Треугольник: вершины, стороны, углы. Высота, биссектриса и медиана
Треугольник — это замкнутая ломаная линия, состоящая из трёх звеньев:
Вершины ломаной называются вершинами треугольника, а её звенья — сторонами треугольника. Углы, образованные двумя сторона треугольника, называются углами треугольника:
В треугольнике ABC вершины A, B и C — это вершины треугольника, звенья AB, BC и CA — стороны треугольника. Три угла — ∠ABC, ∠BCA и ∠CAB — углы треугольника. Часто углы треугольника обозначаются только одной буквой: ∠A, ∠B, ∠C.
Треугольник обычно обозначается тремя буквами, стоящими при его вершинах. Например, треугольник ABC, или BCA, или CBA. Вместо слова треугольник часто используется знак . Так, запись ABC будет читаться: треугольник ABC
.
У каждого треугольника 3 вершины, 3 стороны и 3 угла.
Высота
Высота треугольника — это перпендикуляр, опущенный из вершины треугольника на его основание. Высота треугольника может быть опущена и на продолжение основания.
Отрезок BN — это высота ABC. Отрезок EL высота DEF, опущенная на продолжение стороны DF.
Длина высоты — это длина отрезка от вершины угла до пересечения с основанием.
Каждый треугольник имеет три высоты.
Биссектриса
Биссектриса угла треугольника — прямая, делящая угол треугольника пополам. Длина отрезка этой прямой от вершины угла до точки пересечения с противоположной стороной называется
Отрезок BN — это биссектриса ABC.
Каждый треугольник имеет три биссектрисы.
Медиана
Медиана треугольника — это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Длина этого отрезка называется длиной медианы.
Отрезок BN — это медиана ABC.
Каждый треугольник имеет три медианы.
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия
Серединный перпендикуляр к отрезку
Определение 1. Серединным перпендикуляром к отрезку называют, прямую, перпендикулярную к этому отрезку и проходящую через его середину (рис. 1).
Рис.1
Теорема 1. Каждая точка серединного перпендикуляра к отрезку находится на одном и том же расстоянии от концов этого отрезка.
Доказательство. Рассмотрим произвольную точку D, лежащую на серединном перпендикуляре к отрезку AB (рис.2), и докажем, что треугольники ADC и BDC равны.
Рис.2
Действительно, эти треугольники являются прямоугольными треугольниками, у которых катеты AC и BC равны, а катет DC является общим. Из равенства треугольников ADC и BDC вытекает равенство отрезков AD и DB. Теорема 1 доказана.
Теорема 2 (Обратная к теореме 1). Если точка находится на одном и том же расстоянии от концов отрезка, то она лежит на серединном перпендикуляре к этому отрезку.
Доказательство. Докажем теорему 2 методом «от противного». С этой целью предположим, что некоторая точка E находится на одном и том же расстоянии от концов отрезка, но не лежит на серединном перпендикуляре к этому отрезку. Приведём это предположение к противоречию. Рассмотрим сначала случай, когда точки E и A лежат по разные стороны от серединного перпендикуляра (рис.3). В этом случае отрезок EA пересекает серединный перпендикуляр в некоторой точке, которую мы обозначим буквой D.
Рассмотрим сначала случай, когда точки E и A лежат по разные стороны от серединного перпендикуляра (рис.3). В этом случае отрезок EA пересекает серединный перпендикуляр в некоторой точке, которую мы обозначим буквой D.
Рис.3
Докажем, что отрезок AE длиннее отрезка EB. Действительно,
Таким образом, в случае, когда точки E и A лежат по разные стороны от серединного перпендикуляра, мы получили противоречие.
Рис.4
Теперь рассмотрим случай, когда точки E и A лежат по одну сторону от серединного перпендикуляра (рис.4). Докажем, что отрезок EB длиннее отрезка AE. Действительно,
Полученное противоречие и завершает доказательство теоремы 2
Окружность, описанная около треугольника
Определение 2. Окружностью, описанной около треугольника, называют окружность, проходящую через все три вершины треугольника (рис.5). В этом случае треугольник называют треугольником, вписанным в окружность, или вписанным треугольником.
Рис.5
Свойства описанной около треугольника окружности. Теорема синусов
| Фигура | Рисунок | Свойство |
| Серединные перпендикуляры к сторонам треугольника | Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке. Посмотреть доказательство | |
| Окружность, описанная около треугольника | Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника.Посмотреть доказательство | |
| Центр описанной около остроугольного треугольника окружности | Центр описанной около остроугольного треугольника окружности лежит внутри треугольника. | |
| Центр описанной около прямоугольного треугольника окружности | Центром описанной около прямоугольного треугольника окружности является середина гипотенузы. Посмотреть доказательство | |
| Центр описанной около тупоугольного треугольника окружности | Центр описанной около тупоугольного треугольника окружности лежит вне треугольника. | |
| Теорема синусов | Для любого треугольника справедливы равенства (теорема синусов): , где a , b , c – стороны треугольника, A , B , С – углы треугольника, R – радиус описанной окружности. Посмотреть доказательство | |
| Площадь треугольника | Для любого треугольника справедливо равенство: S = 2R2 sin A sin B sin C , где A , B , С – углы треугольника, S – площадь треугольника, R – радиус описанной окружности. Посмотреть доказательство | |
| Радиус описанной окружности | Для любого треугольника справедливо равенство: где a , b , c – стороны треугольника, S – площадь треугольника, R – радиус описанной окружности. Посмотреть доказательство |
| Серединные перпендикуляры к сторонам треугольника |
Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке. Посмотреть доказательство |
| Окружность, описанная около треугольника |
Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника. Посмотреть доказательство |
| Центр описанной около остроугольного треугольника окружности |
Центр описанной около остроугольного треугольника окружности лежит внутри треугольника. |
| Центр описанной около прямоугольного треугольника окружности |
Центром описанной около прямоугольного треугольника окружности является середина гипотенузы. Посмотреть доказательство |
| Центр описанной около тупоугольного треугольника окружности |
Центр описанной около тупоугольного треугольника окружности лежит вне треугольника. |
| Теорема синусов |
Для любого треугольника справедливы равенства (теорема синусов): , где a , b , c – стороны треугольника, A , B , С – углы треугольника, R – радиус описанной окружности. Посмотреть доказательство |
| Площадь треугольника |
Для любого треугольника справедливо равенство: S = 2R2 sin A sin B sin C , где A , B , С – углы треугольника, S – площадь треугольника, R – радиус описанной окружности. Посмотреть доказательство |
| Радиус описанной окружности |
Для любого треугольника справедливо равенство: где a , b , c – стороны треугольника, S – площадь треугольника, R – радиус описанной окружности. Посмотреть доказательство |
Доказательства теорем о свойствах описанной около треугольника окружности
Теорема 3. Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке.
Доказательство. Рассмотрим два серединных перпендикуляра, проведённых к сторонам AC и AB треугольника ABC, и обозначим точку их пересечения буквой O (рис. 6).
Рис.6
Поскольку точка O лежит на серединном перпендикуляре к отрезку AC, то в силу теоремы 1 справедливо равенство:
CO = AO .
Поскольку точка O лежит на серединном перпендикуляре к отрезку AB, то в силу теоремы 1 справедливо равенство:
AO = BO .
Следовательно, справедливо равенство:
CO = BO ,
откуда с помощью теоремы 2 заключаем, что точка O лежит на серединном перпендикуляре к отрезку BC. Таким образом, все три серединных перпендикуляра проходят через одну и ту же точку, что и требовалось доказать.
Следствие. Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника.
Доказательство. Рассмотрим точку O, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника ABC (рис. 6).
При доказательстве теоремы 3 было получено равенство:
AO = OB = OC ,
из которого вытекает, что окружность с центром в точке O и радиусами OA, OB, OC проходит через все три вершины треугольника ABC, что и требовалось доказать.
Теорема 4 (теорема синусов). Для любого треугольника (рис. 7)
Рис.7
справедливы равенства:
.
Доказательство. Докажем сначала, что длина хорды окружности радиуса R хорды окружности радиуса R, на которую опирается вписанный угол величины φ , вычисляется по формуле:
Рассмотрим сначала случай, когда одна из сторон вписанного угла является диаметром окружности (рис.8).
Рис.8
Угол MPN, как угол,опирающийся на диаметр, является прямым угломугол,опирающийся на диаметр, является прямым углом, и равенство (1) вытекает из определения синуса угла прямоугольного треугольника.
Поскольку все вписанные углы, опирающиеся на одну и ту же дугу, равны, то для произвольного вписанного угла всегда найдется равный ему вписанный угол, у которого одна из сторон является диаметром окружности.
Формула (1) доказана.
Из формулы (1) для вписанного треугольника ABC получаем (рис.7):
Теорема синусов доказана.
На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Урок 63. виды треугольников по видам углов. закрепление изученного материала — Математика — 3 класс
Математика
3 класс
Урок № 63
Виды треугольников по видам углов. Закрепление изученного материала
Перечень вопросов, рассматриваемых в теме:
Какие виды треугольников различают по видам углов?
Как различать треугольники: прямоугольный, тупоугольный, остроугольный?
Тезаурус:
Геометрия – это раздел математики, изучающий геометрические фигуры и их свойства.
Треугольник – геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой.
Виды треугольников по величине углов
Остроугольный треугольник – это треугольник, в котором все три угла острые, т.е. меньше 90°.
Прямоугольный треугольник – это треугольник, в котором один угол прямой, т.е. 90º.
Тупоугольный треугольник – это треугольник, содержащий тупой угол, т.е. один из его углов лежит в пределах между 90° и 180°.
Основная и дополнительная литература:
1. Моро М. И. Учебник для 3 класса четырехлетней начальной школы. М. «Просвещение» — 2017. С. 85-87.
2. Волкова С. И. математика. Тесты. 3 кл. – М.: Просвещение, 2018. С. 60-67.
3. Рудницкая В. Н. Математика. Дидактические материалы. ч.1 3 кл. – М. «Вентана- Граф», 2016, с. 47-53.
Теоретический материал для самостоятельного изучения
Давайте вспомним, что вы уже знаете о видах треугольников.
По длине сторон различают: разносторонние, равнобедренные и равносторонние треугольники.
Но было бы несправедливо разделить все треугольники на 3 вида по длине сторон. Ведь у каждого есть ещё и по три угла.
У вас уже появились идеи?
Углы бывают:
Острые – меньше прямого
Прямые – угол 90 градусов
Тупые – больше прямого
Оказывается, по величине углов все треугольники тоже можно разделить на 3 вида:
те, у которых все углы острые, – остроугольные,
те, у которых есть прямой угол, – прямоугольные,
те, у которых есть тупой угол, – тупоугольные.
Для того чтобы безошибочно определить вид треугольника по величине углов, необходимо измерить все три угла при помощи транспортира.
Обычно вид треугольника можно определить на глаз.
Попробуйте определить виды треугольников по величине углов без измерений.
Проверим.
Прямоугольный –1, 3
Остроугольный – 6
тупоугольный– 2, 4, 7, 5
Сделаем вывод:
По величине углов различают 3 вида треугольников:
Остроугольные, прямоугольные и тупоугольные
Определить вид треугольника можно тремя способами:
с помощью измерений, на глаз и по условным обозначениям.
Теперь вы можете различать виды треугольников по сторонам и по углам. Эти знания необходимы в геометрии.
Задания тренировочного модуля
Закончите предложения:
Остроугольный треугольник – это треугольник, у которого ……………………
Прямоугольный треугольник – это треугольник, у которого есть ……………………
Тупоугольный треугольник – треугольник, все стороны которого есть ……………………
Правильные варианты ответов:
Остроугольный треугольник — это треугольник, у которого все углы острые.
Прямоугольный треугольник — это треугольник, у которого есть прямой угол.
Тупоугольный треугольник — треугольник, все стороны которого есть тупой угол.
Определите вид треугольника по величине углов и выпишите номера треугольников по порядку:
Правильный ответ:
Остроугольные: 1, 2, 10
Прямоугольные: 4, 6, 8, 12
Тупоугольные: 3, 5, 7, 9, 11
Как начертить правильный шестиугольник с помощью циркуля
Урок 35. Геометрия 9 класс
Конспект урока «Построение правильных многоугольников»
На этом уроке мы рассмотрим способы построения некоторых правильных многоугольников с помощью циркуля и линейки. А также изобразим правильный многоугольник графически.
Для начала давайте вспомним определение правильного многоугольника. Итак, правильным многоугольником называется выпуклый многоугольник, у которого все углы равны и все стороны равны.
Для выполнения построений мы используем циркуль и линейку.
– построить дугу окружности,
– отложить на прямой отрезок, равный данному.
– построить прямую линию,
– построить отрезок, соединяющий две точки,
– найти точку пересечения двух прямых.
Ранее мы с вами уже рассматривали построения правильного треугольника и четырехугольника, т.е. квадрата.
Давайте рассмотрим, каким образом можно с помощью циркуля и линейки построить правильный треугольник и правильный четырехугольник, вписанные в окружность.
Задача 1. Вписать в заданную окружность правильный треугольник
Построение. Пусть задана окружность с центром О. Проведем произвольный диаметр BD окружности. Построим прямую l, являющуюся серединным перпендикуляром к радиусу OD. Середину радиуса ОD обозначим точкой К. Отметим точки А и C – пересечения прямой l с окружностью. И построим отрезки BA и BC. Треугольник ABC – правильный.
В Тогда Отсюда, .
Значит,
Задача 2. Вписать в заданную окружность правильный четырехугольник.
Построение. Пусть задана окружность с центром О. Построим диаметр AC. Затем построим диаметр BD перпендикулярный диаметру AC. Точки А, C и B, D – точки пересечения диаметров с окружностью. И построим отрезки АB, BC, CD и АD. Четырехугольник ABCD – правильный.
Т.к. Т.к. Т.к. Т.к. Следовательно, – квадрат.
Значит, – правильный четырехугольник.
Теперь давайте рассмотрим построения правильных n-угольников при n>4. Обычно для построения таких n-угольников используется окружность, описанная около многоугольника.
Задача 3. Построить правильный шестиугольник, сторона которого равна данному отрезку.
Построение. Так как в правильном шестиугольнике сторона а равна радиусу, то достаточно последовательно отложить от одной точки окружности 6 радиусов-хорд. Пусть МN – заданный отрезок. Построим окружность с произвольным центром О и радиуса MN. Отметим на этой окружности произвольную точку А. Затем, не меняя раствора циркуля, последовательно от этой точки А будем делать на окружности засечки, пока последняя засечка не совпадет с взятой первоначально точкой А. Отметим точки B, C, D, Е и F. Теперь соединим последовательно построенные точки отрезками. Получим искомый правильный шестиугольник ABCD.
Равные хорды стягивают равные дуги.
Все углы шестиугольника будут равны, так как опираются на дуги, состоящие из четырех равных меньших дуг.
Для построения правильных многоугольников часто используется следующая задача: дан правильный n-угольник. Построить правильный 2n-угольник.
Построить правильный 2n-угольник.
Задача 4. Дан правильный шестиугольник. Построить правильный двенадцатиугольник.
Пусть ABCDEF – данный правильный шестиугольник. Опишем около него окружность.
1. 2. Окружность .
3. – серединные
перпендикуляры к .
4.
.
5. – правильный двенадцатиугольник.
Применяя указанный способ, можно с помощью циркуля и линейки построить целый ряд правильных многоугольников, если построен один из них. Например, построив правильный четырехугольник, т.е. квадрат, и пользуясь задачей 4, можно построить правильный восьмиугольник, затем правильный шестнадцати-угольник и вообще правильный 2 k угольник, где k – любое целое число, большее 2.
Замечание. Рассмотренные примеры показывают, что многие правильные многоугольники могут быть построены с помощью циркуля и линейки. Но важно заметить, что не все правильные многоугольники могут быть построены таким образом.
С давних времен построению правильных многоугольников математики уделяли большое внимание. Древние греки умели строить правильные треугольники, четырехугольники, пятиугольники. А также многоугольники, получаемые удвоением их сторон, шестиугольники, восьмиугольники, десятиугольники и т.д. Далее дело зашло в тупик. И только 2000 лет спустя великий немецкий математик 17 века Карл Гаусс, которого называли «королем математики», решил эту математическую проблему. Будучи девятнадцати летним юношей, он доказал, что можно построить правильный семнадцати-угольник, а вот семиугольник, девятиугольник, одиннадцатиугольник, тринадцати-угольник циркулем и линейкой построить нельзя. Задача о построении правильного семнадцати-угольника была самым первым его научным открытием.
Подведем итоги урока.
Сегодня мы рассмотрели способы построения некоторых правильных многоугольников с помощью циркуля и линейки. Научились строить правильные треугольник и четырехугольник, вписанные в окружность. А также выполнили задачу на построение правильного многоугольника по заданному отрезку, и задачу на построение правильного 2n-угольника по заданному n-угольнику.
Деление окружности на равные части и построение правильных вписанных многоугольников можно выполнить как циркулем, так и с помощью угольников и рейсшины.
Деление окружности на четыре равные части и построение правильного вписанного четырехугольника. Две взаимно перпендикулярные центровые линии делят окружность на четыре равные части (рис. 115, а). Соединив точки пересечения этих линий с окружностью прямыми, получают правильный вписанный четырехугольник.
Деление окружности на восемь равных частей и построение правильного вписанного восьмиугольника. Две взаимно перпендикулярные линии, проведенные под углом 45° к центровым линиям с помощью угольника с углами 45, 45 и 90° и рейсшины (рис. 115, б), вместе с центровыми линиями разделят окружность на восемь равных частей.
Деление окружности на восемь равных частей можно выполнить циркулем. Для этого из точек 1 и 3 (точки пересечения центровых линий с окружностью) произвольным радиусом делаются засечки до взаимного пересечения, тем же радиусом делают две засечки из точек 3 и 5 (рис. 115, в). Через точки пересечения засечек и центр окружности проводят прямые линии до пересечения с окружностью в точках 2, 4, 6, 8.
Если полученные восемь точек соединить последовательно прямыми линиями, то получится правильный вписанный восьмиугольник (рис. 115, в).
Деление окружности на три равные части и построение правильного вписанного треугольника выполняют с помощью циркуля или угольника с углами 30, 60 и 90° и рейсшины.
При делении окружности циркулем на три равные части из любой точки окружности, например из точки Л пересечения центровых линий с окружностью (рис. 116, а и б), проводят дугу радиусом R, равным радиусу данной окружности, получают точки 1 и 2. Третья точка деления (точка 3) будет находиться на противоположном конце диаметра, проходящего через точку Л. Последовательно соединив точки 1, 2 и 3, получают правильный вписанный треугольник. При построении правильного вписанного треугольника, если задана одна из его вершин, например точка 1, находят точку А. Для этого через заданную точку 1 проводят диаметр (рис. 116, в). Точка А будет находиться на противоположном конце этого диаметра. Затем проводят дугу радиусом R равным радиусу данной окружности, получают точки 2 и 3.
Для этого через заданную точку 1 проводят диаметр (рис. 116, в). Точка А будет находиться на противоположном конце этого диаметра. Затем проводят дугу радиусом R равным радиусу данной окружности, получают точки 2 и 3.
При делении окружности на три равные части с помощью угольника и рейсшины через точку 1 под углом 60° проводят две прямые линии до пересечения с окружностью в точках 2 и 3 (рис. 117, а, б), точки 2 и 3 соединяют и получают правильный вписанный треугольник (рис. 117, в).
Деление окружности на шесть равных частей и построение правильного вписанного шестиугольника выполняют с помощью угольника с углами 30, 60 и 90° и рейсшины или циркуля. При делении окружности на шесть равных частей циркулем из двух концов одного диаметра радиусом, равным радиусу данной окружности, проводят дуги до пересечения с окружностью в точках 2, 6 и 3, 5 (рис. 118). Последовательно соединив полученные точки, получают правильный вписанный шестиугольник. Деление окружности на шесть равных час-1ен и построение правильного вписанного шестиугольника с помощью угольника и рейсшины показано на рис. 119 и 120. Деление окружности на двенадцать равных частей и построение правильного вписанного двенадцатиугольника выполняют с помощью угольника с углами 30, 60 и 90° и рейсшины или циркуля.
При делении окружности циркулем из четырех концов двух взаимно перпендикулярных диаметров окружности проводят радиусом, равным радиусу данной окружности, дуги до пересечения с окружностью (рис. 121). Соединив полученные точки, получают двенадцатиугольник.
При построении двенадцатиугольника с помощью угольника и рейсшины точки деления строят, как показано на рис. 119 и 120.
Деление окружности на пять и десять равных частей и построение правильного вписанного пятиугольника и десятиугольника показано на рис.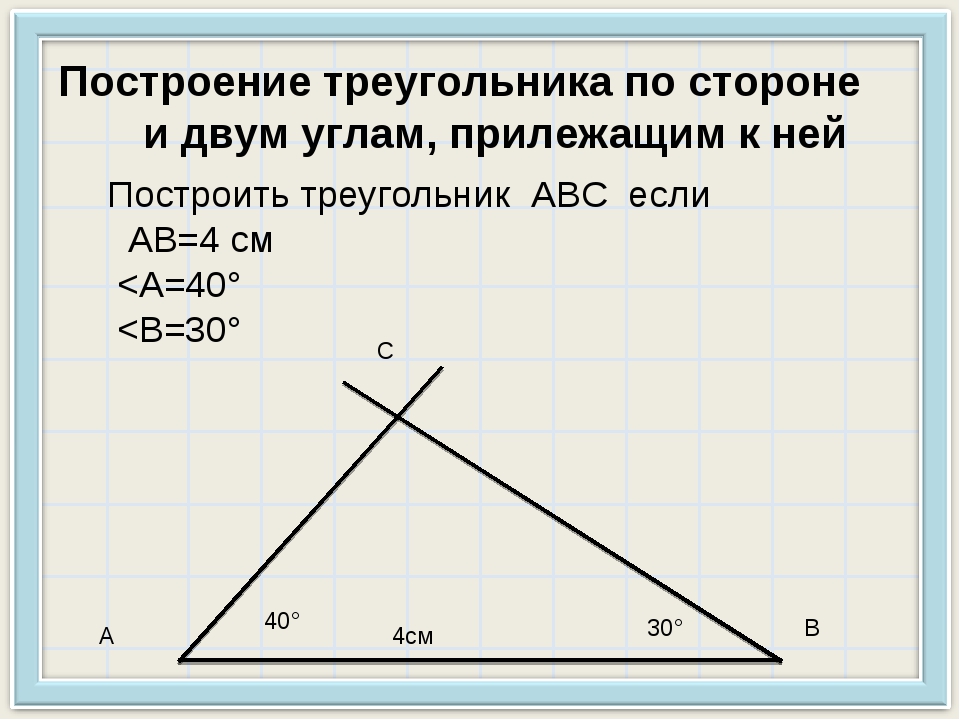 122.
122.
Половину любого диаметра (радиус) делят пополам (рис. 122, а), получают точку А. Из точки А, как из центра, проводят дугу радиусом, равным расстоянию от точки А до точки 1, до пересечения со второй половиной этого диаметра, в точке В (рис. 122, б). Отрезок 1В равен хорде, стягивающей дугу, длина которой равна 1 /5 длины окружности. Делая засечки на окружности (рис. 122, в) радиусом R, равным отрезку 1В, делят окружность на пять равных частей. Начальную точку 1 выбирают в зависимости от расположения пятиугольника. Из точки / строят точки 2 и 5 (рис. 122, в), затем из точки 2 строят точку 3, а из точки 5 строят точку 4. Расстояние от точки 3 до точки 4 проверяют циркулем; если расстояние между точками 3 и 4 равно отрезку 1В, то построения были выполнены точно. Нельзя выполнять засечки последовательно, в одну сторону, так как происходит набегание ошибок и последняя сторона пятиугольника получается перекошенной. Последовательно соединив найденные точки, получают пятиугольник (рис. 122, г).
Деление окружности на десять равных частей выполняют аналогично делению окружности на пять равных частей (рис. 122), но сначала делят окружность на пять частей, начиная построение из точки /, а затем из точки 6, находящейся на противоположном конце диаметра (рис. 123, а). Соединив последовательно все точки, получают правильный вписанный десятиугольник (рис. 123, б).
Деление окружности на семь и четырнадцать равных частей и построение правильного вписанного семиугольника и четырнадцатиугольника показано на рис. 124 и 125.
Из любой точки окружности, например точки Л, радиусом заданной окружности проводят дугу (рис. 124, а) до пересечения с окружностью в точках В и D. Соединим точки В и D прямой. Половина полученного отрезка (в данном случае отрезок ВС) будет равна хорде, которая стягивает дугу, составляющую 1 /7 длины окружности.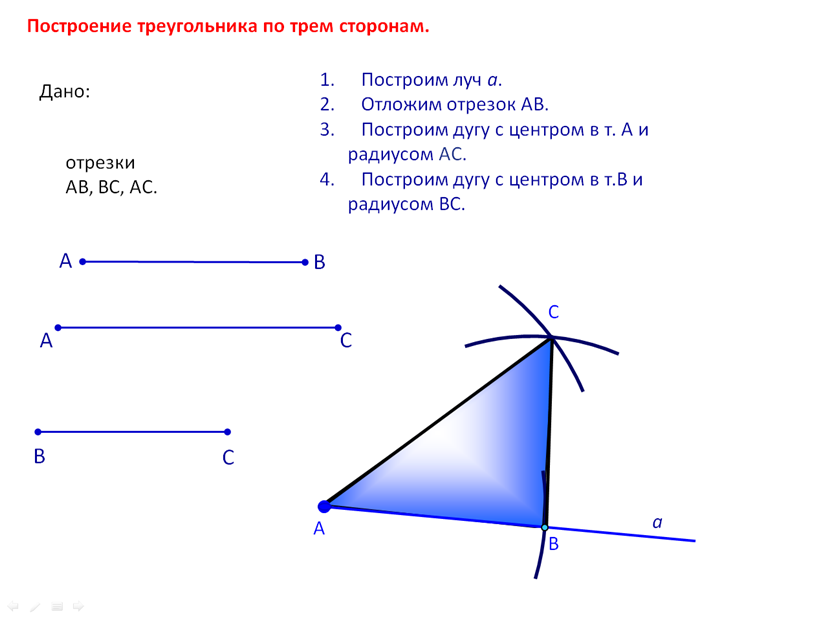 Радиусом, равным отрезку ВС, делают засечки на окружности в последовательности, показанной на рис. 124, б. Соединив последовательно все точки, получают правильный вписанный семиугольник (рис. 124, в).
Радиусом, равным отрезку ВС, делают засечки на окружности в последовательности, показанной на рис. 124, б. Соединив последовательно все точки, получают правильный вписанный семиугольник (рис. 124, в).
Деление окружности на четырнадцать равных частей выполняется делением окружности на семь равных частей два раза от двух точек (рис. 125, а).
Сначала окружность делится на семь равных частей от точки /, затем то же построение выполняется от точки 8. Построенные точки соединяют последовательно прямыми линиями и получают правильный вписанный четырна-дцатиугольник (рис. 125, б).
СОПРЯЖЕНИЯ
Рассматривая детали, видим, что в их конструкции часто одна поверхность переходит в другую. Обычно эти переходы делают плавными, что повышает прочность деталей и делает их более удобными в работе. На чертеже поверхности изображаются линиями, которые также плавно переходят одна в другую.
На рис. 126, а изображена деталь, в которой плавные переходы одних плоскостей в другие представляют собой цилиндрические поверхности. На чертеже (рис. 126, б) эти плоскости изображены прямыми линиями, а цилиндрические поверхности — дугами окружностей. Плавные переходы от одной прямой к другой в этих случаях выполняются дугой заданного радиуса.
Плавный переход одной цилиндрической поверхности в другую может являться цилиндрической поверхностью (рис. 127, а). На чертеже эти цилиндрические поверхности изображены дугами окружностей, (рис. 127, б). В этом случае плавный переход одной дуги окружности в другую осуществляется дугой окружности заданного радиуса.
На рис. 126, а и 127, а рассмотрены простейшие примеры плавных переходов поверхностей. В чертежах более сложных деталей плавные переходы между поверхностями изображаются различными сочетаниями прямых, окружностей и их дуг. Вариантов таких сочетаний может быть много, но их объединяет одно — плавность перехода. Такой плавный переход одной линии (поверхности) в другую линию (поверхность) называют сопряжением. При построении сопряжения необходимо определить границу, где кончается одна линия и начинается другая, т. е. найти на чертеже точку перехода, которая называется точкой сопряжения или точкой касания.
При построении сопряжения необходимо определить границу, где кончается одна линия и начинается другая, т. е. найти на чертеже точку перехода, которая называется точкой сопряжения или точкой касания.
Задачи на сопряжения условно можно разделить на три группы.
Первая группа задачвключает в себя задачи на построение сопряжений, где участвуют прямые линии. Это может быть непосредственное касание прямой и окружности, сопряжение двух прямых дугой заданного радиуса, а также проведение касательной прямой к двум окружностям.
Построение окружности, касательной к прямой, связано с нахождением точки касания и центра окружности.
Задана горизонтальная прямая АВ, требуется построить окружность радиусом R, касательную к данной прямой (рис. 128). Точка касания выбирается произвольно. Так как точка касания не задана, то окружность радиуса R может коснуться данной прямой в любой точке. Таких окружностей можно провести множество. Центры этих окружностей (O1, О2и т. д.) будут находиться на одинаковом расстоянии от заданной прямой, т. е. на линии, расположенной параллельно заданной прямой АВ на расстоянии, равном радиусу заданной окружности (рис. 128). Назовем эту линию линией центров. Проведем линию центров параллельно прямой АВ на расстоянии R. Так как центр касательной окружности не задан, возьмем любую точку на линии центров, например точку О. Прежде чем проводить касательную окружность, следует определить точку касания. Точка касания будет лежать на перпендикуляре, опущенном из точки О на прямую АВ. В пересечении перпендикуляра с прямой АВ получим точку К, которая будет точкой касания. Из центра О радиусом R от точки К проведем окружность. Задача решена.
В детали, которая изображена на рис. 129, а, пластина плавно переходит в цилиндр. При выполнении чертежа этой детали необходимо построить плавный переход прямой в окружность.
Задача аналогична предыдущей, но дополнена условием, что точка касания задана, так как задан размер А (рис. 129, б), который определяет величину прямолинейного участка.
Отложив размер Л, находят точку касания (точку /С), затем из точки К восставляют перпендикуляр, на котором откладывают радиус R заданной окружности, и находят центр окружности (точку О). При обводке сначала от точки касания проводится дуга заданного радиуса, а потом — прямая.
Из сказанного следует:
1) центр окружности, касательной к прямой, лежит на прямой (линия центров), проведенной параллельно заданной прямой, на расстоянии, равном радиусу данной окружности;
Не нашли то, что искали? Воспользуйтесь поиском:
Понимая самые простые закономерности в геометрии, можно научиться строить на плоскости более сложные фигуры. Так, большинство геометрических фигур имеют достаточно сложный вид, однако, зная определённые правила, можно понять, как построить шестиугольник с помощью только лишь циркуля и линейки.
Для начала на листе бумаги необходимо изобразить окружность, делается это с помощью циркуля. Устанавливаем ножки инструмента на определённом уровне друг от друга, чтобы задать радиус, после чего рисуем окружность. Важно помнить, что окружность должна полностью помещаться на листе бумаги. При этом, если ножки циркуля будут сильно близко друг к другу или, наоборот, сильно далеко друг от друга, то может не получиться начертить правильную окружность. Поэтому стоит учитывать, что между ножками должен быть угол примерно в 30 градусов.
Теперь необходимо построить точки, которые будут являться вершинами углов шестиугольника. Для этого, не меняя расстояния между ножками циркуля, устанавливаем иглу в любую точку окружности таким образом, чтобы игла была точно на линии. Чем точнее будут выполнены действия, тем точнее будет дальнейшее построение. Теперь проводим циркулем дугу до тех пор, пока она не пересечётся с линией окружности. Это и будет одной из вершин углов шестиугольника. Далее переставляем иглу в только что полученную точку и совершаем такие же действия. Эту операцию нужно будет проделать ещё четыре раза, в результате чего получится шесть точек, то есть шесть углов.
Теперь проводим циркулем дугу до тех пор, пока она не пересечётся с линией окружности. Это и будет одной из вершин углов шестиугольника. Далее переставляем иглу в только что полученную точку и совершаем такие же действия. Эту операцию нужно будет проделать ещё четыре раза, в результате чего получится шесть точек, то есть шесть углов.
Перед тем как построить правильный шестиугольник, необходимо соединить полученные точки. Все действия необходимо делать с помощью карандаша и линейки, чтобы добиться максимально точного результата. В итоге на листе бумаги появится вписанный в окружность правильный шестиугольник.
Как правильно начертить равносторонний треугольник по черчению. Построение правильных многоугольников
- карандаш,
- стерка,
- лист бумаги,
- пошаговая интсрукция.
- сперва изобразить треугольник,
- затем все его грани, начиная с внешней,
- заштриховать участки свето-тени, чтобы придать объем фигуре,
- при необходимости разукрасить объект.
Нарисуем треугольник 3D с оптической иллюзией поэтапно.
Сначала рисуем обыкновенный равносторонний треугольник карандашом. Внутри него, параллельно каждой из сторон, проводим по линии на равном расстоянии так, что внутри треугольника получается еще один треугольник.
Вновь проводим параллельные линии, отступив на то же расстояние и рисуя еще один меньший треугольник внутри первых двух.
Жирно проводим контур по периметру сторон большого треугольника, обводя его стороны, но срезая острые углы.
Проводим еще один контур из двух прямых, повторяющих одну сторону среднего и одну сторону меньшего треугольников внутри большого, как показано на рисунке.
Проводим еще по контуру, — две прямые, повторяя стороны треугольников, как на рисунке.
И еще раз делаем те же действия, с другими сторонами, — обводим жирным контуром две прямые, как на рисунке.
Лишние линии убираем. Вот получился 3D треугольник, пока не закрашенный.
Заштриховываем стороны треугольника, придавая изображению объемность. Рисунок готов, треугольник 3D иллюзия .
Посмотрим видео, как рисовать оптическую иллюзию треугольник 3D.
Нарисовать треугольную иллюзию несложно, особенно если есть пошаговая инструкция. Понадобится карандаш, бумага и желательно линейка, с ней будет аккуратнее рисунок. По шагам повторить все действия, а потом затенить с помощью растушевки нужные места.
Понадобится карандаш, бумага и желательно линейка, с ней будет аккуратнее рисунок. По шагам повторить все действия, а потом затенить с помощью растушевки нужные места.
Как нарисовать треугольник … Да, при этом не простой, а очень сложный с множеством треугольников внутри. Чтобы все его грани проглядывались, а на бумаге он выглядел реалистичным и четким.
Для этого нам потребуется:
Процесс рисования:
Получается необычайная фигура с множеством завихрений. Смотрится немного завораживающе, так как разум пытается продлить все линии и уловить суть.
Видео-инструкция, как нарисовать треугольник на бумаге:
Треугольник Пенроуза или невозможные фигуры. Был придуман в 1953 году художником Оскаром Реутерсвардом. Первый треугольник был сделан из кубиков.
Уникальность этого объекта в том, что посмотрев на прямые палки под определнным углом можно четко увидеть треугольник. Как например вот на этом памятнике.
Как нарисовать треугольник? Этому учат в процессе изучения геометрии в школе. Чтобы задание было выполнено правильно, важно точно знать, какой треугольник необходимо изобразить: равносторонний, равнобедренный или же вписанный. Правилам начертания этих фигур будет посвящена данная статья.
Как рисовать треугольник с равными сторонами?
Как нарисовать треугольник, стороны у которого равны? Для этого можно воспользоваться одним из трех методов.
Такая фигура имеет три одинаковые по длине стороны, связанные тремя углами равной ширины. Это может быть сложным для рисования треугольника вручную. Поэтому можно использовать круглый объект для выделения углов.
Варианты создания фигуры
Обязательно используйте линейку и один из представленных ниже способов:
- Применение циркуля: надо начертить ровную линию. Проведите карандаш вдоль прямого края бумаги. Этот сегмент линии образует одну из сторон. А это означает, что нужно будет чертить вторую и третью линии одинаковой длины, каждая из которых достигает точки под углом 60° от первой линии. Удостоверьтесь, что достаточно места для рисования всех трех сторон!
- Разделите сегмент циркулем. Вставьте карандаш и убедитесь, что он острый! Поместите точку циркуля на один конец сегмента и установите карандаш на другую. Опишите дугу. Не изменяйте установленную «ширину» инструмента от точки циркуля до точки карандаша. Нарисуйте вторую дугу, чтобы она пересекала первую дугу, которую уже нарисовали. Отметьте точку, в которой пересекаются две дуги. Это вершина (верхняя точка) треугольника. Он должен лежать в точном центре сегмента линии, который нарисовали. Теперь можете сделать две прямые линии, ведущие к этой точке: по одному от каждого конца «нижнего» сегмента линии. Закончите треугольник. Далее с помощью линейки надо нарисовать еще два сегмента прямой линии — это стороны в треугольнике. Подключите каждый конец исходного сегмента линии к точке, в которой пересекаются дуги. Чтобы закончить работу, сотрите дуги, которые нарисовали, так, чтобы остался только треугольник.
- Использование объекта с круглой базой: этот совет подойдет для построения дуги. Предложенный метод по сути такой же, как с использованием циркуля.
Указанные советы помогут выяснить, как нарисовать равносторонний треугольник.
Равнобедренный треугольник представляет собой фигуру с двумя равными сторонами и двумя равными углами. Если знаете длину, основание и высоту стороны, это можно сделать только с линейкой и циркулем (или просто циркулем, если заданы размеры).
Как нарисовать равнобедренный треугольник:
- Учитывая все боковые длины. Чтобы использовать этот метод, важно знать длину основания треугольника и длину двух равных сторон.

- Учитывая две равные стороны и угол между ними. Чтобы использовать этот метод, нужно знать длину двух равных сторон и измерение угла между этими двумя сторонами.
- Учитывая базовые и смежные углы — необходимо знать длину базы, градусы двух углов, смежных с основанием. Помните, что два угла, смежные с основанием равнобедренного треугольника, будут равны.
- Основа и высота. Нужно знать длину основания треугольника, а также высоту этой геометрической фигуры.
Как нарисовать вписанный треугольник? Выберите круглый объект. Используйте предмет с круглым основанием. Выбор компакт-диска станет хорошим вариантом. Но можно взять и другой объект нужного размера. Для этого метода свойственно, что длина каждой стороны равносторонней геометрической фигуры с тремя углами будет равна размерам радиуса (половине диаметра) круга.
Как нарисовать треугольник, если используете компакт-диск? Представьте себе равносторонний треугольник, который вписывается в верхнюю правую часть компакт-диска. Надо начертить первую из сторон. Радиус круглого объекта — расстояние на полпути до получения желаемого результата. Удостоверьтесь, что линии нарисованы ровно.
С помощью линейки просто выполните измерения диаметра объекта и нарисуйте линию на половину длины. Если ее нет, поместите круглый объект на бумагу, затем тщательно проведите по окружности карандашом. Удалите объект — должен быть идеальный круг. Используйте прямой край, чтобы нарисовать линию через точный центр круга: точку, которая полностью равноудалена от любой точки по окружности круга.
Используйте круглый объект для создания дуги. Поместите объект по отрезку линии, с краем круга, расположенным на одном конце линии. Для обеспечения точности убедитесь, что линия проходит четко через центр круга. Используйте карандаш, чтобы начертить дугу — это четверть пути по окружности.
Начертите еще одну дугу. Теперь сдвиньте круглый объект так, чтобы край касался другого конца сегмента линии.
Подведем итоги
В этой статье вы научитесь рисовать в фотошопе разные виды треугольника: равносторонний, равнобедренный, разносторонний и прямоугольный.
Как нарисовать равносторонний треугольник
У равностороннего треугольника все три стороны равны.
Самый простой вариант нарисовать в фотошопе такой треугольник — с помощью инструмента Многоугольник .
Выберите этот инструмент и на панели настроек сразу укажите количество сторон — 3.
Следующим этапом нужно определиться каким должен быть будущий треугольник: векторной фигурой, растровым со сплошной заливкой или нужен только контур. Рассмотри все варианты.
Векторный треугольник
На панели параметров выберите опцию Слой-фигура .
Теперь можно рисовать и сам треугольник. Во время создания вы будете видеть его границы. Это нужно для того, чтобы рассчитать его размеры. Также, пока не отпустили клавишу мыши, можно его крутить.
Векторный треугольник хорош тем, что можно быстро сменить его цвет, а также безболезненно изменить его размеры без потери качества. Для этого вызовете команду — Ctrl+T .
Чтобы позже превратить его в растровый треугольник, используйте команду .
Растровый треугольник со сплошной заливкой
Получится такой же треугольник, что и примером выше, но он будет сразу в растре.
Для этого на панели параметров нужно выбрать настройку Выполнить заливку пикселов .
Перед созданием такого треугольника, нужно первоначально .
Теперь рисуйте фигуру и она будет как самый обычный элемент растрового изображения.
Как нарисовать контур равностороннего треугольника
Для такой фигуры выберите на панели параметров опцию Контуры .
Рисуйте треугольник. У вас, естественно, получится только его контур. Далее, при этом же выбранном инструменте, сделайте клик правой кнопкой мыши внутри контура. Появится контекстное меню. Выберите команду Образовать выделенную область .
Откроется диалоговое окно. Радиус растушевки оставьте 0. Жмите Ок.
В итоге мы из контура сделали .
Для этого выполните команду Редактирование — Выполнить обводку . Появится окно, в котором укажите толщину линии обводки, а также как она будет проходить относительно пунктирной линии выделения: внутри, по центру, снаружи.
Фотошоп сделал обводку, теперь уберите пунктир выделения, чтобы не мешал — Ctrl+D . Результат:
Как нарисовать равнобедренный треугольник
У равнобедренного треугольника две стороны равны.
Разберем пример, когда нужно нарисовать равнобедренный треугольник заданных размеров. Допустим, основание 300 пикселей и высота 400 пикселей.
Готово
Равнобедренный треугольник по заданным размерам нарисован!
В прямоугольном треугольнике один из углов равен 90 градусов.
Если нужен прямоугольный треугольник с заранее известными размерами, например, размеры катетов 200 и 300 пикселей, то проще всего сделать следующим образом:
Шаг 1
Создайте новый документ в фотошопе с высотой и шириной равными размерам катетов: например, ширина пусть 300 пикселей, а высота 200 пикселей.
Рабочая область в фотошопе всегда прямоугольной формы, поэтому угол в 90 градусов будет уже обеспечен. Две стороны прямоугольника — его катеты. Останется только провести диагональ — это будет гипотенузой.
Шаг 2
Будем действовать по аналогии с примером выше. Берем инструмент Линия и ставим опцию Слой-фигура .
Теперь обводим линией по краям и соединяем две точки по диагонали:
Шаг 3
На палитре слоев опять три слоя-фигуры. Их можно объединить в один слой (команда Объединить слои ).
Готово
Прямоугольный треугольник готов, можно закрасить его в какой-нибудь цвет:
Заметили ошибку в тексте — выделите ее и нажмите Ctrl + Enter . Спасибо!
Существует множество областей, в которых вы могли бы применить знания программы Photoshop. Могу с уверенностью вам сказать, что порой для двух разных областей требуются настолько разные навыки, что просто диву даешься. Дизайнер может даже не представлять, как можно отретушировать портрет. А фотограф и понятия иметь не будет, как работать с линейками. Но есть вещи, которые желательно знать всем. Как, например, создание простейших фигур. Разберемся, как нарисовать треугольник в фотошопе.
Могу с уверенностью вам сказать, что порой для двух разных областей требуются настолько разные навыки, что просто диву даешься. Дизайнер может даже не представлять, как можно отретушировать портрет. А фотограф и понятия иметь не будет, как работать с линейками. Но есть вещи, которые желательно знать всем. Как, например, создание простейших фигур. Разберемся, как нарисовать треугольник в фотошопе.
Способов рисования треугольника в Adobe Photoshop CS 6 несколько. Начнем с инструмента «многоугольник».
Создадим новый документ. Справа отыщем инструмент «многоугольник» и выберем его.
Теперь выбираем цвет будущего треугольника. На той же панели инструментов. Этот способ позволит нам создать треугольник залитый цветом.
А теперь на верхней панели устанавливаем кол-во углов треугольника.
Теперь делаем клик на рабочей области и протягиваем. Треугольник готов!
Давайте разберем еще один способ. Как нарисовать треугольник в фотошопе при помощи пера.
Возвращаемся к той же панели инструментов. Выбираем «перо».
Делаем 2 клика по рабочей области и замыкаем контур.
Это способ позволит нам сделать как треугольник залитый цветом, так и контур треугольника. Начнем с контура.
Кликаем по нарисованному треугольнику левой клавишей мыши. В выпадающем списке выбираем «выполнить обводку контура».
Как видите, выскочило окно, позволяющее выбрать нам два варианта. Обводка кистью или карандашом. Я применю кисть.
Знайте, что обводка контура будет выполнена при помощи настроек, которые были выставлены заблаговременно.
Обводка выполнена. Чтобы убрать контур, выберите инструмент «перо» вновь. Кликните левой клавишей мыши, чтобы вызвать контекстное меню. И выберите команду «удалить контур».
А теперь разберемся, как при помощи пера сделать треугольник заполненный цветом. Возвращаемся к контуру. Кликаем левой клавишей мыши. В выпадающем меню выбираем «образовать выделенную область». И переходим к боковой панели, к уже знакомому нам инструменту выбора цвета. Устанавливаем нужный. На той же панели ищем «заливку».
И переходим к боковой панели, к уже знакомому нам инструменту выбора цвета. Устанавливаем нужный. На той же панели ищем «заливку».
Кликаем по выделенной области.
Снимание выделение при помощи комбинации клавиш ctrl+d. Треугольник, залитый цветом готов!
На первый взгляд может показаться, что второй способ гораздо удобнее, потому как мы можем выбрать любую форму треугольника. Но на деле и первый способ позволяет нам проводить любые манипуляции по измене формы. Но это уже совсем другая история.
Построение вписанного в окружность правильного шестиугольника. Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой (фиг. 60, а).
Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг. 60, б), строим стороны 1 -6, 4-3, 4-5 и 7-2, после чего проводим стороны 5-6 и 3-2.
Построение вписанного в окружность равностороннего треугольника . Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля.
Рассмотрим два способа построения вписанного в окружность равностороннего треугольника.
Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, проведённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0-1-2 равен 30°, то для нахождения стороны
1-2 достаточно построить по точке 1 и стороне 0-1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1-2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2-3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника.
Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вершины через одну, то получится равносторонний треугольник.
Для построения треугольника (фиг. 61, б) намечаем на диаметре вершину-точку 1 и проводим диаметральную линию 1-4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника.
Построение квадрата, вписанного в окружность . Это построение можно выполнить при помощи угольника и циркуля.
Первый способ основан на том, что диагонали квадрата пересекаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные стороны квадрата 4-1 и 3-2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1-2 и 4-3.
Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра (фиг. 62, б). Намечаем на концах двух взаимно перпендикулярных диаметров точки А, В и С и из них радиусом у описываем дуги до взаимного их пересечения.
Далее через точки пересечения дуг проводим вспомогательные прямые, отмеченные на фигуре сплошными линиями. Точки их пересечения с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.
Построение вписанного в окружность правильного пятиугольника.
Чтобы вписать в окружность правильный пятиугольник (фиг. 63), производим следующие построения.
Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точках M и В.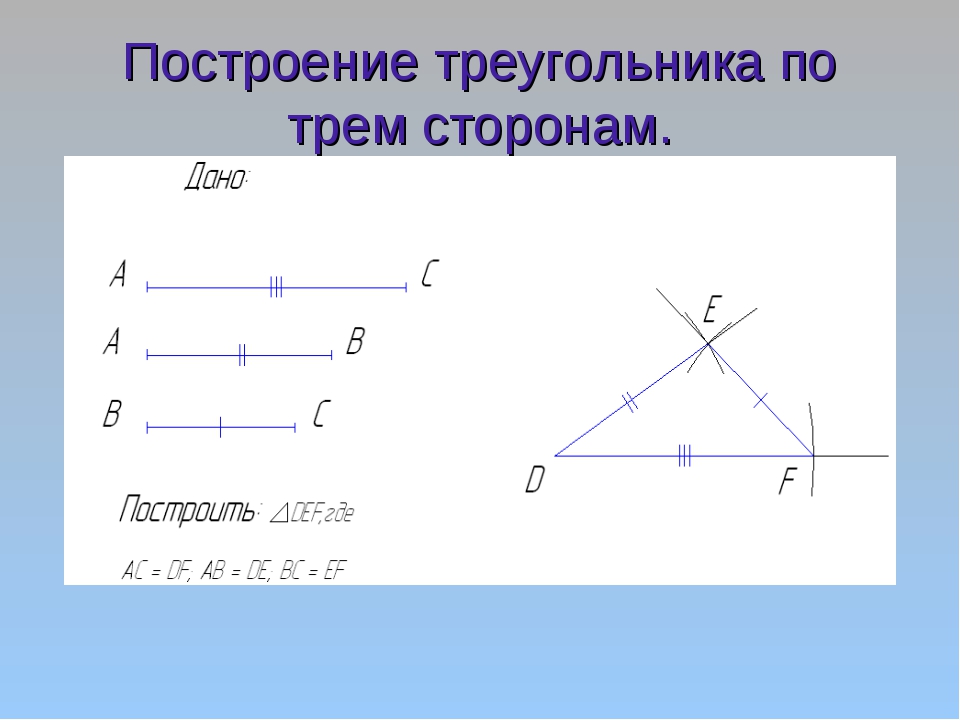 Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой.
Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой.
Построение правильного пятиугольника по данной его стороне.
Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую.
Получим точку 1-вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведёнными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.
Построение вписанного в окружность правильного семиугольника.
Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проводим из полюса F через чётные деления вертикального диаметра лучи, пересечение которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
Приведённый способ годен для построения правильных многоугольников с любым числом сторон.
Деление окружности на любое число равных частей можно производить также, пользуясь данными табл. 2, в которой приведены коэффициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.
Произвольный треугольник по заданным параметрам
| Результат расчета параметров заданного треугольника |
Представляем Вам калькулятор, который позволял рассчитывать все возможные параметры треугольника по заданным параметрам.
Хотелось бы обратить Ваше внимание именно на то, что это универсальный бот. Он рассчитывает все параметры произвольного треугольника, при произвольно заданных параметрах. Такого бота вы не найдете нигде.
Вам известна сторона и две высоты? или две стороны и медиана? Или биссектриса два угла и основание треугольника?
По любым запросам, мы можем получить правильный расчет параметров треугольника.
Вам нет необходимости искать формулы и делать расчет самостоятельно. За вас уже все сделано.
Создайте запрос и получите точный ответ.
Показан произвольный треугольник. Сразу оговоримся как и что обозначается, дабы в дальнейшем не было путаницы и ошибок в расчетах.
Стороны противоположные любому углу называются так же только маленькой буквой. То есть напротив угла А лежит сторона треугольника а, стороне с противостоит угол С.
ma — это медина, падающая на сторону а, соответственно есть еще медианы mb и mc падающие на соответствующие стороны.
lb — это биссектриса , падающая на сторону b, соответственно есть еще биссектрисы la и lc падающие на соответствующие стороны.
hb — это высота, падающая на сторону b, соответственно есть еще высоты ha и hc падающие на соответствующие стороны.
Ну и второе, помните что треугольником является фигура в которой присутствует фундаментальное правило:
Сумма любых(!) двух сторон должна быть больше третьей.
Поэтому не удивляйтесь если получите ошибку При таких данных треугольника не существует при попытке рассчитатать параметры треугольника со сторонами 3, 3 и 7.
Синтаксис
Для позволяателей XMPP клиентов запрос вот такой treug <список параметров>
Для пользователй сайта, все сделано на этой странице.
Список параметров — параметры которые известны, разделенные точкой с запятой
параметр записываетя как параметр=значение
Например если известна сторона а с значением 10, то так и записываем a=10
Более того, значения могут быть не только в виде вещественного числа, но и например как результат какого то выражения
Например если нам нужно посчитать площадь треугольника с сторонами 1, 3, то вот в запросе пишем a=1;b=3;c=sqrt(5)+1
А вот и сам список парметров которые могут фигурировать в расчетах.
Сторона a
Сторона b
Сторона c
Полупериметр p
Угол А
Угол B
Угол C
Площадь треугольника S
Высота ha на сторону a
Высота hb на сторону b
Высота hc на сторону c
Медиана ma на сторону a
Медиана mb на сторону b
Медиана mc на сторону c
Координаты вершин (xa,ya) (xb,yb) (xc,yc)
Примеры
Рассчитать параметры треугольника если известны сторона = 8, угол прилежащей к этой стороне =70 градусов и высота, падающая на эту сторону =2
пишем treug a=8;C=70;ha=2
Параметры треугольника по заданным параметрам
Сторона a = 8
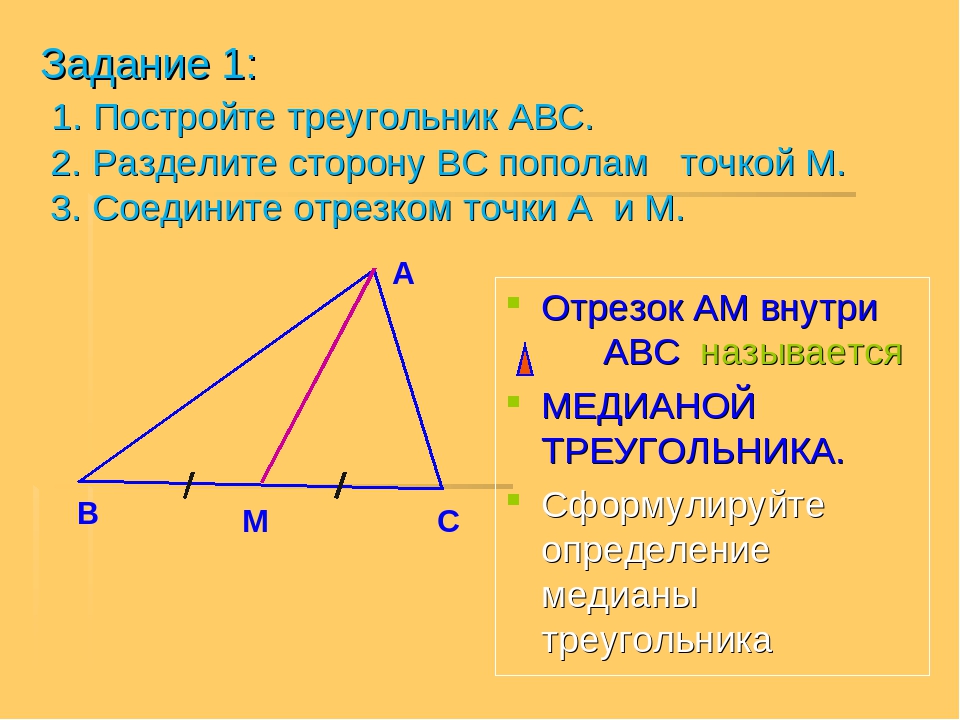
Сторона b = 2.
 1283555449519
1283555449519Сторона c = 7.5420719851515
Полупериметр p = 8.8352137650517
Угол А = 2.1882518638666 в градусах 125.37759631119
Угол B = 2.873202966917 в градусах 164.62240368881
Угол C = 1.221730476396 в градусах 70
Площадь треугольника S = 8
Высота ha на сторону a = 2
Высота hb на сторону b = 7.5175409662872
Высота hc на сторону c = 2.1214329472723
Медиана ma на сторону a = 3.8348889915443
Медиана mb на сторону b = 7.7012304590352
Медиана mc на сторону c = 4.4770789813853
Вот и все, все параметры треугольника.
Вопрос, почему мы сторону назвали а, а не в или с? Это не влияет на решение. Главное выдержать условие о котором я уже сказал «Стороны противоположные любому углу называются так же, только маленькой буквой.» А далее нарисовать в уме треугольник, и применить к заданному вопросу.
Можно было бы взять вместо а в, но тогда прилежащий угол будет не С а А ну и высота будет hb. Результат если вы проверите, будет один и тот же.
Как рассчитать треугольник если известны координаты его вершин?
Например вот такими (xa,ya) =3,4 (xb,yb) =-6,14 (xc,yc)=-6,-3
пишем запрос treug xa=3;ya=4;xb=-6;yb=14;xc=-6;yc=-3
и получаем
Параметры треугольника по заданным параметрам
Сторона a = 17
Сторона b = 11.401754250991
Сторона c = 13.453624047073
Полупериметр p = 20.927689149032
Угол А = 1.4990243938603 в градусах 85.887771155351
Угол B = 0.73281510178655 в градусах 41.987212495819
Угол C = 0.90975315794426 в градусах 52.125016348905
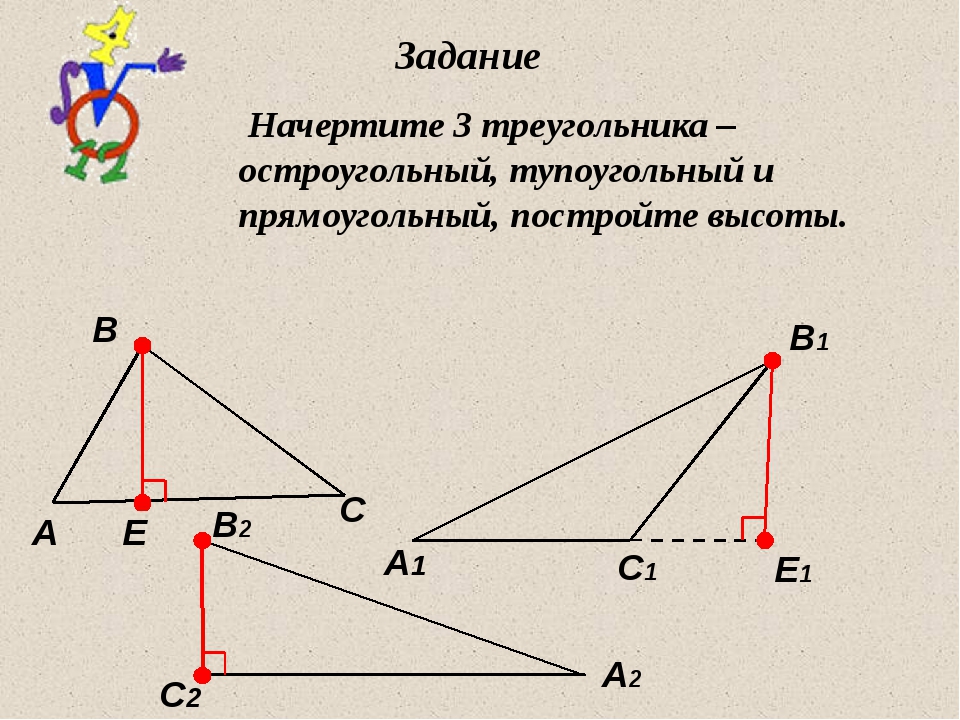
Площадь треугольника S = 76.
 5
5Высота ha на сторону a = 9
Высота hb на сторону b = 13.418987695398
Высота hc на сторону c = 11.372400437582
Медиана ma на сторону a = 9.1241437954466
Медиана mb на сторону b = 14.230249470757
Медиана mc на сторону c = 12.816005617976
Удачных расчетов!!
- Разбиение многоугольника на треугольники >>
Узнаем как правильно нарисовать треугольник: этапы выполнения задания
Как нарисовать треугольник? Этому учат в процессе изучения геометрии в школе. Чтобы задание было выполнено правильно, важно точно знать, какой треугольник необходимо изобразить: равносторонний, равнобедренный или же вписанный. Правилам начертания этих фигур будет посвящена данная статья.
Как рисовать треугольник с равными сторонами?
Как нарисовать треугольник, стороны у которого равны? Для этого можно воспользоваться одним из трех методов.
Такая фигура имеет три одинаковые по длине стороны, связанные тремя углами равной ширины. Это может быть сложным для рисования треугольника вручную. Поэтому можно использовать круглый объект для выделения углов.
Варианты создания фигуры
Обязательно используйте линейку и один из представленных ниже способов:
- Применение циркуля: надо начертить ровную линию. Проведите карандаш вдоль прямого края бумаги. Этот сегмент линии образует одну из сторон. А это означает, что нужно будет чертить вторую и третью линии одинаковой длины, каждая из которых достигает точки под углом 60° от первой линии. Удостоверьтесь, что достаточно места для рисования всех трех сторон!
- Разделите сегмент циркулем. Вставьте карандаш и убедитесь, что он острый! Поместите точку циркуля на один конец сегмента и установите карандаш на другую. Опишите дугу. Не изменяйте установленную «ширину» инструмента от точки циркуля до точки карандаша.
 Нарисуйте вторую дугу, чтобы она пересекала первую дугу, которую уже нарисовали. Отметьте точку, в которой пересекаются две дуги. Это вершина (верхняя точка) треугольника. Он должен лежать в точном центре сегмента линии, который нарисовали. Теперь можете сделать две прямые линии, ведущие к этой точке: по одному от каждого конца «нижнего» сегмента линии. Закончите треугольник. Далее с помощью линейки надо нарисовать еще два сегмента прямой линии – это стороны в треугольнике. Подключите каждый конец исходного сегмента линии к точке, в которой пересекаются дуги. Чтобы закончить работу, сотрите дуги, которые нарисовали, так, чтобы остался только треугольник.
Нарисуйте вторую дугу, чтобы она пересекала первую дугу, которую уже нарисовали. Отметьте точку, в которой пересекаются две дуги. Это вершина (верхняя точка) треугольника. Он должен лежать в точном центре сегмента линии, который нарисовали. Теперь можете сделать две прямые линии, ведущие к этой точке: по одному от каждого конца «нижнего» сегмента линии. Закончите треугольник. Далее с помощью линейки надо нарисовать еще два сегмента прямой линии – это стороны в треугольнике. Подключите каждый конец исходного сегмента линии к точке, в которой пересекаются дуги. Чтобы закончить работу, сотрите дуги, которые нарисовали, так, чтобы остался только треугольник. - Использование объекта с круглой базой: этот совет подойдет для построения дуги. Предложенный метод по сути такой же, как с использованием циркуля.
Указанные советы помогут выяснить, как нарисовать равносторонний треугольник.
Рекомендации по построению равнобедренного треугольника
Равнобедренный треугольник представляет собой фигуру с двумя равными сторонами и двумя равными углами. Если знаете длину, основание и высоту стороны, это можно сделать только с линейкой и циркулем (или просто циркулем, если заданы размеры).
Как нарисовать равнобедренный треугольник:
- Учитывая все боковые длины. Чтобы использовать этот метод, важно знать длину основания треугольника и длину двух равных сторон.
- Учитывая две равные стороны и угол между ними. Чтобы использовать этот метод, нужно знать длину двух равных сторон и измерение угла между этими двумя сторонами.
- Учитывая базовые и смежные углы – необходимо знать длину базы, градусы двух углов, смежных с основанием. Помните, что два угла, смежные с основанием равнобедренного треугольника, будут равны.
- Основа и высота. Нужно знать длину основания треугольника, а также высоту этой геометрической фигуры.
Вписанный треугольник
Как нарисовать вписанный треугольник? Выберите круглый объект. Используйте предмет с круглым основанием. Выбор компакт-диска станет хорошим вариантом. Но можно взять и другой объект нужного размера. Для этого метода свойственно, что длина каждой стороны равносторонней геометрической фигуры с тремя углами будет равна размерам радиуса (половине диаметра) круга.
Используйте предмет с круглым основанием. Выбор компакт-диска станет хорошим вариантом. Но можно взять и другой объект нужного размера. Для этого метода свойственно, что длина каждой стороны равносторонней геометрической фигуры с тремя углами будет равна размерам радиуса (половине диаметра) круга.
Как нарисовать треугольник, если используете компакт-диск? Представьте себе равносторонний треугольник, который вписывается в верхнюю правую часть компакт-диска. Надо начертить первую из сторон. Радиус круглого объекта – расстояние на полпути до получения желаемого результата. Удостоверьтесь, что линии нарисованы ровно.
С помощью линейки просто выполните измерения диаметра объекта и нарисуйте линию на половину длины. Если ее нет, поместите круглый объект на бумагу, затем тщательно проведите по окружности карандашом. Удалите объект – должен быть идеальный круг. Используйте прямой край, чтобы нарисовать линию через точный центр круга: точку, которая полностью равноудалена от любой точки по окружности круга.
Используйте круглый объект для создания дуги. Поместите объект по отрезку линии, с краем круга, расположенным на одном конце линии. Для обеспечения точности убедитесь, что линия проходит четко через центр круга. Используйте карандаш, чтобы начертить дугу – это четверть пути по окружности.
Начертите еще одну дугу. Теперь сдвиньте круглый объект так, чтобы край касался другого конца сегмента линии.
Подведем итоги
В статье были предоставлены рекомендации, как нарисовать треугольник равносторонний, равнобедренный и вписанный в окружность.
Калькулятор треугольников
Укажите 3 значения, включая хотя бы одну сторону в следующих 6 полях, и нажмите кнопку «Рассчитать». Если в качестве единицы угла выбраны радианы, он может принимать такие значения, как пи / 2, пи / 4 и т. Д.
Треугольник — это многоугольник с тремя вершинами. Вершина — это точка, в которой встречаются две или более кривых, линий или ребер; в случае треугольника три вершины соединены тремя отрезками, называемыми ребрами. Треугольник обычно называют его вершинами.Следовательно, треугольник с вершинами a, b и c обычно обозначается как Δabc. Кроме того, треугольники обычно описывают на основе длины их сторон, а также их внутренних углов. Например, треугольник, в котором все три стороны имеют равную длину, называется равносторонним треугольником, а треугольник, в котором две стороны имеют равную длину, называется равнобедренным. Когда ни одна из сторон треугольника не имеет одинаковой длины, он называется разносторонним, как показано ниже.
Треугольник обычно называют его вершинами.Следовательно, треугольник с вершинами a, b и c обычно обозначается как Δabc. Кроме того, треугольники обычно описывают на основе длины их сторон, а также их внутренних углов. Например, треугольник, в котором все три стороны имеют равную длину, называется равносторонним треугольником, а треугольник, в котором две стороны имеют равную длину, называется равнобедренным. Когда ни одна из сторон треугольника не имеет одинаковой длины, он называется разносторонним, как показано ниже.
Отметки на краю треугольника — это обычное обозначение, которое отражает длину стороны, где одинаковое количество отметок означает одинаковую длину.Аналогичные обозначения существуют для внутренних углов треугольника, обозначаемых различным количеством концентрических дуг, расположенных в вершинах треугольника. Как видно из треугольников выше, длина и внутренние углы треугольника напрямую связаны, поэтому логично, что равносторонний треугольник имеет три равных внутренних угла и три стороны равной длины. Обратите внимание, что треугольник, представленный в калькуляторе, не показан в масштабе; хотя он выглядит равносторонним (и имеет маркировку угла, которая обычно считается равной), он не обязательно является равносторонним и представляет собой просто представление треугольника.После ввода фактических значений выходные данные калькулятора будут отражать форму входного треугольника.
Треугольники, классифицируемые на основе их внутренних углов, делятся на две категории: прямые и наклонные. Прямоугольный треугольник — это треугольник, в котором один из углов равен 90 °, и обозначается двумя отрезками прямой, образующими квадрат в вершине, составляющей прямой угол. Самый длинный край прямоугольного треугольника, противоположный прямому углу, называется гипотенузой.Любой треугольник, который не является прямоугольным, классифицируется как наклонный треугольник и может быть тупым или острым. В тупом треугольнике один из углов треугольника больше 90 °, а в остром треугольнике все углы меньше 90 °, как показано ниже.
Факты, теоремы и законы о треугольнике
- Учитывая длины всех трех сторон любого треугольника, каждый угол можно рассчитать с помощью следующего уравнения. Обратитесь к треугольнику выше, предполагая, что a, b и c — известные значения.
Площадь треугольника
Существует несколько различных уравнений для вычисления площади треугольника в зависимости от того, какая информация известна. Вероятно, наиболее известное уравнение для вычисления площади треугольника включает его основание, b , и высоту, h . «Основание» относится к любой стороне треугольника, где высота представлена длиной отрезка линии, проведенного от вершины, противоположной основанию, до точки на основании, образующей перпендикуляр.
Учитывая длину двух сторон и угол между ними, следующую формулу можно использовать для определения площади треугольника. Обратите внимание, что используемые переменные относятся к треугольнику, показанному на калькуляторе выше. Для a = 9, b = 7 и C = 30 °:
Другой метод вычисления площади треугольника основан на формуле Герона. В отличие от предыдущих уравнений, формула Герона не требует произвольного выбора стороны в качестве основания или вершины в качестве начала координат.Однако для этого требуется, чтобы длина трех сторон была известна. Опять же, со ссылкой на треугольник, представленный в калькуляторе, если a = 3, b = 4 и c = 5:
Медиана, внутренний радиус и радиус окружности
Медиана
Медиана треугольника определяется как длина отрезка прямой, который проходит от вершины треугольника до середины противоположной стороны. Треугольник может иметь три медианы, каждая из которых будет пересекаться в центре тяжести (среднее арифметическое положение всех точек в треугольнике) треугольника.См. Рисунок ниже для пояснения.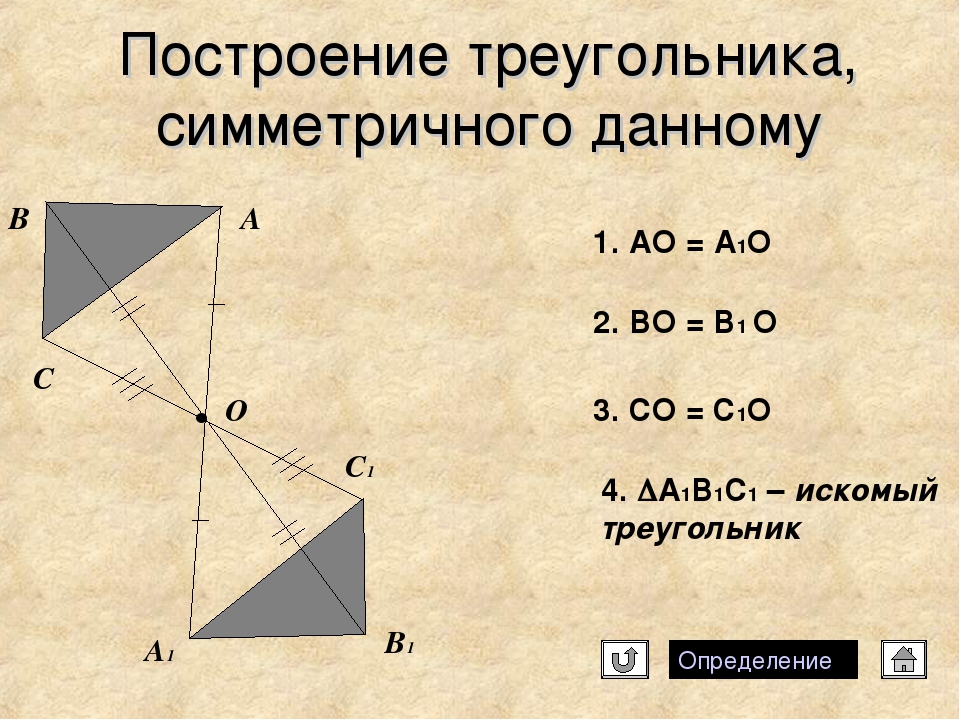
Медианы треугольника представлены отрезками m a , m b и m c . Длину каждой медианы можно рассчитать следующим образом:
Где a, b и c обозначают длину стороны треугольника, как показано на рисунке выше.
В качестве примера, учитывая, что a = 2, b = 3 и c = 4, медиана m a может быть рассчитана следующим образом:
Inradius
Inradius — это радиус наибольшего круга, который может поместиться внутри данного многоугольника, в данном случае треугольника.Внутренний радиус перпендикулярен каждой стороне многоугольника. В треугольнике внутренний радиус можно определить, построив две биссектрисы угла, чтобы определить центр треугольника. Внутренний радиус — это перпендикулярное расстояние между центром вращения и одной из сторон треугольника. Можно использовать любую сторону треугольника, если определено перпендикулярное расстояние между стороной и центром, поскольку центр, по определению, находится на равном расстоянии от каждой стороны треугольника.
В данном калькуляторе внутренний радиус рассчитывается с использованием площади (Area) и полупериметра (ов) треугольника по следующим формулам:
, где a, b и c — стороны треугольника
Круговой радиус
Радиус описанной окружности определяется как радиус окружности, проходящей через все вершины многоугольника, в данном случае треугольника.Центр этой окружности, где пересекаются все срединные перпендикуляры каждой стороны треугольника, является центром описанной окружности и точкой, от которой измеряется радиус описанной окружности. Центр описанной окружности треугольника не обязательно должен находиться внутри треугольника. Стоит отметить, что у всех треугольников есть описанная окружность (окружность, проходящая через каждую вершину) и, следовательно, радиус описанной окружности.
В данном калькуляторе радиус описанной окружности рассчитывается по следующей формуле:
Где a — сторона треугольника, а A — угол, противоположный стороне a
Хотя используются сторона a и угол A, в формуле можно использовать любую из сторон и их соответствующие противоположные углы.
| <сценарий> | |
| функция init () { | |
| // Получить объект холста из DOM | |
| var canvas = document.getElementById («myCanvas»); | |
| // Инициализация контекста WebGL | |
| var gl = canvas.getContext («webgl»); | |
| если (! Gl) { | |
| console.log («Не удалось получить контекст отрисовки для WebGL»); | |
| возврат; | |
| } | |
| // Инициализация шейдеров | |
| var vs = document.getElementById (‘shaderVs’). innerHTML; | |
| var fs = document.getElementById (‘shaderFs’). InnerHTML; | |
| если (! InitShaders (gl, vs, fs)) { | |
| console.log («Не удалось инициализировать шейдеры.»); | |
| возврат; | |
| } | |
| // Записываем позиции вершин в вершинный шейдер | |
| var n = initVertexBuffers (gl); | |
| , если (n <0) { | |
консоль. log (‘Не удалось установить положение вершин’); log (‘Не удалось установить положение вершин’); | |
| возврат; | |
| } | |
| // Чистый холст | |
| gl.clearColor (0,0, 0,0, 0,0, 1,0); | |
| gl.clear (gl.COLOR_BUFFER_BIT); | |
| // Ничья | |
| гл.drawArrays (gl.TRIANGLES, 0, n); | |
| } | |
| функция initVertexBuffers (gl) { | |
| // Вершины | |
| var dim = 3; | |
| var vertices = new Float32Array ([ | |
| 0, 0.5, 0, // Вершина # 1 | |
| -0,5, -0,5, 0, // Вершина # 2 | |
| 0,5, -0,5, 0 // Вершина # 3 | |
| ]); | |
| // Создаем буферный объект | |
| var vertexBuffer = gl.createBuffer (); | |
| если (! VertexBuffer) { | |
консоль. log (‘Не удалось создать буферный объект’); log (‘Не удалось создать буферный объект’); | |
| возврат -1; | |
| } | |
| gl.bindBuffer (gl.ARRAY_BUFFER, vertexBuffer); | |
| gl.bufferData (gl.ARRAY_BUFFER, вершины, gl.STATIC_DRAW); | |
| // Присваиваем вершины в объекте буфера переменной a_Position | |
| var a_Position = gl.getAttribLocation (gl.program, ‘a_Position’); | |
| , если (a_Position <0) { | |
| console.log (‘Не удалось получить место хранения a_Position’); | |
| возврат -1; | |
| } | |
| gl.vertexAttribPointer (a_Position, dim, gl.FLOAT, false, 0, 0); | |
| гл.enableVertexAttribArray (a_Position); | |
| // Возвращаем количество вершин | |
| вернуть vertices.length / dim; | |
| } | |
| функция initShaders (gl, vs_source, fs_source) { | |
| // Компиляция шейдеров | |
var vertexShader = makeShader (gl, vs_source, gl. VERTEX_SHADER); VERTEX_SHADER); | |
| var fragmentShader = makeShader (gl, fs_source, gl.FRAGMENT_SHADER); | |
| // Создать программу | |
| var glProgram = gl.createProgram (); | |
| // Присоединяем и связываем шейдеры с программой | |
| гл.attachShader (glProgram, vertexShader); | |
| gl.attachShader (glProgram, fragmentShader); | |
| gl.linkProgram (glProgram); | |
| if (! Gl.getProgramParameter (glProgram, gl.LINK_STATUS)) { | |
| alert («Не удалось инициализировать программу шейдера»); | |
| return false; | |
| } | |
| // Используйте программу | |
| гл.useProgram (glProgram); | |
| gl.program = glProgram; | |
| вернуть истину; | |
| } | |
| функция makeShader (gl, src, type) { | |
var shader = gl. createShader (тип); createShader (тип); | |
| gl.shaderSource (шейдер, src); | |
| gl.compileShader (шейдер); | |
| если (! Gl.getShaderParameter (шейдер, gl.COMPILE_STATUS)) { | |
| alert («Ошибка компиляции шейдера:» + gl.getShaderInfoLog (шейдер)); | |
| возврат; | |
| } | |
| шейдер возврата; | |
| } | |
Многочисленные способы построения треугольника I
$ m_ {a}, m_ {b}, m_ {c} $
Через $ A $ и $ C $ нарисуйте линии, параллельные $ CM_ {c} $ и $ AM_ {a}, $, соответственно.Пусть $ P $ — точка пересечения. $ APCG $ — это параллелограмм, поэтому его диагонали делятся пополам из-за точки пересечения. Следовательно, они пересекаются в $ M_ {b}, $ и $ CM_ {b} $ — это медиана $ GPC. $ $ PC $ равен $ AG $ и параллелен ему, тогда как $ GM_ {a} $ составляет половину $ AG $ и, следовательно, $ PC. $ Следовательно, медиана $ GK $ $ GPC $ параллельна $ BC $ и равна $ a / 2. $ Третья медиана $ GPC $ аналогичным образом параллельна $ AB $ и равна $ в / 2. $
Тогда есть строительство. Возьмите 2/3 доллара от каждой заданной медианы.Используйте $ SSS $, чтобы построить треугольник $ GPC. $ Найдите в этом треугольнике медианы. Удвойте их. Это даст три стороны искомого треугольника. Нарисуйте его снова, используя $ SSS. $
$ M_ {a}, M_ {b}, M_ {c}
$ Треугольник $ M_ {a} M_ {b} M_ {c} $ похож на $ \ Delta ABC $ и вдвое меньше. Двойные его стороны. Затем используйте $ SSS $, чтобы построить $ ABC. $
Двойные его стороны. Затем используйте $ SSS $, чтобы построить $ ABC. $
$ a, b, m_ {c}
$Треугольник $ M_ {c} M_ {b} C $ имеет следующие стороны: $ a / 2, $ $ b / 2, $ $ m_ {c}. $ Следовательно, его можно построить с помощью $ SSS.$ Теперь увеличьте длину $ CM_ {b} $ вдвое, чтобы получить $ A. $ Затем увеличьте $ AM_ {c} $ до двойной длины, чтобы получить $ B. $
$ a, b, m_ {b}
$Треугольник $ BM_ {b} C $ состоит из следующих сторон: $ m_ {b}, $ $ b / 2, $ $ a. $ Мы можем построить его с помощью $ SSS. $ После этого расширить $ CM_ {b} $ в два раза больше длины, чтобы получить $ A. $
$ H_ {a}, H_ {b}, H_ {c}
$Треугольник $ H_ {a} H_ {b} H_ {c} $ известен как ортогональный треугольник $ \ Delta ABC. $ (Это треугольник педали ортоцентра.) Среди других интересных особенностей ортического треугольника можно отметить тот факт, что высоты $ \ Delta ABC $ являются биссектрисами угла $ H_ {a} H_ {b} H_ {c}. $ Чтобы доказать это, заметим, что $ HH_ {b } CH_ {a} $ — четырехугольник, который можно вписать в круг диаметром $ CH $, потому что его два угла $ HH_ {b} C $ и $ HH_ {a} C $ оба правые. Отсюда углы $ HH_ {a} H_ {b} $ и $ ACH $ равны. Однако $ ACH $ дополняет $ C $ в треугольнике $ ACH_ {c} $, а $ HH_ {a} H_ {b} $ дополняет $ H_ {b} H_ {a} C. $ Следовательно, последний равно $ C.$ Аналогично $ \ angle H_ {c} H_ {a} B = \ angle C. $ Что дает $ \ angle H_ {c} H_ {a} B = \ angle H_ {b} H_ {a} C. $ углы в $ H_ {b} $ и $ H_ {c} $ обрабатываются аналогичным образом.
Таким образом, мы получаем следующую конструкцию. Дан треугольник $ H_ {a} H_ {b} H_ {c}. $ Нарисуйте его биссектрисы. Через вершины проведите прямые, перпендикулярные соответствующим биссектрисам.
(Омар X. из старого CTKExchange отметил, что если все три точки различны, то конструкция фактически приводит к четырем решениям.Однако, имея в виду прямоугольные треугольники, проблема может иметь бесконечно много решений при условии, что две ножки совпадают. )
)
$ A, B, p $
Начните с рисования треугольника $ AB’C ‘$ с двумя заданными углами $ A $ и $ B. $ Как бы вы это ни сделали, полученный треугольник будет похож на треугольник $ \ Delta ABC $, который мы должны найти. На $ cc, $, начиная с точки $ A, $ измеряет перимитер $ p $ точек $ AB’C ‘$ (точка $ P) $ и $ 2p $ (точка $ Q). $ Соедините $ P $ и $ C ‘. $ Через $ Q проведите $ линию, параллельную $ PC’ $, которая пересекает $ bb $ в точке $ C.$ От $ C $ нарисуйте линию, параллельную $ C’B ‘$, чтобы получить $ B. $
Здесь уместно сделать замечание. Два угла полностью определяют форму треугольника . Для однозначного определения треугольника необходимо зафиксировать его размер . Поскольку в подобных треугольниках все линейные элементы находятся в одинаковом соотношении, любой линейный элемент в треугольнике однозначно определяет этот треугольник. Следовательно, вышеуказанное решение будет работать и в других случаях. Например, когда нам даны $ A, B, $ и, скажем, $ l_ {c} $ или $ H_ {a} M_ {b}.$
$ А, м_б, х_а $
Строительство принадлежит Рене Спербу.
Вершина $ A $ имеет своим локусом $ (O) $ с хордами $ BM_b $ длины $ m_b $, соединяющим угол $ A. $ Вершина $ C $ находится на $ AM_b $ на том же расстоянии от $ M_b $, что и $ A, $ означает, что геометрическое место точек $ C $ является окружностью $ (O ‘) $, симметричной $ (O) $ в $ M_b. $
Расстояние от середины $ M_b $ до стороны $ BC $ равно $ \ displaystyle \ frac {h_a} {2}. $ Отсюда следует, что основание перпендикуляра от $ M_b $ до $ BC $ лежит на пересечении окружности $ (BM_b) $ диаметром $ BM_b $ с кругом $ \ displaystyle C (M_b, \ frac {h_a} {2}).$ У двух окружностей всегда есть две точки пересечения. Обозначьте один из них, скажем, $ X, $ и проведите линию $ BX. $ Эта линия пересекает окружность $ (O ‘) $ в одной (когда она касается окружности) или в двух точках. Любая из этих точек может служить вершиной $ C.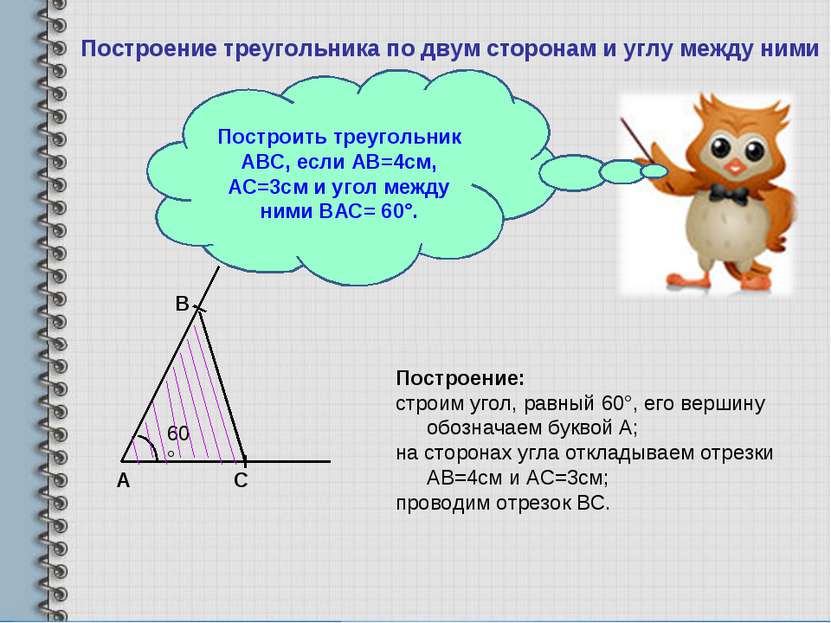 $ После выбора вершина $ A $ будет найдена как второе пересечение $ CM_b $ и $ (O). $ Может быть $ 0,1,2,3,4 $ решения.
$ После выбора вершина $ A $ будет найдена как второе пересечение $ CM_b $ и $ (O). $ Может быть $ 0,1,2,3,4 $ решения.
Как создать треугольник в Illustrator
Выяснить, как создать треугольник в Illustrator, может быть непросто, потому что, в отличие от других фигур, для этого нет специального инструмента.Есть инструмент для создания прямоугольников, кругов, эллипсов и даже звезд. Однако инструмента треугольник нет, но это нормально, потому что мы можем с такой же легкостью использовать инструменты, предназначенные для других фигур.
Ниже приводится краткий обзор того, как мы подойдем к созданию треугольника в Illustrator. Я бы порекомендовал посмотреть видеоурок в верхней части страницы, если вы хотите получить более подробный и понятный урок.
Как создать треугольник в Illustrator
| Чтобы создать треугольник в Illustrator, возьмите инструмент Polygon Tool и щелкните холст, чтобы открыть меню настроек многоугольника.Установите вход Sides на 3 и оставьте значение по умолчанию для Radius . После того, как вы нажмете ОК, на вашем холсте появится треугольник. |
Сначала возьмите инструмент Polygon Tool . Вы, вероятно, не сразу увидите его на панели инструментов, потому что он скрыт внутри Rectangles Tool , поэтому нажмите и удерживайте значок инструмента Rectangles, чтобы вызвать всплывающее меню, в котором отображаются различные другие формы на выбор.
Выберите Инструмент «Многоугольник» и щелкните холст один раз. Это вызовет меню настроек многоугольника.
Оставьте для входа Radius любое значение, которое уже есть, но убедитесь, что вы установили для входа Sides значение 3 . Технически мы будем создавать трехсторонний многоугольник, а не треугольник, но это все равно.
После того, как вы нажмете OK , на вашем холсте будет сгенерирован равносторонний треугольник.Равносторонний треугольник — это треугольник, у которого все три стороны равны по длине.
Равнобедренные треугольники
Равнобедренный треугольник — это треугольник, в котором только 2 стороны равны. Если вы хотите превратить свой треугольник в равнобедренный, просто возьмите инструмент Selection Tool (сочетание клавиш: V ), нажмите и перетащите края, чтобы изменить их размер в соответствии с вашими предпочтениями.
Треугольники из скалена
Разносторонний треугольник — это треугольник, у которого ни одна из трех сторон не равна ширине.Если вы хотите преобразовать свой треугольник в разносторонний треугольник, вы можете сделать это, взяв инструмент Direct Selection Tool (сочетание клавиш: A ), щелкнув и перетащив каждый отдельный угол, чтобы установить его под нужным углом. Вы также можете перетаскивать целые стороны, а не только углы.
Как составлять прямоугольные треугольники
Прямоугольный треугольник — это треугольник, в котором один из углов расположен под углом 90 градусов. Создание прямоугольных треугольников в Illustrator требует другого подхода, чем создание стандартных типов треугольников, описанных выше.
Чтобы создать прямоугольный треугольник в Illustrator, возьмите инструмент Rectangles Tool (сочетание клавиш: M ), затем удерживайте Shift на клавиатуре, щелкните и перетащите холст, чтобы создать идеально симметричный квадрат.
Теперь возьмите инструмент прямого выбора (сочетание клавиш: A ), щелкните и перетащите один из углов квадрата, чтобы выбрать его, затем щелкните значок Удалить выбранные точки привязки в меню вверху панель инструментов.
Значок выглядит примерно так…
Это удалит один из углов квадрата, и у вас останется прямоугольный треугольник.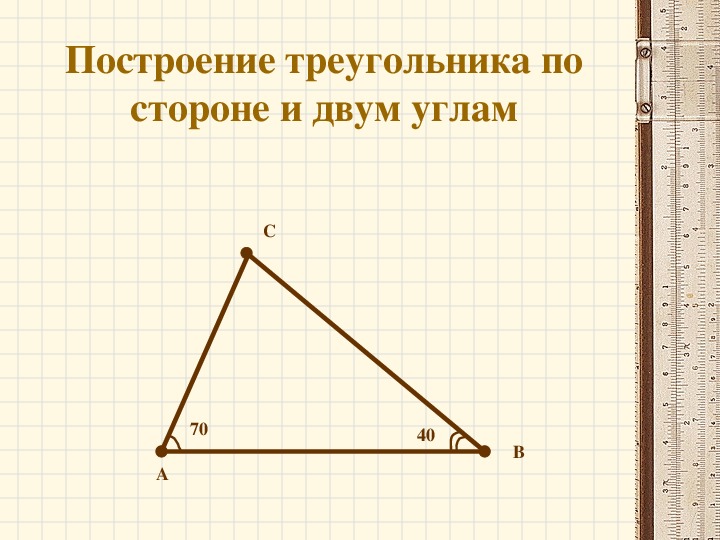
Как создать треугольник с закругленными углами в Illustrator
Чтобы создать треугольник с закругленными углами в Illustrator, просто выполните любой из предыдущих шагов, чтобы создать стандартный треугольник, затем возьмите инструмент Direct Selection Tool (сочетание клавиш: A ) и возьмите один из живых углов, чтобы образовать углы. круглый.
«Живые углы» — это удобная функция в Illustrator, которая позволяет делать острые углы скругленными. Также они позволяют определить радиус закругленного угла. Их можно определить по маленьким синим кружкам внутри каждого угла.
Нажав и перетащив один из активных углов, вы сможете создать закругленный треугольник.
И это основы создания треугольника в Illustrator. Если у вас есть дополнительные вопросы, просто оставьте комментарий ниже.Как всегда, спасибо за просмотр!
Logos By Nick LLC является участником программы Amazon Services LLC Associates, партнерской рекламной программы, предназначенной для предоставления сайтам средств для получения рекламных сборов за счет рекламы и ссылок на Amazon.com. Как партнер Amazon я зарабатываю на соответствующих покупках. Прочтите информацию о партнерских программах здесь.
Инструмент «Треугольник» в Photoshop + Создайте треугольник в Photoshop, как сделать учебник
Как сделать треугольник в фотошопе.Обратите внимание, что в последней версии появился инструмент Photoshop «Треугольник» !! И это обсуждается внизу страницы, а также в видео выше.
Вы можете создать треугольник с помощью инструмента многоугольник. Установите стороны на 3 и установите звездочку на NO.
Используйте его как слой-фигуру и сделайте треугольник. Вы можете вращать его, дублировать треугольник и многое другое. Вы можете заполнить треугольник разными цветами. Вы также можете установить треугольник без цвета и вместо этого сделать обводку.Вы можете создать узор треугольника, определив форму треугольника через меню редактирования в Photoshop. Вы можете использовать инструмент «Перо» для создания любых треугольников. Выделяйте отдельные опорные точки треугольника с помощью инструмента прямого выбора для создания всевозможных различных дизайнов. В этом уроке показано несколько подходов к созданию треугольника в Photoshop
Вы можете вращать его, дублировать треугольник и многое другое. Вы можете заполнить треугольник разными цветами. Вы также можете установить треугольник без цвета и вместо этого сделать обводку.Вы можете создать узор треугольника, определив форму треугольника через меню редактирования в Photoshop. Вы можете использовать инструмент «Перо» для создания любых треугольников. Выделяйте отдельные опорные точки треугольника с помощью инструмента прямого выбора для создания всевозможных различных дизайнов. В этом уроке показано несколько подходов к созданию треугольника в Photoshop
Выберите инструмент «Многоугольник» на панели инструментов Photoshop
Выберите опцию слоя-фигуры
Установите цвет треугольника
Отмените выбор звездочки в параметрах многоугольника
Число сторон установлено на 3
Нарисуйте треугольник, перетащив его из исходной точки
Поверните по мере необходимости
Flatten
Инструмент «Треугольник» для Photoshop
ВPhotoshop теперь есть инструмент «Треугольник», в основном он такой же, как и многоугольник, но вам не нужно устанавливать значение 3.Вы также можете изменить его, используя интерактивные элементы управления. Это также инструмент «живой треугольник», что означает, что вы можете вернуться к нему в любое время, если применить его как фигуру, и изменить настройки. Также можно скруглить углы треугольника. Лучшая панель для управления треугольником — это панель свойств, которую можно найти через меню окна. Выбрав треугольник, вы можете изменить цвет заливки, а также обводку и стиль обводки, а также добавить стили обводки / тире и т. Д.
Нарисуйте в Photoshop базовый треугольник с помощью инструмента «Многоугольник».
Вы можете использовать инструмент «Многоугольник», чтобы нарисовать треугольник. Ключевым моментом является инструмент многоугольника, а для сторон установлено значение 3. Вы можете установить цвет формы треугольника на сплошной цвет, а также градиент и узоры, а также толщину штриха / штриха
Ключевым моментом является инструмент многоугольника, а для сторон установлено значение 3. Вы можете установить цвет формы треугольника на сплошной цвет, а также градиент и узоры, а также толщину штриха / штриха
Выбрать многоугольник на панели инструментов
Установите звездочку на NO
сторон до 3
Выбрать вариант формы
Нарисуйте треугольник
Установить черный цвет
В свойствах можно установить градиентный или сплошной цвет.Вы можете продублировать форму треугольника в Photoshop, выбрав треугольник, alt / option и shift.
Создайте / нарисуйте треугольник обводки с помощью инструмента многоугольник и обведите черным цветом в Photoshop
Инструмент «Выбрать многоугольник» на панели инструментов Photoshop
Установите звездочку на NO
сторон до 3
Выбрать вариант формы
Нарисуйте треугольник
Перейти на панель свойств
Отключить заливку
Установить черную обводку
Установить толщину обводки на 5 пикселей
Затем вы можете добавить стили штрихов, такие как точки, чтобы создать форму точечного треугольника в Photoshop
.Создайте узор треугольника, используя созданный узор, а затем создайте новый слой заливки в Photoshop
.Вы можете сделать узор треугольника, выбрав результаты выше и
Выбрать треугольник
Меню редактирования
Определить шаблон
Меню слоев
Новый слой заливки
Образец
Выберите треугольник
Установить шкалу
ОК
Вы также можете удалить фон (поскольку треугольник был создан как фигура), а затем определить его.![]() Это означает, что треугольные узоры можно добавлять на несколько слоев без необходимости в режимах наложения
Это означает, что треугольные узоры можно добавлять на несколько слоев без необходимости в режимах наложения
Создайте треугольник с помощью инструмента «Перо»
Меню просмотра в Photoshop
Показать сетку (упрощает создание треугольника)
Инструмент «Выбрать перо» на панели инструментов Photoshop
Установить параметр слоя формы
Установить черный цвет заливки
Обводка без цвета
Щелкните инструмент «Перо» в верхнем левом углу
Щелкните инструмент «Перо» посередине внизу
Щелкните инструмент «Перо» в правом верхнем углу
Вернуться к первой точке
Изменить размер ограничивающего прямоугольника треугольника
Повернуть на 90 градусов
С помощью инструмента «Перо» можно создать самые разные треугольники.Вы также можете выбрать точки привязки треугольников и перемещать их для создания различных треугольников
Выберите опорную точку с помощью инструмента прямого выбора
Сдвинуть точку привязки
Выберите другую точку привязки и сдвиньте и т. Д.
Затем вы можете создать много новых треугольников с помощью инструмента прямого выбора
Рисование нестандартного треугольника | КодHS
Команды черепахи
Команды — это то, как мы приказываем Черепашке Трейси что-то делать.
Трейси знает несколько встроенных команд.
Механизм
# Команда вперед заставляет Трейси двигаться вперед на заданное расстояние вперед (10) вперед (50) вперед (200) # Команда назад заставляет Трейси двигаться назад на заданное расстояние назад (10) назад (50) назад (200) # Отрицательные значения также могут использоваться для перемещения Трейси вперед или назад назад (-200) вперед (-200)
Круги для рисования
# Команда круга заставляет Трейси нарисовать круг над собой с указанным радиусом круг (10) круг (100) # Другой параметр может использоваться для рисования только определенных частей круга # Эта команда нарисует полукруг круг (10, 180) # Эта команда нарисует четверть круга круг (10, 90) # Другой параметр может использоваться для управления количеством точек в форме # Эта команда нарисует треугольник круг (10, 360, 3) # Эта команда нарисует квадрат круг (10, 360, 4)
Ручка
# Поднимите перо вверх # Трейси не оставит следов при движении penup () # Положите ручку # Трейси оставит след, когда двинется отложенный () # Изменить размер пера # Нормальный, толщина линии 1 размер карандаша (1) # Больше, ширина линии 10 размер карандаша (10)
Вращение
# Трейси повернется на 90 градусов влево слева (90) # Трейси повернет налево на 180 градусов и # смотреть в противоположную сторону слева (180) # Трейси повернет налево на 360 градусов # и сделайте полный оборот слева (360) # Правильная команда делает то же самое, # но Трейси поворачивает направо, а не налево правый (90) правый (180) право (360) # Отрицательные значения также можно использовать для поворота Трейси вправо или влево право (-90) слева (-90)
Позиция
Трейси расположена в координатной плоскости (x, y) следующим образом:
Каждая точка в мире Трейси может быть расположена по координате (x, y).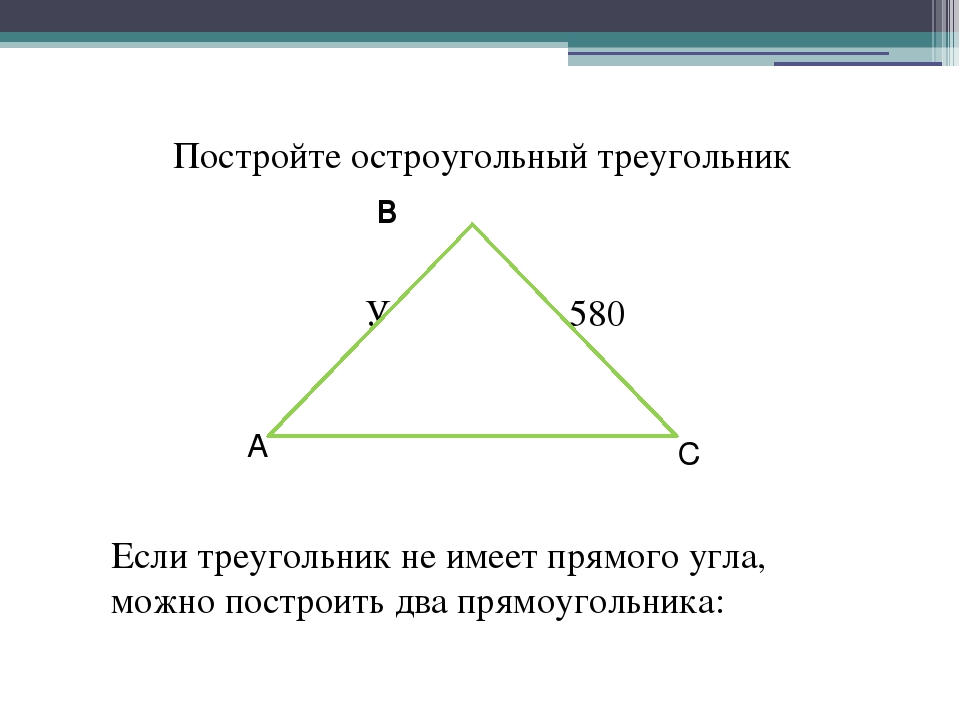 Например:
Например:
- Центр мира (0, 0)
- Верхняя середина мира (0, 200)
- Нижний левый угол мира — (-200, -200)
- И так далее …
Мы можем использовать команду setposition , чтобы отправить Трейси в определенное место
# Отправить Трейси в центр мира setposition (0, 0) # Отправьте Трейси в крайнюю правую середину мира setposition (100, 0) # Отправить Трейси в верхний правый угол мира setposition (200, 200) # Установите позицию x Трейси равной 100 # Положение y остается прежним набор (100) # Установите позицию Y Трейси равной 100 # Положение x остается прежним сети (100)
Скорость
Мы можем установить скорость Трейси с помощью команды speed
Варианты скорости от 0 до 10
# Самый медленный скорость (1) # Обычный скорость (6) # Быстрый скорость (10) # Самый быстрый (без анимации) скорость (0)
Цвет
# Устанавливает фиолетовый цвет фона холста
bgcolor ("фиолетовый")
# Рисует красную линию
красный цвет")
вперед (50)
# Рисует синюю линию
цвет синий")
вперед (50)
# Вот несколько вариантов цвета.# Их можно использовать как для цвета, так и для bgcolor:
черный цвет")
цвет синий")
коричневый цвет")
цвет ("голубой")
цвет («золото»)
цвет («серый»)
цвет («зеленый»)
цвет («индиго»)
оранжевый цвет")
цвет («розовый»)
цвет («пурпурный»)
красный цвет")
цвет («фиолетовый»)
цвет белый")
цвет («желтый»)
Начинка
# Чтобы нарисовать заполненную фигуру, начните с этого вызова
begin_fill ()
# Нарисуйте свою форму
для i в диапазоне (3):
вперед (150)
слева (120)
# Остановить заливку, как только вы нарисовали фигуру
end_fill ()
Очистить экран
# Чтобы очистить экран от любых пометок, используйте команду clear
Чисто()
# Это можно использовать в конце кода
# Это очистит экран после того, как квадрат будет нарисован
для i в диапазоне (4):
вперед (50)
слева (90)
Чисто()
# Это можно использовать во всем коде
# Это очистит экран перед рисованием квадрата
круг (50)
Чисто()
для i в диапазоне (4):
вперед (50)
слева (90)
Петли
Циклы помогают нам повторять команды, что делает наш код намного короче.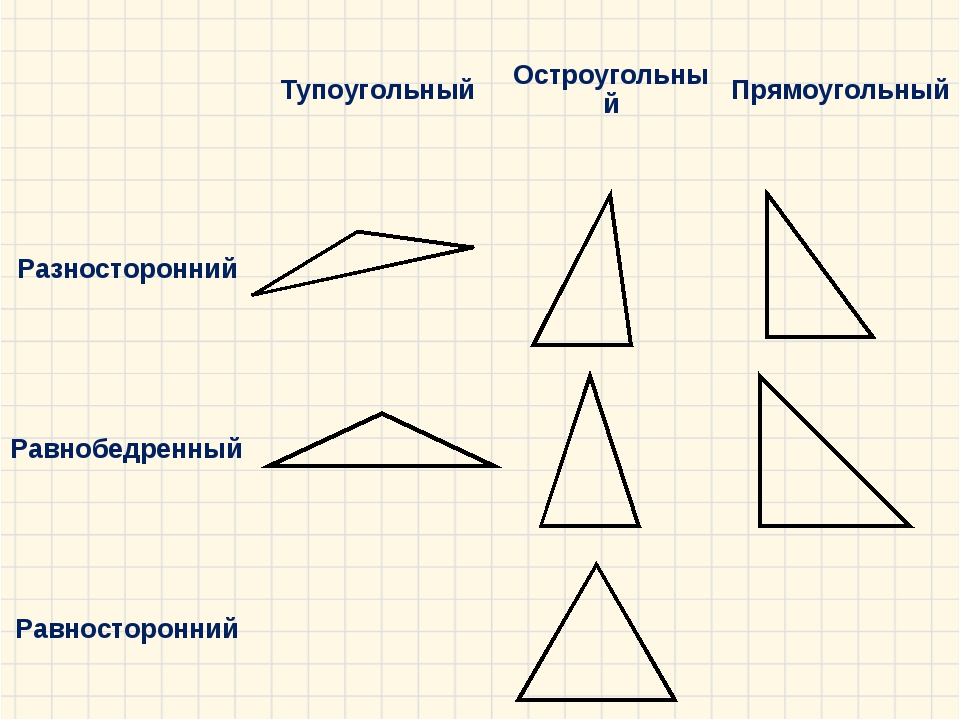
Убедитесь, что все внутри цикла имеет отступ с отступом на один уровень!
Для петель
Используйте циклы for, если вы хотите повторить что-то определенное количество раз.
# Вместо того, чтобы повторять код снова и снова
вперед (10)
слева (90)
вперед (10)
слева (90)
вперед (10)
слева (90)
вперед (10)
слева (90)
# Используйте цикл for, чтобы повторить код!
для i в диапазоне (4):
вперед (10)
слева (90)
# Вы можете использовать переменную i внутри цикла
# i начинается с 0 и увеличивается до COUNT-1
# Это заставит Трейси двигаться вперед 0, затем 1, затем 2
для i в диапазоне (3):
вперед (я)
# Вы можете изменить значение i внутри цикла for, используя математические выражения
для i в диапазоне (3):
вперед (i * 10)
# Вы также можете контролировать значение i, используя расширенные параметры
для i в диапазоне (STARTING_VALUE, ENDING_VALUE, INCREMENT):
# Это переместит Трейси вперед на 25, 50 и 75 пикселей
для i в диапазоне (25, 76, 25):
вперед (я)
Циклы пока
Используйте циклы while, если вы хотите повторить что-то неизвестное количество раз или пока условие не станет ложным.
Если нет точки, где условие становится ложным, вы создадите бесконечный цикл, которого всегда следует избегать!
# Продолжайте рисовать круги, пока переменная count не станет больше 5 # Если переменная счетчика не обновляется, произойдет бесконечный цикл count = 0 пока считатьФункции
Написать функцию - все равно что научить черепаху Трейси новому слову.
Именование функций: вы можете называть свои функции как хотите, но в имени функции не должно быть пробелов.Вместо пробелов используйте символы подчеркивания (_) like_this_for_example
Убедитесь, что весь код внутри вашей функции имеет отступ с отступом на один уровень!
Определение функции
Мы определяем функцию, чтобы научить Трейси инструкциям для нового слова.

def name_of_your_function (): # Код, который запускается, когда вы звоните на # эта функция. # ПРИМЕРЫ # Научите Трейси рисовать край def draw_edge (): вперед (50) слева (90) # Научите Трейси рисовать синий край def draw_blue_edge (): цвет синий") вперед (50) слева (90) # Научите Трейси рисовать квадрат def draw_square (): для i в диапазоне (4): draw_edge ()Использование параметров в функциях
Мы используем параметры для изменения определенных команд в нашей функции.
# Используйте параметр для управления радиусом рисуемого круга def draw_circle (радиус): круг (радиус) # В одной функции можно использовать несколько параметров # Параметры контролируют длину сторон квадрата и цвет def draw_square (длина, выбор цвета): цвет (выбор цвета) для i в диапазоне (4): вперед (длина) слева (90)Вызов функции
Мы вызываем функцию, чтобы Трейси фактически выполнила новую команду.
# Вызов функции draw_edge () один раз # Трейси нарисует одну грань draw_edge () # Вызов функции draw_edge () 3 раза # Трейси нарисует 3 ребра draw_edge () draw_edge () draw_edge () # Вызвать функцию draw_square () с параметрами # Трейси нарисует 3 квадрата разных размеров и цветов draw_square (50, "красный") draw_square (100, «синий») draw_square (75, «оранжевый»)Переменные
Мы используем переменные для хранения значений, которые можно использовать для управления командами в нашем коде.Значения переменных также можно изменять по всему коду.
# Сделать переменную, чтобы что-то отслеживать count = 0 # Обновить значение переменной с помощью математических выражений # Это добавит единицу к значению переменной count count = count + 1 # Значения переменных также могут быть изменены внутри управляющих структур # Значение переменной count будет увеличиваться на 1 на каждой итерации цикла для i в диапазоне (4): вперед (10) count = count + 1Пользовательский ввод
Мы можем использовать ввод от пользователя для управления нашим кодом.
# Спросите пользователя о вводе и сохраните его в переменной, которая будет использоваться в коде # Это будет работать, только если ввод используется как строка circle_color = input («Какого цвета круг?») # Если ввод нужно использовать как число, включите термин «int» radius = int (input («Каков радиус круга?»)) # Этот ввод затем можно использовать для управления различными частями кода цвет (цвет_круга) круг (радиус)Операторы If / Else
Мы можем сказать Трейси, как принимать решения, используя операторы if / else.
Убедитесь, что весь код внутри оператора if / else имеет один уровень отступа!
Если утверждения
Используйте оператор if, чтобы указать Трейси, что нужно что-то делать только тогда, когда условие истинно. Если условие ложно, Трейси пропустит команды, указанные ниже.
# Трейси будет рисовать круг, только если переменная count меньше 5 если считатьОператоры If / Else
Используйте оператор if / else, чтобы заставить Трейси принять решение между несколькими условиями.Если первое условие ложно, Трейси перейдет к следующему условию, пока не найдет истинное. Если ни одно из условий не выполнено, будут выполняться команды внутри блока «else».
# Трейси нарисует круг, если переменная count меньше 5 если счет 5: круг (50,360,4) # В любом другом случае Трейси проведет линию # Единственный другой случай, который существует за пределами указанных границ, это если count = 5 # Мы не включаем условие для операторов else еще: вперед (50)Математика и сравнение
Трейси умеет считать и сравнивать значения.
Математические операторы
| Дополнение | + |
| Вычитание | – |
| Умножение | * |
| Отдел | / |
| Модуль упругости | % |
| Показатель | ** |
Модуль дает вам остаток после деления.
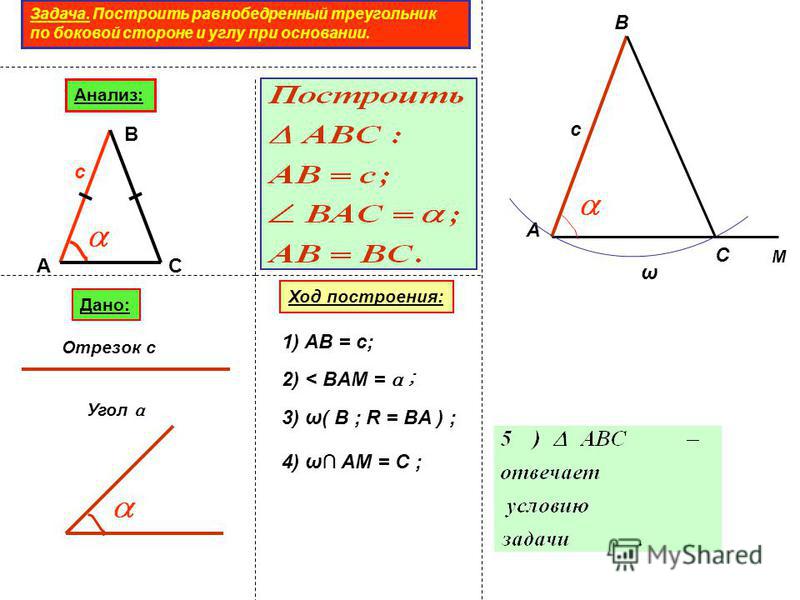
10% 2 равно 0, потому что 10/2 = 5 без остатка.
10% 3 равно 1, потому что 10/3 = 3 с остатком 1.
Сравнение значений
| Равно | == |
| Не равно | ! = |
| Больше | > |
| Больше или равно | > = |
| Менее | |
| Меньше или равно |
Мы используем комментарии, чтобы оставлять читателям заметки о коде.Комментарии на самом деле они не управляются Python, они просто помогают нам читать код.
Мы можем делать многострочные комментарии с "" " и однострочные комментарии с #
"" " Многострочный комментарий описывает ваш код кому-то, кто это читает. "" " # Используйте однострочные комментарии, чтобы прояснить код.
Как нарисовать невозможный треугольник
Простое, пошаговое руководство по рисованию невозможного треугольникаНажмите ЗДЕСЬ, чтобы сохранить учебник в Pinterest!
Невозможный треугольник, также называемый треугольником Пенроуза или невозможным треугольником, был впервые нарисован шведским художником по имени Оскар Реутерсвард в 1934 году.
Он использовался в работах психиатра Лайонела Пенроуза, математика Роджера Пенроуза и голландского художника-математика М. Эшера, а также других художников.
Форма была описана как «невозможная в чистом виде».
Невозможный треугольник — это разновидность оптической иллюзии — изображение, которое из-за восприятия глазами и мозгом отличается от реальности.
Невозможные объекты — это оптические иллюзии, в которых двухмерная фигура (что-то плоское, например, рисунок на бумаге) интерпретируется мозгом как трехмерный объект — объект, который на самом деле не может существовать из-за своих физических пропорций.
Присмотритесь к невозможному треугольнику, и вы увидите, что его стороны необычным образом соединяются.
Прокрутите вниз, чтобы загрузить этот учебник в формате PDF.
В то время как невозможные объекты не могут существовать в реальном мире — вот почему их называют невозможными — художники приложили усилия, чтобы приблизить их.
Скульптура под открытым небом, выставленная в Восточном Перте, Австралия, например, при взгляде под определенным углом принимает вид невозможного треугольника.
Однако, если смотреть под другим углом, становится очевидно, что линии «треугольника» на самом деле не соединяются.
Психологи и другие ученые издавна интересовались оптическими иллюзиями.
Леонардо да Винчи, возможно, был первым, кто нарисовал оптическую иллюзию, серию линий, которые, когда вы наклонили бумагу под правильным углом, превратились в глаз.
Исследователи говорят, что оптические иллюзии возникают потому, что когда наш мозг узнает о нашем окружении, он начинает делать предположения.Иногда эти предположения ошибочны, например, когда плоский рисунок выглядит трехмерным, и этот сдвиг может вызвать чувство замешательства.
Хотите нарисовать невозможный треугольник? Это не невозможно. На самом деле, это легко сделать с помощью этого простого пошагового руководства по рисованию.
Все, что вам понадобится, это карандаш, ручка или маркер и лист бумаги.
Вы также можете использовать линейку, чтобы рисовать прямые линии, и мелки, цветные карандаши или краски, чтобы закрасить законченный рисунок.
Если вам понравился этот урок, см. Также следующие руководства по рисованию: Кристалл, Звезда и Снежинка.
Разблокируйте БЕСПЛАТНЫЕ и ПЕЧАТНЫЕ уроки рисования и раскраски! Узнать большеПошаговые инструкции по рисованию невозможного треугольника
Рисование невозможного треугольника — шаг 11. Начните с рисования небольшого равностороннего треугольника, то есть треугольника со сторонами равной длины. Это сформирует отверстие в середине невозможного треугольника.
Рисование невозможного треугольника — шаг 22. Вытяните короткую прямую линию по диагонали от каждой точки треугольника. Эти линии образуют основу трехмерного изображения невозможного треугольника.
Рисование невозможного треугольника — шаг 33. От самой верхней диагональной линии проведите прямую линию, параллельную стороне маленького треугольника. Затем от этой линии проведите еще одну прямую, параллельную нижней части маленького треугольника.
Рисование невозможного треугольника — шаг 44.Нарисуйте прямую горизонтальную линию от самой нижней из исходных диагоналей. Эта линия должна быть параллельна двум другим горизонтальным линиям и на равном расстоянии от них.
Рисование невозможного треугольника — шаг 55. Проведите длинную прямую линию вверх от оставшейся диагональной линии, параллельную стороне маленького треугольника.
Рисование невозможного треугольника — шаг 66. Из самой верхней точки линии, проведенной на предыдущем шаге, проведите длинную прямую линию, параллельную противоположной стороне треугольника.
Рисование невозможного треугольника — шаг 77. От средней горизонтальной линии вытяните длинную прямую линию вверх, параллельно стороне существующего треугольника.
Рисование невозможного треугольника — шаг 88. Осталось только заключить фигуру невозможного треугольника. Начните с закрытия одного из углов короткой прямой линией.
Рисование невозможного треугольника — шаг 99. Используйте короткие прямые линии, чтобы обвести оставшиеся углы невозможного треугольника.
Завершите рисунок «Невозможный треугольник»10. Раскрасьте свой рисунок. Готовы к большему количеству геометрических рисунков? Ознакомьтесь с нашими руководствами по рисованию кристаллов, снежинок и звезд.
Прокрутите вниз, чтобы загрузить этот учебник в формате PDF.



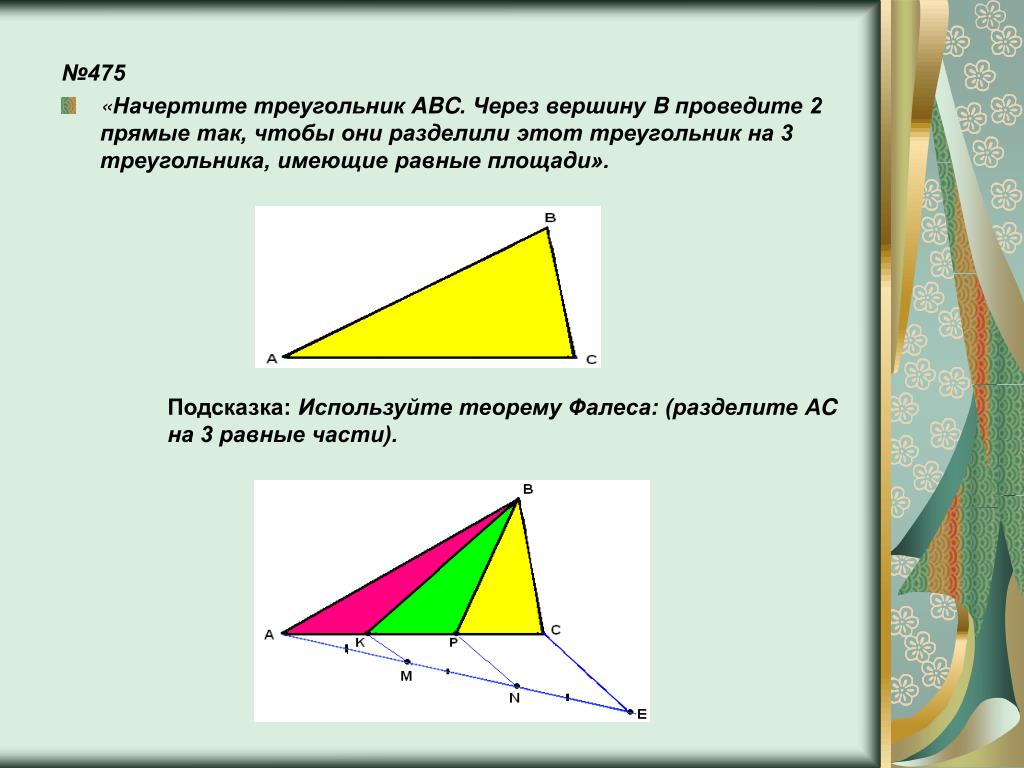
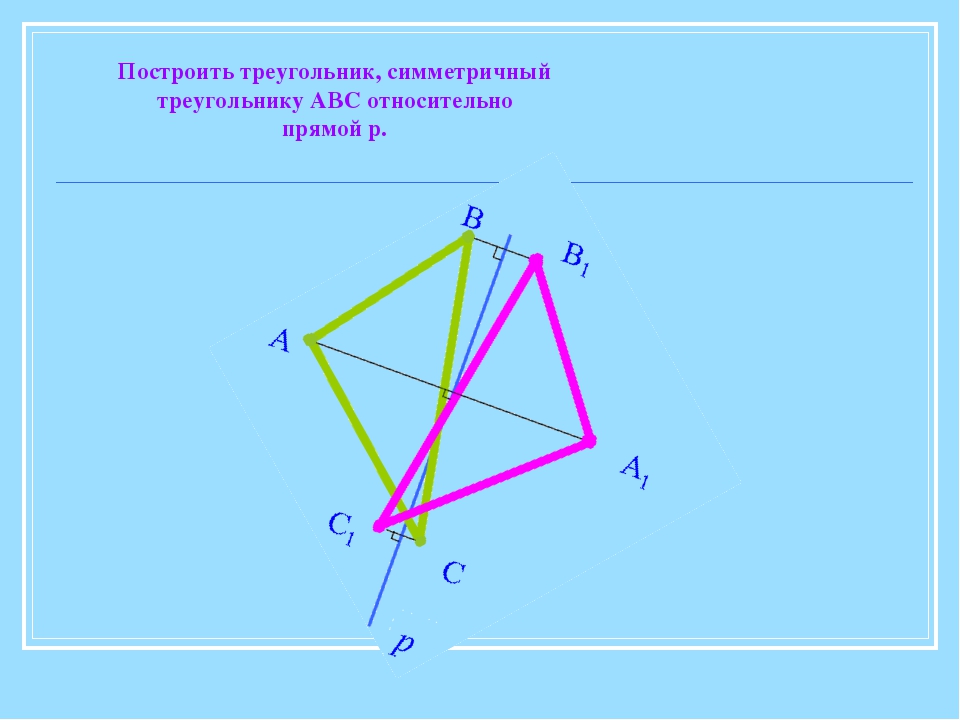 Нарисуйте вторую дугу, чтобы она пересекала первую дугу, которую уже нарисовали. Отметьте точку, в которой пересекаются две дуги. Это вершина (верхняя точка) треугольника. Он должен лежать в точном центре сегмента линии, который нарисовали. Теперь можете сделать две прямые линии, ведущие к этой точке: по одному от каждого конца «нижнего» сегмента линии. Закончите треугольник. Далее с помощью линейки надо нарисовать еще два сегмента прямой линии – это стороны в треугольнике. Подключите каждый конец исходного сегмента линии к точке, в которой пересекаются дуги. Чтобы закончить работу, сотрите дуги, которые нарисовали, так, чтобы остался только треугольник.
Нарисуйте вторую дугу, чтобы она пересекала первую дугу, которую уже нарисовали. Отметьте точку, в которой пересекаются две дуги. Это вершина (верхняя точка) треугольника. Он должен лежать в точном центре сегмента линии, который нарисовали. Теперь можете сделать две прямые линии, ведущие к этой точке: по одному от каждого конца «нижнего» сегмента линии. Закончите треугольник. Далее с помощью линейки надо нарисовать еще два сегмента прямой линии – это стороны в треугольнике. Подключите каждый конец исходного сегмента линии к точке, в которой пересекаются дуги. Чтобы закончить работу, сотрите дуги, которые нарисовали, так, чтобы остался только треугольник.