Нарисовать выпуклый пятиугольник: Attention Required! | Cloudflare – Выпуклый, невыпуклый и звездчатый многоугольник

Выпуклый, невыпуклый и звездчатый многоугольник

Плоская фигура, образованная замкнутым рядом прямолинейных отрезков, называется многоугольником. На рис.1 изображен шестиугольник ABCDEF. Точки А, В, С, D, Е, F — вершины многоугольника; углы при них (углы многоугольника) обозначаются ∠A, ∠В, ∠С, …, ∠F. Отрезки: AC, AD, BE и т.д. — диагонали, АВ; ВС, CD и т. д. — стороны многоугольника; сумма длин сторон АВ + ВС + CD + … + FA называется периметром и обозначается р, а иногда 2р (тогда р — полупериметр).

рис.1

В элементарной геометрии рассматриваются только простые многоугольники, т. е. такие, контур которых не имеет самопересечений.

Многоугольники, контур которых имеет самопересечения, называются звездчатыми многоугольниками

. На рис.2 изображен звездчатый многоугольник ABCDE.

рис.2

Если все диагонали многоугольника лежат внутри него, многоугольник называется выпуклым.

Шестиугольник на рис.1 выпуклый; пятиугольник на рис.3 невыпуклый (диагональ ЕС лежит вне многоугольника).

рис.3

Сумма внутренних углов во всяком выпуклом многоугольнике равна 180° (n-2), где n — число сторон многоугольника*.

* В учебниках геометрии это свойство высказывается обычно только для выпуклых многоугольников. Но оно справедливо для всех простых многоугольников. Но оно справедливо для всех простых многоугольников. Нужно заметить, что в невыпуклом многоугольнике один или несколько внутренних углов превышают 180°. Так, в невыпуклом пятиугольнике, изображенном на рис.3, два угла прямые, два угла имеют по 45°, а один содержит 270°. Суммаа углов составляет 180° (5-2)=540°.

Выпуклый многоугольник — Википедия

Материал из Википедии — свободной энциклопедии

Выпуклым многоугольником называется многоугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.

Существует множество эквивалентных определений:

• многоугольник является выпуклым, если часть плоскости, им ограниченная ( плоский многоугольник) является выпуклым множеством;
• многоугольник будет выпуклым, если для любых двух точек внутри него соединяющий их отрезок полностью лежит в нём;
• многоугольник, для которого продолжения сторон не пересекают других его сторон;
• многоугольник без самопересечений, каждый внутренний угол которого не более 180°;
• многоугольник, все диагонали которого полностью лежат внутри него;
• выпуклая оболочка конечного числа точек на плоскости;
• ограниченное множество, являющееся пересечением конечного числа замкнутых полуплоскостей.

• Пусть {(Xi,Yi)},i=1,2,…,n{\displaystyle \{(X_{i},Y_{i})\},i=1,2,…,n} последовательность координат соседних друг другу вершин n{\displaystyle n}-угольника без самопересечений. Тогда его площадь вычисляется по формуле:

S=12|∑i=1n(Xi+Xi+1)(Yi−Yi+1)|{\displaystyle S={\frac {1}{2}}\left|\sum \limits _{i=1}^{n}(X_{i}+X_{i+1})(Y_{i}-Y_{i+1})\right|}, где (Xn+1,Yn+1)=(X1,Y1){\displaystyle (X_{n+1},Y_{n+1})=(X_{1},Y_{1})}.

Правильный пятиугольник | Формулы и расчеты онлайн

Правильный пятиугольник — это такой пятиугольник у которого все пять сторон равны и его пять углов равны.

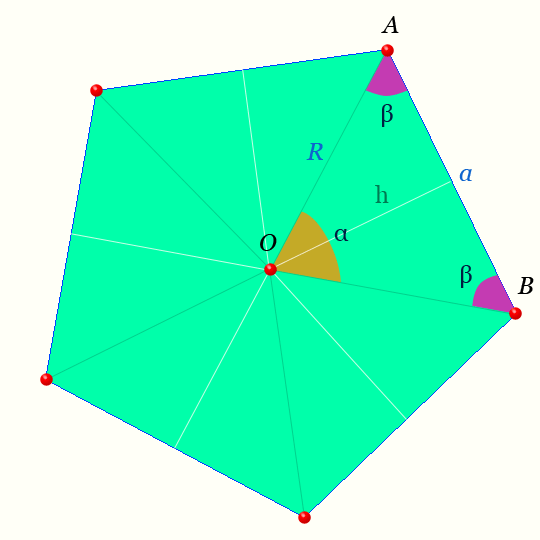
Правильный пятиугольник

Центр правильного пятиугольника — на рисунке точка O равноудалена от вершин.

Светлая линия обозначающая высоту треугольника AOB : h называется — апофемой.

Отрезки OA, OB — радиусы правильного пятиугольника.

Обозначения на рисунке для правильного пятиугольника

n=5	число сторон и вершин правильного пятиугольника,	шт
α	центральный угол правильного пятиугольника,	радианы, °
β	половина внутреннего угла правильного пятиугольника,	радианы, °
γ	внутренний угол правильного пятиугольника,	радианы, °
a	сторона правильного пятиугольника,	м
R	радиусы правильного пятиугольника,	м
p	полупериметр правильного пятиугольника,	м
L	периметр правильного пятиугольника,	м
h	апофемы правильного пятиугольника,	м

Основные формулы для правильного пятиугольника

Периметр правильного пятиугольника

\[ L = 5a \]

Полупериметр правильного пятиугольника

\[ p = \frac{5}{2}a \]

Центральный угол правильного пятиугольника в радианах

\[ α = \frac{2}{5}π \]

Центральный угол правильного пятиугольника в градусах

\[ α = \frac{360°}{5} = 72° \]

Половина внутреннего угла правильного пятиугольника в радианах

\[ β = \frac{3}{10}π \]

Половина внутреннего угла правильного пятиугольника в градусах

\[ β = \frac{3}{10}180° = 54° \]

Внутренний угол правильного пятиугольника в радианах

\[ γ = 2β = \frac{3}{5}π \]

Внутренний угол правильного пятиугольника в градусах

\[ γ = \frac{3}{5}180° = 108° \]

Площадь правильного пятиугольника

\[ S = ph = \frac{5}{2}ha \]

Или учитывая формулу Площади правильного пятиугольника получим

\[ S = \frac{5}{2} · a · \sqrt[-1.0]{(\frac{a}{2 sin(π/5)})^2-\frac{a^2}{4}} \]

Отсюда получим апофему правильного пятиугольника

\[ h = \sqrt[-1.0]{(\frac{a}{2 sin(π/5)})^2-\frac{a^2}{4}} \]

В помощь студенту

Правильный пятиугольник	стр. 268

Открыт новый вид пятиугольников, покрывающих плоскость / Habr

В мире математики сенсация. Открыт новый вид пятиугольников, которые покрывают плоскость без разрывов и без перекрытий.

Это всего 15-й вид таких пятиугольников и первый, открытый за последние 30 лет.

Плоскость покрывается треугольниками и четырехугольниками любой формы, а вот с пятиугольниками все гораздо сложнее и интереснее. Правильные пятиугольники не могут покрыть плоскость, но некоторые неправильные пятиугольники могут. Поиск таких фигур уже сто лет является одной из самых интересных математических задач. Квест начался в 1918 году, когда математик Карл Рейнхард открыл пять первых подходящих фигур.

Долгое время считалось, что Рейнхард рассчитал все возможные формулы и больше таких пятиугольников не существует, но в 1968 году математик Р.Б.Кершнер (R. B. Kershner) нашел еще три, а Ричард Джеймс (Richard James) в 1975 году довел их число до девяти. В том же году 50-летняя американская домохозяйка и любительница математики Марджори Райс (Marjorie Rice) разработала собственный метод нотации и в течение нескольких лет открыла еще четыре пятиугольника. Наконец, в 1985 году Рольф Штайн довел число фигур до четырнадцати.

Пятиугольники остаются единственной фигурой, в отношении которой сохраняется неопределенность и загадка. В 1963 году было доказано, что существует всего три вида шестиугольников, покрывающих плоскость. Среди выпуклых семи-, восьми- и так далее -угольников таких нет. А вот с «пентагонами» пока не все ясно до конца.

До сегодняшнего дня было известно всего 14 видов таких пятиугольников. Они изображены на иллюстрации. Формулы для каждого из них приведены по ссылке.

В течение 30 лет никто не мог найти ничего нового, и вот наконец-то долгожданное открытие! Его сделала группа ученых из Вашингтонского университета: Кейси Манн (Casey Mann), Дженнифер Маклауд (Jennifer McLoud) и Дэвид вон Деро (David Von Derau). Вот как выглядит маленький красавчик.

«Мы открыли фигуру с помощью компьютерного перебора большого, но ограниченного количества вариантов, — говорит Кейси Манн. — Конечно, мы очень взволнованы и немного удивлены, что удалось открыть новый вид пятиугольника».

Открытие кажется чисто абстрактным, но на самом деле оно может найти практическое применение. Например, в производстве отделочной плитки.

Поиск новых пятиугольников, покрывающих плоскость, наверняка продолжится.

Пятиугольник — Википедия

Материал из Википедии — свободной энциклопедии

Пятиугольник — многоугольник с пятью углами. Также пятиугольником называют всякий предмет такой формы.

Площадь пятиугольника без самопересечений, заданного координатами вершин, определяется по общей для многоугольников формуле.

Выпуклым пятиугольником называется пятиугольник, такой, что все его точки лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.

Сумма внутренних углов выпуклого пятиугольника равна 540°.

∑i=15αi=(5−2)⋅180∘=3⋅180∘=540∘{\displaystyle \sum _{i=1}^{5}\alpha _{i}=(5-2)\cdot 180^{\circ }=3\cdot 180^{\circ }=540^{\circ }}

Любые 9 точек в общем положении содержат вершины выпуклого пятиугольника, и существует множество из 8 точек в общем положении, в котором нет выпуклого пятиугольника^[1]. Доказано также, что любые 10 точек на плоскости в общем положении содержат выпуклый пустой пятиугольник, и существует множество из 9 точек в общем положении, в котором нет выпуклого пустого пятиугольника^[2].

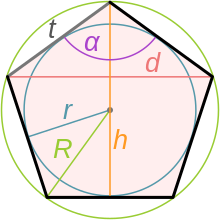
Пентагоном или правильным пятиугольником называется пятиугольник, у которого все стороны и углы равны. Если провести в пентагоне диагонали, то он разобьётся на^[3]:

• меньший пентагон (образуеся точками пересечения диагоналей) — в центре
• Вокруг меньшего пентагона — пять равнобедренных треугольников двух видов (с отношением бедра к основанию, равным золотой пропорции):
  • 1) имеют острые углы в 36° при вершине и острые углы в 72° при основании
  • 2) имеют тупой угол в 108° при вершине и острые углы в 36° при основании

При соединении двух первых и двух вторых треугольников их основаниями получатся два «золотых» ромба (первый имеет острый угол в 36° и тупой угол в 144°). Роджер Пенроуз использовал «золотые» ромбы для конструирования «золотого» паркета (мозаики Пенроуза).

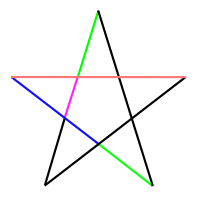
Многоугольник, у которого все стороны и углы равны, а вершины совпадают с вершинами правильного многоугольника называется звёздчатым. Помимо правильного существует ещё один звёздчатый пятиугольник — пентаграмма.

Пентаграмма, как полагал Пифагор, представляет собой математическое совершенство, поскольку демонстрирует золотое сечение (φ = (1+√5)/2 = 1,618…). Если разделить длину любого цветного отрезка на длину самого длинного из оставшихся меньших отрезков, то будет получено золотое сечение φ.

φ=redblue=bluegreen=greenmagenta{\displaystyle \varphi ={\frac {\mathrm {\color {red}red} }{\mathrm {\color {Blue}blue} }}={\frac {\mathrm {\color {Blue}blue} }{\mathrm {\color {Green}green} }}={\frac {\mathrm {\color {Green}green} }{\mathrm {\color {Magenta}magenta} }}}

1. ↑ Kalbfleisch, J.D.; Kalbfleisch, J.G. & Stanton, R.G. (1970), «A combinatorial problem on convex regions», Proc. Louisiana Conf. Combinatorics, Graph Theory and Computing, vol. 1, Congressus Numerantium, Baton Rouge, La.: Louisiana State Univ., с. 180–188 
2. ↑ Harborth, Heiko (1978), «Konvexe Fünfecke in ebenen Punktmengen», Elem. Math. Т. 33 (5): 116–118 
3. ↑ Плитки Пенроуза

16. Многоугольники | учебник для 7 класса «ГЕОМЕТРИЯ»

16. Многоугольники

---

Всякая простая замкнутая ломаная разбивает плоскость на две области — внутреннюю и внешнюю. На рисунке 16.1 внутренние обла­сти закрашены.

Фигура, образованная простой замкнутой ломаной и ограни­ченной ею внутренней областью, называется многоугольникам. Вер­шины ломаной сторонами, — углами многоугольник а. Точки многоугольника, не при­надлежащие его сторонам, называются внутренними.

Периметром многоугольника называется сумма длин всех его сторон.

Многоугольники подразделяются на треугольники — много­угольники с тремя углами (рис. 16.1, а), четырёхугольники — много­угольники с четырьмя углами (рис. 16.1, б) и т. д. Многоугольник, у которого п углов называется п-угольником.

Многоугольник называется правильным, если у него все сторо­ны равны и все углы равны (рис. 16.2).

Правильный четырёхугольник называется также квадратом.

Прямоугольникам называется четырёхугольник, у которого все углы прямые.

Многоугольник называется выпуклым, если вместе с любыми двумя своими точками он содержит и соединяющий их отрезок (рис. 16.3).

Любой треугольник выпуклый. Среди многоугольников с чис­лом углов, большим трёх, могут быть выпуклые (рис. 16.4, а) и невы­пуклые (рис. 16.4, б).

 

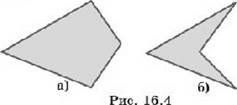
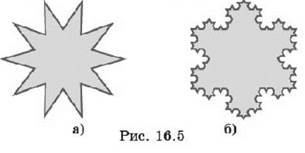
Многоугольники могут иметь и более сложную формы. Приме­ры таких многоугольников показаны на рисунке 16.5.

Диагональю многоугольника называется отрезок, соединяю­щий его несоседние вершины (рис. 16.6).

Ясно, что выпуклый многоугольник содержит все свои диагона­ли. Невыпуклый многоугольник может не содержать некоторые свои диагонали (рис. 16.6, б).

Вопросы

1.        На сколько частей разбивает плоскость простая замкнутая ломаная?

2.        Какая фигура называется многоугольником? Что называется:

а)    вершинами; б) сторонами; в) углами многоугольника?

3.        Какие точки многоугольника называются внутренними?

4.        Что называется периметром многоугольника?

5.        Какой многоугольник называется «-угольником?

6.        Какой многоугольник называется: а) правильным; 6) выпук­лым?

7.        Что называется диагональю многоугольника?

8.        Какой многоугольник содержит все свои диагонали?

Задачи

1.      Проверьте, что линия, изображённая на рисунке 16.7, является простой замкнутой ломаной. Выясните, какая из данных точек лежит:

а)    внутри; 6) вне этой ломаной.

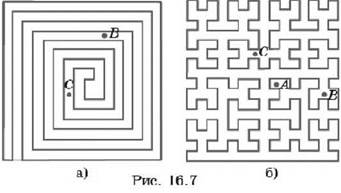
2.              Укажите, какие из представленных на рисунке 16.8 фигур являются многоугольниками, а какие нет.

3. Укажите, какие из представленных на рисунке 16.9 фигур яв­ляются: а) выпуклыми многоугольниками; б) невыпуклыми много­угольниками.

4.        Нарисуйте выпуклые и невыпуклые: а) четырёхугольник;

б)    пятиугольник; в) шестиугольник. Используя линейку, найдите пе­риметры этих многоугольников.

5.        Нарисуйте правильные треугольник, четырёхугольник, пяти­угольник и шестиугольник. Проверьте правильность нарисованных многоугольников с помощью линейки и транспортира.

6.        Являются ли многоугольники, изображенные на рисунке 16.10,      правильными?

7.        На сколько треугольников делится выпуклый: а) четырёх­угольник; 6) пятиугольник; в) шестиугольник своими диагоналями, проведёнными из одной вершины?

8. Сколько всего диагоналей имеет:       а)  четырёхугольник; б)    пятиугольник; в) шестиугольник; г)* n-угольник?

9.        Может ли многоугольник иметь: а) одну диагональ; б) три диагонали; в) восемь диагоналей; г) десять диагоналей; д) двадцать диагоналей?

10. Существует ли многоугольник:  а) число диагоналей которого равно числу его сторон; б) число диагоналей которого меньше числа его сторон; в) число диагоналей которого больше числа его сторон?

11.    Выпуклый многоугольник имеет 14 диагоналей. Сколько у него сторон?

12*. На клетчатой бумаге изобразите какой-нибудь четырёх­угольник, вершинами которого являются точки АД С и D (рис. 16.11). Сколько таких четырёхугольников?

13.             Изобразите два треугольника так, чтобы их общей частью был: а) треугольник; б) четырёхугольник; в) пятиугольник; г) шести­угольник.

Восемнадцатиугольник — Википедия

Материал из Википедии — свободной энциклопедии

Восемнадцатиугольник — это многоугольник с восемнадцатью сторонами^[1].

Правильный восемнадцатиугольник имеет символ Шлефли {18} и может быть построен как квазирегулярный усечённый девятиугольник, t{9}, в котором перемежаются два типа сторон.

Построение[править | править код]

Имея 18 = 2 × 3² сторон, правильный восемнадцатиугольник не может быть построен с помощью циркуля и линейки^[2]. Однако его можно построить с помощью невсиса, или трисекции угла с использованием томагавка.

Точное построение восемнадцатиугольника, основанное на трисекции угла 120° с помощью томагавка. Анимация длится 1м 34с.

Следующее приближённое построение очень близко к построению девятиугольника, поскольку восемнадцатиугольник может быть построен путём усечения девятиугольника. Построение возможно сделать с помощью только циркуля и линейки.

Уменьшаем угол AMC (60°) с помощью четырёх делений угла пополам и строим треть дуги MON с помощью приближённого деления угла между w3 и w4. Для этого проводим прямую через точки O и N, на этой прямой откладываем отрезок OP, равный ON, и строим на полученном отрезке точку Q, так что длина OR равна трети ON. Теперь проводим окружность с центром в точке Q и находим пересечение этой окружности с дугой NO, получаем точку R. Проводим прямую через точку R и центр окружности M. Эта прямая отсекает от исходной окружности дугу, примерно равную 1/18 полной длины окружности. ∠AMR{\displaystyle \scriptstyle \angle {}AMR} = 19,999999994755615…° 360° ÷ 18 = 20° ∠AMR{\displaystyle \scriptstyle \angle {}AMR} — 20° = -5,244…E-9° Пример, иллюстрирующий точность построения: Если взять окружность с радиусом r = 100000 км, абсолютная ошибка длины стороны будет примерно -9 мм. См. также Построение девятиугольника (на немецком) В построении, приведённом на этом сайте, угол ∠{\displaystyle \scriptstyle \angle {}} JMR равен углу ∠{\displaystyle \scriptstyle \angle {}} AMR в приведённом построении восемнадцатиугольника.

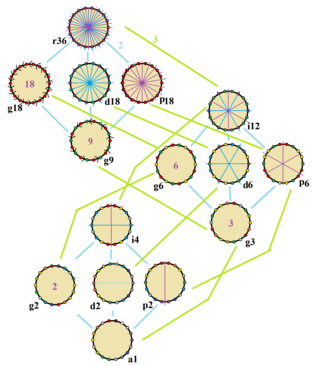Симметрии правильных восемнадцатиугольников. Вершины окрашены согласно их симметриям. Синие зеркала проведены через вершины, а фиолетовые — через середины сторон. Порядок группы вращений указан в центре фигуры.

Правильный восемнадцатиугольник имеет симметрию Dih₁₈ порядка 36. Имеется 5 типов подгрупп диэдральной симметрии: Dih₉, (Dih₆, Dih₃) и (Dih₂, Dih₁), а также 6 циклических групп симметрии: (Z₁₈, Z₉), (Z₆, Z₃) и (Z₂, Z₁).

Справа на рисунке можно видеть 15 симметрий восемнадцатиугольника. Конвей использовал для обозначения симметрий буквы вместе с порядком группы^[3]. Полная симметрия правильной фигуры будет равна r36, а отсутствие симметрии отмечается как a1. Диэдральные симметрии делятся по тому, проходят они через вершины (используется буква

d, от «diagonal») или через середины сторон (используется буква p, от «perpendicular»). Если же оси симметрии проходит через вершины и середины сторон, используется буква i. Циклические симметрии помечаются буквой g (от «gyration»).

Каждая подгруппа симметрии допускает одну или более степеней свободы для неправильных форм. Только подгруппа g18 не даёт свободы, но стороны многоугольника могут рассматриваться как имеющие направление.

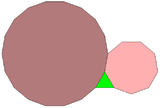
Правильный треугольник, девятиугольник и восемнадцатиугольник могут полностью окружить точку на плоскости, являясь одной из 17 комбинаций правильных многоугольников с таким свойством^[4]. Однако эта комбинация не может быть использована для архимедова замощения плоскости — треугольник и девятиугольник имеют нечётное число сторон, ни одна из этих фигур не может быть окружена чередующимися другими двумя типами многоугольников.

Правильные восемнадцатиугольники могут замощать плоскость, оставляя вогнутые шестиугольные бреши. Другое замощение использует девятиугольники и невыпуклые восьмиугольники. Первая мозаика связана с усечённой шестиугольной мозаикой^[en], а вторая — с усечённой тришестиугольной мозаикой^[en].

Звёздчатые 18-угольники имеют символы {18/n}. Существует два правильных звёздчатых многоугольника: {18/5} и {18/7}. Они используют те же самые вершины, но соединяют каждую пятую или седьмую вершину. Имеются также составные восемнадцатиугольники: {18/2} эквивалентен 2{9} (двум девятиугольникам), {18/3} эквивалентен 3{6} (трём шестиугольникам), {18/4} и {18/8} эквивалентны 2{9/2} и 2{9/4} (двум эннеаграммам), {18/6} эквивалентен 6{3} (6 равносторонним треугольникам), и, наконец, {18/9} эквивалентен 9{2} (девять двуугольников).

Более глубокие усечения правильного многоугольника и правильной эннеаграммы дают равноугольные (вершинно-транзитивные) промежуточные восемнадцатиугольники с находящимися на равном расстоянии вершинами и двумя длинами сторон. Другие усечения дают двойное покрытие: t{9/8}={18/8}=2{9/4}, t{9/4}={18/4}=2{9/2}, t{9/2}={18/2}=2{9} ^[5].

Многоугольники Петри[править | править код]

Правильный восемнадцатиугольник является многоугольником Петри для ряда политопов, что показано в косоортогональных проекциях на плоскость Коксетера^[en]:

1. ↑ Adams, 1907, с. 528.
2. ↑ Conway, 2010, с. 31.
3. ↑ Conway, Burgiel, Goodman-Strauss, 2008, с. 275-278.
4. ↑ Dallas, 1855, с. 134.
5. ↑ Grünbaum, 1994, с. 35-48.

• Henry Adams. Cassell’s Engineer’s Handbook: Comprising Facts and Formulæ, Principles and Practice, in All Branches of Engineering. — D. McKay, 1907. — С. 528.
• John B. Conway. Mathematical Connections: A Capstone Course. — American Mathematical Society, 2010. — С. 31. — ISBN 9780821849798.
• L. Christine Kinsey, Teresa E. Moore. Symmetry, Shape, and Surfaces: An Introduction to Mathematics Through Geometry. — Springer, 2002. — С. 86. — ISBN 9781930190092.
• John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss. Chapter 20, Generalized Schaefli symbols, Types of symmetry of a polygon // The Symmetries of Things. — Wellesley, MA: A K Peters, Ltd., 2008. — ISBN 978-1-56881-220-5.
• Branko Grünbaum. The Lighter Side of Mathematics: Proceedings of the Eugène Strens Memorial Conference on Recreational Mathematics and its History / Richard K.Guy, Robert E. Woodrow. — The Mathematical Association of America, 1994. — (MAA Spectrum). — ISBN 0-88385-516-X.
• Elmslie William Dallas. The Elements of Plane Practical Geometry, Etc. — John W. Parker & Son, 1855.

Многоугольники
Звёздчатые многоугольники
Паркеты на плоскости
Правильные многогранники и сферические паркеты
Многогранники Кеплера — Пуансо
Соты
Четырёхмерные многогранники	{3,3,3} {4,3,3} {3,3,4} {3,4,3} {5,3,3} {3,3,5}