Построение и решение графиков Функций
Понятие функции
Функция — это зависимость y от x, где x является переменной или аргументом функции, а y — зависимой переменной или значением функции.
Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:
- Табличный способ — помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
- Графический способ — наглядно.
- Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.
- Словесный способ.
Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.
Например, для функции вида область определения выглядит так
- х ≠ 0, потому что на ноль делить нельзя.

Область значений — множество у, то есть это значения, которые может принимать функция.
Например, естественная область значений функции y = x² — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.
Понятие графика функции
Графиком функции y = f(x) называется множество точек (x; y), координаты которых связаны соотношением y = f(x). Само равенство y = f(x) называется уравнением данного графика.
График функции — это множество точек (x; y), где x — это
Проще говоря, график функции показывает множество всех точек, координаты которых можно найти, просто подставив в функцию любые числа вместо x.
Для примера возьмём самую простую функцию, в которой аргумент равен значению функции, то есть y = x.
В этом случае нам не придётся вычислять для каждого аргумента значение функции, так как они равны, поэтому у всех точек нашего графика абсцисса будет равна ординате.
Отметим любые три точки на координатной плоскости, например: L (-2; -2), M (0; 0) и N (1; 1).
Если мы последовательно от наименьшего значения аргумента к большему соединим отмеченные точки, то у нас получится прямая линия. Значит графиком функции y = x является прямая. На графике это выглядит так:
Надпись на чертеже y = x — это уравнение графика. Ставить надпись с уравнением на чертеже удобно, чтобы не запутаться в решении задач.
Важно отметить, что прямая линия бесконечна в обе стороны. Хоть мы и называем часть прямой графиком функции, на самом деле на чертеже изображена только малая часть графика.
Не обязательно делать чертеж на целый тетрадный лист, можно выбрать удобный для вас масштаб, который отразит суть задания.
Исследование функции
Важные точки графика функции y = f(x):
- стационарные и критические точки;
- точки экстремума;
- нули функции;
- точки разрыва функции.

Стационарные точки — точки, в которых производная функции f(x) равна нулю.
Критические точки — точки, в которых производная функции f(x) равна нулю либо не существует. Стационарные точки являются подмножеством множества критических точек.
Экстремум в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется
Нули функции — это значения аргумента, при которых функция равна нулю.
Асимптота — прямая, которая обладает таким свойством, что расстояние от точки графика функции до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат. По способам их отыскания выделяют три вида асимптот: вертикальные, горизонтальные, наклонные.
Функция непрерывна в точке k, если предел функции в данной точке равен значению функции в этой точке:
Если функция f(x) не является непрерывной в точке x = a, то говорят, что f(x) имеет разрыв в этой точке.
Если нам нужно построить график незнакомой функции, когда заранее невозможно представить вид графика, полезно применять схему исследования свойств функции. Она поможет составить представление о графике и приступить к построению по точкам.
Схема построения графика функции:
- Найти область определения функции.
- Найти область допустимых значений функции.
- Проверить не является ли функция четной или нечетной.
- Проверить не является ли функция периодической.
- Найти нули функции.
- Найти промежутки знакопостоянства функции, то есть промежутки, на которых она строго положительна или строго отрицательна.
- Найти асимптоты графика функции.

- Найти производную функции.
- Найти критические точки в промежутках возрастания и убывания функции.
- На основании проведенного исследования построить график функции.
Построение графика функции
Чтобы понять, как строить графики функций, потренируемся на примерах.
Задача 1. Построим график функции
Как решаем:
Упростим формулу функции:
Задача 2. Построим график функции
Как решаем:
Выделим в формуле функции целую часть:
График функции — гипербола, сдвинутая на 3 вправо по x и на 2 вверх по y и растянутая в 10 раз по сравнению с графиком функции
Выделение целой части — полезный прием, который применяется в решении неравенств, построении графиков и оценке целых величин.
Задача 3. По виду графика определить знаки коэффициентов общего вида функции y = ax2 + bx + c.
Как решаем:
Вспомним, как параметры a, b и c определяют положение параболы.
Ветви вниз, следовательно, a < 0.
Точка пересечения с осью Oy — c = 0.
Координата вершины
Ветви вверх, следовательно, a > 0.
Точка пересечения с осью Oy — c = 0.
Координата вершины , т.к. неизвестное число при делении на положительное дает отрицательный результат, то это число отрицательное, следовательно, b > 0.
Ветви вниз, следовательно, a < 0.
Точка пересечения с осью Oy — c > 0.
Координата вершины , т.к. неизвестное число при делении на отрицательное дает в результате положительное, то это число отрицательное, следовательно, b < 0.
Задача 4. Построить графики функций:
а) y = 3x — 1
б) y = -x + 2
в) y = 2x
г) y = -1
Как решаем:
Воспользуемся методом построения линейных функций «по точкам».
а) y = 3x — 1
Как видим, k = 3 > 0 и угол наклона к оси Ox острый, b = -1 — смещение по оси Oy.
б) y = -x + 2
k = -1 > 0 и b = 2 можно сделать аналогичные выводы, как и в первом пункте.
в) y = 2x
k = 2 > 0 — угол наклона к оси Ox острый, B = 0 — график проходит через начало координат.
г) y = -1
k = 0 — константная функция, прямая проходит через точку b = -1 и параллельно оси Ox.
Задача 5. Построить график функции
Как решаем:
Это дробно-рациональная функция. Область определения функции D(y): x ≠ 4; x ≠ 0.
Нули функции: 3, 2, 6.
Промежутки знакопостоянства функции определим с помощью метода интервалов.
Вертикальные асимптоты: x = 0, x = 4.
Если x стремится к бесконечности, то у стремится к 1. Значит, y = 1 — горизонтальная асимптота.
Вот так выглядит график:
Задача 6. Построить графики функций:
а) y = x² + 1
б)
в) y = (x — 1)² + 2
г)
д)
Как решаем:
Когда сложная функция получена из простейшей через несколько преобразований, то преобразования графиков можно выполнить в порядке арифметических действий с аргументом.
а)
Преобразование в одно действие типа f(x) + a.
y = x²
Сдвигаем график вверх на 1:
y = x² + 1
б)
Преобразование в одно действие типа f(x — a).
y = √x
Сдвигаем график вправо на 1:
y = √x — 1
в) y = (x — 1)² + 2
В этом примере два преобразования, выполним их в порядке действий: сначала действия в скобках f(x — a), затем сложение f(x) + a.
y = x²
Сдвигаем график вправо на 1:
y = (x — 1)²
Сдвигаем график вверх на 2:
y = (x — 1)² + 2
г)
Преобразование в одно действие типа
y = cos(x)
Растягиваем график в 2 раза от оси ординат вдоль оси абсцисс:
д)
Мы видим три преобразования вида f(ax), f (x + a), -f(x).
Чтобы выполнить преобразования, посмотрим на порядок действий: сначала умножаем, затем складываем, а уже потом меняем знак. Чтобы применить умножение ко всему аргументу модуля в целом, вынесем двойку за скобки в модуле.
Сжимаем график в два раза вдоль оси абсцисс:
Сдвигаем график влево на 1/2 вдоль оси абсцисс:
Отражаем график симметрично относительно оси абсцисс:
Как построить график функции
В этой статье разобран самый простой метод получения графика функции.
Суть метода: найти несколько точек принадлежащих графику, расставить их на координатной плоскости и соединить. Этот способ не лучший (лучший – построение графиков с помощью элементарных преобразований), но если вы все забыли или ничего не учили, то знайте, что у вас всегда есть план Б – возможность построить график по точкам.
Итак, алгоритм по шагам:
1. Представьте, как выглядит ваш график.
Строить гораздо легче, если вы понимаете, что примерно должны получить в итоге. Поэтому сначала посмотрите на функцию и представьте, как примерно должен выглядеть ее график. Все виды графиков элементарных функций вы можете найти здесь. Этот пункт желательный, но не обязательный.
Все виды графиков элементарных функций вы можете найти здесь. Этот пункт желательный, но не обязательный.
Пример: Построить график функции \(y=-\)\(\frac{2}{x}\)
Данная функция — гипербола с ветвями расположенными во второй и четвертой четверти. Её график выглядит как-то так:
2. Составьте таблицу точек, принадлежащих графику:
Теперь подставим разные значения «иксов» в функцию, и для каждого икса посчитаем значение «игрека».
Пример: \(y=-\)\(\frac{2}{x}\)
|
при \(x=-1\) |
\(y=-\)\(\frac{2}{-1}\)\(=2\) |
|
|
при \(x=0\) |
\(y\) — не существует (делить на ноль нельзя) |
|
|
при \(x=1\) |
\(y=-\)\(\frac{2}{1}\)\(=-2\) |
|
|
при \(x=2\) |
\(y=-\)\(\frac{2}{2}\)\(=-1\) |
|
|
при \(x=3\) |
\(y=-\)\(\frac{2}{3}\) |
|
|
при \(x=4\) |
\(y=-\)\(\frac{2}{4}\)\(=-\)\(\frac{1}{2}\) |
Результат вычислений удобно представлять в виде таблицы, примерно такой:
|
\(x\) |
\(-1\) |
\(0\) |
\(1\) |
\(2\) |
\(3\) |
\(4\) |
|
\(y\) |
\(2\) |
\(-\) |
\(-2\) |
\(-1\) |
\(-\)\(\frac{2}{3}\) |
\(-\)\(\frac{1}{2}\) |
Как вы могли догадаться, полученные пары «икс» и «игрек» — это точки, лежащие на нашем графике.
4. Постройте координатную плоскость и отметьте на ней точки из таблицы.
Пример:
5. Если нужно, найдите еще несколько точек и нанесите их на координатную плоскость.
Пример: Чтобы построить график мне не хватает нескольких точек из отрицательной части, а также рядом с осью игрек, поэтому я добавлю столбцы с \(x=-2\), \(x=-4\), \(x=\)\(\frac{1}{2}\) и \(x=-\)\(\frac{1}{2}\)
|
при \(x=-2\) |
\(y=-\)\(\frac{2}{-2}\)\(=1\) |
|
|
при \(x=-4\) |
\(y=-\)\(\frac{2}{-4}\)\(=\)\(\frac{1}{2}\) |
|
|
при \(x=\)\(\frac{1}{2}\) |
\(y=-\)\(\frac{2}{\frac{1}{2}}\)\(=-2:\)\(\frac{1}{2}\)\(=-2 \cdot 2=-4\) |
|
|
при \(x=-\)\(\frac{1}{2}\) |
\(y=-\)\(\frac{2}{-\frac{1}{2}}\)\(=-2:(-\)\(\frac{1}{2}\)\()\)\(=-2 \cdot (-2)=4\) |
|
\(x\) |
\(-1\) |
\(0\) |
\(1\) |
\(2\) |
\(3\) |
\(4\) |
\(-2\) |
\(-4\) |
\(\frac{1}{2}\) |
\(-\)\(\frac{1}{2}\) |
|
\(y\) |
\(2\) |
\(-\) |
\(-2\) |
\(-1\) |
\(-\)\(\frac{2}{3}\) |
\(-\)\(\frac{1}{2}\) |
\(1\) |
\(\frac{1}{2}\) |
\(-4\) |
\(4\) |
6. Постройте график
Постройте график
Теперь аккуратно и плавно соединяем точки.
Готово!
Построение графиков математических функций в OneNote с использованием помощника по преобразованию в математические выражения
Сначала создайте уравнение с помощью рукописного ввода или текста.
На вкладке «Рисовать» напишите или введите уравнение. Используйте инструмент «Лассо», чтобы нарисовать круг вокруг формулы. Затем выберите пункт Математическое выражение. Откроется панель помощника по преобразованию в математические выражения.
В меню Выберите действие в области Математические вычисления выберите пункт Graph двухгодной или Graph двухуголей.
Чтобы изменить граф, созданный помощником по преобразованию в математические выражения, выполните одно из указанных ниже действий (по возможности).
-
Выберите (или нажмите и удерживайте) и перетащите график в любом направлении, чтобы переместить его.
-
Если нужно изменить значения параметров в уравнении, щелкните или коснитесь кнопок увеличительного стекла + и –, чтобы увеличить или уменьшить масштаб.
Примечание: Если вы используете OneNote на сенсорном устройстве, вы также можете настроить граф с помощью пальцев. Используйте один палец, чтобы переместить граф, или два пальца, чтобы изменить масштаб увеличения. В OneNote для Интернета положение графа можно изменить с помощью стрелок, расположенных по сторонам графа.
-
Чтобы восстановить исходное состояние графа, щелкните или коснитесь значка Сброс в форме двойной стрелки.

-
Когда граф приобретет нужный вид, щелкните или коснитесь пункта Вставить на страницу, чтобы поместить его в виде снимка экрана на текущей странице.
Примечание: Чтобы изменить способ измерения графа (градусы, радиан, градианы), щелкните или коснитесь пункта Параметры, когда открыта область «Математическое выражение».
Расширенные функции графики
Другие возможности доступны в зависимости от типа графа.
-
Чтение значений x-y: Чтобы увидеть значения x и y в OneNote для Windows 10, наведите указатель мыши на точку на линии графа.
 Чтобы увидеть значения в OneNote для Интернета, щелкните линию графа.
Чтобы увидеть значения в OneNote для Интернета, щелкните линию графа. -
Управление параметрами Если у вас есть формула с такими параметрами, как ax+b, используйте знаки «плюс» и «минус» под графом, чтобы изменить значения a и b.
-
Основные функции графиков: Помощник по преобразованию в математические выражения рассчитывает интересные сведения о графе (нули, перехваты, минимум, максимум и т. д.). Установите флажки для тех возможностей, которые вы хотите отобразить на графе.
Создание математических формул с помощью рукописного ввода или текста с использованием помощника по преобразованию в математические выражения в OneNote
Решение математических уравнений с использованием помощника по преобразованию в математические выражения в OneNote
Типы задач, поддерживаемые помощником по преобразованию в математические выражения
Создание математического теста для практики
Типы задач, которые можно из графики в двухсмятьных диаграммах
При использовании помощникапо OneNote в формуле вы заметите, что в зависимости от выбранного уравнения изменяется в dropdown Select an action (Выбрать действие) под формулой. С помощью помощника по математическим вычислениям можно построить двухуголовые графики для следующих типов задач.
С помощью помощника по математическим вычислениям можно построить двухуголовые графики для следующих типов задач.
|
Выражения (с переменной) |
|
|
Полиномиальные массивы |
|
|
Формулы |
При работе с уравнениями Graph двухугодными или двухуголными Graph двухугодными. Выберите Graph 2D, чтобы увидеть решение для уравнения.
Выберите Graph обеих сторонах двумеда, чтобы просмотреть график двух функций на противоположной стороне знака равно.
|
|
Системы уравнений |
|
|
Координаты координат |
Для графизации функции в координатах координаты r должны быть выражены как функцияta. |
|
Неравенства |
При работе с Graph двухугодными или двухуголными Graph можно использовать двухуголевую разную сторону. Выберите Graph 2D, чтобы увидеть решение проблемы.
Выберите Graph двухуголовые диаграммы, чтобы просмотреть график двух функций на обеих сторонах знака сравнения.
|
|
Система о-ва |
|
Подробнее
Создание математического теста в Microsoft Forms
Создание математического теста для практики в OneNote с использованием помощника по преобразованию в математические выражения
Решение математических уравнений с помощью помощника по преобразованию в математические выражения в OneNote
Глава 5 Базовая графика | Визуализация и анализ географических данных на языке R
Данный модуль посвящен введению в работу с графическим представлением информации в R. 3\)):
3\)):
Стандартные графики
Графики (точечные и линейные) – базовый и наиболее часто используемый способ визуализации. Универсальная функция plot() позволяет строить графики по координатам \(X\) и \(Y\), которые передаются, соответственно, в первый и второй аргумент. Если переменные \(X\) и \(Y\) не связаны друг с другом явным образом, то такой график называется диаграммой рассеяния.
Диаграммы рассеяния
Диаграмма рассеяния позволяет установить, есть ли зависимость между переменными, а также понять, как объекты дифференцируются по значениям переменных.
par(mar=c(4,4,3,2))
# Диаграмма рассеяния по экспорту и импорту:
plot(sub$МетЭкспорт,
sub$МетИмпорт,
col="red",
xlab="Экспорт, млн. долл. США",
ylab = "Импорт, млн. долл. США",
main = "Экспорт/импорт металлов и изделий из них по субъектам РФ")В данном случае четко выделяется группа субъектов вблизи начала координат, не отличающихся интенсивным экспортом и импортом продукции металлургии, а также очевидно преобладание экспорта над импортом при больших объемах товарооборота.
При построении диаграмм рассеяния важно сохранить одинаковый масштаб по осям \(X\) и \(Y\). Чтобы обеспечить это условие, необходимо использовать параметр asp = 1:
plot(sub$МетЭкспорт,
sub$МетИмпорт,
col="red",
xlab="Экспорт, млн. долл. США",
ylab = "Импорт, млн. долл. США",
main = "Экспорт/импорт металлов и изделий из них по субъектам РФ",
asp = 1)Попробуйте изменить размер окна на вкладке Plots. Вы увидите, что масштаб по осям сохраняется пропорциональным.
Размер и тип значка можно изменить, используя параметры pch = и cex =. Размеры масштабируются параметром cex относительно условной единицы — стандартного размер значка. Сам значок можно выбрать, используя его код в соответствии с нижеприведенным рисунком (на самом деле, вы можете выбирать произвольные символы для визуализации точек):
Типы символов R
plot(sub$МетЭкспорт,
sub$МетИмпорт,
col="red",
xlab="Экспорт, млн. долл. США",
ylab = "Импорт, млн. долл. США",
main = "Экспорт/импорт металлов и изделий из них по субъектам РФ",
asp = 1,
pch = 2,
cex = 0.5)
долл. США",
ylab = "Импорт, млн. долл. США",
main = "Экспорт/импорт металлов и изделий из них по субъектам РФ",
asp = 1,
pch = 2,
cex = 0.5)
plot(sub$МетЭкспорт,
sub$МетИмпорт,
col="red",
xlab="Экспорт, млн. долл. США",
ylab = "Импорт, млн. долл. США",
main = "Экспорт/импорт металлов и изделий из них по субъектам РФ",
asp = 1,
pch = 20,
cex = 1.2)Линейные графики
Линейные графики отражают связь между зависимой и независимой переменной. Существует два способа нанесения линий на график: явное рисование линий поверх уже построенного графика с помощью функции lines(), или создание нового линейного графика с помощью функции plot() с дополнительным параметром type =.
Для иллюстрации принципов работы первого способа откроем еще раз данные по объему сброса загрязненных сточных вод по морям России (млрд куб. м):
м):
tab = read.csv2("data/oxr_vod.csv", encoding = 'UTF-8')
plot(tab$Год, tab$Каспийское, pch=20) # для начала нанесем точки
lines(tab$Год, tab$Каспийское) # теперь нанесем линииПо умолчанию функция plot() рисует именно точки. Однако если точки не нужны, а достаточно только линий, или требуется иной подход к построению графиков, можно задать параметр type =, который принимает следующие значения:
-
"p"for points, -
"l"for lines, -
"b"for both, -
"c"for the lines part alone of “b,” -
"o"for both ‘overplotted,’ -
"h"for ‘histogram’ like (or ‘high-density’) vertical lines, -
"s"for stair steps, -
"S"for other steps, see ‘Details’ below, -
"n"for no plotting.
Попробуем разные методы визуализации:
plot(tab$Год, tab$Карское,pch=20)
plot(tab$Год, tab$Каспийское, type="p")
plot(tab$Год, tab$Каспийское, type="l")
plot(tab$Год, tab$Каспийское, type="b")
plot(tab$Год, tab$Каспийское, type="c")
plot(tab$Год, tab$Каспийское, type="o")
plot(tab$Год, tab$Каспийское, type="h")
plot(tab$Год, tab$Каспийское, type="s")Толщину и тип линии можно изменить, используя параметры lwd = и lty = соответственно. Работают они аналогично параметрам pch и cex для точечных символов. Типов линий по умолчанию в стандартной библиотеке R не так много, но в сочетании с цветовым кодированием и толщиной их оказывается вполне достаточно:
Работают они аналогично параметрам pch и cex для точечных символов. Типов линий по умолчанию в стандартной библиотеке R не так много, но в сочетании с цветовым кодированием и толщиной их оказывается вполне достаточно:
Попробуем разные варианты представления линий:
plot(tab$Год, tab$Каспийское, type="l", lwd = 2, lty = 1)
plot(tab$Год, tab$Каспийское, type="l", lwd = 3, lty = 2)
plot(tab$Год, tab$Каспийское, type="l", lwd = 1, lty = 3)Совмещение графиков
Часто бывает необходимо совместить на одном графике несколько рядов данных. Для этого можно поступить двумя путями:
Нарисовать один ряд данных c помощью функции
plot(), а затем добавить к нему другие ряды с помощью функцийpoints()иlines().Нарисовать пустой график, а затем добавить к нему все ряды данных с помощью функций
points()иlines().
При совмещении нескольких рядов данных на одном графике в первом же вызове функции
plot()необходимо заложить диапазон значений по осям \(X\) и \(Y\), охватывающий все ряды данных. В противном случае будет учтен только разброс значений первого ряда данных, и остальные ряды могут не поместиться в поле графика.
Вариант №1 реализуется следующим образом:
plot(tab$Год,
tab$Каспийское,
pch=20,
type="o",
ylim = c(0,12),
col="red3")
# Добавим теперь на существующий график новый ряд данных, используя функции points() и lines():
points(tab$Год, tab$Карское, pch=20, col="forestgreen")
lines(tab$Год, tab$Карское, pch=20, col="forestgreen")Обратите внимание на то, что если бы мы вызвали еще одну инструкцию
plot()с новым рядом данных, это привело бы к построению нового графика, а не к добавлению его на существующий.
Теперь рассмотрим второй вариант. Заодно устраним недостаток предыдущего кода, в котором диапазон значений по оси \(Y\) указывался вручную.
Заодно устраним недостаток предыдущего кода, в котором диапазон значений по оси \(Y\) указывался вручную.
xrange = range(tab$Год) # вычислим диапазон по оси X
yrange = range(tab$Каспийское, tab$Карское, tab$Азовское) # вычислим диапазон по оси Y
# Построим пустой график, охватывающий полный диапазон данных, и имеющий все необходимые сопроводительные элементы
plot(xrange,
yrange,
main="Объем сброса загрязненных сточных вод",
xlab="Год",
ylab="млрд.куб.м",
type = "n") # n означает, что ряд данных рисоваться не будет
# Теперь добавим на график ряды данных
points(tab$Год, tab$Каспийское, pch=20, col="red3")
lines(tab$Год, tab$Каспийское, pch=20, col="red3")
points(tab$Год, tab$Карское, pch=20, col="forestgreen")
lines(tab$Год, tab$Карское, pch=20, col="forestgreen")
points(tab$Год, tab$Азовское, pch=20, col="steelblue")
lines(tab$Год, tab$Азовское, pch=20, col="steelblue")Функциональные параметры
Графические параметры при построении графиков на самом деле могут быть не константами, а функцией данных. Например, вы можете сказать, что размер точки при построении диаграммы рассеяния должен быть функцией отношения экспорта к импорту, что усилит наглядность отображения:
plot(okr$МетЭкспорт,
okr$МетИмпорт,
col=rgb(1,0,0,0.5),
xlab="Экспорт, млн. долл. США",
ylab = "Импорт, млн. долл. США",
main = "Экспорт/импорт металлов и изделий из них по ФО РФ (2013 г.)",
asp = 1,
pch = 20,
cex = 2+log(sub$МетИмпорт/sub$МетЭкспорт)) # размер кружка зависит от соотношения импорта и экспортаГистограммы
Гистограммы распределения строятся с помощью функции hist(). Чтобы изменить ширину кармана (столбца) гистограммы, необходимо задать параметр breaks =, а цвет задается в параметре col:
hist(sub$ПродЭкспорт)
# Карманы будут от 0 до 3000 через 100. Заодно добавим цвет:
hist(sub$ПродЭкспорт, breaks = seq(0,3000,100), col="olivedrab3")При построении гистограммы (как и любого другого типа графика) вы можете использовать не весь массив данных, а только его подмножество Например, можно посмотреть гистограмму только для субъектов с объемом экспорта менее 300:
hist(sub$ПродЭкспорт[sub$ПродЭкспорт < 300], col = "olivedrab3", breaks = seq(0, 300, 20))Наконец, вы можете осуществить преобразование ряда данных перед построением гистограммы. Например, взять логарифм, чтобы проверить,похоже ли распределение на логнормальное:
hist(log(sub$ПродЭкспорт), col = "olivedrab3")Столбчатые графики
Столбчатые графики — barplot — отображают вектор числовых данных в виде столбиков. Это простейший вид графика (наряду с dotchart), который используется для сравнения абсолютных величин. Для построения необходимо вызвать функцию barplot() и передать ей столбец таблицы:
# Или даже просто вектор натуральных чисел от -5 до 5:
barplot(-5:5)
# Если у каждого столбика есть название,
# нужно передать вектор названий в аргумент names.arg =
barplot(okr$ХимЭкспорт, names.arg = okr$Регион)
# при наличии длинных подписей удобнее столбчатую диаграмму разместить горизонтально, используя параметр horiz = TRUE.
barplot(okr$ХимЭкспорт, names.arg = okr$Регион, horiz=TRUE)Чтобы развернуть подписи перпендикулярно столбцам, следует использовать параметр las =. Справка__R__говорит нам о том, что этот параметр дает следующее поведение подписей:
- 0: всегда параллельно осям (по умолчанию),
- 1: всегда горизонтально,
- 2: всегда перпендикулярно осям,
- 3: всегда вертикально.
Выберем вариант, при котором подписи всегда горизонтальны:
barplot(okr$ХимЭкспорт, names.arg = okr$Регион, horiz=TRUE, las = 1)В данном случае очень массивные названия федеральных не умещаются в пространство графика. Можно было бы вполне убрать словосочетание “федеральный округ.” Для этого используем уже знакомую нам sub().
names = sub("федеральный округ", "", okr$Регион) # "" - означает пустая строка
barplot(okr$ХимЭкспорт, names.arg = names, horiz = TRUE, las = 1)И снова содержимое не поместилось в поле графика. Проблема в том, что вокруг любого графика резервируются поля ограниченного размера для размещения подписей координат и т.д. Автоматически эти поля не пересчитываются, зарезервировать их — ваша задача.
Наберите в консоли ?par. Откроется список всевозможных графических параметров, которые управляют компоновкой и порядком построения графиков. Эти параметры можно установить, вызвав функцию par(). Все дальнейшие вызовы инструкций построения графиков будут учитывать установленные параметры Пролистайте страницу справки вниз и найдите параметр mar = — он отвечает за установку полей в условных единицах. Есть также параметр mai =, который позволяет установить поля графика в дюймах. Обратите внимание на то, что означают параметры этой функции:
# mar=c(bottom, left, top, right)
# The default is c(5, 4, 4, 2) + 0.1.Поскольку в нашем примере проблемы возникают в левым полем, необходимо увеличить второй параметр.
margins.default = par("mar") # запишем текущее значение, чтобы восстановить его потом
par(mar = c(5, 10, 4, 2)) # увеличим поле left до 10 условных единиц
barplot(okr$ХимЭкспорт, names.arg = names, horiz=TRUE, las = 1)Добавим заголовок с помощью параметра main =, а подпись единиц измерения по оси \(X\) — с помощью параметра xlab =. Поскольку количество параметров функции уже достаточно велико, введем каждый из них с новой строчки, чтобы улучшить читаемость кода:
barplot(okr$ХимЭкспорт,
names.arg = names,
main = "Экспорт продукции химической промышленности",
xlab = "млн долл. США",
horiz = TRUE,
las = 1)
# Чтобы увеличить диапазон оси X, можно использовать параметр xlim = c(min, max):
barplot(okr$ХимЭкспорт,
names.arg = names,
main = "Экспорт продукции химической промышленности",
xlab = "млн долл. США",
horiz = TRUE,
las = 1,
xlim = c(0,12000))Работа с цветом на столбчатых диаграммах рассмотрена ниже в отдельном разделе.
Круговые (секторные) диаграммы
Круговые диаграммы (англ. piechart) строятся с помощью функции pie():
par(mar = c(5, 5, 5, 5)) # установим поля
pie(okr$ХимЭкспорт)
# вместо номеров можно использовать подписи секторов, добавив второй параметр:
pie(okr$ХимЭкспорт, names)
# в каждую метку можно добавить процент данного округа в общей массе. Для этого его нужно сначала посчитать:
percentage = 100 * okr$ХимЭкспорт / sum(okr$ХимЭкспорт)
# и округлить до 1 знака после запятой:
percentage = round(percentage, digits = 1)Можно присоединить проценты к названиям округов, добавив обрамляющие скобки. Чтобы функция paste не добавляя пробелы между присоединяемыми строками, необходимо задать параметр sep = , передав ему пустую строку — ““:
names2=paste(names, " (", percentage, "%)", sep = "")
# Используем для аннотирования круговых секторов:
pie(okr$ХимЭкспорт, names2)
# Добавить заголовок можно также с помощью параметра main =
pie(okr$ХимЭкспорт, names2, main = "Доля федеральных округов в экспорте продукции химической промышленности")Чтобы перенести часть заголовка на вторую строку, вы можете использовать управляющий символ перевода строки \n, вставив его в требуемое место:
pie(okr$ХимЭкспорт, names2, main = "Доля федеральных округов в экспорте \n продукции химической промышленности")Управляющие символы играют большое значение в программировании и используются для управления поведением текстового вывода. Нотация
\nназывается escape-последовательностью. Помимо перевода строки, есть и другие полезные управляющие символы. Кстати, именно из-за того, что escape-последовательности начинаются с обратной косой черты (\), при указании системных путей в функцииsetwd()всегда следует использовать прямую косую черту (/). Например, следующий путь не будет найдет, поскольку он содержит управляющие последовательности\nи\t:C:\data\tables\new.
Наконец, при использовании секторных диаграмм важно уметь менять порядок секторов. По умолчанию сектора откладываются против часовой стрелки начиная с восточного направления. Чтобы сектора откладывались по часовой стрелке с северного направления, следует задать параметр clockwise = TRUE.
pie(okr$ХимЭкспорт,
names2,
main = "Доля федеральных округов в экспорте \n продукции химической промышленности",
clockwise = TRUE)Работа с цветом на круговых диаграммах рассмотрена ниже в отдельном разделе.
Цвет и прозрачность
Цвет — одно из основных графических средств, используемых на графиках и диаграммах, поэтому данная тема рассмотрена более подробно в отдельном разделе. Определить цвет можно различными способами. Во-первых, в R есть палитра предопределенных цветов, которые можно выбирать по их названию).
Список названий цветов можно посмотреть, вызвав функцию colors():
head(colors())
## [1] "white" "aliceblue" "antiquewhite" "antiquewhite1"
## [5] "antiquewhite2" "antiquewhite3"Основной цвет любого графика или диаграмма задается параметром col =. Это цвет (или цвета) с помощью которых будут отображаться данные. Попробуем изменить цвет графика с серого на пастельно-синий:
par(mar = c(5, 10, 4, 2)) # увеличим поле left до 10 условных единиц
barplot(okr$ХимЭкспорт,
names.arg = names,
main = "Экспорт продукции химической промышленности",
xlab = "млн долл. США",
horiz = TRUE,
las = 1,
xlim = c(0,12000),
col = "steelblue") Помимо этого вы можете задать цвет с помощью цветовых компонент в различных пространствах. Для этого вы должны быть знакомы с основами теории цвета (посмотрите презентацию UsingColorInR.pdf. Например, фиолетовый цвет в пространстве RGB можно задать с помощью функции rgb(), смешав синюю и красную компоненты:
violet = rgb(0.4, 0, 0.6)
barplot(okr$ХимЭкспорт,
names.arg = names,
main = "Экспорт продукции химической промышленности",
xlab = "млн долл. США",
horiz = TRUE,
las = 1,
xlim = c(0,12000),
col = violet)Чтобы сделать цвет полупрозрачным, есть две возможности:
- При создании нового цвета — передать в функцию
rgb()дополнительный параметрalpha =, который задает долю прозрачности в диапазоне от 0 до 1. - При модификации существующего цвета — вызвать функцию
adjustcolor()с параметромalpha =
Например:
violet.transp = adjustcolor(violet, alpha = 0.5)
barplot(okr$ХимЭкспорт,
names.arg = names,
main = "Экспорт продукции химической промышленности",
xlab = "млн долл. США",
horiz = TRUE,
las = 1,
xlim = c(0,12000),
col = violet.transp)
green.transp = rgb(0, 1, 0, 0.5) # появился четвертый параметр
barplot(okr$ХимЭкспорт,
names.arg = names,
main = "Экспорт продукции химической промышленности",
xlab = "млн долл. США",
horiz = TRUE,
las = 1,
xlim = c(0,12000),
col = green.transp)Функция
adjustcolor()позволяет модифицировать все компоненты цвета, не только прозрачность.
На графике типа barplot вы имеете фактически несколько переменных, которые представлены столбиками. А это означает что для них можно использовать различные цвета. Вы можете передать в параметр col = вектор из цветов, соответствующих столбикам:
colors = c("red", "green", "blue", "orange", "yellow", "pink", "white","black")
barplot(okr$ХимЭкспорт,
names.arg = names,
main = "Экспорт продукции химической промышленности",
xlab = "млн долл. США",
horiz = TRUE,
las = 1,
xlim = c(0,12000),
col = colors)На самом деле, такой винегрет из цветов на столбчатых диаграммах использовать не принято. Но вы должны понимать, что при необходимости можно поменять цвет отдельно выбранных столбиков. Например, мы можем показать красным цветом Центральный и Приволжский округа, которые являются лидерами по экспорту продукции химической промышленности:
colors = rep("gray", 8) # сделаем 8 серых цветов
colors[2] = "red"
colors[7] = "red"
barplot(okr$ХимЭкспорт,
names.arg = names,
main = "Экспорт продукции химической промышленности",
xlab = "млн долл. США",
horiz = TRUE,
las = 1,
xlim = c(0,12000),
col = colors)Еще одна интересная особенность использования цвета заключается в том, что количество указанных цветом может не совпадать с количеством рядов данных. Вы можете указать 2 или 3 цвета, и они будут циклически повторяться при визуализации данных:
colors=c("gray","steelblue")
barplot(okr$ХимЭкспорт,
names.arg = names,
main = "Экспорт продукции химической промышленности",
xlab = "млн долл. США",
horiz =TRUE,
las = 1,
xlim = c(0, 12000),
col = colors)Наконец, вещь, которой совершенно необходимо уметь пользоваться при работе с цветом в R — это цветовые палитры. Палитры чрезвычайно удобны, когда необходимо сгенерировать множество цветов, зная лишь основные оттенки. Для этого нужно создать палитру, используя функцию colorRampPalette():
# задаем 2 опорных цвета: черный белый
palet=colorRampPalette(c("black","white"))
# и автоматически генерируем 8 цветов между ними:
colors=palet(8)
# используем их для отображения:
barplot(okr$ХимЭкспорт,
names.arg = names,
main = "Экспорт продукции химической промышленности",
xlab = "млн долл. США",
horiz = TRUE,
las = 1,
xlim = c(0, 12000),
col= colors)
# вы можете включить в палитру произвольное количество цветов:
palet=colorRampPalette(c("steelblue","white","purple4"))
colors=palet(8)
barplot(okr$ХимЭкспорт,
names.arg = names,
main = "Экспорт продукции химической промышленности",
xlab = "млн долл. США",
horiz=TRUE,
las = 1,
xlim = c(0, 12000),
col= colors)В R существует множество стандартных палитр, их список можно найти в справке и документации. Наиболее полезные из них:
Например, вы можете изменить цвета диаграммы, взяв их из одной из палитр или выбрав случайным образом из полной палитры цветов, используя функцию sample():
pie(okr$ХимЭкспорт, names2, main = "Доля федеральных округов в экспорте \n продукции химической промышленности", col=rainbow(length(names2)))
pie(okr$ХимЭкспорт, names2, main = "Доля федеральных округов в экспорте \n продукции химической промышленности", col=sample(colors(),5))Более богатый набор палитр можно найти в библиотеке RColorBrewer, которая представляет собой интерпретацию палитр, доступных на сайте colorbrewer2.org
library(RColorBrewer) # Откроем библиотеку RColorBrewer:
display.brewer.all() # Посмотрим, какие в ней имеются палитрыК каждой из этих палитр можно обратиться по названию с помощью функции brewer.pal(). Поскольку нам необходимы цвета для категориальных данных, следует использовать палитры из средней части (Set3 — Accent)
# выберем цвета из палитры Set2 по количеству секторов в круге:
colors = brewer.pal(length(names2),"Set1")
# И используем их при визуализации
par(mar = c(5, 5, 5, 5)) # установим поля
pie(okr$ХимЭкспорт, names2, main = "Доля федеральных округов в экспорте \n продукции химической промышленности", col=colors)
# Попробуем палитру Accent:
pie(okr$ХимЭкспорт, names2, main = "Доля федеральных округов в экспорте \n продукции химической промышленности", col=brewer.pal(length(names2),"Accent"))Настройки отображения
Графические параметры
Изменять размеры элементов графика можно независимо друг от друга, используя следующие параметры:
-
cex— общий масштаб элементов на графике -
cex.axis— масштаб подписей координат на оси -
cex.lab— масштаб подписей названий осей -
cex.main— масштаб заголовка графика -
cex.sub— масштаб подзаголовка графика -
cex.names— масштаб подписей факторов (для некоторых типов диаграмм)
Например:
plot(tab$Год,
tab$Каспийское,
pch=20,
type="o",
ylim = c(0,12),
col="red3",
main="Объем сброса загрязненных сточных вод",
xlab="Год",
ylab="млрд.куб.м",
cex.axis=0.8,
cex.lab=0.7,
cex.main=0.9,
cex = 0.8)
points(tab$Год, tab$Карское, pch=20, col="forestgreen",cex = 0.8)
lines(tab$Год, tab$Карское, pch=20, col="forestgreen")
points(tab$Год, tab$Азовское, pch=20, col="steelblue",cex = 0.8)
lines(tab$Год, tab$Азовское, pch=20, col="steelblue")Аналогично происходит тонкая настройка цвета:
-
colцвет графика -
col.axisцвет подписей координат -
col.labцвет названий осей -
col.mainцвет заголовка -
col.subцвет подзаголовка -
fgцвет элементов переднего плана (оси, рамка и т.д.) -
bgцвет фона графика (background)
plot(tab$Год,
tab$Каспийское,
pch=20,
type="o",
ylim = c(0,12),
col="red3",
main="Объем сброса загрязненных сточных вод",
xlab="Год",
ylab="млрд.куб.м",
cex.axis=0.8,
cex.lab=0.7,
cex.main=0.9,
col.lab = "grey50",
fg = "grey40")
points(tab$Год, tab$Карское, pch=20, col="forestgreen")
lines(tab$Год, tab$Карское, pch=20, col="forestgreen")
points(tab$Год, tab$Азовское, pch=20, col="steelblue")
lines(tab$Год, tab$Азовское, pch=20, col="steelblue")Разметка осей, рамка, сетка координат и произвольные линии
По умолчанию R подбирает оптимальный с точки зрения него шаг разметки осей, в зависимости от разброса значений по осям \(X\) и \(Y\), а также размеров графического устройства, на котором производится рисование. Изменяя размер окна прорисовки, вы получите различную разметку осей.
В то же время, часто возникает желание (или необходимость) самостоятельно управлять шагом разметки сетки. Для этого необходимо:
- Вызвать функцию
plot(), передав ей дополнительно параметрaxes = FALSE(убирает при рисовании обе оси) или один из параметровxaxt="n"/yaxt="n"(убирают оси \(X\) и \(Y\) соответственно) - Вызвать столько раз функцию
axis(), сколько вы хотите нарисовать осей, передав ей параметры для рисования каждой оси.
Функция axis() принимает следующие параметры:
-
side— сторона графика, на которой будет нарисована ось (1=bottom,2=left,3=top,4=right) -
at— вектор значений, в которых должны быть нарисованы метки оси -
labels— вектор подписей, которые будут нарисованы в местоположениях, указанных в параметреat. Этот параметр можно пропустить, если подписи совпадают с местоположениями меток -
pos— координата, вдоль которой будет нарисована ось -
lty— тип линии -
col— цвет линии и меток -
las— расположение подписей параллельно (\(0\)) или перпендикулярно (\(2\)) оси -
tck— длина метки относительно размера графика. Отрицательные значения дают метки, выходящие за пределы графика. положительные — внутрь графика. \(0\) убирает метки, \(1\) рисует линии сетки.
При ручном построении осей полезно сразу же нарисовать рамку вокруг графика, используя функцию box().
Например:
plot(tab$Год,
tab$Каспийское,
type = "l",
axes = FALSE)
axis(side = 1,
at = seq(min(tab$Год), max(tab$Год), 1),
tck = -0.02,
labels = FALSE) # разметим ось X через 1 год, но рисовать подписи не будем
axis(side = 1,
at = seq(min(tab$Год), max(tab$Год), 3), # а подписи расставим через 3 года
tck = 0) # но рисовать метки не будем
# разметим ось Y через 1 млрд куб. м., округлив предварительно минимальное и максимальное значение до ближайшего целого снизу и сверху соответственно
axis(side = 2,
at = seq(floor(min(tab$Каспийское)), ceiling(max(tab$Каспийское)), 1),
tck = -0.02)
box() # добавим рамку для красотыДля размещения сетки координат существует функция grid(nx = NULL, ny = nx, col = "lightgray", lty = "dotted", lwd = par("lwd"), equilogs = TRUE). Как видно из набора ее параметров, сетка определяется количеством линий в горизонтальном и вертикальном направлении. Это не всегда бывает удобно, поскольку как правило мы хотим задать шаг сетки конкретной величины. По умолчанию, однако, линии сетки выбираются автоматически, как и метки:
plot(tab$Год,
tab$Каспийское,
type = "l",
col = "red")
grid()Вы, разумеется, можете поменять их количество, однако R не будет за вас согласовывать шаг сетки и шаг меток осей, поскольку метки генерируются на стадии рисования plot() или axis() и не запоминаются.
plot(tab$Год,
tab$Каспийское,
type = "l",
col = "red")
grid(10, 5)Функция grid() на самом деле является оберткой функции abline(), которая позволяет рисовать произвольные линии на графике. Дана функция предоставляет следующие возможности построения линий и серий линий:
-
a, b— коэффициенты уравнения \(y = ax + b\). Таким образом можно определить только одну линию. -
coef— принимает вектор из двух значений, которые интерпретируются какaиb. То есть, это альтернативная форма записи предыдущего случая. -
h— значение (значения) координат \(y\) для горизонтальной линии (серии горизонтальных линий). То есть, вы можете передать в этот параметр как одиночное значение, так и вектор значений. В зависимости это этого нарисуется одна горизонтальная линия или серия горизонтальных линий. -
v— значение (значения) координат \(x\) для вертикальной линии (серии вертикальных линий).3\) по оси \(Y\). Для этого выполним следующую последовательность действий:plot(tab$Год, tab$Каспийское, type="n") # режим 'n' позволяет ничего не рисовать, но заложить поле графика в соответствии с данными, указанными в параметрах x и y # Вычисляем линии сетки xlines = seq(min(tab$Год), max(tab$Год), 1) ylines = seq(ceiling(min(tab$Каспийское)), floor(max(tab$Каспийское)), 1) # Рисуем линии сетки abline(h = ylines, v = xlines, col = "lightgray") # Рисуем график lines(tab$Год, tab$Каспийское, col="red3") points(tab$Год, tab$Каспийское, pch = 20, col="red3") # Выделяем значение 10 по оси Y: abline(h = 10, col = "blue", lwd = 2) # Рисуем дополнительно рамку, т.к. сетку координат мы рисовали после графика box()Аннотации данных (текст на графике)
Аннотации данных добавляются на график с помощью функции
text(). В качестве трех обязательных аргументов ей необходимо передать координаты точек размещения текста, и вектор подписей. Также полезным будет указать параметрpos=, отвечающий за размещение аннотации относительно точки. Значенияpos, равные 1, 2, 3 и 4, соответствуют размещению снизу, слева, сверху и справа от точки:text(tab$Год, tab$Каспийское, labels = tab$Каспийское, cex = 0.75, pos = 3)К сожалению, стандартный механизм размещения аннотаций пакета
graphicsне обладает возможностью устранения конфликтов подписей. Однако это возможно для графиков, построенных с помощью библиотек lattice и ggplot2. Для этого можно воспользоваться пакетом directlabels или ggrepel.Легенда
Легенда к графику размещается с помощью функции
legend(). Эта функция принимает несколько аргументов, включая: местоположение, заголовок, названия элементов, графические параметры. Местоположение может быть задано координатами \((x,y)\) в системе координат графика, но удобнее пользоваться следующими предопределенными константами:"bottomright","bottom","bottomleft","left","topleft","top","topright","right","center".Чтобы в легенде появились точки, необходимо задать параметр
pch=. Для линейной легенды, следует задать, соответственно, параметрlty =и/илиlwd =. Каждый из этих параметров должен быть вектором по количеству элементов легенды:par(mar = margins.default) # Найдем ограничивающий прямоугольник вокруг всех рядов данных xrange = range(tab$Год) yrange = range(tab$Каспийское, tab$Карское, tab$Азовское) # Построим пустой график с разметкой осей и всеми заголовками plot(xrange, yrange, type="n", main="Объем сброса загрязненных сточных вод", xlab="Год", ylab="млрд.куб.м", cex.axis=0.8, cex.lab=0.7, cex.main=0.9, col.lab = "grey50", fg = "grey40") # Добавим на график сетку координат grid() # Добавим на график данные points(tab$Год, tab$Каспийское, pch=20, col="red3") lines(tab$Год, tab$Каспийское, pch=20, col="red3") points(tab$Год, tab$Карское, pch=20, col="forestgreen") lines(tab$Год, tab$Карское, pch=20, col="forestgreen") points(tab$Год, tab$Азовское, pch=20, col="steelblue") lines(tab$Год, tab$Азовское, pch=20, col="steelblue") # Определим положение, названия и цвета: main = "Море" location = "topright" labels = c("Каспийское", "Карское", "Азовское") colors = c("red3", "forestgreen", "steelblue") # Если цвет передать в параметр fill, то по умолчанию # нарисуются цветовые плашки: legend(location, labels, title = main, fill=colors)pts = c(20, 20, 20) # каждый элемент показывается точкой типа 20 lns = c(1, 1, 1) # каждый элемент показывается линией толщиной 1 # теперь посмотрим на легенду (она нарисуется поверх старой) legend(location, labels, title = main, col = colors, pch = pts, lwd = lns)Более подробно с разнообразными опциями размещения легенды на графике вы можете познакомиться, набрав в консоли команду
?legend.Как рисовать графики в Qt?
В статье рассматриваются способы рисования графиков, которые я лично знаю и опробовал (если не говорю иного). Выбирайте, что понравилось, а если знаете что-то иное, то пишите в комментариях.
Содержание
Это стандартные библиотеки для Qt. Они красивые, прикольные, есть 3D, есть для QML, но платные и в базовой комплектации Qt их нет. Крякнутых версий не находил. И эти графики сам не пробовал.
Update 27.01.2016. Появилась новость, что в Qt версии 5.7 данная библиотека появится в Open Source версии.
Посмотреть можно тут:
http://doc-snapshots.qt.io/qtcharts/
https://doc.qt.io/QtCharts/index.html
А тут посмотреть платную версию Qt: https://www.qt.io/download/.
Библиотека для рисования графиков на Widget. Найти их можно тут:
http://www.qcustomplot.com
А еще я писал статью об установке и примере использования библиотеки: http://blog.harrix.org/?p=1813. Вещь удобная!
Моя авторская библиотека. Основана вот на чем: мы генерируем html страницу с графиком, а потом ее выводим в QWebView. Получается такой своеобразный костыль, но это позволяет использовать все javascript библиотеки в теории. Я использую там библиотеку JSXGraph. Удобство библиотеки в прописанных функциях, которые быстро добавляют графики по точкам, а все остальное делают сами. Сам проект можно найти тут:
http://blog.harrix.org/?p=1351
А тут статья про установку и использование:
http://blog.harrix.org/?p=1196
Тоже авторская разработка. Но тут графики рисуются не автоматически. Данная библиотека генерирует LaTeX документы с графиками (включая 3D), которые пользователь потом может скомпилировать. Эта библиотека удобна для сложных генерации отчетов.
Проект можно найти тут:
http://blog.harrix.org/?p=1338
А тут можно найти статью об установке:
http://blog.harrix.org/?p=1164.
Пока всё! Будут новые библиотеки рассмотрены – напишу тут.
15 качественных ресурсов и инструментов для создания визуализации, графиков и диаграмм
Графики и таблицы − верное средство для представления данных в удобном для изучения виде. Ниже представлена подборка из 15 библиотек для создания различных форматов визуализации с использованием программного языка Javascript.
Sigma.js
Библиотека sigmajs предназначена для рисования графов. Она позволяет публиковать графы на веб-страницах и интегрировать их в приложения. Большинство параметров настроек можно настроить по своему усмотрению, включая интерактивность графа.
BonsaiJS
BonsaiJSBonsaiJS − библиотека с открытым кодом, предназначенная для создания графики и анимации. В библиотеке есть функция создания простых форм, а также функция path, позволяющая создавать собственные формы. Также у пользователей есть возможность применять различные цвета, градации и фильтры.
Сайт BonsaiJS.
Chart.js
Chart.jsChart.js использует Javascript и HTML5 Canvas для построения гистограмм и различных типов диаграмм: круговых, полярных, кольцевых и др. Одно из преимуществ Chaart.js − дизайнерское оформление и возможность использования анимационных эффектов.
Aristochart
AristochartAristochart позволяет строить двухмерные линейные статичные графики. Программа предполагает набор возможностей по дизайнерскому оформлению, изменению меток, других элементов графика и его адаптации.
Сайт Aristochart.
JS Charts
JS ChartsJS Сharts − генераторов графиков и схем, не требующий больших знаний в программировании, каких-либо плагинов или серверных модулей. JS Сharts позволяет создавать схемы на основе различных шаблонов, таких как столбцы, круговые диаграммы и простые линии. Библиотека совместима с большинством веб-браузеров.
Сайт JS Charts.
Highcharts JS
Highcharts JSБиблиотека Highcharts JS позволяет легко добавлять интерактивные и анимированные графики на сайт или в веб-приложения. Поддерживается множество видов диаграмм: линейные, круговые, колонные рассеивающие и др. Программа работает со всеми популярными видами браузеров, включая Safari и iPhone.
- Пример использования Highcharts JS;
- Сайт Highcharts JS.
Flot
FlotFlot − Javascript-библиотека, позволяющая быстро создавать динамические графики, совместимые с любыми браузерами и операционными системами. Для использования Flot потребуется библиотека jQuery.
- Инструкции по использованию плагина Flot;
- Сайт Flot.
AwesomeChartJS
AwesomeChartJSAwesomeChartJs − простая в использовании Java-sript библиотека, с помощью которой можно быстро создать следующие виды графиков: вертикальные и горизонтальные столбцы, линейно-столбцовые графики, круговые, круговые раздвижные и кольцевые диаграммы. Настройки внешнего вида сильно ограничены.
Сайт AwesomeChartJs.
FusionCharts
FusionChartsFusionCharts − пакет построения диаграмм с открытым исходным кодом для построения flash-графиков, предназначенных для визуализации данных в приложениях и презентациях. Дополнительные возможности FusionCharts открываются после оплаты.
Сайт FusionCharts.
JSXGraph
JSXGraphJSXGraph − разработанная в Байротском Университете библиотека, используемая для отображения геометрических чертежей в веб-браузере.
- Подробнее об использовании JSXGraph в обзоре Хабрахабр;
- Сайт JSXGraph.
Arbor.js
Arbor.JSArbor.js использует библиотеку jQuery для рисования графов прямо в браузере.
Micropolar
MicropolarMicropolar − минималистичная библиотека, интегрированная с D3.js и предназначенная для построения графиков в полярных системах координат.
Сайт Micropolar.
Morris.js
Morris.jsMorris − библиотека с открытым исходным кодом, с помощью которой можно строить графики на простой сетке горизонтальных линий. Для работы с Morris потребуются библиотеки jQuery и Raphaël.
- Подробнее о библиотеке Morris.js на Хабрахабр;
- Сайт Morris.js.
Dygraphs
DygraphsDygraphs − еще одна библиотека с открытым кодом, предназначенная для рисования временных рядов. Графикам можно добавлять элементы интерактивности.
Сайт Dygraphs.
jFreeChart
jFreeChartjFreeChart − на 100% бесплатная библиотека c открытым кодом, позволяющая создавать графики для приложений. Программа поддерживает широкий спектр типов диаграмм и многие типы выходных форматов.
как строить и где брать информацию
Иллюстрации – их вы замечаете первыми. Любой текст воспринимается лучше, если добавить график, гифку или картинку. Для картинок достаточно фантазии, умения находить ассоциации и доступа к фотостокам или архивам с прикольными базами. Для графиков надо понимать основы восприятия. Надо знать, как выделить нужную информацию, как ее быстрее усвоит мозг, и как выгодно преподнести главное.
C цифрами интереснее
О чем бы вы ни решили написать, цифры делают текст информативнее. Наличие точных данных в статье показывает ее экспертность. Не пишите приблизительно – вокруг миллион источников проверенной информации. Вот 10 официальных открытых источников, на которые не стыдно ссылаться в статье:
- Федеральная служба государственной статистики. Официальная информация обо всех сферах в жизни общества. В архиве данные с 2001 года.
- Сайт Статистика.ру. Справочный ресурс Госкомстата. Статьи, таблицы и аналитика почти по всем отраслям – от туризма и образования до криминологии.
- Статистическая база данных по российской экономике. Раздел сайта Высшей школы экономики. Регулярно размещают информацию по состоянию экономики РФ.
- Статистика Российского образования.
- Портал правовой статистики. Показатели преступности, социальный портрет преступности, преступность в регионах и еще много всего вкусного.
- Всемирная книга фактов – справочник, который регулярно выпускает ЦРУ. Но не ищите там количество высадок инопланетян или кто из президентов – человекоподобный киборг. Официальные данные ограничены основной политической и экономической информацией по странам мира.
- Национальные статистические агентства. Ссылки на официальную статистику по всем странам мира. На английском.
- Доступ к данным ООН. Здесь собраны 35 баз данных и 60 миллионов записей.
- Number of. Или количество чего-то там. Например, муравьев в мире или Богов в религиях.
- Данные о терактах, чрезвычайных происшествиях и прочих катастрофах. Все на сайте Глобальные инциденты.
Когда информации полна коробочка, не пишите цифры полотном в тексте. Таблица – уже хорошо, но еще лучше – наглядная иллюстрация. Мозгу проще воспринимать и понимать информацию в таком виде, плюс – существенная экономия места и времени. В эпоху, когда лишнее предложение, эпитет или прилагательное считается отклонением от нормы, лучше не рисковать и сразу все сводить к графикам.
Но цифры тоже можно использовать по-разному. Можно не заморачиваться и выбрать первую же диаграмму, а можно проявить заботу о читателе и построить красивый и понятный график. Чтобы это сделать, надо знать некоторые особенности восприятия мозгом визуальной и графической информации.
Как мы на самом деле видим
Наши глаза и мозг считывают информацию из пространства совсем иначе, чем фото или видеокамера. Оборудование записывает картинку целиком, насколько это позволяют пиксели и угол съемки. Когда вы смотрите на отснятый материал, в который уместилась 180-градусная панорама, в каждый конкретный момент времени внимание сосредоточено на отрезке в 2-3 градуса. Почему оставшиеся участки не кажутся размытыми пятнами? В дело вмешиваются саккады.
Саккады — быстрые, одновременные, строго согласованные движения глаз в одном направлении. На записи выглядят как вертикальные прямые тонкие линии.
Если выражаться человеческим языком, саккада – это короткое движение глаз между двумя точками фиксации. Почти все движения глаз пользователя на сайте саккадические. Чем больше точек фиксации, тем большую работу совершает нервная система, тем больше информации приходится запоминать. Это одна из причин, почему на главной странице сайта или на первом экране лендинга нельзя лепить все подряд. Даже если есть, что сказать.
Но вернемся к нашим «баранам». Именно саккады помогают видеть картинку целиком. Быстрые движения вырывают из общей информации частички изображения, компонуют их и создают иллюзию того, что вы видите картинку целиком. Чем больше точек фиксации и саккад, тем это сложнее. Это главная причина научиться делать графики одновременно простыми и информативными. Подробнее о тонкостях такого восприятия в своей книге The Functional Art пишет преподаватель Университета Майами Альберто Каиро. Вот как он иллюстрирует процесс восприятия информации.
Мы не зацикливаемся на случайных точках, а выделяем для себя определенные приоритеты – движение, яркие цвета, пятна необычной формы. Эти функции называют по-разному. Мне нравится – первичные атрибуты. Потому что мозг обрабатывает их первыми – еще до того, как составит единую картинку.
Простой пример с контрастным цветом.
Или положением.
Или размером.
Никакого волшебства, всем все и так понятно, логика на уровне первой школьной пятилетки, но почему-то в кейсах и презентациях все еще попадаются шедевры, похожие на график бинарных опционов.
Способность найти и правильно выделить первичный атрибут – важнейшее умение для создания эффективных и эффектных диаграмм и графиков. Как это работает на практике?
1. Выбирайте тип графика без спешки
Выделяем нужные столбцы в Excel, делаем «тыц» в гистограммы, готово. Так я раньше делал диаграммы для большинства своих статей. Скотт Беринато – автор книги Good Charts – дал бы мне за такой подход хороший подзатыльник. Он говорит, что перед тем, как строить какую-то диаграмму, надо спросить себя – исследуем мы что-то или просто заявляем.
Если исследуем, конкретных данных может не быть. Например, когда планируем бизнес-процессы. А может оказаться столько, что не влезут в экран – исследование закономерностей в истории или тенденций в экономике. Здесь уместно использовать ассоциации и метафоры, применять стрелки и сложную структуру, экспериментировать. Если графиком мы ставим аудиторию перед фактом, тогда упрощаем данные, выделяем главное и хорошо изучаем ЦА. Здесь логичнее использовать привычные образы и форматы диаграмм.
2. И снова о целевой аудитории
Снова, но не совсем о том. В книге Harvard Business Review Press говорится, что для построения графика важно определить, на какой стадии и в какой форме произойдет контакт ЦА и вашей иллюстрации. Будет ли это презентация, где вы сами управляете вниманием, или обычный печатный лист, который можно быстро выбросить в ближайшую урну. Чем короче контакт, тем меньше информации должно быть, тем ярче надо выделить основную цифру.
3. И что?
Этот вопрос точно прозвучит в голове у вашей аудитории, так что задача графика дать ответ на него. Проявите заботу. Не делайте график ради графика. Да, мы уже говорили, что цифры в виде иллюстрации усваиваются лучше, но в идеале замахнуться на такой себе графический сторителлинг, когда картинка сама по себе наталкивает на какую-то мысль.
4. А теперь к первичным атрибутам
Улучшить график или диаграмму можно при помощи цвета, размеров, правильной компоновки информации. В Excel диаграммы автоматически формируются с кучей всего необязательного. Если их убрать, ключевое сообщение станет понятнее. Представим, что надо построить прогноз количества населения на планете. Если вбить простенькую табличку, первый результат, который мы получим, будет выглядеть примерно так.
Если 2 минуты над ним поработать, он превратится в более понятную иллюстрацию.
Или еще пример. Изобразим график падения прибыли на фоне роста остальных коммерческих показателей. Числа приблизительные – ради примера. Важно подчеркнуть факт того, что не все радужно в королевстве. Выделить главную мысль.
А если так?
Простые вещи, но приходят к ним не все и не сразу. Необязательно быть крутым дизайнером, чтобы делать понятные каждому графики.
- Не используйте в диаграммах и графиках более 3 цветов. Второстепенные данные заливайте серым. Главные – яркими цветами.
- Легенда должна быть. На графике или в тексте, но пользователь за один взгляд должен понимать, какой столбец или линия, что обозначают.
- Убирайте границы и сетки из диаграмм. Если вы не на уроке геометрии, они не нужны.
- Если возможно, убирайте из поля диаграммы и легенду, оставляя подписи данных непосредственно в теле графика.
Бонус: 17 инструментов для создания графиков, кроме Excel
Программа
Доступ
Формат выгрузки диаграмм
Excel
C регистрацией, платно
gif, jpg, png, bmp
Google Sheets
C регистрацией
html, png
Numbers (Apple)
Платно
pdf, png
Onlinecharts.ru
Бесплатно
jpg, png, bmp, pdf
Creately
Бесплатно на 5 диаграмм
jpg, png, pdf
Visme
Бесплатно
jpg, png, pdf
Raw
Бесплатно с регистрацией
нtml, png, svq
Chartbuilder
Бесплатно
png, svq
Infogr.am
Бесплатно
нtml, png
Vizable
Бесплатно с регистрацией
png
Plot.ly
Бесплатно с регистрацией
нtml, png, svq, pdf
Quadrigram
Бесплатно с регистрацией
нtml, png, svq
Qlik Sense
Бесплатно
нtml, png, jpeg, pdf
Qlik View
Есть бесплатная версия
нtml, png, jpeg, pdf
Illustrator
Платно
png, jpeg, pdf, svq, eps, bmp, ai
Google Charts
Бесплатно
нtml, svq
Highcharts
Бесплатно для некоммерческого использования
нtml, svq
Как нарисовать график в MS Word | Small Business
Ли Джонсон Обновлено 24 мая 2021 г.
Если вы составляете документ Word, в котором вам также необходимо представить данные, вы можете добавить таблицу с данными, но использование диаграммы будет намного более привлекательным визуально и легко интерпретировать. Умение рисовать график или создавать диаграммы MS Word позволяет легко добавлять в документ все типы графиков, включая круговые диаграммы, точечные диаграммы, линейные графики и многое другое.
Вы можете использовать несколько различных подходов, но все современные версии Microsoft Word имеют встроенную функциональность для добавления графика непосредственно через программу, даже если она по существу открывает мини-окно Excel для обработки данных.
Использование Excel и копирование графика
Во многих случаях вы будете создавать график из данных, которые у вас уже есть в Excel, и в этой ситуации вы можете скопировать его в Word, как описано в Computer Hope. Для этого создайте диаграмму, как обычно в Excel (перейдите в «Вставить», а затем выберите нужный тип диаграммы из группы «Диаграммы») и выделите данные при необходимости. Отрегулируйте внешний вид, макет, названия осей и все остальное в графике — вы не сможете этого сделать после его копирования — а затем выделите всю диаграмму.Либо щелкните диаграмму правой кнопкой мыши и выберите «Копировать», либо нажмите «Ctrl» + «C», чтобы скопировать ее.
Перейдите в документ Word и поместите курсор в то место, куда вы хотите поместить диаграмму. Затем щелкните правой кнопкой мыши и выберите «Вставить» или нажмите «Ctrl» + «V». Однако график не будет автоматически обновляться в Word, если вы измените данные в Excel, поэтому убедитесь, что вы используете окончательную версию или скопируйте обновленную версию, когда это необходимо таким же образом.
Создание графика в Word
Если у вас еще нет данных в документе Excel, лучший способ рисовать графики в Word — использовать встроенные функции программы, как описано в Microsoft.Перейдите на вкладку «Вставка» вверху документа и выберите «Диаграмма» из группы «Иллюстрации». Это действие вызывает окно с различными типами доступных диаграмм и конкретными примерами. Выберите нужный тип диаграммы и выберите пример диаграммы, стиль которой вам нравится, дважды щелкнув или выделив и нажав «ОК», когда будете готовы.
Появится электронная таблица, содержащая образцы данных. Отредактируйте окно электронной таблицы, чтобы заменить образцы данных данными, которые вы хотите отобразить на диаграмме, используя предварительно заполненные заголовки в качестве руководства.Например, если вы видите ряд данных и категорий с общими названиями, такими как «Категория 1», замените контент в соответствии с вашими данными. Вы также можете добавить больше столбцов или строк, чем образец, при условии, что вы перетащите правый нижний угол границы, выделив данные соответствующим образом.
Отредактируйте диаграмму, используя параметры, которые отображаются со значком «+», обозначающим «Элементы диаграммы» (например, названия осей и метки данных), и значок кисти, предоставляющий параметры цвета и стиля. Когда будете готовы, закройте окно электронной таблицы, и в документе появится диаграмма.
Использование других версий Word
Как объяснил Альфр, процесс не меняется в большинстве версий Word. Если вы используете Mac, это тот же процесс, и нет изменений между более новой и более старой версиями. Однако если вы используете Word в Интернете, вы не можете добавить график, а на iPhone или Android вам нужно создать диаграмму в Excel, а затем скопировать ее.
методов построения графиков
методов построения графиков Построение графиков — очень важный метод экспериментальной физики.Графики обеспечивают компактный и эффективный способ отображения функциональной взаимосвязи между двумя экспериментальными параметрами и обобщения экспериментальных результатов. Некоторые графики в начале этого лабораторного курса должны быть нарисованы от руки , чтобы убедиться, что вы понимаете все, что нужно для построения эффективного научного графика. Вы также узнаете, как использовать компьютер для построения графиков ваших данных. Если в этом руководстве в лабораторных упражнениях требуются графики, вам будет предложено «построить график A против B» (где A и B — переменные).По соглашению, A ( зависимая переменная ) должна быть нанесена вдоль вертикальной оси (ордината), а B ( независимая переменная ) должна быть нанесена вдоль горизонтальной оси (абсцисса). Ниже приводится типичный пример зависимости расстояния от времени для свободно падающего объекта. Внимательно изучите этот график и обратите внимание на следующие важные правила построения графиков:Рисунок 1
Миллиметровая бумага
Графики, предназначенные для предоставления числовой информации, всегда следует рисовать на миллиметровой бумаге в квадрате или поперечном сечении размером 1 см × 1 см с 10 делениями на см.Для рисования графиков используйте острый карандаш (не ручку), чтобы легко исправить неизбежные ошибки.Название
У каждого графика должен быть заголовок, в котором четко указано, какие переменные появляются на графике. Кроме того, напишите свое имя и дату на графике для удобного использования.Этикетки для осей
Каждая координатная ось графика должна быть помечена словом или символом для переменной, нанесенной вдоль этой оси, и единиц (в скобках), в которых отображается переменная.Выбор шкалы
Масштаб следует выбирать таким образом, чтобы данные было легко построить и легко прочитать. На координатной бумаге каждые 5 -я и / или 10 -я строки немного тяжелее других строк; такая основная линия деления всегда должна представлять собой десятичное число, кратное 1, 2 или 5 (например, 0, 1, 2, 0,05, 20, 500 и т. д.). Другие варианты (например, 0,3) очень затрудняют построение и чтение данных. Шкалы не должны быть мельче самого маленького деления на измерительном приборе, с которого были получены данные.Например, данные с измерительной линейки (имеющей деление 1 мм) должны быть нанесены на шкалу не менее 1 деления = 1 мм. Масштаб меньше 1 дел / мм не обеспечит дополнительной точности построения, поскольку данные с измерительной линейки имеют точность только примерно до 0,5 мм. Часто масштаб должен быть значительно грубее этого предела, чтобы уместить весь график на одном листе миллиметровой бумаги. На иллюстрации были выбраны масштабы, чтобы дать графику примерно квадратную границу; вам следует избегать выбора масштаба, из-за которого оси сильно различаются по длине.Обратите внимание в этой связи, что не всегда необходимо указывать начало координат («ноль») на оси графика; во многих случаях необходимо отобразить только ту часть шкалы, которая покрывает данные.точек данных
Введите точки данных на график, поместив маленькую точку в координаты точки, а затем нарисовав маленький кружок вокруг точки. Если на одном графике должно отображаться более одного набора данных, используйте другие символы (например, θ, , Δ), чтобы различать наборы данных. Для этого пригодится чертежный шаблон.Кривые
Проведите простую плавную кривую через точки данных. Кривая не обязательно будет проходить через все точки, но должна проходить как можно ближе к каждой точке, примерно по половине точек с каждой стороны кривой; эта кривая предназначена для того, чтобы направлять взгляд вдоль точек данных и указывать тенденцию изменения данных. Французская кривая полезна для рисования сегментов кривой. Не , а не соединяют точки данных прямолинейными сегментами по принципу точка-точка. Эта кривая теперь показывает средний тренд данных, и любые прогнозируемые значения следует считывать с этой кривой, а не возвращаться к исходным точкам данных.Прямые графики
Во многих упражнениях в этом руководстве вас попросят построить график ваших экспериментальных результатов таким образом, чтобы между нанесенными на график величинами существовала линейная зависимость. В этих ситуациях вам будет предложено подобрать прямую линию к точкам данных и определить наклон и пересечение y из графика.В приведенном выше примере ожидается, что расстояние до падающего объекта меняется со временем. согласно. Трудно сказать, согласуются ли данные, представленные на первом графике выше, с этим прогнозом. Однако, если построить график d vs. t 2 , должна быть получена прямая линия с наклоном = g /2 и y -intercept = 0.Прямой штуцер
Поместите прозрачную линейку или чертежный треугольник на график и отрегулируйте его положение так, чтобы край находился как можно ближе ко всем точкам данных.Наилучшая настройка приведет к тому, что половина точек данных окажется под линейкой, равномерно распределенных по линии. Нарисуйте линию вдоль края линейки, которая простирается до ближайшей координатной оси на одном конце и немного дальше последней точки данных на другом конце. Степень, в которой данные согласуются с уравнением, отображается тем, насколько близко точки данных находятся к подобранной линии. Построение этой прямой линии выполняет сглаживание необработанных экспериментальных данных и, таким образом, может быть более надежным индикатором результата эксперимента, чем любая пара точек данных.Следовательно, измерения, взятые из графика, должны производиться на подогнанной линии, а не на самих точках данных. Не «заставляйте» подобранную линию проходить через начало вашего графика, даже если предполагаемая математическая функция проходит через (0, 0), как в примере функцииd = (g / 2) t 2 .
Рисунок 2
Получение угла наклона и точки пересечения
Наклон прямой линии вычисляется путем деления «подъема» на «пробег» линии, как показано.Для «пробега» выберите два удобных положения шкалы вдоль горизонтальной оси около концов линии и нарисуйте светлые вертикальные линии, чтобы пересечь нанесенную линию. Считайте положения этих пересечений по вертикальной оси и вычтите, чтобы получить «подъем». Всегда сообщайте рассчитанный уклон на самом графике. Возможно, вам будет полезно пометить точки «подъем» и «бег» и пересечения, как показано в примере, по крайней мере, до тех пор, пока ваша техника построения графиков не будет хорошо развита. Когда вас просят определить точку пересечения с осью y , отметьте точку пересечения, где нанесенная линия пересекает вертикальную ось (при условии, что вертикальная ось расположена в положении «0» по горизонтальной шкале).Неопределенность наклона и пересечения
Неопределенность наклона и пересечения можно оценить, проведя еще две прямые линии с максимальным и минимальным наклоном, которые все еще позволяют линиям проходить через большинство точек данных. Соответствующий диапазон наклонов и значений пересечения можно затем использовать в качестве разумной оценки неопределенности этих значений.Аппарат методом наименьших квадратов
Рассмотрим две физические переменные x и y , которые, как мы ожидаем, связаны линейной зависимостью:y = a + bx.
График y против x должен быть прямой линией, имеющей наклон b и пересекающей ось y в точке пересечения y = a .Рисунок 3
Предположим, мы провели измерения N для x и y со значениями (x 1 , y 1 ), (x 2 , y 2 ),, (x N , y N ). Предположим, что измерения x имеют незначительную ошибку, а измерения y имеют стандартные ошибки σ 1 , σ 2 « σ N .График такого набора измерений показан на рисунке 3. Мы хотим найти прямуюy = a + bx,
, которая составляет наилучшие оценки для a и b . В процедуре линейной аппроксимации методом наименьших квадратов наилучшими оценками для a и b являются те, которые минимизируют взвешенную сумму квадратов (хи-квадрат): Обратите внимание, что величинаa + bx i
является ожидаемым значением y , когдаx = x i ,
, таким образом,y i — (a + bx i )
— это просто отклонение от измеренного значения y от ожидаемого значения.Таким образом, метод наименьших квадратов находит значения a и b , которые минимизируют сумму квадратов этих отклонений, взвешенных по их соответствующей неопределенности. В этой лабораторной работе вы будете использовать программное обеспечение для анализа данных, такое как Excel , которое может автоматически вычислять лучшие значения a и b и их соответствующую ошибку,σ a
иσ b .
Если ваши точки данных содержат самые разные ошибки, то тем с большими ошибками следует придавать меньший вес.Следовательно, для этих случаев следует использовать версию с взвешенным соответствием. Если всем точкам данных необходимо присвоить одинаковый вес, следует использовать невзвешенное соответствие. Линейный график— все, что вам нужно знать о линейных графиках
Что такое линейный график?
Линейный график, также известный как линейная диаграмма, представляет собой тип диаграммы, используемый для визуализации значения чего-либо с течением времени. Например, финансовый отдел может отобразить изменение суммы наличных денег, имеющихся в наличии у компании, с течением времени.
Линейный график состоит из горизонтальной оси x и вертикальной оси y. Большинство линейных графиков имеют дело только с положительными числовыми значениями, поэтому эти оси обычно пересекаются около нижней части оси y и левого конца оси x. Точка пересечения осей всегда (0, 0). Каждая ось помечена типом данных. Например, по оси X могут быть дни, недели, кварталы или годы, а по оси Y — доход в долларах.
Точки данных нанесены на график и соединены линией «точка-точка».
Ось x также называется независимой осью, потому что ее значения ни от чего не зависят. Например, время всегда помещается на ось x, поскольку оно продолжает двигаться вперед независимо от чего-либо еще. Ось Y также называется зависимой осью, потому что ее значения зависят от значений оси X: в то время у компании было столько денег. В результате линия графика всегда движется горизонтально, и каждое значение x имеет только одно значение y (компания не может иметь две суммы денег одновременно).
Более чем одна линия может быть нанесена на одну ось в качестве формы сравнения. Например, вы можете создать линейный график, сравнивающий сумму денег, хранящуюся в каждом филиале, с отдельной строкой для каждого офиса. В этом случае каждая строка будет иметь свой цвет, обозначенный в легенде.
Линейный график — это мощный визуальный инструмент для маркетинга, финансов и других областей. Это также полезно в лабораторных исследованиях, мониторинге погоды или любой другой функции, связанной с корреляцией между двумя числовыми значениями.Если на графике есть две или более линий, это можно использовать для сравнения между ними.
Как создать линейный график
Первый шаг — убедиться, что данные правильно отформатированы для линейного графика.
На вкладке Insert в SmartDraw щелкните Graph и выберите Line Graph. .
Выберите файл данных для импорта, и SmartDraw автоматически сгенерирует график.
После импорта вы можете легко изменить заголовок, размещение легенды и даже быстро изменить тип графика с помощью опций Edit Graph или просто дважды щелкнув импортированную диаграмму.
Графики и диаграммы — Научная работа — KS3 Science — BBC Bitesize
Presenter 2: Мы собираемся сосредоточиться на правильном способе построения графика, а также на построении графика.
Presenter 1: Мы собираемся собирать показания для эксперимента, который включает определение времени, как долго свеча остается гореть под стаканом. График — отличный способ нарисовать картину того, о чем нам говорят данные. Это помогает нам увидеть закономерность в данных.
Presenter 2: Мы ищем связь между объемом воздуха в стакане и продолжительностью горения свечи.
Студент 1: Для этого, я думаю, это будет около 20 … 20 секунд. А может и нет. Что это было?
Студент 2: 22 секунды.
Студент 1: Готовы?
Студент 2: Ага.
Студент 1: Как вы думаете, что произойдет на этот раз?
Студент 2: Думаю, потому что кислорода больше, он прослужит дольше.Итак, я думаю, может быть, 40 секунд?
Presenter 1: Используйте линейный график, если обе переменные используют числа и являются непрерывными. Это означает, что числа могут принимать любое значение.
Presenter 2: При рисовании линейного графика мы используем SALT, что означает масштаб, ось, метки, заголовок.
Presenter 1: Во-первых, нам нужно определить нашу шкалу — и S в SALT — мышлением какова наша самая большая ценность и какова наша наименьшая ценность?
Presenter 2: Для осей нам нужно выбрать единицы, в которых мы поднимаемся.Не забывайте равные промежутки между каждым делением.
Presenter 1: И этикетки.
Presenter 2: И, наконец, название.
Presenter 1: Теперь мы наносим наши точки.
Presenter 2: Стакан кубической формы размером 500 см погас через 21 секунду.
Presenter 1: Стакан кубической формы 250 см погас через девять секунд.
Presenter 2: Стакан кубической формы на 1000 см погас через 40 секунд.
Presenter 1: Мы не соединяем каждую точку, мы рисуем линию наилучшего соответствия, которая имеет равные точки над и под ней. Это покажет нам общую картину. Иногда линия наилучшего соответствия может быть изогнутой. Это может произойти, например, если во время тренировки вы строите график зависимости частоты пульса от времени. Ваша частота пульса увеличится по сравнению с частотой пульса в состоянии покоя …
Студент 1: Быстрее, быстрее!
Presenter 1: .. достичь пика и снова вернуться к своему пульсу в состоянии покоя, когда вы прекратите тренировку.
Presenter 2: Важно, чтобы линия следовала шаблону данных.
Presenter 1: Но здесь, в эксперименте со свечой, наша линия наилучшего соответствия прямая. Это показывает нам, что с увеличением объема воздуха увеличивается время, необходимое для того, чтобы свеча погасла.
Presenter 2: Чтобы подвести итоги, мы увидели, как нарисовать график со всеми правильными метками. Мы также рассмотрели возможность проведения линии наилучшего соответствия по нашим данным.
6: Рисование графиков — статистика LibreTexts
Прежде всего покажите данные.
–Эдвард Тафте 86
Визуализация данных — одна из важнейших задач, стоящих перед аналитиком данных. Это важно по двум различным, но тесно связанным причинам. Во-первых, нужно нарисовать «презентационную графику»: отображение ваших данных в чистом, визуально привлекательном виде помогает вашему читателю понять, что вы пытаетесь им сказать.Не менее важным, а может быть, даже более важным, является тот факт, что рисование графиков помогает и понимать данные. С этой целью важно нарисовать «исследовательскую графику», которая поможет вам узнать о данных в процессе их анализа. Эти моменты могут показаться довольно очевидными, но я не могу сосчитать, сколько раз я видел, как люди их забывали.
Рисунок 6.1: Стилизованный перерисованный рисунок оригинальной карты холеры Джона Сноу.Каждая маленькая точка обозначает местонахождение случая холеры, а каждый большой кружок показывает местонахождение колодца. Как видно из сюжета, очаг вспышки холеры очень близок к насосу Broad St. Это изображение использует данные из пакета## Предупреждение: пакет HistData был собран под R версии 3.5.2HistData@ [Friendly2011] и было нарисовано с незначительными изменениями команд, представленных в файлах справки. Обратите внимание, что на оригинальной нарисованной от руки карте Сноу использовались разные символы и надписи, но идею вы поняли.Чтобы понять важность этой главы, я хочу начать с классической иллюстрации того, насколько мощным может быть хороший граф.С этой целью на рис. 6.1 показана перерисовка одной из самых известных визуализаций данных всех времен: карты смертей от холеры, составленной Джоном Сноу 1854 года. Карта элегантна своей простотой. На заднем плане у нас есть карта улиц, которая помогает сориентировать зрителя. Сверху мы видим большое количество маленьких точек, каждая из которых указывает на место заболевания холеры. Более крупные символы показывают расположение водяных насосов с указанием их названий. Даже самый поверхностный просмотр графика ясно показывает, что источником вспышки почти наверняка является помпа на Брод-стрит.После просмотра этого графика доктор Сноу распорядился снять ручку с насоса, что положило конец вспышке, в результате которой погибло более 500 человек. Такова сила хорошей визуализации данных.
У этой главы двоякая цель: во-первых, обсудить несколько довольно стандартных графиков, которые мы часто используем при анализе и представлении данных, и, во-вторых, показать вам, как создавать эти графики в R. Сами графики, как правило, довольно просты. , так что в этом отношении эта глава довольно проста.Обычно люди борются с тем, чтобы научиться создавать графики, и особенно, как создавать хорошие графики. 87 К счастью, научиться рисовать графики в R достаточно просто, если вы не слишком разборчивы в том, как выглядит ваш график. Когда я говорю об этом, я имею в виду, что в R есть много хороших графических функций , очень , и в большинстве случаев вы можете создавать чистую высококачественную графику без необходимости много изучать низкоуровневые детали. о том, как R обрабатывает графику.К сожалению, в тех случаях, когда вы действительно хотите сделать что-то нестандартное, или если вам нужно внести очень специфические изменения в фигуру, вам действительно нужно немного узнать об этих деталях; и эти детали одновременно сложны и скучны. Имея это в виду, структура этой главы следующая: я начну с очень быстрого обзора того, как графика работает в R. Затем я расскажу о нескольких различных типах графиков и о том, как их рисовать, как и а также показаны основы настройки этих графиков.Затем я более подробно расскажу о графике R, обсудив некоторые из этих сложных и скучных вопросов. В будущей версии этой книги я намерен закончить эту главу, рассказав о том, что делает график хорошим или плохим, но у меня еще не было времени написать этот раздел.
Как нарисовать наиболее подходящую линию в физике
Введение в построение графиков и линий наилучшего соответствия
В этом руководстве мы объясняем важность научных графиков в физике и объясняем, как правильно рисовать научные графики, включая наиболее подходящие линии.Это действительно важный физический навык, и вам необходимо овладеть им, если вы хотите успешно сдать следующий практический экзамен по физике.
В этой статье мы обсуждаем:
Научные графики
Что такое научные графики?
График — это визуальное представление взаимосвязи между двумя переменными: x (независимая переменная) и y (зависимая переменная).
Графики позволяют легко определять тенденции в данных, которые вы собрали и которые можно проанализировать для выполнения вычислений или измерений, связанных с достижением цели эксперимента.
Как нарисовать научный график
Шаг Действие Деталь 1 Определите переменные - Разместите независимый график на оси x вашей переменной и зависимая переменная по оси ординат.
2 Определите диапазон переменной - Вычтите наименьшее значение данных из наибольшего значения данных
3 Определите масштаб графика Определите шкалу (числовое значение для каждого квадрата или деления), которая наилучшим образом соответствует диапазону каждой переменной.- 4
- Используйте масштаб, который позволяет отображать данные как можно больше в отведенном для этого месте.
- Диапазон каждой оси может быть разным . Необязательно начинать с нуля, но рекомендуется, поскольку это позволяет при необходимости экстраполировать.
- Масштаб каждой оси может быть разным , но каждая должна соответствовать . Если одно деление представляет один метр в начале графика на одной оси, одно деление всегда представляет один метр на этой оси.
4 Пронумеруйте и обозначьте каждую ось - Четко обозначьте оси x и y, включая единицы каждого измерения.
5 Нанесите точки данных - Нанесите каждое значение данных на график крестиком (x)
6 Нарисуйте график - 4
Определите тенденцию или взаимосвязь между независимыми и зависимыми переменными. - Исключить из рассмотрения любые выбросы.
- Нарисуйте кривую или линию, которая лучше всего описывает выявленный тренд. Большинство графиков экспериментальных данных по физике являются линейными и нарисованы не как «соединяющие точки».
- Нарисуйте линию (или кривую) только в диапазоне, для которого у вас есть данные. Не выходите за пределы этого диапазона.
- Если требуется экстраполировать (продлить график по тому же наклону за пределы диапазона данных), используйте пунктирную линию, чтобы указать, что вы экстраполируете.
7 Дайте описательный заголовок - В заголовке должно быть четко указано, о чем идет речь. Не просто переформулируйте то, что уже показано на осях.
В 11 и 12 годах по физике тенденции, которые вы будете исследовать, в основном линейны или могут быть преобразованы в линейные графики, и, следовательно, вам потребуется нарисовать линию наилучшего соответствия. .
Рисование линии наилучшего вписывания
Ниже показан пример правильно проведенной линии наилучшего вписывания вместе с неправильной:
Как нарисовать линию наилучшего вписывания
Чтобы нарисовать линию наилучшего вписывания, учтите следующее:
- Выбросы следует игнорировать.
- Линия должна отражать тенденцию в данных, т.е. она должна лучше всего совпадать с большинством данных и меньше — с точками данных, которые отличаются от большинства.
- Линия должна быть сбалансирована, т.е. на обоих концах линии должны быть точки выше и ниже линии.
- НЕ заставляйте линию проходить через какие-либо определенные точки данных или проходить через ноль. Цель линии наилучшего соответствия — выявить тенденцию всех данных.
Почему нам нужно провести линию наилучшего соответствия?
Основными причинами проведения линии наилучшего соответствия являются:
- Уменьшение влияния как систематической, так и случайной ошибки и, таким образом, повышение точности и надежности эксперимента.
- Найдите и используйте градиент линии наилучшего соответствия, чтобы определить неизвестное в эксперименте. Обычно определение этого неизвестного каким-то образом направлено на достижение цели
Каким образом линия наилучшего соответствия уменьшает экспериментальные ошибки?
Рисуя линию наилучшего соответствия, мы ищем наиболее сильную тенденцию в данных и, таким образом, уменьшаем влияние случайных ошибок.Если затем мы используем градиент линии наилучшего соответствия, мы смотрим на различия в значениях, а не на абсолютные значения, что уменьшает или устраняет влияние систематических ошибок.
На графиках ниже показаны четыре примера с различными типами ошибок и без ошибок:
- Идеальные данные без ошибок
- Случайная ошибка
- Случайная ошибка с выбросом
- Случайные и систематические ошибки
Градиент представляет результат эксперимента и должно иметь значение 1, поэтому уравнение линии будет \ (y = x \).
Как использование линии наилучшего соответствия снижает экспериментальные ошибки?
Использование графика дает такие же или лучшие результаты, чем вычисление непосредственно по точкам данных с последующим усреднением, как показано в таблице ниже.
Типы присутствующих ошибок Результат, полученный из градиента линии наилучшего соответствия Результат, полученный в результате расчета с использованием всех точек данных и их усреднения Идеальные данные — без ошибок 1.00 1.00 Случайная ошибка 1.04 1.04 Случайная ошибка с выбросом 1.04 1.07 Случайные и систематические ошибки Из 905 905 905Из таблицы видно, что: - Идеальные данные имеют градиент 1.
- Случайная ошибка дает градиент 1,04, все еще очень близкий к правильному значению 1.
- Выброс игнорируется линией наилучшего соответствия, поэтому градиент по-прежнему равен 1,04, что близко к правильному значению. Усреднение по точкам данных не проигнорирует выброс и даст худший результат 1,07.
- Систематическая ошибка сдвигает данные на ту же величину, но не меняет градиент, который по-прежнему равен 1,01. Это все еще очень близко к правильному значению 1. Однако усреднение по точкам в этом случае дает неправильный ответ 1,47.
Распространенные ошибки при рисовании наиболее подходящих линий
В приведенном ниже примере показаны типичные ошибки учащихся при рисовании наиболее подходящих линий.Ниже перечислены точные ошибки, допущенные учащимися.
Ошибка 1: Отсутствуют ярлыки
В приведенном ниже графике 1 отсутствуют ярлыки:
Ошибки на этом графике включают:
- Отсутствие меток для осей
- Отсутствует описательный заголовок
- Экстраполированная линия не отображается пунктирной линией
6 Распространенные ошибки, которые студенты-физики HSC делают на экзаменах
Ошибка 2 : Неправильный масштаб
График 2, показанный ниже, содержит неправильный масштаб:
Ошибки на этом графике включают:
- Неправильный масштаб по осям x и y.Каждое деление должно представлять одно и то же значение по каждой оси. Например, если для каждого деления установлено значение 0,05 в начале графика для этой оси, то одно деление всегда должно представлять 0,05 для этой оси.
- Учащийся должен начать шкалу с 0 или 0,20 по оси абсцисс.
Хотите успешно сдать следующий практический экзамен по физике?
Загрузите Рабочую тетрадь практических навыков Matrix и отточите свои физические навыки.Узнайте, как:
- Оценить достоверность, надежность и точность любых измерений и вычислений
- Определить источники систематических и случайных ошибок
- Определить и применить соответствующие математические формулы и концепции
- Нарисовать соответствующие графики для отображения взаимосвязей
© Matrix Education и www.matrix.edu.au, 2021. Несанкционированное использование и / или копирование этого материала без явного и письменного разрешения автора и / или владельца этого сайта строго запрещено.Выдержки и ссылки могут быть использованы при условии, что Matrix Education и www.matrix.edu.au полностью и четко указали на исходный контент с соответствующим конкретным указанием.
Рисование двумерных графиков в MatLab® (иллюстрированное выражение)
Двумерные графики часто используются при анализе данных. Кроме того, вам может потребоваться рисовать двумерные графики в Matlab® с различными переменными. В этой статье мы объясним, как рисовать двумерные графики в Matlab®.
Как рисовать двумерные графики в Matlab®?
Рисование 2D-графика в Matlab®.Чтобы рисовать 2D-графики, вам необходимо создать в Matlab® 2 переменные. Например, мы создали комплексное число в Matlab®, чтобы показать вам, как создавать двумерные графики.
Команда для создания двумерных графиков в Matlab® — это «plot ()», как показано в пурпурном поле выше в Matlab®. Вам нужно ввести переменные внутри команды plot (a, b), затем вы также можете добавить указатель, как указано выше, который добавляется как «o».Этот указатель показывает расположение комплексного числа «а», как показано стрелкой выше.
ВЫ МОЖЕТЕ ИЗУЧИТЬ MatLab® НА МЕХАНИЧЕСКОЙ БАЗЕ; Нажмите и начните изучать MatLab®!
С помощью команды «xlabel ()» вы можете определить имя метки x двумерного графика, который вы создаете в Matlab®. Вам нужно ввести имя метки x внутри кода xlabel () как «имя метки x».
Кроме того, вы можете сделать то же самое для метки y нарисованного графика с помощью команды ‘ylabel ()’, как показано выше в Matlab®.
С помощью команды «title ()» вы можете добавить выразительный заголовок к вашему двумерному графику в Matlab®. Использование этого кода аналогично командам xlabel () и ylabel ().
Вы можете определить границы осей с помощью команды axis (), как указано выше. Например, мы вводим граничные значения осей x и y внутри команды axis () как [x x y y], что является начальным и конечным значением оси x и начальным и конечным значением оси y соответственно.
Кроме того, мы хотели расположить наш график в форме квадрата в Matlab®, тогда мы просто набрали «квадрат оси», как показано выше.
Тоже можно делать;
- ось равняется: Автоматически выравнивает оси.
- нормаль оси: Делает оси прямоугольными на графике.
Самая простая задача создания двумерного графа в Matlab® может быть выражена так. Кроме того, мы можем опубликовать гораздо более сложные примеры создания двухмерных осей в Matlab®, если хотите.
Заключение
Оставляйте свои комментарии и вопросы по рисованию двумерных графиков в Matlab®!
Эта статья подготовлена исключительно в познавательных и информационных целях.Изображения любезно предоставлены Matlab®
Ваши ценные отзывы очень важны для нас.
.


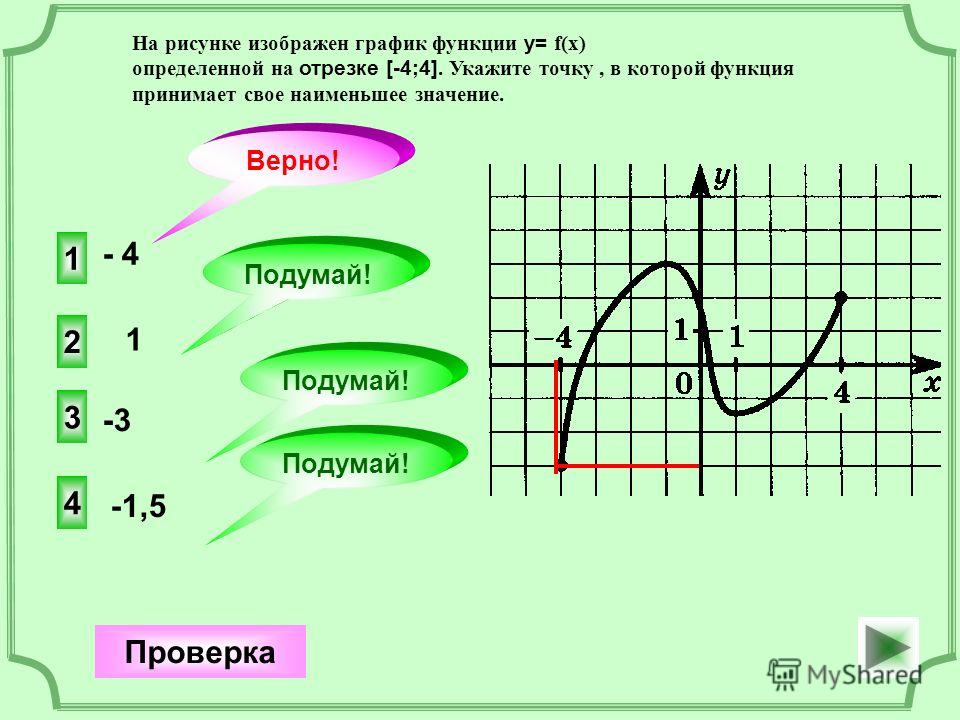


 Чтобы увидеть значения в OneNote для Интернета, щелкните линию графа.
Чтобы увидеть значения в OneNote для Интернета, щелкните линию графа.
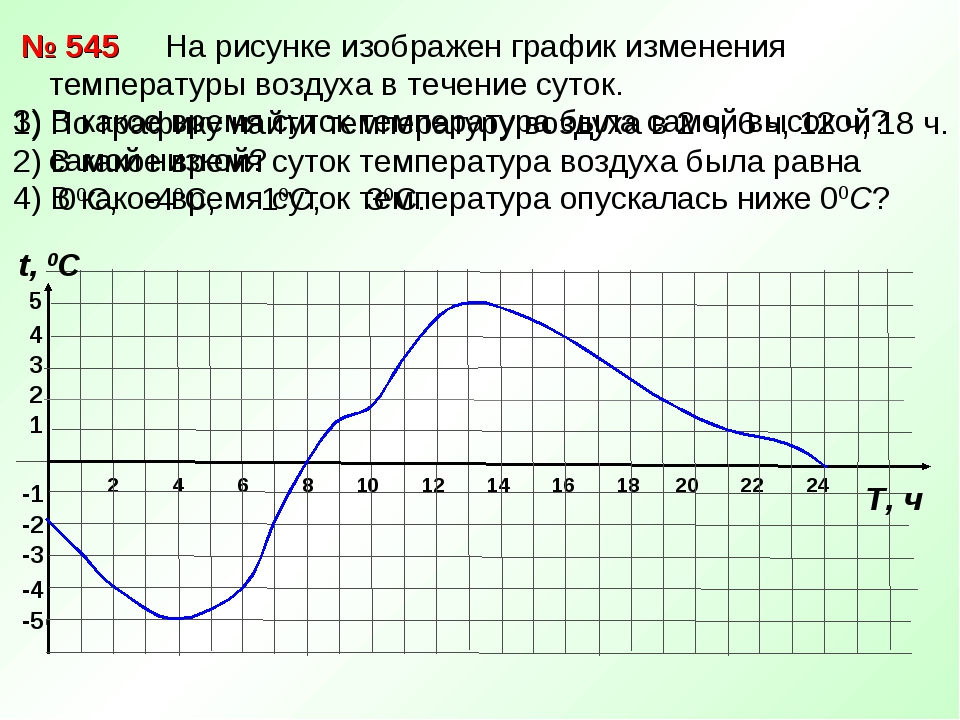
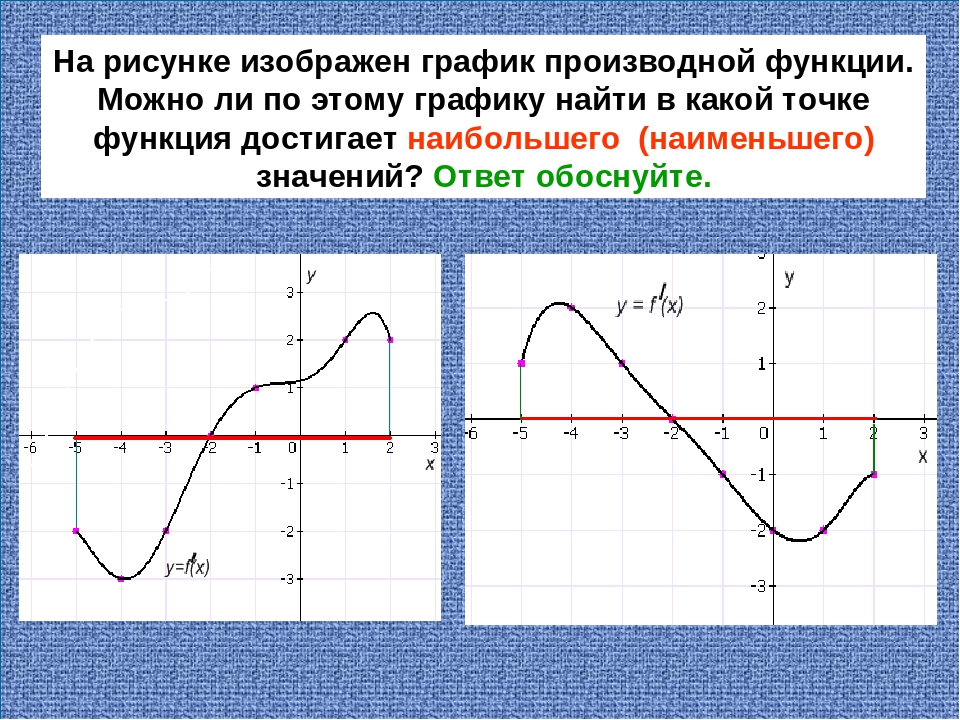 долл. США",
ylab = "Импорт, млн. долл. США",
main = "Экспорт/импорт металлов и изделий из них по субъектам РФ",
asp = 1,
pch = 2,
cex = 0.5)
долл. США",
ylab = "Импорт, млн. долл. США",
main = "Экспорт/импорт металлов и изделий из них по субъектам РФ",
asp = 1,
pch = 2,
cex = 0.5)