Как нарисовать шестиугольник с помощью линейки
Пятиугольник
Здравствуйте коллеги.Сегодня построим правильный пятиугольник в окружности, попробуем начертить циркулем и линейкой фигуру.
Рисунки художников очень тесно связаны с черчением и геометрией. Если мы задумали какую-то композицию, а в ней есть геометрические фигуры, то нам необходимо знать, как изобразить предмет, что бы он не выглядел смешно, и что бы вы не выглядели дилетантом и смогли нарисовать пятиконечную звезду циркулем или в фотошопе. От этого зависит ваш авторитет художника, а значит и заказы.
Построение правильного пятиугольника не так часто встречается в рисунке, но все же есть моменты, когда нам это необходимо.
Например, нам нужно нарисовать пятиконечную звезду (пентаграмму) для картины о Советском прошлом или о настоящем Китая. Правда для этого нужно уметь создать рисунок звезды в перспективе. Это посмотрите в другом уроке.
Мы попробуем нарисовать звезду в фотошопе фронтально. Точно так же вы сможете нарисовать фигуру карандашом на бумаге. Всего лишь с помощью таких инструментов:
Как правильно нарисовать звезду, что бы она выглядела ровно и красиво, сразу не ответишь. Количество углов не четное, поэтому просто разделить окружность на равные части циркулем или линейкой не получится.
Что бы вписанный пятиугольник в окружность был пропорциональный, нам необходимо точно вычислить одну из сторон, а затем отложить этот отрезок пять раз на теле овала.
Как выглядит пятиугольник и звезда
Внизу на фото разберем, как нарисовать звезду поэтапно.
Для начала рисуем окружность с центром О.
Дальше отложим отрезок OA равный радиусу и разделим его пополам точкой B, как показано на фото внизу.
Теперь от точки В до точки С проведем прямую.
Отложим расстояние отрезка ВС на диаметральной линии окружности. Для этого можно воспользоваться циркулем. Таким образом у нас появилась точка D.
И отрезок DB. Картинка внизу.
Дальше, проведя линию от точки D к точке С, Мы получи длину равную стороне пятиугольника.
Дальше этот отрезок можно отложить на окружности. У нас появилась точка Е. Смотрим фото ниже.
Итак, одна из сторон пятиугольника у нас есть, это линия ЕС.
Такие же отрезки наносим на всей части круга. Смотрим картинку.
На этом построение правильного пятиугольника можно закончить. Что бы нарисовать звезду нужно просто соединить углы через один.
Нарисовать пятиконечную звезду циркулем можно так же, как и на нашем уроке в программе Photoshop, весь процесс такой же, только вместо программы графического редактора используем инструменты для черчения.
Так же можно посмотреть уроки построения шестиугольника, разделение на восемь частей, деление круга на семь частей, десять равных частей.
Как построить и нарисовать правильный пятиугольник по окружности
Правильный пятиугольник представляет собой геометрическую фигуру, которая образовывается пересечением пяти прямых, создающих пять одинаковых углов. Такая фигура носит название — пентагон. С пятиугольником тесно связана работа художников — их рисунки строятся на основе правильных геометрических фигур. Для этого необходимо знать то, как быстро построить пентагон.
Чем интересна эта фигура? Форму пентагона имеет здание Министерства обороны Соединенных Штатов Америки. Это можно увидеть на фото, сделанных с высоты полета. В природе не существует кристаллов и камней, форма которых напоминала бы пентагон. Только в этой фигуре количество граней совпадает с числом диагоналей.
Параметры правильного пятиугольника
Прямоугольный пятиугольник, как и каждая фигура в геометрии, имеет свои параметры. Зная необходимые формулы, можно рассчитать эти параметры, что облегчит процесс построения пентагона. Способы и формулы расчетов:
- сумма всех углов в многоугольниках равна 360 градусам. В правильном пятиугольнике все углы равны, соответственно, центральный угол находится таким способом: 360/5 = 72 градуса;
- внутренний угол находится таким образом: 180*(n -2)/ n = 180*(5−2)/5 = 108 градусов.
 Сумма всех внутренних углов: 108*5 = 540 градусов.
Сумма всех внутренних углов: 108*5 = 540 градусов.
Сторона пентагона находится с помощью параметров, которые уже даны в условии задачи:
- если вокруг пятиугольника описана окружность и известен ее радиус, сторона находится по такой формуле: a = 2*R*sin (α/2) = 2*R*sin (72/2) = 1,1756*R.
- Если известен радиус вписанной в пентагон окружности, то формула расчета стороны многоугольника: 2*r*tg (α/2) = 2*r*tg (α/2) = 1,453*r.
- При известной величине диагонали пентагона его сторона рассчитывается таким образом: а = D/1,618.
Площадь пентагона так же, как и его сторона, зависит от уже найденных параметров:
- с помощью известного радиуса вписанной окружности площадь находится так: S = (n*a*r)/2 = 2,5*a*r.
- описанная вокруг пятиугольника окружность позволяет найти площадь по такой формуле: S = (n*R2*sin α)/2 = 2,3776*R2.
- в зависимости от стороны пентагона: S = (5*a2*tg 54°)/4 = 1,7205* a2.
Построение пентагона
Построить правильный пятиугольник можно с помощью линейки и циркуля, на основе вписанной в него окружности или одной из сторон.
Как начертить пятиугольник на основе вписанной окружности? Для этого необходимо запастись циркулем и линейкой и сделать такие шаги:
- Сначала необходимо начертить окружность с центром О, после чего на ней выбрать точку, А — вершину пентагона. От центра к вершине проводится отрезок.
- Затем строится перпендикулярная прямой ОА отрезок, который также проходит через О — центр окружности. Его пересечение с окружностью обозначается точкой В. Отрезок О. В. делится пополам точкой С.
- Точка С станет центром новой окружности, проходящей через А. Точка D — это ее пересечение с прямой ОВ в границах первой фигуры.
- После этого проводится третья окружность через D, центром которой является точка А. Она пересекается с первой фигурой в двух точках, их необходимо обозначить буквами Е и F.
- Следующая окружность имеет центр в точке Е и проходит через А, а ее пересечение с первоначальной находится в новой точке G.

- Последняя окружность в этом рисунке проводится через точку, А с центром F. На ее пересечении с начальной ставится точка Н.
- На первой окружности после всех проделанных шагов появились пять точек, которые необходимо соединить отрезками. Таким образом получился правильный пятиугольник АЕ G Н F.
Как построить правильный пятиугольник иным способом? С помощью линейки и циркуля пентагон можно построить немного быстрее. Для этого необходимо:
- Cначала необходимо с помощью циркуля нарисовать окружность, центр которой — точка О.
- Чертится радиус ОА — отрезок, который откладывается на окружность. Его делят пополам точкой В.
- Перпендикулярно радиусу ОА начерчивается отрезок ОС, точки В и С соединяются прямой.
- Следующим шагом является отложение длины отрезка ВС с помощью циркуля на диаметральной линии. Перпендикулярно отрезку ОА появляется точка D. Точки В и D соединяются, образуя новый отрезок.
- Для того, чтобы получить величину стороны пентагона, необходимо соединить точки С и D.
- D с помощью циркуля переносится на окружность и обозначается точкой Е. Соединив Е и С, можно получить первую сторону правильного пятиугольника. Следуя этой инструкции можно узнать о том, как быстро построить пятиугольник с равными сторонами, продолжая построение остальных его сторон подобно первой.
Интересные факты
В пятиугольнике с одинаковыми сторонами диагонали равны и образуют пятиконечную звезду, которая называется пентаграммой. Золотое сечение — это отношение величины диагонали к стороне пентагона.
Пентагон непригоден для полного заполнения плоскости. Использование любого материала в этой форме оставляет промежутки или образует наложения. Хотя природных кристаллов этой формы не существует в природе, но при образовании льда на поверхности гладких медных изделий возникают молекулы в виде пентагона, которые соединены в цепочки.
Наиболее простой способ получить правильный пятиугольник из полоски бумаги — завязать ее узлом и немного придавить. Этот способ полезен для родителей детей-дошкольников, которые хотят научить своих малышей распознавать геометрические фигуры.
Этот способ полезен для родителей детей-дошкольников, которые хотят научить своих малышей распознавать геометрические фигуры.
Видео
Посмотрите, как можно быстро начертить пятиугольник.
Я РАСТУСайт для детей и их родителейПоследние события
Как из картинки сделать раскраску?
Раскраски любят и дети, и взрослые. И это неудивительно. Ведь даже не умея профессионально рисовать, можно создавать красивые рисунки, вкладывая в них своё умение и виденье .
Рисуем цыпленка
Вот такого цыпленка вы сможете нарисовать, если вы выполните все действия четко по шагам. Пробуйте и все у вас получится!
Елка-раскраска на стену
А так как скоро Новый Год, предлагаю скачать шаблон большой елки-раскраски. Этот шаблон состоит из 22 двух листов формата А4. На них нанесен и основной рисунок, и линии по которым нужно эти листочки склеить.
Дедушка Мороз и дети
Дед Мороз, Снегурочка, Снеговик, птицы и звери в лесу , дети на новогоднем празднике — вот герои этой книжки-раскраски. А создал их художник В. Жигарев.Маша и Медведь. Зимние раскраски
Мультик про шуструю озорную маленькую девочку Машу и ее приятеля медведя нравится всем — и детишкам, и их родителям.Раскраски с дедом Морозом
Новый год наступил. Но впереди еще старый новый год, да и зима еще вся впереди. Раскрашиваем картинки с Дедом Морозом и Снегурочкой.Раскраски к новому году
Новогодние раскраски. Зима, елка, дед Мороз в санях, подарки. Скачайте забавные картинки, пусть они напоминают вам о веселом празднике.
Популярное
Архив
Как нарисовать правильную звездочку
Как нарисовать правильную звездочку? Как нарисовать правильный пятиугольник? Как разделить круг на пять равных частей? На все эти вопросы вы сможете найти ответ, если проделаете вслед за мной эти шаги.Как нарисовать правильную звездочку?
Как нарисовать правильный пятиугольник?
Как разделить круг на пять равных частей?
На все эти вопросы вы сможете найти ответ, если проделаете вслед за мной вот эти шаги.
Конечно же, нам понадобится циркуль с карандашом и линейка.
Для начала нарисуйте циркулем круг.
Разделите его на четыре части линиями сверху вниз и справа налево.
Можно сразу объяснить ребенку, что отрезок, соединяющий две точки на окружности и проходящий через ее центр, называется диаметр.
А отрезок, соединяющий центр и точку на окружности, называется радиус.
С помощью линейки измерьте и разделите пополам один из радиусов.
У меня это отрезок слева от центра.
Серединку радиуса я обозначила
Нам понадобится точка сверху окружности.
Ее я обозначила цифрой 0.
Устанавливаем иголку циркуля
в точку 1, а карандашик в точку 0.
Рисуем дугу до пересечения с горизонтальным диаметром.
Обозначаем точку пересечения
Сейчас устанавливаем иголку циркуля
в точку 0, а карандашик в точку 2.
И рисуем дугу до пересечения с окружностью, причем с двух сторон.
Точки пересечения помечены
Не меняя ширину циркуля, устанавливаем иголку
в точку 3 и отмеряем кусочек окружности.
Точку 6 можно отмерить и от
точки 5 и от точки 4.
Главное, не изменять ширину (раствор) ножек циркуля.
Вот, практически и все.
Если соединим точки, получим правильный пятиугольник.
Построение на плоскости
Наверняка каждому из нас приходилось сталкиваться с тем, что нужно срочно что-то начертить, точный угол или многоугольник, а транспортира как нарочно под рукой нет, или Вы вообще никогда раньше ничего не чертили. Сегодня я хочу поделиться с Вами простыми схемами построения фигур на плоскости. Думаю, этот навык пригодится всем. Продолжение статьи:
http://www.livemaster.ru/topic/383001-postroenie-na-ploskosti-chast-2?ins >
Нам понадобятся: карандаш, линейка, циркуль.
Построение угла в 60
1. Проведём прямую и отметим на ней точку А.
2. Из точки А проведём дугу произвольного радиуса и получим точку В.
3. Из точки В проведём дугу радиуса АВ, чтобы она пересекла ранее начерченную дугу.
4. Проведённая через точку пересечения (С) и точку А прямая будет второй стороной требуемого угла.
Построение угла в 45
1. Построим угол 60, кака описано выше.
2. Разделим полученный угол пополам.
3. Угол между лучами 60 и 30 разделим пополам. В результате получим угол в 45.
Построение угла в 75
1. Построим угол в 60, как описано выше, и разделим его пополам.2. В ходе дальнейшего деления надвое получим угол в 15.
3. Отразим угол в 15 через луч 60 и так получим угол в 75.
Построение угла в 90
1. Построим угол в 60, как описано выше, и разделим его пополам.
2. Получившийся угол в 30 через луч 60 и так получим угол точно в 90.
Разделение отрезка на равные части.
1. Проведём прямую и отметим на ней отрезок АВ.
2. Из точки А проведём вспомогательную прямую и разделим её на столько одинаковых частей, на сколько требуется разделить отрезок АВ. Делить будем при помощи циркуля. Последнюю точку обозначим буквой С.
3. Последнюю точка (С) соединим с концом отрезка АВ. Построим рад параллельных отрезку СВ прямых по всей длине отрезка АВ. Точки пересечения параллельных прямых с отрезком АВ и будут точками раздела отрезка на несколько равных частей.
Построение правильного пятиугольника.
1. Проведём окружность радиусом 50 мм. Через центр окружности проведём взаимно перпендикулярные горизонтальную и вертикальную линии.
2. Разделим пополам расстояние ОВ. Разведём ножки циркуля на расстояние FC . Из точки F проведём дугу через С. Дуга пересечёт горизонтальную линию в точке G .
3. Расстояние CG будет длиной стороны пятиугольника. Из вершины С отложим пять раз расстояние CG .
Построение правильного шестиугольника.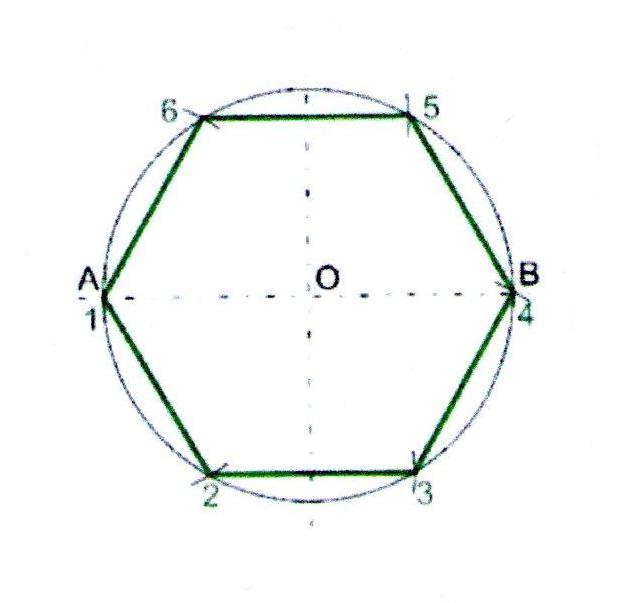
1. Проведём окружность радиусом 50 мм.
2. Через центр окружности проведём взаимно перпендикулярные горизонтальную и вертикальную линии.
3. Из точки А на линии окружности отложим шесть раз радиус нашей окружности. Соединив прямыми точки пересечения, получим шестиугольник.
Построение правильного семиугольника.
1. Проведём окружность заданного радиуса. Через центр окружности проведём взаимно перпендикулярные горизонтальную и вертикальную линии.
2. Из точки D проведём дугу радиусом равным радиусу окружности.
3. Дуга пересечёт окружность в точках E и G .
4. Длина отрезка EF на хорде EG равна длине стороны семиугольника. Из вершины С семь раз отложим расстояние EF .
Общий метод построения многоугольников.
1. Проведём окружность радиусом 50 мм. Через центр окружности проведём взаимно перпендикулярные горизонтальную и вертикальную линии. Продолжим горизонтальную лини. За точки А и В.
2. Из точки D проведём дугу радиусом, равным радиусу окружности так, чтобы дуга пересекла горизонтальную линию.
3. При помощи вспомогательной прямой разделим вертикальную линию на столько равных частей, сколько сторон многоугольника требуется получить. Для примера показано построение одиннадцатиугольника.
4. Из точки Е проведём прямые через нечётные точки раздела вертикальной линии так, чтобы эти прямые пересекли окружность. Такую же операцию проведём из точки G . Полученные лучи пересекают окружность в точках, соединив которые прямыми получаем одиннадцатиугольник.
Линейно-конструктивный рисунок шестигранной призмы
Научимся изображать шестигранную призму в различных положениях.
Изучите различные способы построения правильного шестиугольника, сделайте рисунки шестиугольников, проверьте правильность их построения. На основе шестиугольников постройте шестигранные призмы.
Рассмотрите шестигранную призму на рис. 3.52 и ее ортогональные проекции на рис. 3.53. В основании шестигранной призмы (шестигранника) лежат правильные шестиугольники, боковые грани — одинаковые прямоугольники. Для того, чтобы правильно изобразить шестигранник в перспективе, необходимо сначала научиться грамотно изображать в перспективе его основание (рис. 3.54). В шестиугольнике на рис. 3.55 вершины обозначены цифрами от одного до шести. Если соединить точки 1 и 3, 4 и 6 вертикальными прямыми, можно заметить, что эти прямые вместе с точкой центра окружности делят диаметр 5 — 2 на четыре равных отрезка (эти отрезки обозначены дугами). Противоположные стороны шестиугольника параллельны друг другу и прямой, проходящей через его центр и соединяющей две вершины (например, стороны 6 — 1 и 4 — 3 параллельны прямой 5 — 2). Эти наблюдения помогут вам построить шестиугольник в перспективе, а также проверить правильность этого построения. Построить правильный шестиугольник по представлению можно двумя способами: на основе описанной окружности и на основе квадрата.
3.52 и ее ортогональные проекции на рис. 3.53. В основании шестигранной призмы (шестигранника) лежат правильные шестиугольники, боковые грани — одинаковые прямоугольники. Для того, чтобы правильно изобразить шестигранник в перспективе, необходимо сначала научиться грамотно изображать в перспективе его основание (рис. 3.54). В шестиугольнике на рис. 3.55 вершины обозначены цифрами от одного до шести. Если соединить точки 1 и 3, 4 и 6 вертикальными прямыми, можно заметить, что эти прямые вместе с точкой центра окружности делят диаметр 5 — 2 на четыре равных отрезка (эти отрезки обозначены дугами). Противоположные стороны шестиугольника параллельны друг другу и прямой, проходящей через его центр и соединяющей две вершины (например, стороны 6 — 1 и 4 — 3 параллельны прямой 5 — 2). Эти наблюдения помогут вам построить шестиугольник в перспективе, а также проверить правильность этого построения. Построить правильный шестиугольник по представлению можно двумя способами: на основе описанной окружности и на основе квадрата.
На основе описанной окружности. Рассмотрите рис. 3.56. Все вершины правильного шестиугольника принадлежат описанной окружности, радиус которой равен стороне шестиугольника.
Линейно-конструктивный рисунок шестигранной призмы Линейно-конструктивный рисунок шестигранной призмы Линейно-конструктивный рисунок шестигранной призмыГоризонтальный шестиугольник. Изобразите горизонтальный эллипс произвольного раскрытия, т. е. описанную окружность в перспективе. Теперь необходимо найти на ней шесть точек, являющихся вершинами шестиугольника. Проведите любой диаметр данной окружности через ее центр (рис. 3.57). Крайние точки диаметра — 5 и 2, лежащие на эллипсе, являются вершинами шестиугольника. Для нахождения остальных вершин необходимо разделить этот диаметр на четыре одинаковых отрезка. Диаметр уже разделен точкой центра окружности на два радиуса, остается разделить каждый радиус пополам. На перспективном рисунке все четыре отрезка равномерно сокращаются при удалении от зрителя (рис. 3.58). Теперь проведите через середины радиусов — точки А и В — прямые, перпендикулярные прямой 5 — 2. Найти их направление можно при помощи касательных к эллипсу в точках 5 и 2 (рис. 3.59). Эти касательные будут перпендикулярны диаметру 5 — 2, а прямые, проведенные через точки А и В параллельно этим касательным, будут также перпендикулярны прямой 5 — 2. Обозначьте точки, полученные на пересечении этих прямых с эллипсом, как 1, 3, 4, 6 (рис. 3.60). Соедините все шесть вершин прямыми линиями (рис. 3.61).
3.58). Теперь проведите через середины радиусов — точки А и В — прямые, перпендикулярные прямой 5 — 2. Найти их направление можно при помощи касательных к эллипсу в точках 5 и 2 (рис. 3.59). Эти касательные будут перпендикулярны диаметру 5 — 2, а прямые, проведенные через точки А и В параллельно этим касательным, будут также перпендикулярны прямой 5 — 2. Обозначьте точки, полученные на пересечении этих прямых с эллипсом, как 1, 3, 4, 6 (рис. 3.60). Соедините все шесть вершин прямыми линиями (рис. 3.61).
Проверьте правильность вашего построения разными способами. Если построение верно, то линии, соединяющие противоположные вершины шестиугольника, пересекаются в центре окружности (рис. 3.62), а противоположные стороны шестиугольника параллельны соответствующим диаметрам (рис. 3.63). Еще один способ проверки показан на рис. 3.64.
Вертикальный шестиугольник. В таком шестиугольнике прямые, соединяющие точки 7 и 3, б и 4, а также касательные к описанной окружности в точках 5 и 2, имеют вертикальное направление и сохраняют его на перспективном рисунке. Таким образом, проведя две вертикальные касательные к эллипсу, найдем точки 5 и 2 (точки касания). Соедините их прямой линией, а затем разделите полученный диаметр 5 — 2 на 4 равных отрезка, учитывая их перспективные сокращения (рис. 3.65). Проведите вертикальные прямые через точки А и Б, а на их пересечении с эллипсом найдите точки 1,3,6л4. Затем последовательно соедините точки 1 — 6 прямыми (рис. 3.66). Правильность построения шестиугольника проверьте аналогично предыдущему примеру.
Описанный способ построения шестиугольника позволяет получить эту фигуру на основе окружности, изобразить которую в перспективе проще, чем квадрат заданных пропорций. Поэтому данный способ построения шестиугольника представляется наиболее точным и универсальным. Способ построения на основе квадрата позволяет легко изобразить шестигранник в том случае, когда на рисунке уже есть куб, иными словами, когда пропорции квадрата и направление его сторон определены.
На основе квадрата. Рассмотрите рис. 3.67. Вписанный в квадрат шестиугольник по горизонтальному направлению 5 — 2 равен стороне квадрата, а по вертикали — меньше ее длины.
Вертикальный шестиугольник. Нарисуйте вертикальный квадрат в перспективе. Проведите через пересечение диагоналей прямую, параллельную его горизонтальным сторонам. Разделите полученный отрезок 5 — 2 на четыре равные части и проведите через точки А и В вертикальные прямые (рис. 3.68). Линии, ограничивающие шестиугольник сверху и снизу, не совпадают со сторонами квадрата. Изобразите их на некотором расстоянии (1114 а) от горизонтальных сторон квадрата и параллельно им. Соединив найденные таким образом точки 1 и 3 с точкой 2, а точки 6 и 4 — с точкой 5, получим шестиугольник (рис. 3.69).
Горизонтальный шестиугольник строится в той же последовательности (рис. 3.70 и 3.71).
Этот способ построения уместен только для шестиугольников с достаточным раскрытием. В случае, если раскрытие шестиугольника незначительно, лучше воспользоваться способом на основе описанной окружности. Для проверки шестиугольника, построенного через квадрат, можно использовать уже известные вам методы.
Линейно-конструктивный рисунок шестигранной призмы Линейно-конструктивный рисунок шестигранной призмыКроме того существует еще один — описать вокруг полученного шестиугольника окружность (на вашем рисунке — эллипс). Все вершины шестиугольника должны принадлежать этому эллипсу.
Овладев навыками изображения шестиугольника, вы свободно перейдете к изображению шестигранной призмы. Внимательно рассмотрите схему на рис. 3.72, а также схемы построения шестигранных призм на основе описанной окружности (рис. 3.73; 3.74 и 3.75) и на основе квадрата (рис. 3.76; 3.77 и 3.78). Изобразите вертикальные и горизонтальные шестигранники различными способами. На рисунке вертикального шестигранника длинные стороны боковых граней будут параллельными друг другу вертикальными прямыми, а шестиугольник основания будет тем больше раскрыт, чем дальше он находится от линии горизонта. На рисунке горизонтального шестигранника длинные стороны боковых граней будут сходиться в точке схода на горизонте, а раскрытие шестиугольника основания будет тем больше, чем дальше от зрителя он находится. Изображая шестигранник, следите также за тем, чтобы параллельные грани обоих оснований сходились в перспективе (рис. 3.79; 3.80).
На рисунке горизонтального шестигранника длинные стороны боковых граней будут сходиться в точке схода на горизонте, а раскрытие шестиугольника основания будет тем больше, чем дальше от зрителя он находится. Изображая шестигранник, следите также за тем, чтобы параллельные грани обоих оснований сходились в перспективе (рис. 3.79; 3.80).
Как нарисовать невозможный шестиугольник – Невозможные фигуры
Понравились мои уроки рисования? Получите больше на YouTube:
Нажмите ЗДЕСЬ, чтобы сохранить учебник в Pinterest!
Что такое невозможный объект? Также называемые невозможными фигурами или неразрешимыми фигурами, эти рисунки являются разновидностью оптического обмана. Двумерная фигура кажется трехмерной, но геометрия не похожа ни на что, что могло бы существовать в реальном мире. Невозможные предметы использовались в интригующих произведениях искусства на протяжении всего двадцатого века.
Невозможный шестиугольник в этом руководстве по рисованию основан на треугольнике Пенроуза, который был создан художником в 1934 году. Полигоны Пенроуза, такие как этот шестиугольник, строятся путем добавления дополнительных сторон к треугольнику Пенроуза.
Тем не менее, оптическая иллюзия становится менее яркой, поскольку добавляется больше сторон. Таким образом, шестиугольник может казаться искривленным, заплетенным или искривленным, а не «невозможным».
Шестиугольники являются общими структурами как в искусстве, так и в природе. Вы знали? Соты сделаны из маленьких шестиугольников пчелиного воска. Интересно, что шестиугольник позволяет покрывать большое пространство как можно меньшим количеством воска.
Хотите нарисовать невозможный шестиугольник? Сделать это легко и весело с помощью этого простого, пошагового руководства по рисованию фигур. Все, что вам нужно, это карандаш, ручка или маркер и лист бумаги. Вы также можете покрасить свой законченный рисунок.
Пошаговая инструкция по рисованию – Невозможный шестиугольник
1. Начните с рисования шестиугольника. Шестиугольник — это правильная шестигранная фигура, в которой все стороны имеют одинаковую длину.
2. Нарисуйте короткую линию, идущую от верхнего угла шестиугольника. От этой линии вытяните более длинную линию, параллельную стороне шестиугольника. Затем от конца этой линии протяните прямую линию, параллельную следующей стороне шестиугольника. Обратите внимание, что расстояние между линией и второй стороной больше, чем между линией и первой стороной.
3. Нарисуйте короткую прямую линию, идущую от следующего угла шестиугольника. Протяните от него прямую линию, параллельную стороне шестиугольника.
4. Протяните короткую прямую линию от нижнего угла шестиугольника. Из этой линии нарисуйте прямую линию, параллельную нижней части шестиугольника. Затем продлите еще одну линию вверх, параллельно следующей стороне шестиугольника.
5. Проведите короткую линию от оставшегося нижнего угла шестиугольника. Отсюда нарисуйте прямую линию, параллельную стороне шестиугольника. Затем проведите еще одну линию параллельно следующей стороне шестиугольника.
6. Нарисуйте короткую прямую линию, выходящую из следующего угла шестиугольника. Затем протяните прямую линию, параллельную стороне шестиугольника.
7. Проведите короткую прямую линию от последнего угла шестиугольника. Отсюда вытяните прямую линию, параллельную вершине шестиугольника.
8. Начните соединять внешние края невозможного шестиугольника. Расширьте короткие линии от верхнего угла и стороны формы. Затем соедините эти линии с существующими линиями, заключив верхнюю и верхнюю часть рисунка.
9. Проведите короткую линию, идущую от нижнего угла шестиугольника. Затем соедините все открытые линии, пока фигура не будет полностью заключена.
Цвет и тень вашего невозможного шестиугольника. Обратите внимание, как затенение в нашем примере делает трехмерную иллюзию более яркой.

Построение правильных многоугольников — Техническое черчение
Построение вписанного в окружность правильного шестиугольника. Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой (фиг. 60, а).
Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг. 60, б), строим стороны 1 —6, 4—3, 4—5 и 7—2, после чего проводим стороны 5—6 и 3—2.
Построение вписанного в окружность равностороннего треугольника. Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля.
Рассмотрим два способа построения вписанного в окружность равностороннего треугольника.
Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, проведённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0—1—2 равен 30°, то для нахождения стороны
1—2 достаточно построить по точке 1 и стороне 0—1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1—2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2—3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника.
Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вершины через одну, то получится равносторонний треугольник.
Для построения треугольника (фиг. 61, б) намечаем на диаметре вершину—точку 1 и проводим диаметральную линию 1—4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника.
Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника.
Построение квадрата, вписанного в окружность. Это построение можно выполнить при помощи угольника и циркуля.
Первый способ основан на том, что диагонали квадрата пересекаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные стороны квадрата 4—1 и 3—2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1—2 и 4—3.
Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра (фиг. 62, б). Намечаем на концах двух взаимно перпендикулярных диаметров точки А, В и С и из них радиусом у описываем дуги до взаимного их пересечения.
Далее через точки пересечения дуг проводим вспомогательные прямые, отмеченные на фигуре сплошными линиями. Точки их пересечения с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.
Построение вписанного в окружность правильного пятиугольника.
Чтобы вписать в окружность правильный пятиугольник (фиг. 63), производим следующие построения.
Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5.
Построение правильного пятиугольника по данной его стороне.
Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую.
Далее от точки К на этой прямой откладываем отрезок, равный 4/6 AB.
Получим точку 1—вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведёнными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.
Построение вписанного в окружность правильного семиугольника.
Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проводим из полюса F через чётные деления вертикального диаметра лучи, пересечение которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
Приведённый способ годен для построения правильных многоугольников с любым числом сторон.
Деление окружности на любое число равных частей можно производить также, пользуясь данными табл. 2, в которой приведены коэффициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.
2, в которой приведены коэффициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.
|
В первой колонке этой таблицы указаны числа сторон правильного вписанного многоугольника, а во второй—коэффициенты. Длина стороны заданного многоугольника получится от умножения радиуса данной окружности на коэффициент, соответствующий числу сторон этого многоугольника. |
Как нарисовать шестиугольник в AutoCAD? — Вокруг-Дом
Самый простой способ нарисовать шестиугольник в AutoCAD — это использовать инструмент многоугольника, введя шесть в качестве числа сторон. Если вы знаете радиус, который хотите использовать, то вы можете выбрать размер многоугольника от центра. Затем вы можете выбрать, хотите ли вы, чтобы шестиугольник был вписан в радиус или ограничен радиусом. В качестве альтернативы, если вы знаете длину ребра, которую хотите использовать, вы можете выбрать опцию «Край», выбрать базовую точку и затем ввести длину ребра по вашему выбору.
Шестиугольник, используя радиус
Начало действия Полигон. Кредит: Тим ЭшвудТип POL или же ПОЛИГОН в командной строке или щелкните значок многоугольника.
Ввод числа сторон, для шестиугольника, 6.credit: Tim AshwoodВойти 6 когда предложено для количества сторон.
Выбор, как измерить радиус. Кредит: Тим ЭшвудНажмите в области рисования, чтобы определить свой Центральная точка.
Понимание вписанного против Circumscribeed.credit: Тим Эшвуд Закрытие шестиугольника с помощью radius.credit: Тим Эшвуд
Закрытие шестиугольника с помощью radius.credit: Тим ЭшвудНажмите в области рисования или введите радиус.
Шестиугольник используя длину края
Шаг 1
Тип POL или же ПОЛИГОН в командной строке или щелкните значок многоугольника.
Шаг 2
Войти 6 когда предложено для количества сторон.
Выбор варианта. Кредит: Тим Эшвуднажмите
Нажмите в области рисования, чтобы указать базовая точка для длины ребра.
Закрытие шестиугольника с помощью длины ребра. Кредит: Тим ЭшвудВведите длина по вашему выбору или нажмите в области рисования снова на желаемой длине.
Как нарисовать шестиугольник с равными сторонами
Правильный шестиугольник — это такой шестиугольник у которого все шесть сторон равны и его шесть углов равны.
Центр правильного шестиугольника — на рисунке точка O равноудалена от вершин.
Светлая линия обозначающая высоту треугольника AOB : h называется — апофемой.
Отрезки OA , OB — радиусы правильного шестиугольника.
Обозначения на рисунке для правильного шестиугольника
| n=6 | число сторон и вершин правильного шестиугольника, | шт |
|---|---|---|
| α | центральный угол правильного шестиугольника, | радианы, ° |
| β | половина внутреннего угла правильного шестиугольника, | радианы, ° |
| γ | внутренний угол правильного шестиугольника, | радианы, ° |
| a | сторона правильного шестиугольника, | м |
| R | радиусы правильного шестиугольника, | м |
| p | полупериметр правильного шестиугольника, | м |
| L | периметр правильного шестиугольника, | м |
| h | апофемы правильного шестиугольника, | м |
Основные формулы для правильного шестиугольника
Периметр правильного шестиугольника
Полупериметр правильного шестиугольника
Центральный угол правильного шестиугольника в радианах
Центральный угол правильного шестиугольника в градусах
Половина внутреннего угла правильного шестиугольника в радианах
Половина внутреннего угла правильного шестиугольника в градусах
Внутренний угол правильного шестиугольника в радианах
Внутренний угол правильного шестиугольника в градусах
Площадь правильного шестиугольника
Отсюда получим апофему правильного шестиугольника
Есть ли поблизости от Вас карандаш? Взгляните-ка на его сечение – оно представляет собой правильный шестиугольник или, как его еще называют, гексагон. Такую форму имеет также сечение гайки, поле гексагональных шахмат, кристаллическая решетка некоторых сложных молекул углерода (к примеру, графит), снежинка, пчелиные соты и другие объекты. Гигантский правильный шестиугольник был недавно обнаружен в атмосфере Сатурна. Не кажется ли странным столь частое использование природой для своих творений конструкций именно этой формы? Давайте рассмотрим эту фигуру поподробнее.
Такую форму имеет также сечение гайки, поле гексагональных шахмат, кристаллическая решетка некоторых сложных молекул углерода (к примеру, графит), снежинка, пчелиные соты и другие объекты. Гигантский правильный шестиугольник был недавно обнаружен в атмосфере Сатурна. Не кажется ли странным столь частое использование природой для своих творений конструкций именно этой формы? Давайте рассмотрим эту фигуру поподробнее.
- Длина его сторон соответствует радиусу описанной окружности. Из всех геометрических фигур это свойство имеет лишь правильный шестиугольник.
- Углы равны между собой, и величина каждого составляет 120°.
- Периметр гексагона можно найти по формуле Р=6*R, если известен радиус описанной вокруг него окружности, или Р=4*√(3)*r, если окружность в него вписана. R и r – радиусы описанной и вписанной окружности.
- Площадь, которую занимает правильный шестиугольник, определяется следующим образом: S=(3*√(3)*R 2 )/2. Если радиус неизвестен, вместо него подставляем длину одной из сторон – как известно, она соответствует длине радиуса описанной окружности.
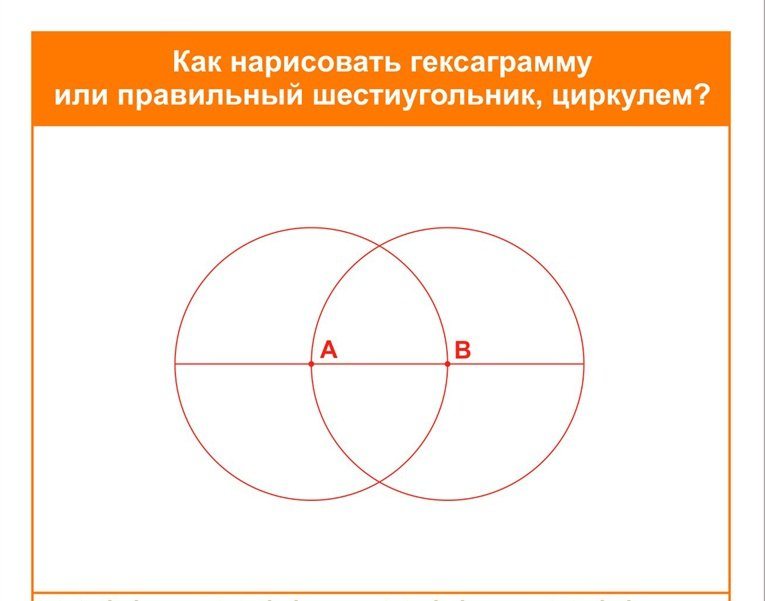
Теперь рассмотрим построение правильного шестиугольника. Есть несколько способов, самый простой из которых предполагает использование циркуля, карандаша и линейки. Вначале рисуем циркулем произвольную окружность, затем в произвольном месте на этой окружности делаем точку. Не меняя раствора циркуля, ставим острие в эту точку, отмечаем на окружности следующую насечку, продолжаем так до тех пор, пока не получим все 6 точек. Теперь остается лишь соединить их между собой прямыми отрезками, и получится искомая фигура.
В широком смысле шестиугольник — это многоугольник с шестью углами. У правильного же шестиугольника углы и стороны равны. Нарисовать такой шестиугольник можно при помощи рулетки и транспортира, грубый шестиугольник — при помощи круглого предмета и линейки или еще более грубый шестиугольник — при помощи интуиции и карандаша. Если вы хотите знать, как нарисовать шестиугольник различными способами, просто читайте далее.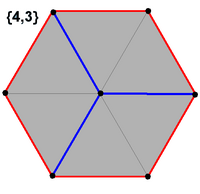
Построение правильного пятиугольника. Построение пятиугольника подробно Как нарисовать идеальный пятиугольник
Эта фигура является многоугольником с минимальным количеством углов, которым невозможно замостить площадь. Только у пятиугольника количество диагоналей совпадает с количеством его сторон. Воспользовавшись формулами для произвольного правильного многоугольника, можно определить все необходимые параметры, которые имеет пентагон. Например, вписать его в окружность с заданным радиусом либо построить на базе заданной боковой стороны.
Как правильно начертить луч и какие принадлежности для черчения вам понадобятся? Возьмите листок бумаги и отметьте в произвольном месте точку. Затем приложите линейку и проведите линию, начиная с указанной точки и до бесконечности. Чтобы начертить ровную линию, нажмите клавишу «Shift»и проведите линию нужной длины. Сразу после начертания откроется вкладка «Формат». Уберите выделение с линии и увидите, что в начале линии появилась точка. Для создания надписи нажмите кнопку «Нарисовать надпись» и создайте поле, где будет находиться надпись.
Первый способ построения пятиугольника считается более «классическим». Получившаяся в результате построения фигура будет правильным пятиугольником. Двенадцатиугольник не является исключением, поэтому его построение будет невозможным без применения циркуля. Задача построения правильного пятиугольника сводится к задаче деления окружности на пять равных частей. Начертить пентаграмму можно с использованием простейших инструментов.
Я долго бился пытаясь этого добиться и самостоятельно найти пропорции и зависимости, но мне этого не удалось. Оказалось, что есть несколько различных вариантов построения правильного пятиугольника, разработанных известными математиками. Инересным моментов является то, что арифметически эту задачу решить только приблизительно точно, поскольку придется использовать иррациональные числа. Зато ее можно решить геометрически.
Деление окружностей. Точки пересечения этих линий с окружностью и являются вершинами квадрата. В окружности радиуса R (Шаг 1) следует провести вертикальный диаметр. В точке сопряжения N прямой и окружности прямая является касательной к окружности.
Получение с помощью полоски бумаги
Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля. Чтобы построить сторону 2-3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника. Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
А на другой конец нитки устанавливаемые карандаш и одержим. Если умеете чертить звезду, но не умеете пятиугольник, начертите звезду карандашом, затем соедините между собой соседние концы звезды, а саму звезду потом сотрите. Затем положите лист бумаги (лучше его закрепить на столе при помощи четырёх кнопок или иголочек). Приколите эти 5 полосочек к листку бумаги кнопками или иголочками, чтобы они оставались неподвижными. Затем обведите полученный пятиугольник и снимите эти полосочки с листка.
Например, нам нужно нарисовать пятиконечную звезду (пентаграмму) для картины о Советском прошлом или о настоящем Китая. Правда для этого нужно уметь создать рисунок звезды в перспективе. Точно так же вы сможете нарисовать фигуру карандашом на бумаге. Как правильно нарисовать звезду, что бы она выглядела ровно и красиво, сразу не ответишь.
С центра опусти на окружность 2 луча, чтоб угол между ними был 72 градуса (транспортиром). Деление круга на пять частей осуществляется с помощью обычного циркуля или транспортира. Поскольку правильный пятиугольник — это одна из фигур, содержащая в себе пропорции золотого сечения, его построением издавна интересовались живописцы и математики.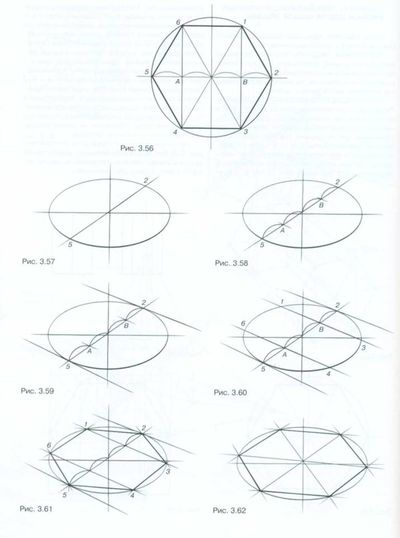 Эти принципы построения с применением циркуля и линейки были изложены еще в эвклидовых «Началах».
Эти принципы построения с применением циркуля и линейки были изложены еще в эвклидовых «Началах».
Первый способ — по данной стороне S с помощью транспортира.
Проводим прямую и откладываем на ней AB = S; принимаем эту линию за радиус и этим радиусом из точек A и В описываем дуги: далее с помощью транспортира строим в этих точках углы в 108°, стороны которых пересекутся с дугами в точках С и D; из этих точек радиусом АВ = 5 описываем дуги, которые пересекутся в Е, и прямыми линиями соединяем точки Л, С, Е, D, В.
Полученный пятиугольник — искомый.
Второй способ. Проведем окружность радиусом r. Из точки А циркулем проводим дугу радиуса AM до пересечения в точках В и С с окружностью. Соединяем В и С линией, которая пересечет горизонтальную ось в точке Е.
Затем из точки Е проводим дугу, которая пересечет горизонтальную линию в точке О. Описываем, наконец, из точки F дугу, которая пересечет окружность в точках Н и К. Отложив по окружности расстояние FO = FH = FK пять раз и соединив точки деления линиями, получим правильный пятиугольник.
Третий способ. В данный круг вписать правильный пятиугольник. Проводим два взаимно перпендикулярных диаметра АВ и МС. Делим радиус АО точкой Е пополам. Из точки Е, как из центра, проводим дугу окружности радиуса ЕМ и засекаем ею диаметр АВ в точке F. Отрезок MF равен стороне искомого правильного пятиугольника. Раствором циркуля, равным MF, делаем засечки N 1 , Р 1 , Q 1 , К 1 и соединяем их прямыми.
На рисунке построен шестиугольник по данной стороне.
Прямой АВ = 5, как радиусом, из точек А и В описываем дуги, которые пересекутся в С; из этой точки тем же радиусом описываем окружность, на которой сторона А В отложится 6 раз.
Шестиугольник ADEFGB — искомый.
«Отделка комнат при ремонте»,
Н.П.Краснов
Основанием для нанесения росписи служат полностью законченные окраской поверхности стен, потолков и других конструкций; роспись делается по высококачественным клеевым и масляным окраскам, сделанным под торцовку или флейц. Приступая к разработке эскиза отделки, мастер должен ясно представить себе всю композицию в бытовой обстановке и отчетливо осознать творческий замысел. Только при соблюдении этого основного условия можно правильно…
Приступая к разработке эскиза отделки, мастер должен ясно представить себе всю композицию в бытовой обстановке и отчетливо осознать творческий замысел. Только при соблюдении этого основного условия можно правильно…
Обмер выполненных работ, за исключением особо оговоренных случаев, производится по площади действительно обработанной поверхности с учетом ее рельефа и за вычетом необработанных мест. Для определения действительно обработанных поверхностей при малярных работах следует пользоваться переводными коэффициентами, приведенными в таблицах. А. Деревянные оконные устройства (обмер производится по площади проемов по наружному обводу коробок) Наименование устройств Коэффициент при…
Мы уже говорили, что для исполнения некоторых видов малярных работ необходимо уметь рисовать. А умение рисовать, в свою очередь, предполагает знание правил построения геометрических фигур. Эскизы на бумаге вычерчивают при помощи треугольников, рейсшин, транспортаpa и циркуля, а на плоскости стен и потолков построения выполняются при помощи веска, линейки, деревянного циркуля и шнура. При этом надо…
Вы находитесь в категории раскраски пятиугольник. Раскраска которую вы рассматриваете описана нашими посетителями следующим образом «» Тут вы найдете множество раскрасок онлайн. Вы можете скачать раскраски пятиугольник и так же распечатать их бесплатно. Как известно творческие занятия играют огромную роль в развитии ребенка. Они активизируют умственную деятельность, формируют эстетический вкус и прививают любовь к искусству. Процесс раскрашивания картинок на тему пятиугольник развивает мелкую моторику, усидчивость и аккуратность, помогает узнать больше об окружающем мире, знакомит со всем разнообразием цветов и оттенков. Мы ежедневно добавляем на наш сайт новые бесплатные раскраски для мальчиков и девочек, которые можно раскрашивать онлайн или скачать и распечатать. Удобный каталог, составленный по категориям, облегчит поиск нужной картинки, а большой выбор раскрасок позволит каждый день находить новую интересную тему для раскрашивания.
Как нарисовать и закрасить массив шестиугольников в python используя matplotlib
У меня есть класс POLYGON, каждый объект этого класса имеет в качестве параметров координаты вершин многоугольника (шестиугольника в данном случае) и параметр «value», который отображает, к примеру, значение какой-либо функции в данном шестиугольнике. Нужное количество шестиугольников в заданных точках я создаю без проблем. Вопрос в том, как нарисовать их, при этом так, чтобы каждый шестиугольник был закрашен в соответствии со значением параметра «value» и нарисовать также colorbar. Все это, используя библиотеку matplotlib. Пример, как должно получиться — на картинке.
Класс POLYGON:
class POLYGON:
def __init__(self,xc,yc,znum,value,st):
self.xc=xc #координата центра на оси абсцисс
self.yc=yc #координата центра на оси ординат
self.znum=znum #для нумерации и поиска
self.value=value #значение функции в данном шестиугольнике
self.st=st #размер под ключ
self.r=st/2 #радиус вписанной окружности
self.R=st/pow(3,.5) #радиус описанной окружности
self.a=self.R #сторона шестиугольника
self.points=[(self.xc+self.a/2,self.yc+self.r), #массив координат вершин
(self.xc+self.R,self.yc),
(self.xc+self.a/2,self.yc-self.r),
(self.xc-self.a/2,self.yc-self.r),
(self.xc-self.R,self.yc),
(self.xc-self.a/2,self.yc+self.r)]
Я могу их нарисовать, используя pylab:
def drawPolygons (axes,points,color):
"""
Рисование многоугольника
"""
polygon_1 = pylab.Polygon (points,
facecolor=color,
edgecolor='black')
axes.add_patch (polygon_1)
#Допустим, есть массив координат центров шестиугольников
xc=[0, 10.392304845413264, 20.784609690826528]
yc=[0, -6.0, -12.0]
poly=[] #Массив, содержащий объекты шестиугольников
for i in range(len(xc)):
#Инициализация шестиугольника с данными координатами центра
#Со случайным параметром "value"
pol=POLYGON(xc[i],yc[i],'znum',random. randint(0,20),12)
poly.append(pol)
pylab.xlim (-50, 50)
pylab.ylim (-50, 50)
axes = pylab.gca()
axes.set_aspect("equal")
for i in range(len(poly)):
a=poly[i].points
drawPolygons (axes,a,(1.0,0.0,0.0,0.7))
pylab.show()
randint(0,20),12)
poly.append(pol)
pylab.xlim (-50, 50)
pylab.ylim (-50, 50)
axes = pylab.gca()
axes.set_aspect("equal")
for i in range(len(poly)):
a=poly[i].points
drawPolygons (axes,a,(1.0,0.0,0.0,0.7))
pylab.show()
Однако, в этом случае приходится явно задавать цвет. Как сделать автоматическую генерацию цветов для любых colormaps из matplotlib, зная значения «value» для всех шестиугольников, и как сделать colorbar не понимаю.
Урок 26. построение правильных многоугольников — Геометрия — 9 класс
Для построения правильных n-угольников при n>4 обычно используется окружность, описанная около многоугольника.
Задача 1. Построим правильный шестиугольник, сторона которого равна данному отрезку
Воспользуемся формулой для стороны правильного шестиугольника:
a6 = 2Rsin (180°)/6 = 2R sin30° = 2R ∙ 1/2 = R, т.е. сторона шестиугольника равна радиусу описанной окружности.
Построим с помощью отрезка PQ окружность, радиусом которой будет являться данный отрезок.
Отметим на окружности точку А1 в произвольном месте. Для построения остальных точек возьмем циркуль. Зафиксируем его раствор размером с выбранный нами отрезок. Не меняя раствора циркуля, построим на окружности точки А2, А3, А4, А5, А6, таким образом, чтобы выполнялись равенства отрезков A1A2 = A2A3 = A3A4 = A4A5 = A5A6.
Соединим точки отрезками. Получим искомый правильный шестиугольник
Задача 2. Дан правильный n-угольник. Построить правильный 2n-угольник.
Пусть А1А2А3Аn правильный n-угольник. Начертим описанную окружность. Для этого построим биссектрисы углов А1 и А2. Точку пересечения биссектрис, а это центр окружности, обозначим буквой О. Из точки пересечения биссектрис проведем окружность радиуса ОА1. Разделим дуги А1А2, А2А3 и так до Аn пополам. Точки деления дуг обозначим как В1, В2 и так до Вn. Для построения точек В1, В2 до Вn можно воспользоваться серединными перпендикулярами к сторонам рассматриваемого нами многоугольника.
Начертим описанную окружность. Для этого построим биссектрисы углов А1 и А2. Точку пересечения биссектрис, а это центр окружности, обозначим буквой О. Из точки пересечения биссектрис проведем окружность радиуса ОА1. Разделим дуги А1А2, А2А3 и так до Аn пополам. Точки деления дуг обозначим как В1, В2 и так до Вn. Для построения точек В1, В2 до Вn можно воспользоваться серединными перпендикулярами к сторонам рассматриваемого нами многоугольника.
Соединим эти точки с концами соответствующей дуги, т.е. с вершинами многоугольника.
Таким образом, построен правильный двенадцатиугольник из шестиугольника.
С помощью данного способа, применяя простые инструменты циркуль и линейку, можно построить целый ряд правильных многоугольников, если построен один из них.
Правило. С помощью циркуля и линейки можно построить любой правильный 2k-угольник, где k любое целое число, большее двух.
Интересные факты.
Семиугольник не может быть построен при помощи циркуля и линейки.
Семнадцатиугольник может быть построен с помощью циркуля и линейки.
Обычное, Идеальное, От Квадрата
Как нарисовать шестиугольник? Как разделить круг на пять равных частей? Вы сможете найти ответ на все эти вопросы, если выполните эти шаги вслед за мной. Слабо определенный шестиугольник — это любой многоугольник с шестью сторонами. Однако правильный шестиугольник состоит из шести равных частей и шести равных углов.
Посмотрите на изображения шестиугольников, чтобы получить четкое представление о том, что вы рисуете. О том, как нарисовать шестиугольник и идеально правильную форму, и пойдет речь в этой статье! Нарисовать шестиугольник просто и понятно, если следовать вашим рекомендациям! В контакте, подумайте, просто начертите доступное изображение шестиугольника.
С помощью линейки и транспортира начертите идеальный шестиугольник. Чтобы получить более грубый шестиугольник, попробуйте использовать круглую форму и линейку, чтобы указать рукой. Если точность не имеет первостепенного значения, не стесняйтесь подготовить легкий шестиугольник, используя всего лишь карандаш и свое чутье. Конечно, нам понадобится циркуль с ручкой и линейкой, чтобы нарисовать красивый шестиугольник!
Чертеж идеального шестиугольника Для начала нарисуйте циркуль.
Разделите его на четыре части линиями сверху вниз и справа налево.
Сразу объясните ребенку, что отрезок, соединяющий две точки на окружности и проходящий через его центр, называется диаметром.
А отрезок, соединяющий центр и точку на окружности, называется радиусом.
Как нарисовать правильную звездочку
С помощью линейки отмерьте и разрежьте пополам одну из радиостанций.
У меня этот сегмент находится слева от центра.
Я отметил середину радиуса.
номер 1.
Нам нужна точка на вершине круга.
Я отметил его цифрой 0.
Установить стрелку компаса
до точки 1 и карандашом указать 0.
Нарисуйте дугу до пересечения с горизонтальным диаметром.
Обозначим точку пересечения
номер 2.
Теперь устанавливаем стрелку компаса.
до точки 0 и карандашом указать 2.
И нарисуйте дугу до пересечения с кругом, причем с двух сторон.
Обозначены точки пересечения.
числа 3 и 4.
Не меняя ширины циркуля, установите стрелку.
в точке 3 и отмерьте кусок круга.
Ставим точку 5.
Точку 6 можно измерить от
точки 5 и из пункта 4.
Главное не менять ширину (раствор) ножек суппорта.
Здесь почти все.
Если соединить точки, получится правильный пятиугольник. А можно звездочку нарисовать!
Вот так звездочка нарисована.
Как нарисовать пятиугольник, шестиугольник и другие многоугольники в Python Turtle?
Многоугольник — это n-сторонняя замкнутая фигура. Все стороны многоугольника одинаковой длины. Название многоугольника зависит от того, сколько у него сторон. Внешний угол многоугольника равен 360 / (количество сторон). Итак, для пятиугольника это будет 72. Для шестиугольника это будет 60. И так далее.
| Количество сторон | Название многоугольника | Внешний угол |
|---|---|---|
| 5 | Пентагон | 72 |
| 6 | Шестиугольник | 60 |
| 7 | Гептагон | 51.42 |
| 8 | восьмиугольник | 45 |
| 9 | Наногон | 40 |
| 10 | декагон | 36 |
Чтобы нарисовать пятиугольник, шестиугольник и другие многоугольники, мы будем использовать вышеупомянутые свойства.
Нарисуйте пятиугольник в Python Turtle
# Программирование Python для рисования пятиугольника в программировании черепах импортная черепаха т = черепаха.Черепаха () для i в диапазоне (5): t.forward (100) # Предполагая, что сторона пятиугольника равна 100 единицам t.right (72) # Поворот черепахи на 72 градуса
Вывод вышеуказанной программы
Расшифровка указанного кода —
для i в диапазоне (5): т. вперед (100) т. правый (72)
Мы предполагаем, что сторона пятиугольника равна 100 единицам. Итак, переместим черепаху вперед на 100 единиц. А затем поверните его по часовой стрелке на 72 °. Поскольку внешний угол пятиугольника равен 72 °.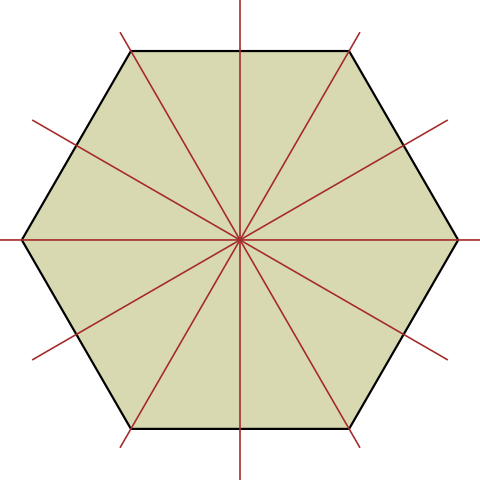 Эти два утверждения повторяются 5 раз, чтобы получить Пентагон.
Эти два утверждения повторяются 5 раз, чтобы получить Пентагон.
Нарисуйте шестиугольник в Python Turtle
# Программирование Python для рисования шестиугольника в программировании черепах импортная черепаха t = черепаха. Черепаха () для i в диапазоне (6): t.forward (100) # Предполагая, что сторона шестиугольника равна 100 единицам t.right (60) # Поворот черепахи на 60 градусов
Вывод вышеуказанной программы
Нарисуйте семиугольник в Python Turtle
# Программирование Python для рисования семиугольника в программировании черепах импортная черепаха t = черепаха. Черепаха () для i в диапазоне (7): т.forward (100) # Предполагая, что сторона семиугольника равна 100 единицам t.right (51,42) # Поворот черепахи на 51,42 градуса
Вывод вышеуказанной программы
Нарисуйте восьмиугольник в Python Turtle
# Программирование Python для рисования восьмиугольника в программировании черепах импортная черепаха t = черепаха. Черепаха () для i в диапазоне (8): t.forward (100) # Предполагая, что сторона восьмиугольника равна 100 единицам t.right (45) # Поворот черепахи на 45 градусов
Вывод вышеуказанной программы
Нарисовать многоугольник в Python Turtle
# Программирование на Python для рисования многоугольника в программировании на черепахах
импортная черепаха
т = черепаха.Черепаха ()
numberOfSides = int (input ('Введите количество сторон многоугольника:'))
lengthOfSide = int (input ('Введите длину стороны многоугольника:'))
externalAngle = 360 / numberOfSides
для i в диапазоне (numberOfSides):
т. вперед (lengthOfSide)
t.right (externalAngle) Вывод вышеуказанной программы
Рекомендуемые сообщения
сообщить об этом объявленииКак нарисовать шестиугольную сетку в React With Canvas | Автор: Джавьер Тимм | The Startup
Побывать в учебном лагере Flatiron School — это действительно потрясающе.Я прошел путь от минимального, почти несуществующего прошлого в кодировании к тому, что теперь я могу создать полноценный веб-сайт практически с нуля.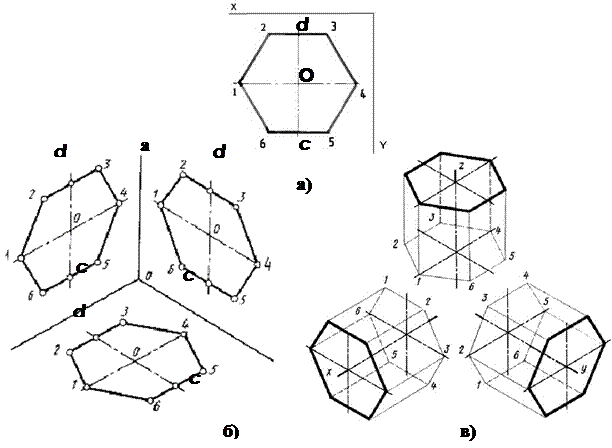 Но даже со всеми предоставленными нам инструментами и информацией мы должны взять непрерывное образование в свои руки, чтобы создавать большие и лучшие вещи. Как программист, ты всегда учишься чему-то новому, и для мода 5 я поступил именно так. Для своего проекта я делаю программу для случайного создания различных карт для игры « Settlers of Catan ».
Но даже со всеми предоставленными нам инструментами и информацией мы должны взять непрерывное образование в свои руки, чтобы создавать большие и лучшие вещи. Как программист, ты всегда учишься чему-то новому, и для мода 5 я поступил именно так. Для своего проекта я делаю программу для случайного создания различных карт для игры « Settlers of Catan ».
Что такое поселенцы Катана? Catan , ранее известная как The Settlers of Catan или просто Settlers , это многопользовательская настольная игра, в которой игроки берут на себя роли поселенцев, каждый из которых пытается строить и развивать владения, торгуя и приобретая Ресурсы. Игроки получают очки по мере роста их поселений, и побеждает тот, кто первым наберет определенное количество очков, обычно 10.
Я видел несколько различных вариантов гексагональной сетки, а также некоторые генераторы плат, но большую часть того, что я видел, было мобильными приложениями.Итак, я хотел попробовать сделать веб-приложение. Итак, на данный момент я не закончил проект, но я установил сетку, и я думаю, что это была самая сложная часть этого проекта.
Я написал свой код, используя React , и вот что я написал:
Если вы не совсем понимаете, что я здесь делаю, не волнуйтесь. Я планирую подробно объяснить, что я написал и как это работает, чтобы получить примерно что-то вроде этого (часть gird):
Я предполагаю, что у вас уже установлен React и вы знаете, как запустить новое приложение для создания реакции. .Я создал класс Cavas и написал операторы рендеринга и возврата как обычно, а также визуализировал холст с помощью опоры.
Не беспокойтесь о функциях внутри класса Canvas, мы займемся этим.Далее мы должны создать состояние. Есть два способа сделать это. Более широко используется конструктор с аргументом props.
Более новый способ и лично более удобный для чтения — это объявление состояния и размещение в нем значений состояния по умолчанию.
Любой способ будет работать нормально и не повлияет на конечный продукт.
Вы можете указать canvasWidth и canvasHeight по своему усмотрению. Мне нужен был прямоугольник такого размера, поэтому я выбралNext, позволяющий распечатать этот холст на экране. Короче говоря, использование компонента componentWillMount позволит нам управлять размером холста до того, как что-либо будет отрисовано в DOM:
После того, как вы его запустите и запустите, давайте также создадим новый файл CSS для нашего холста под названием «Canvas. css ». Я бы рекомендовал поместить все ваши CSS-файлы в папку «Стиль».Как только вы создадите файл, мы напишем холст css:
Это просто даст холсту видимую границу, чтобы вы могли видеть края холста.Теперь мы должны увидеть, что на DOM появится прямоугольник, который выглядит примерно так:
Далее нам понадобится математическое уравнение, чтобы нарисовать шестиугольник, а также получить точки шестиугольника.
ctx — это просто соглашение об именах и означает «контекст», но там может работать все что угодно. getHexCornerCord (center, i) — это именно то, что сказано в соглашении об именах.Это функция, которая позволит нам получить шестиугольник, идеально удаленный от центра. Мы вызываем this.state.hexSize, чтобы получить размер шестиугольника (который можно изменить по своему усмотрению), и мы используем математическую библиотеку для обработки более сложных математических вычислений.
Функция Point просто обрабатывает превращение x и y в объекты, а функция drawLine обрабатывает рисование линий для соединения точек.
Следующий код, который нам понадобится, это то, что на самом деле будет рисовать шестиугольник:
Я не совсем уверен, что такое canvasID и как эта функция полностью работает, но я знаю, что она работает ¯ \ _ (ツ) _ / ¯Теперь просто чтобы шестиугольник появился на экране, вам нужно будет создать новый жизненный цикл и использовать эти переменные:
Компонент, который вы можете поместить прямо под другой жизненный цикл componentWillMount () . По сути, вы просто вызываете функцию drawHex, которую мы создали ранее, и передаете эти переменные, чтобы загрузить этот шестнадцатеричный код. и он должен выглядеть примерно так:
По сути, вы просто вызываете функцию drawHex, которую мы создали ранее, и передаете эти переменные, чтобы загрузить этот шестнадцатеричный код. и он должен выглядеть примерно так:
Теперь, если вы хотите, чтобы шестиугольники отображались в симметричном узоре, это немного Мне сложно разобрать, но по сути код следующий:
Не забудьте закомментировать / удалить неиспользуемый код.Используйте git для резервного копирования и сохранения истории вашего кода.В этом жизненном цикле у нас есть массив, который зацикливается и делит «i% 2», что будет отображать сумму шестиугольников по обе стороны от центрированного шестиугольника. Это также можно расширить, добавив число в массив, я могу увеличить количество шестиугольников, отображаемых из центра. Конечный продукт должен выглядеть примерно так:
Спасибо, что так далеко попали в мой блог. Хлопки приветствуются и приветствуются. Признание также принадлежит Ринату Резяпову за алгоритм шестиугольника.И в этот блог о шестиугольной сетке https://www.redblobgames.com/grids/hexagons/
Приведенный выше текст на самом деле состоит из изображений, поэтому, если вам нужно скопировать часть текста, сделайте это ниже.Спасибо. ОБЫЧНАЯ ШЕСТИГРАННАЯ ПЛОСКОСТЬ. Этот урок является подготовительным к рисованию правильной шестиугольной призмы в следующем уроке. Когда шестиугольная плоскость вертикальна, перпендикулярна линии направления и: вложение на одном краю, как на рис.59, точка 6 будет прямо над 8, точка 7 над 9, а вертикальные линии 6-8 и 7-9 будут пересекать горизонтальную линию 1-2 на четверть от любого конца в точках 4 и 5. Следовательно, для этого положения (рис. 59) нарисуйте горизонтальную диагональ 1-2 и удобную длину и разделите ее на четыре равные части в точках 3, 4 и 5. Через 4 и 5 проведите вертикальные линии 6-7 и 8-9 подходящей длины и нарисуйте линии 1-6, 1-8, 2-7, 2-9, 6-7 и 8-9. Когда плоскость расположена вертикально и в укороченном виде, как на рис.6o, 61, 62 и 63 действуйте как прежде. Нарисуйте 1-2 правильного кажущегося уклона и разделите его на четыре части, которые немного неравны, r -5 немного больше, чем 5-3, и так далее. Через 4 и 5 проведите вертикальные линии соответствующей длины до 6, 7, 8 и 9, от которых проведите точки 6-2, 6-8, 8-1, 1-9, 9-7 и 7-2. Обратите внимание, что 6-8 и 7-9 будут немного сходиться с 1-2 от точки r. ПРАВИЛЬНАЯ ОБЫЧНАЯ ШЕСТИГРАННАЯ ПРИЗМА. Поместите большую правую правильную шестиугольную призму перед классом, сначала с одной прямоугольной гранью на горизонтальной плоскости в нескольких положениях, а затем поставьте на одном конце в нескольких положениях, как показано в мелком масштабе на рис. 7o, 71, 72, 73 и 74; или же маленькие картонные призмы, четыре или пять дюймов длиной, могут быть легко построенные учениками путем разметки, вырезания, складывания и рис.U. вставка формы, показанной на рис. U. Этот урок следует провести на пустой странице Когда призма расположена вертикально, как на рис.73 и 74, нарисуйте видимый конец, как ранее объяснялось для правильной шестиугольной плоскости. Затем проведите вертикальные линии вниз для длинных видимых краев, соответствующей длины по сравнению с горизонтальной шириной объекта, и завершите линии для видимых краев внизу. ПРАВИЛЬНАЯ ОБЫЧНАЯ ШЕСТИГРАННАЯ ПИРАМИДА. Поместите большую правильную шестиугольную пирамиду перед классом, сначала стоя на ее основании в нескольких положениях, а затем опираясь одной из своих треугольных граней на горизонтальную плоскость, в нескольких положениях, как показано в мелком масштабе на рис.75, 76, 77, 78, 79 и 80; или ученики могут легко сделать маленькие пирамиды высотой четыре или пять дюймов из картона, размечая, вырезая, складывая и приклеивая форму, показанную на рис. Когда пирамида стоит на основании, как на рис. 75, 76 и 77 основание 1-8-6, 2-7-9 должно быть сначала нарисовано так, как указано для горизонтальных правильных шестиугольных плоскостей.Проведите любые две диагонали через противоположные углы этого основания, чтобы найти центр, 3, в котором выровняйте вертикальную линию надлежащей высоты для вершины, 10. Соедините вершину с видимыми углами основания прямыми линиями. . Когда пирамида лежит на одной треугольной грани и видно все основание, как на рис. 79 и 80o, сначала можно нарисовать основание, как описано ранее для правильных шестиугольных плоскостей. Путем тщательной оценки и измерения карандашом зафиксируйте точку для вершины и присоедините ее к углам основания, чтобы отобразить видимые края.Если все края основания не видны, как на рис. 78, определите кажущийся уклон и нарисуйте самый длинный край на полу; затем соединяемых с ним краев и так далее, пока рисунок не будет завершен. ПИРАМИДА ПРАВАЯ ПЛОЩАДЬ.Поместите большую правую квадратную пирамиду перед классом, сначала поставив на ее основание в нескольких положениях, а затем положив на одну из ее треугольных граней в нескольких положениях, как это видно и расположено в мелком масштабе на рис.37, 38, 39, 4o, 41 и 42. Пирамида также может быть построена из картона в соответствии с формой, показанной на рис. R, и размещена на столе ученика или на подставке для модели. Вертикальные пирамиды должны быть нарисованы в верхней части пустой страницы 6 и иметь высоту четыре или пять дюймов. Горизонтальные пирамиды должны быть нарисованы в нижней части пустой страницы 6, а высота основания — около двух с половиной дюймов. Когда пирамида стоит на основании, как на рис. 37, 38 и 39, закрепите его за ближайший угол основания. Когда пирамида лежит на одной из своих треугольных граней, как на рис. 40, 41 и 42, сначала найдите кажущийся наклон видимых краев на полу, а затем краев, соединенных с ними, до тех пор, пока все не будет завершено. На домашнем уроке ученики могут нарисовать башню или колокольню церкви или другого здания, или какой-нибудь пирамидальный объект, а затем нарисовать его на одной из ненумерованных чистых страниц тетради для рисования. КВАДРАТНАЯ РАМА.Этот объект может быть изготовлен из картона путем отсечения и разрезания формы, подобной изображенной на рис. S, сгиба ее по пунктирным линиям и склеивания краев вместе, как указано ранее. Размер рамы в готовом виде должен составлять около четырех дюймов. |
Как нарисовать шестиугольник с помощью HTML5 и тега холста
Как нарисовать шестиугольник с помощью HTML5 и тега холстаЕсли вы хотите нарисовать шестиугольную форму на веб-странице, HTML5 предоставляет удобный способ сделать это. используя тег холста и javascript.
Построение шестиугольника на основе предыдущего примера. мы находим, что этот процесс значительно проще, если использовать векторы и линии как часть холста HTML 5. Вот пример, показывающий, как нарисовать шестиугольную форму с помощью HTML5 и тега холста.
В этом примере не представлены параметры стиля CSS из предыдущего примера рисования шестиугольника, но
его легче использовать в отношении других операций программирования, которые вам нужно будет выполнить, если вы пишете сценарии
это для игры. Например, логично предположить, что что-то должно быть помещено «внутри»
форма, которая демонстрируется здесь.
Например, логично предположить, что что-то должно быть помещено «внутри»
форма, которая демонстрируется здесь.
Тег и пример кода
Код, использованный для создания примера, можно увидеть ниже. Тег холста сначала создается в DOM. Здесь применяются некоторые правила стиля CSS с использованием класса my_canvas просто для того, чтобы сопоставьте цветовую схему здесь, а также чтобы показать, что вы можете применить стиль CSS к холсту с помощью атрибутов html класса или стиля. Пример кода javascript запускается кнопкой рядом с холстом. Кнопка использует состояние переключения, чтобы отслеживать, должен ли щелчок «очищать» холст или «рисовать» на холсте.Я подумал, что было бы полезно увидеть здесь контекст, но, оглядываясь назад, я не большой поклонник переключения здесь, потому что он загрязняет взаимодействие с холстом — ваш пример, вероятно, не нужно рисовать или очищать с помощью кнопки. Приношу свои извинения за любую путаницу, я надеюсь пересмотреть это в будущем, чтобы лучше изолировать эти два аспекта.Вот что делает этот пример
- Создать тег холста
- Получите ссылку на тег холста с помощью javascript
- Настройка контекста чертежа («2D» означает двухмерный)
- Установить переменные x и y
- Перемещайтесь по изменениям x и y, необходимым для отслеживания формы шестиугольника.
- Нарисуйте линии для любой из ног, которые нам нужно показать
- Установка характеристик стиля рисования, таких как цвет и толщина линии
- Запуск рисования
- Добавить текст
Холст тег
Пример кода
См. Также
Нарисуйте шестиугольник с помощью циркуля для рисования — Практическое руководство
Я не могу вспомнить, изучал ли я эту технику рисования шестиугольника в начальной школе, но я определенно помню, как моя мама учила меня, делая для нас одеяло из шестиугольника … с помощью циркуля для рисования … Мой первый урок по сшиванию шестиугольника цветка Блок квилта предназначен для рисования этого картонного шаблона шестиугольника. До сегодняшнего дня я все еще слышу бормотание мамы в ушах…
До сегодняшнего дня я все еще слышу бормотание мамы в ушах…
«Идеальный шестигранный цветок для квилтинга получается из точных шестигранных шаблонов» … ..
Пока я не стал немного старше, я научился использовать угловую линейку, чтобы рисовать шестиугольник в моем формальном образовании, например, делить 360 ° на 6 частей по кругу и т. Д. Но мне все еще нравится способ моей мамы, с одним простым инструментом, компасом … так прямолинейно и надежно !!! Если вы используете компьютерное программное обеспечение для создания шаблона шестиугольника, это один из простейших методов….просто замените циркуль кружками.
Нарисуйте шаблон шестиугольника вашего собственного размера, используя этот урок, чтобы сделать свое лоскутное одеяло из шестиугольника.
Как нарисовать шестиугольник для лоскутного одеяла
Инструменты:
1. Циркуль
2. Карандаш (заточенный)
3. Линейка
4. Картон
5. Ножницы
Нарисуйте круг на картоне с помощью циркуля желаемого радиуса.
Радиус — это ширина одной из граней вашего шестиугольника.
Наибольшая ширина шестиугольника — это диаметр круга, который в 2 раза больше радиуса.
Отметьте произвольно первую точку на окружности.
С такими же настройками на компасе поместите стрелку компаса в 1-ю точку и отметьте вторую точку пересечения на окружности.
Поверните циркуль на другую сторону круга, отметьте третью точку пересечения.
Повторите процесс, переместив стрелку компаса на 2-ю точку и 3-ю точку, чтобы отметить 4-ю и 5-ю точки соответственно, а затем — 6-ю точку.
Вы можете выполнить контрпроверку правильности разметки, например, когда ваша стрелка находится на 2-й точке, а вы отмечаете 4-ю точку, поверните циркуль в 1-ю точку и посмотрите, касается ли карандаш той же точки.
После того, как вы отметили все 6 точек на окружности, нарисуйте отрезок прямой линии между ближайшими пересечениями. Вот ваш шестиугольник с 6 равными сегментами на круге.
Вот ваш шестиугольник с 6 равными сегментами на круге.
Вырежьте из картона шестигранник.Используйте его в качестве шаблона и начните рисовать шестиугольники для своего проекта квилтинга.
Проверьте соответствие формы и размера. При необходимости нарисуйте еще один новый шаблон шестиугольника, если первый изношен после выполнения некоторых начертаний.
Нарисуйте еще один шаблон побольше для ткани. Добавьте еще от 1/2 ″ до 3/4 ″ к радиусу шаблона ткани, повторите технику рисования шестиугольника, чтобы создать шаблон ткани. Вам понадобится всего несколько штук, чтобы просто нарисовать шестиугольники на ткани.
Шестиугольники разных размеров, от 1 до 3 дюймов в ширину.
Возьмите достаточно их (1 размера) для запланированного проекта квилтинга и сшейте их вместе.
Как рисовать 2D-фигуры в детском саду — KindergartenWorks
Обучение основам в детском саду может иметь большое значение. Я считаю ключевым обучать мелочам сразу, чтобы преимущества сохранялись круглый год.
Я думаю, что обучение детсадовцев рисованию 2D-форм могло бы уместиться в списке основ.Они не только должны называть 2D-формы, но и описывать их.
Я думаю, что обучение их рисованию 2D-форм в детском саду очень помогает в обучении фигурам, а также улучшает навыки рисования и письма ученикам.
Вот простой совет, который я узнал от лучшего дошкольного воспитателя нашего района.
Обучение рисованию 2D-форм на самом деле сводится к использованию углов / вершин. Я покажу вам треугольник, шестиугольник, прямоугольник и квадрат.Начнем с треугольника, и вы поймете, что я имею в виду.
Чтобы научить киндеров рисовать треугольник, вам нужно всего два шага. В противном случае научиться рисовать треугольник может быть непросто, и часто ученики могут разочароваться в своих результатах.
Попросите учащихся нарисовать на листе три точки. Мне нравится моделировать рисунок один сверху и два снизу (например, букву A в верхнем регистре). Рисуя эти точки, они, по сути, планируют, где будут углы / вершины.
Затем попросите учащихся соединить точки.На этом края треугольника заканчиваются, и они довольны своим рисунком.
А теперь перейдем к квадрату.
Обучение в детском саду рисованию квадрата включает те же два шага. Однако на этот раз им следует поработать, обращая внимание (грубо говоря) на то, насколько близко точки / углы расположены по отношению друг к другу.
Первый шаг — нарисовать четыре точки. Нарисуйте две точки (сверху), а затем нарисуйте соответствующие точки под ними примерно на том же расстоянии ниже.
Затем соедините точки четырьмя прямыми линиями, чтобы закончить рисование квадрата.
Достаточно просто, правда? Я знаю! И все же он учит их этой стратегии, чтобы помочь им научиться успешно делать это самостоятельно.
Обучение рисованию прямоугольника очень похоже.
Нарисуйте две точки (сверху), но далеко друг от друга. Вот так я люблю моделировать, как нарисовать прямоугольник для детского сада. Вы также можете продемонстрировать повернутый прямоугольник.
Затем сопоставьте расстояние, нарисовав две точки внизу, не беспокоясь о равном расстоянии, как мы рисовали квадрат.
Нарисуйте четыре линии, чтобы соединить точки и сделать края.
Мы не будем учиться рисовать круг, потому что, честно говоря, это вопрос развития. Они могут научиться рисовать замкнутый круг только тогда, когда будут готовы.
Последняя форма — шестиугольник. Это может быть немного сложнее, но если вы преподаете в том же формате, выучить его будет легче. Чтобы нарисовать шестиугольник в детском саду, нужно выполнить три шага.
Начните с обучения студентов рисованию квадрата.
Они рисуют четыре точки.Сверху рисуются две точки, а затем они образуют совпадающие точки под ними примерно на одинаковом расстоянии внизу.
Эта часть немного сложна, но разбивает форму на управляемые части.

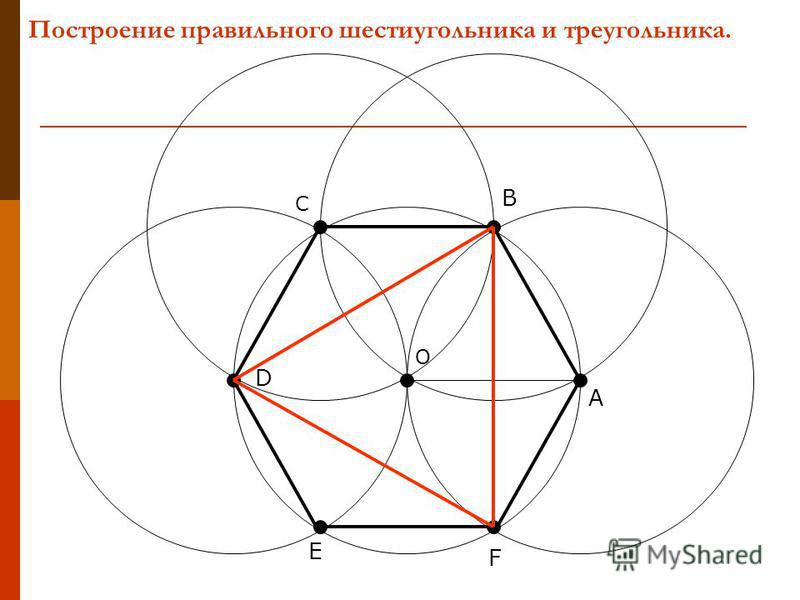 Сумма всех внутренних углов: 108*5 = 540 градусов.
Сумма всех внутренних углов: 108*5 = 540 градусов.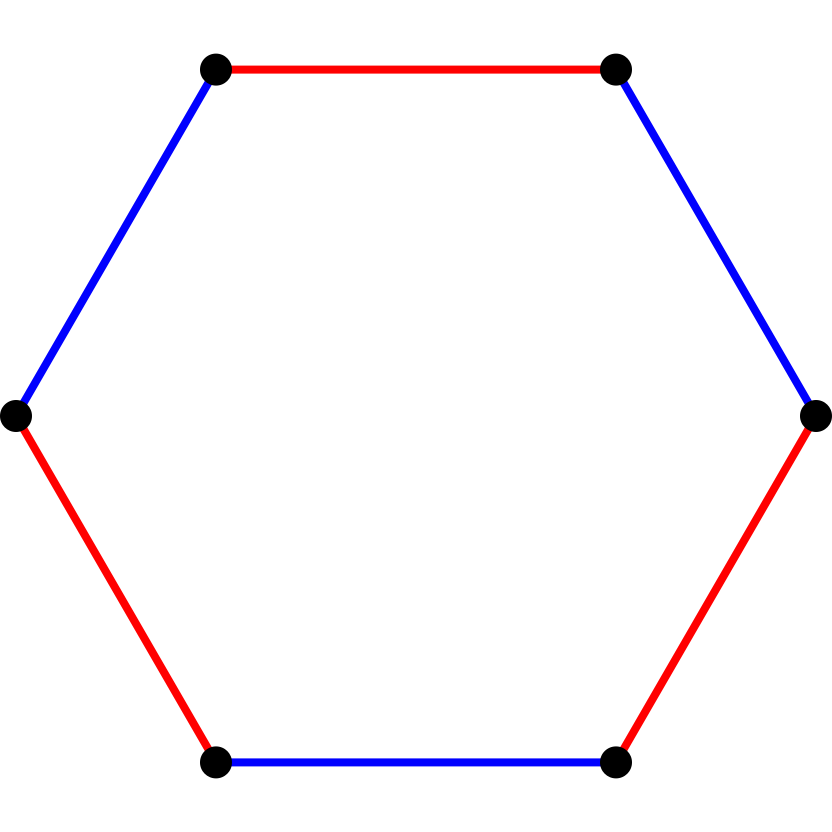
 randint(0,20),12)
poly.append(pol)
pylab.xlim (-50, 50)
pylab.ylim (-50, 50)
axes = pylab.gca()
axes.set_aspect("equal")
for i in range(len(poly)):
a=poly[i].points
drawPolygons (axes,a,(1.0,0.0,0.0,0.7))
pylab.show()
randint(0,20),12)
poly.append(pol)
pylab.xlim (-50, 50)
pylab.ylim (-50, 50)
axes = pylab.gca()
axes.set_aspect("equal")
for i in range(len(poly)):
a=poly[i].points
drawPolygons (axes,a,(1.0,0.0,0.0,0.7))
pylab.show()
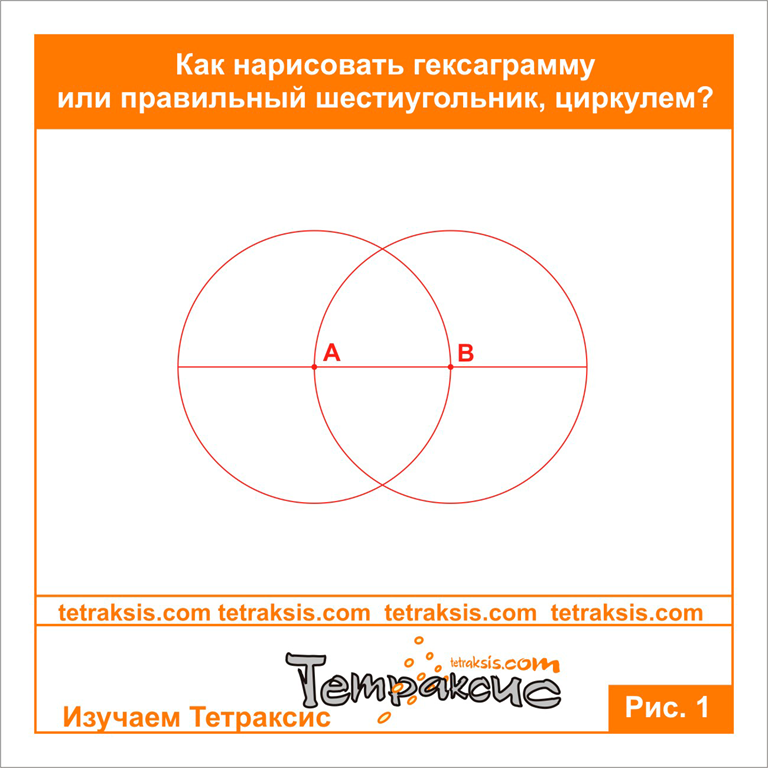 Поместите большую правильную шестиугольную плоскость, вырезанную из жесткого картона или тонкой древесины, перед классом в вертикальном положении, опираясь на один край, сначала плоскостью под прямым углом к линии направления, как на рис.59, а затем так что касается представления в ракурсе, как на рис.6o, 61, 62, 63, 64, 65, 66, 67, 68 и 69; или ученики могут легко вырезать небольшие шестиугольные плоскости с краями длиной два дюйма и разместить их на своих столах или опорах для моделей в необходимых положениях. Этот урок должен быть нарисован на пустой странице 9, вертикальные позиции в верхней половине страницы и горизонтальные позиции в нижней половине.
Поместите большую правильную шестиугольную плоскость, вырезанную из жесткого картона или тонкой древесины, перед классом в вертикальном положении, опираясь на один край, сначала плоскостью под прямым углом к линии направления, как на рис.59, а затем так что касается представления в ракурсе, как на рис.6o, 61, 62, 63, 64, 65, 66, 67, 68 и 69; или ученики могут легко вырезать небольшие шестиугольные плоскости с краями длиной два дюйма и разместить их на своих столах или опорах для моделей в необходимых положениях. Этот урок должен быть нарисован на пустой странице 9, вертикальные позиции в верхней половине страницы и горизонтальные позиции в нижней половине. Через 4 и 5 нарисуйте линии правильного видимого наклона и длины до 6, 7, 8 и 9, из которых проведите точки 6-8, 7-9, I -9, 1-8, 2-7 и 2 — 6.
Через 4 и 5 нарисуйте линии правильного видимого наклона и длины до 6, 7, 8 и 9, из которых проведите точки 6-8, 7-9, I -9, 1-8, 2-7 и 2 — 6. V. позиции в верхней части страницы, пять или шесть дюймов в высоту, и горизонтальные позиции в нижней части страницы.
V. позиции в верхней части страницы, пять или шесть дюймов в высоту, и горизонтальные позиции в нижней части страницы. Определите и нарисуйте наклон видимых краев 1 — 2 и 1 — 3 на полу. Завершите основу, нарисовав 2-4. сходящиеся с 1–3 и 3–4, сходящиеся с 1–2. Нарисуйте диагонали основания 1–4 и 2–3 так, чтобы найти центр 5, в этой точке проведите вертикальную линию надлежащей высоты для вершина 6, так как вершина правой пирамиды, стоящей на ее основании, будет находиться прямо над центром ее основания. От вершины 6 проведите прямые линии до видимых углов основания.
Определите и нарисуйте наклон видимых краев 1 — 2 и 1 — 3 на полу. Завершите основу, нарисовав 2-4. сходящиеся с 1–3 и 3–4, сходящиеся с 1–2. Нарисуйте диагонали основания 1–4 и 2–3 так, чтобы найти центр 5, в этой точке проведите вертикальную линию надлежащей высоты для вершина 6, так как вершина правой пирамиды, стоящей на ее основании, будет находиться прямо над центром ее основания. От вершины 6 проведите прямые линии до видимых углов основания.