Треугольник в круге как нарисовать: Как нарисовать в круге треугольник

Как начертить равнобедренный треугольник в круге. Рисуем треугольник в фотошопе

Как начертить треугольник?

Построение различных треугольников — обязательный элемент школьного курса геометрии. У многих это задание вызывает страх. Но на самом деле, все довольно просто. Далее в статье описано, как начертить треугольник любого типа с помощью циркуля и линейки.

Треугольники бывают

• разносторонние;
• равнобедренные;
• равносторонние;
• прямоугольные;
• тупоугольные;
• остроугольные;
• вписанные в окружность;
• описанные вокруг окружности.

Построение равностороннего треугольника

Равносторонним называется треугольник, у которого все стороны равны. Из всех видов треугольников, начертить равносторонний проще всего.

1. С помощью линейки начертите одну из сторон, заданной длины.
2. Измерьте ее длину с помощью циркуля.
3. Поместите острие циркуля в один из концов отрезка и проведите окружность.
4. Переставьте острие в другой конец отрезка и проведите окружность.
5. У нас получилось 2 точки пересечения окружностей. Соединяя любую из них с краями отрезка, мы получаем равносторонний треугольник.

Построение равнобедренного треугольника

Данный тип треугольников можно построить по основанию и боковым сторонам.

Равнобедренным называется треугольник, у которого две стороны равны. Для того чтобы начертить равнобедренный треугольник по данным параметрам, необходимо выполнить следующие действия:

1. С помощью линейки откладываем отрезок, равный по длине основанию. Обозначаем его буквами АС.
2. Циркулем измеряем необходимую длину боковой стороны.
3. Рисуем из точки А, а затем из точки С, окружности, радиус которых равен длине боковой стороны.
4. Получаем две точки пересечения. Соединив одну из них с точками А и С, получаем необходимый треугольник.

Построение прямоугольного треугольника

Треугольник, у которого один угол прямой, называют прямоугольным. Если нам даны катет и гипотенуза, начертить прямоугольный треугольник не составит труда. Его можно построить по катету и гипотенузе.

Построение тупоугольного треугольника по углу и двум прилегающим сторонам

Если один из углов треугольника тупой (больше 90 градусов), его называют тупоугольным. Чтобы начертить по указанным параметрам тупоугольный треугольник необходимо сделать следующее:

1. С помощью линейки откладываем отрезок, равный по длине одной из сторон треугольника. Обозначим его буквами А и D.
2. Если в задании уже нарисован угол, и вам необходимо начертить такой же, то на его изображении отложить два отрезка, оба конца которых лежат в вершине угла, а длина равняется указанным сторонам. Соедините полученные точки. У нас получился искомый треугольник.
3. Чтобы его перенести на свой чертеж, вам необходимо измерить длину третьей стороны.

Построение остроугольного треугольника

Остроугольный треугольник (все углы меньше 90 градусов) строится по тому же принципу.

1. Нарисуйте две окружности. Центр одной из них лежит в точке D, а радиус равен длине третьей стороны, а у второй центр находится в точке А, а радиус равен длине указанной в задании стороны.
2. Соедините одну из точек пересечения окружности с точками А и D. Искомый треугольник построен.

Вписанный треугольник

Для того чтобы начертить треугольник в окружности, нужно помнить теорему, в которой говорится, что центр описанной окружности лежит на пересечении серединных перпендикуляров:

У тупоугольного треугольника центр описанной окружности лежит за пределами треугольника, а у прямоугольного — на середине гипотенузы.

Чертим описанный треугольник

Описанный треугольник — это треугольник, в центре которого нарисована окружность, касающаяся всех его сторон. Центр вписанной окружности лежит на пересечении биссектрис. Для их построения необходимо:

Построение вписанного в окружность правильного шестиуголь­ника. Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения доста­точно разделить окружность на шесть равных частей и соединить най­денные точки между собой (фиг. 60, а).

Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг. 60, б), строим стороны 1 -6, 4-3, 4-5 и 7-2, после чего прово­дим стороны 5-6 и 3-2.

Построение вписанного в окружность равностороннего треуголь­ника . Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного цир­куля.

Рассмотрим два способа построения вписанного в окружность рав­ностороннего треугольника.

Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, прове­дённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0-1-2 равен 30°, то для нахождения стороны

1-2 достаточно построить по точке 1 и стороне 0-1 угол в 30°.

Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1-2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2-3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 прово­дим прямую, которая определит третью вершину треугольника.

Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вер­шины через одну, то получится равносторонний треугольник.

Для построения треугольника (фиг. 61, б) намечаем на диаметре вершину-точку 1 и проводим диаметральную линию 1-4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окруж­ностью в точках 3 и 2. Полученные точки будут двумя другими вер­шинами искомого треугольника.

Построение квадрата, вписанного в окружность . Это построение можно выполнить при помощи угольника и циркуля.

Первый способ основан на том, что диагонали квадрата пере­секаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные сто­роны квадрата 4-1 и 3-2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1-2 и 4-3.

Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра (фиг. 62, б). Намечаем на концах двух взаимно перпендикулярных диа­метров точки А, В и С и из них радиусом у описываем дуги до вза­имного их пересечения.

Далее через точки пересечения дуг проводим вспомогательные пря­мые, отмеченные на фигуре сплошными линиями. Точки их пересече­ния с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.

Построение вписанного в окружность правильного пятиугольника.

Чтобы вписать в окружность правильный пятиугольник (фиг. 63), про­изводим следующие построения.

Намечаем на окружности точку 1 и принимаем её за одну из вер­шин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точ­ках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вер­шины 3 и 4. Найденные точки последовательно соединяем между собой.

Построение правильного пятиугольника по данной его стороне.

Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую.

Получим точку 1-вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведён­ными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.

Построение вписанного в окружность правильного семиугольника.

Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиу­сом, равным диаметру окружности D, описываем дугу до пересечения с про­должением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, прово­дим из полюса F через чётные деления вертикального диаметра лучи, пересече­ние которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые.

Найденные вершины соединяем после­довательно между собой. Семиугольник может быть построен путём проведе­ния лучей из полюса F и через нечётные деления вертикального диаметра.

Приведённый способ годен для построения правильных многоуголь­ников с любым числом сторон.

Деление окружности на любое число равных частей можно произ­водить также, пользуясь данными табл. 2, в которой приведены коэф­фициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.

Равносторонний треугольник в фотошопе рисуется при помощи векторных объектов. Можно нарисовать закрашенный треугольник, можно треугольник с рамкой. Выбираем рисование многоугольников (Polygon tool).

Рисование многоугольников (Polygon tool)

Выбираем фигуры (гор. клавиша U ), затем Polygon tool (Инструмент Многоугольник), см. скриншот ниже.

Устанавливаем свойство «Fill Pixels».

Выбираем цвет заливки треугольника (первый цвет в панели инструментов), рисуем мышкой треугольник.

Треугольник с рамкой

Треугольник следует рисовать на новом пустом слое , без какой-либо заливки. Создать новый слой можно одновременным нажатием клавиш Alt + Ctrl + Shift + N .

Устанавливаем значение «Paths» (по-русски пути).

Рисуем мышкой треугольник.

Преобразуем векторный треугольник в выделение (Select), нажатием клавиш Ctrl + Enter .

Закрашиваем выделение (в данном случае белым цветом).

Alt + ← BackSpace — первый выбранный цвет.

Ctrl + ← BackSpace — второй выбранный цвет.

В свою бытность «чайником», я столкнулся с необходимостью нарисовать треугольник в Фотошопе. Тогда с этой задачей без посторонней помощи мне справиться не удалось.

Оказалось, что все не настолько сложно, как могло показаться на первый взгляд. В этом уроке я поделюсь с Вами опытом в рисовании треугольников.

Существуют два (известных мне) способа.

Первый способ позволяет изобразить равносторонний треугольник. Для этого нам нужен инструмент под названием «Многоугольник» . Находится он в разделе фигур на правой панели инструментов.

Этот инструмент позволяет рисовать правильные многоугольники с заданным числом сторон. В нашем случае их (сторон) будет три.

После настройки цвета заливки

ставим курсор на холст, зажимаем левую кнопку мыши и рисуем нашу фигуру. В процессе создания треугольник можно вращать, не отпуская кнопку мыши.

Полученный результат:

Кроме того, можно нарисовать фигуру без заливки, но с контуром. Линии контура настраиваются в верхней панели инструментов. Там же настраивается и заливка, вернее ее отсутствие.

У меня получились такие треугольники:

С настройками можно экспериментировать, добиваясь нужного результата.

Следующий инструмент для рисования треугольников – «Прямолинейное лассо» .

Этот инструмент позволяет рисовать треугольники с любыми пропорциями. Давайте попробуем изобразить прямоугольный.

Для прямоугольного треугольника нам понадобится точно нарисовать прямой (кто бы мог подумать…) угол.

Воспользуемся направляющими. Как работать с направляющими линиями в Фотошопе, читайте в этой статье .

Итак, статью прочитали, тянем направляющие. Одну вертикальную, другую горизонтальную.

Чтобы выделение «притягивалось» к направляющим, включаем функцию привязки.

Затем кликаем правой кнопкой мыши внутри выделения и выбираем, в зависимости от потребностей, пункты контекстного меню «Выполнить заливку» или «Выполнить обводку» .

Цвет заливки настраивается следующим образом:

Для обводки также можно настроить ширину и расположение.

Получаем следующие результаты:
Заливка.

Для получения острых углов обводку нужно выполнять «Внутри» .

После снятия выделения (CTRL+D ) получаем готовый прямоугольный треугольник.

Вот такие два простейших способа рисования треугольников в программе Фотошоп.

Как нарисовать остроугольный треугольник. Как построить равнобедренный треугольник. Построение равностороннего треугольника

Инструкция

Поставьте иглу циркуля в отмеченную точку. Нарисуйте ножкой с грифелем дугу окружности отмеренного радиуса.

В любом месте по окружности нарисованной дуги поставьте точку. Это будет вторая вершина B создаваемого треугольника.

Аналогичным способом поставьте ножку на вторую вершину. Проведите еще одну окружность так, чтобы она пресекалась с первой.

В точке пересечения обоих проведенных дуг и находится третья вершина C создаваемого треугольника. Отметьте ее на рисунке.

Получив все три вершины, соедините их прямыми линиями с помощью любой ровной поверхности (лучше линейки). Треугольник ABC построен.

Если окружность касается всех трех сторон данного треугольника, а её центр находится внутри треугольника, то ее называют вписанной в треугольник.

Вам понадобится

• линейка, циркуль

Инструкция

Из вершин треугольника (стороны противоположной делимому углу) циркулем проводят дуги окружности произвольного радиуса до пересечения их между собой;

Точку пересечения дуг по линейке соединяют с вершиной делимого угла;

Тоже самое проделывают с любым другим углом;

Радиусом вписанной в треугольник окружности будет отношение площади треугольника и его полупериметра: r=S/p , где S — площадь треугольника, а p=(a+b+c)/2 — полупериметр треугольника.

Радиус вписанной в треугольник окружности равноудален от всех сторон треугольника.

Источники:

• http://www.alleng.ru/d/math/math52.htm

Рассмотрим задачу построения треугольника при условии, что известны три его стороны или одна сторона и два угла.

Вам понадобится

• — циркуль
• — линейка
• — транспортир

Инструкция

Допустим, даны три стороны : a, b и с. Пользуясь , несложно с такими сторонами. Для начала выберем самую длинную из этих сторон, пусть это будет сторона с, и начертим ее. Затем установим раствор циркуля на величину другой стороны, стороны a, и начертим циркулем окружность радиуса a с центром на одном из концов стороны c. Теперь установим раствор циркуля на величину стороны b и начертим окружность с центром на другом конце стороны c. Радиус этой окружности равен b. Соединим точку пересечения окружностей с центрами и получим треугольник с искомыми сторонами.

Чтобы начертить треугольник с заданной стороной и двумя прилегающими углами, возьмите транспортир. Начертите сторону указанной длины. На краях ее отложите транспортиром углы. На пересечении сторон углов получите третью вершину треугольника.

Видео по теме

Обратите внимание

Для сторон треугольника справедливо следующее утверждение: сумма длин двух любых сторон должна быть больше третьей. Если это не выполняется, то построить такой треугольник невозможно.

Окружности в шаге 1 пересекаются в двух точках. Можно выбрать любую, треугольники будут равными.

Правильный треугольник — тот, у которого все стороны обладают одинаковой длиной. Исходя из этого определения, построение подобной разновидности треугольника является нетрудной задачей.

Вам понадобится

• Линейка, лист разлинованной бумаги, карандаш

Инструкция

С помощью линейки соединить отмеченные на листке точки последовательно, друг за другом так, как это показано на рисунке 2.

Обратите внимание

В правильном (равностороннем) треугольнике все углы равны 60 градусам.

Полезный совет

Равносторонний треугольник так же является и равнобедренным. Если треугольник равнобедренный, то это означает, что 2 из 3-х его сторон равны, а третья сторона считается основанием. Любой правильный треугольник является равнобедренным, в то время как обратное утверждение не верно.

У любого равностороннего треугольника одинаковы не только стороны, но и углы, каждый из которых равен 60 градусам. Однако чертеж такого треугольника, построенный при помощи транспортира, не будет обладать высокой точностью. Поэтому для построения данной фигуры лучше воспользоваться циркулем.

Вам понадобится

• Карандаш, линейка, циркуль

Инструкция

Затем возьмите циркуль, установите его в из концов (будущей вершине треугольника) и проведите окружность с радиусом, равным длине этого отрезка. Можно не проводить окружность целиком, а начертить лишь ее четверть, от противоположного края отрезка.

Теперь переставьте циркуль в другой конец отрезка и снова начертите окружность того же радиуса. Здесь будет достаточно построить окружности, проходящую от дальнего конца отрезка до пересечения с уже построенной дугой. Полученная точка будет третьей вершиной вашего треугольника.

Чтобы закончить построение, снова возьмите линейку с карандашом и соедините точку пересечения двух окружностей с обоими концами отрезка. Вы получите треугольник, все три стороны которого абсолютно равны, – это можно будет легко проверить с помощью линейки.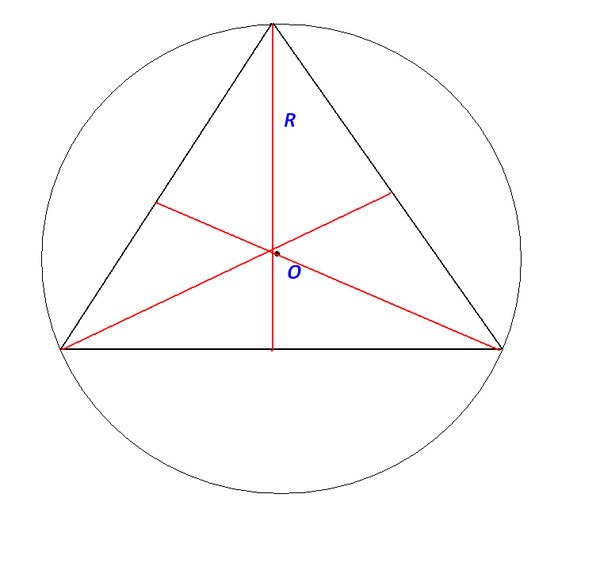

Видео по теме

Треугольник – это многоугольник, у которого три стороны. Равносторонним или правильным треугольником называют треугольник, у которого все стороны и углы равны. Рассмотрим, как можно нарисовать правильный треугольник.

Вам понадобится

• Линейка, циркуль.

Инструкция

С помощью циркуля нарисуйте еще одну окружность, центр которой будет в точке В, а радиус равен отрезку ВА.

Окружности будут пересекаться в двух точках. Выберите любую из них. Назовите ее С. Это будет третьей вершиной треугольника.

Соедините вершины между собой. Получившийся треугольник будет правильным. Убедитесь в этом, померив его стороны линейкой.

Рассмотрим способ построения правильного треугольника с помощью двух линеек. Начертите отрезок ОК, он будет одной из сторон треугольника, а точки О и К его вершинами.

Не сдвигая линейки после построения отрезка ОК, приложите перпендикулярно к ней еще одну линейку. Проведите прямую m пересекающую отрезок ОК в середине.

С помощью линейки отмерьте отрезок ОЕ, равный отрезку ОК так, чтобы один его конец совпадал с точкой О, а другой находился на прямой m. Точка Е буде третьей вершиной треугольника.

Закончите построение треугольника, соединив точки Е и К. Проверьте правильность построения с помощью линейки.

Обратите внимание

Убедиться в том, что треугольник правильный можете с помощью транспортира, измерив углы.

Полезный совет

Равносторонний треугольник так же можно начертить на листе в клетку с помощью одной линейки. Вместо другой линейки используйте перпендикулярные линии.

Источники:

• Классификация треугольников. Равносторонние треугольники
• Что такое треугольник
• построение правильного треугольника

Вписанным называется такой треугольник, все вершины которого находятся на окружности. Построить его можно, если знать хотя бы одну сторону и угол. Окружность называется описанной, и она будет единственной для данного треугольника.

Вам понадобится

• — окружность;
• — сторона и угол треугольника;
• — лист бумаги;
• — циркуль;
• — линейка;
• — транспортир;
• — калькулятор.

Инструкция

От точки А с помощью транспортира отложите заданный угол. Продолжите сторону угла до пересечения с окружностью и поставьте точку С. Соедините точки В и С. У вас получился треугольник АВС. Он может быть любого типа. Центр окружности у остроугольного треугольника него, у тупоугольного — вне, а у прямоугольного — на гипотенузе. Если вам задан не угол, а, например, три стороны треугольника, вычислите один из углов по радиусу и известной стороне.

Значительно чаще приходится иметь дело с обратным построением, когда задан треугольник и надо вокруг него описать окружность. Вычислите его радиус. Сделать это можно по нескольким формулам, в зависимости от того, что вам дано. Радиус можно найти, например, по стороне и синусу противолежащего угла. В этом случае он равен длине стороны, разделенной на удвоенный синус противолежащего угла. То есть R=a/2sinCAB. Можно его выразить и через произведение сторон, в этом случае R=abc/‭√(‬a+b+c)(a+b-c)(a+c-b)(b+c-a).

Определите центр окружности. Разделите все стороны пополам и проведите серединам перпендикуляры. Точка их пересечения и будет центром окружности. Начертите ее так, чтобы она пересекла все вершины углов.

Две короткие стороны прямоугольного треугольника, которые принято называть катетами, по определению должны быть перпендикулярны между собой. Это свойство фигуры значительно облегчает ее построение. Однако возможность точно определить перпендикулярность есть не всегда. В таких случаях можно рассчитать длины всех сторон — они позволят построить треугольник единственно возможным, а поэтому правильным, способом.

Вам понадобится

• Бумага, карандаш, линейка, транспортир, циркуль, угольник.

Как начертить треугольник?

Построение различных треугольников — обязательный элемент школьного курса геометрии. У многих это задание вызывает страх. Но на самом деле, все довольно просто. Далее в статье описано, как начертить треугольник любого типа с помощью циркуля и линейки.

Треугольники бывают

• разносторонние;
• равнобедренные;
• равносторонние;
• прямоугольные;
• тупоугольные;
• остроугольные;
• вписанные в окружность;
• описанные вокруг окружности.

Построение равностороннего треугольника

Равносторонним называется треугольник, у которого все стороны равны. Из всех видов треугольников, начертить равносторонний проще всего.

1. С помощью линейки начертите одну из сторон, заданной длины.
2. Измерьте ее длину с помощью циркуля.
3. Поместите острие циркуля в один из концов отрезка и проведите окружность.
4. Переставьте острие в другой конец отрезка и проведите окружность.
5. У нас получилось 2 точки пересечения окружностей. Соединяя любую из них с краями отрезка, мы получаем равносторонний треугольник.

Построение равнобедренного треугольника

Данный тип треугольников можно построить по основанию и боковым сторонам.

Равнобедренным называется треугольник, у которого две стороны равны. Для того чтобы начертить равнобедренный треугольник по данным параметрам, необходимо выполнить следующие действия:

1. С помощью линейки откладываем отрезок, равный по длине основанию. Обозначаем его буквами АС.
2. Циркулем измеряем необходимую длину боковой стороны.
3. Рисуем из точки А, а затем из точки С, окружности, радиус которых равен длине боковой стороны.
4. Получаем две точки пересечения. Соединив одну из них с точками А и С, получаем необходимый треугольник.

Построение прямоугольного треугольника

Треугольник, у которого один угол прямой, называют прямоугольным. Если нам даны катет и гипотенуза, начертить прямоугольный треугольник не составит труда.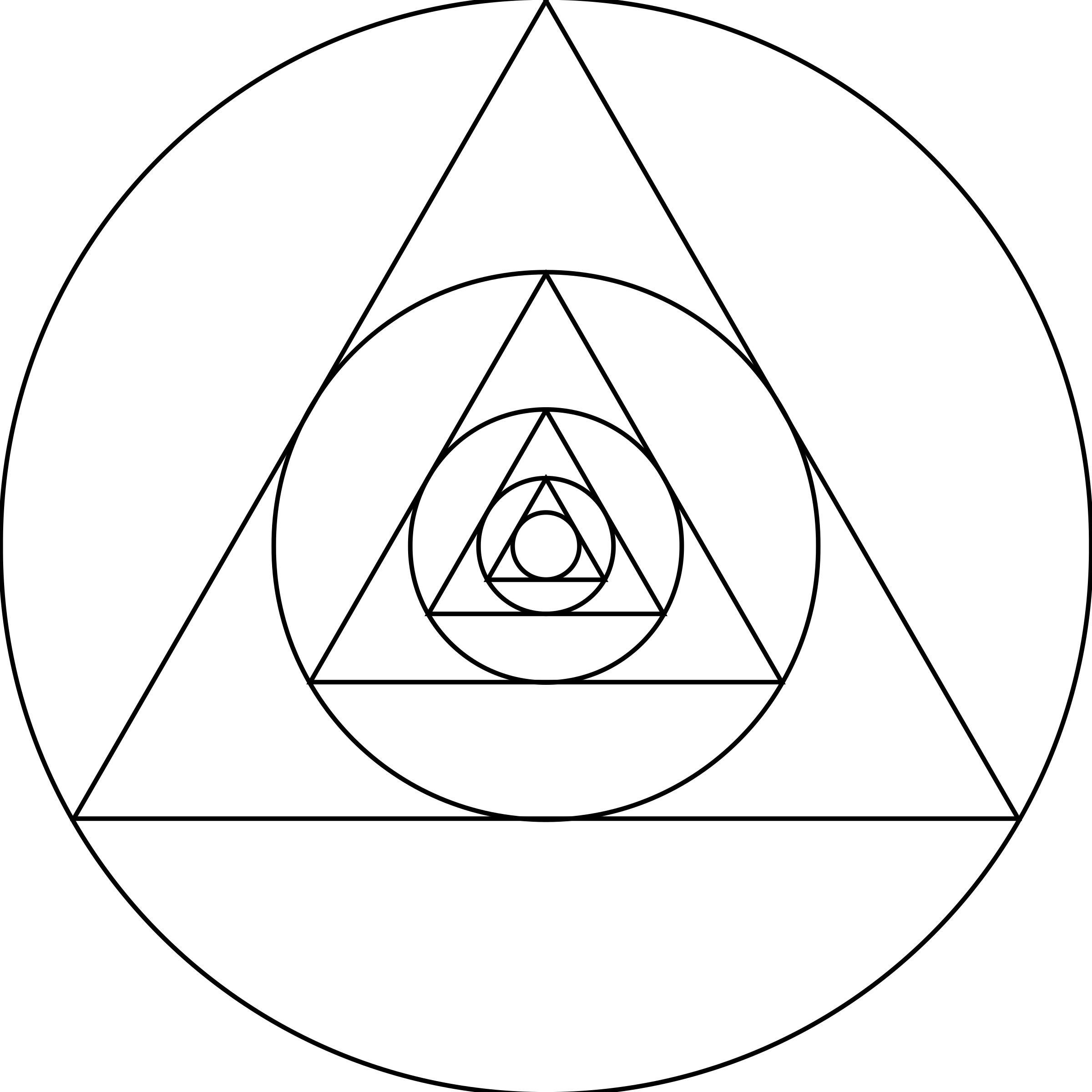 Его можно построить по катету и гипотенузе.

Построение тупоугольного треугольника по углу и двум прилегающим сторонам

Если один из углов треугольника тупой (больше 90 градусов), его называют тупоугольным. Чтобы начертить по указанным параметрам тупоугольный треугольник необходимо сделать следующее:

1. С помощью линейки откладываем отрезок, равный по длине одной из сторон треугольника. Обозначим его буквами А и D.
2. Если в задании уже нарисован угол, и вам необходимо начертить такой же, то на его изображении отложить два отрезка, оба конца которых лежат в вершине угла, а длина равняется указанным сторонам. Соедините полученные точки. У нас получился искомый треугольник.
3. Чтобы его перенести на свой чертеж, вам необходимо измерить длину третьей стороны.

Построение остроугольного треугольника

Остроугольный треугольник (все углы меньше 90 градусов) строится по тому же принципу.

1. Нарисуйте две окружности. Центр одной из них лежит в точке D, а радиус равен длине третьей стороны, а у второй центр находится в точке А, а радиус равен длине указанной в задании стороны.
2. Соедините одну из точек пересечения окружности с точками А и D. Искомый треугольник построен.

Вписанный треугольник

Для того чтобы начертить треугольник в окружности, нужно помнить теорему, в которой говорится, что центр описанной окружности лежит на пересечении серединных перпендикуляров:

У тупоугольного треугольника центр описанной окружности лежит за пределами треугольника, а у прямоугольного — на середине гипотенузы.

Чертим описанный треугольник

Описанный треугольник — это треугольник, в центре которого нарисована окружность, касающаяся всех его сторон. Центр вписанной окружности лежит на пересечении биссектрис. Для их построения необходимо:

Как построить равнобедренный треугольник? Это легко сделать с помощью линейки, карандаша и клеточек тетради.

Построение равнобедренного треугольника начинаем с основания. Чтобы рисунок получился ровным, количество клеточек в основании должно быть четным числом.

Делим отрезок — основание треугольника — пополам.

Вершину треугольника можно выбрать на любой высоте от основания, но обязательно ровно над срединой.

Как построить остроугольный равнобедренный треугольник?

Углы при основании равнобедренного треугольника могут быть только острыми. Чтобы равнобедренный треугольник получился остроугольным, угол при вершине тоже должен быть острым.

Для этого вершину треугольника выбираем повыше, подальше от основания.

Чем выше вершина, тем меньше угол при вершине. Углы при основании при этом, соответственно, увеличиваются.

Как построить тупоугольный равнобедренный треугольник?

С приближением вершины равнобедренного треугольника к основанию градусная мера угла при вершине увеличивается.

Значит, чтобы построить равнобедренный тупоугольный треугольник, вершину выбираем пониже.

Как построить равнобедренный прямоугольный треугольник?

Чтобы построить равнобедренный прямоугольный треугольник, надо вершину выбрать на расстоянии, равном половине основания (это обусловлено свойствами равнобедренного прямоугольного треугольника).

Например, если длина основания — 6 клеточек, то вершину треугольника располагаем на высоте 3 клеточек над серединой основания. Обратите внимание: при этом каждая клеточка у углов при основании делится по диагонали.

Построение равнобедренного прямоугольного треугольника можно начать с вершины.

Выбираем вершину, от нее под прямым углом откладываем равные отрезки вверх и вправо. Это — боковые стороны треугольника.

Соединим их и получим равнобедренный прямоугольный треугольник.

Построение равнобедренного треугольника с помощью циркуля и линейки без делений рассмотрим в другой теме.

Еще дети дошкольного возраста знают, как выглядит треугольник. А вот с тем, какие они бывают, ребята уже начинают разбираться в школе. Одним из видов является тупоугольный треугольник. Понять, что это такое, проще всего, если увидеть картинку с его изображением. А в теории это так называют «простейший многоугольник» с тремя сторонами и вершинами, одна из которых является

Разбираемся с понятиями

В геометрии различают такие виды фигур с тремя сторонами: остроугольный, прямоугольный и тупоугольный треугольники.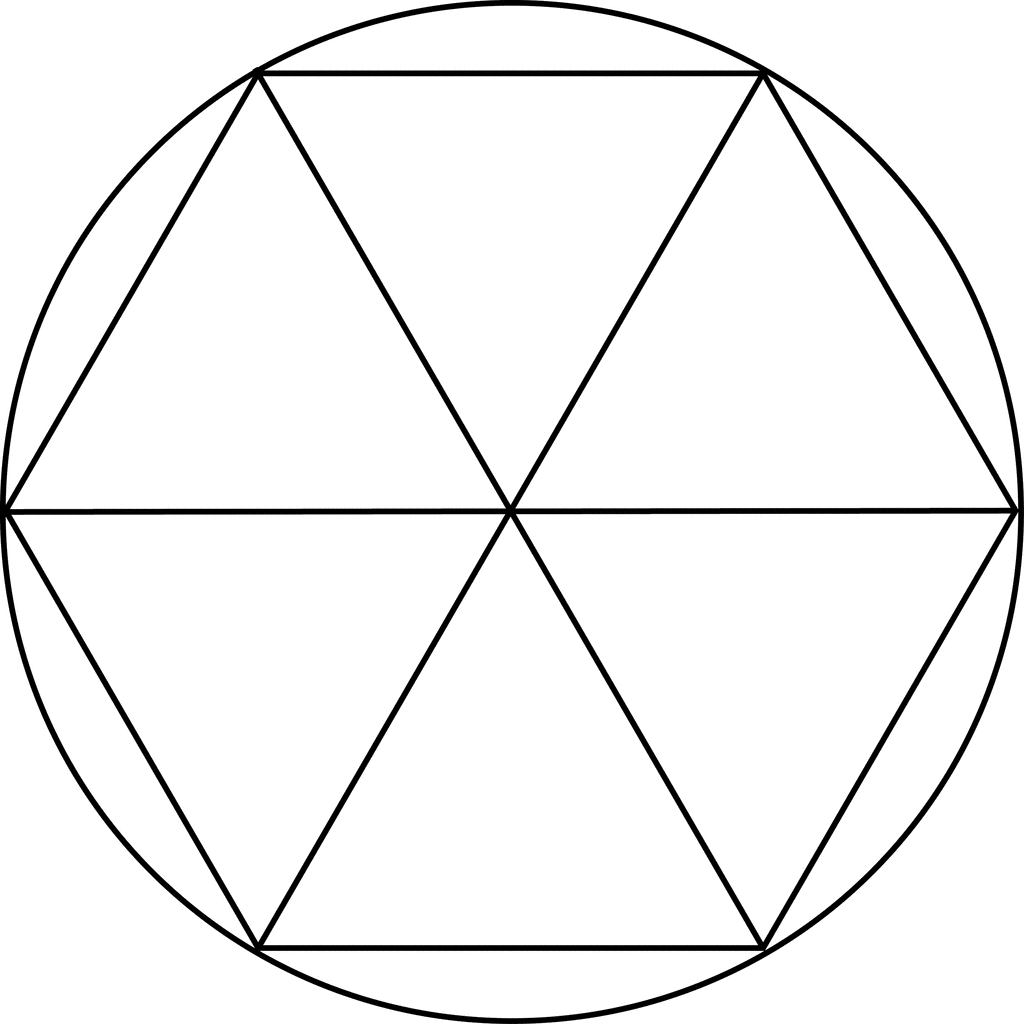 При этом свойства этих простейших многоугольников одинаковы для всех. Так, для всех перечисленных видов будет соблюдаться такое неравенство. Сумма длин любых двух сторон обязательно будет больше протяженности третьей стороны.

Но для того чтобы быть уверенным, что речь идет именно о законченной фигуре, а не о наборе отдельных вершин, необходимо проверить, чтобы соблюдалось основное условие: сумма углов тупоугольного треугольника равняется 180 о. Это же верно и для других видов фигур с тремя сторонами. Правда, в тупоугольном треугольнике один из углов будет еще больше 90 о, а два оставшихся обязательно будут острыми. При этом именно наибольший угол будет находиться напротив самой длинной стороны. Правда, это далеко не все свойства тупоугольного треугольника. Но и зная лишь эти особенности, школьники могут решать многие задачи по геометрии.

Для каждого многоугольника с тремя вершинами верно и то, что, продолжая любую из сторон, мы получим угол, размер которого будет равен сумме двух несмежных с ним внутренних вершин. Периметр тупоугольного треугольника рассчитывается так же, как и для других фигур. Он равняется сумме длин всех его сторон. Для определения математиками были выведены различные формулы, в зависимости от того, какие изначально присутствуют данные.

Правильное начертание

Одним из важнейших условий решения задач по геометрии является верный рисунок. Часто учителя математики говорят о том, что он поможет не только наглядно представить, что дано и что от вас требуется, но на 80% приблизиться к правильному ответу. Именно поэтому важно знать, как построить тупоугольный треугольник. Если вам нужна просто гипотетическая фигура, то вы можете нарисовать любой многоугольник с тремя сторонами так, чтобы один из углов был больше 90 о.

Если даны определенные значения длин сторон или градусы углов, то чертить тупоугольный треугольник необходимо в соответствии с ними. При этом необходимо стараться максимально точно изобразить углы, высчитывая их при помощи транспортира, и пропорционально данным в задании условиям отобразить стороны.

Основные линии

Зачастую школьникам мало знать только то, как должны выглядеть те или иные фигуры. Они не могут ограничиться лишь информацией о том, какой треугольник тупоугольный, а какой прямоугольный. Курсом математики предусмотрено, что их знания об основных особенностях фигур должны быть более полными.

Так, каждому школьнику должно быть понятно определение биссектрисы, медианы, серединного перпендикуляра и высоты. Кроме того, он должен знать и их основные свойства.

Так, биссектрисы делят угол пополам, а противоположную сторону — на отрезки, которые пропорциональны прилегающим сторонам.

Медиана делит любой треугольник на два равных по площади. В точке, в которой они пересекаются, каждая из них разбивается на 2 отрезка в пропорции 2: 1, если смотреть от вершины, из которой она вышла. При этом большая медиана всегда проведена к его наименьшей стороне.

Не меньше внимания уделяется и высоте. Это перпендикуляр к противоположной от угла стороне. Высота тупоугольного треугольника имеет свои особенности. Если она проведена из острой вершины, то она попадает не на сторону этого простейшего многоугольника, а на ее продолжение.

Серединный перпендикуляр — это отрезок, который выходит из центра грани треугольника. При этом он расположен к ней под прямым углом.

Работа с окружностями

В начале изучения геометрии детям достаточно понять, как начертить тупоугольный треугольник, научиться отличать его от остальных видов и запомнить его основные свойства. А вот старшеклассникам этих знаний уже мало. Например, на ЕГЭ часто встречаются вопросы про описанные и вписанные окружности. Первая из них касается всех трех вершин треугольника, а вторая имеет по одной общей точке со всеми сторонами.

Построить вписанный или описанный тупоугольный треугольник уже намного сложнее, ведь для этого необходимо для начала выяснить, где должен находиться центр окружности и ее радиус. Кстати, необходимым инструментом станет в этом случае не только карандаш с линейкой, но и циркуль.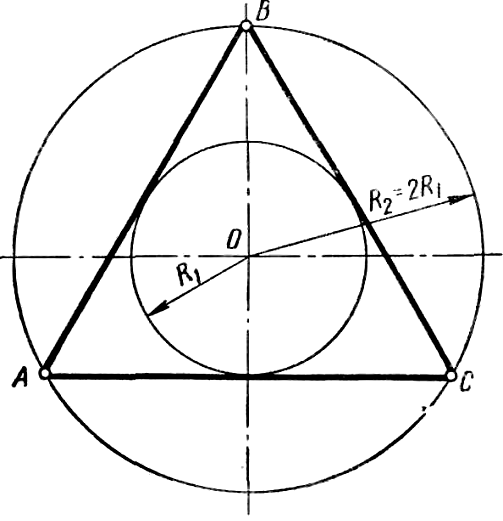

Те же сложности возникают при построении вписанных многоугольников с тремя сторонами. Математиками были выведены различные формулы, которые позволяют определить их месторасположение максимально точно.

Вписанные треугольники

Как уже было сказано ранее, если круг проходит через все три вершины, то это называется описанной окружностью. Главным ее свойством является то, что она единственная. Чтобы выяснить, как должна располагаться описанная окружность тупоугольного треугольника, необходимо помнить, что ее центр находится на пересечении трех серединных перпендикуляров, которые идут к сторонам фигуры. Если в остроугольном многоугольнике с тремя вершинами эта точка будет находиться внутри него, то в тупоугольном — за его пределами.

Зная, например, что одна из сторон тупоугольного треугольника равна его радиусу, можно найти угол, который лежит напротив известной грани. Его синус будет равен результату от деления длины известной стороны на 2R (где R — это радиус окружности). То есть sin угла будет равен ½. Значит, угол будет равен 150 о.

Если вам необходимо найти радиус описанной окружности тупоугольного треугольника, то вам пригодятся сведения о длине его сторон (c, v, b) и его площади S. Ведь радиус высчитывается так: (c х v х b) : 4 х S. Кстати, неважно, какого именно у вас вида фигура: разносторонний тупоугольный треугольник, равнобедренный, прямо- или остроугольный. В любой ситуации, благодаря приведенной формуле, вы можете узнать площадь заданного многоугольника с тремя сторонами.

Описанные треугольники

Также довольно часто приходится работать со вписанными окружностями. По одной из формул, радиус такой фигуры, умноженный на ½ периметра, будет равняться площади треугольника. Правда, для ее выяснения вам необходимо знать стороны тупоугольного треугольника. Ведь для того чтобы определить ½ периметра, необходимо сложить их длины и разделить на 2.

Чтобы понять, где должен находиться центр круга, вписанного в тупоугольный треугольник, необходимо провести три биссектрисы. Это линии, которые делят углы пополам. Именно на их пересечении и будет находиться центр окружности. При этом он будет равноудален от каждой из сторон.

Радиус такой окружности, вписанной в тупоугольный треугольник, равняется из частного (p-c) х (p-v) х (p-b) : p. При этом p — это полупериметр треугольника, c, v, b — его стороны.

Как нарисовать треугольник на листе чтобы вырезать. Как нарисовать несуществующий объемный треугольник поэтапно. Построение остроугольного треугольника

Как нарисовать треугольник? Этому учат в процессе изучения геометрии в школе. Чтобы задание было выполнено правильно, важно точно знать, какой треугольник необходимо изобразить: равносторонний, равнобедренный или же вписанный. Правилам начертания этих фигур будет посвящена данная статья.

Как рисовать треугольник с равными сторонами?

Как нарисовать треугольник, стороны у которого равны? Для этого можно воспользоваться одним из трех методов.

Такая фигура имеет три одинаковые по длине стороны, связанные тремя углами равной ширины. Это может быть сложным для рисования треугольника вручную. Поэтому можно использовать круглый объект для выделения углов.

Варианты создания фигуры

Обязательно используйте линейку и один из представленных ниже способов:

1. Применение циркуля: надо начертить ровную линию. Проведите карандаш вдоль прямого края бумаги. Этот сегмент линии образует одну из сторон. А это означает, что нужно будет чертить вторую и третью линии одинаковой длины, каждая из которых достигает точки под углом 60° от первой линии. Удостоверьтесь, что достаточно места для рисования всех трех сторон!
2. Разделите сегмент циркулем. Вставьте карандаш и убедитесь, что он острый! Поместите точку циркуля на один конец сегмента и установите карандаш на другую. Опишите дугу. Не изменяйте установленную «ширину» инструмента от точки циркуля до точки карандаша. Нарисуйте вторую дугу, чтобы она пересекала первую дугу, которую уже нарисовали. Отметьте точку, в которой пересекаются две дуги. Это вершина (верхняя точка) треугольника. Он должен лежать в точном центре сегмента линии, который нарисовали. Теперь можете сделать две прямые линии, ведущие к этой точке: по одному от каждого конца «нижнего» сегмента линии. Закончите треугольник. Далее с помощью линейки надо нарисовать еще два сегмента прямой линии — это стороны в треугольнике. Подключите каждый конец исходного сегмента линии к точке, в которой пересекаются дуги. Чтобы закончить работу, сотрите дуги, которые нарисовали, так, чтобы остался только треугольник.
3. Использование объекта с круглой базой: этот совет подойдет для построения дуги. Предложенный метод по сути такой же, как с использованием циркуля.

Указанные советы помогут выяснить, как нарисовать равносторонний треугольник.

Равнобедренный треугольник представляет собой фигуру с двумя равными сторонами и двумя равными углами. Если знаете длину, основание и высоту стороны, это можно сделать только с линейкой и циркулем (или просто циркулем, если заданы размеры).

Как нарисовать равнобедренный треугольник:

1. Учитывая все боковые длины. Чтобы использовать этот метод, важно знать длину основания треугольника и длину двух равных сторон.
2. Учитывая две равные стороны и угол между ними. Чтобы использовать этот метод, нужно знать длину двух равных сторон и измерение угла между этими двумя сторонами.
3. Учитывая базовые и смежные углы — необходимо знать длину базы, градусы двух углов, смежных с основанием. Помните, что два угла, смежные с основанием равнобедренного треугольника, будут равны.
4. Основа и высота. Нужно знать длину основания треугольника, а также высоту этой геометрической фигуры.

Как нарисовать вписанный треугольник? Выберите круглый объект. Используйте предмет с круглым основанием. Выбор компакт-диска станет хорошим вариантом. Но можно взять и другой объект нужного размера. Для этого метода свойственно, что длина каждой стороны равносторонней геометрической фигуры с тремя углами будет равна размерам радиуса (половине диаметра) круга.

Как нарисовать треугольник, если используете компакт-диск? Представьте себе равносторонний треугольник, который вписывается в верхнюю правую часть компакт-диска. Надо начертить первую из сторон. Радиус круглого объекта — расстояние на полпути до получения желаемого результата. Удостоверьтесь, что линии нарисованы ровно.

С помощью линейки просто выполните измерения диаметра объекта и нарисуйте линию на половину длины. Если ее нет, поместите круглый объект на бумагу, затем тщательно проведите по окружности карандашом. Удалите объект — должен быть идеальный круг. Используйте прямой край, чтобы нарисовать линию через точный центр круга: точку, которая полностью равноудалена от любой точки по окружности круга.

Используйте круглый объект для создания дуги. Поместите объект по отрезку линии, с краем круга, расположенным на одном конце линии. Для обеспечения точности убедитесь, что линия проходит четко через центр круга. Используйте карандаш, чтобы начертить дугу — это четверть пути по окружности.

Начертите еще одну дугу. Теперь сдвиньте круглый объект так, чтобы край касался другого конца сегмента линии.

Подведем итоги

Как начертить треугольник?

Построение различных треугольников — обязательный элемент школьного курса геометрии. У многих это задание вызывает страх. Но на самом деле, все довольно просто. Далее в статье описано, как начертить треугольник любого типа с помощью циркуля и линейки.

Треугольники бывают

• разносторонние;
• равнобедренные;
• равносторонние;
• прямоугольные;
• тупоугольные;
• остроугольные;
• вписанные в окружность;
• описанные вокруг окружности.

Построение равностороннего треугольника

Равносторонним называется треугольник, у которого все стороны равны. Из всех видов треугольников, начертить равносторонний проще всего.

1. С помощью линейки начертите одну из сторон, заданной длины.
2. Измерьте ее длину с помощью циркуля.
3. Поместите острие циркуля в один из концов отрезка и проведите окружность.
4. Переставьте острие в другой конец отрезка и проведите окружность.
5. У нас получилось 2 точки пересечения окружностей. Соединяя любую из них с краями отрезка, мы получаем равносторонний треугольник.

Построение равнобедренного треугольника

Данный тип треугольников можно построить по основанию и боковым сторонам.

Равнобедренным называется треугольник, у которого две стороны равны. Для того чтобы начертить равнобедренный треугольник по данным параметрам, необходимо выполнить следующие действия:

1. С помощью линейки откладываем отрезок, равный по длине основанию. Обозначаем его буквами АС.
2. Циркулем измеряем необходимую длину боковой стороны.
3. Рисуем из точки А, а затем из точки С, окружности, радиус которых равен длине боковой стороны.
4. Получаем две точки пересечения. Соединив одну из них с точками А и С, получаем необходимый треугольник.

Построение прямоугольного треугольника

Треугольник, у которого один угол прямой, называют прямоугольным. Если нам даны катет и гипотенуза, начертить прямоугольный треугольник не составит труда. Его можно построить по катету и гипотенузе.

Построение тупоугольного треугольника по углу и двум прилегающим сторонам

Если один из углов треугольника тупой (больше 90 градусов), его называют тупоугольным.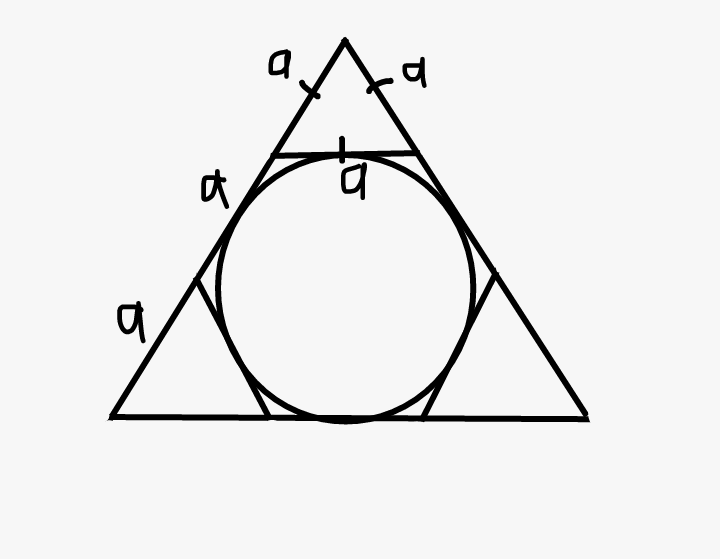 Чтобы начертить по указанным параметрам тупоугольный треугольник необходимо сделать следующее:

1. С помощью линейки откладываем отрезок, равный по длине одной из сторон треугольника. Обозначим его буквами А и D.
2. Если в задании уже нарисован угол, и вам необходимо начертить такой же, то на его изображении отложить два отрезка, оба конца которых лежат в вершине угла, а длина равняется указанным сторонам. Соедините полученные точки. У нас получился искомый треугольник.
3. Чтобы его перенести на свой чертеж, вам необходимо измерить длину третьей стороны.

Построение остроугольного треугольника

Остроугольный треугольник (все углы меньше 90 градусов) строится по тому же принципу.

1. Нарисуйте две окружности. Центр одной из них лежит в точке D, а радиус равен длине третьей стороны, а у второй центр находится в точке А, а радиус равен длине указанной в задании стороны.
2. Соедините одну из точек пересечения окружности с точками А и D. Искомый треугольник построен.

Вписанный треугольник

Для того чтобы начертить треугольник в окружности, нужно помнить теорему, в которой говорится, что центр описанной окружности лежит на пересечении серединных перпендикуляров:

У тупоугольного треугольника центр описанной окружности лежит за пределами треугольника, а у прямоугольного — на середине гипотенузы.

Чертим описанный треугольник

Описанный треугольник — это треугольник, в центре которого нарисована окружность, касающаяся всех его сторон. Центр вписанной окружности лежит на пересечении биссектрис. Для их построения необходимо:

Построение вписанного в окружность правильного шестиуголь­ника. Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения доста­точно разделить окружность на шесть равных частей и соединить най­денные точки между собой (фиг. 60, а).

Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°.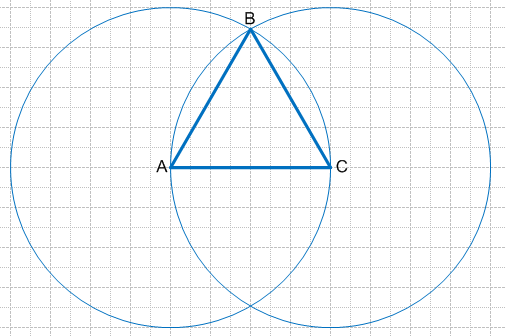 Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг. 60, б), строим стороны 1 -6, 4-3, 4-5 и 7-2, после чего прово­дим стороны 5-6 и 3-2.

Построение вписанного в окружность равностороннего треуголь­ника . Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного цир­куля.

Рассмотрим два способа построения вписанного в окружность рав­ностороннего треугольника.

Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, прове­дённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0-1-2 равен 30°, то для нахождения стороны

1-2 достаточно построить по точке 1 и стороне 0-1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1-2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2-3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 прово­дим прямую, которая определит третью вершину треугольника.

Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вер­шины через одну, то получится равносторонний треугольник.

Для построения треугольника (фиг. 61, б) намечаем на диаметре вершину-точку 1 и проводим диаметральную линию 1-4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окруж­ностью в точках 3 и 2. Полученные точки будут двумя другими вер­шинами искомого треугольника.

Построение квадрата, вписанного в окружность . Это построение можно выполнить при помощи угольника и циркуля.

Первый способ основан на том, что диагонали квадрата пере­секаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные сто­роны квадрата 4-1 и 3-2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1-2 и 4-3.

Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра (фиг. 62, б). Намечаем на концах двух взаимно перпендикулярных диа­метров точки А, В и С и из них радиусом у описываем дуги до вза­имного их пересечения.

Далее через точки пересечения дуг проводим вспомогательные пря­мые, отмеченные на фигуре сплошными линиями. Точки их пересече­ния с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.

Построение вписанного в окружность правильного пятиугольника.

Чтобы вписать в окружность правильный пятиугольник (фиг. 63), про­изводим следующие построения.

Намечаем на окружности точку 1 и принимаем её за одну из вер­шин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точ­ках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вер­шины 3 и 4. Найденные точки последовательно соединяем между собой.

Построение правильного пятиугольника по данной его стороне.

Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую.

Получим точку 1-вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведён­ными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.

Построение вписанного в окружность правильного семиугольника.

Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиу­сом, равным диаметру окружности D, описываем дугу до пересечения с про­должением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, прово­дим из полюса F через чётные деления вертикального диаметра лучи, пересече­ние которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем после­довательно между собой. Семиугольник может быть построен путём проведе­ния лучей из полюса F и через нечётные деления вертикального диаметра.

Приведённый способ годен для построения правильных многоуголь­ников с любым числом сторон.

Деление окружности на любое число равных частей можно произ­водить также, пользуясь данными табл. 2, в которой приведены коэф­фициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.

Сегодня мы расскажем вам, как легко прослыть художником среди своих друзей или показать девушке, какой ты весь разносторонний (о, они это любят!). Итак начнем!

Нам понадобится: 50 грамм для храбрости, 2 карандаша (один жесткий, другой мягкий), лист бумаги, линейка и ластик. Да начнется магия!

Шаг 1.

Рисуем обычный треугольник – он не должен являть собой венец геометрической мысли: просто соедини три линии.

Шаг 2.

Теперь нарисуй внутри линии, прямо как у нас. Старайся сделаить их одной ширины, ты ж не рукожоп, как мы!

Шаг 3.

Нарисовал? Молодец! Теперь нарисуй еще, как мы показали. Мы знаем, ты устал, но скоро все закончится.

Шаг 4.

Спили вершины треугольника как на рисунке.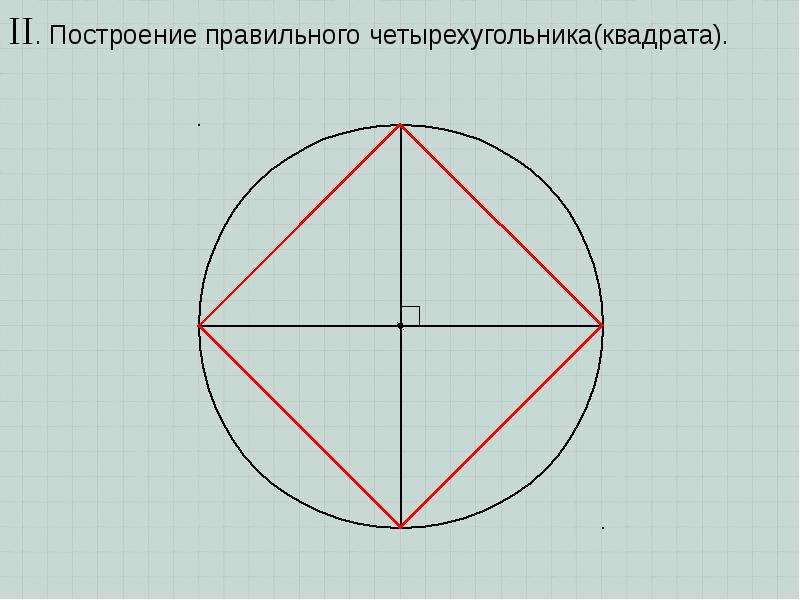

Шаг 5.

Теперь обведи все линии, которые выделили мы, жирным карандашом, пером или гелевой ручкой. Или маркером. Или фломастером. Может надо бутерброд забацать?

Шаг 6.

Сотри все ненужное. Мы близко к цели, видишь?

Шаг 7.

Тут мы обратились к богам Олимпа и они нарисовали нам тени. Ты рисуй сам.

Шаг 8.

Теперь можно вырезать наше творение лезвием или ножницами и ломать хрупкие разумы своих друзей. Этот треугольник входит в число фигур, которые геометрически не имеют право на существование или по по-другому “несуществующие фигуры”.

Надеемся, тебе понравилось, ибо мы старались и крали этот урок рисования несуществующего треугольника поэтапно. И теперь тебе лучше нарисовать героев

Нарисуем треугольник 3D с оптической иллюзией поэтапно.

Сначала рисуем обыкновенный равносторонний треугольник карандашом. Внутри него, параллельно каждой из сторон, проводим по линии на равном расстоянии так, что внутри треугольника получается еще один треугольник.

Вновь проводим параллельные линии, отступив на то же расстояние и рисуя еще один меньший треугольник внутри первых двух.

Жирно проводим контур по периметру сторон большого треугольника, обводя его стороны, но срезая острые углы.

Проводим еще один контур из двух прямых, повторяющих одну сторону среднего и одну сторону меньшего треугольников внутри большого, как показано на рисунке.

Проводим еще по контуру, — две прямые, повторяя стороны треугольников, как на рисунке.

И еще раз делаем те же действия, с другими сторонами, — обводим жирным контуром две прямые, как на рисунке.

Лишние линии убираем. Вот получился 3D треугольник, пока не закрашенный.

Заштриховываем стороны треугольника, придавая изображению объемность. Рисунок готов, треугольник 3D иллюзия .

Посмотрим видео, как рисовать оптическую иллюзию треугольник 3D.

Нарисовать треугольную иллюзию несложно, особенно если есть пошаговая инструкция. Понадобится карандаш, бумага и желательно линейка, с ней будет аккуратнее рисунок. По шагам повторить все действия, а потом затенить с помощью растушевки нужные места.

Как нарисовать треугольник … Да, при этом не простой, а очень сложный с множеством треугольников внутри. Чтобы все его грани проглядывались, а на бумаге он выглядел реалистичным и четким.

Для этого нам потребуется:

• карандаш,
• стерка,
• лист бумаги,
• пошаговая интсрукция.

Процесс рисования:

• сперва изобразить треугольник,
• затем все его грани, начиная с внешней,
• заштриховать участки свето-тени, чтобы придать объем фигуре,
• при необходимости разукрасить объект.

Получается необычайная фигура с множеством завихрений. Смотрится немного завораживающе, так как разум пытается продлить все линии и уловить суть.

Видео-инструкция, как нарисовать треугольник на бумаге:

Треугольник Пенроуза или невозможные фигуры. Был придуман в 1953 году художником Оскаром Реутерсвардом. Первый треугольник был сделан из кубиков.

Уникальность этого объекта в том, что посмотрев на прямые палки под определнным углом можно четко увидеть треугольник. Как например вот на этом памятнике.

Вписанный и описанный треугольник — материалы для подготовки к ЕГЭ по Математике

Вписанный треугольник — треугольник, все вершины которого лежат на окружности. Тогда окружность называется описанной вокруг треугольника.

Очевидно, расстояние от центра описанной окружности до каждой из вершин треугольника одинаково и равно радиусу этой окружности.

Вокруг любого треугольника можно описать окружность, причем только одну.

Окружность вписана в треугольник, если она касается всех его сторон. Тогда сам треугольник будет описанным вокруг окружности. Расстояние от центра вписанной окружности до каждой из сторон треугольника равно радиусу этой окружности.

В любой треугольник можно вписать окружность, причем только одну.

Попробуйте сами описать окружность вокруг треугольника и вписать окружность в треугольник.

Как вы думаете, почему центр вписанной окружности — это точка пересечения биссектрис треугольника, а центр описанной окружности — точка пересечения серединных перпендикуляров к его сторонам?

В задачах ЕГЭ чаще всего встречаются вписанные и описанные правильные треугольники.

Есть и другие задачи. Для их решения вам понадобятся еще две формулы площади треугольника, а также теорема синусов.

Вот еще две формулы для площади.
Площадь треугольника равна половине произведения его периметра на радиус вписанной окружности.

,

где — полупериметр,

— радиус окружности, вписанной в треугольник.

Есть и еще одна формула, применяемая в основном в задачах части :

где — стороны треугольника, — радиус описанной окружности.

Для любого треугольника верна теорема синусов:

Ты нашел то, что искал? Поделись с друзьями!

. Радиус окружности, вписанной в равнобедренный прямоугольный треугольник, равен . Найдите гипотенузу c этого треугольника. В ответе укажите .

Треугольник прямоугольный и равнобедренный. Значит, его катеты одинаковы. Пусть каждый катет равен . Тогда гипотенуза равна .

Запишем площадь треугольника АВС двумя способами:

Приравняв эти выражения, получим, что . Поскольку , получаем, что . Тогда .

В ответ запишем .

Ответ: .

. Сторона АС треугольника АВС с тупым углом В равна радиусу описанной около него окружности. Найдите угол В. Ответ дайте в градусах.

По теореме синусов,

Получаем, что . Угол — тупой. Значит, он равен .

Ответ: .

. Боковые стороны равнобедренного треугольника равны , основание равно . Найдите радиус описанной окружности этого треугольника.

Углы треугольника не даны. Что ж, выразим его площадь двумя разными способами.

, где — высота треугольника. Ее найти несложно — ведь в равнобедренном треугольнике высота является также и медианой, то есть делит сторону пополам. По теореме Пифагора найдем . Тогда .

Задачи на вписанные и описанные треугольники особенно необходимы тем, кто нацелен на решения задания .

Квадрат, треугольник, круг. Для вас, мальчишки

Квадрат, треугольник, круг

Предлагаем нарисовать из геометрических фигур человечка. Используем круги, прямоугольники и треугольники. В твоем рисунке могут присутствовать равносторонние треугольники, треугольники с прямым углом, вертикальные прямоугольники, горизонтальные прямоугольники, очень вытянутые прямоугольники, квадраты, овалы и т. д., но не должно быть звезд, пятиугольников, трапеций и прочих геометрических фигур, которые не относятся ни к одной из требуемых групп. Ты можешь использовать фигуры разных размеров, накладывать одну фигуру на другую. Главное – придерживаться следующих требований:

1. Общее количество фигур в одном человечке должно быть равно 10, ни больше и ни меньше.

2. В изображении человечка должны быть использованы все три вида геометрических фигур.

Если к концу рисования ты обнаружишь, что человечек содержит более 10 элементов, то лишние фигуры необходимо удалить.

Следуя правилам, из геометрических фигур необходимо нарисовать 3 человечка. При этом каждый следующий человечек выполняется на отдельном листке бумаги. Первый человечек – это, как говорится, росчерк пера. Он необходим для того, чтобы ты попробовал задание «на вкус».

После выполнения задания подсчитай количество кругов, прямоугольников и треугольников отдельно во втором и в третьем человечке. Полученные результаты запиши в виде двух трехзначных чисел. Трехзначное число – это «формула рисунка», в которой первая цифра означает количество треугольников, вторая цифра – количество кругов и третья цифра – количество прямоугольников. Например, 325 – это 3 треугольника, 2 круга и 5 прямоугольников.

А теперь самое интересное. Дело в том, что соотношение геометрических элементов в нарисованных тобой человеческих фигурках неслучайно. Изображая человечка из треугольников, кругов и квадратов, ты как бы рисуешь свой автопортрет. Какой именно – смотри ниже.

Все возможные формулы рисунка можно объединить в 8 типов.

Лидер: этому типу соответствуют формулы 901, 910, 802, 811, 820, 703, 712, 721, 730, 604, 613, 622, 631, 640.

Если твои рисунки относятся к данному типу, то у тебя, определенно, есть склонности к организаторской деятельности и лидерские способности. Ты любишь руководить, и у тебя это неплохо получается. Ты легко приспосабливаешься к любой ситуации. Особенно сильно черты лидера выражены у подтипов 901, 910, 802, 811 и 820. Подтипы 703, 712, 421 и 730 проявляют лидерские качества время от времени. А 604, 613, 622, 631 и 640 являются хорошими рассказчиками и обладают редким даром убеждения, благодаря которому могут воздействовать на других людей.

Труженик: 505, 514, 523, 532, 541, 550. Труженик очень похож на Лидера, но в отличие от него в ответственные минуты, когда требуется принять важное решение, начинает колебаться, взвешивать все «за» и «против». У тебя сильно развито чувство ответственности и стремление к совершенству. Что бы ты не делал, ты все пытаешься выполнить на «отлично». Высокая требовательность себе соседствует с неменьшей требовательностью к окружающим тебя людям. Осторожно, ты склонен к нервным перенапряжениям!

Артист: 406, 415, 424, 433, 442, 451, 460. У тебя много талантов и, как следствие, много увлечений. Ты физически не переносишь грязь и беспорядок, что может стать причиной для конфликта с людьми, менее щепетильными в данном вопросе. Ты очень раним, часто сомневаешься в себе, но если тебя хвалят, то расцветаешь буквально на глазах. Подтип 415 часто обладает поэтической одаренностью, а 424 отличается особой тщательностью в работе.

Ученый: 307, 316, 325, 334, 343, 352, 361, 370. У тебя буквально на все есть своя теория. Любой свой поступок, прежде чем совершить, ты тщательно продумываешь. И вообще, отличаешься «концептуальным» умом и редким душевным равновесием.

Психолог: 208, 217, 226, 235, 244, 253, 262, 271, 280.

Тебя отличает высокая чувствительность и заботливость в отношении других людей. В ситуациях несправедливости ты часто встаешь на сторону обиженных. При этом отрицательно реагируешь на любые попытки посягнуть на твою личную свободу. Любишь все новое, часто обладаешь богатым воображением и ручными умениями в прикладных видах искусства. Если ты – подтип 235, то не пора ли тебе заняться психологией? Подтип 244 нередко обладает литературными способностями, а 217 – способностями к изобретательской деятельности.

Изобретатель: 109, 118, 127, 136, 145, 019, 028, 037, 046.

Природа наградила тебя богатым воображением и «технической жилкой», позволяющей заниматься самыми разными видами технического творчества. Особенно сильно выраженными возможностями к изобретательской деятельности отличается подтип 118. Ты не любишь, когда тебя норовят подвести под общую гребенку, и всегда поступаешь так, как сам считаешь нужным. Свой богатый внутренний мир предпочитаешь шумным вечеринкам и праздному веселью. Часто бываешь одержим собственными оригинальными идеями.

Чувствительный: 550, 451, 460, 352, 361, 370, 253, 262, 271, 280, 154, 163, 172, 181, 190, 055, 064, 073, 082, 091.

Ты тяжело переживаешь жестокие сцены в кино и близко к сердцу принимаешь несчастья и проблемы окружающих тебя людей. Неприятные события, произошли ли они в жизни или были увидены тобой по телевизору, ты переживаешь долго и глубоко. На сопереживание и сочувствие другим людям у тебя уходит слишком много энергии, в результате становится затруднительной реализация твоих собственных способностей.

Эгоист: 901, 802, 703, 604, 505, 406, 307, 208, 109.

Если ты относишься к данному типу, то чужие переживания и эмоции для тебя словно не существуют. Ты невнимателен и время от времени черств. Особенно сильно твоя эгоистичность проявляется в тех случаях, когда тебя одолевают собственные проблемы. Ты склонен заставлять других людей делать то, что хочется именно тебе, не считаясь с их потребностями.

Данный текст является ознакомительным фрагментом.

Продолжение на ЛитРес

Как влиять на других с помощью изображений, даже если вы не Микеланджело?

Эта статья не поможет вам научиться рисовать подобно талантливому художнику, зато она продемонстрирует, как использовать изображения как мыслящий человек.

Если вы считаете, что не умеете рисовать, вы увидите, что ошибаетесь. Вы способны рисовать, просто нужно узнать о двух простых инструментах, увидеть их в действии и пару раз попробовать применить их самому. Вот и все. Тут можно провести аналогию с говорением. Когда вы только учились говорить, у вас не все получалось с первого раза. Но со временем, после практики, повторений, каких-то вспомогательных инструментов вы стали хорошо разговаривать. Ситуация с рисованием похожа: вам не нужно быть писателем, чтобы уметь писать, и не обязательно быть художником, чтобы уметь представлять вещи визуально.

Рисование аналогично говорению, только вместо слов вы используете фигуры. Вот пример того, как простые формы (квадрат, круг, шестиугольник) могут стать наглядной историей о том, как пчела собрала нектар и полетела домой, в улей

Что важнее в веб-дизайне, изображения или текст?

Первая линия — самая сложная. Так не думайте о ней

Есть одно мгновение в рисовании, когда вы ни о чем не задумываетесь, — момент нанесения первой линии. Первая линия является самой сложной, и нам приходится давать мозгу команду «не думать», чтобы затем поместить карандаш на бумагу и нарисовать круг.  

• Нарисуйте круг. Вот вы и начали рисовать. Затем снова подключите мозговую деятельность и придумайте этому кругу имя. Выберите абсолютно любое, какое только придет вам на ум. Оно может быть связано с важной для вас идеей: я, ты, сегодня, завтра, прибыль, наш продукт, моя компания, мир. Как только вы станете придумывать название, вы вновь запустите мыслительный процесс.
• Впишите придуманное слово в круг. Теперь вы уже обдумываете вещи и явления.

Как начать рисовать: пойдем от простого — круг и «я» в середине 

Есть первый круг — теперь дело за малым

Добавьте несколько других фигур рядом с кругом — квадрат, треугольник и звезду. Теперь соедините их стрелками. А затем как-нибудь отметьте их: вот вы и создали схематическую диаграмму идеи, как по мановению волшебной палочки.

Первый круг выделен красным цветом. Всем фигурам присвоена маркировка «шаг 1», «шаг 2» и т.д. Теперь все это можно назвать, скажем, бизнес-процессом, и тогда звезда станет его финалом 

Зачастую все, что вам нужно сделать для начала, — это нарисовать и назвать первый круг. А потом лишь продолжить процесс: один рисунок приводит к другому, а тот к следующему. 

Что маркетологу нужно знать про инфографику?

Добавляя (и называя) круги, вы сможете нарисовать любую идею!

Посмотрите на первый круг на рисунке ниже. Видите, какое количество разных идей вы способны выразить, просто прибавив еще круги, обозначения и несколько деталей?

Рассмотрим несколько рисунков, созданных с применением «концепта первого круга». 

Рисунок №1 

Три пересекающихся круга образуют диаграмму (ее еще называют «диаграммой Венна» для перекрывающихся множеств), иллюстрирующую пересечение трех компонентов идеи, в данном случае — как сделать идеальную чашечку кофе. 

(Тот же рисунок может демонстрировать ваш бизнес-оффер, клиентские сегменты или маркетинговый план.)

Схема «чашечки счастья» начинается с первого (красного) круга, означающего кофе, два других пересекающихся круга — это молоко и сахар

Рисунок №2

Три круга, изображающих простые рожицы, становятся картой конкурентного ландшафта. Здесь получился почти «любовный треугольник», о который разбиваются человеческие сердца. (Подобный рисунок может иллюстрировать ваше конкурентоспособное позиционирование, подход клиента к процессу приобретения или ваши кадровые потребности).

«Любовный треугольник» от бизнеса: клиент-продавец-конкурент

Рисунок №3

Два больших круга, два маленьких и один треугольник превращаются в велосипед. Или любое количество других объектов. (Так же можно показать ваше предложение или стратегию поставки продукции и услуг на рынок.)

Визуальное восприятие и применение принципов гештальта в веб-дизайне

Рисовать легко, когда вы начинаете с базовых форм

Поскольку из одного первого круга можно произвести так много рисунков, как только вы управитесь с ним, остальное придет само. Не успеете вы опомниться, а у вас уже нарисованы квадраты и треугольники, линии и стрелки, и идея, запрятанная глубоко в голове, принимает форму на ваших глазах. Более того, самой тяжелой частью процесса станет попытка остановиться. Такова сила нашего визуального мышления: главное — начать, потом идеи будут приходить сами собой. Такой простой пусковой механизм, как круг с названием, — это все, что требуется машине сознания, чтобы запустить обороты.

А если рисование вдруг застопорилось, всегда можно вновь зажечь ваше воображение, подбросив в его огонь новые формы, стрелки и названия.

90% всех изображений, относящихся к бизнесу, состоят всего лишь из 7 базовых блоков:

1. Точка
2. Линия
3. Стрелка
4. Квадрат
5. Треугольник
6. Круг
7. Клякса

Используя только эти 7 фигур, вы можете нарисовать практически все, что угодно. 

Начните с точки — и, оттолкнувшись от нее, карандаш побежит дальше. В конце концов, с точки начинаются даже те самые 7 строительных блоков, что мы только что перечислили.

Рисование как говорение: пока вы не скажете первое слово, будет царить тишина. Так скажите «Точка», а затем нарисуйте ее. Говорите визуально, для чего, подержав кончик карандаша на точке, продолжите рисовать линию в нужном направлении.

А какое направление нужно? Зависит от базовой фигуры, которую вы желаете нарисовать.

Инструмент 3A: семь базовых «строительных» фигур 

Вот, как рисуются основные фигуры:

1. Точка — начало всех линий.
2. Линия — начало всех фигур.
3. Стрелка — линия, обозначающая направление, влияние или изменение.
4. Квадрат — четыре точки, соединенные четырьмя линиями. Удлиняя линии, вы получите прямоугольник, наклоняя — трапецию.
5. Треугольник — три точки, соединенные тремя линиями. Удлиняя линии, вы получите любую трехстороннюю фигуру.
6. Круг — линия, «кусающая себя за хвост». Немного сжав круг, получаем овал.
7. Клякса — линия, «отправившаяся погулять, прежде чем вернуться домой». Кляксой обозначаются неструктурируемые вещи и явления, часто характеризующиеся проблематичностью.

Все бизнес-рисунки представляют собой комбинацию этих простых форм.

Для создания более значимых картинок вы просто комбинируете семь блоков. Комбинации также не отличаются сложностью. Есть всего лишь 6 основных бизнес-картинок, иллюстрирующих и объясняющих почти любую идею.

Как сделать продающую инфографику

Комбинации фигур 

Большая часть базовых объектов состоит из комбинаций фигур, в которых при необходимости стираются скрытые линии. 

1. Простые объекты и изображения людей создаются с помощью комбинации квадратов, кругов и треугольников.

2. Можно построить таблицу, поместив прямоугольники рядом друг с другом, или создать круговую диаграмму, «разрезав на куски» круг.

3. Карта получится, если перекрестить две стрелки и поместить фигуры в соответствующие секторы. 

4. История в хронологии создается путем выстраивания в ряд больших, толстых стрелок (представляющих собой прямоугольники, соединенные с треугольниками).

5. Вы нарисуете детальную схему, сортируя фигуры в определенном порядке и соединяя их стрелками.

6. Можно представлять зрителям уравнения путем объединения любого количества простых форм.

Попрактикуйтесь в создании таких 6 изображений за счет комбинаций базовых фигур. Даже если вы сможете рисовать только их, это уже составит 90% рисунков, необходимых для ваших бизнес-целей.

Высоких вам конверсий!

По материалам: neurosciencemarketing.com.

25-10-2016

Как нарисовать круг (окружность) в Автокад

[Видео курс Автокад] Как нарисовать круг (окружность) AutoCAD

---

Команда рисования в AutoCAD

Круг

Определение

Круг (окружность) в Автокад — это простейший плоский объект, представляющий собой замкнутую кривую, все точки которой равноудалены от центра.

Инструмент

Инструмент Автокад Круг — команда, позволяющая строить двухмерный объект круг (по умолчанию по центральной точке и радиусу)

Команда

Круг

Объект

Круг

Инструмент Круг в AutoCAD довольно часто используется и уступает по частоте вызовов только инструменту Отрезок.

Команда Круг

За создание окружностей в Автокад отвечает команда Круг, вызвать которую можно следующими способами (начать построение круга):

• постоить окружность в AutoCAD вы можете из строки меню пункт Рисование — строка Круг;
• Нарисовать круг можно из вкладки Главная ленты инструментов — в группе инструментов Рисование кнопка Круг;
• создать его можно из панели инструментов Рисование — кнопка Круг;
• начать построение окружности в AutoCAD можно также из командной строки, прописав наименование команды в командной строке Круг .

Всего доступно 6 способов построения круга в Автокад, которые поделены на 3 группы:

• Центр, Радиус, Диаметр.
• 2 Точки, 3 Точки.
• 2 Точки касания, Радиус (3 точки касания).

По умолчанию доступ ко всем методам построения окружности в Автокад можно получить из строки меню пункт Рисование — строка Круг c раскрывающемся списком способов построения, а также на вкладке «Главная» ленты инструментов — в группе инструментов Рисование кнопка в AutoCAD Круг с вложенными кнопками методов построения окружности.

Примечание

Вы можете создать вложенную панель инструментов Круг в Автокад в панели инструментов Рисование, содержащую все необходимые методы построения.

Построение в AutoCAD окружности по умолчанию (по центральной точке и радиусу)

Вызываем инструмент Круг в Автокад. В командной строке появится запрос:

Центр круга или [3T/2T/KKP]:

В ответ на запрос укажем точку центра круга Автокад щелчком мыши в нужном месте чертежа либо вводом координат в командную строку. Отобразится предварительный вид окружности, радиус которого изменяется в соответствии с перемещением указателя-перекрестия. По умолчанию появится штриховая линия желтого цвета, которая следует от центральной точки окружуности Автокад до указателя-перекрестия. Система выдаст запрос:

Радиус круга или [Диаметр]:

Задайте радиус окружности, выбрав точку на чертеже или введя значение радиуса круга в командную строку. Как только вы его укажите, окружность в Автокад будет вычерчена, работа команды Круг завершится.

Построение круга (окружности) в Автокад специальными способами

Довольно часто возникает необходимость построить окружность в AutoCAD по центральной точке и диаметру, т.к. большинство размеров окружностей на чертеже обозначаются ее диаметром. Построить круг в AutoCAD таким образом, чтобы он проходил через определенные точки или чтобы он касался каких-либо объектов.

Как построить окружность по центральной точке и диаметру

Вызываем команду Круг в AutoCAD. В командной строке появится запрос:

Центр круга или [3T/2T/KKP]:

В ответ на запрос укажем точку центра круга Автокад щелчком мыши в нужном месте чертежа либо вводом координат в командную строку. Отобразится предварительный вид окружности, диаметр которого изменяется в соответствии с перемещением указателя-перекрестия. По умолчанию появится штриховая линия желтого цвета, которая следует от центральной точки окружности в AutoCAD до указателя-перекрестия. Программа выдаст запрос:

Радиус круга или [Диаметр]:

Выбираем опцию «Диаметр». Система отобразит запрос:

Диаметр круга:

Зададим диаметр окружности Автокад, указав точку щелчком мыши на чертеже. Как только вы зададите диаметр, она будет построена, а команда Круг завершит выполнение.

Как сделать в Автокад круг по двум точкам

Вызываем команду Круг в AutoCAD. В командной строке появится запрос:

Центр круга или [3T/2T/KKP]:

В ответ на запрос выбираем опцию «2Т». Далее последовательно необходимо будет задать 2 точки будущего диаметра круга. Программа выдаст запрос:

Первая конечная точка диаметра круга:

Укажем точку щелчком мыши на чертеже. Отобразится предварительный вид круга AutoCAD, диаметр которого будет изменяться вместе с перемещением положения курсора-перекрестия. Появится желтая штриховая линия, которая следует от первой конечной точки диаметра круга до курсора-перекрестия. Отобразится следующий запрос в командной строке:

Вторая конечная точка диаметра круга:

Укажем точку щелчком мыши на чертеже. Как только вы зададите диаметр круга двумя точками, окружность в AutoCAD будет построена, а команда Круг завершит свое выполнение.

Как начертить окружность в AutoCAD по трем точкам

Вызываем в Автокад инструмент Круг. В командной строке появится запрос:

Центр круга или [3T/2T/KKP]:

В ответ на запрос выбираем опцию «3Т». Далее последовательно необходимо будет указать 3 точки, через которые будет проходить окружность Автокад. Система выдаст запрос:

Первая точка круга:

Укажем точку щелчком мыши на чертеже. Появится штриховая линия желтого цвета, которая будет следовать от первой точки окружности в Автокад до курсора-перекрестия. Программа отобразит следующий запрос:

Вторая точка круга:

Укажем в Автокад вторую точку окружности щелчком мыши на чертеже. Отобразится ее предварительный вид, который будет проходить через 1 и 2 точки и изменяться вместе с перемещением курсора-перекрестия. Штриховая желтая линия будет выходить из 2 указанной точки до курсора-перекрестия. Программа выдаст запрос:

Третья точка круга:

Укажем точку щелчком мыши на чертеже. Как только вы укажете 3 точку, окружность Автокад будет построена, команда «Круг» завершит выполнение.

Примечание

При построении окружности по 3 точкам — эти точки не должны лежать на одной прямой, иначе построение окружности будет невозможно.

Как построить круг по двум точкам касания и радиусу

Вызываем команду Круг в Автокад. В командной строке появится запрос:

Центр круга или [3T/2T/KKP]:

Выбираем опцию «ККР (построение в Автокад окружности по 2 точкам касания и радиусу)» . Программа отобразит запрос:

Укажите точку на объекте, задающую первую касательную:

Подведем курсор к отрезку. Программа распознает отрезок, обозначив объектную привязку «Касательная». По умолчанию появится подсказка «Задержанная касательная». Щелкнем мышкой по отрезку. Автокад выдаст запрос:

Укажите точку на объекте, задающую вторую касательную:

В ответ на запрос выберем щелчком мыши ломаную линию. Появится следующий запрос:

Радиус круга:

Радиус круга Автокад можно задать, введя его значение в командную строку или указав две точки на чертеже, расстояние между которыми станет величиной радиуса. Как только вы зададите радиус, окружность в AutoCAD будет построена, команда Круг завершит выполнение.

Построение окружности в Автокад по трем точкам касания

Выберем опцию «3 точки касания» команды «Круг» в AutoCAD из строки меню пункт «Рисование» — строка «Круг» — в раскрывающемся списке выберем строку 3 точки касания.

Теперь необходимо указать 3 точки касания окружности к объектам, последовательно ответив на запросы командной строки:

Первая точка круга: к
Вторая точка круга: к
Третья точка круга: к

Выбираем отрезки щелчком мыши. Как только вы укажете 3 точку касания, окружность в AutoCAD будет построена, а команда Круг завершит свое выполнение.

Полезные уроки схожих тематик и рекомендации

Рекомендую ознакомиться с подобными уроками по Автокад:

Читайте и смотрите также:

Курсы, самоучители Автокад:

1. 2D проектирование.
2. 3D моделирование.
3. Начертательная геометрия.
4. Инженерная графика.
5. План дома.
6. Сборочный чертеж цилиндрической зубчатой передачи.
7. Модель кухни 3D.

Видео «Как нарисовать в Автокад круг (окружность), дугу»

Как построить равносторонний треугольник, вписанный в данный круг, с помощью циркуля и линейки или линейки

ПРИМЕЧАНИЕ. Шаги с 1 по 7 такие же, как и для построения шестиугольника, вписанного в круг. В случае вписанного равностороннего треугольника мы используем все остальные точки на окружности.
1	A, B, C, D, E, F все лежат в центре окружности O	По конструкции.
2	AB = BC = CD = DE = EF	Все они были нарисованы с одинаковой шириной циркуля.
Из (2) видно, что пять сторон равны по длине, но последняя сторона FA не была нарисована циркулем. Это было «оставшееся» пространство, когда мы обошли круг и остановились у F. Итак, мы должны доказать, что это соответствует остальным пяти сторонам.
3	OAB — равносторонний треугольник	AB был нарисован с шириной компаса, установленной на OA, и OA = OB (оба радиуса круга).
4	м∠AOB = 60 °	Все внутренние углы равностороннего треугольника равны 60 °.
5	м∠AOF = 60 °	Как и в (4) m∠BOC, m∠COD, m∠DOE, m∠EOF все равны & 60deg; Так как все центральные углы складываются в 360 °, м∠AOF = 360 — 5 (60)
6	Треугольник BOA, AOF совпадают	SAS См. Тест на конгруэнтность, бок-угол-бок.
7	AF = AB	CPCTC — Соответствующие части конгруэнтных треугольников конгруэнтны
Итак, теперь мы можем доказать, что BDF — это равносторонний треугольник
8	Все шесть центральных углов (∠AOB, ∠BOC, ∠COD, ∠DOE, ∠EOF, ∠FOA) совпадают.	Из (4) и повторением для других 5 углов все шесть углов имеют меру 60 °.
9	Углы ∠BOD, ∠DOF, ∠BOF равны	Из (8) — Каждый из них представляет собой сумму двух углов по 60 °
10	Треугольники BOD, DOF и BOF совпадают.	Стороны представляют собой равные радиусы окружности, а из (9) включенные углы совпадают. См. Тест на соответствие, сторона-угол-сторона
11	BDF — равносторонний треугольник.	Из (10) BD, DF, FB конгруэнтно. CPCTC — соответствующие части конгруэнтных треугольников конгруэнтны. Это, в свою очередь, удовлетворяет определению равносторонний треугольник.
12	BDF — равносторонний треугольник, вписанный в данную окружность	Из (11) и все три вершины B, D, F лежат на данной окружности.

Иллюстративная математика

Задача

Предположим, нам дан круг радиуса $ r $. Цель этой задачи — построить равносторонний треугольник, три вершины которого лежат на окружности. Предположим, что $ \ overline {AB} $ — диаметр окружности. Нарисуйте круг с центром $ A $ и радиусом $ r $ и обозначьте две точки пересечения кругов $ P $ и $ Q $, как показано ниже:

1. Докажите, что $ m (\ angle ABP) = 30 $ и $ m (\ angle ABQ) = 30 $.
2. Покажи это $ \ треугольник PBQ $ — это равносторонний треугольник, вписанный в данную окружность.

IM Комментарий

Построение равностороннего треугольника, вписанного в круг, требует творческого подхода и хорошего знания геометрии и / или тригонометрии. Подход, принятый в данном решении, использует тот факт, что $ \ sin {30} = \ frac {1} {2} $. Следовательно, чтобы построить угол в 30 градусов, достаточно уметь построить прямоугольный треугольник, гипотенуза которого в два раза больше длины катета.Студентам необходимо знать, что $ \ angle APB $ правильный, поскольку он вписан в круг с одним лучом по диаметру круга. Отношение $ (2: 1) $ для гипотенузы к катету определяется с использованием диаметра окружности для гипотенузы и радиуса конгруэнтной окружности для катета.

Эта задача реализует многие важные идеи из геометрии, включая тригонометрические отношения, важные факты о треугольниках и отражения, если учащиеся предпочитают рассматривать $ \ треугольник ABQ $ как отражение $ \ треугольника ABP $ относительно $ \ overleftrightarrow {AB} $.В результате рекомендуется выполнять эту задачу относительно поздно в учебной программе по геометрии. Он также может быть дан в открытой форме, то есть с просьбой создать вписанный равносторонний треугольник внутри данного круга без предложения подхода или изображения. Альтернативный метод начинается с того, что если $ O $ — центр исходной окружности, то $ \ треугольник AOP $ равносторонний (все три стороны являются радиусами конгруэнтных окружностей). Мы можем продолжать рисовать круги с центрами $ P $ и $ Q $, и каждый раз мы получаем еще один равносторонний треугольник.Конечным результатом будет правильный шестиугольник, вписанный в круг: соединение всех остальных вершин этого шестиугольника дает равносторонний треугольник, вписанный в круг. Вариант этого аргумента, сфокусированный только на шестиугольнике, представлен на http://www.illustrativemat Mathematics.org/illustrations/786.

Работа над этой задачей может развить навыки, связанные с MP1, понимать проблемы и настойчиво решать их, а также MP3, создавать жизнеспособные аргументы и критиковать рассуждения других.В первом случае аргумент сложен и требует объединения нескольких абстрактных аргументов, которые необходимо связать с построением желаемого равностороннего треугольника. Из-за своей сложности он идеально подходит для групповой работы, чтобы учащиеся могли объединить свои сильные стороны и навыки.

Превращение кругов в треугольники — игровое обучение

загрузка …

Несколько лет назад я взял в руки книгу Майкла Шнайдера «Руководство для начинающих по построению Вселенной ».Это было именно то, что я искал, чтобы улучшить уроки геометрии моих детей. Сегодня я делюсь одним из первых уроков из книги и одним из любимых моих детей — лепкой треугольников из кругов.

Вам понадобится:

• Миллиметровая бумага
• Линейка или другой инструмент с прямой кромкой
• Циркуль с заточенным карандашом. Примечание. Если ребенку сложно управлять компасом, круги можно также нарисовать с помощью картонной полоски, канцелярской кнопки и карандаша или ручки, как показано на фотографии выше.

Урок начинается с того, что ваш ребенок рисует круг вокруг центральной точки (созданной точкой компаса). Точка на миллиметровой бумаге — идеальное место для начала. Для этого упражнения важно отметить центр круга. Вы скоро поймете, почему. После того, как круг нарисован, мне нравится делать карандашную точку в центре, чтобы его было легко увидеть.

Теперь поместите конец циркуля (или булавку на картонную полоску) на окружность круга по горизонтали от центральной точки круга.Вы можете проследить линию на миллиметровой бумаге. Нарисуйте второй круг и снова затемните центральную точку. Каждый круг должен пересекать центр другого.

Нарисуйте точку на пересечении кругов вверху. Используя линейку, проведите прямую линию от верхней точки к каждой центральной точке. Затем соедините каждую центральную точку горизонтальной линией. Это рождение треугольника! Насколько это аккуратно?

Но это еще не конец. Это прекрасное время, чтобы задавать вопросы типа «Интересно» и глубже исследовать, добавляя больше точек для связи.Наша распечатка поможет вам начать работу.

После завершения печати вы увидите, что все созданные треугольники являются равносторонними треугольниками. Если соединить другие точки, появится ли треугольник другого типа? Вы замечаете другие формы?

Получайте удовольствие и не бойтесь экспериментировать или добавлять свое чутье!

Нарисуйте фигуру в Visio с помощью инструментов «Карандаш», «Линия», «Дуга» или «Произвольная форма»

Вы можете создавать свои собственные пользовательские фигуры, используя в Visio фигуры прямоугольника, эллипса, дуги, произвольной формы и карандаша.

Если вы хотите иметь возможность применять цвета заливки к вашей новой форме, вам необходимо создать замкнутую форму. Если вы используете инструмент Прямоугольник или Эллипс , вы автоматически получаете замкнутые формы. По умолчанию замкнутые фигуры залиты сплошным цветом.

В этом примере прямоугольник является замкнутой формой, потому что он залит сплошным цветом. Вы можете сказать, что треугольник не замкнут, потому что он не залит сплошным цветом, и вы можете видеть фон рисунка через фигуру.

Что ты хочешь сделать?

Нарисуйте прямоугольник или круг

1. На вкладке Главная в группе Инструменты щелкните стрелку рядом с Прямоугольник , а затем выполните одно из следующих действий:

   • Чтобы нарисовать прямоугольник, выберите инструмент Прямоугольник .

   • Чтобы нарисовать круг или овал, выберите инструмент Эллипс .

2. Перетащите, чтобы нарисовать фигуру на странице документа.

3. Чтобы вернуться к обычному редактированию, в группе Инструменты щелкните указатель инструмент.

Верх страницы

Нарисуйте произвольную форму

1. На вкладке Главная в группе Инструменты щелкните стрелку рядом с Прямоугольник , а затем выполните одно из следующих действий:

   • Чтобы нарисовать прямую линию, выберите инструмент Линия .

   • Чтобы нарисовать неправильную форму, выберите инструмент Freeform .

   • Чтобы нарисовать изогнутую линию, выберите инструмент Дуга .

2. Чтобы нарисовать первый сегмент, наведите указатель мыши на то место, где вы хотите начать фигуру, а затем перетащите его, пока сегмент не станет нужного размера.

3. Чтобы нарисовать второй сегмент, наведите указатель на вершину первого сегмента и перетащите его.

4. Чтобы нарисовать дополнительные сегменты, наведите указатель на вершину в конце последнего добавленного сегмента, а затем перетащите его, чтобы нарисовать следующий сегмент.

   Примечание. Чтобы отменить сегмент, нажмите Ctrl + Z. Сегменты удаляются в том порядке, в котором они были нарисованы.

5. Чтобы замкнуть фигуру, перетащите конечную точку последнего сегмента, который вы создаете, над вершиной в начале первого сегмента. Форма становится непрозрачной, что указывает на то, что это замкнутая форма.

6. Чтобы вернуться к обычному редактированию, на вкладке Home в группе Tools щелкните инструмент Pointer .

Верх страницы

Редактировать фигуру

Вы можете редактировать большинство фигур в Visio, добавляя, удаляя и изменяя формы сегментов в фигуре.

Удалить сегмент фигуры

1. На вкладке Главная в группе Инструменты щелкните стрелку рядом с Прямоугольник , а затем щелкните инструмент Карандаш .

2. Выберите фигуру, из которой вы хотите удалить сегмент, щелкните вершину который вы хотите удалить, а затем нажмите клавишу DELETE.

Добавить сегмент к фигуре

1. На вкладке Главная в группе Инструменты щелкните стрелку рядом с Прямоугольник , а затем щелкните инструмент Карандаш .

2. Выберите фигуру, к которой вы хотите добавить сегмент, наведите указатель на то место, куда вы хотите добавить сегмент, и, удерживая клавишу Ctrl, нажмите.

   Новая вершина появляется там, где вы щелкнули по фигуре, создавая новый сегмент.

Изменение формы

1. На вкладке Главная в группе Инструменты щелкните стрелку рядом с Прямоугольник , а затем щелкните инструмент Карандаш .

2. Выберите форму, щелкните вершину который вы хотите переместить, а затем перетащите вершину в новое положение.

Верх страницы

Создать новый образец формы

Вы можете повторно использовать свою произвольную форму в других чертежах, сделав ее образцом. Чтобы превратить пользовательскую фигуру в эталонную, выполните следующие действия?

1. На панели Shapes щелкните More Shapes , а затем выберите настраиваемый набор или создайте новый настраиваемый набор, выбрав New Stencil (US units) или New Stencil (Metric) .

2. На странице документа выберите пользовательскую фигуру и перетащите ее в новый набор элементов на панели Фигуры .

3. Чтобы переименовать новую форму-образец, щелкните ее правой кнопкой мыши, выберите Переименовать образец , а затем введите имя для новой формы-образца.

4. На панели Фигуры на настраиваемом наборе элементов нажмите Сохранить , чтобы сохранить изменения настраиваемого набора элементов с новой основной формой.

Дополнительные сведения о создании новой формы-образца см. В разделах Создание формы или Редактирование основной формы.

Верх страницы

Как нарисовать равносторонний треугольник в круге »OrigamiTree.com

Поиск по ключевому слову

ДОБРО ПОЖАЛОВАТЬ!

Origami Tree предлагает БЕСПЛАТНЫЕ уроки ремесла на YouTube — дом для миллионов посетителей с ноября 2013 года.

Копаться в архивах

Копаться в архивах Выберите месяц Апрель 2021 Сентябрь 2020 Октябрь 2019 Сентябрь 2019 Август 2019 Июль 2019 Июнь 2019 Май 2019 Апрель 2019 Март 2019 Февраль 2019 Январь 2019 Декабрь 2018 Ноябрь 2018 Октябрь 2018 Сентябрь 2018 Август 2018 Июль 2018 Июнь 2018 Май 2018 Апрель 2018 Март 2018 Февраль 2018 Январь 2018 Декабрь 2017 Ноябрь 2017 Октябрь 2017 Сентябрь 2017 Август 2017 Июль 2017 Июнь 2017 Май 2017 Апрель 2017 Март 2017 Февраль 2017 Январь 2017 Декабрь 2016 Ноябрь 2016 Октябрь 2016 Сентябрь 2016 Август 2016 Июль 2016 Июнь 2016 Май 2016 Апрель 2016 Март 2016 Февраль 2016 Январь 2016 Декабрь 2015 Ноябрь 2015 Октябрь 2015 Сентябрь 2015 Август 2015 Июль 2015 Июнь 2015 Май 2015 Апрель 2015 Март 2015 Февраль 2015 Январь 2015 Декабрь 2014 Ноябрь 2014 Октябрь 2014 Сентябрь 2014 Август 2014 Июль 2014 Июнь 2014 Май 2014 Апрель 2014 Март 2014 Февраль 2014 Январь 2014 Январь 2014 Декабрь 2013 Ноябрь 2013 Октябрь 201 3 июня 2013 г. март 2013 г. июнь 2011 г. декабрь 2010 г.

Хотите помочь?

Поддержите продолжение бесплатных обучающих программ, сделав пожертвование сегодня!

В этом уроке я покажу вам простой способ нарисовать треугольник внутри круга.С помощью этого метода вы можете построить равносторонний треугольник (все стороны треугольника равны) в данном круге. Вы можете изучить это для помощи в домашнем задании по геометрии / математике, или вы можете создать из них бумажный орнамент! Ага, верно! Вам понадобится циркуль, линейка, ручка или карандаш и лист бумаги.

Больше веселья!

Как сделать орнамент из бумаги (треугольник в единицах круга)

Нравится:

Нравится Загрузка…

Связанные

19 декабря 2016 г. в Back-to-School, Tips & Tricks. Теги: круг, геометрия, математика, орнамент, треугольник

Круги и использование циркуля

Части круга

Дуга является частью окружности.

Сектор — это часть окружности между двумя радиусами.

Сегмент — это часть окружности, которая находится между хордой и окружностью.

Полукруг — это половина круга.

Компас

Компас — это инструмент, используемый для рисования кругов или частей окружности называются дугами.Он состоит из двух подвижных рычагов, шарнирно соединенных между собой. где одна рука имеет заостренный конец, а другая держит карандаш.

Обратите внимание, что компас также называется парой циркуля.

Чтобы нарисовать круг (или дугу) с помощью циркуля:

• убедитесь, что петля в верхней части компаса затянут так, чтобы не скользила
• затяните держатель карандаша, чтобы он не соскальзывал
• совместите грифель карандаша с иглой циркуля
• нажмите на иглу и поверните ручку в верхней части циркуль для рисования круга (или дуги)

Пример 2

С помощью циркуля начертите круг радиусом 4 см.

Решение:

Шаг 1: С помощью линейки установите расстояние от точки компаса до грифель карандаша на 4 см.
Шаг 2: Поместите конец циркуля в центр круга.
Шаг 3: Нарисуйте круг, повернув циркуль на 360.

Действие 10,1

1. С помощью циркуля начертите круг радиусом 5 см.
2. С помощью циркуля начертите круг диаметром 12 см.

3а. С помощью циркуля начертите круг радиусом 4,5 см.
3б. Нарисуйте диаметр круга; и используйте линейку, чтобы измерить длина диаметра.
3с. Напишите уравнение для представления отношения между радиусом, r , и диаметром d .

4а. С помощью циркуля начертите круг радиусом 5,5 см.
4б. Нарисуйте диаметр и обозначьте его PQ .
4с. Нарисуйте треугольник PQR , где R находится на полукруге.
4д. С помощью транспортира измерьте размер уголка PRQ .

5а. С помощью циркуля начертите круг радиусом 6,5 см.
5б. Нарисуйте диаметр и обозначьте его PQ .
5с. Нарисуйте треугольник PQR , где R находится на полукруге.
5д. С помощью транспортира измерьте размер уголка PRQ .

6а.С помощью циркуля начертите круг радиусом 7,5 см.
6б. Нарисуйте диаметр и обозначьте его PQ .
6с. Нарисуйте треугольник PQR , где R находится на полукруге.
6д. С помощью транспортира измерьте размер уголка PRQ .

7. Используйте результаты вопросов 4, 5 и 6, чтобы заполнить следующие выписки:
а. Размер угла на диаметр окружности с вершиной на круг —
б.Если треугольник нарисован полукругом, используя диаметр как ребро, угол касания изогнутой части треугольника равен

Ключевые термины

круг, центр круга, радиус, периметр, окружность, радиусы, линии круга, секущая, хорда, диаметр, касательная, части круга, дуга, сектор, сегмент, полукруг, циркуль, циркуль

Как рисовать прямоугольник, Круг и основная форма на странице PDF

Как нарисовать прямоугольник, круг и простую форму на странице PDF

PDFill | Обзор | Первый | Предыдущая | Далее | Последние

PDFill PDF чертеж: Инструмент «Прямоугольник, круг и основная форма»
(см. Пример PDF и пример файла проекта PDFill)

Вы можете использовать этот инструмент для рисования прямоугольника, квадрат, круглый угол, круг, эллипс, дуга и круговая диаграмма и многое другое. формы в PDF документ.

Больше базовой формы Рисунки включают равнобедренный треугольник, прямоугольный треугольник, ромб, пятиугольник, Шестиугольник, стрелка влево, стрелка вправо, стрелка вверх, стрелка вниз, 4-конечная звезда, 5-конечная звезда, 6-конечная звезда, закругленное прямоугольное обозначение, овальное обозначение, Облако выноски, сердце, молния и смайлик.

Ты можешь изменение рисунков Ширина линии, Стиль пунктирной линии, Цвет линии, Заливка Цвет и прозрачность.

1. Как нарисовать прямоугольник, круг или Основная форма на странице PDF:

• Выбрать Вставить меню > Чертеж > Выбрать Прямоугольник , Круг или Базовая форма

или щелкните Прямоугольник , Круг или Базовая форма Кнопка в Панель инструментов рисования .

Нажмите кнопку «Основные типы», чтобы показать меню и затем выбрать базовую фигуру

• Удерживайте левую кнопку мыши, чтобы создать площадь необходимого размер, а затем отпустите его

2. Откройте свойства:

• Нажмите кнопку Selection первый.
• Щелкните внутри строки, чтобы выделить ее, и щелкните Кнопка «Свойства»
• Или щелкните строку и снова дважды щелкните
• Или, клавиша F4

3.Задайте свойства:

Вот список свойств.

Вес линии	Толщина линии.
Цвет линии	Цвет для линия.
Штриховая линия	Есть 8 штриховых стилей: Сплошная, круглая точка, квадратная точка, тире, тире точка, длинная тире, Длинная точка тире, точка длинная тире
Цвет заливки	Фон цвет внутри формы.
Повернуть	Вращение градус от 3 часов относительно центра формы.
Прозрачный	Прозрачность рисунка объект
Прямоугольник	Если установлено, это будет прямоугольник или квадрат типа
Угловой радиус	Если установлено, прямоугольник будет закругленный угол радиусом
Круг	Если установлено, это будет эллипс, тип круга
Арка	Если установлено, то не будет полный круг / эллипс на 360 градусов
Пирог	Будет нарисован край.
Начальный угол	степень от 3 часов
Концевой уголок	степень в области Направление против часовой стрелки
Основные формы	Равнобедренный треугольник, Прямой треугольник, Алмаз, Пентагон, Шестиугольник, Стрелка влево, Стрелка вправо, Вверх Стрелка, Стрелка вниз, 4-конечная звезда, 5-конечная звезда, 6-конечная звезда, закругленное прямоугольное обозначение, овал Выноска, Выноска из облака, Сердце, Молния и Смайлик Лицо.
Положение (слева, справа, сверху, снизу)	X и Y координата поля для определения положения поле.
Режим наложения	Цвет Режим наложения для Прямоугольник или круг. Сохраните в новый PDF-файл, чтобы увидеть эффект смешивания.
Заказать	Это будет отображаться на переднем или заднем плане PDF-файла документ
Слой PDF	Выбрать имя слоя PDF, если он принадлежит слою PDF. Делать он пуст, если не принадлежит слою PDF. Видеть детали в PDF Layer.
Действие: добавить ссылку, отправить, JavaScript и многое другое…	Видеть Действия с PDF.
Установить это поле по умолчанию	Если установлено, новый объект будет иметь те же свойства как этот. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт