Равнобедренный треугольник. Свойства, Признаки, Высота
Определение равнобедренного треугольника
Какой треугольник называется равнобедренным?
| Равнобедренным называется треугольник, у которого две стороны равны. |
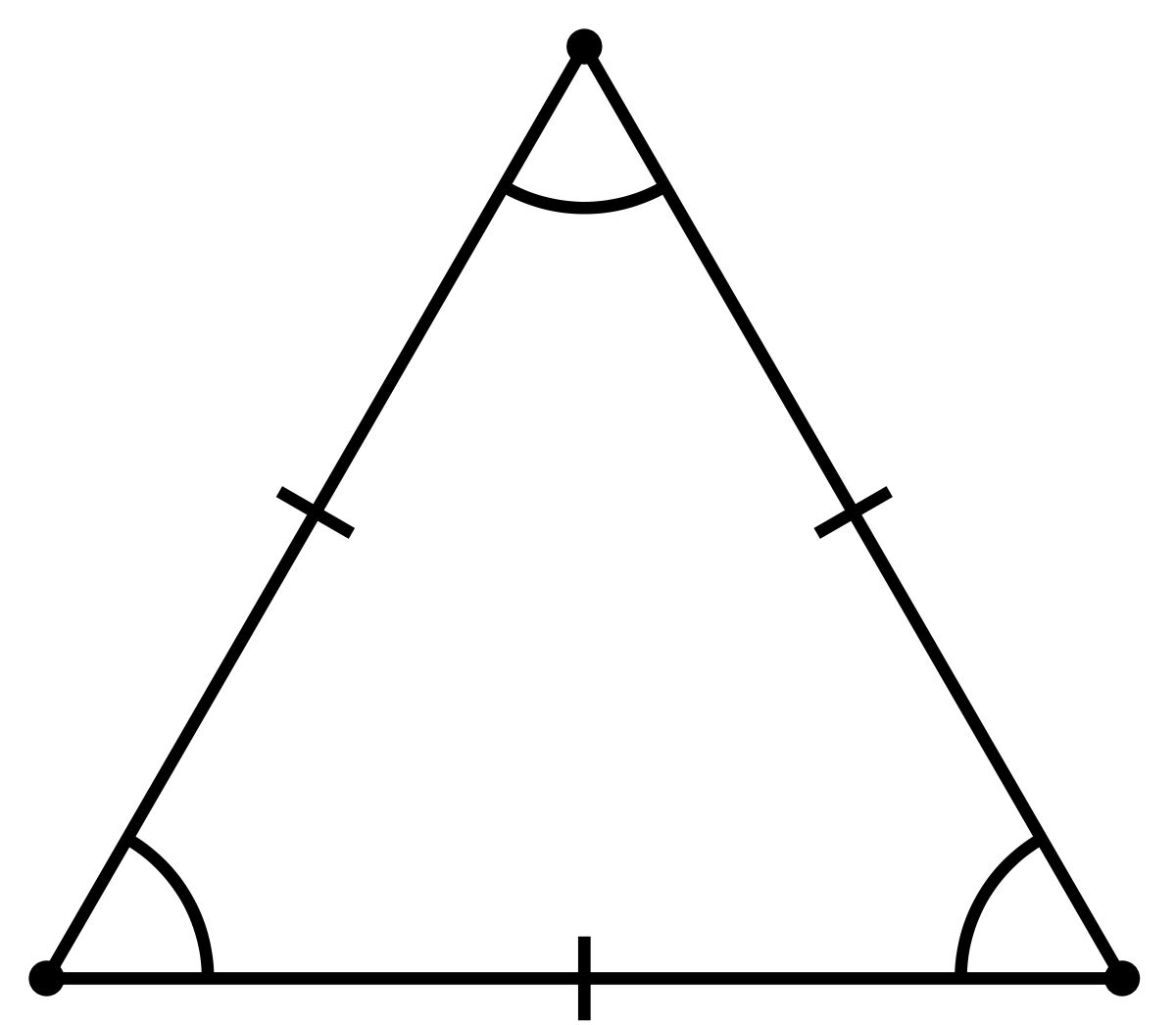
Давайте посмотрим на такой треугольник:
На рисунке хорошо видно, что боковые стороны равны. Это равенство и делает треугольник равнобедренным.
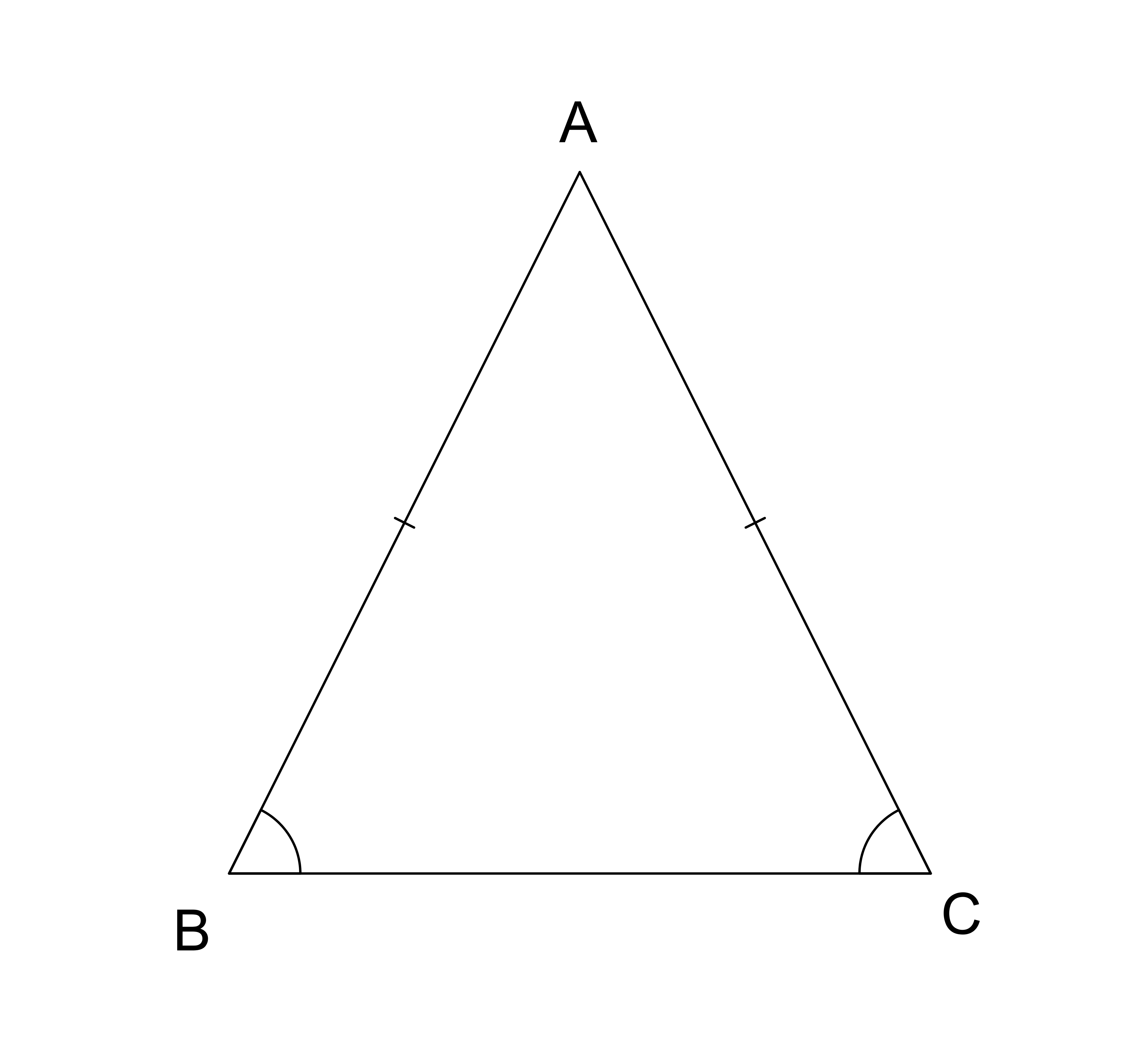
А вот как называются стороны равнобедренного треугольника:
AB и BC — боковые стороны,
AC — основание треугольника.
Чтобы найти основание равнобедренного треугольника, используйте формулу: b = 2a cos
Свойства равнобедренного треугольника
Чтобы понять суть равнобедренного треугольника, нужно думать как равнобедренный треугольник, стать равнобедренным треугольником — и выучить 5 теорем.
Теоремы помогут доказать, что треугольник равнобедренный, а не какой-нибудь ещё. Давайте приступим.
Давайте приступим.
Теорема 1. В равнобедренном треугольнике углы при основании равны.
Доказательство теоремы:
Мы выяснили, что AС — основание равнобедренного треугольника. Поскольку боковые стороны треугольника равны AB = СB, то и углы при основании — равны. ∠ BАC = ∠ BСA. Изи!
Теорема 2: В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
Теорема 3: В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
Теорема 4: В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.
Биссектриса — луч, который исходит из вершины угла и делит этот угол на два равных угла.
Даже если вы не знаете определения, то про крысу, бегающую по углам и делящую их пополам, наверняка слышали.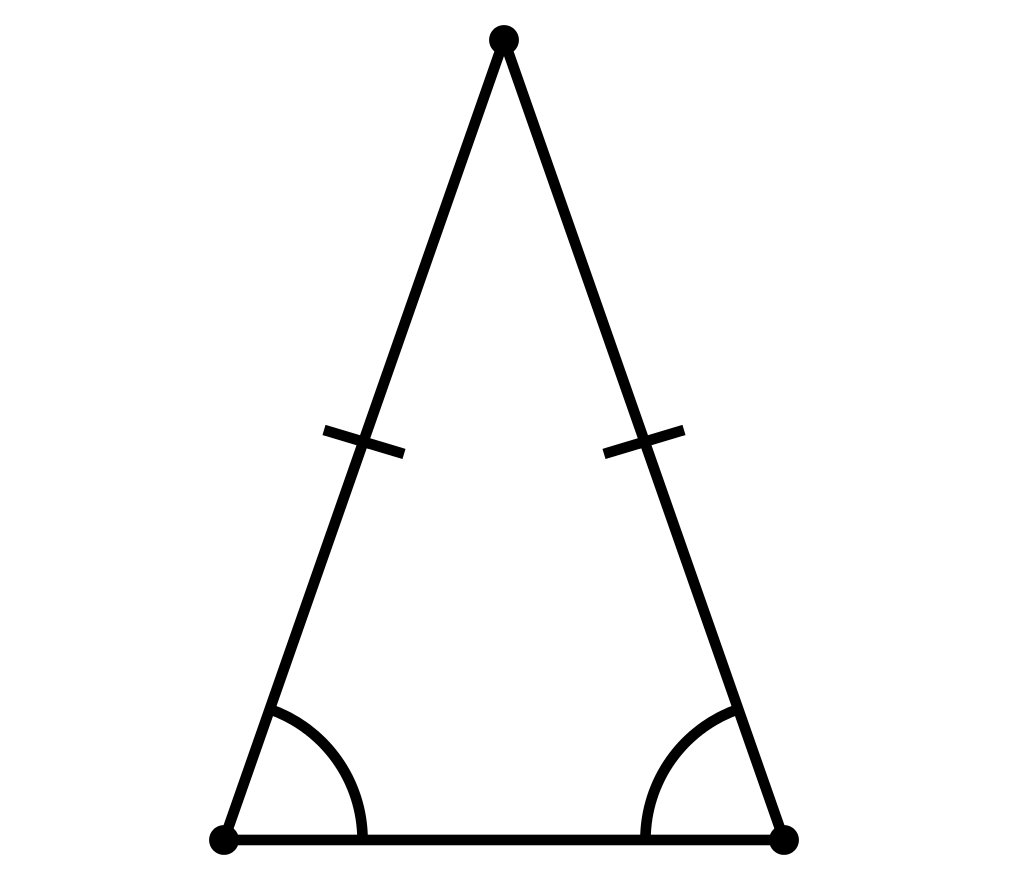 Она не даст вам забыть, что такое биссектриса. А если вам не очень приятны крысы, то вместо нее бегать может кто угодно. Биссектриса — это киса. Биссектриса — это лИса. Никаких правил для воображения нет. Все правила — для геометрии.
Она не даст вам забыть, что такое биссектриса. А если вам не очень приятны крысы, то вместо нее бегать может кто угодно. Биссектриса — это киса. Биссектриса — это лИса. Никаких правил для воображения нет. Все правила — для геометрии.
Обратите внимание на рисунок. В представленном равнобедренном треугольнике биссектрисой будет отрезок BH.
Медиана — линия, которая соединяет вершину треугольника с серединой противолежащей стороны.
Для медианы не придумали веселого правила, как с биссектрисой, но можно его придумать. Например, буддийская запоминалка: «Медиана — это Лама, бредущий из вершины треугольника к середине его основания и обратно».
В данном треугольнике медианой является отрезок BH.
Высота треугольника — перпендикуляр, опущенный из вершины треугольника на противоположную сторону.
Высотой в представленном равнобедренном треугольнике является отрезок BH.
Доказательство теорем 2, 3, 4 будет коллективным, поскольку из определений видно, что биссектриса, медиана и высота равнобедренного треугольника — это одно и то же.
А вот и доказательство:
- Δ ABC
- Высота BH делит Δ ABC на два прямоугольных треугольника ABH и CBH
- Δ ABH = Δ CBH, поскольку гипотенузы и катет равны по теореме Пифагора
- Согласно теореме 1: в треугольниках ABH и BCH ∠ BАH = ∠ BСH, поскольку углы при основании равнобедренного треугольника равны
- Так как Δ ABC — равнобедренный, то его боковые стороны равны AB = BC
- AH = CH, поскольку точка H делит основание Δ ABC на две равные части
- Δ ABH = Δ BCH
- Значит, отрезок BH одновременно биссектриса, медиана и высота равнобедренного треугольника ABC
Вуаля, сразу три теоремы доказаны.
Теорема 5: Если три стороны одного треугольника равны трем сторонам другого треугольника, то такие треугольники равны (третий признак равенства треугольников).
Доказательство:
Дано два Δ ABC = Δ A1B1C1.
Чтобы доказать равенство треугольников, мысленно наложите один треугольник на другой так, чтобы стороны совпали.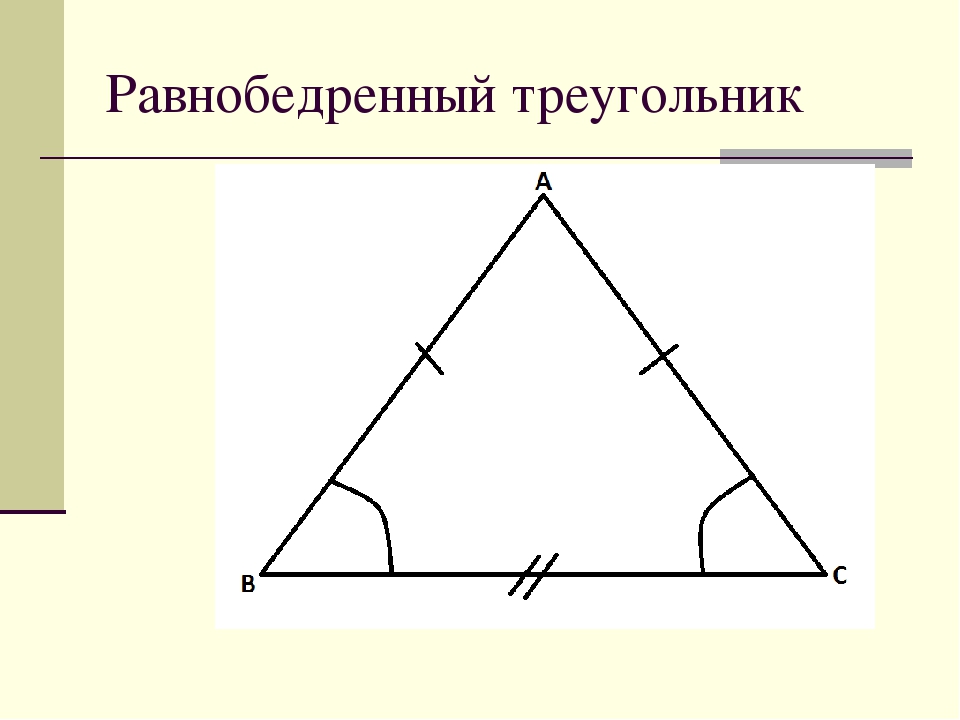 Точка A должна совпасть с точкой А1, точка B должна совпасть с точкой B2, точка С — с точкой С1.
Точка A должна совпасть с точкой А1, точка B должна совпасть с точкой B2, точка С — с точкой С1.
Если все стороны совпадают — треугольники равны, а теорема доказана.
Признаки равнобедренного треугольника
Вот несколько нехитрых правил, по которым легко определить, что перед вами не что иное, как его величество равнобедренный треугольник.
- Если у треугольника два угла равны, то этот треугольник — равнобедренный.
- Если высота треугольника совпадает с его медианой, то такой треугольник — равнобедренный.
- Если высота треугольника совпадает с его биссектрисой, то такой треугольник — равнобедренный.
- Если биссектриса треугольника совпадает с его медианой, то такой треугольник снова равнобедренный!
- Если два угла треугольника равны, такой треугольник является равнобедренным.
Свойства углов равнобедренного треугольника
|
Формулы равнобедренного треугольника
Формулы сторон равнобедренного треугольника
b — основание равнобедренного треугольника
a — равные стороны равнобедренного треугольника
α — углы при основании
β — угол, образованный равными сторонами
Формулы длины стороны (основания b) равнобедренного треугольника
Формулы длины равных сторон равнобедренного треугольника (стороны a):
Формулы высоты, медианы, биссектрисы равнобедренного треугольника
b — основание равнобедренного треугольника
α — углы при основании
β — угол, образованный равными сторонами
L — высота, биссектриса и медиана
Формулы высоты, биссектрисы и медианы равнобедренного треугольника, через сторону и угол (L)
Формула высоты, биссектрисы и медианы равнобедренного треугольника, через стороны (L)
Примеры решения задач
Нет ничего приятнее, чем поупражняться и поискать градусы и длины в равнобедренном треугольнике.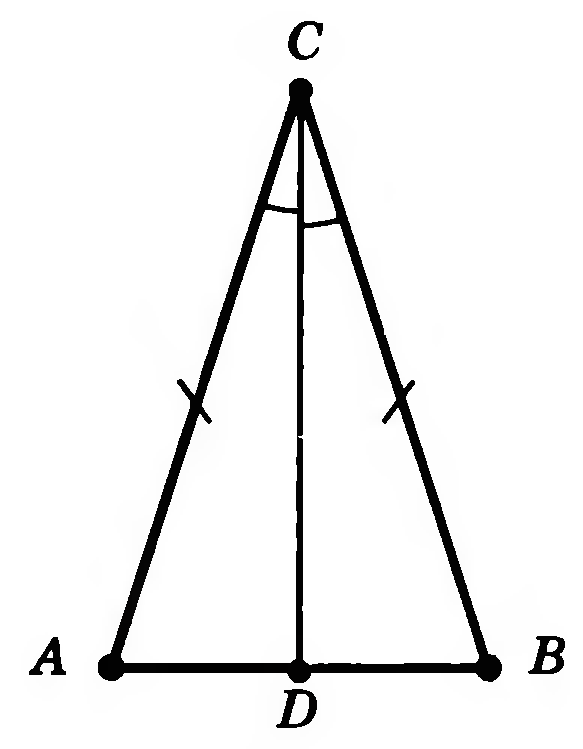 Ну… почти ничего.
Ну… почти ничего.
Задачка раз. Дан ABC: ∠C = 80∘, AB = BC. Найдите ∠B.
Поскольку вы уже знакомы с пятью теоремами, то для вас не секрет, что углы при основании в равнобедренном треугольнике равны.
∠A = ∠C = 80∘.
Не должно вас удивить и то, что сумма углов треугольника равна 180∘
∠B = 180∘ − 80∘ − 80∘ = 20∘.
∠B = 20∘
Задачка два. В равнобедренном треугольнике один из углов равен 110∘. Найдите наибольший из внешних углов этого треугольника.
Вспоминаем первую теорему о равенстве углов при основании (а лучше не забываем вовсе). Поскольку сумма углов = 180∘, то второго угла в 110∘ в нём быть не может. Соответственно, известный угол в 110∘ — это угол при вершине. (180∘−110∘)/2=35∘. Внешние углы треугольника равны: 180∘−110∘=70∘,180∘−35∘=145∘,180∘−35∘=145∘. Больший внешний угол равен 145∘
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия
| Тип утверждения | Фигура | Рисунок | Формулировка |
| Определение | Равнобедренный треугольник | Равнобедренным треугольником называют треугольник, у которого две стороны равны. Равные стороны называют боковыми сторонами равнобедренного треугольника, третью сторону называют основанием равнобедренного треугольника. | |
| Свойство | Углы при основании равнобедренного треугольника | Если треугольник является равнобедренным треугольником, то углы при его основании равны. | |
| Признак | Два равных угла треугольника | Если у треугольника два угла равны, то этот треугольник является равнобедренным треугольником. | |
| Свойство | Медиана, биссектриса и высота, проведённые к основанию равнобедренного треугольника | В равнобедренном треугольнике медиана, биссектриса и высота, проведённые из вершины, противолежащей основанию, совпадают. | |
| Признак | Высота треугольника, совпадающая с медианой | Если в треугольнике высота совпадает с медианой, то этот треугольник является равнобедренным | |
| Признак | Высота треугольника, совпадающая с биссектрисой | Если в треугольнике высота совпадает с биссектрисой, то этот треугольник является равнобедренным | |
| Признак | Биссектриса треугольника, совпадающая с медианой | Если в треугольнике биссектриса совпадает с медианой, то этот треугольник является равнобедренным |
| Определение: равнобедренный треугольник | |
Равнобедренным треугольником называют треугольник, у которого две стороны равны. Равные стороны называют боковыми сторонами равнобедренного треугольника, третью сторону называют основанием равнобедренного треугольника. | |
| Свойство: углы при основании равнобедренного треугольника | |
Если треугольник является равнобедренным треугольником, то углы при его основании равны. | |
| Признак: два равных угла треугольника | |
Если у треугольника два угла равны, то этот треугольник является равнобедренным треугольником. | |
| Свойство: медиана, биссектриса и высота, проведённые к основанию равнобедренного треугольника | |
| В равнобедренном треугольнике медиана, биссектриса и высота, проведённые из вершины, противолежащей основанию, совпадают. | |
| Признак: высота треугольника, совпадающая с медианой | |
Если в треугольнике высота совпадает с медианой, то этот треугольник является равнобедренным | |
| Признак: высота треугольника, совпадающая с биссектрисой | |
Если в треугольнике высота совпадает с биссектрисой, то этот треугольник является равнобедренным | |
| Признак: биссектриса треугольника, совпадающая с медианой | |
Если в треугольнике биссектриса совпадает с медианой, то этот треугольник является равнобедренным | |
| Определение равнобедренного треугольника |
Определение: Равнобедренным треугольником называют треугольник, у которого две стороны равны. Равные стороны называют боковыми сторонами равнобедренного треугольника, третью сторону называют основанием равнобедренного треугольника. |
| Свойство углов при основании равнобедренного треугольника |
Свойство: Если треугольник является равнобедренным треугольником, то углы при его основании равны. |
| Признак равнобедренного треуголька: два равных угла треугольника |
Признак: Если у треугольника два угла равны, то этот треугольник является равнобедренным треугольником. |
| Свойство медианы, биссектрисы и высоты, проведённых к основанию равнобедренного треугольника |
Свойство: В равнобедренном треугольнике медиана, биссектриса и высота, проведённые из вершины, противолежащей основанию, совпадают. |
| Признак равнобедренного треугольника: высота треугольника, совпадающая с медианой |
Признак: Если в треугольнике высота совпадает с медианой, то этот треугольник является равнобедренным |
| Признак равнобедренного треугольника: высота треугольника, совпадающая с биссектрисой |
Признак: Если в треугольнике высота совпадает с биссектрисой, то этот треугольник является равнобедренным |
| Признак равнобедренного треугольника: биссектриса треугольника, совпадающая с медианой |
Признак: Если в треугольнике биссектриса совпадает с медианой, то этот треугольник является равнобедренным |
На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
свойства, признаки и формулы / Блог / Справочник :: Бингоскул
Содержание:
- Свойства равнобедренного треугольника.
- Признаки равнобедренного треугольника.
- Формулы равнобедренного треугольника:
- формулы длины стороны;
- формулы длины равных сторон;
- формулы высоты, медианы, биссектрисы равнобедренного треугольника.
Равнобедренным называется треугольник, у которого две стороны равны. Эти стороны называются боковыми, а третья сторона — основанием.
АВ = ВС — боковые стороны
АС — основание
Свойства равнобедренного треугольника
Свойства равнобедренного треугольника выражаются через 5 теорем:
Теорема 1. В равнобедренном треугольнике углы при основании равны.
Доказательство теоремы:
Рассмотрим равнобедренный Δ ABC с основанием АС.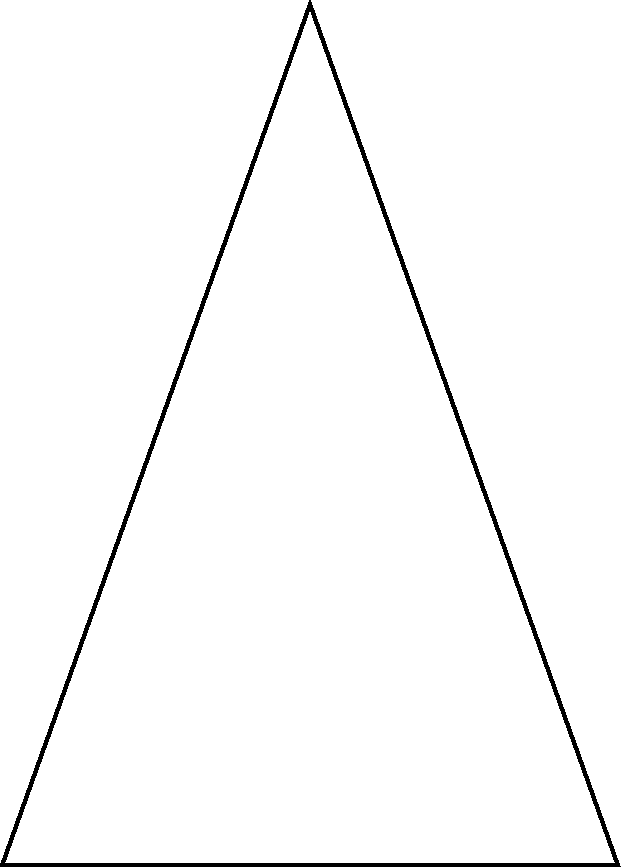
Боковые стороны равны АВ = ВС,
Следовательно углы при основании ∠ BАC = ∠ BСA.
Теорема о биссектрисе, медиане, высоте, проведенной к основанию равнобедренного треугольника
- Теорема 2. В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
- Теорема 3. В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
- Теорема 4. В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.
Доказательство теоремы:
- Дан Δ ABC.
- Из точки В проведем высоту BD.
- Треугольник разделился на Δ ABD и ΔCBD. Эти треугольники равны, т.
 к. гипотенузы и общий катет у них равны (теорема Пифагора).
к. гипотенузы и общий катет у них равны (теорема Пифагора). - Прямые АС и BD называются перпендикуляром.
- В Δ ABD и Δ BCD ∠ BАD = ∠ BСD (из Теоремы 1).
- АВ = ВС — боковые стороны равны.
- Стороны АD = СD, т.к. точка D отрезок делит пополам.
- Следовательно Δ ABD = ΔBCD.
- Биссектриса, высота и медиана это один отрезок — BD
Вывод:
- Высота равнобедренного треугольника, проведенная к основанию, является медианой и биссектрисой.
- Медиана равнобедренного треугольника, проведенная к основанию, является высотой и биссектрисой.
- Биссектриса равнобедренного треугольника, проведенная к основанию, является медианой и высотой.

Запомни! При решении таких задач опусти высоту на основание равнобедренного треугольника. Чтобы разделить его на два равных прямоугольных треугольника.
- Теорема 5. Если три стороны одного треугольника равны трем сторонам другого треугольника, то такие треугольники равны.
Доказательство теоремы:
Дано два Δ ABC и Δ A1B1C1. Стороны AB = A1B1; BC = B1C1; AC = A1C1.
Доказательство от противного.
- Пусть треугольники не равны (а то треугольники были равны по первому признаку).
- Пусть Δ A1B1C2 = Δ ABC, у которого вершина C2 лежит в одной полуплоскости с вершиной C1 относительно прямой A1B1. По предположению вершины C1 и C2 не совпадают. Пусть D – середина отрезка C1C2.
 Δ A1C1C2 и Δ B1C1C2 – равнобедренные с общим основанием C1C2. Поэтому их медианы A1D и B1D являются высотами. Значит, прямые A1D и B1D перпендикулярны прямой C1C2. A1D и B1D имеют разные точки A1 и B1, следовательно, не совпадают. Но через точку D прямой C1C2 можно провести только одну перпендикулярную ей прямую.
Δ A1C1C2 и Δ B1C1C2 – равнобедренные с общим основанием C1C2. Поэтому их медианы A1D и B1D являются высотами. Значит, прямые A1D и B1D перпендикулярны прямой C1C2. A1D и B1D имеют разные точки A1 и B1, следовательно, не совпадают. Но через точку D прямой C1C2 можно провести только одну перпендикулярную ей прямую. - Отсюда пришли к противоречию и теорему доказали.
Признаки равнобедренного треугольника
- Если в треугольнике два угла равны.
- Сумма углов треугольника 180°.
- Если в треугольнике биссектриса является медианой или высотой.
- Если в треугольнике медиана является биссектрисой или высотой.
- Если в треугольнике высота является медианой или биссектрисой.
Формулы равнобедренного треугольника
Формулы сторон равнобедренного треугольника
- b — сторона (основание)
- а — равные стороны
- a — углы при основании
- b — угол образованный равными сторонами
Формулы длины стороны (основания — b):
- b = 2a \sin( \beta /2)= a \sqrt { 2-2 \cos \beta }
- b = 2a \cos \alpha
Формулы длины равных сторон — (а):
- a=\frac { b } { 2 \sin(\beta /2) } = \frac { b } { \sqrt { 2-2 \cos \beta } }
- a=\frac { b } { 2 \cos\alpha }
Формулы высоты, медианы, биссектрисы равнобедренного треугольника
- L — высота=биссектриса=медиана
- b — сторона (основание)
- а — равные стороны
- a — углы при основании
- b — угол образованный равными сторонами
Формулы высоты, биссектрисы и медианы, через сторону и угол, (L):
- L = a sina
- L = \frac { b } { 2 } *\tg\alpha
- L = a \sqrt { (1 + \cos \beta)/2 } =a \cos (\beta)/2)
Формула высоты, биссектрисы и медианы, через стороны, (L):
- L = \sqrt { a^ { 2 } -b^ { 2 } /4 }
Площадь равнобедренного треугольника
- b — сторона (основание)
- а — равные стороны
- h — высота
Формула площади треугольника через высоту h и основание b, (S):
S=\frac { 1 } { 2 } *bh
Смотри также:
Свойства равнобедренного треугольника.
 Третий признак равенства треугольников. [wiki.eduVdom.com]
Третий признак равенства треугольников. [wiki.eduVdom.com]Свойства равнобедренного треугольника выражают следующие теоремы.
Теорема 1. В равнобедренном треугольнике углы при основании равны.
Теорема 2. В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
Теорема 3. В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
Теорема 4. В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.
Докажем одну из них, например теорему 2.5.
Рис.1
Доказательство. Рассмотрим равнобедренный треугольник ABC с основанием ВС и докажем, что ∠ В = ∠ С. Пусть AD — биссектриса треугольника ABC (рис.1). Треугольники ABD и ACD равны по первому признаку равенства треугольников (АВ = АС по условию, AD — общая сторона, ∠ 1 = ∠ 2, так как AD — биссектриса). Из равенства этих треугольников следует, что ∠ В = ∠ С. Теорема доказана.
Из равенства этих треугольников следует, что ∠ В = ∠ С. Теорема доказана.
С использованием теоремы 1 устанавливается следующая теорема.
Рис.2
Теорема 5. Третий признак равенства треугольников. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны (рис. 2).
Замечание. Предложения, установленные в примерах 1 и 2, выражают свойства серединного перпендикуляра к отрезку. Из этих предложений следует, что серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.
Пример 1. Доказать, что точка плоскости, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к этому отрезку.
Решение. Пусть точка М равноудалена от концов отрезка АВ (рис. 3), т. е. AM = ВМ.
3), т. е. AM = ВМ.
Рис.3
Тогда Δ АМВ равнобедренный. Проведем через точку М и середину О отрезка АВ прямую р. Отрезок МО по построению есть медиана равнобедренного треугольника АМВ, а следовательно (теорема 3), и высота, т. е. прямая МО, есть серединный перпендикуляр к отрезку АВ.
Пример 2. Доказать, что каждая точка серединного перпендикуляра к отрезку равноудалена от его концов.
Решение. Пусть р — серединный перпендикуляр к отрезку АВ и точка О — середина отрезка АВ (см. рис. 3).
Рис.3
Рассмотрим произвольную точку М, лежащую на прямой р. Проведем отрезки AM и ВМ. Треугольники АОМ и ВОМ равны, так как у них углы при вершине О прямые, катет ОМ общий, а катет ОА равен катету ОВ по условию. Из равенства треугольников АОМ и ВОМ следует, что AM = ВМ.
Пример 3. В треугольнике ABC (см. рис. 4) АВ = 10 см, ВС = 9 см, АС = 7 см; в треугольнике DEF DE = 7 см, EF = 10 см, FD = 9 см.
В треугольнике ABC (см. рис. 4) АВ = 10 см, ВС = 9 см, АС = 7 см; в треугольнике DEF DE = 7 см, EF = 10 см, FD = 9 см.
Рис.4
Сравнить треугольники ABC и DEF. Найти соответственно равные углы.
Решение. Данные треугольники равны по третьему признаку. Соответственно равные углы: А и Е (лежат против равных сторон ВС и FD), В и F (лежат против равных сторон АС и DE), С и D (лежат против равных сторон АВ и EF).
Пример 4. На рисунке 5 АВ = DC, ВС = AD, ∠B = 100°.
Рис.5
Найти угол D.
Решение. Рассмотрим треугольники ABC и ADC. Они равны по третьему признаку (АВ = DC, ВС = AD по условию и сторона АС — общая). Из равенства этих треугольников следует, что ∠ В = ∠ D, но угол В равен 100°, значит, и угол D равен 100°.
Пример 5.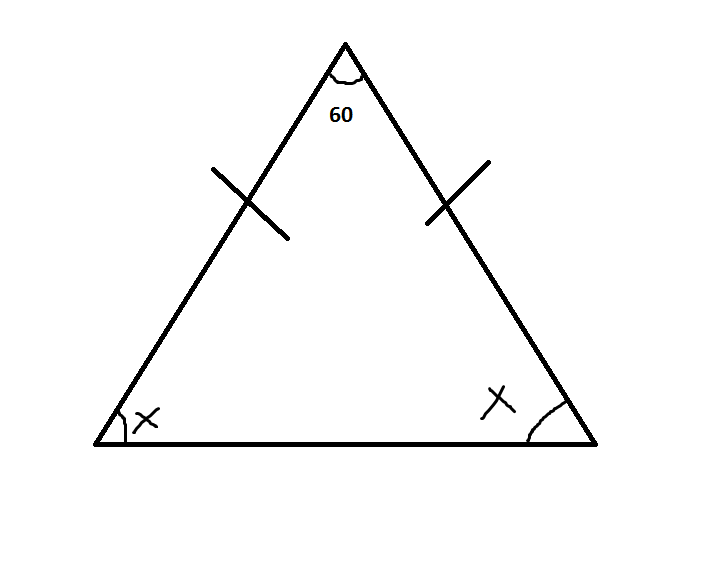 В равнобедренном треугольнике ABC с основанием AC внешний угол при вершине C равен 123°. Найдите величину угла ABC . Ответ дайте в градусах.
В равнобедренном треугольнике ABC с основанием AC внешний угол при вершине C равен 123°. Найдите величину угла ABC . Ответ дайте в градусах.
Видео-решение.
Если в треугольнике два угла равны
Теорема (Признак равнобедренного треугольника)
Если в треугольнике два угла равны, то этот треугольник — равнобедренный.
Дано:
∆ ABC,
∠A=∠B
Доказать:
∆ ABC — равнобедренный.
Доказательство:
Проведем биссектрису CF.
Рассмотрим треугольники ACF и BCF.
1) ∠ACF=∠BCF (так как CF — биссектриса (по построению))
2) CF — общая сторона
∠A=∠B (по условию)
Сумма углов треугольника равна 180º.
В треугольнике ACF
∠AFC=180º — (∠A+∠ACF).
В треугольнике BCF
∠BCF =180º — (∠B+∠BCF).
Из 180º вычли сумму равных углов. Получили равные углы:
Таким образом, имеем:
3)∠AFC=∠BFC.
Следовательно, ∆ACF = ∆BCF (по стороне и двум прилежащим к ней углам).
Из равенства треугольников следует равенство соответствующих сторон: AC=BC.
Значит, треугольник ABC — равнобедренный с основанием AB (по определению равнобедренного треугольника).
Что и требовалось доказать.
Данный признак равнобедренного треугольника можно доказать другими способами.
2 способ
Рассмотрим треугольники ABC и BAC.
(это — два разных треугольника. Подробнее — смотрите «Два треугольника равны«)
1) AB=BA (по условию)
2) ∠A=∠B (по условию)
3) ∠B =∠A (по условию)
Следовательно, ∆ACF = ∆BCF (по стороне и двум прилежащим к ней углам).
Из равенства треугольников следует равенство соответствующих сторон: AC=BC.
Вывод: ∆ ABC — равнобедренный с основанием AB.
3 способ
По соотношениям между углами треугольника и противолежащими сторонами, в треугольнике против б’ольшего угла лежит б’ольшая сторона. Следствие: против равных углов лежат равные стороны. Таким образом, если в треугольнике два угла равны, то лежащие напротив этих углов стороны тоже равны, а значит, треугольник — равнобедренный.
Медиана треугольника является его биссектрисой
Выясним, какой вывод следует из того, что медиана треугольника является его биссектрисой?
Утверждение.
Если медиана треугольника является его биссектрисой, то этот треугольник — равнобедренный.
Дано:
∆ ABC,
CK — медиана и биссектриса
Доказать:
∆ ABC — равнобедренный.
Проведем анализ задачи.
На основе каких данных можно утверждать, что треугольник — равнобедренный? Если у него две стороны равны либо два угла равны. Значит, нам нужно доказать либо равенство сторон AC и BC, либо равенство углов A и B. Любое из этих равенств следует из равенства треугольников.
В треугольниках AKC и BKC биссектриса CK образует равные углы ACK и BCK, медиана CK — равные отрезки AK и BK. Сторона CK — общая.
Что мы имеем? Две стороны, но нет угла между ними. Ни к одной из сторон нет двух прилежащих углов. Признаки равенства треугольников применить не можем.
В таком случае придется выполнять дополнительные построения.
На луче CK отложим отрезок KE так, чтобы KE=CK, и точки A и E соединим отрезком. Получили еще один треугольник AKE.
Мы можем доказать, что этот треугольник равен треугольнику BKC (по двум сторонам и углу между ними).
Из равенства этих треугольников следует равенство сторон AE и BC и углов AEK и BCK.
Получается, что в треугольнике ACE имеется два равных угла AEK и ACK. Поэтому он — равнобедренный, откуда легко доказывается и равенство сторон AC и ВС. Осталось записать доказательство.
Доказательство:
На луче CK отложим отрезок KE, KE=CK.
Рассмотрим треугольники AKE и BKC:
1) AK=BK (так как CK — медиана по условию)
2) KE=CK (по построению)
3) ∠AKE=∠BKC (как вертикальные).
Следовательно, ∆ AKE=∆ BKC (по двум сторонам и углу между ними).
Из равенства треугольников следует равенство соответствующих сторон: AE=BC и соответствующих углов: ∠AEK=∠BCK.
По условию, ∠BCK=∠AСK. Поэтому ∠AEK=∠AСK.
Таким образом получили, что в треугольнике ACE два угла равны. Значит, ∆ ACE — равнобедренный с основанием CE (по признаку). Следовательно, его боковые стороны равны: AE=AC.
А поскольку уже доказали, что AE=BC, то и AС=BС. Поэтому ∆ ABC — равнобедренный с основанием AB (по определению).
Что и требовалось доказать.
Если в треугольнике совпадают медиана и биссектриса, проведенные к каждой из сторон, то такой треугольник — равносторонний (каждые две его стороны равны между собой, значит, равны все три стороны).
§ 2. Признаки равенства треугольников. Равнобедренный треугольник. Прямоугольный треугольник. Теоремы об углах. — ЗФТШ, МФТИ
Для повторения мы выбрали эти темы. Приводить доказательство теорем, содержащихся в учебнике, не будем, лишь напомним основные теоремы. Также обсудим некоторые важные вопросы, приведём примеры решения задач, докажем несколько дополнительных теорем (Всякое утверждение, сформулированное в общем виде и доказанное, есть теорема, но их так много и они часто столь просты, что наполнять ими учебник не имеет смысла, а вот учиться на них применению основных теорем, умению рассуждать, делать выводы, — очень полезно). Такие теоремы мы будем называть леммами.
В учебнике доказаны три признака равенства треугольников.
Первый признак: по двум сторонам и углу между ними.
Второй признак: по стороне и прилежащим к ней углам.
Третий признак: по трём сторонам.
Мы напомнили их краткую формулировку.
Отметим также важный момент.@`, и $$ △KAM=△KBC$$ Делаем вывод: $$ KC=CM=KM$$ т. е. треугольник $$ KCM$$ – равносторонний.
(В решении использовано утверждение, что все углы равностороннего треугольника равны $$ 60°$$).
II. Равнобедренный треугольник.
В учебнике доказаны теоремы:
Т1. В равнобедренном треугольнике углы при основании равны.
Т2. В равнобедренном треугольнике медиана, проведённая к основанию, является высотой и биссектрисой.
Т3. (Признак равнобедренного треугольника). Если два угла в треугольнике равны, то он равнобедренный.
Обратим внимание, что признаком фигуры $$ A$$ называется теорема с формулировкой: «если имеет место … , то это фигура $$ A$$». Сформулируем следующие, часто применяемые в задачах, признаки равнобедренного треугольника:
а) если в треугольнике высота является медианой, то треугольник равнобедренный;
б) если в треугольнике высота является биссектрисой, то треугольник равнобедренный;
в) если в треугольнике медиана является биссектрисой, то треугольник равнобедренный.
Доказательство признака а) вполне простое. Если $$ BD\perp AC$$ и $$ AD=DC$$ (рис. 9), то $$ △ADB=△CDB$$ по двум сторонам ( $$ BD$$ – общая, $$ AD=DC$$) и углу между ними ($$ \angle ADB$$ смежный с $$ \angle BDC=90°$$ поэтому $$ \angle ADB=90°$$ ).
Из равенства треугольников следует $$ AB=BC$$ и треугольник $$ ABC$$ по определению равнобедренный.
| Рис. 9 | Рис. 10 |
Доказательство признака б) Столь же простое, докажите его самостоятельно.
Докажем признак в) Пусть в треугольнике $$ ABC$$ биссектриса $$ BM$$ является медианой: $$ AM=MC$$ (рис. 10). На продолжении биссектрисы $$ BM$$ отложим отрезок $$ MD$$ равный $$ BM$$ Треугольники $$ ABM$$ и $$ CDM$$ равны по первому признаку: у них углы при вершине $$ M$$ равны, как вертикальные, и $$ AM=CM$$, $$ BM=DM$$ Из равенства треугольников следует
$$ CD=AB$$ (1)
и $$ \angle CDM=\angle ABM$$. Но $$ \angle ABM=\angle CBM$$ поэтому $$ \angle CDM=\angle CBM$$, т. е. в треугольнике $$ BCD$$ углы при основании $$ BD$$ равны. По признаку Т3 этот треугольник равнобедренный: $$ BC=CD$$ Отсюда и из (1) заключаем: $$ BC=AB$$. Утверждение доказано.
В следующем примере применяются признак параллельности прямых и две теоремы об углах треугольника (и следствия этих теорем):
Т. Сумма углов треугольника равна $$ 180°$$.
Т. Внешний угол треугольника равен сумме двух внутренних углов, не
смежных с ним.
Точка $$ K$$ лежит на основании $$ AC$$ равнобедренного треугольника $$ ABC$$ ($$ AB=BC$$). Через точку $$ K$$ проведена прямая, пересекающая прямую $$ AB$$ и отрезок $$ BC$$, при этом образовалось два равнобедренных треугольника (рис. 11).
Найти углы треугольника $$ ABC$$.
Решение
Обозначим точки пересечения $$ M$$ и $$ D$$.
1. Углы при основании равнобедренного треугольника равны и они острые, значит угол $$ MAK$$ – тупой.
2. В треугольнике может быть только один тупой угол, значит, если треугольник $$ MAK$$ равнобедренный, то равными могут быть только углы при вершинах $$ M$$ и $$ K$$. Обозначим их $$ \alpha $$.
3. $$ \angle BAK=2\alpha $$ (как внешний угол треугольника $$ MAK$$), $$ \angle BCA=2\alpha $$ (углы при основании равнобедренного треугольника равны) и $$ \angle DKC=\alpha $$ ($$ \angle DKC=\angle AKM$$ как вертикальные).
Расставим углы.
4. Треугольник $$ KDC$$ по условию равнобедренный. Возможны, вообще говоря, два случая: а) $$ \angle KDC=\alpha $$ и б) $$ \angle KDC=2\alpha $$.
а) Если $$ \angle KDC=\alpha $$, то накрест лежащие углы при секущей $$ MD$$ равны $$ \alpha $$; это по теореме означало бы параллельность прямых $$ MB$$ и $$ CB$$, что противоречит их пересечению. Этот случай невозможен.
б) Если $$ \angle KDC=2\alpha $$, то по теореме о сумме углов треугольника (для треугольника $$ KDC$$) $$ \alpha +2\alpha +2\alpha =180°$$ ,$$ \alpha =36°$$. Находим углы треугольника $$ ABC$$ :$$ \angle A=\angle C=2\alpha =72°$$ , $$ \angle B=180°-2·\angle A=36°$$.
III. Для прямоугольных треугольников справедливы признаки равенства (их надо уметь доказывать):
1. по двум катетам;
2. по гипотенузе и катету;
3. по гипотенузе и острому углу;
4. по катету и острому углу.
Применяя признаки равенства прямоугольных треугольников, докажем ещё один признак равнобедренного треугольника:
Доказать, что если две высоты треугольника равны, то он равнобедренный.
Решение
Пусть высоты $$ A{A}_{1}$$ и $$ C{C}_{1}$$ треугольника $$ ABC$$ равны друг другу.
1. (Треугольник остроугольный. Обе высоты внутри треугольника, (рис. 12а). Прямоугольные треугольники $$ A{A}_{1}B$$ и $$ C{C}_{1}B$$ равны по катету ($$ A{A}_{1}=C{C}_{1}$$) и противолежащему острому углу (угол $$ B$$ – общий). Тогда
равны их гипотенузы $$ AB=CB$$, а это и означает, что треугольник $$ ABC$$ равнобедренный.
| Рис. 12a | Рис. 12б |
Рис. 12в |
2. (Треугольник тупоугольник, угол $$ В$$ тупой. Обе высоты вне треугольника, рис. 12б). Прямоугольные треугольники $$ A{A}_{1}B$$ и $$ C{C}_{1}B$$ имеют равные катеты $$ A{A}_{1}=C{C}_{1}$$ и равные противолежащие углы $$ \angle AB{A}_{1}=\angle CB{C}_{1}$$ как вертикальные . Треугольники равны, равны их гипотенузы $$ AB=CB$$. Треугольник $$ ABC$$ – равнобедренный.
3. Случай равенства двух высот равнобедренного треугольника, одна из которых внутри треугольника, другая – вне треугольника, невозможен. Действительно, если $$ B{B}_{1}=A{A}_{1}=h$$ (рис. 12в), то $$ △A{A}_{1}B=△B{B}_{1}A$$ по гипотенузе (у них общая $$ AB$$) и катету $$ A{A}_{1}=B{B}_{1}$$. Тогда $$ \angle BA{A}_{1}=\angle AB{B}_{1}$$ (обозначен $$ \alpha $$ ), т. е. накрест лежащие углы при секущей $$ AB$$ равны и прямые $$ A{A}_{1}$$ и $$ {B}_{1}B$$ параллельны, что неверно.
4. Если угол $$ B$$ – прямой, то высоты из вершин $$ A$$ и $$ C$$ совпадают с катетами $$ AB$$ и $$ CB$$.
При равных высотах равны и катеты, треугольник $$ ABC$$ – равнобедренный.
Доказать, что медиана прямоугольного треугольника, проведённая из вершины прямого угла, равна половине гипотенузы.
Решение
| Рис. 13 |
Точка $$ M$$ – середина гипотенузы $$ AB$$ прямоугольного треугольника $$ ABC$$ (рис. 13). Проведём через точку $$ M$$ прямую $$ MK\perp AC$$.
Из $$ BC\perp AC$$ и $$ MK\perp AC$$ следует $$ BC\parallel MK$$.
Из параллельности прямых $$ BC$$ и $$ MK$$ и равенства отрезков $$ BM$$ и $$ MA$$ по теореме Фалеса следует $$ CK=KA$$.
В прямоугольных треугольниках $$ CMK$$ и $$ AMK$$ катет $$ MK$$ общий и, как установили, равны катеты $$ CK$$ и $$ AK$$. Эти треугольники равны, значит, равны и их гипотенузы, т. е. $$ CM=AM$$, или $$ CM={\displaystyle \frac{1}{2}}AB$$.
Дополнение. Для многих учащихся при решении задач возникает проблема: с чего начать? С рисунка! В геометрической задаче очень важен рисунок, он должен отвечать условиям задачи, быть наглядной формой их записи.
| Рис. 14a | Рис. 14б |
Например, в задаче рассматривается равнобедренный треугольник. Его можно нарисовать по-разному (рис. 14а и 14б), поэтому сначала рисуют на черновике, от руки, и из других условий определяют вид треугольника.
Если сказано, что один отрезок в два раза длиннее другого, – отразите это на рисунке; если какие-то прямые параллельны – так и рисуйте, т. е. после таких рассмотрений делаете чёткий хороший рисунок, отвечающий условиям задачи.
Хороший рисунок – помощник в решении, особенно если на нём Вы отмечаете равные углы, перпендикулярность отрезков, отношение длин и т. п. и ставите данные задачи. Посмотрите, например, на рис. 7, 8, 11 и подумайте, как рисунок помогает в решении.
В треугольнике $$ ABC$$ медиана $$ BM$$ перпендикулярна биссектрисе $$ AD$$. Найти длину стороны $$ AB$$, если $$ AC=6$$.
Решение
△ 1. Подумаем, как построить рисунок. Возьмём луч $$ AK$$ (рис. 15) и отложим от точки $$ A$$ какие-то равные углы (т. е. считаем, что биссектриса $$ AD$$ лежит на этом луче).
| Рис. 15 |
Выберем точку $$ B$$, проведём через точку $$ B$$ прямую, перпендикулярно $$ AK$$ и отметим точку $$ M$$, $$ BM$$ – медиана, поэтому отложим отрезок $$ MC=MA$$. Треугольник $$ ABC$$ – тот, что нужен: $$ AD$$ – биссектриса, $$ BM$$ – медиана, $$ AD\perp BM$$.
2. Решение очевидно: $$ △ABO=△AMO$$ (по катету и острому углу), значит $$ AB=AM$$ и $$ AC=2AM=2AB$$. Зная, что $$ AC=6$$, находим $$ AB=3$$.
Равнобедренный треугольник — математический путь
Равнобедренный треугольник представляет собой многоугольник из трех сторон и двух равных сторон . Другая неравная сторона называется основанием треугольника.
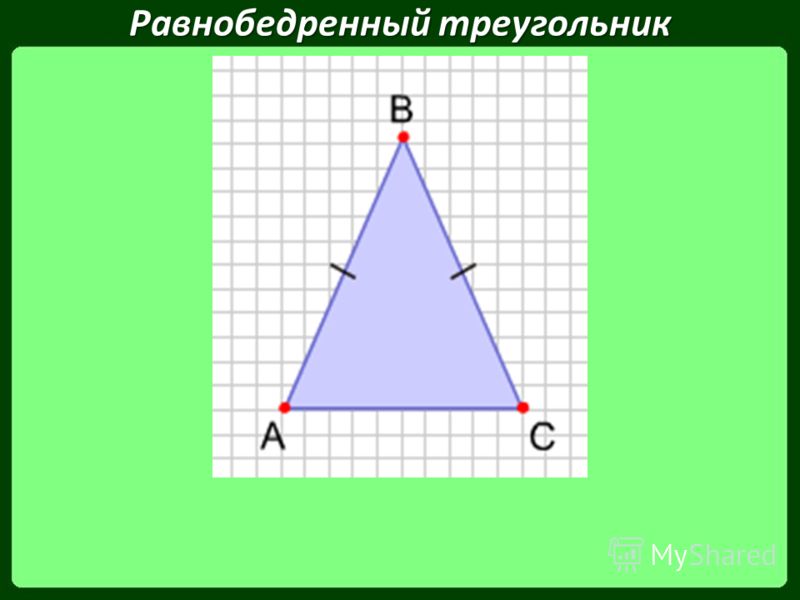
Следовательно, два угла также будут равными (α), а другие — разными (β), т.е. это угол, образованный двумя равными сторонами ( a ).
Двумя частными случаями равнобедренных треугольников являются равносторонний треугольник и равнобедренный прямоугольный треугольник .
Высота равнобедренного треугольника
Высота ( h ) равнобедренного треугольника (или высота ) может быть вычислена по теореме Пифагора. Стороны a , b / 2 и h образуют прямоугольный треугольник. Стороны b / 2 и h являются катетами, а и — гипотенузами.
По теореме Пифагора:
И получается, что высота h составляет:
В равнобедренном треугольнике высота , соответствующая основанию ( b ), также является биссектрисой угла, серединным перпендикуляром и серединой.
Площадь равнобедренного треугольника вычисляется из основания b (неповторяющаяся сторона) и высоты ( h ) треугольника, соответствующего основанию. Площадь является произведением базы и высоты, разделенной на два, и ее формула следующая:
.
Периметр равнобедренного треугольника получается сложением трех сторон треугольника.Имея две равные стороны, периметр равен удвоенной повторяющейся стороне ( a ) плюс другая сторона ( b ).
Если повторяющаяся сторона ( a ) и угол двух равных сторон известны, другая сторона ( b ) должна быть найдена по закону косинусов .
Загрузите этот калькулятор , чтобы получить результаты формул на этой странице. Выберите исходные данные и введите их в верхнем левом поле. Для получения результатов нажмите ENTER.
Triangle-total.rar или Triangle-total.exe
Примечание. Предоставлено автором: Хосе Мария Пареха Маркано . Химик. Севилья, испания.
Решенные упражнения
Упражнение в области равнобедренного треугольника
Определите площадь равнобедренного треугольника , зная его две равные стороны ( a = 3 см) и неравную, длина которой составляет 2 см ( b = 2 см).
Каков его район ?
Рассчитайте площадь по приведенной выше формуле, умножив основание на высоту:
Площадь равнобедренного треугольника равна 2.83 см 2 .
Упражнение по периметру равнобедренного треугольника
Равнобедренный треугольник с двумя равными сторонами, a = 3 см, а другая сторона b = 2 см.
Каков его периметр ?
Чтобы вычислить периметра , мы добавляем повторяющуюся сторону, умноженную на два, плюс неравную сторону, то есть:
Получается, что периметр равнобедренного треугольника равен 8 см .
Упражнение на высоту равнобедренного треугольника
Найдите стороны и периметр равнобедренного треугольника, высота которого относительно неровной стороны составляет h = 6 см, а противоположный угол, также неровный, 40 °.
Найдено с помощью тригонометрических соотношений из одного прямоугольного треугольника, на который делится равнобедренный треугольник по высоте h .
Отрезок, противоположный углу β / 2, который является отрезком b /2, мы нашли его через касательную:
Сторона b меры 4.36 см.
Образуется гипотенуза прямоугольного треугольника, то есть сторона и находится по косинусу:
Сторона и имеет размер 6,38 см.
Наконец, периметр треугольника составит:
Получается, что периметр этого равнобедренного треугольника будет составлять 17,12 см.
Равнобедренный треугольник
Треугольник с двумя сторонами равной длины называется равнобедренным треугольником.
Введение
На английском языке слово «равнобедренный» означает две стороны равной длины.
Геометрически треугольник образован соединением концов трех отрезков прямой. В некоторых треугольниках длины любых двух сторон могут быть одинаковыми. Следовательно, к треугольнику добавлено слово «равнобедренный» для обозначения таких треугольников, в которых длины двух сторон равны. Следовательно, треугольники называются в геометрии равнобедренными треугольниками.
Равнобедренный треугольник представлен графически путем проведения одной и двух небольших перпендикулярных линий к сторонам треугольника в их средних точках.
Из-за свойства равенства сторон в равнобедренном треугольнике два внутренних угла любого равнобедренного треугольника равны.
Строительство
Давайте узнаем, как построить равнобедренный треугольник и полезно изучить его свойства.
- Нарисуйте отрезок линии от точки $ C $ до $ D $ по горизонтали с помощью линейки. Здесь длина горизонтального отрезка $ 9 \, см $.
- Установите расстояние между острием и острием карандаша циркуля на некоторую длину с помощью линейки.В данном случае он равен $ 7 \, cm $. Затем нарисуйте дугу на плоскости из точки $ C $.
- Аналогичным образом нарисуйте циркулем из точки $ D $ другую дугу той же длины, но она должна пересекать ранее нарисованную дугу, чтобы завершить построение равнобедренного треугольника.
Таким образом, треугольник можно построить геометрически за три простых шага, и в математике он выражается просто как $ \ Delta ECD $.
Недвижимость
Свойства равнобедренного треугольника можно изучить из построенного выше треугольника.
Стороны
Теперь перечислите длины всех трех сторон треугольника $ ECD $.
$ (1). \, \, \, $ Длина стороны $ \ overline {CD} $ равна $ CD \, = \, 9 \, см $
$ (2). \, \, \, $ Длина стороны $ \ overline {CE} $ равна $ CE \, = \, 7 \, cm $
$ (3). \, \, \, $ Длина стороны $ \ overline {DE} $ равна $ DE \, = \, 7 \, см $
В $ \ Delta ECD $ длины двух сторон равны, но длина третьей стороны различна. Следовательно, треугольник геометрически называется равнобедренным треугольником.° $
Понятно, что два угла равны, но третий угол различен.
$ \ следовательно \, \, \, \, \, \, $ $ \ angle CED $ $ \, \ ne \, $ $ \ angle ECD $ $ \, = \, $ $ \ angle CDE $
В равнобедренном треугольнике два угла равны из-за двух равных сторон треугольника.Что такое равнобедренный треугольник? — [Определение, факты и пример]
Что такое равнобедренный треугольник?
Треугольник с двумя сторонами равной длины является равнобедренным треугольником. Две равные стороны равнобедренного треугольника известны как «ноги», тогда как третья или неравная сторона известна как «основание».
В равнобедренном треугольнике углы, противоположные равным сторонам, всегда равны. В данном равнобедренном треугольнике, если AB = AC, то ∠B = ∠C
Вот несколько примеров равнобедренного треугольника:
Примеры из жизни
Многие вещи в мире имеют форму равнобедренного треугольника. Некоторые популярные примеры равнобедренного треугольника в реальной жизни — кусок пиццы, пара серег.
Без примеров
Общая недвижимость
Равные стороны равнобедренного треугольника известны как «ноги».
Третья и неравная сторона равнобедренного треугольника известна как «основание».
Угол, образованный двумя равными сторонами равнобедренного треугольника, известен как «угол при вершине».
Углы, составляющие основу равнобедренного треугольника, известны как «углы основания».’
Углы, расположенные напротив равных сторон равнобедренного треугольника, всегда равны.
Все три угла, расположенные внутри равнобедренного треугольника, являются острыми, что означает, что углы меньше 90 °.
Сумма трех углов равнобедренного треугольника всегда равна 180 °, что означает, что мы можем определить третий угол треугольника, если известны два угла равнобедренного треугольника.
Интересные факты
|
Равнобедренный треугольник
Равнобедренный треугольник — это треугольник, у которого есть как минимум две стороны равной длины. На рисунке ниже приведены два примера.
AB≅AC
Части равнобедренного треугольника
Для равнобедренного треугольника только с двумя конгруэнтными сторонами конгруэнтные стороны называются катетами. Третья сторона называется базой. Угол, противоположный основанию, называется углом при вершине, а углы, противоположные ногам, называются углами основания.
Длины равнобедренного треугольника
Высота равнобедренного треугольника — это отрезок перпендикулярной линии, проведенный от основания треугольника к противоположной вершине.
Используя теорему Пифагора, мы можем найти, что основание, катеты и высота равнобедренного треугольника имеют следующие отношения:
Углы основания равнобедренного треугольника
Углы основания равнобедренного треугольника одинаковы по мере. См. Треугольник ABC ниже.
AB ≅AC, значит, треугольник ABC равнобедренный. ABC можно разделить на два равных треугольника, нарисовав отрезок AD, который также является высотой треугольника ABC.
Используя теорему Пифагора, где l — длина ног,. Исходя из этого, ADB≅ △ ADC по теореме Side-Side-Side для конгруэнтных треугольников, поскольку BD ≅CD, AB ≅ AC и AD ≅AD. Итак, ∠B≅∠C, поскольку соответствующие части конгруэнтных треугольников также конгруэнтны.
Симметрия в равнобедренном треугольнике
Высота равнобедренного треугольника также является линией симметрии.
Участок AB отражается на высоте AD в участок AC. Точно так же нога AC отражается в ногу AB.База BC отражается сама на себя, когда отражается на высоте.
45-45-90 треугольников
Когда углы основания равнобедренного треугольника составляют 45 °, треугольник представляет собой специальный треугольник, называемый треугольником 45 ° -45 ° -90 °. Длина основания, называемого гипотенузой треугольника, умножена на длину его катета.
Апофема правильного многоугольника
Апофема правильного многоугольника — это также высота равнобедренного треугольника, образованного центром и стороной многоугольника, как показано на рисунке ниже.
Для правильного пятиугольника ABCDE выше высота равнобедренного треугольника BCG является апофемой многоугольника.
равнобедренных треугольников — Бесплатная справка по математике
В мире геометрии существует множество типов треугольников. Существует особый треугольник, называемый равнобедренным треугольником и . В равнобедренном треугольнике базовые углы имеют одинаковую степень и, как следствие, равны (конгруэнтны). Точно так же, если два угла треугольника имеют одинаковую длину, тогда стороны , противоположные этим углам, имеют одинаковую длину.Самый простой способ определить равнобедренный треугольник — у него две равные стороны .
В равнобедренном треугольнике есть две стороны, называемые ногами, и третья сторона, называемая основанием. Угол, расположенный напротив основания, называется вершиной.
Образец A:
Угол при вершине B равнобедренного треугольника ABC составляет 120 градусов. Найдите градус каждого базового угла.
Решение:
(1) Пусть x = мера каждого базового угла.
(2) Составьте уравнение и решите относительно x.
базовый угол + базовый угол + 120 градусов = 180 градусов
x + x + 120 градусов = 180 градусов
2х + 120 = 180
2х = 180–120
2х = 60
х = 60/2
х = 30
Каждый угол основания треугольника ABC составляет 30 градусов.
Образец B:
В равнобедренном треугольнике RST угол S — это угол при вершине. Базовые углы R и T равны 64 градусам. Найдите градус угла при вершине S.
Решение:
(1) Пусть x = мера угла при вершине S.
(2) Составьте уравнение и решите относительно x.
базовый угол + базовый угол + угол при вершине S = 180 градусов
64 градуса + 64 градуса + x = 180 градусов
128 + х = 180
х = 180 — 128
х = 52
Угол при вершине S в треугольнике RST составляет 52 градуса.
Образец C:
Угол основания равнобедренного треугольника XYZ в градусах в три раза превышает градус вершины Y на 60.Найдите градус угла при вершине Y. Обратите внимание, что трудно нарисовать картинку, не зная, какие углы наибольшие.
Нам нужно составить уравнение из этой проблемы, поэтому давайте разберемся, что она пытается нам сказать. Сначала мы читаем «Мера базового угла в градусах», поэтому начнем с X =
.Наше уравнение на данный момент: X =
Теперь мы видим «превышает в три раза … Y … на 60», что означает 3Y + 60.
Теперь наше уравнение: X = 3Y + 60
Поскольку мы знаем, что X = Z, потому что это равнобедренный треугольник, мы можем найти меры всех углов.
базовый угол + базовый угол + вершина = 180
Х + Y + Z = 180
(3Y + 60) + Y + (3Y + 60) = 180
7лет + 120 = 180
7Y = 60
Y = 60/7
Y = 8,57 градуса
Угол при вершине Y треугольника XYZ равен 8,57 градуса.
Урок, проводимый г-ном Фелизом
Равносторонний и равнобедренный треугольники
На этом уроке геометрии 5-го класса рассматриваются равносторонние, равнобедренные и разносторонние треугольники, а также предлагаются различные упражнения, в том числе рисование. упражнения на эти темы для студентов.
Если все три стороны треугольника равны конгруэнтный (тот же длины), он называется равносторонним треугольником . Equi — относится к «одинаковым» или «Равный» и боковой, означает «односторонний». Подумай об этом как «односторонний» треугольник. | Если только , две стороны треугольника равны равнобедренный треугольник . Подумай об этом в виде «одноногого» треугольника, причем «ноги» — это две стороны одинаковой длины. Отметьте два совпадающих стороны каждого равнобедренного треугольника: |
Наконец, если ни одна из сторон треугольника конгруэнтны (все разной длины), это разносторонний треугольник . |
1.Классифицируйте треугольники по Вы можете отметить каждую |
2. Заполните таблицу, классифицируя треугольники, помеченные как (a), (d), (e) и
(g) выше как «острый», «правый»,
или «тупые» (по углам), а также как
«Равносторонний», «равнобедренный» или «разносторонний» (по бокам).
| Треугольник | Классификация по сторонам | Классификация по углам |
| д | ||
| e | ||
| г |
3.Постройте точки и соедините их
с линией Треугольник 1: (0, 0), (4, 0), (0, 4) ___________________________ и ___________________________ Треугольник 2: (5, 5), (1, 8), (9, 4) ___________________________ и ___________________________ |
4.Постройте в координатной сетке острый разносторонний треугольник.
6. а. Нарисуйте разносторонний тупой треугольник, одна сторона которого равна 3 см, а другая — 7 см.
Подсказка:
Сначала нарисуйте 7-сантиметровую сторону, затем 3-сантиметровую, образуя любой тупой угол с
первая сторона.
г. Измерьте третью сторону.
Сравните свой треугольник с треугольниками одноклассников или нарисуйте другой
один себе.
Вы можете нарисовать несколько
разно выглядящие треугольники с этой информацией,
или все они идентичны
(конгруэнтно)?
7. а. Нарисуйте равнобедренный прямоугольный треугольник, две стороны которого
отмерьте 5 см.
Подсказка: сначала нарисуйте прямой угол. Затем отмерьте стороны по 5 см. Затем втяните
последняя сторона.
г. Измерьте третью сторону. Это ____________ см.
Сравните свой треугольник с
те из ваших одноклассников, или нарисуйте другой
один себе.
Вы можете нарисовать несколько
разно выглядящие треугольники с этой информацией,
или все они идентичны
(конгруэнтно)?
8. а. Нарисуйте любой равнобедренный треугольник.
Подсказка:
Нарисуйте любой угол. Затем отмерьте две совпадающие стороны, убедившись, что они
такой же длины.
Затем нарисуйте последнюю сторону.
г. Измерьте углы вашего треугольника. Они Измерьте ________ °, ________ ° и ________ °.
Сумма углов равна ________ °.
9. Измерьте все углы в
равнобедренные треугольники (а) и (б).
При необходимости продолжите их стороны.
| а. | г. |
| _________ °, _________ ° и ________ °. Сумма углов составляет ________ °. | _________ °, _________ ° и ________ °. Сумма углов составляет ________ °. |
Что ты заметил?
__________________________________________________________________________________
__________________________________________________________________________________
Там
два угла в равнобедренном треугольнике, которые имеют Остающийся угол называется верхним углом . | Вы можете найти верхний угол и |
10. Угол при A составляет 40 °.
Нарисуйте еще один угол 40 ° в точке B, а затем продолжите его стороной
так что вы получите равнобедренный треугольник с углами основания 40 °.
Измерьте верхний угол. Это _______ °. Сумма трех угловых мер составляет _______ °.
11. а. Нарисуйте равнобедренный треугольник с углами при основании 75 °. (Длина
стороны могут быть любыми.)
Подсказка: начните с рисования
сторона основания (любой длины). Затем нарисуйте углы 75 °.
г. Измерьте верхний угол. Это _______ °.Сумма трех угловых мер составляет _______ °.
г. Сравните ваш треугольник с
те из ваших одноклассников, или нарисуйте другой
один себе.
Вы можете нарисовать несколько
разные на вид треугольники с этой информацией, или все они идентичны?
| 14. а. Может ли равносторонний треугольник быть прямоугольным? Если да, нарисуйте пример. Если нет, объясните Почему нет. |
г. Может ли разносторонний треугольник быть тупым?
Если да, нарисуйте пример. Если нет, объясните
Почему нет.
г. Может ли острый треугольник быть разносторонним?
Если да, нарисуйте пример. Если нет, объясните
Почему нет.
г. Может ли прямоугольный треугольник быть разносторонним?
Если да, нарисуйте пример.Если нет, объясните
Почему нет.
e. Может ли тупой треугольник быть равносторонним?
Если да, нарисуйте пример. Если нет, объясните
Почему нет.
Этот урок взят из книги Марии Миллер Math Mammoth Geometry 1 и размещен на сайте www.HomeschoolMath.net с разрешения автора. Авторские права © Мария Миллер.
Как нарисовать прямоугольный равнобедренный треугольник
Выписка
Хорошо, теперь мы рассмотрим, как нарисовать равнобедренный прямоугольный треугольник с помощью черепахи.Этот треугольник равнобедренный, потому что эти две стороны имеют одинаковую длину, и это прямоугольный треугольник, потому что здесь у нас прямой угол.
Давайте поместим нашу черепаху прямо сюда, и пока я не буду ничего рисовать на экране, я просто хочу посмотреть, смогу ли я заставить черепаху следовать по пути этого края.
Итак, я случайно знаю, что в этом конкретном треугольнике 100 шагов с этой стороны и 100 с этой стороны. Итак, старт легкий, я могу просто сказать «вперед 100», и это подводит меня к углу.
Теперь я хочу выяснить, сколько поворота мне нужно здесь сделать. Что ж, давайте на минутку рассмотрим, как мы составляем равнобедренный прямоугольный треугольник.
Если мы посмотрим на этот квадрат, мы увидим, что этот треугольник состоит из квадрата и его диагонали. Ну, эта диагональ разрезает этот угол пополам, не так ли?
Мы знаем, что каждый угол квадрата равен 90 градусам. Если мы разрежем этот угол пополам, у нас будет 45 градусов прямо здесь.
Итак, мы знаем, что этот угол составляет 45 градусов.Сколько нам нужно сделать поворота? Сколько поворота должна сделать черепаха?
Давайте посмотрим на поворот, ладно? В общем, когда мы поворачиваем за угол, вы видите, что мы все еще смотрим в этом направлении, на этот, весь этот угол, если мы возьмем синий угол треугольника вместе с этим маленьким сектором, равным 180 градусам. И мы знаем, что эта маленькая синяя часть здесь, этот маленький угол составляет 45 градусов. Таким образом, общий угол поворота во всем секторе составляет 180 минус 45 или 135 градусов.
Итак, давайте повернем направо на 135 градусов и посмотрим, как это выглядит. Хорошо, похоже, это правильно. Теперь мы должны вычислить длину этой линии прямо здесь, и это немного сложнее. Хм, давайте на минутку подумаем, что нам нужно посмотреть, так это то, что мы начнем с двух квадратов здесь и на минуту подумаем о площади квадратов, а затем все станет ясно через Минуту, почему мы должны беспокоиться об областях. Но мы сказали, что это 100 шагов, на самом деле давайте составим нашу собственную единицу, мы скажем, что это один гектостаг, хорошо, гектометр — это 100 метров, гектостаг — это 100 шагов.Итак, это один гектостаг, поэтому эти квадраты расположены один за другим.
Таким образом, если каждая сторона равна 1, то в целом площадь составляет 1 гектостаг. И эти два квадрата составляют два квадратных гектара.
Теперь давайте на минутку переставим эти кусочки.
Хорошо, мы знаем, что площадь этого квадрата составляет два гектара, потому что площадь этого квадрата — один гектостаг, площадь этого квадрата — один гектостаг в квадрате, так что это должно быть два гектара в квадрате.
Так что это значит о длине этой строки? Длина этой линии, умноженная на длину этой линии, составляет 2 гектостага. Это означает, что одна из этих линий является квадратным корнем из двух гектостадий.А поскольку гектостаг равен 100 шагам, это означает, что мы хотим продвинуться вперед в 100 раз больше квадратного корня из 2.
Так что, если мы будем смотреть на эту черепаху, когда я нажму «Return» и пойдем вперед, мы должны пройти весь путь до другого угла. Давайте посмотрим.
Да, это сработало, хорошо?
Итак, давайте посмотрим. Давайте вернем наш исходный треугольник на место, и теперь мы хотим выяснить, сколько поворота нам нужно сделать с этой стороны. Помните, мы здесь повернулись на 135 градусов.
Давайте посмотрим на этот поворот.Ну, это тоже 45 градусов, поэтому нам нужно сделать поворот на 180 минус 45 или 135 градусов.
Пойдем направо, 135. Выглядит правильно. И теперь мы знали, что это 100 шагов. Когда мы пошли отсюда сюда, это было 100 шагов, и это тоже 100 шагов.
И, наконец, просто чтобы вернуться в исходное состояние, в исходное положение, мы пойдем направо на 90. И на этом все нарисовано.
Так что давайте просто дважды проверим. Мы переместим этого парня сюда и положим ручку.Теперь я просто вернусь и пройду через все шаги, которые мы делали раньше. Мы пошли вперед 100, вправо 135, вперед 100, умноженное на квадратный корень из 2, вправо 135, вперед 100 и вправо 90.
Вот так получается равнобедренный прямоугольный треугольник.
.
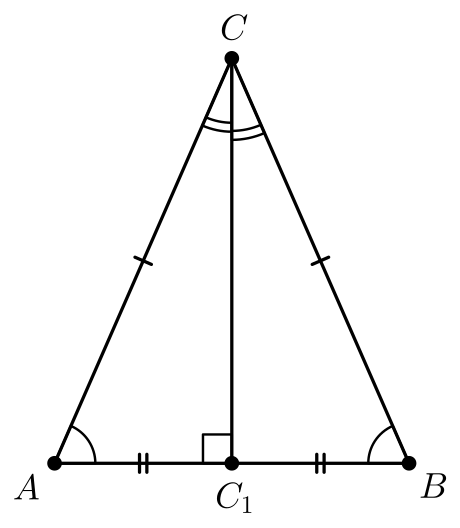
 к. гипотенузы и общий катет у них равны (теорема Пифагора).
к. гипотенузы и общий катет у них равны (теорема Пифагора).
 Δ A1C1C2 и Δ B1C1C2 – равнобедренные с общим основанием C1C2. Поэтому их медианы A1D и B1D являются высотами. Значит, прямые A1D и B1D перпендикулярны прямой C1C2. A1D и B1D имеют разные точки A1 и B1, следовательно, не совпадают. Но через точку D прямой C1C2 можно провести только одну перпендикулярную ей прямую.
Δ A1C1C2 и Δ B1C1C2 – равнобедренные с общим основанием C1C2. Поэтому их медианы A1D и B1D являются высотами. Значит, прямые A1D и B1D перпендикулярны прямой C1C2. A1D и B1D имеют разные точки A1 и B1, следовательно, не совпадают. Но через точку D прямой C1C2 можно провести только одну перпендикулярную ей прямую.