Треугольник равнобедренный рисунок: Равнобедренный треугольник. Подробная теория с примерами. – Виды треугольников (по сторонам). Видеоурок. Математика 3 Класс

Виды треугольников (по сторонам). Видеоурок. Математика 3 Класс

На данном уроке учащимся предоставляется возможность обобщить знания о названиях и изученных свойствах геометрических фигур, познакомиться с основными свойствами треугольника, узнать виды треугольников по величине угла, по числу равных сторон, потренироваться в распознавании названных видов.

Сегодня мы отправляемся в страну Геометрия, где познакомимся с различными видами треугольников.

Рассмотрите геометрические фигуры и найдите среди них «лишнюю» (рис. 1).

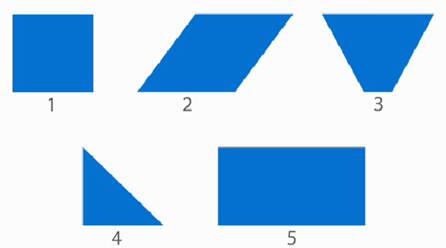
Рис. 1. Иллюстрация к примеру

Мы видим, что фигуры № 1, 2, 3, 5 – четырехугольники. Каждая из них имеет свое название (рис. 2).

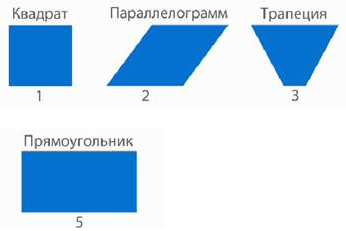
Рис. 2. Четырехугольники

Значит, «лишней» фигурой является треугольник (рис. 3).

Рис. 3. Иллюстрация к примеру

Треугольником называется фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех отрезков, попарно соединяющих эти точки.

Точки называются вершинами треугольника, отрезки – его сторонами. Стороны треугольника образуют в вершинах треугольника три угла.

Основными признаками треугольника являются три стороны и три угла. По величине угла треугольники бывают остроугольные, прямоугольные и тупоугольные.

Треугольник называется остроугольным, если все три угла его острые, то есть меньше 90° (рис. 4).

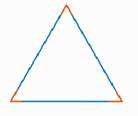
Рис. 4. Остроугольный треугольник

Треугольник называется прямоугольным, если один из его углов равен 90° (рис. 5).   

 

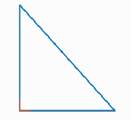
Рис. 5. Прямоугольный треугольник

Треугольник называется тупоугольным, если один из его углов тупой, то есть больше 90° (рис. 6).

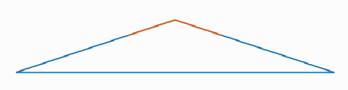
Рис. 6. Тупоугольный треугольник

По числу равных сторон треугольники бывают равносторонние, равнобедренные, разносторонние.

Равнобедренным называется треугольник, у которого две стороны равны (рис. 7). 

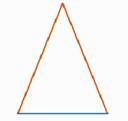
Рис. 7. Равнобедренный треугольник

Эти стороны называются боковыми, третья сторона – основанием. В равнобедренном треугольнике углы при основании равны.

Равнобедренные треугольники бывают остроугольными и тупоугольными

(рис. 8).

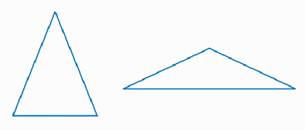
Рис. 8. Остроугольный и тупоугольный равнобедренные треугольники 

Равносторонним называется треугольник, у которого все три стороны равны (рис. 9). 

Рис. 9. Равносторонний треугольник

В равностороннем треугольнике все углы равны

. Равносторонние треугольники всегда остроугольные.

Разносторонним называется треугольник, у которого все три стороны имеют разную длину (рис. 10). 

Рис. 10. Разносторонний треугольник

Выполните задание. Распределите данные треугольники на три группы (рис. 11).

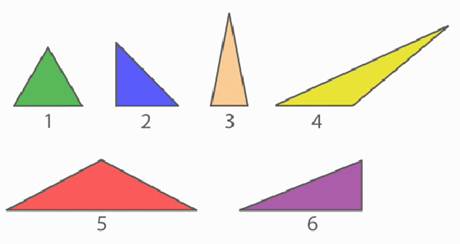
Рис. 11. Иллюстрация к заданию

Сначала распределим по величине углов.

Остроугольные треугольники: № 1, № 3.

Прямоугольные треугольники: № 2, № 6.

Тупоугольные треугольники: № 4, № 5.

Эти же треугольники распределим на группы по числу равных сторон.

Разносторонние треугольники: № 4, № 6.

Равнобедренные треугольники: № 2, № 3, № 5.

Равносторонний треугольник: № 1.

Рассмотрите рисунки.

Подумайте, из какого куска проволоки сделали каждый треугольник (рис. 12).

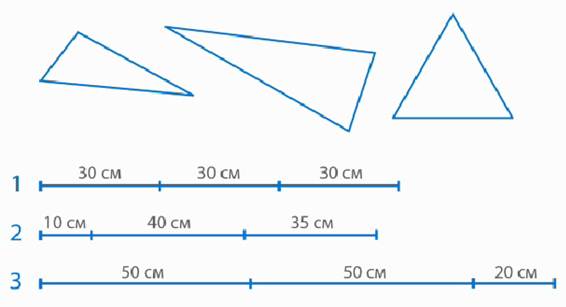
Рис. 12. Иллюстрация к заданию

Можно рассуждать так.

Первый кусок проволоки разделен на три равные части, поэтому из него можно сделать равносторонний треугольник. На рисунке он изображен третьим.

Второй кусок проволоки разделен на три разные части, поэтому из него можно сделать разносторонний треугольник. На рисунке он изображен первым.

Третий кусок проволоки разделен на три части, где две части имеют одинаковую длину, значит, из него можно сделать равнобедренный треугольник. На рисунке он изображен вторым.

Сегодня на уроке мы познакомились  с различными видами треугольников.

 

Список литературы

1. М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 1. – М.: «Просвещение», 2012.
2. М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 2. – М.: «Просвещение», 2012.
3. М.И. Моро. Уроки математики: Методические рекомендации для учителя. 3 класс. – М.: Просвещение, 2012.
4. Нормативно-правовой документ. Контроль и оценка результатов обучения. – М.: «Просвещение», 2011.
5. «Школа России»: Программы для начальной школы. – М.: «Просвещение», 2011.
6. С.И. Волкова. Математика: Проверочные работы. 3 класс. – М.: Просвещение, 2012.
7. В.Н. Рудницкая. Тесты. – М.: «Экзамен», 2012.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Nsportal.ru (Источник).
2. Prosv.ru (Источник).
3. Do.gendocs.ru (Источник).

 

Домашнее задание

1. Закончите фразы.

а) Треугольником называется фигура, которая состоит из …, не лежащих на одной прямой, и …, попарно соединяющих эти точки.

б) Точки называются …, отрезки – его …. Стороны треугольника образуют в вершинах треугольника ….

в) По величине угла треугольники бывают … , … , … .

г) По числу равных сторон треугольники бывают … , … , … .

2. Начертите

а) прямоугольный треугольник;

б) остроугольный треугольник;

в) тупоугольный треугольник;

г) равносторонний треугольник;

д) разносторонний треугольник;

е) равнобедренный треугольник.

3. Составьте задание по теме урока для своих товарищей.

свойства, признаки и формулы / Блог :: Бингоскул

Содержание:

1. Свойства равнобедренного треугольника.
2. Признаки равнобедренного треугольника.
3. Формулы равнобедренного треугольника:
   • формулы длины стороны;
   • формулы длины равных сторон;
   • формулы высоты, медианы, биссектрисы равнобедренного треугольника.

Равнобедренным называется треугольник, у которого две стороны равны. Эти стороны называются боковыми, а третья сторона — основанием.

АВ = ВС — боковые стороны

АС — основание

 

Свойства равнобедренного треугольника

Свойства равнобедренного треугольника выражаются через 5 теорем:

Теорема 1. В равнобедренном треугольнике углы при основании равны.

Доказательство теоремы:

Рассмотрим равнобедренный Δ ABC с основанием АС.

Боковые стороны равны АВ = ВС,

Следовательно углы при основании ∠ BАC = ∠ BСA.

 

 

Теорема о биссектрисе, медиане, высоте, проведенной к основанию равнобедренного треугольника

• Теорема 2. В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
• Теорема 3. В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
• Теорема 4. В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.

Доказательство теоремы:

• Дан Δ ABC.
• Из точки В проведем высоту BD.
• Треугольник разделился на Δ ABD и ΔCBD. Эти треугольники равны, т.к. гипотенузы и общий катет у них равны (теорема Пифагора).
• Прямые АС и BD называются перпендикуляром.
• В Δ ABD и Δ BCD ∠ BАD = ∠ BСD (из Теоремы 1).
• АВ = ВС — боковые стороны равны.
• Стороны АD = СD, т.к. точка D отрезок делит пополам.
• Следовательно Δ ABD = ΔBCD.
• Биссектриса, высота и медиана это один отрезок — BD

Вывод:

1. Высота равнобедренного треугольника, проведенная к основанию, является медианой и биссектрисой.
2. Медиана равнобедренного треугольника, проведенная к основанию, является высотой и биссектрисой.
3. Биссектриса равнобедренного треугольника, проведенная к основанию, является медианой и высотой.

Запомни! При решении таких задач опусти высоту на основание равнобедренного треугольника. Чтобы разделить его на два равных прямоугольных треугольника.

• Теорема 5. Если три стороны одного треугольника равны трем сторонам другого треугольника, то такие треугольники равны.

Доказательство теоремы:

Дано два Δ ABC и Δ A₁B₁C₁. Стороны AB = A₁B₁; BC = B₁C₁; AC = A₁C₁.

Доказательство от противного.

• Пусть треугольники не равны (а то треугольники были равны по первому признаку).
• Пусть Δ A₁B₁C₂ = Δ ABC, у которого вершина C₂ лежит в одной полуплоскости с вершиной C₁ относительно прямой A₁B₁. По предположению вершины C₁ и C₂ не совпадают. Пусть D – середина отрезка C₁C₂. Δ A₁C₁C₂ и Δ B₁C₁C₂ – равнобедренные с общим основанием C₁C₂. Поэтому их медианы A₁D и B₁D являются высотами. Значит, прямые A₁D и B₁D перпендикулярны прямой C₁C₂. A₁D и B₁D имеют разные точки A₁ и B₁, следовательно, не совпадают. Но через точку D прямой C₁C₂ можно провести только одну перпендикулярную ей прямую.
• Отсюда пришли к противоречию и теорему доказали.

 

Признаки равнобедренного треугольника

1. Если в треугольнике два угла равны.
2. Сумма углов треугольника 180°.
3. Если в треугольнике биссектриса является медианой или высотой.
4. Если в треугольнике медиана является биссектрисой или высотой.
5. Если в треугольнике высота является медианой или биссектрисой.

 

 

Формулы равнобедренного треугольника

Формулы сторон равнобедренного треугольника

 

• b — сторона (основание)
• а — равные стороны
• a — углы при основании
• b — угол образованный равными сторонами

 

Формулы длины стороны (основания — b):

• b = 2a \sin( \beta /2)= a \sqrt { 2-2 \cos \beta }
• b = 2a \cos \alpha

Формулы длины равных сторон — (а):

• a=\frac { b } { 2 \sin(\beta /2) } = \frac { b } { \sqrt { 2-2 \cos \beta } }
• a=\frac { b } { 2 \cos\alpha }

Формулы высоты, медианы, биссектрисы равнобедренного треугольника

• L — высота=биссектриса=медиана
• b — сторона (основание)
• а — равные стороны
• a — углы при основании
• b — угол образованный равными сторонами

 

Формулы высоты, биссектрисы и медианы, через сторону и угол, (L):

• L = a sina
• L = \frac { b } { 2 } *\tg\alpha
• L = a \sqrt { (1 + \cos \beta)/2 } =a \cos (\beta)/2)

 

Формула высоты, биссектрисы и медианы, через стороны, (L):

• L = \sqrt { a^ { 2 } -b^ { 2 } /4 }

 

Площадь равнобедренного треугольника

• b — сторона (основание)
• а — равные стороны
• h — высота

Формула площади треугольника через высоту h и основание b, (S):

S=\frac { 1 } { 2 } *bh

---

 

Смотри также:

Решение задач по теме «Равнобедренный треугольник» . Видеоурок. Геометрия 7 Класс

Данный видеоурок предназначен для самостоятельного изучения темы «Решение задач по теме “Равнобедренный треугольник”». Вы вспомните определение равнобедренного треугольника и повторите его свойства. Разберете несколько задач на треугольники, для решения которых понадобятся полученные ранее знания.

Вспомним предварительно определение равнобедренного треугольника.     



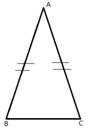
Рис. 1. Равнобедренный треугольник

Определение: Треугольник называется равнобедренным, если у него две стороны равны.                                                                                                     

АВ = АС,  треугольник АВС – равнобедренный. АВ и АС – боковые стороны, ВС – основание.

Определение: Треугольник называется равносторонним, если у него все три стороны равны.



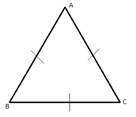
Рис. 2. Равносторонний треугольник

АВ = АС = ВС, треугольник АВС – равносторонний.

Следует повторить следующие свойства равнобедренного треугольника:

1. Углы при основании равнобедренного треугольника равны. ∠В = ∠С.

2. Пусть точка D – середина ВС. Отрезок AD является медианой, биссектрисой и высотой треугольника.



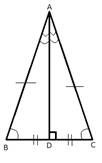
Рис. 3. Свойства равнобедренного треугольника

Рассмотрим следующие задачи:

Пример 1: На рисунке АВ = ВС, ∠1 = 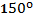. Найдите ∠2.

Решение: Выполним пояснительный рисунок:

 

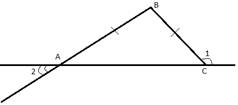
Рис. 4. Чертеж к примеру 1

1. ∠АСВ = – 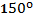= 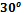(по свойству смежных углов). Значит, угол при основании равнобедренного треугольника равен .

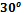2. ∠ВАС = ∠АСВ = 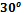(поскольку углы при основании равнобедренного треугольника равны).

3. ∠2 = ∠ВАС (как вертикальные), значит, ∠2 = ∠ВАС = .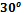

Ответ:.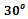

Пример 2: Периметр равнобедренного треугольника АВС с основанием ВС равен 40 см, а периметр равностороннего треугольника ВСD равен 45 см. Найдите стороны

Как построить равнобедренный треугольник | Треугольники

Как построить равнобедренный треугольник? Это легко сделать с помощью линейки, карандаша и клеточек тетради.

Построение равнобедренного треугольника начинаем с основания. Чтобы рисунок получился ровным, количество клеточек в основании должно быть четным числом.

    Делим отрезок — основание треугольника — пополам.

Вершину треугольника можно выбрать на любой  высоте от основания, но обязательно ровно над срединой.

Как построить остроугольный равнобедренный треугольник?

Углы при основании равнобедренного треугольника могут быть только острыми. Чтобы равнобедренный треугольник получился остроугольным, угол при вершине тоже должен быть острым.

    Для этого вершину треугольника выбираем повыше, подальше от основания.

Чем выше вершина, тем меньше угол при вершине. Углы при основании при этом, соответственно, увеличиваются.

Как построить тупоугольный равнобедренный треугольник?

    С приближением вершины равнобедренного треугольника к основанию градусная мера угла при вершине увеличивается.

Значит, чтобы построить равнобедренный тупоугольный треугольник, вершину выбираем пониже.

Как построить равнобедренный прямоугольный треугольник?

   Чтобы построить равнобедренный прямоугольный треугольник, надо вершину выбрать на расстоянии, равном половине основания (это обусловлено свойствами равнобедренного прямоугольного треугольника).

Например, если длина основания — 6 клеточек, то вершину треугольника располагаем на высоте 3 клеточек над серединой основания. Обратите внимание: при этом каждая клеточка у углов при основании делится по диагонали.

  Построение равнобедренного прямоугольного треугольника можно начать с вершины.

Выбираем  вершину, от нее под прямым углом откладываем равные отрезки вверх и вправо. Это — боковые стороны треугольника.

Соединим их и получим равнобедренный прямоугольный треугольник.

Построение равнобедренного треугольника с помощью циркуля и линейки без делений рассмотрим в другой теме.

ПНШ 3 класс. Математика. Учебник № 1, с. 133

Разносторонние и равнобедренные треугольники

Ответы к с. 133


439. Может ли равнобедренный треугольник быть остроугольным? Попробуй начертить такой треугольник.


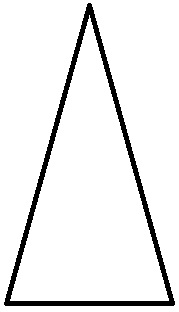
Да, может. На рисунке у равнобедренного треугольника все углы острые.


440. Начерти равнобедренный прямоугольный треугольник.



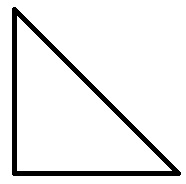
441. Начерти равнобедренный тупоугольный треугольник.



442. Начерти равнобедренный треугольник, у которого две стороны имеют длину 5 см.



443. Начерти равнобедренный треугольник, у которого только одна сторона – 5 см.



444. Является ли равнобедренный треугольник симметричной фигурой? Проверь этот факт с помощью модели равнобедренного треугольника, сделанной из бумаги.


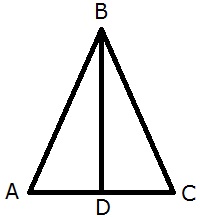
Треугольник АВС является равнобедренным. В нём проведён отрезок ВD, проходящий через середину треугольника и перпендикулярный основанию треугольника АС, делящий основание треугольника на два равных отрезка. Поскольку сторона АВ равна стороне ВС, а отрезки АD и DС равны между собой, то треугольник АВD равен треугольнику DВС. Получается, что равнобедренный треугольник – симметричная фигура и осью симметрии в нём является отрезок (или прямая) ВD. Бумажную модель треугольника нужно сложить пополам (линия сгиба – отрезок ВD) и убедиться, что половины равны.

445. Можно ли равнобедренный треугольник разбить на два равных прямоугольных треугольника? Покажи на чертеже, как это можно сделать.

На рисунке из предыдущего задания 444 видно, что нужно провести перпендикуляр из вершины треугольника на основание. Получаются два равных прямоугольных треугольника: АВD и ВDC.

446. Может ли разносторонний треугольник быть равнобедренным? Почему?


Не может, потому что у равнобедренного треугольника две стороны равны между собой, а у разностороннего треугольника все стороны разные по длине.


Ответы к заданиям. Математика. Учебник. Часть 1. Чекин А.Л. 2013 г.

Математика. 3 класс. Чекин А.Л.

Понравилось? Оцени!