Треугольник начертить: Как нарисовать треугольник: этапы выполнения задания – Как начертить равносторонний треугольник 🚩 как начертить окружность описанную около треугольника 🚩 Математика

Как нарисовать треугольник: этапы выполнения задания

Как нарисовать треугольник? Этому учат в процессе изучения геометрии в школе. Чтобы задание было выполнено правильно, важно точно знать, какой треугольник необходимо изобразить: равносторонний, равнобедренный или же вписанный. Правилам начертания этих фигур будет посвящена данная статья.

Как рисовать треугольник с равными сторонами?

Как нарисовать треугольник, стороны у которого равны? Для этого можно воспользоваться одним из трех методов.

Такая фигура имеет три одинаковые по длине стороны, связанные тремя углами равной ширины. Это может быть сложным для рисования треугольника вручную. Поэтому можно использовать круглый объект для выделения углов.

Варианты создания фигуры

Обязательно используйте линейку и один из представленных ниже способов:

1. Применение циркуля: надо начертить ровную линию. Проведите карандаш вдоль прямого края бумаги. Этот сегмент линии образует одну из сторон. А это означает, что нужно будет чертить вторую и третью линии одинаковой длины, каждая из которых достигает точки под углом 60° от первой линии. Удостоверьтесь, что достаточно места для рисования всех трех сторон!
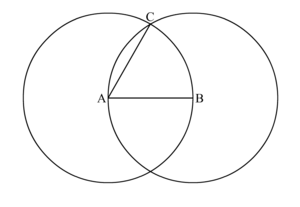
2. Разделите сегмент циркулем. Вставьте карандаш и убедитесь, что он острый! Поместите точку циркуля на один конец сегмента и установите карандаш на другую. Опишите дугу. Не изменяйте установленную «ширину» инструмента от точки циркуля до точки карандаша. Нарисуйте вторую дугу, чтобы она пересекала первую дугу, которую уже нарисовали. Отметьте точку, в которой пересекаются две дуги. Это вершина (верхняя точка) треугольника. Он должен лежать в точном центре сегмента линии, который нарисовали. Теперь можете сделать две прямые линии, ведущие к этой точке: по одному от каждого конца «нижнего» сегмента линии. Закончите треугольник. Далее с помощью линейки надо нарисовать еще два сегмента прямой линии – это стороны в треугольнике. Подключите каждый конец исходного сегмента линии к точке, в которой пересекаются дуги. Чтобы закончить работу, сотрите дуги, которые нарисовали, так, чтобы остался только треугольник.
3. Использование объекта с круглой базой: этот совет подойдет для построения дуги. Предложенный метод по сути такой же, как с использованием циркуля.

Указанные советы помогут выяснить, как нарисовать равносторонний треугольник.

Рекомендации по построению равнобедренного треугольника

Равнобедренный треугольник представляет собой фигуру с двумя равными сторонами и двумя равными углами. Если знаете длину, основание и высоту стороны, это можно сделать только с линейкой и циркулем (или просто циркулем, если заданы размеры).

Как нарисовать равнобедренный треугольник:

1. Учитывая все боковые длины. Чтобы использовать этот метод, важно знать длину основания треугольника и длину двух равных сторон.
2. Учитывая две равные стороны и угол между ними. Чтобы использовать этот метод, нужно знать длину двух равных сторон и измерение угла между этими двумя сторонами.
3. Учитывая базовые и смежные углы – необходимо знать длину базы, градусы двух углов, смежных с основанием. Помните, что два угла, смежные с основанием равнобедренного треугольника, будут равны.
4. Основа и высота. Нужно знать длину основания треугольника, а также высоту этой геометрической фигуры.

Вписанный треугольник

Как нарисовать вписанный треугольник? Выберите круглый объект. Используйте предмет с круглым основанием. Выбор компакт-диска станет хорошим вариантом. Но можно взять и другой объект нужного размера. Для этого метода свойственно, что длина каждой стороны равносторонней геометрической фигуры с тремя углами будет равна размерам радиуса (половине диаметра) круга.

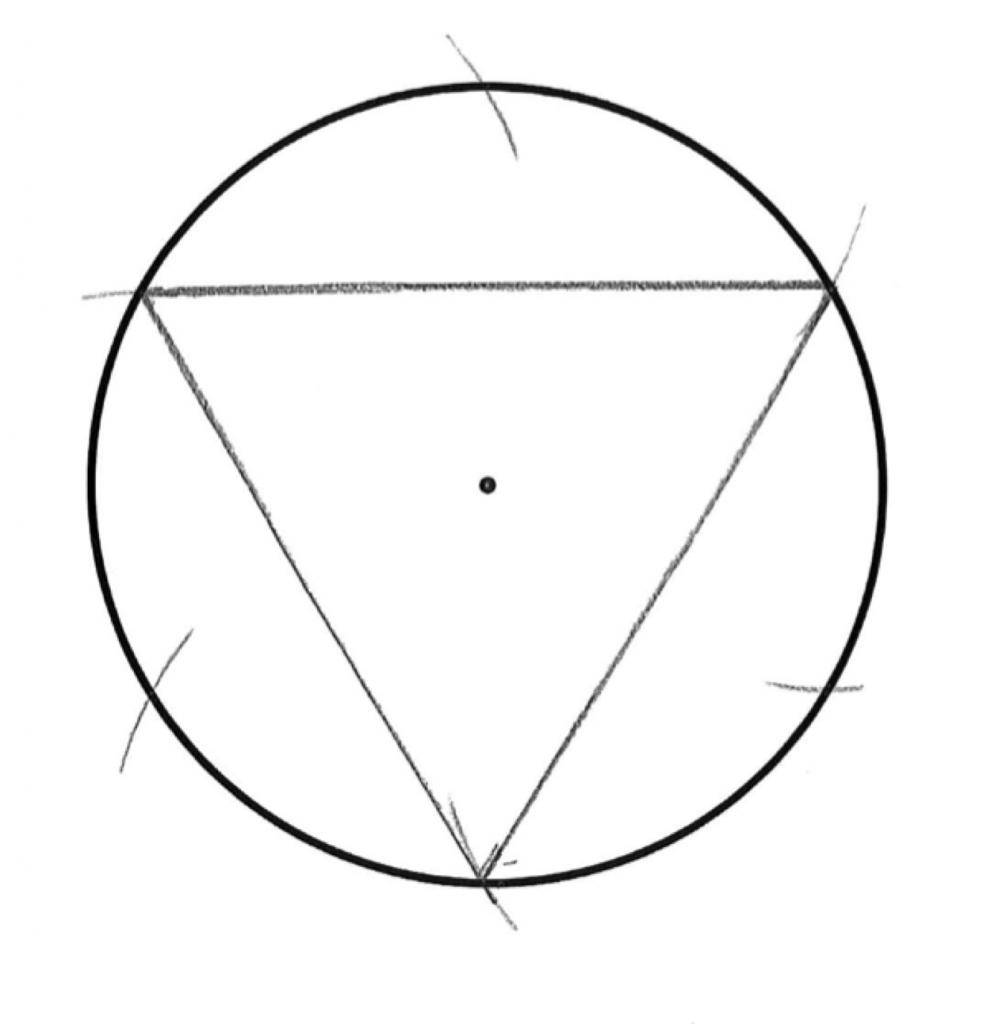
Как нарисовать треугольник, если используете компакт-диск? Представьте себе равносторонний треугольник, который вписывается в верхнюю правую часть компакт-диска. Надо начертить первую из сторон. Радиус круглого объекта – расстояние на полпути до получения желаемого результата. Удостоверьтесь, что линии нарисованы ровно.

С помощью линейки просто выполните измерения диаметра объекта и нарисуйте линию на половину длины. Если ее нет, поместите круглый объект на бумагу, затем тщательно проведите по окружности карандашом. Удалите объект – должен быть идеальный круг. Используйте прямой край, чтобы нарисовать линию через точный центр круга: точку, которая полностью равноудалена от любой точки по окружности круга.

Используйте круглый объект для создания дуги. Поместите объект по отрезку линии, с краем круга, расположенным на одном конце линии. Для обеспечения точности убедитесь, что линия проходит четко через центр круга. Используйте карандаш, чтобы начертить дугу – это четверть пути по окружности.

Начертите еще одну дугу. Теперь сдвиньте круглый объект так, чтобы край касался другого конца сегмента линии.

Подведем итоги

В статье были предоставлены рекомендации, как нарисовать треугольник равносторонний, равнобедренный и вписанный в окружность.

Как начертить треугольник?

Как начертить треугольник?

Построение различных треугольников – обязательный элемент школьного курса геометрии. У многих это задание вызывает страх. Но на самом деле, все довольно просто. Далее в статье описано, как начертить треугольник любого типа с помощью циркуля и линейки.

Треугольники бывают

• разносторонние;
• равнобедренные;
• равносторонние;
• прямоугольные;
• тупоугольные;
• остроугольные;
• вписанные в окружность;
• описанные вокруг окружности.

Построение равностороннего треугольника

Равносторонним называется треугольник, у которого все стороны равны. Из всех видов треугольников, начертить равносторонний проще всего.

1. С помощью линейки начертите одну из сторон, заданной длины.
2. Измерьте ее длину с помощью циркуля.
3. Поместите острие циркуля в один из концов отрезка и проведите окружность.
4. Переставьте острие в другой конец отрезка и проведите окружность.
5. У нас получилось 2 точки пересечения окружностей. Соединяя любую из них с краями отрезка, мы получаем равносторонний треугольник.

Построение равнобедренного треугольника

Данный тип треугольников можно построить по основанию и боковым сторонам.

Равнобедренным называется треугольник, у которого две стороны равны. Для того чтобы начертить равнобедренный треугольник по данным параметрам, необходимо выполнить следующие действия:

1. С помощью линейки откладываем отрезок, равный по длине основанию. Обозначаем его буквами АС.
2. Циркулем измеряем необходимую длину боковой стороны.
3. Рисуем из точки А, а затем из точки С, окружности, радиус которых равен длине боковой стороны.
4. Получаем две точки пересечения. Соединив одну из них с точками А и С, получаем необходимый треугольник.

Построение прямоугольного треугольника

Треугольник, у которого один угол прямой, называют прямоугольным. Если нам даны катет и гипотенуза, начертить прямоугольный треугольник не составит труда. Его можно построить по катету и гипотенузе.

1. С помощью линейки чертим гипотенузу заданной длины. Назовем этот отрезок АВ.
2. Ставим острие циркуля в точку А и проводим полуокружность, радиус которой немного больше, чем половина отрезка.
3. Переставляем острие циркуля в точку В и проводим аналогичное действие. Наши дуги пересекаются в двух места. Соединяем эти точки. Точка пересечения данной линии и отрезка АВ – его середина, точка О.
4. С помощью циркуля рисуем окружность, центр которой находится в точке О, а радиус равен отрезку АО.
5. Из точки А проводим циркулем дугу, радиус которой равен заданному катету. Точка пересечения дуги и окружности – искомая третья вершина треугольника. Соединяем ее с точками А и В. Задача выполнена.

Построение тупоугольного треугольника по углу и двум прилегающим сторонам

Если один из углов треугольника тупой (больше 90 градусов), его называют тупоугольным. Чтобы начертить по указанным параметрам тупоугольный треугольник необходимо сделать следующее:

1. С помощью линейки откладываем отрезок, равный по длине одной из сторон треугольника. Обозначим его буквами А и D.
2. Если в задании уже нарисован угол, и вам необходимо начертить такой же, то на его изображении отложить два отрезка, оба конца которых лежат в вершине угла, а длина равняется указанным сторонам. Соедините полученные точки. У нас получился искомый треугольник.
3. Чтобы его перенести на свой чертеж, вам необходимо измерить длину третьей стороны.

Построение остроугольного треугольника

Остроугольный треугольник (все углы меньше 90 градусов) строится по тому же принципу.

1. Нарисуйте две окружности. Центр одной из них лежит в точке D, а радиус равен длине третьей стороны, а у второй центр находится в точке А, а радиус равен длине указанной в задании стороны.
2. Соедините одну из точек пересечения окружности с точками А и D. Искомый треугольник построен.

Вписанный треугольник

Для того чтобы начертить треугольник в окружности, нужно помнить теорему, в которой говорится, что центр описанной окружности лежит на пересечении серединных перпендикуляров:

1. Циркулем проводим две окружности, центры которых лежат на разных концах отрезка одной из сторон, а радиусы (одинаковые) немного больше половины его длины. Соединяем точки пересечения окружностей. Это и будет нашим серединным перпендикуляром.
2. Строим два серединных перпендикуляра к двум любым сторонам. Точка пересечения (назовем ее О) – центр искомой описанной окружности. Согласно аксиоме, у двух прямых может быть только одна точка пересечения, поэтому нет надобности чертить все три перпендикуляра.
3. Измеряем циркулем расстояние от точки О до любой из вершин треугольника и рисуем окружность. Задание выполнено.

У тупоугольного треугольника центр описанной окружности лежит за пределами треугольника, а у прямоугольного – на середине гипотенузы.

Чертим описанный треугольник

Описанный треугольник – это треугольник, в центре которого нарисована окружность, касающаяся всех его сторон. Центр вписанной окружности лежит на пересечении биссектрис. Для их построения необходимо:

1. Произвольным радиусом чертим дугу, центр которой одна из вершин треугольника. Точки пересечения дуги со сторонами назовем Р и М.
2. Тем же радиусом рисуем еще две дуги, с центрами в точках Р и М. Соединяем точку их пересечения с исходной вершиной. Биссектриса построена.
3. Чертим 2 биссектрисы. Точка их пересечения (обозначим ее О) – центр нашей будущей окружности.
4. Для того, чтобы определить радиус окружности, необходимо построить перпендикуляр из точки О на любую из сторон.
5. Произвольным радиусом рисуем дугу с центром в точке О так, чтобы она пересекала выбранную сторону (пускай это будет сторона АС) в двух местах.
6. Радиусом АО рисуем две окружности, с центрами в точках А и С. Соединяем места пересечения окружностей.  Точка пересечения этой линии и стороны АС  (обозначим ее Е) – искомый перпендикуляр.
7. Измеряем циркулем отрезок ЕО и чертим вписанную окружность.
8. Таким образом вы сможете начертить описанный треугольник.

Виды треугольников. Построение прямоугольного треугольника на нелинованной бумаге

На этом уроке мы рассмотрим виды треугольников и научимся строить прямоугольный треугольник на нелинованной бумаге. Вначале вспомним определение треугольника и его элементы, какие существуют виды углов, узнаем, как на нелинованной бумаге построить прямой угол. Далее узнаем, как делятся треугольники на виды в зависимости от типа углов в них. Рассмотрим несколько задач на нахождение вида треугольников и на построение 

Треугольник – это геометрическая фигура, состоящая из трех точек, не лежащих на одной прямой и трех соединяющих их отрезков. В любом треугольнике различают следующие элементы:

Вершины (рис. 1). Это точки.

Рис. 1. Элементы треугольника: вершины

Стороны (Рис. 2). Это отрезки.

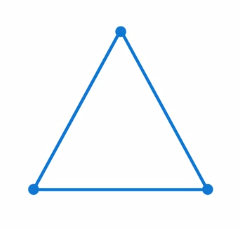
Рис. 2. Элементы треугольника: стороны

Углы (Рис. 3)

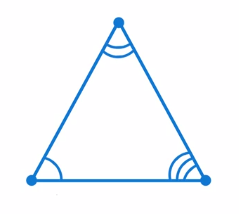
Рис. 3. Элементы треугольника: углы

Развернутый угол. (Рис. 4)

Угол называется развернутым, если его стороны лежат на одной прямой.

Рис. 4. Виды углов: развернутый

Прямой угол (Рис. 5)

Прямой угол составляет половину развернутого.

Рис. 5. Виды углов: прямой угол

Прямой угол можно получить путем складывания бумаги. Сложив лист дважды, мы получим модель прямого угла, его составляют линии сгиба.

Приложим модель угла к углу на чертеже (Рис. 5) таким образом, чтобы углы и стороны совпали (Рис. 6).

Рис. 5. Модель угла и угол на чертеже

Рис. 6. Модель угла, приложенная к углу на чертеже

Мы убедились, что на чертеже действительно изображен прямой угол.

Для удобства определения, прямой угол или нет, используют особый инструмент – прямоугольный треугольник (Рис. 7).

Рис. 7. Прямоугольный треугольник

Непрямые углы делятся на острые (Рис. 8) и тупые (Рис. 11).

Прямоугольный треугольник (Рис. 13). Угол 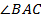 – прямой.

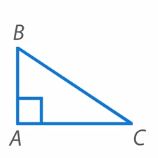
Рис. 13. Виды треугольников: прямоугольный треугольник

Остроугольный треугольник (Рис. 14). Все углы  данного треугольника острые.

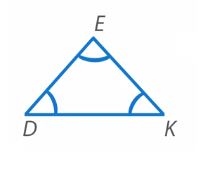
Рис. 14. Виды треугольников: остроугольный треугольник

Тупоугольный треугольник (Рис. 15). Угол 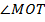 – тупой.

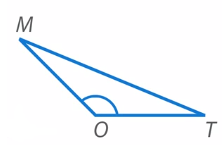
Рис. 15. Виды треугольников: тупоугольный треугольник 

Назовите номера тупоугольных, остроугольных и прямоугольных треугольников на рисунке 16.

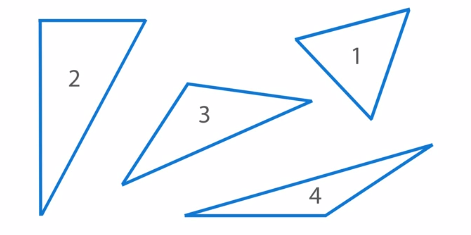
Рис. 16. Иллюстрация к заданию 1

Треугольник номер 1 – остроугольный, у него все углы острые. Треугольники номер 3 и 4 – тупоугольные, каждый из них имеет один тупой угол. Фигура номер 2 – прямоугольный треугольник. Проверим, действительно ли эта фигура имеет прямой угол, с помощью прямоугольного треугольника (Рис. 17).

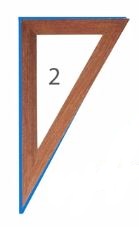
Рис. 17. Проверка треугольника номер 2

Мы видим, что вершины и стороны прямого угла совпали, значит, угол прямой, а треугольник прямоугольный.

Постройте на нелинованной бумаге треугольник 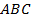, чтобы угол  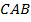был прямым, длина стороны  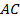равнялась 15 см, а длина сторогы  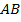– 20 см.

Построим точку 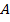 (Рис. 18).

Рис. 18. Точка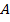

Проведем через точку 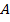 прямую (Рис. 19).

Рис. 19. Прямая, проведенная через точку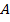

Для построения прямого угла воспользуемся прямоугольным треугольником. Приложим треугольник так, чтобы вершина прямого угла совпала с точкой 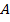, а одна из сторон совпала с лучом, как показано на рис. 20.

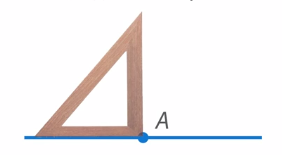
Рис. 20. Построение прямого угла

Проведем по второй стороне прямого угла треугольника луч из точки 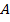 и получим прямой угол (Рис. 21).

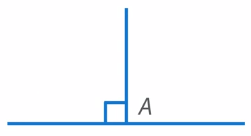
Рис. 21. Полученный прямой угол

Выполним построение сторон треугольника. Построим отрезок 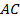, который равен 15 см (Рис. 22).

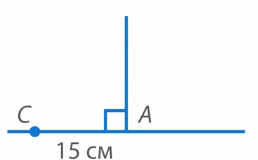
Рис. 22. Отрезок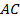

Построим отрезок 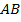, который равен 20 см (Рис. 23).

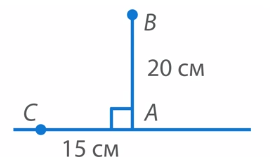
Рис. 23. Отрезок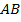

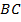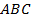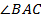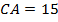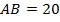Соединим полученные точки отрезком . Мы получили прямоугольный треугольник  (Рис. 24) с прямым углом  и сторонами  см и  см.

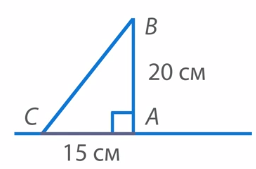
Рис. 24. Треугольник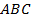

В зависимости от длины сторон можно выделить разносторонние и равнобедренные треугольники. Вспомним, если у треугольника длины всех сторон различные, то такой треугольник называется разносторонним. Если в треугольнике две стороны по длине равны, то такой треугольник называется равнобедренным, а равные по длине стороны называют боковыми сторонами треугольника, а третья сторона называется основанием треугольника.

Постройте равнобедренный треугольник 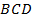 с прямым углом  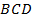и сторонам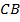и  и 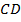 по 20 см. Дополните этот треугольник до прямоугольника.

Построим точку 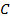 (Рис. 25).

Рис. 25. Точка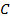

Проведем через точку 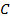 прямую (Рис. 26).

Рис. 26. Прямая, проведенная через точку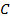

Для построения прямого угла воспользуемся прямоугольным треугольником. Приложим прямоугольный треугольник так, чтобы вершина прямого угла совпала с точкой 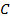, а одна из сторон треугольника – с лучом (Рис. 27).

Геометрия для средней школы/Построение правильного треугольника — Викиучебник

Материал из Викиучебника — открытых книг для открытого мира

В этой главе мы покажем как построить равносторонний треугольник. Что значит «Равносторонний»? Это просто значит, что все три стороны треугольника имеют одинаковую длину.
Любой треугольник, вершинами которого являются точки A, B и C записывается как △ABC{\displaystyle \triangle ABC}.
И если он равносторонний, то выглядит как показано на рисунке снизу:

Построение (метод, которым мы нарисуем △ABC{\displaystyle \triangle ABC}) основано на Book I, proposition 1.

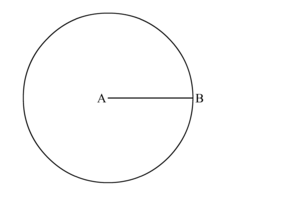
1. Используя вашу линейку, начертите линию любой длины. Это будет одна из сторон вашего треугольника.
   Назовем один конец отрезка — A другой — B.
   Теперь мы имеем отрезок с названием AB¯{\displaystyle {\overline {AB}}}.
   Он должен выглядеть как на рисунке ниже.
   
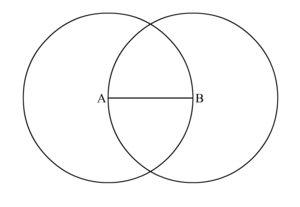
2. Используя ваш циркуль, нарисуйте окружность ∘A,{\displaystyle \circ A,} центр которого будет в точке A, а радиус будет AB¯{\displaystyle {\overline {AB}}}.
   
3. Снова используя ваш циркуль, нарисуйте окружность ∘A,{\displaystyle \circ A,} центр которого будет в точке B, а радиус будет AB¯{\displaystyle {\overline {AB}}}.
   
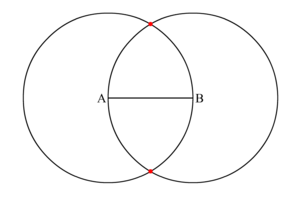
4. Вы можете увидеть как круги пересекаются (накладываются друг на друга) в двух точках.
   Точки отмечены красным цветом на картинке снизу.
   
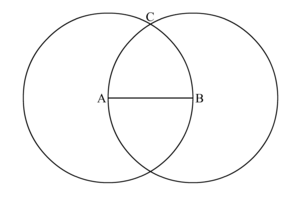
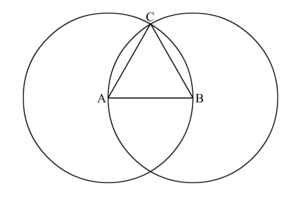
5. Выберите одну из этих точек и назовем её C.
   Мы выбрали верхнюю точку, но вы можете выбрать нижнюю если вам так больше нравится. Если вы выберите нижнюю точку, ваш треугольник будет выглядеть «вверх тормашками», но он всё равно будет правильным.
   
6. Начертите линию между A и C и получите отрезок AC¯{\displaystyle {\overline {AC}}}.
   
7. Начертите линию между B и C и получите отрезок BC¯{\displaystyle {\overline {BC}}}.
   
8. Построение △ABC{\displaystyle \triangle ABC} завершено.

Треугольник △ABC{\displaystyle \triangle ABC} — правильный.

Доказательство[править]

Как нарисовать равносторонний треугольник

Как нарисовать равносторонний треугольник, используя только линейку и карандаш? Этот способ позволяет быстро сделать рисунок правильного или равнобедренного треугольника.

Как нарисовать равнобедренный треугольник

Рисунок начинаем с основания. Длину основания подбираем такой, чтобы ее удобно было делить пополам (берем четное количество клеточек).  Вершину треугольника отмечаем  ровно над серединой основания:

 

 

Если нужен равнобедренный треугольник, у которого боковая сторона больше основания, вершину ставим повыше:

 

 

Если требуется треугольник, основание которого больше боковой стороны, то вершину отмечаем ниже:

 

 

Как нарисовать равносторонний треугольник

От конца основания откладываем отрезок равной ему длины так, чтобы второй конец этого отрезка расположился ровно над серединой основания. Соединяем вершину треугольника с другим концом основания:

 

 

Бонус.

Если в задаче о равнобедренном треугольнике речь идет о высоте, биссектрисе и медиане, проведенным к основанию, достаточно соединить вершину треугольника с отмеченной серединой основания:

 

Как построить треугольник с помощью циркуля Как

Как построить треугольник с помощью циркуля

Как построить треугольник с помощью циркуля Циркуль – инструмент не только для построения окружности. Он позволяет также отложить равные отрезки заданной длины. Это и поможет нам с его помощью построить треугольник.

Вам понадобится: лист бумаги, циркуль, линейка. Инструкция. 1. возьмите любой листок бумаги. В центре листа поставьте точку. Это будет первая вершина A создаваемого треугольника. A

Инструкция 2. Раскройте циркуль на расстояние, соответствующее требуемой стороне создаваемого треугольника. Жестко зафиксируйте ножки циркуля в данном положении.

Инструкция 3. Поставьте иглу циркуля в отмеченную точку. Нарисуйте ножкой с грифелем дугу окружности отмеренного радиуса.

Инструкция 4. В любом месте по окружности нарисованной дуги поставьте точку. Это будет вторая вершина B создаваемого треугольника.

Инструкция 5. Аналогичным способом поставьте ножку на вторую вершину. Проведите еще одну окружность так, чтобы она пресекалась с первой.

Инструкция 6. В точке пересечения обоих проведенных дуг и находится третья вершина C создаваемого треугольника. Отметьте ее на рисунке.

Инструкция 7. Получив все три вершины, соедините их прямыми линиями с помощью любой ровной поверхности (лучше линейки). Треугольник ABC построен. .

Источник: http: //www. kakprosto. ru/kak-17118 -kak-postroit -treugolnik-s-pomoshchyu-cirkulya#ixzz 4 TOIkn. Sn 5 Источник шаблона: Ранько Елена Алексеевна, учитель начальных классов МАОУ лицей № 21, г. Иваново

Как построить высоту треугольника | Треугольники

Рассмотрим, как построить высоту треугольника с помощью чертежного угольника.

Чтобы построить высоту остроугольного треугольника, надо приложить угольник так, чтобы одна сторона прямого угла проходила через вершину треугольника, а вторая — через противоположную этой вершине сторону.

AK⊥BC.

AK — высота треугольника ABC, проведённая из вершины A к противолежащей стороне BC.

 

BF⊥AC.

BF — высота треугольника ABC, опущенная из вершины B на сторону AC.

 

CH⊥AB.

CH — высота треугольника ABC, проведённая из вершины C к стороне AB.

 

Все высоты треугольника пересекаются в одной точке.

В остроугольном треугольнике точка пересечения высот лежит внутри треугольника.

Если требуется построить все высоты треугольника, достаточно построить две, а третью провести из вершины треугольника через точку пересечения двух высот.

 

В прямоугольном треугольнике две стороны (катеты) являются также его высотами. Остаётся построить третью высоту.

Угольник прикладываем прямым углом так, чтобы одна сторона проходила через гипотенузу, а другая — через прямой угол.

CD⊥AB.

CD — высота прямоугольного треугольника ABC, проведённая из вершины прямого угла C к гипотенузе AB.

Точка пересечения высот прямоугольного треугольника — вершина прямого угла.

Высоты AC, BC и CD прямоугольного треугольника ABC пересекаются в точке C, ∠C=90°.

 

 

В тупоугольном треугольнике проще всего построить высоту, выходящую из вершины тупого угла.

Прикладываем угольник прямым углом так, чтобы одна его сторона проходила через наибольшую сторону треугольника, а другая — через тупой угол.

AP⊥BC.

AP — высота тупоугольного треугольника ABC, проведённая из вершины тупого угла A к стороне BC.

Только высота, проведённая из вершины тупого угла, лежит внутри треугольника. Две другие высоты находятся вне него.

Высоты тупоугольного треугольника, выходящие из вершин острых углов, проведены не к противолежащим сторонам, а к прямым, содержащим эти стороны.

Чтобы построить высоту, продлеваем противолежащую сторону и прикладываем угольник прямым углом таким образом, чтобы одна сторона угольника проходила через построенную прямую, а другая — через вершину острого угла.

BM⊥AC,

BM — высота тупоугольного треугольника ABC, проведённая из вершины острого угла B к прямой, содержащей противолежащую сторону AC.

 

 

CN⊥AB,

CN — высота тупоугольного треугольника ABC, проведённая из вершины острого угла С к прямой, содержащей противолежащую сторону AB.

 

 

Точка пересечения высот тупоугольного треугольника лежит вне него, за тупым углом, напротив наибольшей стороны.

Чтобы построить точку пересечения высот треугольника ABC, продлим прямые BM, CN и AP до пересечения.

Мы рассмотрели, как строить высоты треугольника с помощью угольника.

Построение высот с помощью циркуля и линейки будем рассматривать в теме «Задачи на построение».