Симметрический рисунок: Рисование симметричных орнаментов в режиме симметрии – «Как научиться рисовать симметричные объекты симметричными? Глаза например» – Яндекс.Кью — DesignLessons – все о дизайне

Содержание

Прямоугольник, ромб и квадрат. Осевая и центральная симметрии

Данный урок посвящён осевой и центральной симметрии.

Определение

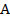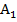Две точки и называются симметричными относительно прямой 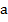, если:

1. прямая 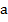проходит через середину отрезка ;

2. прямая

перпендикулярна отрезку

На Рис. 1 изображены примеры симметричных относительно прямой точек и ,

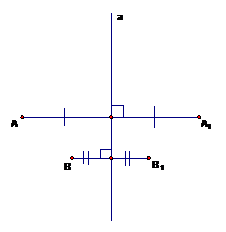
Рис. 1

Отметим также тот факт, что любая точка прямой симметрична сама себе относительно этой прямой.

Симметричными относительно прямой могут быть и фигуры.

Сформулируем строгое определение.

Определение

Фигура называется симметричной относительно прямой

, если для каждой точки фигуры симметричная ей относительно этой прямой точка также принадлежит фигуре. В этом случае прямая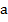

называется осью симметрии. Фигура при этом обладает осевой симметрией.

Рассмотрим несколько примеров фигур, обладающих осевой симметрией, и их оси симметрии.

Пример 1

Угол обладает осевой симметрией. Осью симметрии угла является биссектриса. Действительно: опустим из любой точки угла перпендикуляр к биссектрисе и продлим его до пересечения с другой стороной угла (см. Рис. 2).

Рис. 2

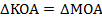(так как – общая сторона,

(свойство биссектрисы), а треугольники – прямоугольные). Значит,

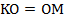. Поэтому точки

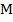симметричны относительно биссектрисы угла.

Из этого следует, что и равнобедренный треугольник обладает осевой симметрии относительно биссектрисы (высоты, медианы), проведённой к снованию.

Пример 2

Равносторонний треугольник обладает тремя осями симметрии (биссектрисы/медианы/высоты каждого из трёх углов (см. Рис. 3).

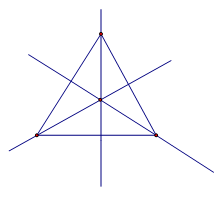
Рис. 3

Пример 3

Прямоугольник обладает двумя осями симметрии, каждая из которых проходит через середины двух его противоположных сторон (см. Рис. 4).

Рис. 4

Пример 4

Ромб также обладает двумя осями симметрии: прямые, которые содержат его диагонали (см. Рис. 5).

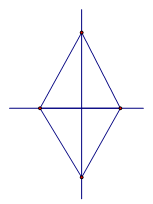
Рис. 5

Пример 5

Квадрат, являющийся одновременно ромбом и прямоугольником, обладает 4 осями симметрии (см. Рис. 6).

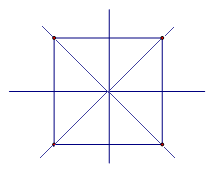
Рис. 6

Пример 6

У окружности осью симметрии является любая прямая, проходящая через её центр (то есть содержащая диаметр окружности). Поэтому окружность имеет бесконечно много осей симметрии (см. Рис. 7).

Рис. 7

Рассмотрим теперь понятие центральной симметрии.

Определение

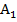Точки и называются симметричными относительно точки

, если:

– середина отрезка

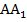Рассмотрим несколько примеров: на Рис. 8 изображены точк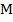и и 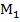, а также

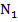, которые являются симметричными относительно точки

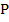, а точки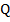

не являются симметричными относительно этой точки.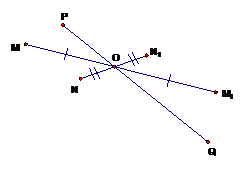

Рис. 8

Некоторые фигуры являются симметричными относительно некоторой точки. Сформулируем строгое определение.

Определение

Фигура называется симметричной относительно точки , если для любой точки фигуры точка, симметричная ей, также принадлежит данной фигуре. Точка называется центром симметрии, а фигура обладает

центральной симметрией.

Рассмотрим примеры фигур, обладающих центральной симметрией.

Пример 7

У окружности центром симметрии является центр окружности (это легко доказать, вспомнив свойства диаметра и радиуса окружности) (см. Рис. 9).

Рис. 9

Пример 8

У параллелограмма центром симметрии является точка пересечения диагоналей (см. Рис. 10).

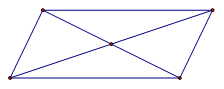
Рис. 10

Решим несколько задач на осевую и центральную симметрию.

Задача 1.

Сколько осей симметрии имеет отрезок ?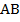

Решение:

Отрезок имеет две оси симметрии. Первая из них – это прямая, содержащая отрезок (так как любая точка прямой симметрична сама себе относительно этой прямой). Вторая – серединный перпендикуляр к отрезку, то есть прямая, перпендикулярная отрезку и проходящая через его середину.

Ответ: 2 оси симметрии.

Задача 2.

Сколько осей симметрии имеет прямая ?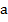

Решение:

Прямая имеет бесконечно много осей симметрии. Одна из них – это сама прямая (так как любая точка прямой симметрична сама себе относительно этой прямой). А также осями симметрии являются любые прямые, перпендикулярные данной прямой.

Ответ: бесконечно много осей симметрии.

Задача 3.

Сколько осей симметрии имеет луч ?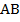

Решение:

Луч имеет одну ось симметрии, которая совпадает с прямой, содержащей луч (так как любая точка прямой симметрична сама себе относительно этой прямой).

Ответ: одна ось симметрии.

Задача 4.

Доказать, что прямые, содержащие диагонали ромба, являются его осями симметрии.

Доказательство:

Рассмотрим ромб 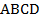. Докажем, к примеру, что прямая 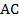является его осью симметрии. Очевидно, что точк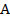и и 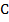являются симметричными сами себе, так как лежат на этой прямой. Кроме того, точки и симметричны относительно этой прямой, так как 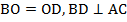. Выберем теперь произвольную точку и докажем, что симметричная ей относительно 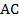точка также принадлежит ромбу (см. Рис. 11).

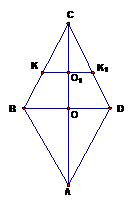
Рис. 11

Проведём через точку перпендикуляр к прямой 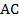и продлим его до пересечения с 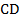. Рассмотрим треугольники 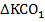и . Эти треугольники прямоугольные (по построению), кроме того, в них: 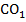– общий катет, а (так как диагонали ромба являются его биссектрисами). Значит, эти треугольники равны: . Значит, равны и все их соответствующие элементы, поэтому: 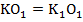. Из равенства этих отрезков следует то, что точки и 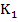являются симметричными относительно прямой 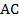. Это означает, что 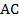является осью симметрии ромба. Аналогично можно доказать этот факт и для второй диагонали.

Доказано.

Задача 5.

Доказать, что точка пересечения диагоналей параллелограмма является его центром симметрии.

Доказательство:

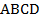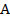Рассмотрим параллелограмм . Докажем, что точка является его центром симметрии. Очевидно, что точки 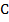и , и 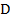являются попарно симметричными относительно точки , так как диагонали параллелограмма точкой пересечения делятся пополам. Выберем теперь произвольную точку и докажем, что симметричная ей относительно точка также принадлежит параллелограмму (см. Рис. 12).

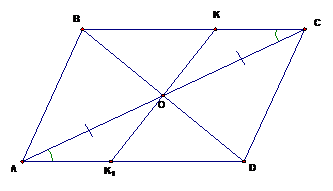
Рис. 12

Соединим точку с точкой и продлим линию до пересечения с противоположной стороной. Рассмотрим треугольники и 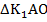. Эти треугольники равны по второму признаку равенства треугольников (сторона и два угла). Действительно: 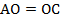(так как диагонали параллелограмма точкой пересечения делятся пополам), 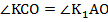(как внутренние накрест лежащие при параллельных прямых), (как вертикальные углы). Значит, эти треугольники равны: . Значит, равны и все их соответствующие элементы, поэтому: . Из равенства этих отрезков следует то, что точки и 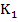являются симметричными относительно точки . Это означает, что является центром симметрии параллелограмма.

Доказано.

На этом уроке мы заканчиваем изучение темы «виды четырёхугольников» (параллелограмм, трапеция, прямоугольник, ромб, квадрат). Мы рассмотрели осевую и центральную симметрию и её примеры для различных геометрических фигур. Кроме того, были решены несколько задач на эту тему.

На следующих уроках мы перейдём к изучению новой темы: «Площадь».

Список литературы

Александров А.Д. и др. Геометрия, 8 класс. – М.: Просвещение, 2006.
Бутузов В.Ф., Кадомцев С.Б., Прасолов В.В. Геометрия, 8 класс. – М.: Просвещение, 2011.
Мерзляк А.Г., Полонский В.Б., Якир С.М. Геометрия, 8 класс. – М.: ВЕНТАНА-ГРАФ, 2009.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

Фестиваль педагогических наук «Открытый урок» (Источник).
Docme.ru (Источник).
Ikt.oblcit.ru (Источник).

Домашнее задание

№ 59, 60. Бутузов В.Ф., Кадомцев С.Б., Прасолов В.В. Геометрия, 8 класс. – М.: Просвещение, 2011.
Дан угол и точка , которая лежит внутри него. Построить угол, симметричный углу относительно точки .
Постройте окружность радиусом . Проведите прямую, которая не проходит через центр окружности. Постройте окружность, симметричную данной относительно этой прямой.

Уроки дизайна вышивки. Урок 4. Симметрия

Урок 4. Симметрия, или правила спокойствия.

В этом уроке мы научимся создавать уравновешенные гармоничные композиции и откроем секрет хороших отношений в коллективе.

Что вы предпочитаете больше — конфеты или сосиски? Если бы вы были рыжим котом, думаю, что сомнений бы у вас не было. Поэтому, рассматривать понятие симметрии будем на примере с сосисками.

Симметрия в переводе с древнегреческого означает соразмерность, соответствие, неизменность, проявляемые при изменениях и преобразованиях чего-либо. В нашем случеае «что-либо» — это не кто-либо, а рыжий кот Василий, получивший от хозяйки за свою красоту и обаяние три свежих сосиски. Но, дело в том, что есть у него брат Кузьма, не менее обаятельный и привлекательный, но опаздавший к завтраку. На рисунке вверху вы видите их портрет. Кажется, что что-то не так, ощущается некое напряжение, назревает конфликт. В чем же причина? — в неуравновешенности, точнее в несправедливости. Усы, лапы, хвост те-же, а сосисок не дали.

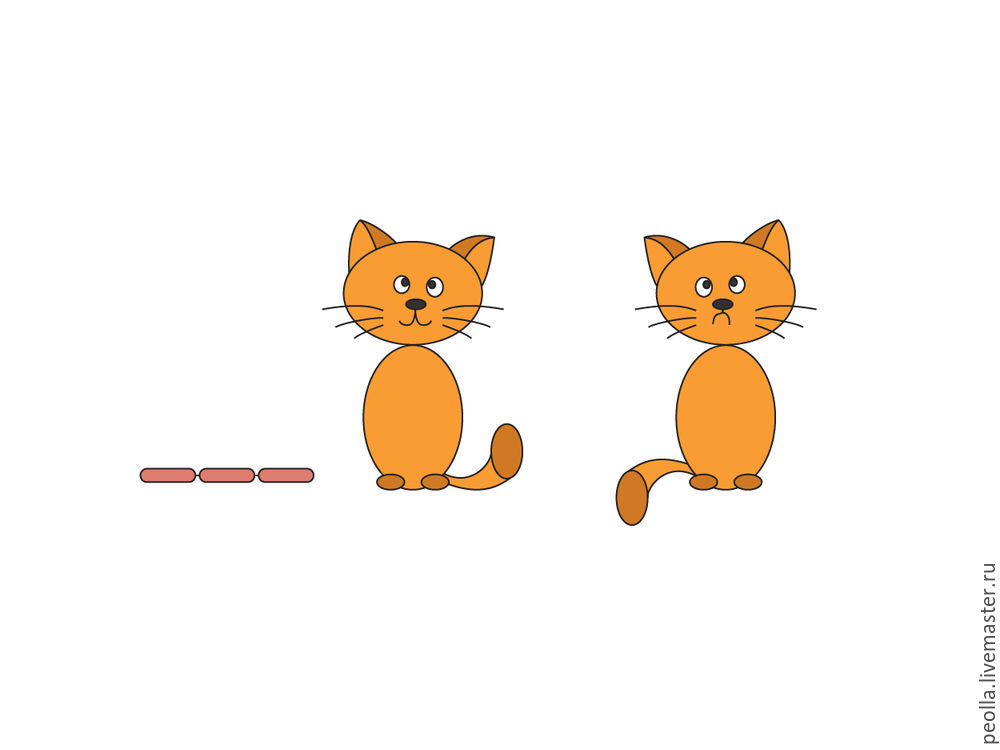
Попробуем исправить ситуацию и дадим также и Кузе три свежих сосиски. — Совсем другое дело! Гармония и благодать, дружба, мир и всем хорошо. Это с кошачьей точки зрения, а с позиции геометрии, можно сказать, что мы выполнили преобразование отражения, то есть, получили зеркальную симметрию. Другими словами, если посадить Василия с сосисками рядом с зеркалом, то мы увидим в зеркале его копию, но в отраженном виде. Композиция стала абсолютно уравновешена. Древние греки часто использовали такой вид симметрии, полагая, что она олицетворяет идею гармонии и совершенства.

Если вам захочется глубоко изучить законы симметрии, то могу порекомендовать книгу: А.В. Шубников, В.А. Копцик «Симметрия в науке и искусстве». Мы же начнем с самого простого, необходимого и достаточного для создания дизайна вышивки, мы рассмотрим три вида симметрии: симметрия скольжения, отражения и вращения. Если вы со школьных времен боитесь геомерии — не бойтесь, смело пропускайте все текстовые описания и просто внимательно рассматривайте картинки — вы все обязательно поймете!

1. Симметрия скольжения.

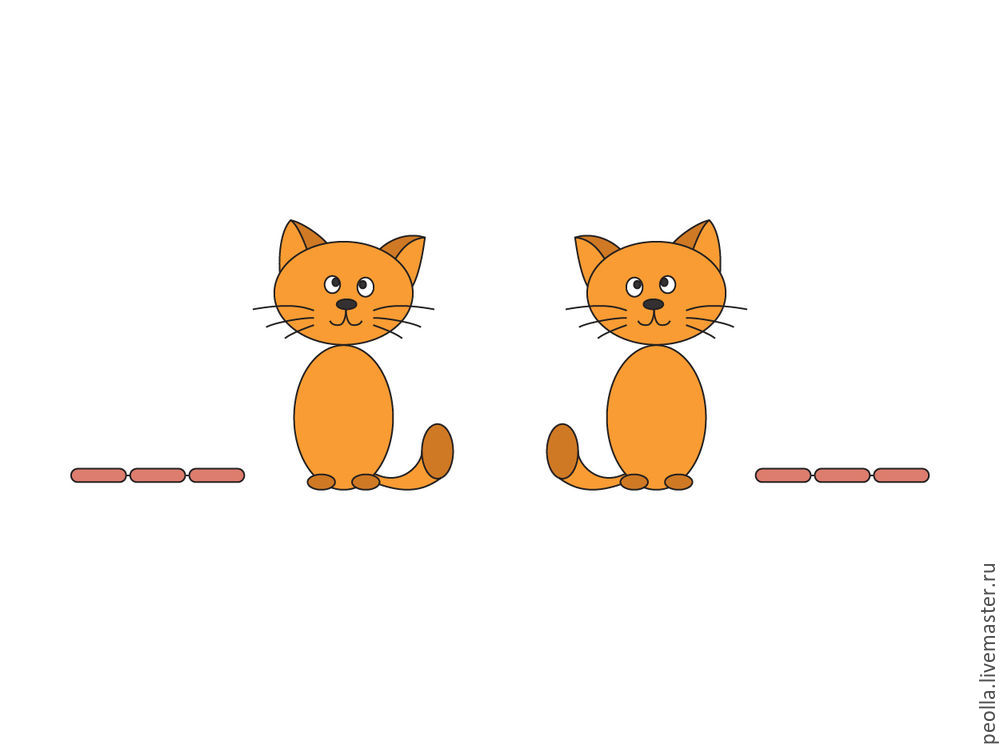
Все очень просто, объяснение смысла этого вида симметрии дано в его названии. Допустим, вы хотите сделать фото Василия, сидящего на подоконнике и, для получения прекрасного снимка, просите его пару раз немного подвинуться вдоль подоконника на некоторое одинаковое расстояние. Последовательные перемещения Василия будут выглядеть примерно так, как показано на рисунке внизу, а расстояние, на которое перемещался Василий будет называться раппортом. Сам же подоконник в данном случае будет выполнять роль прямой а, вдоль которой двигался Василий и будет называться «осью переносов», в нашем случае, осью переносов кота:)

Посмотрите на рисунок внизу. Фигура А — (желтый треугольник) скользит вдоль прямой а, в результате чего мы получаем фигуру А’ — точную копию фигуры А, но смещенную на расстояние раппорта. Следует уточнить, что раппорт может быть меньше, равен или больше элемента по отношению к которому выполняется преобразование скольжения. Этот вид симметрии дает ощущение движения, очень распространен и используется при построении декоративных бордюров, а также, в сочетании с другими видами симметрии, для создания более сложных композиций.

2. Симметрия отражения (зеркальная).

Этот вид симметрии мы уже рассмотрели на примере с котом Василием в начале статьи. Уточним лишь рисунок, обозначив зеркало (а еще правильнее, след плоскости зеркала на плоскости рисунка) — прямую b. В рассматриваемом примере зеркало стоит строго вертикально и перпендикулярно плоскости рисунка, поэтому мы видим лишь его торец. Отражение Василия является его точной копией, но, все что у Василия было слева — стало справа и наоборот (сосиски были слева, хвост справа, у отражения Василия все в другую сторону). Это свойство зеркала и, соответственно, зеркальной симметрии.

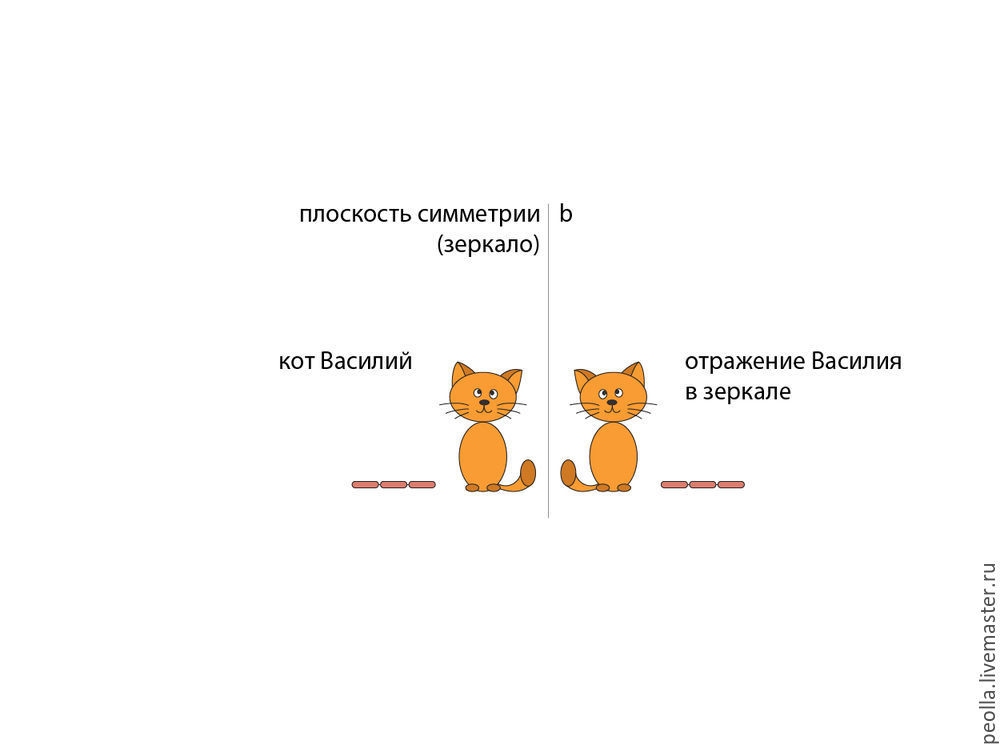
На рисунке внизу желтый треугольник (фигура А) отражается в зеркале, в результате, получаем фигуру А’ — точную копию фигуры А, но, все что было слева, стало на таком же расстоянии от плоскости симметрии (прямая b) справа. Это самый распространенный вид симметрии — мы видим его повсюду в природе, а также в искусстве, технике и даже в музыке, лингвистике и других науках.

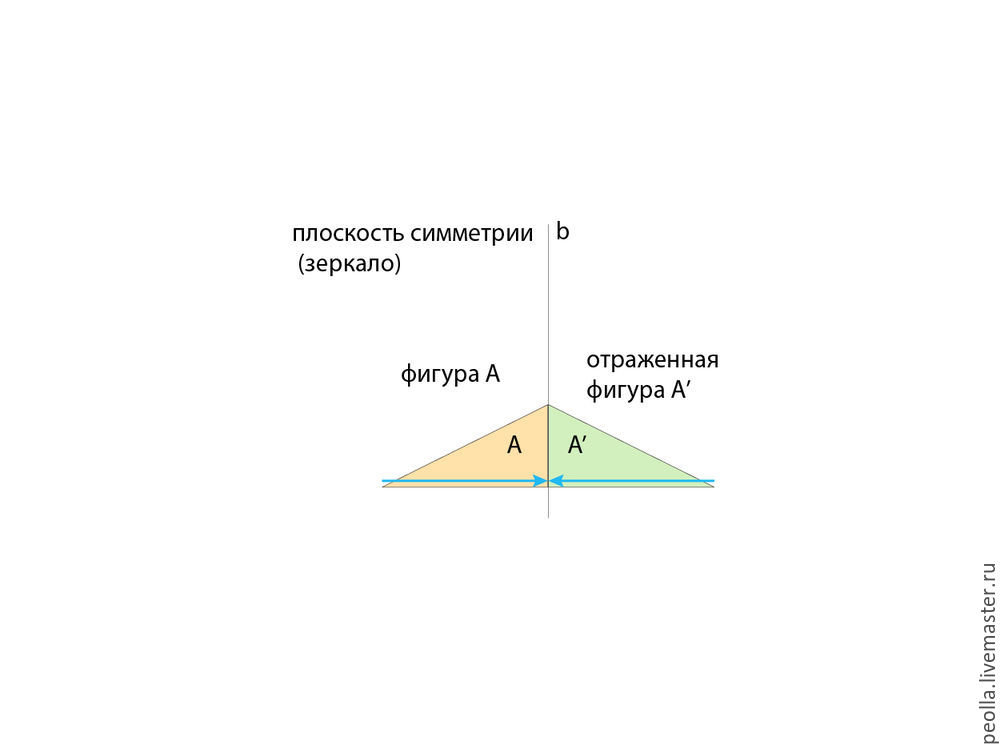
Часто симметрии отражения и скольжения используются вместе. Если вам удастся рассадить братьев Василия зеркальными парочками, затем переместить эти парочки на одинковое расстояние друг от друга, то вы получите картину небывалой красоты и умиротворения.

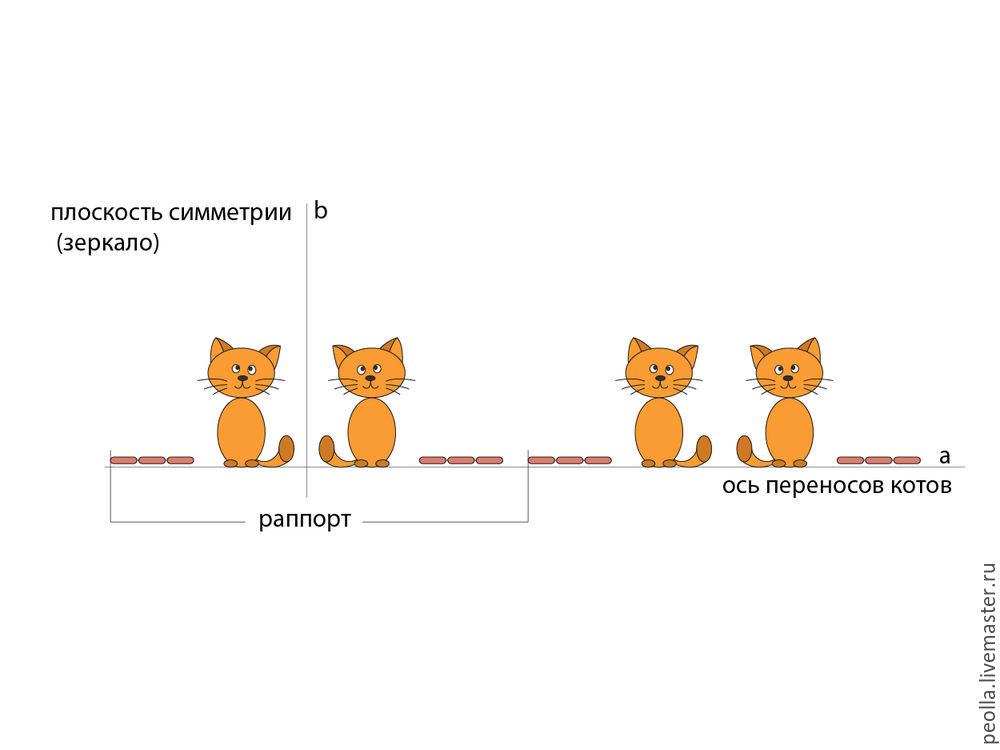
На следующем рисунке вы видите схему построений комбинированной симметрии отражения и скольжения. Вначале фигура А отражается зеркально относительно вертикальной плоскости симметрии, а затем обе фигуры (первоначальная А и отраженная А’) становятся единым элементом и для этого элемента выполняется преобразование скольжения (перенос) вдоль оси а на расстояние раппорта.

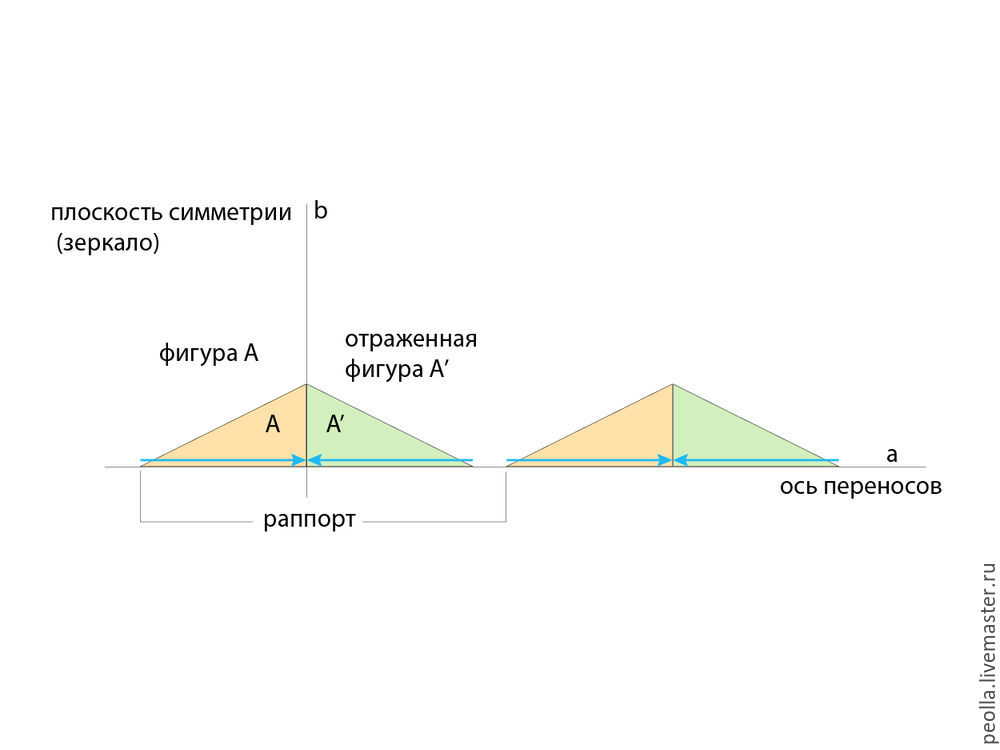
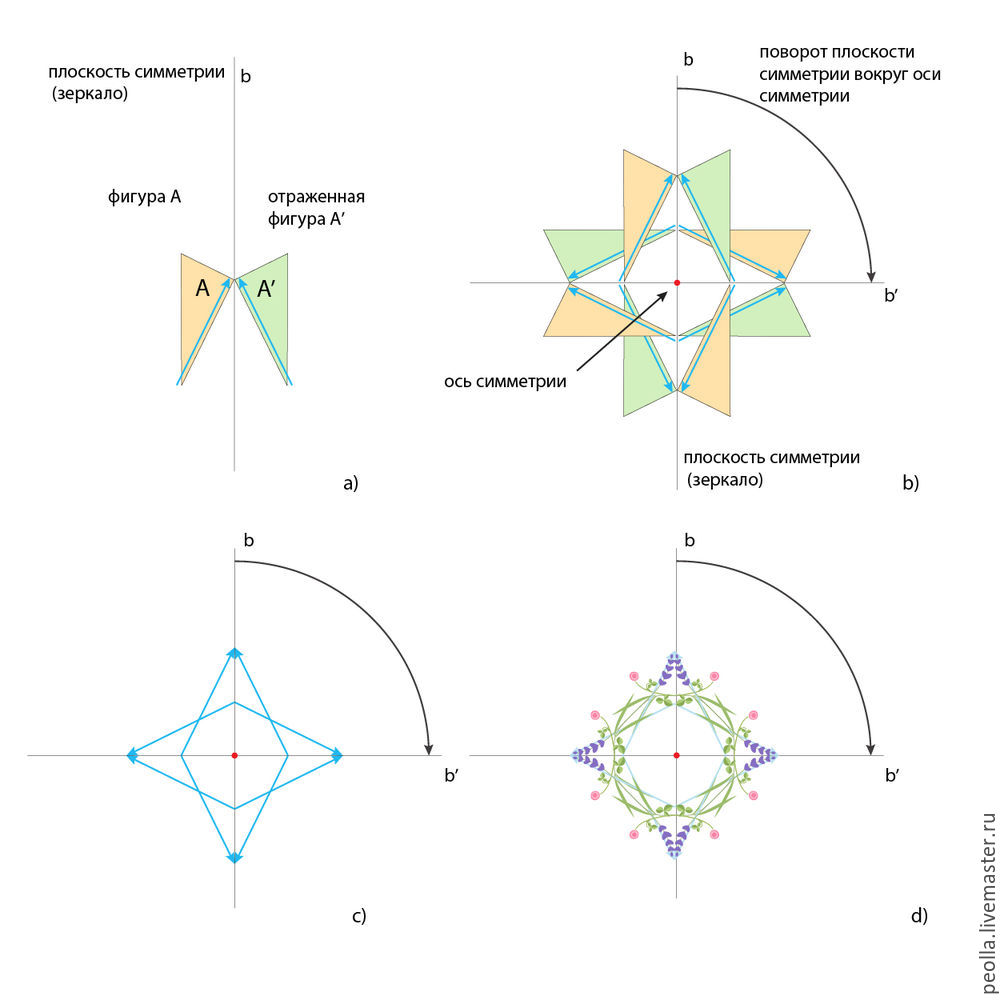
Рассмотрим варианты применения симметрий отражения и скольжения для создания декоративных бордюров. Как мы договорились ранее, желтый треугольник — первоначальная фигура, зеленый треугольник — ее зеркальное отражение (в этом примере для отражения мы будем использовать только вертикальные и горизонтальные плоскости симметрии, перпендикулярные плоскости рисунка). Заметим также, что преобразование отражения может быть выполнено с одной и той же фигурой несколько раз, то есть, например, мы можем отразить фигуру относительно вертикальной плоскости симметрии, а потом, уже отраженную фигуру еще раз отразить относительно горизонтальной плоскости симметрии. На рисунке ниже даны 7 вариантов симметрии бордюров (подробнее в книге А.В. Шубников, В.А. Копцик «Симметрия в науке и искусстве»).

Справа, напротив каждого примера с треугольниками, помещен пример с растительными мотивами. Синяя стрелка на треугольниках дана для удобства восприятия, она же служит ориентиром того, как следует располагать растительные мотивы для создания бордюра с заданной симметрией.

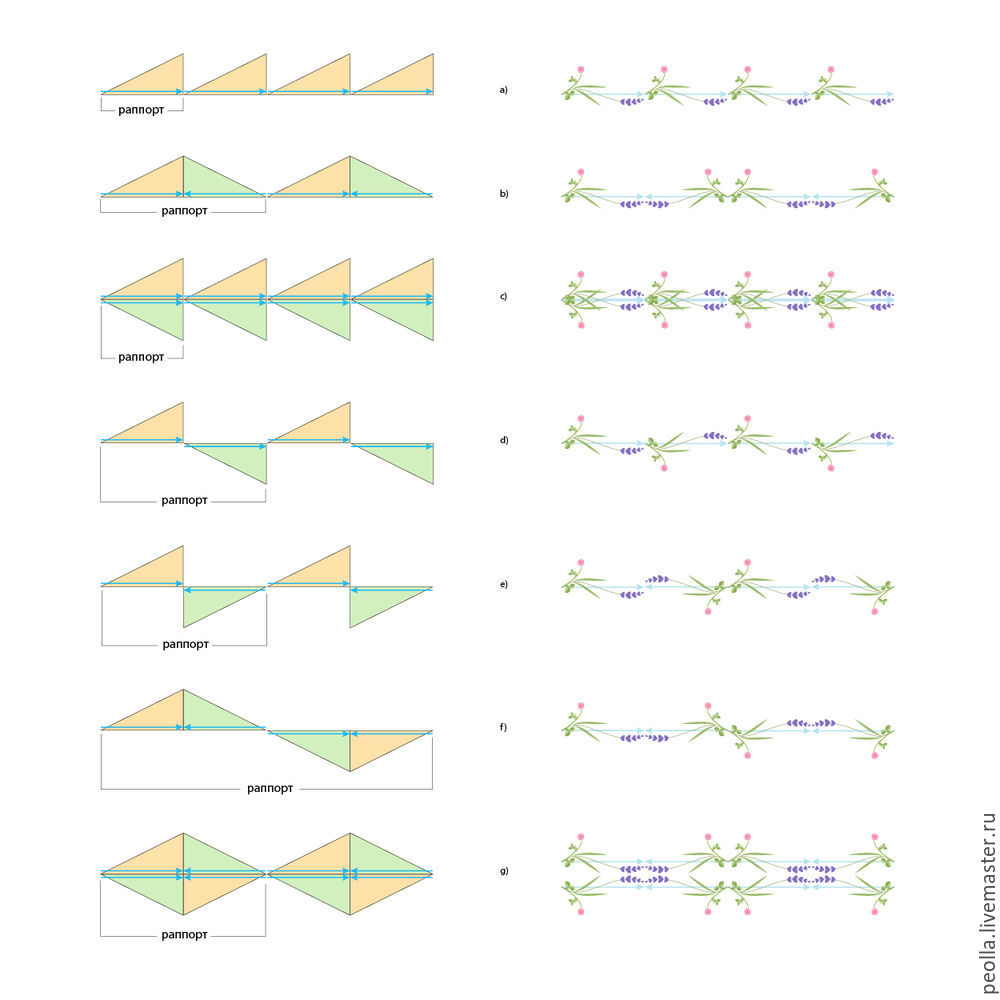
Как видите, мы получили достаточно разнообразный набор бордюров. Обратите внимание, во всех примерах, за исключением примера а), после преобразований отражения, мы имеем уже составные мотивы, которые далее участвуют в преобразованиях переноса. Открою вам еще один большой секрет — вариантов бордюров на основе представленных схем симметрии может быть гораздо больше, если перед выполнением отражения попробовать подвигать мотив, подводя его ближе или дальше к плоскости отражения, а также прислоняя его под разными углами (в примере на рисунке использовано лишь горизонтальное положение мотивов). Кроме того, данные бордюры можно использовать для заполнения больших поверхностей, располагая их параллельными рядами.

3. Симметрия вращения.

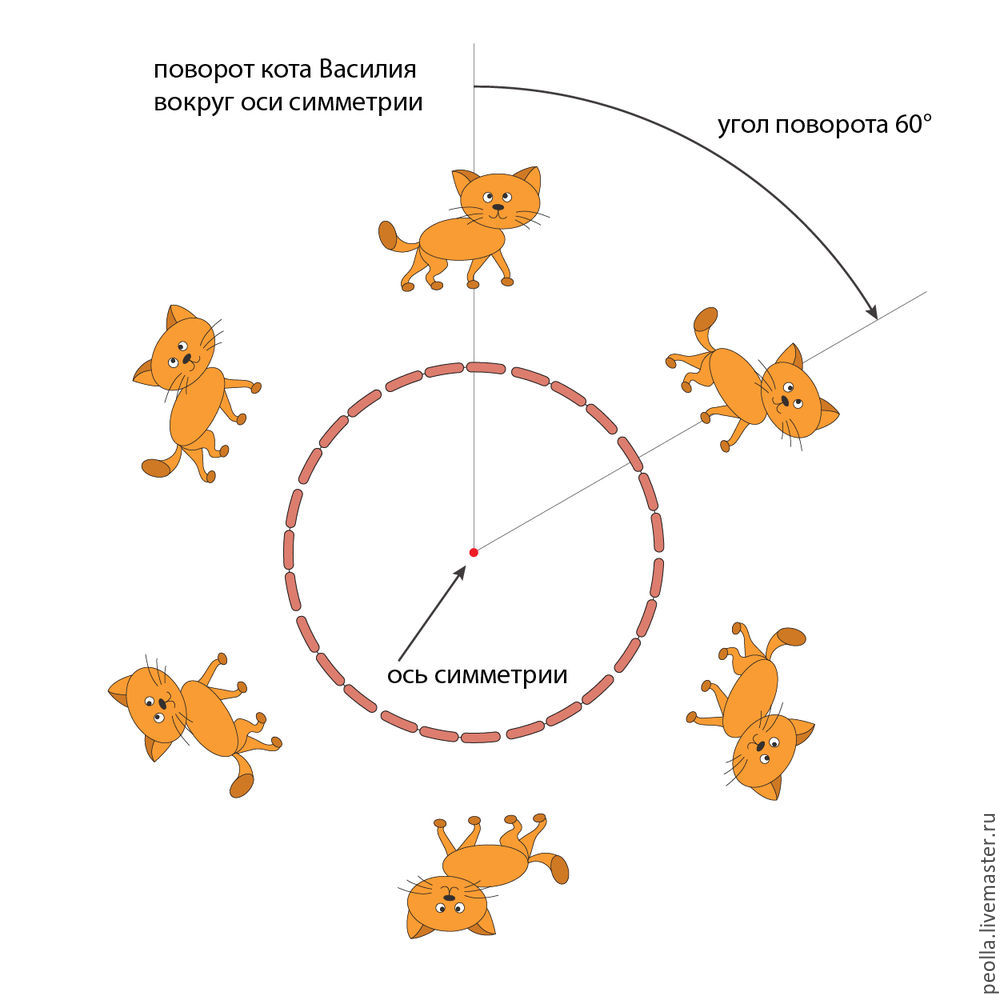
Помните, у Пушкина: «И днем и ночью кот ученый все ходит по цепи кругом…». Если нашего Василия отправить в такое путешествие вместе с его братьями, то получим вот такую картину (при условии, что они не будут догонять друг друга, а будут ходить гуськом, с одинаковым интервалом). Это и будет симметрия вращения. Точка, вокруг которой ходит Василий с братьями — на самом деле не точка, а проекция оси, перпендикулярной плоскости рисунка. Эта самая ось будет называться осью симметрии.

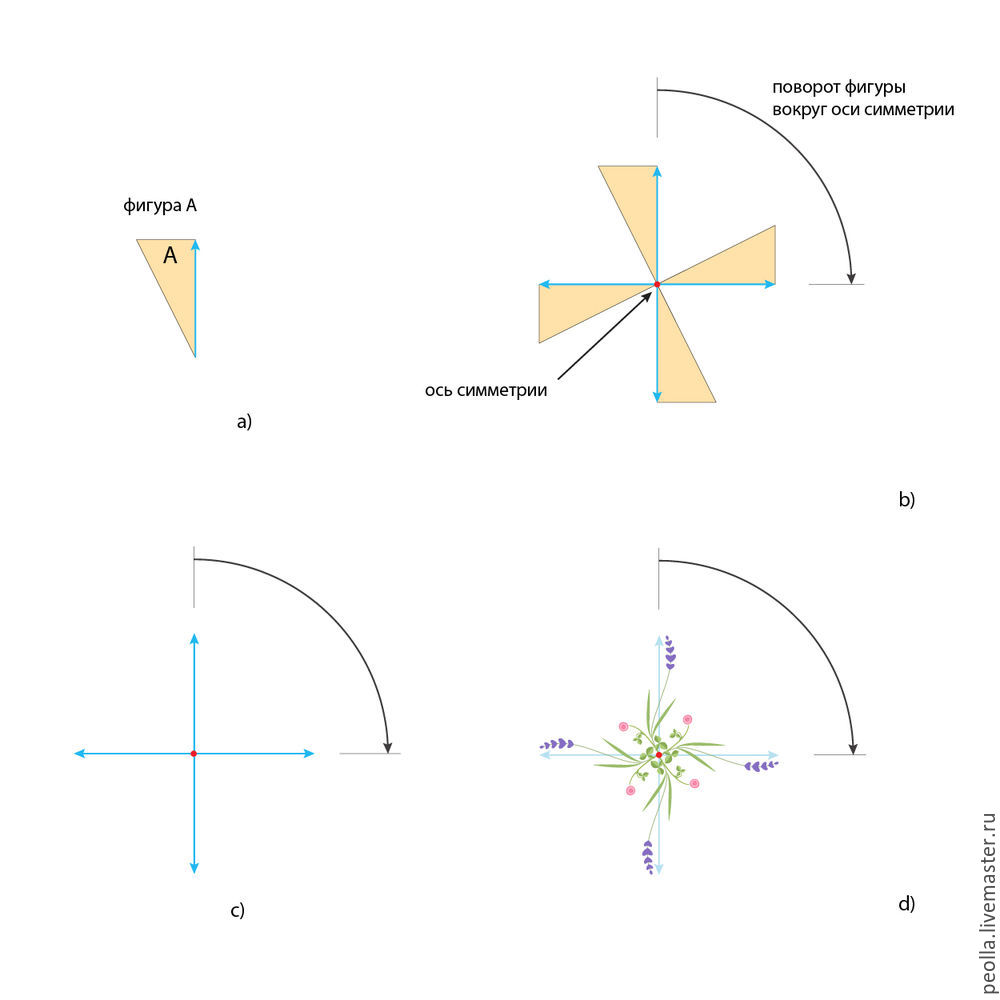
На следующем рисунке симметрия вращения рассмотрена на примере с треугольниками. Фигура А осуществляет поворот вокруг оси симметрии (красная точка). Угол поворота на этом примере равен 90°, соответственно за полный оборот вокруг оси симметрии фигура совместится сама с собой: 360° : 90° = 4 раза. На рис. с) вы видите общую схему данного преобразования. Заменив треугольники на цветочные мотивы, получим декоративную розетку (рис. d). Данный вид симметрии позволяет передать вращательное «движение» в композиции.

На рисунке ниже дан еще один пример симметрии вращения, но уже совмещенной с зеркальной симметрией. Первое преобразование — отражение фигуры А относительно вертикальной плоскости симметрии. Второе преобразование — вращение плоскости симметрии, фигуры А и ее отражения — фигуры А’ вокруг оси симметрии. Фигуры А и А’ теперь становятся единым мотивом. Как и в предыдущем примере, угол поворота равен 90°. Вообще, угол поворота может быть и другим, вы просто должны предварительно решить — сколько копий вашего мотива должно уместиться в одном полном обороте, затем разделить 360° на выбранное вами количество повторений мотива. Например, вы хотите разместить 3 мотива, расчет будет таким: 360° : 3 = 120°. Если же вы решили расположить ваш мотив 7 раз, то угол поворота должен быть: 360° : 7 = 51,43° . Скажем, не очень удобный результат, но, если у вас есть транспортир, то вы с этим справитесь. Для удобства, приведу здесь таблицу «целочисленного» деления окружности, т.е. определения угла поворота, выраженного в целых градусах.

Количество

мотивов

Угол

поворота, °

180

120

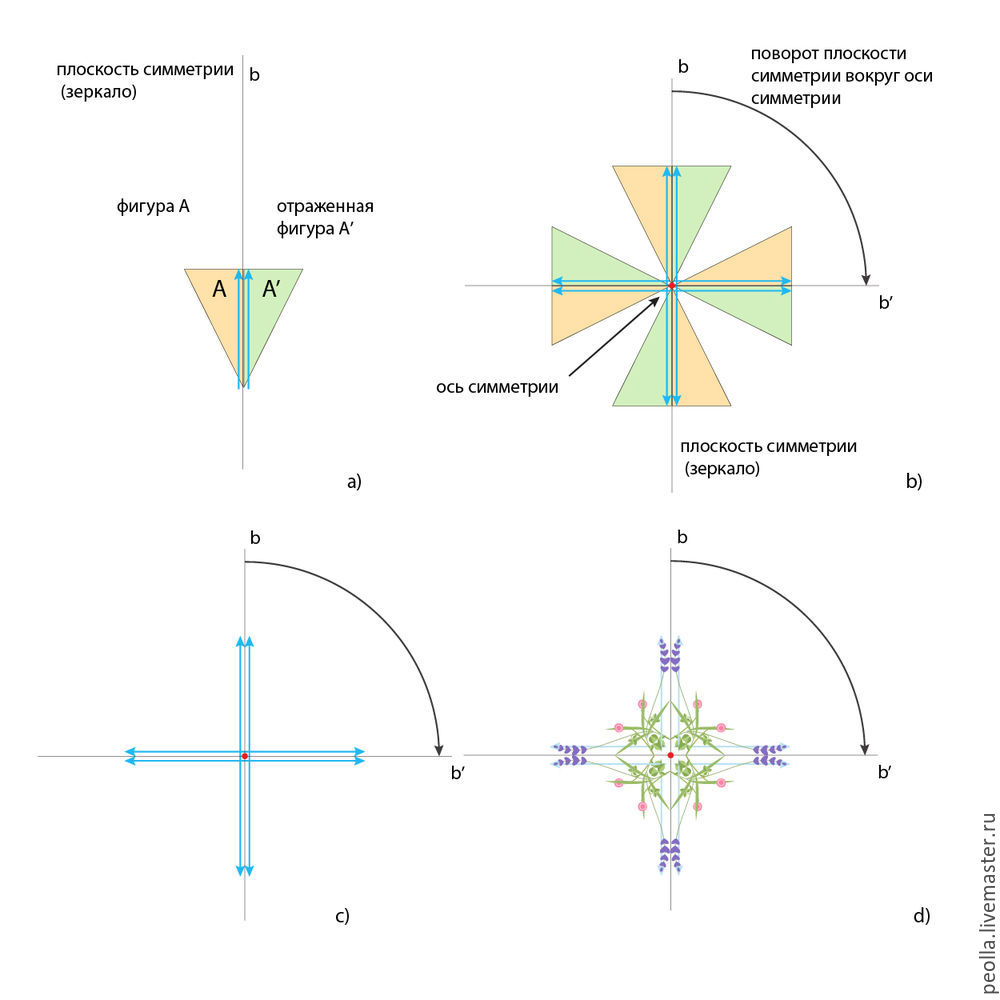
Ниже представлен еще один вариант использования симметрии вращения и симметрии отражения. Здесь мы расположили фигуру А под углом к плоскости симметрии, получив при этом немного иной вид конечного мотива (фигура А + фигура A’). На рис. с) дана общая схема симметрии. Заменив треугольники на цветочные мотивы, получаем декоративную розетку (рис. d). Отметим, что в этом примере был использован тот же цветочный мотив, что и в предыдущем, а результаты получились разными. Как и в случае с симметрией бордюров, мы можем легко изменять положение исходного мотива относительно плоскости симметрии — двигать его ближе или дальше, поворачивать разными сторонами к плосксти симметрии. В итоге этот метод дает бесчисленное множество вариантов симметричных розеток.

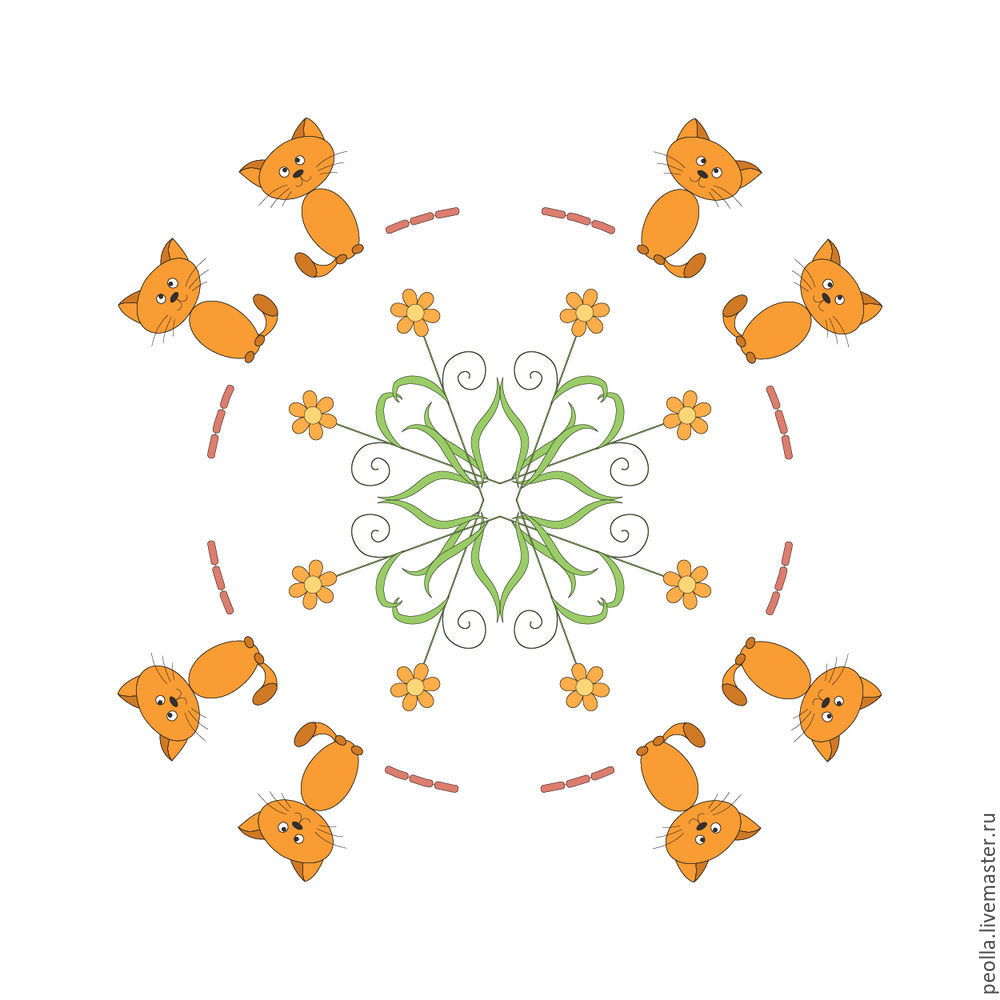
И наконец, изучив достаточно тщательно науку о симметрии котов, мы можем нарисовать великолепную картину под названием «Кошачье счастье». Таким же образом рисуются картины: «Цыплячья дружба», «Заячья радость» и др. Как видим, преобразования симметрии делают нас практически волшебниками и дают нам возможность из одного или нескольких мотивов создавать бесконечно разнообразные композиции, уравновешенные и гармоничные. Основываясь на изученных принципах вы можете придумывать также и намного более сложные конструкции, комбинируя виды симметрии и меняя мотивы.

Этот урок получился очень теоретическим. Спасибо всем, кто дошел до конца и прочитал все! В уроке №6 будет рассмотрена практическая часть — применение полученных знаний для создания декоративных композиций, будем рисовать диковинные узоры 🙂

Симметрия — Википедия

Равнобедренный треугольник с зеркальной симметрией. Пунктирная линия является осью симметрии

Рисунок бабочки с двусторонней симметрией

(др.-греч. συμμετρία = «соразмерность»; от συμ- «совместно» + μετρέω «мерю»), в широком смысле — соответствие, неизменность (инвариантность), проявляемые при каких-либо изменениях, преобразованиях (например: положения, энергии, информации, другого). Так, например, сферическая симметрия тела означает, что вид тела не изменится, если его вращать в пространстве на произвольные углы (сохраняя центр на месте и если поверхность тела однородна). Двусторонняя симметрия означает, что правая и левая сторона относительно какой-либо плоскости выглядят одинаково.

Симметрия — основополагающий принцип самоорганизации материальных форм в природе и формообразования в искусстве^[1]. Отсутствие или нарушение симметрии называется асимметрией или диссимметрией^[2].

Общие симметрийные свойства описываются с помощью теории групп.

Симметрии могут быть точными или приближёнными.

Два треугольника с точечной симметрией отражения в плоскости. Треугольник А’В’С может быть получен из треугольника ABC поворотом на 180 ° вокруг точки O.
Геометрическая симметрия — это наиболее известный тип симметрии для многих людей. Геометрический объект называется симметричным, если после того как он был преобразован геометрически, он сохраняет некоторые исходные свойства. Например, круг, повёрнутый вокруг своего центра, будет иметь ту же форму и размер, что и исходный круг. Поэтому круг называется симметричным относительно вращения (имеет осевую симметрию). Виды симметрий, возможных для геометрического объекта, зависят от множества доступных геометрических преобразований и того, какие свойства объекта должны оставаться неизменными после преобразования.
Виды геометрических симметрий:
Зеркальная симметрия[править | править код]
Зеркальная симметрия или отражение— движение евклидова пространства, множество неподвижных точек которого является гиперплоскостью (в случае трехмерного пространства — просто плоскостью). Термин зеркальная симметрия употребляется также для описания соответствующего типа симметрии объекта, то есть, когда объект при операции отражения переходит в себя. Это математическое понятие в оптике описывает соотношение объектов и их (мнимых) изображений при отражении в плоском зеркале. Проявляется во многих законах природы (в кристаллографии, химии, физике, биологии и т. д., а также в искусстве и искусствоведении).
Осевая симметрия[править | править код]
Фигура называется симметричной относительно прямой А, если для каждой точки фигуры симметричная ей точка относительно прямой А также принадлежит этой фигуре.
Вращательная симметрия[править | править код]
Вращательная симметрия — термин, означающий симметрию объекта относительно всех или некоторых собственных вращений m-мерного евклидова пространства. Собственными вращениями называются разновидности изометрии, сохраняющие ориентацию. Таким образом, группа симметрии, отвечающая вращениям, есть подгруппа группы E⁺(m) (см. Евклидова группа).
Трансляционная симметрия может рассматриваться как частный случай вращательной — вращение вокруг бесконечно-удалённой точки. При таком обобщении группа вращательной симметрии совпадает с полной E⁺(m). Такого рода симметрия неприменима к конечным объектам, поскольку делает всё пространство однородным, однако она используется в формулировке физических закономерностей.
Совокупность собственных вращений вокруг фиксированной точки пространства образуют специальную ортогональную группу SO(m) — группу ортогональных матриц m×m с определителем, равным 1. Для частного случая m = 3 группа носит специальное название — группа вращений.
В физике инвариантность относительно группы вращений называется изотропностью пространства (все направления в пространстве равноправны) и выражается в инвариантности физических законов, в частности, уравнений движения, относительно вращений. Теорема Нётер связывает эту инвариантность с наличием сохраняющейся величины (интеграла движения) — углового момента.
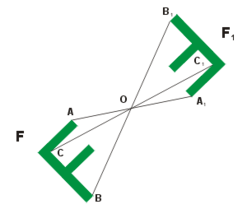Центральная симметрия
Симметрия относительно точки[править | править код]
Центра́льной симме́трией (иногда центра́льной инве́рсией) относительно точки A называют преобразование пространства, переводящее точку X в такую точку X′, что A — середина отрезка XX′. Центральная симметрия с центром в точке A обычно обозначается через ZA{\displaystyle Z_{A}}, в то время как обозначение SA{\displaystyle S_{A}} можно перепутать с осевой симметрией. Фигура называется симметричной относительно точки A, если для каждой точки фигуры симметричная ей точка относительно точки A также принадлежит этой фигуре. Точка A называется центром симметрии фигуры. Говорят также, что фигура обладает центральной симметрией. Другие названия этого преобразования — симметрия с центром A. Центральная симметрия в планиметрии является частным случаем поворота, точнее, является поворотом на 180 градусов.
Скользящая симметрия[править | править код]
Скользящая симметрия — изометрия евклидовой плоскости. Скользящей симметрией называют композицию симметрии относительно некоторой прямой l{\displaystyle l} и переноса на вектор, параллельный l{\displaystyle l} (этот вектор может быть и нулевым). Скользящую симметрию можно представить в виде композиции 3 осевых симметрий (теорема Шаля).
В теоретической физике поведение физической системы описывается некоторыми уравнениями. Если эти уравнения обладают какими-либо симметриями, то часто удаётся упростить их решение путём нахождения сохраняющихся величин (интегралов движения). Так, уже в классической механике формулируется теорема Нётер, которая каждому типу непрерывной симметрии сопоставляет сохраняющуюся величину. Из неё, например, следует, что инвариантность уравнений движения тела с течением времени приводит к закону сохранения энергии; инвариантность относительно сдвигов в пространстве — к закону сохранения импульса; инвариантность относительно вращений — к закону сохранения момента импульса.
Суперсимметрия[править | править код]
Суперсимме́трия или симме́трия Ферми́ — Бозе́ — гипотетическая симметрия, связывающая бозоны и фермионы в природе. Абстрактное преобразование суперсимметрии связывает бозонное и фермионное квантовые поля, так что они могут превращаться друг в друга. Образно можно сказать, что преобразование суперсимметрии может переводить вещество во взаимодействие (или в излучение), и наоборот.
По состоянию на начало 2009 года суперсимметрия является физической гипотезой, не подтверждённой экспериментально. Совершенно точно установлено, что наш мир не является суперсимметричным в смысле точной симметрии, так как в любой суперсимметричной модели фермионы и бозоны, связанные суперсимметричным преобразованием, должны обладать одинаковыми массой, зарядом и другими квантовыми числами (за исключением спина). Данное требование не выполняется для известных в природе частиц. Предполагается, тем не менее, что существует энергетический лимит, за пределами которого поля подчиняются суперсимметричным преобразованиям, а в рамках лимита — нет. В таком случае частицы-суперпартнёры обычных частиц оказываются очень тяжёлыми по сравнению с обычными частицами. Поиск суперпартнёров обычных частиц — одна из основных задач современной физики высоких энергий. Ожидается, что Большой адронный коллайдер^[3] сможет открыть и исследовать суперсимметричные частицы, если они существуют, или поставить под большое сомнение суперсимметричные теории, если ничего не будет обнаружено.
Трансляционная симметрия[править | править код]
Трансляционная симметрия — тип симметрии, при которой свойства рассматриваемой системы не изменяются при сдвиге на определённый вектор, который называется вектором трансляции. Например, однородная среда совмещается сама с собой при сдвиге на любой вектор, поэтому для неё свойственна трансляционная симметрия.
Трансляционная симметрия свойственна также для кристаллов. В этом случае векторы трансляции не произвольны, хотя их существует бесконечное число. Среди всех векторов трансляций кристаллической решётки можно выбрать 3 линейно независимых таким образом, что любой другой вектор трансляции был бы целочисленно-линейной комбинацией этих трёх векторов. Эти три вектора составляют базис кристаллической решётки.
Теория групп показывает, что трансляционная симметрия в кристаллах совместима только с поворотами на углы θ=2π/n, где n может принимать значения 1, 2, 3, 4, 6.
При повороте на углы 180, 120, 90, 60 градусов положение атомов в кристалле не меняется. Говорят, что кристаллы имеют ось вращения n-го порядка.^{[уточнить]}
Перенос в плоском четырёхмерном пространстве-времени не меняет физических законов. В теории поля трансляционная симметрии, согласно теореме Нётер, соответствует сохранению тензора энергии-импульса. В частности, чисто временные трансляции соответствуют закону сохранения энергии, а чисто пространственные сдвиги — закону сохранения импульса.
Сложные узоры на крыльях бабочки являются одним из примеров двусторонней симметрии
Симметрия в биологии — это закономерное расположение подобных (одинаковых, равных по размеру) частей тела или форм живого организма, совокупности живых организмов относительно центра или оси симметрии. Тип симметрии определяет не только общее строение тела, но и возможность развития систем органов животного. Строение тела многих многоклеточных организмов отражает определённые формы симметрии. Если тело животного можно мысленно разделить на две половины, правую и левую, то такую форму симметрии называют билатеральной. Этот тип симметрии свойственен подавляющему большинству видов, а также человеку. Если тело животного можно мысленно разделить не одной, а несколькими плоскостями симметрии на равные части, то такое животное называют радиально-симметричным. Этот тип симметрии встречается значительно реже.
Асимметрия — отсутствие симметрии. Иногда этот термин используется для описания организмов, лишённых симметрии первично, в противоположность диссимметрии — вторичной утрате симметрии или отдельных её элементов.
Понятия симметрии и асимметрии обратны. Чем более симметричен организм, тем менее он асимметричен и наоборот. Небольшое количество организмов полностью асимметричны. При этом следует различать изменчивость формы (например у амёбы) от отсутствия симметрии. В природе и, в частности, в живой природе симметрия не абсолютна и всегда содержит некоторую степень асимметрии. Например, симметричные листья растений при сложении пополам в точности не совпадают.
У биологических объектов встречаются следующие типы симметрии:
Радиальная симметрия[править | править код]
В биологии о радиальной симметрии говорят, когда через трёхмерное существо проходят одна или более осей симметрии. При этом радиальносимметричные животные могут и не иметь плоскостей симметрии. Так, у сифонофоры Velella имеется ось симметрии второго порядка и нет плоскостей симметрии^[4]
Обычно через ось симметрии проходят две или более плоскости симметрии. Эти плоскости пересекаются по прямой — оси симметрии. Если животное будет вращаться вокруг этой оси на определённый градус, то оно будет отображаться само на себе (совпадать само с собой). Таких осей симметрии может быть несколько (полиаксонная симметрия) или одна (монаксонная симметрия). Полиаксонная симметрия распространена среди протистов (например, радиолярий).
Как правило, у многоклеточных животных два конца (полюса) единственной оси симметрии неравноценны (например, у медуз на одном полюсе (оральном) находится рот, а на противоположном (аборальном) — верхушка колокола. Такая симметрия (вариант радиальной симметрии) в сравнительной анатомии называется одноосно-гетеропольной. В двухмерной проекции радиальная симметрия может сохраняться, если ось симметрии направлена перпендикулярно к проекционной плоскости. Иными словами, сохранение радиальной симметрии зависит от угла наблюдения.
Радиальная симметрия характерна для многих стрекающих, а также для большинства иглокожих. Среди них встречается так называемая пентасимметрия, базирующаяся на пяти плоскостях симметрии. У иглокожих радиальная симметрия вторична: их личинки двустороннесимметричны, а у взрослых животных наружная радиальная симметрия нарушается наличием мадрепоровой пластинки.
Кроме типичной радиальной симметрии существует двулучевая радиальная симметрия (две плоскости симметрии, к примеру, у гребневиков). Если плоскость симметрии только одна, то симметрия билатеральная (такую симметрию имеют животные из группы Bilateria).
У цветковых растений часто встречаются радиальносимметричные цветки: 3 плоскости симметрии (водокрас лягушачий), 4 плоскости симметрии (лапчатка прямая), 5 плоскостей симметрии (колокольчик), 6 плоскостей симметрии (безвременник). Цветки с радиальной симметрией называются актиноморфные, цветки с билатеральной симметрией — зигоморфные.
Билатеральная симметрия[править | править код]
Билатера́льная симме́трия (двусторонняя симметрия) — симметрия зеркального отражения, при которой объект имеет одну плоскость симметрии, относительно которой две его половины зеркально симметричны. Если на плоскость симметрии опустить перпендикуляр из точки A и затем из точки О на плоскости симметрии продолжить его на длину AО, то он попадёт в точку A₁, во всём подобную точке A. Ось симметрии у билатерально симметричных объектов отсутствует. У животных билатеральная симметрия проявляется в схожести или почти полной идентичности левой и правой половин тела. При этом всегда существуют случайные отклонения от симметрии (например, различия в папиллярных линиях, ветвлении сосудов и расположении родинок на правой и левой руках человека). Часто существуют небольшие, но закономерные различия во внешнем строении (например, более развитая мускулатура правой руки у праворуких людей) и более существенные различия между правой и левой половиной тела в расположении внутренних органов. Например, сердце у млекопитающих обычно размещено несимметрично, со смещением влево.
У животных появление билатеральной симметрии в эволюции связано с ползанием по субстрату (по дну водоема), в связи с чем появляются спинная и брюшная, а также правая и левая половины тела. В целом среди животных билатеральная симметрия более выражена у активно подвижных форм, чем у сидячих.
Билатеральная симметрия свойственна всем достаточно высокоорганизованным животным, кроме иглокожих. В других царствах живых организмов билатеральная симметрия свойственна меньшему числу форм. Среди протистов она характерна для дипломонад (например, лямблий), некоторых форм трипаносом, бодонид, раковинок многих фораминифер. У растений билатеральную симметрию имеет обычно не весь организм, а его отдельные части — листья или цветки. Билатерально симметричные цветки ботаники называют зигоморфными.
Симметрия важна для химии, так как она объясняет наблюдения в спектроскопии, квантовой химии и кристаллографии.
Кристаллографическая точечная группа симметрии — это точечная группа симметрии, которая описывает макросимметрию кристалла. Поскольку в кристаллах допустимы оси (поворотные и несобственного вращения) только 1, 2, 3, 4 и 6 порядков, из всего бесконечного числа точечных групп симметрии только 32 относятся к кристаллографическим.
Анизотропия (от др.-греч. ἄνισος — неравный и τρόπος — направление) — различие свойств среды (например, физических: упругости, электропроводности, теплопроводности, показателя преломления, скорости звука или света и др.) в различных направлениях внутри этой среды; в противоположность изотропии. Причиной анизотропности кристаллов является то, что при упорядоченном расположении атомов, молекул или ионов силы взаимодействия между ними и межатомные расстояния (а также некоторые не связанные с ними прямо величины, например, поляризуемость или электропроводность) оказываются неодинаковыми по различным направлениям. Причиной анизотропии молекулярного кристалла может быть также асимметрия его молекул. Макроскопически эта неодинаковость проявляется, как правило, лишь если кристаллическая структура не слишком симметрична.

Предполагается, что тенденция людей видеть цель в симметрии, является одной из причин, почему симметрия часто является неотъемлемой частью символов мировых религий. Вот лишь некоторые из многих примеров, изображённые на рисунке справа.
Люди наблюдают симметричную природу (также включающую асимметричный баланс) социального взаимодействия в различных контекстах. Они включают оценки взаимности, эмпатии, извинения, диалога, уважения, справедливости и мести. Симметричные взаимодействия посылают сигналы «мы одинаковые», а асимметричные взаимодействия выражают мысль «я особый, лучше, чем ты». Взаимоотношения со сверстниками строятся на основе симметрии, а властные отношения — на асимметрии^[5].
Типы симметрий, встречающиеся в математике и в естественных науках:

Краб-скрипач, Uca pugnax

Камбала
Асимметрией (др.-греч. ασυμμετρία «несоразмерность» от μετρέω «измеряю») можно считать любое нарушение симметрии. Чаще всего термин употребляется в отношении зрительных объектов и в изобразительном искусстве. В художественном творчестве асимметрия может выступать (и очень часто выступает) в качестве одного из основных средств формообразования (или композиции). Одно из близких понятий в искусстве — аритмия.
В связи с постоянным делением клеток в организме асимметрия в организмах является обычным явлением по крайней мере в одном измерении наравне с биологической симметрией (также см. Межполушарная асимметрия). Луи Пастер полагал, что биологические молекулы асимметричны из-за космических [то есть физических] сил, которые осуществляют контроль над их формированием, закладывая свойства (асимметричность), аналогичные своим. Хоть и в его время, и даже сейчас, симметрии в физических процессах придаётся большее значение, так же известны фундаментальные физические асимметрии, начиная с времени.
Существует понятие «преобладающая рука», означающее асимметрию в развитии навыков людей и животных. Тренировка нервных путей во время обучения навыку с одной рукой (лапой) занимает меньше времени, чем та же тренировка с двумя.^[6]
Понятие асимметрии существует также в физике (Барионная асимметрия Вселенной, Омическая асимметрия, Ёмкостная асимметрия), математике (Коэффициент асимметрии, Асимметричное отношение, Асимметрический атом, Асимметричная криптография) архитектуре и т. д.
Урманцев Ю. А. Симметрия природы и природа симметрии. — М., Мысль, 1974.
Вигнер Е. Этюды о симметрии. — М., Мир, 1971. — 320 с.
Нокс Р., Голд А. Симметрия в твердом теле. — М., Наука, 1970. — 424 с.
Шубников А. В., Копцик В. А. Симметрия в науке и искусстве. — М., Наука, 1972. — 340 с.
Вернадский В. И. Химическое строение биосферы Земли и её окружения. — М., Наука, 1965. — 373 с.
Болтянский В. Г., Виленкин Н. Я. Симметрия в алгебре. — М., Наука, 1967. — 284 с.
Под ред. Сенешаль М., Флека Дж. Узоры симметрии. — М., Мир, 1980. — 269 с.
Ю. К. Егоров-Тисменко, Г. П. Литвинская Теория симметрии кристаллов, ГЕОС, 2000.
П. М. Зоркий Симметрия молекул и кристаллических структур, МГУ, 1986.
А. В. Шубников Симметрия и антисимметрия конечных фигур, Изд-во АН СССР, 1951
И. Харгиттаи, М. Харгиттаи Симметрия глазами химика. — М., Мир, 1989. — 494 с.
ОСНОВЫ КОМПОЗИЦИИ: Равновесие (симметрия и асимметрия)
04 Мая 2016
Из первой части статьи мы знаем что такое равновесие в фотографии и что оно является одним из наиболее важных элементов композиции. Размеры, характер и расположение в пространстве элементов композиции должны быть подчинены зрительному равновесию. Но вот как сбалансировать изображение, какие есть способы — рассмотрим в этой статье.
СИММЕТРИЯ
Симметрия — это наиболее очевидный и простой способ достичь композиционного равновесия. Симметрия прослеживается во всем: в природе, в строении человеческого тела, в предметах повседневной жизни.
Не все уравновешенные или сбалансированные фотографии симметричны – все симметричные композиции по умолчанию находятся в равновесии.
Фото: Robert Biondo
Симметричное равновесие на фотографии достигается тогда, когда объекты с одинаковым визуальным весом будут размещены равноудалённо от центра изображения. Но, создавая такую композицию, необходимо учитывать, что нарушить равновесие может даже небольшой элемент, присутствующий на одной из частей композиции, но отсутствующий на другой. Композиция уже не будет восприниматься симметричной — появится дисбаланс и визуальное напряжение. Происходит это от того, что при восприятии симметрии наш мозг устанавливает определённый ритм объектов и интервалов между ними, предполагает наличие определённой последовательности и интервала. А если этого не происходит — испытывает беспокойство.
Фото: Bramham
В фотографии наиболее часто используются три вида симметрии:
Зеркальная (двусторонняя). Как уже понятно из названия, в основе лежит равенство двух частей композиции, которые расположены по разные стороны центральной оси снимка и являются практически зеркальными отражениями друг друга. Ориентация оси может быть как вертикальная, так и горизонтальная. Симметрию называют чистой, если две половины композиции отражают друг друга абсолютно точно. Но в природе такое встречается достаточно редко, ведь ни для кого не секрет, что даже человеческое тело не полностью симметрично. В большинстве случаев мы имеем дело с неполной симметрией — когда отражения не полностью идентичны и имеют незначительные отличия.

Фото: Hesham Alhumaid

Фото: Stefan Krebs

Фото: Bildwerker Freidburg

Фото: Davor Plesa
Радиальная (лучевая или круговая). В её основе лежит равное удаление всех элементов композиции относительно центральной точки (или общего центра). Количество объектов, как и угол их расположения относительно центра, могут быть различны. Главное понимать, что пока есть некий общий центр — симметрия сохраняется.

Фото: Victor Mozqueda

Фото: Markus Studtmann
Трансляционная (кристаллографическая). Это вид симметрии, в которой элементы композиции повторяются через определенные промежутки. Как пример — колонны или окна здания. В трансляционной симметрии ключевую роль играет совпадение направления элементов. С помощи такой симметрии можно создать ритм, движение, показать скорость или очень динамичное действие.

Фото: Hans Wolfgang Hawerkamp

Фото: Massimo Cuomo
АСИММЕТРИЯ
Асимметрия — это отсутствие или нарушение симметрии. Но это вовсе не значит, что асимметрия – это отсутствие равновесия композиции.
Асимметричное равновесие достигается тогда, когда элементы композиции, находящиеся по разные стороны от центра, имеют одинаковую визуальную массу. Достичь равновесия при помощи асимметрии сложнее, чем в симметричной композиции, так как между композиционными элементами более сложные пространственные отношения. Асимметричное равновесие более динамичное и интересное для привлечения внимания, чем симметричное.
Фото: Josef Sieberer

Фото: Uros Podlogar
Фото: Ute Scherhag
С его помощью можно дать ощущение движения, жизни и энергии. И если симметричная композиция воспринимается «как есть» — легко и сразу, то асимметричную нужно «читать» постепенно. Асимметричное равновесие сложнее построить, но у него есть огромное преимущество — оно оставляет нам большой простор для творчества.
Применяя знания на практике, вы можете совмещать симметрию с асимметрией и добиваться прекрасных результатов и привлекать больше внимания. Вот несколько примеров:
композиция приближается к абсолютной или чистой симметрии:

Фото: Stefan Neuweger
Фото: C.S. Tjandra
Фото: Karthi KN Raveendiran
симметричное равновесие асимметричных форм:

Фото: Jozef Kiss
Фото: Christian Muller
Фото: Ute Scherhag
Фото: Suzy Mead
асимметричная в целом композиция состоит из симметричных частей:

Фото: Ali Ayer

Фото: Jacqueline Hammer
Фото: Jacqueline Hammer

Фото: Plosz Zoltan
композиция может быть и в целом, и в деталях полностью асимметрична:

Фото: E. Amer

Фото: Piet Haaksma

Фото: Vedran Vidak
Фото: Knut Borge Strom
Сталкивая симметрию с асимметрией, необходимо помнить, что:
визуальная масса симметричной фигуры будет больше, чем масса асимметричной фигуры подобного размера и формы;

симметрия создаёт баланс сама по себе и, как правило, считается красивой и гармоничной. Но есть и обратная сторона медали — она зачастую лишена динамики и может показаться статичной и скучной;

асимметрия, как антипод статичной симметрии, обычно привносит в композицию динамику.

Симметрия и асимметрия окружают нас каждое мгновение в повседневной жизни, понятие данных терминов позволяет более осознанно и гармонично наблюдать за красотой окружающего мира и позволяет создавать неповторимые фотографии!
Читайте ещё о композиции в других наших статьях:
Золотое сечение в фотографии
Сила линий в фотографии
Формат кадра в фотографии
Контраст в фотографии (Часть 1)
Контраст в фотографии (Часть 2)
Точка съемки и выбор плана
Ракурс
Геометрия в фотографии
Понятие симметрии для дошкольников
Значение сформированности у ребёнка понятия симметрии на пороге школы велико. Симметрия – одно из основных понятий в математике, письме и чтении. Словом везде, где мы сталкиваемся с пространственным мышлением:
в математике это геометрия, стереометрия, работа в системе координат;

в химии – строение химических веществ;

сюда же черчение и физика.

Существует не один вид симметрии, не будем на них останавливаться. В дошкольном детстве важнее всего освоить зеркальную симметрию, в животном мире называющуюся билатеральной.
У большинства детей понятие симметрии формировалось и формируется стихийно через рисование, конструирование, лепку и прочую ручную деятельность.
Проблема в том, что ручная деятельность в детсадовской программе сокращена значительно. Поэтому понятие симметрии надо формировать специально. Как это делать?
Как формировать понятие симметрии у дошкольников?
Ориентировка в пределах собственного тела, начиная с раннего возраста.
Подготовишкам полезно чётко знать, что у каждого человека есть середина тела и правая и левая часть тела. Вот про эту середину, которая есть линия симметрии, взрослые чаще всего и забывают. Главное: правая/левая рука. А должна быть полная картина.
Складывание листа бумаги
Во второй младшей группе учите сгибать лист бумаги пополам, так, чтобы уголки совпадали. Не погружаясь в пространные разъяснения, стоит обратить внимание на линию сгиба и показать малышу, что части листа одинаковые. Кстати, не все старшие ребята делаю это правильно.
Вырезание симметричных фигурок.
В средней группе ребёнок способен вырезать фигурку из сложенного пополам листа.
Возьмите небольшой прямоугольный лист бумаги, примерно 14*7 см, чтобы он удобно удерживался в руке малыша. Согните пополам.

Нарисуйте половинку предмета. Предмет нужен простой. Мы берём ёлочку.

Держа бумагу за сгиб, вырезайте её по линиям.

Разворачивание вырезанной фигурки приводит детей в восторг. Можно взять не ёлку, а что попроще, шарик, к примеру. Подготовишки вырезают целые гирлянды ёлок, человечков, держащихся за руки, и прочее.

Взрослые часто возражают: сложно для четырёхлетки. Отвечу так. Если ничему не учить, сложно будет до пенсии. Конечно, если ребёнок ножницы в руках держать не умеет, то сперва этому надо научить. Научить просто резать, разрезать, а уж потом вырезать.
Надо всегда помнить, что ребёнку полезно работать в зоне ближайшего развития. Зона ближайшего развития – это то, что он сам ещё сделать не может, но с помощью взрослого – вполне. Расскажите, покажите, похвалите… Видите – освоил действие, легко справляется, дайте задание немножко посложнее.
Дорисовывание предметов.
Начиная со средней группы, ребята способны дорисовать часть предмета по контурным линиям.
Усложнение.
дорисовать предмет без контурных линий.

сам предмет потихоньку усложняется добавлением деталей.

рисование двумя руками одновременно (зеркальное рисование).

Рисование по клеточками.
Выбираете симметричную фигурку. Мы берём робота. По вашей инструкции ребята рисуют половину робота. Вторую половину предложите им дорисовать самостоятельно.

К выпуску подготовишкам полезно освоить понятие симметрии на интуитивном уровне через деятельность.
Ребёнок не усвоил понятие симметрии?
Как узнать, что симметрия не «дошла» по назначению? Проведите простой тест. Берём рисунок (ниже), распечатанный на А4, другим листом, размером А5, закрываем его половину. Закрепляем скрепкой или «прихватываем» клеем.

Квадратное зеркальце (без рамки) ставим на край закрывающего листа. Детально рассматриваем с ребёнком всё, отражающееся в зеркальце.

Задание. Нарисуй на чистом листе за зеркалом всё, что ты увидел в зеркале.
Возможные варианты на рисунке ниже. Из них только один, самый нижний, показывает, что понятие симметрии у ребёнка сформировано.

Если он с заданием не справился, то надо поработать. Упражнения проводим с помощью того же зеркала до полного усвоения понятия симметрии. Советуем для упражнений сперва брать отдельные, достаточно простые фигурки, которые ребёнку будет несложно воспроизвести.
Может быть, вам придётся не один раз показать ему, как вы рисуете симметричные рисунки, потом сделать это вместе, и только потом предложить самостоятельную работу. Наберитесь терпения, и вперёд за хорошей успеваемостью. Сайт Нестандартные дети желает успехов!
Правила композиции в фотографии: симметрия
Симметрия – это мощный прием композиции, при помощи которого создаются и гармонизируются произведения искусства: архитектуры, дизайна, живописи, графики, фотографии. Но этот прием не придуман человеком, он подсмотрен у природы. Тело человека, цветок, снежинка – это все примеры симметрии в природе.

Проще всего симметрию в фотографии описать так: если вы сложите идеально симметричную фотографию пополам вдоль линии симметрии, у вас получится две идентичные фотографии.

Но симметричная композиция не предусматривает идеального совпадения элементов обеих половинок изображения. Взгляд зрителя может быстро устать от однообразия, поэтому несовершенность симметрии дает взгляду зацепиться и отдохнуть. Сознательное нарушение симметрии также может привлекать взгляд к изображению, автоматически делать его более интересным.

Типы симметрии

Есть три основных типа симметрии, которые вы видите вокруг себя каждый день.

1. Вертикальная симметрия

Здания, сооружения и дороги являются хорошими объектами для симметричных изображений. Если дорога находится в центре композиции, линия посередине уже разделяет изображение на две части.

Колонны также являются отличным примером вертикальной симметрии.

Если вы фотографируете архитектуру, симметрия в композиции – достаточно очевидный прием. Но когда вы фотографируете людей, это может быть сложнее. Например, знаменитый фотограф Родни Смит использовал симметрию как основной художественный прием своих работ.

В крупноплановых портретах найти симметрию не составит проблемы.

Также симметричная композиция часто используется при съемке людей, вписанных в окружающую среду.

Даже гости на свадьбе у входа в храм располагаются так, чтобы жених и невеста оказывались в центре симметрии, когда друзья и родственники будут кидать конфетти или лепестки роз. И неидеально симметричные ряды гостей вносят в изображение некую небрежность, отчего фотография выглядит еще интереснее.

Симметричным является снимок молодоженов у алтаря от входа в храм с рядами скамей с гостями. Это также приводит зрителя к точке фокусировки, жениху и невесте в центре изображения.

Кстати, вертикальную симметрию создают также отображения в витринах, зеркалах и стеклянных зданиях.

2. Горизонтальная симметрия

Отражения в воде являются отличным примером горизонтальной симметрии.

При использовании отражений в воде очень легко сочетать симметрию с правилом третей. Если ваш главный объект находится в пересечении линий сетки по правилу третей, а сцена отражается в воде, вы естественным образом объедините эти два правила в одном кадре.

3. Радиальная симметрия

Такие изображения, как спицы на велосипедном колесе, лепестки на ромашке или круги на воде, имеют радиальную симметрию.

Узоры листьев и лепестков создают радиальную симметрию у растений. Но иногда даже фото архитектуры или людей могут иметь радиальную симметрию.

Симметрия в композиции достигается, когда две половины изображения имеют одинаковый вес. Однако симметрия не обязательно должна быть буквальной. Эффект также может быть достигнут, когда различные элементы используются, чтобы казаться симметричными.

Как используют симметрию фотографы, которые преподают в нашей фотошколе?

Этот прием часто используют наши преподаватели в своих коммерческих и творческих съемках:

Фото: Денис Бондарев

Фото: Иван Малигон

Фото: Иван Малигон

Фото: Иван Малигон

Фото: Сергей Аринохин

Фото: Сергей Аринохин

Фото: Виталий Шохан

Фото: Виталий Шохан

Фото: Виталий Шохан

Фото: Виталий Шохан

Фото: Виталий Шохан

Фото: Виталий Шохан

Фото: Виталий Шохан

Фото: Наталья Прядко

Фото: Наталья Прядко

Фото: Наталия Никитик

Фото: Ольга Павловская

Фото: Наталия Никитик

Фото: Александр Меклер

Фото: Александр Меклер

Фото: Александр Меклер

Фото: Александр Меклер

Фото: Александр Меклер

Фото: Виталий Шохан

На доске в пинтерест мы собрали 350 фото с симметрией в основе композиции. Вдохновляйтесь и подписывайтесь на нас!

Все фото, использованные в материале (кроме фотографий наших преподавателей), взяты из интернета и несут чисто иллюстративный характер.
Поделиться в социальных сетях
Вконтакте
Facebook
Twitter
3114