Рисунки треугольниками: D1 82 d1 80 d0 b5 d1 83 d0 b3 d0 be d0 bb d1 8c d0 bd d0 b8 d0 ba d0 b8 d0 b6 d0 b8 d0 b2 d0 be d1 82 d0 bd d1 8b d0 b5: стоковые векторные изображения, иллюстрации

Портрет из треугольников или низкополигональный рисунок

Решила я разнообразить свои аватарки в ВК и добавить новое фото, что-нибудь нарисовав. Думала-думала и пришли на ум полигоны.

В сети гуляет множество рисунков с треугольниками: цветные и чёрно-белые, несложные и замысловатые, есть даже потрясающие эскизы низкополигональных татуировок. Но как же сделать подобное фото, и в какой программе?

Для меня проще всего это было сделать во флэше. Открываем программу Macromedia Flash Professional. Создаём новый документ, кидаем в него нужное фото.
Лучше выбрать фотографию с минимумом деталей и цветов, ведь множество мелочей на фото вы устанетесь превращать в треугольники, да и изображение в итоге должно быть легкоугадываемое, а не «рябь на картинке», по которой невозможно узнать, кто или что там на рисунке.

Я масштабирую на 400% изображение, и оно становится размытым. Не беда, ведь треугольники мы нарисуем в векторе. Готовую иллюстрацию можно будет уменьшать и увеличивать как угодно, она не потеряет качества.

Теперь создадим новый слой (сверху слева на фото, где написано Layer 1, и на новом слое начнем инструментом Line Tool (N) рисовать треугольники, соединяя их друг с другом.
Затем нужно их залить заливкой Paint Bucket Tool (K), взяв пипеткой преобладающий в данном треугольнике цвет прямо с изображения (фото).

Получается примерно так:

Когда вы обрисуете нужную вам часть, треугольники нарисованные инструментом Line Tool, можно удалить все разом, фото тоже следует удалить. Останутся лишь полигоны:

Такое готовое низкополигональное изображение можно трансформировать как угодно — бесконечно увеличивать или уменьшать, качества оно не потеряет.

Также есть способ сделать подобную картинку в Фотошопе. Подробно вы можете изучить кучу видео по теме размещённых на youtube, благо их там тьма.

Но кратенько я расскажу. Открываем Фотошоп, оздаем новый документ, на него новым слоем добавляем нужное вам фото. Можете сделать копию слоя с фото на всякий случай, но я прямо по фото начинаю рисовать полигоны — треугольники.

На видео советуют сделать сетку и много чего еще, но проще всего рисовать магнитным лассо прямо по фото. Выбираем какую-то деталь на фото и начинаем рисовать треугольники, примерно ориентируясь на форму или цвет изображения:

Рисуем магнитным лассо 2 стороны треугольника и кликаем 2 раза, третья сторона автоматически добавляется сама.

Теперь заливаем тругольник цветом, который является усреднённым в этом полигоне: Filter-Blur-Average. В следующий раз — просто команда ctrl+F повторит этот фильтр.

Рисуем несколько таких треугольников, сразу же заливая их средним цветом. Вот, что получается:

Обведя так нужное пространство, остальное — ненужное, обводим магнитным лассо и заливаем белой заливкой (как вариант).

Вот и всё!

Рисунок из трех треугольников

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

Рис. 1. Иллюстрация к примеру

Мы видим, что фигуры № 1, 2, 3, 5 – четырехугольники. Каждая из них имеет свое название (рис. 2).

Рис. 2. Четырехугольники

Значит, «лишней» фигурой является треугольник (рис. 3).

Рис. 3. Иллюстрация к примеру

Треугольником называется фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех отрезков, попарно соединяющих эти точки.

Точки называются вершинами треугольника, отрезки – его сторонами. Стороны треугольника образуют в вершинах треугольника три угла.

Знакомство с основными свойствами треугольника

Основными признаками треугольника являются три стороны и три угла. По величине угла треугольники бывают остроугольные, прямоугольные и тупоугольные.

Знакомство с видами треугольников по величине угла

Треугольник называется остроугольным, если все три угла его острые, то есть меньше 90° (рис. 4).

Рис. 4. Остроугольный треугольник

Треугольник называется прямоугольным, если один из его углов равен 90° (рис. 5).

Рис. 5. Прямоугольный треугольник

Треугольник называется тупоугольным, если один из его углов тупой, то есть больше 90° (рис. 6).

Рис. 6. Тупоугольный треугольник

Знакомство с видами по числу равных сторон

По числу равных сторон треугольники бывают равносторонние, равнобедренные, разносторонние.

Равнобедренным называется треугольник, у которого две стороны равны (рис. 7).

Рис. 7. Равнобедренный треугольник

Эти стороны называются боковыми, третья сторона – основанием. В равнобедренном треугольнике углы при основании равны.

Равнобедренные треугольники бывают остроугольными и тупоугольными (рис. 8).

Рис. 8. Остроугольный и тупоугольный равнобедренные треугольники

Равносторонним называется треугольник, у которого все три стороны равны (рис.

9).

Рис. 9. Равносторонний треугольник

В равностороннем треугольнике все углы равны. Равносторонние треугольники всегда остроугольные.

Разносторонним называется треугольник, у которого все три стороны имеют разную длину (рис. 10).

Рис. 10. Разносторонний треугольник

Выполнение тренировочных упражнений, деление на группы

Выполните задание. Распределите данные треугольники на три группы (рис. 11).

Рис. 11. Иллюстрация к заданию

Сначала распределим по величине углов.

Остроугольные треугольники: № 1, № 3.

Прямоугольные треугольники: № 2, № 6.

Тупоугольные треугольники: № 4, № 5.

Эти же треугольники распределим на группы по числу равных сторон.

Разносторонние треугольники: № 4, № 6.

Равнобедренные треугольники: № 2, № 3, № 5.

Равносторонний треугольник: № 1.

Решение геометрической задачи

Подумайте, из какого куска проволоки сделали каждый треугольник (рис. 12).

Рис. 12. Иллюстрация к заданию

Можно рассуждать так.

Первый кусок проволоки разделен на три равные части, поэтому из него можно сделать равносторонний треугольник. На рисунке он изображен третьим.

Второй кусок проволоки разделен на три разные части, поэтому из него можно сделать разносторонний треугольник. На рисунке он изображен первым.

Третий кусок проволоки разделен на три части, где две части имеют одинаковую длину, значит, из него можно сделать равнобедренный треугольник. На рисунке он изображен вторым.

Сегодня на уроке мы познакомились с различными видами треугольников.

Список литературы

1. М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 1. – М.: «Просвещение», 2012.
2. М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 2. – М.: «Просвещение», 2012.
3. М.И. Моро. Уроки математики: Методические рекомендации для учителя. 3 класс. – М.: Просвещение, 2012.
4. Нормативно-правовой документ. Контроль и оценка результатов обучения. – М.: «Просвещение», 2011.
5. «Школа России»: Программы для начальной школы. – М.: «Просвещение», 2011.
6. С.И. Волкова. Математика: Проверочные работы. 3 класс. – М.: Просвещение, 2012.
7. В.Н. Рудницкая. Тесты. – М.: «Экзамен», 2012.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

Домашнее задание

1. Закончите фразы.

а) Треугольником называется фигура, которая состоит из …, не лежащих на одной прямой, и …, попарно соединяющих эти точки.

б) Точки называются …, отрезки – его …. Стороны треугольника образуют в вершинах треугольника ….

в) По величине угла треугольники бывают … , … , … .

г) По числу равных сторон треугольники бывают … , … , … .

а) прямоугольный треугольник;

б) остроугольный треугольник;

в) тупоугольный треугольник;

г) равносторонний треугольник;

д) разносторонний треугольник;

е) равнобедренный треугольник.

3. Составьте задание по теме урока для своих товарищей.

Если вы нашли ошибку или неработающую ссылку, пожалуйста, сообщите нам – сделайте свой вклад в развитие проекта.

Главное нужно указать файл картинки на вашем компьютере или телефоне, нажать кнопку ОК. Остальные настройки выставлены по умолчанию.

Пример фотографии розы без изменений и сделанная на этом сайте картинка из треугольников:

Обратите внимание, что обработка длится около 1 минуты, на выходе получается картинка из треугольников не более 0.5 мегапикселей, примерно 800×600 и этого размера хватит с запасом, например, чтобы выложить на сайте vk.com. Если нужна картинка из треугольников без уменьшения, то присылайте на контактный ящик фото или картинку, которую нужно обработать и выставленные настройки (если они изменялись) — будет сделано бесплатно в течение суток.

Ещё картинку можно сделать из: квадратов | треугольников | кругов | звёзд

Исходное изображение никак не изменяется. Вам будет предоставлена другая обработанная картинка.

Веселые и красочные задания для детей «Рисунки из геометрических фигур» являются очень удобным обучающим материалом для детей дошкольного и младшего школьного возраста по изучению и запоминанию основных геометрических форм: треугольника, круга, овала, квадрата, прямоугольника и трапеции. Все задания предназначены для самостоятельной работы ребенка под наблюдением взрослых. Родитель или педагог должны правильно объяснить ребенку, что он должен сделать в каждом задании.

Также вам может понравиться наш онлайн тренажер по математике для 1 класса «Геометрические фигуры»:

Геометрические фигуры 1 класс — Онлайн-тренажер

Онлайн-тренажер по математике «Геометрические фигуры 1 класс» поможет первоклассникам потренироваться в умении различать основные геометрические фигуры: квадрат, круг, овал, прямоугольник и треугольник.

1. Рисунки из геометрических фигур — Условия к выполнению заданий:

Чтобы начать выполнять задания, скачайте во вложениях бланк, в котором вы найдете 2 типа заданий: рисунки из геометрических фигур для раскрашивания и задание для рисования фигур с помощью логического и образного мышления.

Распечатайте скачанную страницу на цветном принтере и дайте ребенку вместе с цветными карандашами или фломастерами.

• В первом задании малышу нужно мысленно соединить каждые две части представленных фигур в одну и нарисовать полученную геометрическую форму в соответствующей клетке. Объясните ребенку, что детали можно поворачивать в уме в разные стороны до тех пор, пока он не получит нужную комбинацию для составления фигуры. Например, два треугольника можно повернуть так, чтобы получился квадрат. После этого квадрат нужно нарисовать в клетке рядом с треугольником. По такому же принципу необходимо сделать и остальные рисунки.
• Во втором задании дети должны правильно назвать фигуры из которых состоят нарисованные картинки. Затем эти картинки нужно раскрасить, используя цвета рядом с геометрическими фигурами. Каждую фигуру нужно раскрасить только в указанный цвет.

Чтобы придать занятию больше энергии и энтузиазма — можно объединить несколько детей в группу и предоставить им выполнение заданий на время. Тот ребенок, который первый выполнит все задания без ошибок, признается победителем. В качестве приза можно повесить его работу на стену достижений (такая стена обязательно должна присутствовать как дома, так и в детском саду).

Скачать задание «Рисунки из геометрических фигур» вы можете во вложениях внизу страницы.

2. Геометрические фигуры в рисунках — 3 задания-раскраски:

Следующее занятие также скрывает основные геометрические фигуры в рисунках. Ребенку нужно найти эти фигуры, назвать их, а затем раскрасить таким образом, чтобы каждой фигуре соответствовал определенный цвет (руководствуясь инструкцией на бланке с заданием).

Во втором задании нужно нарисовать на всех этажах любые геометрические фигуры, но при этом необходимо соблюдать условие: на каждом этаже фигуры должны находиться в разном порядке. В последствии можно это задание видоизменить. Для этого достаточно начертить на бумаге точно такой домик и попросить ребенка заполнить его фигурами так, чтобы в каждом подъезде не встречались одинаковые фигуры (подъезд — вертикальный ряд квадратов).

В третьем задании нужно, руководствуясь стрелками, нарисовать точно такие же геометрические фигуры внутри или снаружи данных фигур.

Не торопите ребенка и не подсказывайте ему, пока он сам вас об этом не попросит. Если у малыша что-то получилось неправильно — вы всегда можете распечатать еще один экземпляр учебного бланка с заданием.

Скачать задание «Геометрические фигуры в рисунках» вы можете во вложениях внизу страницы.

3. Развивающая раскраска для детей — Смешные рисунки из фигур

В этом занятии детям опять предстоит отыскать геометрические фигуры среди рисунков. После предыдущих занятий им будет уже легче ориентироваться в знакомых формах, так что, я думаю, оба задания не вызовут у них затруднений.

Второе задание также дает возможность малышу повторить математические знаки и усвоить счет до десяти, так как ему понадобится посчитать количество фигур и поставить знаки «больше» «меньше» между картинками.

Скачать раскраску «Смешные рисунки из фигур» вы можете во вложениях внизу страницы.

Также вам будут полезны и другие материалы по изучению геометрических фигур:

Здесь вы с ребенком можете изучить геометрические фигуры и их названия с помощью веселых заданий в картинках.

Задания ознакомят ребенка с основными фигурами геометрии — кругом, овалом, квадратом, прямоугольником и треугольником. Только здесь не занудное зазубривание названий фигур, а своеобразная игра-раскраска.

Как правило, геометрию начинают изучать, рисуя плоские геометрические фигуры. Восприятие правильной геометрической формы невозможно без выведения ее своими руками на листе бумаги.

Это занятие изрядно позабавит ваших юных математиков. Ведь теперь им придется находить знакомые формы геометрических фигур среди множества картинок.

Наложение фигур друг на друга — это занятие по геометрии для дошкольников и младших школьников. Смысл упражнения состоит в решении примеров на сложение. Только это необычные примеры. Вместо цифр здесь нужно складывать геометрические фигуры.

Это задание составлено в виде игры, в которой ребенку предстоит менять свойства геометрических фигур: форму, цвет или размер.

Здесь вы можете скачать задания в картинках, в которых представлен счет геометрических фигур для занятий по математике.

В этом задании ребенок познакомится с таким понятием, как чертежи геометрических тел. По сути, это занятие представляет собой мини-урок по начертательной геометрии

Здесь мы подготовили для вас объемные геометрические фигуры из бумаги, которые нужно вырезать и склеить. Куб, пирамиды, ромб, конус, цилиндр, шестигранник, распечатать их на картоне (или цветной бумаге, а затем наклеить на картон), а затем дать ребенку для запоминания.

Дети любят раскрашивать и обводить, поэтому данные задания сделают ваши занятия по обучению счету максимально эффективными.

И еще можете поиграть в математические игры онлайн от лисенка Бибуши:

В этой развивающей онлайн игре ребенку предстоит определить, что является лишним среди 4 картинок. При этом необходимо руководствоваться признаками геометрических форм.

«>

1 класс, 2 класс (круг, овал, квадрат, треугольник и многоугольник)

Рисунок из геометрических фигур — это задание для детей дошкольного и младшего школьного возраста, позволяющее развить пространственное воображение, знание геометрических фигур и улучшить моторные навыки черчения.

Для вашего удобства мы сделали рисунки-раскраски из геометрических фигур, которые можно распечатать и раскрасить (для дошкольников). После каждой раскраски представлен пример рисунка на эту же тему. Рисунок дети выполняют самостоятельно по линейке и раскрашивают красками или карандашами (для школьников). Раскраски и рисунки выполнены на следующие темы:

• «Воздушный транспорт»
• «Игрушки»
• Животные из геометрических фигур «Кошка и мышка»
• «Транспорт»
• «Домик в деревне»
• «Море и корабль»
• «Железная дорога»
• «Лесная новогодняя сказка»
• «Летняя поляна»
• «Космический полет»

Рисунки из геометрических фигур для детей — план занятия

• Начните занятие с того, что выясните какие геометрические фигуры помнит ребенок. Он должен уверенно называть и видеть круг (полукруг), овал, квадрат, треугольник и многоугольник . Дети постарше смогут увидеть в рисунках ломаную линию.
• Найдите геометрические фигуры на рисунке. Чем больше ребенок найдет геометрических фигур — тем лучше. Можно их посчитать.
• Заполните цветом раскраску или нарисуйте и выбранную композицию. Очень хорошо, если ребенок пойдет дальше и нарисует свои элементы рисунка.

Композиция из геометрических фигур рисунок «Воздушный транспорт»

Рисунок из геометрических фигур 1 класс — воздушный транспорт. Самолет, воздушный шар и вертолет вызовут интерес у мальчиков. Можно рассказать интересные факты об устройстве транспорта, его скорости, истории создания и роли в наши дни.

Раскраска «Воздушный транспорт из геометрических фигур»Рисунок «Воздушный транспорт из геометрических фигур»

Рисунок из геометрических фигур «Игрушки»

Тема игрушек подойдет для самых маленьких художников. Сюда можно нарисовать любимого мишку или зайчика, выполнив его из геометрических фигур.

Раскраска «Игрушки из геометрических фигур»Рисунок «Игрушки из геометрических фигур»

Животные из геометрических фигур рисунки — «Кошка и мышка»

Самый любимый сюжет — война кошки и мышки.

Раскраска из геометрических фигур»Кошка и мышка»Рисунок из геометрических фигур»Кошка и мышка»

Рисунок из геометрических фигур «Транспорт»

Рисуя транспорт можно повторить его виды и предназначение.

Раскраска из геометрических фигур»Транспорт»Рисунок из геометрических фигур»Транспорт»

Рисунок из геометрических фигур»Домик в деревне»

Нежный яркий рисунок с уточками и домиком понравиться всем.

Раскраска из геометрических фигур»Домик в деревне»Рисунок из геометрических фигур»Домик в деревне»

Рисунок из геометрических фигур»Море и корабль»

Дети обожают рисовать море, рыбок и других морских жителей.

Раскраска из геометрических фигур»Море и корабль»Рисунок из геометрических фигур»Море и корабль»

Рисунок из геометрических фигур»Железная дорога»

Раскраска из геометрических фигур»Железная дорога»Рисунок из геометрических фигур»Железная дорога»

Рисунок из геометрических фигур «Лесная новогодняя сказка»

Раскраска из геометрических фигур»Лесная новогодняя сказка»Рисунок из геометрических фигур»Лесная новогодняя сказка»

Рисунок из геометрических фигур»Летняя поляна»

Любимый сюжет — лето, поляна, цветы и различные насекомые.

Раскраска из геометрических фигур»Летняя поляна»Рисунок из геометрических фигур»Летняя поляна»

Рисунок из геометрических фигур»Космический полет»

Раскраска из геометрических фигур»Космический полет»Рисунок из геометрических фигур»Космический полет»

Рисунки из геометрических фигур (подборка из интернета)

Раскраска из геометрических фигур «Петушок»Рисунок из геометрических фигур «Петушок»Раскраска из геометрических фигур «Домик»Рисунок из геометрических фигур «Домик»Раскраска из геометрических фигур «Робот-солдат»Рисунок из геометрических фигур «Робот-солдат»Раскраска из геометрических фигур «Цветок»Рисунок из геометрических фигур «Цветок»Пчелка из геометрических фигурРаскраска из геометрических фигур «Солнечная улица»

Рисунки из геометрических фигур (видео)

Картинки из геометрических фигур:

Рисунок из геометрических фигур «Домик»:

Аппликации из геометрических фигур 1 класс:

Аппликации тренируют моторику, ведь каждую деталь надо вырезать ножницами. Аппликации помогут научиться представлять целое и его части, помогут не только вспомнить фигуры, но и ощутить их руками.

Рисунки из геометрических фигур (идеи из интернета)

Ракета из овалов, башня из квадратов, ракета из треугольников, человечек из квадратов, человечек из треугольников, человечек из овалов

Легкие рисунки из треугольников — Домострой

Художник, работающий с детьми, показал, как при помощи простых фигур нарисовать забавных животных, которые своим видом порадуют всех. По этой простой технологии, освоить которую могут даже самые маленькие, каждый сможет научиться рисовать.

Веселые и красочные задания для детей «Рисунки из геометрических фигур» являются очень удобным обучающим материалом для детей дошкольного и младшего школьного возраста по изучению и запоминанию основных геометрических форм: треугольника, круга, овала, квадрата, прямоугольника и трапеции. Все задания предназначены для самостоятельной работы ребенка под наблюдением взрослых. Родитель или педагог должны правильно объяснить ребенку, что он должен сделать в каждом задании.

Также вам может понравиться наш онлайн тренажер по математике для 1 класса «Геометрические фигуры»:

Геометрические фигуры 1 класс — Онлайн-тренажер

Онлайн-тренажер по математике «Геометрические фигуры 1 класс» поможет первоклассникам потренироваться в умении различать основные геометрические фигуры: квадрат, круг, овал, прямоугольник и треугольник.

1. Рисунки из геометрических фигур — Условия к выполнению заданий:

Чтобы начать выполнять задания, скачайте во вложениях бланк, в котором вы найдете 2 типа заданий: рисунки из геометрических фигур для раскрашивания и задание для рисования фигур с помощью логического и образного мышления. Распечатайте скачанную страницу на цветном принтере и дайте ребенку вместе с цветными карандашами или фломастерами.

• В первом задании малышу нужно мысленно соединить каждые две части представленных фигур в одну и нарисовать полученную геометрическую форму в соответствующей клетке. Объясните ребенку, что детали можно поворачивать в уме в разные стороны до тех пор, пока он не получит нужную комбинацию для составления фигуры. Например, два треугольника можно повернуть так, чтобы получился квадрат. После этого квадрат нужно нарисовать в клетке рядом с треугольником. По такому же принципу необходимо сделать и остальные рисунки.
• Во втором задании дети должны правильно назвать фигуры из которых состоят нарисованные картинки. Затем эти картинки нужно раскрасить, используя цвета рядом с геометрическими фигурами. Каждую фигуру нужно раскрасить только в указанный цвет.

Чтобы придать занятию больше энергии и энтузиазма — можно объединить несколько детей в группу и предоставить им выполнение заданий на время. Тот ребенок, который первый выполнит все задания без ошибок, признается победителем. В качестве приза можно повесить его работу на стену достижений (такая стена обязательно должна присутствовать как дома, так и в детском саду).

Скачать задание «Рисунки из геометрических фигур» вы можете во вложениях внизу страницы.

2. Геометрические фигуры в рисунках — 3 задания-раскраски:

Следующее занятие также скрывает основные геометрические фигуры в рисунках. Ребенку нужно найти эти фигуры, назвать их, а затем раскрасить таким образом, чтобы каждой фигуре соответствовал определенный цвет (руководствуясь инструкцией на бланке с заданием).

Во втором задании нужно нарисовать на всех этажах любые геометрические фигуры, но при этом необходимо соблюдать условие: на каждом этаже фигуры должны находиться в разном порядке. В последствии можно это задание видоизменить. Для этого достаточно начертить на бумаге точно такой домик и попросить ребенка заполнить его фигурами так, чтобы в каждом подъезде не встречались одинаковые фигуры (подъезд — вертикальный ряд квадратов).

В третьем задании нужно, руководствуясь стрелками, нарисовать точно такие же геометрические фигуры внутри или снаружи данных фигур.

Не торопите ребенка и не подсказывайте ему, пока он сам вас об этом не попросит. Если у малыша что-то получилось неправильно — вы всегда можете распечатать еще один экземпляр учебного бланка с заданием.

Скачать задание «Геометрические фигуры в рисунках» вы можете во вложениях внизу страницы.

3. Развивающая раскраска для детей — Смешные рисунки из фигур

В этом занятии детям опять предстоит отыскать геометрические фигуры среди рисунков. После предыдущих занятий им будет уже легче ориентироваться в знакомых формах, так что, я думаю, оба задания не вызовут у них затруднений.

Второе задание также дает возможность малышу повторить математические знаки и усвоить счет до десяти, так как ему понадобится посчитать количество фигур и поставить знаки «больше» «меньше» между картинками.

Скачать раскраску «Смешные рисунки из фигур» вы можете во вложениях внизу страницы.

Также вам будут полезны и другие материалы по изучению геометрических фигур:

Здесь вы с ребенком можете изучить геометрические фигуры и их названия с помощью веселых заданий в картинках.

Задания ознакомят ребенка с основными фигурами геометрии — кругом, овалом, квадратом, прямоугольником и треугольником. Только здесь не занудное зазубривание названий фигур, а своеобразная игра-раскраска.

Как правило, геометрию начинают изучать, рисуя плоские геометрические фигуры. Восприятие правильной геометрической формы невозможно без выведения ее своими руками на листе бумаги.

Это занятие изрядно позабавит ваших юных математиков. Ведь теперь им придется находить знакомые формы геометрических фигур среди множества картинок.

Наложение фигур друг на друга — это занятие по геометрии для дошкольников и младших школьников. Смысл упражнения состоит в решении примеров на сложение. Только это необычные примеры. Вместо цифр здесь нужно складывать геометрические фигуры.

Это задание составлено в виде игры, в которой ребенку предстоит менять свойства геометрических фигур: форму, цвет или размер.

Здесь вы можете скачать задания в картинках, в которых представлен счет геометрических фигур для занятий по математике.

В этом задании ребенок познакомится с таким понятием, как чертежи геометрических тел.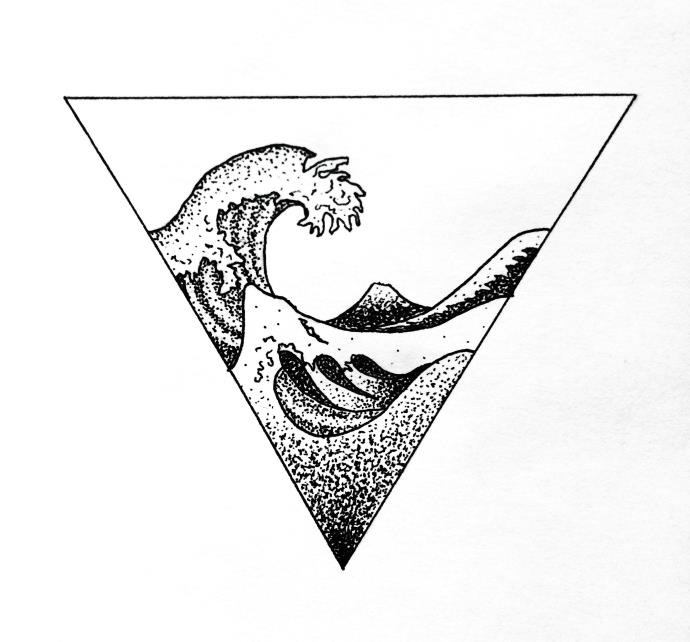 По сути, это занятие представляет собой мини-урок по начертательной геометрии

Здесь мы подготовили для вас объемные геометрические фигуры из бумаги, которые нужно вырезать и склеить. Куб, пирамиды, ромб, конус, цилиндр, шестигранник, распечатать их на картоне (или цветной бумаге, а затем наклеить на картон), а затем дать ребенку для запоминания.

Дети любят раскрашивать и обводить, поэтому данные задания сделают ваши занятия по обучению счету максимально эффективными.

И еще можете поиграть в математические игры онлайн от лисенка Бибуши:

В этой развивающей онлайн игре ребенку предстоит определить, что является лишним среди 4 картинок. При этом необходимо руководствоваться признаками геометрических форм.

Главное нужно указать файл картинки на вашем компьютере или телефоне, нажать кнопку ОК. Остальные настройки выставлены по умолчанию.

Пример фотографии розы без изменений и сделанная на этом сайте картинка из треугольников:

Обратите внимание, что обработка длится около 1 минуты, на выходе получается картинка из треугольников не более 0. 5 мегапикселей, примерно 800×600 и этого размера хватит с запасом, например, чтобы выложить на сайте vk.com. Если нужна картинка из треугольников без уменьшения, то присылайте на контактный ящик фото или картинку, которую нужно обработать и выставленные настройки (если они изменялись) — будет сделано бесплатно в течение суток.

Ещё картинку можно сделать из: квадратов | треугольников | кругов | звёзд

Исходное изображение никак не изменяется. Вам будет предоставлена другая обработанная картинка.

Урок 28. треугольники — Математика — 5 класс

Математика

5 класс

Урок №28

Треугольники

Перечень рассматриваемых вопросов:

— треугольники;

— элементы треугольника;

— виды треугольников.

Тезаурус

Треугольник – это геометрическая фигура, состоящая из трёх точек, не лежащих на одной прямой и соединённых между собой.

Периметр треугольника – сумма длин всех сторон треугольника.

Обязательная литература

Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений. // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017. – 272 с.

Дополнительная литература

1. Чулков П. В. Математика: тематические тесты. 5 класс. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. – М.: Просвещение, 2009. – 142 с.

2. Шарыгин И. Ф. Задачи на смекалку: 5-6 классы. // И. Ф. Шарыгин, А. В. Шевкин. – М.: Просвещение, 2014. – 95 с.

Теоретический материал для самостоятельного изучения

Среди всех многоугольников наименьшее число сторон и углов имеет треугольник. Он является простейшей фигурой, и казалось бы, его изучение не может быть интересным. Однако существует множество видов треугольников. О них мы и поговорим.

Отметим какие-нибудь три точки, не лежащие на одной прямой – например, А, В, С. Соединим их с помощью линейки. Получим геометрическую фигуру, которая называется треугольником. Отмеченные три точки А, В, С называются вершинами, отрезки АВ, ВС, АС – сторонами треугольника, а углы А, В, С – углами треугольника.

Все треугольники можно разделить на группы по сторонам:

— если равных сторон нет – это разносторонний треугольник;

— если две стороны равны – это равнобедренный треугольник;

— если все стороны равны – это равносторонний треугольник.

Треугольники можно разделить на группы в зависимости от углов:

— если есть тупой угол – это тупоугольный треугольник;

— если все углы острые – это остроугольный треугольник;

— если есть прямой угол – это прямоугольный треугольник.

Треугольники, соединяясь друг с другом, могут образовывать другие фигуры.

Попробуем нарисовать прямоугольный треугольник на листе в клетку. Мы знаем, что сторона стандартной клетки – пять миллиметров, следовательно, две клетки – это один сантиметр.

По сторонам клетки проведём отрезки заданной длины из одной точки. В нашем случае из точки А проведём отрезки длиной четыре и три сантиметра, что соответствует восьми и шести клеткам. На концах отрезков поставим точки В и С и соединим их между собой. Таким образом, мы построили прямоугольный треугольник АВС.

А теперь рассмотрим свойства треугольников. Одно из них – жёсткость. Это свойство заключается в том, что, если взять три рейки и соединить их попарно, то получится треугольник, изменить форму которого можно лишь сломав рейку.

Рассмотрим ещё одно свойство треугольников. Оно заключается в том, что длина каждой стороны треугольника всегда меньше суммы двух других сторон.

Это свойство можно использовать для проверки возможности построения треугольника по определённым сторонам. То есть, если свойство не выполняется, то такого треугольника не может быть.

Если мы знаем стороны треугольника, то можем найти его периметр как сумму длин всех его сторон. Например, периметр треугольника АВС – это сумма сторон АВ, АС и ВС.

Р = АВ + ВС + АС

Измерим с помощью линейки стороны треугольника и рассчитаем его периметр.

По результатам измерения стороны, соответственно, равны пяти, шести и семи сантиметрам.

Значит, периметр равен восемнадцати сантиметрам, то есть сумме всех сторон.

Говоря о треугольниках, стоит упомянуть, что они бывают как одинаковыми, так и разными. Определить, равные или разные треугольники, можно способом наложения. Если треугольник полностью накладывается на другой треугольник, такие треугольники равны. В противном случае треугольники не будут равными.

Рисунки из треугольников

Многие люди, как маленькие, так и взрослые, очень любят рисовать. Но иногда одного желания рисовать недостаточно. Для того чтобы облегчить процесс создания простейших картинок, инженер Эриф Мд. Вейлиула Байан, разработчик инновационного контента для детей, создал схемы, по которым, имея базовые навыки работы с чертёжными инструментами, можно создать милые и забавные картинки с животными и птицами.

Похожие схемы частично есть в открытом доступе, поэтому каждый желающий может приобщиться к миру изобразительного искусства через поэтапное прорисовывание простых картинок.

Тренировочные задания

№ 1. В треугольнике все стороны равны 15 см. Чему равен периметр треугольника?

Решение: для нахождения периметра используем формулу Р = АВ + АС + ВС.

Так как у этого треугольника стороны равны, то Р = 15 см + 15 см + 15 см = 45 см

№ 2. Сопоставьте треугольники с их видами (по углам).

Решение: в задаче требуется сопоставить треугольники со следующими видами по углам: остроугольный, прямоугольный, тупоугольный. Согласно определению, прямоугольный треугольник имеет один угол 90 градусов: этому треугольнику соответствует второй треугольник. А тупоугольный треугольник имеет один угол больше 90 градусов: он отображён третьим по счёту. Как мы знаем, остроугольный треугольник имеет три угла меньше 90 градусов, так что в этом случае подходит треугольник, изображённый первым слева.

значение, эскизы, лучшие примеры на фото

Татуировка треугольник – очень распространенный вариант среди девушек. Какие же самые актуальные и неповторимые эскизы предлагают нам современные мастера тату в 2018 году?

Тату треугольник: значение геометрического нательного рисунка

Татуировка в виде треугольника – очень распространенный вариант у современных девушек. Данные символы встречаются довольно часто в самых различных частях женского тела. Очень часто мастера тату любят включать в центр треугольника всевозможные цветочные композиции, абстракции и другие замысловатые сюжеты. С точки зрения мистики геометрическая фигура треугольник на теле трактуется как что-то таинственное. Смысловое значение сводится к человеческой составляющей, а именно: душе, телу и разуму.  Альтернативное восприятие татуировки треугольник трактуется как взаимосвязь между появлением на свет, этапами жизни и смертью. Женщины воспринимают татуировку в виде треугольника как особенную нить, связывающую молодость и старость, а между этими этапами – время материнства. Тату треугольник считается довольно универсальным нательным рисунком. Это обозначает лишь то, что тату может сделать себе не только молодая девушка, но и женщины постарше.

Самые оригинальные эскизы тату треугольник

Обыкновенный равнобедренный треугольник встречается крайне редко в качестве эскиза. Обычно его дополняют различные композиции и рисунки, хотя минималистическое исполнение треугольника смотрится весьма аккуратно. Существует масса разнообразных эскизов, в которых треугольник является основным элементом. Острота углов треугольника на теле компенсируется за счет сопутствующих деталей, которые в основном выполнены в плавных очертаниях.  Например, если в треугольнике изображено дерево, то это обозначает лишь то, что обладательница любит и ценит жизнь во всех ее проявлениях. А линии, которые ограничивают изображение дерева, символизируют цикличность. Среди различных вариантов эскизов тату с треугольниками можно обязательно найти подходящий.

 

Тату глаз в треугольнике – один из популярнейших женских рисунков на теле

Самой распространенной татуировкой треугольника является его изображение с глазом посередине, этакое всевидящее око. Глядя на изображение тату с глазом в треугольнике, возникают двойственные чувства, которые свойственны мистицизму и необъяснимым явлениям. Значение данного изображение трактуется как озарение или просветление сознания, хотя внешне глаз ограничивается сторонами треугольника. Специфические направления в религии берут рисунок в виде глаза в треугольнике в качестве основы для своих символов, ведь у каждой религии свое видение на окружающий мир. Многие культуры считают тату треугольника с глазом внутри символическим изображением, предназначенным лицезреть за всем происходящим.

Цветное и черное тату треугольник на руке: настоящие примеры художественного искусства

Большинство примеров татуировок с треугольником на руке выполнены цветными чернилами. Особенно эффектно на запястьях смотрится тату треугольника в акварельной технике. Необычный нательный дизайн подойдет девушкам, которые не унывают по жизни, а стараются все видеть через разноцветную призму счастья. Если говорить о черном варианте тату на руке, то треугольник в данном формате смотрится аккуратно, что, в любом случае, уже считается модным.

Женское тату роза в треугольнике: красивые варианты

Очень часто девушки выбирают для себя изображение в виде треугольника, заполненного цветочными мотивами. Розы – самое распространенное из них. С помощью татуировки роз в треугольнике девушка привлекает к себе внимание. Данная нательная композиция прекрасно смотрится как в маленьком, так и большом формате. Место для расположения татуировки треугольника с розами могут быть самыми различными. Все зависит от выбранного размера. Вообще, значение комбинации треугольника с розой трактуется как женская энергетика. Представительницы прекрасного пола, на теле которых можно увидеть тату с розой в комбинации с треугольником, отличаются особым отношением к художественному искусству, музыке и творчеству в целом.

Тату два треугольника: парные рисунки для двух половинок

Мужчины считают татуировку треугольник, сделанную в паре со второй половинкой, символом мощи, красоты и ума. Парное тату символизирует о слиянии душ в одно целое и единство отношений. Определенные детали в парных татуировка указывают на то, что между влюбленными существует определенная неразрывная нить, которая поддерживает отношения. Перевернутые изображения треугольников указывают на то, что оба человека поддерживают друг друга во всем. В целом, все парные изображения носят определенный характер, в том числе дополнительные орнаменты к треугольнику.

Тату треугольник на ногах девушек

Интересно и оригинально смотрится тату треугольника на ногах девушек, причем в любой ее части. На бедре стараются сделать татуировку покрупней, а в районе щиколотки встречаются более минималистические изображения. Модные композиции с разносторонними и равносторонними треугольниками на ногах, как и на многих других частях тела, украшаются дополнительными элементами. Цветные изображения животных, цветочные композиции или непонятная абстракция смотрится на ноге довольно эффектно, особенно если тату сделано качественно и со вкусом.

Тату треугольник: фото примеры актуального и современного нательного дизайна

Неповторимость татуировки гарантирует обладательнице только свойственную ей индивидуальность и неповторимость. Выбирая тату треугольника по фото, обязательно старайтесь внести что-то свое, личное в нательное изображение. Нельзя сделать татуировку как под копирку. Важно вложить в нее особый смысл, понятный только вам и вашим близким людям. Тем более, что вы знаете о том, что при выборе необходимо основываться на значение тату треугольника и дополнительных орнаментов. Цветовое решение в данной ситуации тоже играет немаловажную роль. Если вы жизнерадостны, то не стоит выбирать сплошное черное тату с треугольником, а лучше внести живые нотки ярких красок в рисунок, который будет сопутствовать с вами по жизни.

конструктивный рисунок человека из геометрических форм

Анализ рисунка человека по предпочтению семантики треугольников, кругов и квадратов

Анализ рисунка человека по предпочтению треугольников, кругов и квадратов проводился на основе метода семантического дифференциала. Результаты нашего исследования (подробнее см. главу 18) легли в основу приведенной ниже интерпретационной схемы. Семантика каждой из геометрических форм выступает в качестве отдельного психологического признака:

ТРЕУГОЛЬНИК характеризуется как «острая», «наступательная» форма, связанная с доминирующим началом.

Семантическое значение КРУГА связано с «обтекаемостью» или округлостью его формы, которая психологически созвучна с мягкостью характера, сочувствием и женственностью.

КВАДРАТ обладает «устойчивостью» и «стабильностью», а также ассоциируется с маскулинностью. Квадрат и прямоугольник в тесте имеют одинаковое семантическое значение, хотя различаются по другим признакам.

В таблице 1 приведены индивидуальные психологические свойства, соответствующие предпочтению каждой из геометрических форм.

Степень выраженности в конструктивном рисунке человека психологических признаков той или иной геометрической формы определяется по шкале от 1 до 8, где 8 показывает максимальное значение данного признака, в то время как 1 соответствует минимальному его значению.

8, 7 и 6 геометрических форм данного типа означают преобладание признака;

5 геометрических форм – признак выражен, но не доминирует;

4 и 3 – признак мало выражен, хотя и присутствует в структуре индивидуально-психологических свойств;

2 и 1 – признак не выражен или вытеснен значением признака другой геометрической формы.

Рис. 6. Формула рисунка 811 (восемь треугольников, один круг и один квадрат в изображении фигуры человека).

В качестве примера рассмотрим изображение фигуры человека, имеющего восемь треугольников, один круг и один квадрат (формула рисунка 811). Предпочтение восьми треугольников указывает на максимальную выраженность присущих треугольнику свойств, таких как интенсивность, настойчивость, возбудимость, стремление к доминированию и соперничеству (см. таблицу 1).

Таблица 1. Интерпретация основных показателей психографического теста ТиГр на основе семантики предпочтения геометрических форм

В то же время четыре треугольника, три круга и три квадрата в изображении человека (формула рисунка 433) указывают скорее на присутствие, чем выраженность присущих треугольнику свойств.

Рис 7. Формула рисунка 433 (четыре треугольника, три круга и три квадрата в изображении фигуры человека).

Данный текст является ознакомительным фрагментом.

Продолжение на ЛитРес

рисунков треугольников | E.J.Kaplan

Проекты | 2021 | Ссылки: .zip файлов svg

Рисование изображений, сделанных из множества и множества треугольников

Я сделал несколько изображений птиц, используя треугольники с помощью Axidraw v3 и цветного маркера с острым концом. Изображения были сгенерированы с помощью специальной программы обработки, а затем перед печатью настроены в Inkscape. Если вы хотите построить их самостоятельно, я связал файлы svg выше. Однако большинство из вас заинтересуются изображениями и таймлапсами, так что вот они.Подробнее о том, как работает программа, я расскажу ниже. Приношу свои извинения за плохое качество изображений — очевидно, мне нужно вложить деньги в лучшую камеру / сканер, если я собираюсь хвастаться своей работой.

The Work

Timelapse (10x)

Хохлатая синичка

Hummingbird

Flamingo

Подробности реализации

Я не собираюсь делиться кодом в данный момент, не потому, что Я не хочу делиться, потому что сейчас очень грязно.Но основы таковы: я начинаю с присвоения каждому пикселю исходного изображения значения от 0 до 1, указывающего вероятность того, что вершина будет назначена в этом месте. Алгоритм отдает предпочтение размещению вершин в темных областях изображения и по краям. Создавая конкретное изображение, мне приходится тратить много времени на настройку параметров, наиболее важным из которых является то, какой вес нужно придать в пользу правильного затенения изображения (размещение вершин в темных областях) по сравнению с взвешиванием в пользу стилизации (размещение вершин). по краям).После размещения всех вершин выполняется триангуляция Делоне для получения треугольной сетки. Триангуляция Делоне создает основную часть сетки, однако на этом этапе мне нужно выполнить несколько ручных настроек — в основном обрезать края, которые соединяют части изображения, которые должны быть разделены. Иногда также не хватает деталей, которые должны присутствовать, поэтому я добавляю еще несколько краев. После этого svg готов к построению.

Авторы изображений

Это лицензии CC для фотографий птиц, которые я использовал для этого проекта.

• «Колибри» от szeke имеет лицензию CC BY-SA 2.0. Чтобы просмотреть копию этой лицензии, посетите https://creativecommons.org/licenses/by-sa/2.0/
• «Фотография недели — хохлатая синичка (Массачусетс)» Службы охраны рыбных ресурсов и дикой природы США — Северо-восточный регион отмечен под CC PDM 1.0. Чтобы ознакомиться с условиями, посетите https://creativecommons.org/publicdomain/mark/1.0/
• «Фламинго» от Спасибо за более 2 миллионов просмотров !! имеет лицензию CC BY 2.0. Чтобы просмотреть копию этой лицензии, посетите https: // creativecommons.org / licenses / by / 2.0 /

---

Около

Элиот Дж. Каплан (он / он) — изобретательный программист, сомелье настольных игр, художник по процедурам, временный GM, бывший учитель CS в средней школе, Trekkie и профессиональное программное обеспечение инженер.

Другие проекты

---

Лицензировано по международной лицензии Creative Commons Attribution-ShareAlike 4.0.

---

Масштабные чертежи и рабочие листы свойств треугольников от Free to Discover

В этих рабочих таблицах для разработки концепций учащиеся решают задачи, связанные с масштабными чертежами геометрических фигур и рисуют треугольники с заданными условиями.В первом упражнении ученикам дается масштабный рисунок. Они определяют фактическую длину с учетом масштаба, оценивают стоимость, вычисляют фактическую площадь, воспроизводят масштабный чертеж в другом масштабе и обобщают основные идеи. Затем у учащихся есть возможность создать собственный масштабный рисунок и выполнить аналогичный процесс. Во втором упражнении учащиеся работают в парах, чтобы построить треугольники с помощью транспортира с учетом меры угла. Они сравнивают длину сторон со своим партнером, чтобы показать, что, хотя стороны не совпадают, они пропорциональны.Студенты обобщают свои выводы и размышляют над основными идеями. Затем они строят треугольники с заданной длиной сторон и обсуждают, когда построить треугольник невозможно.

Этот продукт является частью серии Discovery-Based Worksheet. Рабочие листы на основе открытий были специально разработаны для вовлечения студентов в обучение, выходящее за рамки традиционной практики навыков. Студенты получат более глубокое понимание большой идеи и установят связи между концепциями. Эти рабочие листы являются отличным введением в новую тему или резюме в конце урока или раздела.Попробуйте сегодня!

Включено:

-2 двухстраничных рабочих листа

-1 страница последующего действия

— Руководство для учителя с CCSS, целями, материалами и процедурой

— Ответные ключи (включая образец последующей деятельности)

Вам также могут понравиться:

Станции масштабных чертежей

Карты задач измерения 2D и 3D

Марди Гра: аналогичные цифры и пропорциональные отношения

Карты задач на день числа числа пи

************** ************************************************* **********

Советы покупателям

☺ Зарабатывайте кредиты TpT, чтобы использовать их для будущих покупок, оставляя отзывы о платных продуктах.(Мы также будем благодарны за отзывы о бесплатных продуктах!)

☺ Подпишитесь на меня, чтобы получать уведомления о новых продуктах. Это поможет вам получить скидку 50% в течение первых 48 часов. Вы также будете время от времени получать сообщения с предупреждениями о распродажах, рекламных акциях и другими интересными новостями.

☺ Не совсем понимаете, что ищете? Оставьте мне сообщение во вкладке «Задать вопрос». Я был бы рад создать продукт, отвечающий потребностям вас и ваших учеников.

Информация об авторских правах и условия использования:

Приобретение этого продукта дает право одному пользователю воспроизводить ресурс только для использования в классе. Если вы хотите поделиться с другими учителями, можно приобрести дополнительные лицензии со скидкой. Продукт предназначен только для образовательного использования. Продукт нельзя использовать в коммерческих целях или перепродавать в какой-либо форме. Его нельзя загрузить в Интернет, в том числе на школьные сайты.

© Free to Discover (Аманда Никс)

Рисование фигур с помощью холста — веб-API

Теперь, когда мы настроили среду холста, мы можем перейти к деталям того, как рисовать на холсте.К концу этой статьи вы научитесь рисовать прямоугольники, треугольники, линии, дуги и кривые, познакомившись с некоторыми из основных фигур. Работа с контурами важна при рисовании объектов на холсте, и мы увидим, как это можно сделать.

Прежде чем мы сможем начать рисовать, нам нужно поговорить о сетке холста или пространстве координат . Наш скелет HTML с предыдущей страницы имел элемент холста шириной 150 пикселей и высотой 150 пикселей.

Обычно 1 единица сетки соответствует 1 пикселю на холсте.Начало этой сетки расположено в верхнем левом углу в координате (0,0). Все элементы размещаются относительно этого начала координат. Таким образом, положение верхнего левого угла синего квадрата становится x пикселей слева и y пикселей сверху, в координатах (x, y). Позже в этом уроке мы увидим, как мы можем перевести начало координат в другое положение, повернуть сетку и даже масштабировать ее, но пока мы будем придерживаться значения по умолчанию.

В отличие от SVG, поддерживает только две примитивные формы: прямоугольники и пути (списки точек, соединенных линиями).Все остальные формы должны быть созданы путем объединения одного или нескольких контуров. К счастью, у нас есть набор функций рисования контуров, которые позволяют создавать очень сложные формы.

Сначала посмотрим на прямоугольник. Есть три функции, которые рисуют прямоугольники на холсте:

fillRect (x, y, ширина, высота)

Рисует закрашенный прямоугольник.

strokeRect (x, y, ширина, высота)

Рисует прямоугольный контур.

clearRect (x, y, ширина, высота)

Очищает указанную прямоугольную область, делая ее полностью прозрачной.

Каждая из этих трех функций принимает одни и те же параметры. x и y определяют положение на холсте (относительно исходной точки) верхнего левого угла прямоугольника. Ширина и высота обеспечивают размер прямоугольника.

Ниже представлена ​​функция draw () с предыдущей страницы, но теперь она использует эти три функции.

Пример прямоугольной формы

  function draw () {
  var canvas = document.getElementById ('холст');
  if (canvas.getContext) {
    var ctx = canvas.getContext ('2d');

    ctx.fillRect (25, 25, 100, 100);
    ctx.clearRect (45, 45, 60, 60);
    ctx.strokeRect (50, 50, 50, 50);
  }
}
  

Результат этого примера показан ниже.

Скриншот	Живой образец

Функция fillRect () рисует большой черный квадрат по 100 пикселей с каждой стороны. Затем функция clearRect () стирает квадрат 60×60 пикселей из центра, а затем вызывается strokeRect () для создания прямоугольного контура 50×50 пикселей внутри очищенного квадрата.

На следующих страницах мы увидим два альтернативных метода для clearRect () , а также увидим, как изменить цвет и стиль обводки визуализированных фигур.

В отличие от функций контура, которые мы увидим в следующем разделе, все три прямоугольные функции рисуют непосредственно на холсте.

Теперь посмотрим на пути. Путь — это список точек, соединенных отрезками линий разной формы, изогнутыми или нет, разной ширины и разного цвета. Путь или даже подпуть можно закрыть. Чтобы сделать фигуры с помощью контуров, мы предпримем несколько дополнительных шагов:

1. Сначала вы создаете путь.
2. Затем вы используете команды рисования, чтобы нарисовать контур.
3. После того, как путь был создан, вы можете обвести его или заполнить, чтобы отобразить его.

Вот функции, используемые для выполнения этих шагов:

beginPath ()

Создает новый путь. После создания будущие команды рисования направляются в путь и используются для построения пути.

Методы пути

Способы задания разных путей для объектов.

closePath ()

Добавляет прямую линию к пути, идущему до начала текущего вложенного пути.

ход ()

Рисует фигуру, обводя ее контур.

заполнить ()

Рисует сплошную фигуру, заполняя область содержимого контура.

Первым шагом для создания пути является вызов beginPath () . Внутри контуры хранятся в виде списка подпутей (линий, дуг и т. Д.), Которые вместе образуют форму. Каждый раз, когда вызывается этот метод, список сбрасывается, и мы можем начать рисовать новые фигуры.

Примечание: Когда текущий путь пуст, например, сразу после вызова beginPath () , или на вновь созданном холсте, первая команда построения пути всегда обрабатывается как moveTo () , независимо от того, что она на самом деле есть. По этой причине вам почти всегда нужно специально устанавливать начальную позицию после сброса пути.

Второй шаг — это вызов методов, которые фактически определяют пути, которые нужно нарисовать. Мы увидим это в ближайшее время.

Третий и необязательный шаг — вызвать closePath () . Этот метод пытается замкнуть фигуру, проведя прямую линию от текущей точки до начала. Если фигура уже закрыта или в списке только одна точка, эта функция ничего не делает.

Примечание: Когда вы вызываете fill () , все открытые фигуры закрываются автоматически, поэтому вам не нужно вызывать closePath () . Это , а не , когда вы вызываете stroke () .

Рисование треугольника

Например, код для рисования треугольника будет выглядеть примерно так:

  function draw () {
  var canvas = document.getElementById ('холст');
  if (canvas.getContext) {
    var ctx = canvas.getContext ('2d');

    ctx.beginPath ();
    ctx.moveTo (75, 50);
    ctx.lineTo (100, 75);
    ctx.lineTo (100, 25);
    ctx.наполнять();
  }
}
  

Результат выглядит так:

Снимок экрана	Живой образец

Перемещение пера

Одна очень полезная функция, которая на самом деле ничего не рисует, но становится частью список путей, описанный выше, — это функция moveTo () . Вероятно, вы можете представить себе это как то, что вы поднимаете ручку или карандаш с одного места на листе бумаги и кладете их на другое.

moveTo (x, y)

Перемещает перо к координатам, указанным в x и y .

Когда холст инициализируется или вызывается beginPath () , вы обычно хотите использовать функцию moveTo () , чтобы разместить начальную точку в другом месте. Мы также можем использовать moveTo () для рисования несвязанных путей. Взгляните на смайлик ниже.

Чтобы попробовать это на себе, вы можете использовать приведенный ниже фрагмент кода.Просто вставьте его в функцию draw () , которую мы видели ранее.

  function draw () {
  var canvas = document.getElementById ('холст');
  if (canvas.getContext) {
     var ctx = canvas.getContext ('2d');

    ctx.beginPath ();
    ctx.arc (75, 75, 50, 0, Math.PI * 2, истина);
    ctx.moveTo (110, 75);
    ctx.arc (75, 75, 35, 0, Math.PI, ложь);
    ctx.moveTo (65, 65);
    ctx.arc (60, 65, 5, 0, Math.PI * 2, истина);
    ctx.moveTo (95, 65);
    ctx.arc (90, 65, 5, 0, Math.PI * 2, истина);
    ctx.stroke ();
  }
}
  

Результат выглядит следующим образом:

Снимок экрана	Живой образец

Если вы хотите увидеть соединительные линии, вы можете удалить линии, которые вызывают moveTo ( ) .

Примечание: Чтобы узнать больше о функции arc () , см. Раздел «Дуги» ниже.

Линии

Для рисования прямых линий используйте метод lineTo () .

lineTo (x, y)

Рисует линию из текущей позиции рисования в позицию, заданную параметрами x и y .

Этот метод принимает два аргумента: x и y , которые являются координатами конечной точки линии. Начальная точка зависит от ранее нарисованных путей, где конечная точка предыдущего пути является отправной точкой для следующих и т. Д.Начальную точку также можно изменить с помощью метода moveTo () .

Пример ниже рисует два треугольника: один с заливкой и один с контуром.

  function draw () {
  var canvas = document.getElementById ('холст');
  if (canvas.getContext) {
    var ctx = canvas.getContext ('2d');

    
    ctx.beginPath ();
    ctx.moveTo (25, 25);
    ctx.lineTo (105, 25);
    ctx.lineTo (25, 105);
    ctx.fill ();

    
    ctx.beginPath ();
    ctx.moveTo (125, 125);
    ctx.lineTo (125, 45);
    ctx.lineTo (45, 125);
    ctx.closePath ();
    ctx.stroke ();
  }
}
  

Это начинается с вызова beginPath () , чтобы начать новый контур формы. Затем мы используем метод moveTo () , чтобы переместить начальную точку в желаемое положение. Ниже нарисованы две линии, составляющие две стороны треугольника.

Скриншот	Живой образец

Вы заметите разницу между закрашенным и заштрихованным треугольником.Как упоминалось выше, это происходит потому, что фигуры автоматически закрываются при заливке контура, но не при обводке. Если бы мы пропустили closePath () для обведенного треугольника, были бы нарисованы только две линии, а не полный треугольник.

Дуги

Для рисования дуг или окружностей мы используем методы arc () или arcTo () .

arc (x, y, radius, startAngle, endAngle, против часовой стрелки)

Рисует дугу с центром в позиции (x, y) с радиусом r , начиная с startAngle и заканчивая endAngle в заданном направлении, обозначенном против часовой стрелки (по умолчанию по часовой стрелке).

arcTo (x1, y1, x2, y2, radius)

Рисует дугу с заданными контрольными точками и радиусом, соединенную с предыдущей точкой прямой линией.

Давайте более подробно рассмотрим метод arc , который принимает шесть параметров: x и y — координаты центра окружности, на которой должна быть нарисована дуга. радиус не требует пояснений. Параметры startAngle и endAngle определяют начальную и конечную точки дуги в радианах вдоль кривой окружности.Они отсчитываются от оси x. Параметр против часовой стрелки — это логическое значение, которое, когда истинно , рисует дугу против часовой стрелки; в противном случае дуга рисуется по часовой стрелке.

Примечание. Углы в функции arc измеряются в радианах, а не в градусах. Чтобы преобразовать градусы в радианы, вы можете использовать следующее выражение JavaScript: радиан = (Math.PI / 180) * градусов .

Следующий пример немного сложнее, чем те, которые мы видели выше.Он рисует 12 разных дуг с разными углами и заливками.

Две петли на предназначены для прохода по рядам и столбцам дуг. Для каждой дуги мы начинаем новый путь, вызывая beginPath () . В коде каждый из параметров дуги для ясности указан в переменной, но в реальной жизни это не обязательно.

Координаты x и y должны быть достаточно четкими. radius и startAngle фиксированы. endAngle начинается с 180 градусов (полукруга) в первом столбце и увеличивается с шагом 90 градусов, завершаясь полным кругом в последнем столбце.

Оператор для параметра по часовой стрелке приводит к тому, что первая и третья строки рисуются как дуги по часовой стрелке, а вторая и четвертая строки — как дуги против часовой стрелки. Наконец, оператор if делает верхнюю половину заштрихованной дугой, а нижнюю половину — заполненной дугой.

Примечание: В этом примере требуется холст немного большего размера, чем другие на этой странице: 150 x 200 пикселей.

  function draw () {
  var canvas = document.getElementById ('холст');
  if (canvas.getContext) {
    var ctx = canvas.getContext ('2d');

    for (var i = 0; i <4; i ++) {
      for (var j = 0; j <3; j ++) {
        ctx.beginPath ();
        var x = 25 + j * 50;
        var y = 25 + i * 50;
        var radius = 20;
        вар startAngle = 0;
        var endAngle = Math.PI + (Math.PI * j) / 2;
        var против часовой стрелки = i% 2! == 0;

        ctx.arc (x, y, радиус, startAngle, endAngle, против часовой стрелки);

        if (i> 1) {
          ctx.fill ();
        } еще {
          ctx.stroke ();
        }
      }
    }
  }
}
  

Снимок экрана	Живой образец

Кривые Безье и квадратичные

Следующим типом доступных траекторий являются кривые Безье, доступные как в кубическом, так и в квадратичном вариантах.Обычно они используются для рисования сложных органических форм.

quadraticCurveTo (cp1x, cp1y, x, y)

Рисует квадратичную кривую Безье от текущего положения пера до конечной точки, указанной параметрами x и y , используя контрольную точку, указанную параметрами cp1x и cp1y .

bezierCurveTo (cp1x, cp1y, cp2x, cp2y, x, y)

Рисует кубическую кривую Безье от текущего положения пера до конечной точки, заданной параметрами x и y , с использованием контрольных точек, заданных параметрами ( cp1x , cp1y ) и (cp2x, cp2y).

Разница между ними заключается в том, что квадратичная кривая Безье имеет начальную и конечную точки (синие точки) и только одну контрольную точку (обозначена красной точкой), в то время как кубическая кривая Безье использует две контрольные точки.

Параметры x и y в обоих этих методах являются координатами конечной точки. cp1x и cp1y — координаты первой контрольной точки, а cp2x и cp2y — координаты второй контрольной точки.

Использование квадратичных и кубических кривых Безье может быть довольно сложной задачей, потому что в отличие от программного обеспечения для рисования векторных изображений, такого как Adobe Illustrator, у нас нет прямой визуальной обратной связи относительно того, что мы делаем. Из-за этого довольно сложно рисовать сложные формы. В следующем примере мы будем рисовать несколько простых органических форм, но если у вас есть время и, самое главное, терпение, можно создать гораздо более сложные формы.

В этих примерах нет ничего сложного. В обоих случаях мы видим последовательность нарисованных кривых, которые в конечном итоге приводят к завершенной форме.

Квадратичные кривые Безье

В этом примере используется несколько квадратичных кривых Безье для визуализации выноски речи.

  function draw () {
  var canvas = document.getElementById ('холст');
  if (canvas.getContext) {
    var ctx = canvas.getContext ('2d');

    
    ctx.beginPath ();
    ctx.moveTo (75, 25);
    ctx.quadraticCurveTo (25, 25, 25, 62.5);
    ctx.quadraticCurveTo (25, 100, 50, 100);
    ctx.quadraticCurveTo (50, 120, 30, 125);
    ctx.quadraticCurveTo (60, 120, 65, 100);
    ctx.quadraticCurveTo (125, 100, 125, 62,5);
    ctx.quadraticCurveTo (125, 25, 75, 25);
    ctx.stroke ();
  }
}
  

Скриншот	Живой образец

Кубические кривые Безье

В этом примере сердце нарисовано с использованием кубических кривых Безье.

  function draw () {
  var canvas = document.getElementById ('холст');
  if (canvas.getContext) {
    var ctx = canvas.getContext ('2d');

    
    ctx.beginPath ();
    ctx.moveTo (75, 40);
    ctx.bezierCurveTo (75, 37, 70, 25, 50, 25);
    ctx.bezierCurveTo (20, 25, 20, 62,5, 20, 62,5);
    ctx.bezierCurveTo (20, 80, 40, 102, 75, 120);
    ctx.bezierCurveTo (110, 102, 130, 80, 130, 62,5);
    ctx.bezierCurveTo (130, 62,5, 130, 25, 100, 25);
    ctx.bezierCurveTo (85, 25, 75, 37, 75, 40);
    ctx.fill ();
  }
}
  

Скриншот	Живой образец

Прямоугольники

В дополнение к трем методам, которые мы видели в Рисование прямоугольников, которые рисуют прямоугольники прямо на холсте, rect () , который добавляет прямоугольный путь к текущему открытому пути.

прямоугольник (x, y, ширина, высота)

Рисует прямоугольник, верхний левый угол которого задан как ( x , y ) с указанной шириной и высотой .

Перед выполнением этого метода автоматически вызывается метод moveTo () с параметрами (x, y). Другими словами, текущее положение пера автоматически сбрасывается до координат по умолчанию.

Создание комбинаций

До сих пор в каждом примере на этой странице использовался только один тип функции контура для каждой формы.Однако нет ограничений на количество или типы путей, которые вы можете использовать для создания формы. Итак, в этом последнем примере давайте объединим все функции пути, чтобы создать набор очень известных игровых персонажей.

  function draw () {
  var canvas = document.getElementById ('холст');
  if (canvas.getContext) {
    var ctx = canvas.getContext ('2d');

    округленныйRect (ctx, 12, 12, 150, 150, 15);
    округленныйRect (CTX, 19, 19, 150, 150, 9);
    Round RoundRect (CTX, 53, 53, 49, 33, 10);
    Round RoundRect (CTX, 53, 119, 49, 16, 6);
    округленныйRect (ctx, 135, 53, 49, 33, 10);
    округленныйRect (ctx, 135, 119, 25, 49, 10);

    ctx.beginPath ();
    ctx.arc (37, 37, 13, Math.PI / 7, -Math.PI / 7, ложь);
    ctx.lineTo (31, 37);
    ctx.fill ();

    for (var i = 0; i <8; i ++) {
      ctx.fillRect (51 + я * 16, 35, 4, 4);
    }

    for (i = 0; i <6; i ++) {
      ctx.fillRect (115, 51 + я * 16, 4, 4);
    }

    for (i = 0; i <8; i ++) {
      ctx.fillRect (51 + я * 16, 99, 4, 4);
    }

    ctx.beginPath ();
    ctx.moveTo (83, 116);
    ctx.lineTo (83, 102);
    ctx.bezierCurveTo (83, 94, 89, 88, 97, 88);
    ctx.bezierCurveTo (105, 88, 111, 94, 111, 102);
    ctx.lineTo (111, 116);
    ctx.lineTo (106,333, 111,333);
    ctx.lineTo (101,666, 116);
    ctx.lineTo (97, 111.333);
    ctx.lineTo (92.333, 116);
    ctx.lineTo (87,666, 111,333);
    ctx.lineTo (83, 116);
    ctx.fill ();

    ctx.fillStyle = 'белый';
    ctx.beginPath ();
    ctx.moveTo (91, 96);
    ctx.bezierCurveTo (88, 96, 87, 99, 87, 101);
    ctx.bezierCurveTo (87, 103, 88, 106, 91, 106);
    ctx.bezierCurveTo (94, 106, 95, 103, 95, 101);
    ctx.bezierCurveTo (95, 99, 94, 96, 91, 96);
    ctx.moveTo (103, 96);
    ctx.bezierCurveTo (100, 96, 99, 99, 99, 101);
    ctx.bezierCurveTo (99, 103, 100, 106, 103, 106);
    ctx.bezierCurveTo (106, 106, 107, 103, 107, 101);
    ctx.bezierCurveTo (107, 99, 106, 96, 103, 96);
    ctx.fill ();

    ctx.fillStyle = 'черный';
    ctx.beginPath ();
    ctx.arc (101, 102, 2, 0, Math.PI * 2, истина);
    ctx.fill ();

    ctx.beginPath ();
    ctx.arc (89, 102, 2, 0, Math.PI * 2, истина);
    ctx.fill ();
  }
}



function roundedRect (ctx, x, y, width, height, radius) {
  ctx.beginPath ();
  ctx.moveTo (x, y + радиус);
  ctx.lineTo (x, y + height - радиус);
  ctx.arcTo (x, y + высота, x + радиус, y + высота, радиус);
  ctx.lineTo (x + width - радиус, y + высота);
  ctx.arcTo (x + ширина, y + высота, x + ширина, y + высота-радиус, радиус);
  ctx.lineTo (x + ширина, y + радиус);
  ctx.arcTo (x + width, y, x + width - радиус, y, радиус);
  ctx.lineTo (x + радиус, y);
  ctx.arcTo (x, y, x, y + радиус, радиус);
  ctx.stroke ();
}
  

Полученное изображение выглядит так:

Снимок экрана	Живой образец

Мы не будем вдаваться в подробности, так как это на самом деле удивительно просто.Наиболее важные моменты, на которые следует обратить внимание, - это использование свойства fillStyle в контексте рисования и использование служебной функции (в данном случае roundedRect () ). Использование служебных функций для фрагментов рисования, которые вы часто делаете, может быть очень полезным и уменьшить объем необходимого кода, а также его сложность.

Мы еще раз рассмотрим fillStyle более подробно позже в этом руководстве. Здесь все, что мы делаем, это используем его для изменения цвета заливки контуров с черного цвета по умолчанию на белый, а затем обратно.

Как мы видели в последнем примере, может быть серия путей и команд рисования для рисования объектов на вашем холсте. Чтобы упростить код и повысить производительность, объект Path3D , доступный в последних версиях браузеров, позволяет кэшировать или записывать эти команды рисования. Вы можете быстро воспроизвести свои пути. Давайте посмотрим, как мы можем построить объект Path3D :

Path3D ()

Конструктор Path3D () возвращает вновь созданный объект Path3D , необязательно с другим путем в качестве аргумента (создает копию) или необязательно со строкой, состоящей из данных пути SVG.

  новый Path3D ();
новый Path3D (путь);
новый Path3D (d);
  

Все методы пути, такие как moveTo , rect , arc или quadraticCurveTo и т. Д., О которых мы узнали выше, доступны для объектов Path3D .

API Path3D также добавляет способ объединения путей с помощью метода addPath . Это может быть полезно, например, когда вы хотите построить объекты из нескольких компонентов.

Path3D.addPath (путь [, преобразование])

Добавляет путь к текущему пути с дополнительной матрицей преобразования.

Пример Path3D

В этом примере мы создаем прямоугольник и круг. Оба хранятся как объект Path3D , поэтому они доступны для дальнейшего использования. С новым Path3D API несколько методов были обновлены, чтобы опционально принимать объект Path3D для использования вместо текущего пути.Здесь, например, для рисования обоих объектов на холсте используются обводка и заливка с аргументом пути.

  function draw () {
  var canvas = document.getElementById ('холст');
  if (canvas.getContext) {
    var ctx = canvas.getContext ('2d');

    var rectangle = new Path3D ();
    прямоугольник. прямоугольник (10, 10, 50, 50);

    var circle = new Path3D ();
    круг.дуга (100, 35, 25, 0, 2 * Math.PI);

    ctx.stroke (прямоугольник);
    ctx.fill (кружок);
  }
}
  

Снимок экрана	Живой образец

Использование путей SVG

Еще одна мощная функция нового холста Path3D API - инициализация данных пути для вашего пути к данным SVG. . Это может позволить вам передавать данные пути и повторно использовать их как в SVG, так и в холсте.

Путь переместится в точку ( M10 10 ), а затем переместится по горизонтали на 80 точек вправо ( h 80 ), затем на 80 точек вниз ( v 80 ), затем на 80 точек влево ( h - 80 ), а затем обратно в начало ( z ).Вы можете увидеть этот пример на странице конструктора Path3D .

  var p = new Path3D ('M10 10 h 80 v 80 h -80 Z');
  

Математика 7 класс, Раздел 1 - Семейные материалы

Масштабированные копии

На этой неделе ваш ученик узнает о масштабировании фигур. Изображение представляет собой масштабную копию оригинала, если форма растянута таким образом, чтобы не искажать ее. Например, вот оригинальная картинка и пять копий. Изображения C и D являются копиями оригинала в масштабе, а изображения A, B и E - нет.

В каждой масштабированной копии стороны в определенное количество раз превышают длину соответствующих сторон оригинала. Мы называем это число масштабным коэффициентом . Размер масштабного коэффициента влияет на размер копии. Коэффициент масштабирования больше 1 делает копию больше оригинала. Коэффициент масштабирования меньше 1 делает копию меньше.

Вот задание, которое стоит попробовать со своим учеником:

1. Для каждой копии укажите, является ли она масштабированной копией исходного треугольника.Если да, то каков масштабный коэффициент?
2. Нарисуйте еще одну масштабированную копию исходного треугольника с другим масштабным коэффициентом.

Решение:

1. 1. Копия 1 - это уменьшенная копия исходного треугольника. Коэффициент масштабирования равен 2, потому что каждая сторона в копии 1 вдвое длиннее соответствующей стороны в исходном треугольнике. 5 \ boldcdot 2 = 10, 4 \ boldcdot 2 = 8, (6.4) \ boldcdot 2 = 12.8
   2. Копия 2 - это уменьшенная копия исходного треугольника. Масштабный коэффициент равен \ frac12 или 0.5, потому что каждая сторона копии 2 вдвое короче соответствующей стороны исходного треугольника. 5 \ boldcdot (0,5) = 2,5, 4 \ boldcdot (0,5) = 2, (6,4) \ boldcdot (0,5) = 3,2
   3. Копия 3 не является масштабированной копией исходного треугольника. Форма была искажена. Углы бывают разных размеров, и нет одного числа, которое мы могли бы умножить на длину каждой стороны исходного треугольника, чтобы получить соответствующую длину стороны в Копии 3.
2. Ответы различаются. Пример ответа: прямоугольный треугольник со сторонами 12, 15 и 19.2 единицы будут копией исходного треугольника в масштабе с использованием коэффициента масштабирования 3.

Чертежи в масштабе

На этой неделе ваш ученик будет изучать масштабные чертежи. Чертеж в масштабе - это двухмерное представление реального объекта или места. Карты и планы этажей являются примерами масштабных чертежей.

Масштаб говорит нам, какую длину на чертеже в масштабе представляет в действительной длине. Например, масштаб «от 1 дюйма до 5 миль» означает, что 1 дюйм на чертеже представляет 5 фактических миль.Если на рисунке показана дорога длиной 2 дюйма, мы знаем, что на самом деле она имеет длину 2 \ boldcdot 5 или 10 миль.

Масштаб может быть записан с единицами измерения (например, от 1 дюйма до 5 миль) или без единиц (например, от 1 до 50 или от 1 до 400). Если на шкале нет единиц измерения, для расстояний на чертеже шкалы и фактических расстояний используются одни и те же единицы. Например, шкала «от 1 до 50» означает, что 1 сантиметр на чертеже соответствует 50 фактическим сантиметрам, 1 дюйм представляет 50 дюймов и т. Д.

Вот задание, которое стоит попробовать со своим учеником:

Киран нарисовал план этажа своего класса, используя масштаб от 1 дюйма до 6 футов.

1. Рисунок Кирана имеет ширину 4 дюйма и длину 5 \ frac12 дюймов. Каковы размеры фактического класса?
2. Стол в классе имеет ширину 3 фута и длину 6 футов. Какого размера она должна быть на чертеже в масштабе?
3. Киран хочет сделать увеличенный чертеж того же класса. Какие из этих весов он мог использовать?
   1. 1 до 50
   2. 1 до 72
   3. 1 до 100

Решение:

1. 24 фута в ширину и 33 фута в длину.Поскольку каждый дюйм на рисунке соответствует 6 футам, мы можем умножить его на 6, чтобы найти фактические размеры. Фактическая ширина классной комнаты составляет 24 фута, потому что 4 \ boldcdot 6 = 24. Классная комната имеет длину 33 фута, потому что 5 \ frac12 \ boldcdot 6 = 5 \ boldcdot 6 + \ frac12 \ boldcdot 6 = 30 + 3 = 33.
2. \ frac12 дюймов в ширину и 1 дюйм в длину. Мы можем разделить на 6, чтобы найти размеры на чертеже. 6 \ div 6 = 1 и 3 \ div 6 = \ frac12.
3. A, от 1 до 50. Шкала «от 1 дюйма до 6 футов» эквивалентна шкале «от 1 до 72», потому что в 6 футах 72 дюйма.Масштаб «от 1 до 100» сделает чертеж в масштабе меньше, чем масштаб «от 1 до 72», потому что каждый дюйм на новом чертеже будет представлять более фактическую длину. Масштаб «от 1 до 50» сделает чертеж в масштабе больше, чем масштаб «от 1 до 72», потому что Kiran потребуется больше дюймов на чертеже, чтобы представить ту же фактическую длину.

Как нарисовать невозможный треугольник

Простое, пошаговое руководство по рисованию невозможного треугольника

Нажмите ЗДЕСЬ, чтобы сохранить учебник в Pinterest!

Невозможный треугольник, также называемый треугольником Пенроуза или невозможным треугольником, был впервые нарисован шведским художником по имени Оскар Реутерсвард в 1934 году.

Он использовался в работах психиатра Лайонела Пенроуза, математика Роджера Пенроуза и голландского художника-математика М. Эшера, а также других художников.

Форма была описана как «невозможная в чистом виде».

Невозможный треугольник - это разновидность оптической иллюзии - изображение, которое из-за восприятия глазами и мозгом отличается от реальности.

Невозможные объекты - это оптические иллюзии, в которых двухмерная фигура (что-то плоское, например, рисунок на бумаге) интерпретируется мозгом как трехмерный объект, который не может существовать на самом деле из-за своих физических пропорций.

Прокрутите вниз, чтобы загрузить этот учебник в формате PDF.

Присмотритесь к невозможному треугольнику, и вы увидите, что его стороны необычным образом соединяются.

В то время как невозможные объекты не могут существовать в реальном мире - вот почему их называют невозможными - художники приложили усилия, чтобы приблизить их.

Скульптура под открытым небом, показанная в Восточном Перте, Австралия, например, принимает вид невозможного треугольника, если смотреть под определенным углом.Однако, если смотреть под другим углом, становится очевидным, что линии «треугольника» на самом деле не соединяются.

Психологи и другие ученые издавна интересовались оптическими иллюзиями.

Леонардо да Винчи, возможно, был первым, кто нарисовал оптическую иллюзию, серию линий, которые, когда вы наклонили бумагу под правильным углом, превратились в глаз.

Исследователи говорят, что оптические иллюзии возникают потому, что когда наш мозг узнает о нашем окружении, он начинает делать предположения.

Иногда эти предположения ошибочны, например, когда плоский рисунок выглядит трехмерным, и этот сдвиг может вызвать чувство замешательства.

Хотите нарисовать невозможный треугольник? Это не невозможно. На самом деле, это легко сделать с помощью этого простого пошагового руководства по рисованию.

Все, что вам понадобится, это карандаш, ручка или маркер и лист бумаги.

Вы также можете использовать линейку, чтобы рисовать прямые линии, и мелки, цветные карандаши или краски, чтобы закрасить законченный рисунок.

Если вам понравился этот урок, см. Также следующие руководства по рисованию: Кристалл, Звезда и Снежинка.

Пошаговые инструкции по рисованию невозможного треугольника

Рисование невозможного треугольника - шаг 1

1. Начните с рисования небольшого равностороннего треугольника, то есть треугольника со сторонами равной длины. Это сформирует отверстие в середине невозможного треугольника.

Рисование невозможного треугольника - шаг 2

2. Вытяните короткую прямую линию по диагонали от каждой точки треугольника.Эти линии образуют основу трехмерного изображения невозможного треугольника.

Рисование невозможного треугольника - шаг 3

3. От самой верхней диагональной линии проведите прямую линию, параллельную стороне маленького треугольника. Затем от этой линии проведите еще одну прямую, параллельную нижней части маленького треугольника.

Рисование невозможного треугольника - шаг 4

4. Проведите прямую горизонтальную линию от самой нижней из исходных диагоналей. Эта линия должна быть параллельна двум другим горизонтальным линиям и на равном расстоянии от них.

Рисование невозможного треугольника - шаг 5

5. Проведите длинную прямую линию вверх от оставшейся диагональной линии, параллельную стороне маленького треугольника.

Рисование невозможного треугольника - шаг 6

6. Из самой верхней точки линии, проведенной на предыдущем шаге, проведите длинную прямую линию, параллельную противоположной стороне треугольника.

Рисование невозможного треугольника - шаг 7

7. От средней горизонтальной линии вытяните длинную прямую линию вверх, параллельно стороне существующего треугольника.

Рисование невозможного треугольника - шаг 8

8. Осталось только заключить фигуру невозможного треугольника. Начните с закрытия одного из углов короткой прямой линией.

Рисование невозможного треугольника - шаг 9

9. Обведите оставшиеся углы невозможного треугольника короткими прямыми линиями.

Полный рисунок невозможного треугольника

10. Раскрасьте свой рисунок.

Готовы к другим геометрическим рисункам? Ознакомьтесь с нашими руководствами по рисованию кристаллов, снежинок и звезд.

Прокрутите вниз, чтобы загрузить этот учебник в формате PDF.

Распечатать Учебник по рисованию

УСТРАНЕНИЕ НЕПОЛАДОК УЧАСТНИКА

Все еще видите рекламу или не можете загрузить PDF-файл?

Сначала убедитесь, что вы вошли в систему. Вы можете войти в систему на странице входа в систему.

Если вы по-прежнему не можете загрузить PDF-файл, наиболее вероятным решением будет перезагрузка страницы.

Это можно сделать, нажав кнопку перезагрузки браузера.

Это значок в виде круглой стрелки в верхней части окна браузера, обычно в верхнем левом углу (вы также можете использовать сочетания клавиш: Ctrl + R на ПК и Command + R на Mac).

Мы не можем найти эту страницу

(* {{l10n_strings.REQUIRED_FIELD}})

{{l10n_strings.CREATE_NEW_COLLECTION}} *

{{l10n_strings.ADD_COLLECTION_DESCRIPTION}}

{{l10n_strings.COLLECTION_DESCRIPTION}} {{addToCollection.description.length}} / 500 {{l10n_strings.TAGS}} {{$ item}} {{l10n_strings.PRODUCTS}} {{l10n_strings.DRAG_TEXT}}

{{l10n_strings.DRAG_TEXT_HELP}}

{{l10n_strings.ЯЗЫК}} {{$ select.selected.display}}

{{article.content_lang.display}}

{{l10n_strings.AUTHOR}}

{{l10n_strings.AUTHOR_TOOLTIP_TEXT}}

{{$ select.selected.display}} {{l10n_strings.CREATE_AND_ADD_TO_COLLECTION_MODAL_BUTTON}} {{l10n_strings.CREATE_A_COLLECTION_ERROR}}

Построение треугольников - Локусы и конструкции - Edexcel - Редакция математики GCSE - Edexcel

Треугольники и другие формы можно точно построить с помощью транспортира, циркуля и линейки.

Чтобы нарисовать треугольник, необходимы три свойства:

1. SAS - Боковой угол Сторона
2. ASA - Боковой угол
3. SSS - Боковой бок Сторона

Построение треугольников согласно SAS

Требуются длины двух сторон и размер угла между ними.

Пример

Нарисуйте точный рисунок треугольника длиной 4 см и 6 см с углом 40 ° между ними.

Нарисуйте самую длинную сторону с помощью линейки.

С помощью транспортира измерьте угол 40 °.Поместите центр транспортира в точку А. Отсчитайте от нуля градусов от горизонтальной линии до 40 ° и поставьте отметку в этой точке. Это точка B

Используйте линейку, чтобы провести линию от A до B, чтобы она была длиной 4 см

Нарисуйте третью сторону треугольника от B до C

Построение треугольников согласно ASA

Размеры двух углов и длина стороны между ними необходимы.

Пример

Нарисуйте точный рисунок треугольника с углами 40 ° и 70 ° со стороной длиной 8 см между ними.

Нарисуйте сторону с помощью линейки

С помощью транспортира измерьте угол 40 °. Поместите центр транспортира в точку D. Отсчитайте от нуля градусов по горизонтали до 40 °. Нанесите строительную отметку под углом 40 °

С помощью линейки проведите линию от D через строительную отметку. Сделайте его длинным

С помощью транспортира измерьте угол 70 ° от E. Поместите центр транспортира в точку E. Отсчитывайте от нуля градусов от горизонтальной линии до 70 °. Поставьте отметку под углом 70 °, точка F

С помощью линейки проведите линию от E до F.Убедитесь, что он пересекает линию 40 °.

Построение треугольников согласно SSS

Необходимы длины всех трех сторон.

Пример

Нарисуйте точный треугольник со сторонами длиной 3 см, 5 см и 6 см.

Нарисуйте самую длинную сторону с помощью линейки.

Раскройте циркуль, пока он не станет шириной 5 см. Используйте линейку, чтобы измерить это. Нарисуйте дугу от точки H над линией

Раскройте циркуль, пока он не станет шириной 3 см. Используйте линейку, чтобы измерить это.Нарисуйте дугу из точки J над линией

Соедините дугу с точками H и J с помощью линейки

Как и во всех конструкциях, убедитесь, что вспомогательные линии не стираются.