Рисуем сами симметрические и механические формы
Раньше, чем перейти к рисованию механических форм, необходимо проделать ряд упражнений, организующих правильное восприятие сложных форм, и рисование симметричных форм, какие встречаются в большинстве предметов.
Под схемой предмета понимается линейная фигура, в которой каждая линия по своей форме и размеру характеризует отдельную часть предмета.
Такая схема рисуется, как скелет вещи, после чего уже производится наполнение этой схемы материалом. Таковы, например, схемы стула (рис. 149) и велосипеда (рис. 150).
Полезно нарисовать схемы по предлагаемым рисункам: ключа (рис. 151), подковы (рыс. 152), тисков (рис. 153), плуга (рис. 154).
СИММЕТРИЧНЫЕ ФОРМЫ
Симметрией называется отображенное равенство частей фигуры, подобное предмету и его зеркальному изображению.
Симметрия может быть на плоскости (рис. 155), причем она тогда строится относительно оси симметрии, то есть линии.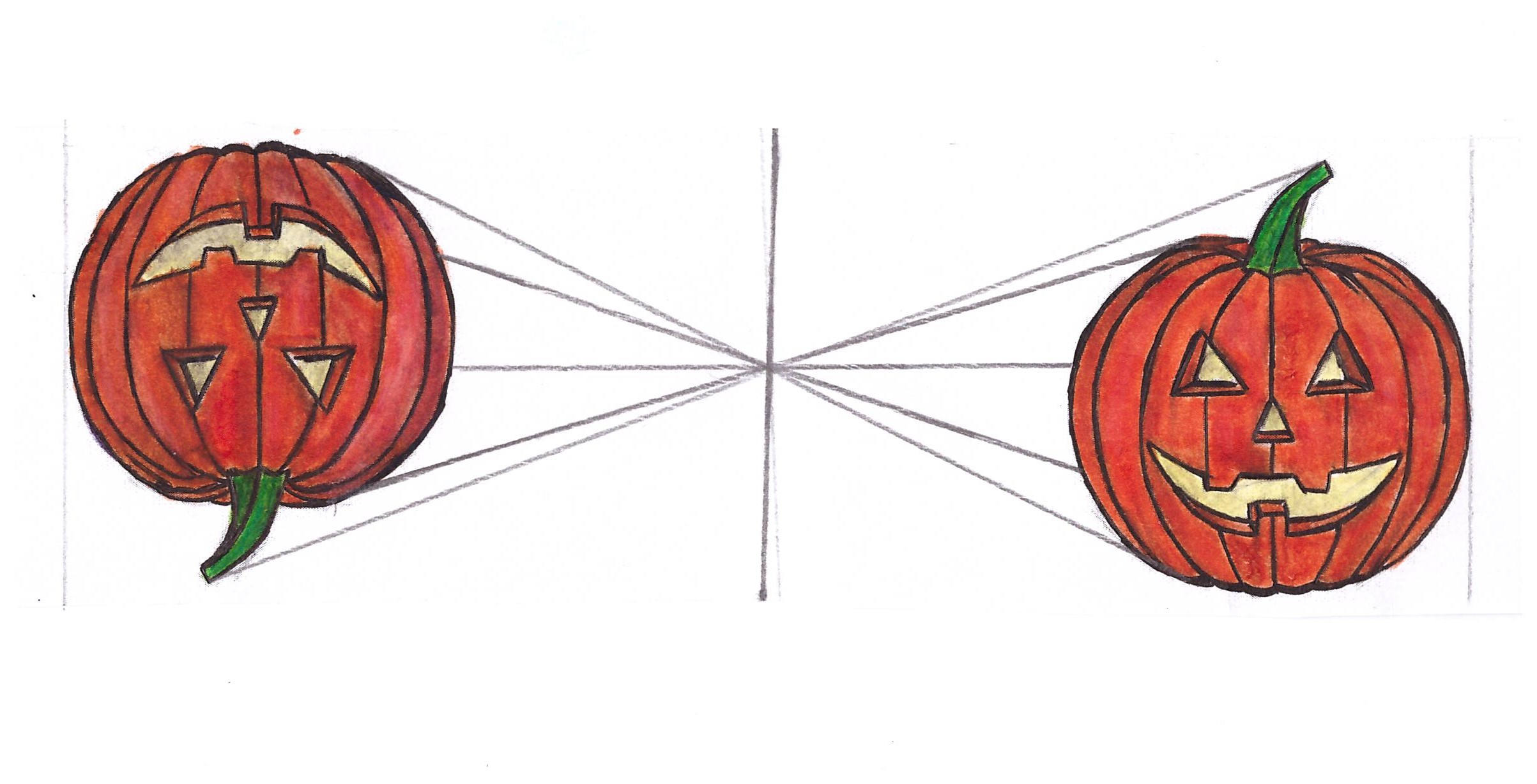
Симметрия может быть и в пространстве (рис. 156), тогда она строится уже относительно плоскости симметрии.
Имея перед собой рис. 157—160, дорисуем симметричные части фигуры.
МЕХАНИЧЕСКИЕ ФОРМЫ
Рисуем коленчатый вал (рис. 161) — деталь, встречающуюся во многих механизмах для преобразования прямолинейного движения во вращательное и обратно.
Коленчатый вал представляет собой основной вал, состоящий из трех частей, расположенных строго на одной оси (иначе он не будет вращаться), прерванный двумя «кривошипами», расположенными под прямым углом друг к другу (кривошипы могут находиться и в одной плоскости, и под углом в 120°).
Каждый кривошип, в свою очередь, состоит из цилиндрической шейки и двух призматических щек. Оканчивается коленчатый вал цилиндрическим фланцем с отверстиями. К нему прикрепляется движимая часть механизма.
Рисуем сами симметрические и механические формыРаньше всего рисуем схему, в которой прямой линией определяем положение вала, и уже на этой прямой отмечаем направление и величины кривошипов.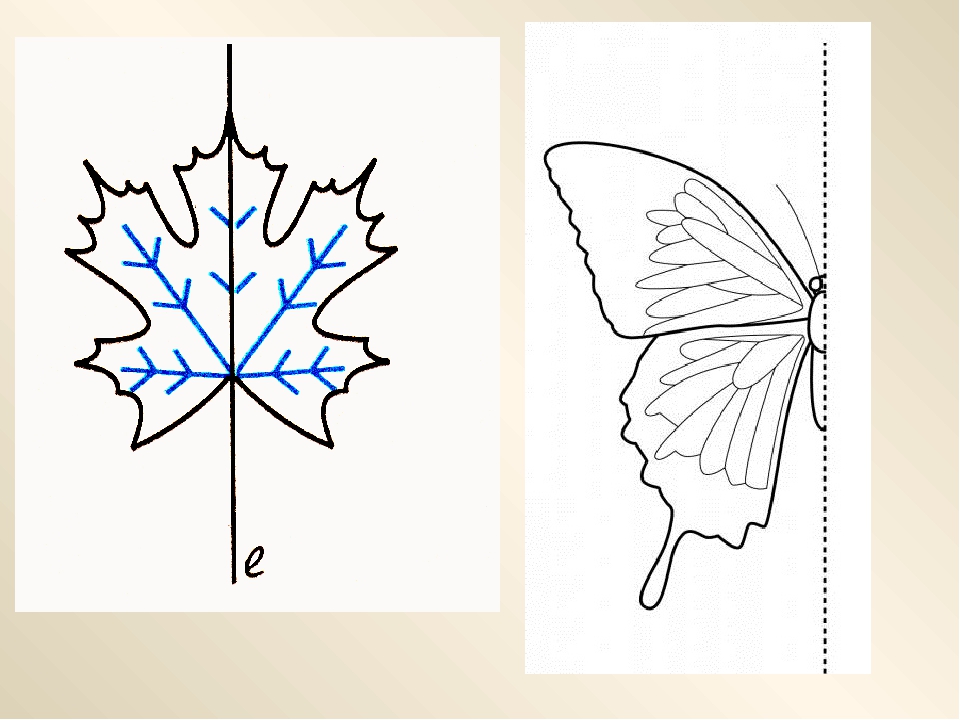
Направления и относительные величины (на бумаге) определяем при помощи вспомогательного куба (pиc. 162), который пристраиваем при избранном направлении вала. В правую сторону куба вписываем круг — он нужен нам для определения величины зрительного сжатия оснований цилиндров, которые расположены по направлению основной оси, а ребра куба укажут на зрительные величины щек кривошипов.
Важно установить место составных частей вала. Если ось рисовать не общей, а двигаться последовательно по пути всего вала, заходя в кривошипы, то легко может получиться ошибка, и три части вала не окажутся на одной прямой (рис. 163).
Когда предварительная осевая наметка готова — можно уже наполнить ее массой. Устанавливаем толщину вала и шеек кривошипа и прорисовываем окружности пересечений оснований цилиндрических частей {рис. 164) главного вала и шеек со щеками.
Считая, что оси щек идут на нашем рисунке не внутри, на пересечении этих осей с продольной осью вала, строим толщину щеки и повторяем эту же грань по ту сторону щеки
(рис. 165).
165).
Подобное же построение повторяем еще три раза, пристраиваем фланец, и рисунок готов (рис. 166). Надо помнить, что круглые отверстия во фланце (для болтов) будут иметь такое же сжатие, как остальные круги, находящиеся в этом же положении.
Рисуем сами симметрические и механические формыОсевая и центральная симметрия — урок. Математика, 6 класс.
Симметрия — соразмерность, соответствие, сходность, порядок в расположении частей. Это слово, как и многие другие математические понятия, произошли от греческих слов.
Смотря на объекты вокруг, мы не раз восклицаем: «Какая симметрия!»
Рис. \(1\). Симметрия в архитектуре.
Люди с давних времён использовали симметрию в рисунках, орнаментах, предметах быта, в архитектуре, художестве, строительстве.
Но симметрия широко распространена и в природе, где не было вмешательства человеческой руки. Её можно наблюдать в форме листьев и цветов растений, в расположении различных органов животных, в форме кристаллических тел, в порхающей бабочке, загадочной снежинке, морской звезде.
Рис. \(2\). Симметрия в природе.
Пока рассмотрим две симметрии на плоскости: относительно точки и прямой.
Центральная симметрия
Симметрию относительно точки называют центральной симметрией.
Точки M и M1 симметричны относительно некоторой точки \(O\), если точка \(O\) является серединой отрезка MM1.
Рис. \(3\). Центральная симметрия.
Точка \(O\) называется центром симметрии.
Алгоритм построения центрально-симметричных фигур.
Рис. \(4\). Треугольники симметричны относительно точки \(O\).
Построим треугольник A1B1C1, симметричный треугольнику \(ABC\) относительно центра (точки) \(O\):
1. для этого соединим точки \(A\), \(B\), \(C\) с центром \(O\) и продолжим эти отрезки;
2. измерим отрезки \(AO\), \(BO\), \(CO\) и отложим с другой стороны от точки \(O\) равные им отрезки AO=OA1;BO=OB1;CO=OC1;
3. соединим получившиеся точки отрезками и получим треугольник A1B1C1, симметричный данному треугольнику \(ABC\).
Фигуры, симметричные относительно некоторой точки, равны.
Фигура симметрична относительно центра симметрии, если для каждой точки этой фигуры симметричная ей точка также лежит на этой фигуре. Такая фигура имеет центр симметрии (фигура с центральной симметрией).
Осевая симметрия
Осевая симметрия — это симметрия относительно проведённой прямой (оси).
Точки M и M1 симметричны относительно некоторой прямой (оси симметрии), если эти точки лежат на прямой, перпендикулярной данной, и на одинаковом расстоянии от оси симметрии.
Рис. \(5\). Осевая симметрия.
Алгоритм построения фигуры, симметричной относительно некоторой прямой.
Рис. \(6\). Треугольники симметричны относительно прямой.
\(6\). Треугольники симметричны относительно прямой.
Построим треугольник A1B1C1, симметричный треугольнику \(ABC\) относительно красной прямой:
1. для этого проведём из вершин треугольника \(ABC\) прямые, перпендикулярные оси симметрии, и продолжим их дальше на другой стороне оси.
2. Измерим расстояния от вершин треугольника до получившихся точек на прямой и отложим с другой стороны прямой такие же расстояния.
3. Соединим получившиеся точки отрезками и получим треугольник A1B1C1, симметричный данному треугольнику \(ABC\).
Фигуры, симметричные относительно прямой, равны.
Фигура считается симметричной относительно прямой, если для каждой точки рассматриваемой фигуры симметричная для неё точка относительно данной прямой также находится на этой фигуре. Прямая является в этом случае осью симметрии фигуры.
Иногда у фигур несколько осей симметрии:
- для неразвёрнутого угла существует единственная ось симметрии — это биссектриса данного угла.

- Для равнобедренного треугольника есть единственная ось симметрии.
- Для равностороннего треугольника — три оси.
- Для квадрата — целых четыре.
- Для окружности осей симметрии бесчисленное множество — это каждая прямая, которая проходит через центр этой фигуры.
- Есть фигуры без осей симметрии — это параллелограмм и треугольник, все стороны которого различны.
Источники:
Рис. 1 Симметрия в архитектуре. Указание авторства не требуется, 2021-06-02, Архитектура/Здания, бесплатно для коммерческого использования, https://clck.ru/VFC5B.
Рис. 2. Симметрия в природе. Указание авторства не требуется, 2021-06-02, бесплатно для коммерческого использования, https://clck.ru/VFECn.
Рис. 3. Центральная симметрия, © ЯКласс.
Рис. 4. Треугольники симметричны относительно точки O, © ЯКласс.
Рис. 5. Осевая симметрия, © ЯКласс.
Рис. 6. Треугольники симметричны относительно прямой, © ЯКласс.
Как нарисовать симметричный предмет. Понятие о симметрии
Вам понадобится
- — свойства симметричных точек;
- — свойства симметричных фигур;
- — линейка;
- — угольник;
- — циркуль;
- — карандаш;
- — лист бумаги;
- — компьютер с графическим редактором.
Инструкция
Проведите прямую a, которая будет являться осью симметрии. Если ее координаты не заданы, начертите ее произвольно. С одной стороны от этой прямой поставьте произвольную точку A. необходимо найти симметричную точку.
Полезный совет
Свойства симметрии постоянно используются в программе AutoCAD. Для этого используется опция Mirror. Для построения равнобедренного треугольника или равнобедренной трапеции достаточно начертить нижнее основание и угол между ним и боковой стороной. Отразите их с помощью указанной команды и продлите боковые стороны до необходимой величины. В случае с треугольником это будет точка их пересечения, а для трапеции — заданная величина.
С симметрией вы постоянно сталкиваетесь в графических редакторах, когда пользуетесь опцией «отразить по вертикали/горизонтали». В этом случае за ось симметрии берется прямая, соответствующая одной из вертикальных или горизонтальных сторон рамки рисунка.
Источники:
- как начертить центральную симметрию
Построение сечения конуса не такая уж сложная задача. Главное — соблюдать строгую последовательность действий. Тогда данная задача будет легко выполнима и не потребует от Вас больших трудозатрат.
Вам понадобится
- — бумага;
- — ручка;
- — циркль;
- — линейка.
Инструкция
При ответе на этот вопрос, сначала следует определиться – какими параметрами задано сечение.
Пусть это будет прямая пересечения плоскости l с плоскостью и точка О, которая местом пересечения с его сечением.
Построение иллюстрирует рис.1. Первый шаг построения сечения – это через центр сечения его диаметра, продленного до l перпендикулярно этой линии. В итоге получается точка L. Далее через т.О проведите прямую LW, и постройте две направляющие конуса, лежащие в главном сечении О2М и О2С. В пересечении этих направляющих лежат точка Q, а также уже показанная точка W. Это первые две точки искомого сечения.
В итоге получается точка L. Далее через т.О проведите прямую LW, и постройте две направляющие конуса, лежащие в главном сечении О2М и О2С. В пересечении этих направляющих лежат точка Q, а также уже показанная точка W. Это первые две точки искомого сечения.
Теперь проведите в основании конуса ВВ1 перпендикулярный МС и постройте образующие перпендикулярного сечения О2В и О2В1. В этом сечении через т.О проведите прямую RG, параллельную ВВ1. Т.R и т.G — еще две точки искомого сечения. Если бы сечения бал известен, то его можно было бы построить уже на этой стадии. Однако это вовсе не эллипс, а нечто эллипсообразное, имеющее симметрию относительно отрезка QW. Поэтому следует строить как можно больше точек сечения, чтобы соединяя их в дальнейшем плавной кривой получить наиболее достоверный эскиз.
Постройте произвольную точку сечения. Для этого проведите в основании конуса произвольный диаметр AN и постройте соответствующие направляющие О2A и O2N. Через т.О проведите прямую, проходящую через PQ и WG, до ее пересечения с только что построенными направляющими в точках P и E. Это еще две точки искомого сечения. Продолжая так же и дальше, можно сколь угодно искомых точек.
Это еще две точки искомого сечения. Продолжая так же и дальше, можно сколь угодно искомых точек.
Правда, процедуру их получения можно немного упростить пользуясь симметрией относительно QW. Для этого можно в плоскости искомого сечения провести прямые SS’, параллельные RG до пересечения их с поверхность конуса. Построение завершается скруглением построенной ломаной из хорд. Достаточно построить половину искомого сечения в силу уже упомянутой симметрии относительно QW.
Видео по теме
Вам требуется начертить график тригонометрической функции ? Освойте алгоритм действий на примере построения синусоиды. Для решения поставленной задачи используйте метод исследования.
Вам понадобится
- — линейка;
- — карандаш;
- — знание основ тригонометрии.
Инструкция
Видео по теме
Обратите внимание
Если две полуоси однополосного гиперболоида равны, то фигуру можно получить путем вращения гиперболы с полуосями, одна из которых вышеуказанная, а другая, отличающаяся от двух равных, вокруг мнимой оси.
Полезный совет
При рассмотрении этой фигуры относительно осей Oxz и Oyz видно, что ее главными сечениями являются гиперболы. А при разрезе данной пространственной фигуры вращения плоскостью Oxy ее сечение представляет собой эллипс. Горловой эллипс однополосного гиперболоида проходит через начало координат, ведь z=0.
Горловой эллипс описывается уравнением x²/a² +y²/b²=1, а другие эллипсы составляются по уравнению x²/a² +y²/b²=1+h²/c².
Источники:
- Эллипсоиды, параболоиды, гиперболоиды. Прямолинейные образующие
Форма пятиконечной звезды повсеместно используется человеком с древних времен. Мы считаем ее форму прекрасной, так как бессознательно различаем в ней соотношения золотого сечения, т.е. красота пятиконечной звезды обоснована математически. Первым описал построение пятиконечной звезды Евклид в своих «Началах». Давайте же приобщимся к его опыту.
Вам понадобится
- линейка;
- карандаш;
- циркуль;
- транспортир.

Инструкция
Построение звезды сводится к построению с последующим соединением его вершин друг с другом последовательно через одну. Для того чтобы построить правильный необходимо разбить окружность на пять .
Постройте произвольную окружность при помощи циркуля. Обозначьте ее центр точкой O.
Отметьте точку A и при помощи линейки начертите отрезок ОА. Теперь необходимо разделить отрезок OA пополам, для этого из точки А проведите дугу радиусом ОА до пересечения ее с окружностью в двух точках M и N. Постройте отрезок MN. Точка Е, в которой MN пересекает OA, будет делить отрезок OA пополам.
Восстановите перпендикуляр OD к радиусу ОА и соедините точку D и E. Сделайте засечку B на OA из точки E радиусом ED.
Теперь при помощи отрезка DB разметьте окружность на пять равных частей. Обозначьте вершины правильного пятиугольника последовательно цифрами от 1 до 5. Соедините точки в следующей последовательности: 1 с 3, 2 с 4, 3 с 5, 4 с 1, 5 с 2. Вот и правильная пятиконечная звезда, в правильный пятиугольник. Именно таким способом строил
Именно таким способом строил
Фридрих В.А. 1
Дементьева В.В. 1
1 Муниципальное бюджетное общеобразовательное учреждение «Средняя общеобразовательная школа № 6», г. Александровск, Пермский край
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
Введение
«Стоя перед черной доской и рисуя на ней
мелом разные фигуры,
я вдруг был поражен мыслью:
почему симметрия приятна глазу?
Что такое симметрия?
Это врожденное чувство, отвечал я сам себе»
Л.Н. Толстой
В учебнике математика 6 класс, автор Никольский С. М., на страницах 132 — 133 раздел Дополнительные задачи к главе № 3, имеются задания для исследования фигур на плоскости, симметричных относительно прямой. Меня заинтересовала данная тема, я решила выполнить задания и более подробно изучить данную тему.
Объект исследования — симметрия.
Предмет исследования — симметрия как основополагающий закон вселенной.
Какую гипотезу я буду проверять:
Я считаю, что осевая симметрия является не только математическим и геометрическим понятием, и применяется только для решения соответствующих задач, но и является основой гармонии, красоты, равновесия и устойчивости. Принцип симметрии используется практически во всех науках, в нашей повседневной жизни и является одним из «краеугольных» законов, на котором базируется мироздание в целом.
Актуальность темы
Понятие симметрия проходит через всю многовековую историю человеческого творчества. Оно встречается уже у истоков его развития. В наше время, наверное, трудно найти человека, который не имел бы какого-либо представления о симметрии. Мир, в котором мы живём, наполнен симметрией домов, улиц, творениями природы и человека. С симметрией мы встречаемся буквально на каждом шагу: в технике, искусстве, науке.
Поэтому, знание и понимание о симметрии в окружающем нас мире, является обязательным и необходимым, которое пригодится в дальнейшем для изучения других научных дисциплин.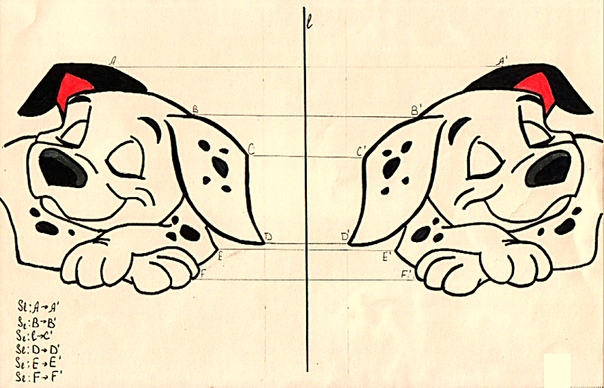 В этом и заключается актуальность избранной мной темы.
В этом и заключается актуальность избранной мной темы.
Цель и задачи
Цель работы: выяснить, какую роль играет симметрия в повседневной жизни человека, в природе, архитектуре, в быту, музыке и других науках.
Для достижения поставленной цели, мне необходимо выполнить следующие задачи:
1. Найти необходимую информацию, литературу и фотографии. Установить наибольшее количество данных, необходимых для моей работы, с помощью доступных для меня источников: учебники, энциклопедии или другие носители информации, соответствующих заданной теме.
2. Дать общие понятие о симметрии, видах симметрии и истории происхождения термина.
3. Для подтверждения своей гипотезы, создать поделки и провести эксперимент с данными фигурами, имеющими симметрию и не несимметричными.
4. Продемонстрировать и представить результаты наблюдений в своём исследовании.
Для практической части исследовательской работы мне необходимо сделать следующее, для чего я составила план работы:
1. Создать своими руками поделки с заданными свойствами — симметричные и не симметричные модели, композицию, используя цветную бумагу, картон, ножницы, фломастеры, клей и т.д.;
Создать своими руками поделки с заданными свойствами — симметричные и не симметричные модели, композицию, используя цветную бумагу, картон, ножницы, фломастеры, клей и т.д.;
2. Провести эксперимент с моими поделками, с двумя вариантами симметрии.
3. Исследовать, проанализировать и систематизировать полученные результаты, составив таблицу.
4. Для наглядного и интересного закрепления полученных знаний, с помощью приложения «Paint 3 D» создать рисунки для наглядности, а так же нарисовать картинки, с заданиями — дорисовать симметричную половинку (начиная с простых рисунков и заканчивая сложными) и объединить их, создав электронную книгу.
Методы исследования:
1. Анализ статей и всей информации о симметрии.
2. Компьютерное моделирование (обработка фотографий средствами графического редактора).
3. Обобщение и систематизация полученных данных.
Основная часть.
Осевая симметрия и понятие совершенства
С древних времен человек выработал представления о красоте и пытался постигнуть смысл совершенства. Красивы все творения природы. По-своему прекрасны люди, восхитительны животные и растения. Радует взор зрелище драгоценного камня или кристалла соли, сложно не любоваться снежинкой или бабочкой. Но почему так происходит? Нам кажется правильным и завершенным вид объектов, правая и левая половина которых выглядит одинаково.
Красивы все творения природы. По-своему прекрасны люди, восхитительны животные и растения. Радует взор зрелище драгоценного камня или кристалла соли, сложно не любоваться снежинкой или бабочкой. Но почему так происходит? Нам кажется правильным и завершенным вид объектов, правая и левая половина которых выглядит одинаково.
Видимо, первыми о сути красоты задумывались люди искусства.
Впервые обосновали это понятие художники, философы и математики Древней Греции. Древние скульпторы, изучавшие строение человеческого тела, еще в V веке до н.э. стали применять понятие «симметрия». Это слово имеет греческое происхождение и означает гармоничность, пропорциональность и похожесть расположения составляющих частей. Древнегреческий мыслитель и философ Платон утверждал, что прекрасным может быть лишь то, что симметрично и соразмерно.
И действительно, «радуют глаз» те явления и формы, которые имеют пропорциональность и завершенность. Их мы называем правильными.
Виды симметрии
В геометрии и математике рассматриваются три вида симметрии: осевая симметрия (относительно прямой), центральная (относительно точки) и зеркальная (относительно плоскости).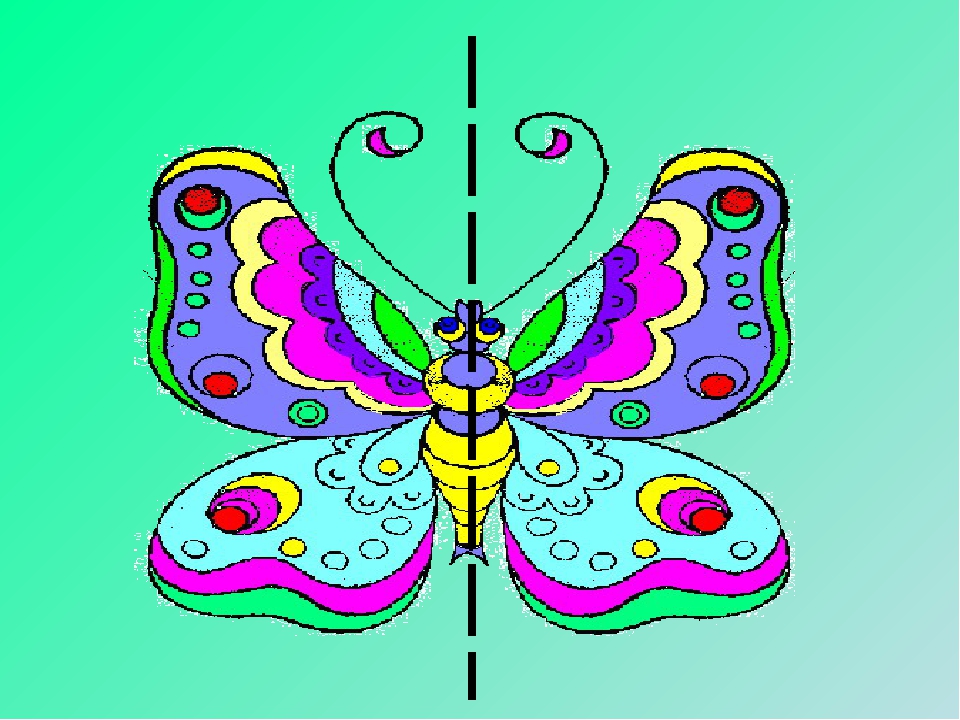
Осевая симметрия как математическое понятие
Точки симметричны относительно некой прямой (оси симметрии), если они лежат на прямой, перпендикулярной данной прямой, и на одинаковом расстоянии от оси симметрии.
Фигура считается симметричной относительно прямой, если для каждой точки рассматриваемой фигуры, симметричная для неё точка относительно данной прямой также находится на этой фигуре. Прямая является в этом случае осью симметрии фигуры.
Фигуры, симметричные относительно прямой равны. Если геометрической фигуре свойственна осевая симметрия, определение зеркальных точек можно наглядно представить, просто перегнув ее по оси и сложив равные половинки «лицом к лицу». Искомые точки при этом соприкоснутся.
Примеры оси симметрии: биссектриса неразвернутого угла равнобедренного треугольника, любая прямая, проведенная через центр окружности, и т.д. Если геометрической фигуре свойственна осевая симметрия, определение зеркальных точек можно наглядно представить, просто перегнув ее по оси и сложив равные половинки «лицом к лицу». Искомые точки при этом соприкоснутся.
Искомые точки при этом соприкоснутся.
Фигуры могут иметь несколько осей симметрии:
· осью симметрии угла является прямая, на которой лежит его биссектриса;
· осью симметрии окружности и круга является любая прямая, проходящая через их диаметр;
· равнобедренный треугольник имеет одну ось симметрии, равносторонний треугольник — три оси симметрии;
· прямоугольник имеет 2 оси симметрии, квадрат — 4, ромб — 2 оси симметрии.
Ось симметрии — это воображаемая линия разделяющая объект на симметричные части. На моём рисунке она изображена для наглядности.
Имеются фигуры, у которых нет ни одной оси симметрии. К таким фигурам относится параллелограмм, отличный от прямоугольника и ромба, разносторонний треугольник.
Осевая симметрия в природе
Природа мудра и рациональна, поэтому почти все ее творения имеют гармоничное строение. Это относится и к живым существам, и к неодушевленным объектам.
Внимательное наблюдение показывает, что основу красоты многих форм, созданных природой, составляет симметрия.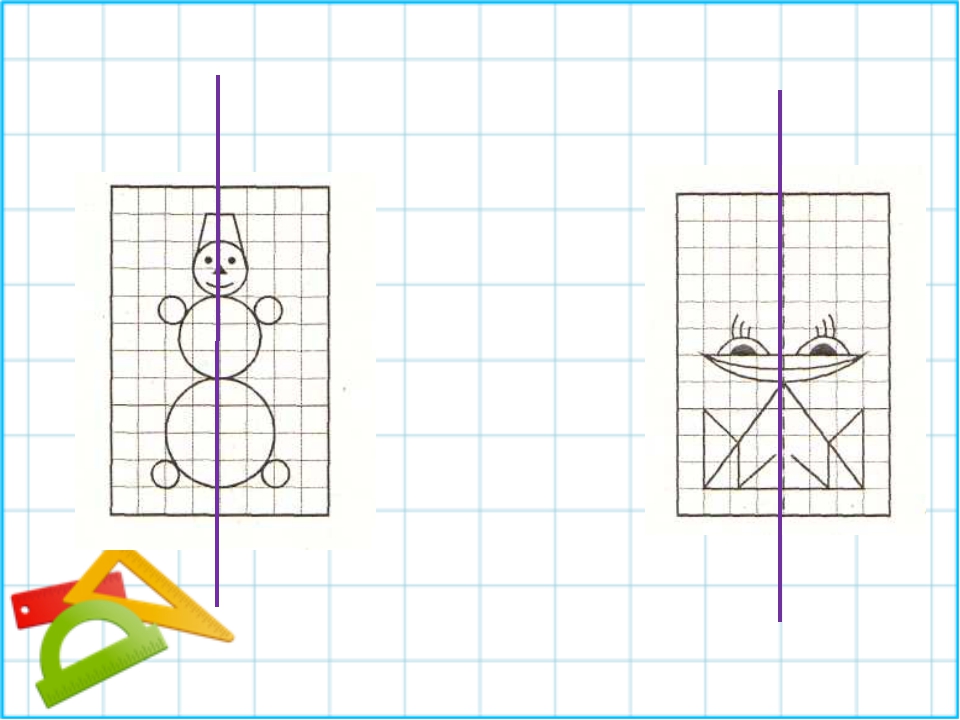 Ярко выраженной симметрией обладают листья, цветы, плоды. Их зеркальная, радиальная, центральная, осевая симметрия — очевидны. В значительной степени она обусловлена явлением гравитации.
Ярко выраженной симметрией обладают листья, цветы, плоды. Их зеркальная, радиальная, центральная, осевая симметрия — очевидны. В значительной степени она обусловлена явлением гравитации.
Геометрические формы кристаллов с их плоскими поверхностями представляют собой удивительное явление природы. Однако подлинная физическая симметрия кристалла проявляется не столько в его внешнем виде, сколько во внутреннем строении кристаллического вещества.
Осевая симметрия в животном мире
Симметрия в мире живых существ, проявляется в закономерном расположении одинаковых частей тела относительно центра или оси. Чаще в природе встречается осевая симметрия. Она обуславливает не только общее строение организма, но и возможности его последующего развития. Каждому виду животных присущ характерный окрас. Если в расцветке фигурирует рисунок, то, как правило, он дублируется с обеих сторон.
Осевая симметрия и человек
Если взглянуть на любое живое существо, сразу бросается в глаза симметричность устройства организма. Человек: две руки, две ноги, два глаза, два уха и так далее.
Человек: две руки, две ноги, два глаза, два уха и так далее.
Это означает, что существует некая линия, по которой животные и люди могут быть визуально «поделены» на две идентичные половинки, то есть в основе их геометрического устройства лежит осевая симметрия.
Как видно из приведённых примеров, любой живой организм природа создает не хаотично и бессмысленно, а согласно общим законам мироустройства, ведь во Вселенной ничто не имеет чисто эстетического, декоративного назначения. Это обусловлено закономерной необходимостью.
Конечно, природе редко присуща математическая точность, но похожесть элементов организма все равно поразительна.
Симметрия в архитектуре
С древнейших времен архитекторы хорошо знали математическую пропорцию и симметрию, и использовали их при строительстве архитектурных сооружений. Например, архитектура русских православных храмов и соборов Руси: Кремль, собор Христа Спасителя г. Москва, Казанский и Исаакиевский соборы г. Санкт-Петербург и др.
А также другие всемирно известные достопримечательности, многие из которых во всех странах мира, мы можем видеть и сейчас: Египетские пирамиды, Лувр, Тадж-Махал, Кёльнский собор и т.д. Все они, как мы видим, имеют симметрию.
Симметрия в музыке
Я учусь в музыкальной школе, для меня было интересно найти примеры симметрии в данной области. Не только музыкальные инструменты обладают явной симметрией, но и части музыкальных произведений звучат в определённом порядке, в соответствии с партитурой и замыслом композитора.
Например, реприза — (франц. reprise, от reprendre -возобновлять). Повторение темы или группы тем после этапа её (их) развития или изложения нового тематического материала.
Также в одномерном повторении во времени через равные интервалы состоит музыкальный принцип ритма.
Симметрия в технике
Мы живем в стремительно — меняющемся высокотехнологическом, информационном обществе, и не задумываемся, почему некоторые окружающие нас предметы и явления пробуждают чувство прекрасного, а другие нет. Мы их не замечаем, даже не задумываемся, об их свойствах.
Мы их не замечаем, даже не задумываемся, об их свойствах.
Но кроме этого, данные технические и механические устройства, детали, механизмы, агрегаты не смогут правильно работать и вообще функционировать, если при этом не будет соблюдена симметрия, а вернее, некая ось, в механике это — центр тяжести.
Сбалансированность по центру, в данном случае, является обязательным техническим требованием, соблюдение которого строго регламентируется ГОСТ или ТУ и должно соблюдаться.
Симметрия и космические объекты
Но, пожалуй, самыми загадочными, волновавшими умы многих, ещё с древнейших времён, являются космические объекты. Которые также имеют симметрию — солнце, луна, планеты.
Эту цепочку можно продолжать, но мы сейчас говорим о чем-то едином: о том, что осевая симметрия является основополагающим законом вселенной, является основой красоты, гармонии и пропорциональности, и во взаимосвязи этого с математикой.
Практическая часть
Найдя необходимую информацию, изучив литературу, я убедилась в правоте своей гипотезы и сделала вывод о том, что в глазах человека несимметричность чаще всего ассоциируется с неправильностью или ущербностью. Поэтому в большинстве творений людских рук прослеживается симметричность и гармония, как необходимое и обязательное требование.
Поэтому в большинстве творений людских рук прослеживается симметричность и гармония, как необходимое и обязательное требование.
Это хорошо видно на моём рисунке, где изображён поросёнок, с непропорциональными частями тела, что сразу бросается в глаза!
И только после того, как подольше приглядишься к нему, посчитаешь его милым?
Несмотря на то, что данная тема известна, хорошо изучена, но все эти данные рассмотрены отдельно в каждой дисциплине. Обобщённых данных о том, что принцип симметрии используется, и именно на нём базируются многие другие науки, и их взаимосвязи с математикой я не встретила.
Поэтому я решила доказать своё утверждение с помощью самого простого и доступного для меня способа. Таким решением, я считаю, будет проведение эксперимента с испытаниями.
Для наглядного доказательства того, что асимметричные модели не устойчивы, не обладают необходимыми требованиями и жизненно необходимыми навыками, и подтверждения своей гипотезы мне необходимо создать поделки, рисунки и композицию:
1 вариант — симметричны относительно оси;
2 вариант — с явным нарушением симметрии.
Поскольку я считаю, что такой дисбаланс будет хорошо виден на следующих примерах, для чего я создала поделки-оригами (самолёт и лягушонок) из цветной бумаги. Для чистоты эксперимента они сделаны из одинаковой цветной бумаги и тестировались в одинаковых условиях. И композицию «Маяк», где маяк сделан из пустой пластиковой бутылки, обклеен цветной бумагой. Для украшения композиции использованы игрушечные фигуры человека, модели парусника и лодки, декоративные камни, а для имитации света я использовала светящийся от батарейки элемент.
Я провела испытания с данными поделками, все показатели зафиксировала и занесла в таблицу (все показатели можно посмотреть в приложении № 1 стр. 18 — 21).
Все поделки делались с соблюдением техники безопасности (приложение № 2 стр. 21)
Все полученные данные я проанализировала, вот что у меня получилось.
Анализ полученных данных
Эксперимент № 1
Испытание — прыжок лягушек в длину, замер этого расстояния.
Лягушонок Зелёный (симметричный) прыгает ровно, на большее расстояние, а Красный (не симметричный) ни разу не прыгнул ровно, всегда с поворотом или переворотом в сторону, на расстояние в 2 — 3 раза меньше.
Таким образом, можно сделать вывод, что такое животное не сможет быстро охотиться или наоборот убегать, эффективно добывать пищу, что уменьшает шансы на выживание, это доказывает, что в природе всё сбалансировано, пропорционально, правильно — симметрично.
Эксперимент № 2
Вид испытания — запуск самолётов в полёт и измерение расстояния длины полёта.
Самолётик № 1 «Розовый» (симметричный) летит из 10 раз, 8 раз ровно и прямо, на максимальную длину, (т.е. на всю длину моей комнаты), а траектория полёта самолётика № 2 «Оранжевый» (не симметричный) из 10 раз — ни разу не летел ровно, всегда с поворотом или переворотом, на меньшее расстояние. То есть, если бы это был настоящий самолёт, то он не смог бы лететь ровно, в правильном направлении. Такой полёт был бы очень неудобен или даже опасен для человека (также как и для птиц), а машины и другие транспортные средства передвижения, не смогли бы ехать, плыть и т.д. в необходимую сторону.
Такой полёт был бы очень неудобен или даже опасен для человека (также как и для птиц), а машины и другие транспортные средства передвижения, не смогли бы ехать, плыть и т.д. в необходимую сторону.
Эксперимент № 3
Вид испытания — проверка устойчивости здания «Маяка», при уменьшении угла наклона сооружения, относительно поверхности.
1. Создав композицию «Маяка», я установила его прямо, т.е. перпендикулярно (под углом 90 0) относительно стен сооружения к поверхности. Данная конструкция стоит ровно, выдерживает установленный световой элемент и фигурку человека.
2. Для дальнейшего проведения эксперимента мне было необходимо расчертить основание башни на углы, равные 10 0 .
После чего я отрезала от основания угол равный 10 0 .
Под углом в 80 0 здание стоит криво, шатается, но дополнительную нагрузку выдерживает.
3. Отрезав ещё 10 0 , получился угол наклона в 70 0 , при котором вся моя конструкция рушится.
Данный опыт доказывает, что исторически сложившиеся традиция строительства под прямым углом и соблюдение при этом симметрии самого здания, является необходимым условием для устойчивого, надёжного возведения и эксплуатации архитектурных зданий и сооружений.
Для наглядного примера осевой симметрии и доказательства утверждения о том, что человек воспринимает любые окружающие его предметы, образы животных и т.д. только симметрично, то есть, когда обе стороны, «половинки» одинаковы, равны, я создала электронную раскраску, которую можно распечатать, составив детскую книжку-раскраску. Данное пособие поможет всем желающим лучше усвоить тему, интересно и с удовольствием провести свободное время (Титульный лист изображён на этом рисунке, остальные рисунки расположены в приложении № 3 стр. 21 -24).
Проведённые мною эксперименты доказывают, что симметрия является не только математическим и геометрическим понятием, а является сферой, средой нашего проживания, неким техническим требованием, так же необходимым условием для выживания в целом, как для людей, так и для животных. Симметрия объединяет всё это воедино, и уходит далеко за пределы обычной науки!
Заключение
Выводы:
Я выяснила, что симметрия является одной из главных составляющих в повседневной жизни человека, в предметах быта, в архитектуре, технике, в природе, музыке, науке и т. д.
д.
Результат:
Я нашла необходимую информацию, доказала свою гипотезу, проверила и подтвердила её опытным путём. Я создала поделки, композицию, рисунки и электронную раскраску для наглядного проведения эксперимента.
Я выяснила, что все законы природы — биологические, химические, генетические, астрономические связаны с симметрией. Практически, всё то, что нас окружает, что создано человеком — подчинено общим для нас всех принципам симметрии, поскольку имеют завидную системность. Таким образом, сбалансированность, тождественность как принцип имеет всеобщий масштаб.
Можно сказать, что симметрия является основополагающим законом, на котором базируются основные законы науки? Наверное, да.
Эту тайну пытались осмыслить великие мыслители человечества. Сегодня в разгадку этой тайны погрузились и мы.
Один из известных математиков Герман Вейль писал, что «симметрия — является той идеей, посредством которой человек на протяжении веков пытался постичь и создать порядок, красоту и совершенство».
Может мы нашли секрет создания красоты, совершенства или даже создания основных законов вселенной? Может это симметрия?
Приложения
Приложение № 1 Таблица испытаний:
Эксперимент № 1 | |||
Попытка № | Вид испытания | «Зелёная лягушка» (симметричная) | Результат и характеристика испытания «Красная лягушка» (не симметричная) |
Прыжок лягушки в длину (измерение в см.) | 6,0 в левую сторону | ||
14,4 с небольшим поворотом вправо | 9,0 переворот назад | ||
10,5 почти ровно | 2,0 переворот | ||
9,5 с небольшим поворотом вправо | 5,0 переворот в левую сторону | ||
10,6 с небольшим поворотом вправо | 3,0 в левую сторону | ||
9,0 переворот | 9,0 поворот влево | ||
13,5 почти ровно | 1,5 назад, с поворотом влево | ||
9,5 влево с переворотом | |||
21,2 почти ровно | 4,5 влево с переворотом | ||
Эксперимент № 2 | |||
Самолёт «Розовый» (Симметричный) | Самолёт «Оранжевый» (Не симметричный) | ||
Запуск самолётика в длину Максимальная (5,1 метра) | 5,1 с 2 переворотами | 3,04 с переворотами вправо | |
2,78 с переворотами вправо | |||
5,1 с наклоном вправо | 3, 65 с переворотами вправо | ||
5,1 с наклоном вправо | 1,51 почти ровно | ||
5,1 почти ровно | 4,73 с переворотами вправо | ||
5,1 с наклоном в левую сторону | 3,82 поворот вправо | ||
5,1 почти ровно | 3,41 с переворотами | ||
5,1 почти ровно | 3,37 поворот влево | ||
5,1 с переворотом | 3,51 с переворотами влево | ||
5,1 почти ровно | 3,19 с переворотами вправо | ||
Эксперимент № 3 | |||
Попытка № | Характеристика свойств объекта | Вид и характеристика испытания | Результат |
Сооружение стоит перпендикулярно поверхности (т. | Установка дополнительной нагрузки: светящийся элемент и игрушечная фигура человека | Маяк стоит ровно, надёжно | |
Под углом 80 0 | От основания маяка я наметала и отрезала угол в 10 0 | Маяк выдерживает нагрузку, но стоит ненадёжно, шатается | |
Под углом 70 0 | От основания маяка я ещё раз отрезала 10 0 | Сооружение падает и рушится | |
Приложение № 2
При изготовлении моих поделок соблюдалась техника безопасности, а именно:
Ножницы или нож должны быть хорошо заточены и отрегулированы.
Хранить необходимо в определенном и безопасном месте или коробке.
При пользовании ножниц (ножа), нельзя отвлекаться, нужно быть максимально внимательными, дисциплинированными.
Передавая ножницы (нож), держать их за сомкнутые лезвия (остриё).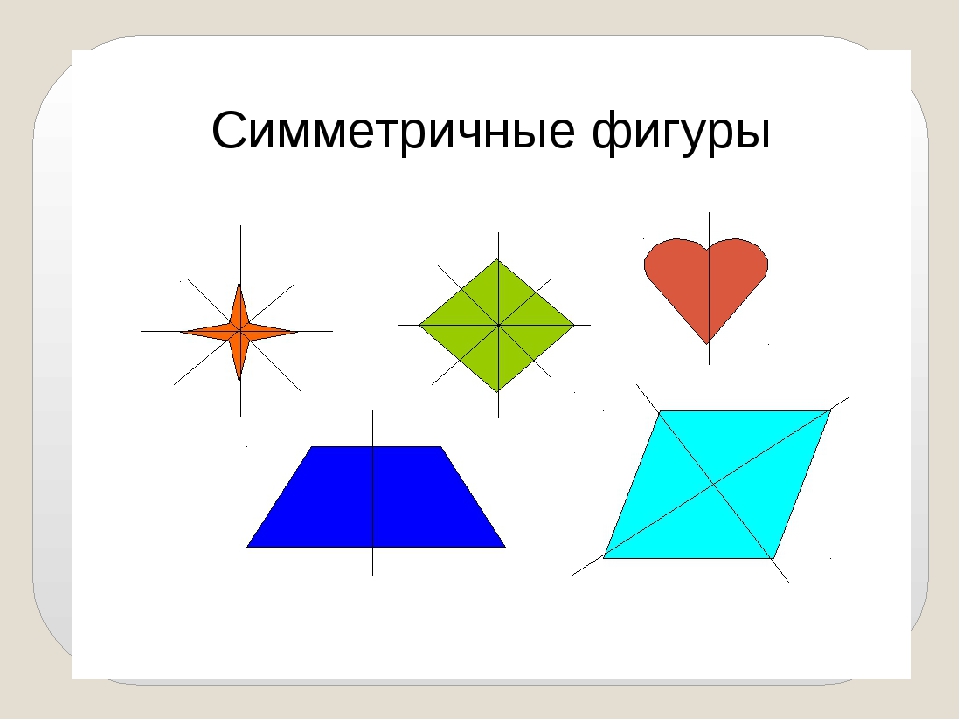
Ножницы (нож) класть справа сомкнутыми лезвиями (остриём) направленными от себя.
При резании узкое лезвие ножниц (остриё ножа) должно быть внизу.
После использования клея вымыть руки.
Приложение № 3
Электронная книга-раскраска
Симметрия-
Это означает то, что одна часть предмета похожа на другую.
Осевая симметрия- это симметрия относительно прямой (линии).
Ось симметрии — это воображаемая линия разделяющая объект на симметричные части. На рисунках она изображена для наглядности.
В этой книге нужно закончить рисунки, соединяя точки.
Затемможнораскрашиватьто, чтополучилось.
Попробуй закончить эти рисунки:
Сердечко
Треугольник Домик
Звёздочка Листочек
Мышка Ёлочка
Собачка Замок
К роме осевой симметрии есть и симметрия относительно точки.
Этот шар симметричен
И ёщё один вид симметрии — зеркальная симметрия.
Зеркальная симметрия-
это симметрия относительно плоскости. Например, относительно зеркала.
Симметрия это—
Используемая литература
2. Герман Вейль «Симметрия» (Издательство «Наука» главная редакция физико-математической литературы, Москва 1968 г.)
4. Мои рисунки и фотографии.
5. Справочник машиностроителя, том 1, (Государственное научно — техническое издательство машиностроительной литературы, Москвы 1960 г.)
6. Фотографии и рисунки из сети «Интернет».
Точки М и М1 называются симметричными относительно заданной прямой L , если эта прямая является серединным перпендикуляром к отрезку МM1 (рис 1). Каждая точка прямой L симметрична сама себе. Преобразование плоскости, при котором каждая точка отображается на симметричную ей точку относительно данной прямой L , называется осевой симметрией с осью L и обозначается SL : SL (M) = M1 .
Точки М и М1 взаимно симметричны относительно L , поэтому SL (M1 )=M . Следовательно, преобразование, обратное осевой симметрии, есть та же осевая симметрия: SL -1 = SL , SL ° SL = E . Иначе говоря, осевая симметрия плоскости является инволютивным преобразованием.
Образ данной точки при осевой симметрии можно просто построить, пользуясь только одним циркулем. Пусть L — ось симметрии, A и B — произвольные точки этой оси (рис 2). Если и SL (M) = M1 , то по свойству точек серединного перпендикуляра к отрезку имеем: AM = AM1 и BM = BM1 . Значит, точка M1 принадлежит двум окружностям: окружности с центром A радиуса AM и окружности с центром B радиуса BM (M — данная точка). Фигура F и её образ F1 при осевой симметрии называются симметричными фигурами относительно прямой L (рис 3).
Фигура F и её образ F1 при осевой симметрии называются симметричными фигурами относительно прямой L (рис 3).
Теорема. Осевая симметрия плоскости есть движение.
Если А и В — любые точки плоскости и SL (A) = A1 , SL (B) = B1 , то надо доказать, что A1 B1 = AB . Для этого введем прямоугольную систему координат OXY так, чтобы ось OX совпала с осью симметрии. Точки А и В имеют координаты А(x1 ,-y1 ) и B(x1 ,-y2 ) .Точки А1 и В1 имеют координаты A1 (x1 ,y1 ) и B1 (x1 ,y2 ) (рис 4 — 8). По формуле расстояния между двумя точками находим:
Из этих соотношений ясно, что АВ=А1 В1 , что и требовалось доказать.
Из сравнения ориентаций треугольника и его образа получаем, что осевая симметрия плоскости есть движение второго рода .
Осевая симметрия отображает каждую прямую на прямую. В частности, каждая из прямых, перпендикулярных оси симметрии, отображается этой симметрией на себя.
Теорема. Прямая, отличная от перпендикуляра к оси симметрии, и её образ при этой симметрии пересекаются на оси симметрии или ей параллельны.
Доказательство. Пусть дана прямая, не перпендикулярная оси L симметрии. Если m ? L= P и SL (m)=m1 , то m1 ?m и SL (P)=P , поэтому Pm1 (рис 9). Если же m || L , то m1 || L , так как в противном случае прямые m и m1 пересекались бы в точке прямой L , что противоречит условию m ||L (рис 10).
В силу определения равных фигур, прямые, симметричные относительно прямой L , образуют с прямой L равные углы (рис 9).
Прямая L называется осью симметрии фигуры F , если при симметрии с осью L фигура F отображается на себя: SL (F) =F . Говорят, что фигура F симметрична относительно прямой L .
Например, всякая прямая, содержащая центр окружности, является осью симметрии этой окружности. Действительно, пусть М — произвольная точка окружности щ с центром О , ОL , SL (M)= M1 . Тогда SL (O) = O и OM1 =OM , т. е. M1 є щ . Итак, образ любой точки окружности принадлежит этой окружности. Следовательно, SL (щ)=щ .
Осями симметрии пары непараллельных прямых служат две перпендикулярные прямые, содержащие биссектрисы углов между данными прямыми. Осью симметрии отрезка является содержащая его прямая, а также серединный перпендикуляр к этому отрезку.
Свойства осевой симметрии
- 1.
 При осевой симметрии образом прямой является прямая, образом параллельных прямых являются параллельные прямые
При осевой симметрии образом прямой является прямая, образом параллельных прямых являются параллельные прямые - 3. Осевая симметрия сохраняет простое отношение трех точек.
- 3. При осевой симметрии отрезок переходит в отрезок, луч — в луч, полуплоскость — в полуплоскость.
- 4. При осевой симметрии угол переходит в равный ему угол.
- 5. При осевой симметрии с осью d всякая прямая, перпендикулярная оси d остается на месте.
- 6. При осевой симметрии ортонормированный репер переходит в ортонормированный репер. При этом точка М с координатами х и у относительно репера R переходит в точку M` с теми же самыми координатами х и у, но относительно репера R`.
- 7. Осевая симметрия плоскости переводит правый ортонормированный репер в левый и, наоборот, левый ортонормированный репер — в правый.
- 8. Композиция двух осевых симметрий плоскости с параллельными осями есть параллельный перенос на вектор, перпендикулярный данным прямым, длина которого в два раза больше расстояния между данными прямыми
Жизнь людей наполнена симметрией. Это удобно, красиво, не нужно выдумывать новых стандартов. Но что она есть на самом деле и так ли красива в природе, как принято считать?
Это удобно, красиво, не нужно выдумывать новых стандартов. Но что она есть на самом деле и так ли красива в природе, как принято считать?
Симметрия
С древних времен люди стремятся упорядочить мир вокруг себя. Поэтому что-то считается красивым, а что-то не очень. С эстетической точки зрения как привлекательные рассматриваются золотое и серебряное сечения, а также, разумеется, симметрия. Этот термин имеет греческое происхождение и дословно означает «соразмерность». Разумеется, речь идет не только о совпадении по этому признаку, но также и по некоторым другим. В общем смысле симметрия — это такое свойство объекта, когда в результате тех или иных образований результат равен исходным данным. Это встречается как в живой, так и в неживой природе, а также в предметах, сделанных человеком.
Прежде всего термин «симметрия» употребляется в геометрии, но находит применение во многих научных областях, причем его значение остается в общем и целом неизменным. Это явление достаточно часто встречается и считается интересным, поскольку различается несколько его видов, а также элементов. Использование симметрии также интересно, ведь она встречается не только в природе, но и в орнаментах на ткани, бордюрах зданий и многих других рукотворных предметах. Стоит рассмотреть это явление поподробнее, поскольку это крайне увлекательно.
Использование симметрии также интересно, ведь она встречается не только в природе, но и в орнаментах на ткани, бордюрах зданий и многих других рукотворных предметах. Стоит рассмотреть это явление поподробнее, поскольку это крайне увлекательно.
Употребление термина в других научных областях
В дальнейшем симметрия будет рассматриваться с точки зрения геометрии, однако стоит упомянуть, что данное слово используется не только здесь. Биология, вирусология, химия, физика, кристаллография — все это неполный список областей, в которых данное явление изучается с различных сторон и в разных условиях. От того, к какой науке относится этот термин, зависит, например, классификация. Так, разделение на типы серьезно варьируется, хотя некоторые основные, пожалуй, остаются неизменными везде.
Видео по теме
Классификация
Различают несколько основных типов симметрии, из которых наиболее часто встречаются три:
Кроме того, в геометрии различают также следующие типы, они встречаются значительно реже, но не менее любопытны:
- скользящая;
- вращательная;
- точечная;
- поступательная;
- винтовая;
- фрактальная;
- и т.
 д.
д.
В биологии все виды называются несколько иначе, хотя по сути могут быть такими же. Подразделение на те или иные группы происходит на основании наличия или отсутствия, а также количества некоторых элементов, таких как центры, плоскости и оси симметрии. Их следует рассмотреть отдельно и более подробно.
Базовые элементы
В явлении выделяют некоторые черты, одна из которых обязательно присутствует. Так называемые базовые элементы включают в себя плоскости, центры и оси симметрии. Именно в соответствии с их наличием, отсутствием и количеством определяется тип.
Центром симметрии называют точку внутри фигуры или кристалла, в которой сходятся линии, соединяющие попарно все параллельные друг другу стороны. Разумеется, он существует не всегда. Если есть стороны, к которым нет параллельной пары, то такую точку найти невозможно, поскольку ее нет. В соответствии с определением, очевидно, что центр симметрии — это то, через что фигура может быть отражена сама на себя. Примером может служить, например, окружность и точка в ее середине. Этот элемент обычно обозначается как C.
Примером может служить, например, окружность и точка в ее середине. Этот элемент обычно обозначается как C.
Плоскость симметрии, разумеется, воображаема, но именно она делит фигуру на две равные друг другу части. Она может проходить через одну или несколько сторон, быть параллельной ей, а может делить их. Для одной и той же фигуры может существовать сразу несколько плоскостей. Эти элементы обычно обозначаются как P.
Но, пожалуй, наиболее часто встречается то, что называют «оси симметрии». Это нередкое явление можно увидеть как в геометрии, так и в природе. И оно достойно отдельного рассмотрения.
Оси
Часто элементом, относительно которого фигуру можно назвать симметричной,
выступает прямая или отрезок. В любом случае речь идет не о точке и не о плоскости. Тогда рассматриваются оси симметрии фигур. Их может быть очень много, и расположены они могут быть как угодно: делить стороны или быть параллельными им, а также пересекать углы или не делать этого. Оси симметрии обычно обозначаются как L.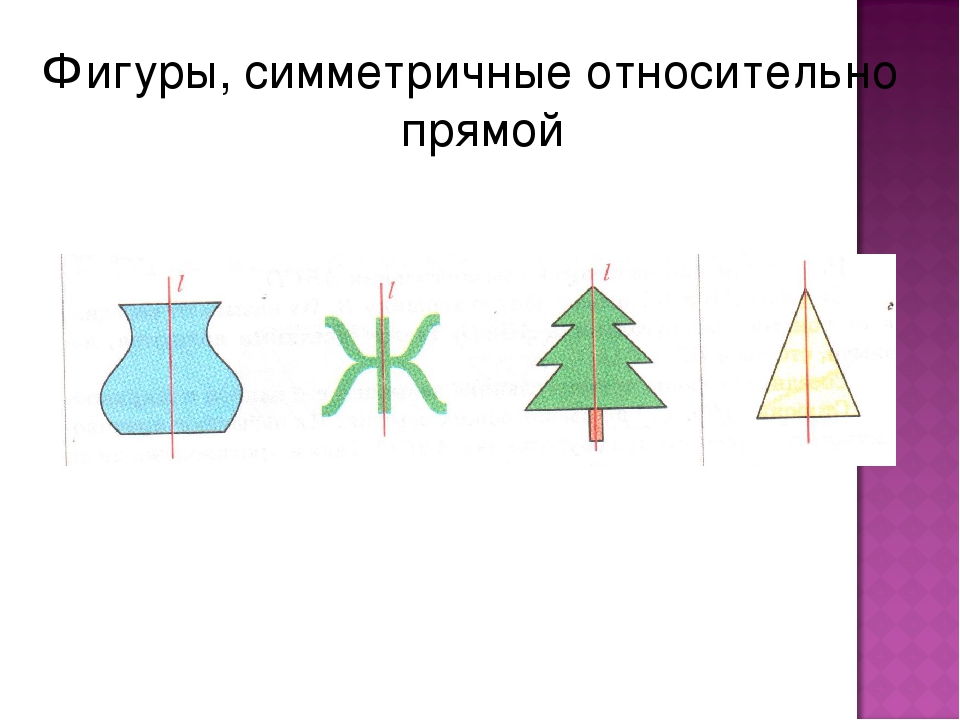
Примерами могут служить равнобедренные и равносторонние треугольники. В первом случае будет вертикальная ось симметрии, по обе стороны от которой равные грани, а во втором линии будут пересекать каждый угол и совпадать со всеми биссектрисами, медианами и высотами. Обычные же треугольники ею не обладают.
Кстати, совокупность всех вышеназванных элементов в кристаллографии и стереометрии называется степенью симметрии. Этот показатель зависит от количества осей, плоскостей и центров.
Примеры в геометрии
Условно можно разделить все множество объектов изучения математиков на фигуры, имеющие ось симметрии, и такие, у которых ее нет. В первую категорию автоматически попадают все правильные многоугольники, окружности, овалы, а также некоторые частные случаи, остальные же попадают во вторую группу.
Как и в случае, когда говорилось про ось симметрии треугольника, данный элемент для четырехугольника существует не всегда. Для квадрата, прямоугольника, ромба или параллелограмма он есть, а для неправильной фигуры, соответственно, нет. Для окружности оси симметрии — это множество прямых, которые проходят через ее центр.
Для окружности оси симметрии — это множество прямых, которые проходят через ее центр.
Кроме того, интересно рассмотреть и объемные фигуры с этой точки зрения. Хотя бы одной осью симметрии помимо всех правильных многоугольников и шара будут обладать некоторые конусы, а также пирамиды, параллелограммы и некоторые другие. Каждый случай необходимо рассматривать отдельно.
Примеры в природе
Зеркальная симметрия в жизни называется билатеральной, она встречается наиболее
часто. Любой человек и очень многие животные тому пример. Осевая же называется радиальной и встречается гораздо реже, как правило, в растительном мире. И все-таки они есть. Например, стоит подумать, сколько осей симметрии имеет звезда, и имеет ли она их вообще? Разумеется, речь идет о морских обитателях, а не о предмете изучения астрономов. И правильным ответом будет такой: это зависит от количества лучей звезды, например пять, если она пятиконечная.
Кроме того, радиальная симметрия наблюдается у многих цветков: ромашки, васильки, подсолнухи и т. д. Примеров огромное количество, они буквально везде вокруг.
д. Примеров огромное количество, они буквально везде вокруг.
Аритмия
Этот термин, прежде всего, напоминает большинству о медицине и кардиологии, однако он изначально имеет несколько другое значение. В данном случае синонимом будет «асимметрия», то есть отсутствие или нарушение регулярности в том или ином виде. Ее можно встретить как случайность, а иногда она может стать прекрасным приемом, например, в одежде или архитектуре. Ведь симметричных зданий очень много, но знаменитая Пизанская башня чуть наклонена, и хоть она не одна такая, но это самый известный пример. Известно, что так получилось случайно, но в этом есть своя прелесть.
Кроме того, очевидно, что лица и тела людей и животных тоже не полностью симметричны. Проводились даже исследования, согласно результатам которых «правильные» лица расценивались как неживые или просто непривлекательные. Все-таки восприятие симметрии и это явление само по себе удивительны и пока не до конца изучены, а потому крайне интересны.
Что же такое ось симметрии? Это множество точек, которые образуют прямую, являющуюся основой симметрии, то есть, если от прямой отложили определенное расстояние с одной стороны, то оно отразится и в другую сторону в таком же размере. Осью может выступать все, что угодно, — точка, прямая, плоскость и так далее. Но об этом лучше говорить на наглядных примерах.
Симметрия
Для того чтобы понять, что такое ось симметрии, нужно вникнуть в само определение симметрии. Это соответствие определенного фрагмента тела относительно какой-либо оси, когда его структура неизменна, а свойства и форма такого объекта остаются прежними относительно его преобразований. Можно сказать, что симметрия — свойство тел к отображению. Когда фрагмент не может иметь подобного соответствия, это называется асимметрией или же аритмией.
Некоторые фигуры не имеют симметрии, поэтому они и называются неправильными или же асимметричными. К таким относятся различные трапеции (кроме равнобедренной), треугольники (кроме равнобедренного и равностороннего) и другие.
Виды симметрии
Также обсудим некоторые виды симметрии, чтобы до конца изучить это понятие. Их разделяют так:
История симметрии
Само понятие симметрии часто бывает отправной точкой в теориях и гипотезах ученых древних времен, которые были уверены в математической гармонии мироздания, а также в проявлении божественного начала. Древние греки свято верили в то, что Вселенная симметрична, потому что симметрия великолепна. Человек очень давно использовал идею симметрии в своих познаниях картины мироздания.
В V веке до нашей эры Пифагор считал сферу самой совершенной формой и думал, что Земля имеет форму сферы и таким же образом движется. Также он полагал, что Земля движется по форме какого-то «центрального огня», вокруг которого должны были вращаться 6 планет (известные на то время), Луна, Солнце и все другие звезды.
А философ Платон считал многогранники олицетворением четырех природных стихий:
- тетраэдр — огонь, так как его вершина направлена вверх;
- куб — земля, так как это самое устойчивое тело;
- октаэдр — воздух, нет каких-либо объяснений;
- икосаэдр — вода, так как тело не имеет грубых геометрических форм, углов и так далее;
- образом всей Вселенной являлся додекаэдр.
Из-за всех этих теорий правильные многогранники называют телами Платона.
Симметрией пользовались еще зодчие Древней Греции. Все их постройки были симметричны, об этом свидетельствуют изображения древнего храма Зевса в Олимпии.
Голландский художник М. К. Эшер также прибегал к симметрии в своих картинах. В частности, мозаика из двух птиц, летящих навстречу, стала основой картины «День и ночь».
К. Эшер также прибегал к симметрии в своих картинах. В частности, мозаика из двух птиц, летящих навстречу, стала основой картины «День и ночь».
Также и наши искусствоведы не пренебрегали правилами симметрии, что видно на примере картины Васнецова В. М. «Богатыри».
Что уж там говорить, симметрия — ключевое понятие для всех деятелей искусства на протяжении многих веков, но в XX веке ее смысл оценили также все деятели точных наук. Точным свидетельством являются физические и космологические теории, например, теория относительности, теория струн, абсолютно вся квантовая механика. Со времен Древнего Вавилона и, заканчивая передовыми открытиями современной науки, прослеживаются пути изучения симметрии и открытия ее основных законов.
Симметрия геометрических фигур и тел
Рассмотрим внимательнее геометрические тела. Например, осью симметрии параболы является прямая, проходящая через ее вершину и рассекающая данное тело пополам. У этой фигуры имеется одна единственная ось.
А с геометрическими фигурами дело обстоит иначе. Ось симметрии прямоугольника — также прямая, но их несколько. Можно провести ось параллельно отрезкам ширины, а можно — длины. Но не все так просто. Вот прямая не имеет осей симметрии, так как ее конец не определен. Могла существовать только центральная симметрия, но, соответственно, и таковой не будет.
Следует также знать то, что некоторые тела имеют множество осей симметрии. Об этом догадаться несложно. Даже не нужно говорить о том, сколько осей симметрии имеет окружность. Любая прямая, проходящая через центр окружности, является таковой и этих прямых — бесконечное множество.
У некоторые четырехугольников может быть две оси симметрии. Но вторые должны быть перпендикулярны. Это происходит в случае с ромбом и прямоугольником. В первом оси симметрии — диагонали, а во втором — средние линии. Множество таковых осей только у квадрата.
Симметрия в природе
Природа поражает множеством примеров симметрии. Даже наше человеческое тело устроено симметрично. Два глаза, два уха, нос и рот расположены симметрично относительно центральной оси лица. Руки, ноги и все тело в общем устроено симметрично оси, проходящей через середину нашего тела.
А сколько примеров окружает нас постоянно! Это цветы, листья, лепестки, овощи и фрукты, животные и даже соты пчел имеют ярко выраженную геометрическую форму и симметрию. Вся природа устроена упорядоченно, всему есть свое место, что еще раз подтверждает совершенство законов природы, в которых симметрия — основное условие.
Вывод
Нас постоянно окружают какие-либо явления и предметы, например, радуга, капля, цветы, лепестки и так далее. Их симметрия — очевидна, в какой-то степени она обусловлена гравитацией. Часто в природе под понятием «симметрия» понимают регулярную смену дня и ночи, времен года и так далее.
Подобные свойства наблюдаются везде, где есть порядок и равенство. Также и сами законы природы — астрономические, химические, биологические и даже генетические подчинены определенным принципам симметрии, так как имеют совершенную системность, а значит, сбалансированность имеет всеохватывающий масштаб. Следовательно, осевая симметрия — один из основополагающих законов мироздания в целом.
Как использовать Paint Symmetry в Photoshop CC 2019
Узнайте, как использовать новую функцию Paint Symmetry в Photoshop CC 2019, чтобы легко создавать забавные, симметричные рисунки и рисунки!
Симметрия рисования в Photoshop позволяет рисовать сразу несколько мазков кисти для создания зеркальных, симметричных рисунков и узоров. Он работает с Brush Tool, Pencil Tool и Eraser Tool, а также с масками слоев.
Впервые добавленная в качестве технического предварительного просмотра в Photoshop CC 2018, Paint Symmetry теперь является официальной частью Photoshop начиная с CC 2019. Все более базовые параметры симметрии из CC 2018, такие как вертикальная, горизонтальная и диагональная, включены. Кроме того, CC 2019 также добавляет два новых режима симметрии, Radial и Mandala, которые позволяют создавать удивительные, очень сложные симметричные изображения за считанные секунды! Посмотрим, как это работает.
Чтобы следовать, вам понадобится Photoshop CC. И если вы уже являетесь подписчиком Creative Cloud, убедитесь, что ваша копия Photoshop CC обновлена. Давайте начнем!
Как рисовать с симметрией в фотошопе
Мы начнем с изучения основ того, как использовать Paint Symmetry для создания симметричных иллюстраций и дизайнов. Как только мы познакомимся с основами, я покажу вам, как комбинировать Paint Symmetry с масками слоев для более креативных эффектов!
Шаг 1: Добавьте новый пустой слой
Начните с добавления нового пустого слоя в ваш документ. Это будет держать ваши мазки кисти отдельно от всего остального. Чтобы добавить новый слой, щелкните значок « Новый слой» в нижней части панели «Слои»:
Нажав на иконку Новый слой.
Шаг 2: Выберите инструмент Brush Tool, Pencil Tool или Eraser Tool
Paint Symmetry работает с инструментами Brush Tool, Pencil Tool и Eraser Tool, которые находятся на панели инструментов. Я выберу инструмент Brush Tool :
Выбор инструмента «Кисть».
Как загрузить более 1000 кистей в Photoshop
Шаг 3: Откройте меню Paint Symmetry
При выбранном инструменте «Кисть», «Карандаш» или «Ластик» на панели параметров появляется значок «Симметрия краски» (маленькая бабочка). Нажмите на значок, чтобы открыть меню Paint Symmetry:
Нажав на значок симметрии краски (бабочка).
Шаг 4: Выберите опцию симметрии
А затем в меню выберите опцию симметрии из списка. В CC 2019 можно выбирать из десяти различных стилей, включая новые опции Radial и Mandala внизу:
Параметры рисования симметрии в Photoshop CC 2019.
Параметры рисования симметрии в Photoshop CC 2019
Вот краткий обзор того, как работает каждый из десяти параметров Photoshop Paint Symmetry:
- Вертикальный: Делит холст вертикально и отражает мазки кисти с одной стороны на другую.
- Горизонтально: Делит холст по горизонтали и отражает мазки кисти сверху вниз или снизу вверх.
- Двойная ось: делит холст по вертикали и горизонтали на четыре равные части (вверху слева, вверху справа, внизу слева и внизу справа). Рисование в одном разделе отражает ваши мазки кистью в других трех.
- Диагональ: Делит холст по диагонали и отражает мазки кисти с одной стороны на другую.
- Волнистый: похож на вертикальный, но с изогнутой волнистой линией вместо прямой.
- Круг: зеркальные мазки, нарисованные внутри круга за пределами круга, и наоборот.
- Спираль: зеркально отображает мазки кистью, нанесенные по обе стороны спиральной дорожки.
- Параллельные линии: Делит холст на три вертикальных секции, используя две параллельные вертикальные линии. Мазки кисти, нарисованные в средней части, отражаются в левой и правой частях.
- Радиальный: Делит холст на диагональные сегменты или «кусочки». Мазки кисти, нарисованные в одном сегменте, отражаются в других.
- Мандала: аналогично Radial, но также отражает мазки кисти в каждом сегменте, создавая в два раза больше мазков кисти, чем Radial.
Мы не будем здесь рассматривать все варианты симметрии, так как вы можете легко попробовать их самостоятельно. Но чтобы показать вам основы их работы, я выберу простую, например, Dual Axis . Двойная ось представляет собой комбинацию перечисленных выше вертикальных и горизонтальных режимов:
Выберите один из десяти вариантов Paint Symmetry.
Путь симметрии
Выбор параметра в меню добавляет синий путь симметрии к документу. В данном случае это путь симметрии Dual Axis, делящий холст по вертикали и горизонтали на четыре равные части:
Путь симметрии появляется.
Шаг 5: измените размер и примите путь
Прежде чем вы сможете рисовать с симметричной траекторией, Photoshop сначала помещает поле Transform вокруг пути, чтобы вы могли масштабировать и изменять его размер при необходимости. Но обратите внимание, что путь только для визуальной ссылки . Пути симметрии всегда влияют на весь холст, независимо от фактического размера пути. Поскольку рисование вне границы пути имеет тот же эффект, что и рисование внутри него, изменение размера симметрии на самом деле не дает никакой выгоды. Так что в большинстве случаев вам не нужно изменять его размер.
Однако, если вы хотите изменить размер пути, просто перетащите любой из маркеров преобразования, чтобы пропорционально масштабировать путь. Чтобы масштабировать путь от его центра, нажмите и удерживайте Alt (Win) / Option (Mac) при перетаскивании ручки. Вы также можете переместить путь в другое место в документе, щелкнув и перетащив его в поле «Преобразование»:
Масштабирование пути симметрии путем перетаскивания угловой ручки.
Связанные: новые функции и изменения Free Transform в CC 2019
Чтобы принять путь (даже если вы не изменили его размер) и выйти из команды «Преобразовать», щелкните флажок на панели параметров или нажмите клавишу « Ввод» (Win) / « Return» (Mac) на клавиатуре:
Нажмите на галочку, чтобы зафиксировать путь.
Шаг 6: Нарисуйте в одном из разделов, чтобы создать симметрию
Затем, имея путь симметрии, просто нарисуйте внутри одного из разделов. Фотошоп автоматически скопирует и отразит ваш мазок кисти в других разделах, создав симметричный дизайн:
Рисование одного мазка кисти создает несколько зеркальных мазков.
Чем больше мазков кисти вы рисуете, тем сложнее становится дизайн. Даже имея ограниченные навыки рисования, Photoshop позволяет легко придумать что-нибудь интересное:
Картина более мазков кисти добавляет к симметричному дизайну.
Как скрыть путь симметрии
Чтобы просмотреть изображение, не мешая синему пути симметрии, спрячьте его, щелкнув значок Paint Symmetry (бабочка) на панели параметров и выбрав « Скрыть симметрию» :
Выбор «Скрыть симметрию» в параметрах «Симметрия краски».
Поскольку путь предназначен только для визуальной ссылки, вы можете продолжить рисовать и добавлять в дизайн даже со скрытым путем:
Сокрытие пути по-прежнему позволяет рисовать симметрично.
Как показать путь симметрии
Чтобы снова показать путь, щелкните значок бабочки на панели параметров и выберите « Показать симметрию» :
Выбор Показать симметрию из опций рисования симметрии.
И теперь путь снова виден:
Это искусство? Наверное, нет, но это было, конечно, легко.
Просмотр пути симметрии на панели «Пути»
Как и обычные контуры в Photoshop, контуры симметрии отображаются на панели «Контуры» . Путь именуется в зависимости от режима симметрии (в данном случае «Симметрия двойной оси 1»). И значок бабочки в правом нижнем углу эскиза говорит нам не только о том, что это путь симметрии, но и о том, что он в данный момент активен. Вы можете иметь несколько путей симметрии в одном документе (как мы увидим чуть позже), но одновременно может быть активен только один:
Пути симметрии можно просматривать и выбирать на панели «Пути».
Новые опции радиальной и мандалевой симметрии
В Photoshop CC 2019 появилось два новых варианта Paint Symmetry — Radial и Mandala . Посмотрим, как они работают.
Как использовать параметр радиальной симметрии
Режим радиальной симметрии делит холст на диагональные сегменты или «кусочки» (например, кусочки пиццы). Картина в одном срезе отражает ваши мазки кистью в других.
Шаг 1: Выберите Radial из опций симметрии пути
Нажмите значок бабочки на панели параметров и выберите Радиальный из списка:
Выбор Radial из опций Paint Symmetry.
Шаг 2: Установите количество сегментов
Затем выберите нужное количество сегментов пути (срезов) от 2 до 12. Я пойду с 5:
Выбор количества сегментов, на которые нужно разделить холст.
Шаг 3: Нарисуйте в одном из сегментов
А затем просто нарисуйте в одном из сегментов. Photoshop будет отражать ваш мазок кисти в других сегментах, создавая радиальный рисунок:
Создание дизайна радиальной симметрии.
Как использовать опцию симметрии мандалы
Как и Radial, режим симметрии Mandala также делит холст на диагональные сегменты. Разница между Radial и Mandala заключается в том, что, наряду с отражением мазка кисти в других сегментах, Mandala также отражает штрих в том же сегменте. Это добавляет в два раза больше мазков кисти, чем Radial, что позволяет создавать очень сложные симметричные узоры с минимальными затратами времени и усилий.
Шаг 1: Выберите Mandala из опций симметрии пути
Нажмите значок бабочки на панели параметров и выберите Мандала из списка:
Выбор мандалы из опций Paint Symmetry.
Шаг 2: Установите количество сегментов
Затем, как и в случае с Radial, выберите необходимое количество отрезков пути. В то время как Radial позволяет выбирать до 12 сегментов, Mandala ограничена до 10. Я пойду с 8:
Выбор количества сегментов.
Шаг 3: Нарисуйте в одном из сегментов
А затем, как и раньше, нарисуйте один из сегментов. Photoshop будет отражать ваш мазок кисти в том же сегменте, в котором вы рисуете, и он будет отражать оба мазка кисти в других сегментах. Этот сложный дизайн занял у меня всего пару минут:
Мандала — самый впечатляющий (и забавный) из вариантов Photoshop’s Paint Symmetry.
Как отменить мазки кисти, если вы допустили ошибку
Создание симметричных рисунков в Photoshop — это весело и легко, но может потребовать много проб и ошибок. Если вам не нравится мазок кисти, который вы только что нарисовали, вы можете отменить его с клавиатуры, нажав Ctrl + Z (Победа) / Command + Z (Mac). Продолжайте нажимать на ярлык, чтобы отменить несколько мазков кисти. Чтобы повторить мазки кисти, нажмите Shift + Ctrl + Z (Победа) / Shift + Command + Z (Mac).
Как переключаться между путями симметрии
Фотошоп позволяет нам добавить несколько путей симметрии к одному и тому же документу, и каждый из них будет добавлен на панель « Пути» . Значок бабочки в правом нижнем углу миниатюры указывает активный в данный момент путь симметрии. Только один путь может быть активным одновременно. В этом случае мой путь мандалы активен:
Значок бабочки показывает активный путь.
Чтобы переключиться на один из других путей в списке, щелкните правой кнопкой мыши (Win) / Control-click (Mac) на нужном пути:
Щелчок правой кнопкой мыши (Win) / Control-click (Mac) на пути радиальной симметрии.
И затем выберите Make Symmetry Path из меню:
Выбор команды «Создать путь симметрии».
Это деактивирует предыдущий путь и активирует новый, чтобы вы могли рисовать его в документе:
Путь радиальной симметрии теперь активен.
Параметр «Последняя использованная симметрия»
Вы также можете переключиться с текущего пути симметрии на ранее использовавшийся путь, щелкнув значок бабочки на панели параметров и выбрав « Последняя использованная симметрия» :
Путь радиальной симметрии теперь активен.
Как отключить Paint Symmetry
Чтобы отключить рисование симметрии и продолжить рисование без эффекта симметрии, щелкните значок бабочки на панели параметров и выберите « Выключить симметрию» :
В меню выберите «Выключить симметрию».
Как использовать Paint Symmetry с маской слоя
Теперь, когда мы изучили основы работы Paint Symmetry, давайте посмотрим, как мы можем использовать путь симметрии с маской слоя, чтобы создать что-то еще более интересное.
В этом документе у меня есть радиальный градиент на фоновом слое:
Радиальный градиент спектра.
И если мы посмотрим на панель «Слои», то увидим, что у меня также есть сплошной черный слой над градиентом. Я включу верхний слой, щелкнув его значок видимости:
Включение верхнего слоя в документе.
И теперь документ заполнен черным, блокируя градиент из вида:
Верхний слой теперь скрывает градиент.
Шаг 1: Добавьте маску слоя
Выделив верхний слой, я добавлю маску слоя, щелкнув значок « Добавить маску слоя» в нижней части панели «Слои»:
Нажав значок Добавить маску слоя.
Эскиз маски слоя появляется на верхнем слое:
Эскиз маски слоя.
Шаг 2: Выберите инструмент Brush Tool
Я выберу инструмент Brush Tool на панели инструментов:
Выбор инструмента «Кисть».
Шаг 3: Установите цвет переднего плана на черный
И поскольку я хочу скрыть верхний слой в областях, где появляется эффект симметрии, я позабочусь о том, чтобы мой цвет переднего плана (цвет кисти) был установлен на черный :
Установка цвета кисти на черный.
Шаг 4: Выберите опцию Paint Symmetry
Я выберу мандалу из опций Paint Symmetry на панели параметров:
Выбор варианта симметрии.
А Photoshop добавляет путь симметрии мандалы к документу. Чтобы принять его, я нажму Enter (Win) / Return (Mac) на моей клавиатуре:
Путь симметрии добавляется в документ.
Шаг 5: Нарисуйте симметричный дизайн на маске слоя
Затем, чтобы скрыть текущий слой и показать слой под ним, просто нарисуйте маску слоя. Поскольку эффект симметрии расширяется, все больше и больше слоя ниже раскрывается. В этом случае цвета от моего градиента отображаются через мазки кисти:
Рисуем с симметричной траекторией на маске слоя, чтобы показать изображение ниже.
Я продолжу рисовать, чтобы добавить больше мазков к эффекту Мандала. И вот мой окончательный, красочный результат:
Окончательный дизайн мандалы.
И там у нас это есть! Вот как использовать Paint Symmetry в Photoshop CC 2019! Посетите наш раздел «Основы фотошопа» для получения дополнительных уроков И не забывайте, все наши учебники теперь доступны для скачивания в формате PDF!
Зеркальное рисование в Adobe Illustrator — Советы
Цель урока
Во многих графических и 3D редакторах есть функция зеркального рисования, но, к сожалению, такой функции нет в Adobe Illustrator. Однако это настолько мощное и многофункциональное приложение, что мы можем осуществить зеркальное рисование, используя только его стандартные функции. Как это сделать вы узнаете, прочитав сегодняшнюю статью.
Создание шаблона для зеркального рисования
Шаг 1
Открываем Adobe Illustrator и создаем новый документ (File > New). Размеры рабочей области и цветовой режим нового документа зависят только от ваших предпочтений. Берем Rectangle Tool (M) и создаем прямоугольник без заливки, размеры которого больше, чем размеры рабочей области. Цвет обводки этого прямоугольника не имеет абсолютно никакого значения.
Шаг 2
Включите линейки (Rulers) (Command/Ctrl + R) и создайте горизонтальную и вертикальную направляющую, перетащив их с соответствующих линеек. Направляющие должны проходить через центр созданного прямоугольника.
Создавать направляющие не обязательно, просто они указывают на положение осей симметрии. То есть мы создали их для удобства.
Шаг 3
Создадим произвольный объект на рабочей области. Я создал стрелку, для того чтобы обозначить направление пути.
Шаг 4
Выделяем весь слой в панеле Layer.
Теперь переходим Effect > Distort & Transform > Transform… и в открывшемся диалоговом окне указываем ось симметрии и количество копий, равное 1. Для визуального контроля над происходящим отмечаем опцию Preview и нажимаем OK.
Шаблон готов, можно приступать к рисованию.
Зеркальное рисование
Шаг 5
Отключим видимость созданного объекта (в моем случае это стрелка) в панели Layers.
Теперь берем любой из инструментов рисования, например Paint Brush Tool (B) и создаем путь.
Как вы можете видеть, мы получили мгновенную симметрию относительно горизонтальной оси. При этом вы можете рисовать с обеих сторон от оси симметрии.
Шаг 6
К сожалению, данный способ имеет два недостатка, о которых я, конечно, должен вас предупредить. При пересечении оси симметрии не происходит соединение создаваемого пути и его зеркальной копии.
То есть создаваемый путь существует по обе стороны от оси симметрии. Это нужно учитывать и стараться не пересекать ось симметрии, если, конечно, это не входит в ваши планы.
Шаг 7
Также вы не должны пересекать границы прямоугольника, созданного в первом шаге и рисовать за его границами, так как это нарушит всю систему симметрии. Именно поэтому мы создали прямоугольник больше, чем наша рабочая область.
Настройка шаблона при зеркальном рисовании
Шаг 8
Вы всегда можете перенастроить шаблон. Для этого выделите слой с шаблоном и кликните на Transform effect в панели Appearance (Window > Appearance), что приведет к открытию диалогового окна с параметрами эффекта.
Например, вы можете изменить ось симметрии.
Шаг 9
Вы даже можете установить несколько осей симметрии, выбрав одновременно опции Reflect X, Reflect Y и установив требуемое количество копий и угол поворота.
Только в этом случае помимо симметрии мы также получаем поворот относительно точки пересечения осей.
Завершение процесса зеркального рисования
Шаг 10
Теперь давайте что-нибудь нарисуем. Я создал абстрактный узор в стиле Freehand Pinstriping.
Когда рисование закончено, выделяем весь слой, затем переходим Object > Expand Appearance. Зеркальное отражение материализовалось в виде обычных векторных объектов.
Вспомогательные элементы в виде стрелок и прямоугольников теперь могут быть удалены. Итоговая работа выглядит так:
Сегодня я рассказал вам о том, как осуществить зеркальное рисование при помощи стандартных функций Adobe Illustrator. Может этот путь показался вам неудобным и имеющим некоторые ограничения. Хочу заметить, что это не единственный способ осуществить зеркальное рисование. Недавно появился плагин MirrorMe для осуществления мгновенной симметрии в Adobe Illustrator, пользоваться которым намного удобней, и который имеет больше функций.
Урок математики. Тема: «Ось симметрии»
Цели:
- образовательные:
- дать представление о симметрии;
- познакомить с основными видами симметрии на плоскости и в пространстве;
- выработать прочные навыки построения симметричных фигур;
- расширить представления об известных фигурах, познакомив со свойствами, связанных с симметрией;
- показать возможности использования симметрии при решении различных задач;
- закрепить полученные знания;
- общеучебные:
- научить настраивать себя на работу;
- научить вести контроль за собой и соседом по парте;
- научить оценивать себя и соседа по парте;
- развивающие:
- активизировать самостоятельную деятельность;
- развивать познавательную деятельность;
- учить обобщать и систематизировать полученную информацию;
- воспитательные:
- воспитываать у учащихся “чувство плеча”;
- воспитывать коммуникативность;
- прививать культуру общения.
ХОД УРОКА
Перед каждым лежат ножницы и лист бумаги.
Задание 1 (3 мин).
– Возьмем лист бумаги, сложим его попалам и вырежем какую-нибудь фигурку. Теперь развернем лист и посмотрим на линию сгиба.
Вопрос: Какую функцию выполняет эта линия?
Предполагаемый ответ: Эта линия делит фигуру пополам.
Вопрос: Как расположены все точки фигуры на двух получившихся половинках?
Предполагаемый ответ: Все точки половинок находятся на равном расстоянии от линии сгиба и на одном уровне.
– Значит, линия сгиба делит фигурку пополам так, что 1 половинка является копией 2 половинки, т.е. эта линия непростая, она обладает замечательным свойством (все точки относительно ее находятся на одинаковом расстоянии), эта линия – ось симметрии.
Задание 2 (2 мин).
– Вырезать снежинку, найти ось симметрии, охарактеризовать ее.
Задание 3 (5 мин).
– Начертить в тетради окружность.
Вопрос: Определить, как проходит ось симметрии?
Предполагаемый ответ: По-разному.
Вопрос: Так сколько осей симметрии имеет окружность?
Предполагаемый ответ: Много.
– Правильно, окружность имеет множество осей симметрии. Такой же замечательной фигурой является шар (пространственная фигура)
Вопрос: Какие еще фигуры имеют не одну ось симметрии?
Предполагаемый ответ: Квадрат, прямоугольник, равнобедренный и равносторонний треугольники.
– Рассмотрим объемные фигуры: куб, пирамиду, конус, цилиндр и т.д. Эти фигуры тоже имеют ось симметрии. Определите, сколько осей симметрии у квадрата, прямоугольника, равностороннего треугольника и у предложенных объемных фигур?
Раздаю учащимся половинки фигурок из пластилина.
Задание 4 (3 мин).
– Используя полученную информацию, долепить недостающую часть фигурки.
Примечание: фигурка может быть и плоскостной, и объемной. Важно, чтобы учащиеся определили, как проходит ось симметрии, и долепили недостающий элемент. Правильность выполнения определяет сосед по парте, оценивает, насколько правильно проделана работа.
Из шнурка одного цвета на рабочем столе выложена линия (замкнутая, незамкнутая, с самопересечением, без самопересечения).
Задание 5 (групповая работа 5 мин).
– Определить визуально ось симметрии и относительно нее достроить из шнурка другого цвета вторую часть.
Правильность выполненной работы определяется самими учениками.
Перед учащимися представлены элементы рисунков
Задание 6 (2 мин).
– Найдите симметричные части этих рисунков.
Для закрепления пройденного материала предлагаю следующие задания, предусмотренные на 15 мин.:
1. Прямая ОР – ось симметрии треугольника КОМ.
Назовите все равные элементы треугольника КОР и КОМ. Каков вид этих треугольников?
2. Начертите в тетради несколько равнобедренных треугольников с общим основанием равным 6 см.
3. Начертите отрезок АВ. Постройте прямую перпендикулярную отрезку АВ и проходящую через его середину. Отметьте на ней точки С и D так, чтобы четырехугольник АСВD был симметричен относительно прямой АВ.
– Наши первоначальные представления о форме
относятся к очень отдаленной эпохе древнего
каменного века – палеолита. В течение сотен
тысячелетий этого периода люди жили в пещерах, в
условиях мало отличавшихся от жизни животных.
Люди изготовляли орудия для охоты и рыболовства,
вырабатывали язык для общения друг с другом, а в
эпоху позднего палеолита украшали свое
существование, создавая произведения искусства,
статуэтки и рисунки, в которых обнаруживается
замечательное чувство формы.
Когда произошел переход от простого собирания
пищи к активному ее производству, от охоты и
рыболовства к земледелию, человечество вступает
в новый каменный век, в неолит.
Человек неолита обладал острым чувством
геометрической формы. Обжиг и раскраска глиняных
сосудов, изготовление камышовых циновок, корзин,
тканей, позже – обработка металлов вырабатывали
представления о плоскостных и пространственных
фигурах. Неолитические орнаменты радовали глаз,
выявляя равенство и симметрию.
– А где в природе встречается симметрия?
Предполагаемый ответ: крылья бабочек, жуков, листья деревьев…
– Симметрию можно наблюдать и в архитектуре. Строя здания, строители четко придерживаются симметрии.
Поэтому здания получаются такие красивые. Также примером симметрии служит человек, животные.
Задание на дом:
1. Придумать свой орнамент, изобразить его на
листе формат А4 (можно нарисовать в виде ковра).
2. Нарисовать бабочек, отметить, где присутствуют
элементы симметрии.
Нарисовать фигуру с осевой симметрией. Симметрия и асимметрия
I . Симметрия в математике :
Основные понятия и определения.
Осевая симметрия (определения, план построения, примеры)
Центральная симметрия (определения, план построения, при меры)
Обобщающая таблица (все свойства, особенности)
II . Применения симметрии:
1) в математике
2) в химии
3) в биологии, ботанике и зоологии
4) в искусстве, литературе и архитектуре
1. Основные понятия симметрии и ее виды.Понятие симметрии пр оходит через всю историю человечества. Оно встречается уже у истоков человеческого знания. Возникло оно в связи с изучением живого организма, а именно человека. И употреблялось скульпторами ещё в 5 веке до н. э. Слово “симметрия” греческое, оно означает “соразмерность, пропорциональность, одинаковость в расположении частей”. Его широко используют все без исключения направления современной науки. Об этой закономерности задумывались многие великие люди. Например, Л. Н. Толстой говорил: “Стоя перед черной доской и рисуя на ней мелом разные фигуры, я вдруг был поражен мыслью: почему симметрия понятна глазу? Что такое симметрия? Это врожденное чувство, отвечал я сам себе. На чем же оно основано?”. Действительно симметричность приятна глазу. Кто не любовался симметричностью творений природы: листьями, цветами, птицами, животными; или творениями человека: зданиями, техникой, – всем тем, что нас с детства окружает, тем, что стремится к красоте и гармонии. Герман Вейль сказал: “Симметрия является той идеей, посредством которой человек на протяжении веков пытался постичь и создать порядок, красоту и совершенство”. Герман Вейль – это немецкий математик. Его деятельность приходится на первую половину ХХ века. Именно он сформулировал определение симметрии, установил по каким признакам усмотреть наличие или, наоборот, отсутствие симметрии в том или ином случае. Таким образом, математически строгое представление сформировалось сравнительно недавно – в начале ХХ века. Оно достаточно сложное. Мы же обратимся и еще раз вспомним те определения, которые даны нам в учебнике.
2. Осевая симметрия.
2.1 Основные определения
Определение. Две точки А и А 1 называются симметричными относительно прямой а, если эта прямая проходит через середину отрезка АА 1 и перпендикулярна к нему. Каждая точка прямой а считается симметричной самой себе.
Определение. Фигура называется симметричной относительно прямой а , если для каждой точки фигуры симметричная ей точка относительно прямой а также принадлежит этой фигуре. Прямая а называется осью симметрии фигуры. Говорят также, что фигура обладает осевой симметрией.
2.2 План построения
И так, для построения симметричной фигуры относительно прямой от каждой точки проводим перпендикуляр к данной прямой и продлеваем его на такое же расстояние, отмечаем полученную точку. Так поступаем с каждой точкой, получаем симметричные вершины новой фигуры. Затем последовательно их соединяем и получаем симметричную фигуру данной относительной оси.
2.3 Примеры фигур, обладающих осевой симметрией.
3. Центральная симметрия
3.1 Основные определения
Определение . Две точки А и А 1 называются симметричными относительно точки О, если О — середина отрезка АА 1 . Точка О считается симметричной самой себе.
Определение. Фигура называется симметричной относительно точки О, если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре.
3.2 План построения
Построение треугольника симметричного данному относительно центра О.
Чтобы построить точку, симметричную точке А относительно точки О , достаточно провести прямую ОА (рис. 46) и по другую сторону от точки О отложить отрезок, равный отрезку ОА . Иными словами, точки А и ; В и ; С и симметричны относительно некоторой точки О. На рис. 46 построен треугольник, симметричный треугольнику ABC относительно точки О. Эти треугольники равны.
Построение симметричных точек относительно центра.
На рисунке точки М и М 1 , N и N 1 симметричны относительно точки О, а точки Р и Q не симметричны относительно этой точки.
Вообще фигуры, симметричные относительно некоторой точки, равны.
3.3 Примеры
Приведём примеры фигур, обладающие центральной симметрией. Простейшими фигурами, обладающими центральной симметрией, является окружность и параллелограмм.
Точка О называется центром симметрии фигуры. В подобных случаях фигура обладает центральной симметрией. Центром симметрии окружности является центр окружности, а центром симметрии параллелограмма- точка пересечения его диагоналей.
Прямая также обладает центральной симметрией, однако в отличие от окружности и параллелограмма, которые имеют только один центр симметрии (точка О на рисунке) у прямой их бесконечно много — любая точка прямой является её центром симметрии.
На рисунках показан угол симметричный относительно вершины, отрезок симметричный другому отрезку относительно центра А и четырехугольник симметричный относительно своей вершины М.
Примером фигуры, не имеющей центра симметрии, является треугольник.
4. Итог урока
Обобщим полученные знания. Сегодня на уроке мы познакомились с двумя основными видами симметрии: центральная и осевая. Посмотрим на экран и систематизируем полученные знания.
Обобщающая таблица
Осевая симметрия | Центральная симметрия | |
Особенность | Все точки фигуры должны быть симметричны относительно какой-нибудь прямой. | Все точки фигуры должны, симметричны относительно точки, выбранной в качестве центра симметрии. |
Свойства | 1. Симметричные точки лежат на перпендикулярах к прямой. 3. Прямые переходят в прямые, углы в равные углы. 4. Сохраняются размеры и формы фигур. | 1. Симметричные точки лежат на прямой, проходящей через центр и данную точку фигуры. 2. Расстояние от точки до прямой равно расстоянию от прямой до симметричной точки. 3. Сохраняются размеры и формы фигур. |
II. Применение симметрии
Математика | На уроках алгебры мы изучили графики функций y=x и y=x На рисунках представлены различные картинки, изображенные с помощью ветвей парабол. (а) Октаэдр, (б) ромбический додекаэдр, (в) гексагональной октаэдр. | |
Русский язык | Печатные буквы русского алфавита тоже обладают различными видами симметрий. В русском языке есть «симметричные» слова — палиндромы , которые можно читать одинаково в двух направлениях. | А Д Л М П Т Ф Ш – вертикальная ось В Е З К С Э Ю — горизонтальная ось Ж Н О Х — и вертикальная и горизонтальная Б Г И Й Р У Ц Ч Щ Я – ни какой оси Радар шалаш Алла Анна |
Литература | Могут быть палиндромичес- кими и предложения. Брюсов написал стихотворение «Голос луны», в котором каждая строка — палиндром. Посмотрите на четверости -шие А.С.Пушкина «Медный всадник». Если провести линию после второй строчки мы можем заметить элементы осевой симметрии | А роза упала на лапу Азора. Я иду с мечем судия. (Державин) «Искать такси» «Аргентина манит негра», «Ценит негра аргентинец», «Леша на полке клопа нашел». В гранит оделася Нева; Мосты повисли над водами; Темно-зелеными садами Ее покрылись острова… |
Биология | Тело человека построено по принципу двусторонней симметрии. Большинство из нас рассматривает мозг как единую структуру, в действительности он разделён на две половины. Эти две части — два полушария — плотно прилегают друг к другу. В полном соответствии с общей симметрией тела человека каждое полушарие представляет собой почти точное зеркальное отображение другого Управление основными движениями тела человека и его сенсорными функциями равномерно распределено между двумя полушариями мозга. Левое полушарие контролирует правую сторону мозга, а правое — левую сторону. |
Ботаника | Цветок считается симметричным, когда каждый околоцветник состоит из равного числа частей. Цветки, имея парные части, считаются цветками с двойной симметрией и т.д. Тройная симметрия обычна для однодольных растений, пятерная — для двудольных Характерной чертой строения растений и их развития является спиральность. Обратите внимание на побеги листорасположения – это тоже своеобразный вид спирали – винтовая. Еще Гёте, который был не только великим поэтом, но и естествоиспытателем, считал спиральность одним из характерных признаков всех организмов, проявлением самой сокровенной сущности жизни. Спирально закручиваются усики растений, по спирали происходит рост тканей в стволах деревьев, по спирали расположены семечки в подсолнечнике, спиральные движения наблюдаются при росте корней и побегов. | Характерной чертой строения растений и их развития является спиральность. Посмотрите на сосновую шишку. Чешуйки на ее поверхности расположены строго закономерно — по двум спиралям, которые пересекаются приблизительно под прямым углом. Число таких спиралей у сосновых шишек равно 8 и 13 или 13 и 21. |
Зоология | Под симметрией у животных понимают соответствие в размерах, форме и очертаниях, а также относительное расположение частей тела, находящихся на противоположных сторонах разделяющей линии. При радиальной или лучистой симметрии тело имеет форму короткого или длинного цилиндра либо сосуда с центральной осью, от которого отходят в радиальном порядке части тела. Это кишечнополостные, иглокожие, морские звёзды. При билатеральной симметрии осей симметрии три, но симметричных сторон только одна пара. Потому что две другие стороны — брюшная и спинная — друг на друга не похожи. Этот вид симметрии характерен для большинства животных, в том числе насекомых, рыб, земноводных, рептилий, птиц, млекопитающих. | Осевая симметрия |
Различные виды симметрии физических явлений: симметрия электрического и магнитного полей (рис. 1) Во взаимно перпендикулярных плоскостях симметрично распространение электромагнитных волн (рис. 2) | рис.1 рис.2 | |
Искусство | В произведениях искусства часто можно наблюдать зеркальную симметрию. Зеркальная» симметрия широко встречается в произведениях искусства примитивных цивилизаций и в древней живописи. Средневековые религиозные картины также характеризуются этим видом симметрии. Одно из лучших ранних произведений Рафаэля – «Обручение Марии» — создано в 1504 году. Под солнечным голубым небом раскинулась долина, увенчанная белокаменным храмом. На первом плане – обряд обручения. Первосвященник сближает руки Марии и Иосифа. За Марией – группа девушек, за Иосифом – юношей. Обе части симметричной композиции скреплены встречным движением персонажей. На современный вкус композиция такой картины скучна, поскольку симметрия слишком очевидна. |
Химия | Молекула воды имеет плоскость симметрии (прямая вертикальная линия).Исключительно важную роль в мире живой природы играют молекулы ДНК (дезоксирибонуклеиновая кислота). Это двуцепочечный высокомолекулярный полимер, мономером которого являются нуклеотиды. Молекулы ДНК имеют структуру двойной спирали, построенной по принципу комплементарности. | |
Архите ктура | Издавна человек использовал симметрию в архитектуре. Особенно блистательно использовали симметрию в архитектурных сооружениях древние зодчие. Причем древнегреческие архитекторы были убеждены, что в своих произведениях они руководствуются законами, которые управляют природой. Выбирая симметричные формы, художник тем самым выражал свое понимание природной гармонии как устойчивости и равновесия. В городе Осло, столице Норвегии, есть выразительный ансамбль природы и художественных произведений. Это Фрогнер – парк – комплекс садово-парковой скульптуры, который создавался в течение 40 лет. | Дом Пашкова Лувр (Париж) |
© Сухачева Елена Владимировна, 2008-2009гг.
Цели:
- образовательные:
- дать представление о симметрии;
- познакомить с основными видами симметрии на плоскости и в пространстве;
- выработать прочные навыки построения симметричных фигур;
- расширить представления об известных фигурах, познакомив со свойствами, связанных с симметрией;
- показать возможности использования симметрии при решении различных задач;
- закрепить полученные знания;
- общеучебные:
- научить настраивать себя на работу;
- научить вести контроль за собой и соседом по парте;
- научить оценивать себя и соседа по парте;
- развивающие:
- активизировать самостоятельную деятельность;
- развивать познавательную деятельность;
- учить обобщать и систематизировать полученную информацию;
- воспитательные:
- воспитываать у учащихся “чувство плеча”;
- воспитывать коммуникативность;
- прививать культуру общения.
ХОД УРОКА
Перед каждым лежат ножницы и лист бумаги.
Задание 1 (3 мин).
– Возьмем лист бумаги, сложим его попалам и вырежем какую-нибудь фигурку. Теперь развернем лист и посмотрим на линию сгиба.
Вопрос: Какую функцию выполняет эта линия?
Предполагаемый ответ: Эта линия делит фигуру пополам.
Вопрос: Как расположены все точки фигуры на двух получившихся половинках?
Предполагаемый ответ: Все точки половинок находятся на равном расстоянии от линии сгиба и на одном уровне.
– Значит, линия сгиба делит фигурку пополам так, что 1 половинка является копией 2 половинки, т.е. эта линия непростая, она обладает замечательным свойством (все точки относительно ее находятся на одинаковом расстоянии), эта линия – ось симметрии.
Задание 2 (2 мин).
– Вырезать снежинку, найти ось симметрии, охарактеризовать ее.
Задание 3 (5 мин).
– Начертить в тетради окружность.
Вопрос: Определить, как проходит ось симметрии?
Предполагаемый ответ: По-разному.
Вопрос: Так сколько осей симметрии имеет окружность?
Предполагаемый ответ: Много.
– Правильно, окружность имеет множество осей симметрии. Такой же замечательной фигурой является шар (пространственная фигура)
Вопрос: Какие еще фигуры имеют не одну ось симметрии?
Предполагаемый ответ: Квадрат, прямоугольник, равнобедренный и равносторонний треугольники.
– Рассмотрим объемные фигуры: куб, пирамиду, конус, цилиндр и т.д. Эти фигуры тоже имеют ось симметрии.Определите, сколько осей симметрии у квадрата, прямоугольника, равностороннего треугольника и у предложенных объемных фигур?
Раздаю учащимся половинки фигурок из пластилина.
Задание 4 (3 мин).
– Используя полученную информацию, долепить недостающую часть фигурки.
Примечание: фигурка может быть и плоскостной, и объемной. Важно, чтобы учащиеся определили, как проходит ось симметрии, и долепили недостающий элемент. Правильность выполнения определяет сосед по парте, оценивает, насколько правильно проделана работа.
Из шнурка одного цвета на рабочем столе выложена линия (замкнутая, незамкнутая, с самопересечением, без самопересечения).
Задание 5 (групповая работа 5 мин).
– Определить визуально ось симметрии и относительно нее достроить из шнурка другого цвета вторую часть.
Правильность выполненной работы определяется самими учениками.
Перед учащимися представлены элементы рисунков
Задание 6 (2 мин).
– Найдите симметричные части этих рисунков.
Для закрепления пройденного материала предлагаю следующие задания, предусмотренные на 15 мин.:
Назовите все равные элементы треугольника КОР и КОМ. Каков вид этих треугольников?
2. Начертите в тетради несколько равнобедренных треугольников с общим основанием равным 6 см.
3. Начертите отрезок АВ. Постройте прямую перпендикулярную отрезку АВ и проходящую через его середину. Отметьте на ней точки С и D так, чтобы четырехугольник АСВD был симметричен относительно прямой АВ.
– Наши первоначальные представления о форме
относятся к очень отдаленной эпохе древнего
каменного века – палеолита. В течение сотен
тысячелетий этого периода люди жили в пещерах, в
условиях мало отличавшихся от жизни животных.
Люди изготовляли орудия для охоты и рыболовства,
вырабатывали язык для общения друг с другом, а в
эпоху позднего палеолита украшали свое
существование, создавая произведения искусства,
статуэтки и рисунки, в которых обнаруживается
замечательное чувство формы.
Когда произошел переход от простого собирания
пищи к активному ее производству, от охоты и
рыболовства к земледелию, человечество вступает
в новый каменный век, в неолит.
Человек неолита обладал острым чувством
геометрической формы. Обжиг и раскраска глиняных
сосудов, изготовление камышовых циновок, корзин,
тканей, позже – обработка металлов вырабатывали
представления о плоскостных и пространственных
фигурах. Неолитические орнаменты радовали глаз,
выявляя равенство и симметрию.
– А где в природе встречается симметрия?
Предполагаемый ответ: крылья бабочек, жуков, листья деревьев…
– Симметрию можно наблюдать и в архитектуре. Строя здания, строители четко придерживаются симметрии.
Поэтому здания получаются такие красивые. Также примером симметрии служит человек, животные.
Задание на дом:
1. Придумать свой орнамент, изобразить его на
листе формат А4 (можно нарисовать в виде ковра).
2. Нарисовать бабочек, отметить, где присутствуют
элементы симметрии.
Если на минутку задуматься и представить у себя в воображении какой-либо предмет, то в 99% случаев фигура, пришедшая на ум, будет правильной формы. Лишь 1 % людей, точнее их воображение, нарисует замысловатый объект, выглядящий совсем неправильно или непропорционально. Это скорее исключение из правил и относится к нетрадиционно размышляющим личностям с особым взглядом на вещи. Но возвращаясь к абсолютному большинству, стоит сказать, что существенная доля правильных предметов все же преобладает. В статье пойдет речь исключительно о них, а именно о симметричном рисовании таковых.
Изображение правильных предметов: всего несколько шагов до законченного рисунка
Прежде чем приступить к рисованию симметричного предмета, нужно его выбрать. В нашем варианте это будет ваза, но даже если она никак не напоминает то, что решили изображать вы, не отчаивайтесь: все шаги абсолютно идентичны. Придерживайтесь последовательности и все получится:
- У всех предметов правильной формы есть так называемая центральная ось, которую при симметричном рисовании обязательно стоит выделить. Для этого можно даже воспользоваться линейкой и провести по центру альбомного листа прямую линию.
- Далее внимательно посмотрите на выбранный вами предмет и постарайтесь перенести его пропорции на лист бумаги. Сделать это несложно, если с обеих сторон проведенной заранее линии, наметить легкие штрихи, которые впоследствии станут очертаниями рисуемого предмета. В случае с вазой необходимо выделить горлышко, донышко и самую широкую часть корпуса.
- Не забывайте о том, что симметричное рисование не терпит неточностей, поэтому если есть некоторые сомнения относительно намеченных штрихов, или вы не уверены в правильности собственного глазомера, перепроверьте отложенные расстояния при помощи линейки.
- Последний шаг — соединение всех линий воедино.
Симметричное рисование доступно компьютерным пользователям
В силу того что большинство окружающих нас предметов имеют правильные пропорции, иначе говоря симметричны, разработчики компьютерных приложений создали программы, в которых легко можно нарисовать абсолютно все. Достаточно лишь скачать их и наслаждаться творческим процессом. Однако помните, машина никогда не станет заменой остро наточенному карандашу и альбомному листу.
ТРЕУГОЛЬНИКИ.
§ 17. СИММЕТРИЯ ОТНОСИТЕЛЬНО ПРЯМОЙ.
1. Фигуры, симметричные друг другу.
Начертим на листе бумаги чернилами какую-нибудь фигуру, а карандашом вне её — произвольную прямую. Затем, не давая чернилам высохнуть, перегнём лист бумаги по этой прямой так, чтобы одна часть листа налегла на другую. На этой другой части листа получится, таким образом, отпечаток данной фигуры.
Если затем лист бумаги опять распрямить, то на нём окажутся две фигуры, которые называются симметричными относительно данной прямой (черт. 128).
Две фигуры называются симметричными относительно некоторой прямой, если при перегибании плоскости чертежа по этой прямой они совмещаются.
Прямая, относительно которой данные фигуры симметричны, называется их осью симметрии .
Из определения симметричных фигур следует, что всякие симметричные фигуры равны.
Получить симметричные фигуры можно и не пользуясь перегибанием плоскости, а с помощью геометрического построения. Пусть требуется построить точку С», симметричную данной точке С относительно прямой АВ. Опустим из точки С перпендикуляр
СD на прямую АВ и на продолжении его отложим отрезок DС» = DС. Если перегнём плоскость чертежа по АВ, то точка С совместится с точкой С»: точки С и С» симметричны (черт. 129).
Пусть требуется теперь построить отрезок С»D», симметричный данному отрезку СD относительно прямой АВ. Построим точки С» и D», симметричные точкам С и D. Если перегнём плоскость чертежа по АВ, то точки С и D совместятся соответственно с точками С» и D» (черт. 130).Поэтому отрезки СD и С»D» совместятся, они будут симметричны.
Построим теперь фигуру, симметричную данному многоугольнику АВСDЕ относительно данной оси симметрии МN (черт. 131).
Для решения этой задачи опустим перпендикуляры Аа , Вb , Сс , Dd и Ее на ось симметрии МN. Затем на продолжениях этих перпендикуляров отложим отрезки
а А» = Аа , b В» = Вb , с С» = Сс; d D»» =Dd и е Е» = Ее .
Многоугольник А»В»С»D»Е» будет симметричным многоугольнику АВСDЕ. Действительно, если перегнуть чертёж по прямой МN, то соответствующие вершины обоих многоугольников совместятся, а значит, совместятся и сами многоугольники; это и доказывает, что многоугольники АВСDЕ и А»В»С»D»Е» симметричны относительно прямой MN.
2. Фигуры, состоящие из симметричных частей.
Часто встречаются геометрические фигуры, которые какой-нибудь прямой разделяются на две симметричные части. Такие фигуры называются симметричными.
Так, например, угол — фигура симметричная, и биссектриса угла является его осью симметрии, так как при перегибании по ней одна часть угла совмещается с другой (черт. 132).
В круге осью симметрии является его диаметр, так как при перегибании по нему один полукруг совмещается с другим (черт. 133). Точно так же симметричны фигуры на чертежах 134, а, б.
Симметричные фигуры часто встречаются в природе, строительстве, в украшениях. Изображения, помещённые на чертежах 135 и 136, симметричны.
Следует заметить, что симметричные фигуры совместить простым передвижением по плоскости можно лишь в некоторых случаях. Чтобы совместить симметричные фигуры, как правило, необходимо одну из них повернуть обратной стороной,
Эта пара средств определяет расположение элементов композиции относительно главной оси. Если оно одинаково, то композиция выступает как симметричная, если в нем есть небольшое отклонение в сторону, то композиция является дисимметричной. При значительном таком отклонении она становится асимметричной.
Очень часто симметрия, как и асимметрия, выражается в сопоставлении нескольких композиционных осей. Самый простой случай – соотношение главной оси и подчиненных ей осей, определяющих положение второстепенных частей композиции. При значительном расхождении второстепенных осей с главной осью композиция может разрушиться. Для достижения ее целостности используются разные приемы: сближение осей, их слияние, принятие общего направления. На рисунке 17 представлены формальные композиции (схемы), построенные на их основе.
Рисунок 17 — Композиции с разными осями симметрии
1 Создать симметричную композицию (разные виды симметрии) (Приложение А, рисунки 15-16).
2 Создать асимметричную композицию (Приложение А, рисунок 17).
Требования:
выполняется 7-10 поисковых вариантов композиции;
внимательно отнестись к компоновке элементов; при реализации основной идеи заботиться об аккуратности исполнения.
Карандаш, тушь, акварель, цветные карандаши. Формат листа – А3.
Равновесие
Правильно построенная композиция является уравновешенной.
Равновесие – это размещение элементов композиции, при котором каждый предмет находится в устойчивом положении. Его местонахождение не вызывает сомнения и желания передвинуть его по изобразительной плоскости. При этом не требуется точного зеркального соответствия правой и левой сторон. Количественное соотношение тональных и цветовых контрастов левой и правой частей композиции должно быть равным. Если же в одной части число контрастных пятен больше, необходимо усилить контрастные отношения в другой части либо ослабить контрасты в первой. Можно изменить очертания предметов, увеличив периметр контрастных отношений.
Для установления равновесия в композиции важны форма, направление, место расположения изобразительных элементов (рисунок 18).
Рисунок 18 — Равновесие контрастных пятен в композиции
Неуравновешенная композиция выглядит случайной и необоснованной, вызывающей желание дальше работать над ней (производить перекомпоновку элементов и их деталей) (рисунок 19).
Рисунок 19 — Уравновешенная и неуравновешенная композиция
Правильно построенная композиция не может вызывать сомнения и чувства неопределенности. В ней должна быть успокаивающая глаз ясность соотношений, пропорций.
Рассмотрим простейшие схемы построения композиций:
Рисунок 20 – Схемы уравновешенности композиции
Изображение А – уравновешенное. В сочетании его квадратов и прямоугольников различных размеров и пропорций чувствуется жизнь, ничего не хочется изменить или добавить, есть композиционная ясность пропорций.
Можно сравнить устойчивую вертикальную линию на рисунке 20, А с колеблющейся на рисунке 20, Б. Пропорции на рисунке Б основаны на небольших различиях, которые мешают определить их равноценность, понять, что изображено — прямоугольник или квадрат.
На рисунке 20, В каждый диск в отдельности выглядит неуравновешенным. Вместе они образуют пару, которая находится в состоянии покоя. На рисунке 20, Г та же самая пара выглядит совершенно несбалансированной, т.к. сдвинута относительно осей квадрата.
Равновесие бывает двух видов.
Статическое равновесие возникает при симметричном расположении фигур на плоскости относительно вертикальной и горизонтальной осей формата композиции симметричной формы (рисунок 21).
Рисунок 21 — Статическое равновесие
Динамическое равновесие возникает при асимметричном расположении фигур на плоскости, т.е. при их сдвиге вправо, влево, вверх, вниз (рисунок 22).
Рисунок 22 — Динамическое равновесие
Чтобы фигура казалась изображенной в центре плоскости, ее нужно немного передвинуть вверх относительно осей формата. Круг, расположенный в центре, кажется смещенным вниз, этот эффект усиливается, если низ круга окрасить в темный цвет (рисунок 23).
Рисунок 23 – Уравновешенность круга
Крупную фигуру в левой части плоскости в состоянии уравновесить небольшой контрастный элемент в правой, который активен в силу своих тональных отношений с фоном (рисунок 24).
Рисунок 24 – Уравновешенность крупного и мелкого элемента
1 Выполнить уравновешенную композицию, используя любые мотивы (Приложение А, рисунок 18).
2 Выполнить неуравновешенную композицию (Приложение А, рисунок 19).
Требования:
выполнить поисковые варианты (5-7 шт.) в ахроматическом исполнении с нахождением тональных отношений;
работа должна быть аккуратной.
Материал и размеры композиции
Тушь. Формат листа – А3.
Как использовать Paint Symmetry в Photoshop CC 2019
Узнайте, как использовать новую функцию Paint Symmetry в Photoshop CC 2019, чтобы с легкостью создавать забавные симметричные рисунки и дизайны!
Автор Стив Паттерсон.
Paint Symmetry в Photoshop позволяет рисовать сразу несколько мазков кистью для создания зеркальных, симметричных рисунков и узоров. Он работает с инструментами «Кисть», «Карандаш» и «Ластик», а также с масками слоев.
Впервые добавленная в качестве технической превью в Photoshop CC 2018, Paint Symmetry теперь является официальной частью Photoshop с CC 2019. Включены все основные параметры симметрии из CC 2018, такие как Vertical, Horizontal и Diagonal. Plus CC 2019 также добавляет два новых режима симметрии, Radial и Mandala, которые позволяют создавать удивительные, очень сложные симметричные изображения за секунды! Посмотрим, как это работает.
Чтобы продолжить, вам понадобится Photoshop CC. А если вы уже являетесь подписчиком Creative Cloud, убедитесь, что у вас установлена последняя версия Photoshop CC.Давайте начнем!
Загрузите это руководство в виде готового к печати PDF-файла!
Как рисовать симметрично в Photoshop
Мы начнем с изучения основ использования Paint Symmetry для создания симметричных иллюстраций и дизайнов. Когда мы узнаем основы, я покажу вам, как комбинировать Paint Symmetry с масками слоя для получения более творческих эффектов!
Шаг 1: Добавьте новый пустой слой
Начните с добавления в документ нового пустого слоя. Это позволит отделить мазки кисти от всего остального.Чтобы добавить новый слой, щелкните значок New Layer в нижней части панели «Слои»:
Щелкните значок «Новый слой».
Шаг 2. Выберите инструмент «Кисть», «Карандаш» или «Ластик».
Paint Symmetry работает с инструментами «Кисть», «Карандаш» и «Ластик», которые находятся на панели инструментов. Я выберу инструмент «Кисть » :
.Выбор инструмента «Кисть».
Как загрузить еще более 1000 кистей в Photoshop
Шаг 3. Откройте меню Paint Symmetry
Выбрав инструмент «Кисть, Карандаш или Ластик», на панели параметров появится значок Paint Symmetry (маленькая бабочка).Щелкните значок, чтобы открыть меню Paint Symmetry:
Щелкните значок «Симметрия рисования» (бабочка).
Шаг 4: Выберите вариант симметрии
Затем в меню выберите вариант симметрии из списка. В CC 2019 есть десять различных стилей на выбор, включая новые параметры Radial и Mandala внизу:
Параметры Paint Symmetry в Photoshop CC 2019.
Параметры симметрии краски в Photoshop CC 2019
Вот краткое описание того, как работает каждая из десяти опций Paint Symmetry в Photoshop:
- По вертикали: Делит холст по вертикали и отражает мазки кисти с одной стороны на другую.
- По горизонтали: Делит холст по горизонтали и отражает мазки кисти сверху вниз или снизу вверх.
- Dual Axis: Делит холст по вертикали и по горизонтали на четыре равные части (верхний левый, верхний правый, нижний левый и нижний правый). Рисование в одном разделе отражает мазки кисти в трех других.
- Диагональ: Делит холст по диагонали и отражает мазки кисти с одной стороны на другую.
- Волнистый: Подобен вертикальному, но с изогнутой волнистой линией вместо прямой.
- Круг: Отражает мазки кисти, нарисованные внутри круга за пределами круга, и наоборот.
- Спираль: Отражает мазки кисти, нарисованные по обе стороны спирального пути.
- Параллельные линии: Делит холст на три вертикальные части с помощью двух параллельных вертикальных линий. Мазки кисти, нарисованные в средней части, отражаются в левой и правой частях.
- Radial: Делит холст на диагональные сегменты, или «кусочки». Мазки кисти, нарисованные в одном сегменте, отражаются в других.
- Мандала: Подобно Радиальному, но также отражает мазки кисти в пределах каждого сегмента, создавая вдвое больше мазков кисти, чем Радиальный.
Мы не будем рассматривать здесь все варианты симметрии, так как вы легко можете попробовать их самостоятельно. Но чтобы показать вам основы их работы, я выберу простой, например Dual Axis .Двойная ось — это комбинация вертикального и горизонтального режимов, перечисленных выше:
Выбор одного из десяти вариантов симметрии краски.
Путь симметрии
При выборе параметра в меню к документу добавляется синий контур симметрии . В данном случае это путь симметрии Dual Axis, разделяющий холст по вертикали и горизонтали на четыре равные части:
Появляется симметричный путь.
Шаг 5: Измените размер и примите путь
Прежде чем вы сможете рисовать симметричным контуром, Photoshop сначала помещает прямоугольник Transform вокруг контура, чтобы вы могли масштабировать и изменять его размер при необходимости.Но обратите внимание, что путь предназначен только для визуальной ссылки . Пути симметрии всегда влияют на весь холст независимо от фактического размера пути. Поскольку рисование за пределами контура имеет тот же эффект, что и рисование внутри него, на самом деле нет ничего нового, изменяя размер контуров симметрии. Поэтому в большинстве случаев изменять его размер не требуется.
Однако, если вы действительно хотите изменить размер пути, просто перетащите любой из маркеров преобразования, чтобы пропорционально масштабировать путь. Чтобы масштабировать путь от его центра, нажмите и удерживайте Alt (Win) / Option (Mac) при перетаскивании маркера.Вы также можете переместить путь в другое место в документе, щелкнув и перетащив курсор в поле преобразования:
Масштабирование пути симметрии путем перетаскивания углового маркера.
Связано: новые функции Free Transform и изменения в CC 2019
Чтобы принять путь (даже если вы не изменяли его размер) и выйти из команды «Преобразовать», щелкните галочку на панели параметров или нажмите Введите (Win) / Верните (Mac) на клавиатуре. :
Щелкните галочку, чтобы подтвердить путь.
Шаг 6: Закрасьте одну из секций, чтобы создать симметрию
Затем, установив путь симметрии, просто нарисуйте внутри одной из секций. Photoshop автоматически скопирует и отразит ваш мазок кисти в других разделах, создавая симметричный дизайн:
Рисование одним мазком кисти создает несколько зеркальных мазков.
Чем больше мазков кисти вы рисуете, тем сложнее становится рисунок. Даже при ограниченных навыках рисования Photoshop позволяет легко придумать что-нибудь интересное:
Рисование большего количества мазков добавляет симметричному дизайну.
Как скрыть путь симметрии
Чтобы просмотреть изображение без синего контура симметрии, скройте его, щелкнув значок Paint Symmetry (бабочка) на панели параметров и выбрав Hide Symmetry :
Выбор «Скрыть симметрию» в параметрах «Раскрашивание симметрии».
Так как путь предназначен только для визуального ознакомления, вы можете продолжать рисовать и добавлять в дизайн, даже если путь скрыт:
Скрытие контура по-прежнему позволяет рисовать симметрично.
Как показать путь симметрии
Чтобы снова показать путь, щелкните значок бабочки на панели параметров и выберите Показать симметрию :
Выбор «Показать симметрию» в параметрах «Рисование симметрии».
И вот путь снова виден:
Это искусство? Наверное, нет, но это было, конечно, легко.
Просмотр пути симметрии на панели «Контуры»
Как и обычные контуры в Photoshop, контуры симметрии отображаются на панели «Контуры » .Путь назван в соответствии с его режимом симметрии (в данном случае «Dual Axis Symmetry 1»). Значок бабочки в правом нижнем углу миниатюры говорит нам не только о том, что это путь симметрии, но и о том, что он в настоящее время активен. В одном документе может быть несколько путей симметрии (как мы вскоре увидим), но одновременно может быть активен только один:
Пути симметрииможно просмотреть и выбрать на панели «Пути».
Загрузите это руководство в виде готового к печати PDF-файла!
Новые возможности радиальной симметрии и симметрии мандалы
Новым в Photoshop CC 2019 являются два новых параметра Paint Symmetry: Radial и Mandala .Посмотрим, как они работают.
Как использовать опцию радиальной симметрии
Режим радиальной симметрии делит холст на диагональные сегменты или «кусочки» (например, кусочки пиццы). Рисование в одном фрагменте отражает мазки кисти в других.
Шаг 1. Выберите «Радиальный» в параметрах «Симметрия траектории».
Щелкните значок бабочки на панели параметров и выберите Radial из списка:
Выбор радиальной из опций симметрии краски.
Шаг 2: Установите количество сегментов
Затем выберите необходимое количество сегментов (срезов) пути от 2 до 12.Я пойду с 5:
Выбор количества сегментов для разделения холста.
Шаг 3: Закрасьте один из сегментов
А затем просто закрасьте один из сегментов. Photoshop отразит ваш мазок кисти в других сегментах, создав радиальный узор:
Создание конструкции радиальной симметрии.
Как использовать параметр симметрии мандалы
Как и Radial, режим симметрии Mandala также разделяет холст на диагональные сегменты. Разница между Radial и Mandala заключается в том, что, помимо отражения мазка кисти в других сегментах, Mandala также отражает мазок в том же сегменте и .Это добавляет вдвое больше мазков кисти, чем Radial, что позволяет создавать очень сложные симметричные узоры с минимальными затратами времени и усилий.
Шаг 1. Выберите «Мандала» в параметрах «Симметрия пути».
Щелкните значок бабочки на панели параметров и выберите Мандала из списка:
Выбор мандалы из опций Paint Symmetry.
Шаг 2: Установите количество сегментов
Затем, как и в случае с Radial, выберите необходимое количество сегментов пути.В то время как Radial позволяет вам выбрать до 12 сегментов, Mandala ограничена 10. Я выберу 8:
.Выбор количества сегментов.
Шаг 3: Закрасьте один из сегментов
А затем, как и раньше, закрасьте один из сегментов. Photoshop отразит ваш мазок кисти в том же сегменте, в котором вы рисуете, и отразит и мазков кисти в других сегментах. Этот сложный дизайн занял у меня всего пару минут:
Мандала — самая впечатляющая (и увлекательная) из возможностей Photoshop Paint Symmetry.
Как отменить мазки кистью, если вы сделали ошибку
Создание симметричного дизайна в Photoshop — это весело и легко, но также может потребоваться много проб и ошибок. Если вам не нравится только что нарисованный мазок кисти, вы можете отменить его с клавиатуры, нажав Ctrl + Z (Win) / Command + Z (Mac). Продолжайте нажимать ярлык, чтобы отменить несколько мазков кистью. Чтобы повторить мазки кисти, нажмите Shift + Ctrl + Z (Win) / Shift + Command + Z (Mac).
Как переключаться между путями симметрии
Photoshop позволяет нам добавлять несколько контуров симметрии в один и тот же документ, и каждый добавляемый вами путь появляется на панели Paths . Значок «бабочка» в правом нижнем углу эскиза указывает активный в настоящее время путь симметрии. Одновременно может быть активен только один путь. В этом случае активен мой путь мандалы:
Значок бабочки показывает активный путь.
Чтобы переключиться на один из других путей в списке, щелкните правой кнопкой мыши (Win) / , удерживая клавишу Control, щелкните (Mac) по нужному пути:
Щелкните правой кнопкой мыши (Win) / щелкните, удерживая клавишу Control (Mac), на пути радиальной симметрии.
Затем выберите в меню Make Symmetry Path :
Выбор команды «Создать путь симметрии».
Это деактивирует предыдущий путь и активирует новый, чтобы вы могли рисовать им в документе:
Путь радиальной симметрии теперь активен.
Последний использованный параметр симметрии
Вы также можете переключиться с текущего пути симметрии на ранее использовавшийся путь, щелкнув значок бабочки на панели параметров и выбрав Последняя использованная симметрия :
Путь радиальной симметрии теперь активен.
Как выключить Paint Symmetry
Чтобы выключить Paint Symmetry и продолжить рисование без эффекта симметрии, щелкните значок бабочки на панели параметров и выберите Symmetry Off :
Выбор в меню «Симметрия выключена».
Как использовать Paint Symmetry с маской слоя
Теперь, когда мы узнали основы того, как работает Paint Symmetry, давайте посмотрим, как мы можем использовать путь симметрии с маской слоя, чтобы создать что-то еще более интересное.
В этом документе у меня есть радиальный градиент на фоновом слое:
Радиальный градиент спектра.
И если мы посмотрим на панель Layers, мы увидим, что у меня также есть сплошной черный слой, расположенный над градиентом. Я включу верхний слой, щелкнув его значок видимости:
Включение верхнего слоя в документе.
И теперь документ заполнен черным цветом, закрывая вид градиента:
Верхний слой скрывает градиент.
Шаг 1: Добавьте маску слоя
Выбрав верхний слой, я добавлю маску слоя, щелкнув значок Добавить маску слоя в нижней части панели «Слои»:
Щелкните значок «Добавить маску слоя».
Миниатюра маски слоя появляется на верхнем слое:
Миниатюра маски слоя.
Шаг 2. Выберите инструмент «Кисть»
.Я выберу Brush Tool на панели инструментов:
Выбор инструмента «Кисть».
Шаг 3: Установите черный цвет переднего плана
И поскольку я хочу скрыть верхний слой в областях, где проявляется эффект симметрии, я сделаю так, чтобы мой цвет переднего плана (цвет кисти) был установлен на черный :
Установка черного цвета кисти.
Шаг 4. Выберите параметр «Симметрия окраски»
Я выберу Mandala из параметров Paint Symmetry на панели параметров:
Выбор варианта симметрии.
И Photoshop добавляет в документ путь симметрии мандалы. Чтобы принять его, я нажимаю Enter (Win) / Return (Mac) на моей клавиатуре:
Симметричный путь добавлен в документ.
Шаг 5. Нарисуйте симметричный рисунок на маске слоя
.Затем, чтобы скрыть текущий слой и показать слой под ним, просто закрасьте маску слоя.По мере расширения эффекта симметрии раскрывается все больше и больше нижележащего слоя. В этом случае цвета моего градиента видны через мазки кисти:
Рисование симметричным контуром на маске слоя, чтобы открыть изображение ниже.
Я продолжу рисовать, чтобы добавить больше мазков кисти к эффекту мандалы. И вот мой окончательный красочный результат:
.Окончательный дизайн мандалы.
И вот оно! Вот как использовать Paint Symmetry в Photoshop CC 2019! Посетите наш раздел «Основы Photoshop», чтобы получить дополнительные уроки! И не забывайте, что все наши руководства теперь доступны для скачивания в формате PDF!
Симметрия красок — Artrage
Симметрия красок ArtRage
Система Paint Symmetry автоматически создает зеркальные штрихи на холст во время рисования и позволяет контролировать такие свойства, как количество зеркала созданы и центральная точка симметрии.
Paint Symmetry можно активировать и контролировать с помощью Paint Symmetry. меню в меню инструментов.
При включении симметрии любой штрих, который вы делаете на холсте, будет зеркально отражается в других положениях в зависимости от выбранных вами настроек. Есть две важные настройки, которые определяют, как это работает:
- Количество сегментов: Это значение определяет, сколько различных симметрий сегменты есть. Ваш ход повторяется в каждом сегменте на холст.
- Тип симметрии: Это значение определяет, являются ли повторяющиеся штрихи прямое зеркальное отражение или вращение вокруг центральной точки.
Объясняется, как эти две настройки определяют внешний вид зеркальной краски.
ниже:
Пунктирными линиями на холсте обозначены линии симметрия между сегментами. Это «зеркала» отражающие вашу краску.
Когда вы рисуете в сегменте, обведенном пунктирной линией, ваш мазок краски повторяется в других сегментах. То, как именно повторяются штрихи, определяется Тип симметрии (см. ниже).
Вы можете установить количество сегментов, выбрав Set Number of Параметр «Сегменты» в меню «Симметрия».
Если вы используете зеркальную симметрию (см. Ниже), количество сегменты должны быть четным числом.
Выбранный тип симметрии определяет, как краска в каждом сегмент ведет себя. Есть два типа:
Зеркальная симметрия: Этот тип симметрии линии между сегментами как зеркала, отражающие нарисованный контент.
В этом примере стрелка в левом верхнем углу была окрашен вправо, произведен правый сегмент стрелка, которая нарисовала себя влево.
Вращательная симметрия: Этот тип симметрии учитывает линии между сегментами как срезы циферблат и все, что вы рисуете в срезе, будет точно повторяется в следующем срезе, повернут на угол вокруг центра симметрии.
В этом примере стрелка в левом верхнем углу была окрашен вправо, произведен правый сегмент стрелка, также нарисованная в сторону правой руки край своего сегмента.
Тип симметрии можно установить с помощью параметров в меню «Симметрия».
Управление симметрией
Когда вы включаете Paint Symmetry на симметрии, шайба появляется посередине холста. Эта шайба находится в центральной точке системы симметрии ( точка, вокруг которой будет вращаться вращательная симметрия).
Этот значок представляет зеркальную симметрию.
Этот значок обозначает симметрию вращения.
Можно щелкнуть центральную кнопку шайбы симметрии, чтобы открыть окно симметрии. Меню. Вы также можете манипулировать самой шайбой, чтобы редактировать свойства симметрии:
- Щелкните и перетащите шайбу, чтобы переместить центр симметрии.Удерживайте Shift чтобы ограничить движение одной осью.
- Удерживая Ctrl (Windows) / Cmd (OS X), щелкните и перетащите шайбу на повернуть оси симметрии. Удерживайте Shift, чтобы ограничить вращение с шагом 15 градусов.
- Удерживая нажатой клавишу Alt (Windows) / Option (OS X), щелкните и перетащите шайбу на изменить количество осей. Обратите внимание, что если вы используете зеркальную симметрию в режиме количество осей всегда будет четным.
В меню симметрии есть две опции, которые определяют, как вы можете
манипулировать осями симметрии:
- Показать контроль симметрии: Этот параметр устанавливает, будет ли шайба симметрии видно.Если это не так, вы можете показать его снова, используя меню симметрии в меню «Инструменты».
- Разрешить перетаскивание оси: Если эта опция включена, вы сможете вращать осей симметрии, щелкнув и перетащив пунктирные линии на холст. По умолчанию он отключен, чтобы предотвратить случайное редактирование топоры.
Рисование с симметрией
Когда включена симметрия, вы не ограничены рисованием в одном сегменте или «Внутри линий». Линии действуют как зеркала, но мазки краски могут проходить мимо их сколько угодно.Это означает, что мазок, который вы рисуете, может взаимодействовать с другими штрихами, которые создаются автоматически.
Большинство инструментов без проблем взаимодействуют с этой системой, как если бы вы рисовать вручную несколько мазков одновременно. Некоторые инструменты не взаимодействовать с Symmetry или отображать другое особое поведение:
- Наклейка-спрей: Если наклейка-спрей настроена на распыление со случайными вариациями форма вашего штриха останется той же в каждом сегменте, но в любом Применяемое случайное свойство будет рандомизировано для каждого сегмента независимо.
- Инструмент выделения: Единственный тип выделения, который отражается, пока вы создать это раскрашенный тип. Выбор отменяет систему симметрии и если у вас есть выделенная область, только краска, созданная симметрией внутри эта область будет применена.
- Инструмент преобразования: Инструмент преобразования игнорирует симметрию.
- Инструмент Sampler: Инструмент Sampler игнорирует симметрию.
- Инструмент заливки: Инструмент заливки игнорирует симметрию.
- Инструмент «Текст»: Инструмент «Текст» игнорирует симметрию.
Рисуйте с симметрией в Photoshop CC и дайте волю своему творчеству
Рисование с симметрией в Photoshop CC — отличный способ раскрыть свой творческий потенциал, ускорить и повысить точность вашей работы. Новая функция симметрии имеет несколько режимов симметрии, которые вы можете использовать в соответствии со своими потребностями.
На мой взгляд, это не обязательный инструмент в концепции и философии Photoshop и в том, что вы должны с ним делать, но иметь его действительно приятно.
После стольких лет отсутствия инструмента симметрии в Photoshop, хотя он уже есть в какой-то другой программе для редактирования изображений, я подумал, что этого никогда не произойдет. Я рада, что ошиблась.
Если вы новичок в Adobe Photoshop, вы можете взглянуть на КАК И ЗАЧЕМ УЗНАТЬ PHOTOSHOP
Как рисовать с симметрией в Photoshop:
Как использовать симметрию:
Рисовать с симметрией в Photoshop очень просто. процесс. Единственное, что вам нужно сделать, это включить функцию симметрии в Photoshop, и вы готовы творить великие дела с ее помощью.
Мы можем использовать функцию симметрии как с кистью, так и с инструментами карандаша. Конечно, инструмент стирания тоже работает с симметрией.
Чтобы включить симметрию, выберите один из этих инструментов, нажмите значок бабочки и выберите один из режимов симметрии на верхней панели Photoshop (в дальнем правом углу). При этом появится путеводитель. Теперь мы можем начать рисовать или рисовать с симметрией в нашем документе Photoshop.
инструмент симметрии включить (значок в правом углу)Примечание: Инструмент симметрии не поддерживается все кисти в Photoshop
Направляющие контура инструмента симметрии:
Каждый раз, когда мы выбираем режим симметрии, Photoshop автоматически создает контур в палитре контуров которые могут располагаться под окнами — дорожки.
Допустим, мы выбираем режим вертикальной симметрии и рисуем с ним что-то. Затем мы выбираем другой режим симметрии, например, горизонтальный или любой другой режим симметрии, и снова рисуем что-то. Если мы хотим снова рисовать с первым выбранным режимом, который был режимом вертикальной симметрии, мы могли бы повторно использовать первый путь, который Photoshop уже создал для нас в палитре контуров, и не создавать с самого начала другой контур вертикальной симметрии.
Повторное использование пути симметрии:
Способ повторно использовать уже существующий путь режима симметрии — перейти к палитрам путей и выбрать путь, который вы хотите использовать в качестве руководства по симметрии.Щелкните его правой кнопкой мыши и выберите «Сделать путь симметрии». Значок бабочки появляется рядом с выбранным путем, что указывает на активный путь симметрии в вашем конкретном документе.
Примечание. Пути симметрии всегда влияют на весь холст, а не только на область, которую он покрывает в документе Photoshop. Нам не нужно его расширять или сжимать. Кроме того, мы могли скрыть это, не влияя на функцию симметрии. Следовательно, это только для визуальных целей.
Поскольку мы рассмотрели, как использовать инструмент симметрии, теперь мы следуем некоторой теории о каждом режиме.Некоторые из них говорят сами за себя.
Различные режимы симметрии в Photoshop:
Вот краткое описание того, как работает каждый из десяти параметров симметрии краски в Photoshop:
- По вертикали: Делит холст по вертикали и отражает мазки кисти с одной стороны на другую.
- По горизонтали: Делит холст по горизонтали и отражает мазки кисти сверху вниз или снизу вверх.
- Dual Axis: Делит холст по вертикали и по горизонтали на четыре равные части (верхний левый, верхний правый, нижний левый и нижний правый).Рисование в одном разделе отражает мазки кисти в трех других.
- Диагональ: Делит холст по диагонали и отражает мазки кисти с одной стороны на другую.
- Волнистый: Подобен вертикальному, но с изогнутой волнистой линией вместо прямой.
- Круг: Отражает мазки кисти, нарисованные внутри круга за пределами круга, и наоборот.
- Спираль: Отражает мазки кисти, нарисованные по обе стороны спиральной траектории.
- Параллельные линии: Делит холст на три вертикальные части с помощью двух параллельных вертикальных линий. Мазки кисти, нарисованные в средней части, отражаются в левой и правой частях.
- Радиально: Делит холст на диагональные сегменты или «кусочки». Мазки кисти, нарисованные в одном сегменте, отражаются в других.
- Мандала: Подобно Радиальному, но также отражает мазки кисти в пределах каждого сегмента, создавая вдвое больше мазков кисти, чем Радиальный.
Я нашел интересный пост в блоге, который более подробно описывает пошаговый процесс на сайте photoshopessentials.com, если вы хотите его проверить.
Рисование с режимами симметрии в Photoshop в действии:
Когда мы поняли, как можно использовать инструмент симметрии в Photoshop и его различные режимы, пришло время для забавной части. Чтобы на самом деле что-то из этого сделать. Немного поиграв с инструментом симметрии, я создал несколько примеров с некоторыми из режимов симметрии ниже.
Примеры режимов симметрии:
мужской портрет — режим вертикальной симметрии — лабиринт — режим двухосной симметрии — цветной вортекст — режим радиальной симметрии — сложные формы паттерна — режим симметрии мандалыВот и все:
Инструмент симметрии в Photoshop — в конце концов, отличный инструмент.
Помимо очевидного использования каждого из режимов симметрии, вы могли бы использовать свое воображение и свое творчество, чтобы встряхнуть вещи.
Режим радиальной симметрии и симметрии мандалы действительно эффективен, вам обязательно стоит попробовать их.Это простой способ сделать действительно сложный узор очень простым. Конечно, вы можете смешать все вышеперечисленные режимы симметрии, чтобы создать окончательный шедевр, такой как персонаж, окружающая среда, природа — все, что вас вдохновляет.
5.10. Диалог «Рисование симметрии»
5.10. Диалог рисования симметрии5.10. Диалог рисования симметрии
Рисование симметрии — это новая функция рисования в GIMP-2.10 при поддержке инструменты на основе кисти (Карандаш, Кисть, Ластик, Аэрограф, Кисть MyPaint, Clone, Smudge, Dodge), а также инструмент Ink. Есть несколько видов симметрия, все настраивается.
5.10.1. Активация диалога
Вы можете получить доступ к этому диалоговому окну из строки меню изображения через: → →
Диалог «Рисование симметрии» стыкуется.Прочтите Раздел 2.3, «Диалоги и стыковка», чтобы узнать больше. о концепции стыковки.
5.10.2. Использование диалогового окна «Рисование симметрии»
Рисунок 15.85. Диалог рисования симметрии
Этот диалог очень прост. У вас есть только симметрия элемент с раскрывающимся списком, который предлагает четыре варианта.Как только вы проверите тип симметрии, оси симметрии отображаются на изображении как пунктирные зеленые линии окно, и вы можете начать рисовать выбранной кистью.
Опции
- никто
Это вариант по умолчанию; рисование симметрии не активировано.
- Зеркало
Рисунок 15.86. Диалоговое окно «Зеркальное отражение симметрии» .
Это симметрия, как в зеркале. Вы можете выбрать Горизонтальная симметрия, Вертикальная симметрия или центральная симметрия. Ты также можно выбрать несколько симметрий.
Положение оси симметрии по умолчанию — середина изображения. окно. Вы можете разместить ось там, где хотите, используя Положение горизонтальной оси и Положение вертикальной оси.
Отключить преобразование кисти: при преобразовании рисунок, сама кисть тоже преобразится. Для Например, при зеркальном преобразовании не только ваш рисунок на правая часть холста должна быть зеркально отражена слева, но сама кисть очевидно «перевернутый» слева. Если по какой-то причине вы хотите нарисованные линии должны быть отражены (или другое преобразование), но не сам контур кисти, вы можете установить этот флажок.По понятной причине вы не увидите этого с симметричными кистями. хотя. Вот почему вы не видите эффекта, так как многие по умолчанию кисти симметричные.
- Черепица
«Тайлинг» — это трансляционная симметрия, которая может быть конечный (с максимумом штрихов) или бесконечный. В последнем случае, это идеальный инструмент для создания узоров или бесшовных плиток на время покраски.
Рисунок 15.87. Диалог мозаики симметрии
В этом режиме изображение покрывается штрихами.
Здесь нет топоров. Возможные варианты:
Интервал X Интервал Y: это интервалы по осям X и Y в пикселях между инсультные центры.
Shift: это сдвиг между линиями на Ось X в пикселях.
Макс ходов X, Макс. штрихов Y: это максимальное количество кистей штрихи по осям X и Y. По умолчанию 0, что означает отсутствие ограничений, по размеру изображения.
- Мандала
Рисунок 15.88. Диалог симметрии «Мандала»
Штрихи нанесены вокруг центра координат оси.
Возможные варианты:
Центр абсцисс, Центр ордината для позиционирования центра координат.
Количество баллов: количество штрихов.
Отключить преобразование кисти: см. Выше.
Кисточка для перца выбрана. Используется карандаш.
- Пример для зеркала
Рисунок 15.89. Вертикальная симметрия
- Пример плитки
-
- Пример для мандалы
-
Симметрия бабочки — Супер простой
Что такое симметрия?
Симметрия — это когда две части целого абсолютно идентичны.Что-то будет симметричным, если вы проведете по нему линию, и каждая сторона будет выглядеть одинаково. Это называется линией симметрии . Возьмем, к примеру, сердце. У него одна линия симметрии. Если бы вы поместили зеркало на вертикальную линию, показанную ниже, вы бы увидели в зеркале другую сторону сердца. Две одинаковые стороны. Это симметрия. Другие формы, например квадрат, имеют множество линий симметрии, то есть вы можете поставить зеркало на любую из линий, показанных выше, и все они будут симметричными в отражении зеркала.
Природа любит симметрию. Люди даже симметричны. Да, ты и я. У нас есть линия симметрии, которую можно провести прямо посередине нас. По обе стороны от этой линии у нас есть глаз, ухо, ноздря, половина наших губ и рука, рука с пятью пальцами, нога и ступня с пятью пальцами на ногах.
Какие животные в природе симметричны? Давайте подумаем о нескольких. Почему бы не достать несколько книг или не поискать в Интернете, чтобы помочь им найти некоторые.
Используя приложение iNaturalist в Интернете или на телефоне, выполните поиск бабочек и просматривайте картинки вместе со своими детьми.Поговорите с ними о том, что вы узнали, используя глаза, чтобы видеть, и соедините их обучение с визуальным. Что они видят, глядя на бабочек? Каждое из их крыльев такое же, как другое? Есть ли у них линия симметрии? Значит ли это, что они симметричны?
Ученые, астрономы, математики, художники, скульпторы, философы, архитекторы и дизайнеры интерьеров были и продолжают увлекаться симметрией. На самом деле никто не смог объяснить, почему нас так привлекает это или почему симметрия окружает нас повсюду.Фактически, как только вы начнете искать его, вы скоро обнаружите, что не можете остановиться и что он повсюду.
Факты о бабочках
- Это насекомые.
- У них есть четыре стадии в их жизненном цикле. Яйцо, гусеница (личинка), куколка (куколка) и бабочка (взрослая особь).
- У меня четыре крыла.
- Они живут как бабочки, в зависимости от вида от недели до года.
- Узоры на их крыльях сделаны из крошечных чешуек.
- Как пчелы, они едят нектар из цветов.
- Какой-то вкус ногами.
- Изображения бабочек можно увидеть на древнеегипетских фресках в Фивах. Им 3500 лет!
- Бабочки старше этого, они старые динозавры. Самая ранняя найденная окаменелость бабочки датируется 56 миллионами лет назад! Палеонтологи и ученые считают, что они появились вместе с цветами.
Как сделать ваш сад или балкон манящими бабочек
Взрослым бабочкам нужны цветы, чтобы питаться, поэтому посадите несколько цветов нектара.Проведите небольшое исследование, чтобы узнать, какие бабочки живут в вашем районе и какими цветами они любят питаться.
Они любят есть и отдыхать на солнышке (кому не нравится есть на солнышке ?!), поэтому сажайте цветы в местах, где их ударит солнце.
Держите почву влажной, так как они любят пить воду из влажных мест.
Знаете ли вы, что они тоже любят есть цитрусовые, такие как апельсины и ананасы. Если вы выжали из апельсинов сок, а черенки ананаса остались, верните их на природу, чтобы они могли их съесть.Возвращение к природе не должно быть сложным.
Симметричная активность бабочки
Обучить детей симметрии может быть непросто, не показывая им физически и не заставляя их взаимодействовать с заданием о симметрии. Таким образом, они могут претворять в жизнь то, что они изучают, и, скорее всего, они и дальше будут помнить это. В нашей деятельности «Симметрия бабочек» мы используем простую старинную поделку, которую я, помню, делал сам, когда был маленьким. Это простой, но очень эффективный способ научить симметрии.Симметрия прекрасна, и каждая созданная вами бабочка станет уникальным шедевром, иллюстрирующим это. Присоединяйтесь к нам и приступайте к творчеству!
Что понадобится:
- Альбом для рисования или более толстая бумага
- Черная плотная бумага (для тела, по желанию)
- Клей-карандаш (опционально — для кузова)
- Кисти
- Краска
- Палитра
- Ножницы
- Карандаш
Инструкции:
- Вытащите лист бумаги из своего блокнота или используйте любую более толстую бумагу, которая у вас есть в руке.Поместите его горизонтально перед собой, возьмите левую сторону и сложите пополам так, чтобы левая сторона соприкасалась с правой.
- На сложенном листе нарисуйте одну сторону бабочки. Убедитесь, что вы нарисовали туловище бабочки на сгибе бумаги.
- Ножницами вырежьте бабочку, обрезая обе стороны бумаги. Если ваши дети умеют обращаться с ножницами, обязательно позвольте им делать стрижки. В противном случае эту часть должны выполнять родитель или опекун.
- Откройте бумагу, и вы увидите симметрично вырезанную бабочку. Ура! Теперь самое интересное.
- Возьмите одну сторону внутренней части сложенной бабочки, чтобы нанести на нее краску. Наносить краску нужно только с одной стороны. После того, как вы выбрали, дайте ребенку начать рисовать, убедившись, что он нанес достаточно краски.
A ПРИМЕЧАНИЕ : на этом этапе вы можете либо позволить им нарисовать одну сторону кистью, либо позволить им брызнуть краской на сторону прямо из тюбика с краской. На нем должно быть достаточно влажной краски, чтобы она могла перейти на другую сторону при нажатии, поэтому не позволяйте им долго красить, иначе краска высохнет. - Когда вы довольны количеством краски на одной стороне, попросите ребенка осторожно сложить неокрашенную сторону в сторону с краской. Осторожно нажмите вниз, убедившись, что вся бумага разглажена и прижата. Мы советуем убедиться, что у вас есть газета или коврик под ним, так как немного краски будет просачиваться.
- Осторожно откройте обе стороны и посмотрите на красивую симметричную бабочку, которую вы создали!
- Оставьте на безопасной поверхности до полного высыхания.
- После высыхания вы можете вырезать форму туловища бабочки и нанести на нее клей-карандаш.
Не забудьте подписаться на нас в Twitter, Instagram, Pinterest и Facebook!
Автор
Грейс Селус Булл — автор художественного образования и блогер-фрилансер. Ее книга «Горшок о горшках: декоративно-прикладное искусство для дома и школы» предназначена для детей от 5 до 12 лет и знакомит их с путешествием керамики во времени. Ее блог «Радужное дерево» исследует все аспекты декоративно-прикладного искусства и предназначен для детей всех возрастов.Она — мама двух девочек, обе из которых любят заниматься творчеством, и замужем за своим мужем Эндрю, который этого не делает. Следите за ней в твиттере.
Оригинальное содержание © 2018 Super Simple. Запрещается перепечатывать без письменного разрешения. Условия обслуживания.
Как нарисовать симметрию сердца на День святого Валентина
Используйте эту технику рисования симметрии, чтобы создать уникальное сердечное искусство на День святого Валентина. Легкое и увлекательное занятие по искусству!
Обновлено в январе 2021 г.
Здравствуйте, друзья.Наверняка вы пробовали какую-нибудь разновидность симметричной раскраски со своими детьми, верно?
Вы также можете знать это как рисование пятнами, рисование с помощью туши (со шнурком или без него) или рисование с помощью сплющивания. Но как бы вы это ни называли, это очень увлекательное художественное занятие.
Симметричное рисование — это когда вы добавляете несколько капель краски на одну сторону листа бумаги, загибаете вторую сторону поверх краски и прижимаете бутерброд с краской вместе руками. Затем, когда вы открываете сложенную бумагу?
Вуаля! У вас уникальный симметричный дизайн сплющенной краски.
Это большой успех среди малышей и дошкольников, но я должен сказать вам, что старики (и, кстати, так называемые взрослые) тоже любят это.
Существует множество забавных вариаций, в том числе струнные принты с зеркальным отображением, с использованием рисунков симметрии в качестве подсказок для рисования (мы использовали их в прошлом для забавных лиц и животных), с использованием их для бабочек или монстров, но мы недавно сделали Картины симметрии сердца с Дня святого Валентина уже не за горами . Они такие красивые!
Не забудьте посмотреть наше видео на Youtube, посвященное рисованию симметрии!
Сердце Smush Painting
МАТЕРИАЛЫ
- Прочная бумага
- Температурная краска двух или более цветов
- Кисть или ложка для каждого цвета краски
ИНСТРУКЦИИ
- Вырежьте бумажные сердечки
Сначала нарежьте из бумаги сердечки любого размера.Сложите лист бумаги пополам и вырежьте по сгибу половину сердца. Откройте, чтобы раскрыть свою сердечную бумагу.
- Добавьте краску
Используйте кисть или ложку, чтобы нанести капли краски на одну сторону сердечка.
- Сложите и раздавите
Осторожно сложите вторую половину сердечка поверх краски и нажмите. Раздавите бутерброд с краской руками.
- Раскройте свой рисунок симметрии!
Откройте сердце, чтобы раскрыть свое интересное и уникальное симметричное сердечное искусство!
Здесь Майя использовала цвета краски, которые она смешала, чтобы сделать сердце омбре.
- Осушите свои сердца
Повесьте сердца или разложите их, чтобы они полностью высохли. Вот наши сердечные картины на сушильной / выставочной стене в студии. Разве они не прекрасно выглядят ?!
Мы сделали наше большое — от одного до двух сердечек на лист бумаги 12 × 18 дюймов, — но вы можете сделать свое настолько маленьким, насколько захотите. Кучка маленьких подойдет, например, для классных валентинок. И я почти уверен, что ваш ребенок с радостью сделает около 20 таких штук.
Другие мероприятия по рисованию симметрии
Прикрепите его для использования в дальнейшем
Страница 404 не найдена
Страница 404 не найдена Диалог сообщений Показать сообщение об обновленииКанада
Мексика
Общая информация
Наши продукты доступны по всей Южной Америке, см. Адреса ниже или свяжитесь с нами по адресу [email protected].
Аргентина
Наши продукты доступны по всей Южной Америке, см. Адреса ниже или свяжитесь с нами по адресу globalsales @ sherwin.com.
Бразилия
Наши продукты доступны по всей Южной Америке, см. Адреса ниже или свяжитесь с нами по адресу [email protected].
Чили
Наши продукты доступны по всей Южной Америке, см. Адреса ниже или свяжитесь с нами по адресу [email protected].
Колумбия
Наши продукты доступны по всей Южной Америке, см. Адреса ниже или свяжитесь с нами по адресу [email protected].
Эквадор
Наши продукты доступны по всей Южной Америке, см. Адреса ниже или свяжитесь с нами по адресу globalsales @ sherwin.com.
Уругвай
Наши продукты доступны по всей Южной Америке, см. Адреса ниже или свяжитесь с нами по адресу [email protected].
Общая информация
Наши продукты доступны по всей Центральной Америке, см. Адреса ниже или свяжитесь с нами по адресу [email protected].
Коста-Рика
Наши продукты доступны по всей Центральной Америке, см. Адреса ниже или свяжитесь с нами по адресу globalsales @ sherwin.com.
Сальвадор
Наши продукты доступны по всей Центральной Америке, см. Адреса ниже или свяжитесь с нами по адресу [email protected].
Гватемала
Наши продукты доступны по всей Центральной Америке, см. Адреса ниже или свяжитесь с нами по адресу [email protected].
Гондурас
Наши продукты доступны по всей Центральной Америке, см. Адреса ниже или свяжитесь с нами по адресу globalsales @ sherwin.com.
Мексика
Наши продукты доступны по всей Центральной Америке, см. Адреса ниже или свяжитесь с нами по адресу [email protected].
Никарагуа
Наши продукты доступны по всей Центральной Америке, см. Адреса ниже или свяжитесь с нами по адресу [email protected].
Панама
Наши продукты доступны по всей Центральной Америке, см. Адреса ниже или свяжитесь с нами по адресу [email protected].
Общая информация
Наши продукты доступны по всему Карибскому региону, см. Адреса ниже или свяжитесь с нами по адресу globalsales @ sherwin.com.
Багамы
Наши продукты доступны по всему Карибскому региону, см. Адреса ниже или свяжитесь с нами по адресу [email protected].
Bermuda
Наши продукты доступны по всему Карибскому региону, см. Адреса ниже или свяжитесь с нами по адресу [email protected].
Бонайре, Синт-Эстатиус и Саба
Наши продукты доступны по всему Карибскому региону, см. Адреса ниже или свяжитесь с нами по адресу globalsales @ sherwin.com.
Каймановы острова
Наши продукты доступны по всему Карибскому региону, см. Адреса ниже или свяжитесь с нами по адресу [email protected].
Доминиканская Республика
Наши продукты доступны по всему Карибскому региону, см. Адреса ниже или свяжитесь с нами по адресу [email protected].
Гаити
Наши продукты доступны по всему Карибскому региону, см. Адреса ниже или свяжитесь с нами по адресу [email protected].
Ямайка
Наши продукты доступны по всему Карибскому региону, см. Адреса ниже или свяжитесь с нами по адресу globalsales @ sherwin.com.
Пуэрто-Рико
Наши продукты доступны по всему Карибскому региону, см. Адреса ниже или свяжитесь с нами по адресу [email protected].
Сент-Китс и Невис
Наши продукты доступны по всему Карибскому региону, см. Адреса ниже или свяжитесь с нами по адресу [email protected].
Острова Теркс и Кайкос
Наши продукты доступны по всему Карибскому региону, см. Адреса ниже или свяжитесь с нами по адресу globalsales @ sherwin.com.
Виргинские острова (Британские)
Наши продукты доступны по всему Карибскому региону, см. Адреса ниже или свяжитесь с нами по адресу [email protected].
Другие островные страны Карибского бассейна
Наши продукты доступны по всему Карибскому региону, см. Адреса ниже или свяжитесь с нами по адресу [email protected].
Общая информация
Наши продукты доступны во всем Азиатско-Тихоокеанском регионе, см. Адреса ниже или свяжитесь с нами по адресу globalsales @ sherwin.com.
Китай
Наши продукты доступны во всем Азиатско-Тихоокеанском регионе, см. Адреса ниже или свяжитесь с нами по адресу [email protected].
Индонезия
Наши продукты доступны во всем Азиатско-Тихоокеанском регионе, см. Адреса ниже или свяжитесь с нами по адресу [email protected].
Япония
Наши продукты доступны во всем Азиатско-Тихоокеанском регионе, см. Адреса ниже или свяжитесь с нами по адресу [email protected].
Малайзия
Наши продукты доступны во всем Азиатско-Тихоокеанском регионе, см. Адреса ниже или свяжитесь с нами по адресу globalsales @ sherwin.com.
Сингапур
Наши продукты доступны во всем Азиатско-Тихоокеанском регионе, см. Адреса ниже или свяжитесь с нами по адресу [email protected].
Южная Корея
Наши продукты доступны во всем Азиатско-Тихоокеанском регионе, см. Адреса ниже или свяжитесь с нами по адресу [email protected].
Таиланд
Наши продукты доступны во всем Азиатско-Тихоокеанском регионе, см. Адреса ниже или свяжитесь с нами по адресу [email protected].
Вьетнам
Наши продукты доступны во всем Азиатско-Тихоокеанском регионе, см. Адреса ниже или свяжитесь с нами по адресу globalsales @ sherwin.com.
Общая информация
Наши продукты доступны по всей Европе, см. Адреса ниже или свяжитесь с нами по адресу [email protected].
Хорватия
Наши продукты доступны по всей Европе, см. Адреса ниже или свяжитесь с нами по адресу [email protected].
Кипр
Наши продукты доступны по всей Европе, см. Адреса ниже или свяжитесь с нами по адресу [email protected].
Чешская Республика
Наши продукты доступны по всей Европе, см. Адреса ниже или свяжитесь с нами по адресу globalsales @ sherwin.com.
Дания
Наши продукты доступны по всей Европе, см. Адреса ниже или свяжитесь с нами по адресу [email protected].
Общие промышленные покрытия
Danske
Промышленные покрытия для древесины
Danske
Упаковочные покрытия
Английский
Защитные и морские покрытия
Danske
Финляндия
Наши продукты доступны по всей Европе или см. Адреса ниже свяжитесь с нами по адресу globalsales @ sherwin.com.
Общие промышленные покрытия
Suomi
Промышленные покрытия для древесины
Suomi
Упаковочные покрытия
Английский
Защитные и морские покрытия
Suomi
Франция
Наши продукты доступны по всей Европе, см. Адреса ниже или свяжитесь с нами по адресу [email protected].
Германия
Наши продукты доступны по всей Европе, см. Адреса ниже или свяжитесь с нами по адресу globalsales @ sherwin.com.
Венгрия
Наши продукты доступны по всей Европе, см. Адреса ниже или свяжитесь с нами по адресу [email protected].
Италия
Наши продукты доступны по всей Европе, см. Адреса ниже или свяжитесь с нами по адресу [email protected].
Литва
Наши продукты доступны по всей Европе, см. Адреса ниже или свяжитесь с нами по адресу [email protected].
Норвегия
Наши продукты доступны по всей Европе, см. Адреса ниже или свяжитесь с нами по адресу globalsales @ sherwin.com.
Общие промышленные покрытия
Norsk
Промышленные покрытия для древесины
Norsk
Упаковочные покрытия
Английский
Защитные и морские покрытия
Nynorsk
Польша
Наши продукты доступны по всей Европе, см. свяжитесь с нами по адресу [email protected].
Общепромышленные покрытия
Polski
Промышленные покрытия для древесины
Polski
Упаковочные покрытия
Английский
Защитные и морские покрытия
Polski
Португалия
Наши продукты доступны по всей Европе, см. Адреса ниже свяжитесь с нами по адресу globalsales @ sherwin.com.
Румыния
Наши продукты доступны по всей Европе, см. Адреса ниже или свяжитесь с нами по адресу [email protected].
Россия
Наши продукты доступны по всей Европе, см. Адреса ниже или свяжитесь с нами по адресу [email protected].
Сербия
Наши продукты доступны по всей Европе, см. Адреса ниже или свяжитесь с нами по адресу [email protected].
Словакия
Наши продукты доступны по всей Европе, см. Адреса ниже или свяжитесь с нами по адресу globalsales @ sherwin.com.
Словения
Наши продукты доступны по всей Европе, см. Адреса ниже или свяжитесь с нами по адресу [email protected].
Испания
Наши продукты доступны по всей Европе, см. Адреса ниже или свяжитесь с нами по адресу [email protected].
Швеция
Наши продукты доступны по всей Европе, см. Адреса ниже или свяжитесь с нами по адресу [email protected].
Украина
Наши продукты доступны по всей Европе, см. Адреса ниже или свяжитесь с нами по адресу globalsales @ sherwin.com.
Великобритания
Наши продукты доступны по всей Европе, см. Адреса ниже или свяжитесь с нами по адресу [email protected].
Ближний Восток
Наши продукты доступны по всему Ближнему Востоку, см. Адреса ниже или свяжитесь с нами по адресу [email protected].
Австралия
Наши продукты доступны по всей Австралии, см. Адреса ниже или свяжитесь с нами по адресу [email protected].
сгенерировано: Вт, 19 октября, 02:56:03 UTC 2021
Хост: tsapp-556449d66-xdw8b
Порт сервера: 443
Локальный порт: 5443
Экземпляр: server1
Создание этой страницы заняло 1 миллисекунду.
.

 е. под углом в 90 0)
е. под углом в 90 0) При осевой симметрии образом прямой является прямая, образом параллельных прямых являются параллельные прямые
При осевой симметрии образом прямой является прямая, образом параллельных прямых являются параллельные прямые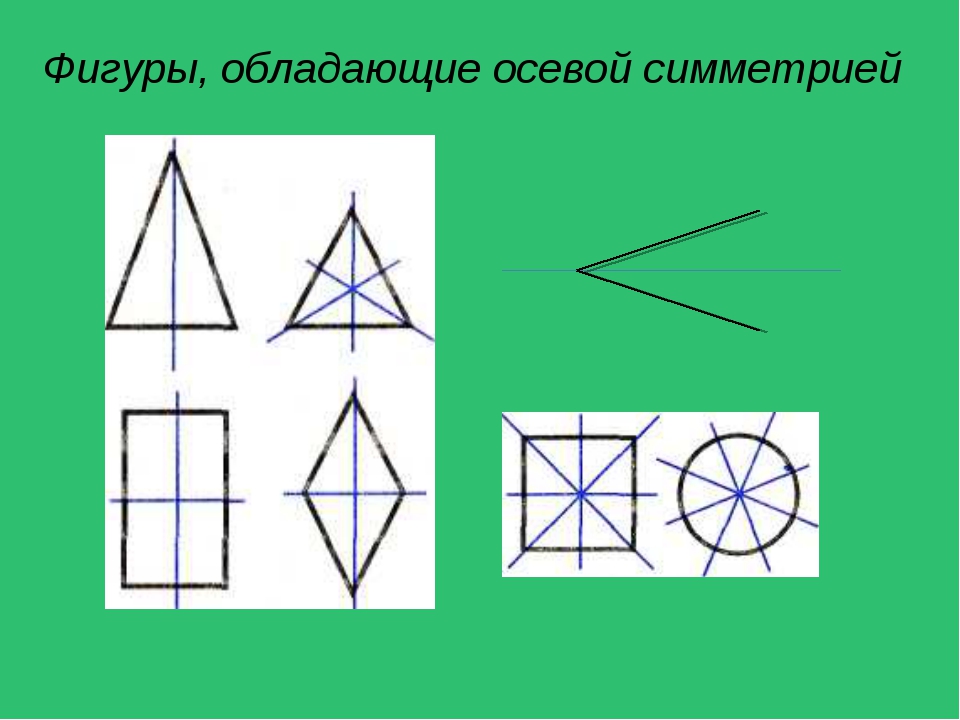 д.
д.