Как нарисовать правильный треугольник вписанный в окружность
Popular
Основы черчения
Строительное
Машиностроительное
Построение вписанного в окружность правильного шестиугольника. Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой (фиг. 60, а).
Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг. 60, б), строим стороны 1 —6, 4—3, 4—5 и 7—2, после чего проводим стороны 5—6 и 3—2.
Построение вписанного в окружность равностороннего треугольника. Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля.
Рассмотрим два способа построения вписанного в окружность равностороннего треугольника.
Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, проведённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0—1—2 равен 30°, то для нахождения стороны
1—2 достаточно построить по точке 1 и стороне 0—1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1—2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2—3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника.
Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вершины через одну, то получится равносторонний треугольник.
Для построения треугольника (фиг. 61, б) намечаем на диаметре вершину—точку 1 и проводим диаметральную линию 1—4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника.
Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника.
Построение квадрата, вписанного в окружность
Первый способ основан на том, что диагонали квадрата пересекаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные стороны квадрата 4—1 и 3—2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1—2 и 4—3.
Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра (фиг. 62, б). Намечаем на концах двух взаимно перпендикулярных диаметров точки А, В и С и из них радиусом у описываем дуги до взаимного их пересечения.
Далее через точки пересечения дуг проводим вспомогательные прямые, отмеченные на фигуре сплошными линиями. Точки их пересечения с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.
Построение вписанного в окружность правильного пятиугольника.
Чтобы вписать в окружность правильный пятиугольник (фиг. 63), производим следующие построения.
Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой.
Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой.
Построение правильного пятиугольника по данной его стороне.
Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую.
Далее от точки К на этой прямой откладываем отрезок, равный 4/6 AB.
Получим точку 1—вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведёнными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.
Построение вписанного в окружность правильного семиугольника.
Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проводим из полюса F через чётные деления вертикального диаметра лучи, пересечение которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проводим из полюса F через чётные деления вертикального диаметра лучи, пересечение которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
Приведённый способ годен для построения правильных многоугольников с любым числом сторон.
Деление окружности на любое число равных частей можно производить также, пользуясь данными табл. 2, в которой приведены коэффициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.
В первой колонке этой таблицы указаны числа сторон правильного вписанного многоугольника, а во второй—коэффициенты.
Длина стороны заданного многоугольника получится от умножения радиуса данной окружности на коэффициент, соответствующий числу сторон этого многоугольника.
Деление окружности на равные части и построение правильных вписанных многоугольников можно выполнить как циркулем, так и с помощью угольников и рейсшины.
Деление окружности на четыре равные части и построение правильного вписанного четырехугольника. Две взаимно перпендикулярные центровые линии делят окружность на четыре равные части (рис. 115, а). Соединив точки пересечения этих линий с окружностью прямыми, получают правильный вписанный четырехугольник.
Деление окружности на восемь равных частей и построение правильного вписанного восьмиугольника. Две взаимно перпендикулярные линии, проведенные под углом 45° к центровым линиям с помощью угольника с углами 45, 45 и 90° и рейсшины (рис.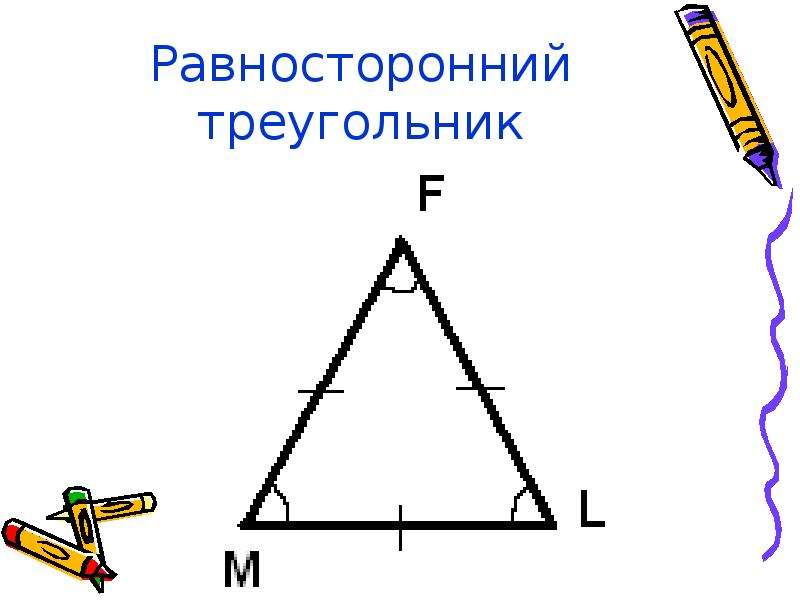 115, б), вместе с центровыми линиями разделят окружность на восемь равных частей.
115, б), вместе с центровыми линиями разделят окружность на восемь равных частей.
Деление окружности на восемь равных частей можно выполнить циркулем. Для этого из точек 1 и 3 (точки пересечения центровых линий с окружностью) произвольным радиусом делаются засечки до взаимного пересечения, тем же радиусом делают две засечки из точек 3 и 5 (рис. 115, в). Через точки пересечения засечек и центр окружности проводят прямые линии до пересечения с окружностью в точках 2, 4, 6, 8.
Если полученные восемь точек соединить последовательно прямыми линиями, то получится правильный вписанный восьмиугольник (рис. 115, в).
Деление окружности на три равные части и построение правильного вписанного треугольника выполняют с помощью циркуля или угольника с углами 30, 60 и 90° и рейсшины.
При делении окружности циркулем на три равные части из любой точки окружности, например из точки Л пересечения центровых линий с окружностью (рис. 116, а и б), проводят дугу радиусом R, равным радиусу данной окружности, получают точки 1 и 2.
При делении окружности на три равные части с помощью угольника и рейсшины через точку 1 под углом 60° проводят две прямые линии до пересечения с окружностью в точках 2 и 3 (рис. 117, а, б), точки 2 и 3 соединяют и получают правильный вписанный треугольник (рис. 117, в).
Деление окружности на шесть равных частей и построение правильного вписанного шестиугольника выполняют с помощью угольника с углами 30, 60 и 90° и рейсшины или циркуля. При делении окружности на шесть равных частей циркулем из двух концов одного диаметра радиусом, равным радиусу данной окружности, проводят дуги до пересечения с окружностью в точках 2, 6 и 3, 5 (рис.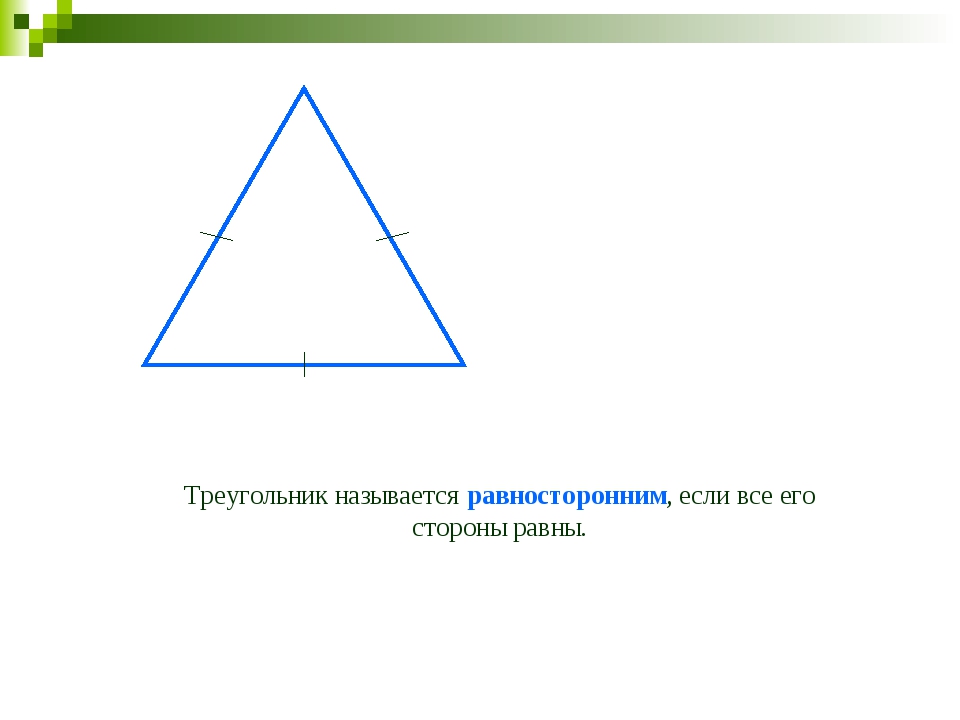 118). Последовательно соединив полученные точки, получают правильный вписанный шестиугольник. Деление окружности на шесть равных час-1ен и построение правильного вписанного шестиугольника с помощью угольника и рейсшины показано на рис. 119 и 120. Деление окружности на двенадцать равных частей и построение правильного вписанного двенадцатиугольника выполняют с помощью угольника с углами 30, 60 и 90° и рейсшины или циркуля.
118). Последовательно соединив полученные точки, получают правильный вписанный шестиугольник. Деление окружности на шесть равных час-1ен и построение правильного вписанного шестиугольника с помощью угольника и рейсшины показано на рис. 119 и 120. Деление окружности на двенадцать равных частей и построение правильного вписанного двенадцатиугольника выполняют с помощью угольника с углами 30, 60 и 90° и рейсшины или циркуля.
При делении окружности циркулем из четырех концов двух взаимно перпендикулярных диаметров окружности проводят радиусом, равным радиусу данной окружности, дуги до пересечения с окружностью (рис. 121). Соединив полученные точки, получают двенадцатиугольник.
При построении двенадцатиугольника с помощью угольника и рейсшины точки деления строят, как показано на рис.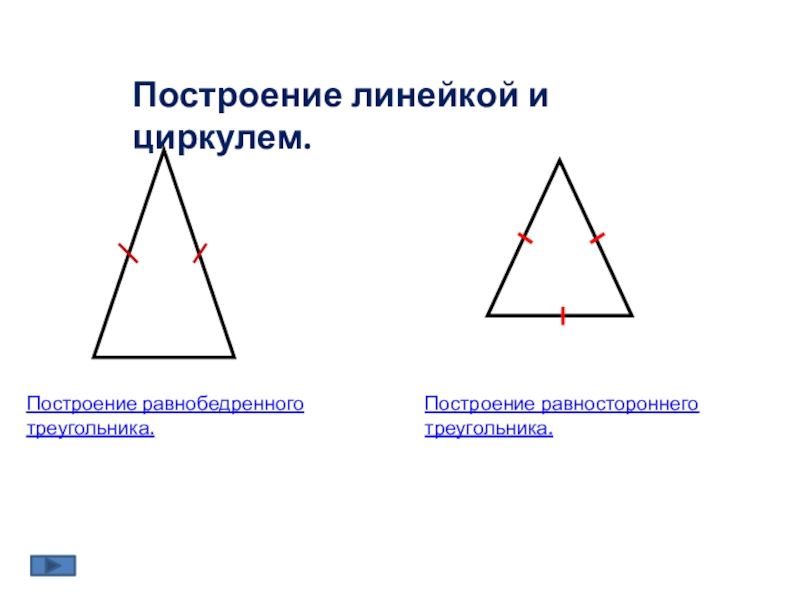 119 и 120.
119 и 120.
Деление окружности на пять и десять равных частей и построение правильного вписанного пятиугольника и десятиугольника показано на рис. 122.
Половину любого диаметра (радиус) делят пополам (рис. 122, а), получают точку А. Из точки А, как из центра, проводят дугу радиусом, равным расстоянию от точки А до точки 1, до пересечения со второй половиной этого диаметра, в точке В (рис. 122, б). Отрезок 1В равен хорде, стягивающей дугу, длина которой равна 1 /5 длины окружности. Делая засечки на окружности (рис. 122, в) радиусом R, равным отрезку 1В, делят окружность на пять равных частей. Начальную точку 1 выбирают в зависимости от расположения пятиугольника. Из точки / строят точки 2 и 5 (рис. 122, в), затем из точки 2 строят точку 3, а из точки 5 строят точку 4. Расстояние от точки 3 до точки 4 проверяют циркулем; если расстояние между точками 3 и 4 равно отрезку 1В, то построения были выполнены точно. Нельзя выполнять засечки последовательно, в одну сторону, так как происходит набегание ошибок и последняя сторона пятиугольника получается перекошенной. Последовательно соединив найденные точки, получают пятиугольник (рис. 122, г).
Последовательно соединив найденные точки, получают пятиугольник (рис. 122, г).
Деление окружности на десять равных частей выполняют аналогично делению окружности на пять равных частей (рис. 122), но сначала делят окружность на пять частей, начиная построение из точки /, а затем из точки 6, находящейся на противоположном конце диаметра (рис. 123, а). Соединив последовательно все точки, получают правильный вписанный десятиугольник (рис. 123, б).
Деление окружности на семь и четырнадцать равных частей и построение правильного вписанного семиугольника и четырнадцатиугольника показано на рис. 124 и 125.
Из любой точки окружности, например точки Л, радиусом заданной окружности проводят дугу (рис. 124, а) до пересечения с окружностью в точках В и D. Соединим точки В и D прямой. Половина полученного отрезка (в данном случае отрезок ВС) будет равна хорде, которая стягивает дугу, составляющую 1 /7 длины окружности. Радиусом, равным отрезку ВС, делают засечки на окружности в последовательности, показанной на рис. 124, б. Соединив последовательно все точки, получают правильный вписанный семиугольник (рис. 124, в).
Радиусом, равным отрезку ВС, делают засечки на окружности в последовательности, показанной на рис. 124, б. Соединив последовательно все точки, получают правильный вписанный семиугольник (рис. 124, в).
Деление окружности на четырнадцать равных частей выполняется делением окружности на семь равных частей два раза от двух точек (рис. 125, а).
Сначала окружность делится на семь равных частей от точки /, затем то же построение выполняется от точки 8. Построенные точки соединяют последовательно прямыми линиями и получают правильный вписанный четырна-дцатиугольник (рис. 125, б).
СОПРЯЖЕНИЯ
Рассматривая детали, видим, что в их конструкции часто одна поверхность переходит в другую. Обычно эти переходы делают плавными, что повышает прочность деталей и делает их более удобными в работе. На чертеже поверхности изображаются линиями, которые также плавно переходят одна в другую.
На рис. 126, а изображена деталь, в которой плавные переходы одних плоскостей в другие представляют собой цилиндрические поверхности.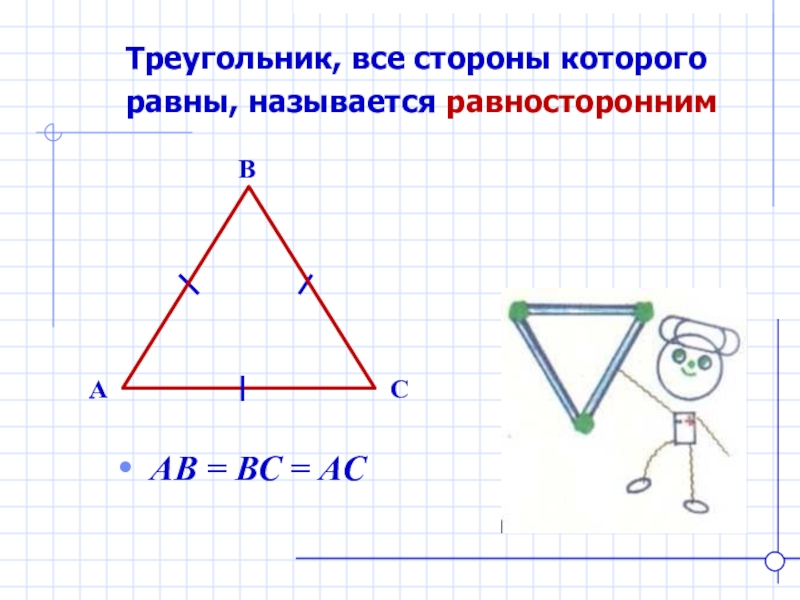 На чертеже (рис. 126, б) эти плоскости изображены прямыми линиями, а цилиндрические поверхности — дугами окружностей. Плавные переходы от одной прямой к другой в этих случаях выполняются дугой заданного радиуса.
На чертеже (рис. 126, б) эти плоскости изображены прямыми линиями, а цилиндрические поверхности — дугами окружностей. Плавные переходы от одной прямой к другой в этих случаях выполняются дугой заданного радиуса.
Плавный переход одной цилиндрической поверхности в другую может являться цилиндрической поверхностью (рис. 127, а). На чертеже эти цилиндрические поверхности изображены дугами окружностей, (рис. 127, б). В этом случае плавный переход одной дуги окружности в другую осуществляется дугой окружности заданного радиуса.
На рис. 126, а и 127, а рассмотрены простейшие примеры плавных переходов поверхностей. В чертежах более сложных деталей плавные переходы между поверхностями изображаются различными сочетаниями прямых, окружностей и их дуг. Вариантов таких сочетаний может быть много, но их объединяет одно — плавность перехода. Такой плавный переход одной линии (поверхности) в другую линию (поверхность) называют сопряжением. При построении сопряжения необходимо определить границу, где кончается одна линия и начинается другая, т. е. найти на чертеже точку перехода, которая называется точкой сопряжения или точкой касания.
е. найти на чертеже точку перехода, которая называется точкой сопряжения или точкой касания.
Задачи на сопряжения условно можно разделить на три группы.
Первая группа задачвключает в себя задачи на построение сопряжений, где участвуют прямые линии. Это может быть непосредственное касание прямой и окружности, сопряжение двух прямых дугой заданного радиуса, а также проведение касательной прямой к двум окружностям.
Построение окружности, касательной к прямой, связано с нахождением точки касания и центра окружности.
Задана горизонтальная прямая АВ, требуется построить окружность радиусом R, касательную к данной прямой (рис. 128). Точка касания выбирается произвольно. Так как точка касания не задана, то окружность радиуса R может коснуться данной прямой в любой точке. Таких окружностей можно провести множество. Центры этих окружностей (O1, О2и т. д.) будут находиться на одинаковом расстоянии от заданной прямой, т. е. на линии, расположенной параллельно заданной прямой АВ на расстоянии, равном радиусу заданной окружности (рис. 128). Назовем эту линию линией центров. Проведем линию центров параллельно прямой АВ на расстоянии R. Так как центр касательной окружности не задан, возьмем любую точку на линии центров, например точку О. Прежде чем проводить касательную окружность, следует определить точку касания. Точка касания будет лежать на перпендикуляре, опущенном из точки О на прямую АВ. В пересечении перпендикуляра с прямой АВ получим точку К, которая будет точкой касания. Из центра О радиусом R от точки К проведем окружность. Задача решена.
е. на линии, расположенной параллельно заданной прямой АВ на расстоянии, равном радиусу заданной окружности (рис. 128). Назовем эту линию линией центров. Проведем линию центров параллельно прямой АВ на расстоянии R. Так как центр касательной окружности не задан, возьмем любую точку на линии центров, например точку О. Прежде чем проводить касательную окружность, следует определить точку касания. Точка касания будет лежать на перпендикуляре, опущенном из точки О на прямую АВ. В пересечении перпендикуляра с прямой АВ получим точку К, которая будет точкой касания. Из центра О радиусом R от точки К проведем окружность. Задача решена.
В детали, которая изображена на рис. 129, а, пластина плавно переходит в цилиндр. При выполнении чертежа этой детали необходимо построить плавный переход прямой в окружность.
Задача аналогична предыдущей, но дополнена условием, что точка касания задана, так как задан размер А (рис. 129, б), который определяет величину прямолинейного участка.
129, б), который определяет величину прямолинейного участка.
Отложив размер Л, находят точку касания (точку /С), затем из точки К восставляют перпендикуляр, на котором откладывают радиус R заданной окружности, и находят центр окружности (точку О). При обводке сначала от точки касания проводится дуга заданного радиуса, а потом — прямая.
Из сказанного следует:
1) центр окружности, касательной к прямой, лежит на прямой (линия центров), проведенной параллельно заданной прямой, на расстоянии, равном радиусу данной окружности;
Не нашли то, что искали? Воспользуйтесь поиском:
Как нарисовать треугольник? Этому учат в процессе изучения геометрии в школе. Чтобы задание было выполнено правильно, важно точно знать, какой треугольник необходимо изобразить: равносторонний, равнобедренный или же вписанный. Правилам начертания этих фигур будет посвящена данная статья.
Правилам начертания этих фигур будет посвящена данная статья.
Как рисовать треугольник с равными сторонами?
Как нарисовать треугольник, стороны у которого равны? Для этого можно воспользоваться одним из трех методов.
Такая фигура имеет три одинаковые по длине стороны, связанные тремя углами равной ширины. Это может быть сложным для рисования треугольника вручную. Поэтому можно использовать круглый объект для выделения углов.
Варианты создания фигуры
Обязательно используйте линейку и один из представленных ниже способов:
- Применение циркуля: надо начертить ровную линию. Проведите карандаш вдоль прямого края бумаги. Этот сегмент линии образует одну из сторон. А это означает, что нужно будет чертить вторую и третью линии одинаковой длины, каждая из которых достигает точки под углом 60° от первой линии. Удостоверьтесь, что достаточно места для рисования всех трех сторон!
- Разделите сегмент циркулем. Вставьте карандаш и убедитесь, что он острый! Поместите точку циркуля на один конец сегмента и установите карандаш на другую.
 Опишите дугу. Не изменяйте установленную «ширину» инструмента от точки циркуля до точки карандаша. Нарисуйте вторую дугу, чтобы она пересекала первую дугу, которую уже нарисовали. Отметьте точку, в которой пересекаются две дуги. Это вершина (верхняя точка) треугольника. Он должен лежать в точном центре сегмента линии, который нарисовали. Теперь можете сделать две прямые линии, ведущие к этой точке: по одному от каждого конца «нижнего» сегмента линии. Закончите треугольник. Далее с помощью линейки надо нарисовать еще два сегмента прямой линии – это стороны в треугольнике. Подключите каждый конец исходного сегмента линии к точке, в которой пересекаются дуги. Чтобы закончить работу, сотрите дуги, которые нарисовали, так, чтобы остался только треугольник.
Опишите дугу. Не изменяйте установленную «ширину» инструмента от точки циркуля до точки карандаша. Нарисуйте вторую дугу, чтобы она пересекала первую дугу, которую уже нарисовали. Отметьте точку, в которой пересекаются две дуги. Это вершина (верхняя точка) треугольника. Он должен лежать в точном центре сегмента линии, который нарисовали. Теперь можете сделать две прямые линии, ведущие к этой точке: по одному от каждого конца «нижнего» сегмента линии. Закончите треугольник. Далее с помощью линейки надо нарисовать еще два сегмента прямой линии – это стороны в треугольнике. Подключите каждый конец исходного сегмента линии к точке, в которой пересекаются дуги. Чтобы закончить работу, сотрите дуги, которые нарисовали, так, чтобы остался только треугольник. - Использование объекта с круглой базой: этот совет подойдет для построения дуги. Предложенный метод по сути такой же, как с использованием циркуля.
Указанные советы помогут выяснить, как нарисовать равносторонний треугольник.
Рекомендации по построению равнобедренного треугольника
Равнобедренный треугольник представляет собой фигуру с двумя равными сторонами и двумя равными углами. Если знаете длину, основание и высоту стороны, это можно сделать только с линейкой и циркулем (или просто циркулем, если заданы размеры).
Как нарисовать равнобедренный треугольник:
- Учитывая все боковые длины. Чтобы использовать этот метод, важно знать длину основания треугольника и длину двух равных сторон.
- Учитывая две равные стороны и угол между ними. Чтобы использовать этот метод, нужно знать длину двух равных сторон и измерение угла между этими двумя сторонами.
- Учитывая базовые и смежные углы – необходимо знать длину базы, градусы двух углов, смежных с основанием. Помните, что два угла, смежные с основанием равнобедренного треугольника, будут равны.
- Основа и высота. Нужно знать длину основания треугольника, а также высоту этой геометрической фигуры.
Вписанный треугольник
Как нарисовать вписанный треугольник? Выберите круглый объект. Используйте предмет с круглым основанием. Выбор компакт-диска станет хорошим вариантом. Но можно взять и другой объект нужного размера. Для этого метода свойственно, что длина каждой стороны равносторонней геометрической фигуры с тремя углами будет равна размерам радиуса (половине диаметра) круга.
Используйте предмет с круглым основанием. Выбор компакт-диска станет хорошим вариантом. Но можно взять и другой объект нужного размера. Для этого метода свойственно, что длина каждой стороны равносторонней геометрической фигуры с тремя углами будет равна размерам радиуса (половине диаметра) круга.
Как нарисовать треугольник, если используете компакт-диск? Представьте себе равносторонний треугольник, который вписывается в верхнюю правую часть компакт-диска. Надо начертить первую из сторон. Радиус круглого объекта – расстояние на полпути до получения желаемого результата. Удостоверьтесь, что линии нарисованы ровно.
С помощью линейки просто выполните измерения диаметра объекта и нарисуйте линию на половину длины. Если ее нет, поместите круглый объект на бумагу, затем тщательно проведите по окружности карандашом. Удалите объект – должен быть идеальный круг. Используйте прямой край, чтобы нарисовать линию через точный центр круга: точку, которая полностью равноудалена от любой точки по окружности круга.
Используйте круглый объект для создания дуги. Поместите объект по отрезку линии, с краем круга, расположенным на одном конце линии. Для обеспечения точности убедитесь, что линия проходит четко через центр круга. Используйте карандаш, чтобы начертить дугу – это четверть пути по окружности.
Начертите еще одну дугу. Теперь сдвиньте круглый объект так, чтобы край касался другого конца сегмента линии.
Подведем итоги
В статье были предоставлены рекомендации, как нарисовать треугольник равносторонний, равнобедренный и вписанный в окружность.
3 СПОСОБА НАРИСОВАТЬ РАВНОСТОРОННИЙ ТРЕУГОЛЬНИК — ЧАЕВЫЕ
Равносторонний треугольник состоит из трех сторон равного размера, соединенных между собой тремя одинаковыми углами. Нарисовать от руки идеально равносторонний треугольник может быть непросто. Однако
Равносторонний треугольник состоит из трех сторон равного размера, соединенных между собой тремя одинаковыми углами. Нарисовать от руки идеально равносторонний треугольник может быть непросто. Однако вы можете использовать круглый объект, чтобы отметить углы формы. Не забудьте использовать линейку, чтобы линии оставались прямыми! Продолжайте читать, чтобы узнать, как нарисовать равносторонний треугольник.
Однако вы можете использовать круглый объект, чтобы отметить углы формы. Не забудьте использовать линейку, чтобы линии оставались прямыми! Продолжайте читать, чтобы узнать, как нарисовать равносторонний треугольник.
меры
Метод 1 из 3: Использование компаса
- Проведите прямую линию. Положите линейку на бумагу и проведите карандашом по прямому краю. Этот отрезок линии будет составлять одну сторону вашего равностороннего треугольника, а это означает, что вы должны нарисовать еще две линии одинакового размера, каждая из которых соединена с другой под углом 60 °. Важно, чтобы было достаточно места для рисования трех сторон.
- Измерьте отрезок линии с помощью компаса. Вставьте карандаш в циркуль и убедитесь, что он острый. Поместите конец циркуля на один конец отрезка линии, а кончик карандаша — на другой.
- Нарисуйте дугу, соответствующую окружности. Не изменяйте положение циркуля и не меняйте «ширину» между ним и кончиком карандаша.
 Проденьте кончик карандаша в сторону от отрезка линии в форме полукруга.
Проденьте кончик карандаша в сторону от отрезка линии в форме полукруга. - Поменять компас в сторону. Не меняя ширины циркуля, переместите точку в другую сторону.
- Нарисуйте вторую дугу. Осторожно проведите кончиком циркуля, чтобы новая дуга пересеклась с нарисованной ранее.
- Отметьте точку пересечения обеих арок. Это будет вершина (верхний край) треугольника, который должен располагаться точно в центре нарисованного отрезка линии. Теперь вы можете нарисовать две прямые линии, которые приходят к этой точке: по одной с каждой стороны нижнего сегмента линии.
- Закончите треугольник. С помощью линейки нарисуйте еще два прямых отрезка: оставшиеся стороны треугольника. Соедините каждый конец исходного сегмента линии с точкой, в которой обе дуги пересекаются, не забывая рисовать прямые линии. Наконец, сотрите нарисованные дуги, чтобы остался только треугольник.

- Рассмотрите возможность рисования этого треугольника на другой странице. Итак, вы можете начать заново, по-новому.
- Если вам нужен треугольник большего или меньшего размера, повторите процесс, отрегулировав длину начального отрезка линии. Чем больше стороны, тем больше треугольник.
Метод 2 из 3: использование объекта с круговой основой
Если у вас нет доступа к компасу или транспортиру, вы можете использовать объект с круглым основанием, чтобы нарисовать лук. По сути, этот метод идентичен использованию компаса, но вы должны использовать его с умом.
- Выберите свой круглый объект. Вы можете использовать практически любой цилиндрический предмет с круглым основанием, например бутылку с жидким мылом. Попробуйте использовать рулон ленты или компакт-диск. Если вы хотите заменить дугу этого объекта на дугу циркуля, вам нужно будет выбрать что-то подходящего размера. В этом методе каждая сторона равностороннего треугольника будет равна радиусу (половине диаметра) рассматриваемого круглого объекта.

- Если вы хотите использовать компакт-диск в качестве объекта, представьте себе равносторонний треугольник, который умещается в верхнем правом квадранте его поверхности.
- Нарисуйте первую сторону. Он должен быть идентичен по размеру радиусу круглого объекта — на полпути вниз. Важно, чтобы она была идеально ровной.
- Если у вас есть линейка, просто измерьте диаметр объекта и проведите линию вдвое меньшего размера.
- Если у вас нет линейки, поместите круглый предмет на лист бумаги, а затем аккуратно нарисуйте его окружность карандашом. Удалите объект, и, наконец, у вас должен получиться идеальный круг. С помощью линейки проведите линию через точный центр круга: точку, которая полностью равноудалена от любой другой точки по его окружности.
- Используйте круглый объект, чтобы нарисовать дугу. Поместите объект на отрезок линии так, чтобы край круга находился на одном конце линии. Для большей точности важно, чтобы линия проходила прямо через центр круга.
 Карандашом нарисуйте дугу, примерно равную ¼ периметра круга.
Карандашом нарисуйте дугу, примерно равную ¼ периметра круга. - Сделайте еще один поклон. Теперь переместите круглый объект так, чтобы его край касался другого конца отрезка линии. Такой отрезок должен проходить точно через центр круга. Нарисуйте еще одну дугу, которая пересекает первую в точке прямо над отрезком линии. Эта точка представляет собой вершину треугольника.
- Завершите треугольник. Нарисуйте оставшиеся стороны треугольника: две прямые линии, которые соединят вершину с двумя открытыми концами отрезка. Теперь у вас будет идеально равносторонний треугольник.
Метод 3 из 3: Использование транспортира
- Нарисуйте первую сторону. С помощью линейки или прямой стороны транспортира нарисуйте отрезок нужного размера. Это будет представлять первую сторону вашего треугольника, и каждая из других сторон будет иметь такую же меру — не забывайте всегда рисовать их правильного размера.

- Используйте транспортир для определения угла 60 ° по отношению к одному концу.
- Сделайте вторую сторону. Нарисуйте еще один отрезок линии того же размера, что и первый. Начните с одного конца исходного семени, от которого вы определите угол 60 °. От вершины (точки) угла проводите прямой стороной транспортира, пока не дойдете до следующей «точки».
- Закончите треугольник. Используйте прямую сторону транспортира, чтобы нарисовать последнюю сторону треугольника. Присоедините точку на конце второго отрезка к свободному концу первого. Теперь у вас будет равносторонний треугольник.
подсказки
- Метод компаса обычно является наиболее точным, поскольку он не зависит от точного измерения каждого угла.
- Не делайте линии компаса сильными; вы должны сделать их тонкими и легкими, чтобы потом их можно было легко стереть.
- Используйте фиксирующий компас, чтобы предотвратить нежелательные изменения его ширины.

Предупреждения
- Не помечайте поверхность под бумагой.
Необходимые материалы
- Компас
- Поверхность, которую следует разместить под компасом, чтобы предотвратить его скольжение
- Линейка
- Карандаш (избегайте использования механических карандашей, которые могут не поместиться на подставке в компасе) — важно, чтобы он был очень острым!
длина сторон, сумма углов. Описанный тупоугольный треугольник Как рисуется остроугольный треугольник
Как начертить треугольник?
Построение различных треугольников — обязательный элемент школьного курса геометрии. У многих это задание вызывает страх. Но на самом деле, все довольно просто. Далее в статье описано, как начертить треугольник любого типа с помощью циркуля и линейки.
Треугольники бывают
- разносторонние;
- равнобедренные;
- равносторонние;
- прямоугольные;
- тупоугольные;
- остроугольные;
- вписанные в окружность;
- описанные вокруг окружности.

Построение равностороннего треугольника
Равносторонним называется треугольник, у которого все стороны равны. Из всех видов треугольников, начертить равносторонний проще всего.
- С помощью линейки начертите одну из сторон, заданной длины.
- Измерьте ее длину с помощью циркуля.
- Поместите острие циркуля в один из концов отрезка и проведите окружность.
- Переставьте острие в другой конец отрезка и проведите окружность.
- У нас получилось 2 точки пересечения окружностей. Соединяя любую из них с краями отрезка, мы получаем равносторонний треугольник.
Построение равнобедренного треугольника
Данный тип треугольников можно построить по основанию и боковым сторонам.
Равнобедренным называется треугольник, у которого две стороны равны. Для того чтобы начертить равнобедренный треугольник по данным параметрам, необходимо выполнить следующие действия:
- С помощью линейки откладываем отрезок, равный по длине основанию.
 Обозначаем его буквами АС.
Обозначаем его буквами АС. - Циркулем измеряем необходимую длину боковой стороны.
- Рисуем из точки А, а затем из точки С, окружности, радиус которых равен длине боковой стороны.
- Получаем две точки пересечения. Соединив одну из них с точками А и С, получаем необходимый треугольник.
Построение прямоугольного треугольника
Треугольник, у которого один угол прямой, называют прямоугольным. Если нам даны катет и гипотенуза, начертить прямоугольный треугольник не составит труда. Его можно построить по катету и гипотенузе.
Построение тупоугольного треугольника по углу и двум прилегающим сторонам
Если один из углов треугольника тупой (больше 90 градусов), его называют тупоугольным. Чтобы начертить по указанным параметрам тупоугольный треугольник необходимо сделать следующее:
- С помощью линейки откладываем отрезок, равный по длине одной из сторон треугольника. Обозначим его буквами А и D.
- Если в задании уже нарисован угол, и вам необходимо начертить такой же, то на его изображении отложить два отрезка, оба конца которых лежат в вершине угла, а длина равняется указанным сторонам.
 Соедините полученные точки. У нас получился искомый треугольник.
Соедините полученные точки. У нас получился искомый треугольник. - Чтобы его перенести на свой чертеж, вам необходимо измерить длину третьей стороны.
Построение остроугольного треугольника
Остроугольный треугольник (все углы меньше 90 градусов) строится по тому же принципу.
- Нарисуйте две окружности. Центр одной из них лежит в точке D, а радиус равен длине третьей стороны, а у второй центр находится в точке А, а радиус равен длине указанной в задании стороны.
- Соедините одну из точек пересечения окружности с точками А и D. Искомый треугольник построен.
Вписанный треугольник
Для того чтобы начертить треугольник в окружности, нужно помнить теорему, в которой говорится, что центр описанной окружности лежит на пересечении серединных перпендикуляров:
У тупоугольного треугольника центр описанной окружности лежит за пределами треугольника, а у прямоугольного — на середине гипотенузы.
Чертим описанный треугольник
Описанный треугольник — это треугольник, в центре которого нарисована окружность, касающаяся всех его сторон.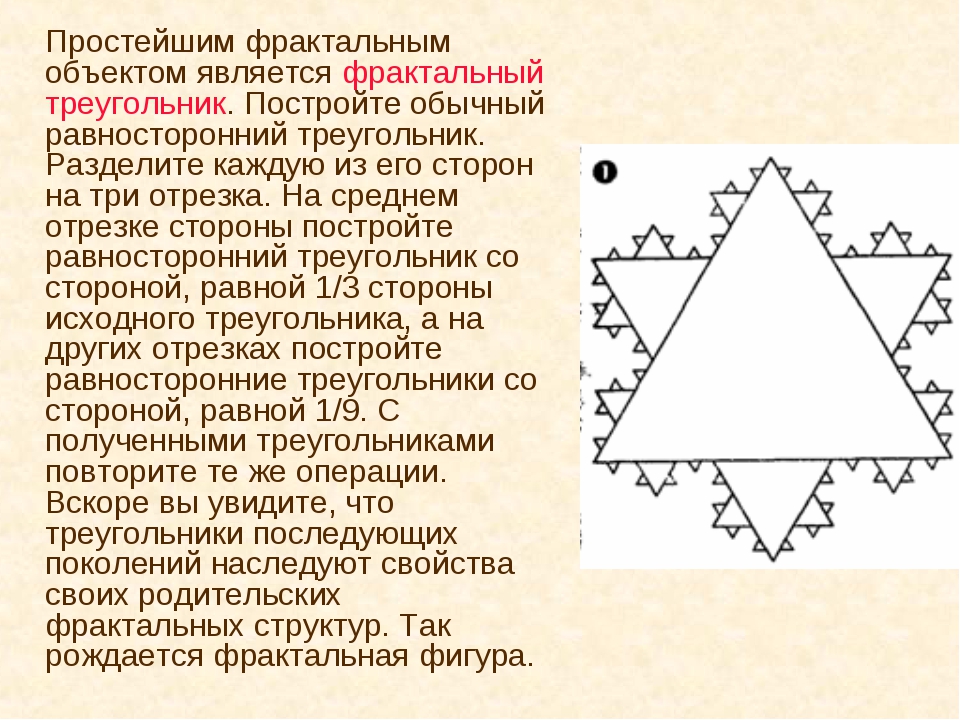 Центр вписанной окружности лежит на пересечении биссектрис. Для их построения необходимо:
Центр вписанной окружности лежит на пересечении биссектрис. Для их построения необходимо:
Еще дети дошкольного возраста знают, как выглядит треугольник. А вот с тем, какие они бывают, ребята уже начинают разбираться в школе. Одним из видов является тупоугольный треугольник. Понять, что это такое, проще всего, если увидеть картинку с его изображением. А в теории это так называют «простейший многоугольник» с тремя сторонами и вершинами, одна из которых является
Разбираемся с понятиями
В геометрии различают такие виды фигур с тремя сторонами: остроугольный, прямоугольный и тупоугольный треугольники. При этом свойства этих простейших многоугольников одинаковы для всех. Так, для всех перечисленных видов будет соблюдаться такое неравенство. Сумма длин любых двух сторон обязательно будет больше протяженности третьей стороны.
Но для того чтобы быть уверенным, что речь идет именно о законченной фигуре, а не о наборе отдельных вершин, необходимо проверить, чтобы соблюдалось основное условие: сумма углов тупоугольного треугольника равняется 180 о.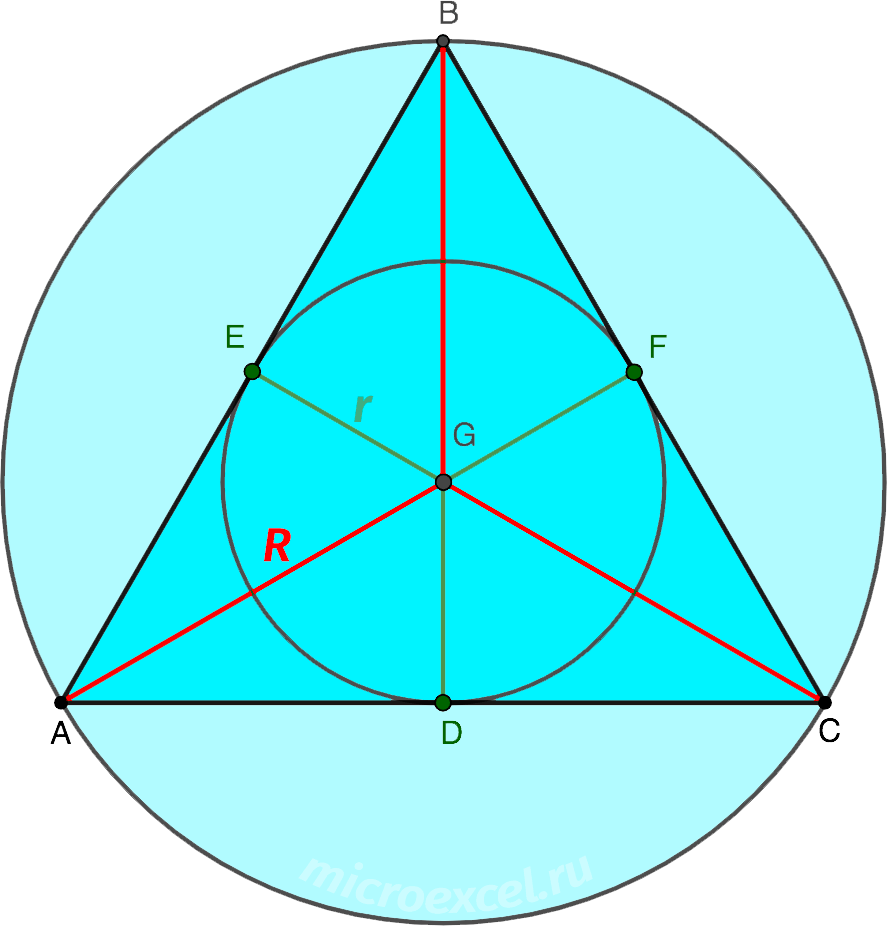 Это же верно и для других видов фигур с тремя сторонами. Правда, в тупоугольном треугольнике один из углов будет еще больше 90 о, а два оставшихся обязательно будут острыми. При этом именно наибольший угол будет находиться напротив самой длинной стороны. Правда, это далеко не все свойства тупоугольного треугольника. Но и зная лишь эти особенности, школьники могут решать многие задачи по геометрии.
Это же верно и для других видов фигур с тремя сторонами. Правда, в тупоугольном треугольнике один из углов будет еще больше 90 о, а два оставшихся обязательно будут острыми. При этом именно наибольший угол будет находиться напротив самой длинной стороны. Правда, это далеко не все свойства тупоугольного треугольника. Но и зная лишь эти особенности, школьники могут решать многие задачи по геометрии.
Для каждого многоугольника с тремя вершинами верно и то, что, продолжая любую из сторон, мы получим угол, размер которого будет равен сумме двух несмежных с ним внутренних вершин. Периметр тупоугольного треугольника рассчитывается так же, как и для других фигур. Он равняется сумме длин всех его сторон. Для определения математиками были выведены различные формулы, в зависимости от того, какие изначально присутствуют данные.
Правильное начертание
Одним из важнейших условий решения задач по геометрии является верный рисунок. Часто учителя математики говорят о том, что он поможет не только наглядно представить, что дано и что от вас требуется, но на 80% приблизиться к правильному ответу. Именно поэтому важно знать, как построить тупоугольный треугольник. Если вам нужна просто гипотетическая фигура, то вы можете нарисовать любой многоугольник с тремя сторонами так, чтобы один из углов был больше 90 о.
Именно поэтому важно знать, как построить тупоугольный треугольник. Если вам нужна просто гипотетическая фигура, то вы можете нарисовать любой многоугольник с тремя сторонами так, чтобы один из углов был больше 90 о.
Если даны определенные значения длин сторон или градусы углов, то чертить тупоугольный треугольник необходимо в соответствии с ними. При этом необходимо стараться максимально точно изобразить углы, высчитывая их при помощи транспортира, и пропорционально данным в задании условиям отобразить стороны.
Основные линии
Зачастую школьникам мало знать только то, как должны выглядеть те или иные фигуры. Они не могут ограничиться лишь информацией о том, какой треугольник тупоугольный, а какой прямоугольный. Курсом математики предусмотрено, что их знания об основных особенностях фигур должны быть более полными.
Так, каждому школьнику должно быть понятно определение биссектрисы, медианы, серединного перпендикуляра и высоты. Кроме того, он должен знать и их основные свойства.
Так, биссектрисы делят угол пополам, а противоположную сторону — на отрезки, которые пропорциональны прилегающим сторонам.
Медиана делит любой треугольник на два равных по площади. В точке, в которой они пересекаются, каждая из них разбивается на 2 отрезка в пропорции 2: 1, если смотреть от вершины, из которой она вышла. При этом большая медиана всегда проведена к его наименьшей стороне.
Не меньше внимания уделяется и высоте. Это перпендикуляр к противоположной от угла стороне. Высота тупоугольного треугольника имеет свои особенности. Если она проведена из острой вершины, то она попадает не на сторону этого простейшего многоугольника, а на ее продолжение.
Серединный перпендикуляр — это отрезок, который выходит из центра грани треугольника. При этом он расположен к ней под прямым углом.
Работа с окружностями
В начале изучения геометрии детям достаточно понять, как начертить тупоугольный треугольник, научиться отличать его от остальных видов и запомнить его основные свойства.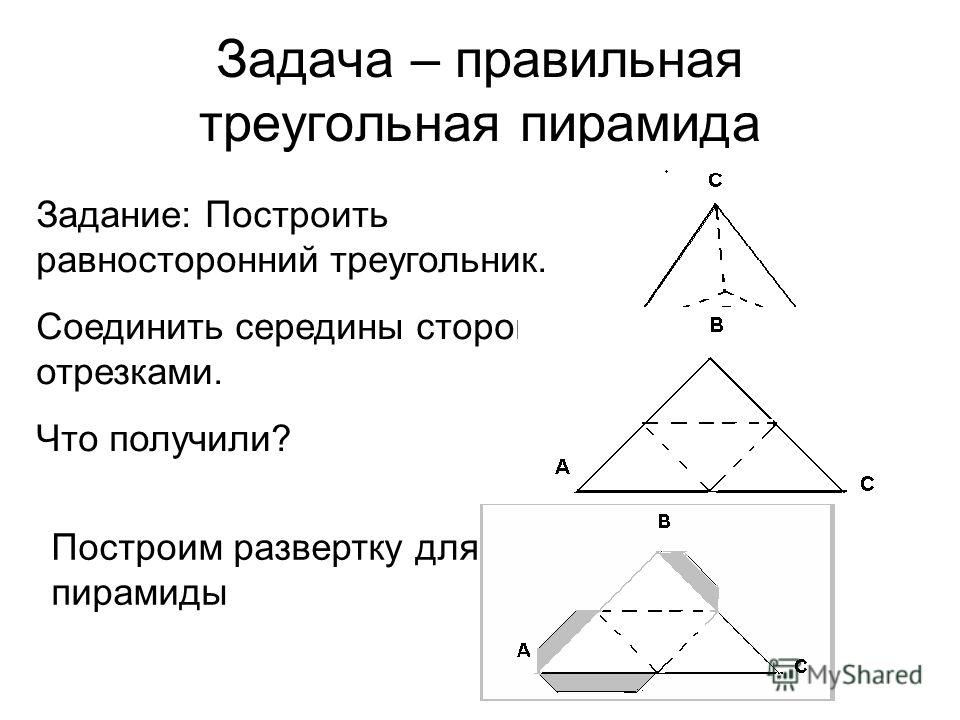 А вот старшеклассникам этих знаний уже мало. Например, на ЕГЭ часто встречаются вопросы про описанные и вписанные окружности. Первая из них касается всех трех вершин треугольника, а вторая имеет по одной общей точке со всеми сторонами.
А вот старшеклассникам этих знаний уже мало. Например, на ЕГЭ часто встречаются вопросы про описанные и вписанные окружности. Первая из них касается всех трех вершин треугольника, а вторая имеет по одной общей точке со всеми сторонами.
Построить вписанный или описанный тупоугольный треугольник уже намного сложнее, ведь для этого необходимо для начала выяснить, где должен находиться центр окружности и ее радиус. Кстати, необходимым инструментом станет в этом случае не только карандаш с линейкой, но и циркуль.
Те же сложности возникают при построении вписанных многоугольников с тремя сторонами. Математиками были выведены различные формулы, которые позволяют определить их месторасположение максимально точно.
Вписанные треугольники
Как уже было сказано ранее, если круг проходит через все три вершины, то это называется описанной окружностью. Главным ее свойством является то, что она единственная. Чтобы выяснить, как должна располагаться описанная окружность тупоугольного треугольника, необходимо помнить, что ее центр находится на пересечении трех серединных перпендикуляров, которые идут к сторонам фигуры. Если в остроугольном многоугольнике с тремя вершинами эта точка будет находиться внутри него, то в тупоугольном — за его пределами.
Если в остроугольном многоугольнике с тремя вершинами эта точка будет находиться внутри него, то в тупоугольном — за его пределами.
Зная, например, что одна из сторон тупоугольного треугольника равна его радиусу, можно найти угол, который лежит напротив известной грани. Его синус будет равен результату от деления длины известной стороны на 2R (где R — это радиус окружности). То есть sin угла будет равен ½. Значит, угол будет равен 150 о.
Если вам необходимо найти радиус описанной окружности тупоугольного треугольника, то вам пригодятся сведения о длине его сторон (c, v, b) и его площади S. Ведь радиус высчитывается так: (c х v х b) : 4 х S. Кстати, неважно, какого именно у вас вида фигура: разносторонний тупоугольный треугольник, равнобедренный, прямо- или остроугольный. В любой ситуации, благодаря приведенной формуле, вы можете узнать площадь заданного многоугольника с тремя сторонами.
Описанные треугольники
Также довольно часто приходится работать со вписанными окружностями. По одной из формул, радиус такой фигуры, умноженный на ½ периметра, будет равняться площади треугольника. Правда, для ее выяснения вам необходимо знать стороны тупоугольного треугольника. Ведь для того чтобы определить ½ периметра, необходимо сложить их длины и разделить на 2.
По одной из формул, радиус такой фигуры, умноженный на ½ периметра, будет равняться площади треугольника. Правда, для ее выяснения вам необходимо знать стороны тупоугольного треугольника. Ведь для того чтобы определить ½ периметра, необходимо сложить их длины и разделить на 2.
Чтобы понять, где должен находиться центр круга, вписанного в тупоугольный треугольник, необходимо провести три биссектрисы. Это линии, которые делят углы пополам. Именно на их пересечении и будет находиться центр окружности. При этом он будет равноудален от каждой из сторон.
Радиус такой окружности, вписанной в тупоугольный треугольник, равняется из частного (p-c) х (p-v) х (p-b) : p. При этом p — это полупериметр треугольника, c, v, b — его стороны.
Как построить равнобедренный треугольник? Это легко сделать с помощью линейки, карандаша и клеточек тетради.
Построение равнобедренного треугольника начинаем с основания. Чтобы рисунок получился ровным, количество клеточек в основании должно быть четным числом.
Делим отрезок — основание треугольника — пополам.
Вершину треугольника можно выбрать на любой высоте от основания, но обязательно ровно над срединой.
Как построить остроугольный равнобедренный треугольник?
Углы при основании равнобедренного треугольника могут быть только острыми. Чтобы равнобедренный треугольник получился остроугольным, угол при вершине тоже должен быть острым.
Для этого вершину треугольника выбираем повыше, подальше от основания.
Чем выше вершина, тем меньше угол при вершине. Углы при основании при этом, соответственно, увеличиваются.
Как построить тупоугольный равнобедренный треугольник?
С приближением вершины равнобедренного треугольника к основанию градусная мера угла при вершине увеличивается.
Значит, чтобы построить равнобедренный тупоугольный треугольник, вершину выбираем пониже.
Как построить равнобедренный прямоугольный треугольник?
Чтобы построить равнобедренный прямоугольный треугольник, надо вершину выбрать на расстоянии, равном половине основания (это обусловлено свойствами равнобедренного прямоугольного треугольника).
Например, если длина основания — 6 клеточек, то вершину треугольника располагаем на высоте 3 клеточек над серединой основания. Обратите внимание: при этом каждая клеточка у углов при основании делится по диагонали.
Построение равнобедренного прямоугольного треугольника можно начать с вершины.
Выбираем вершину, от нее под прямым углом откладываем равные отрезки вверх и вправо. Это — боковые стороны треугольника.
Соединим их и получим равнобедренный прямоугольный треугольник.
Построение равнобедренного треугольника с помощью циркуля и линейки без делений рассмотрим в другой теме.
Инструкция
Поставьте иглу циркуля в отмеченную точку. Нарисуйте ножкой с грифелем дугу окружности отмеренного радиуса.
В любом месте по окружности нарисованной дуги поставьте точку. Это будет вторая вершина B создаваемого треугольника.
Аналогичным способом поставьте ножку на вторую вершину. Проведите еще одну окружность так, чтобы она пресекалась с первой.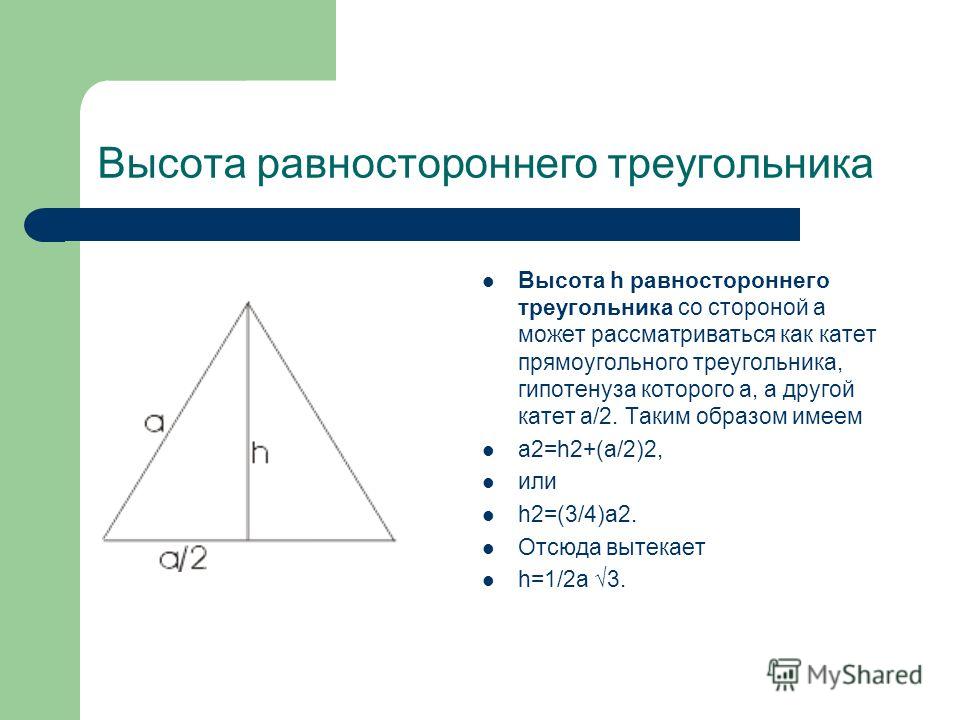
В точке пересечения обоих проведенных дуг и находится третья вершина C создаваемого треугольника. Отметьте ее на рисунке.
Получив все три вершины, соедините их прямыми линиями с помощью любой ровной поверхности (лучше линейки). Треугольник ABC построен.
Если окружность касается всех трех сторон данного треугольника, а её центр находится внутри треугольника, то ее называют вписанной в треугольник.
Вам понадобится
- линейка, циркуль
Инструкция
Из вершин треугольника (стороны противоположной делимому углу) циркулем проводят дуги окружности произвольного радиуса до пересечения их между собой;
Точку пересечения дуг по линейке соединяют с вершиной делимого угла;
Тоже самое проделывают с любым другим углом;
Радиусом вписанной в треугольник окружности будет отношение площади треугольника и его полупериметра: r=S/p , где S — площадь треугольника, а p=(a+b+c)/2 — полупериметр треугольника.
Радиус вписанной в треугольник окружности равноудален от всех сторон треугольника.
Источники:
- http://www.alleng.ru/d/math/math52.htm
Рассмотрим задачу построения треугольника при условии, что известны три его стороны или одна сторона и два угла.
Вам понадобится
- — циркуль
- — линейка
- — транспортир
Инструкция
Допустим, даны три стороны : a, b и с. Пользуясь , несложно с такими сторонами. Для начала выберем самую длинную из этих сторон, пусть это будет сторона с, и начертим ее. Затем установим раствор циркуля на величину другой стороны, стороны a, и начертим циркулем окружность радиуса a с центром на одном из концов стороны c. Теперь установим раствор циркуля на величину стороны b и начертим окружность с центром на другом конце стороны c. Радиус этой окружности равен b. Соединим точку пересечения окружностей с центрами и получим треугольник с искомыми сторонами.
Чтобы начертить треугольник с заданной стороной и двумя прилегающими углами, возьмите транспортир.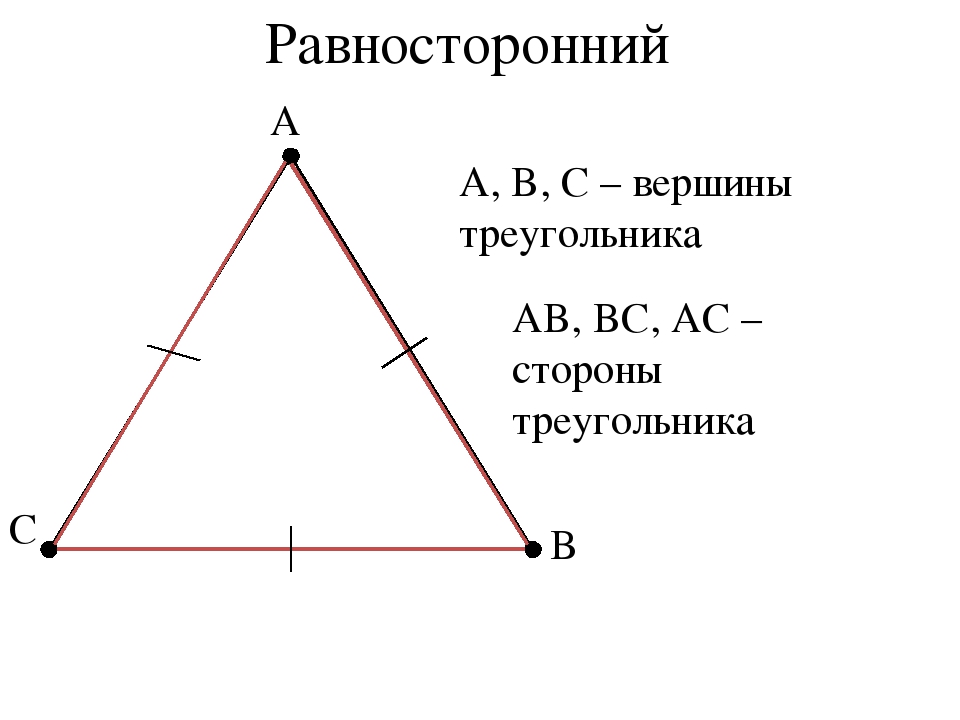 Начертите сторону указанной длины. На краях ее отложите транспортиром углы. На пересечении сторон углов получите третью вершину треугольника.
Начертите сторону указанной длины. На краях ее отложите транспортиром углы. На пересечении сторон углов получите третью вершину треугольника.
Видео по теме
Обратите внимание
Для сторон треугольника справедливо следующее утверждение: сумма длин двух любых сторон должна быть больше третьей. Если это не выполняется, то построить такой треугольник невозможно.
Окружности в шаге 1 пересекаются в двух точках. Можно выбрать любую, треугольники будут равными.
Правильный треугольник — тот, у которого все стороны обладают одинаковой длиной. Исходя из этого определения, построение подобной разновидности треугольника является нетрудной задачей.
Вам понадобится
- Линейка, лист разлинованной бумаги, карандаш
Инструкция
С помощью линейки соединить отмеченные на листке точки последовательно, друг за другом так, как это показано на рисунке 2.
Обратите внимание
В правильном (равностороннем) треугольнике все углы равны 60 градусам.
Полезный совет
Равносторонний треугольник так же является и равнобедренным. Если треугольник равнобедренный, то это означает, что 2 из 3-х его сторон равны, а третья сторона считается основанием. Любой правильный треугольник является равнобедренным, в то время как обратное утверждение не верно.
У любого равностороннего треугольника одинаковы не только стороны, но и углы, каждый из которых равен 60 градусам. Однако чертеж такого треугольника, построенный при помощи транспортира, не будет обладать высокой точностью. Поэтому для построения данной фигуры лучше воспользоваться циркулем.
Вам понадобится
- Карандаш, линейка, циркуль
Инструкция
Затем возьмите циркуль, установите его в из концов (будущей вершине треугольника) и проведите окружность с радиусом, равным длине этого отрезка. Можно не проводить окружность целиком, а начертить лишь ее четверть, от противоположного края отрезка.
Теперь переставьте циркуль в другой конец отрезка и снова начертите окружность того же радиуса. Здесь будет достаточно построить окружности, проходящую от дальнего конца отрезка до пересечения с уже построенной дугой. Полученная точка будет третьей вершиной вашего треугольника.
Здесь будет достаточно построить окружности, проходящую от дальнего конца отрезка до пересечения с уже построенной дугой. Полученная точка будет третьей вершиной вашего треугольника.
Чтобы закончить построение, снова возьмите линейку с карандашом и соедините точку пересечения двух окружностей с обоими концами отрезка. Вы получите треугольник, все три стороны которого абсолютно равны, – это можно будет легко проверить с помощью линейки.
Видео по теме
Треугольник – это многоугольник, у которого три стороны. Равносторонним или правильным треугольником называют треугольник, у которого все стороны и углы равны. Рассмотрим, как можно нарисовать правильный треугольник.
Вам понадобится
- Линейка, циркуль.
Инструкция
С помощью циркуля нарисуйте еще одну окружность, центр которой будет в точке В, а радиус равен отрезку ВА.
Окружности будут пересекаться в двух точках. Выберите любую из них. Назовите ее С. Это будет третьей вершиной треугольника.
Это будет третьей вершиной треугольника.
Соедините вершины между собой. Получившийся треугольник будет правильным. Убедитесь в этом, померив его стороны линейкой.
Рассмотрим способ построения правильного треугольника с помощью двух линеек. Начертите отрезок ОК, он будет одной из сторон треугольника, а точки О и К его вершинами.
Не сдвигая линейки после построения отрезка ОК, приложите перпендикулярно к ней еще одну линейку. Проведите прямую m пересекающую отрезок ОК в середине.
С помощью линейки отмерьте отрезок ОЕ, равный отрезку ОК так, чтобы один его конец совпадал с точкой О, а другой находился на прямой m. Точка Е буде третьей вершиной треугольника.
Закончите построение треугольника, соединив точки Е и К. Проверьте правильность построения с помощью линейки.
Обратите внимание
Убедиться в том, что треугольник правильный можете с помощью транспортира, измерив углы.
Полезный совет
Равносторонний треугольник так же можно начертить на листе в клетку с помощью одной линейки. Вместо другой линейки используйте перпендикулярные линии.
Вместо другой линейки используйте перпендикулярные линии.
Источники:
- Классификация треугольников. Равносторонние треугольники
- Что такое треугольник
- построение правильного треугольника
Вписанным называется такой треугольник, все вершины которого находятся на окружности. Построить его можно, если знать хотя бы одну сторону и угол. Окружность называется описанной, и она будет единственной для данного треугольника.
Вам понадобится
- — окружность;
- — сторона и угол треугольника;
- — лист бумаги;
- — циркуль;
- — линейка;
- — транспортир;
- — калькулятор.
Инструкция
От точки А с помощью транспортира отложите заданный угол. Продолжите сторону угла до пересечения с окружностью и поставьте точку С. Соедините точки В и С. У вас получился треугольник АВС. Он может быть любого типа. Центр окружности у остроугольного треугольника него, у тупоугольного — вне, а у прямоугольного — на гипотенузе.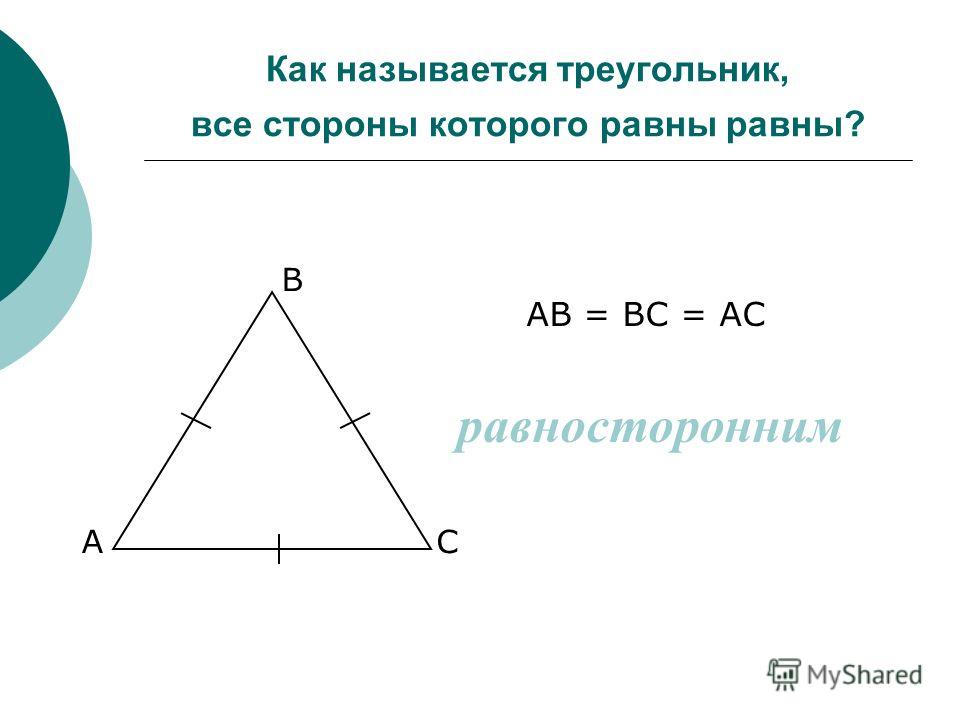 Если вам задан не угол, а, например, три стороны треугольника, вычислите один из углов по радиусу и известной стороне.
Если вам задан не угол, а, например, три стороны треугольника, вычислите один из углов по радиусу и известной стороне.
Значительно чаще приходится иметь дело с обратным построением, когда задан треугольник и надо вокруг него описать окружность. Вычислите его радиус. Сделать это можно по нескольким формулам, в зависимости от того, что вам дано. Радиус можно найти, например, по стороне и синусу противолежащего угла. В этом случае он равен длине стороны, разделенной на удвоенный синус противолежащего угла. То есть R=a/2sinCAB. Можно его выразить и через произведение сторон, в этом случае R=abc/√(a+b+c)(a+b-c)(a+c-b)(b+c-a).
Определите центр окружности. Разделите все стороны пополам и проведите серединам перпендикуляры. Точка их пересечения и будет центром окружности. Начертите ее так, чтобы она пересекла все вершины углов.
Две короткие стороны прямоугольного треугольника, которые принято называть катетами, по определению должны быть перпендикулярны между собой. Это свойство фигуры значительно облегчает ее построение. Однако возможность точно определить перпендикулярность есть не всегда. В таких случаях можно рассчитать длины всех сторон — они позволят построить треугольник единственно возможным, а поэтому правильным, способом.
Это свойство фигуры значительно облегчает ее построение. Однако возможность точно определить перпендикулярность есть не всегда. В таких случаях можно рассчитать длины всех сторон — они позволят построить треугольник единственно возможным, а поэтому правильным, способом.
Вам понадобится
- Бумага, карандаш, линейка, транспортир, циркуль, угольник.
Как начертить равнобедренный треугольник в круге. Рисуем треугольник в фотошопе
Как начертить треугольник?
Построение различных треугольников — обязательный элемент школьного курса геометрии. У многих это задание вызывает страх. Но на самом деле, все довольно просто. Далее в статье описано, как начертить треугольник любого типа с помощью циркуля и линейки.
Треугольники бывают
- разносторонние;
- равнобедренные;
- равносторонние;
- прямоугольные;
- тупоугольные;
- остроугольные;
- вписанные в окружность;
- описанные вокруг окружности.

Построение равностороннего треугольника
Равносторонним называется треугольник, у которого все стороны равны. Из всех видов треугольников, начертить равносторонний проще всего.
- С помощью линейки начертите одну из сторон, заданной длины.
- Измерьте ее длину с помощью циркуля.
- Поместите острие циркуля в один из концов отрезка и проведите окружность.
- Переставьте острие в другой конец отрезка и проведите окружность.
- У нас получилось 2 точки пересечения окружностей. Соединяя любую из них с краями отрезка, мы получаем равносторонний треугольник.
Построение равнобедренного треугольника
Данный тип треугольников можно построить по основанию и боковым сторонам.
Равнобедренным называется треугольник, у которого две стороны равны. Для того чтобы начертить равнобедренный треугольник по данным параметрам, необходимо выполнить следующие действия:
- С помощью линейки откладываем отрезок, равный по длине основанию.
 Обозначаем его буквами АС.
Обозначаем его буквами АС. - Циркулем измеряем необходимую длину боковой стороны.
- Рисуем из точки А, а затем из точки С, окружности, радиус которых равен длине боковой стороны.
- Получаем две точки пересечения. Соединив одну из них с точками А и С, получаем необходимый треугольник.
Построение прямоугольного треугольника
Треугольник, у которого один угол прямой, называют прямоугольным. Если нам даны катет и гипотенуза, начертить прямоугольный треугольник не составит труда. Его можно построить по катету и гипотенузе.
Построение тупоугольного треугольника по углу и двум прилегающим сторонам
Если один из углов треугольника тупой (больше 90 градусов), его называют тупоугольным. Чтобы начертить по указанным параметрам тупоугольный треугольник необходимо сделать следующее:
- С помощью линейки откладываем отрезок, равный по длине одной из сторон треугольника. Обозначим его буквами А и D.
- Если в задании уже нарисован угол, и вам необходимо начертить такой же, то на его изображении отложить два отрезка, оба конца которых лежат в вершине угла, а длина равняется указанным сторонам.
 Соедините полученные точки. У нас получился искомый треугольник.
Соедините полученные точки. У нас получился искомый треугольник. - Чтобы его перенести на свой чертеж, вам необходимо измерить длину третьей стороны.
Построение остроугольного треугольника
Остроугольный треугольник (все углы меньше 90 градусов) строится по тому же принципу.
- Нарисуйте две окружности. Центр одной из них лежит в точке D, а радиус равен длине третьей стороны, а у второй центр находится в точке А, а радиус равен длине указанной в задании стороны.
- Соедините одну из точек пересечения окружности с точками А и D. Искомый треугольник построен.
Вписанный треугольник
Для того чтобы начертить треугольник в окружности, нужно помнить теорему, в которой говорится, что центр описанной окружности лежит на пересечении серединных перпендикуляров:
У тупоугольного треугольника центр описанной окружности лежит за пределами треугольника, а у прямоугольного — на середине гипотенузы.
Чертим описанный треугольник
Описанный треугольник — это треугольник, в центре которого нарисована окружность, касающаяся всех его сторон.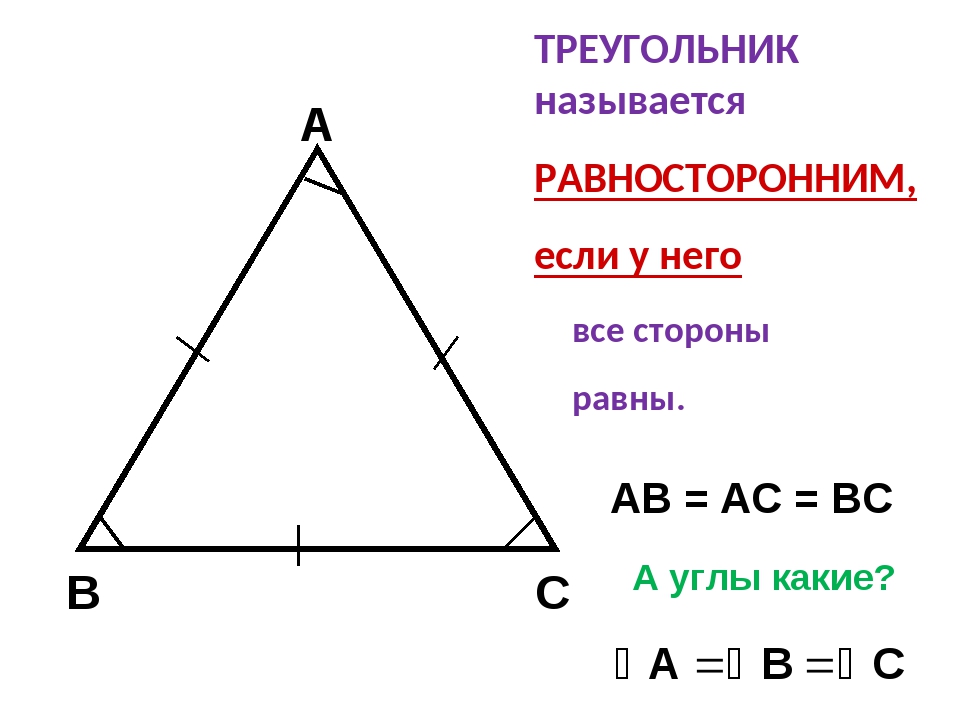 Центр вписанной окружности лежит на пересечении биссектрис. Для их построения необходимо:
Центр вписанной окружности лежит на пересечении биссектрис. Для их построения необходимо:
Построение вписанного в окружность правильного шестиугольника. Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой (фиг. 60, а).
Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг. 60, б), строим стороны 1 -6, 4-3, 4-5 и 7-2, после чего проводим стороны 5-6 и 3-2.
Построение вписанного в окружность равностороннего треугольника . Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля.
Рассмотрим два способа построения вписанного в окружность равностороннего треугольника.
Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, проведённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0-1-2 равен 30°, то для нахождения стороны
61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, проведённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0-1-2 равен 30°, то для нахождения стороны
1-2 достаточно построить по точке 1 и стороне 0-1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1-2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2-3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника.
Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вершины через одну, то получится равносторонний треугольник.
Для построения треугольника (фиг. 61, б) намечаем на диаметре вершину-точку 1 и проводим диаметральную линию 1-4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника.
Полученные точки будут двумя другими вершинами искомого треугольника.
Построение квадрата, вписанного в окружность . Это построение можно выполнить при помощи угольника и циркуля.
Первый способ основан на том, что диагонали квадрата пересекаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные стороны квадрата 4-1 и 3-2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1-2 и 4-3.
Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра (фиг. 62, б). Намечаем на концах двух взаимно перпендикулярных диаметров точки А, В и С и из них радиусом у описываем дуги до взаимного их пересечения.
Далее через точки пересечения дуг проводим вспомогательные прямые, отмеченные на фигуре сплошными линиями. Точки их пересечения с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.
Точки их пересечения с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.
Построение вписанного в окружность правильного пятиугольника.
Чтобы вписать в окружность правильный пятиугольник (фиг. 63), производим следующие построения.
Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4.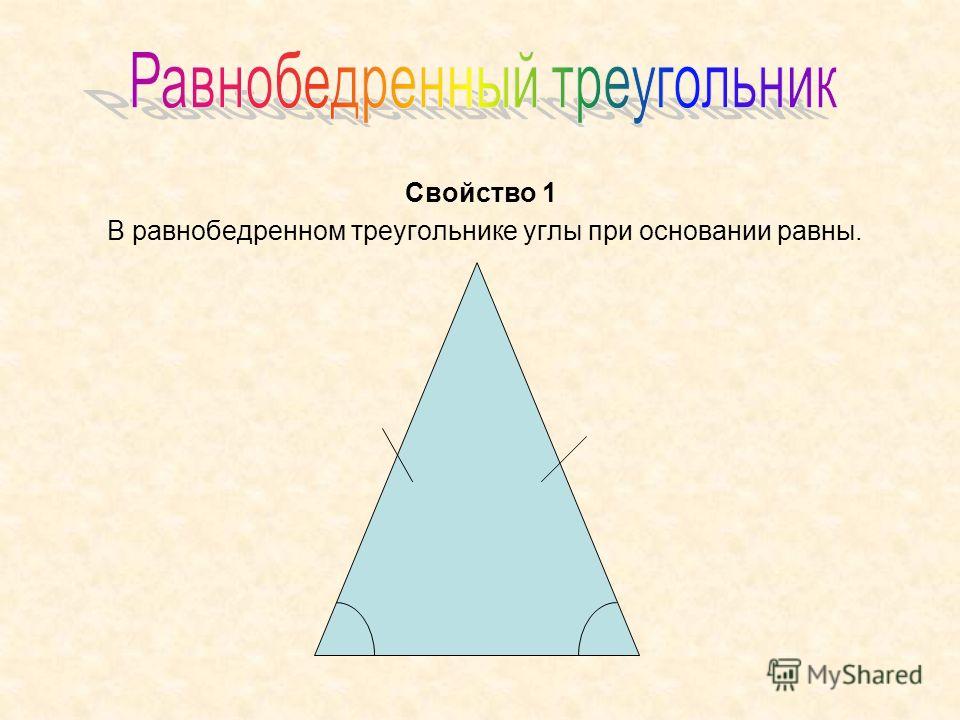 Найденные точки последовательно соединяем между собой.
Найденные точки последовательно соединяем между собой.
Построение правильного пятиугольника по данной его стороне.
Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую.
Получим точку 1-вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведёнными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.
Построение вписанного в окружность правильного семиугольника.
Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проводим из полюса F через чётные деления вертикального диаметра лучи, пересечение которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проводим из полюса F через чётные деления вертикального диаметра лучи, пересечение которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
Приведённый способ годен для построения правильных многоугольников с любым числом сторон.
Деление окружности на любое число равных частей можно производить также, пользуясь данными табл. 2, в которой приведены коэффициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.
Равносторонний треугольник в фотошопе рисуется при помощи векторных объектов. Можно нарисовать закрашенный треугольник, можно треугольник с рамкой. Выбираем рисование многоугольников (Polygon tool).
Выбираем рисование многоугольников (Polygon tool).
Рисование многоугольников (Polygon tool)
Выбираем фигуры (гор. клавиша U ), затем Polygon tool (Инструмент Многоугольник), см. скриншот ниже.
Устанавливаем свойство «Fill Pixels».
Выбираем цвет заливки треугольника (первый цвет в панели инструментов), рисуем мышкой треугольник.
Треугольник с рамкой
Треугольник следует рисовать на новом пустом слое , без какой-либо заливки. Создать новый слой можно одновременным нажатием клавиш Alt + Ctrl + Shift + N .
Устанавливаем значение «Paths» (по-русски пути).
Рисуем мышкой треугольник.
Преобразуем векторный треугольник в выделение (Select), нажатием клавиш Ctrl + Enter .
Закрашиваем выделение (в данном случае белым цветом).
Alt + ← BackSpace — первый выбранный цвет.
Ctrl + ← BackSpace — второй выбранный цвет.
В свою бытность «чайником», я столкнулся с необходимостью нарисовать треугольник в Фотошопе. Тогда с этой задачей без посторонней помощи мне справиться не удалось.
Тогда с этой задачей без посторонней помощи мне справиться не удалось.
Оказалось, что все не настолько сложно, как могло показаться на первый взгляд. В этом уроке я поделюсь с Вами опытом в рисовании треугольников.
Существуют два (известных мне) способа.
Первый способ позволяет изобразить равносторонний треугольник. Для этого нам нужен инструмент под названием «Многоугольник» . Находится он в разделе фигур на правой панели инструментов.
Этот инструмент позволяет рисовать правильные многоугольники с заданным числом сторон. В нашем случае их (сторон) будет три.
После настройки цвета заливки
ставим курсор на холст, зажимаем левую кнопку мыши и рисуем нашу фигуру. В процессе создания треугольник можно вращать, не отпуская кнопку мыши.
Полученный результат:
Кроме того, можно нарисовать фигуру без заливки, но с контуром. Линии контура настраиваются в верхней панели инструментов. Там же настраивается и заливка, вернее ее отсутствие.
У меня получились такие треугольники:
С настройками можно экспериментировать, добиваясь нужного результата.
Следующий инструмент для рисования треугольников – «Прямолинейное лассо» .
Этот инструмент позволяет рисовать треугольники с любыми пропорциями. Давайте попробуем изобразить прямоугольный.
Для прямоугольного треугольника нам понадобится точно нарисовать прямой (кто бы мог подумать…) угол.
Воспользуемся направляющими. Как работать с направляющими линиями в Фотошопе, читайте в этой статье .
Итак, статью прочитали, тянем направляющие. Одну вертикальную, другую горизонтальную.
Чтобы выделение «притягивалось» к направляющим, включаем функцию привязки.
Затем кликаем правой кнопкой мыши внутри выделения и выбираем, в зависимости от потребностей, пункты контекстного меню «Выполнить заливку» или «Выполнить обводку» .
Цвет заливки настраивается следующим образом:
Для обводки также можно настроить ширину и расположение.
Получаем следующие результаты:
Заливка.
Для получения острых углов обводку нужно выполнять «Внутри» .
После снятия выделения (CTRL+D ) получаем готовый прямоугольный треугольник.
Вот такие два простейших способа рисования треугольников в программе Фотошоп.
Построение равносторонего треугольника
← →boriskb © (2012-04-11 10:27) [0]
без транспортира и циркуля.
Прямо сейчас понадобилось. Ниего кроме карандаша и линейки без делений нет. Размер стороны можно на глаз.
Научите?
← →
RWolf © (2012-04-11 10:30) [1]
сдаётся мне, для таких фокусов нужны минимум циркуль и линейка.
← →
Jeer © (2012-04-11 10:31) [2]
Сверлишь две дырочки в линейке — вот тебе и циркуль 🙂
← →
CRLF (2012-04-11 10:33) [3]
в нашей нищей школе математик, помнится, кусок мела и тряпку для вытирания доски успешно использовал в качестве циркуля %-)
← →
Boriskb © (2012-04-11 10:33) [4]
> Сверлишь две дырочки в линейке — вот тебе и циркуль 🙂
Ниего кроме карандаша и линейки без делений нет.
← →
oldman © (2012-04-11 10:33) [5]
высота расчитывается по теореме Пифагора
Проводить перпендикуляр с помощью только линейки научить?
← →
Медвежонок Пятачок © (2012-04-11 10:35) [6]
ломаем линейку на три примерно равные части.
складываем вместе, карандашом наносим риски с краев.
получили три стороны одинаковой длины.
выкладываем их на листе бумаги, совмещая риски.
вуаля….
← →
Boriskb © (2012-04-11 10:36) [7]
Ладно. Уточним вопрос: как простейшим способом соорудить циркуль?
← →
AV © (2012-04-11 10:37) [8]
> Сверлишь две дырочки в линейке — вот тебе и циркуль 🙂
рисуешь любой треугольник, объявляешь его находящимся в таком искривленном пространстве, что он становится равносторонним по его искривлению.
по сабжу — имхо, никак. Циркуль, все-таки, нужен.
← →
Boriskb © (2012-04-11 10:38) [9]
> oldman © (11.04.12 10:33) [5]
> высота расчитывается по теореме ПифагораПроводить перпендикуляр
> с помощью только линейки научить?
Нет спасибо — лучше науите откладывать на линейке без делений корень из 2
← →
oldman © (2012-04-11 10:38) [10]
> Ладно. Уточним вопрос: как простейшим способом соорудить
> циркуль?
Карандаш, нитка, кнопка
← →
Boriskb © (2012-04-11 10:40) [11]
Блин…
Есть куча графических редакторов, но нет принтера :))
← →
RWolf © (2012-04-11 10:42) [12]
> как простейшим способом соорудить циркуль?
ножницы должны подойти.
← →
oldman © (2012-04-11 10:44) [13]
1. Рисуешь известную тебе одну сторону треугольника AB.
2. С помощью линейки рисуешь с двух сторон равноудаленные параллельные прямые 1 и 2 (прикладывая линейку к АВ и чертя с другой стороны линейки)
3. Находишь на прямой точки A1 и В1, а на прямой 2 точки А2 и В2
(AA1=AA2=BB1=BB2>половины стороны)
4. соединяешь точки пересечения АА1 с ВВ1 и АА2 с ВВ2
Получаешь перпендикуляр четко в середине стороны. Он высота. Далее Пифагор.
← →
sniknik © (2012-04-11 10:46) [14]
> Карандаш, нитка, кнопка
кусок бумаги пробитый в одном месте спичкой в другом карандашом.
← →
Boriskb © (2012-04-11 10:46) [15]
> Карандаш, нитка, кнопка
Это первое что пришло в голову, но нет кнопки. На иголке завязать чтоли… И карандашь обвязать? Амне их надо штук 20 разного размера — с моими кривыми руками я их буду бог знает скаолько времени завязывать…
На иголке завязать чтоли… И карандашь обвязать? Амне их надо штук 20 разного размера — с моими кривыми руками я их буду бог знает скаолько времени завязывать…
Сижу дома.
По всем соседям уже сбегал.
← →
Boriskb © (2012-04-11 10:47) [16]
> RWolf © (11.04.12 10:42) [12]
> > как простейшим способом соорудить циркуль?ножницы должны
> подойти.
ну вот почему сам не догадался? Пока самый реальный метод.
← →
oldman © (2012-04-11 10:47) [17]
> По всем соседям уже сбегал.
А по магазинам нет?
«Знаю я тут одно место с офигенными циркулями» (ДМБ ©)
← →
Boriskb © (2012-04-11 10:49) [18]
> Пока самый реальный метод
Хотя. . как я след на бумаге от такого циркуля получу? Глазки старенькие уже :))
. как я след на бумаге от такого циркуля получу? Глазки старенькие уже :))
← →
Boriskb © (2012-04-11 10:50) [19]
> А по магазинам нет?
Денег жалко :))
На один раз покупать — потом выбросить..
← →
oldman © (2012-04-11 10:50) [20]
Привяжи карандаш к ножницам!!!
← →
oldman © (2012-04-11 10:54) [21]
> > Карандаш, нитка, кнопка
>
> Это первое что пришло в голову, но нет кнопки. На иголке
> завязать чтоли… И карандашь обвязать? Амне их надо штук
> 20 разного размера — с моими кривыми руками я их буду бог
> знает скаолько времени завязывать. ..
..
Завязать на карандаше. Отмотать нитку большой длины. Начать с большого треугольника. Малые радиусы получаться путем наматывания нитки вокруг карандаша.
Блин! Я больше не могу смеяться. Закройте ветку.
← →
Boriskb © (2012-04-11 10:56) [22]
> Блин! Я больше не могу смеяться. Закройте ветку.
:))
Еще веселей будет если сам, на практике, попробуешь решить задачу с указанными ограничениями
← →
han_malign (2012-04-11 10:59) [23]
> надо штук 20 разного размера
— нарисуй один большой, и 19-ть вложенных — используй как трафарет…
← →
Плохиш © (2012-04-11 10:59) [24]
Сначала создать трудности, а после героически их решать. Как всё знакомо и не смешно.
Как всё знакомо и не смешно.
← →
RWolf © (2012-04-11 11:01) [25]
почему бы просто не нарисовать треугольник на экране, после чего приложить лист бумаги и отметить на нём вершины треугольника на просвет?
а их уж и линейкой обвести можно.
← →
Inovet © (2012-04-11 11:07) [26]
Так ниток тоже нет.
А у линейкм есть ширина? Прямой угол? Лист сгибать можно?
← →
AV © (2012-04-11 11:09) [27]
имхо, дядя Боря дисер пишет
«Мониторинг инет-сообщества технического уклона по вопросам готовности помочь ближнему»
наиболее реальное — нарисовать, добавить яркости, приложить, обвести.
Я так дочери солдата-победителя нарисовал в школу на А2. Кусками двигал изображение и лист, обводил. Даже на выставку оправили 🙂
Кусками двигал изображение и лист, обводил. Даже на выставку оправили 🙂
← →
Inovet © (2012-04-11 11:11) [28]
> [27] AV © (11.04.12 11:09)
> наиболее реальное — нарисовать, добавить яркости, приложить,
> обвести.
Монитора тоже нет
← →
Boriskb © (2012-04-11 11:15) [29]
Ну хоть тренинг в остроумии получился 🙂
> Монитора тоже нет
Монитор есть :))
Сейчас расскажу историю вопроса.
← →
Inovet © (2012-04-11 11:17) [30]
> [29] Boriskb © (11.04.12 11:15)
> Монитор есть :))
Может и принтер есть?
← →
CRLF (2012-04-11 11:18) [31]
а прямой угол у нас есть?
← →
Inovet © (2012-04-11 11:20) [32]
> [31] CRLF (11.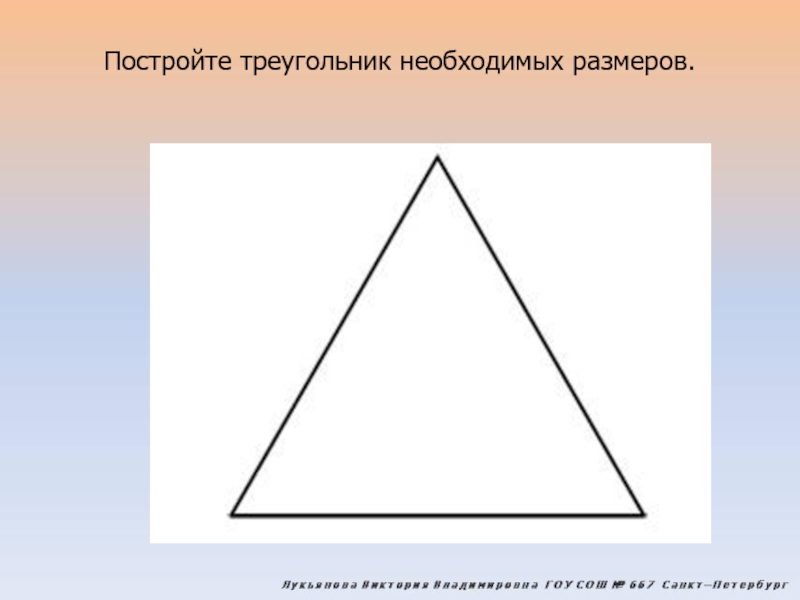 04.12 11:18)
04.12 11:18)
> а прямой угол у нас есть?
Монитор прямокгольный. Можно положить на стол и пользоваться как прямоугольником.
← →
CRLF (2012-04-11 11:22) [33]
впрочем, не поможет.
← →
Boriskb © (2012-04-11 11:23) [34]
История следущая:
Ко мне пришла внучка — 14 лет . Захотел ей показать сою любимую игрушку в ее возрасте и около того.
Гексафлексагоны http://www.arbuz.uz/z_flex.html
На ней и мои дети выросли. Тогда известный кубик еще не был изобретен
Требуется ее сначала сделать :))
← →
Boriskb © (2012-04-11 11:24) [35]
Циркуль сбегал — купил.
Ножницы бы все равно не подошли — трудно зафиксировать раствор.
← →
Inovet © (2012-04-11 11:25) [36]
> [33] CRLF (11.04.12 11:22)
> впрочем, не поможет.
Чё иа не поможет, очень даже поможет.
← →
Anatoly Podgoretsky © (2012-04-11 11:29) [37]
Бумаги нет
← →
Inovet © (2012-04-11 11:34) [38]
> [37] Anatoly Podgoretsky © (11.04.12 11:29)
> Бумаги нет
Придётся линейку пилить ей же самой и карандашом.
← →
Boriskb © (2012-04-11 11:34) [39]
> Бумаги нет
Да, кстати — тоже не так просто.
Надо было найти подходящий картон белый с обеих сторон. Не так просто.
Еще не знаю — есть ли чем скреплять…
Липкой ленты точно нет. Полезу в аптечку — пластырь рулонный искать…
← →
Inovet © (2012-04-11 11:35) [40]
> [39] Boriskb © (11.04.12 11:34)
> Липкой ленты точно нет.
Скотч надо было вместе с циркулем купить и картон там же.
← →
oldman © (2012-04-11 11:41) [41]
> Скотч надо было вместе с циркулем купить и картон там же.
Проще купить гексафлексагон
← →
Boriskb © (2012-04-11 11:42) [42]
> Inovet © (11.04.12 11:35) [40]
Не понимаете вы ничего в воспитании.
Лучше было бы и циркуль не покупать. Дал слабину…
← →
Труп Васи Доброго © (2012-04-11 11:46) [43]
Найди/создай/отмерь угол в 60 градусов (раздели 180 на 3). Нарисуй этот «длинный» угол на весь ватман, а потом при помощи любой штуки отметь на обоих сторонах угла одинаковое расстояние. Соедини отметки и вот тебе сколь угодно равносторонних треугольников.
← →
Inovet © (2012-04-11 11:47) [44]
> [42] Boriskb © (11.04.12 11:42)
> Не понимаете вы ничего в воспитании.
Внучка может не понять изюминку изготовления и заодно ей станет неинтересна сама суть игрушки. Даже во всяких Очумелых ручках применяют скотч, чтобы понятно было — он же есть в магазине, чем он хуже картона. Ну а нет, так ткашь и нитки с иголкой, но их тоже нет по условию задачи.
← →
Inovet © (2012-04-11 11:49) [45]
> [43] Труп Васи Доброго © (11.04.12 11:46)
> Нарисуй этот «длинный» угол на весь ватман, а потом при
> помощи любой штуки отметь на обоих сторонах угла одинаковое
> расстояние. Соедини отметки и вот тебе сколь угодно равносторонних
> треугольников.
Надо, как оказалось, много одинаковых.
← →
Inovet © (2012-04-11 11:51) [46]
> [43] Труп Васи Доброго © (11.04.12 11:46)
> Найди/создай/отмерь угол в 60 градусов (раздели 180 на 3).
Нечем — нет ничего.
← →
Boriskb © (2012-04-11 11:56) [47]
Задача ясна из [34]
Попробуйте в реале bepyftnt методом проб и ошибок (я их сделал несколько десятков штук) что ни бумага, картон не всякий, иголка и нитка и много чего еще не подойдет для хоть мало мальски долгоживущей игрушки.
> Проще купить гексафлексагон
Это точно — зачем учить арифметику — ведь калькулятор есть :))
← →
Anatoly Podgoretsky © (2012-04-11 11:59) [48]
> Inovet (11.04.2012 11:34:38) [38]
Ничего нет, вот в этом ничего и надо рисовать
← →
CRLF (2012-04-11 12:02) [49]
Ничего есть!
← →
Anatoly Podgoretsky © (2012-04-11 12:13) [50]
> CRLF (11.04.2012 12:02:49) [49]
Ничего есть нельзя.
← →
Игорь Шевченко © (2012-04-11 12:20) [51]
Boriskb © (11. 04.12 11:23) [34]
04.12 11:23) [34]
Статья в «Науке и жизни» занимательная была, помнится
← →
Boriskb © (2012-04-11 12:27) [52]
> Игорь Шевченко © (11.04.12 12:20) [51]
Я про них вычитал в книге Мартина Гарднера. Подарила учительница математики. Потом купили еще 3 наименования его книг.
Помнится на этом форуме его уже упоминали
← →
Jeer © (2012-04-11 14:30) [53]
Что-то мне напомнило «Как выжить с товарищем в пустыне без воды» 🙂
Варианты ? 🙂
← →
Думкин © (2012-04-11 14:36) [54]
> Jeer © (11.04.12 14:30) [53]
А товарищ тоже должен выжить?
← →
Anatoly Podgoretsky © (2012-04-11 14:46) [55]
> Думкин (11.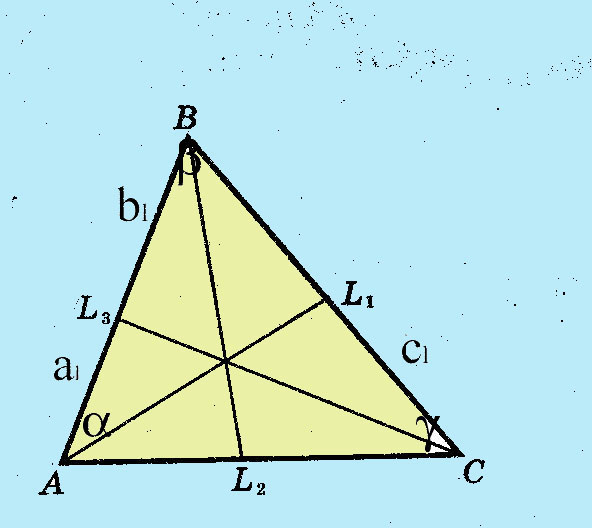 04.2012 14:36:54) [54]
04.2012 14:36:54) [54]
А потом будем выяснить можно ли пить кровь
← →
Думкин © (2012-04-11 14:49) [56]
> Anatoly Podgoretsky © (11.04.12 14:46) [55]
нужно!
Постперестроечный помойный фильм как-то был — так там сын в пустыне папку съел, так и выжил.
← →
Jeer © (2012-04-11 14:58) [57]
> Думкин © (11.04.12 14:36) [54]
>
>
> > Jeer © (11.04.12 14:30) [53]
>
> А товарищ тоже должен выжить?
А как же ? Иначе это уже не товарищ, а корм 🙂
← →
БарЛог © (2012-04-11 15:03) [58]
Я за 20 секунд нарисовал 🙂
Рисуешь квадрат.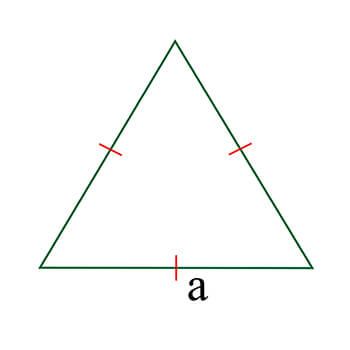 Делишь верхнюю сторону пополам, соединяешь точки.
Делишь верхнюю сторону пополам, соединяешь точки.
Из точки, которая лежит на середине верхней стороны квадрата проводишь отрезки до нижних точек.
← →
Труп Васи Доброго © (2012-04-11 15:12) [59]
> Я за 20 секунд нарисовал 🙂
Учителем тебе не быть! Ничего не понял из твоего «рассказа».
Сдаётся мне что если вырезать из бумаги три одинаковые полоски и сложить из них замкнутую фигуру, то получится совершенно равносторонний треугольник.
← →
boriskb © (2012-04-11 15:13) [60]
> БарЛог © (11.04.12 15:03) [58]
Не понял.
Нарисуй — покажи.
PS
:))
вспомнил анекдот про «не понял»
← →
Inovet © (2012-04-11 15:21) [61]
> [58] БарЛог © (11. 04.12 15:03)
04.12 15:03)
> Рисуешь квадрат
Как?
← →
Boriskb © (2012-04-11 15:21) [62]
К
> boriskb © (11.04.12 15:13) [60]
Старый рабочий передает своё хозяйство молодому.
— Значит так: ты работаешь дежурныи электриком. Утром приходишь — включаешь рубильник. Вечером уходишь — выключаешь. Понял?
-Неа. Не понял.
-Видишь рубильник. Утром его надо включить, люди придут, будут работать. Вечером, все уйдут. В целях пожарной безопасности рубильник дадо выключить. Понял?
-Да не понял я!
-Ну идрит твою… Рубильник знаешь? Включать-выключать умеешь? Утром ты первый приходишь, надо дать электричество цеху — поворачивашь рубильник в эту сторону. Вечером, когда все уйдут, повернешь его в другую сторону — выключишь. Понял?
— Мужик, ты что — тупой чтоли? Я тебе уже сколько раз говорю: Я не понял!! А ты всё переспрашиваешь!
← →
CRLF (2012-04-11 15:32) [63]
> Как?
Кстати. .. Загибаем угол бумажной полоски под 45 градусов (короткий край параллельно длинному краю). Загибаем полоску вдоль катета получившегося треугольника, имеем квадрат.
.. Загибаем угол бумажной полоски под 45 градусов (короткий край параллельно длинному краю). Загибаем полоску вдоль катета получившегося треугольника, имеем квадрат.
← →
icWasya © (2012-04-11 15:44) [64]
Как тот же Гарднер советовал — сначала взять ленту от кассового аппарата.
Если аккуратно сложить втрое лист бумаги — можно получить угол в 60 градусов.
← →
Думкин_ (2012-04-11 15:50) [65]
> А как же ? Иначе это уже не товарищ, а корм 🙂
Какая скучная задача, однако! Но может так оказаться, что в пустыне только товарищ, а не я.
Как с таким товарищем, который в пустыне без воды, выжить — вроде понятно.
А вот если в пустые и он и я. А пустыня — это центр Сахары, то думаю, что привет. Даже та дикая идея, что пробегает по некоторому взаимному сохранению жидкости — кажется безнадежной. И неприятной.
И неприятной.
← →
Inovet © (2012-04-11 15:53) [66]
> [63] CRLF (11.04.12 15:32)
> [64] icWasya © (11.04.12 15:44)
На мой вопрос положительного ответа не было
> [26] Inovet © (11.04.12 11:07)
> А у линейкм есть ширина? Прямой угол? Лист сгибать можно?
И вообще
> [37] Anatoly Podgoretsky © (11.04.12 11:29)
> Бумаги нет
← →
CRLF (2012-04-11 15:59) [67]
> Inovet © (11.04.12 15:53) [66]
У топикстартера задача — сделать гексафлексагон. Как нарисовать сферический квадрат в вакууме, он не спрашивал. Ты спрашиваешь, да. 🙂
← →
CRLF (2012-04-11 15:59) [68]
> Inovet © (11. 04.12 15:53) [66]
04.12 15:53) [66]
У топикстартера задача — сделать гексафлексагон. Как нарисовать сферический квадрат в вакууме, он не спрашивал. Ты спрашиваешь, да. 🙂
← →
Inovet © (2012-04-11 16:18) [69]
> [67] CRLF (11.04.12 15:59)
> Как нарисовать сферический квадрат в вакууме, он не спрашивал.
ТС хочет нарисовать только линейкой, больше ничего нет. Сгибать лист не разрешил. Потом купил циркуль, тут уже всё просто.
← →
CRLF (2012-04-11 16:30) [70]
> Захотел ей показать сою любимую игрушку в ее возрасте и около того.
> Требуется ее сначала сделать :))
Задача — сделать игрушку, а не мысленный эксперимент «как построить всё, не имея ничего» %-)
← →
TUser © (2012-04-11 16:33) [71]
> У топикстартера задача — сделать гексафлексагон.
Только вопрос в топике задан в стиле, на который тут обычно отвечают ссылкой на «Как задавать вопросы хакерам?»
← →
Владислав © (2012-04-11 16:35) [72]
Надо до появления внуков циркуль купить.
← →
CRLF (2012-04-11 16:36) [73]
Обычно разным людям отвечают по-разному, на основе экспертной оценки их предыдущих постов, ага.
← →
boriskb © (2012-04-11 16:43) [74]
Друзья, мне конечно льстит, что меня причисляют к великим писателям (Ведь только в произведениях великих писателей каждый видит что-то своё?).
Но, право же — я не достоин. :))
Всё проще.
Я лишь хотел воказать внучке, чем дед занимался в её возрасте :))
Идействительно, ни линейки нормальной (не говоря о большем) дома давно нет.
Отучились все.
← →
БарЛог © (2012-04-11 18:12) [75]
http://savepic.su/1656425m.jpg
← →
Владислав © (2012-04-11 18:22) [76]
> БарЛог © (11.04.12 18:12) [75]
Ну все бы ничего, но нужен равносторонний.
← →
Inovet © (2012-04-11 18:24) [77]
> [75] БарЛог © (11.04.12 18:12)
> http://savepic.su/1656425m.jpg
И как это сделать одной линейкой?
← →
Inovet © (2012-04-11 18:25) [78]
> [76] Владислав © (11.04.12 18:22)
> Ну все бы ничего, но нужен равносторонний.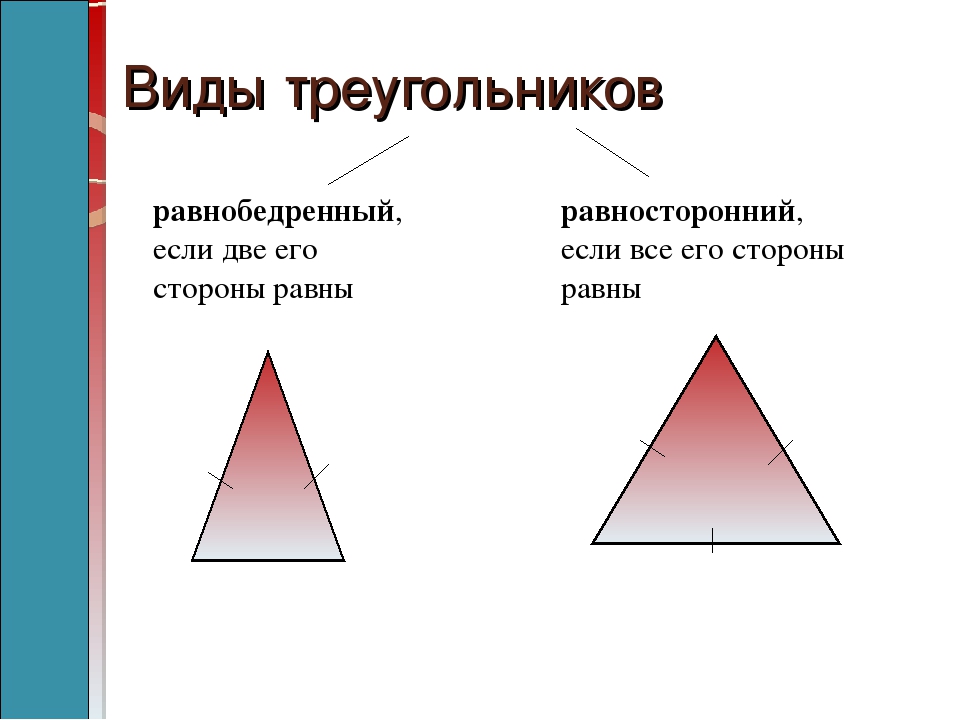
Там не понятно какой он.
← →
БарЛог © (2012-04-11 18:30) [79]
> Ну все бы ничего, но нужен равносторонний.
Да, задача не решена 🙁
← →
CRLF (2012-04-11 18:34) [80]
Без эталона прямого угла задачка нерешаема %-)
← →
Дмитрий С © (2012-04-11 18:52) [81]
Тему не читал.
Решение задачи:
Берем линейку, карандаш. Начинаем случайным образом рисовать линии до тех пор пока какие нибудь из них не образуют равносторонний треугольник.
← →
CRLF (2012-04-11 18:54) [82]
А линейка-то зачем?. .
.
← →
boriskb © (2012-04-11 20:04) [83]
Инет всё знает :))
Получаем эталон угла в 60 градусов. Он решит все наши проблемы.
http://505sovetov.ru/231/
Правда получаем вопрос: как построить квадрат? Я думаю в наших условиях можно воспользоваться тетрадкой в клеточку — она у меня есть.
← →
Sha © (2012-04-11 20:10) [84]
> boriskb © (11.04.12 20:04) [83]
> Инет всё знает :))
не верь:
у того треугольника отношение катетов 2:1,
а надо гипотенуза к катету 2:1
← →
Inovet © (2012-04-11 20:18) [85]
> [83] boriskb © (11.04.12 20:04)
> Инет всё знает :))
Врёт инет всё
a — сторона квадрата
a / (1/2 * a) = 2 = tng(CAB)
CAB = 1,1071487177940905030170654601785
CAB <> Pi / 3 = 1,0471975511965977461542144610932
← →
Inovet © (2012-04-11 20:20) [86]
И гнуть ты запретил. Если можно гнуть, то равносторонний легко строится с помощью линейки.
Если можно гнуть, то равносторонний легко строится с помощью линейки.
← →
Inovet © (2012-04-11 20:24) [87]
Ты так плохому научишь внучку.
← →
Boriskb © (2012-04-11 20:25) [88]
> Inovet © (11.04.12 20:18) [85]
Да уж…
Как школьник.
← →
Boriskb © (2012-04-11 20:26) [89]
> И гнуть ты запретил
Где? Цитата?
> Если можно гнуть, то равносторонний легко строится с помощью
> линейки.
Покажи
← →
Sha © (2012-04-11 20:32) [90]
Если у нас есть прямой угол, то задача сводится к построению отрезка длиной 3^1/2. 1/2.
1/2.
← →
Inovet © (2012-04-11 20:34) [91]
> [89] Boriskb © (11.04.12 20:26)
> > И гнуть ты запретил
>
> Где? Цитата?
Ты не ответил на вопрос о гнутье.:)
> [26] Inovet © (11.04.12 11:07)
> А у линейкм есть ширина? Прямой угол? Лист сгибать можно?
> [89] Boriskb © (11.04.12 20:26)
> Покажи
Чертим отрезок на длину линейки. Складываем лист так, чтобы концы отрезка совпали — линия изгиба будет срединным перпендикуляром. Совмежаем один конец линейки с концом отрезка, второй с перпендикуляром, проводим линию. Аналогично поступаем с другим.
← →
Inovet © (2012-04-11 20:35) [92]
> [90] Sha © (11.04.12 20:32)
> то задача сводится к построению отрезка длиной
Делений нет на линейке.
← →
Inovet © (2012-04-11 20:37) [93]
> [92] Inovet © (11.04.12 20:35)
> Делений нет на линейке.
Вообще никаких, тем более логарифмической разметки.
← →
Sha © (2012-04-11 20:38) [94]
> Inovet © (11.04.12 20:35) [92]
> Делений нет на линейке.
Они не нужны.
В качестве единичного отрезка выбери любую длину.
Этого достаточно.
← →
Inovet © (2012-04-11 20:42) [95]
> [94] Sha © (11.04.12 20:38)
> Они не нужны.
А, ну да. Прямой угол тоже двумя сгибаниями можно сделать.
← →
oldman © (2012-04-11 21:02) [96]
> БарЛог © (11. 04.12 18:30) [79]
04.12 18:30) [79]
> Да, задача не решена 🙁
>
> CRLF (11.04.12 18:34) [80]
> Без эталона прямого угла задачка нерешаема %-)
Задача решена еще в [13]
Если на линейке нет делений, до две риски карандашом помогают не прибегать даже к теореме Пифагора.
Построив срединный перпендикуляр найти на нем точку, удаленную от концов отрезка на длину отрезка элементарно.
Кстати, отложив на перпендикуляре длину отрезка, получим эталонный треугольник с углами 30 и 60.
Математики, блин! Геометрия, средняя школа.
← →
oldman © (2012-04-11 21:04) [97]
Елки! Про эталонный треугольник я ошибся. там не 30 и 60!!!
← →
CRLF (2012-04-11 21:07) [98]
> Построив срединный перпендикуляр
Как его построить без циркуля или эталонного прямого угла?
← →
Sha © (2012-04-11 21:09) [99]
> oldman © (11. 04.12 21:02) [96]
04.12 21:02) [96]
> Построив срединный перпендикуляр найти на нем точку,
> удаленную от концов отрезка на длину отрезка элементарно.
Без циркуля? Это задача на построение или где?
← →
oldman © (2012-04-11 21:19) [100]
> CRLF (11.04.12 21:07) [98]
> Как его построить без циркуля или эталонного прямого угла?
Учитывая [13] и написанное ниже в этом посте, можно. Используя поворот линейки с двумя рисками как циркуль. Вернее, как нахождение угла поворота.
> Sha © (11.04.12 21:09) [99]
> Без циркуля? Это задача на построение или где?
Без циркуля!
Задача на построение в домашних условиях.
Прикладывая первую риску линейки к концу основания, найти точку пересечения перпендикуляра с другой риской можно просто поворачивая линейку.
Да, похоже на циркуль. Но человеку было надо построить треугольник.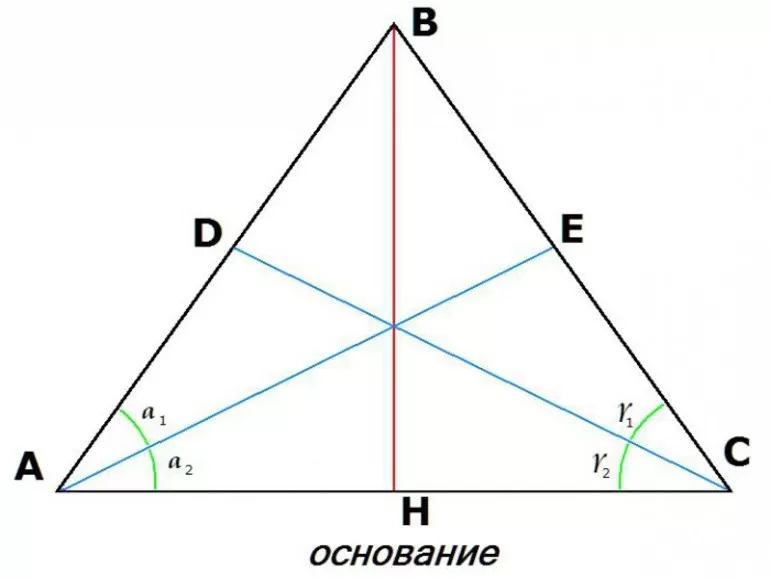
А с точки зрения геометрии нужен циркуль.
← →
Sha © (2012-04-11 21:25) [101]
Похоже, есть 2 решения задачи, кпждое при 1 дополнительном условии
1. при условии, что линейка имеет постоянную по длине ширину
2. при условии, что разрешено на любой прямой отмерять некий единичный отрезок
← →
Sha © (2012-04-11 21:28) [102]
> oldman © (11.04.12 21:19) [100]
> Задача на построение в домашних условиях.
немного беременной быть нельзя:
— или на построение
— или в домашних условиях
← →
oldman © (2012-04-11 21:29) [103]
Замечание по поводу.
Что же это за линейка такая, без делений? Это называется как-то по другому. ..
..
← →
oldman © (2012-04-11 21:32) [104]
> Sha © (11.04.12 21:28) [102]
Когда Пифагор сказал землемерам, что может доказать, что квадрат Г равен сумме квадратов К, землемеры сказали: «Мы знаем, что это так по опыту, а доказательство засунь себе…»
Немного беременной быть можно. ты никогда в саду ничего не строил, имея из измерительных инструментов карандаш, молоток и лопату?
← →
Sha © (2012-04-11 21:33) [105]
> oldman © (11.04.12 21:29) [103]
> Что же это за линейка такая, без делений?
В задачах на построение только такие используются
← →
Inovet © (2012-04-11 21:34) [106]
> [103] oldman © (11. 04.12 21:29)
04.12 21:29)
> Что же это за линейка такая, без делений? Это называется
> как-то по другому…
Линейка от линия, а деления уже для измерения длины линии.
← →
CRLF (2012-04-11 21:35) [107]
> 2. при условии, что разрешено на любой прямой отмерять некий
> единичный отрезок
Линейка и есть единичный отрезок
← →
Sha © (2012-04-11 21:37) [108]
> oldman © (11.04.12 21:32) [104]
> ты никогда в саду ничего не строил, имея из измерительных инструментов карандаш, молоток и лопату?
еще как строил и египетский треугольник активно юзал,
только, вроде, задача не для сада была сформулирована
← →
Sha © (2012-04-11 21:41) [109]
> CRLF (11.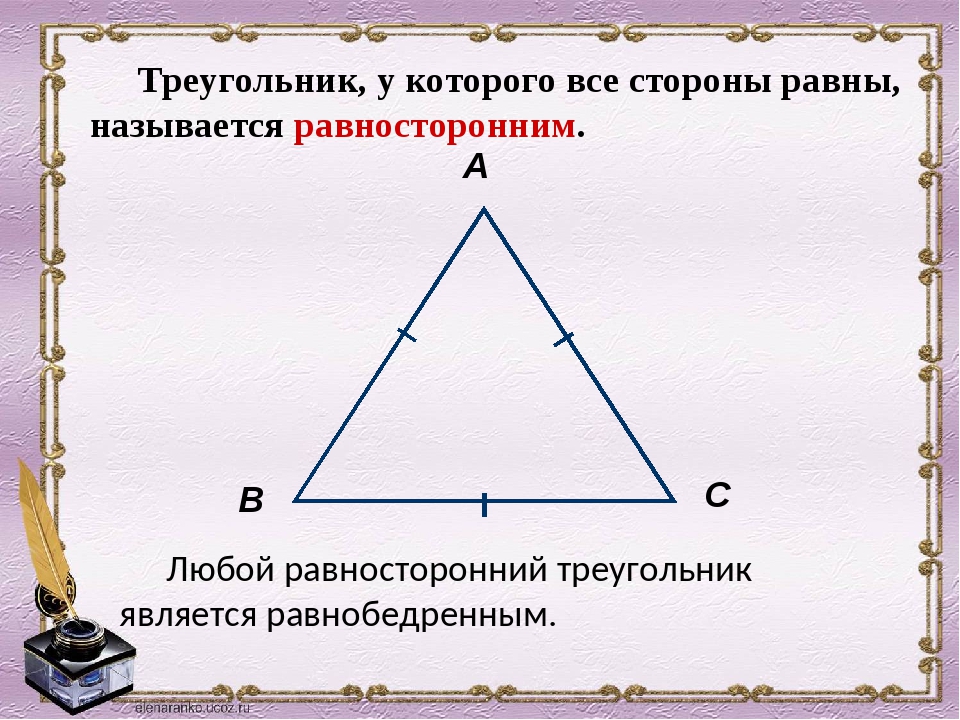 04.12 21:35) [107]
04.12 21:35) [107]
> Линейка и есть единичный отрезок
Не совсем так.
В задачах на построение для построения равных по длине отрезков
используется линейка и циркуль, как бы смешно это не звучало.
← →
CRLF (2012-04-11 21:43) [110]
Чего уж тут смешного… Но учитывая, что циркуля у нас нет, придётся линейку в качестве единичного отрезка использовать имхо.
← →
oldman © (2012-04-11 21:47) [111]
> Sha © (11.04.12 21:37) [108]
> только, вроде, задача не для сада была сформулирована
Построение равносторонего треугольника
boriskb © (11.04.12 10:27)
без транспортира и циркуля.
Прямо сейчас понадобилось. Ниего кроме карандаша и линейки без делений нет.
И правда не для сада. Для детсада.
Для детсада.
В общем, спасибо boriskb© за классную разминку для затекших мозгов. Попахивает разводом в стиле 1 апреля, да ладно.
← →
Sha © (2012-04-11 21:55) [112]
> oldman © (11.04.12 21:47) [111]
Никто задачу в такой формулировке и не решает.
Мне, например, интересно другое:
что надо добавить в условия задачи, чтобы она имела решение?
← →
oldman © (2012-04-11 21:58) [113]
> что надо добавить в условия задачи, чтобы она имела решение?
естественно, циркуль!
← →
MBo © (2012-04-11 22:08) [114]
Достаточно одной таблэтки, т.е. тонкой линейки.
Отмеряем полоску бумаги шириной точно в линейку — приложить, загнуть, оторвать.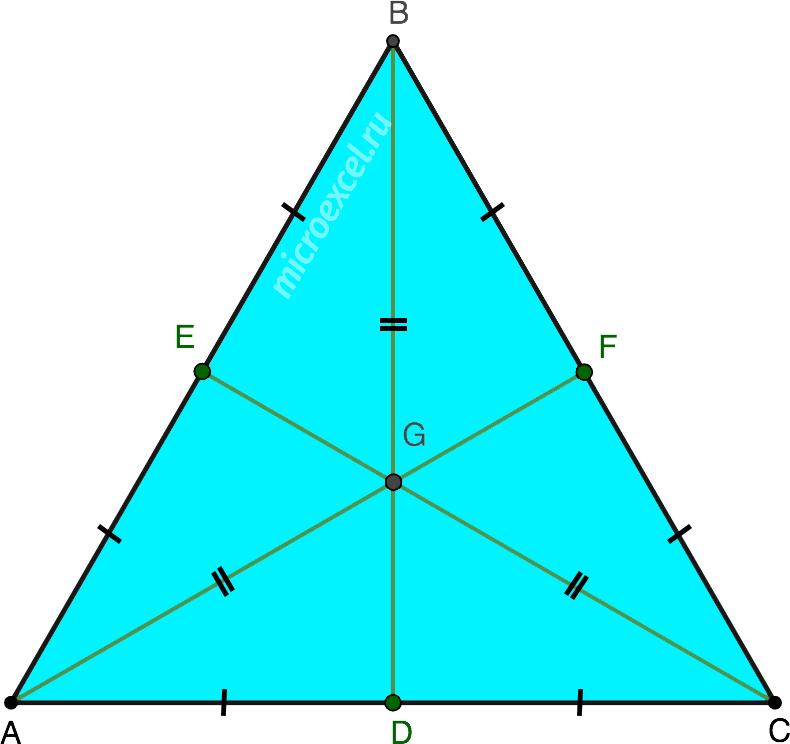 1/2.
1/2.
При помощи вспомогательного треугольника со сторонами,
перпендикулярными только что построенному,
строим треугольник с углом 30 градусов.
← →
Sha © (2012-04-11 22:23) [116]
> MBo © (11.04.12 22:08) [114]
> Ромбы 60-градусные.
а почему у меня параллелограммы не ромбические выходят? )
← →
Anatoly Podgoretsky © (2012-04-11 23:03) [117]
> Inovet (11.04.2012 21:34:46) [106]
Делилка — деление
← →
MBo © (2012-04-11 23:14) [118]
>Sha © (11.04.12 22:23) [116]
Хм… Пусть линейка горизонтальна, ширина линейки А. Половинка параллелограмма симметрична относительно вертикали (угол отражения) — треугольник равнобедренный. Высота треугольника А — как ширина линейки, высота к левому плечу тоже А — как ширина полоски, высота к правому плечу такая же ввиду равнобедренности. Разве три равные высоты не гарантируют, что треугольник равносторонний? Или я что-то упустил?
Высота треугольника А — как ширина линейки, высота к левому плечу тоже А — как ширина полоски, высота к правому плечу такая же ввиду равнобедренности. Разве три равные высоты не гарантируют, что треугольник равносторонний? Или я что-то упустил?
← →
Sha © (2012-04-11 23:35) [119]
> MBo © (11.04.12 23:14) [118]
В теории все верно.
Практическому воплощению могут помешать 3 вещи
1 материал может растягиваться и тогда угол будет гулять
2 материал не растягивается и из большего шага трудно будет
перейти к правильному
3 материал не растягивается и если шаг меньше нужного,
то небольшой зазор между одним краем ленты и линейкой
можно исправить только ценой зазора между витками.
Т.е. получается, что шаг надо угадать сразу.
← →
MBo © (2012-04-11 23:49) [120]
Ну на практике даже и с предварительной разметкой качественный флексагон второго порядка может не с первого раза получиться.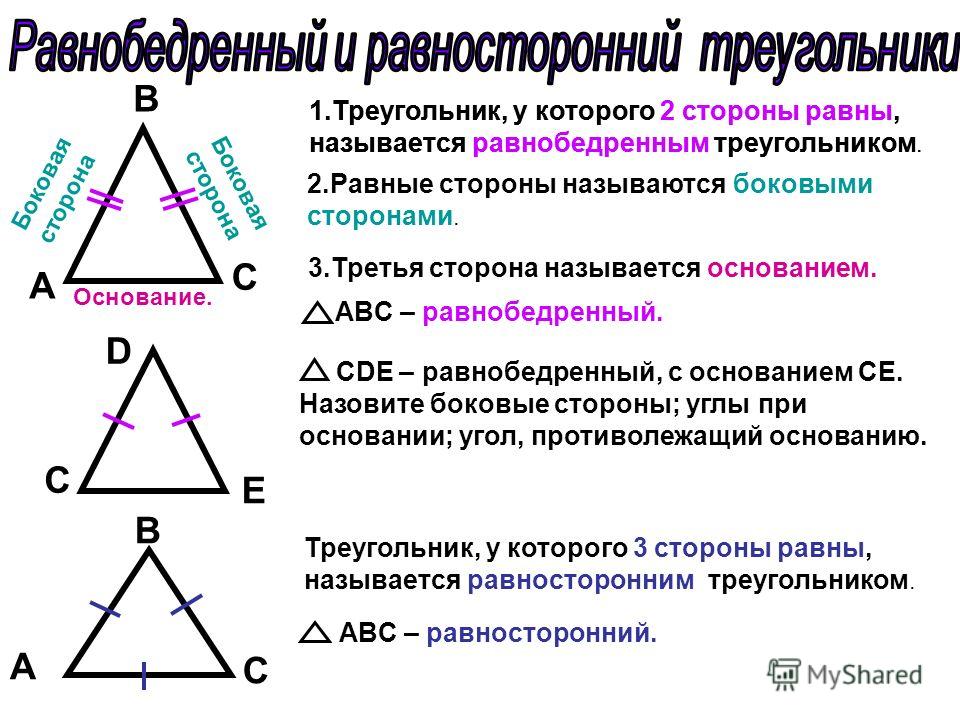
Всё-таки построение фигур с помощью искусственно ограниченных средств подразумевает условность идеальной точности.
← →
Inovet © (2012-04-11 23:50) [121]
> [119] Sha © (11.04.12 23:35)
> то небольшой зазор между одним краем ленты и линейкой
> можно исправить только ценой зазора между витками.
Так атрэзать, всё равно рэзать надо.
← →
Sha © (2012-04-12 00:03) [122]
> MBo © (11.04.12 23:49) [120]
> условность идеальной точности.
Тут даже не ясно с чего мы начинаем.
Примерно так: кладем линейку на бумажную полоску, загибаем концы
полоски навстречу друг другу, если стороны полоски не соприкасаются,
то повторяем процесс…
> Inovet © (11.04.12 23:50) [121]
просто много раз приходилось наматывать полоску не линейку или трубку,
не просто это сделать красиво
← →
MBo © (2012-04-12 05:32) [123]
Блин, у меня уже полтретьего ночи было, жена заинтересовалась рваньём бумажек, объяснял, что я не просто так, а детство вспомнил, гексагексафлексагон собираю 🙂
С накруткой на слесарную линейку вышло довольно коряво.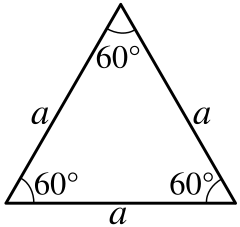 Выворачивается, но всё друг за друга зацепляется, бумага для принтера — быстро рвётся.
Выворачивается, но всё друг за друга зацепляется, бумага для принтера — быстро рвётся.
← →
MBo © (2012-04-12 05:39) [124]
>Тут даже не ясно с чего мы начинаем
Вроде это не вызвало особых затруднений — накидываем виток-два ленты на линейку, подтягиваем не до излома, чуть шевелим вправо-влево до совмещения.
В детстве я, насколько помню, использовал бумагу для слепых (по плотности похоже на перфокарту, но другой консистенции, не хрупкая), у нас была пачка для поделок. Не накручивал, конечно, а предварительную разметку делал. Задним концом иглы двойные швы нужной толщины проминал.
← →
oldman © (2012-04-12 08:05) [125]
> уже полтретьего ночи было, жена заинтересовалась рваньём
> бумажек
А могла и санитаров позвать )))
← →
Sha © (2012-04-12 08:44) [126]
>> что надо добавить в условия задачи, чтобы она имела решение?
> oldman © (11. 04.12 21:58) [113]
04.12 21:58) [113]
> естественно, циркуль!
По условию задачи у ТС нет его. Если есть циркуль, то линейка не нужна.
Решение [115] вполне строгое.
С одним дополнительным требованием, меньше требования наличия циркуля.
← →
oldman © (2012-04-12 08:52) [127]
> Линейка от линия, а деления уже для измерения длины линии.
Линия бесконечна, можно не измерять
← →
Inovet © (2012-04-12 08:55) [128]
> [127] oldman © (12.04.12 08:52)
> Линия бесконечна, можно не измерять
Отрезка линии, но ножниц тоже нет.
← →
han_malign (2012-04-12 09:48) [129]
Вот зараза ведь. 1/2:
1/2:
Нумеруем вершины квадрата по часовой стрелке 1, 2, 3, 4.
Продолжим сторону 1-2 на единичный отрезок, получим точку 5.
На отрезке 1-4 отложим единичный отрезок от точки 4, получим точку 6.
Проведем прямую через точки 6 и 3, отложим на ней единичные отрезки
от точки 3 в обе стороны, получим точки 7 и 8.
Треугольник 7-5-8 равносторонний.
Треугольник 3-5-8 прямоугольный, с углами 90, 30, 60 градусов
Как правильно рисовать треугольник
Как нарисовать треугольник? Этому учат в процессе изучения геометрии в школе. Чтобы задание было выполнено правильно, важно точно знать, какой треугольник необходимо изобразить: равносторонний, равнобедренный или же вписанный. Правилам начертания этих фигур будет посвящена данная статья.
Как рисовать треугольник с равными сторонами?
Как нарисовать треугольник, стороны у которого равны? Для этого можно воспользоваться одним из трех методов.
Такая фигура имеет три одинаковые по длине стороны, связанные тремя углами равной ширины. Это может быть сложным для рисования треугольника вручную. Поэтому можно использовать круглый объект для выделения углов.
Это может быть сложным для рисования треугольника вручную. Поэтому можно использовать круглый объект для выделения углов.
Варианты создания фигуры
Обязательно используйте линейку и один из представленных ниже способов:
- Применение циркуля: надо начертить ровную линию. Проведите карандаш вдоль прямого края бумаги. Этот сегмент линии образует одну из сторон. А это означает, что нужно будет чертить вторую и третью линии одинаковой длины, каждая из которых достигает точки под углом 60° от первой линии. Удостоверьтесь, что достаточно места для рисования всех трех сторон!
- Разделите сегмент циркулем. Вставьте карандаш и убедитесь, что он острый! Поместите точку циркуля на один конец сегмента и установите карандаш на другую. Опишите дугу. Не изменяйте установленную «ширину» инструмента от точки циркуля до точки карандаша. Нарисуйте вторую дугу, чтобы она пересекала первую дугу, которую уже нарисовали. Отметьте точку, в которой пересекаются две дуги. Это вершина (верхняя точка) треугольника.
 Он должен лежать в точном центре сегмента линии, который нарисовали. Теперь можете сделать две прямые линии, ведущие к этой точке: по одному от каждого конца «нижнего» сегмента линии. Закончите треугольник. Далее с помощью линейки надо нарисовать еще два сегмента прямой линии – это стороны в треугольнике. Подключите каждый конец исходного сегмента линии к точке, в которой пересекаются дуги. Чтобы закончить работу, сотрите дуги, которые нарисовали, так, чтобы остался только треугольник.
Он должен лежать в точном центре сегмента линии, который нарисовали. Теперь можете сделать две прямые линии, ведущие к этой точке: по одному от каждого конца «нижнего» сегмента линии. Закончите треугольник. Далее с помощью линейки надо нарисовать еще два сегмента прямой линии – это стороны в треугольнике. Подключите каждый конец исходного сегмента линии к точке, в которой пересекаются дуги. Чтобы закончить работу, сотрите дуги, которые нарисовали, так, чтобы остался только треугольник. - Использование объекта с круглой базой: этот совет подойдет для построения дуги. Предложенный метод по сути такой же, как с использованием циркуля.
Указанные советы помогут выяснить, как нарисовать равносторонний треугольник.
Рекомендации по построению равнобедренного треугольника
Равнобедренный треугольник представляет собой фигуру с двумя равными сторонами и двумя равными углами. Если знаете длину, основание и высоту стороны, это можно сделать только с линейкой и циркулем (или просто циркулем, если заданы размеры).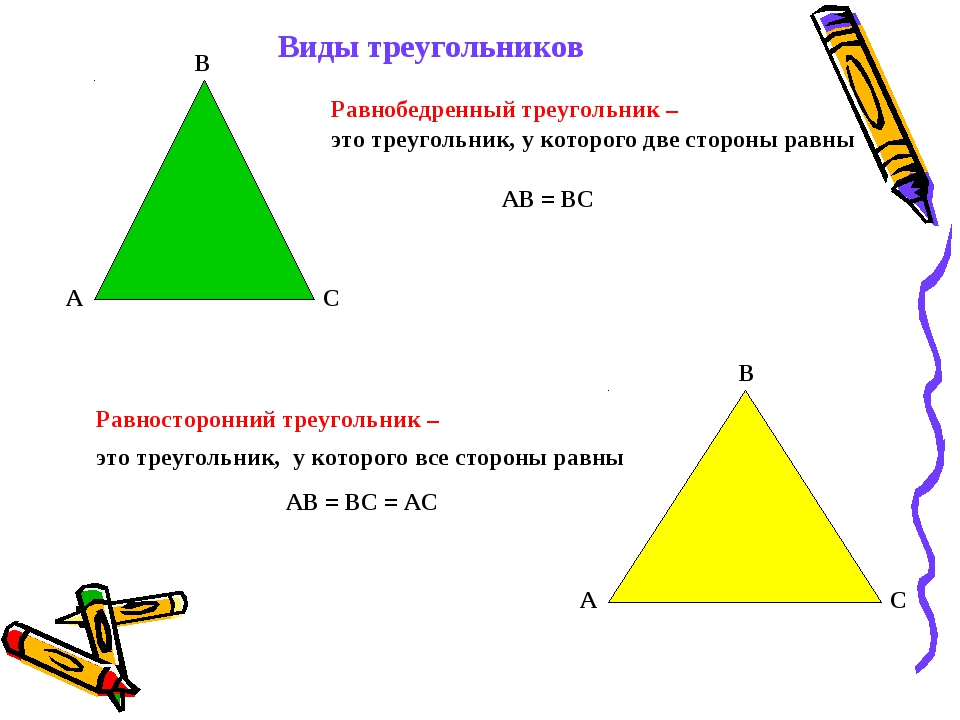
Как нарисовать равнобедренный треугольник:
- Учитывая все боковые длины. Чтобы использовать этот метод, важно знать длину основания треугольника и длину двух равных сторон.
- Учитывая две равные стороны и угол между ними. Чтобы использовать этот метод, нужно знать длину двух равных сторон и измерение угла между этими двумя сторонами.
- Учитывая базовые и смежные углы – необходимо знать длину базы, градусы двух углов, смежных с основанием. Помните, что два угла, смежные с основанием равнобедренного треугольника, будут равны.
- Основа и высота. Нужно знать длину основания треугольника, а также высоту этой геометрической фигуры.
Вписанный треугольник
Как нарисовать вписанный треугольник? Выберите круглый объект. Используйте предмет с круглым основанием. Выбор компакт-диска станет хорошим вариантом. Но можно взять и другой объект нужного размера. Для этого метода свойственно, что длина каждой стороны равносторонней геометрической фигуры с тремя углами будет равна размерам радиуса (половине диаметра) круга.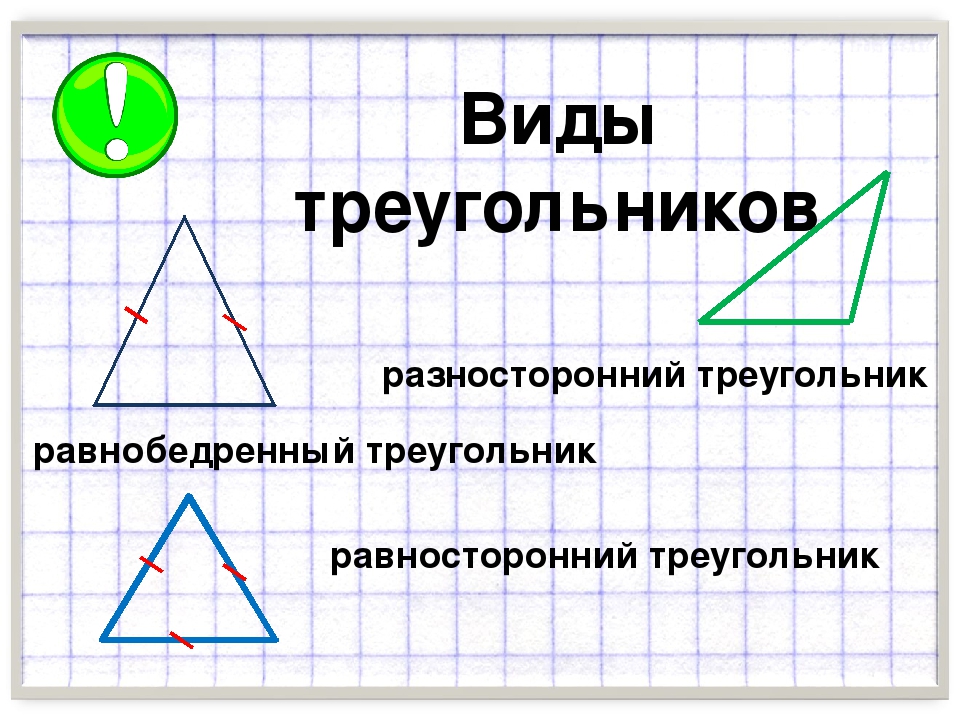
Как нарисовать треугольник, если используете компакт-диск? Представьте себе равносторонний треугольник, который вписывается в верхнюю правую часть компакт-диска. Надо начертить первую из сторон. Радиус круглого объекта – расстояние на полпути до получения желаемого результата. Удостоверьтесь, что линии нарисованы ровно.
С помощью линейки просто выполните измерения диаметра объекта и нарисуйте линию на половину длины. Если ее нет, поместите круглый объект на бумагу, затем тщательно проведите по окружности карандашом. Удалите объект – должен быть идеальный круг. Используйте прямой край, чтобы нарисовать линию через точный центр круга: точку, которая полностью равноудалена от любой точки по окружности круга.
Используйте круглый объект для создания дуги. Поместите объект по отрезку линии, с краем круга, расположенным на одном конце линии. Для обеспечения точности убедитесь, что линия проходит четко через центр круга. Используйте карандаш, чтобы начертить дугу – это четверть пути по окружности.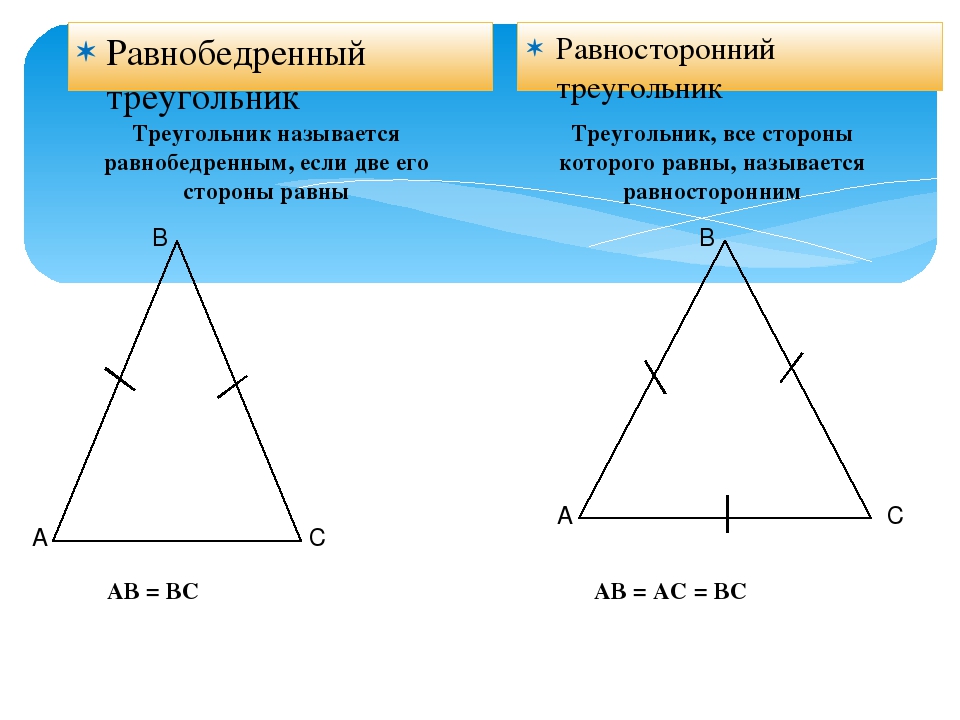
Начертите еще одну дугу. Теперь сдвиньте круглый объект так, чтобы край касался другого конца сегмента линии.
Подведем итоги
В статье были предоставлены рекомендации, как нарисовать треугольник равносторонний, равнобедренный и вписанный в окружность.
Знание — сила. Познавательная информация
Как нарисовать равносторонний треугольник
Как нарисовать равносторонний треугольник, используя только линейку и карандаш? Этот способ позволяет быстро сделать рисунок правильного или равнобедренного треугольника.
Как нарисовать равнобедренный треугольник
Рисунок начинаем с основания. Длину основания подбираем такой, чтобы ее удобно было делить пополам (берем четное количество клеточек). Вершину треугольника отмечаем ровно над серединой основания:
Если нужен равнобедренный треугольник, у которого боковая сторона больше основания, вершину ставим повыше:
Если требуется треугольник, основание которого больше боковой стороны, то вершину отмечаем ниже:
Как нарисовать равносторонний треугольник
От конца основания откладываем отрезок равной ему длины так, чтобы второй конец этого отрезка расположился ровно над серединой основания. Соединяем вершину треугольника с другим концом основания:
Соединяем вершину треугольника с другим концом основания:
Если в задаче о равнобедренном треугольнике речь идет о высоте, биссектрисе и медиане, проведенным к основанию, достаточно соединить вершину треугольника с отмеченной серединой основания:
В создании этой статьи участвовала наша опытная команда редакторов и исследователей, которые проверили ее на точность и полноту.
Количество источников, использованных в этой статье: 6. Вы найдете их список внизу страницы.
Команда контент-менеджеров wikiHow тщательно следит за работой редакторов, чтобы гарантировать соответствие каждой статьи нашим высоким стандартам качества.
В равностороннем треугольнике все стороны и углы равны. Вручную нарисовать идеальный равносторонний треугольник довольно сложно. Но вы можете воспользоваться транспортиром, чтобы точно отложить углы. Также используйте линейку, чтобы проводить абсолютно прямые линии. Эта статья расскажет вам, как нарисовать равносторонний треугольник.
Как нарисовать треугольник в Indesign — Вокруг-Дом
Создание геометрических форм и дизайнов может быть как сложным, так и одновременно простым, в зависимости от того, какое приложение вы выберете. Использование Adobe InDesign делает его простым и красноречивым как в создании, так и в цвете. Рисование треугольника или серии треугольников — это одна из тех задач, которая может вас как развлечь, так и озадачить, опять же в зависимости от того, какой тип треугольников, таких как острые треугольники, тупые треугольники, равнобедренные треугольники и разносторонние треугольники или равносторонние. Это удобно для студентов, изучающих геометрию или тригонометрию, которым необходимо подготовить экзамен или курсовую работу, а также для тех, кто хочет экспериментировать с дизайном логотипов или баннеров. В любом случае, этот метод выполняется быстро и просто.
Быстрое создание треугольников с помощью четырех наборов в Adobe InDesign.
Шаг 1
Откройте Adobe InDesign и создайте новый документ, удерживая клавишу «Ctrl» и одновременно нажимая «N» (или нажмите «Файл», «Новый» и «Документ»). Откроется окно «Новый документ». Выберите параметры страницы, которые вы предпочитаете, такие как ширина и высота. Параметр Количество страниц должен быть установлен на «1». На подпанели «Столбцы» оставьте в раскрывающемся поле «Число» значение «1» и «Ориентация» в «Портрет» (первый значок после «Ширина»). Нажмите «ОК», и появится новое пустое окно документа.
Шаг 2
Выберите «Rectangle Tool» в меню «Tools» или нажмите букву «M» на клавиатуре. Если меню «Инструменты» не отображается, перейдите в главное меню «Windows» и выберите пункт «Инструменты». С помощью мыши нарисуйте прямоугольник шириной 3 дюйма и высотой 2 дюйма.
Шаг 3
Выберите «Pen Tool» из меню «Tools» или нажмите «P» на клавиатуре. Нажмите один раз прямо в верхнем левом углу вашего прямоугольника. Прямоугольный треугольник появляется. Чтобы создать равносторонний треугольник, просто выберите «Инструмент многоугольника» в меню «Инструменты», дважды щелкните его значок и введите число «3» в поле ввода текста «Число сторон» в «Многоугольнике». Настройки ». Удерживая нажатой клавишу Shift, перетаскивая курсор, создайте равносторонний треугольник со всеми равными сторонами.
Чтобы создать равносторонний треугольник, просто выберите «Инструмент многоугольника» в меню «Инструменты», дважды щелкните его значок и введите число «3» в поле ввода текста «Число сторон» в «Многоугольнике». Настройки ». Удерживая нажатой клавишу Shift, перетаскивая курсор, создайте равносторонний треугольник со всеми равными сторонами.
Шаг 4
Выберите инструмент «Заливка» в меню «Инструменты» или нажмите «X» на клавиатуре. Дважды щелкните заливку и выберите цвет.
Как построить (нарисовать) равносторонний треугольник с циркулем и линейкой или линейкой
Как построить (нарисовать) равносторонний треугольник с циркулем и линейкой или линейкой — Math Open Reference На этой странице показано, как построить
равносторонний треугольник
с циркулем и линейкой или линейкой. Равносторонний треугольник — это треугольник со всеми тремя сторонами одинаковой длины. Это начинается с заданного
отрезок
которая является длиной каждой стороны желаемого равностороннего треугольника.
Это работает, потому что ширина компаса не меняется между рисованием каждой стороны, гарантируя, что все они конгруэнтный (такой же длины). Это похоже на Конструкция под углом 60 градусов, потому что внутренние углы равностороннего треугольника все 60 градусов.
Пошаговые инструкции для печати
Вышеупомянутая анимация доступна как распечатываемый лист с пошаговыми инструкциями, который можно использовать для изготовления раздаточных материалов или когда компьютер недоступен.
Проба
Изображение ниже — это окончательный рисунок выше.
| Аргумент | Причина | |
|---|---|---|
| 1 | PQ, PR и QR — все конгруэнтно AB, поэтому все они имеют одинаковую длину | Ширина компаса, установленная от AB, чтобы нарисовать их все |
| 2 | Треугольник RPQ — равносторонний треугольник с заданной длиной стороны AB. | Все три стороны совпадают.См. Определение равностороннего треугольника. |
— Q.E.D
Попробуйте сами
Щелкните здесь, чтобы распечатать лист с двумя проблемами, которые можно попробовать. Когда вы перейдете на страницу, используйте команду печати браузера, чтобы распечатать столько, сколько хотите. Печатная продукция не защищена авторскими правами.Другие конструкции, страницы на сайте
линий
Уголки
Треугольники
Правые треугольники
Центры треугольника
Окружности, дуги и эллипсы
Полигоны
Неевклидовы конструкции
(C) Открытый справочник по математике, 2011 г.
Все права защищены.
Как построить (нарисовать) равносторонний треугольник
Содержание
- Построение равностороннего треугольника
- Как нарисовать равносторонний треугольник с помощью циркуля
- Как построить равносторонний треугольник, вписанный в круг
- Постройте равносторонний треугольник, вписанный в круг Доказательство
- Как нарисовать равносторонний треугольник
- Нарисуйте доказательство равностороннего треугольника
Построение равностороннего треугольника
Равносторонние треугольники легко построить с помощью циркуля, линейки и карандаша, поскольку внутренние углы 60 ° можно найти, используя только радиус окружности вокруг треугольника (описанной окружности).
Предположим, вам дана длина одной стороны требуемого равностороннего треугольника. Вы должны построить две одинаковые стороны, которые каким-то образом образуют три внутренних угла в 60 °.
Вот сегмент CE:
[вставить чертеж линейного сегмента CE]
- Поместите иглу циркуля для рисования в точку C, затем отрегулируйте рычаг карандаша так, чтобы он касался точки E.
- Поверните дугу вверх, образуя легкую строительную линию.
- Не регулируя компас, переместите стрелку в точку E.
- Поверните дугу вверх от точки C, образуя еще одну легкую строительную линию. [вставить чертеж, показывающий дуги поворота компаса для этих точек]
- В месте пересечения двух дуг находится точка третьей вершины равностороннего треугольника. Назовите это точкой А. Используйте линейку, чтобы соединить точки A и C, точки A и E. У вас есть равносторонний треугольник ACE!
Как нарисовать равносторонний треугольник с помощью циркуля
Точки C и E — центры конгруэнтных окружностей с радиусами, равными CE. Длины AC и CE являются радиусами окружности C. Длины AE и CE также являются радиусами окружности E. По транзитивному свойству:
Длины AC и CE являются радиусами окружности C. Длины AE и CE также являются радиусами окружности E. По транзитивному свойству:
Три совпадающие стороны означают, что треугольник должен быть равносторонним.
Как построить равносторонний треугольник, вписанный в круг
Предположим, вам дан круг, а не сторона. Предположим, вас попросили построить внутри этого круга равносторонний треугольник:
[вставить чертеж круга S]
Вы знаете только центральную точку, точку S, но исходя из нее, вы можете скопировать радиус (расстояние от центра, точки S, до самой окружности).
- Настройте циркуль для рисования, чтобы установить радиус.
- Сделайте отметку на круге в любом месте. Установите игольную консоль в эту точку.
- Не меняя компаса, поверните две небольшие дуги выше и ниже точки окружности, чтобы дуги пересекали окружность.
- Переместите стрелку циркуля для рисования на одну из этих дуг.

- Снова поверните циркуль, чтобы образовать небольшую дугу на окружности.
- Повторите это еще два раза, чтобы создать шесть точек на окружности (исходная точка плюс шесть маленьких дуг, пересекающих ее).
- Используйте линейку, чтобы соединить все остальные точки на окружности. То есть нарисуйте отрезки линии, скажем, от вашей первой точки на окружности до третьей точки, и еще один отрезок линии от третьей точки до пятой точки. Еще одна линия, от пятой точки обратно к исходной точке, и вот она. Вы вписали в круг равносторонний треугольник!
[вставьте рисунок, показывающий это, или оживите конструкцию трех сторон]
Постройте равносторонний треугольник, вписанный в круг Доказательство
Представьте, что этот равносторонний треугольник состоит из трех меньших равнобедренных треугольников, имеющих точку S как общую вершину.Это означает, что каждый из трех треугольников имеет центральный угол (в точке S) 120 °, полученный путем деления полных 360 ° круга на 3 (количество центральных углов).
Каждый из этих меньших равнобедренных треугольников имеет две вершины на окружности, и каждый из них имеет одинаковые стороны с другими треугольниками. Это делает две из трех сторон треугольников конгруэнтными.
Если две стороны равнобедренного треугольника совпадают, то третья сторона также определяется теоремой стороны-угла-стороны.
Как нарисовать равносторонний треугольник
Этот метод позволяет вам контролировать размер вашего равностороннего треугольника, потому что вы строите его с нуля.
- Настройте циркуль для рисования, чтобы нарисовать круг; назовем его Circle E.
- Используйте линейку, чтобы установить диаметр (отрезок прямой через центральную точку E с конечными точками на самой окружности). Обозначьте конечные точки Точки B и R. [вставьте рисунок или анимацию, показывающую эти шаги]
- Не трогая компас, опустите стрелку в точку R и сделайте еще один полный круг. Там, где новый круг пересекает старый в двух точках выше и ниже диаметра BR, обозначьте эти точки A и S.

- Соедините точку B с A, точку A с S и точку A с B. Это МЕДВЕДЬ замечает, что вы построили равносторонний треугольник!
Нарисуйте доказательство равностороннего треугольника
Вы можете доказать, что треугольник равносторонний, используя свои знания о том, что любой угол, вписанный в полукруг, является прямым углом, что дает вам прямые углы ∠BAR и ∠BSR, что создает два конгруэнтных прямоугольных треугольника △ BAR и △ BSR, имеющих общую гипотенузу, BR .
Таким образом, AB ≅ BS (соответствующие стороны конгруэнтных треугольников), что означает, что △ BAS равнобедренный.Это делает BAS и ∠BSA конгруэнтными (углы основания равнобедренного треугольника совпадают). Мы знаем, что ∠ABS составляет 60 °, оставляя два оставшихся угла в сумме до 120 °, так что каждый из них составляет 60 °. Все три внутренних угла △ BAS равны, что делает его равносторонним треугольником.
Следующий урок:
Как построить биссектрису угла
Как найти высоту равностороннего треугольника
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает
или больше ваших авторских прав, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
то
информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении может быть направлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как так как ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатов), если вы искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к адвокату.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись владельца авторских прав или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного расположения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить преподавателям Varsity Tutors найти и точно идентифицировать этот контент; например нам требуется
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении прав, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении прав, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Планшет Геометра
ОПРЕДЕЛЕНИЯ:
- Key означает Key Curriculum Press, Inc., 1150 65th Street, Emeryville, CA 94608, США.
 Программное обеспечение
Программное обеспечение - означает компьютерную программу Geometer Sketchpad версии 5, полученную вами из любого источника.
- Документация означает печатные или электронные справочные материалы и другие печатные или электронные материалы, сопровождающие Программное обеспечение.
- Продукт означает Программное обеспечение и Документацию.
- Использование означает установку, использование, доступ, отображение, запуск или иное взаимодействие с Продуктом. Лицензия
- означает Однопользовательскую лицензию, Лицензию для учебного заведения / учреждения, Студенческую лицензию, Студенческую лицензию на 1 год или любую другую лицензию, которая время от времени определяется Ключом.
- Лицензиат означает физическое или юридическое лицо, получившее Лицензию на законных основаниях и имеющее законную возможность Использовать Продукт в соответствии с условиями этой Лицензии, или любое физическое лицо, которое использует Продукт в соответствии с Лицензией с Ограниченным Предварительным просмотром.

- Название лицензии означает имя, присвоенное Лицензии Лицензиатом или Ключом с целью идентификации Лицензии, обычно это название школы или учреждения или имя отдельного Лицензиата, если Лицензиат не выберет другое идентифицирующее имя.
- Администратор лицензии означает лицо, назначенное Лицензиатом для администрирования Лицензии от имени Лицензиата. Код авторизации
- означает уникальный код, предоставленный Лицензиату вместе с Лицензией и позволяющий использовать Программное обеспечение в соответствии с условиями Лицензии.
- Режим предварительного просмотра означает ограниченное и ограниченное по времени состояние Программного обеспечения до регистрации Программного обеспечения с помощью кода авторизации, необходимого для использования по лицензии.
- Limited Preview License означает лицензию на Использование Программного обеспечения в режиме предварительного просмотра.
- Подтверждение заказа или Подтверждение лицензии означает распечатанную или электронную копию счета-фактуры или записи подтверждения счета, полученную Лицензиатом от Key или от одного из авторизованных образовательных дилеров или дистрибьюторов Key, или любое другое печатное или электронное подтверждение Лицензии, полученное Лицензиатом от Ключ или отображается Программным обеспечением при регистрации.

- Срок действия лицензии означает период времени, связанный с Лицензией, если таковая имеется.
ПРЕДОСТАВЛЕНИЕ ЛИЦЕНЗИИ
Key предоставляет Лицензиату ограниченную неисключительную лицензию на Использование Продукта на одном или нескольких компьютерах Лицензиата в соответствии с условиями, изложенными ниже. Если будет установлено, что Лицензиат нарушил эти условия использования, Ключ может аннулировать Лицензию Лицензиата и расторгнуть настоящее Соглашение. Все остальные права прямо принадлежат Key.
- Однопользовательские лицензии: Лицензиат с однопользовательской лицензией может использовать Продукт максимум на трех персональных компьютерах при условии, что одновременно используется только одна копия Продукта.
- Лицензии для учебного заведения / учреждения: Лицензиат с лицензией для учебного заведения / учреждения может использовать Программное обеспечение или разрешить Использование Программного обеспечения на количестве физических или виртуальных компьютеров, как указано в Подтверждении заказа или Подтверждении лицензии.
 Использование инструктором на персональном или домашнем компьютере считается одним из случаев использования в соответствии с Школьной / институциональной лицензией.
Использование инструктором на персональном или домашнем компьютере считается одним из случаев использования в соответствии с Школьной / институциональной лицензией. - Студенческие лицензии: Студенческий лицензиат со студенческой лицензией может использовать Продукт максимум на трех личных или семейных компьютерах при условии, что одновременно используется только одна копия Продукта.Учащийся, получивший Продукт и / или код авторизации от школы или учебного заведения для использования Программного обеспечения на личном или семейном компьютере, считается Лицензиатом и должен соблюдать условия Студенческой лицензии. Пользователь Студенческой лицензии должен быть студентом образовательного учреждения на момент покупки или получения лицензии.
Срок действия лицензии: Если Лицензия имеет Срок действия лицензии или если Подтверждение заказа или Подтверждение лицензии указывает Срок действия лицензии, Лицензиат может использовать Программное обеспечение в течение указанного Срока действия лицензии, начинающегося в день выдачи лицензии (дата, на которую Код авторизации был сгенерирован). Использование Программного обеспечения вне Срока действия лицензии или вмешательство в программное обеспечение с целью его использования вне Срока действия лицензии является нарушением настоящего Соглашения.
Использование Программного обеспечения вне Срока действия лицензии или вмешательство в программное обеспечение с целью его использования вне Срока действия лицензии является нарушением настоящего Соглашения.
ПРЕДОСТАВЛЕНИЕ ОГРАНИЧЕННОЙ ЛИЦЕНЗИИ НА ПРЕДВАРИТЕЛЬНЫЙ ПРОСМОТР: Key предоставляет каждому человеку, устанавливающему Продукт на компьютер, ограниченную неисключительную лицензию на Использование Продукта в режиме предварительного просмотра на компьютере, на котором он установлен.
ПРОВЕРКА ЛИЦЕНЗИИ: Лицензиат должен зарегистрировать Продукт на компьютере с действующим именем лицензии и кодом авторизации, чтобы разблокировать полный набор функций Продукта.При запуске Продукт может связываться через Интернет с сервером лицензий, обслуживаемым Key, с целью проверки лицензии. Это сообщение содержит название лицензии и код авторизации, связанные с лицензией, а также соответствующую информацию о компьютерах, на которых зарегистрирована и используется лицензия. Чтобы помочь администраторам лицензий в устранении проблем с регистрацией, если они возникнут, в случае лицензий для учебных заведений / учебных заведений и специальных лицензий, обмен данными включает адрес управления доступом к среде (MAC) каждого компьютера, другую информацию, относящуюся к компьютеру, и адрес Интернет-протокола (IP).Чтобы защитить конфиденциальность лицензиатов с однопользовательской лицензией или студенческой лицензией, вся информация, идентифицирующая конкретный компьютер, на котором используется Sketchpad, шифруется таким образом, чтобы создать уникальную подпись, обеспечивая при этом конфиденциальность. Key будет использовать эту информацию только для проверки действительности Лицензии, помощи Лицензиатам в решении технических проблем и для улучшения Продукта. Эта информация не будет передана сторонам, кроме назначенного Лицензиатом Администратора лицензий и лиц, отвечающих за обслуживание Продукта, а также проверку и администрирование Лицензий на продукт.
Чтобы помочь администраторам лицензий в устранении проблем с регистрацией, если они возникнут, в случае лицензий для учебных заведений / учебных заведений и специальных лицензий, обмен данными включает адрес управления доступом к среде (MAC) каждого компьютера, другую информацию, относящуюся к компьютеру, и адрес Интернет-протокола (IP).Чтобы защитить конфиденциальность лицензиатов с однопользовательской лицензией или студенческой лицензией, вся информация, идентифицирующая конкретный компьютер, на котором используется Sketchpad, шифруется таким образом, чтобы создать уникальную подпись, обеспечивая при этом конфиденциальность. Key будет использовать эту информацию только для проверки действительности Лицензии, помощи Лицензиатам в решении технических проблем и для улучшения Продукта. Эта информация не будет передана сторонам, кроме назначенного Лицензиатом Администратора лицензий и лиц, отвечающих за обслуживание Продукта, а также проверку и администрирование Лицензий на продукт.
ОГРАНИЧЕНИЯ НА ИСПОЛЬЗОВАНИЕ: Продукт лицензируется как единый продукт, и его составные части не могут быть разделены для использования на большем количестве компьютеров, чем указано в Лицензии и / или как указано в Подтверждении заказа или Подтверждении лицензии. Права, предоставленные по настоящему Соглашению, являются личными для Лицензиата. Ни Продукт, ни права, предоставленные по настоящему Соглашению, не могут быть перепроданы, сублицензированы, назначены, сданы в аренду, сданы в аренду или сданы в аренду за плату или иным образом, за исключением предварительно утвержденных Ключевыми реселлерами или в соответствии с условиями настоящего Соглашения.Название лицензии и код авторизации, связанные с лицензией, не могут публиковаться для публичного доступа и использования, включая, помимо прочего, веб-сайты в Интернете. Продукт не должен использоваться в рамках соглашения о таймшеринге или бюро обслуживания. Продукт нельзя модифицировать, реконструировать, декомпилировать или разбирать. Обозначения прав собственности, содержащиеся на Продукте и внутри него, нельзя удалять или скрывать.
Права, предоставленные по настоящему Соглашению, являются личными для Лицензиата. Ни Продукт, ни права, предоставленные по настоящему Соглашению, не могут быть перепроданы, сублицензированы, назначены, сданы в аренду, сданы в аренду или сданы в аренду за плату или иным образом, за исключением предварительно утвержденных Ключевыми реселлерами или в соответствии с условиями настоящего Соглашения.Название лицензии и код авторизации, связанные с лицензией, не могут публиковаться для публичного доступа и использования, включая, помимо прочего, веб-сайты в Интернете. Продукт не должен использоваться в рамках соглашения о таймшеринге или бюро обслуживания. Продукт нельзя модифицировать, реконструировать, декомпилировать или разбирать. Обозначения прав собственности, содержащиеся на Продукте и внутри него, нельзя удалять или скрывать.
ПЕРЕДАЧА ИСПОЛЬЗОВАНИЯ ШКОЛАМИ: школы или образовательные учреждения, которые приобретают либо лицензию школы / учреждения, либо студенческую лицензию на домашнее использование, могут передать или продать сублицензию на такой Продукт для использования инструктором или студентом, зачисленным в школу или образовательное учреждение. Для целей данной Лицензии такой преподаватель или студент считается Лицензиатом при соблюдении всех условий использования Продукта в качестве первоначального Лицензиата.
Для целей данной Лицензии такой преподаватель или студент считается Лицензиатом при соблюдении всех условий использования Продукта в качестве первоначального Лицензиата.
ПРЕДСТАВЛЕНИЯ ЛИЦЕНЗИАТА: Лицензиат заявляет, что он получил все необходимое согласие и полномочия для импорта и использования Продукта в юрисдикции, в которой Лицензиат намеревается использовать Продукт.
ПРАВА НА ИНТЕЛЛЕКТУАЛЬНУЮ СОБСТВЕННОСТЬ: Ключевые и / или правообладатели, указанные в Продукте, являются владельцами и сохраняют за собой право собственности на все права собственности и интеллектуальной собственности на Продукт, включая авторские права, коммерческую тайну, товарные знаки и ноу-хау, защищенные как законами США и Канады об авторском праве, а также положениями международных договоров.Копирование Продукта, кроме случаев, явно указанных в данном документе, представляет собой нарушение прав правообладателей на интеллектуальную собственность. Лицензиат признает вышесказанное и соглашается с тем, что он не имеет никаких прав, титулов или интересов в отношении Продукта, за исключением случаев, специально оговоренных в настоящем документе, и что Лицензиат не имеет прав на какие-либо товарные знаки, определенные как принадлежащие правообладателям.
: Key может предоставлять Лицензиату услуги поддержки, связанные с Продуктом («Услуги поддержки»).Использование Служб поддержки регулируется политиками и программами Key, описанными в справочном руководстве по программному обеспечению пользователя, в онлайн-документации и / или в других материалах, предоставленных Key. Любое дополнительное программное обеспечение, предоставленное Лицензиату в рамках Услуг поддержки, считается частью Продукта и регулируется положениями настоящего Соглашения. В случае, если Лицензиат предоставляет Key техническую информацию в связи с предоставлением Услуг поддержки, Key может использовать эту информацию в своих деловых целях, включая поддержку и разработку продукта.
ПРЕКРАЩЕНИЕ: Без ущерба для каких-либо других прав, Key может прекратить действие настоящего Соглашения, если Лицензиат не соблюдает его положения и условия. В таком случае Лицензиат соглашается удалить все копии Продукта со всех компьютеров, на которых они были установлены, и уничтожить все такие копии.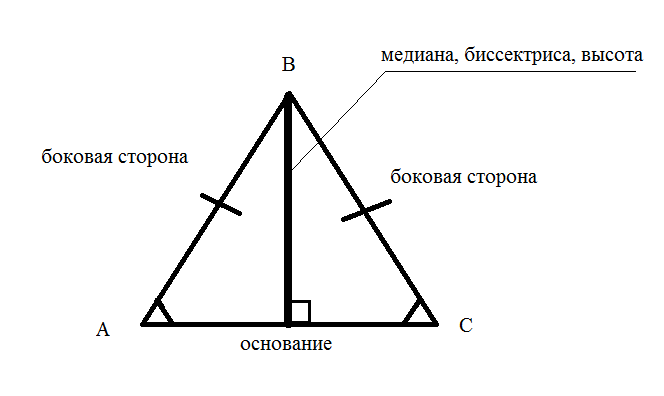
ОГРАНИЧЕННАЯ ГАРАНТИЯ: ПРОДУКТ ПРЕДОСТАВЛЯЕТСЯ «КАК ЕСТЬ», БЕЗ КАКИХ-ЛИБО ГАРАНТИЙ, ЯВНЫХ ИЛИ ПОДРАЗУМЕВАЕМЫХ, ВКЛЮЧАЯ, НО НЕ ОГРАНИЧИВАЯСЬ, ПОДРАЗУМЕВАЕМЫЕ ГАРАНТИИ ТОВАРНОЙ ЦЕННОСТИ, ПРИГОДНОСТИ ДЛЯ КОНКРЕТНОЙ ЦЕЛИ, НАЗВАНИЯ, НАЗВАНИЯ И ОТНОСИТЕЛЬНО НАИМЕНОВАНИЯ. ПРОДУКТ И ПРЕДОСТАВЛЕНИЕ ИЛИ ОТСУТСТВИЕ УСЛУГ ПОДДЕРЖКИ.В НЕКОТОРЫХ ЮРИСДИКЦИЯХ НЕ ДОПУСКАЕТСЯ ИСКЛЮЧЕНИЕ ПОДРАЗУМЕВАЕМЫХ ГАРАНТИЙ, ПОЭТОМУ ВЫШЕУКАЗАННОЕ ИСКЛЮЧЕНИЕ МОЖЕТ НЕ ОТНОСИТЬСЯ К ВАМ.
ОГРАНИЧЕНИЕ ОТВЕТСТВЕННОСТИ: В СЛУЧАЕ ИСКЛЮЧЕНИЯ ПОДРАЗУМЕВАЕМЫХ ГАРАНТИЙ НЕ ПРИМЕНЯЕТСЯ И В СЛУЧАЕ НАРУШЕНИЯ ТАКИХ ГАРАНТИЙ КЛЮЧЕВЫЕ И ЕГО ДИЛЕРЫ И ДИСТРИБЬЮТОРЫ ДЕЙСТВУЮТ ВСЯ ОТВЕТСТВЕННОСТЬ И ИСКЛЮЧИТЕЛЬНОЕ ОБЕСПЕЧЕНИЕ ЗАЩИТЫ A) ВОЗВРАТ УПЛАЧЕННОЙ ЦЕНЫ, ЕСЛИ ЕСТЬ ЕСТЬ; ИЛИ (B) РЕМОНТ ИЛИ ЗАМЕНА ПРОДУКТА, ВОЗВРАЩЕННОГО КЛЮЧОМ С ЧЕТОМ ПОКУПКИ.В МАКСИМАЛЬНОЙ СТЕПЕНИ, РАЗРЕШЕННОЙ ДЕЙСТВУЮЩИМ ЗАКОНОДАТЕЛЬСТВОМ, НИ ПРИ КАКИХ ОБСТОЯТЕЛЬСТВАХ KEY ИЛИ ЕГО ПОСТАВЩИКИ НЕ НЕСЕТ ОТВЕТСТВЕННОСТИ ЗА ЛЮБЫЕ ОСОБЫЕ, СЛУЧАЙНЫЕ, КОСВЕННЫЕ ИЛИ КОСВЕННЫЕ УБЫТКИ (ВКЛЮЧАЯ, БЕЗ ОГРАНИЧЕНИЙ, УБЫТКИ ОТ ПОТЕРИ ДЕЛОВОЙ ИНФОРМАЦИИ, ПОТЕРЯ ДЕЛОВОЙ ИНФОРМАЦИИ ИЛИ ЛЮБЫЕ ДРУГИЕ УБЫТКИ), ВЫЗВАННЫЕ ИСПОЛЬЗОВАНИЕМ ИЛИ НЕВОЗМОЖНОСТЬЮ ИСПОЛЬЗОВАТЬ ПРОДУКТ, ИЛИ ПРЕДОСТАВЛЕНИЕМ ИЛИ НЕОБХОДИМОМ ПРЕДОСТАВЛЕНИЯ УСЛУГ ПОДДЕРЖКИ, ДАЖЕ ЕСЛИ КЛЮЧ БЫЛ ПРЕДЪЯВЛЕН О ВОЗМОЖНОСТИ ТАКИХ УБЫТКОВ. Поскольку НЕКОТОРЫЕ ЮРИСДИКЦИИ НЕ ДОПУСКАЮТ ИСКЛЮЧЕНИЯ ИЛИ ОГРАНИЧЕНИЯ ОТВЕТСТВЕННОСТИ, ВЫШЕУКАЗАННОЕ ОГРАНИЧЕНИЕ МОЖЕТ НЕ ПРИМЕНЯТЬСЯ В ОПРЕДЕЛЕННЫХ ЮРИСДИКЦИЯХ.
Поскольку НЕКОТОРЫЕ ЮРИСДИКЦИИ НЕ ДОПУСКАЮТ ИСКЛЮЧЕНИЯ ИЛИ ОГРАНИЧЕНИЯ ОТВЕТСТВЕННОСТИ, ВЫШЕУКАЗАННОЕ ОГРАНИЧЕНИЕ МОЖЕТ НЕ ПРИМЕНЯТЬСЯ В ОПРЕДЕЛЕННЫХ ЮРИСДИКЦИЯХ.
ПОЛНОЕ СОГЛАШЕНИЕ: Лицензиат соглашается с тем, что настоящее Соглашение является полным и единственным заявлением соглашения между Лицензиатом, Ключом и дистрибьюторами и дилерами Ключа и заменяет собой все заявления, сделанные в отношении Продукта, и все другие соглашения (письменные или устные. ), относящиеся к предмету настоящего Соглашения.
ЧАСТИЧНАЯ НЕЗАКОННОСТЬ: Если какие-либо положения настоящего Соглашения будут истолкованы как незаконные или недействительные, это не повлияет на законность или действительность любого другого его положения, а незаконные или недействительные положения будут считаться перечеркнутыми и удаленными из него в той же степени. и действуют так, как если бы они никогда не были включены в настоящий документ, но все остальные положения остаются в полной силе.
ПРИМЕНИМЫЕ ЗАКОНЫ: Права и обязанности сторон по настоящему Соглашению не регулируются Конвенцией Организации Объединенных Наций о договорах международной купли-продажи товаров. Вместо этого, если это прямо не запрещено местным законодательством, права и обязанности сторон по настоящему Соглашению регулируются штатом Калифорния и применимыми законами Соединенных Штатов.
Key Curriculum Press 1150 65th Street Emeryville, CA 94608 Телефон: 510-595-7000 Факс: 510-595-7040 Интернет: www.keypress.com
Летняя игра 2020 № 2: Инструменты для рисования и равносторонние треугольники
Вам нравится лето? Играете в карточные игры? В этом году игры ждут вас каждую неделю, а все игры прошлого года доступны для вас и ваших детей, чтобы они могли практиковать математические навыки. А вам понравились занятия на прошлой неделе с Math Balance? Что ж, на этой неделе давайте поработаем с инструментами для рисования и добавим немного художественного вкуса в наши летние математические забавы и игры.
На этой неделе я возьму задания из RightStart Math, уровень C, второе издание, урок 70, и из RightStart Math, уровень G, второе издание, урок 7.Это задание станет приложением по математике, которую изучают дети. Обучение геометрии с помощью практических инструментов помогает ребенку изучать неформальную, практическую сторону геометрии. Это также помогает развивать координацию, которая улучшается с практикой. Готовы повеселиться?
Прежде всего, вам понадобится доска для рисования, Т-образный квадрат и треугольник 30-60. Используйте механический карандаш или хороший острый карандаш. Тусклый карандаш создаст толстые линии, и точность будет снижена.
Приклейте чистый лист бумаги к доске для рисования.Используйте ленту на двух верхних углах. Съемный скотч лучше всего подходит, потому что тогда он не оторвет уголки бумаги. Не наклеивайте липкую ленту на нижние углы, так как она будет мешать перемещению Т-образного квадрата.
Для правшей Т-образный квадрат помещается вдоль левой стороны доски. Левша поместит Т-образный квадрат с правой стороны. Крепко прижмите Т-образный квадрат к доске одной рукой, пока вы проводите линии вдоль вершины Т-образного квадрата доминирующей рукой для письма.Перед проведением каждой линии убедитесь, что Т-образный квадрат «обнимает» доску. Начнем с рисования базовой линии внизу нашей страницы.
При использовании треугольника он должен касаться Т-образного квадрата, в то время как Т-квадрат обнимает доску. Т-образный квадрат должен быть по крайней мере на сантиметр или четверть дюйма ниже нижней начальной точки, чтобы провести точную линию с треугольником.
Вот как работать с Т-квадратом и треугольником, если предположить, что человек правша. Левша отразит эти инструкции.
1. Левая рука перемещает Т-образный квадрат ниже начальной точки и удерживает его на месте. Слегка потяните вправо, чтобы он плотно прилегал к доске.
2. Правая рука перемещает треугольник в правильное место на Т-образном квадрате.
3. Обе руки на мгновение возьмутся за инструменты.
4. Левая рука берет на себя оба инструмента. Опять же, создайте небольшое натяжение, чтобы Т-образный квадрат плотно прилегал к доске.
Когда у нас есть Т-образный квадрат и треугольник, нарисуйте одну сторону равностороннего треугольника.Конечно, мы не знаем, сколько времени нужно сделать, поэтому просто нарисуйте его дольше, чем вы считаете необходимым. Сотрем то, что нам не нужно.
Переверните треугольник и нарисуйте последнюю сторону нашего треугольника.
Теперь, поскольку мы собираемся разбить наши равносторонние треугольники на девятые, вот так:
нам нужно найти центр нашего треугольника. Видите, как три указанные выше линии проходят через центр треугольника и параллельны его сторонам? Сделайте это с отметками, как показано ниже.Обратите внимание, что отметки — это просто маленькие частичные линии, «тикающие» от центра. Они нарисованы не полностью.
Затем нарисуйте линии, чтобы образовать девять маленьких равносторонних треугольников.
На этой фигуре есть интересный узор, особенно если на него добавить. Вот моя с одной добавленной строкой внизу.
Обратите внимание на количество маленьких треугольников в каждом ряду.
Посмотрите на таблицу ниже, чтобы увидеть некоторые закономерности.В первом столбце диаграммы указан номер строки. Второй столбец — это первый столбец, умноженный на два. Третий столбец — это количество маленьких треугольников в каждой строке. Как видите, я заполнил первые две строки. Каковы ответы на следующие две строки? Используйте схему выше, чтобы ответить на вопросы.
Что вы получили за третий ряд? Должны быть ряды 3, 6 (3 × 2) и 5 маленьких треугольников. А четвертый? Ответы — маленькие треугольники 4, 8 и 7 рядов. Видите здесь образец?
Давайте продолжим …… Если нужно, нарисуйте еще треугольников.Мы могли бы взглянуть на это и математически. Посмотрите на выкройки.
В последней строке диаграммы n означает любое число. Дважды любое число можно записать как 2 n . Кроме того, любое число плюс 1 записывается как n + 1; любое число минус 1 равно n — 1. Посмотрите на второй и третий столбцы. Сколько равносторонних треугольников в каждом ряду? По отношению к номеру строки это будет 2 n — 1 . Ответы можно найти здесь.
Используйте инструменты рисования, чтобы продолжить рисование и создать новые. Поделитесь ими с нами по адресу [email protected]. Удачного рисования!
Иллюстративная математика
Задача
Существует ли равносторонний треугольник $ ABC $, так что $ \ overline {AB} $ лежит на оси $ x $, а координаты $ A $, $ B $ и $ C $ целые числа $ x $ и $ y $? ? Объясни.
IM Комментарий
Цель этой задачи — изучить углы треугольников, вершины которых имеют определенные целочисленные координаты.Исследуемые углы образованы тремя точками с целыми координатами, две из которых находятся на оси $ x $. Таких углов много, поскольку единственным ограничением негоризонтального луча является то, что он принадлежит прямой с рациональным наклоном. Оказывается, влияние рациональности этого наклона состоит в том, что при этих условиях угол в 60 градусов становится невозможным, и поэтому не существует равностороннего треугольника, удовлетворяющего этим ограничениям. Студенты должны будут знать или уметь рассчитать длину равностороннего треугольника или знать синус и косинус угла 60 градусов.Это можно сделать с помощью знания тригонометрических функций или теоремы Пифагора. Учителю, возможно, потребуется дать совет: хорошей отправной точкой было бы нарисовать несколько треугольников, как в решении, и определить, являются ли эти частные случаи равносторонними.
Задачу можно естественным образом расширить, чтобы показать, что на плоскости не существует равностороннего треугольника, вершины которого имеют целочисленные координаты: другими словами, ответ на задачу тот же, без предположения, что две из вершин находятся на $ x $ — ось.Аргумент этой более общей проблемы представлен с использованием формул суммы и разности для касательной функции. Это дополнительный стандарт, и, вероятно, потребуется указать формулы. Однако важны не сами точные формулы, а их структура: эту задачу можно рассматривать не только как применение этих формул, но и как мотивацию для их исследования.
Идея этого задания возникла на собрании кружка учителей математики в Альбукерке 1 октября 2013 года.
Решения
Решение: 1 Тригонометрические функции
Предположим, что существует равносторонний треугольник $ ABC $, удовлетворяющий заданным условиям. Мы можем сделать горизонтальный сдвиг так, чтобы $ A = (0,0) $, и для простоты предположим, что $ B $ лежит на положительной оси $ x $. Ниже приведено изображение примера, в котором координата $ y $ для $ C $ положительна:
Предположим, что $ m (\ angle A) = 60 $. Мы можем вычислить тригонометрические функции для $ \ angle A $, составив прямоугольный треугольник, как показано ниже:
Поскольку линии сетки перпендикулярны, $ \ angle O $ в $ \ треугольнике AOC $ является прямым углом, и мы имеем $$ \ tan (\ angle A) = \ frac {| OC |} {| AO |}.$$ Для конкретного треугольника, который мы нарисовали, $ | OC | = 5 $ и $ | AO | = 2 $, но в общем случае, если $ C $ имеет целочисленные координаты (a, b), то мы получим рациональное число $ \ frac {b} {a} $ для значения $ \ tan (\ angle A) $. Поскольку $ \ tan (60) = \ sqrt {3} $ и $ \ sqrt {3} $ — иррациональное число, это означает, что $ m (\ angle BAC) $ не может быть 60. Дробь $ \ frac {b} {a} $, задающий значение $ \ tan {\ angle A} $, имеет смысл только тогда, когда $ a \ neq 0 $, но если $ a = 0 $, тогда $ \ angle A $ будет прямым углом, а $ \ треугольник ABC $ все равно не будет равносторонним.Следовательно, не существует равностороннего треугольника $ ABC $ с двумя вершинами на оси $ x $ и всеми вершинами, имеющими целочисленные координаты.
Решение: 2 Теорема Пифагора
Предположим, что существует равносторонний треугольник $ ABC $, удовлетворяющий заданным условиям. Мы можем сделать горизонтальный сдвиг так, чтобы $ A = (0,0) $, и для простоты предположим, что $ B $ лежит на положительной оси $ x $. На рисунке $ \ overleftrightarrow {CO} $ перпендикулярен $ \ overleftrightarrow {AB} $.2 $ и, следовательно, $$ \ sqrt {3} | АО | = | OC | $$ и $ \ sqrt {3} = \ frac {| OC |} {| AO |} $. Если бы $ \ треугольник ABC $ был равносторонним, то $ | AC | = | AB | $ и $ | AO | = \ frac {| AB |} {2} $ — рациональные числа. Это означало бы, что $ \ sqrt {3} $ — рациональное число. Однако это неверно, поэтому $ \ треугольник ABC $ не может быть равносторонним.
Решение: 3 формулы сложения для тригонометрических функций (F-TF.9)
Это решение основано на первом решении с использованием тригонометрии. Цель здесь — использовать формулу суммы / разности для касательной функции, которая гласит, что $$ \ tan {(a \ pm b)} = \ frac {\ tan {a} \ pm \ tan {b}} {1 \ mp \ tan {a} \ tan {b}}.$$ Напомним, что $ \ tan {x} = \ frac {\ sin {x}} {\ cos {x}} $, и это имеет смысл когда $ \ cos {x} \ neq 0 $. Таким образом, мы должны убедиться в нашем аргументе ниже, что $ a, b, $ и $ a \ pm b $ не являются $ \ pm 90 $. Отметим также, что разные знаки касательных выражений в числителе и знаменателе.
На рисунке ниже показан конкретный треугольник, к которому мы можем применить приведенную выше формулу суммы:
В этом случае мы имеем $ m (\ angle A) = a + b $ и, используя формулу выше
$$ \ begin {align} \ tan {\ angle A} & = \ tan {(a + b)} \\ & = \ frac {\ tan {a} + \ tan {b}} {1 — \ tan {a} \ tan {b}}.\ end {align} $$
Как видно из первого решения, $ \ tan {a} $ и $ \ tan {b} $ являются рациональными числами: в этом случае $ \ tan {a} = \ frac {1} {3} $ и $ \ tan {b} = \ frac {2} {2} $. Используя формулу выше, мы находим, что $ \ tan {\ angle A} $ — рациональное число. С другой стороны, если $ m (\ angle A) = 60 $, то $ \ tan {A} = \ sqrt {3} $, иррациональное число. Таким образом, это невозможно для $ m (\ angle A) = 60 $, и не может быть, чтобы $ \ треугольник ABC $ был равносторонним треугольником.
Любой треугольник, вершины которого имеют целые координаты, можно перевести так что одна из вершин, скажем, $ A $, находится в точке (0,0), а две другие вершины имеют целочисленные координаты.Мы также можем применить поворот на 90 градусов относительно начала координат (который преобразует целочисленные координаты в целые координаты) так, чтобы одна из других вершин, которые мы помечаем как $ C $, лежала в первом квадранте и $ m (\ angle BAC) \ gt 0 $. Единственный способ сделать треугольник равносторонним — это если третья вершина $ B $ лежит либо в четвертом, либо в первом квадранте. Случай, когда $ B $ лежит в четвертом квадранте, был рассмотрен выше (знаменатель $ 1 — \ tan {a} \ tan {b} $ не может быть нулевым, если $ \ angle A $ равен углу 60 градусов).Если $ B $ лежит в первом квадранте, применяется аналогичный аргумент с использованием формулы тангенса разности двух углов. Изображение этой другой ситуации дано ниже:
Мы не можем найти эту страницу
(* {{l10n_strings.REQUIRED_FIELD}})
{{l10n_strings.CREATE_NEW_COLLECTION}} *
{{l10n_strings.ADD_COLLECTION_DESCRIPTION}}
{{l10n_strings.COLLECTION_DESCRIPTION}} {{addToCollection.description.length}} / 500 {{l10n_strings.TAGS}} {{$ item}} {{l10n_strings.PRODUCTS}} {{l10n_strings.DRAG_TEXT}}{{l10n_strings.DRAG_TEXT_HELP}}
{{l10n_strings.LANGUAGE}} {{$ select.selected.display}}{{article.content_lang.display}}
{{l10n_strings.АВТОР}}{{l10n_strings.AUTHOR_TOOLTIP_TEXT}}
{{$ select.selected.display}} {{l10n_strings.CREATE_AND_ADD_TO_COLLECTION_MODAL_BUTTON}} {{l10n_strings.CREATE_A_COLLECTION_ERROR}} .
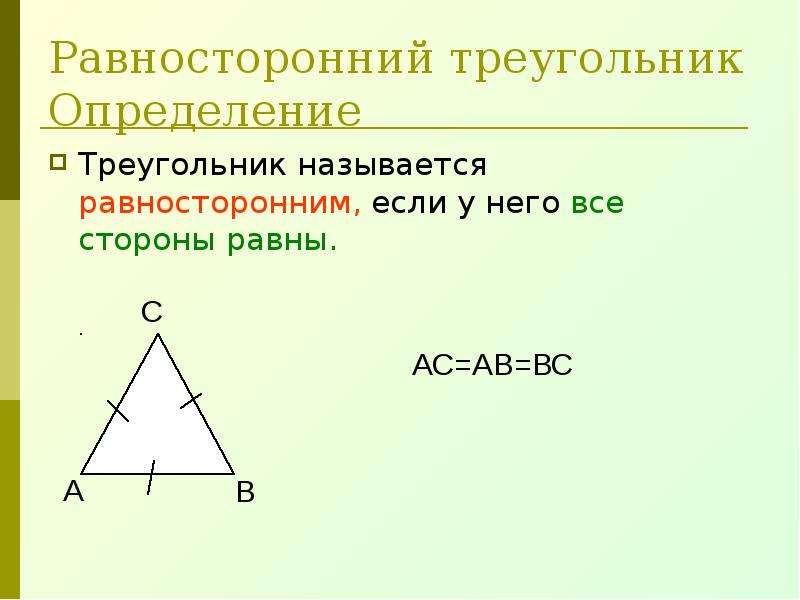 Опишите дугу. Не изменяйте установленную «ширину» инструмента от точки циркуля до точки карандаша. Нарисуйте вторую дугу, чтобы она пересекала первую дугу, которую уже нарисовали. Отметьте точку, в которой пересекаются две дуги. Это вершина (верхняя точка) треугольника. Он должен лежать в точном центре сегмента линии, который нарисовали. Теперь можете сделать две прямые линии, ведущие к этой точке: по одному от каждого конца «нижнего» сегмента линии. Закончите треугольник. Далее с помощью линейки надо нарисовать еще два сегмента прямой линии – это стороны в треугольнике. Подключите каждый конец исходного сегмента линии к точке, в которой пересекаются дуги. Чтобы закончить работу, сотрите дуги, которые нарисовали, так, чтобы остался только треугольник.
Опишите дугу. Не изменяйте установленную «ширину» инструмента от точки циркуля до точки карандаша. Нарисуйте вторую дугу, чтобы она пересекала первую дугу, которую уже нарисовали. Отметьте точку, в которой пересекаются две дуги. Это вершина (верхняя точка) треугольника. Он должен лежать в точном центре сегмента линии, который нарисовали. Теперь можете сделать две прямые линии, ведущие к этой точке: по одному от каждого конца «нижнего» сегмента линии. Закончите треугольник. Далее с помощью линейки надо нарисовать еще два сегмента прямой линии – это стороны в треугольнике. Подключите каждый конец исходного сегмента линии к точке, в которой пересекаются дуги. Чтобы закончить работу, сотрите дуги, которые нарисовали, так, чтобы остался только треугольник.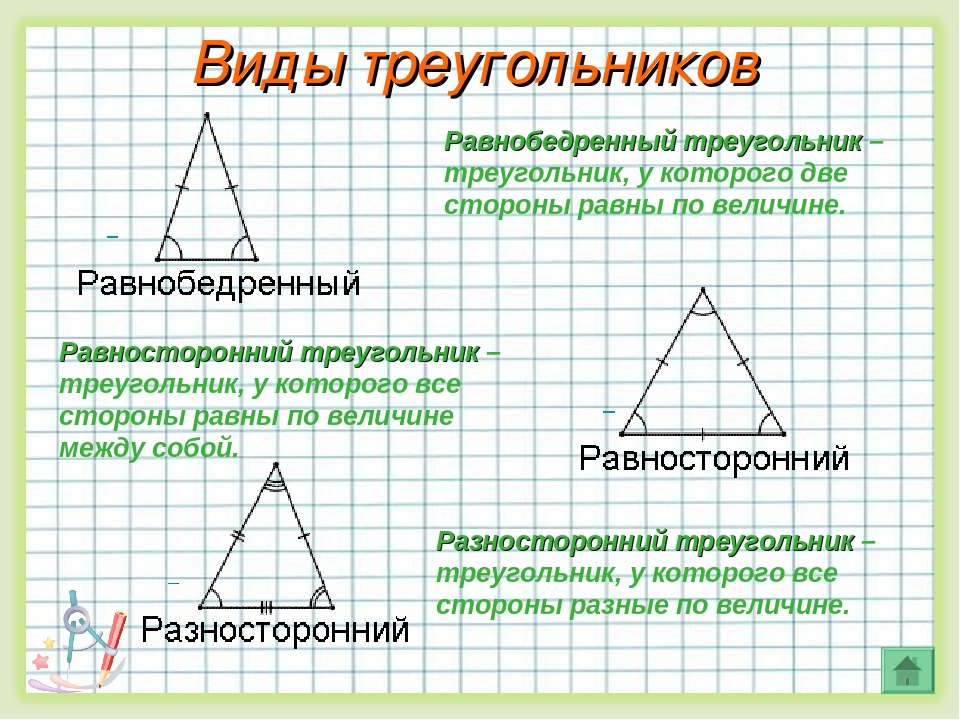 Проденьте кончик карандаша в сторону от отрезка линии в форме полукруга.
Проденьте кончик карандаша в сторону от отрезка линии в форме полукруга.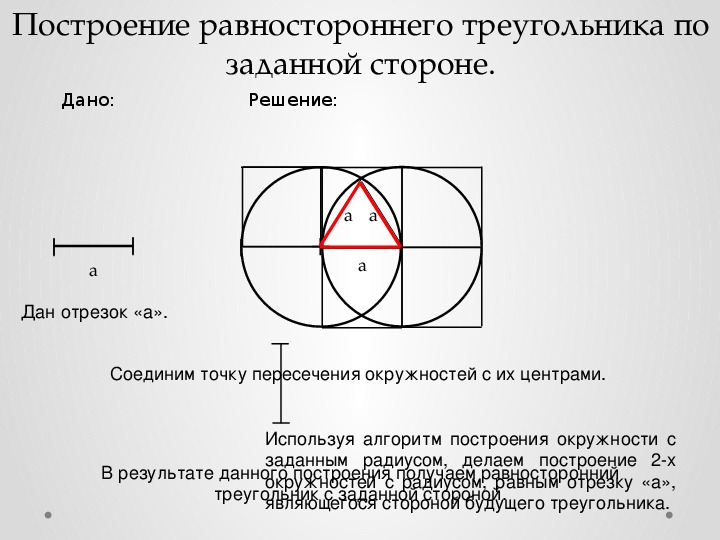
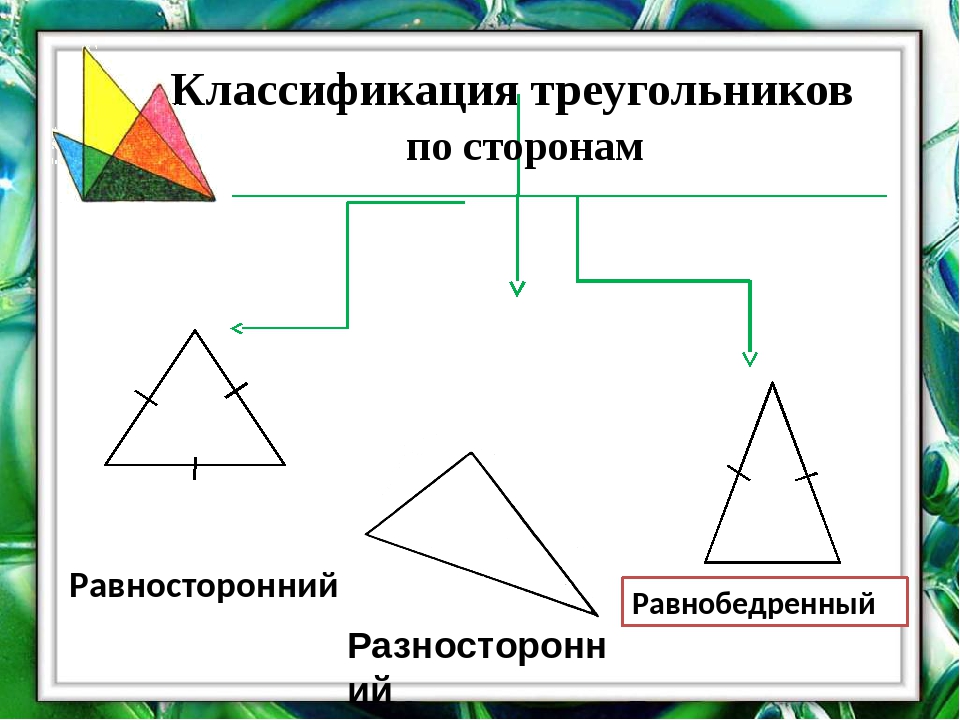 Карандашом нарисуйте дугу, примерно равную ¼ периметра круга.
Карандашом нарисуйте дугу, примерно равную ¼ периметра круга.


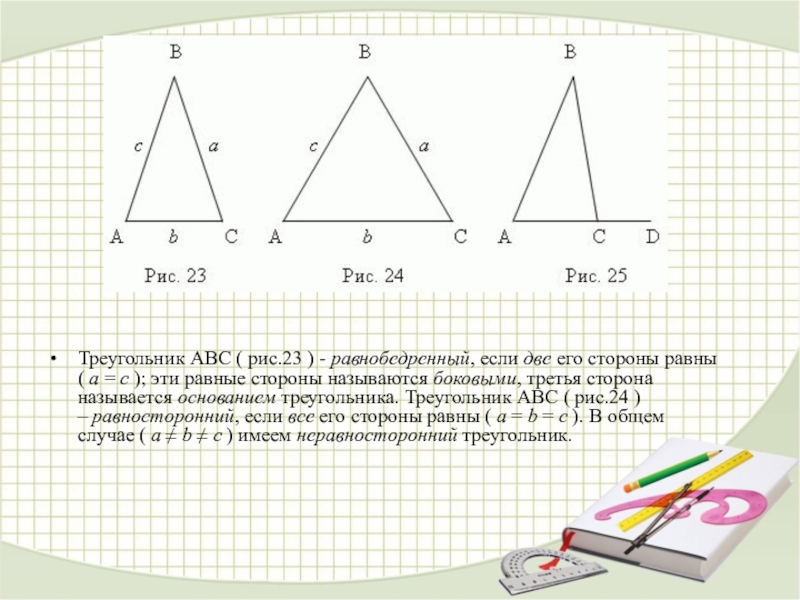 Обозначаем его буквами АС.
Обозначаем его буквами АС. Соедините полученные точки. У нас получился искомый треугольник.
Соедините полученные точки. У нас получился искомый треугольник.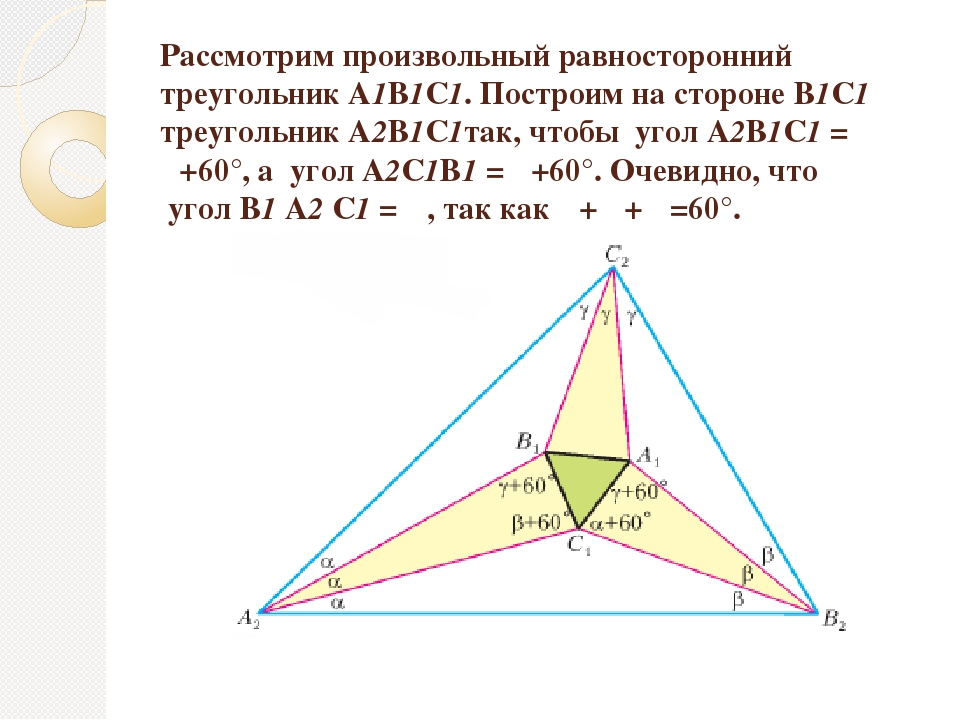
 Обозначаем его буквами АС.
Обозначаем его буквами АС. Соедините полученные точки. У нас получился искомый треугольник.
Соедините полученные точки. У нас получился искомый треугольник. Он должен лежать в точном центре сегмента линии, который нарисовали. Теперь можете сделать две прямые линии, ведущие к этой точке: по одному от каждого конца «нижнего» сегмента линии. Закончите треугольник. Далее с помощью линейки надо нарисовать еще два сегмента прямой линии – это стороны в треугольнике. Подключите каждый конец исходного сегмента линии к точке, в которой пересекаются дуги. Чтобы закончить работу, сотрите дуги, которые нарисовали, так, чтобы остался только треугольник.
Он должен лежать в точном центре сегмента линии, который нарисовали. Теперь можете сделать две прямые линии, ведущие к этой точке: по одному от каждого конца «нижнего» сегмента линии. Закончите треугольник. Далее с помощью линейки надо нарисовать еще два сегмента прямой линии – это стороны в треугольнике. Подключите каждый конец исходного сегмента линии к точке, в которой пересекаются дуги. Чтобы закончить работу, сотрите дуги, которые нарисовали, так, чтобы остался только треугольник.

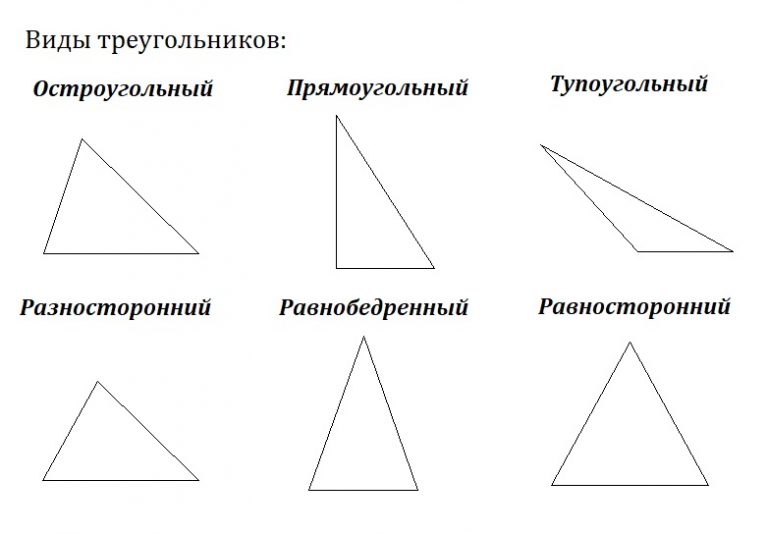
 Использование инструктором на персональном или домашнем компьютере считается одним из случаев использования в соответствии с Школьной / институциональной лицензией.
Использование инструктором на персональном или домашнем компьютере считается одним из случаев использования в соответствии с Школьной / институциональной лицензией.