стороны, вершины, диагонали. Периметр многоугольника
Многоугольник — это геометрическая фигура, ограниченная замкнутой ломаной линией, не имеющей самопересечений.
Звенья ломаной называются сторонами многоугольника, а её вершины — вершинами многоугольника.
Углами многоугольника называются внутренние углы, образованные соседними сторонами. Число углов многоугольника равно числу его вершин и сторон.
Многоугольникам даются названия по количеству сторон. Многоугольник с наименьшим количеством сторон называется треугольником, он имеет всего три стороны. Многоугольник с четырьмя сторонами называется четырёхугольником, с пятью — пятиугольником и т. д.
Обозначение многоугольника составляют из букв, стоящих при его вершинах, называя их по порядку (по часовой или против часовой стрелки). Например, говорят или пишут: пятиугольник ABCDE
:
В пятиугольнике
Выпуклые и вогнутые
Многоугольник называется выпуклым, если ни одна из его сторон, продолженная до прямой линии, его не пересекает. В обратном случае многоугольник называется вогнутым:
Периметр
Сумма длин всех сторон многоугольника называется его периметром.
Периметр многоугольника ABCDE равен:
AB + BC + CD + DE + EA.
Если у многоугольника равны все стороны и все углы, то его называют
Диагональ
Диагональ многоугольника — это отрезок, соединяющий вершины двух углов, не имеющих общей стороны. Например, отрезок AD является диагональю:
Например, отрезок AD является диагональю:
Единственным многоугольником, который не имеет ни одной диагонали, является треугольник, так как в нём нет углов, не имеющих общих сторон.
Если из какой-нибудь вершины многоугольника провести все возможные диагонали, то они разделят многоугольник на треугольники:
Треугольников будет ровно на два меньше, чем сторон:
t = n — 2,
где t — это количество треугольников, а n — количество сторон.
Разделение многоугольника на треугольники с помощью диагоналей используется для нахождения площади многоугольника, так как чтобы найти площадь какого-нибудь многоугольника, нужно разбить его на треугольники, найти площадь этих треугольников и полученные результаты сложить.
Индивидуальное домашнее задание по геометрии для учащихся 8 класса по теме «Многоугольник»
Начертить две фигуры, одна из которых является многоугольником, а другая — нет. Указать вершины, стороны данного многоугольника.
Начертить выпуклый и невыпуклый четырехугольники. У выпуклого четырехугольника указать противоположные вершины и противоположные стороны. Отметить по две точки, принадлежащие внутренней и внешней области невыпуклого четырехугольника.
Начертить выпуклый пятиугольник и указать все его диагонали.
Что такое периметр многоугольника?
Чему равна сумма углов выпуклого «-угольника? 4-угольника? Каков план доказательства теоремы о сумме углов выпуклого «-угольника?
Как найти угол выпуклого «-угольника, если известно, что все его углы равны?
уровень (карточка № 1)
Найдите сумму углов выпуклого восьмиугольника.
В четырехугольнике АВСИ противолежащие стороны параллельны,АВ = 10 см, ВС = 14 см. Найдите периметр АВСИ.
уровень (карточка № 2)
Сколько сторон имеет выпуклый «-угольник, если сумма его улов равна 540°?
В випуклом четырехугольнике длины сторон относятся как 1 ‘Л : 9 : 10, а его периметр равен 68 см.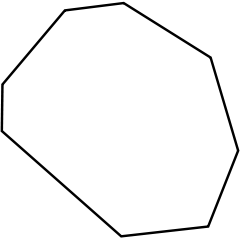 Найдите стороны четырехугольника.
Найдите стороны четырехугольника.
уровень (карточка № 3)
Найдите число сторон выпуклого многоугольника, если каждый угол равен 108°.
Выпуклый четырехугольник АВСй имеет две пары равных между собой смежных сторон: АВ = ЛД ВС = СД О — точка
пересечения диагоналей четырехугольника. Сравните периметры пятиугольников АВСОО и АВОСО.
а)Найдите сумму углов выпуклого 7-угольника. (900°)
б)Найдите угол выпуклого 5-угольника, если известно, что все его углы равны. (108°)
в)Найдите число сторон выпуклого о-угольника, если известно, что сумма его углов равна 1080°.
4.Решить самостоятельно с последующим обсуждением. (Эти задачи решают более подготовленные учащиеся, обсуждение проводится индивидуально во время самостоятельной работы.) а) Докажите, что выпуклый четырехугольник с неравными углами должен иметь хотя бы один тупой угол.
б) В выпуклом многоугольнике имеется пять углов с градусной мерой 140° каждый, остальные углы острые. Найдите число сторон этого многоугольника. (Ответ-, п = 6.)
вариант
Найдите сумму углов выпуклого двенадцатиугольника.
В выпуклом пятиугольнике две стороны равны, третья сторона на 3 см больше, а четвертая в 2 раза больше первой стороны, пятая — на 4 см меньше четвертой. Найдите стороны пятиугольника, если известно, что его периметр равен 34 см.
вариант
Найдите сумму углов выпуклого тринадцатиугольника.
В выпуклом шестиугольнике три стороны равны, четвертая в 2 раза больше первой стороны, пятая — на 3 см меньше четвертой, а шестая — на 1 см больше второй. Найдите стороны шестиугольника, если известно, что его периметр равен 30 см.
II уровень
I вариант
Сколько сторон имеет выпуклый многоугольник, если сумма его углов равна 2160°?
Выпуклый четырехугольник АВСБ имеет две пары равных между собой смежных сторон: АВ = ЛД ВС = СО, О — точка пересечения диагоналей четырехугольника. Сравните периметры пятиугольников АВСОО и АВОСй.
Сравните периметры пятиугольников АВСОО и АВОСй.
Сколько сторон имеет выпуклый многоугольник, если сумма его углов равна 2520°?
ДиагональАС невыпуклого четырехугольника ЛЯСО разделяет этот четырехугольник на два треугольника, причем АВ > ВС, АВ = ЛО, ОС = СО, а прямые, содержащие диагонали четырехугольника, пересекаются в точкеО. Сравните периметры пятиугольниковВ СОИ А и ОСОБА.
III уровень
I вариант1. Каждый угол выпуклого многоугольника равен 162°. Найдите число сторон этого многоугольника.
2. В выпуклом шестиугольнике ABCDEF все стороны равны. Большая диагональ, проведенная из вершины А, параллельна стороне ВС,ZBAD=ZCDA. Сравните периметры пятиугольниковABDEFи ACDEF.
II вариант
Каждый угол выпуклого многоугольника равен 165°. Найдите число сторон этого многоугольника.
В выпуклом пятиугольнике ABCDE все стороны имеют равные длины. Диагональ, проведенная из вершины А, параллельна стороне ED,ZEAC = ZDCA. Сравните периметры четырехугольниковЕАВС и DCBA.
Адрес публикации: https://www.prodlenka.org/metodicheskie-razrabotki/365704-individualnoe-domashnee-zadanie-po-geometrii-
Построить пятиугольник, избегая использования компаса
правила
Вы начнете с только два элемента: Точки и такие , что . Эти точки занимают плоскость, которая бесконечна во всех направлениях.AABBA≠BA≠B
На любом этапе процесса вы можете выполнить одно из следующих трех действий:
Нарисуйте линию, которая проходит через две точки.
Нарисуйте круг с центром в одной точке, так что другая точка лежит на круге.
Добавьте новую точку, где два объекта (линии и круги) пересекаются.
Ваша цель состоит в том, чтобы создать 5 точек таким образом, чтобы они образовывали вершины правильного пятиугольника (выпуклый многоугольник с 5 сторонами, равными по длине), используя как можно меньше кругов. Конечно, у вас могут быть и другие очки, но 5 из них должны иметь обычный пятиугольник. Вам не нужно рисовать края пятиугольника для вашей оценки.
Конечно, у вас могут быть и другие очки, но 5 из них должны иметь обычный пятиугольник. Вам не нужно рисовать края пятиугольника для вашей оценки.
счет
При сравнении двух ответов лучше использовать тот, который рисует меньше кругов. В случае ничьей в кругах ответ, который рисует наименьшее количество линий, лучше. В случае равенства в кругах и линиях ответ, который добавляет наименьшее количество баллов, будет лучше.
Анти-правила
Хотя список правил является исчерпывающим и детализирует все, что вы можете сделать, этого списка нет, но то, что я не говорю, что вы не можете что-то делать, не означает, что вы можете.
Вы не можете создавать «произвольные» объекты. Некоторые конструкции, которые вы найдете, будут думать, как добавить точку в «произвольном» месте и работать оттуда. Вы не можете добавлять новые точки в местах, отличных от перекрестков.
Вы не можете скопировать радиус. Некоторые конструкции будут включать компас, устанавливая его на радиус между двумя точками, а затем подбирая его и рисуя круг в другом месте. Ты не сможешь это сделать.
Вы не можете выполнять ограничивающие процессы. Все конструкции должны пройти конечное число шагов. Недостаточно подходить к ответу асимптотически.
Вы не можете нарисовать дугу или часть круга, чтобы не считать его кругом при подсчете очков. Если вы хотите визуально использовать дуги при показе или объяснении своего ответа, потому что они занимают меньше места, продолжайте, но они считаются кругом для подсчета очков.
инструменты
Вы можете продумать проблему на GeoGebra . Просто перейдите на вкладку формы. Три правила эквивалентны точке, линии и окружности с центральными инструментами.
Бремя доказательства
Это стандартно, но я хотел бы повторить. Если возникает вопрос о том, является ли конкретный ответ действительным, бремя доказывания лежит на ответчике, чтобы показать, что его ответ является действительным, а не на публике, чтобы показать, что ответ не является.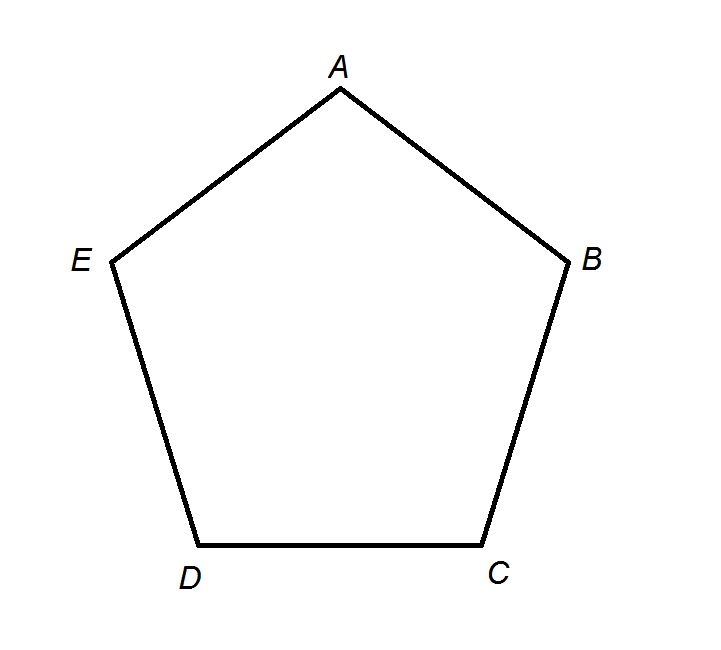
Что это делает на моем сайте Code-Golf ?!
Это форма атомно-кодового гольфа, похожего на корректный гольф, хотя и немного странного языка программирования. В настоящее время существует + 22 / -0 консенсус в отношении того, что подобные вещи разрешены.
| ||||||||||||||||||||||
| ||||||||||||||||||||||||||||||
Отрывок, характеризующий Правильный пятиугольник
Петя не знал, как долго это продолжалось: он наслаждался, все время удивлялся своему наслаждению и жалел, что некому сообщить его. Его разбудил ласковый голос Лихачева.
Его разбудил ласковый голос Лихачева.– Готово, ваше благородие, надвое хранцуза распластаете.
Петя очнулся.
– Уж светает, право, светает! – вскрикнул он.
Невидные прежде лошади стали видны до хвостов, и сквозь оголенные ветки виднелся водянистый свет. Петя встряхнулся, вскочил, достал из кармана целковый и дал Лихачеву, махнув, попробовал шашку и положил ее в ножны. Казаки отвязывали лошадей и подтягивали подпруги.
– Вот и командир, – сказал Лихачев. Из караулки вышел Денисов и, окликнув Петю, приказал собираться.
Быстро в полутьме разобрали лошадей, подтянули подпруги и разобрались по командам. Денисов стоял у караулки, отдавая последние приказания. Пехота партии, шлепая сотней ног, прошла вперед по дороге и быстро скрылась между деревьев в предрассветном тумане. Эсаул что то приказывал казакам. Петя держал свою лошадь в поводу, с нетерпением ожидая приказания садиться. Обмытое холодной водой, лицо его, в особенности глаза горели огнем, озноб пробегал по спине, и во всем теле что то быстро и равномерно дрожало.
– Ну, готово у вас все? – сказал Денисов. – Давай лошадей.
Лошадей подали. Денисов рассердился на казака за то, что подпруги были слабы, и, разбранив его, сел. Петя взялся за стремя. Лошадь, по привычке, хотела куснуть его за ногу, но Петя, не чувствуя своей тяжести, быстро вскочил в седло и, оглядываясь на тронувшихся сзади в темноте гусар, подъехал к Денисову.
– Василий Федорович, вы мне поручите что нибудь? Пожалуйста… ради бога… – сказал он. Денисов, казалось, забыл про существование Пети. Он оглянулся на него.
– Об одном тебя пг»ошу, – сказал он строго, – слушаться меня и никуда не соваться.
Во все время переезда Денисов ни слова не говорил больше с Петей и ехал молча. Когда подъехали к опушке леса, в поле заметно уже стало светлеть. Денисов поговорил что то шепотом с эсаулом, и казаки стали проезжать мимо Пети и Денисова. Когда они все проехали, Денисов тронул свою лошадь и поехал под гору. Садясь на зады и скользя, лошади спускались с своими седоками в лощину. Петя ехал рядом с Денисовым. Дрожь во всем его теле все усиливалась. Становилось все светлее и светлее, только туман скрывал отдаленные предметы. Съехав вниз и оглянувшись назад, Денисов кивнул головой казаку, стоявшему подле него.
– Сигнал! – проговорил он.
Казак поднял руку, раздался выстрел. И в то же мгновение послышался топот впереди поскакавших лошадей, крики с разных сторон и еще выстрелы.
В то же мгновение, как раздались первые звуки топота и крика, Петя, ударив свою лошадь и выпустив поводья, не слушая Денисова, кричавшего на него, поскакал вперед. Пете показалось, что вдруг совершенно, как середь дня, ярко рассвело в ту минуту, как послышался выстрел. Он подскакал к мосту. Впереди по дороге скакали казаки. На мосту он столкнулся с отставшим казаком и поскакал дальше. Впереди какие то люди, – должно быть, это были французы, – бежали с правой стороны дороги на левую. Один упал в грязь под ногами Петиной лошади.
У одной избы столпились казаки, что то делая. Из середины толпы послышался страшный крик. Петя подскакал к этой толпе, и первое, что он увидал, было бледное, с трясущейся нижней челюстью лицо француза, державшегося за древко направленной на него пики.
– Ура!.. Ребята… наши… – прокричал Петя и, дав поводья разгорячившейся лошади, поскакал вперед по улице.
Впереди слышны были выстрелы. Казаки, гусары и русские оборванные пленные, бежавшие с обеих сторон дороги, все громко и нескладно кричали что то. Молодцеватый, без шапки, с красным нахмуренным лицом, француз в синей шинели отбивался штыком от гусаров. Когда Петя подскакал, француз уже упал. Опять опоздал, мелькнуло в голове Пети, и он поскакал туда, откуда слышались частые выстрелы. Выстрелы раздавались на дворе того барского дома, на котором он был вчера ночью с Долоховым. Французы засели там за плетнем в густом, заросшем кустами саду и стреляли по казакам, столпившимся у ворот. Подъезжая к воротам, Петя в пороховом дыму увидал Долохова с бледным, зеленоватым лицом, кричавшего что то людям. «В объезд! Пехоту подождать!» – кричал он, в то время как Петя подъехал к нему.
– Подождать?.. Ураааа!.. – закричал Петя и, не медля ни одной минуты, поскакал к тому месту, откуда слышались выстрелы и где гуще был пороховой дым. Послышался залп, провизжали пустые и во что то шлепнувшие пули. Казаки и Долохов вскакали вслед за Петей в ворота дома. Французы в колеблющемся густом дыме одни бросали оружие и выбегали из кустов навстречу казакам, другие бежали под гору к пруду. Петя скакал на своей лошади вдоль по барскому двору и, вместо того чтобы держать поводья, странно и быстро махал обеими руками и все дальше и дальше сбивался с седла на одну сторону. Лошадь, набежав на тлевший в утреннем свето костер, уперлась, и Петя тяжело упал на мокрую землю. Казаки видели, как быстро задергались его руки и ноги, несмотря на то, что голова его не шевелилась. Пуля пробила ему голову.
Переговоривши с старшим французским офицером, который вышел к нему из за дома с платком на шпаге и объявил, что они сдаются, Долохов слез с лошади и подошел к неподвижно, с раскинутыми руками, лежавшему Пете.
– Готов, – сказал он, нахмурившись, и пошел в ворота навстречу ехавшему к нему Денисову.
– Убит?! – вскрикнул Денисов, увидав еще издалека то знакомое ему, несомненно безжизненное положение, в котором лежало тело Пети.
– Готов, – повторил Долохов, как будто выговаривание этого слова доставляло ему удовольствие, и быстро пошел к пленным, которых окружили спешившиеся казаки. – Брать не будем! – крикнул он Денисову.
Как начертить ровный шестиугольник
Обычный шестиугольник, также называемый идеальным шестиугольником, имеет шесть равных сторон и шесть равных углов. Вы можете нарисовать шестиугольник при помощи рулетки и транспортира, грубый шестиугольник – при помощи круглого предмета и линейки или еще более грубый шестиугольник – при помощи только карандаша и немного интуиции. Если вы хотите знать, как нарисовать шестиугольник различными способами – просто читайте далее.
Геометрические построения являются одной из главных частей обучения. Они формируют пространственное и логическое мышление, а также разрешают понять примитивные и натуральные геометрические обоснованности. Построения производятся на плоскости при помощи циркуля и линейки. Этими инструментами дозволено возвести крупное число геометрических фигур. При этом многие фигуры, кажущиеся довольно трудными, строятся с использованием простейших правил. Скажем, то, как возвести верный шестиугольник, дозволено описать каждого в нескольких словах.
Вам понадобится
- Циркуль, линейка, карандаш, лист бумаги.
Инструкция
1. Нарисуйте окружность. Установите некоторое расстояние между ножками циркуля. Это расстояние будет являться радиусом окружности. Выберите радиус таким образом, дабы вычерчивание окружности было довольно комфортным. Окружность должна всецело помещаться на листе бумаги. Слишком огромное либо слишком маленькое расстояние между ножками циркуля может привести к его изменению во время черчения. Оптимальным будет расстояние, при котором угол между ножками циркуля равен 15-30 градусов.
2. Постройте точки вершин углов верного шестиугольника. Установите ножку циркуля, в которой закреплена игла, в всякую точку окружности. Игла должна проткнуть начерченную линию. Чем вернее будет установлен циркуль, тем вернее будет построение. Проведите дугу окружности так, дабы она пересекла начерченную ранее окружность. Переставьте иглу циркуля в точку пересечения только что начерченной дуги с окружностью. Начертите еще одну дугу, пересекающую окружность. Вновь переставьте иглу циркуля в точку пересечения дуги и окружности и вновь начертите дугу. Произведите данное действие еще три раза, перемещаясь в одном направлении по окружности. Каждого должно получиться шесть дуг и шесть точек пересечения.
3. Постройте положительный шестиугольник. Ступенчато объедините все шесть точек пересечения дуг с изначально начерченной окружностью. Соединяйте точки прямыми, вычерчиваемыми при помощи линейки и карандаша. Позже произведенных действий будет получен верный шестиугольник, вписанный в окружность.
Шестиугольником считается многоугольник, владеющий шестью углами и шестью сторонами. Многоугольники бывают как выпуклыми, так и вогнутыми. У выпуклого шестиугольника все внутренние углы тупые, у вогнутого один либо больше угол является острым. Шестиугольник довольно легко возвести. Это делается в пару шагов.
Вам понадобится
- Карандаш, лист бумаги, линейка
Инструкция
1. Берется лист бумаги и на нем отмечается 6 точек приблизительно так, как это показано на рис. 1.
2. Позже того, как были подмечены точки, берется линейка, карандаш и с их подмогой ступенчато, друг за ином соединяются точки так, как это выглядит на рис. 2.
Видео по теме
Обратите внимание!
Сумма всех внутренних углов шестиугольника равна 720 градусам.
Шестиугольник – это многоугольник, тот, что владеет шестью углами. Для того, дабы начертить произвольный шестиугольник, надобно проделать каждого 2 действия.
Вам понадобится
- Карандаш, линейка, лист бумаги.
Инструкция
1. Нужно взять в руку карандаш и разметить на листе 6 произвольных точек. В дальнейшем эти точки будут исполнять роль углов в шестиугольнике. (рис.1)
2. Взять линейку и начертить по данным точкам 6 отрезков, которые бы соединялись друг с ином по начерченным ранее точкам (рис.2)
Видео по теме
Обратите внимание!
Специальным типом шестиугольника является положительный шестиугольник. Он именуется таковым потому, что все его стороны и углы равны между собой. Вокруг такого шестиугольника дозволено описать либо вписать окружность. Стоит подметить, что в точках, которые получились путем касания вписанной окружности и сторон шестиугольника, стороны положительного шестиугольника делятся напополам.
Полезный совет
В природе положительные шестиугольники владеют крупный популярностью. К примеру, вся пчелиная сота владеет положительной шестиугольной формой. Либо кристаллическая решетка графена (модификация углерода) тоже владеет формой положительного шестиугольника.
Как возвести тот либо другой угол – крупной вопрос. Но для некоторых углов задача невидимо упрощается. Одним из таких углов является угол в 30 градусов. Он равен ?/6, то есть число 30 является делителем 180. Плюс к этому его синус вестим. Это и помогает при его построении.
Вам понадобится
- транспортир, угольник, циркуль, линейка
Инструкция
1. Для начала разглядим особенно примитивную обстановку, когда у вас на руках есть транспортир. Тогда прямую под углом 30 градусов к данной дозволено легко отложить с поддержкой него.
2. Помимо транспортира существуют и угол ьники, один из углов которых равен 30 градусам. Тогда иной угол угол ьника будет равен 60 градусам, то есть вам необходим визуально меньший угол для построения требуемой прямой.
3. Перейдем сейчас к нетривиальным способам построения угла 30 градусов. Как вестимо, синус угла 30 градусов равен 1/2. Для его построения нам надобно возвести прямоугол ьный треугол ьник. Возможен, мы можем возвести две перпендикулярные прямые. Но тангенс 30 градусов – иррациональное число, следственно соотношение между катетами мы можем посчитать лишь примерно (исключительно, если нет калькулятора), а, значит, и возвести угол в 30 градусов примерно.
4. В этом случае дозволено сделать и точное построение. Возведем вновь две перпендикулярные прямые, на которых будут располагаться катеты прямоугол ьного треугол ьника. Отложим по одной прямой катет BC какой-нибудь длины с поддержкой циркуля (B – прямой угол ). После этого увеличим длину между ножками циркуля в 2 раза, что элементарно. Проводя окружность с центром в точке C с радиусом этой длины, обнаружим точку пересечения окружности с иной прямой. Эта точка и будет точкой A прямоугол ьного треугол ьника ABC, а угол A будет равен 30 градусам.
5. Возвести угол в 30 градусов дозволено и с поддержкой окружности, применяя то, что он равен ?/6. Возведем окружность с радиусом OB. Разглядим в теории треугол ьник, где OA = OB = R – радиус окружности, где угол OAB = 30 градусов. Пускай OE – высота этого равнобедренного треугол ьника, а, следственно, и его биссектриса и медиана. Тогда угол AOE = 15 градусов, и, по формуле половинного угла, sin(15o) = (sqrt(3)-1)/(2*sqrt(2)).Следственно, AE = R*sin(15o). Отсель, AB = 2AE = 2R*sin(15o). Строя окружность радиусом BA с центром в точке B, обнаружим точку пересечения A этой окружности с начальной. Угол AOB будет равен 30 градусам.
6. Если мы можем определять длину дуг каким-нибудь образом, то, отложив дугу длиной ?*R/6, мы также получим угол в 30 градусов.
Обратите внимание!
Нужно помнить, что в 5 пункте мы можем возвести угол лишь приближенно, потому что в вычислениях будут фигурировать иррациональные числа.
Шестиугольником называют частный случай полигона – фигуры, образованной большинством точек плоскости, ограниченным замкнутой полилинией. Положительный шестиугольник (гексагон), в свою очередь, также является частным случаем – это полигон с шестью равными сторонами и равными углами. Эта фигура знаменательна тем, что длина всей из ее сторон равна радиусу описанной вокруг фигуры окружности.
Вам понадобится
Инструкция
1. Выберите длину стороны шестиугольника. Возьмите циркуль и установите расстояние между концом иглы, расположенной на одной из его ножек, и концом грифеля, расположенным на иной ножке, равным длине стороны вычерчиваемой фигуры. Для этого дозволено воспользоваться линейкой либо предпочесть случайное расстояние, если данный момент несущественен. Зафиксируйте ножки циркуля винтом, если есть такая вероятность.
2. Нарисуйте окружность при помощи циркуля. Выбранное расстояние между ножками будет являться радиусом окружности.
3. Разбейте окружность точками на шесть равных частей. Эти точки будут являться вершинами углов шестиугольника и, соответственно, окончаниями отрезков, представляющих его стороны.
4. Ножку циркуля с иглой установите в произвольную точку, находящуюся на линии очерченной окружности. Игла должна верно проткнуть линию. От точности установки циркуля напрямую зависит точность построений. Очертите циркулем дугу так, дабы она пересекла в 2-х точках окружность, начерченную первой.
5. Переставьте ножку циркуля с иглой в одну из точек пересечения начерченной дуги с изначальной окружностью. Вычертите еще одну дугу, также пересекающую окружность в 2-х точках (одна из них совпадет с точкой предыдущего расположения иглы циркуля).
6. Сходственным же образом переставляйте иглу циркуля и вычерчивайте дуги еще четыре раза. Перемещайте ножку циркуля с иглой в одном направлении по окружности (неизменно по либо вопреки часовой стрелки). В итоге обязаны быть выявлены шесть точек пересечения дуг с изначально построенной окружностью.
7. Нарисуйте положительный шестиугольник. Ступенчато попарно объедините отрезками полученные на предыдущем шаге шесть точек. Вычерчивайте отрезки при помощи карандаша и линейки. В итоге будет получен верный шестиугольник. Позже осуществления построения дозволено стереть вспомогательные элементы (дуги и окружность).
Обратите внимание!
Имеет толк выбирать такое расстояние между ножками циркуля, дабы угол между ними был равен 15-30 градусов, напротив при осуществлении построений данное расстояние может легко сбиться.
При строительстве либо разработке домашних дизайн-планов зачастую требуется возвести угол , равный теснее имеющемуся. На поддержка приходят образцы и школьные умения геометрии.
Инструкция
1. Угол образуют две прямые, исходящие из одной точки. Эта точка будет именоваться вершиной угла, а линии будут являться сторонами угла.
2. Для обозначения углов используйте три буквы: одна у вершины, две у сторон. Называют угол , начиная с той буквы, которая стоит у одной стороны, дальше называют букву, стоящую у вершины, и после этого букву у иной стороны. Используйте и другие методы для обозначения углов, если вам комфортнее напротив. Изредка называют только одну букву, которая стоит у вершины. А дозволено обозначать углы греческими буквами, скажем, α, β, γ.
3. Встречаются обстановки, когда нужно начертить угол , дабы он был равен теснее данному углу. Если при построении чертежа применять транспортир вероятности нет, дозволено обойтись только линейкой и циркулем. Возможен, на прямой, обозначенной на чертеже буквами MN, надобно возвести угол у точки К, так, дабы он был равен углу В. То есть из точки K нужно провести прямую, образующую с линией MN угол , тот, что будет равен углу В.
4. В начале подметьте по точке на всей стороне данного угла, скажем, точки А и С, дальше объедините точки С и А прямой линией. Получите треугол ьник АВС.
5. Теперь постройте на прямой MN такой же треугол ьник, дабы его вершина В находилась на линии в точке К. Используйте правило построения треугол ьника по трем сторонам. Отложите от точки К отрезок KL. Он должен быть равен отрезку ВС. Получите точку L.
6. Из точки K вычертите окружность радиусом равным отрезку ВА. Из L вычертите окружность радиусом СА. Полученную точку (Р) пересечения 2-х окружностей объедините с К. Получите треугол ьник КPL, тот, что будет равен треугол ьнику ABC. Так вы получите угол К. Он и будет равен углу В. Дабы это построение сделать комфортнее и стремительней, от вершины В отложите равные отрезки, применяя один раствор циркуля, не сдвигая ножек, опишите этим же радиусом из точки К окружность.
Видео по теме
Обратите внимание!
Избегайте случайного метаморфозы расстояния между ножками циркуля. В этом случае шестиугольник может получиться неправильным.
Полезный совет
Имеет толк изготавливать построения при помощи циркуля с отлично заточенным грифелем. Так построения будут особенно точны.
Первый способ — по данной стороне S с помощью транспортира.
Проводим прямую и откладываем на ней AB = S; принимаем эту линию за радиус и этим радиусом из точек A и В описываем дуги: далее с помощью транспортира строим в этих точках углы в 108°, стороны которых пересекутся с дугами в точках С и D; из этих точек радиусом АВ = 5 описываем дуги, которые пересекутся в Е, и прямыми линиями соединяем точки Л, С, Е, D, В.
Полученный пятиугольник — искомый.
Первый способ построения пятиугольника
Второй способ. Проведем окружность радиусом r. Из точки А циркулем проводим дугу радиуса AM до пересечения в точках В и С с окружностью. Соединяем В и С линией, которая пересечет горизонтальную ось в точке Е.
Затем из точки Е проводим дугу, которая пересечет горизонтальную линию в точке О. Описываем, наконец, из точки F дугу, которая пересечет окружность в точках Н и К. Отложив по окружности расстояние FO = FH = FK пять раз и соединив точки деления линиями, получим правильный пятиугольник.
Второй способ построения пятиугольника
Третий способ. В данный круг вписать правильный пятиугольник. Проводим два взаимно перпендикулярных диаметра АВ и МС. Делим радиус АО точкой Е пополам. Из точки Е, как из центра, проводим дугу окружности радиуса ЕМ и засекаем ею диаметр АВ в точке F. Отрезок MF равен стороне искомого правильного пятиугольника. Раствором циркуля, равным MF, делаем засечки N1, Р1, Q1, К1 и соединяем их прямыми.
Третий способ построения пятиугольника
На рисунке построен шестиугольник по данной стороне.
Построение шестиугольника
Прямой АВ = 5, как радиусом, из точек А и В описываем дуги, которые пересекутся в С; из этой точки тем же радиусом описываем окружность, на которой сторона А В отложится 6 раз.
Шестиугольник ADEFGB — искомый.
«Отделка комнат при ремонте»,
Н.П.Краснов
Построение вписанных и описанных правильных многоугольников сводится, как уже было сказано, к делению окружности на столько равных частей, сколько в многоугольнике сторон. Однако точное деление окружности путем геометрического построения возможно лишь на 3, 4, 5 и 15 равных частей, а также при делении на число частей, получаемое последовательным удвоением этих чисел. В остальных случаях приходится…
Построение овала (коробовой кривой) по данной длине АВ. Делим длину ЛВ на 3 равные части и из D и Е радиусом DF описываем дуги которые пересекутся в F и G; соединяем D и E c F и G и продолжаем эти прямые, как на фигуре; далее радиусом AD = BE из точек D и Е…
Первый способ построения. Проводим горизонтальную (АВ) и вертикальную (CD) оси и из точки их пересечения М откладываем в соответствующем масштабе полуоси. Наносим малую полуось от точки М на большой оси до точки Е. Эллипс, первый способ построения Делим BE на 2 части и одну наносим от точки М на большой оси (до F или H)…
Основанием для нанесения росписи служат полностью законченные окраской поверхности стен, потолков и других конструкций; роспись делается по высококачественным клеевым и масляным окраскам, сделанным под торцовку или флейц. Приступая к разработке эскиза отделки, мастер должен ясно представить себе всю композицию в бытовой обстановке и отчетливо осознать творческий замысел. Только при соблюдении этого основного условия можно правильно…
Обмер выполненных работ, за исключением особо оговоренных случаев, производится по площади действительно обработанной поверхности с учетом ее рельефа и за вычетом необработанных мест. Для определения действительно обработанных поверхностей при малярных работах следует пользоваться переводными коэффициентами, приведенными в таблицах. А. Деревянные оконные устройства (обмер производится по площади проемов по наружному обводу коробок) Наименование устройств Коэффициент при…
Пятиугольник построение. Как построить и нарисовать правильный пятиугольник по окружности
Построение вписанного в окружность правильного пятиугольника. Дан правильный многоугольник, число сторон которого представляет собой произведение натуральных чисел k и m, где m>2. Как построить правильный m-угольник? Гаусс показал также возможность построения правильного 257-угольника с помощью циркуля и линейки.
Построить пятиугольник и поможет именно эта окружность. В первую очередь необходимо построить циркулем окружность. Аналогичным образом необходимо построить еще один круг. Центр его в G. Точка пересечения его с первоначальной окружностью пусть будет H. Это последняя вершина правильного многоугольника.
Правда, процесс это достаточно длительный, как, впрочем, и построение любого правильного многоугльника с нечетным количеством сторон. Она и представляет собой многоугольник, остается только ввести параметры. Число сторон может достигать 1024. Можно использовать и командную строку, в зависимости от версии набрав « _polygon» или «мн.-угол».
Деление окружности на равные части и вписывание правильных многоугольников.
Введите туда цифру «5» и нажмите Enter. Вам будет предложено определить центр пятиугольника. Можно обозначить их как (0,0), но могут быть и любые другие данные. Пятиугольник может быть описанным вокруг окружности или вписанным в нее, но можно построить его и по заданному размеру стороны. Пятиугольник по заданной стороне сначала строится точно так же. Выберите «Рисование», замкнутую полилинию и введите число сторон.
В командной строке наберите координаты начальной и конечной точек одной из сторон пятиугольника. После этого пятиугольник появится на экране. Таким нехитрым способом можно построить не только пятиугольник. Для того чтобы построить треугольник, необходимо разведите ножки циркуля на расстояние, равное радиусу окружности.
Две точки пересечения окружностей, а так же точка, в которой была ножка циркуля образуют три вершины правильного треугольника. Оказалось, что есть несколько различных вариантов построения правильного пятиугольника, разработанных известными математиками. Восьмиугольник — это геометрическая фигура с восемью углами. Правильный восьмиугольник – это восьмиугольник, у которого все стороны (и углы) равны. Эта статья расскажет вам, как сделать восьмиугольник.
Окружность, дуги и многоугольники.
Определите длину стороны восьмиугольника (углы правильного восьмиугольника известны). На листе бумаги при помощи линейки нарисуйте прямую линию выбранной длины. Это первая сторона восьмиугольника (нарисуйте ее так, чтобы оставить место для рисования других сторон). Используя транспортир, отложите угол в 135o (от начала или конца первой стороны). Нарисуйте третью линию выбранной длины под углом в 135o ко второй линии. Продолжайте до тех пор, пока у вас не получится правильный восьмиугольник.
Таким образом, чем больше окружность, тем больше фигура (и наоборот). Нарисуйте вторую большую окружность, установив иглу циркуля в центре первой окружности. Установите иглу циркуля в прямо противоположной точке пересечения внутренней (малой) окружности и ее диаметра. У вас получится «глаз» в середине окружности. Нарисуйте две дуги, пересекающие внутреннюю окружность.
Построение правильных многоугольников по заданной стороне
Сотрите окружности, линии и дуги, оставив только восьмиугольник. Таким образом, вы придадите ему восьмиугольную форму. Используйте линейку, чтобы убедиться, что все стороны получились равными (так как вы делаете правильный восьмиугольник). Не загибайте углы так, чтобы они соприкасались друг с другом; в этом случае вы получите не восьмиугольник, а небольшой квадрат. Зачастую, когда говорят «восьмиугольник», имеют в виду правильный восьмиугольник.
Смотреть что такое «Правильный пятиугольник» в других словарях:
Таким образом, создав фигуру с восемью сторонами разной длины, вы получите неправильный восьмиугольник. Существуют многоугольники с пересекающимися сторонами. Например, пятиконечная звезда является многоугольником с пересекающимися сторонами. Правильные многоугольники уже в глубокой древности считались символом красоты и совершенства. Практическая задача построения таких многоугольников с помощью циркуля и линейки имеет давнюю историю.
Лишь в 1796 г. К. Ф. Гаусc доказал принципиальную невозможность этого построения с помощью только циркуля и линейки. В настоящем параграфе мы предлагаем вам самим поискать способы построения правильных многоугольников, вписанных в данную окружность или имеющих заданную сторону. Не менее важное практическое значение имеют методы приближенного построения в тех случаях, когда точное построение циркулем и линейкой неосуществимо.
Правильный пятиугольник — это многоугольник, у которого все пять сторон и все пять углов равны между собой. Вокруг него легко описать окружность. Теперь на окружности радиуса AО от любой точки последовательно отложим 11 дуг, каждая из которых равна дуге АВ. Получим вершины правильного двенадцатиугольника. Построение правильного пятиугольника по данной его стороне. Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника.
Уровень сложности: Несложно
1 шаг
Сначала, выбирайте, где разместить центр окружности. Там нужно поставить начальную точку, пусть она называется О. С помощью циркуля вычерчиваем вокруг нее окружность заданного диаметра или радиуса.
2 шаг
Затем проводим две оси через точку О, центр окружности, одна горизонтальная, другая под 90 градусов по отношению к ней – вертикальная. Точки пересечения по горизонтали назовем слева на право А и В, по вертикали, сверху вниз – М и Н. Радиус, который лежит на любой оси, например, на горизонтальной в правой части, делим пополам. Это можно сделать так: циркуль с радиусом известной нам окружности устанавливаем острием в точку пересечения горизонтальной оси и окружности – В, отчеркиваем пересечения с окружностью, полученные точки называем, соответственно сверху вниз – С и Р, соединяем их отрезком, который будет пересекать ось ОВ, точку пересечения называем К.
3 шаг
Соединяем точки К и М и получаем отрезок КМ, устанавливаем циркуль в точку М, задаем на нем расстояние до точки К и очерчиваем метки на радиусе ОА, эту точку называем Е, далее ведем циркуль до пересечения с левой верхней частью окружности ОМ. Эту точку пересечения называем F. Расстояние равное отрезку МЕ является искомой стороной равностороннего пятиугольника. При этом точка М будет являться одной вершиной встраиваемого в окружность пятиугольника, а точка F – другой.
4 шаг
Далее из полученных точек по всей окружности отчерчиваем циркулем расстояния, равные отрезку МЕ, всего точек должно получиться 5. Соединяем все точки отрезками – получаем пятиугольник, вписанный в окружность.
- При черчении будьте аккуратны в измерениях расстояний, не допускайте погрешностей, чтобы пятиугольник действительно полчился равносторонним
Эта фигура является многоугольником с минимальным количеством углов, которым невозможно замостить площадь. Только у пятиугольника количество диагоналей совпадает с количеством его сторон. Воспользовавшись формулами для произвольного правильного многоугольника, можно определить все необходимые параметры, которые имеет пентагон. Например, вписать его в окружность с заданным радиусом либо построить на базе заданной боковой стороны.
Как правильно начертить луч и какие принадлежности для черчения вам понадобятся? Возьмите листок бумаги и отметьте в произвольном месте точку. Затем приложите линейку и проведите линию, начиная с указанной точки и до бесконечности. Чтобы начертить ровную линию, нажмите клавишу «Shift»и проведите линию нужной длины. Сразу после начертания откроется вкладка «Формат». Уберите выделение с линии и увидите, что в начале линии появилась точка. Для создания надписи нажмите кнопку «Нарисовать надпись» и создайте поле, где будет находиться надпись.
Первый способ построения пятиугольника считается более «классическим». Получившаяся в результате построения фигура будет правильным пятиугольником. Двенадцатиугольник не является исключением, поэтому его построение будет невозможным без применения циркуля. Задача построения правильного пятиугольника сводится к задаче деления окружности на пять равных частей. Начертить пентаграмму можно с использованием простейших инструментов.
Я долго бился пытаясь этого добиться и самостоятельно найти пропорции и зависимости, но мне этого не удалось. Оказалось, что есть несколько различных вариантов построения правильного пятиугольника, разработанных известными математиками. Инересным моментов является то, что арифметически эту задачу решить только приблизительно точно, поскольку придется использовать иррациональные числа. Зато ее можно решить геометрически.
Деление окружностей. Точки пересечения этих линий с окружностью и являются вершинами квадрата. В окружности радиуса R (Шаг 1) следует провести вертикальный диаметр. В точке сопряжения N прямой и окружности прямая является касательной к окружности.
Получение с помощью полоски бумаги
Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля. Чтобы построить сторону 2-3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника. Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
А на другой конец нитки устанавливаемые карандаш и одержим. Если умеете чертить звезду, но не умеете пятиугольник, начертите звезду карандашом, затем соедините между собой соседние концы звезды, а саму звезду потом сотрите. Затем положите лист бумаги (лучше его закрепить на столе при помощи четырёх кнопок или иголочек). Приколите эти 5 полосочек к листку бумаги кнопками или иголочками, чтобы они оставались неподвижными. Затем обведите полученный пятиугольник и снимите эти полосочки с листка.
Например, нам нужно нарисовать пятиконечную звезду (пентаграмму) для картины о Советском прошлом или о настоящем Китая. Правда для этого нужно уметь создать рисунок звезды в перспективе. Точно так же вы сможете нарисовать фигуру карандашом на бумаге. Как правильно нарисовать звезду, что бы она выглядела ровно и красиво, сразу не ответишь.
С центра опусти на окружность 2 луча, чтоб угол между ними был 72 градуса (транспортиром). Деление круга на пять частей осуществляется с помощью обычного циркуля или транспортира. Поскольку правильный пятиугольник — это одна из фигур, содержащая в себе пропорции золотого сечения, его построением издавна интересовались живописцы и математики. Эти принципы построения с применением циркуля и линейки были изложены еще в эвклидовых «Началах».
5.3. Золотой пятиугольник; построение Евклида.
Замечательный пример «золотого сечения» представляет собой правильный пятиугольник – выпуклый и звездчатый (рис. 5).
Для построения пентаграммы необходимо построить правильный пятиугольник.
Пусть О — центр окружности, А — точка на окружности и Е — середина отрезка ОА. Перпендикуляр к радиусу ОА, восстановленный в точке О, пересекается с окружностью в точке D. Пользуясь циркулем, отложим на диаметре отрезок CE = ED. Длина стороны вписанного в окружность правильного пятиугольника равна DC. Откладываем на окружности отрезки DC и получим пять точек для начертания правильного пятиугольника. Соединяем углы пятиугольника через один диагоналями и получаем пентаграмму. Все диагонали пятиугольника делят друг друга на отрезки, связанные между собой золотой пропорцией.
Каждый конец пятиугольной звезды представляет собой золотой треугольник. Его стороны образуют угол 36° при вершине, а основание, отложенное на боковую сторону, делит ее в пропорции золотого сечения.
Есть и золотой кубоид- это прямоугольный параллелепипед с ребрами, имеющими длины 1.618, 1 и 0.618.
Теперь рассмотрим доказательство, предложенное Евклидом в «Началах».
Посмотрим теперь, как Евклид использует золотое сечение для того, чтобы построить угол в 72 градуса – именно под таким углом видна сторона правильного пятиугольникаиз центра описанной окружности. Начнем с
отрезка АВЕ, разделенного в среднем и
Итак, пусть АС=АЕ. Обозначим через a равные углы ЕВС и СЕВ. Так как АС=АЕ, то угол АСЕ также равен a. Теорема о том, что сумма углов треугольника равна 180 градусов, позволяет найти угол ВСЕ: он равен 180-2a, а угол ЕАС — 3a — 180. Но тогда угол АВС равен 180-a. Суммируя углы треугольника АВС получаем,
180=(3a -180) + (3a-180) + (180 — a)
Откуда 5a=360, значит a=72.
Итак, каждый из углов при основании треугольника ВЕС вдвое больше угла при вершине, равного 36 градусов. Следовательно, чтобы построить правильный пятиугольник, необходимо лишь провести любую окружность с центром в точке Е, пересекающую ЕС в точке Х и сторону ЕВ в точке Y: отрезок XY служит одной из сторон вписанного в окружность правильного пятиугольника; Обойдя вокруг всей окружности, можно найти и все остальные стороны.
Докажем теперь, что АС=АЕ. Предположим, что вершина С соединена отрезком прямой с серединой N отрезка ВЕ. Заметим, что поскольку СВ=СЕ, то угол СNЕ прямой. По теореме Пифагора:
CN 2 = а 2 – (а/2j) 2 = а 2 (1-4j 2)
Отсюда имеем (АС/а) 2 = (1+1/2j) 2 + (1-1/4j 2) = 2+1/j = 1 + j =j 2
Итак, АС = jа = jАВ = АЕ, что и требовалось доказать
5.4.Спираль Архимеда.
Последовательно отсекая от золотых прямоугольников квадраты до бесконечности, каждый раз соединяя противоположные точки четвертью окружности, мы получим довольно изящную кривую. Первым внимание на неё обратил древнегреческий ученый Архимед, имя которого она и носит. Он изучал её и вывел уравнение этой спирали.
В настоящее время спираль Архимеда широко используется в технике.
6.Числа Фибоначчи.
С золотым сечением косвенно связано имя итальянского математика Леонардо из Пизы, который известен больше по своему прозвищу Фибоначчи (Fibonacci — сокращенное filius Bonacci, то есть сын Боначчи)
В 1202г. им была написана книга «Liber abacci», то есть «Книга об абаке» . «Liber abacci» представляет собой объемистый труд, содержащий почти все арифметические и алгебраические сведения того времени и сыгравший заметную роль в развитии математики в Западной Европе в течение нескольких следующих столетий. В частности, именно по этой книге европейцы познакомились с индусскими («арабскими») цифрами.
Сообщаемый в книге материал поясняется на большом числе задач, составляющих значительную часть этого трактата.
Рассмотрим одну такую задачу:
«Сколько пар кроликов в один год от одной пары рождается?
Некто поместил пару кроликов в некоем месте, огороженном со всех сторон стеной, дабы узнать, сколько пар кроликов родится в течение этого года, если природа кроликов такова, что через месяц пара кроликов воспроизведет другую, а рождают кролики со второго месяца после своего рождения»
| Месяцы | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Пары кроликов | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 | 377 |
Перейдем теперь от кроликов к числам и рассмотрим следующую числовую последовательность:
u 1 , u 2 … u n
в которой каждый член равен сумме двух предыдущих, т.е. при всяком n>2
u n =u n -1 +u n -2 .
Данная последовательность асимптотически (приближаясь все медленнее и медленнее) стремится к некоторому постоянному соотношению. Однако, это соотношение иррационально, то есть представляет собой число с бесконечной, непредсказуемой последовательностью десятичных цифр в дробной части. Его невозможно выразить точно.
Если какой-либо член последовательности Фибоначчи разделить на предшествующий ему (например, 13:8), результатом будет величина, колеблющаяся около иррационального значения 1.61803398875… и через раз то превосходящая, то не достигающая его.
Асимптотическое поведение последовательности, затухающие колебания ее соотношения около иррационального числа Ф могут стать более понятными, если показать отношения нескольких пеpвых членов последовательности. В этом примере приведены отношения второго члена к первому, третьего ко второму, четвертого к третьему, и так далее:
1:1 = 1.0000, что меньше фи на 0.6180
2:1 = 2.0000, что больше фи на 0.3820
3:2 = 1.5000, что меньше фи на 0.1180
5:3 = 1.6667, что больше фи на 0.0486
8:5 = 1.6000, что меньше фи на 0.0180
По мере продвижения по суммационной последовательности Фибоначчи каждый новый член будет делить следующий со все большим и большим приближением к недостижимому Ф.
Человек подсознательно ищет Божественную пропорцию: она нужна для удовлетворения его потребности в комфорте.
Пpи делении любого члена последовательности Фибоначчи на следующий за ним получается просто обратная к 1.618 величина (1: 1.618=0.618). Hо это тоже весьма необычное, даже замечательное явление. Поскольку пеpвоначальное соотношение – бесконечная дpобь, у этого соотношения также не должно быть конца.
При делении каждого числа на следующее за ним через одно, получаем число 0.382
Подбирая таким образом соотношения, получаем основной набор коэффициентов Фибоначчи: 4.235 ,2.618 ,1.618,0.618,0.382,0.236.Упомянем также 0.5.Все они играют особую роль в природе и в частности в техническом анализе.
Тут необходимо отметить, что Фибоначчи лишь напомнил свою последовательность человечеству, так как она была известна еще в древнейшие времена под названием Золотое сечение.
Золотое сечение, как мы видели, возникает в связи с правильным пятиугольником, поэтому и числа Фибоначчи играют роль во всем, что имеет отношение к правильным пятиугольникам — выпуклым и звездчатым.
Ряд Фибоначчи мог бы остаться только математическим казусом, если бы не то обстоятельство, что все исследователи золотого деления в растительном и в животном мире, не говоря уже об искусстве, неизменно приходили к этому ряду как арифметическому выражению закона золотого деления. Ученые продолжали активно развивать теорию чисел Фибоначчи и золотого сечения. Ю. Матиясевич с использованием чисел Фибоначчи решает 10-ю проблему Гильберта (о решении Диофантовых уравнений). Возникают изящные методы решения ряда кибернетических задач (теории поиска, игр, программирования) с использованием чисел Фибоначчи и золотого сечения. В США создается даже Математическая Фибоначчи-ассоциация, которая с 1963 года выпускает специальный журнал.
Одним из достижений в этой области является открытие обобщенных чисел Фибоначчи и обобщенных золотых сечений. Ряд Фибоначчи (1, 1, 2, 3, 5, 8) и открытый им же «двоичный» ряд чисел 1, 2, 4, 8, 16…(то есть ряд чисел до n , где любое натуральное число, меньшее n можно представить суммой некоторых чисел этого ряда) на первый взгляд совершенно разные. Но алгоритмы их построения весьма похожи друг на друга: в первом случае каждое число есть сумма предыдущего числа с самим собой 2 = 1 + 1; 4 = 2 + 2…, во втором – это сумма двух предыдущих чисел 2 =1 + 1, 3 = 2 + 1, 5 = 3 + 2…. Нельзя ли отыскать общую математическую формулу, из которой получаются и «двоичный» ряд, и ряд Фибоначчи?
Действительно, зададимся числовым параметром S, который может принимать любые значения: 0, 1, 2, 3, 4, 5… Рассмотрим числовой ряд, S + 1 первых членов которого – единицы, а каждый из последующих равен сумме двух членов предыдущего и отстоящего от предыдущего на S шагов. Если n-й член этого ряда мы обозначим через S (n), то получим общую формулу S (n) = S (n – 1) + S (n – S – 1).
Очевидно, что при S = 0 из этой формулы мы получим «двоичный» ряд, при S = 1 –ряд Фибоначчи, при S = 2, 3, 4. новые ряды чисел, которые получили название S-чисел Фибоначчи.
В общем виде золотая S-пропорция есть положительный корень уравнения золотого S-сечения x S+1 – x S – 1 = 0.
Нетрудно показать, что при S = 0 получается деление отрезка пополам, а при S = 1 – знакомое классическое золотое сечение.
Отношения соседних S-чисел Фибоначчи с абсолютной математической точностью совпадают в пределе с золотыми S-пропорциями! То есть золотые S-сечения являются числовыми инвариантами S-чисел Фибоначчи.
7.Золотое сечение в искусстве.
7.1. Золотое сечение в живописи.
Переходя к примерам «золотого сечения» в живописи, нельзя не остановить своего внимания на творчестве Леонардо да Винчи. Его личность – одна из загадок истории. Сам Леонардо да Винчи говорил: «Пусть никто, не будучи математиком, не дерзнет читать мои труды».
Нет сомнений, что Леонардо да Винчи был великим художником, это признавали уже его современники, но его личность и деятельность останутся покрытыми тайной, так как он оставил потомкам не связное изложение своих идей, а лишь многочисленные рукописные наброски, заметки, в которых говорится «обо всем на свете».
Портрет Монны Лизы (Джоконды) долгие годы привлекает внимание исследователей, которые обнаружили, что композиция рисунка основана на золотых треугольниках, являющихся частями правильного звездчатого пятиугольника..
Также пропорция золотого сечения проявляется в картине Шишкина. На этой знаменитой картине И. И. Шишкина с очевидностью просматриваются мотивы золотого сечения. Ярко освещенная солнцем сосна (стоящая на первом плане) делит длину картины по золотому сечению. Справа от сосны — освещенный солнцем пригорок. Он делит по золотому сечению правую часть картины по горизонтали.
В картине Рафаэля «Избиение младенцев» просматривается другой элемент золотой пропорции — золотая спираль. На подготовительном эскизе Рафаэля проведены красные линии, идущие от смыслового центра композиции — точки, где пальцы воина сомкнулись вокруг лодыжки ребенка — вдоль фигур ребенка, женщины, прижимающей его к себе, воина с занесенным мечом и затем вдоль фигур такой же группы в правой части эскиза. Неизвестно, строил ли Рафаэль золотую спираль или чувствовал её.
Т.Кук использовал при анализе картины Сандро Боттичелли «рождение Венеры» золотое сеченеие.
7.2. Пирамиды золотого сечения.
Широко известны медицинские свойства пирамид, особенно золотого сечения. По некоторым наиболее распространенным мнениям, комната, в которой находится такая пирамида, кажется больше, а воздух — прозрачнее. Сны начинают запоминаться лучше. Также известно, что золотое сечение широко применялась в архитектуре и скульптуре. Примером тому стали: Пантеон и Парфенон в Греции, здания архитекторов Баженова и Малевича
8. Заключение.
Необходимо сказать, что золотое сечение имеет большое применение в нашей жизни.
Было доказано, что человеческое тело делится в пропорции золотого сечения линией пояса.
Раковина наутилуса закручена подобно золотой спирали.
Благодаря золотому сечению был открыт пояс астероидов между Марсом и Юпитером – по пропорции там должна находиться ещё одна планета.
Возбуждение струны в точке, делящей её в отношении золотого деления, не вызовет колебаний струны, то есть это точка компенсации.
На летательных аппаратах с электромагнитными источниками энергии создаются прямоугольные ячейки с пропорцией золотого сечения.
Джоконда построена на золотых треугольниках, золотая спираль присутствует на картине Рафаэля «Избиение младенцев».
Пропорция обнаружена в картине Сандро Боттичелли «Рождение Венеры»
Известно много памятников архитектуры, построенных с использованием золотой пропорции, в том числе Пантеон и Парфенон в Афинах, здания архитекторов Баженова и Малевича.
Иоанну Кеплеру, жившему пять веков назад, принадлежит высказывание: «Геометрия обладает двумя великими сокровищами. Первое — это теорема Пифагора, второе — деления отрезка в крайнем и среднем отношении»
Список литературы
1. Д. Пидоу. Геометрия и искусство. – М.: Мир, 1979.
2. Журнал «Наука и техника»
3. Журнал «Квант», 1973, № 8.
4. Журнал «Математика в школе», 1994, № 2; № 3.
5. Ковалев Ф.В. Золотое сечение в живописи. К.: Выща школа, 1989.
6. Стахов А. Коды золотой пропорции.
7.Воробьев Н.Н. «Числа Фибоначчи» — М.: Наука 1964
8. «Математика — Энциклопедия для детей» М.: Аванта +, 1998
9. Информация из интернета.
Матриц Фибоначчи и так называемых «золотых» матриц, новые компьютерные арифметики, новая теорию кодирования и новая теория криптографии. Суть новой науки, в пересмотре с точки зрения золотого сечения всей математики, начиная с Пифагора, что, естественно, повлечет в теории новые и наверняка очень интересные математические результаты. В практическом отношении – «золотую» компьютеризацию. А поскольку…
Не повлияют на этот результат. Основание золотой пропорции является инвариантом рекурсивных соотношений 4 и 6. В этом проявляется «устойчивость» золотого сечения, одного из принципов организации живой материи. Так же, основание золотой пропорции является решением двух экзотических рекурсивных последовательностей (рис 4.) Рис. 4 Рекурсивных последовательности Фибоначчи так…
Уха — j5, а расстояние от уха до макушки — j6 . Таким образом, в этой статуе мы видим геометрическую прогрессию со знаменателем j: 1, j, j2, j3, j4, j5, j6. (рис.9). Таким образом, золотое сечение – один из основополагающих принципов в искусстве античной Греции. Ритмы сердца и мозга. Равномерно бьется сердце человека – около 60 ударов в минуту в состоянии покоя. Сердце как поршень сжимает…
Без изучения техники этого процесса не обойтись. Существует несколько вариантов выполнения работы. Как нарисовать звезду с помощью линейки, помогут понять самые известные методы этого процесса.
Разновидности звезд
Существует множество вариантов внешнего вида такой фигуры, как звезда.
Еще с древних времен пятиконечная ее разновидность использовалась для начертания пентаграмм. Это объясняется ее свойством, которое позволяет сделать рисунок, не отрывая ручки от бумаги.
Существуют также шестиконечные, хвостатые кометы.
Пять вершин традиционно имеет морская звезда. Такой же формы нередко встречаются изображения рождественского варианта.
В любом случае, чтобы нарисовать пятиконечную звезду поэтапно, необходимо прибегнуть к помощи специальных инструментов, так как изображение от руки вряд ли будет выглядеть симметрично и красиво.
Выполнение чертежа
Чтобы понять, как нарисовать ровную звезду, следует осознать суть этой фигуры.
Основой для ее начертания является ломаная линия, концы которой сходятся в начальной точке. Она образовывает правильный пятиугольник — пентагон.
Отличительными свойствами такой фигуры являются возможности вписания ее в окружность, а также окружности в этот многоугольник.
Все стороны пентагона равны между собой. Понимая, как правильно выполнить чертеж, можно осознать суть процесса построения всех фигур, а также разнообразных схем деталей, узлов.
Для достижения такой цели, как нарисовать звезду с помощью линейки, необходимо владеть знаниями о простейших математических формулах, являющихся основополагающими в геометрии. А также потребуется умение считать на калькуляторе. Но самое главное — это логическое мышление.
Работа не является сложной, но она потребует точности и скрупулезности. Потраченные усилия будут вознаграждены хорошим симметричным, а потому и красивым изображением пятиконечной звезды.
Классическая техника
Самый известный способ того, как нарисовать звезду при помощи циркуля, линейки и транспортира, является достаточно несложным.
Для этой методики понадобится несколько инструментов: циркуль или транспортир, линейка, простой карандаш, ластик и лист белой бумаги.
Чтобы понять, как красиво нарисовать звезду, действовать следует последовательно, этап за этапом.
Можно в работе воспользоваться специальными вычислениями.
Расчет фигуры
На этом этапе рисования правильной звезды проступают контуры готовой фигуры.
Если все сделано правильно, полученное изображение будет ровным. Это можно проверить визуально, вращая лист бумаги и оценивая форму. Она будет неизменной при каждом повороте.
Основные контуры наводятся при помощи линейки и простого карандаша более четко. Все вспомогательные линии убираются.
Чтобы понять, как нарисовать звезду поэтапно, следует проводить все действия вдумчиво. В случае ошибки можно подправить рисунок ластиком или провести все манипуляции заново.
Оформление работы
Готовую форму можно украсить самыми разнообразными способами. Главное — не нужно бояться экспериментировать. Фантазия подскажет оригинальный и красивый образ.
Можно разукрасить нарисованную ровную звезду простым карандашом или использовать самые разнообразные цвета и оттенки.
Чтобы разобраться в том, как нарисовать правильную звезду, необходимо придерживаться идеальных линий во всем. Поэтому самый популярный вариант оформления заключается в разделении каждого луча фигуры на две равные части линией, исходящей от вершины до центра.
Можно не разделять стороны звезды линиями. Допускается просто закрасить каждый луч фигуры более темным оттенком с одного бока.
Такой вариант также будет ответом на вопрос о том, как нарисовать правильную звезду, ведь все ее линии будут симметричны.
По желанию при эстетическом оформлении фигуры можно добавить орнамент или другие всевозможные элементы. Добавив кружочки к вершинам, можно получить звезду шерифа. Применив плавную растушевку теневых сторон, можно получить морскую звезду.
Эта техника является самой распространенной, так как без особых усилий позволяет понять, как нарисовать пятиконечную звезду поэтапно. Не прибегая к сложным математическим вычислениям, возможно получить правильное, красивое изображение.{\cir ..
Пользователи также искали:
как построить пятиугольник с заданной стороной, правильный пятиугольник диагонали, правильный пятиугольник по клеточкам, пятиугольник, Правильный, правильный, Правильный пятиугольник, правильный пятиугольник свойства, правильный пятиугольник диагонали, правильный пятиугольник площадь, неправильный пятиугольник, правильный пятиугольник по клеточкам, правильный пятиугольник углы, формулы, свойства, диагонали, площадь, неправильный, клеточкам, построить, заданной, стороной, углы, правильный пятиугольник формулы, как построить пятиугольник с заданной стороной, правильный пятиугольник, правильные многоугольники. правильный пятиугольник,
Определение выпуклого многоугольника — математическая открытая ссылка
Определение выпуклого многоугольника — математическая открытая ссылка Определение: многоугольник, в котором есть все внутренние углы менее 180 °(Результат: все вершины направлены «наружу», от центра.)
Попробуй это Отрегулируйте многоугольник ниже, перетащив любую оранжевую точку. Если какая-либо вершина указывает «внутрь» к центру многоугольника, она перестает быть выпуклым многоугольником.
Выпуклый многоугольник определяется как многоугольник, все внутренние углы которого меньше 180 °.Это означает, что все вершины многоугольник будет указывать наружу, от внутренней части фигуры. Думайте об этом как о «выпуклом» многоугольнике. Обратите внимание, что треугольник (3-угольник) всегда выпуклый.
Выпуклый многоугольник противоположен вогнутому многоугольнику. Видеть Вогнутый многоугольник.
На рисунке выше перетащите любую из вершин с помощью мыши. Обратите внимание на то, что нужно, чтобы сделать многоугольник выпуклым или вогнутым. Также измените количество сторон.
Свойства выпуклого многоугольника
Линия, проведенная через выпуклый многоугольник , пересечет многоугольник ровно дважды, как это видно на рисунке слева.Вы также можете видеть, что линия разделит многоугольник ровно на две части.
Все диагонали выпуклого многоугольника целиком лежат внутри многоугольника. См. Рисунок слева. (В вогнутый многоугольник, некоторые диагонали будут лежать вне многоугольника).
Площадь неправильного выпуклого многоугольника можно найти, разделив его на треугольники и просуммировав площади треугольника. См. Площадь неправильного многоугольника
Правильные многоугольники всегда выпуклые по определению.См. Определение правильного многоугольника. На рисунке вверху страницы нажмите «Сделать регулярным», чтобы многоугольник всегда был правильным многоугольником. Тогда вы увидите, что, что бы вы ни делали, он останется выпуклым.
Другие темы многоугольников
Общие
Типы полигонов
Площадь различных типов полигонов
Периметр различных типов полигонов
Углы, связанные с многоугольниками
Именованные полигоны
(C) Открытый справочник по математике, 2011 г.
Все права защищены.
типов многоугольников (видео) 17 различных типов и примеров
Содержание
- Что такое многоугольник?
- Типы полигонов
Многоугольники — одни из первых фигур, которые мы учимся рисовать в детстве, и они появляются вокруг нас. Многоугольники могут быть правильными или неправильными. Они могут быть простыми и сложными, выпуклыми или вогнутыми.Это могут быть знакомые формы, которые вы видите в учебниках по геометрии, или они могут быть странными, как дротики и бабочки.
Слово «многоугольник» означает «многоугольник», в переводе с греческого. Чтобы быть многоугольником, плоская замкнутая форма должна использовать только линейные сегменты для создания сторон. Таким образом, круг или любая форма, имеющая кривую, — это , а не многоугольник.Три идентифицирующих свойства любого многоугольника заключаются в следующем:
- Двумерная форма
- Закрытие в пространстве (имеющем внутреннее и внешнее)
- Сделано с прямыми сторонами
Типы полигонов
Давайте посмотрим на огромное множество форм, которые представляют собой многоугольники, и рассмотрим детали.
- Выпуклый многоугольник не имеет внутреннего угла более 180 ° (у него нет сторон, направленных внутрь). Один внутренний угол вогнутого многоугольника превышает 180 °.
- Простой многоугольник охватывает единое внутреннее пространство (границу) и не имеет самопересекающихся сторон. У сложных многоугольников есть самопересекающиеся стороны!
- Неправильный многоугольник не имеет совпадающих сторон и внутренних углов.
- Правильный многоугольник имеет совпадающие стороны и внутренние углы.
Правильные и неправильные многоугольники
Правильные многоугольники имеют совпадающие стороны и внутренние углы. Каждая сторона равна по длине любой другой стороне, и каждый внутренний угол равен всем другим внутренним углам. Количество правильных многоугольников безгранично.
Неправильные многоугольники от до , но не , имеют совпадающие стороны и углы. Домашняя пластина на поле для софтбола или бейсбола представляет собой неправильный пятиугольник, потому что у него пять сторон с двумя углами 90 °.
Выпуклые и вогнутые многоугольники
Выпуклый многоугольник замыкается во внутренней области, не выглядя «помятым». Ни один из его внутренних углов не направлен внутрь. В геометрии у вас может быть четырехсторонний многоугольник, который указывает наружу во всех направлениях, как змей , или у вас могут быть те же четыре стороны, чтобы две из них были направлены внутрь, образуя дротик . Воздушный змей выпуклый; дротик вогнутый.
Каждый внутренний угол выпуклого многоугольника меньше 180 °.Вогнутый многоугольник имеет как минимум один угол больше 180 °. Представьте себе простой шестиугольник (6 сторон) в форме галстука-бабочки. Он будет иметь два внутренних угла больше 180 °.
Простые и сложные многоугольники
Простые многоугольники не имеют самопересекающихся сторон. Сложные многоугольники , также называемые самопересекающимися многоугольниками, имеют пересекающиеся друг с другом стороны. Классическая звезда представляет собой сложный многоугольник. Большинство людей могут быстро нарисовать звезду на бумаге, но немногие называют ее пентаграммой , , сложным многоугольником или самопересекающимся многоугольником.
Семейство сложных многоугольников в форме звезды обычно имеет префикс греческого числа и суффикс -грамму: пентаграмма, гексаграмма, октаграмма и т. Д.
Вы не можете нарисовать сложный треугольник. Для каждого многоугольника с четырьмя или более сторонами можно нарисовать сложный многоугольник. Сложный четырехугольник — это знакомая форма бабочки, но считается, что у него только четыре стороны, потому что одна пара противоположных сторон скручена, чтобы пересекать друг друга.
Так же, как вы не учитываете пересекающиеся стороны как четыре отрезка линии, вы не учитываете два угла, которые они создают, как внутренние углы.Сложный четырехугольник по-прежнему имеет только четыре стороны и четыре внутренних угла.
Сложные многоугольники трудно представить, если вы не думаете о них с упругими сторонами. Если бы вы могли поднять часть многоугольника вверх и повернуть ее так, чтобы две стороны пересекались друг с другом, а затем снова положили бы ее ровно, вы бы получили сложный многоугольник. Поскольку вы скрутили две стороны, у вас все еще есть эти две стороны (их количество не удваивается при пересечении). Они также не создают новых вершин в местах пересечения.
Антипараллелограмм
Необычным сложным многоугольником является антипараллелограмм , который немного похож на крылья птицы. Антипараллелограмм (или скрещенный параллелограмм) имеет две нормальные пары совпадающих противоположных сторон, но одна пара пересекается, образуя два соприкасающихся треугольника.
Однако, как и любой параллелограмм, у антипараллелограмма есть только четыре стороны и четыре внутренних угла. Однако его диагонали выходят за рамки формы!
Имена полигонов
| Форма многоугольника | Количество сторон |
|---|---|
| Треугольник | 3-х сторонний |
| Квадрат | 4-х сторонний |
| Прямоугольник | 4-х сторонний |
| Четырехугольник | 4-х сторонний |
| Параллелограмм | 4-х сторонний |
| Ромб | 4-х сторонний |
| Дротик | 4-х сторонний |
| Воздушный змей | 4-х сторонний |
| Пентагон | 5-ти сторонний |
| Шестигранник | 6 сторон |
| Гептагон | 7 сторон |
| восьмиугольник | 8 сторон |
| Nonagon | 9 сторон |
| Десятиугольник | 10 сторон |
| Додекагон | 12 сторон |
| Икосагон | 20 сторон |
| Шестиугольник | 100 сторон |
| угольник | n стороны |
Это многоугольник?
Внутренние части всех многоугольников можно разбить на треугольники, что является удобным способом найти сумму их внутренних углов.Возьмите на два меньше, чем количество сторон, n , и умножьте на 180 °: ( n — 2) x 180 °.
Окружность — это не многоугольник, а icosikaihenagon. — это многоугольник. Икосикаихенагон — это многоугольник с 21 стороной. Большинство математиков и студентов математиков просто написали бы «21-угольник», чтобы назвать его.
Краткое содержание урока
Полигоны можно изучать и классифицировать разными способами. Теперь вы видите, что многоугольники могут быть правильными или неправильными, выпуклыми или вогнутыми, а также простыми или сложными.Когда вы видите незнакомый многоугольник, вы можете определить его свойства и правильно классифицировать.
Чтобы быть многоугольником, фигура должна быть плоской, закрытой в пространстве и состоять только из прямых сторон. Многоугольники с совпадающими сторонами и углами правильные; все остальные нерегулярны. Многоугольники со всеми внутренними углами менее 180 ° являются выпуклыми; если у многоугольника есть хотя бы один внутренний угол больше 180 °, он вогнутый. Простые многоугольники не пересекают свои стороны; у сложных многоугольников есть самопересекающиеся стороны.Многоугольники вокруг вас!
Следующий урок:
Что такое правильный многоугольник?
Что такое многоугольник? Типы | Формулы | Части | Специальные многоугольники | Имена Типы многоугольников
Формулы многоугольника Площадь правильного многоугольника = (1/2) N sin (360 ° / N) S 2 Сумма внутренних углов многоугольника = (N — 2) x 180 ° Число диагоналей в многоугольнике = 1/2 N (N-3) Части многоугольника
Особые полигоны Специальный Треугольники — правый, равносторонний, равнобедренный, разносторонний, острый, тупой. Многоугольник
Имена
Предложены имена для других полигонов.
Чтобы создать имя, объедините префикс + суффикс
Примеры: 28-сторонний многоугольник — Icosikaioctagon Однако многие люди используют форму n-угольник, например, 46-угольник или 28-угольник. этих имен. |
Полигоны — Основы работы с полигонами — Подробно
Слово многоугольник представляет собой сочетание двух греческих слов: «поли» означает «много» и «гон». означает угол.У многоугольника помимо углов есть стороны и вершины. «Три» означает «три», поэтому самый простой многоугольник называется треугольник, потому что у него три угла. Он также имеет три стороны и три вершины. Треугольник всегда компланарен, чего нельзя сказать о многих из них. другие полигоны.
Правильный многоугольник — многоугольник, все углы и стороны которого совпадают или равны. Вот некоторые правильные многоугольники.
Мы можем использовать формула, чтобы найти сумму внутренних углов любого многоугольника.В этой формуле буква n обозначает количество сторон или углов многоугольника.
сум углов = (n — 2) 180 °
Давайте использовать формула, чтобы найти сумму внутренних углов треугольника. Запасной 3 для п. Получаем, что сумма равна 180 градусам. Это важный факт, о котором следует помнить.
сум
углов = (n — 2) 180 °
= (3 — 2) 180 ° = (1) 180 ° = 180 °
Чтобы найти сумма внутренних углов четырехугольника, мы можем снова использовать формулу.На этот раз замените n на 4. Мы находим, что сумма внутренних углов четырехугольника 360 градусов.
сум
углов = (n — 2) 180 °
= (4-2) 180 ° = (2) 180 ° = 360 °
Полигоны могут быть разделенными на треугольники, нарисовав все диагонали, которые можно нарисовать из одной единственной вершины. Давайте попробуем это с четырехугольником, показанным здесь. Из вершине A мы можем провести только одну диагональ, к вершине D.Четырехугольник может поэтому разделим на два треугольника.
Если вы посмотрите вернувшись к формуле, вы увидите, что n — 2 дает количество треугольников в многоугольнике, и это число умножается на 180, сумма мер всех внутренних углов в треугольнике. Вы видите, где «н — 2 «? Это дает нам количество треугольников в многоугольнике. Как Как вы думаете, много ли треугольников будет у 5-стороннего многоугольника?
Вот пятиугольник, 5-сторонний многоугольник.Из вершины A можно провести две диагонали, разделяющие пятиугольник на три треугольника. Умножаем 3 раза на 180 градусов, чтобы найти сумма всех внутренних углов пятиугольника, составляющая 540 градусов.
сум
углов = (n — 2) 180 °
= (5-2) 180 ° = (3) 180 ° = 540 °
Ссылки по теме:
Определения многоугольников,
формулы полигонов (площадь, периметр) и имена полигонов (таблицы и формулы)
Основная геометрия: Многоугольники Учебное пособие
Многоугольники
Многоугольник — это любая замкнутая фигура с тремя или более прямыми сторонами .«Закрыто» означает, что в нем нет зияющих отверстий и что все стороны соединяются вместе.
Это многоугольники:
Это не многоугольники:
Первая фигура — это линия, которая определенно не является фигурой с более чем тремя сторонами. Извини, брат, тебя нет. У следующей формы более трех сторон, но не все они соединяются. Плохие новости, чувак, тебя тоже нет. Правильно, круг — это тоже не многоугольник . Хотя это замкнутая фигура, очень сложно подсчитать количество сторон у круга, потому что у него их нет.Окончательная форма замкнута, и у нее более трех сторон, но две из них изогнуты. Это не прямые линии, так что еще раз извините, Чарли.
Названия некоторых общих многоугольников
| Число сторон | Число углов | Название | ||
| 3 | 3 | Треугольник | 4184 | 4186 9019 Четырехугольник |
| 5 | 5 | Пятиугольник | ||
| 6 | 6 | Шестигранник | ||
| 7 | 7 | Септагон | 6 | |
| 9 | 9 | Nonagon | ||
| 10 | 10 | Decagon | ||
| 12 | 12 | Dodecab | Dodecabab |
- Угол : форма, образующаяся, когда два луча встречаются в общей точке. АКА «уголок».
- Вершина : точка, где встречаются два луча; угловая точка многоугольника. Множественное число вершин — это вершины.
- Сторона : прямая кромка многоугольника.
- Выпуклый многоугольник: многоугольник, внутренний угол которого не превышает 180 °.
- Вогнутый многоугольник: многоугольник с хотя бы одним внутренним углом больше 180 °.
- Равноугольный : фигура, где все углы равны по размеру.
- Равносторонний : фигура, у которой все стороны равны по длине.
- Правильный многоугольник : равносторонний равносторонний многоугольник.
Многоугольники могут быть выпуклыми или вогнутыми. Мы привыкли видеть чаще всего выпуклые многоугольники: квадраты, треугольники, пятиугольники и т. Д.Все вершины выпуклых многоугольников направлены наружу от центра. Официально каждый внутренний угол выпуклого многоугольника меньше 180 °, и это то, что указывает на все вершины. Это примеры выпуклых многоугольников.
Если мы проведем линию через любой из этих выпуклых многоугольников, линия будет пересекать только 2 стороны многоугольника.
Вогнутые многоугольники имеют некоторые углы, которые обращены к центру, как пещера, для мошенников… вогнутая… понятно? Пример вогнутого многоугольника — пятиконечная звезда.Обратите внимание, что некоторые углы направлены от центра, как точки звезды, а некоторые — к центру, как углы между точками звезды. Вогнутый многоугольник имеет один или несколько внутренних углов больше 180 °. Вот несколько примеров вогнутых многоугольников.
Если мы проведем линию через любой из этих вогнутых многоугольников, возможно, что линия может пересекать более чем две стороны.
Равносторонние и равносторонние
Некоторые полигоны любят играть честно.Они следят за тем, чтобы все их углы были одинаковыми, чтобы ни один угол не был больше или меньше любого другого. Такие многоугольники называются равноугольными. Прямоугольники равноугольные, потому что все четыре угла равны 90 °. Чтобы многоугольник был равноугольным, стороны не должны быть равной длины.
Некоторые многоугольники , например , имеют одинаковую длину всех сторон, их называют равносторонними. Ромб — это пример равностороннего многоугольника, потому что у него четыре равные стороны, хотя углы не равны.
А еще есть многоугольники, которые действительно хороши и хотят, чтобы все их стороны были равны, а все их углы были равны. Это один супер-красивый, равносторонний и равносторонний многоугольник. Он настолько хорош, что получил собственное название: это правильный многоугольник.
Правильные многоугольники
Вы, наверное, знакомы с этими формами. Все стороны имеют одинаковую длину и все углы одинаковой меры.
Они не являются правильными
Основание и высота многоугольника
- Основание : нижняя сторона многоугольника.
- Высота : высота многоугольника — это расстояние по перпендикуляру от самой верхней вершины до основания. Высота и основание ВСЕГДА образуют прямой угол.
Сумма углов многоугольников
Когда вы начинаете с многоугольника с четырьмя или более сторонами и рисуете все возможные диагонали из одной вершины, многоугольник затем делится на несколько неперекрывающихся треугольников. Рисунок иллюстрирует это деление с помощью семиугольного многоугольника. Сумма внутренних углов этого многоугольника теперь может быть найдена умножением количества треугольников на 180 °.При исследовании обнаруживается, что количество треугольников всегда на два меньше, чем количество сторон. Этот факт утверждается в виде теоремы.
Рисунок 1 Триангуляция семистороннего многоугольника для нахождения суммы внутренних углов.
Теорема 39: Если у выпуклого многоугольника n сторон, то сумма его внутренних углов определяется следующим уравнением: S = ( n −2) × 180 °.
Многоугольник на рисунке 1 имеет семь сторон, поэтому, используя теорему 39, дает:
Внешний угол многоугольника образуется продолжением только одной из его сторон. Непрямым углом, примыкающим к внутреннему углу, является внешний угол. Рисунок может предложить следующую теорему:
Рисунок 2 Внешние (непрямые) углы многоугольника. {\ circ} $$
Что делать, если вам нужен только 1 внутренний угол?
Чтобы найти размер одного внутреннего угла правильного многоугольника (многоугольника со сторонами равной длины и углами одинаковой меры) с n сторонами, мы вычисляем сумму внутренних углов или $$ (\ red n-2) \ cdot 180 $$ и затем разделите эту сумму на количество сторон или $$ \ red n $$.{\ circ}
долл. СШАНахождение 1 внутреннего угла правильного многоугольника
Задача 5
Каков размер 1 внутреннего угла правильного восьмиугольника?
Покажи ответЗадача 6
Вычислить размер 1 внутреннего угла правильного двенадцатиугольника (12-сторонний многоугольник)?
Покажи ответЗадача 7
Вычислить размер 1 внутреннего угла правильного шестиугольника (16-стороннего многоугольника)?
Покажи ответЗадача вызова
Каков размер 1 внутреннего угла пятиугольника?
Покажи ответНа этот вопрос нельзя ответить , потому что форма не является правильным многоугольником .Вы можете использовать эту формулу, чтобы найти единственный внутренний угол, только если многоугольник правильный!
Рассмотрим, например, неправильный пятиугольник внизу.
Вы можете сказать, просто взглянув на картинку, что $$ \ angle A и \ angle B $$ не совпадают.
Мораль этой истории. Хотя вы можете использовать нашу формулу, чтобы найти сумму внутренних углов любого многоугольника (правильного или неправильного), вы можете использовать формулу , а не для единичной меры углов, кроме случаев, когда полигон правильный .
Как насчет меры внешнего угла?
Внешние углы многоугольника Формула суммы внешних углов:
Сумма размеров внешних углов многоугольника, по одному в каждой вершине, равна 360 °.
Измерение единственного внешнего угла
Формула для нахождения 1 угла правильного выпуклого многоугольника с n сторонами =
$$ \ angle1 + \ angle2 + \ angle3 = 360 ° $$
$$ \ угол1 + \ угол2 + \ угол3 + \ угол4 = 360 ° $$
$$ \ угол1 + \ угол2 + \ угол3 + \ угол4 + \ угол5 = 360 ° $$
Практика ПроблемыЗадача 8
Вычислить размер 1 внешнего угла правильного пятиугольника?
Покажи ответЗадача 9
Чему равен 1 внешний угол правильного десятиугольника (10-сторонний многоугольник)?
Покажи ответЗадача 10
Каков размер 1 внешнего угла правильного двенадцатиугольника (12-стороннего многоугольника)?
Покажи ответЗадача вызова
Каков размер 1 внешнего угла пятиугольника?
Покажи ответНа этот вопрос нельзя ответить , потому что форма не является правильным многоугольником .

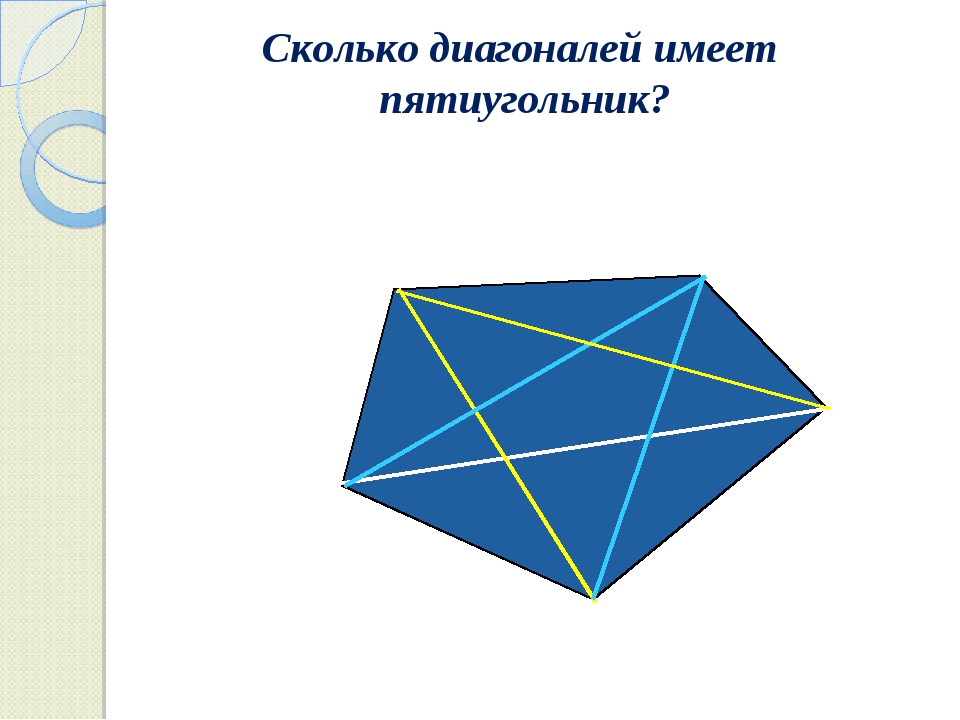


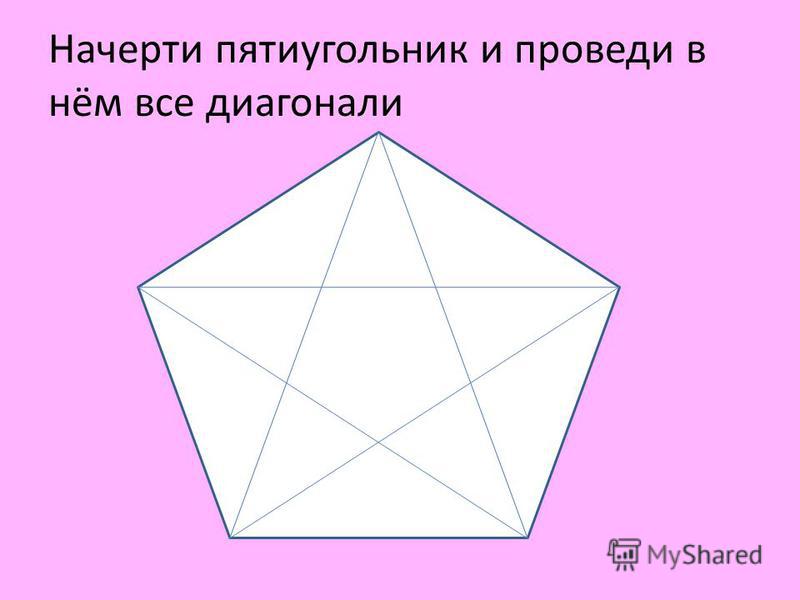 Затем в любую точку установите иглу. Проведите тонкую вспомогательную окружность. Две точки пересечения окружностей, а так же точка, в которой была ножка циркуля образуют три вершины правильного треугольника.
Затем в любую точку установите иглу. Проведите тонкую вспомогательную окружность. Две точки пересечения окружностей, а так же точка, в которой была ножка циркуля образуют три вершины правильного треугольника.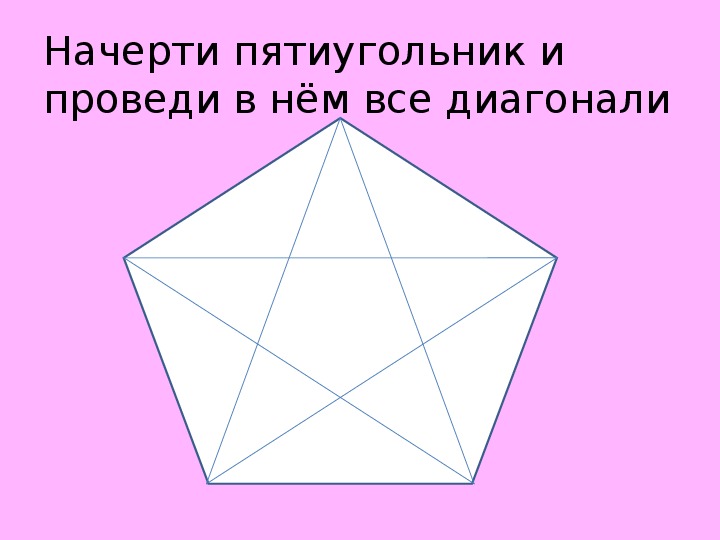
 Неудивительно, что способы построения окружности начали интересовать математиков еще в древности.
Неудивительно, что способы построения окружности начали интересовать математиков еще в древности. Многоугольники бывают как выпуклыми, так и вогнутыми. У выпуклого шестиугольника все внутренние углы тупые, у вогнутого один или более угол является острым. Шестиугольник достаточно легко построить. Это делается в пару шагов.
Многоугольники бывают как выпуклыми, так и вогнутыми. У выпуклого шестиугольника все внутренние углы тупые, у вогнутого один или более угол является острым. Шестиугольник достаточно легко построить. Это делается в пару шагов. Далее разделите ваш отрезок на 6 равных частей. В нашем случае длина каждой части будет составлять 1,5 см. Теперь возьмите циркуль, поставьте его в один из концов отрезка и проведите окружность или дугу с радиусом, равным длине отрезка (АВ). Затем переставьте циркуль в другой конец и повторите операцию. Полученные окружности (или дуги) пересекутся в одной точке. Назовем ее C.
Далее разделите ваш отрезок на 6 равных частей. В нашем случае длина каждой части будет составлять 1,5 см. Теперь возьмите циркуль, поставьте его в один из концов отрезка и проведите окружность или дугу с радиусом, равным длине отрезка (АВ). Затем переставьте циркуль в другой конец и повторите операцию. Полученные окружности (или дуги) пересекутся в одной точке. Назовем ее C. Нарисуйте полукруг с радиусом, равным длине отрезка ОВ. Отметьте точки пересечения с границей круга. Через них проведите вертикальную линию. Она будет пересекаться с горизонтальной осевой линией. В точку пересечения С поставьте ножку циркуля и измерьте расстояние до А. Изобразите круг с радиусом равным полученному расстоянию СА.
Нарисуйте полукруг с радиусом, равным длине отрезка ОВ. Отметьте точки пересечения с границей круга. Через них проведите вертикальную линию. Она будет пересекаться с горизонтальной осевой линией. В точку пересечения С поставьте ножку циркуля и измерьте расстояние до А. Изобразите круг с радиусом равным полученному расстоянию СА. Теперь найдены несколько способов построения правильного многоугольника, вписанного в заданную окружность.
Теперь найдены несколько способов построения правильного многоугольника, вписанного в заданную окружность. Эти окружности пересекаются в точке С. Точка C при этом лежит на луче, исходящем перпендикулярно вверх из середины AB. Отложите от C вверх по этому лучу расстояние, равное 4/6 от длины AB, обозначьте эту точку D. Постройте окружность радиуса AB с центром в точке D. Пересечение этой окружности с двумя вспомогательными построенными ранее даст последние две вершины пятиугольника.
Эти окружности пересекаются в точке С. Точка C при этом лежит на луче, исходящем перпендикулярно вверх из середины AB. Отложите от C вверх по этому лучу расстояние, равное 4/6 от длины AB, обозначьте эту точку D. Постройте окружность радиуса AB с центром в точке D. Пересечение этой окружности с двумя вспомогательными построенными ранее даст последние две вершины пятиугольника.

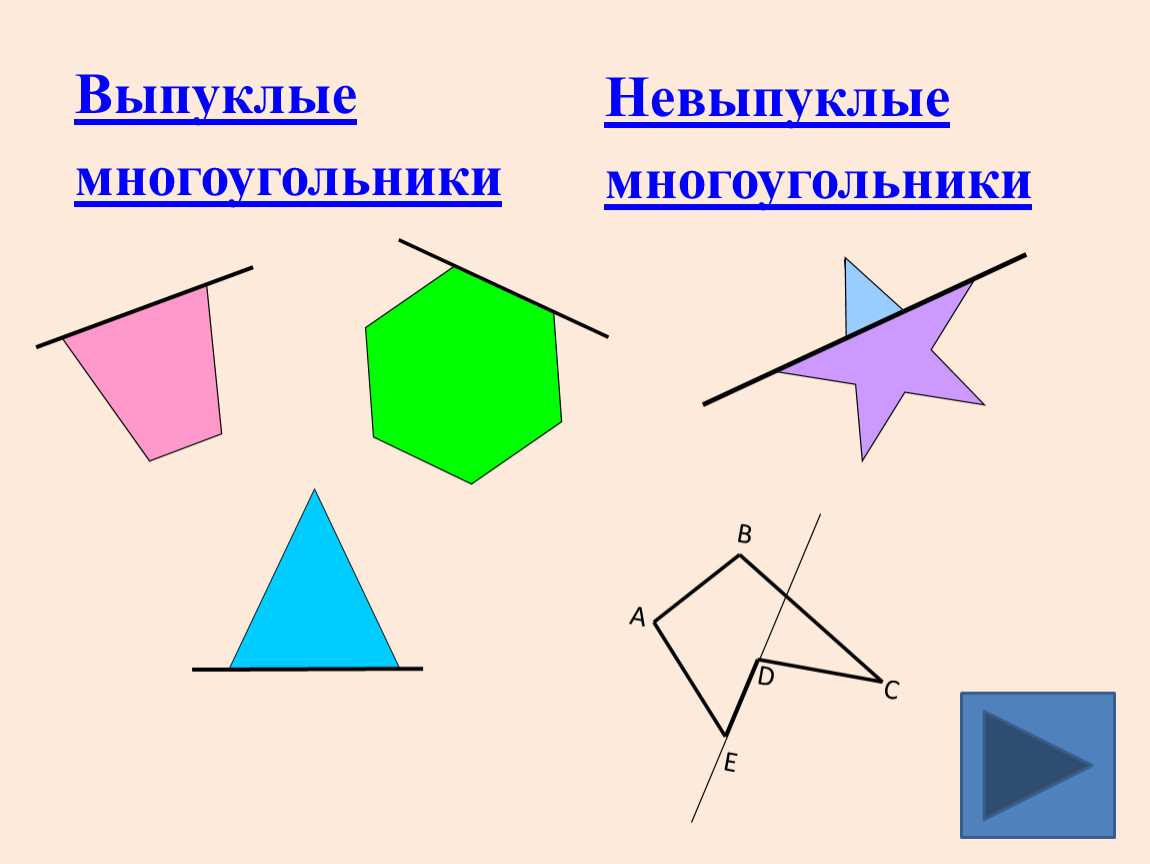
 Появится панель «Рисование». Появятся разные типы линий. Выберите замкнутую полилинию. Она и представляет собой многоугольник, остается только ввести параметры. AutoCAD. Позволяет рисовать самые разные правильне многоугольники. Число сторон может достигать 1024. Можно использовать и командную строку, в зависимости от версии набрав « _polygon» или «мн.-угол».
Появится панель «Рисование». Появятся разные типы линий. Выберите замкнутую полилинию. Она и представляет собой многоугольник, остается только ввести параметры. AutoCAD. Позволяет рисовать самые разные правильне многоугольники. Число сторон может достигать 1024. Можно использовать и командную строку, в зависимости от версии набрав « _polygon» или «мн.-угол». Две точки пересечения окружностей, а так же точка, в которой была ножка циркуля образуют три вершины правильного треугольника.
Две точки пересечения окружностей, а так же точка, в которой была ножка циркуля образуют три вершины правильного треугольника.
 2}{4}\sqrt{\frac{5+\sqrt{5
2}{4}\sqrt{\frac{5+\sqrt{5