Построение правильных многоугольников
На этом уроке мы рассмотрим способы построения некоторых правильных многоугольников с помощью циркуля и линейки. А также изобразим правильный многоугольник графически.
Для начала давайте вспомним определение правильного многоугольника. Итак, правильным многоугольником называется выпуклый многоугольник, у которого все углы равны и все стороны равны.
Для выполнения построений мы используем циркуль и линейку.
Циркуль позволяет:
– построить окружность,
– построить дугу окружности,
– отложить на прямой отрезок, равный данному.
Линейка позволяет:
– построить прямую линию,
– построить отрезок, соединяющий две точки,
– найти точку пересечения двух прямых.
Ранее мы с вами уже рассматривали построения правильного треугольника и четырехугольника, т.е. квадрата.
Давайте рассмотрим, каким образом можно с помощью циркуля и линейки построить правильный треугольник и правильный четырехугольник, вписанные в окружность.
Задача 1. Вписать в заданную окружность правильный треугольник
Решение.
Первый способ.
Построение. Пусть задана окружность с центром О. Проведем произвольный диаметр BD окружности. Построим прямую l, являющуюся серединным перпендикуляром к радиусу OD. Середину радиуса ОD обозначим точкой К. Отметим точки А и C – пересечения прямой l с окружностью. И построим отрезки BA и BC. Треугольник ABC – правильный.
Доказательство.
В 
катет
Тогда 
,
.
Отсюда, 
.
Значит, 
–
правильный.Второй способ построения.
Пусть задана окружность с центром О. Раствором циркуля, равным радиусу, последовательно от одной точки окружности делаем на ней засечки, пока последняя засечка не совпадет с взятой первоначально точкой. Соединив полученные точки через одну, получим правильный треугольник.
Задача 2.
Решение.
Построение. Пусть задана окружность с центром О. Построим диаметр AC. Затем построим диаметр BD перпендикулярный диаметру AC. Точки А, C и B, D – точки пересечения диаметров с окружностью. И построим отрезки АB, BC, CD и АD. Четырехугольник ABCD – правильный.
Доказательство.
Т.к. 
,
–
параллелограмм.Т.к. 
,то
–
прямоугольник.
Т.к. 
,то
Т.к. 
,то
–
квадрат.
Следовательно, –
квадрат.
Значит, –
правильный четырехугольник.
Теперь давайте рассмотрим построения правильных n-угольников при n>4. Обычно для построения таких n-угольников используется окружность, описанная около многоугольника.
Задача 3. Построить правильный шестиугольник, сторона которого равна данному отрезку.
Решение.
Построение. Так как в правильном шестиугольнике сторона а равна радиусу, то достаточно последовательно отложить от одной точки окружности 6 радиусов-хорд. Пусть МN – заданный отрезок. Построим окружность с произвольным центром О и радиуса MN. Отметим на этой окружности произвольную точку А. Затем, не меняя раствора циркуля, последовательно от этой точки А будем делать на окружности засечки, пока последняя засечка не совпадет с взятой первоначально точкой А. Отметим точки B, C, D, Е и F. Теперь соединим последовательно построенные точки отрезками. Получим искомый правильный шестиугольник ABCD.
Доказательство.
Равные хорды стягивают равные дуги.
Для построения правильных многоугольников часто используется следующая задача: дан правильный n-угольник. Построить правильный 2n-угольник.
Задача 4. Дан правильный шестиугольник. Построить правильный двенадцатиугольник.
Решение.
Построение.
Пусть ABCDEF – данный правильный шестиугольник. Опишем около него окружность.
1. 
и
.2. Окружность 
.
3. 
–
серединные
перпендикуляры к 
4. 
.
5. 
–
правильный двенадцатиугольник.
Применяя указанный способ, можно с
помощью циркуля и линейки построить целый ряд правильных многоугольников, если
построен один из них. Например, построив правильный четырехугольник, т.е.
квадрат, и пользуясь задачей 4, можно построить правильный восьмиугольник,
затем правильный шестнадцати-угольник и вообще правильный 2
Замечание. Рассмотренные примеры показывают, что многие правильные многоугольники могут быть построены с помощью циркуля и линейки. Но важно заметить, что не все правильные многоугольники могут быть построены таким образом.
С давних времен построению правильных многоугольников математики уделяли большое внимание. Древние греки умели строить правильные треугольники, четырехугольники, пятиугольники. А также многоугольники, получаемые удвоением их сторон, шестиугольники, восьмиугольники, десятиугольники и т.д. Далее дело зашло в тупик. И только 2000 лет спустя великий немецкий математик 17 века Карл Гаусс, которого называли «королем математики», решил эту математическую проблему. Будучи девятнадцати летним юношей, он доказал, что можно построить правильный семнадцати-угольник, а вот семиугольник, девятиугольник, одиннадцатиугольник, тринадцати-угольник циркулем и линейкой построить нельзя. Задача о построении правильного семнадцати-угольника была самым первым его научным открытием.
Подведем итоги урока.
Сегодня мы рассмотрели способы построения некоторых правильных многоугольников с помощью циркуля и линейки. Научились строить правильные треугольник и четырехугольник, вписанные в окружность. А также выполнили задачу на построение правильного многоугольника по заданному отрезку, и задачу на построение правильного 2n-угольника по заданному n-угольнику.
Как нарисовать многоугольник — Полезные советы
Здравствуйте коллеги. Как нарисовать многоугольник вопрос не сложный. Это просто — если умеешь. Для специалиста нет трудностей.
Предлагаю вам стать специалистом в этой области.
Будем рисовать фигуру с шестью вершинами. С пятью вершинами (звезда), с семью, или разделить на восемь и четыре части, на десять, а так же на двенадцать можно найти в заметках сайта.
В процессе рисования вы часто будете сталкиваться с построением. Все окружение человека состоит из геометрических фигур, большая часть «всего».
Возьмем интерьер. Сама комната — это геометрическая фигура, предметы мебели тоже геометрия, посуда, ковры, картины, окна и т. д.
На улице нас окружают дома, машины, тротуары, заборы ну и много предметов, которые нужно уметь правильно рисовать.
Первое, что приходит на ум при слове шестигранник — это колесики в часах, окно — иллюминатор, призма, алмаз. Карандаш тоже имеет шесть сторон.
Сегодня построим фигуру фронтально.
В перспективе нарисуем в следующем уроке.
Если у нас получиться сделать предмет с шестью гранями, то с тремя вершинами сделать не сложно. Рассмотрим это более подробно.
Как правильно нарисовать многоугольник
Нашу фигуру создадим в фотошопе. В этой статье я не буду разбирать, возможности программы. Кто умеет ею пользоваться, то разберется, а наша задача понять принцип. Замечу, что и простыми карандашами, линейкой, циркулем тоже получиться.
Вы можете онлайн рисовать за мной, обучение запомнится надежней. Практика всегда тесно шла с теорией. Делая руками, запоминаешь быстрее.
Берем лист бумаги и циркулем произвольно, наносим круг. Смотрим ниже.
Теперь через центр O чертим горизонтальную прямую F, F1 (зеленая линия).
Дальше ставим циркуль в точку F1, и создадим еще одну окружность через центр первой, через центр O. Картинка ниже.
Нарисовать многоугольник с шестью вершинами. Рисовать онлайн в фотошопе на artatac
Здравствуйте коллеги. Как нарисовать многоугольник вопрос не сложный. Это просто — если умеешь. Для специалиста нет трудностей.
Предлагаю вам стать специалистом в этой области.
Будем рисовать фигуру с шестью вершинами. С пятью вершинами (звезда), с семью, или разделить на восемь и четыре части, на десять, а так же на двенадцать можно найти в заметках сайта.
В процессе рисования вы часто будете сталкиваться с построением. Все окружение человека состоит из геометрических фигур, большая часть «всего».
Возьмем интерьер. Сама комната — это геометрическая фигура, предметы мебели тоже геометрия, посуда, ковры, картины, окна и т. д.
На улице нас окружают дома, машины, тротуары, заборы ну и много предметов, которые нужно уметь правильно рисовать.
Первое, что приходит на ум при слове шестигранник — это колесики в часах, окно — иллюминатор, призма, алмаз. Карандаш тоже имеет шесть сторон.
Сегодня построим фигуру фронтально.
В перспективе нарисуем в следующем уроке.
Если у нас получиться сделать предмет с шестью гранями, то с тремя вершинами сделать не сложно. Рассмотрим это более подробно.
Как правильно нарисовать многоугольник
Нашу фигуру создадим в фотошопе. В этой статье я не буду разбирать, возможности программы. Кто умеет ею пользоваться, то разберется, а наша задача понять принцип. Замечу, что и простыми карандашами, линейкой, циркулем тоже получиться.
Вы можете онлайн рисовать за мной, обучение запомнится надежней. Практика всегда тесно шла с теорией. Делая руками, запоминаешь быстрее.
Берем лист бумаги и циркулем произвольно, наносим круг. Смотрим ниже.
Теперь через центр O чертим горизонтальную прямую F, F1 (зеленая линия).
Дальше ставим циркуль в точку F1, и создадим еще одну окружность через центр первой, через центр O. Картинка ниже.
Давайте обозначим пересечения. Это будут точки B, C.
Теперь проведем две прямые линии через центр O. Первая это B, B1. Вторая C, C1 (они у нас синего цвета). Картинка ниже.
У нас появились шесть точек, соединив их можно получить шестигранник.
Вывод: «Сторона шестиугольника равна радиусу окружности»
Если соединить прямые, как на фото внизу, получим трехгранники. Еще такой знак называют «Звездой Давида»
Знаете другие способы построения шестигранника? Поделитесь в комментариях.
Предлагаю к просмотру статьи по построению тени от фигур.
Объект Многоугольник в Автокаде — как построить его в AutoCAD различными способами
[Уроки Автокад] Как нарисовать (начертить) многоугольник в AutoCAD
| Команда рисования в AutoCAD | |
| Многоугольник | |
 |
|
| Определение | |
| Многоугольник в Автокад — является замкнутой 2D-полилинией, состоящей из трех и более сегментов. Правильный многоугольник — это многоугольник у которого все стороны и углы равны. |
|
| Инструмент | |
| Инструмент Автокад Многоугольник — строит правильный многоугольник либо по конечным точкам одной стороны, либо по точке центра и радиусу вписанной или описанной окружности. | |
| Команда | |
| МН-Угол | |
| Объект | |
| Полилиния |
Команда МН-Угол в AutoCAD
За создание в Автокад правильного многоугольника отвечает команда MH-Угол.
Вызвать данную команду можно следующими способами (начать построение в AutoCAD многоугольника):
- построить многоугольник в Автокад можно из строки меню пункт Рисование — строка Многоугольник;
- начертить его можно из ленты инструментов на вкладке «Главная» — в группе Рисование кнопка Многоугольник;
- нарисовать многоугольник в Автокад можно из классической панели инструментов Рисование кнопка Многоугольник;
- либо прописать наименование команды в командной строке МН-Угол.
Построение многоугольника в Автокад вписанного в окружность
Как уже отмечалось, в вписанный в AutoCAD многоугольник в окружность задается центральной точкой и расстоянием от центра до любой из вершин. Следовательно, радиус описанной окружности — это расстояние от центра многоугольника до одной из его вершин.
Вызываем команду МН-Угол. В командной строке появляется запрос:
Число сторон <4>:
В ответ на который вы должны ввести число сторон, которое должно быть у многоугольника в AutoCAD (от 3 до 1024). Введем значение 5. Нажимаем «Enter». Появляется следующий запрос:
Укажите центр многоугольника:
Зададим центр многоугольника в AutoCAD щелчком мыши. Система отобразит запрос:
Задайте параметр размещения [Вписанный в окружность/Описанный вокруг окружности] <В>:
Выбираем опцию «Вписанный в окружность». Отобразится предварительный вид многоугольника AutoCAD, который прикреплен к линии, проходящей из заданного центра до указателя. Размер его будет изменяться вместе с изменением положения указателя. В командной строке появится запрос:
Радиус окружности:
Радиус окружности можно задать, введя значение в командную строку или щелчком мыши, указав точку на чертеже. Введем значение 20 мм в командную строку и нажмем «Enter». Правильный пятиугольник (многоугольник) в Автокад с радиусом описанной окружности 20 мм построен.
Как начертить многоугольник в AutoCAD описанный вокруг окружности
Многоугольник Автокад описанный вокруг окружности задается центральной точкой и расстоянием от центра до средней точки одной из его сторон. Следовательно, радиус вписанной окружности — это расстояние от центра многоугольника до средней точки одной из его сторон.
Вызываем команду «МН-Угол». Система отобразит запрос:
Число сторон <5 — предыдущее значение>:
Соглашаемся со значением по умолчанию, нажимаем «Enter». Появляется следующий запрос:
Укажите центр многоугольника:
Указываем в Автокад центр многоугольника. Появляется запрос в командной строке:
Задайте параметр размещения [Вписанный в окружность/Описанный вокруг окружности] <В>:
Выбираем опцию «Описанный вокруг окружности» команды МН-Угол. Отобразится предварительный вид многоугольника Автокад, который прикреплен к линии, проходящей из заданного центра до указателя, соответствующего середине одной из сторон многоугольника. Размер многоугольника в Автокад будет изменяться вместе с изменением положения указателя. В командной строке появится запрос:
Радиус окружности:
Повторим ввод координат и зададим радиус описанной окружности с помощью задания относительных полярных координат. Введем в командную строку следующее значение @20<0, что означает:
- «@» — отсчет координат ведется от центральной точки многоугольника Автокад;
- «20» — расстояние от центральной точки, т.е. радиус вписанной окружности;
- «<» обозначение полярности координат — возможности привязки к определенному углу;
- «0» — значение угла, т.е. 0 градусов.
Правильный многоугольник в Автокад с радиусом вписанной окружности 20 мм построен.
Совет
Задав радиус вписанной или описанной окружности в командной строке путем ввода значения радиуса, многоугольник в Автокад автоматически выравнивается так, чтобы его нижняя сторона располагалась параллельно оси X текущей ПСК. Если задать радиус при помощи мыши (различными методами задания координат), то можно повернуть многоугольник вокруг центра на нужный угол.Как построить многоугольник по конечным точкам одной стороны (по стороне)
Как в Автокад начертить многоугольник по стороне (алгоритм):
Вызываем команду МН-Угол в AutoCAD. В командной строке появляется запрос:
Число сторон <5 — предыдущее значение>:
Соглашаемся со значением по умолчанию, т.е. 5 сторон многоугольника Автокад. Нажимаем «Enter». Система отобразит запрос:
Укажите центр многоугольника или [Сторона]:
Выбираем опцию «Сторона», чтобы начать строить в AutoCAD многоугольник по одной из сторон. Появляется следующий запрос:
Первая конечная точка стороны:
Укажем первую конечную точку стороны многоугольника Автокад щелчком мыши. Отобразиться его предварительный вид, который прикреплен к линии, проходящей от заданной первой конечной точки стороны до второй конечной точки. Появится запрос:
Вторая конечная точка стороны:
Вторую конечную точку стороны многоугольника в AutoCAD можете указать щелчком мыши или вводом координат в командную строку. Укажем точку щелчком мыши.
Правильный пятиугольник (многоугольник) в Автокад произвольных размеров по стороне построен.
Полезные уроки схожих тематик и рекомендации
Рекомендую ознакомиться с подобными уроками по Автокад:
Читайте и смотрите также:
Курсы, самоучители Автокад:
- 2D проектирование.
- 3D моделирование.
- Начертательная геометрия.
- Инженерная графика.
- План дома.
- Сборочный чертеж цилиндрической зубчатой передачи.
- Модель кухни 3D.
Видео «Как начертить прямоугольник и правильный многоугольник в Автокад»
Построение многоугольников в autocad
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
Урок №5 Построение многоугольников в AutoCAD.
Правильные многоугольники, частными случаями которых являются равносторонние треугольники, квадраты и шестигранники можно построить тремя способами:
- Описанный многоугольник;
- Вписанный многоугольник;
- Многоугольник с заданной стороной.
Рассмотрим каждый способ отдельно.
1. Для построения описанного многоугольника на вкладке «Главная» открываем панель «Рисование», нажимаем на кнопку «Многоугольник» (создание равносторонней замкнутой полилинии).
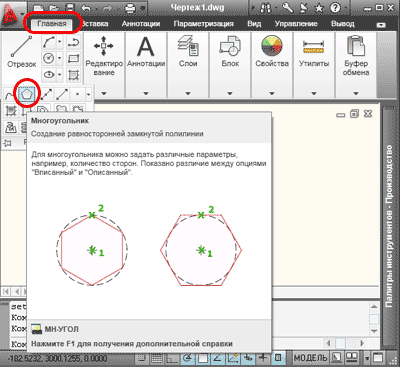
Кроме того можно использовать командную строку. Для русифицированных версий программы набираем команду «МН-УГОЛ», для англоязычных, команду «_polygon». После набора команды нажимаем клавишу «Enter». На экране появится рамка, в которую нужно ввести число сторон (по умолчанию четыре). Число сторон допускается от 3 до 1024, значение можно вводить в командную строку. Зададим в нашем примере значение 6, нажмем клавишу «Enter», программа попросит указать центр многоугольника.
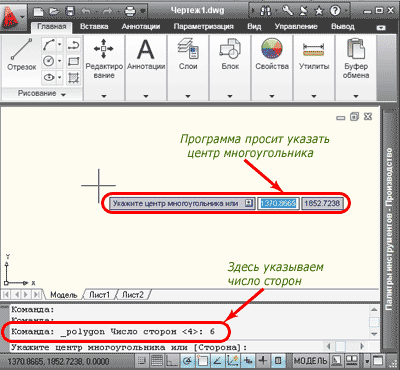
Указываем точку с координатами (0,0), нажимаем «Enter» и задаем параметр размещения «Описанный вокруг окружности».
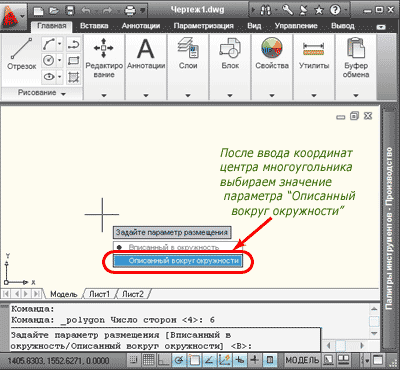
Данный параметр можно задавать через контекстное меню, которое вызывается щелчком правой клавиши мыши.
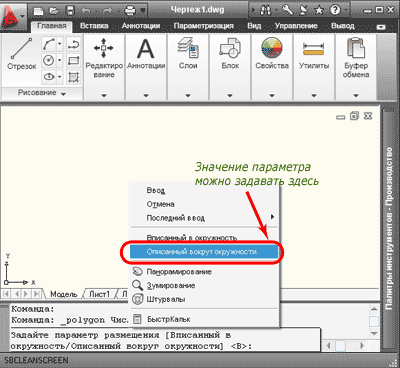
Теперь достаточно задать радиус окружности, например 500 и нажать клавишу «Enter».
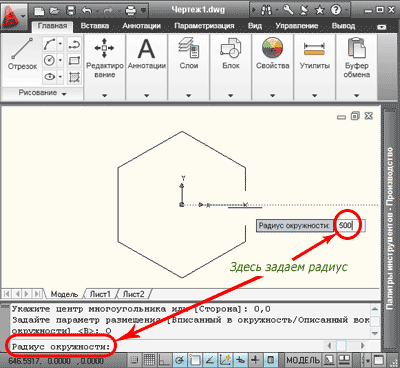
При необходимости, до ввода значения радиуса, многоугольник можно развернуть под любым углом.
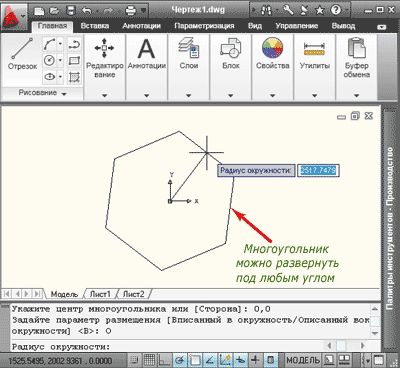
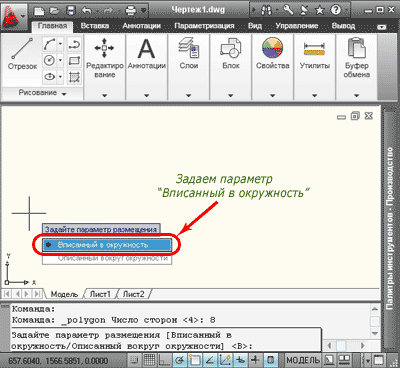
2. Вписанный многоугольник строится аналогично, разница лишь в том, что параметр размещения указываем «Вписанный в окружность».
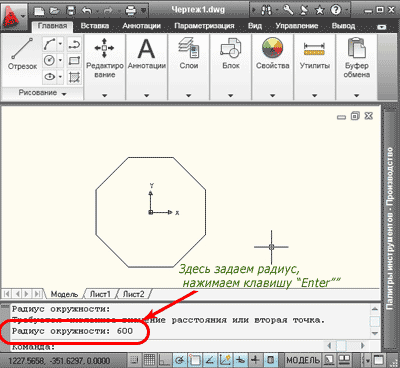
Задаем радиус в командной строке, или указываем точку курсором, щелкая левой кнопкой мыши в требуемом месте на экране.
При первом и втором способе параметр размещения можно задавать через командную строку. Для описанного многоугольника пишется русская буква «О», для вписанного буква «В». Если версия программы англоязычная, то пишем «_с» (от Circumscribed about circle) для описанного, и «_i» (от Inscribed in circle) для вписанного многоугольника (раскладка клавиатуры английская).
3.Построение многоугольника с заданной стороной начинается, как и в предыдущих случаях. На вкладке «Главная» открываем панель «Рисование», нажимаем на кнопку «Многоугольник» и указываем число сторон. Далее щелчком правой клавиши мыши вызываем контекстное меню, нажимаем команду «Сторона» в английских версиях «Edge».
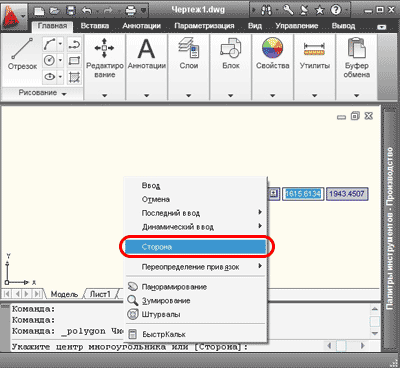
Теперь нужно задать в командной строке координаты первой конечной точки (к примеру: 0,0), и второй конечной точки (например: 100,500). Нажимаем клавишу «Enter» — многоугольник построен.
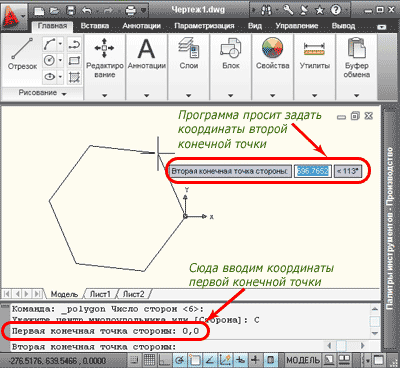
Чтобы построить многоугольник с заданной стороной при помощи командной строки, после ввода числа сторон, пишем в командной строке русскую букву «С», нажимаем клавишу «Enter». Для англоязычных программ пишем «_e» (от Edge). Далее указываем координаты конечных точек, при помощи курсора, или вводим их координаты.
В следующем уроке рассмотрим построение прямоугольников.
Если у Вас есть вопросы можно задать их ЗДЕСЬ.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
Список последних уроков по программе AutoCAD.
 Автор: Дмитрий Родин | «AutoCAD ЭКСПЕРТ» Видео самоучитель По AutoCAD
|
 Автор: Саляхутдинов Роман | «БОСК 5.0» Новый Видеокурс. «Твердотельное и Поверхностное Моделирование в КОМПАС-3D»
>> Читать Полное Описание << |
 Автор: Саляхутдинов Роман | «БОСК 8.0» Познай Все Cекреты КОМПАС-3D
>> Читать Полное Описание << |
Построение на плоскости | Журнал Ярмарки Мастеров
Наверняка каждому из нас приходилось сталкиваться с тем, что нужно срочно что-то начертить, точный угол или многоугольник, а транспортира как нарочно под рукой нет, или Вы вообще никогда раньше ничего не чертили. Сегодня я хочу поделиться с Вами простыми схемами построения фигур на плоскости. Думаю, этот навык пригодится всем. Продолжение статьи:
http://www.livemaster.ru/topic/383001-postroenie-na-ploskosti-chast-2?inside=1&wf=&cp=1&vr=1
Нам понадобятся: карандаш, линейка, циркуль.
Построение угла в 60
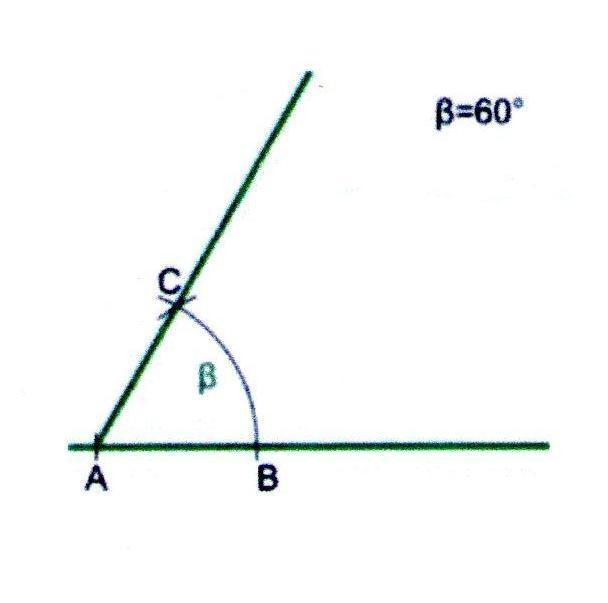
1. Проведём прямую и отметим на ней точку А.
2. Из точки А проведём дугу произвольного радиуса и получим точку В.
3. Из точки В проведём дугу радиуса АВ, чтобы она пересекла ранее начерченную дугу.
4. Проведённая через точку пересечения (С) и точку А прямая будет второй стороной требуемого угла.
Построение угла в 45
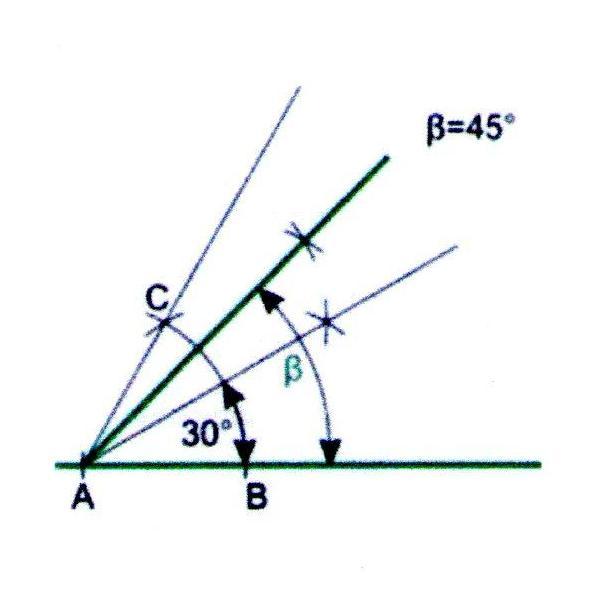1. Построим угол 60, кака описано выше.
2. Разделим полученный угол пополам.
3. Угол между лучами 60 и 30 разделим пополам. В результате получим угол в 45.
Построение угла в 75
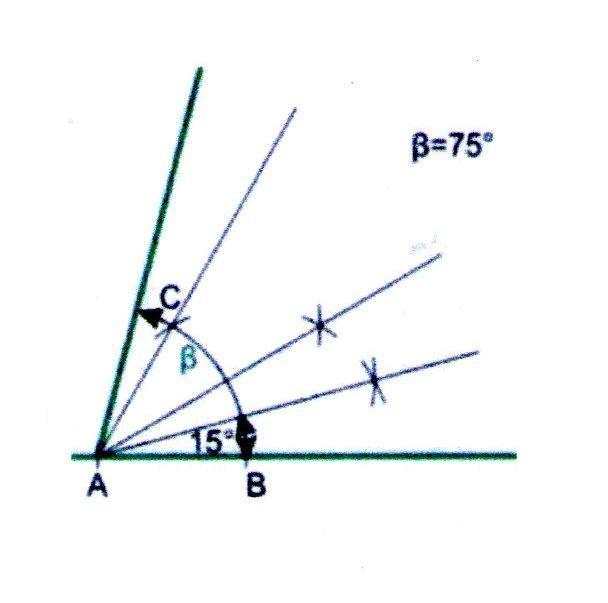1. Построим угол в 60, как описано выше, и разделим его пополам.
2. В ходе дальнейшего деления надвое получим угол в 15.
3. Отразим угол в 15 через луч 60 и так получим угол в 75.
Построение угла в 90
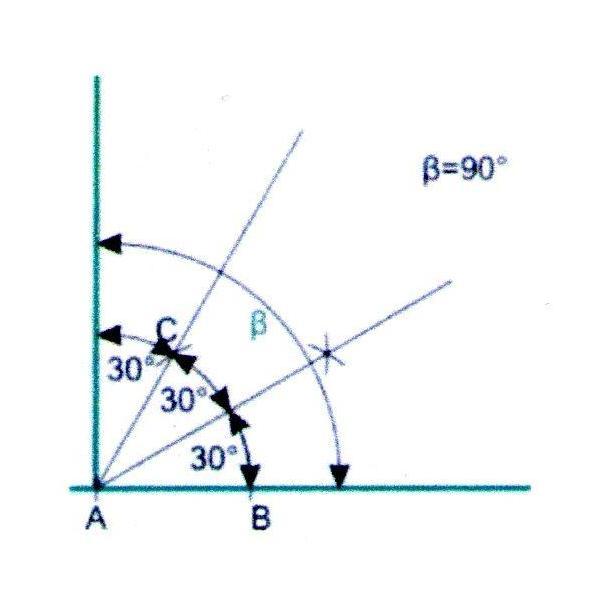
1. Построим угол в 60, как описано выше, и разделим его пополам.
2. Получившийся угол в 30 через луч 60 и так получим угол точно в 90.
Разделение отрезка на равные части.
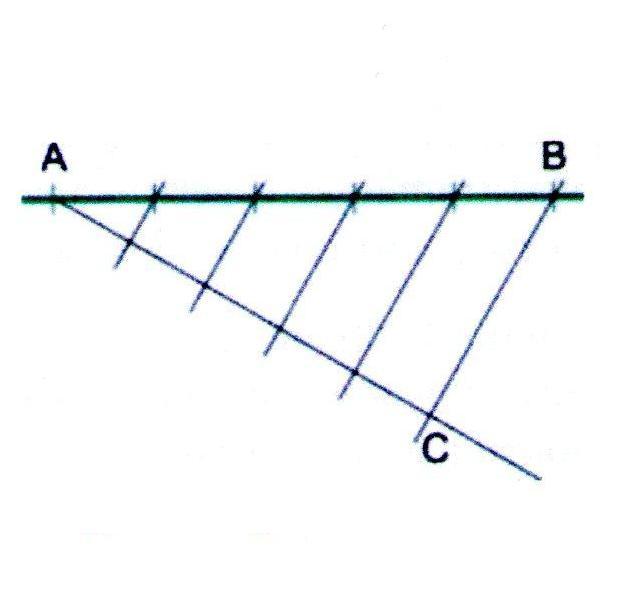
1. Проведём прямую и отметим на ней отрезок АВ.
2. Из точки А проведём вспомогательную прямую и разделим её на столько одинаковых частей, на сколько требуется разделить отрезок АВ. Делить будем при помощи циркуля. Последнюю точку обозначим буквой С.
3. Последнюю точка (С) соединим с концом отрезка АВ. Построим рад параллельных отрезку СВ прямых по всей длине отрезка АВ. Точки пересечения параллельных прямых с отрезком АВ и будут точками раздела отрезка на несколько равных частей.
Построение правильного пятиугольника.
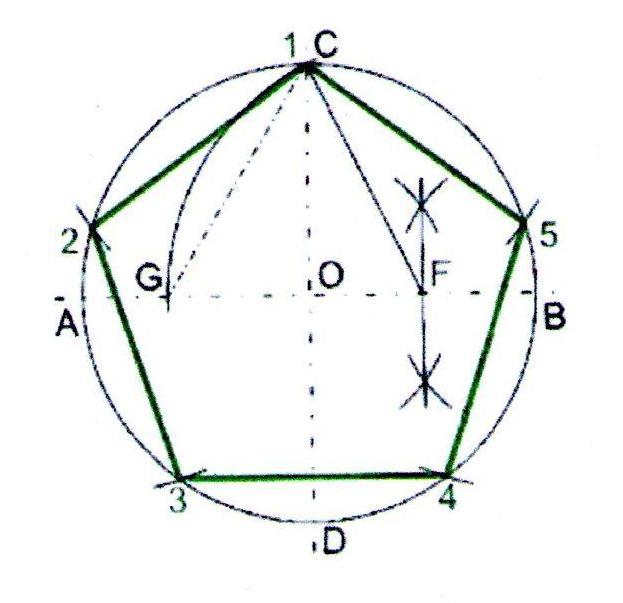
1. Проведём окружность радиусом 50 мм. Через центр окружности проведём взаимно перпендикулярные горизонтальную и вертикальную линии.
2. Разделим пополам расстояние ОВ. Разведём ножки циркуля на расстояние FC. Из точки F проведём дугу через С. Дуга пересечёт горизонтальную линию в точке G.
3. Расстояние CG будет длиной стороны пятиугольника. Из вершины С отложим пять раз расстояние CG.
Построение правильного шестиугольника.
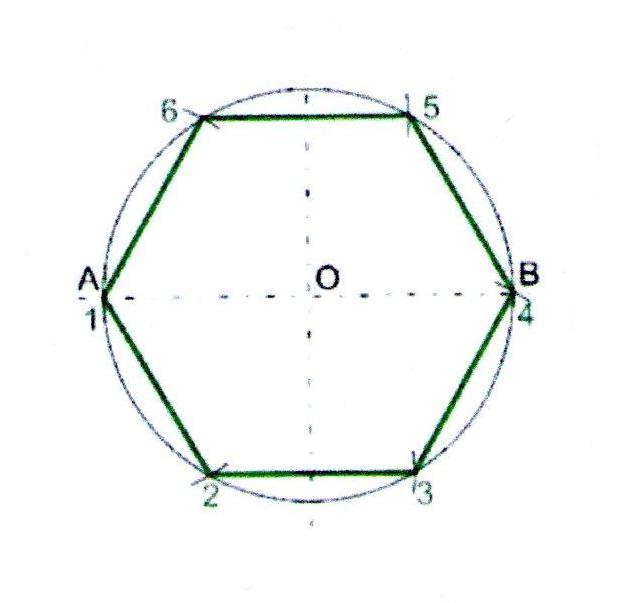
1. Проведём окружность радиусом 50 мм.
2. Через центр окружности проведём взаимно перпендикулярные горизонтальную и вертикальную линии.
3. Из точки А на линии окружности отложим шесть раз радиус нашей окружности. Соединив прямыми точки пересечения, получим шестиугольник.
Построение правильного семиугольника.
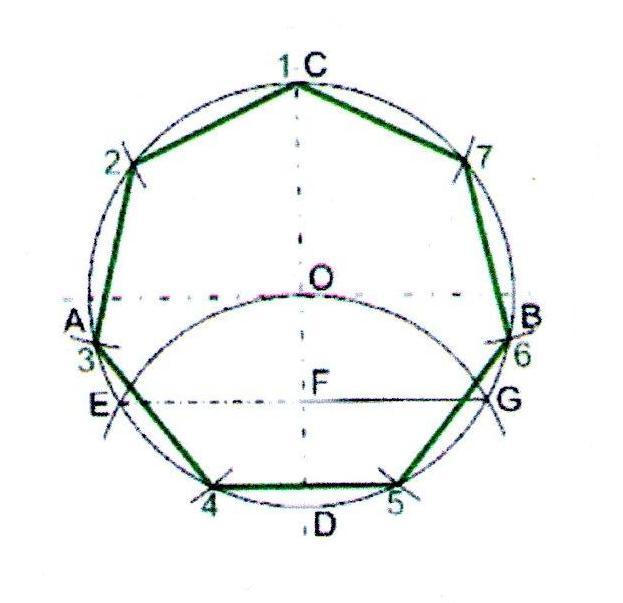
1. Проведём окружность заданного радиуса. Через центр окружности проведём взаимно перпендикулярные горизонтальную и вертикальную линии.
2. Из точки D проведём дугу радиусом равным радиусу окружности.
3. Дуга пересечёт окружность в точках E и G.
4. Длина отрезка EF на хорде EG равна длине стороны семиугольника. Из вершины С семь раз отложим расстояние EF.
Общий метод построения многоугольников.
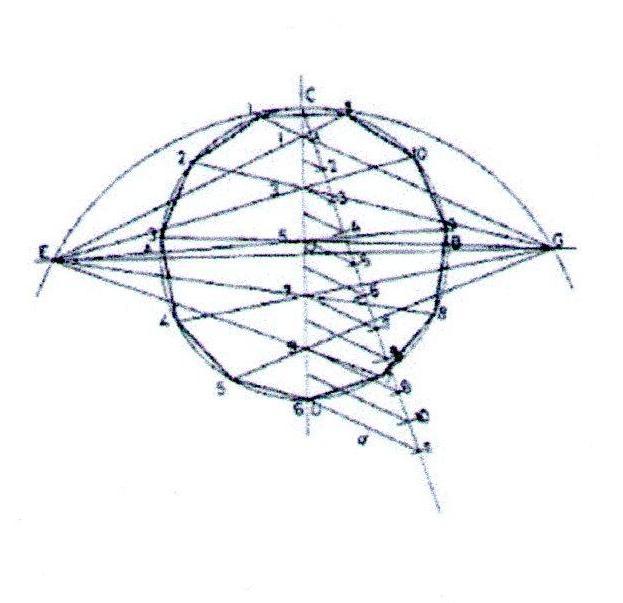
1. Проведём окружность радиусом 50 мм. Через центр окружности проведём взаимно перпендикулярные горизонтальную и вертикальную линии. Продолжим горизонтальную лини. За точки А и В.
2. Из точки D проведём дугу радиусом, равным радиусу окружности так, чтобы дуга пересекла горизонтальную линию.
3. При помощи вспомогательной прямой разделим вертикальную линию на столько равных частей, сколько сторон многоугольника требуется получить. Для примера показано построение одиннадцатиугольника.
4. Из точки Е проведём прямые через нечётные точки раздела вертикальной линии так, чтобы эти прямые пересекли окружность. Такую же операцию проведём из точки G. Полученные лучи пересекают окружность в точках, соединив которые прямыми получаем одиннадцатиугольник.
Построение с помощью циркуля и линейки — Википедия
Построе́ния с по́мощью ци́ркуля и лине́йки — раздел евклидовой геометрии, известный с античных времён.
В задачах на построение циркуль и линейка предполагаются идеальными инструментами, в частности:
- Линейка не имеет делений и имеет сторону бесконечной длины, но только одну.
- Циркуль может иметь какой угодно большой или малый раствор (то есть может чертить окружность произвольного радиуса).
Разбиение отрезка пополамЗадача на бисекцию. С помощью циркуля и линейки разбить данный отрезок AB на две равные части. Одно из решений показано на рисунке:
- Циркулем проводим окружности с центром в точках A и B радиусом AB.
- Находим точки пересечения P и Q двух построенных окружностей (дуг).
- По линейке проводим отрезок или линию, проходящую через точки P и Q.
- Находим искомую середину отрезка AB — точку пересечения AB и PQ.
В задачах на построение рассматривается множество следующих объектов: все точки плоскости, все прямые плоскости и все окружности плоскости. В условиях задачи изначально задается (считается построенными) некоторое множество объектов. К множеству построенных объектов разрешается добавлять (строить):
- произвольную точку;
- произвольную точку на заданной прямой;
- произвольную точку на заданной окружности;
- точку пересечения двух заданных прямых;
- точки пересечения/касания заданной прямой и заданной окружности;
- точки пересечения/касания двух заданных окружностей;
- произвольную прямую, проходящую через заданную точку;
- прямую, проходящую через две заданные точки;
- произвольную окружность с центром в заданной точке;
- произвольную окружность с радиусом, равным расстоянию между двумя заданными точками;
- окружность с центром в заданной точке и с радиусом, равным расстоянию между двумя заданными точками.
Требуется с помощью конечного количества этих операций построить другое множество объектов, находящееся в заданном соотношении с исходным множеством.
Решение задачи на построение содержит в себе три существенные части:
- Описание способа построения заданного множества.
- Доказательство того, что множество, построенное описанным способом, действительно находится в заданном соотношении с исходным множеством. Обычно доказательство построения производится как обычное доказательство теоремы, опирающееся на аксиомы и другие доказанные теоремы.
- Анализ описанного способа построения на предмет его применимости к разным вариантам начальных условий, а также на предмет единственности или неединственности решения, получаемого описанным способом.
- Задача Аполлония о построении окружности, касающейся трех заданных окружностей. Если ни одна из заданных окружностей не лежит внутри другой, то эта задача имеет 8 существенно различных решений.
- Задача Брахмагупты о построении вписанного четырехугольника по четырем его сторонам.
Построение правильных многоугольников[править | править код]
Построение правильного пятиугольникаАнтичным геометрам были известны способы построения правильных n-угольников для n=2k{\displaystyle n=2^{k}}, n=3⋅2k{\displaystyle n=3\cdot 2^{k}}, n=5⋅2k{\displaystyle n=5\cdot 2^{k}} и n=3⋅5⋅2k{\displaystyle n=3\cdot 5\cdot 2^{k}}.
В 1796 году Гаусс показал возможность построения правильных n-угольников при n=2k⋅p1⋯pm{\displaystyle n=2^{k}\cdot p_{1}\cdots p_{m}}, где pi{\displaystyle p_{i}} — различные простые числа Ферма. В 1836 году Ванцель доказал, что других правильных многоугольников, которые можно построить циркулем и линейкой, не существует.
Неразрешимые задачи[править | править код]
Следующие три задачи на построение были поставлены ещё древними греками:
Лишь в XIX веке было строго доказано, что все эти три задачи неразрешимы при использовании только циркуля и линейки. Доказательство неразрешимости этих задач построения было достигнуто с помощью алгебраических методов, основанными на теории Галуа[1]. В частности, невозможность построения квадратуры круга следует из трансцендентности числа π.
Другая известная и неразрешимая с помощью циркуля и линейки задача — построение треугольника по трём заданным длинам биссектрис[2]. Эта задача остаётся неразрешимой даже при наличии инструмента, выполняющего трисекцию угла, например томагавка.[3]
Допустимые отрезки для построения с помощью циркуля и линейки[править | править код]
Построение квадратного корня из 2. 
Построение квадратного корня из 3.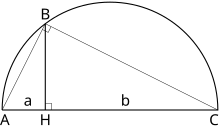 
С помощью этих инструментов возможно построение отрезка, который по длине:
- равен сумме длин нескольких отрезков;
- равен разности длин двух отрезков;
- численно равен произведению длин двух отрезков;
- численно равен частному от деления длин двух отрезков;
- численно равен квадратному корню из длины заданного отрезка (следует из возможности построения среднего геометрического двух отрезков, см. иллюстрацию).[4]
Для построения отрезка с длиной численно равной произведению, частному и квадратному корню из длин заданных отрезков необходимо задание на плоскости построения единичного отрезка (то есть отрезка длины 1), иначе задача неразрешима из-за отсутствия масштаба. Извлечение корней из отрезков с иными натуральными степенями, не являющимися степенью числа 2, невозможны с помощью циркуля и линейки. Так, например, невозможно при помощи циркуля и линейки из единичного отрезка построить отрезок длиной 23{\displaystyle {\sqrt[{3}]{2}}}. Из этого факта, в частности, следует неразрешимость задачи об удвоении куба.[5]
С формальной точки зрения, решение любой задачи на построение сводится к графическому решению некоторого алгебраического уравнения, причем коэффициенты этого уравнения связаны с длинами заданных отрезков. Поэтому можно сказать, что задача на построение сводится к отысканию действительных корней некоторого алгебраического уравнения.
Поэтому удобно говорить о построении числа — графического решения уравнения определенного типа.
Исходя из возможных построений отрезков возможны следующие построения:
Иначе говоря, возможно строить лишь отрезки, равные арифметическим выражениям с использованием квадратного корня из исходных чисел (заданных длин отрезков).
Важно отметить, что существенно, что решение должно выражаться при помощи квадратных корней, а не радикалов произвольной степени. Если даже алгебраическое уравнение имеет решение в радикалах, то из этого не следует возможность построения циркулем и линейкой отрезка, равного его решению. Простейшее такое уравнение: x3−2=0,{\displaystyle x^{3}-2=0,} связанное со знаменитой задачей на удвоение куба, сводящаяся к этому кубическому уравнению. Как было сказано выше, решение этого уравнения (23{\displaystyle {\sqrt[{3}]{2}}}) невозможно построить циркулем и линейкой.
Возможность построить правильный 17-угольник следует из выражения для косинуса центрального угла его стороны:
- cos(2π17)=−116+11617+11634−217+{\displaystyle \cos {\left({\frac {2\pi }{17}}\right)}=-{\frac {1}{16}}\;+\;{\frac {1}{16}}{\sqrt {17}}\;+\;{\frac {1}{16}}{\sqrt {34-2{\sqrt {17}}}}\;+\;}
- +1817+317−34−217−234+217,{\displaystyle +{\frac {1}{8}}{\sqrt {17+3{\sqrt {17}}-{\sqrt {34-2{\sqrt {17}}}}-2{\sqrt {34+2{\sqrt {17}}}}}},}
- что, в свою очередь, следует из возможности сведения уравнения вида xFn−1=0,{\displaystyle x^{F_{n}}-1=0,} где Fn{\displaystyle F_{n}} — любое простое число Ферма, с помощью замены переменной к квадратному уравнению.
- Построения с помощью одного циркуля. По теореме Мора — Маскерони с помощью одного циркуля можно построить любую фигуру, которую можно построить циркулем и линейкой. При этом прямая считается построенной, если на ней заданы две точки.
- Построения с помощью одной линейки. Очевидно, что с помощью одной линейки можно проводить только проективно-инвариантные построения. В частности,
- невозможно даже разбить отрезок на две равные части,
- также невозможно найти центр данной окружности.
- Однако,
- при наличии на плоскости заранее проведённой окружности с отмеченным центром с одной линейкой можно провести те же построения, что и циркулем и линейкой (теорема Штейнера — Понселе).
- Если на линейке есть две засечки, то построения с её помощью эквивалентны построениям с помощью циркуля и линейки (важный шаг в доказательстве этого сделал Наполеон).
- Построения с помощью инструментов с ограниченными возможностями. В задачах такого рода инструменты (в противоположность классической постановке задачи) считаются не идеальными, а ограниченными: прямую через две точки с помощью линейки можно провести только при условии, что расстояние между этими точками не превышает некоторой величины; радиус окружностей, проводимых с помощью циркуля, может быть ограничен сверху, снизу или одновременно и сверху, и снизу.
- Построения с помощью плоского оригами см. правила Фудзиты
- Построения с помощью шарнирных механизмов — это построения на плоскости и в пространстве с помощью единичных стержней, связанных на концах шарнирами. Этим способом можно построить любое алгебраическое число[6].
- Программные пакеты динамической геометрии позволяют выполнять виртуальные построения с помощью циркуля и линейки на мониторе компьютера.
- ↑ Кириченко, 2005, с. 1.
- ↑ Кто и когда доказал невозможность построения треугольника по трем биссектрисам?. Дистанционный консультационный пункт по математике МЦНМО.
- ↑ Можно ли построить треугольник по трем биссектрисам, если кроме циркуля и линейки разрешается использовать трисектор. Дистанционный консультационный пункт по математике МЦНМО.
- ↑ Кириченко, 2005, с. 4.
- ↑ Кириченко, 2005, с. 9.
- ↑ Maehara, Hiroshi (1991), «Distances in a rigid unit-distance graph in the plane», Discrete Applied Mathematics Т. 31 (2): 193–200, DOI 10.1016/0166-218X(91)90070-D .
- ↑ Стандарт флага Ирана Архивная копия от 21 июня 2012 на Wayback Machine (перс.)
- Адлер А. Теория геометрических построений / Перевод с немецкого Г. М. Фихтенгольца. — Издание третье. — Л.: Учпедгиз, 1940. — 232 с.
- Александров И. И. Сборник геометрических задач на построение. — Издание восемнадцатое. — М.: Учпедгиз, 1950. — 176 с.
- Аргунов Б. И., Балк М. Б. Геометрические построения на плоскости. Пособие для студентов педагогических институтов. — Издание второе. — М.: Учпедгиз, 1957. — 268 с.
- Воронец А. М. Геометрия циркуля. — М.-Л.: ОНТИ, 1934. — 40 с. — (Популярная библиотека по математике под общей редакцией Л. А. Люстерника).
- Гейлер В. А. Неразрешимые задачи на построение // СОЖ. — 1999. — № 12. — С. 115—118.
- Кириченко В. А. Построения циркулем и линейкой и теория Галуа // Летняя школа «Современная математика». — Дубна, 2005.
- Манин Ю. И. Книга IV. Геометрия // Энциклопедия элементарной математики. — М.: Физматгиз, 1963. — 568 с.
- Петерсен Ю. Методы и теории решения геометрических задач на построение. — М.: Типография Э. Лисснера и Ю. Романа, 1892. — 114 с.
- Прасолов В. В. Три классические задачи на построение. Удвоение куба, трисекция угла, квадратура круга. — М.: Наука, 1992. — 80 с. — (Популярные лекции по математике).
- Геометрические построения // Справочник по математике (для ср. уч. заведений)/ Цыпкин А.Г., под ред. Степанова С.А. — 3-е изд. — М.: Наука, Гл. редакция физ.-мат. литературы, 1983. — С. 200–213. — 480 с.
- Штейнер Я. Геометрические построения, выполняемые с помощью прямой линии и неподвижного круга. — М.: Учпедгиз, 1939. — 80 с.
- Факультативный курс по математике. 7-9 / Сост. И. Л. Никольская. — М.: Просвещение, 1991. — С. 80. — 383 с. — ISBN 5-09-001287-3.