Многоугольник фигура: МНОГОУГОЛЬНИК — это… Что такое МНОГОУГОЛЬНИК? — DesignLessons – все о дизайне

Содержание

Многоугольники — урок. Геометрия, 8 класс.

Ломаной называется фигура, которая состоит из точек и соединяющих их отрезков.

Точки называются вершинами ломаной, а отрезки — звеньями ломаной.

Виды ломаных

Ломаная называется замкнутой, если у неё концы совпадают.

Если концы ломаной не совпадают, то она называется незамкнутой.

Ломаная называется простой, если она не имеет самопересечений. Обе ломаные выше являются простыми.

На следующем рисунке — ломаная с самопересечением.

Многоугольник

Многоугольник — это простая замкнутая ломаная линия и конечная часть

плоскости, которую она ограничивает.

Вершины ломаной линии называются вершинами многоугольника, а её звенья — сторонами многоугольника.

Отрезок, соединяющий две вершины, не лежащие на одной стороне, называется диагональю многоугольника.

\(A\), \(B\), \(C\), \(D\), \(E\) — вершины;
\(AB\), \(BC\), \(CD\), \(DE\), \(AE\) — стороны;
\(AC\), \(AD\), \(BE\), \(BD\), \(CE\) — диагонали.

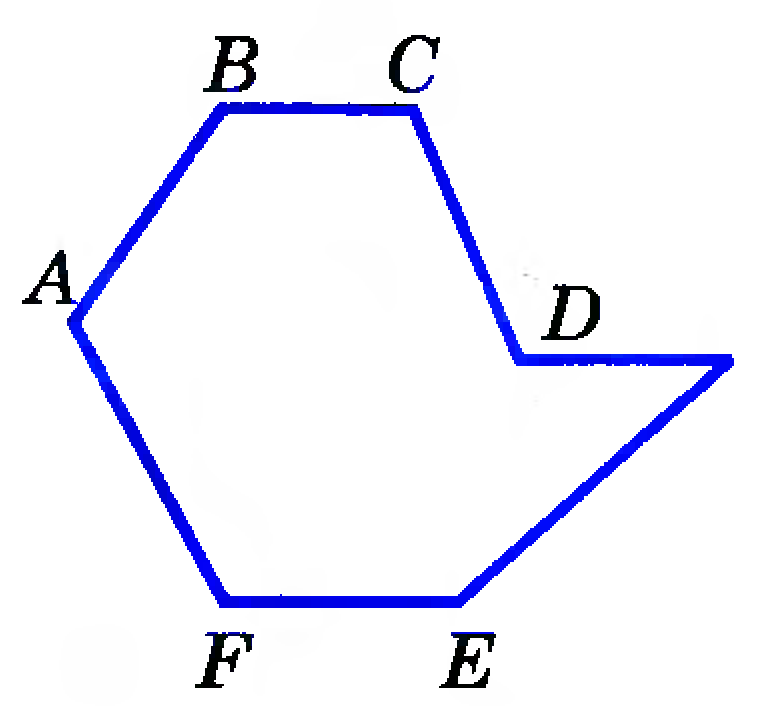
Многоугольник, у которого все углы меньше 180°, называется выпуклым многоугольником.

Пятиугольник \(ABCDE\) является выпуклым многоугольником.

Сумма углов выпуклого \(n\)-угольника

В общем случае многоугольник можно назвать \(n\)-угольником, это означает, что у данного многоугольника \(n\) сторон и \(n\) вершин.

Сумма углов выпуклого \(n\)-угольника равна 180°⋅n−2.

Любой выпуклый многоугольник можно разделить на треугольники. Количество треугольников на \(2\) меньше, чем количество сторон в многоугольнике.

Сумма внутренних углов любого треугольника равна 180°.

Поэтому сумма углов выпуклого \(n\)-угольника равна 180°⋅n−2.

Пример:

вычисли сумму внутренних углов выпуклого одиннадцатиугольника.

Можно нарисовать рисунок, но это не обязательно для решения задачи.
Используем формулу:
180°⋅n−2=180°⋅11−2=180°⋅9=1620°.

стороны, вершины, диагонали. Периметр многоугольника

Многоугольник — это геометрическая фигура, ограниченная замкнутой ломаной линией, не имеющей самопересечений.

Звенья ломаной называются сторонами многоугольника

, а её вершины — вершинами многоугольника.

Углами многоугольника называются внутренние углы, образованные соседними сторонами. Число углов многоугольника равно числу его вершин и сторон.

Многоугольникам даются названия по количеству сторон. Многоугольник с наименьшим количеством сторон называется треугольником, он имеет всего три стороны. Многоугольник с четырьмя сторонами называется четырёхугольником, с пятью — пятиугольником и т. д.

Обозначение многоугольника составляют из букв, стоящих при его вершинах, называя их по порядку (по часовой или против часовой стрелки). Например, говорят или пишут: пятиугольник

ABCDE:

В пятиугольнике ABCDE точки A, B, C, D и E — это вершины пятиугольника, а отрезки AB, BC, CD, DE и EA — стороны пятиугольника.

Выпуклые и вогнутые

Многоугольник называется выпуклым, если ни одна из его сторон, продолженная до прямой линии, его не пересекает. В обратном случае многоугольник называется вогнутым:

Периметр

Сумма длин всех сторон многоугольника называется его периметром

Периметр многоугольника ABCDE равен:

AB + BC + CD + DE + EA.

Если у многоугольника равны все стороны и все углы, то его называют правильным. Правильными многоугольниками могут быть только выпуклые многоугольники.

Диагональ

Диагональ многоугольника — это отрезок, соединяющий вершины двух углов, не имеющих общей стороны. Например, отрезок AD является диагональю:

Единственным многоугольником, который не имеет ни одной диагонали, является треугольник, так как в нём нет углов, не имеющих общих сторон.

Если из какой-нибудь вершины многоугольника провести все возможные диагонали, то они разделят многоугольник на треугольники:

Треугольников будет ровно на два меньше, чем сторон:

t = n — 2,

где t — это количество треугольников, а n — количество сторон.

Разделение многоугольника на треугольники с помощью диагоналей используется для нахождения площади многоугольника, так как чтобы найти площадь какого-нибудь многоугольника, нужно разбить его на треугольники, найти площадь этих треугольников и полученные результаты сложить

Многоугольники | Математика

Часть плоскости, ограниченная со всех сторон прямыми, называется фигурой.

Линия или совокупность отрезков, ограничивающих фигуру, называется периметром.

Фигуры разделяются на прямолинейные и криволинейные. Прямолинейная есть фигура, ограниченная только прямыми линиями. Криволинейная есть фигура, ограниченная одной или несколькими кривыми линиями.

Чертежи 71 и 72 представляют прямолинейные, а чертеж 73 криволинейную фигуры.

Из прямолинейных фигур заслуживают особого внимания многоугольники.

Многоугольником называется часть плоскости, ограниченная со всех сторон прямыми линиями.

Прямая линия, ограничивающая многоугольник, называется его стороной.

Точки пересечения сторон называются вершинами многоугольника.

Число углов многоугольника равно числу сторон.

По числу сторон многоугольники получают название четырехугольник, пятиугольник, шестиугольник и т. д.

На чертеже 74 мы имеем пятиугольник ABCDE.

Периметр многоугольника есть совокупность всех его сторон.

Отрезки AB, BC, CD, DE, AE (черт. 74) будут сторонами, точки A, B, C, D, E вершинами многоугольника. При этих вершинах расположены внутренние углы многоугольника того же названия.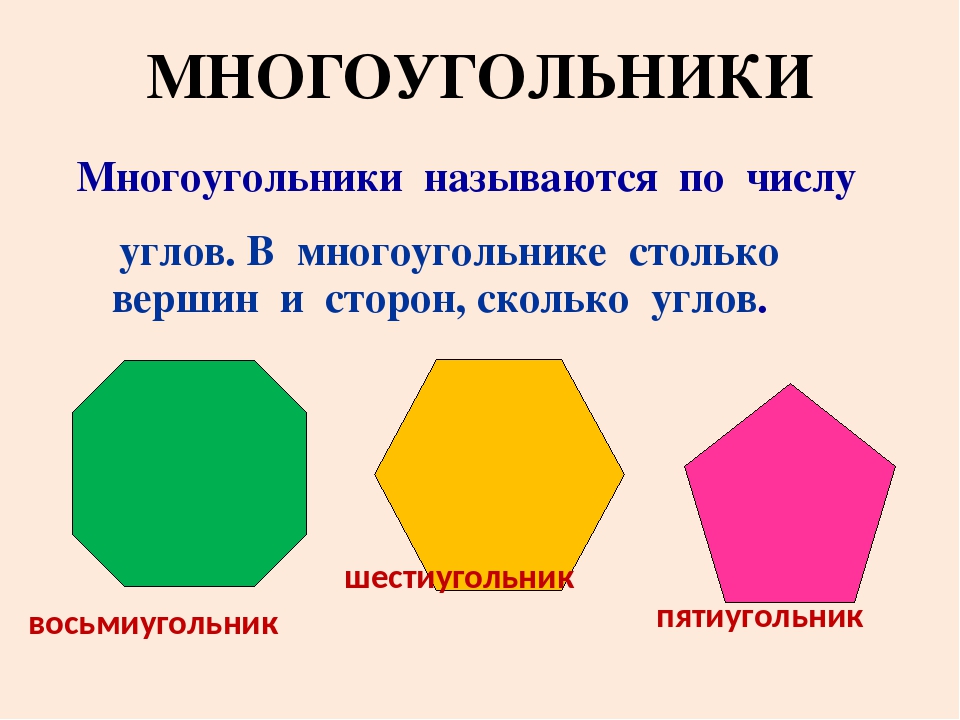

Угол, образуемый стороной многоугольника и продолжением другой смежной с ней, называется внешним углом многоугольника.

Внутренний угол многоугольника называется исходящим и входящим, смотря по тому, будет ли он меньше или больше двух прямых.

На чертеже 72 угол FAB есть исходящий, а EDC входящий угол многоугольника, ибо первый меньше, а второй больше двух прямых. Мы будем рассматривать только многоугольники с одними исходящими углами.

Всякая линия, соединяющая две вершины и проходящая внутри многоугольника, называется его диагональю.

Отрезки AC, AD (черт. 74) есть диагонали.

Из каждой вершины можно провести диагонали ко всем углам многоугольника кроме двух смежных.

Диагоналями многоугольник разбивается на треугольники.

Если n есть число сторон многоугольника, то число диагоналей, которые можно провести из какой-нибудь вершины, равно n — 3.

Число треугольников, на которые разбивается многоугольник диагоналями, проведенными из одной вершины, равно n — 2.

Теорема 47. Сумма всех внутренних углов многоугольника равна двум прямым, умноженным на число сторон без двух.

Доказательство. Многоугольник разбивается диагоналями, проведенными из какой-нибудь вершины на n — 2 треугольников. Сумма всех внутренних углов многоугольника равна сумме углов всех треугольников, на которые он разбивается.

Обозначив сумму всех внутренних углов многоугольника через S, имеем:

S = (n — 2) 2d или S = 2dn — 4d.

Сумма внутренних углов многоугольника равна двум прямым, умноженным на число сторон без четырех прямых.

Из этой формулы вытекает, что сумма углов четырехугольника равна 4d, пятиугольника 6d, шестиугольника 8d, семиугольника 10d и т. д.

Теорема 48. Сумма внешних углов многоугольника равна четырем прямым.

Доказательство

. Продолжим все стороны многоугольника, имеющего n сторон, в одну сторону (черт. 75) и назовем внешние углы буквами α, β, γ и т.

д.

Обозначив внутренние углы через A, B, C и т. д., имеем равенства:

A + α = 2d
B + β = 2d
C + γ = 2d

и т. д.

Сложив эти равенства, имеем:

A + B + C + … + α + β + γ + … = 2dn

Сумма внутренних углов будет

A + B + C + … = 2d(n — 2) = 2dn — 4d

следовательно,

2dn — 4d + α + β + γ + … = 2dn

откуда сумма внешних углов многоугольника будет

α + β + γ + … = 4d (ЧТД).

Четырехугольники

Четырехугольники получают различные названия, смотря по взаимному расположению их четырех сторон. Они называются трапециями, параллелограммами, ромбами, прямоугольниками, квадратами.

Трапеция есть такой четырехугольник, у которого две стороны параллельны, а остальные две не параллельны между собой.

Четырехугольник ABCD (черт. 76) есть трапеция. У ней стороны AD и BC параллельны, а стороны AB и CD не параллельны.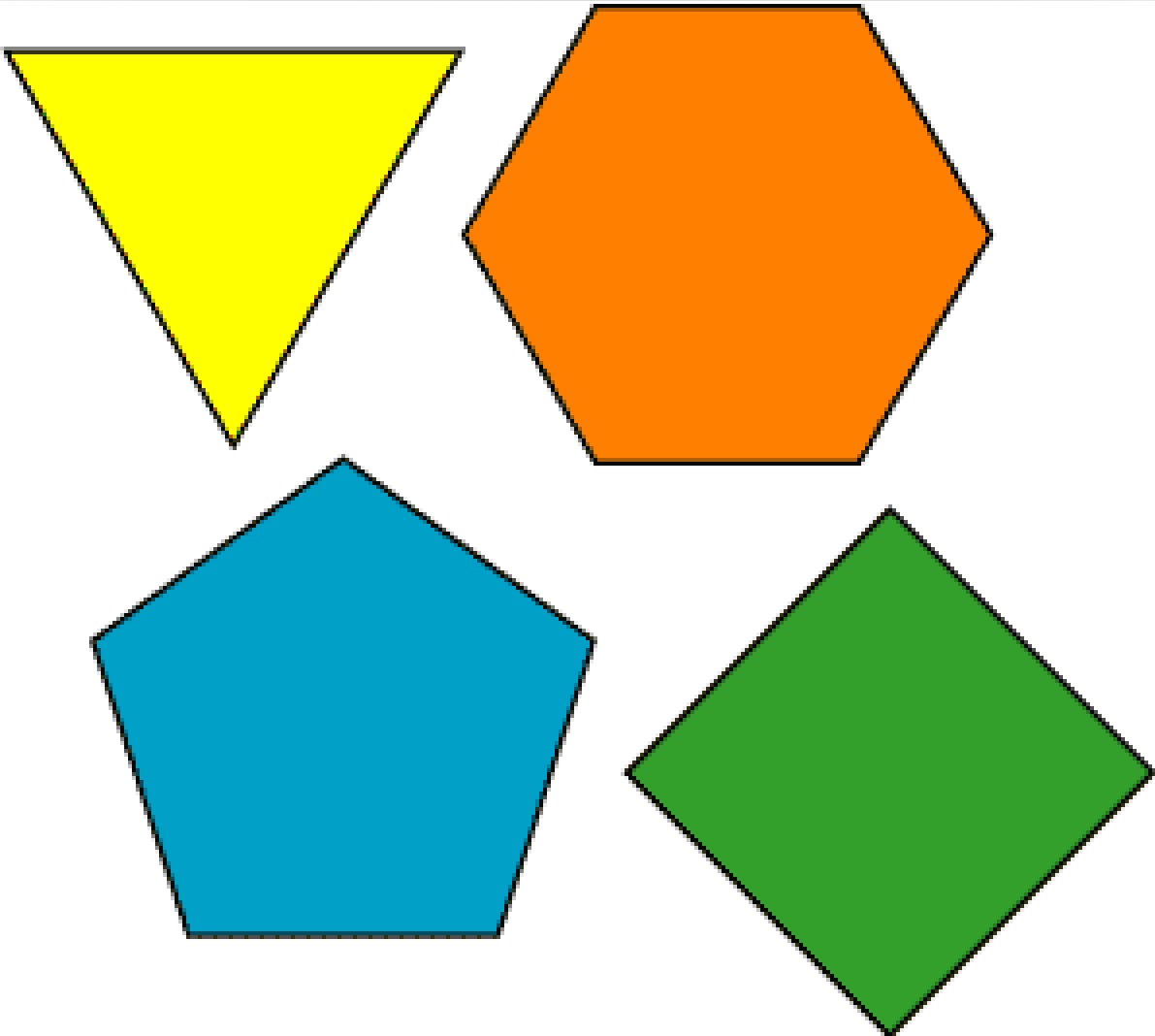

Высота трапеции есть расстояние двух ее параллельных сторон. BH есть высота трапеции.

Параллелограмм есть четырехугольник, у которого каждые две противоположные стороны параллельны. Одна из сторон его называется основанием.

Высота параллелограмма есть расстояние основания от другой параллельной ему стороны, считаемое по перпендикуляру.

Четырехугольник ABCD есть параллелограмм (черт. 77, 78, 79, 80), ибо AB || CD и BC || AD. Сторона AD (черт. 77) будет основанием, а отрезок BE высотой параллелограмма.

Ромб есть параллелограмм, у которого все четыре стороны равны.

Четырехугольник ABCD (черт. 78 и 80) есть ромб, ибо у него AB || CD, AD || BC и в то же время AB = BC = CD = AD.

Прямоугольник есть параллелограмм, у которого все углы прямые.

Четырехугольник ABCD (черт. 79 и 80) есть прямоугольник, ибо у него AB || CD, BC || AD и углы равны A = B = C = D = d прямому углу.

Квадрат есть параллелограмм, у которого все углы и все стороны равны.

Квадрат есть одновременно и прямоугольник и ромб.

Четырехугольник ABCD (черт. 80) есть квадрат, ибо у него AB || CD, BC || AD, углы равны A = B = C = D = d и стороны AB = BC = DC = AD.

Теорема 49. В параллелограмме противоположные углы и стороны равны.

Дано. Четырехугольник ABCD есть параллелограмм, следовательно, AC || CD и BC || AD (черт. 81).

Требуется доказать, что

AB = CD, BC = AD, ∠A = ∠C, ∠B = ∠D

Доказательство. Противоположные стороны равны как части параллельных между параллельными (теорема 43), следовательно,

AB = CD, AD = BC

Проведя диагональ BD, имеем два равных треугольника ABD и BCD, ибо BD сторона общая, AB = CD и AD = BC по доказанному.

Против общей стороны BD лежат равные углы, следовательно,

∠A = ∠C (ЧТД).

Равенство углов B и D доказывается аналогично (через диагональ AC).

Теорема 50 (обратная 49). Четырехугольник, у которого противоположные стороны равны, есть параллелограмм.

Дано. В четырехугольнике ABCD противоположные стороны равны (черт. 81)

AB = CD, BC = AD.

Требуется доказать, что AB || CD и BC || AD.

Доказательство. На основании теоремы 45 заключаем, что BC || AD и AB || CD, следовательно, четырехугольник ABCD есть параллелограмм (ЧТД).

Теорема 51. Диагонали параллелограмма пересекаются пополам.

Дано. Четырехугольник ABCD есть параллелограмм (черт. 82), следовательно, BC || AD, AB || CD и проведены диагонали AC и BD, которые пересекаются в точке O.

Требуется доказать, что AO = OC и BO = OD.

Доказательство. При точке O соприкасаются вершинами два равных треугольника BOC и AOD, ибо у них

BC = AD как равные противоположные стороны параллелограмма.

∠γ = ∠β (как накрест-лежащие углы от пересечения параллельных BC и AD прямой AC).

∠α = ∠δ (как накрест-лежащие от пересечения параллельных BC и AD прямой BD).

Против равных углов γ и β лежат равные стороны BO и OD, следовательно, точка O есть середина диагонали BD.

Против равных углов δ и α лежат равные стороны AO и OC, следовательно, точка O есть середина диагонали AC (ЧТД).

Теорема 52. Диагонали ромба перпендикулярны.

Дано. Параллелограмм ABCD (черт. 83) есть ромб, следовательно,

AB || CD, BC || AD и AB = BC = CD = AD.

Требуется доказать, что BD ⊥ AC.

Доказательство. Два треугольника ABO и BOC равны, ибо BO общая сторона, AB = BC по условию, AO = OC по предыдущей теореме (51), следовательно,

∠AOB = ∠BOC,

откуда вытекает, что ∠AOB как один из равных смежных есть прямой угол и потому BO ⊥ AO и BD ⊥ AC (ЧТД).

Теорема 53. Диагонали прямоугольника равны.

Дано. Параллелограмм ABCD есть прямоугольник (черт. 84), следовательно, AB = CD, BC = AD, и углы A, B, C, D прямые.

Требуется доказать, что BD = AC.

Доказательство. Треугольник ABD равен треугольнику ACD, ибо они оба прямоугольные треугольники и у них AD сторона общая.

AB = CD как противоположные стороны параллелограмма, следовательно, AC = BD.

Так как квадрат есть одновременно параллелограмм, ромб и прямоугольник, то диагонали квадрата пересекаются пополам, перпендикулярны и равны.

При помощи этих теорем легко может быть доказана следующая теорема.

Теорема 54. Перпендикуляры, опущенные из трех вершин треугольника на его стороны, встречаются в одной точке.

Дано. Отрезки AD, BE и CF перпендикулярны к сторонам треугольника ABC (черт. 85).

Требуется доказать, что они пересекаются в одной точке.

Доказательство. Проведем через вершины треугольника ABC прямые, параллельные его сторонам, так что

A’B’ || AC, B’C’ || BC, A’B’ || AB,

и продолжим их до взаимного пересечения.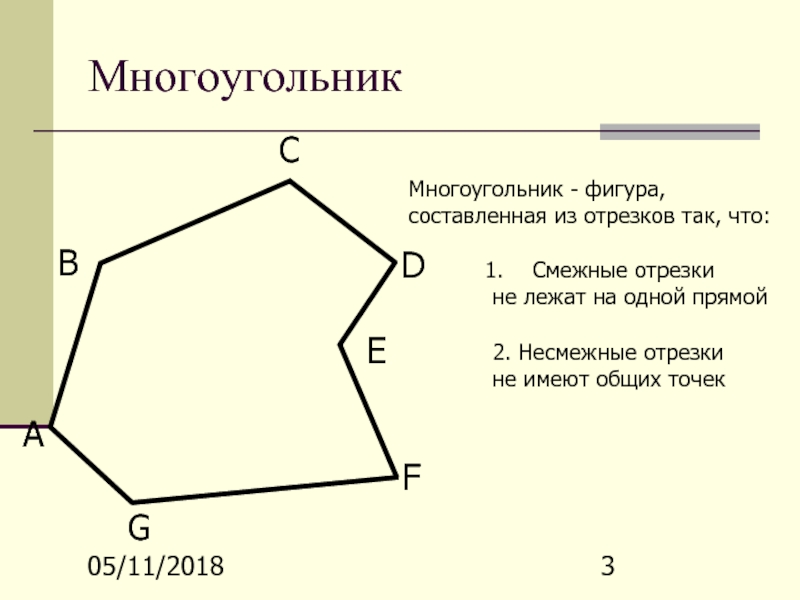

Четырехугольники AC’BC, AB’CB, ABA’C суть параллелограммы, ибо у них противоположные стороны параллельны, поэтому

AC’ = CB и AB’ = CB

откуда

AC’ = AB’

следовательно, точка A есть середина BC’.

Подобным же образом можно доказать, что точка B есть середина отрезка A’C’ и C середина отрезка A’B’.

Прямые AD, BE, CF как перпендикуляры, восставленные из середины сторон треугольника A’B’C’, должны встретиться в одной точке (теорема 32) (ЧТД).

Многоугольники. Выпуклый многоугольник. Четырехугольник 8 класс онлайн-подготовка на Ростелеком Лицей

Многоугольники. Выпуклый многоугольник. Четырехугольник.

Треугольник – это частный случай многоугольника.

В самом названии уже подчеркивается, что это фигура, у которой три угла. Следовательно, в многоугольнике их может быть много, т.е. больше, чем три. Например, изобразим пятиугольник – фигуру с пятью углами.

Многоугольник – фигура, состоящая из нескольких точек (больше двух) и соответствующего количества отрезков, которые их последовательно соединяют. Эти точки называются вершинами многоугольника, а отрезки – сторонами. При этом никакие две смежные стороны не лежат на одной прямой и никакие две несмежные стороны не пересекаются.

Любой многоугольник разделяет плоскость на две области: внутреннюю и внешнюю. Внутреннюю область также относят к многоугольнику.

Иными словами, например, когда говорят о пятиугольнике А₁А₂А₃А₄А₅, имеют в виду и всю его внутреннюю область, и границу. А ко внутренней области относятся и все точки, которые лежат внутри многоугольника.

Многоугольники еще иногда называют n-угольниками, чтобы подчеркнуть, что рассматривается общий случай наличия какого-то неизвестного количества углов (n штук).

Периметр многоугольника – сумма длин сторон многоугольника.

Отрезок, соединяющий любые две противоположные вершины, называется диагональю многоугольника.

Многоугольники делятся на выпуклые и невыпуклые. Например, многоугольник, изображенный на рисунке выше, является выпуклым, а на рисунке ниже – невыпуклым.

Многоугольник называется выпуклым, если при проведении прямой через любую из его сторон весь многоугольник лежит только по одну сторону от этой прямой. Невыпуклыми являются все остальные многоугольники.

Правильный многоугольник – это выпуклый многоугольник, у которого все стороны и углы равны.

Существенное отличие четырехугольника от треугольника в том, что он может быть выпуклым или невыпуклым.

Очень важное различие, о котором знает каждый плотник, состоит в том, что треугольник – «жесткая» фигура, а четырехугольник (как и все остальные многоугольники) – «нежесткая».

У треугольника невозможно изменить его форму, не изменив длин сторон. При этом у любого четырехугольника можно изменить его форму, не меняя длины сторон. На практике это будет означать, что треугольник, сколоченный из трех дощечек, будет жестким, не будет сминаться даже при сильных воздействиях, а четырехугольник при достаточной нагрузке со стороны изменит свою форму.

Для описания свойств многоугольников существуют две важнейшие теоремы об их углах: теорема о сумме внутренних углов выпуклого многоугольникаитеорема о сумме внешних углов выпуклого многоугольника.

Теорема. О сумме внутренних углов выпуклого многоугольника (n-угольника).

Сумма углов n-угольника равна 180°·(n-2).

Математическая запись: ∠A1+∠A2+…+∠An=180°(n-2), где n – количество его углов (сторон).

Вспомним, что любой четырехугольник состоит из двух треугольников (достаточно провести диагональ). Но сумма углов каждого из них одинакова и равна 180⁰, значит, сумма углов четырехугольника 360⁰.

Теорема. О сумме внешних углов выпуклого многоугольника (n-угольника).

∠1’+∠2’+…+∠n’=360°, где n – количество его углов (сторон), а ∠1′,…,∠n’ – внешние углы, по одному от каждой вершины.

Урок 37. многоугольники — Математика — 5 класс

Математика

5 класс

Урок №37

Многоугольники

Перечень рассматриваемых вопросов:

— наглядные представления о фигурах на плоскости;

— многоугольники;

— периметр многоугольника;

— выпуклые многоугольники;

— изображение геометрических фигур.

Тезаурус

Многоугольник – это фигура, образованная ломаной, у которой никакие два звена не имеют общих точек, кроме концов соседних звеньев ломаной.

Периметр многоугольника – это сумма всех его сторон.

Диагональ многоугольника – это отрезок, соединяющий две несмежные вершины многоугольника.

Обязательная литература

Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений. // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017. – 272 с.

Дополнительная литература

1. Чулков П. В. Математика: тематические тесты. 5 класс. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. – М.: Просвещение, 2009. – 142 с.

2. Шарыгин И. Ф. Задачи на смекалку: 5-6 классы. // И. Ф. Шарыгин, А. В. Шевкин. – М.: Просвещение, 2014. – 95 с.

Теоретический материал для самостоятельного изучения

Мы уже знаем, из каких элементов состоят некоторые геометрические фигуры и как их изобразить на плоскости. Сегодня мы рассмотрим многоугольник.

Ломаная линия лежит в основе построения многоугольника.

Построим ломаную. Для этого отметим на плоскости несколько точек – например, пять. Соединим их так, чтобы никакие два из отрезков, имеющих общие точки, не лежали на одной прямой. Полученная фигура и будет ломаной, которую обозначают A, B, C, D, E.

Отрезки АВ, ВС, СD,DE называются звеньями ломаной.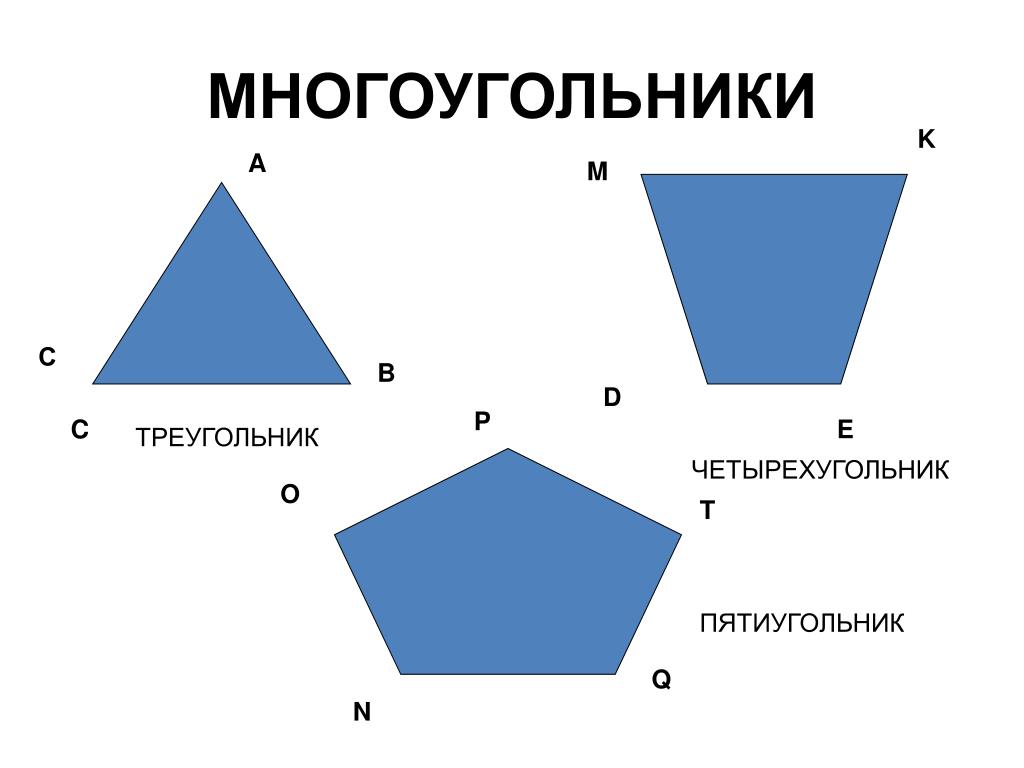 У ломаной, которую мы изобразили, четыре звена.

Если измерить длину каждого звена и найти их сумму, то получится длина ломаной.

Измерим длину ломаной.

АВ = 4 см

ВС = 2 см

СD = 3 см

DE = 5 см

Сумма длин всех звеньев равна:

АВ + ВС + СD + DЕ = 14 см – длина ломаной

Теперь нарисуем ломаную таким образом, чтобы её конец совпадал с началом. Получается замкнутая ломаная A, B, C, D, E, А.

Фигуру, образованную таким образом, называют многоугольником. То есть многоугольник – это фигура, образованная ломаной, у которой никакие два звена не имеют общих точек, кроме концов соседних звеньев ломаной.

Стоит помнить, что многоугольником является как замкнутая линия, так и эта линия вместе с плоскостью внутри неё.

Такие звенья называются сторонами многоугольника. В нашем случае это стороны АВ, ВС, СD,DE, ЕА.

Углы, образованные двумя соседними сторонами, называют углами многоугольника, а их вершины – вершинами многоугольника.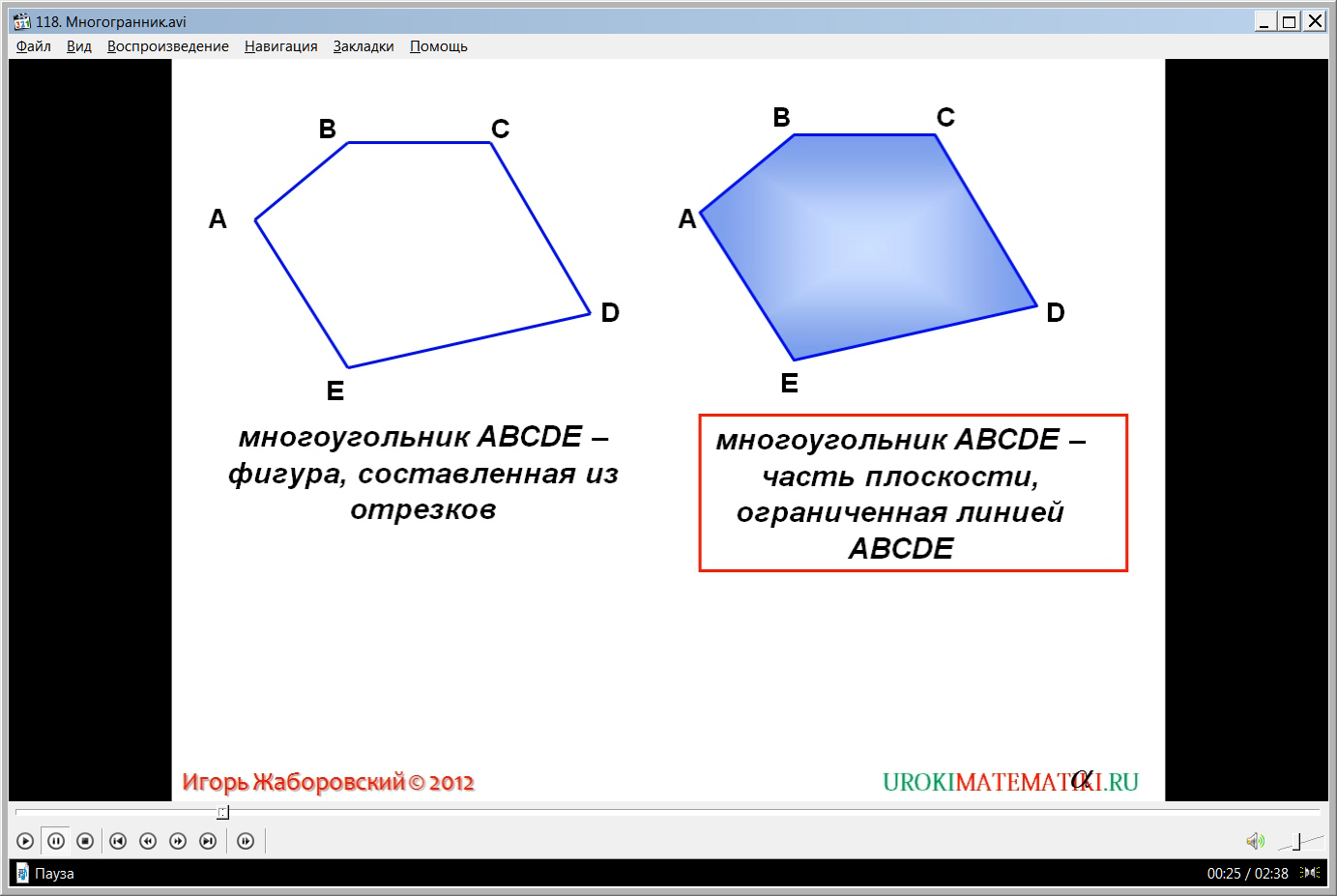

∠А, ∠В, ∠С, ∠D, ∠E – углы многоугольника

Точки А, В, С, D, E – вершины многоугольника

Кроме того, у многоугольника есть ещё и диагонали.

Диагональ – это отрезок, соединяющий две несмежные вершины многоугольника. АС, СЕ – диагонали.

Сумма всех сторон многоугольника составляет периметр многоугольника.

P = АВ + ВС + СD + DЕ + ЕА

Рассмотрим разновидности многоугольников.

Многоугольник называется выпуклым, если он расположен по одну сторону от каждой прямой, содержащей его сторону.

Например, многоугольник ABCDE – выпуклый. А многоугольник MNKLO – нет.

По числу сторон многоугольники делятся на треугольники, пятиугольники и так далее.

Кроме того, многоугольники, у которых все стороны и все углы равны, называют правильными. Например, квадрат.

Многоугольники можно сравнить путём наложения. Если они полностью накладываются друг на друга, то считаются равными. При этом стоит помнить, они имеют одинаковые площади.

Для определения площади многоугольника надо выяснить, сколько раз выбранная единица измерения содержится в этой фигуре.

Не только человек может рисовать многоугольники. Природа тоже создаёт многоугольники в большом разнообразии. Рассмотрим, где они встречаются. Например, шестиугольники можно увидеть в сотах пчёл и – под микроскопом – в строении глаза мухи или некоторых других насекомых.

Панцирь черепахи тоже изобилует большим количеством многоугольников. Как и кожа змеи: она буквально покрыта многоугольниками. В общем, природа постаралась и разнообразила мир геометрическими фигурами.

Тренировочные задания

№ 1. Чему равен периметр правильного шестиугольника со стороной 4 см?

Решение: для решения этой задачи достаточно вспомнить, что в правильных фигурах все стороны равны, следовательно, все стороны шестиугольника равны 4 см. Вычислим периметр шестиугольника, это сумма всех его сторон.

Р = 4 см + 4 см + 4 см + 4 см + 4 см + 4 см = 24 см

Ответ: 24 см.

№ 2. Из листа железа размером 10 × 14 см вырезали два квадрата со стороной 4 см и три прямоугольника со сторонами 2см и 6см.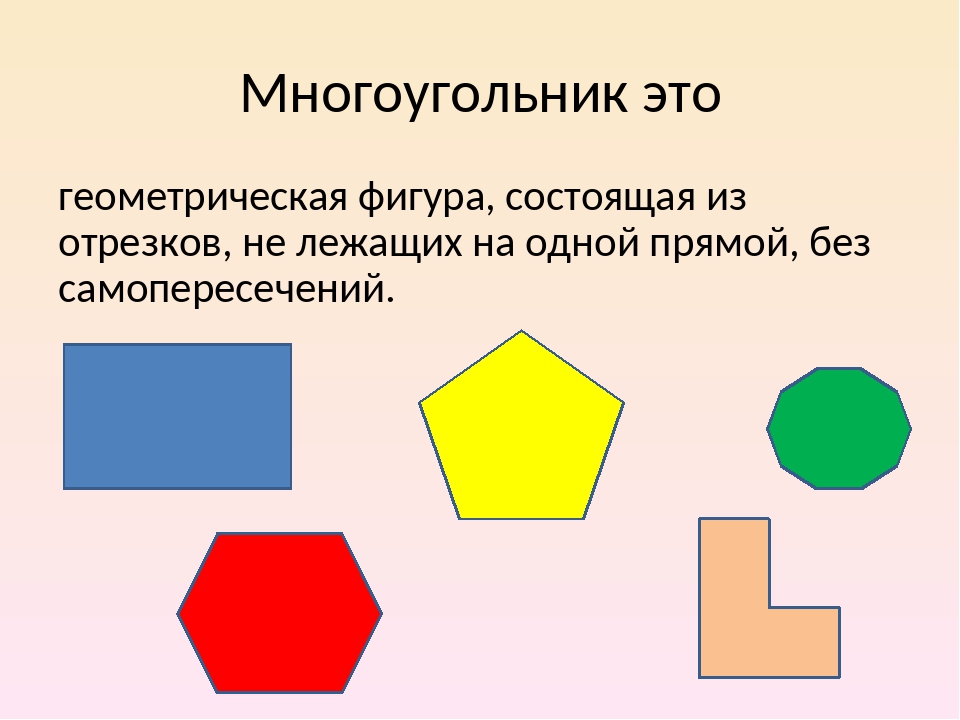 Определите площадь остатка.

Решение: сначала найдём площадь листа:

S = 10 cм · 14 см = 140 см²

Далее вычислим площадь квадратов со сторонами 4см:

S = 4 cм · 4 см = 16 см²

Тогда площадь двух квадратов равна:

16 см²· 2 = 32 см²

Найдём площадь прямоугольника:

S = 2 cм · 6 см = 12 см²

Тогда площадь трёх прямоугольников равна:

12 см²· 3 = 36 см²

Определим площади всех квадратов и прямоугольников, вырезанных из листа:

32 см²+ 36 см²= 68 см²

А теперь найдём площадь остатка: 140 см² – 68 см² = 72 см²

Ответ 72 см²

Простейшие многоугольники и их свойства — Алексей Лавриненко | Oleksiy Lavrynenko

Привет всем! В этой записи мы рассмотрели простейшую геометрическую фигуру — угол, познакомились с видами углов, и узнали об основных свойствах этой фигуры, а так же методах их обозначений. Сегодня мы узнаем, какие основные фигуры могут получиться из нескольких углов (многоугольники). И начнем, пожалуй, с треугольника.

Итак, треугольник — как следует из названия — геометрическая фигура состоящая из трех ( 🙂 ) углов (которые являются вершинами треугольника) и трех сторон:

Самой важной особенностью треугольника является тот факт, что сумма углов треугольника всегда равна 180° (пример на картинках ниже):

Как видно из картинок — сумма углов каждого из треугольников равна 180 градусам — какой бы треугольник мы не создавали.

В тексте треугольник обозначается знаком Δ и тремя заглавными латинскими буквами, которые обозначают вершины треугольника. Например, на рисунке ниже у нас имеется треугольник ABC (ΔABC) со сторонами a, b, c:

Что касается видов треугольников, то их всего три:
— прямоугольный (два угла острых (меньше 90°), и один угол прямой (равен 90°):

— остроугольный (каждый из трех углов меньше 90°):

— тупоугольный (один угол больше 90°, два других меньше 90°):

С треугольниками и их видами мы закончили. А теперь зададим себе вопрос: а что будет, если сторон и вершин у фигуры будет не три, а четыре? Начнем с квадрата. Строгое научное объяснение квадрата звучит так: квадрат — это прямоугольник, у которого все стороны равны.

А если говорить простым языком — квадрат — это фигура, у которой четыре вершины, а длина всех сторон — равная. Суть одна, а звучит, как по мне — проще, и не так сухо. Но решать — вам 🙂

В тексте квадрат обозначается заглавными латинскими буквами, обозначающими вершины квадрата. Например, на рисунке ниже у нас имеется квадрат ABCD:

Нужно отметить, что квадрат состоит из четырех углов: BAD, ABC, BCD, CDA. Что касается сторон квадрата — то они (стороны: a, b, c, d) совершенно равны:

А что будет, если в квадрате не все стороны равны? Оказывается, если в квадрате равны не все стороны, а только противоположные,а и углы равны 90° — то это будет не квадрат, а прямоугольник. Обозначается прямоугольник в тексте так же, как и квадрат — заглавными латинскими буквами. На рисунке ниже — прямоугольник ABCD (заглавные буквы обозначают вершины прямоугольника), со сторонами a, b, c, d — причем, как видно из рисунка — противоположные стороны равны друг другу: сторона a = стороне c, а сторона b = стороне d:

Ок… с прямоугольником разобрались … и перейдем к многоугольникам: геометрическим фигурам различной формы, которые, подобно треугольникам, квадратам и прямоугольникам состоят из сторон (отрезки, из которых состоит многоугольник) и вершин (точки, в которых пересекаются стороны). На рисунке ниже — многоугольник ABCDEFG (кстати, многоугольник в тексте обозначается аналогично с треугольником/квадратом/прямоугольником — заглавными латинскими буквами), состоящий из вершин и сторон a, b, c, d, e, f, g:

На этом — пока все 🙂 В следующей записи, посвященной основам геометрии мы поговорим об окружности и круге. Будет интересно!

Похожее

Урок в 8-м классе по теме « многоугольник и его элементы&quot цели урока — Урок

Урок в 8-м классе по теме « Многоугольник и его элементы»

Цели урока:

Образовательные: изучение понятия многоугольник, его элементы; вписанный и описанный многоугольник;
Развивающие: активизация познавательной деятельности учащихся через решение практических задач, умение выбирать правильное решение, лаконично излагать свои мысли, анализировать и делать выводы.
Воспитательные: организация совместной деятельности, воспитание у учащихся интереса к предмету, доброжелательности, умения выслушивать ответы товарищей.

Ход урок:

1. Организационный момент

2. Мотивация урока.

Дорогие ребята!

Я надеюсь, что этот урок пройдет интересно, с большой пользой для всех. Очень хочу, чтобы те, кто еще равнодушен к царице всех наук, с нашего урока ушел с глубоким убеждением, что геометрия – интересный и нужный предмет.

Французский писатель XIX столетия Анатоль Франс однажды заметил: “Учиться можно только весело… Чтобы переваривать знания, надо поглощать их с аппетитом”.

Давайте последуем совету писателя на сегодняшнем уроке: будьте активны, внимательны, поглощайте с большим желанием знания, которые пригодятся вам в дальнейшей жизни.

3. Актуализация опорных знаний.

Какие геометрические фигуры нами уже изучены?

Каковы их элементы?

Фронтальный опрос:

Какая фигура называется четырехугольником?
Какие вершины четырехугольника называются соседними, какие противолежащими?
Что такое диагонали четырехугольника?
Какие стороны четырехугольника называются соседними? Какие стороны называются противолежащими?
Что такое периметр четырехугольника?
Как проверить, можно ли из четырех данных отрезков построить четырехугольник?
Чему равна сумма внутренних углов четырехугольника?
Могут ли все углы четырехугольника быть тупыми? острыми? прямыми?

4. Изучение нового материала.

Среди множества различных геометрических фигур на плоскости выделяется большое семейство МНОГОУГОЛЬНИКОВ.

Названия геометрических фигур имеют вполне определенный смысл. Присмотритесь внимательно к слову “многоугольник”, и скажите из каких частей оно состоит. Слово “многоугольник” указывает на то, что у всех фигур этого семейства “много углов”.

Подставьте в слово “многоугольник” вместо части “много” конкретное число, например 5. Вы получите ПЯТИУГОЛЬНИК. Или 6. Тогда – ШЕСТИУГОЛЬНИК. Заметьте, сколько углов, столько и сторон, поэтому эти фигуры вполне можно было бы назвать и многосторонниками.

На рисунке геометрические фигуры. Используя рисунок, назовите эти фигуры.

Каким наименьшим числом можно заменить “много” в многоугольнике? (Ответ: 3)

Фигура, ограниченная простой замкнутой ломаной, называется многоугольником. Вершины ломаной называются вершинами многоугольника, стороны ломаной — сторонами многоугольника, а углы, образованные соседними сторонами, — углами многоугольника. Точки многоугольника, не принадлежащие его сторонам, называются внутренними.

Периметром многоугольника называется сумма длин всех его сторон.

Многоугольник, у которого n углов называется n — угольником. Многоугольник называется выпуклым, если вместе с любыми двумя своими точками он содержит и соединяющий их отрезок.

Любой треугольник выпуклый. Среди многоугольников, с числом углов большим трех, могут быть выпуклые и невыпуклые.

Диагональю многоугольника называется отрезок, соединяющий его несоседние вершины.

Исследовательская работа по группам.

Каждая группа работает по учебно-исследовательской карте.

1.Задача.

Чему равна сумма углов выпуклого пятиугольника?

2.Проблема.

Как зависит сумма углов выпуклого n-угольника от числа углов

многоугольника и от числа треугольников, на которые он разбивается

диагоналями, проведенными из одной вершины?

3.Пробы.

1 проба-180⁰ 2 проба-360⁰ 3 проба-540⁰ 4 проба-720⁰

4.Таблица результатов.

Пробы	1	2	3	4
Число углов	3	4	5	6
Число треугольников	1	2	3	4
Сумма углов	180⁰	360⁰	540⁰	720⁰

Вывод: Формула для суммы внутренних углов n-угольника. 180° (n-2 ).

Сумма внешних углов выпуклого многоугольника не зависит от числа сторон п- угольника и равна 360.

Вписанным в круг многоугольником называется такой многоугольник, вершины которого лежат на окружности. Описанным около круга многоугольником называется такой многоугольник, стороны которого касаются окружности.

Построить № 667, 668(1).

5. Закрепление нового материала.

Решение задач по рисункам устно №655, 657, 662(1, 2).

Решить № 663(1), 664(1), 665(2), 671(устно), 673(1), 666(устно).

6. Физминутка для глаз.

-Не поворачивая головы, обведите взглядом стену класса по периметру по часовой стрелке, классную доску по периметру против часовой стрелки, треугольник, изображенный на стенде по часовой стрелке и равный ему треугольник против часовой стрелки. Поверните голову налево и посмотрите на линию горизонта, а теперь на кончик своего носа. Закройте глаза, сосчитайте до 5, откройте глаза и …

Мы ладонь к глазам приставим,
Ноги крепкие расставим.
Поворачиваясь вправо,
Оглядимся величаво.
И налево надо тоже
Поглядеть из под ладошек.
И – направо! И еще
Через левое плечо!
а теперь продолжим работу.

7. Самостоятельная работа учащихся.

Решить № 665(1).

8.Итоги урока. Рефлексия.

Что больше всего тебе запомнилось на уроке?

Что удивило?

Что понравились больше всего?

Каким ты хочешь увидеть следующий урок?

Домашнее задание: выучить п.15, вопросы с.128, решить №664(2), 665(3), 668(2), 673(2).

Тема: Площадь. Площадь прямоугольника и квадрата.

Цели урока:

 Обучающие: формирование понятия площади, организация работы учащихся по самостоятельному нахождению способов сравнения площадей фигур, повторить формулы для определения площади прямоугольника и квадрата.

 Развивающие: развитие мышления и элементов познавательной деятельности (смекалки, умений сравнивать, анализировать), умения работать в проблемной ситуации.

 Воспитательные: воспитание интереса и любви к предмету через содержание учебного материала, умения применять преемстенность в изучении отдельных тем математики.

Ход урока.

1. Организационный момент.

Чтобы спорилось нужное дело,

Чтобы в жизни не знать неудач,

В математики мир отправимся смело,

В мир примеров и разных задач.

А девизом нашего урока буду такие слова:

Думать — коллективно!

Решать — оперативно!

Отвечать — доказательно!

Бороться — старательно!

И открытия нас ждут обязательно!

2. Мотивация урока.

В обычной жизни на каждом шагу мы встречаемся с понятием “площадь”. Что такое “площадь”, знает каждый. Каждый понимает смысл слов: площадь комнаты, площадь садового участка. Подумайте и самостоятельно ответьте на вопрос? что такое “площадь”? И вы увидите, что не так-то это просто. Даже математики смогли создать соответствующую математическую теорию сравнительно недавно. Правда, это никому не мешало успешно использовать понятие площади и в науке, и на практике с незапамятных времен.

Измерение площадей считают одним из самых древних разделов геометрии; в частности название “геометрия” (т.е. “землемерие”) связывают именно с измерением площадей. Согласно легенде, эта наука возникла в Древнем Египте, где после каждого разлива Нила приходилось заново производить разметку участков, покрытых плодоносным илом, и вычисление их площадей.

У римлян мерой земляных участков был югер (от «югум» — «ярмо»). Это участок земли, вспахиваемый за день двумя волами, впряженными в деревянное ярмо.

В древней Руси слабо знали основы геометрии и испытывали трудности их приложения к измерению земельных участков неправильной формы. С течением времени для пахотных земель главенствующую роль стала играть четверть — площадь, на которую высевали четверть (меру объема) ржи.

И сегодня мы с вами определим четкое понятие «площади фигуры».

3. Актуализация опорных знаний.

Площади каких фигур вы уже умеете вычислять?

4. Объяснение нового материала

– Что показывает площадь? (Сколько места занимает фигура на плоскости)

— у вас на партах разные фигуры, сравните их, выберите самую большую, самую маленькую.

Как измерить площадь фигуры? Сначала нужно выбрать единицу площади, т.е. указать единичный квадрат, т.е. квадрат, сторона которого служит единицей длины.

При выбранной единице измерения площадей площадь каждого многоугольника показывает сколько раз единица измерения и ее части укладываются в данном многоугольнике.

— у вас на партах в конвертах различные единицы измерения площади- квадраты, со стороной 1 см, 1 дм. Какую единицу вы выберите, чтобы найти площадь вашего прямоугольника? Работая в парах, найдите площадь фигуры 1. (Ученики укладывают квадраты, со стороной 1 см. в фигуре, сообщают учителю количество) Мы нашли площадь нашей фигуры.

Запишем S = … см2

А чтобы найти площадь моей фигуры, квадрат с какой стороной нужно выбрать? (Учитель показывает большую фигуру)

К доске выходят несколько учеников, выбирают квадраты, укладывают на фигуре, сообщают площадь.

Чтобы найти площадь класса, квадрат с какой стороной нужно выбрать? Удобно ли пользоваться теми, что есть у нас?

Найдите площадь каждой фигуры, изображенной на рисунке 68, если условиться, что длина стороны каждой клетки равна 1 см.

Итак, чтобы найти площадь фигуры, нужно:

1. Выбрать единицу измерения, посчитать, сколько раз эта единица укладывается в данной фигуре.

Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников. Это свойство площади многоугольника.

Равные многоугольники имеют равные площади.

Найдите площадь прямоугольника, который есть у вас.

Удобно ли каждый раз укладывать единичные квадраты в наших фигурах?

Предложите способ, который позволяет вычислить площадь прямоугольника, не используя способ подсчета уместившихся квадратов.

S = a * b

А как называется прямоугольник, у которого длина и ширина равны? (Квадрат)

Он давно знакомый мой.

Каждый угол в нем прямой,

Все четыре стороны одинаковой длины.

Вам его представить рад,

А зовут его …(квадрат).

Как найти его площадь?

S = a∙a = a²

Площадь многоугольника — положительная величина, численное значение которой обладает такими свойствами:

Свойство 1°. Равные многоугольники имеют равные площади.

Свойство 2°. Если многоугольник состоит из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.

Свойство 3°. Площадь квадрата равна квадрату его стороны.

Найти площадь фигуры.

5. Первичное закрепление нового материала.

Решить:

устно № 686, 687, 688, 691;

письменно № 688, 694(1, 2), 697(1), 693.

6. Самостоятельная работа учащихся.

Найдите площадь треугольника ВСМ

Найти: S_МВС−?

Ответ: S_ВСМ=14 см²

Есть ли вопросы, как находить площадь сложной плоской фигуры?

7. Итог урока.

Работа с карточками «+», «-».

Верно ли утверждение.

1. Равные фигуры имеют равные площади.

2. Неравные фигуры имеют различные площади.

3. Если фигуры равновеликие, то они равны.

4. Если площадь квадрата равна сумме площадей двух других квадратов, то длина стороны большего квадрата равна сумме длин сторон этих квадратов.

5. Если сторону квадрата увеличить в 2 раза, то его площадь увеличится в 2 раза.

Сформулировать свойства площадей.

8. Рефлексия. Д/з.

Ребята, продолжите предложения, написанные на доске.

На уроке сегодня я узнал…

Мне было интересно, когда…

Я так и не понял…

Знания, полученные на уроке, мне пригодятся…

Выучить п.16, вопросы с.136. Решить № 692, 694(3, 4), 697(2).

Творческое задание: сообщение «Как измеряли площадь в старину».

Урок геометрии в 8-м классе по теме «Площадь параллелограмма»

Цели урока:

Повторить свойства площадей фигур; формулы площади прямоугольника и квадрата; вывести формулу для нахождения площади параллелограмма; рассмотреть задачи с её применением.
Развивать умения анализировать, сопоставлять, логически мыслить, обобщать; развивать внимание, память, активность и самостоятельность.
Воспитывать ответственное отношение к учебному труду, настойчивость для достижения конечного результата, умение работать в коллективе; воспитывать в учащихся личностную рефлексию: стал ли он сам для себя изменяющимся субъектом деятельности.

Ход урока.

1. Организационный момент.

2. Мотивация урока.

Ребята, урок я начну с высказывания Г.Галилея: «Геометрия является самым могущественным средством для изощрения наших умственных способностей и дает нам возможность правильно мыслить и рассуждать». Я хочу, чтобы вы на уроке думали и рассуждали.

3. Актуализация опорных знаний. Проверка д/з.

6 cм

о рисунку составить задачу и решить.

S₂

S₁=S₂.

S₁

4 см

2) А D

S_ABCD = Q

S_{Δ ABC}=?

В С

Найдите площадь дачного участка такой формы.

Определение и свойства параллелограмма

— А какие Вы знаете свойства? (сторон, углов, диагоналей).

— Дети, Вы всё знаете о данной фигуре? (нет, площадь).

— Площадь каких фигур Вы знаете? (S_кв=а²; S_прям=а*b).

— А Вы знаете, чему равна площадь параллелограмма? (нет).

— О чём мы сегодня будем говорить на уроке геометрии? (S_парал).

Итак, вы сегодня на уроке будет учениками «Евклида» и исследуете параллелограмм и докажите чему равна площадь параллелограмма.

4. Объяснение нового материала

Вывод формулы площади параллелограмма.

Задача.

Как «перекроить» параллелограмм, чтобы получить прямоугольник с такой же площадью?

После вывода формулы учитель требует ее словесное описание. Несколько учеников «проговариваются» вслух, тем самым, развивая математическую речь.

Найти площадь фигуры.

Теорема о площади ромба по его диагоналям.

Площадь ромба равна половине произведения его диагоналей.

Рассмотреть доказательство теоремы на с. 142.

5. Минутки релаксации:

Быстро поморгать, закрыть глаза и посидеть спокойно, медленно считая до пяти. Повторить 4-5 раз.
Вытянуть правую руку вперёд. Следить глазами, не поворачивая головы, за медленным движением указательного пальца вытянутой руки влево и вправо, вверх и вниз. Повторить 4-5 раз.
В среднем темпе проделать 3-4 круговых движения глазами в правую сторону, столько же в левую сторону. Расслабив глазные мышцы, посмотреть вдаль на счет 1-6. Повторить 1-2 раза.

6. Первичное закрепление нового материала.

Решить:

устно № 721, 722, 723, 724;

письменно № 725 (1, 2), 726(1, 2), 727(1, 2), 732, 743(1).

7. Самостоятельная работа учащихся.

Решить № 725(3), 726(3).

8. Итог урока.

9. Рефлексия. Д/з.

Выучить п.17, решить № 727(3, 4), 743(2), 729(1).

Урок геометрии в 8-м классе по теме «Площадь треугольника»

Цели урока:

Повторить свойства площадей фигур; формулы площади прямоугольника и квадрата, параллелограмма. ромба; вывести формулу для нахождения площади треугольника; рассмотреть задачи с её применением.
Развивать умения анализировать, сопоставлять, логически мыслить, обобщать; развивать внимание, память, активность и самостоятельность.
Воспитывать ответственное отношение к учебному труду, настойчивость для достижения конечного результата, умение работать в коллективе; воспитывать в учащихся личностную рефлексию: стал ли он сам для себя изменяющимся субъектом деятельности.

Ход урока.

1. Организационный момент.

2. Мотивация урока.

3. Актуализация опорных знаний. Проверка д/з.

Дан периметр параллелограмма ABCD равный 80 см, высота ВН = 3 см. А стороны относятся как 2:3. Найдите Площадь параллелограмма.

КРОССВОРД

По горизонтали:

Перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону.
Четырехугольник, у которого противоположные стороны попарно параллельны.

7. Параллелограмм, у которого все стороны равны.

Сторона прямоугольного треугольника, лежащая против прямого угла.

По вертикали:

Четырехугольник, у которого две стороны параллельны, а две другие не параллельны.
Геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки.
Отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Геометрическая фигура, состоящая из трех точек, не лежащих на одной прямой и трех отрезков, попарно соединяющих эти точки.

4. Первичное усвоение нового материала.

Учитель показывает листочки с фигурами:

Задача: узнать площади этих фигур.

Итак, площади фигур 1 и 2 мы можем узнать, измерив длины их сторон и использовав формулы площадей прямоугольника и квадрата; площадь фигур 3 и 4 мы можем узнать, используя вторую аксиому площадей.

Чтобы узнать площадь фигуры 5 мы тоже могли бы воспользоваться 2 аксиомой площадей, т.е. разбить фигуру на более простые фигуры, площади которых мы можем измерять.

? Можно ли данную фигуру разбить на прямоугольники? на квадраты?

? На какие многоугольники можно разбить любой n-угольник? [треугольники]

Если бы мы смогли найти способ измерения площади треугольника, то мы бы нашли способ измерения площади любого n-угольника. Цель нашего урока — найти такой способ.

Любой исследование начинается с обобщения уже имеющихся знаний. Давайте вспомним, что мы знаем о треугольниках. (несколько фактов ребята предлагают сами, затем учитель задает наводящие вопросы)

? Вспомним, что называется высотой треугольника (отвечает команда, первая поднявшая сигнальную табличку).

На доске изображены треугольники:

В каждом треугольнике необходимо опустить высоту из вершины А на прямую, содержащую сторону ВС ( по 1 человеку от команды; команда 1 — первый треугольник, команда 2 — второй треугольник и т.д.).

? Как в данных случаях будет называться сторона ВС треугольника АВС. [основание]

? Вспомним, по какой формуле вычисляется площадь прямоугольника. (необходим ответ, в котором прозвучали бы “смежные стороны”).

Командам выдается листочек с планом исследования. Выполняя задания в соответствии с этим планом, ученики все промежуточные действия и конечные выводы записывают в тетради.

Что такое многоугольник? — Определение, формы и углы — Видео и стенограмма урока

Правильные многоугольники

Существует особый класс многоугольников; это происходит с многоугольниками, у которых все стороны одинаковой длины и все углы одинаковы. Когда это происходит, многоугольники называются правильными многоугольниками . Знак остановки — это пример правильного многоугольника с восемью сторонами. Все стороны одинаковы, и как бы вы его не сложили, он будет выглядеть одинаково. Вы не сможете сказать, какой путь был вверху, потому что все стороны одинаковы и все углы одинаковы.

Когда у треугольника все стороны и углы совпадают, мы знаем его как равносторонний или правильный треугольник. Четырехугольник, у которого все стороны и углы совпадают, называется квадратом или правильным четырехугольником. Пятиугольник, у которого все стороны и углы одинаковы, называется правильным пятиугольником. n -угольник с одинаковыми сторонами и углами называется правильным n -угольником.

Правильные многоугольники

Вот правильный треугольник, правильный четырехугольник и правильный пятиугольник.Вы видите, что все стороны одинаковы, и как бы вы их ни перевернули, они будут выглядеть одинаково?

Углы правильных многоугольников

Правильные многоугольники также имеют два разных угла, связанных с ними. Первый называется внешним углом , и это расстояние между формой и каждым отрезком линии, когда вы растягиваете его за пределы формы.

Внешний угол

У многоугольника столько же сторон, сколько и внешних углов.Итак, пятиугольник с пятью сторонами имеет пять внешних углов. У шестиугольника будет шесть внешних углов и так далее. Для правильных многоугольников мы можем вычислить измерение внешнего угла, но для неправильных многоугольников мы не можем. Вот формула для правильных многоугольников:

Формула внешнего угла

n обозначает количество сторон многоугольника. Итак, пятиугольник имеет внешние углы, которые составляют 360/5 = 72 градуса.

Второй угол называется внутренним углом , который является дополнительным углом к внешнему углу. Это означает, что внутренний угол вместе с внешним углом в сумме составит 180 градусов.

Внутренний угол

Вы также можете сказать, что внутренний угол — это измерение каждого угла многоугольника. Вот формула для внутреннего угла:

Формула внутреннего угла

Вторая формула такая же, как первая, только с перестановкой.Не беспокойтесь о том, как мы попали туда прямо сейчас; просто запомните одно или другое, и все будет в порядке. Второй вариант чаще встречается в математическом мире. Давайте посмотрим на пример. Для нашего пятиугольника с пятью сторонами первое уравнение дает 180 — 360/5 = 180 — 72 = 108 градусов. Используя второе уравнение, мы получаем (5-2) * 180/5 = 3 * 180/5 = 540/5 = 108 градусов. Обе формулы дадут нам одинаковый ответ. Выберите формулу, которую вам легче запомнить.

Резюме урока

Многоугольники окружают нас.Кто из нас когда-либо видел треугольник или квадрат? Многоугольник определяется как двумерная фигура с прямыми сторонами. Правильные многоугольники имеют одинаковые стороны и углы. Хотя вы можете найти измерения внешних и внутренних углов правильных многоугольников, вы не можете найти их для неправильных многоугольников.

Результаты обучения

После этого урока вы должны уметь:

Определить многоугольник и правильный многоугольник
Определите примеры многоугольников и правильных многоугольников
Объясните, как найти внешние и внутренние углы правильных многоугольников

Полигоны

Многоугольник — это плоская форма с прямыми сторонами.

Это многоугольник?

Многоугольники — это двумерные фигуры. Они состоят из прямых линий, а форма «замкнута» (все линии соединяются).


Многоугольник (прямые стороны)	Не Полигон (с изгибом)	Не Полигон (открытый, не закрытый)

Многоугольник происходит от греческого языка. Poly- означает «много», а -угольник означает «угол».

Типы полигонов

Обычное или нестандартное

У правильного многоугольника все углы и стороны равны, в противном случае это неправильный


Обычный		Нерегулярное

вогнутый или выпуклый

Выпуклый многоугольник не имеет углов, направленных внутрь.Точнее, внутренний угол не может быть больше 180 °.

Если какой-либо внутренний угол больше 180 °, то многоугольник вогнутый . ( Подумайте: в вогнутой части есть «пещера» )


выпуклый		вогнутый

Простой или сложный

Простой многоугольник имеет только одну границу и не пересекает себя. сложный полигон пересекает сам себя! Многие правила, касающиеся многоугольников, не работают, когда они сложны.


Простой многоугольник (это Пентагон)		Сложный многоугольник (также Пентагон)

Другие примеры


Шестигранник неправильной формы		Вогнутый восьмиугольник		Сложный многоугольник («звездообразный многоугольник», в данном случае пентаграмма)

Играй с ними!

Попробуйте интерактивные многоугольники… сделайте их правильными, вогнутыми или сложными.

Имена полигонов

С помощью этого метода можно делать имена:

Стороны		Начать с …
20		Икоси …
30		Triaconta…
40		Тетраконта …
50		Пентаконта …
60		Гексаконта …
70		Heptaconta…
80		Octaconta …
90		Эннеаконта …
100		Гектара …
и т. Д.

Стороны		… закончить с
+1		… шестигранник
+2		… Дигон
+3		… тригон
+4		…тетрагон
+5		… пятиугольник
+6		… шестигранник
+7		… семиугольник
+8		…octagon
+9		… эннеагон

Пример: 62-сторонний многоугольник — это гексаконтадигон

НО, для многоугольников с 13 или более сторонами нормально (и проще) написать « 13-угольник », « 14-угольник » … « 100-угольник» и т. Д.

Вспоминая

Четырехугольник (4 стороны)

A Quad Велосипед с 4 колесами

Пентагон (5 сторон)

« Пентагон » в Вашингтоне, округ Колумбия, имеет 5 сторон

Шестигранник (6 сторон)

H oneycomb имеет H эксагонов

Септагон (7 сторон)

Think Sept agon — это «Seven- agon»

Восьмиугольник (8 сторон)

Гной Octo имеет 8 щупалец

Nonagon (9 сторон)

Think Non agon — это «Nine- agon»

Десятиугольник (10 сторон)

Think Dec agon имеет 10 сторон,
точно так же, как наша Dec imal система имеет 10 цифр

свойств полигонов | SkillsYouNeed

На этой странице рассматриваются свойства двумерных или «плоских» многоугольников.Многоугольник — это любая форма, состоящая из прямых линий, которую можно нарисовать на плоской поверхности, например на листе бумаги. Такие формы включают квадраты, прямоугольники, треугольники и пятиугольники, но не круги или любую другую форму, которая включает кривую.

Понимание форм важно в математике. Вам, безусловно, потребуется изучать формы в школе, но понимание свойств форм имеет много практических применений в профессиональных и реальных ситуациях.

Многие профессионалы должны понимать свойства форм, включая инженеров, архитекторов, художников, агентов по недвижимости, фермеров и строителей.

Возможно, вам понадобится разбираться в формах, когда вы делаете ремонт дома или делаете все своими руками, когда садитесь в сад и даже планируете вечеринку.

При работе с полигонами важны следующие свойства:

Число сторон формы.
Элемент расположен под углом между сторонами фигуры.
Длина сторон формы.

Количество сторон

Многоугольники обычно определяются количеством сторон, которые у них есть.

Трехсторонние многоугольники: треугольники

Трехсторонний многоугольник — это треугольник. Существует несколько различных типов треугольников (см. Диаграмму), в том числе:

Равносторонний — все стороны равны по длине, а все внутренние углы равны 60 °.
Равнобедренный — имеет две равные стороны, у третьей разной длины. Два внутренних угла равны.
Scalene — все три стороны и все три внутренних угла разные.

Треугольники также можно описать в терминах их внутренних углов (см. Нашу страницу Углы для получения дополнительной информации об именах углов). Сумма внутренних углов треугольника всегда составляет 180 °.

Треугольник, имеющий только острых углов и внутренних углов, называется острым (или остроугольным) треугольником. Один с одним тупым углом и двумя острыми углами называется тупоугольным (тупоугольным), а другой с прямым углом известен как прямоугольный.

Каждый из них будет и будет либо равносторонним, равнобедренным, или разносторонним .

Четырехсторонние многоугольники — четырехугольники

Четырехсторонние многоугольники обычно называют четырехугольниками, четырехугольниками или иногда четырехугольниками. В геометрии обычно используется термин четырехугольник . Термин четырехугольник часто используется для описания прямоугольного замкнутого открытого пространства, например «новички, собранные в четырехугольнике колледжа». Термин четырехугольник соответствует многоугольнику, пятиугольнику и т. Д. Вы можете встретить его время от времени, но на практике он обычно не используется.

Семейство четырехугольников включает квадрат, прямоугольник, ромб и другие параллелограммы, трапецию / трапецию и воздушный змей.

Внутренние углы всех четырехугольников в сумме составляют 360 °.

Квадрат : четыре стороны равной длины, четыре внутренних прямых угла.
Прямоугольник : четыре внутренних прямых угла, противоположные стороны равной длины.
Параллелограмм : Противоположные стороны параллельны, противоположные стороны равны по длине, противоположные углы равны.
Ромб : особый тип параллелограмма, в котором все четыре стороны имеют одинаковую длину, как квадрат, сдавленный в стороны.
Трапеция (или трапеция) : две стороны параллельны, а две другие — нет. Длина сторон и углы не равны.
Равнобедренная трапеция (или трапеция) : Две стороны параллельны, а углы основания равны, что означает, что непараллельные стороны также равны по длине.
Воздушный змей : две пары соседних сторон имеют одинаковую длину; форма имеет ось симметрии.
Неправильный четырехугольник : четырехсторонняя форма, у которой нет одинаковых сторон и внутренние углы. Все внутренние углы по-прежнему составляют 360 °, как и у всех других правильных четырехугольников.

Более четырех сторон

Пятиугольник называется пятиугольником.

Шестигранная форма — это шестиугольник, семигранная форма — семиугольник, а восьмиугольник имеет восемь сторон…

Имена многоугольников

Имена многоугольников образованы от префиксов древнегреческих чисел. Греческий числовой префикс встречается во многих названиях повседневных предметов и понятий. Иногда они могут быть полезны, чтобы помочь вам вспомнить, сколько сторон имеет многоугольник. Например:

У осьминога восемь ног — у восьмиугольника восемь сторон.
Десятилетие — это десять лет — у десятиугольника десять сторон.
Современное пятиборье состоит из пяти видов — пятиугольник имеет пять сторон.
Олимпийское семиборье состоит из семи этапов, семиугольник имеет семь сторон.

Префикс «поли-» просто означает «множественный», поэтому многоугольник — это фигура с множеством сторон, точно так же, как «полигамия» означает множественность супругов.

Есть имена для многих различных типов многоугольников, и обычно количество сторон более важно, чем имя формы.

Есть два основных типа многоугольников — правильный и неправильный.

Правильный многоугольник имеет стороны равной длины с равными углами между ними. Любой другой многоугольник представляет собой неправильный многоугольник , у которого по определению есть стороны неравной длины и неравные углы между сторонами.

Окружности и формы, включающие кривые, не являются многоугольниками. — многоугольник по определению состоит из прямых линий. Смотрите наши страницы о кругах и изогнутых формах для получения дополнительной информации.

Углы между сторонами

Углы между сторонами фигур важны при определении многоугольников и работе с ними. См. Нашу страницу об углах, чтобы узнать больше о том, как измерять углы.

Существует полезная формула для определения суммы (или суммы) внутренних углов для любого многоугольника, а именно:

(количество сторон — 2) × 180 °

Пример:

Для пятиугольника (пятиугольной формы) расчет будет:

5–2 = 3

3 × 180 = 540 °.

Сумма внутренних углов любого (несложного) пятиугольника составляет 540 °.

Кроме того, если форма представляет собой правильный многоугольник (все углы и длины сторон равны), вы можете просто разделить сумму внутренних углов на количество сторон, чтобы найти каждый внутренний угол.

540 ÷ 5 = 108 °.

Следовательно, правильный пятиугольник имеет пять углов, каждый из которых равен 108 °.

Длина сторон

Помимо количества сторон и углов между сторонами, длина каждой стороны фигур также важна.

Длина сторон плоской фигуры позволяет вычислить периметра фигуры, (расстояние вокруг внешней стороны фигуры) и области (количество пространства внутри фигуры).

Если ваша фигура представляет собой правильный многоугольник (например, квадрат в приведенном выше примере), то необходимо измерить только одну сторону, поскольку, по определению, другие стороны правильного многоугольника имеют одинаковую длину. Обычно используются отметки, чтобы показать, что все стороны имеют одинаковую длину.

В примере с прямоугольником нам нужно было измерить две стороны — две неизмеренные стороны равны двум измеренным сторонам.

Обычно некоторые размеры не отображаются для более сложных форм. В таких случаях можно рассчитать недостающие размеры.

В приведенном выше примере отсутствуют две длины.

Недостающую длину по горизонтали можно вычислить. Возьмите более короткую известную длину по горизонтали из известной длины по горизонтали.

9 м — 5,5 м = 3,5 м.

По такому же принципу можно определить недостающую длину по вертикали. То есть:

3 м — 1 м = 2 м.

Объединение всей информации: расчет площади многоугольников

Самым простым и основным многоугольником для вычисления площади является четырехугольник. Чтобы получить площадь, вы просто умножаете длину на высоту по вертикали.

Для параллелограммов обратите внимание, что высота по вертикали составляет НЕ длины наклонной стороны, а расстояние по вертикали между двумя горизонтальными линиями.

Это потому, что параллелограмм представляет собой прямоугольник с треугольником, обрезанным с одного конца и наклеенным на другой:

Вы можете видеть, что если вы удалите левый синий треугольник и прикрепите его к другому концу, прямоугольник превратится в параллелограмм.

Площадь — это длина (верхняя горизонтальная линия), умноженная на высоту, расстояние по вертикали между двумя горизонтальными линиями.

Чтобы вычислить площадь треугольника , вы умножаете длину на высоту по вертикали (то есть высоту по вертикали от нижней линии до верхней точки) и делите ее пополам.По сути, это потому, что треугольник — это половина прямоугольника.

Чтобы вычислить площадь любого правильного многоугольника , проще всего разделить его на треугольники и использовать формулу для площади треугольника.

Итак, для шестиугольника, например:

На диаграмме видно, что имеется шесть треугольников.

Площадь:

Высота (красная линия) × длина стороны (синяя линия) × 0,5 × 6 (потому что треугольников шесть).

Вы также можете определить площадь любого правильного многоугольника с помощью тригонометрии, но это намного сложнее.

См. Нашу страницу Расчет площади для получения дополнительной информации, включая примеры.

Вы также можете определить площадь любого правильного многоугольника с помощью тригонометрии, но это намного сложнее. См. Нашу страницу Введение в тригонометрию для получения дополнительной информации.

Многоугольник | Математика ∞ Блог

В математике у каждой фигуры есть имя, которое отличает ее от других фигур. Вместо простых треугольников существует несколько типов треугольников.Например, равносторонний треугольник отличается от равностороннего треугольника. Также есть названия для типов фигур. Любая фигура с тремя и более плоскими сторонами и углами называется многоугольником.

Многоугольники — это плоские формы, они имеют только ширину и длину. Слово «многоугольник» происходит от корневого слова «поли», что означает «много», и «гон», что означает стороны.

Отличительные аспекты многоугольников отличают их друг от друга, но все они подпадают под одно определение. Все многоугольники представляют собой двумерные фигуры с плоскими сторонами и состоят из прямых линий, образующих замкнутую форму.

У правильных многоугольников равные стороны, у неправильных многоугольников одни стороны длиннее других.

Они также могут быть вогнутыми или выпуклыми, а также простыми или сложными. У каждого из этих типов многоугольников есть определение, которое отличает их от других форм. Вот исчерпывающий список названий и определений многоугольников.

Измерительные полигоны

Многоугольники могут показаться сложной формой, но на самом деле это не так. Формулы для определения площади многоугольника просты и требуют только элементарных математических вычислений.Например, измерить периметр правильного многоугольника так же просто, как найти длину одной стороны и умножить ее на количество сторон.

Найдя апофему формы, можно задать формулу для вычисления площади. Апофема — это расстояние от центра до одной стороны многоугольника. Радиус можно найти, измерив расстояние от центра до угла или вершины.

Формула для определения площади правильного многоугольника: A = ½ периметра x апофема.

Измерение пятиугольника со сторонами восемь дюймов даст площадь.Периметр 40 и апофема 8 будут выглядеть так: A = ¹/₂ (40 x 8). Площадь многоугольника будет 160. Неправильные многоугольники и более сложные формы потребуют различных формул для решения, но применяются те же принципы.

Неправильные и сложные многоугольники

В отличие от правильных многоугольников, сложные и неправильные многоугольники не имеют стороны одинаковой длины. Это означает, что при измерении одной стороны умножение длины на количество сторон не дает периметра.

Для неправильных многоугольников сначала измерьте длину всех сторон. Найдя сумму длин и разделив ее на количество сторон, мы получим длину стороны.

Затем длину стороны можно использовать для вычисления периметра, умножив ее на количество сторон. Если длина стороны 8 дюймов и имеется 5 сторон, периметр будет равен 40.

Сложные многоугольники могут быть решены аналогично, но есть несколько дополнительных шагов. Линии, составляющие сложный многоугольник, часто пересекаются и образуют несколько других форм.Эти лишние формы нужно будет разделить и измерить.

Преобразуя измерения неправильных и сложных многоугольников, проблема решается с помощью простых формул.

Чтобы найти апофему любого периметра, данные должны быть вставлены в форму правильного многоугольника. Периметр можно разделить на количество сторон, чтобы найти длину стороны соответствующей правильной формы, такой как пятиугольник. Формулы, используемые для нахождения апофемы и площади формы, теперь можно использовать для решения измерений неправильного или сложного многоугольника.

Интерактивный урок математики | Полигоны

Интерактивное математическое упражнение — Полигоны

Практикуйте геометрические навыки с помощью этого увлекательного математического упражнения, посвященного полигонам! Ваши третьеклассники научатся определять свойства многоугольника, решая различные практические вопросы в этой интерактивной математической игре. По завершении этого задания учащиеся приобретут уверенность и навыки в своем базовом понимании многоугольников.

Эта игра с геометрией для третьего класса представляет многоугольники с множеством забавных, но сложных математических вопросов.Студентов могут попросить определить, является ли данная форма многоугольником. Их могут спросить, сколько сторон или углов имеет данный многоугольник. Студентам может потребоваться выбрать, какая форма не является многоугольником. Или студентам может потребоваться указать, сколько пар параллельных сторон имеет данная форма, а также сколько прямых углов у нее. Если учащиеся не могут ответить на вопрос, они могут выбрать вариант «Подсказка». Подсказка состоит из полезной письменной и / или графической подсказки, которая даст представление о задаваемом вопросе, не давая ответа.Если учащиеся ответят на вопрос неправильно, им будет показана страница с подробным объяснением, на которой они смогут узнать, где они ошиблись, а также как получить правильный ответ в будущем. Таким образом, учащиеся проходят урок, извлекая уроки из своих ошибок.

Эта интерактивная математическая игра для третьего класса оснащена несколькими практическими функциями, которые помогают учащимся максимально использовать их практические занятия по математике. Индикатор прогресса в правом верхнем углу экрана практики показывает учащимся, на сколько вопросов они ответили из общего количества вопросов в уроке.Счетчик результатов позволяет учащимся узнать, сколько баллов они уже заработали на уроке. Напротив, значок динамика указывает на функцию чтения вслух; учащиеся могут нажать кнопку, чтобы вопрос был прочитан им вслух и четким голосом. Это отличный вариант для студентов ESL / ELL и детей, которые хорошо обучаются на слух. Все функции урока разработаны с учетом интересов учащихся!

Почему преподаватели и ученики любят «Я знаю это»

Учителя начальных классов и учителя на дому в равной степени с удовольствием используют программу практической математической практики «Я знаю» вместе со своим традиционным учебным планом по математике для дополнительной практики.Учителя ценят широкий спектр увлекательных заданий по математике, которые мы предлагаем для детского сада до пятого класса. Наши уроки математики охватывают популярные темы элементарной математики от числовых значений до базовой алгебры. Все практические занятия по математике на сайте I Know It приведены в соответствие со стандартом Common Core и организованы на веб-сайте по классам и темам. Легко найти именно то, что вы ищете, именно тогда, когда вам это нужно.

Студенты тоже любят использовать программу I Know It для отработки своих математических навыков! Каждое упражнение по математике представляет собой веселую, но сложную математическую игру.Глупые анимированные персонажи приветствуют учеников на каждом математическом задании, готовые подбодрить их каждый раз, когда они правильно ответят на вопрос. Множество положительных отзывов побуждают детей «Продолжать!» даже когда они делают ошибки. Кроме того, учащиеся могут получать награды за свои виртуальные «трофеи» за каждый новый математический навык, который они изучают. Кто знал, что занятия по математике могут быть такими увлекательными ?!

Мы надеемся, что вам и вашим третьеклассникам понравится изучать многоугольники в этой интерактивной математической игре! Обязательно ознакомьтесь с сотнями других уроков математики для 3-го класса, которые доступны на нашем веб-сайте.

Испытайте воды и присоединяйтесь к нашему сообществу!

Хотели бы вы испытать воду и попробовать программу практики математики I Know It со своими учениками сегодня? Ты можешь! Воспользуйтесь нашей бесплатной шестидесятидневной пробной версией. С нашей бесплатной пробной версией вы и ваш класс можете бесплатно изучить все интерактивные математические упражнения на нашем веб-сайте — кредитная карта не требуется! Мы уверены, что вам понравится ощутить разницу, которую может иметь интерактивная математическая практика, поэтому, когда ваша бесплатная пробная версия закончится, мы надеемся, что вы подумаете о присоединении к сообществу I Know It в качестве члена нашего сайта! Таким образом, вы и ваши ученики продолжите пользоваться преимуществами интерактивной математической практики в течение всего календарного года!

Ваше членство в программе I Know It открывает доступ к удобным административным функциям веб-сайта, призванным упростить вам мониторинг успеваемости ваших учеников в их математической практике.Наши административные инструменты позволяют вам создавать список классов, назначать уникальные имена пользователей и пароли своим ученикам, изменять основные настройки урока, давать различные задания уроков отдельным ученикам, отслеживать успеваемость учеников с помощью подробных, легко читаемых отчетов об успеваемости и распечатывать , загрузите и отправьте по электронной почте отчеты об успеваемости учащихся.

Когда учащиеся входят в систему «Я знаю это», используя свое уникальное имя пользователя и пароль, им будет показана адаптированная для детей версия домашней страницы. Отсюда они могут получить доступ к урокам, которые вы им назначили для практики.Если вы разрешите в настройках администратора, учащиеся могут также изучить другие практические занятия по математике на своем уровне — и выше — для дополнительного обзора или дополнительной задачи. Уровни успеваемости в студенческом режиме «Я знаю» обозначаются буквами вместо цифр, что упрощает назначение уроков по математике в зависимости от уникальных потребностей и уровня навыков ребенка.

Уровень

Этот онлайн-урок математики относится к Уровню C. Он может быть идеальным для третьего класса.

Стандарт Common Core

3.G.A.1
Геометрия
Учащиеся рассуждают с помощью форм и их атрибутов. Учащиеся продемонстрируют понимание того, что фигуры в разных категориях могут иметь общие атрибуты и что общие атрибуты могут определять более крупную категорию. Учащиеся поймут, что ромбы, прямоугольники и квадраты являются примерами четырехугольников.

Возможно, вас также заинтересует …

Сплошные фигуры (уровень C)
На этом третьем уроке математики на уровне своего класса учащиеся будут практиковаться в распознавании твердых форм.Вопросы представлены в формате с множественным выбором и заполнением пустых полей.

Классифицирующие углы (уровень C)
На этом уроке математики, предназначенном для третьего класса, ученики будут практиковать классификационные углы. Вопросы представлены в формате с множественным выбором и заполнением пустых полей.

Полигонов — объяснения и примеры

Вы слышали о многоугольнике? Что ж, полигонов нас окружают! Большинство обычных форм, которые вы видите или изучаете каждый день, — это многоугольники.Вы видите, что стена прямоугольной формы представляет собой многоугольник.

Вид спереди игральной кости, имеющей квадратную форму, представляет собой многоугольник. Кусочек пиццы имеет форму треугольника, а значит, и многоугольника.

Из этой статьи вы узнаете:

Что такое многоугольники и как они выглядят.
Различные типы полигонов.

Что такое многоугольник?

В математике многоугольник — это замкнутая двумерная фигура, состоящая из отрезков прямых, но не кривых.Термин «многоугольник» происходит от греческого слова «поли -», означающего «много», и «- гон», что означает «углы».

Самыми распространенными примерами многоугольников являются треугольник, прямоугольник и квадрат. Проще говоря, многоугольники — это простые фигуры или фигуры, состоящие только из отрезков линий.

Примечание. Круги, трехмерные объекты, любые формы, включающие кривые, и любые незамкнутые формы не являются многоугольниками.

Полигоны были известны человеку с древних времен. Греки изучали невыпуклый правильный многоугольник в 7 ^-м веке до нашей эры на кратере Аристофана. Томас Брэдвардайн был первым известным человеком, изучавшим невыпуклые многоугольники в 14 ^{-х годах} века. Концепция многоугольников была обобщена в 1952 году Джеффри Колином.

Теперь, когда вы поняли, что такое многоугольник, давайте исследуем различные многоугольники и то, как они выглядят.

Типы многоугольников

В зависимости от сторон и углов, многоугольников подразделяются на различных типов, а именно

Правильный многоугольник
Неправильный многоугольник
Выпуклый многоугольник
Вогнутый многоугольник

Правильный многоугольник 901 Правильный многоугольник — это многоугольник, в котором все внутренние углы равны, а также все стороны равны.Есть разные типы правильных многоугольников.

Это:

Треугольник : Равносторонний треугольник — это правильный многоугольник с тремя равными длинами сторон и тремя равными углами.

Четырехугольник. Четырехугольник — это правильный многоугольник с четырьмя углами и четырьмя сторонами. Примеры четырехугольников:

a. Квадрат : Четырехугольник, у которого 4 стороны равны, а четыре угла равны 90 градусам каждый.

б. Прямоугольник:

c. Параллелограмм : Противоположные стороны параллельны, противоположные стороны равны по длине, противоположные углы равны

d. Воздушный змей : Две пары соседних сторон имеют одинаковую длину; форма имеет ось симметрии.

эл. Ромб : особый тип параллелограмма, в котором все четыре стороны имеют одинаковую длину, как квадрат, сдавленный в стороны.

Пентагон : многоугольник с 5 равными сторонами и углом

Шестиугольник: Правильный многоугольник с 6 равными сторонами и 6 равными углами.

Шестиугольник: Правильный многоугольник с 7 равными длинами сторон и 7 одинаковыми углами.

Восьмиугольник: Восьмиугольник имеет 8 равных сторон и 8 равных углов. Лучшим примером восьмиугольника из реальной жизни является дорожный знак STOP.

Nonagon: Имеет 9 равных сторон и 9 одинаковых углов.

Хендекагон: Имеет 11 равных сторон и 11 равных углов.
Додекагон: правильный многоугольник с 12 равными сторонами и 12 одинаковыми углами
Трехугольник: Имеет 13 равных сторон и 13 одинаковых углов.
Tetrakaidecagon : имеет 14 равных сторон и 14 одинаковых углов.
Пятиугольник: Пятиугольник — это правильный многоугольник с 15 равными сторонами и 15 одинаковыми углами.
Hexakaidecagon : имеет 16 сторон и углов.
Heptadecagon : Имеет 17 сторон и углов.
Octakaidecagon: Имеет 18 сторон и углов
Enneadecagon: 19 сторон и 19 углов.
Икосагон: Имеет равные стороны и 20 равных углов
Шестиугольник: Имеет 100 равных сторон и 100 равных углов.
Chiliagon: Имеет 1000 сторон
Myriagon: 10000 сторон.
Мегагон: Один миллион сторон.
n-угольник : имеет n равных сторон.

Неправильный многоугольник

Неправильный многоугольник — это многоугольник с разными углами и длинами сторон.

Примеры неправильных многоугольников:

Выпуклый многоугольник

Это тип многоугольника, все внутренние углы которого строго меньше 180 градусов. Вершина выпуклого многоугольника всегда направлена наружу от центра фигуры.

Вогнутый многоугольник

Если один или несколько внутренних углов многоугольника больше 180 градусов, он называется вогнутым многоугольником. Вогнутый многоугольник может иметь как минимум четыре стороны — вершина указывает внутрь многоугольника.

Ниже приведены несколько мнемоник, которые помогут запомнить названия некоторых многоугольников:

Квадроцикл имеет 4 колеса и, следовательно, четырехугольник.
Вашингтон, округ Колумбия, в США имеет 5 сторон (Пентагон).
A H oneycomb имеет 6 сторон ( H exagon).
S эптагон имеет 7 сторон ( S даже).
У осьминога 8 щупалец (восьмиугольник).
Обе термины N, onagon и N начинаются с буквы N.
Десятиугольник имеет 10 сторон, как и десятичная запятая D имеет 10 цифр.

Реальные приложения многоугольников

Понимание форм важно в геометрии. Формы находят широкое применение в реальных приложениях.

Например:

Плитки, по которым вы идете, имеют квадратную форму, что означает, что они являются многоугольниками.
Ферма здания или моста, стены здания и т. Д., являются примерами многоугольников. Фермы имеют треугольную форму, а стены — прямоугольную.
Прямоугольная часть стула, на которой вы сидите, является примером многоугольника.
Прямоугольный экран вашего ноутбука, телевизора или мобильного телефона является примером многоугольника.
Прямоугольное футбольное поле или игровая площадка является примером многоугольника.
Бермудский треугольник треугольной формы представляет собой многоугольник.
Пирамиды Египта также являются примером многоугольника (треугольника)
Фигуры в форме звезды являются примерами многоугольника.
Дорожные знаки также являются примером многоугольников.

Пример

У Джона есть прямоугольный лист бумаги. Он хочет разрезать бумагу так, чтобы получить еще два многоугольника (кроме прямоугольника) того же размера и формы. Подскажите возможные пути.

Решение

Есть два возможных способа вырезать прямоугольный лист бумаги таким образом, чтобы он получил еще два многоугольника (кроме прямоугольника) того же размера и формы:

Он может вырезать прямоугольник лист бумаги ровно от центра по вертикали, чтобы получить два квадрата одинакового размера и формы.
Он может разрезать прямоугольный лист бумаги по диагонали, чтобы получить два треугольника одинакового размера и формы.

Практические вопросы

Угадай многоугольник:

Я плоская фигура с 4 сторонами равной длины и углами 90 градусов по бокам.
Я — плоская фигура с двумя сторонами одинаковой длины и углами 90 градусов по бокам.
Я плоская фигура с 6 сторонами, и все внутренние углы больше 90 градусов.

Ответы

Квадрат
Прямоугольник
Шестиугольник

Предыдущий урок | Главная страница | Следующий урок

Многоугольники: 3, 5, 7 сторон и многое другое

Кредит: WikiCommons CC0 1.0

Один из видов фигур, изучаемых в геометрии и алгебре, — это многоугольники. Многоугольники — это фигуры, состоящие из конечного числа прямых линий, закрывающих некоторую область пространства.Многоугольники относятся к числу простейших форм и тщательно исследуются еще со времен древних греков. Слово «многоугольник» происходит от двух греческих слов, означающих «многоугольник». Все многоугольники имеют 3 основных свойства:

1. Они двумерны
2. У них есть внутренняя и внешняя части (они ограничивают пространство)
3. Они состоят из прямых линий

Elements Of Polygons

Все полигоны можно разбить на части.Отдельные линейные сегменты называются ребрами или сторонами , а точки, где встречаются ребра, называются вершинами (единственная вершина). Область, ограниченная многоугольником, называется телом . Диагональ многоугольника — это любой отрезок линии, который можно нарисовать для соединения двух несмежных вершин.

Части многоугольника. Предоставлено: Автор

Классификация многоугольников

Многоугольники можно классифицировать несколькими способами в зависимости от:

количества сторон
выпуклых или вогнутых
самопересекающихся или простых
правильных или неправильных

Стороны

В большинстве случаев многоугольники классифицируются на основе количества их сторон.Согласно евклидовой геометрии, минимально возможное количество сторон многоугольника — 3. Требуется не менее 3 прямых линий, чтобы охватить некоторую область пространства. Следовательно, треугольник — это самый простой из возможных многоугольников в евклидовой геометрии. Большинство многоугольников имеют специальное имя, соответствующее количеству сторон (четырехугольник — 4 стороны, пятиугольник — 5 сторон, шестиугольник, 6 сторон и т. Д.), Или их можно просто назвать n -угольником, где n соответствует количество сторон (3-угольник, 4-угольник, 5-угольник и т. д.).

А как насчет круга? Считается ли круг многоугольником? Ответ: нет , круг не считается многоугольником. Это потому, что круг состоит не из прямых линий, это кривая.

Выпуклые или вогнутые

Многоугольники можно классифицировать как выпуклые или вогнутые . Выпуклый многоугольник — это любой многоугольник, внутренние углы которого меньше 180 градусов. Это означает, что каждая диагональ выпуклого многоугольника попадет внутрь области, ограниченной фигурой.Напротив, вогнутый многоугольник — это любой многоугольник, имеющий хотя бы один угол, размер которого превышает 180 градусов. Вогнутый многоугольник всегда будет иметь по крайней мере одну диагональ, выходящую за пределы области, ограниченной фигурой.

Самопересекающиеся или простые

Многоугольники также различаются как самопересекающиеся или простые. Самопересекающийся многоугольник имеет как минимум одну пару пересекающихся линий. Напротив, у простого многоугольника есть линии, которые не пересекаются друг с другом.Самопересекающиеся многоугольники иногда называют сложными многоугольниками. Их сложно представить. Представьте себе упругий простой многоугольник, который поднят и скручен так, что некоторые его стороны пересекают друг друга. Например, прямоугольник превратится в форму, похожую на бабочку. В самопересекающемся многоугольнике пересечение линий НЕ создает новую вершину или новый внутренний угол. Форма бабочки, образованная из квадрата, по-прежнему имеет 4 внутренних угла и 4 вершины.

Обычные или неправильные

Многоугольники также классифицируются в соответствии с их симметрией.Правильный многоугольник — это такой многоугольник, у которого все стороны равны по длине и все углы равны. Неправильный многоугольник — это такой многоугольник, в котором стороны и углы имеют неравные размеры. Например, квадрат — это правильный четырехугольник. Углы и стороны квадрата равны.

Первые несколько правильных многоугольников. Предоставлено: Texample CC-BY SA 2.5

Углы многоугольников

Каждый многоугольник имеет одинаковое количество сторон и вершин. Таким образом, каждый многоугольник имеет одинаковое количество вершин и углов.Для любого простого многоугольника сумма его внутренних углов может быть определена по формуле:

Угол = (n − 2) × 180

Итак, квадрат имеет внутренние углы, которые в сумме составляют 360 градусов ((4−2) × 180), внутренние углы шестиугольника составляют 720 градусов ((6−2) × 180). Эта формула выпадает из того факта, что любой простой многоугольник можно разделить на n– 2 треугольников, каждый из которых имеет внутренние углы, в сумме равные 180 градусам (или пи радианам). Для любого правильного многоугольника размер и каждый внутренний угол — это просто сумма внутренних углов, разделенных на количество сторон.Таким образом, каждый угол правильного треугольника составляет 60 градусов (180/3), каждый угол правильного пятиугольника составляет 108 градусов (540/5), а каждый угол 7-угольника (семиугольника) составляет 128,57 градусов.

Площадь многоугольников

В этом разделе мы расскажем, как найти внутренний угол многоугольников. Наш анализ будет сосредоточен на обнаружении области правильных многоугольников, поскольку они имеют определенные формулы, которые одинаковы независимо от размера многоугольника. Неправильные многоугольники имеют общие формулы, но решить эту математическую задачу гораздо сложнее.

Для любого правильного многоугольника с n сторонами длиной s общая формула для площади:

Площадь = ( n × s × a ) / 2

, где a это апофема; длина линии, проведенной от центра перпендикулярно одной из сторон. В этом выражении величина n × s равна периметру (длина сторон × количество сторон), поэтому выражение можно записать как:

Площадь = P × a /2

Выяснить апофему немного сложнее.Апофема — это кратчайшее расстояние от центра до одной из сторон, образующее прямой угол. Формула для нахождения апофемы угольника n :

a = s / 2tan (180/ n )

На английском языке: апофема равна длине стороны s делится на два, умноженные на тангенс 180, деленный на количество сторон n .

Давайте попробуем эту формулу на простом примере: скажем, у нас есть шестиугольник со сторонами длиной 10.У шестиугольника 6 сторон, поэтому мы можем рассчитать периметр как:

P = 6 × 10 = 60

Чтобы найти апофему, мы подставляем значения n и s в формулу апофемы:

a = 10 / 2tan (180/6)

a = 8,66

Включение P и a в полную формулу дает:

Площадь = (60 × 8,66) / 2

Площадь = 259,8 кв. Единиц

Таким образом, правильный шестиугольник со стороной 10 имеет площадь 259.8 кв. Шт.

Как понять формулу площади

Почему эта формула работает? Во-первых, примите во внимание тот факт, что внутреннюю часть любого правильного многоугольника можно разделить на равные треугольники.

Кредит: общественное достояние

Каждая сторона может рассматриваться как основание каждого треугольника, а апофема — это высота каждого треугольника. Таким образом, формулу площади можно рассматривать как простую формулу для площади треугольника, умноженной на количество треугольников.

Примеры правильных многоугольников

Ниже приведен список различных правильных многоугольников и некоторые из их уникальных свойств.

Имя	Ребра	Свойства
треугольник	3	Простейший многоугольник в евклидовой геометрии. Может создавать мозаику
четырехугольник	4	Простейший многоугольник, который может быть вогнутым или самопересекающимся. Может создавать мозаику
пятиугольник	5	Простейший многоугольник, который может быть звездой
шестиугольник	6	Последний из правильных многоугольников, который может разбить плоскость
семиугольник	7	Первый многоугольник, который не может быть построен с помощью циркуля и прямой кромки
восьмиугольник	8	Каждый внутренний угол восьмиугольника составляет 135 градусов
nonagon	9	Невозможно построить с помощью компаса и прямая кромка
декагон	10	Использует золотое сечение для построения с компасом и линейкой
пятиугольник	11	Невозможно построить с помощью компаса и линейки
семиугольник	17	Обнаружен Гауссом в 1796 году.Первый новый правильный многоугольник, обнаруженный более чем за 2000 лет
гектогон	100
chiliagon	1000	Используется Декартом в философских мысленных экспериментах. Бывший. четко определенного многоугольника, который невозможно визуализировать
65537-угольник	65537	Впервые построенный в 1894 году Йоханн Гермес
апейрогон	исчисляемо бесконечный	Вырожденный многоугольник, который эквивалентен (но не идентичен) ) в круг.

Многоугольники в более высоких измерениях

Слово «многоугольник» обычно конкретно относится к двумерным формам, состоящим из прямых линий. Концепция многоугольника может быть обобщена на более высокие измерения. Обобщение многоугольника называется многогранником . Итак, многоугольник — это конкретный двумерный пример более общей идеи многогранника.

Многогранники определенного размера n можно понимать как построенные из элементов размерности n -1.Например, двумерный многогранник (многоугольник) состоит из одномерных элементов, то есть линий. Точно так же трехмерный многогранник называется многогранником (мн. Многогранники) и представляет собой трехмерное тело, состоящее из двухмерных многоугольников.

В отличие от правильных многоугольников, которых существует практически бесконечное количество, в трехмерном пространстве существует только 5 правильных многогранников. Эти 5 правильных многогранников — это тетраэдр , куб , октаэдр , додекаэдр и икосаэдр .Эти 5 правильных многогранников иногда называют «Платоновыми телами» в честь греческого философа Платона, который считал, что правильные многогранники имеют форму пяти классических элементов огня (тетраэдр), земли (куб), воды (икосаэдр) и воздуха. (октаэдр). Последний правильный многогранник, додекаэдр, был связан с эфиром , пятым классическим элементом, который, как говорили, составлял небеса и небесные объекты, такие как солнце, луна, планеты и звезды.

Пять «Платоновых тел» Источник: WikiCommons CC-BY SA 4.0

Почему правильных многогранников всего 5? Ответ связан с внутренними углами трехмерных фигур. Короче говоря, двумерные многоугольники могут быть организованы в правильный трехмерный многогранник, если внутренние углы по крайней мере трех многоугольников, которые встречаются в конкретной вершине, составляют менее 360 градусов.

Итак, представьте себе треугольник. Все внутренние углы правильного треугольника составляют 60 градусов. Значит, у нас может быть многогранник с вершинами, в которых пересекаются 3, 4 и 5 треугольников:

3 × 60 <360

4 × 60 <360

5 × 60 <360

Они соответствуют тетраэдру, октаэдру. , и икосаэдр.

В случае квадрата только 3 квадрата могут пересекаться в вершине, а сумма их внутренних углов меньше 360 градусов. Углы квадрата составляют 90 градусов каждый, поэтому:

3 × 90 <360

Это соответствует кубу. Для пятиугольника возможно только три пятиугольника, пересекающиеся в вершине, и сумма внутренних углов меньше 360:

3 × 108 <360

Это расположение соответствует додекаэдру.

А как насчет шестиугольников? Ответ — нет.Из правильных шестиугольников не получится сделать правильный многогранник. Это потому, что внутренние углы по крайней мере трех шестиугольников, которые встречаются в одной вершине, составляют в сумме 360 градусов. Следовательно, такое расположение шестиугольников может существовать только в двумерном пространстве; не остается «лишнего» места, чтобы форма могла согнуться в 3 измерения.

Итак, шестиугольник — это первый из правильных многоугольников, который нельзя использовать для создания правильного многогранника. Фактически, никакие другие формы, кроме треугольника, квадрата и пятиугольника, не могут образовать правильный многогранник; законы трехмерного пространства делают это невозможным.

Была ли эта статья полезной?

😊 ☹️ Приятно слышать! Хотите больше научных тенденций? Подпишитесь на нашу рассылку новостей науки! Нам очень жаль это слышать! Мы любим отзывы 🙂 и хотим, чтобы вы внесли свой вклад в то, как сделать Science Trends еще лучше.

Многоугольники — урок. Геометрия, 8 класс.

стороны, вершины, диагонали. Периметр многоугольника

Выпуклые и вогнутые

Периметр

Диагональ

Многоугольники | Математика

Четырехугольники

Многоугольники. Выпуклый многоугольник. Четырехугольник 8 класс онлайн-подготовка на Ростелеком Лицей

Урок 37. многоугольники — Математика — 5 класс

Простейшие многоугольники и их свойства — Алексей Лавриненко | Oleksiy Lavrynenko

Урок в 8-м классе по теме « многоугольник и его элементы&quot цели урока — Урок

Что такое многоугольник? — Определение, формы и углы — Видео и стенограмма урока

Правильные многоугольники

Углы правильных многоугольников

Резюме урока

Результаты обучения

Полигоны

Это многоугольник?

Типы полигонов

Обычное или нестандартное

вогнутый или выпуклый

Простой или сложный

Другие примеры

Играй с ними!

Имена полигонов

Вспоминая

Четырехугольник (4 стороны)

Пентагон (5 сторон)

Шестигранник (6 сторон)

Септагон (7 сторон)

Восьмиугольник (8 сторон)

Nonagon (9 сторон)

Десятиугольник (10 сторон)

свойств полигонов | SkillsYouNeed

Количество сторон

Трехсторонние многоугольники: треугольники

Четырехсторонние многоугольники — четырехугольники

Более четырех сторон

Углы между сторонами

Длина сторон

Объединение всей информации: расчет площади многоугольников

Многоугольник | Математика ∞ Блог

Интерактивный урок математики | Полигоны

Интерактивное математическое упражнение — Полигоны

Почему преподаватели и ученики любят «Я знаю это»

Испытайте воды и присоединяйтесь к нашему сообществу!

Уровень

Стандарт Common Core

Возможно, вас также заинтересует …

Полигонов — объяснения и примеры

Что такое многоугольник?

Типы многоугольников

Неправильный многоугольник

Выпуклый многоугольник

Вогнутый многоугольник

Реальные приложения многоугольников

Многоугольники: 3, 5, 7 сторон и многое другое

Elements Of Polygons

Классификация многоугольников

Углы многоугольников

Площадь многоугольников

Как понять формулу площади

Примеры правильных многоугольников

Многоугольники в более высоких измерениях

Добавить комментарий Отменить ответ