Картинки пятиугольники: Картинки d0 bf d1 8f d1 82 d0 b8 d1 83 d0 b3 d0 be d0 bb d1 8c d0 bd d0 b8 d0 ba, Стоковые Фотографии и Роялти-Фри Изображения d0 bf d1 8f d1 82 d0 b8 d1 83 d0 b3 d0 be d0 bb d1 8c d0 bd d0 b8 d0 ba

%d0%bf%d1%8f%d1%82%d0%b8%d1%83%d0%b3%d0%be%d0%bb%d1%8c%d0%bd%d0%b8%d0%ba PNG, векторы, PSD и пнг для бесплатной загрузки

естественный цвет bb крем цвета

1200*1200

green environmental protection pattern garbage can be recycled green clean

2000*2000

три группы 3d реалистичное декоративное яйцо с золотым цветом на гнезде bd с золотым всплеском текстовый баннер

5000*5000

дизайн плаката премьера фильма кино с белым вектором экрана ба

1200*1200

be careful to slip fall warning sign carefully

2500*2775

3d модель надувной подушки bb cream

2500*2500

цвет перо на воздушной подушке bb крем трехмерный элемент

1200*1200

в первоначальном письме bd логотипа

1200*1200

bd письмо 3d круг логотип

1200*1200

в первоначальном письме ба логотипа

1200*1200

облака комиксов

5042*5042

в первоначальном письме bd шаблон векторный дизайн логотипа

1200*1200

розовый бб крем красивый бб крем ручная роспись бб крем мультфильм бб крем

2000*3000

я люблю моих фб хорошо за футболку

1200*1200

в первоначальном письме bf логотип шаблон векторный дизайн

1200*1200

номер 82 золотой шрифт

1200*1200

элегантный серебряный золотой bb позже логотип значок символа

1200*1200

в первоначальном письме bd логотип шаблон

1200*1200

в первоначальном письме bd шаблон векторный дизайн логотипа

1200*1200

первый логотип bf штанга

4500*4500

первый логотип bf штанга

4500*4500

логотип fb или bf

2223*2223

круглая буквица bd или db дизайн логотипа вектор

5000*5000

буква bf фитнес логотип дизайн коллекции

3334*3334

Векторная иллюстрация мультфильм различных овощей на деревянном ба

800*800

фб письмо логотип

1200*1200

82 летняя годовщина векторный дизайн шаблона иллюстрация

4083*4083

в первоначальном письме bf логотип шаблон

1200*1200

аэрозольный баллончик увлажняющий лосьон bb cream парфюм для рук

3072*4107

bb кремовый плакат белый макияж косметический На воздушной подушке

3240*4320

bb логотип дизайн шаблона

2223*2223

Креативное письмо bb дизайн логотипа черно белый вектор минималистский

1202*1202

жидкая подушка крем bb

1200*1200

испуганные глаза комиксов

5042*5042

bb логотип градиент с абстрактной формой

1200*1200

b8 b 8 письма и номер комбинации логотипа в черном и gr

5000*5000

bd письмо логотип

1200*1200

фб письмо логотип

1200*1200

серые облака png элемент для вашего комикса bd

5042*5042

bd письмо логотип

1200*1200

blue series frame color can be changed text box streamer

1024*1369

фб письмо логотип

1200*1200

red bb cream cartoon cosmetics

2500*2500

в первоначальном письме bd логотип шаблон

1200*1200

bd tech логотип дизайн вектор

8542*8542

bb градиентный логотип с абстрактной формой

1200*1200

две бутылки косметики жидкая основа белая бутылка крем bb

2000*2000

ма дурга лицо индуистский праздник карта

5000*5000

bf письмо дизайн логотипа внутри черного круга вектор

1200*1200

bb логотип письмо дизайн вектор простые и минималистские ключевые слова lan

1202*1202

Как выглядит пятиугольник фото

Правильный пятиугольник (или пентагон от греч. <4>=3Phi +2=<frac <3<sqrt <5>>+7><2>>approx 6<,>8541>где Φ <displaystyle Phi >— отношение золотого сечения.

Построение [ править | править код ]

Правильный пятиугольник может быть построен с помощью циркуля и линейки или вписыванием его в заданную окружность, или построением на основе заданной стороны. Этот процесс описан Евклидом в его «Началах» около 300 года до н. э.

Вот один из методов построения правильного пятиугольника в заданной окружности:

1. Постройте окружность, в которую будет вписан пятиугольник, и обозначьте её центр как O. (Это зелёная окружность на схеме справа).
2. Выберите на окружности точку A, которая будет одной из вершин пятиугольника. Постройте прямую через O и A.
3. Постройте прямую перпендикулярно прямой OA, проходящую через точку O. Обозначьте одно её пересечение с окружностью как точку B.
4. Постройте точку C посередине между O и B.
5. Проведите окружность с центром в точке C через точку A. Обозначьте её пересечение с прямой OB (внутри первоначальной окружности) как точку D.
6. Проведите окружность с центром в A через точку D, пересечение данной окружности с оригинальной (зелёной окружностью) обозначьте как точки E и F.
7. Проведите окружность с центром в E через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку
   G.
8. Проведите окружность с центром в F через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку H.
9. Постройте правильный пятиугольник AEGHF.

Получение с помощью полоски бумаги [ править | править код ]

Правильный пятиугольник можно получить, завязав узлом полоску бумаги.

В природе [ править | править код ]

Исследования формирования водяного льда на ровной поверхности меди при температурах 100—140 K показали, что сначала на поверхности возникают цепочки молекул шириной около 1 нм не гексагональной, а пентагональной структуры.

[1] Пентасимметрию можно увидеть во многих цветах и некоторых фруктах, например в таких как эта мушмула германская.

Иглокожие, например морские звёзды, обладают пентасимметрией.

Пентасимметрию можно увидеть во многих цветах и некоторых фруктах, например в таких как мушмула германская.

Правильный пятиугольник представляет собой геометрическую фигуру, которая образовывается пересечением пяти прямых, создающих пять одинаковых углов. Такая фигура носит название — пентагон. С пятиугольником тесно связана работа художников — их рисунки строятся на основе правильных геометрических фигур. Для этого необходимо знать то, как быстро построить пентагон.

Чем интересна эта фигура? Форму пентагона имеет здание Министерства обороны Соединенных Штатов Америки. Это можно увидеть на фото, сделанных с высоты полета. В природе не существует кристаллов и камней, форма которых напоминала бы пентагон. Только в этой фигуре количество граней совпадает с числом диагоналей.

Параметры правильного пятиугольника

Прямоугольный пятиугольник, как и каждая фигура в геометрии, имеет свои параметры. Зная необходимые формулы, можно рассчитать эти параметры, что облегчит процесс построения пентагона. Способы и формулы расчетов:

• сумма всех углов в многоугольниках равна 360 градусам. В правильном пятиугольнике все углы равны, соответственно, центральный угол находится таким способом: 360/5 = 72 градуса;
• внутренний угол находится таким образом: 180*(n -2)/ n = 180*(5−2)/5 = 108 градусов. Сумма всех внутренних углов: 108*5 = 540 градусов.

Сторона пентагона находится с помощью параметров, которые уже даны в условии задачи:

• если вокруг пятиугольника описана окружность и известен ее радиус, сторона находится по такой формуле: a = 2*R*sin (α/2) = 2*R*sin (72/2) = 1,1756*R.
• Если известен радиус вписанной в пентагон окружности, то формула расчета стороны многоугольника: 2*r*tg (α/2) = 2*r*tg (α/2) = 1,453*r.
• При известной величине диагонали пентагона его сторона рассчитывается таким образом: а = D/1,618.

Площадь пентагона так же, как и его сторона, зависит от уже найденных параметров:

• с помощью известного радиуса вписанной окружности площадь находится так: S = (n*a*r)/2 = 2,5*a*r.
• описанная вокруг пятиугольника окружность позволяет найти площадь по такой формуле: S = (n*R2*sin α)/2 = 2,3776*R2.
• в зависимости от стороны пентагона: S = (5*a2*tg 54°)/4 = 1,7205* a2.

Построение пентагона

Построить правильный пятиугольник можно с помощью линейки и циркуля, на основе вписанной в него окружности или одной из сторон.

Как начертить пятиугольник на основе вписанной окружности? Для этого необходимо запастись циркулем и линейкой и сделать такие шаги:

1. Сначала необходимо начертить окружность с центром О, после чего на ней выбрать точку, А — вершину пентагона. От центра к вершине проводится отрезок.
2. Затем строится перпендикулярная прямой ОА отрезок, который также проходит через О — центр окружности. Его пересечение с окружностью обозначается точкой В. Отрезок О. В. делится пополам точкой С.
3. Точка С станет центром новой окружности, проходящей через А. Точка D — это ее пересечение с прямой ОВ в границах первой фигуры.
4. После этого проводится третья окружность через D, центром которой является точка А. Она пересекается с первой фигурой в двух точках, их необходимо обозначить буквами Е и F.
5. Следующая окружность имеет центр в точке Е и проходит через А, а ее пересечение с первоначальной находится в новой точке G.
6. Последняя окружность в этом рисунке проводится через точку, А с центром F. На ее пересечении с начальной ставится точка Н.
7. На первой окружности после всех проделанных шагов появились пять точек, которые необходимо соединить отрезками. Таким образом получился правильный пятиугольник АЕ G Н F.

Как построить правильный пятиугольник иным способом? С помощью линейки и циркуля пентагон можно построить немного быстрее.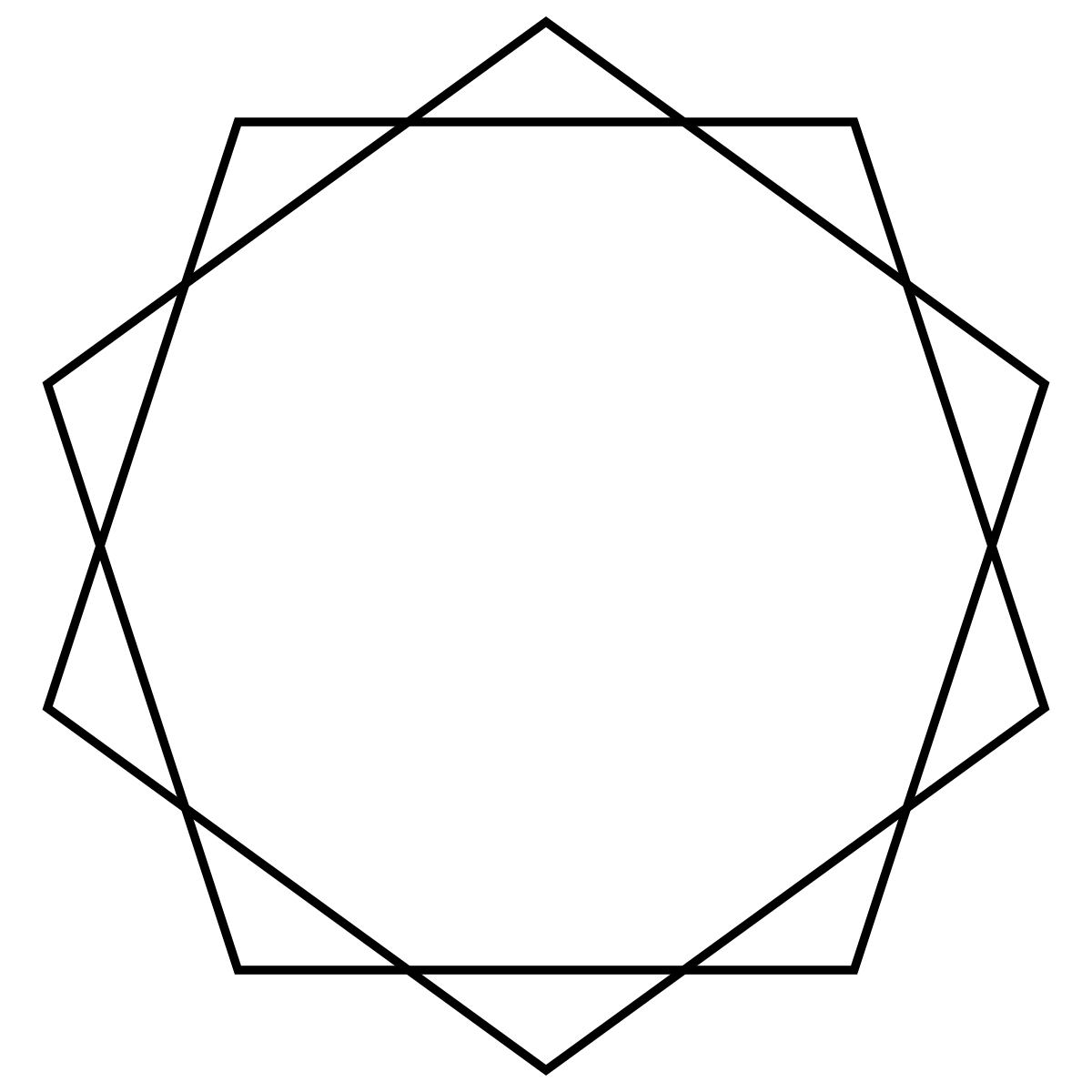

Для этого необходимо:

1. Cначала необходимо с помощью циркуля нарисовать окружность, центр которой — точка О.
2. Чертится радиус ОА — отрезок, который откладывается на окружность. Его делят пополам точкой В.
3. Перпендикулярно радиусу ОА начерчивается отрезок ОС, точки В и С соединяются прямой.
4. Следующим шагом является отложение длины отрезка ВС с помощью циркуля на диаметральной линии. Перпендикулярно отрезку ОА появляется точка D. Точки В и D соединяются, образуя новый отрезок.
5. Для того, чтобы получить величину стороны пентагона, необходимо соединить точки С и D.
6. D с помощью циркуля переносится на окружность и обозначается точкой Е. Соединив Е и С, можно получить первую сторону правильного пятиугольника. Следуя этой инструкции можно узнать о том, как быстро построить пятиугольник с равными сторонами, продолжая построение остальных его сторон подобно первой.

Интересные факты

В пятиугольнике с одинаковыми сторонами диагонали равны и образуют пятиконечную звезду, которая называется пентаграммой. Золотое сечение — это отношение величины диагонали к стороне пентагона.

Пентагон непригоден для полного заполнения плоскости. Использование любого материала в этой форме оставляет промежутки или образует наложения. Хотя природных кристаллов этой формы не существует в природе, но при образовании льда на поверхности гладких медных изделий возникают молекулы в виде пентагона, которые соединены в цепочки.

Наиболее простой способ получить правильный пятиугольник из полоски бумаги — завязать ее узлом и немного придавить. Этот способ полезен для родителей детей-дошкольников, которые хотят научить своих малышей распознавать геометрические фигуры.

Видео

Посмотрите, как можно быстро начертить пятиугольник.

Здравствуйте коллеги.
Сегодня построим правильный пятиугольник в окружности, попробуем начертить циркулем и линейкой фигуру.

Рисунки художников очень тесно связаны с черчением и геометрией.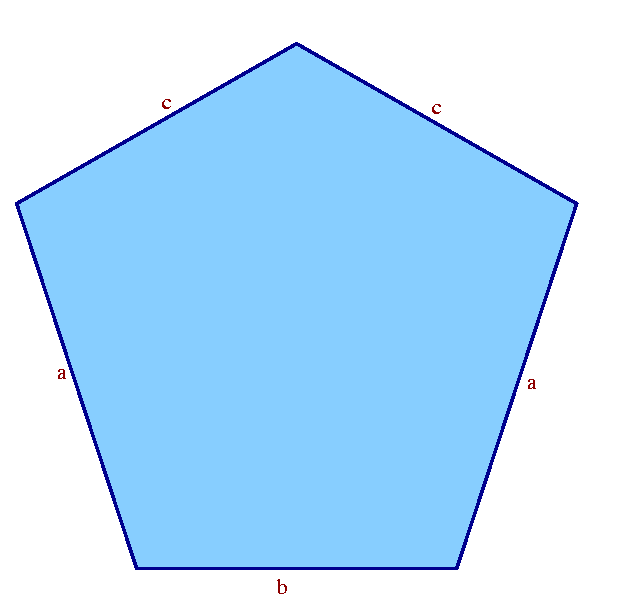

Если мы задумали какую-то композицию, а в ней есть геометрические фигуры, то нам необходимо знать, как изобразить предмет, что бы он не выглядел смешно, и что бы вы не выглядели дилетантом и смогли нарисовать пятиконечную звезду циркулем или в фотошопе. От этого зависит ваш авторитет художника, а значит и заказы.

Построение правильного пятиугольника не так часто встречается в рисунке, но все же есть моменты, когда нам это необходимо.

Например, нам нужно нарисовать пятиконечную звезду (пентаграмму) для картины о Советском прошлом или о настоящем Китая. Правда для этого нужно уметь создать рисунок звезды в перспективе. Это посмотрите в другом уроке.

Мы попробуем нарисовать звезду в фотошопе фронтально. Точно так же вы сможете нарисовать фигуру карандашом на бумаге. Всего лишь с помощью таких инструментов:

Как правильно нарисовать звезду, что бы она выглядела ровно и красиво, сразу не ответишь. Количество углов не четное, поэтому просто разделить окружность на равные части циркулем или линейкой не получится.

Что бы вписанный пятиугольник в окружность был пропорциональный, нам необходимо точно вычислить одну из сторон, а затем отложить этот отрезок пять раз на теле овала.

Как выглядит пятиугольник и звезда

Внизу на фото разберем, как нарисовать звезду поэтапно.
Для начала рисуем окружность с центром О.

Дальше отложим отрезок OA равный радиусу и разделим его пополам точкой B, как показано на фото внизу.

Теперь от точки В до точки С проведем прямую.

Отложим расстояние отрезка ВС на диаметральной линии окружности. Для этого можно воспользоваться циркулем. Таким образом у нас появилась точка D.

И отрезок DB. Картинка внизу.

Дальше, проведя линию от точки D к точке С, Мы получи длину равную стороне пятиугольника.

Дальше этот отрезок можно отложить на окружности. У нас появилась точка Е. Смотрим фото ниже.

Итак, одна из сторон пятиугольника у нас есть, это линия ЕС.

Такие же отрезки наносим на всей части круга. Смотрим картинку.

На этом построение правильного пятиугольника можно закончить. Что бы нарисовать звезду нужно просто соединить углы через один.

Нарисовать пятиконечную звезду циркулем можно так же, как и на нашем уроке в программе Photoshop, весь процесс такой же, только вместо программы графического редактора используем инструменты для черчения.

Так же можно посмотреть уроки построения шестиугольника, разделение на восемь частей, деление круга на семь частей, десять равных частей.

Создание потока процесса в PowerPoint :: think-cell

С помощью think-cell вы можете легко и быстро создать линейный поток процесса, который состоит из пятиугольников, шевронов и текстовых полей.

16.1

Создание потока процесса

16.2

Изменение структуры потока процесса

16.3

Размещение потока процесса на слайде

16.4

Стилизация потока процесса

16.1 Создание потока процесса

Чтобы начать создание потока процесса, вставьте первый пятиугольник. Для этого выберите  Пятиугольник/Шеврон в меню Элементы. Оранжевый контур вставки пятиугольника появится на слайде рядом с указателем мыши. Вы также заметите серые границы на слайде, которые соответствуют заполнителям PowerPoint выбранного макета из образца слайда.

Нажмите в пределах границ, чтобы вставить элемент в нужной позиции. Неважно, где вы нажмете — пятиугольник будет размещен автоматически в пределах этих границ. Элемент выбирается автоматически после вставки, и текст можно вставить напрямую в него. Допустим, этот элемент представляет «Этап 1» вашего потока, поэтому вы можете просто ввести текст в этот пятиугольник. Размер пятиугольника изменяется автоматически по мере ввода текста.

Самый быстрый способ добавить шевроны в поток — использовать кнопку  Дублировать справа или слева от выбранного элемента. Если нажать на него, элемент и его текст будут скопированы на соответствующей стороне, а копия будет автоматически выровнена. Или же вы можете удерживать клавиши Ctrl и Alt и нажать одну из клавиш со стрелкой, чтобы создать копию в этом направлении. При необходимости пятиугольник станет шевроном.

Это также можно сделать для нескольких выбранных элементов. Когда все будет готово, нажмите на каждый пятиугольник или шеврон, чтобы вставить или изменить текст. Удерживая клавишу Alt и нажимая клавиши со стрелкой, можно легко перемещаться от одного элемента к другому.

После создания заголовков для потока с пятиугольниками и шевронами добавим в него таблицу. Выберите строку с несколькими пятиугольниками и шевронами с помощью мыши, а затем нажмите кнопку  Дублировать под выделением. Ниже будет вставлена строка текстовых полей, выровненная с элементами выше. Предположим, для потока процесса вам необходимо еще две строки содержимого: просто дважды нажмите кнопку  Дублировать под выделением, что приведет к получению следующей структуры:

Чтобы детализировать поток, добавив предшествующий столбец текстовых полей для категорий строк, в этом случае это «что», «как» и «кто». Выберите первый столбец текстовых полей с помощью мыши:

Затем нажмите кнопку  Дублировать слева от выделения. Появится выровненная копия первого столбца.

Нажмите на каждое текстовое поле первого столбца и введите «Что», «Как» и «Кто». Вы можете заполнить оставшиеся поля в таблице таким же образом:

Размер и позиция отдельных текстовых полей и всего потока автоматически адаптируются под введенный текст.

16.2 Изменение структуры потока процесса

Удалить отдельные текстовые поля, строки или столбцы так же просто, как и вставить их. Просто выберите текстовое поле, строку или столбец, который требуется удалить, и нажмите клавишу Delete. Вы также можете нажать правой кнопкой мыши на выделение, а затем на красную кнопку  Удалить в контекстном меню.

Чтобы изменить последовательность в потоке процесса позднее, перетащите столбец в другую позицию (например, переместите «Этап 3» в позицию между «Этап 1» и «Этап 2»):&

1. Выберите соответствующий пятиугольник и текстовые поля с помощью мыши.
2. Нажмиите на синий контур выбранных элементов и удерживайте кнопку мыши.
3. Удерживая клавишу Shift, перетащите выделение в позицию между двумя столбцами, чтобы оранжевые границы, которые отображаются во время перетаскивания, обозначили перемещение.

   Удерживая клавишу Shift, можно перетаскивать элементы только по горизонтали, что упрощает поиск нужной точки вставки между двумя столбцами.

4. Отпустите кнопку мыши.

16.3 Размещение потока процесса на слайде

После ввода всех данных для потока разместим все элементы и настроим их размер. По умолчанию размещение и определение размеров элементов think-cell или выровненной группы элементов происходит автоматически в соответствующих границах заполнителя образца слайда. Рекомендуем использовать автоматическое размещение, так как это сэкономит много времени и позволит получить более сбалансированный макет слайда.

Однако вы можете вручную определить другую позицию и максимальный размер потока процесса, если хотите. Для этого выберите весь поток. Вы заметите небольшие значка замка в углах выделения. Их можно использовать для ограничения размера и позиции потока процесса или любого другого элемента.

Допустим, вы хотите оставить зазор по бокам слайда, чтобы ваш поток не выходил за эти границы.

1. Щелкните крайний левый горизонтальный значок замка и удерживайте кнопку мыши.

   Значок замка отображается в области линейки в текущей выбранной позиции. Сама линейка не должна быть видимой.

2. Перетаскивайте замок вправо до тех пор, пока размер зазора не будет вас устраивать.
3. Отпустите кнопку мыши. Левый край потока теперь зафиксирован в этой позиции.

Повторите операцию для правого зазора, перетащив крайний правый значок замка в нужную позицию. Существуют также замки для вертикальных измерений потока, которые можно использовать аналогичным образом.

Чтобы восстановить автоматическое размещение и определение размеров think-cell, нажмите на значок замка на линейке, чтобы удалить замок. Повторите операцию для каждого замка, который размещен на линейке.

16.4 Стилизация потока процесса

После размещения и изменения размера вы можете добавить финальные штрихи в ваш поток процесса, настроив стиль. Допустим, вы хотите задать для каждого пятиугольника и шеврона разный цвет для обозначения различных этапов проекта. Нажмите левой кнопкой мыши каждый пятиугольник и шеврон, а затем выберите нужный цвет в раскрывающемся меню цвета заливки на перемещаемой панели инструментов (см. раздел Цвет и заливка). Вы также можете изменить цвет и тип линии пятиугольников. Выберите все пятиугольники, нажмите на выделение левой кнопкой мыши, откройте раскрывающееся меню цвета контура и измените цвет линии, например, на Фон 2 (см. раздел Цвета структуры. Еще раз нажмите на выделение, откройте раскрывающееся меню типа линии и измените тип линии на 3 пт. сплошная, чтобы получить толстый контур (см. раздел Тип линии).

Чтобы улучшить удобочитаемость потока, вы также можете назначить альтернативные цвета фона для строк или столбцов с помощью функции «Чередование». Просто выберите текстовые поля, которые хотите заполнить и нажмите на любое из них, чтобы открыть Откройте раскрывающееся меню «Чередование» и нажмите Вертикальные полосы, чтобы использовать чередующиеся оттенки столбцов, или Горизонтальные полосы, чтобы использовать оттенки строк. После этого в плавающей панели инструментов вы можете выбрать два цвета в качестве чередующихся цветов фона. Просто откройте соответствующее раскрывающееся меню и выберите в списке предпочитаемый оттенок цвета.

Наконец, чтобы отображать названия столбцов и строк полужирным шрифтом, выделите соответствующий столбец или строку, нажмите на выделение, откройте раскрывающееся меню шрифта и выберите полужирную версию предпочитаемого шрифта (см. раздел Шрифт).

%d0%bf%d1%8f%d1%82%d0%b8%d1%83%d0%b3%d0%be%d0%bb%d1%8c%d0%bd%d0%b8%d0%ba на турецкий — Русский-Турецкий

В настоящий 83-й год правления Царства, возглавляемого Иисусом, некоторые, возможно, думают, что сейчас как раз период замедления.

İsa’nın Gökteki Krallık yönetiminin 83. yılında bulunduğumuzdan, bazıları şimdi gecikme döneminde olduğumuzu düşünebilir.

jw2019

Этот отчисленный ученик умер в 82 года, в здравом уме, будучи основателем и первым директором Еврейского университета в Иерусалиме и основателем издательства Шокен Букс. Это популярное издательство в дальнейшем было поглощено издательским домом Рандом Хаус.

Bu liseden terk 82 yaşında öldüğünde, müthiş bir entelektüel, Kudüs İbrani Üniversitesi’nin kurucu ortağı ve ilk genel müdürü ve Schocken Books’un, ki ileride Random House tarafından satın alınan alkışlanacak bir markanın kurucusuydu.

ted2019

82-летний мужчина, диабетик, похищен около своего маленького милого дома среди бела дня.

82 yaşında şeker hastası adam, günün ortasında güzel ve küçük evinin önünden kaçırılıyor.

OpenSubtitles2018.v3

▪ Ежедневно в ЮАР осуждаются 82 ребенка за «изнасилование или словесное оскорбление других детей».

▪ Tüm Güney Afrika’da günde 82 çocuk “başka çocuklara tecavüz etmek veya saldırmak” suçundan mahkemeye çıkıyor.

jw2019

82 7 Иметь детей — ответственность и награда

79 7 Çocuklar Bir Sorumluluk ve Bir Mükâfat

jw2019

Какое же счастливое освобождение настанет для людей, жаждущих мирного, справедливого правления! (Псалом 36:9–11; 82:18, 19).

Böylelikle, barışçı, adil bir hükümdarlığı özleyen insanlara, mutluluk dolu ne büyük bir ferahlık gelecektir!—Mezmur 37:9-11; 83:17, 18.

jw2019

Урок: Ясно покажи, как применяется библейский стих (be с. 154, абз. 4 — с. 155, абз.

Konuşma Özelliği: Ayetlerin Uygulanışı Net Olsun (be s. 154 p. 4-s. 155 p.

jw2019

Пройдите к выходу 82 через 40 минут.

Lütfen 40 dakika içerisinde 82 nolu peronda olun.

OpenSubtitles2018.v3

Относительно 82 процентов слов, приписываемых Иисусу в Евангелиях, они проголосовали черным шаром.

Aslında, onlar İncillerde İsa’ya atfedilen sözlerin yüzde 82’si için siyah oy kullandı.

jw2019

Урок: Объясняй незнакомые термины (be с. 227, абз.

Konuşma Özelliği: Bilinmeyen Terimleri Açıklamak (be s. 227 p. 2-s. 228 p.

jw2019

MBI нашла 83 процента.

MBI %83’ünü tespit etti.

ted2019

Как вам известно, Эль- Ниньо 1982- 83 годов погубило 95 процентов всех кораллов на Галапагосах.

Ama az önce öğrendiğiniz gibi 1982- 1983 ́te olan El Nino, Galapagos’taki mercanların% 95 ́ini öldürdü.

QED

Что это, номер 82?

OpenSubtitles2018.v3

(«Too Fat, Too Thin, Will We Ever Be Content?») на фестивале Vogue в составе группы, под председательством главного редактора Vogue Fiona Golfar, а также моделями Daisy Lowe, Patsy Kensit и содействующим редактором Vogue Christa D’Souza.

Bu panelde, moderatör olarak Vogue’un baş editörü Fiona Golfar, diğer katılımcılar manken Daisy Lowe, çocuk yıldız Patsy Kensit ve Vogue yardımcı editörü Christa D’Souza’dır.

WikiMatrix

Это оправдает владычество Иеговы и освободит послушных Богу людей — а значит, и нас — от унаследованного греха (1 Паралипоменон 29:11; Псалом 82:19; Деяния 4:24; 1 Иоанна 3:8; Евреям 2:14, 15).

Yehova bunu yaparak egemenlik hakkını pekiştirecek ve miras alınan günahın itaatli insanlardan kaldırılmasını mümkün kılacak. (I.

jw2019

Урок: Будь тактичным, когда свидетельствуешь (be с. 197, абз. 4 — с. 199, абз.

Konuşma Özelliği: Taktla Şahitlik Etmek (be s. 197 p. 4–s. 198 p.

jw2019

(Воспользуйся вопросником «Твой гардероб» на страницах 82 и 83.)

(Özdeyişler 15:22; 82 ve 83. sayfadaki “Gardırop Değerlendirmesi” çizelgesini kullan.)

jw2019

Урок: Интересуйся людьми (be с. 186, абз.

Konuşma Özelliği: Karşımızdaki Kişiye İlgi Göstermek (be s. 186 p.

jw2019

Те, кто полагаются на Иегову, «приходят от силы в силу» (Псалом 83:6, 8).

Gücünü Yehova’dan alan kişiler “gittikçe kuvvetlenir.”

jw2019

83:12). Происходит ли подобное в наши дни?

83:12). Günümüzde de benzer bir şey oldu mu?

jw2019

◆ 83:4 — Почему здесь упоминаются птицы?

◆ 84:3—Burada neden kuşlardan söz edilir?

jw2019

Число найденных шаровых скоплений продолжало расти, достигнув 83 единиц к 1915 году, 93 — к 1930 году и 97 — к 1947 году.

Keşfedilen küresel yıldız kümesi sayısı gittikçe artmaya devam etti, 1915’te 83’e ulaştı, 1930’da 93’ye ulaştı ve 1947 yılı itibarıyla 97’ye ulaştı.

WikiMatrix

Урок: Вступление, вызывающее интерес (be с. 215, абз. 1 — с. 216, абз.

Konuşma Özelliği: İlgi Uyandıran Giriş (be s. 215 p. 1–s. 216 p.

jw2019

Урок: Главных пунктов должно быть немного (be с. 213, абз. 2 — с. 214, абз.

Konuşma Özelliği: Çok Fazla Ana Nokta Ele Almamak (be s. 213 p. 2–s. 214 p.

jw2019

Желаю лучше быть у порога в доме Божием, нежели жить в шатрах нечестия» (Псалом 83:11).

Kötülük çadırlarında oturmaktansa, Allahın evinde eşikte durmak benim için iyidir.”

jw2019

Декоративные картинки, пятиугольник, фото для подарков и сувениров

О продукте и поставщиках:

Alibaba.com предлагает невероятные коллекции красивого, элегантного и потрясающего. картинки, пятиугольник, фото для различных подарочных, декоративных и сувенирных целей. Эти обаятельные и привлекательные. картинки, пятиугольник, фото очень привлекательны с эстетической точки зрения и изготовлены из высококачественных материалов, благодаря которым они служат долго. Широкий ассортимент. картинки, пятиугольник, фото на сайте замысловато созданы, демонстрируя истинное мастерство, и доступны в различных индивидуальных вариантах. Ведущие поставщики и проверенные оптовики на сайте предлагают эти товары по заманчивым ценам. 
Безупречный. картинки, пятиугольник, фото товары на сайте изготовлены из различных прочных материалов, таких как АБС-пластик, закаленный пластик и ПВХ, для обеспечения большей долговечности в будущем. Файл. картинки, пятиугольник, фото являются идеальными элементами декора для вашего интерьера и могут вписаться в любой стиль или декор. Эти. картинки, пятиугольник, фото доступны во всех типах современного, классического и старинного дизайна в соответствии с вашими индивидуальными предпочтениями. 
Alibaba.com предлагает несколько различных вариантов. картинки, пятиугольник, фото различных дизайнов, форм, размеров, цветов и материалов в зависимости от продуктов и ваших требований. Вы можете выбрать из выдающихся. картинки, пятиугольник, фото, которые идеально подходят для любых типов рекламных мероприятий, деловых подарков, сувениров, произведений искусства и других товаров.  предметы коллекционирования или даже украшения. Эти. картинки, пятиугольник, фото экологически безопасны и обладают более высокой устойчивостью, чтобы противостоять всем видам внешних воздействий благодаря регулярному использованию. 
Исследуйте обширное царство. картинки, пятиугольник, фото на Alibaba.com и приобретайте продукты в рамках своего бюджета и требований. Эти продукты доступны как OEM-заказы и поставляются в индивидуальной упаковке при оптовых закупках. Они имеют сертификаты ISO, CE для обеспечения качества.

Что можно нарисовать из пяти и шестиугольников. Построение пятиугольника подробно. Получение с помощью полоски бумаги

Вы находитесь в категории раскраски пятиугольник. Раскраска которую вы рассматриваете описана нашими посетителями следующим образом «» Тут вы найдете множество раскрасок онлайн. Вы можете скачать раскраски пятиугольник и так же распечатать их бесплатно. Как известно творческие занятия играют огромную роль в развитии ребенка. Они активизируют умственную деятельность, формируют эстетический вкус и прививают любовь к искусству. Процесс раскрашивания картинок на тему пятиугольник развивает мелкую моторику, усидчивость и аккуратность, помогает узнать больше об окружающем мире, знакомит со всем разнообразием цветов и оттенков. Мы ежедневно добавляем на наш сайт новые бесплатные раскраски для мальчиков и девочек, которые можно раскрашивать онлайн или скачать и распечатать. Удобный каталог, составленный по категориям, облегчит поиск нужной картинки, а большой выбор раскрасок позволит каждый день находить новую интересную тему для раскрашивания. 8 июня 2011

Первый способ — по данной стороне S с помощью транспортира.

Проводим прямую и откладываем на ней AB = S; принимаем эту линию за радиус и этим радиусом из точек A и В описываем дуги: далее с помощью транспортира строим в этих точках углы в 108°, стороны которых пересекутся с дугами в точках С и D; из этих точек радиусом АВ = 5 описываем дуги, которые пересекутся в Е, и прямыми линиями соединяем точки Л, С, Е, D, В.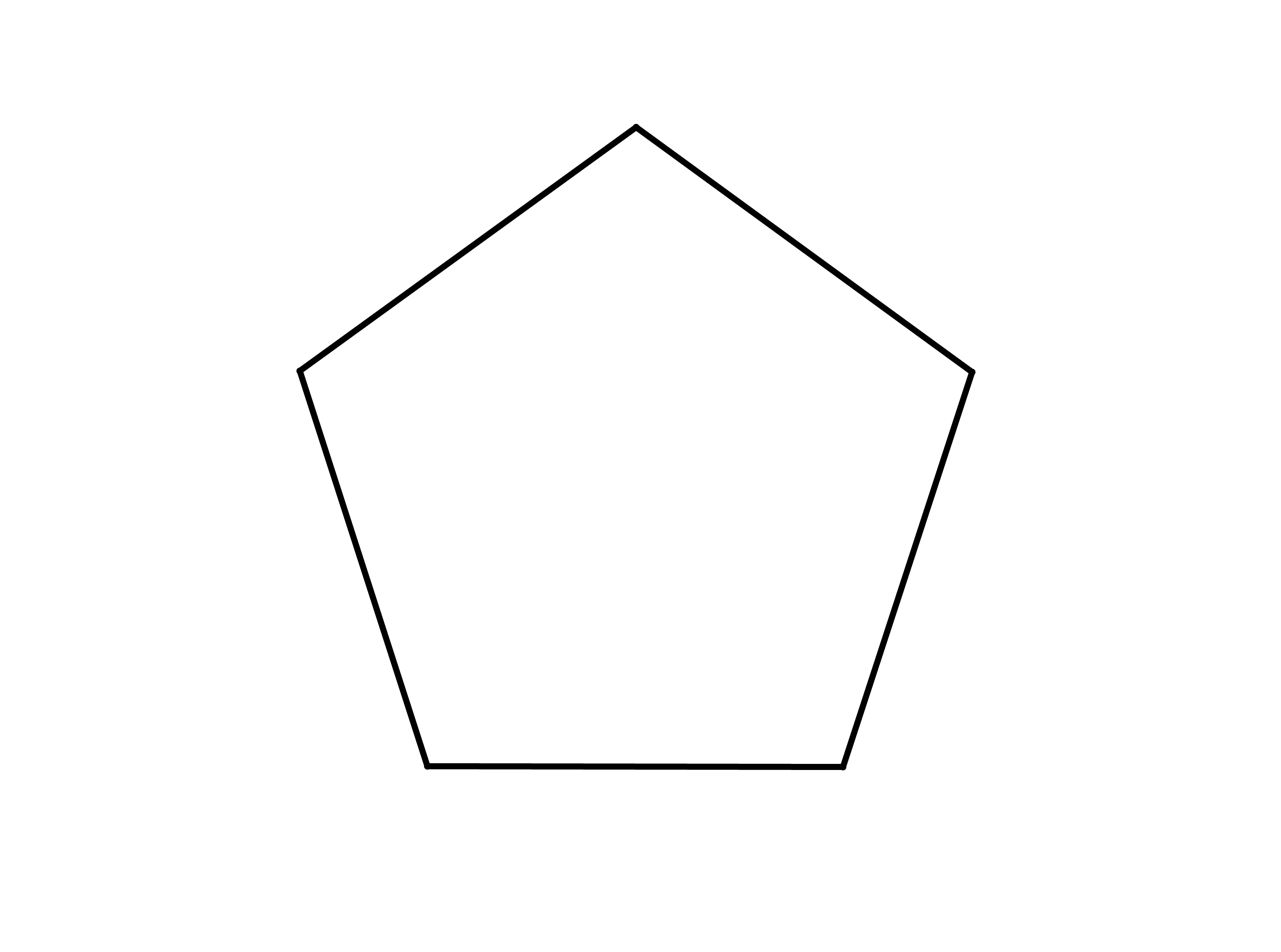

Полученный пятиугольник — искомый.

Второй способ. Проведем окружность радиусом r. Из точки А циркулем проводим дугу радиуса AM до пересечения в точках В и С с окружностью. Соединяем В и С линией, которая пересечет горизонтальную ось в точке Е.

Затем из точки Е проводим дугу, которая пересечет горизонтальную линию в точке О. Описываем, наконец, из точки F дугу, которая пересечет окружность в точках Н и К. Отложив по окружности расстояние FO = FH = FK пять раз и соединив точки деления линиями, получим правильный пятиугольник.

Третий способ. В данный круг вписать правильный пятиугольник. Проводим два взаимно перпендикулярных диаметра АВ и МС. Делим радиус АО точкой Е пополам. Из точки Е, как из центра, проводим дугу окружности радиуса ЕМ и засекаем ею диаметр АВ в точке F. Отрезок MF равен стороне искомого правильного пятиугольника. Раствором циркуля, равным MF, делаем засечки N 1 , Р 1 , Q 1 , К 1 и соединяем их прямыми.

На рисунке построен шестиугольник по данной стороне.

Прямой АВ = 5, как радиусом, из точек А и В описываем дуги, которые пересекутся в С; из этой точки тем же радиусом описываем окружность, на которой сторона А В отложится 6 раз.

Шестиугольник ADEFGB — искомый. 

«Отделка комнат при ремонте»,
Н.П.Краснов

Основанием для нанесения росписи служат полностью законченные окраской поверхности стен, потолков и других конструкций; роспись делается по высококачественным клеевым и масляным окраскам, сделанным под торцовку или флейц. Приступая к разработке эскиза отделки, мастер должен ясно представить себе всю композицию в бытовой обстановке и отчетливо осознать творческий замысел. Только при соблюдении этого основного условия можно правильно…

Обмер выполненных работ, за исключением особо оговоренных случаев, производится по площади действительно обработанной поверхности с учетом ее рельефа и за вычетом необработанных мест. Для определения действительно обработанных поверхностей при малярных работах следует пользоваться переводными коэффициентами, приведенными в таблицах. А. Деревянные оконные устройства (обмер производится по площади проемов по наружному обводу коробок) Наименование устройств Коэффициент при…

Мы уже говорили, что для исполнения некоторых видов малярных работ необходимо уметь рисовать. А умение рисовать, в свою очередь, предполагает знание правил построения геометрических фигур. Эскизы на бумаге вычерчивают при помощи треугольников, рейсшин, транспортаpa и циркуля, а на плоскости стен и потолков построения выполняются при помощи веска, линейки, деревянного циркуля и шнура. При этом надо…

Эта фигура является многоугольником с минимальным количеством углов, которым невозможно замостить площадь. Только у пятиугольника количество диагоналей совпадает с количеством его сторон. Воспользовавшись формулами для произвольного правильного многоугольника, можно определить все необходимые параметры, которые имеет пентагон. Например, вписать его в окружность с заданным радиусом либо построить на базе заданной боковой стороны.

Как правильно начертить луч и какие принадлежности для черчения вам понадобятся? Возьмите листок бумаги и отметьте в произвольном месте точку. Затем приложите линейку и проведите линию, начиная с указанной точки и до бесконечности. Чтобы начертить ровную линию, нажмите клавишу «Shift»и проведите линию нужной длины. Сразу после начертания откроется вкладка «Формат». Уберите выделение с линии и увидите, что в начале линии появилась точка. Для создания надписи нажмите кнопку «Нарисовать надпись» и создайте поле, где будет находиться надпись.

Первый способ построения пятиугольника считается более «классическим». Получившаяся в результате построения фигура будет правильным пятиугольником. Двенадцатиугольник не является исключением, поэтому его построение будет невозможным без применения циркуля. Задача построения правильного пятиугольника сводится к задаче деления окружности на пять равных частей. Начертить пентаграмму можно с использованием простейших инструментов.

Я долго бился пытаясь этого добиться и самостоятельно найти пропорции и зависимости, но мне этого не удалось. Оказалось, что есть несколько различных вариантов построения правильного пятиугольника, разработанных известными математиками. Инересным моментов является то, что арифметически эту задачу решить только приблизительно точно, поскольку придется использовать иррациональные числа. Зато ее можно решить геометрически.

Деление окружностей. Точки пересечения этих линий с окружностью и являются вершинами квадрата. В окружности радиуса R (Шаг 1) следует провести вертикальный диаметр. В точке сопряжения N прямой и окружности прямая является касательной к окружности.

Получение с помощью полоски бумаги

Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного цир­куля. Чтобы построить сторону 2-3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 прово­дим прямую, которая определит третью вершину треугольника. Намечаем на окружности точку 1 и принимаем её за одну из вер­шин пятиугольника. Найденные вершины соединяем после­довательно между собой. Семиугольник может быть построен путём проведе­ния лучей из полюса F и через нечётные деления вертикального диаметра.

А на другой конец нитки устанавливаемые карандаш и одержим. Если умеете чертить звезду, но не умеете пятиугольник, начертите звезду карандашом, затем соедините между собой соседние концы звезды, а саму звезду потом сотрите. Затем положите лист бумаги (лучше его закрепить на столе при помощи четырёх кнопок или иголочек). Приколите эти 5 полосочек к листку бумаги кнопками или иголочками, чтобы они оставались неподвижными. Затем обведите полученный пятиугольник и снимите эти полосочки с листка.

Например, нам нужно нарисовать пятиконечную звезду (пентаграмму) для картины о Советском прошлом или о настоящем Китая. Правда для этого нужно уметь создать рисунок звезды в перспективе. Точно так же вы сможете нарисовать фигуру карандашом на бумаге. Как правильно нарисовать звезду, что бы она выглядела ровно и красиво, сразу не ответишь.

С центра опусти на окружность 2 луча, чтоб угол между ними был 72 градуса (транспортиром). Деление круга на пять частей осуществляется с помощью обычного циркуля или транспортира. Поскольку правильный пятиугольник — это одна из фигур, содержащая в себе пропорции золотого сечения, его построением издавна интересовались живописцы и математики. Эти принципы построения с применением циркуля и линейки были изложены еще в эвклидовых «Началах».

Фотообои «Мраморные пятиугольники» №dec_5357pw на заказ под свой размер

Фотообои «Мраморные пятиугольники» №dec_5357pw на заказ под свой размер — picwalls.ru

Загрузите свое

изображение

cloud_upload

Ваше сообщение

отправлено



Фотообои

• Фотообои
• Обои

По типу помещения

0 руб
Цена 0 руб
0 руб

Непонятно как будет смотреться у меня

Непонятно как будет смотреться у меня. Заказать бесплатный макет

Заказать в 1 клик Заказать в 1 клик Полный заказ

Укажите размер для фотообоев

Выберите материал

Папирус АКЦИЯ

★★★★★

★★★★★

740 руб/м²

keyboard_arrow_right

Бумажные фотообои

Постер

?

★★★★★

★★★★★

390 руб/м²

Папирус

?

★★★★★

★★★★★

740 руб/м²

Флизелиновые фотообои

Сатин

?

★★★★★

★★★★★

940 руб/м²

Виниловые на флизелиновой основе

Сафьян

?

★★★★★

★★★★★

1270 руб/м²

Мелкая нить

?

★★★★★

★★★★★

1400 руб/м²

Песок

?

★★★★★

★★★★★

1190 руб/м²

Прованс

?

★★★★★

★★★★★

1200 руб/м²

Декоративная штукатурка

?

★★★★★

★★★★★

1440 руб/м²

Роспись

?

★★★★★

★★★★★

1540 руб/м²

Самоклеющиеся фотообои

Авангард

?

★★★★★

★★★★★

1350 руб/м²

Папирус

★★★★★

★★★★★

740 руб/м² 

Дополнительно

Отзывы

Показать больше 

Благодарим за подписку!



zabtest

Фигур пятиугольника: Урок для детей

Математический словарь

Пентагон : многоугольник (форма), имеющий 5 сторон и 5 углов.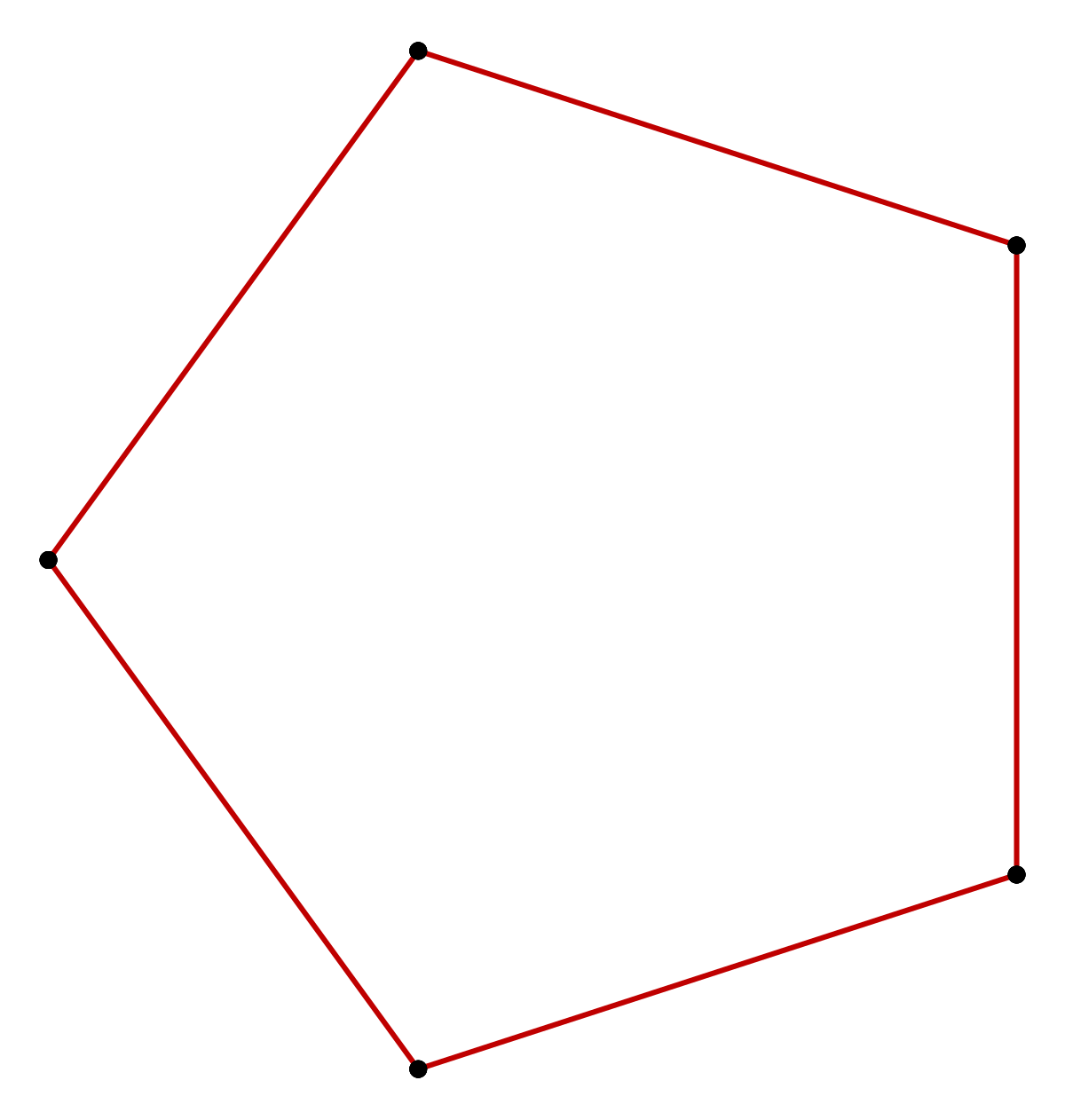 Он должен состоять из прямых линий и быть замкнутой (без отверстий) фигурой.

Неправильный пятиугольник : пятиугольник, стороны которого различаются по длине.

Правильный пятиугольник : пятиугольник, стороны и углы которого одинаковы. На схеме показаны примеры каждого типа пятиугольника.

Подключение к реальной жизни

Вам может быть интересно, как нарисовать пятиугольник. Самый простой способ нарисовать настоящую форму — это представить себе дом. Крыша может иметь две наклонные стороны, а остальные 3 стороны будут составлять стены и пол дома. Взгляните на пример на картинке. Помните, что пятиугольник может выглядеть по-разному, но самый простой способ нарисовать его — это просто вспомнить, как выглядит дом.

В Вашингтоне, округ Колумбия, есть знаменитое здание, которое также называют пятиугольником. Взгляните на его изображение и посмотрите, сможете ли вы выяснить, как он получил такое название. Пентагон в Вашингтоне, округ Колумбия, является штаб-квартирой Министерства обороны. У здания 5 сторон и 5 углов, как вы можете видеть на картинке, отсюда и название — Пентагон.

Здание Пентагона в Вашингтоне, округ Колумбия.

Резюме урока

Пента означает 5, поэтому слово Пентагон означает форму, имеющую 5 сторон и 5 углов.Пентагоны могут быть правильными, имеющими одинаковые стороны и углы, или неправильными, иметь разную длину и углы. В Вашингтоне, округ Колумбия, есть знаменитая достопримечательность, называемая Пентагоном, которая представляет собой здание, состоящее из 5 сторон и углов — это штаб-квартира Министерства обороны США

.

Пентагоны в дикой природе

В этом упражнении учащиеся создадут фото-дневник и отражение пятиугольников, которые они видят в своем окружении.Учащиеся могут использовать смартфон, одноразовую камеру или блокнот, чтобы рисовать пятиугольники, которые они находят. Для каждой фотографии или эскиза учащиеся должны объяснить, где они нашли объект, и дать его описание. Например, учащиеся могут найти подставки в форме пятиугольника на журнальном столике, сфотографировать их и написать описание, например: «Эти подставки имеют форму пятиугольника, потому что они имеют пять сторон и используются для защиты стола от холодных и горячих напитков. . »

Проезд

На этом уроке вы будете находить пятиугольники в своей повседневной жизни в виде фотожурнала.Этот проект может длиться от нескольких часов до нескольких дней, насколько смело вы хотите получить, зависит только от вас! Для начала возьмите фотоаппарат, смартфон или просто альбом для рисования и карандаш и начните искать пятиугольники. Для каждого найденного объекта запишите краткое описание сцены и объекта и решите, является ли пятиугольник правильным или неправильным. Убедитесь, что вы включили не менее 10 пятиугольников в свой фотожурнал, и поделитесь своими результатами с кем-нибудь, когда закончите. Вы должны уметь объяснить, почему каждая форма представляет собой пятиугольник и почему она правильная или неправильная.

Критерии успеха

• В фотожурнале не менее 10 фотографий
• На каждой фотографии есть описание и объяснение того, является ли пятиугольник правильным или неправильным.
• Фоторепортаж опубликован вместе с объяснением того, почему на каждой из фотографий есть пятиугольник

Пентагон. Калькулятор | Определение | Формула

С помощью этого калькулятора пятиугольника вы найдете основные свойства правильного пятиугольника: сторону, диагональ, высоту, периметр и площадь, а также радиус описанной и вписанной окружности.Введите любое значение, и остальные параметры будут рассчитаны на месте. Если вы не уверены, что такое пятиугольник или сколько сторон у него, продолжайте прокручивать, и вы найдете проясняющие картинки с кратким пояснением.

Что такое пятиугольник? Сколько сторон у пятиугольника?

Пентагон — это 5-сторонний многоугольник . Пентагон может быть простым или самопересекающимся.

Сумма внутренних углов в простом пятиугольнике составляет 540 °, поэтому каждый внутренний угол равен 108 °.У правильного простого пятиугольника все пять сторон равны по длине. (В этой статье мы используем термин «правильный пятиугольник» для описания правильного простого пятиугольника).

Площадь и периметр правильного пятиугольника

Площадь правильного пятиугольника можно рассчитать по формуле:

площадь = a² * √ (25 + 10√5) / 4 , где — сторона правильного пятиугольника.

Также вы можете найти область с радиусом вписанной окружности:

площадь = 5 * r² * √ [(5 + √5) / 2] / 4 , где r — радиус вписанной окружности.

Периметр P правильного пятиугольника равен длине стороны, умноженной на количество вершин. Пентагон — это 5-сторонний многоугольник, поэтому периметр:

.

периметр = 5 *

Высота и диагональ правильного пятиугольника

Чтобы рассчитать высоту и диагональ правильного пятиугольника, все, что вам нужно, это длина стороны a :

диагональ = a * (1 + √5) / 2

высота = a * √ (5 + 2√5) / 2

Пентагон имеет пять диагоналей равной длины, которые образуют пентаграмму.

Как решить правильный пятиугольник с помощью этого калькулятора пятиугольника?

Теперь, когда мы знаем определение пятиугольника, мы можем взглянуть на этот пошаговый пример:

1. Узнайте, что дано . Для правильного пятиугольника достаточно одного параметра, чтобы найти оставшиеся шесть.
2. Введите значение в пятиугольник калькулятора . Возьмем для примера самый известный почти правильный пятиугольник — здание Пентагона, штаб-квартиру Министерства обороны США.Со страницы Википедии мы узнаем, что его ширина 1414 футов — это , высота пентаграммы.

Пентагон, 1414 футов, 431 м (голубой)
RMS Queen Mary 2, 1132 футов, 345 м (розовый)
USS Enterprise с ядерным двигателем ВМС США, 1123 фута, 342 м (желтый)
Дирижабль LZ 129 Hindenburg, 804 фута , 245 м (зеленый)
Ямато Императорского флота Японии, 863 фута, 263 м (темно-синий)
Эмпайр-стейт-билдинг, 1454 фута, 443 м (серый)
Супертанкер Knock Nevis, 1503 фута, 458 м (красный) Главное здание Apple Park, 1522 фута, 458 м (зеленый)

3. Появляются параметры пятиугольника! Это:

• сторона — 918.9 футов
Диагональ
• — 1486,8 футов
• периметр — 4594 футов (0,87 миль)
• площадь — 33,35 акров
• Радиус описанной окружности — 781,6 фута
• радиус вписанной окружности — 632,4 фута

Вы заметили, насколько он огромен? Посмотрите по периметру — это почти миля! На самом деле каждая сторона здания составляет ~ 921 фут в длину — похоже, это практически правильный пятиугольник!

Прочая правильная форма

Если вас интересуют другие правильные формы, обратите внимание на наши замечательные инструменты:

27 фотографий Пентагона от ФБР на 9/11, которые вы должны увидеть

Большая часть того, что валяется на пыльном пространстве кладбищ самолетов вокруг Тусона, штат Аризона, легко идентифицировать и не совсем примечательно.

Катапультные кресла от старых Ф-4 Фантомов. Старый корпус вертолета CH-53. Интересная находка — часть фюзеляжа советского МиГ-23 Флоггер. Понятия не имею, как он сюда попал. В остальном это просто длинные ряды старых, сломанных, бесшумных самолетов внутри высоких заборов, окруженные кактусами, пылью, песком и еще большим количеством песка. Заблудший элерон на мертвом крыле тихо лязгает на фоне жаркого полуденного бриза, словно желая вернуться в воздух. Но, как и все здесь, дни его полетов закончились.

---

Но вот … Что это за странное, пыльно-черное существо в форме ската манты, лежащее под углом по другую сторону забора? Это может быть старый аэродромный флюгер или испытательный образец радара. Но также может быть…

Lockheed D-21B в Национальном музее ВВС США. (фото ВВС США)

Я только читал об этом и видел зернистые фотографии. Я знаю, что это невозможно. Проект был настолько секретным, что даже сегодня существует мало информации о деталях.Но я стою и смотрю сквозь забор из цепей, а обломки других самолетов молчаливо свидетельствуют. Как будто трупы других самолетов побуждают меня присмотреться. Не уходить. Их безмолвное достоинство умоляет меня рассказать эту историю.

После почти минуты изучения этого через забор я понимаю; Я не ошибаюсь. Это прямо у меня на глазах. В десяти футах от меня. Несмотря на 100-градусную жару, у меня мурашки по коже. И я начинаю бежать.

Я быстро нахожу место, где открывается вся линия забора.Я обхожу забор и через пару минут, бегая вокруг песчаных трупов самолетов, оказываюсь внутри. Прямо передо мной на дряхлой транспортной тележке, присыпанной ветром песком, заброшенной в пустыне Сонора, находится один из самых амбициозных секретных проектов Келли Джонсон и Бена Рича легендарной компании Lockheed Skunk Works.

Ранее засекреченная фотография беспилотника Lockheed D-21 на заводе Skunkworks. (фото Lockheed Martin)

Я только что нашел сверхсекретную цифру 3 числа Маха ЦРУ.3+ Д-21 Дрон-разведчик дальнего действия. D-21 был настолько странным, столь амбициозным, настолько маловероятным, что он остается одним из самых невероятных концептов в истории зачастую причудливого мира сверхсекретных «черных» авиационных проектов. А теперь он лежит в пустыне. История, стоящая за этим, настолько причудлива, что трудно поверить, но это правда.

30 июля 1966 года: эшелон полета 920 (92000 футов), скорость 3,25 Маха, испытательный центр военно-морских ракет над точкой Мугу, Окснард, Калифорния.

Только SR-71 Blackbird достаточно быстр и может летать достаточно высоко, чтобы сфотографировать это, самый засекреченный тест национальной безопасности. Одна из самых амбициозных и причудливых штуковин в истории человечества летит быстрее винтовочной пули на высоте 91 000 футов, близкой к высоте во внутреннем космосе.

«Табло» — его кодовое имя. Из-за катастрофического сбития в мае 1960 года высотного самолета-разведчика Lockheed U-2 Фрэнсиса Гэри Пауэрса над Советским Союзом ЦРУ отчаянно нуждается в другом способе слежения за растущей угрозой коммунистических ядерных испытаний. Хуже того, другая «красная угроза», китайцы, испытывают массивные водородные бомбы в отдаленном месте пустыни Гоби, недалеко от монгольско-китайской границы.Было бы легче наблюдать за испытаниями, если бы китайцы проводили их на Луне.

Цель простая, но проблема титаническая. Сделайте фотографии сверхсекретных испытаний водородной бомбы красного Китая недалеко от границы с Монголией в глубине Азии, а затем получите их обратно, не будучи обнаруженными.

Босс Lockheed Skunkworks Келли Джонсон и небольшая элитная сверхсекретная небольшая группа аэрокосмических инженеров построили самолет настолько, что опередили свое время, что даже яркое воображение не может его вообразить.

Плоский, треугольный, черный, безликий, за исключением странной формы в плане, если смотреть сверху, как плащ демона, у него заостренный нос, углубленный в обращенное вперед отверстие. Вот и все. Ни навеса, ни кабины, ни вооружения. Ничего внешнего не прикреплено. Даже больше, чем у винтовочной пули, ее форма гладкая и простая. Это сверхсекретный дрон Д-21.

Фотография ВВС Д-21, установленного на самолет-носитель М-21. Самолет-носитель М-21 был особым вариантом SR-71 Blackbird.Всего было выпущено два. (фото ВВС США)

D-21 действительно «дрон», а не беспилотный летательный аппарат (ДПВС). Его план полета запрограммирован в систему наведения. Он запускается с базового самолета-носителя на скорости и высоте. Он выполняет заранее определенную шпионскую миссию с высоты 17 миль над землей и мигает со скоростью, в три раза превышающей скорость звука. Он фотографирует огромные участки земли с невероятной детализацией и разрешением. А из-за его удивительно незаметной формы никто никогда не узнает, что он там был.

Сегодня D-21 едет на задней части Lockheed M-21, специализированного варианта SR-71 Blackbird, знаменитого высотного самолета-разведчика со скоростью 3+ Маха. Версия SR-71 M-21 несет на своей спине дрон D-21, обеспечивающий скорость и высоту пуска. Он запускает уникальный прямоточный воздушно-реактивный двигатель D-21 RJ43-MA20S-4 и запускает его в заранее запрограммированном полете.

Сегодня в погоне за комбинацией M-21 и D-21 будет Lockheed SR-71, единственное, что может не отставать от этой комбинации самолетов.Задача SR-71 — фотографировать и снимать тестовый запуск беспилотника D-21 с самолета-носителя M-21.

К настоящему времени выполнено три успешных отделения запуска Д-21 от самолета-носителя М-21. В каждом из этих полетов, даже несмотря на то, что запуск был успешным, дрон D-21 падал жертвой небольшого механического отказа, который разрушил его, потому что на скорости более 3 Маха и

футов действительно не было «мелких» отказов.

Сегодня Билл Парк и Рэй Торик — летный экипаж на борту самолета-носителя М-21.Они сидят внутри самолета-носителя М-21, одетые в герметичные высотные летные костюмы, напоминающие скафандры.

При заданной стартовой скорости и высоте комбинация M-21 / D-21 летит рядом с самолетом камеры SR-71. Кейт Бесвик снимает пусковые испытания с фотоаппарата SR-71. Рэй Торик, диспетчер запуска дронов, сидящий на заднем сиденье тандема М-21, запускает D-21 с его позиции на фюзеляже М-21 между массивными двигателями.

Что-то пошло не так.

Дрон Д-21 отделяется и немного перекатывается влево. Он поражает левый вертикальный стабилизатор базового корабля М-21. Затем он падает обратно в верхнюю часть фюзеляжа М-21, оказывая на самолет М-21 огромные тройные сверхзвуковые силы. М-21 начинает набирать обороты, и физика берет верх, когда Билл Парк и Рэй Торик совершают мгновенный переход от летчиков-испытателей к беспомощным пассажирам и жертвам аварии.

Тройная сверхзвуковая сила разрывает оба самолета в разреженном, ледяном воздухе.Осколки титана и шрапнель от деталей двигателя оставляют следы дыма и замороженного пара, распадаясь в верхних слоях атмосферы. Не существует такой вещи, как незначительная авария на скорости 3+ Маха и высоте 92 000 футов.

Чудесным образом Билл Парк и Рэй Торик катапультируются с разбитого корабля-носителя М-21. Что еще более примечательно, они действительно пережили изгнание. Пара приземляется в Тихом океане в 150 милях от побережья Калифорнии. Билл Парк успешно разворачивает небольшой спасательный плот, прикрепленный к его катапультному креслу.Рэй Торик приземляется в океане, но открывает козырек на своем шлеме, похожем на скафандр, прикрепленном к герметичному летному костюму. Костюм проливается сквозь отверстие в шлеме. Торик тонет, прежде чем его успевают спасти. Кейт Бесвик, пилот, снимавший аварию с самолета-погонщика SR-71, должен отправиться в морг, чтобы вырезать тело Рэя Торика из герметичного высотного летного костюма, прежде чем его можно будет похоронить.

Сверхсекретная программа испытаний по запуску беспилотника D-21 с вершины самолета-носителя M-21 на скорости более 3 Маха и

футов отменяется.

Программа D-21 продвигается сама по себе. Теперь дрон сбрасывается с неуклюжего базового корабля B-52. Затем D-21 разгоняется до большой высоты и до 3+ Маха с помощью ракетного ускорителя. После достижения скорости и высоты ускоритель падает, и дрон D-21 начинает свою шпионскую миссию.

После более чем года тестовых запусков с базового корабля B-52 дрон D-21 был готов к своим первым боевым вылетам над Красным Китаем. Президент Никсон одобрил первый разведывательный полет на 9 ноября 1969 года.Миссия была запущена с авиабазы ​​Бил в Калифорнии.

Несмотря на успешный запуск, беспилотник Д-21 был утерян. В середине 1972 года после четырех попыток облететь Красный Китай с помощью беспилотника D-21 и четырех неудачных миссий программа была отменена. Это было творчески. Это было новаторски. Это было гениально. Но это было невозможно.

Так закончился один из самых амбициозных и возмутительных шпионских проектов в истории.

1604 Часов. 20 декабря 2009 года. На заднем дворе музея авиакосмического пространства Пима за пределами Тусона, штат Аризона.

Я гладлю самолеты, когда могу. Я не совсем уверен, почему, возможно, чтобы сказать, что сделал. Может быть, чтобы попытаться осязать их историю. Может быть, поглотить что-нибудь из них, если такое возможно. Может быть, чтобы, когда я состарюсь и умираю, я смогу вспомнить, каково было стоять рядом с ними и трогать их. Я не знаю, почему я прикасаюсь к ним и глажу их, но знаю.

Полностью отреставрированный дрон Lockheed D-21 в Музее авиакосмической авиации Пима, недалеко от Тусона, штат Аризона.

(фото из Музея космонавтики в Пиме)

D-21 пыльное и теплое в лучах дневного аризонского солнца. Его титановая оболочка тверда, не прощает ошибок, как алюминиевый самолет. Он ничего не дает. Тихий. Задумчивый. После того, как я прикоснулся к нему, с моей руки отошла пыль. Я не вытираю.

Когда-нибудь в ближайшие годы дрон D-21B, номер 90-0533, будет доставлен в обширное реставрационное здание Музея авиакосмоса Пима и прекрасно отреставрирован.Сейчас он находится в государстве, выставлен в музее.

Но когда я впервые нашел его брошенным на складе, пыльным и запекавшимся под солнцем пустыни Сонора, мне показалось, что в его теплой титановой коже все еще есть какая-то тайная жизнь.

Эта статья впервые появилась на сайте The Aviationist. Подпишитесь на @theaviationist в Twitter.

Подробнее о We are the Mighty

изображений полигонов

Мы получили множество отличных решений этой проблемы, поэтому спасибо Питеру из Даремской школы Джонстон в Дареме, Тому, Ронану, Карми, Нардиа, Брин, Джастину, Вивеку, Прие, Адену, Тегану и Люси из Школа Святого Стефана Каррамар в Австралии, Алекс из Межобщинной школы Цюриха в Швейцарии, Махди из Международной школы Махатмы Ганди в Индии и Беркли из начальной школы Мэри Хоган в США за то, что прислали нам свои решения. \ circ $.

Махди прислал нам это подробное и ясное объяснение того, как найти все углы на диаграмме пятиугольника.

Итак, вы хотите знать о пятиугольниках?

В геометрии учащиеся работают с множеством различных форм. Один из самых важных полигонов, с которым нужно познакомиться, — это пятиугольник.

7 фактов о пятиугольниках, которых вы могли не знать

1. У всех пятиугольников пять прямых сторон, но стороны не обязательно должны быть одинаковой длины.
2. У правильного пятиугольника пять равных сторон и пять равных углов. В базовой геометрии большинство проблем связаны с правильными многоугольниками.
3. Каждый внутренний угол правильного пятиугольника = 108 градусов.
4. Каждый внешний угол правильного пятиугольника = 72 градуса.
5. Сумма внутренних углов правильного пятиугольника = 540 градусов.
6. Проведение диагональных линий между точками пятиугольника приведет к идеальной форме звезды или пентаграммы.
7. Если пять сторон фигуры НЕ соединены или у фигуры есть изогнутые стороны, это НЕ пятиугольник.

Типы пятиугольников

1. Правильный или равносторонний пятиугольник: пять равных сторон и углов
2. Неправильный пятиугольник: пять неравных сторон и неравные углы
3. Выпуклый пятиугольник: внутренний угол не может превышать 180 градусов
4. Вогнутый пятиугольник: имеет внутренний угол более 180 градусов, из-за чего две стороны «погружаются», как «пещера».

Части пятиугольника

1. Сторона: один из пяти отрезков линии
2. Вершина: две стороны встречаются в точке, называемой вершиной
3. Диагональ: линия, соединяющая две вершины, не являющиеся одной из пяти сторон
4. Внутренний угол : внутренний угол, образованный двумя сторонами пятиугольника
5. Внешний угол : угол на внешней стороне пятиугольника, образованный двумя смежными сторонами

Как рассчитать площадь пятиугольника

1. Начало с одной стороны и апофемы *
2. Разделите пятиугольник на 5 треугольников, проведя 5 линий из центра пятиугольника
3. Вычислить площадь треугольника **
4. Умножьте на 5, чтобы найти общую площадь

* Апофема — это линия от центра пятиугольника к стороне, пересекающая сторону под прямым углом 90º.

** Запомните формулу для вычисления площади треугольника: ½ x основание x высота

Пентагоны — несколько забавных фактов

Почему Пентагон — это пятиугольник: Штаб-квартира Министерства обороны США в Вашингтоне, округ Колумбия, называется Пентагоном. Это массивное здание из бетона и стали имеет общую площадь почти 7 миллионов квадратных футов и 17,5 миль коридоров. В начале Второй мировой войны в 1941 году президент Рузвельт решил, что для Военного департамента необходимо новое здание.

Архитектор решил воспользоваться свойствами симметричного пятиугольника. Это сократило расстояние, которое люди должны были бы пройти от одного офиса к другому в этом огромном здании, по сравнению с традиционным прямоугольным зданием. Круглое здание также должно было включать более короткие пешеходные расстояния, но построить здание с прямыми сторонами, такими как пятиугольник, было намного проще и быстрее.

Бамия: В следующий раз, когда вы будете есть жареную окра или гамбо, обратите внимание на ломтик бамии.Он имеет форму пятиугольника.

Морская звезда: Почти все морские звезды имеют пятикратную радиальную симметрию или имеют форму пятиугольника.

Поэзия: На самом деле существует нечто, известное как поэзия пятиугольника.

Музыкальные пятиугольники: Если вам нравится музыка 1980-х годов, обратите внимание на группу Pentagon Band Рича Клэра. Для чего-то другого, в Южной Корее есть бойз-бэнд под названием Pentagon.

Как видите, пятиугольник — очень полезная форма. Мало того, что пятиугольник часто используется в базовой геометрии, это форма, полезная в архитектуре и встречающаяся во всем мире природы.

Есть кое-что о пятиугольниках |

В прошлом месяце исследователи Кейси Манн, Дженнифер Маклауд и Дэвид фон Дерау из Вашингтонского университета Ботелл обнаружили новый пятиугольник, который облицовывает самолет, и толпа обезумела. Исследовательской математике сложно получить освещение в новостях, но этот отважный маленький пятиугольник был идеальной историей для СМИ. Всем нравятся формы, и они понимают, что значит выложить плитку на плоскости. У задачи также есть интересная история, и это хороший способ показать людям, как думают математики: как только мы отвечаем на вопрос в одном контексте, скажем, для правильных многоугольников, мы видим, что меняется при изменении контекста.

Представители 15 типов пятиугольников, покрывающих плоскость. Самый новый находится в правом нижнем углу. Изображение: Эд Пегг-младший, через Wikimedia Commons.

Несколько хороших математиков написали историю маленького пятиугольника, который мог. Алекс Беллос написал об этом для Guardian, у NPR была хорошая статья Эйдера Перальты, Кевин Кнудсон написал об этом пост в своей недавно запущенной колонке Forbes, Кэти Стеклес осветила это для Aperiodical, а Робби Гонсалес написал небольшой пост для io9. .

В некоторых новостях упускается из виду тот факт, что большинство пятиугольных мозаик — это не отдельные пятиугольники, которые работают, а бесконечные семейства пятиугольников, поэтому существует бесконечно много пятиугольников, а не только 15. Это тонкий момент, но тот, который вызвал небольшая путаница. К счастью, в Wolfram есть интерактивная демонстрация различных типов мозаик, которая помогает прояснить ситуацию. У Решана Ричардса также есть пятиугольный тайловый модуль в своем приложении Explain Everything. (У меня нет «Объяснить все», поэтому мое упоминание об этом здесь не является одобрением или обзором.)

Вопрос о пятиугольных мозаиках — это два вопроса в одном: какие пятиугольники могут мозаить плоскость и как они могут мозаить плоскость? Другими словами, это различие между плитками и плитками. Текущее открытие связано с новой плиткой, другой формой, покрывающей плоскость. У Фрэнка Моргана есть пост по другому вопросу: как можно расположить плитки в мозаику? В частности, он наставлял студентов бакалавриата, изучающих мозаики, состоящие из двух различных пятиугольных плиток. В посте полно изображений этих двух плиток во всевозможных разных узорах плитки с такими названиями, как Рождественская елка, Зубастая улыбка и Космические пилюли. В статье AMS его группы об их работе (pdf) есть еще больше иллюстраций.

Впервые я узнал об истории пятиугольных плиток, когда Мат Мунк написал о Марджори Райс в 2013 году. Райс, одно из громких имен в области пятиугольных плиток, не был математиком, но узнал о проблеме из статьи Мартина Гарднера в Scientific American .Редко, когда настоящие любители совершают прорывы в исследовательской математике, но она открыла четыре новых класса пятиугольников, покрывающих плоскость, и ее история трогательна и вдохновляет. Иварс Петерсон, турист-математик, написал о ней и о том, как облицован вход в MAA.

Пока я исследовал этот пост, я наткнулся на другую статью Петерсона о пятиугольниках и мозаиках. Это о парадоксальном куполе Биосферы в Монреале. Это купол, поэтому скорее сферический, чем плоский, но он, кажется, выложен правильными шестиугольниками.«Откуда искривление?» — спрашивает Петерсон. «Я знаю, что пятиугольники есть, и я пытался их найти, но мне не удалось найти даже один».

Интересно, нашли ли мы все пятиугольные плитки или кому-то еще удастся найти еще одну.

полигонов — математика для учителей начальных классов

Может показаться, что изучение геометрии в начальной школе — это не что иное, как изучение множества определений и последующей классификации объектов.В этой части вы исследуете некоторые действия по решению проблем и рассуждению, основанные на геометрии. Но определения по-прежнему важны! Итак, начнем с этого.

Определение

Полигон равен:

1. плоская фигура
2. , ограниченный конечным числом отрезков прямых
3. , в котором каждый сегмент встречается ровно с двумя другими, по одному на каждой из своих конечных точек.

Думать / Пара / Поделиться

Точно так же, как первый шаг в решении проблемы — это понять проблему, первый шаг в чтении математического определения — это понять определение.

• Используйте определение выше, чтобы нарисовать несколько примеров фигур, которые определенно являются многоугольниками. (Вы должны быть в состоянии сказать, почему ваш пример подходит под определение.)
• Нарисуйте также несколько не-примеров: фигуры, которые определенно не являются многоугольниками. (Вы должны быть в состоянии сказать, какая часть определения не соответствует вашим примерам.)

Несколько комментариев о полигонах:

• Сегменты линии, составляющие многоугольник, называются его ребрами , а точки, где они встречаются, называются его вершинами (особая: вершина ).
• Из-за свойств (2) и (3) в определении границы многоугольников не являются самопересекающимися.

Не многоугольник.

• Многоугольники именуются в зависимости от количества сторон, которые у них есть.

название	Кол-во сторон	примеров
треугольник	3
четырехугольник	4
пятиугольник	5
шестигранник	6
семиугольник	7
восьмиугольник	8
неугольник	9
декагон	10

• В общем, мы называем многоугольник со сторонами n n-угольником n .

Задача 6

На рисунках ниже многоугольники скрыты в дизайне. В каждом дизайне найдите все треугольники, четырехугольники, пятиугольники и шестиугольники. Как вы можете быть уверены, что нашли их все и не пересчитали дважды?

Вы знаете, что сумма внутренних углов в любом треугольнике равна 180 °. Что вы можете сказать об углах в других многоугольниках?

Вы, наверное, знаете, что у прямоугольников четыре угла по 90 °.Итак, , если все четырехугольники имеют одинаковую сумму внутренних углов , она должна быть 360 ° (поскольку 4 × 90 ° = 360 °).

Но обратите внимание: у нас нет никаких оснований полагать, что эта постоянная сумма верна. Помните, что сравнение SSS верно для треугольников, но не для любых других многоугольников. Треугольники особенные, и мы не должны предполагать, что истинные утверждения о треугольниках будут верны и для других форм.

Думать / Пара / Поделиться

Любой четырехугольник можно разделить на два треугольника, все вершины которых совпадают с вершинами четырехугольника:

Используйте изображения выше, чтобы внимательно объяснить, почему все четырехугольники действительно имеют сумму углов 360 °.

Самостоятельно

Работайте над следующими упражнениями самостоятельно или с партнером.

1. Нарисуйте на бумаге несколько разных пятиугольников. Покажите, что каждый из них можно разбить ровно на три треугольника таким образом, чтобы все вершины треугольников совпадали с вершинами пятиугольника.
2. Воспользуйтесь тем фактом, что каждый пятиугольник можно разделить на три треугольника, чтобы найти сумму углов в любом пятиугольнике.
3. Нарисуйте на бумаге несколько разных шестиугольников.Покажите, что каждый из них можно разбить ровно на четыре треугольника так, чтобы все вершины треугольников совпадали с вершинами шестиугольника.
4. Воспользуйтесь тем фактом, что каждый шестиугольник можно разделить на четыре треугольника, чтобы найти сумму углов в любом шестиугольнике.

Проблема 7

Используйте свою работу над упражнениями выше, чтобы завершить это общее утверждение:

Сумма углов в многоугольниках

Сумма внутренних углов n-угольника (многоугольника с n сторонами) равна

__________________________.