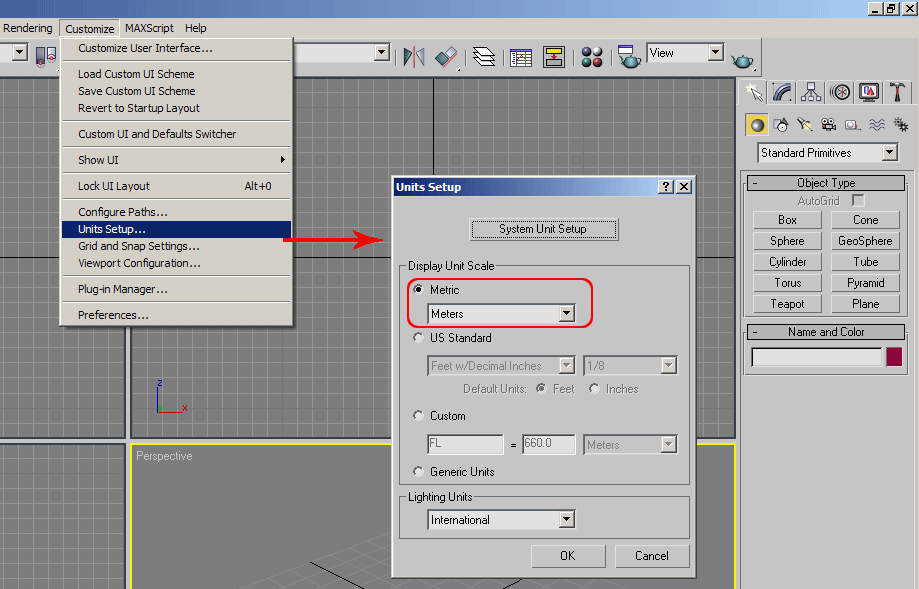
Не удается найти страницу | Autodesk Knowledge Network
(* {{l10n_strings.REQUIRED_FIELD}})
{{l10n_strings.CREATE_NEW_COLLECTION}}*
{{l10n_strings.ADD_COLLECTION_DESCRIPTION}}
{{l10n_strings.COLLECTION_DESCRIPTION}} {{addToCollection.description.length}}/500 {{l10n_strings.TAGS}} {{$item}} {{l10n_strings.PRODUCTS}} {{l10n_strings.DRAG_TEXT}}{{l10n_strings.DRAG_TEXT_HELP}}
{{l10n_strings.LANGUAGE}} {{$select.selected.display}}{{l10n_strings.AUTHOR_TOOLTIP_TEXT}}
{{$select.selected.display}} {{l10n_strings.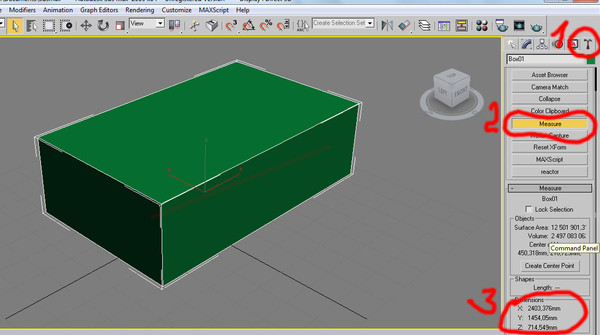
Панель Utilities в 3ds Max и что она умеет
Панель Utilities содержит в себе множество полезных инструментов. Некоторые из них устанавливаются в виде плагинов, поэтому их количество не всегда одинаково. Вся панель состоит из одного раздела, который можно изменять.
1. Выбор инструментов.
Кнопка More… открывает окно со всеми доступным утилитами. Выделив какой-либо инструмент и нажав OK, откроются его настройки под панелью Utilities.
При нажатии на любую кнопку, вынесенную на панель, ее функции откроются сразу. Но вынесенные на панель Utilities инструменты будут отсутствовать в окне More. То есть в двух меню один и тот же инструмент быть не может.
2. Конфигурация
Изменить наполнение панели можно с помощью кнопок Sets и Configurate Button Sets
. Sets открывает выбор уже созданных наборов.
Configurate Button Sets открывает окно настройки всей панели и создания наборов. В строку Sets вводится название нового набора, который можно сохранить кнопкой Save. Существующие наборы можно удалить кнопкой Delete. Total Buttons определяет, сколько кнопок и, следовательно, сколько инструментов будет в наборе. Из левого окна Utilities на созданные кнопки перетаскиваются инструменты.
Заполнив кнопки инструментами, набор необходимо сохранить указанным выше образом. После этого его можно будет установить кнопкой
3.
 Набор Max Default
Набор Max DefaultPerspective Match – позволяет настраивать перспективу сцены, ориентируясь на фоновое изображение. Настройка осуществляется с помощью нескольких отрезков, которые нужно выставить по ориентирам на картинке. Включить и отключить линии можно кнопкой Hide Vanishing Lines.
Отрезки и их точки можно только перемещать. Никакие стандартные инструменты перемещения при этом не работают.
Collapse – позволяет превратить один или несколько объектов в Editable Mesh. В зависимости от настроек, несколько объектов модно конвертировать в один, раздельно, применить Boolean.
Color Clipboard – позволяет точно копировать цвета материалов и переносить его на другой материал. Для этого нужно взять цветное окно в настройках материала и перетащить на панель Color Clipboard. Чтобы назначить цвет другому материалу нужно сделать то же самое в обратной последовательности.
Measure – измеряет основные размеры объекта. Измерение осуществляется не для самого объекта, а габаритного контейнера. Показывает площадь, объем, координаты центра масс и размер по каждой из осей.
А если нужно измерить длину на части сложного объекта, стоит воспользоваться инструментом Tape, описанным в статье «Объекты-помощники Helpers в 3ds Max»
Motion Capture – позволяет управлять анимацией с помощью периферийных устройств и записывать ее в режиме реального времени.
Reset XForm – превращает вращение и масштабирование объекта в модификатор XForm. Благодаря этой утилите (модификатору) можно легко отменять последние перемещения или переносить их на другие объекты.
MAXScript – позволяет писать и запускать сценарии для 3ds Max. Для использования этой утилиты желательно предварительно научиться программировать. Однако скрипты бывают очень полезны. Хороший скрипт может сильно упростить и ускорить моделирование, что хорошо видно в статье «Скрипты для ускорения моделирования в 3ds Max».
Flight Studio (c) – с помощью этой утилиты можно редактировать объекты формата
Базовый набор утилит содержит как полезные инструменты, так и не очень. Каждый пользователь 3ds Max может настроить окно утилит под себя и иметь к ним быстрый доступ. Со временем количество доступных утилит может увеличиться за счет установки плагинов и скриптов. Поэтому удобство панели зависит исключительно от ваших настроек.
Определите зеленые линии на этом изображении и вычислите их длину
Примеры Изображений
Изображение может быть более шумным в те моменты, когда на заднем плане появляется больше объектов. Прямо сейчас я использую различные методы, использующие цветовое пространство RGB, чтобы обнаружить линии, но это не удается, когда происходит изменение цвета из-за промежуточных препятствий со стороны фона. Я использую opencv и python. Я читал, что HSV лучше подходит для определения цвета и используется, но пока не добился успеха. Я не могу найти общего решения этой проблемы. Любые намеки или подсказки в этом направлении были бы очень полезны.
Поделиться Источник Abhyudai 25 июля 2016 в 14:06
2 ответа
- OpenCV определите линии на этом изображении
Я не могу применить преобразование HoughLines из OpenCV к изображению, которое я публикую.

- Удаление линии из изображения
Я использовал преобразования Хафа для обнаружения прямых линий на изображении. Функция houghlines возвращает конечные точки линий, которые можно построить. Однако я хочу удалить обнаруженную линию из изображения, создав черную линию на изображении шириной в два пикселя. Вот примерный график линии…
1
Вы должны использовать тот факт, что вы знаете, что пытаетесь обнаружить линию с помощью преобразования линии Хафа. http://docs.opencv.org/2.4/ doc/tutorials/imgproc/imgtrans/hough_lines/hough_lines.html
- Когда препятствие также выглядит как линия, используйте тот факт, что вы примерно знаете, какова ориентация зеленых линий.
- Если вы не знаете ориентацию линии используйте тот факт что есть несколько зеленых линий с одинаковой ориентацией и только одна линия которая является препятствием
Вот код того, что я имел в виду:
import cv2
import numpy as np
# Params
minLineCount = 300 # min number of point alogn line with the a specif orientation
minArea = 100
# Read img
img = cv2.imread('i.png')
greenChannel = img[:,:,1]
# Do noise reduction
iFilter = cv2.bilateralFilter(greenChannel,5,5,5)
# Threshold data
#ret,iThresh = cv2.threshold(iFilter,0,255,cv2.THRESH_BINARY+cv2.THRESH_OTSU)
iThresh = (greenChannel > 4).astype(np.uint8)*255
# Remove small areas
se1 = cv2.getStructuringElement(cv2.MORPH_RECT, (5,5))
iThreshRemove = cv2.morphologyEx(iThresh, cv2.MORPH_OPEN, se1)
# Find edges
iEdge = cv2.Canny(iThreshRemove,50,100)
# Hough line transform
lines = cv2.HoughLines(iEdge, 1, 3.14/180,75)
# Find the theta with the most lines
thetaCounter = dict()
for line in lines:
theta = line[0, 1]
if theta in thetaCounter:
thetaCounter[theta] += 1
else:
thetaCounter[theta] = 1
maxThetaCount = 0
maxTheta = 0
for theta in thetaCounter:
if thetaCounter[theta] > maxThetaCount:
maxThetaCount = thetaCounter[theta]
maxTheta = theta
# Find the rhos that corresponds to max theta
rhoValues = []
for line in lines:
rho = line[0, 0]
theta = line[0, 1]
if theta == maxTheta:
rhoValues.
append(rho)
# Go over all the lines with the specific orientation and count the number of pixels on that line
# if the number is bigger than minLineCount draw the pixels in finaImage
lineImage = np.zeros_like(iThresh, np.uint8)
for rho in range(min(rhoValues), max(rhoValues), 1):
a = np.cos(maxTheta)
b = np.sin(maxTheta)
x0 = round(a*rho)
y0 = round(b*rho)
lineCount = 0
pixelList = []
for jump in range(-1000, 1000, 1):
x1 = int(x0 + jump * (-b))
y1 = int(y0 + jump * (a))
if x1 < 0 or y1 < 0 or x1 >= lineImage.shape[1] or y1 >= lineImage.shape[0]:
continue
if iThreshRemove[y1, x1] == int(255):
pixelList.append((y1, x1))
lineCount += 1
if lineCount > minLineCount:
for y,x in pixelList:
lineImage[y, x] = int(255)
# Remove small areas
## Opencv 2.4
im2, contours, hierarchy = cv2.findContours(lineImage,cv2.RETR_CCOMP,cv2.CHAIN_APPROX_NONE )
finalImage = np.zeros_like(lineImage)
finalShapes = []
for contour in contours:
if contour.size > minArea:
finalShapes.append(contour)
cv2.fillPoly(finalImage, finalShapes, 255)
## Opencv 3.0
# output = cv2.connectedComponentsWithStats(lineImage, 8, cv2.CV_32S)
#
# finalImage = np.zeros_like(output[1])
# finalImage = output[1]
# stat = output[2]
# for label in range(output[0]):
# if label == 0:
# continue
# cc = stat[label,:]
# if cc[cv2.CC_STAT_AREA] < minArea:
# finalImage[finalImage == label] = 0
# else:
# finalImage[finalImage == label] = 255
# Show image
#cv2.imwrite('finalImage2.jpg',finalImage)
cv2.imshow('a', finalImage.astype(np.uint8))
cv2.waitKey(0)
и результат для изображений:
Поделиться Amitay Nachmani 26 июля 2016 в 23:01
1
ВСЕ ЕЩЕ ПРОДОЛЖАЕТСЯ
Прежде всего, изображение RGB состоит из 3 изображений в оттенках серого. Поскольку вам нужен зеленый цвет, вы будете иметь дело только с одним каналом. Тот, зеленый. Для этого вы можете разделить изображение, вы можете использовать
Поскольку вам нужен зеленый цвет, вы будете иметь дело только с одним каналом. Тот, зеленый. Для этого вы можете разделить изображение, вы можете использовать b,g,r = cv2.split('Your Image') . Вы получите такой вывод, если будете показывать зеленый канал:
После этого вы должны пороговать изображение, используя желаемый способ. В данном случае я предпочитаю Otsu's thresholding . Выход после порогового значения равен:
Очевидно, что пороговое изображение чрезвычайно шумно. Таким образом, выполнение erosion немного уменьшит шум. Изображение с уменьшенным шумом будет выглядеть следующим образом:
Я попробовал использовать closing вместо dilation , но closing сохраняет некоторый нежелательный шум. Поэтому я отдельно выполнил erosion , а затем dilation . После dilation вывод будет следующим:
Обратите внимание, что : Вы можете сделать свой собственный путь в морфологической операции. Вы можете использовать opening вместо того, что я сделал. Результаты субъективны от
одного человека к другому.
Теперь вы можете попробовать один из этих двух методов:
1. Обнаружение Больших Двоичных Объектов. HoughLine трансформация.
TODO
Попробуйте эти два метода и выберите лучший.
Поделиться Tes3awy 27 июля 2016 в 21:49
Похожие вопросы:
Как измерить длину линии, которая нарисована на изображении в java?
Я делаю приложение на платформе netbeans в java с использованием технологии Swing для стоматолога. я хочу измерить длину линии, которая рисуется пользователем на изображении зубов? Итак, тогда врач. ..
..
3ds max визуализированное изображение-зеленые линии по краям
Я пытаюсь текстурировать сцену на Autodesk 3ds max, что я делаю: Выберите объект и добавьте модификатор Unwrap UVW Выберите все грани и откройте УФ редактор Сгладить сопоставления шаблона и…
вычислите длину строки с помощью toString
Мне нужно реализовать классы Point и Line Метод toString точки должен выводить точку в виде (x,y) Метод toString линии должен выводить точку в виде (x1,y1)->(x2,y2) Затем мне нужно создать класс под…
OpenCV определите линии на этом изображении
Я не могу применить преобразование HoughLines из OpenCV к изображению, которое я публикую. Все линии должны быть ориентированы на 15 градусов, но это приводит к большому количеству линий в…
Удаление линии из изображения
Я использовал преобразования Хафа для обнаружения прямых линий на изображении. Функция houghlines возвращает конечные точки линий, которые можно построить. Однако я хочу удалить обнаруженную линию…
Плиточный редактор карт, зеленые линии на столкновениях
Я работаю над картой в Редакторе плиточных карт. Когда я запускаю игру, мой игрок стоит на границе столкновений, которые я сделал с объектом Rectangel. Это хорошо. Но я не хочу, чтобы зеленые линии…
Зеленые линии в видео GStreamer
я использую Gstreamer 1.0 для воспроизведения видео, и у меня есть пользовательская область, установленная для показа видео gst_video_overlay_set_window_handle . Проблема в том, что в некоторых…
создайте красные и зеленые точки На изображении
Я добавляю свой код здесь. У меня есть таблица с именем points, с полями id,name и status. значения имеют статус 0 и 1 Если значение имеет статус 1,то покажите его в виде зеленой точки Если значение…
Как сгладить линии на изображении?
Есть ли способ с помощью OpenCV сгладить края, как показано на этом маленьком черно-белом изображении? Я попробовал cv2. blur и cv2.GaussianBlur , но это просто размывает изображение. Я хочу сгладить…
blur и cv2.GaussianBlur , но это просто размывает изображение. Я хочу сгладить…
Вертикальные синие, зеленые или серые линии в Android Studio
Я вижу эти вертикальные синие и зеленые линии на правой границе Android Studio: Что означают эти строки? Есть ли способ удалить их, так как они немного раздражают. Я не помню, чтобы видел их в…
Как проставить реальные размеры скатов крыши в ArchiCAD. Уроки ArchiCAD
Давно уже обещал какой-нибудь урок по поводу размеров и разверток крыш в ArchiCAD. С развертками пока ничего не придумал, кроме как рисовать вручную, а вот с размерами оказалось проще.
Всем известно, что размеры объектов в ArchiCAD в 3D не показываются. Чтобы обойти это досадное недоразумение, в Graphisoft в конце-концов придумали так называемые 3D-документы, в которых можно рисовать линии, ставить размеры прямо по трехмерной модели здания. Использование таких 3D-документов — это пока что единственный способ узнать реальные длины наклонных ребер кровли, поскольку на плане мы видим только проекцию на горизонтальную плоскость.
Порядок действий по простановке размеров несложен и выглядит примерно так.
Открываем нашу кровлю в 3D окне
Перспектива или аксонометрия — это дело вкуса, на сами размеры никак не влияет. Только учтите, что в перспективном виде некоторые размеры могут выглядеть не параллельными измеряемым ребрам.
Сохраняем как 3D-документ
В навигаторе выбираем папку 3D-документы, щелкаем на кнопке «Новый взгляд» в нижней части навигатора.
Меняем параметры отображения
Это можно сделать и потом, но я сразу поменял опции модельного вида на «05 Планы потолков», чтобы отключить показ штриховки, и заменил набор перьев на гостовский, чтобы сразу все линии стали черными.
Выбираем инструмент Линейный размер
Поменяйте параметр «Геометрический вариант» на «Любая плоскость», чтобы появилась возможность сразу выравнивать размеры в родной для ската плоскости.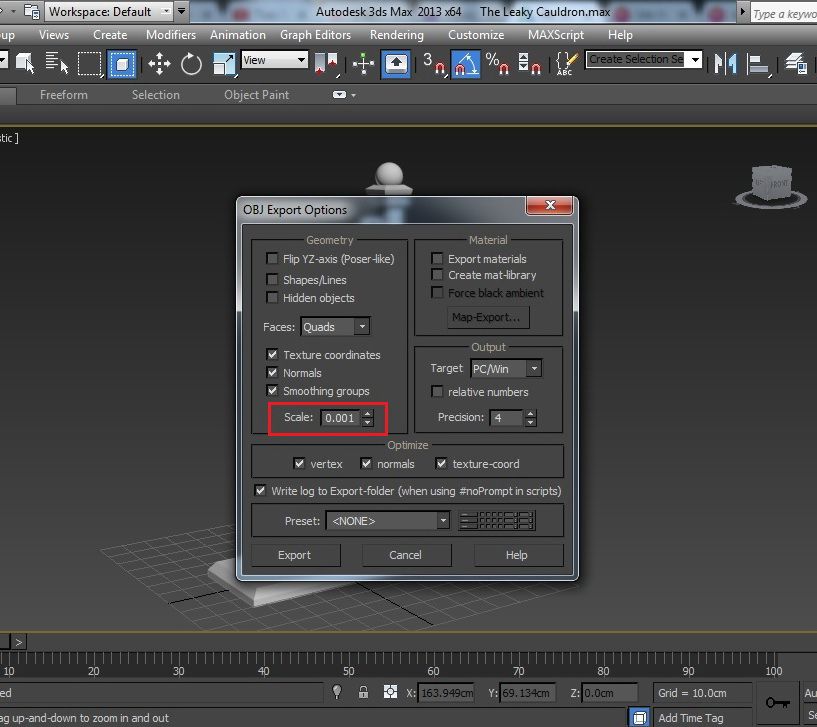
Ставим размер
Щелчками мыши поставьте размерные точки на концах измеряемого ребра и сделайте двойной щелчок. Курсор как обычно превратится в молоточек, которым надо щелкнуть по скату кровли, чтобы выбрать плоскость для размера.
Следующим щелчком ставим размер где-нибудь рядом.
Выравниваем
Выберите размер инструментом «Указатель», в появившейся локальной панели выберите «Выравнивание размерной линии», наведите курсор на ребро ската и выполните щелчок мышью.
Передвиньте этот и другие проставленные размеры поближе к измеряемому объекту.
Texel density. Зачем нужен и как его применять / Хабр
Эта статья предназначена 3d художникам, техническим художникам, а также всем разработчикам, которые связаны с 3д графикой, текстурами и составлением технических заданий. В ней я покажу чем может быть полезно следование одному текселю, как его считать и на что он может влиять. Основные действующие лица — чеккер, модели, текстуры, мыльцо, UV и прочие радости разработки 3d контента.0. Что такое texel density.
Для начала, что такое тексель. Texel (аббревиатура от двух слов «TEXture» и «ELement» — текстура и элемент) — элемент текстуры, «точка». Текстура, в свою очередь, представляет собой массив текселей. Тексель может представлять собой цветную точку в изображении. Но, поскольку, текстура может быть не только изображением (двумерным массивом цветных точек), а также и другими массивами данных различных типов и размерности, то тексель, как текстурный элемент — более общее понятие.
Texel density (текселерация, тексель (сокращенно, в контексте)) — это величина, которая является отношением размера текстуры (в пикселях) к габаритам 3d модели в сцене. Texel density характеризует плотность, «качество» текстуры, в общем смысле. Выглядит в техзадании примерно так: 256px/m, 128px/inch, и так далее. Таким образом, текселерация определяет какая площадь текстуры будет отдана на модель исходя из ее размеров. Высокий texel density означает большую детализацию текстуре, низкий — меньшую, размытую текстуру.
Высокий texel density означает большую детализацию текстуре, низкий — меньшую, размытую текстуру.
1. Применимость texel density.
Наибольшее значение работа с текселерацией имеет при работе с окружением. Это связано с тем, что в окружение чаще используются тайленные текстуры, текстурные атласы и на объекты окружения редко выделяют отдельные карты (на пропсы, разве что). Например, к персонажам, абсолютная текселерация не имеет такого важного значения, т.к. в основном, все персонажи имеют схожие физические размеры. В техзадании на персонажа вполне может быть такое: использовать 2 сета текстур, 2048*2048 для тела, 1024*1024 для головы, и задача художника выжать максимальный тексель, правильно сделав UV развертку. Для элементов окружения, обычно указывают абсолютный тексель (например, 256px/m), т.к. они сильно разнятся по размерам (стена дома, автомобиль, дорога, почтовый ящик).
2. Относительная и абсолютная текселерация
Деление условное, но, думаю, будет полезно сделать на этом акцент. Существует относительная текселерация (в пределах одной модели) и абсолютная — в пределах всей игрых/сцены.
Относительная текселерация должна удовлетворять следующим требованиям:
Единый texel density по всей модели (допускается незначительное увеличение текселя на мелких деталях UV) Из этого правила есть ряд исключений: важные детали должны занимать больше места на развертке (и на текстуре), например лицо персонажа должно иметь больший texel density. Те детали, которые не видны или плохо видны должны иметь меньший тексель (например, днище автомобиля, подошвы ботинок у персонажа).
Максимально возможная текселерация на уникальных моделях. Это общее требование к качеству, упомянутое выше.
Пример хорошей и плохой текселерации (Источник: quixel.se/tutorial/uv-mapping-for-the-suite)
Пример исключения. Обратите внимание на разницу между четкостью текстур на лице и одежде — и это правильно, т.к. внимание игрока больше направленно на лицо, а не на одежду. (Источник: Fallout 4)
(Источник: Fallout 4)
3. Как рассчитывается texel density
Тексель рассчитывается очень просто: необходимо знать размер геометрии и разрешение текстуры, а потом поделить разрешение текстуры на размер геометрии.
Посмотрите на иллюстрацию. Тут изображен куб размерами 1м*1м и плоскости разных размеров. На все объекты применена текстура 1024*1024 пикселей, соответственно, мы имеем следующие texel density для объектов, слева направо: 512px/m, 1024px/m, 2048px/m. Используется только одна текстура, но объекты разные по размерам и, следовательно, мы получаем разный texel density.
Также 3d художники используют различные скрипты и инструменты для подсчета texel density. Помимо показанного выше способа подсчета (т.е. создание специальной эталонной текстуры и подгонки вручную «под квадратики»), существую ряд скриптов для измерения и установки нужного texel density:
3ds Max
Advanced UV Normalizer
Textools
Maya
Nightshade UV
UV Deluxe
Blender
UPD: Texel Density Checker:
mrven.ru/2017/03/update-my-blender-add-on-texel-density-checker-1-0-1
4. Как можно привести ассеты к одной плотности?
1. Редактирование UV, использование тайлов
Слева направо: увеличена развертка UV в два раза, без изменений, уменьшена в 2 раза. Таким образом на иллюстрации все объекты имеют один texel density равный 1024px/m.
2. Изменения размера текстур
Для большого объекта использована большая текстура, для меньшего — меньшая.
3. Изменения размеров объекта. Да, таким образом можно повлиять на texel density, но на практике никто ведь не будет делать автомобиль меньше в два раза лишь оттого, что по texel density не хватает плотности текстуры?
5. Как использовать texel density, выводы и полезные советы
1. Начните с правильных размеров.
В движке, в редакторе, следует установить эталонный масштаб и единицы измерения.
 Это следует сделать в самом начале разработки и придерживаться до конца.
Это следует сделать в самом начале разработки и придерживаться до конца.2. В документации попробуйте определить важность ассетов и соответственно, качество текстур для них. Ассеты первого плана (например, оружие, руки в FPS, персонаж в TPS, вблизи глаз VR приложения), предметы важные для геймплея (например, броня в Fallout 4, верстак, HL2 аптечка на стене и т.д.), предметы окружения и предметы дальнего плана. Тут не помешает сделать тесты прямо в движке с эталонными текстурами, прикинуть как это будет смотреться. Для каждого типа ассета можно использовать собственный texel density.
3. Продолжать следовать этим значениям и при постановке задачи указывать их в ТЗ.
Следование одному texel density для предметов схожих планов и одной значимости даст возможность сделать арт игры более цельным, из него не будут выпадать отдельные элементы в стиле «Вы плохо прорисованы, вас скоро убьют». Также, при использовании этого подхода, будет меньше вероятность потратить ресурсы нерационально (в симуляторе машиниста, на костыли ЖД полотна использовать текстуры 1024*1024, например).
4. Пока я писал черновик Leonardo Iezzi сделал отличный урок по texel density. Обязательно ознакомьтесь со статьей Leonardo, если данная тема интересна.
Как определить параметры созданного объекта
Примитивы и их параметры в Maya®
Простейший способ создать трехмерный объект в Maya® — воспользоваться подходящим примитивом. Создавать и редактировать объекты можно в любой проекции, но некоторые возможности редактирования в разных проекциях отличаются друг от друга. Принцип создания любого примитива в Maya одинаков — достаточно указать нужный примитив на панели Shelf или в меню Create и растянуть его до нужных размеров.
Любой объект может состоять из большего или меньшего числа составных элементов, а значит, иметь разный уровень детализации, от чего зависит его внешний вид в окне проекций. В Maya® предусмотрено три варианта детализации: низкая, средняя или высокая — выбор нужного варианта осуществляется путем нажатия клавиш 1, 2 и 3 соответственно.
В Maya® предусмотрено три варианта детализации: низкая, средняя или высокая — выбор нужного варианта осуществляется путем нажатия клавиш 1, 2 и 3 соответственно.
Каждый созданный объект имеет имя и обладает некоторыми параметрами. Под параметрами объекта понимается набор свойств, описывающих объект в трехмерном пространстве, например его координаты, длина, ширина и высота.
Параметры могут задаваться в процессе создания объекта в окне опций либо затем корректироваться в окне каналов или в окне редактора атрибутов. Чтобы определить нужные параметры объекта непосредственно в процессе его создания, следует щелкать не на соответствующей объекту строке меню Create, а на расположенном справа от названия типа объекта квадратике. В этом случае перед созданием объекта открывается диалоговое окно с параметрами выбранной команды, в котором можно отредактировать установленные по умолчанию параметры инструмента. Чтобы восстановить исходные параметры создания объектов, воспользуйтесь командой Edit=>Reset Settings из командного меню окна параметров объекта.
Следует отметить, что изменить любые параметры любого объекта можно в любой момент времени, так как в программе запоминаются все этапы их создания и редактирования.
история фракталов и области их применения / Offсянка
Самые гениальные открытия в науке способны кардинально изменить человеческую жизнь. Изобретенная вакцина может спасти миллионы людей, создание оружия, наоборот, эти жизни отнимает. Совсем недавно (в масштабе человеческой эволюции) мы научились «укрощать» электричество — и теперь не можем себе представить жизнь без всех этих удобных устройств, использующих электроэнергию. Но есть и такие открытия, которым мало кто придает значение, хотя они тоже сильно влияют на нашу жизнь.
Одно из таких «незаметных» открытий — фракталы. Вам наверняка доводилось слышать это запоминающееся слово, но знаете ли вы, что оно означает и как много интересного скрыто в этом термине?
В каждом человеке заложена природная любознательность, стремление познавать окружающий его мир. И в этом стремлении человек старается придерживаться логики в суждениях. Анализируя процессы, происходящие вокруг него, он пытается найти логичность происходящего и вывести некоторую закономерность. Самые большие умы на планете заняты этой задачей. Грубо говоря, ученые ищут закономерность там, где ее быть не должно. Тем не менее даже в хаосе можно найти связь между событиями. И эта связь — фрактал.
И в этом стремлении человек старается придерживаться логики в суждениях. Анализируя процессы, происходящие вокруг него, он пытается найти логичность происходящего и вывести некоторую закономерность. Самые большие умы на планете заняты этой задачей. Грубо говоря, ученые ищут закономерность там, где ее быть не должно. Тем не менее даже в хаосе можно найти связь между событиями. И эта связь — фрактал.
Наша маленькая дочь, четырех с половиной лет, сейчас находится в том прекрасном возрасте, когда число вопросов «Почему?» многократно превышает число ответов, которые взрослые успевают давать. Не так давно, рассматривая поднятую с земли ветку, дочка вдруг заметила, что эта ветка, с сучками и ответвлениями, сама похожа на дерево. И, конечно, дальше последовал привычный вопрос «Почему?», на который родителям пришлось искать простое объяснение, понятное ребенку.
Обнаруженная ребенком схожесть отдельной веточки с целым деревом — это очень точное наблюдение, которое лишний раз свидетельствует о принципе рекурсивного самоподобия в природе. Очень многие органические и неорганические формы в природе формируются аналогично. Облака, морские раковины, «домик» улитки, кора и крона деревьев, кровеносная система и так далее — случайные формы всех этих объектов могут быть описаны фрактальным алгоритмом.
⇡#Бенуа Мандельброт: отец фрактальной геометрии
Само слово «фрактал» появилось благодаря гениальному ученому Бенуа Мандельброту (Benoît B. Mandelbrot).
Он сам придумал этот термин в семидесятых годах прошлого века, позаимствовав слово fractus из латыни, где оно буквально означает «ломанный» или «дробленный». Что же это такое? Сегодня под словом «фрактал» чаще всего принято подразумевать графическое изображение структуры, которая в более крупном масштабе подобна сама себе.
Математическая база для появления теории фракталов была заложена за много лет до рождения Бенуа Мандельброта, однако развиться она смогла лишь с появлением вычислительных устройств. В начале своей научной деятельности Бенуа работал в исследовательском центре компании IBM. В то время сотрудники центра трудились над передачей данных на расстояние. В ходе исследований ученые столкнулись с проблемой больших потерь, возникающих из-за шумовых помех. Перед Бенуа стояла сложная и очень важная задача — понять, как предсказать возникновение шумовых помех в электронных схемах, когда статистический метод оказывается неэффективным.
В начале своей научной деятельности Бенуа работал в исследовательском центре компании IBM. В то время сотрудники центра трудились над передачей данных на расстояние. В ходе исследований ученые столкнулись с проблемой больших потерь, возникающих из-за шумовых помех. Перед Бенуа стояла сложная и очень важная задача — понять, как предсказать возникновение шумовых помех в электронных схемах, когда статистический метод оказывается неэффективным.
Просматривая результаты измерений шума, Мандельброт обратил внимание на одну странную закономерность — графики шумов в разном масштабе выглядели одинаково. Идентичная картина наблюдалась независимо от того, был ли это график шумов за один день, неделю или час. Стоило изменить масштаб графика, и картина каждый раз повторялась.
При жизни Бенуа Мандельброт неоднократно говорил, что он не занимается формулами, а просто играет с картинками. Этот человек мыслил очень образно, а любую алгебраическую задачу переводил в область геометрии, где, по его словам, правильный ответ всегда очевиден.
Неудивительно, что именно человек с таким богатым пространственным воображением стал отцом фрактальной геометрии. Ведь осознание сути фракталов приходит именно тогда, когда начинаешь изучать рисунки и вдумываться в смысл странных узоров-завихрений.
Фрактальный рисунок не имеет идентичных элементов, но обладает подобностью в любом масштабе. Построить такое изображение с высокой степенью детализации вручную ранее было просто невозможно, на это требовалось огромное количество вычислений. Например, французский математик Пьер Жозе Луи Фату (Pierre Joseph Louis Fatou) описал это множество более чем за семьдесят лет до открытия Бенуа Мандельбротом. Если же говорить про принципы самоподобия, то о них упоминалось еще в трудах Лейбница и Георга Кантора.
Один из первых рисунков фрактала был графической интерпретацией множества Мандельброта, которое родилось благодаря исследованиям Гастона Мориса Жюлиа (Gaston Maurice Julia).
Гастон Жюлиа (всегда в маске — травма с Первой мировой войны)
Этот французский математик задался вопросом, как будет выглядеть множество, если построить его на основе простой формулы, проитерированной циклом обратной связи. Если объяснить «на пальцах», это означает, что для конкретного числа мы находим по формуле новое значение, после чего подставляем его снова в формулу и получаем еще одно значение. Результат — большая последовательность чисел.
Если объяснить «на пальцах», это означает, что для конкретного числа мы находим по формуле новое значение, после чего подставляем его снова в формулу и получаем еще одно значение. Результат — большая последовательность чисел.
Чтобы получить полное представление о таком множестве, нужно проделать огромное количество вычислений — сотни, тысячи, миллионы. Вручную это сделать было просто нереально. Но когда в распоряжении математиков появились мощные вычислительные устройства, они смогли по-новому взглянуть на формулы и выражения, которые давно вызывали интерес. Мандельброт был первым, кто использовал компьютер для просчета классического фрактала. Обработав последовательность, состоящую из большого количества значений, Бенуа перенес результаты на график. Вот что он получил.
Впоследствии это изображение было раскрашено (например, один из способов окрашивания цветом — по числу итераций) и стало одним из самых популярных изображений, какие только были созданы человеком.
Как гласит древнее изречение, приписываемое Гераклиту Эфесскому, «В одну и ту же реку нельзя войти дважды». Оно как нельзя лучше подходит для трактования геометрии фракталов. Как бы детально мы ни рассматривали фрактальное изображение, мы все время будем видеть схожий рисунок.
Желающие посмотреть, как будет выглядеть изображение пространства Мандельброта при многократном увеличении, могут сделать это, загрузив анимационный GIF.
⇡#Лорен Карпентер: искусство, созданное природой
Теория фракталов скоро нашла практическое применение. Поскольку она тесно связана с визуализацией самоподобных образов, неудивительно, что первыми, кто взял на вооружение алгоритмы и принципы построения необычных форм, были художники.
Будущий сооснователь легендарной студии Pixar Лорен Карпентер (Loren C. Carpenter) в 1967 году начал работать в компании Boeing Computer Services, которая была одним из подразделений известной корпорации, занимающейся разработкой новых самолетов.
В 1977 году он создавал презентации с прототипами летающих моделей. В обязанности Лорена входила разработка изображений проектируемых самолетов. Он должен был создавать картинки новых моделей, показывая будущие самолеты с разных сторон. В какой-то момент в голову будущему основателю Pixar Animation Studios пришла в голову креативная идея использовать в качестве фона изображение гор. Сегодня такую задачу может решить любой школьник, но в конце семидесятых годов прошлого века компьютеры не могли справиться со столь сложными вычислениями — графических редакторов не было, не говоря уже о приложениях для трехмерной графики. В 1978 году Лорен случайно увидел в магазине книгу Бенуа Мандельброта «Фракталы: форма, случайность и размерность». В этой книге его внимание привлекло то, что Бенуа приводил массу примеров фрактальных форм в реальной жизни и доказывал, что их можно описать математическим выражением.
В обязанности Лорена входила разработка изображений проектируемых самолетов. Он должен был создавать картинки новых моделей, показывая будущие самолеты с разных сторон. В какой-то момент в голову будущему основателю Pixar Animation Studios пришла в голову креативная идея использовать в качестве фона изображение гор. Сегодня такую задачу может решить любой школьник, но в конце семидесятых годов прошлого века компьютеры не могли справиться со столь сложными вычислениями — графических редакторов не было, не говоря уже о приложениях для трехмерной графики. В 1978 году Лорен случайно увидел в магазине книгу Бенуа Мандельброта «Фракталы: форма, случайность и размерность». В этой книге его внимание привлекло то, что Бенуа приводил массу примеров фрактальных форм в реальной жизни и доказывал, что их можно описать математическим выражением.
Такая аналогия была выбрана математиком не случайно. Дело в том, что как только он обнародовал свои исследования, ему пришлось столкнуться с целым шквалом критики. Главное, в чем упрекали его коллеги, — бесполезность разрабатываемой теории. «Да, — говорили они, — это красивые картинки, но не более. Практической ценности теория фракталов не имеет». Были также те, кто вообще считал, что фрактальные узоры — просто побочный результат работы «дьявольских машин», которые в конце семидесятых многим казались чем-то слишком сложным и неизученным, чтобы всецело им доверять. Мандельброт пытался найти очевидное применение теории фракталов, но, по большому счету, ему и не нужно было это делать. Последователи Бенуа Мандельброта в следующие 25 лет доказали огромную пользу от подобного «математического курьеза», и Лорен Карпентер был одним из первых, кто опробовал метод фракталов на практике.
Проштудировав книжку, будущий аниматор серьезно изучил принципы фрактальной геометрии и стал искать способ реализовать ее в компьютерной графике. Всего за три дня работы Лорен смог визуализировать реалистичное изображение горной системы на своем компьютере. Иными словами, он с помощью формул нарисовал вполне узнаваемый горный пейзаж.
Иными словами, он с помощью формул нарисовал вполне узнаваемый горный пейзаж.
Принцип, который использовал Лорен для достижения цели, был очень прост. Он состоял в том, чтобы разделять более крупную геометрическую фигуру на мелкие элементы, а те, в свою очередь, делить на аналогичные фигуры меньшего размера.
Используя более крупные треугольники, Карпентер дробил их на четыре мелких и затем повторял эту процедуру снова и снова, пока у него не получался реалистичный горный ландшафт. Таким образом, ему удалось стать первым художником, применившим в компьютерной графике фрактальный алгоритм для построения изображений. Как только стало известно о проделанной работе, энтузиасты по всему миру подхватили эту идею и стали использовать фрактальный алгоритм для имитации реалистичных природных форм.
Одна из первых визуализаций 3D по фрактальному алгоритму
Всего через несколько лет свои наработки Лорен Карпентер смог применить в куда более масштабном проекте. Аниматор создал на их основе двухминутный демонстрационный ролик Vol Libre, который был показан на Siggraph в 1980 году. Это видео потрясло всех, кто его видел, и Лоурен получил приглашение от Lucasfilm.
Анимация рендерилась на компьютере VAX-11/780 от Digital Equipment Corporation с тактовой частотой пять мегагерц, причем прорисовка каждого кадра занимала около получаса.
Работая для Lucasfilm Limited, аниматор создавал по той же схеме трехмерные ландшафты для второго полнометражного фильма саги Star Trek. В фильме «Гнев Хана» (The Wrath of Khan) Карпентер смог создать целую планету, используя тот же самый принцип фрактального моделирования поверхности.
В настоящее время все популярные приложения для создания трехмерных ландшафтов используют аналогичный принцип генерирования природных объектов. Terragen, Bryce, Vue и прочие трехмерные редакторы полагаются на фрактальный алгоритм моделирования поверхностей и текстур.
⇡#Фрактальные антенны: лучше меньше, да лучше
За последние полвека жизнь стремительно стала меняться. Большинство из нас принимает достижения современных технологий как должное. Ко всему, что делает жизнь более комфортной, привыкаешь очень быстро. Редко кто задается вопросами «Откуда это взялось?» и «Как оно работает?». Микроволновая печь разогревает завтрак — ну и прекрасно, смартфон дает возможность поговорить с другим человеком — отлично. Это кажется нам очевидной возможностью.
Но жизнь могла бы быть совершенно иной, если бы человек не искал объяснения происходящим событиям. Взять, например, сотовые телефоны. Помните выдвижные антенны на первых моделях? Они мешали, увеличивали размеры устройства, в конце концов, часто ломались. Полагаем, они навсегда канули в Лету, и отчасти виной тому… фракталы.
Фрактальные рисунки завораживают своими узорами. Они определенно напоминают изображения космических объектов — туманностей, скопления галактик и так далее. Поэтому вполне закономерно, что, когда Мандельброт озвучил свою теорию фракталов, его исследования вызвали повышенный интерес у тех, кто занимался изучением астрономии. Один из таких любителей по имени Натан Коэн (Nathan Cohen) после посещения лекции Бенуа Мандельброта в Будапеште загорелся идеей практического применения полученных знаний. Правда, сделал он это интуитивно, и не последнюю роль в его открытии сыграл случай. Будучи радиолюбителем, Натан стремился создать антенну, обладающую как можно более высокой чувствительностью.
Единственный способ улучшить параметры антенны, который был известен на то время, заключался в увеличении ее геометрических размеров. Однако владелец жилья в центре Бостона, которое арендовал Натан, был категорически против установки больших устройств на крыше. Тогда Натан стал экспериментировать с различными формами антенн, стараясь получить максимальный результат при минимальных размерах. Загоревшись идеей фрактальных форм, Коэн, что называется, наобум сделал из проволоки один из самых известных фракталов — «снежинку Коха». Шведский математик Хельге фон Кох (Helge von Koch) придумал эту кривую еще в 1904 году. Она получается путем деления отрезка на три части и замещения среднего сегмента равносторонним треугольником без стороны, совпадающей с этим сегментом. Определение немного сложное для восприятия, но на рисунке все ясно и просто.
Существуют также другие разновидности «кривой Коха», но примерная форма кривой остается похожей
Когда Натан подключил антенну к радиоприемному устройству, он был очень удивлен — чувствительность резко увеличилась. После серии экспериментов будущий профессор Бостонского университета понял, что антенна, сделанная по фрактальному рисунку, имеет высокий КПД и покрывает гораздо более широкий частотный диапазон по сравнению с классическими решениями. Кроме того, форма антенны в виде кривой фрактала позволяет существенно уменьшить геометрические размеры. Натан Коэн даже вывел теорему, доказывающую, что для создания широкополосной антенны достаточно придать ей форму самоподобной фрактальной кривой.
Автор запатентовал свое открытие и основал фирму по разработке и проектированию фрактальных антенн Fractal Antenna Systems, справедливо полагая, что в будущем благодаря его открытию сотовые телефоны смогут избавиться от громоздких антенн и станут более компактными.
В принципе, так и произошло. Правда, и по сей день Натан ведет судебную тяжбу с крупными корпорациями, которые незаконно используют его открытие для производства компактных устройств связи. Некоторые известные производители мобильных устройств, как, например, Motorola, уже пришли к мирному соглашению с изобретателем фрактальной антенны.
⇡#Фрактальные измерения: умом не понять
В своей книге Мандельброт рассказывает об одном очень интересном математическом парадоксе. Пятая глава книги «Фрактальная геометрия природы» посвящена, на первый взгляд, довольно простому вопросу: «Какова длина береговой линии Британии?» (аналогичная статья была опубликована им в журнале Science от 1967 года).
Этот вопрос Бенуа позаимствовал у знаменитого американского ученого Эдварда Каснера.
Последний, как и многие другие известные математики, очень любил общаться с детьми, задавая им вопросы и получая неожиданные ответы. Иногда это приводило к удивительным последствиям. Так, например, девятилетний племянник Эдварда Каснера придумал хорошо всем известное теперь слово «гугол», обозначающее единицу со ста нулями. Но вернемся к фракталам. Американский математик любил задавать вопрос, какова длина береговой линии США. Выслушав мнение собеседника, Эдвард сам говорил правильный ответ. Если измерять длину по карте ломаными отрезками, то результат окажется неточным, ведь береговая линия имеет большое количество неровностей. А что будет, если измерять максимально точно? Придется учитывать длину каждой неровности — нужно будет измерять каждый мыс, каждую бухту, скалу, длину скалистого уступа, камня на ней, песчинки, атома и так далее. Поскольку число неровностей стремится к бесконечности, измеренная длина береговой линии будет при измерении каждой новой неровности увеличиваться до бесконечности.
Чем меньше мера при измерении, тем больше измеряемая длина
Интересно, что, следуя подсказкам Эдварда, дети намного быстрее взрослых говорили правильное решение, в то время как у последних были проблемы с принятием такого невероятного ответа.
На примере этой задачи Мандельброт предложил использовать новый подход к измерениям. Поскольку береговая линия близка к фрактальной кривой, значит, к ней можно применить характеризующий параметр — так называемую фрактальную размерность.
Что такое обычная размерность — понятно любому. Если размерность равна единице, мы получаем прямую, если два — плоскую фигуру, три — объем. Однако такое понимание размерности в математике не срабатывает с фрактальными кривыми, где этот параметр имеет дробное значение. Фрактальную размерность в математике можно условно рассматривать как «неровность». Чем выше неровность кривой, тем больше ее фрактальная размерность. Кривая, обладающая, по Мандельброту, фрактальной размерностью выше ее топологической размерности, имеет аппроксимированную протяженность, которая не зависит от количества измерений.
В настоящее время ученые находят все больше и больше областей для применения теории фракталов. С помощью фракталов можно анализировать колебания котировок на бирже, исследовать всевозможные естественные процессы, как, например, колебание численности видов, или моделировать динамику потоков. Фрактальные алгоритмы могут быть использованы для сжатия данных, например для компрессии изображений. И кстати, чтобы получить на экране своего компьютера красивый фрактал, не обязательно иметь докторскую степень.
⇡#Фрактал в браузере
Пожалуй, один из самых простых способов получить фрактальный узор — воспользоваться онлайновым векторным редактором от молодого талантливого программиста Toby Schachman. В основе инструментария этого простого графического редактора лежит все тот же принцип самоподобия.
В вашем распоряжении имеется всего две простейших формы — четырехугольник и круг. Вы можете добавлять их на холст, масштабировать (чтобы масштабировать вдоль одной из осей, удерживайте клавишу Shift) и вращать. Перекрываясь по принципу булевых операций сложения, эти простейшие элементы образуют новые, менее тривиальные формы. Далее эти новые формы можно добавлять в проект, а программа будет повторять генерирование этих изображений до бесконечности. На любом этапе работы над фракталом можно возвращаться к любой составляющей сложной формы и редактировать ее положение и геометрию. Увлекательное занятие, особенно если учесть, что единственный инструмент, который вам нужен для творчества, — браузер. Если вам будет непонятен принцип работы с этим рекурсивным векторным редактором, советуем вам посмотреть видео на официальном сайте проекта, на котором подробно показывается весь процесс создания фрактала.
⇡#XaoS: фракталы на любой вкус
Многие графические редакторы имеют встроенные средства для создания фрактальных узоров. Однако эти инструменты обычно являются второстепенными и не позволяют выполнить тонкую настройку генерируемого фрактального узора. В тех случаях, когда необходимо построить математически точный фрактал, на помощь придет кроссплатформенный редактор XaoS. Эта программа дает возможность не только строить самоподобное изображение, но и выполнять с ним различные манипуляции. Например, в режиме реального времени вы можете совершить «прогулку» по фракталу, изменив его масштаб. Анимированное движение вдоль фрактала можно сохранить в виде файла XAF и затем воспроизвести в самой программе.
XaoS может загружать случайный набор параметров, а также использовать различные фильтры постобработки изображения — добавлять эффект смазанного движения, сглаживать резкие переходы между точками фрактала, имитировать 3D-картинку и так далее.
⇡#Fractal Zoomer: компактный фрактальный генератор
По сравнению с другими генераторами изображений фракталов Fractal Zoomer имеет несколько преимуществ. Во-первых, он совсем небольшой по размеру и не требует установки. Во-вторых, в нем реализована возможность определять цветовую палитру рисунка. Вы можете выбирать оттенки в цветовых моделях RGB, CMYK, HVS и HSL.
Также очень удобно использовать опцию случайного подбора цветовых оттенков и функцию инвертирования всех цветов на картинке. Для настройки цвета имеется функция цикличного перебора оттенков — при включении соответствующего режима программа анимирует изображение, циклично меняя на нем цвета.
Fractal Zoomer может визуализировать 85 различных фрактальных функций, причем в меню программы наглядно показываются формулы. Фильтры для постобработки изображения в программе имеются, хотя и в небольшом количестве. Каждый назначенный фильтр можно в любой момент отменить.
⇡#Mandelbulb3D: редактор трехмерных фракталов
Когда употребляется термин «фрактал», чаще всего подразумевается плоское двухмерное изображение. Однако фрактальная геометрия выходит за рамки 2D-измерения. В природе можно найти как примеры плоских фрактальных форм, скажем, геометрию молнии, так и трехмерные объемные фигуры. Фрактальные поверхности могут быть трехмерными, и одна из очень наглядных иллюстраций 3D-фракталов в повседневной жизни — кочан капусты. Наверное, лучше всего фракталы можно разглядеть в сорте романеско — гибриде цветной капусты и брокколи.
А еще этот фрактал можно съесть
Создавать трехмерные объекты с похожей формой умеет программа Mandelbulb3D. Чтобы получить трехмерную поверхность с использованием фрактального алгоритма, авторы данного приложения, Дениэл Уайт (Daniel White) и Пол Ниландер (Paul Nylander), преобразовали множество Мандельброта в сферические координаты. Созданная ими программа Mandelbulb3D представляет собой самый настоящий трехмерный редактор, который моделирует фрактальные поверхности разных форм. Поскольку в природе мы часто наблюдаем фрактальные узоры, то искусственно созданный фрактальный трехмерный объект кажется невероятно реалистичным и даже «живым».
Он может походить на растение, может напоминать странное животное, планету или что-нибудь другое. Этот эффект усиливается благодаря продвинутому алгоритму визуализации, который дает возможность получать реалистичные отражения, просчитывать прозрачность и тени, имитировать эффект глубины резкости и так далее. В Mandelbulb3D имеется огромное количество настроек и параметров визуализации. Можно управлять оттенками источников света, выбирать фон и уровень детализации моделируемого объекта.
Фрактальный редактор позволяет создавать анимацию. Вы не только конфигурируете трехмерное множество Мандельброта, но и можете его вращать, масштабировать и менять параметры с течением времени.
⇡#Генератор трехмерных фракталов Incendia
Incendia — это мультипроцессорный генератор трехмерных фракталов, разработанный испанским программистом Ramiro Perez, который изучает фракталы с 1989 года.
Фрактальный редактор Incendia поддерживает двойное сглаживание изображения, содержит библиотеку из полусотни различных трехмерных фракталов и имеет отдельный модуль для редактирования базовых форм.
Приложение использует фрактальный скриптинг, с помощью которого можно самостоятельно описывать новые типы фрактальных конструкций. В Incendia есть редакторы текстур и материалов, а движок визуализации позволяет использовать эффекты объемного тумана и различные шейдеры. В программе реализована опция сохранения буфера при длительном рендеринге, поддерживается создание анимации.
Incendia позволяет экспортировать фрактальную модель в популярные форматы трехмерной графики — OBJ и STL. В состав Incendia включена небольшая утилита Geometrica — специальный инструмент для настройки экспорта фрактальной поверхности в трехмерную модель. С помощью этой утилиты можно определять разрешение 3D-поверхности, указывать число фрактальных итераций. Экспортированные модели могут быть использованы в 3D-проектах при работе с такими трехмерными редакторами, как Blender, 3ds max и прочие.
В последнее время работа над проектом Incendia несколько затормозилась. На данный момент автор ищет спонсоров, которые помогли бы ему развивать программу.
Если вам не хватает фантазии нарисовать в этой программе красивый трехмерный фрактал — не беда. Воспользуйтесь библиотекой параметров, которая находится в папке INCENDIA_EX\parameters. С помощью файлов PAR вы сможете быстро найти самые необычные фрактальные формы, в том числе и анимированные.
⇡#Aural: как поют фракталы
Мы обычно не рассказываем о проектах, работа над которыми только ведется, однако в данном случае мы должны сделать исключение, уж очень это необычное приложение. Проект под названием Aural придумал тот же человек, что и Incendia. Правда, на этот раз программа не визуализирует фрактальное множество, а озвучивает его, превращая в электронную музыку. Идея очень любопытная, особенно если учесть необычные свойства фракталов. Aural — это аудиоредактор, генерирующий мелодии с использованием фрактальных алгоритмов, то есть, по сути, это звуковой синтезатор-секвенсор.
Последовательность звуков, выдаваемая этой программой, необычна и… красива. Она вполне может пригодиться для написания современных ритмов и, как нам кажется, особенно хорошо подходит для создания звуковых дорожек к заставкам телевизионных и радиопередач, а также «петель» фоновой музыки к компьютерным играм. Рамиро пока не предоставил демонстрационной версии своей программы, но обещает, что, когда он это сделает, для того, чтобы работать с Aural, не нужно будет изучать теорию фракталов — достаточно просто поиграться с параметрами алгоритма генерирования последовательности нот. Послушать, как звучат фракталы, можно здесь и тут.
Фракталы: музыкальная пауза
Вообще-то фракталы могут помочь написать музыку даже без программного обеспечения. Но это может сделать только тот, кто по-настоящему проникнут идеей природной гармонии и при этом не превратился в несчастного «ботана». Тут есть смысл брать пример с музыканта по имени Джонатан Колтон (Jonathan Coulton), который, помимо всего прочего, пишет композиции для журнала Popular Science. И не в пример другим исполнителям, Колтон все свои произведения публикует под лицензией Creative Commons Attribution-Noncommercial, которая (при использовании в некоммерческих целях) предусматривает свободное копирование, распространение, передачу произведения другим лицам, а также его изменение (создание производных произведения), чтобы приспособить его к своим задачам.
У Джонатана Колтона, конечно же, есть песня про фракталы.
⇡#Заключение
Во всем, что нас окружает, мы часто видим хаос, но на самом деле это не случайность, а идеальная форма, разглядеть которую нам помогают фракталы. Природа — лучший архитектор, идеальный строитель и инженер. Она устроена очень логично, и если где-то мы не видим закономерности, это означает, что ее нужно искать в другом масштабе. Люди все лучше и лучше это понимают, стараясь во многом подражать естественным формам. Инженеры проектируют акустические системы в виде раковины, создают антенны с геометрией снежинок и так далее. Уверены, что фракталы хранят в себе еще немало секретов, и многие из них человеку еще лишь предстоит открыть.
Если Вы заметили ошибку — выделите ее мышью и нажмите CTRL+ENTER.
Мы не можем найти эту страницу
(* {{l10n_strings.REQUIRED_FIELD}})
{{l10n_strings.CREATE_NEW_COLLECTION}} *
{{l10n_strings.ADD_COLLECTION_DESCRIPTION}}
{{l10n_strings.COLLECTION_DESCRIPTION}} {{addToCollection.description.length}} / 500 {{l10n_strings.TAGS}} {{$ item}} {{l10n_strings.PRODUCTS}} {{l10n_strings.DRAG_TEXT}}{{l10n_strings.DRAG_TEXT_HELP}}
{{l10n_strings.ЯЗЫК}} {{$ select.selected.display}}{{article.content_lang.display}}
{{l10n_strings.AUTHOR}}{{l10n_strings.AUTHOR_TOOLTIP_TEXT}}
{{$ select.selected.display}} {{l10n_strings.CREATE_AND_ADD_TO_COLLECTION_MODAL_BUTTON}} {{l10n_strings.CREATE_A_COLLECTION_ERROR}}Как измерить размер объекта в Autodesk 3ds max | 3ds Max
(* {{l10n_strings.REQUIRED_FIELD}})
{{l10n_strings.CREATE_NEW_COLLECTION}} *
{{l10n_strings.ADD_COLLECTION_DESCRIPTION}}
{{l10n_strings.COLLECTION_DESCRIPTION}} {{addToCollection.description.length}} / 500 {{l10n_strings.TAGS}} {{$ item}} {{l10n_strings.ТОВАРЫ}} {{l10n_strings.DRAG_TEXT}}{{l10n_strings.DRAG_TEXT_HELP}}
{{l10n_strings.LANGUAGE}} {{$ select.selected.display}}{{article.content_lang.display}}
{{l10n_strings.AUTHOR}}{{l10n_strings.AUTHOR_TOOLTIP_TEXT}}
{{$ select.selected.display}} {{l10n_strings.CREATE_AND_ADD_TO_COLLECTION_MODAL_BUTTON}} {{l10n_strings.CREATE_A_COLLECTION_ERROR}}Мы не можем найти эту страницу
(* {{l10n_strings.REQUIRED_FIELD}})
{{l10n_strings.CREATE_NEW_COLLECTION}} *
{{l10n_strings.ADD_COLLECTION_DESCRIPTION}}
{{l10n_strings.COLLECTION_DESCRIPTION}} {{addToCollection.description.length}} / 500 {{l10n_strings.TAGS}} {{$ item}} {{l10n_strings.PRODUCTS}} {{l10n_strings.DRAG_TEXT}}{{l10n_strings.DRAG_TEXT_HELP}}
{{l10n_strings.LANGUAGE}} {{$ select.selected.display}}{{article.content_lang.display}}
{{l10n_strings.AUTHOR}}{{l10n_strings.AUTHOR_TOOLTIP_TEXT}}
{{$ select.selected.display}} {{l10n_strings.CREATE_AND_ADD_TO_COLLECTION_MODAL_BUTTON}} {{l10n_strings.CREATE_A_COLLECTION_ERROR}}resize — как я могу установить определенный размер для многоугольника в 3ds max
resize — как я могу установить определенный размер для многоугольника в 3ds max — Graphic Design Stack ExchangeСеть обмена стеком
Сеть Stack Exchange состоит из 176 сообществ вопросов и ответов, включая Stack Overflow, крупнейшее и пользующееся наибольшим доверием онлайн-сообщество, где разработчики могут учиться, делиться своими знаниями и строить свою карьеру.
Посетить Stack Exchange- 0
- +0
- Авторизоваться Зарегистрироваться
Graphic Design Stack Exchange — это сайт вопросов и ответов для профессионалов, студентов и энтузиастов графического дизайна.Регистрация займет всего минуту.
Зарегистрируйтесь, чтобы присоединиться к этому сообществуКто угодно может задать вопрос
Кто угодно может ответить
Лучшие ответы голосуются и поднимаются наверх
Спросил
Просмотрено 3к раз
Закрыто. Этот вопрос не по теме. В настоящее время он не принимает ответы.Хотите улучшить этот вопрос? Обновите вопрос, чтобы он соответствовал теме обмена стеками графического дизайна.
Закрыт 5 лет назад.
Я работаю над моделью в 3ds max, и мне нужно ввести конкретные размеры после преобразования в съедобный поли.есть ли способ установить конкретный многоугольник после его выбора?
спасибо
Создан 04 мар.
Джад Чидиак1311 серебряный знак55 бронзовых знаков
1Выберите инструмент равномерного масштабирования, затем перейдите в Edit> Transform Type-In.Это позволит вам масштабировать поли на процентной основе.
Единственный способ, которым я знаю, как сопоставить размер многоугольника с конкретным размером, — это создать новую плоскость с этими конкретными размерами, разместить ее в ортогональном окне просмотра, включить привязку кромок и соответствующим образом перемещать контуры кромок, пока они не будут привязаны к края плоскости.
Создан 31 мар.
БреннБренн30111 серебряный знак77 бронзовых знаков
Не тот ответ, который вы ищете? Посмотрите другие вопросы с метками resize 3ds-max или задайте свой вопрос.
Graphic Design Stack Exchange лучше всего работает с включенным JavaScriptВаша конфиденциальность
Нажимая «Принять все файлы cookie», вы соглашаетесь с тем, что Stack Exchange может хранить файлы cookie на вашем устройстве и раскрывать информацию в соответствии с нашей Политикой в отношении файлов cookie.
Принимать все файлы cookie Настроить параметры
Помощники по моделированию | 3ds Max 9 Библия
На панели «Создать» (и в меню «Создать») есть категория разных объектов, называемых помощниками (значок выглядит как рулетка).Эти объекты полезны для позиционирования объектов и измерения размеров. К кнопкам в категории Помощник относятся: Dummy, Crowd, Delegate, ExposeTM, Grid, Point, Tape, Protractor и Compass.
| CROSS-REF | Помощники Crowd и Delegate обсуждаются в главе 42 «Создание и анимация Bipeds», а вспомогательный объект Expose Transform рассматривается в главе 31 «Использование модификаторов анимации и параметров подключения». |
Использование фиктивных и точечных объектов
Фиктивный объект — полезный объект для управления сложными иерархиями объектов.Объект-пустышка отображается в окнах просмотра как простой куб с точкой поворота в центре, но объект не будет отображаться и не имеет параметров. Он используется только как объект для преобразования объектов. Например, вы можете создать объект-пустышку, за которым камера будет следовать в последовательности анимации. В оставшейся части книги во многих примерах используются фиктивные объекты.
Объект Point очень похож на объект Dummy в том, что он также не отображается и имеет минимальные параметры.Объект Point определяет точку в пространстве и идентифицируется как X, штатив оси или простой прямоугольник. Опция Center Marker помещает X в центр объекта Point (так что X действительно отмечает точку). Опция Axis Tripod отображает оси X, Y и Z, опция Cross увеличивает длину маркера вдоль каждой оси, а опция Box отображает объект Point как Box. Значение Size определяет размер объекта Point. Параметр «Постоянный размер экрана» сохраняет размер объекта Point постоянным, независимо от того, насколько вы увеличиваете или отдаете масштаб сцены.Параметр «Нарисовать сверху» рисует объект «Точка» над всеми остальными объектами сцены, что упрощает поиск. Основная цель объекта Point — отмечать позиции внутри сцены.
| Осторожно | Точечные объекты трудно увидеть и легко потерять. Если вы используете точечный объект, не забудьте присвоить ему имя, чтобы его можно было легко найти в диалоговом окне «Выбор по имени». |
Измерение координатных расстояний
Категория Помощники также включает несколько удобных утилит для измерения размеров и направлений.Это объекты «Лента», «Транспортир» и «Компас». Все единицы измерения основаны на текущих выбранных системных единицах.
Использование инструмента «Измерение расстояния»
В меню «Инструменты» есть команда для измерения расстояния. Этот инструмент прост в использовании. Просто выберите его и щелкните в начальной точке и еще раз в конечной точке; расстояние между двумя щелчками показано в строке состояния в нижней части интерфейса. Измерение расстояния также сообщает значения дельты в направлениях X, Y и Z.Вы можете использовать этот инструмент с включенной функцией Snap для точных измерений.
Использование помощника «Лента»
Вы используете объект «Лента» для измерения расстояний. Чтобы использовать его, просто перетащите расстояние, которое вы хотите измерить, и просмотрите полученный размер в свитке Parameters. Вы также можете установить длину объекта «Лента» с помощью параметра «Указать длину». Вы можете перемещать и переставлять конечные точки объекта ленты с помощью кнопок «Выбрать» и «Переместить», но кнопки «Повернуть» и «Масштаб» не действуют.
Использование помощника транспортира
Объект транспортира работает аналогично объекту ленты, но измеряет угол между двумя объектами. Чтобы использовать объект Protractor, щелкните в области просмотра, чтобы разместить объект Protractor. (Объект Protractor выглядит как две пирамиды, выровненные точка к точке, и представляет начало угла.) Затем нажмите кнопку «Выбрать объект 1» и выберите объект в сцене. Линия проводится от объекта транспортира к выбранному объекту.Затем нажмите кнопку «Выбрать объект 2». Угловые объекты и объект Protractor отображаются в свитке Parameters. Значение изменяется при перемещении одного из выбранных объектов или транспортира.
| Примечание | Все значения измерений представлены в серых полях в свитке Parameters. Это серое поле указывает на то, что значение не может быть изменено. |
Использование помощника Compass
Объект Compass определяет север, восток, запад и юг на плоском объекте в форме звезды.Вы можете перетащить объект «Компас», чтобы увеличить его размер.
| CROSS-REF | Вспомогательный объект Grid обсуждается вместе с сетками в главе 8 «Преобразование объектов — перемещение, поворот и масштабирование». Объект «Компас» в основном используется вместе с системой солнечного света, о которой вы можете узнать в главе 27 «Использование света и основные методы освещения». |
Использование утилиты «Измерить»
На панели «Утилиты» есть еще один полезный инструмент для получения информации о текущем выбранном объекте: утилита «Измерить».Вы можете открыть утилиту Measure в виде всплывающего диалогового окна, показанного на рисунке 13.10. В этом диалоговом окне отображается имя объекта, а также его площадь поверхности, объем, центр масс, длина (для фигур) и размеры. Он также включает возможность заблокировать текущий выбор.
Рис. 13.10. В диалоговом окне утилиты «Измерение» отображается некоторая полезная информация.
Использование утилиты «Уровень детализации»
Во время анимации сцены некоторые объекты находятся близко к камере, а другие — далеко от нее.Рендеринг сложного объекта, находящегося далеко от камеры, не имеет особого смысла. Используя утилиту уровня детализации (LOD), вы можете заставить Макс визуализировать более простую версию модели, когда она находится дальше от камеры, и более сложную версию, когда она находится близко к камере.
| CROSS-REF | Модификатор MultiRes также может создавать обновления уровня детализации в реальном времени. Он рассматривается в главе 16 «Деформирование поверхностей и использование модификаторов сетки». |
Чтобы открыть служебную программу, нажмите кнопку «Еще» на панели служебных программ и выберите служебную программу «Уровень детализации».Один свиток загружается в панель Utility, как показано на рисунке 13.11. Чтобы использовать эту утилиту, вам нужно создать несколько версий объекта и сгруппировать их вместе. Кнопка «Создать новый набор» позволяет выбрать группу объектов из видовых экранов. Объекты в группе индивидуально перечислены на панели развертывания.
Рисунок 13.11: Утилита «Уровень детализации» (разделенная на две части) может определять способ просмотра объектов на основе заданных пороговых значений.
Если вы выберете объект в списке, вы можете указать пороговые единицы в пикселях или в процентах от целевого изображения.Для каждого элемента в списке вы можете указать минимальный и максимальный пороговые значения. Значения «Размер выходного изображения» используются для указания размера выходного изображения, а различные используемые модели основаны на размере объекта в конечном изображении. Флажок «Отображать в видовых экранах» приводит к тому, что соответствующая модель LOD появляется в видовом экране.
Live Measure Pro от miauu — скрипты и инструменты miauu для 3ds Max
версия 2.8.01
+ NEW: добавлена поддержка 3ds Max 2021.
в.2,8
+ NEW: при масштабировании закрытой группы Live Update покажет изменения размера группы.
+ NEW: измерения объема и площади будут следовать за объектом при его перемещении.
версия 2.7
+ NEW: размер пользовательского интерфейса можно изменять.
— ИСПРАВЛЕНО: ошибка при обновлении угла между гранями.
версия 2.6
+ NEW: добавлены новые измерения — расстояние между двумя выбранными вершинами.
+ NEW: добавлены новые измерения — расстояние между центрами двух выбранных кромок.
+ NEW: добавлены новые измерения — расстояние между центрами двух выбранных граней.
версия 2.5
— ИСПРАВЛЕНО: длина выбранного сегмента сплайна не обновляется в реальном времени.
версия 2.4
+ НОВИНКА: всю длину выбранной линии можно измерить, нажав кнопку [Измерение длины / площади] (первая кнопка слева направо в пользовательском интерфейсе) средней кнопкой мыши.
— ИСПРАВЛЕНО: ошибка при нажатии кнопки [Обновить] и необходимости обновления длины сплайна.
— ИСПРАВЛЕНО: ошибка в 3ds max 2019.1, препятствующая запуску скрипта.
версия 2.3
+ НОВИНКА: добавлено в 3ds Max 2009, 2010, 2011, 2012, площадь и объем будут отображаться как «m2» для квадратного метра и «m3» для кубического метра.
+ NEW: добавлено «копирование в буфер обмена» — нажатие Ctrl + щелчок по измерению в пользовательском интерфейсе скопирует только числовую часть измеренного значения в буфер обмена.
версия 2.2
+ NEW: добавлена поддержка 3ds Max 2019.
в.2,1
+ NEW: добавлена запись в свойства, определяемые пользователем.
— ИСПРАВЛЕНО: ошибка, при которой все измерения стираются при нажатии кнопки LiveMeasure, когда одна уже открыта.
версия 2.0
+ NEW: добавлена поддержка 3ds Max 2018.
версия 1.9
+ NEW: добавлено отображение пользовательского текста для каждого измерения в области просмотра.
вер. 1.8
+ НОВИНКА: Измерьте площадь и объем в мм2, см2, м2 или мм3, см3, м3.Измерьте общую площадь выбранного объекта на уровне объекта. Для этого нажмите кнопку Длина / Площадь средней кнопкой мыши.
— ИСПРАВЛЕНО: при выборе группы и измерении размера скрипт будет измерять размер всей группы. Чтобы измерить размер объектов — откройте группу и выберите нужный объект. Если выбрана открытая группа, скрипт измерит ее размер.
Когда выбрана группа и измерен объем, скрипт будет измерять объем каждого объекта индивидуально, поэтому будьте осторожны, если группа содержит сотни объектов.
вер. 1.7
+ NEW: Добавлена возможность измерять размер и объем сразу нескольких объектов.
вер. 1.6
+ NEW: Добавлена возможность добавлять собственные примечания к каждому измерению.
вер. 1.5
+ NEW: добавлена поддержка 3ds Max 2017.
+ NEW: добавлен экспорт всех измерений в виде файла TXT.
версия 1.4
+ НОВИНКА: Новые типы измерений — Радиус и Диаметр.
версия 1.3
+ НОВИНКА: добавлены линейные размеры — измерение расстояний между точками, но только по осям X, Y или Z.
+ NEW: добавлена десятичная точность отображаемых измерений — ограничивает количество цифр после десятичного знака.
версия 1.2
+ NEW: Добавлена возможность скрыть свиток с экрана.
версия 1.1
— ИСПРАВЛЕНО: ошибка, когда в качестве единиц измерения использовались дюймы.
единиц и масштаб — исправьте масштабирование сцены | Изучите V-Ray
Урок Чиро Саннино | Официальный учебный материал 5SRW
[sc: yellowbox] ВАЖНО:
При открытии наших файлов появляется всплывающее окно с запросом единиц и масштаба.. JUST ACCEPT
Это заставит вашу сцену принять сцену с правильным масштабом, который в наших файлах всегда равен 1: 1 [sc: enddiv]
Что действительно важно для работы в 3ds Max, V-Ray и фотореализме, так это просто
ПОВТОРЕНИЕ РЕАЛЬНОГО МИРА .
Если я скажу вам, что высота двери составляет 2,20 метра, или я скажу, что это 220 сантиметров, это будет точно так же. Также могу сказать, что высота двери в дюймах 86,6 дюйма, это эквивалент 220 сантиметров.
Единицы измерения не влияют на реальную высоту двери.
2,20 м = 220 см = 86,6 дюйма и т.д ..
Выберите см для интерьера или метра для экстерьера, потому что это более удобно для вас, но V-Ray считает метры, сантиметры и дюймы точно так же.
ПРОБЛЕМА НАЧИНАЕТСЯ, КОГДА ВЫ НЕ РАБОТАЕТЕ В МАСШТАБЕ 1: 1
Работа в масштабе 1: 1 означает, что 1 метр в вашем проекте соответствует 1 метру в реальном мире, и это нормально. Но иногда 3D-модели имеют другой / неправильный масштаб, например масштаб 1:20.Это означает, что 20 реальных метров будут представлены 1 метром в вашем трехмерном мире!
Эта ситуация создает ложный / уменьшенный мир, который не является реальным. Это настоящая проблема.
Когда вы работаете за пределами шкалы, измерения совершенно неверны. Дело не в небольших различиях, а в огромных различиях: у вас может быть дверь размером 2 сантиметра или 2 километра.
БЫСТРО УБЕДИТЕСЬ, ЧТО ВАШИ ВЕСЫ
Если я хочу быстро проверить, правильно ли я работаю в масштабе, я просто использую инструмент «Лента »..
.. затем активный инструмент 3D Snap для измерения расстояния, которое я знаю. Например высота двери:
В « Длина » я прочитал 225 сантиметров , что соответствует реальной двери в реальном мире.
Это говорит мне, что я работаю в правильном масштабе.
И наоборот, когда я нахожусь в неправильном масштабе, этот параметр может отображать 2 сантиметра или 2 километра. Я имею в виду, что-то совершенно нереальное.
ИЗМЕНИТЬ МАСШТАБ СЦЕНЫ
Прежде всего вам необходимо правильно настроить свои единицы перед началом работы.