Урок по рисунку №1
Это первый урок из курса по рисованию простым карандашом. В этом уроке вы научитесь правильно держать карандаш и правильно рисовать им простые линии.
1. Положите лист бумаги на вертикальную или наклонную поверхность. Возьмите карандаш HB. Начинаем урок с постановки руки. Чтобы ваш рисунок не смазывался графитом, при длительной работе с тональным рисунком руку нужно держать так, чтобы на лист опирался только мизинец. При растушевке рука держится «на весу». Для набросков и линий построения вы можете держать карандаш так же, как ручку.
2. Чтобы овладеть техникой карандаша, сначала нужно научиться твердо держать карандаш.Учимся проводить ровные линии без отрыва карандаша от бумаги. Нарисуйте прямоугольник. Тренируйтесь до тех пор, пока он не станет у вас ровным. Лист при этом не переворачиваем!
3. Нарисуйте ровный треугольник. Затем заштрихуйте его параллельными штрихами.
4. Теперь учимся рисовать плавные кривые, не отрывая карандаш от бумаги.
5. Рисуем более сложную кривую. Линия должна быть длиной не менее 10 см. Такие упражнения необходимы, чтобы овладеть разными техниками рисунка, чтобы не карандаш руководил вами, а вы – уверенно руководили карандашом.
6. Теперь попробуйте нарисовать вертикальные кривые, похожие на латинскую «S», так же без отрыва грифеля.
7-8. Продолжаем рисовать кривые.
9. Рисуем орнаментальный элемент. Цифры показывают начала линий.
10. Теперь попробуем нарисовать этот элемент более ровно. Для этого рисуем каждую S-образную кривую в два-три приема.
Во втором уроке по рисованию простыми карандашами мы продолжим работать с линиями на примере несложных орнаментов и фигур.
Рекомендуем самоучители по рисованию простыми карандашами
Похожие записи:
Это первый урок из курса по рисованию простым карандашом. В этом уроке вы научитесь правильно держать карандаш и правильно рисовать им простые линии. |
Теги: цветок, уроки, рисования, ракушку, раковину, простым, новичков, нарисовать, колокольчик, карандашом, как, для, детей |
| 12 февраля 2014 — DRAWSCHOOL.RU
| Подробнее
| 0 комментариев
| 80227 просмотров Теги: |
| 12 февраля 2014 — DRAWSCHOOL.RU
| Подробнее
| 0 комментариев
| 69002 просмотра |
| 14 февраля 2014 — DRAWSCHOOL.RU
| Подробнее
| 0 комментариев
| 40009 просмотров |
| 14 февраля 2014 — DRAWSCHOOL.RU
| Подробнее
| 0 комментариев
| 33281 просмотр |
| 24 декабря 2014 — DRAWSCHOOL.RU
| Подробнее
| 0 комментариев
| 31685 просмотров |
Урок 13. Построение и преобразование графиков функций. Обзор графиков основных функций. Теория
Подготовка к ЕГЭ по математике
Эксперимент
Урок 13. Построение и преобразование графиков функций. Обзор графиков основных функций
Теория
Конспект урока
Начнем с построения графиков основных функций.
1) Линейная функция. Ее графиком является прямая.
Общий вид линейной функции:
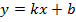
где под  и
и  понимают следующие параметры:
понимают следующие параметры:
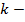 угловой коэффициент;
угловой коэффициент;
 свободный член или смещение по оси ординат.
свободный член или смещение по оси ординат.
Рассмотрим основные формы таких графиков в зависимости от значений параметров и поймем их названия.
 показывает координату пересечения прямой с осью ординат;
показывает координату пересечения прямой с осью ординат;

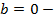 прямая проходит через начало координат;
прямая проходит через начало координат;
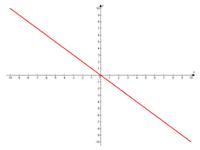
 угол наклона прямой к положительному направлению оси абсцисс острый;
угол наклона прямой к положительному направлению оси абсцисс острый;

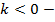 угол наклона прямой к положительному направлению оси абсцисс тупой;
угол наклона прямой к положительному направлению оси абсцисс тупой;

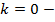 прямая параллельна оси абсцисс.
прямая параллельна оси абсцисс.
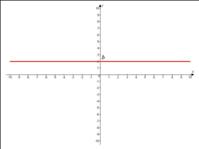
Как видим, параметр « » определяет наклон прямой к оси абсцисс.
» определяет наклон прямой к оси абсцисс.
Метод построения графика линейной функции самый стандартный, и называется «построение по точкам». Поскольку любая прямая может быть однозначно восстановлена по двум точкам, то нам будет достаточно определить координаты двух точек, удовлетворяющих функции, и затем провести через них прямую линию, которая и будет необходимым графиком.
Обычно для этого используется небольшая табличка, в которую записывают произвольно выбранные координаты точек по оси абсцисс, а затем для них вычисляют координаты точек по оси ординат.
Пример. Проделаем эти действия для функции 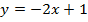 .
.
Решение.
Для вычисления необходимых игреков подставляем значения иксов в формулу, которая задает функцию. При этом удобно выбирать минимальные по модулю целые значения иксов для простоты расчетов:
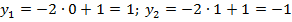
После этого точки наносятся на координатную плоскость, и через них проводится прямая линия, которая и будет графиком.

Обратите внимание, что форма графика соответствует знакам коэффициентов функции.
2) Теперь рассмотрим квадратичную функцию и ее график, который принято называть параболой.
Общий вид квадратичной функции:
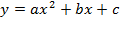
Где под параметрами  понимают:
понимают:
 старший коэффициент;
старший коэффициент;
 второй коэффициент;
второй коэффициент;
 свободный член.
свободный член.
От знаков этих параметров зависит расположение параболы:
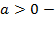 ветки параболы направлены вверх;
ветки параболы направлены вверх;
 ветки параболы направлены вниз;
ветки параболы направлены вниз;
Знаки коэффициента  явно и наглядно ничего не определяют;
явно и наглядно ничего не определяют;
 показывает координату пересечения параболы с осью ординат.
показывает координату пересечения параболы с осью ординат.
Уже можно было обратить внимание, что в графиках функций, которые представлены в виде многочленов, свободный коэффициент показывает точку пересечения с осью ординат. А в общем случае такой точкой является значение функции при подстановке аргумента, равного нулю.
Для ознакомления с изображением параболы построение следует начать с простейшего частного случая рассматриваемой функции  .
.
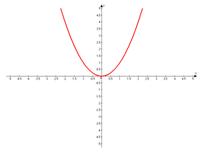
Для построения параболы по общему виду функции есть несколько стандартных приемов, укажем один наиболее простой и удобный из них.
Метод построения «по вершине».
В этом способе сначала находят координаты вершины, а затем в зависимости от знака старшего коэффициента строят эскиз графика.
Координаты вершины находят по следующим формулам:

Как видим, для вычисления значения игрековой координаты вершины выполняется подстановка в функцию найденного значения иксовой координаты вершины.
После этого вершина обозначается в системе координат и с учетом известного нам направления веток параболы в зависимости от знака старшего коэффициента функции изображается эскиз графика.
Пример. Построить график функции 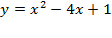 .
.
Решение. Воспользуемся указанными формулами для 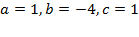 .
.
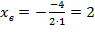 ,
, 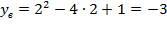 .
.
Учтем, что  , т.е. ветки параболы направлены вверх. Для точности нанесем точку пересечения с осью
, т.е. ветки параболы направлены вверх. Для точности нанесем точку пересечения с осью 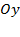 :
:  .
.
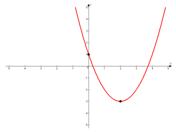
Чтобы увеличить точность построения графика, можно найти и точки его пересечения с осью  . Решим для этого уравнение
. Решим для этого уравнение  , как мы уже знаем, приравняв функцию к нулю. Но мы не будем делать этого в примере, если вам интересно, то можете проделать это действие самостоятельно и решить квадратное уравнение.
, как мы уже знаем, приравняв функцию к нулю. Но мы не будем делать этого в примере, если вам интересно, то можете проделать это действие самостоятельно и решить квадратное уравнение.
3) Перейдем к простейшему виду дробно-рациональной функции, графиком которой является гипербола.
Общий вид такой функции  , т.е. в числителе и знаменателе дроби находятся линейные двучлены.
, т.е. в числителе и знаменателе дроби находятся линейные двучлены.
У указанных параметров нет общепринятых названий.
Начнем знакомство с графиком, который называют гиперболой, с изображения простейшего частного случая дробно-рациональной функции, когда 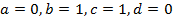 , т.е.
, т.е.  . Он имеет вид:
. Он имеет вид:
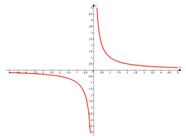
Как видим, у графика есть вспомогательные элементы, которые называются «асимптоты». Их две: горизонтальная и вертикальная.
Вспомним, что вертикальная асимптота строится в координате по оси абсцисс, при которой знаменатель дроби превращается в ноль.
Горизонтальная асимптота проводится в том значении координаты по оси ординат, к которому стремится функция при аргументе, стремящемся к бесконечности. Для функций указанного типа горизонтальную асимптоту можно найти и проще, значением ее игрековой координаты будет отношение коэффициента при иксе в числителе и в знаменателе. Разобраться почему так вы можете изучив тему «Предел функции».
Пример. Построим график дробно-рациональной функции общего положения  .
.
Способ построения мы назовем «по асимптотам» и он будет состоять из трех шагов:
1. Находим уравнение вертикальной асимптоты:  ;
;
2. Находим уравнение горизонтальной асимптоты:  . Можно так же воспользоваться способом приведения числителя к константе, который мы показали в предыдущем уроке.
. Можно так же воспользоваться способом приведения числителя к константе, который мы показали в предыдущем уроке.
3. Расположение веток гиперболы неоднозначно: или справа вверху и слева внизу, например, в простейшем случае
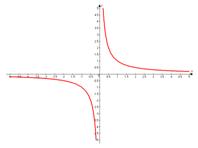
или слева вверху и справа внизу, например,

Поэтому необходимо точно определить, как они будут изображаться. Для этого просто подставим любое целое значение икса в функцию из области определения и найдем одну точку, которая принадлежит графику.
Подставим, например,  и построим ее в системе координат с найденными асимптотами.
и построим ее в системе координат с найденными асимптотами.
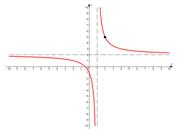
Ветки гиперболы должны прижиматься к асимптотам и по расположению построенной точки мы определяем положение одной из веток гиперболы, а соответственно и другой, т.к. ветки всегда лежат наискось относительно друг друга, если к графику не применялись специальные преобразования.
Урок по рисунку на тему «Графика. Рисунок» (1 класс)
МАУ ДО «ДШИ»
Задонского муниципального района
Липецкой области
Методическая разработка Григорьевой ТН.
Задонск, 2016г.
Конспект урока по предмету «Рисунок» (1 класс)
Тема: Графика. Рисунок.
Вводная беседа о рисунке. Организация рабочего места. Правильная посадка за мольбертом.
Цели и задачи: знакомство с материалами, принадлежностями, инструментами; приемы работы карандашом, постановка руки; знакомство с понятиями «линия», «штрих», «пятно».
Беседа по теме урока.
1. Графика. Рисунок.
Графика — искусство рисования тоном, пятном, линией. Графикой называются рисунки, сделанные карандашом, тушью, гравюры. Язык графики и главные его выразительные средства — это линия, штрих, контур, силуэт, пятно, тон, белый фон бумаги.
Добиться выразительности можно даже при использовании только черного и белого (без серых) и других цветов. Именно поэтому графику часто называют искусством черного и белого. Цвет тоже может использоваться, но не так смело, как в живописи (где он главный).
Рисунки, наброски, станковая графика, книжная графика, прикладная графика (открытки, визитки, упаковка, плакат), а в последнее время и компьютерная графика — все это ее разновидности.
РИСУНОК — изображение, выполненное от руки с помощью графических средств — контурной линии, штриха, пятна. Различными сочетаниями этих средств достигается пластическая моделировка, тональные и светотеневые переходы. Рисунок — это основа для реалистического изображения действительности любыми техническими средствами и приемами. Обучение рисунку составляет важнейшую часть профессионального образования живописца, графика или скульптора.
Разновидности рисунка различаются в зависимости от технических средств и возможностей рисования. В отличие от живописи, рисунок исполняется преимущественно твердым красящим веществом — карандашом, углем, сангиной, пастелью, как правило, посредством штриха и линии, при вспомогательной роли цвета. Такой рисунок может быть как беглой зарисовкой с натуры, так и завершенной графической композицией — иллюстрацией, карикатурой, плакатом. В отдельных случаях, например в технике акварели и пастели, рисунок близко соприкасается с живописью и может отличаться от нее лишь общим характером исполнения.
2. Материалы, принадлежности, инструменты.
Карандаши и бумага. Рисунки можно выполнять обычными графитными карандашами на плотной бумаге, выдерживающей многочисленные поправки в работе.
Карандаши по своим свойствам делятся на твердые и мягкие. Значок обозначения находится на конце деревянной оправы грифеля. Буква М или латинская В определяет мягкие номера. Буква Т или латинская Н — твердые номера. В соответствии с возрастанием номера возрастает твердость или мягкость грифеля. Название карандаша стоит перед номером, например, отечественный «Конструктор» или чешский «KOH-I-NOOR».
Художник-график рисует графитными и цветными карандашами, пером и кистью, тушью и чернилами, углём, пастелью и фломастерами, а также другими художественными материалами.
Графические материалы: графитный карандаш, цветные карандаши, тушь, уголь, фломастеры, пастель (цветные мелки), восковые мелки, гелиевые ручки и др.
Инструменты графика: карандаш, перо, кисть, шариковые ручки, резцы для гравюры.
3. Графические изобразительные средства.
Основными средствами художественной выразительности графики являются линия, точка, пятно.
Итак, линия. Как средство передачи изображения линия появилась в самом начале зарождения искусства. С помощью линии можно изобразить видимый контур предмета. Она может быть тонкой и широкой, прерывистой и непрерывной, одинаковой по всей длине, разной по толщине и насыщенности.
Линия — наиболее часто применяемое в рисунке изобразительное средство. По характеру линии бывают прямые и кривые; по размеру — длинные и короткие, а также ровные и неровные, тонкие и толстые; по светлоте — темные и светлые; по назначению — контурные и вспомогательные; по направлению — горизонтальные, вертикальные и наклонные.
Эмоциональную выразительность линий можно заменить, сопоставив их: горизонтальная линия вызывает чувство покоя, ассоциируясь с линией горизонта; вертикальная — передает стремление вверх; наклонная — неустойчивость, падение; ломаная — переменное движение; волнообразная линия — равномерное движение, качание, спиральная линия — вращение.
Существуют понятия «вялая линия», «напряженная линия», «динамичная линия», они показывают, как применяемые здесь эпитеты и метафоры передают способность человека придавать эмоциональный характер малейшим оттенкам видимых свойств реального мира. Такая реакция на, казалось бы, ничего не выражающие линии показывает, что зрительные ощущения являются исходной точкой сложного психологического процесса осмысления и переработки реальной действительности в зачатки художественного образа.
Штрих — короткая линия, выполненная одним движением (ударом) руки. В зависимости от направлений линий штрихи могут быть разными. Выразительность штриха зависит от мастерства рисовальщика и его вкуса.
Штрих может быть темным и светлым, в зависимости от силы нажима на инструмент или количества накладываемых слоев. Штриховая линия может быть длинной, короткой, широкой, тонкой, едва заметной. Техника штриха, особенно штрихов по форме, играет особую роль в выявлении поверхностей предмета, его конструкции, объема.
Прием работы штрихом называется штриховкой. Чем высполняется штриховка? (Карандашом, углем, тушью, сажей (художественной), пастелью, фломастерами.)
Положенные рядом штрихи воспринимаются тоновым пятном. Плотность тона достигается сближением одних штрихов с другими, повторным нанесением ряда штрихов на поверхности листа бумаги.
Тональное пятно можно создать на бумаге штриховкой карандашом, углем, сангиной, пастелью; кистью, растушевкой или просто пальцем. Очень часто в одной работе художники используют весь цветовой и тоновой спектр графических материалов.
— Давайте рассмотрим произведения художников-графиков и ответим на вопросы:
1. С помощью каких выразительных средств дается изображение? ‘
2. Что делает черно-белые картины «живыми» и выразительными?
3. С помощью каких выразительных средств (линия, пятно, силуэт, свет, тень, ритм) художник создает свое произведение?
II. Практическая деятельность учащихся.
1. Правильная посадка за мольбертом.
Сесть надо прямо, развернув плечи. Посмотрите на себя со стороны — вы должны сидеть как балерина! Теперь возьмите в руку карандаш так, как показано на рисунке. Вытяните вперед руку с карандашом — его острие должно коснуться поверхности бумаги, которую вы накололи на планшет или укрепили на мольберте. Теперь вы будете сидеть вот так и не иначе! Поначалу будет немного трудно, но эта поза складывалась веками: правильная осанка не позволяет перетрудиться позвоночнику и тренирует мышечный корсет.
2. Постановка руки.
Как держать карандаш? Часто начинающие художники держат его так же, как и при письме. Это неправильно. Карандаш следует держать так, как показано на рис., прикасаясь к поверхности листа бумаги только грифелем и изредка мизинцем. Этим обеспечивается свобода движения руки, ее кисти, направляющей штрихи по форме, как бы обвивая ее штрихами. Этот способ позволяет видеть рисунок в целом и предохраняет его от затирания рукой. Положение пальцев руки, находящихся на определенном расстоянии от грифеля, дает художнику возможность видеть и наблюдать рисунок на расстоянии. В таком положении карандаш касается листа, а не режет его острием, не продавливает бумагу, как это часто бывает у еще неопытных любителей рисования.

3.Приемы работы карандашом.
Работа острием карандаша дает, когда это необходимо, или очень легкие воздушные линии, или четкие и уверенные. Касание бумаги боком грифеля оставляет сочные рыхлые штрихи, широко закрывающие более темные тона и большие поверхности.

4. Выполнение упражнений.
Проведение вертикальных, горизонтальных, наклонных линий.
Основные правила преобразования графиков функций. Видеоурок. Алгебра 9 Класс
Наверняка многие из вас могут быстро и правильно построить графики некоторых функций, не прибегая к вычислениям значений точек. Всем известно, что график функции  – это прямая, а график функции
– это прямая, а график функции 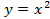 – это парабола. Но как построить, например, график функции
– это парабола. Но как построить, например, график функции 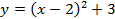 , не вычисляя значения точек? Для этого существуют правила преобразования графиков функций.
, не вычисляя значения точек? Для этого существуют правила преобразования графиков функций.
Предположим, что у нас есть функция  (график этой функции – это парабола) и необходимо построить график функции
(график этой функции – это парабола) и необходимо построить график функции  . Вычислим значения некоторых точек для графиков этих функций.
. Вычислим значения некоторых точек для графиков этих функций.

Из таблиц видно, что одним и тем же значениям аргумента соответствуют противоположные значения функций. Графически это означает, что графики расположены симметрично относительно оси абсцисс. То есть заданная парабола ( ) зеркально отобразится относительно оси
) зеркально отобразится относительно оси  (см. Рис. 1).
(см. Рис. 1).

Рис. 1. Графики функций  и
и 
Таким образом, если у нас есть произвольный график 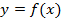 , то для построения графика
, то для построения графика  необходимо график
необходимо график 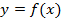 симметрично отразить относительно оси
симметрично отразить относительно оси  (см. Рис. 2). Такое преобразование называется преобразованием симметрии относительно оси
(см. Рис. 2). Такое преобразование называется преобразованием симметрии относительно оси  .
.

Рис. 2. Преобразование симметрии относительно оси 
Преобразование симметрии – зеркальное отражение относительно прямой. График  получается из графика функции
получается из графика функции  преобразованием симметрии относительно оси
преобразованием симметрии относительно оси  .
.
На рисунке 3 показаны примеры симметрии относительно оси  .
.
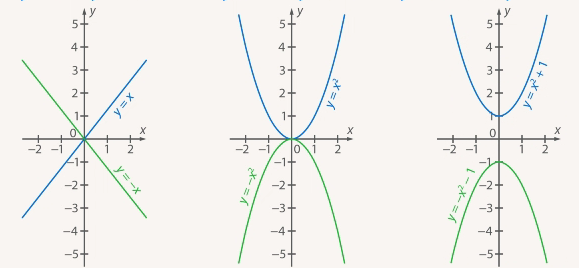
Рис. 3. Симметрия относительно оси Ox
Предположим, что у нас есть функция  (график этой функции – это парабола) и необходимо построить график функции
(график этой функции – это парабола) и необходимо построить график функции 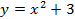 . Вычислим значения некоторых точек для графиков этих функций.
. Вычислим значения некоторых точек для графиков этих функций.

Из таблиц видно, что при одних и тех же значениях аргумента значения функции у графика 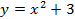 больше на 3 единицы. Графически это означает, что график функции
больше на 3 единицы. Графически это означает, что график функции 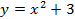 находится на 3 единицы выше, чем график функции
находится на 3 единицы выше, чем график функции  (см. Рис. 4).
(см. Рис. 4).
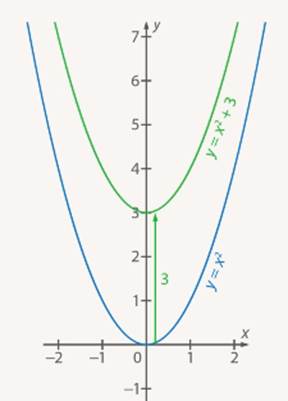
Рис. 4. Графики функций  и
и 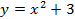
График  получается из графика функции
получается из графика функции параллельным переносом последнего вдоль оси ординат на
параллельным переносом последнего вдоль оси ординат на 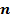 единиц вверх, если
единиц вверх, если 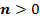 , и на
, и на  единиц вниз, если
единиц вниз, если 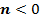 (см. Рис. 5, 6).
(см. Рис. 5, 6).
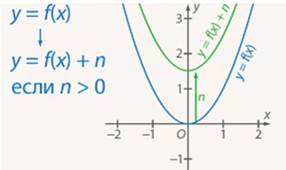
Рис. 5. Параллельный перенос вдоль оси  (при
(при  )
)
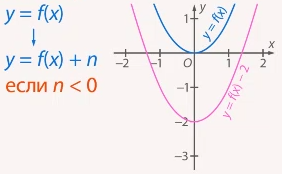
Рис. 6. Параллельный перенос вдоль оси  (при
(при  )
)
Предположим, что у нас есть функция  (график этой функции – это парабола) и необходимо построить график функции
(график этой функции – это парабола) и необходимо построить график функции  . Вычислим значения некоторых точек для графиков этих функций.
. Вычислим значения некоторых точек для графиков этих функций.

Из таблиц видно, что при одних и тех же значениях аргумента значения функции у графика  больше в 2 раза. Графически это означает, что график функции
больше в 2 раза. Графически это означает, что график функции  сужается по сравнению с графиком функции
сужается по сравнению с графиком функции  (см. Рис. 7).
(см. Рис. 7).
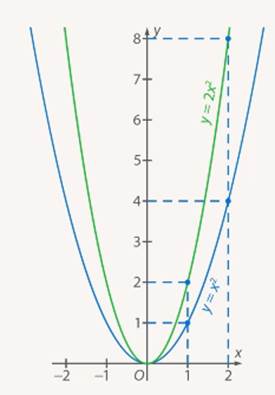
Рис. 7. Графики функций  и
и 
Если необходимо построить график функций 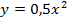 , то из таблиц видно, что при одних и тех же значениях аргумента значения функции у графика
, то из таблиц видно, что при одних и тех же значениях аргумента значения функции у графика 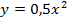 меньше в 2 раза, чем у
меньше в 2 раза, чем у  . Графически это означает, что график функции
. Графически это означает, что график функции 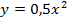 расширяется по сравнению с графиком функции
расширяется по сравнению с графиком функции  (см. Рис. 8).
(см. Рис. 8).

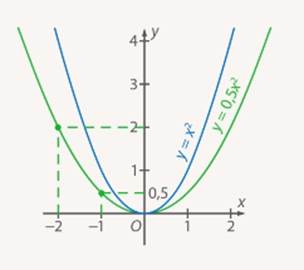
Рис. 8. Графики функций  и
и 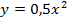
Чтобы построить график функции  , где
, где  и
и  , нужно ординаты точек заданного графика умножить на
, нужно ординаты точек заданного графика умножить на  . Такое преобразование называется растяжением от оси
. Такое преобразование называется растяжением от оси  с коэффициентом
с коэффициентом  , если
, если  , и сжатием к оси
, и сжатием к оси , если
, если  (см. Рис. 9, 10).
(см. Рис. 9, 10).

Рис. 9. Растяжение от оси 

Рис. 10. Сжатие к оси 
Предположим, что у нас есть функция  , необходимо построить график функции
, необходимо построить график функции 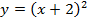 . Вычислим значения некоторых точек для графиков этих функций.
. Вычислим значения некоторых точек для графиков этих функций.

Из таблиц видно, что одинаковым значениям функции соответствуют значения аргумента, отличающиеся на 2 единицы. Это означает, что график данной функции переместился на 2 единицы относительно оси ординат влево (см. Рис. 11), так как для получения одинаковых значений функций приходится брать значения аргумента на 2 меньше:
 , при
, при 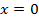
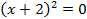 при
при 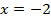
Следовательно, если необходимо было построить график функции  , то сдвиг на 3 единицы относительно оси ординат был бы вправо (по сравнению с графиком функции
, то сдвиг на 3 единицы относительно оси ординат был бы вправо (по сравнению с графиком функции  ) (см. Рис. 11).
) (см. Рис. 11).

Рис. 11. Графики функций  ,
, 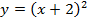 и
и 
График  получается из графика функции
получается из графика функции  параллельным переносом последнего на
параллельным переносом последнего на  единиц влево, если
единиц влево, если  , и на
, и на  единиц вправо, если
единиц вправо, если 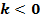 (см. Рис. 12, 13).
(см. Рис. 12, 13).
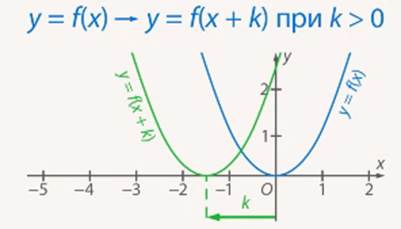
Рис. 12. Параллельный перенос влево при 

Рис. 13. Параллельный перенос вправо при 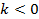
Обратите внимание на то, что по этому принципу из графика 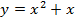 не построить график
не построить график 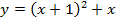 , ведь мы добавили 1 не ко всем вхождениям
, ведь мы добавили 1 не ко всем вхождениям 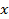 в это выражение. А вот график
в это выражение. А вот график 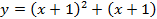 построить можно, сдвинув исходный график на 1 влево (см. Рис. 14).
построить можно, сдвинув исходный график на 1 влево (см. Рис. 14).
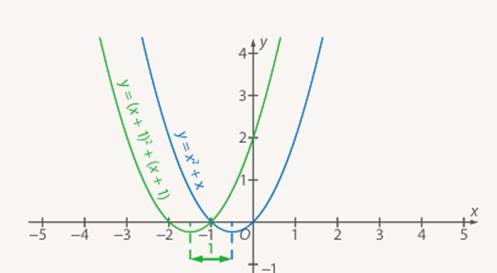
Рис. 14. Графики функции 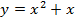 и
и 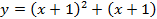
График функции 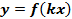 , где
, где  и
и  , получается из графика функции
, получается из графика функции  сжатием с коэффициентом
сжатием с коэффициентом  к оси
к оси 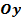 (если
(если  указанное «сжатие» фактически является растяжением с коэффициентом
указанное «сжатие» фактически является растяжением с коэффициентом  ) (см. Рис. 15, 16).
) (см. Рис. 15, 16).

Рис. 15. Сжатие к оси 

Рис. 16. Растяжение от оси 
Подобное преобразование мы уже рассматривали в случае построения графика функции  .
.
Ранее мы рассматривали преобразование симметрии относительно оси Ox, то есть функция умножалась на (-1). Рассмотрим случай, когда на (-1) умножается только аргумент.

В этом случае график симметрично отображается относительно оси ординат, так как значения функций будут одинаковы при противоположных значениях аргумента:
для функции 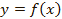 :
:
при 
при 
для функции 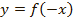 :
:
при 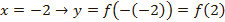
при 
График 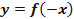 получается из графика функции
получается из графика функции  преобразованием симметрии относительно оси
преобразованием симметрии относительно оси 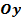 (см. Рис. 17).
(см. Рис. 17).

Рис. 17. Преобразование симметрии относительно оси Oy
Построение графиков  и
и 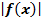
Пусть дан график  , построим график
, построим график  . Для начала раскроем модуль по определению:
. Для начала раскроем модуль по определению:
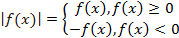
Следовательно, те точки, в которых значения функции положительны или равны 0, остаются на месте, а все точки, в которых значения отрицательны, – отражаются относительно оси  (см. Рис. 18).
(см. Рис. 18).
Урок 13. Построение и преобразование графиков функций. Обзор графиков основных функций. Практика
Подготовка к ЕГЭ по математике
Эксперимент
Урок 13. Построение и преобразование графиков функций. Обзор графиков основных функций
Практика
Конспект урока
Сначала разберем примеры на построение графиков основных функций.
Задача №1. Построить графики функций: а) 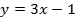 ; б)
; б) 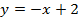 ; в)
; в) 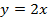 ; г)
; г)  .
.
Решение. Воспользуемся методом построения линейных функций «по точкам».
а) 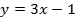
|
|
|
|
0 |
-1 |
|
1 |
2 |

Как видим, 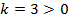 и угол наклона к оси
и угол наклона к оси  острый,
острый,  смещение по оси
смещение по оси 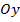 .
.
б) 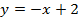
|
|
|
|
0 |
2 |
|
1 |
1 |

 и
и 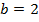 можно сделать аналогичные выводы, как и в первом пункте.
можно сделать аналогичные выводы, как и в первом пункте.
в) 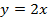
|
|
|
|
0 |
0 |
|
1 |
2 |
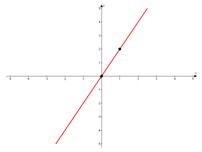
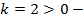 угол наклона к оси
угол наклона к оси острый,
острый,  график проходит через начало координат.
график проходит через начало координат.
г) 

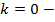 константная функция, прямая проходит через точку
константная функция, прямая проходит через точку  и параллельно оси
и параллельно оси  .
.
Задача №2. Построить графики функций: а)  ; б)
; б) 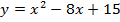 ; в)
; в) 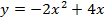 .
.
Решение. Воспользуемся методом построения квадратичных функций «по вершине».
а) 
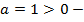 ветки параболы направлены вверх,
ветки параболы направлены вверх, 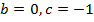 .
.
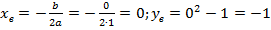
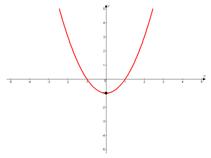
Если возникает вопрос, как точно строится парабола, т.е. с какой именно скоростью растут и убывают ее ветки, то можно запомнить следующий факт: если старший коэффициент  или
или  , как это часто бывает, то при смещении от иксовой координаты вершины на единицу влево или вправо значение функции сначала изменяется на 1, потом на 3, затем на 5 и т.д., т.е. на нечетные числа.
, как это часто бывает, то при смещении от иксовой координаты вершины на единицу влево или вправо значение функции сначала изменяется на 1, потом на 3, затем на 5 и т.д., т.е. на нечетные числа.
Например, в нашем графике:
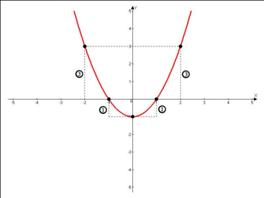
Для функций, у которых старший коэффициент  , значения изменений функции умножаются на это «
, значения изменений функции умножаются на это « ». Например, построение функции
». Например, построение функции  выглядит так:
выглядит так:

Но, как правило такая точность построения не важна, а нужен только эскиз графика, поэтому в дальнейшем мы не будем это учитывать.
б) 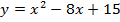
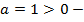 ветки параболы направлены вверх,
ветки параболы направлены вверх, 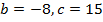 .
.
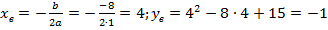
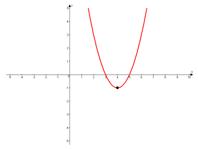
в) 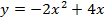
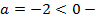 ветки параболы направлены вниз,
ветки параболы направлены вниз,  .
.
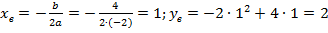

Кстати, график проходит через ноль, что легко проверить подстановкой в функцию точки 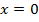 или обратив внимание на то, что
или обратив внимание на то, что  .
.
Задача №3. Построить графики функций: а) 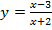 ; б)
; б) 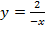 ; в)
; в) 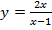 .
.
Решение. Воспользуемся нашим методом построения дробно-рациональных функций «по асимптотам».
а) 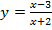
Вертикальная асимптота определяется решением уравнения, которое показывает, что знаменатель дроби равен нулю:  .
.
Горизонтальную асимптоту определим по тому быстрому способу, который мы указали в лекции. Она определяется отношением коэффициентов при иксах в числителе и знаменателе: 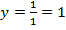 .
.
Для определения расположения веток гиперболы подставим в функцию любую точку из области определения, т.е. кроме , например,
, например, 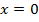 :
: 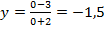 , т.е. координаты этой точки
, т.е. координаты этой точки  через нее и проведем одну ветку гиперболы, вторая будет располагаться наискось.
через нее и проведем одну ветку гиперболы, вторая будет располагаться наискось.
Теперь строим гиперболу, прижимая ее к асимптотам:

Остальные пункты строим аналогично.
б) 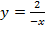
Вертикальная асимптота:  .
.
Горизонтальная асимптота:  , т.е. асимптотами являются оси координат.
, т.е. асимптотами являются оси координат.
Проверочная точка: 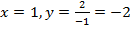 .
.
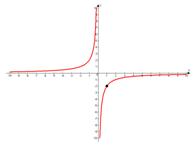
в) 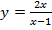
Вертикальная асимптота:  .
.
Горизонтальная асимптота: 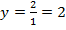 .
.
Проверочная точка: 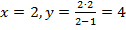 .
.

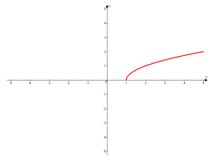
Задача №4. Построить графики функций: а)  , б)
, б)  , в)
, в) 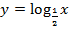 .
.
Решение. По сути дела, указаны функции, которые не имеют особых методов построения их графиков. Поэтому если необходимо изобразить их эскиз, то просто вспоминаем теорию, а если необходимо построить графики более точно, то следует подставить несколько контрольных точек, так и поступим.
а) 
Подставим полные квадраты, чтобы вычислить из них целые значения корня.
|
|
|
|
0 |
0 |
|
1 |
1 |
|
4 |
2 |

б) 
Подставим несколько значений и учтем общий вид графика.
|
|
|
|
0 |
1 |
|
1 |
3 |
|
2 |
9 |
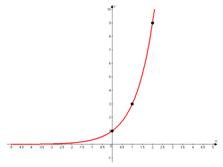
Т.к. основание степени  , то функция растет.
, то функция растет.
в) 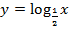
Подставим такие значения аргумента, при которых значения логарифма будут целыми. При построении учтем общий вид графика.

Т.к. основание логарифма  , то функция убывает.
, то функция убывает.
Теперь давайте попробуем научиться решать обратную задачу – по изображенному графику исследовать функцию.
Задача №5. По виду графика определить знаки коэффициентов общего вида функции 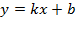 :
:
а) 
б) 
в) 
г) 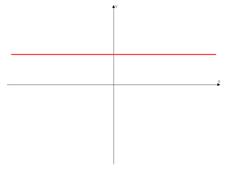
Решение. Для определения знаков коэффициентов  и
и  вспомним, как от них зависят формы графиков.
вспомним, как от них зависят формы графиков.
а) Острый угол наклона прямой к оси 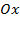 (функция возрастает) – это
(функция возрастает) – это 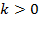 . Точка пересечения с осью
. Точка пересечения с осью  — это
— это  .
.
Далее аналогичные рассуждения.
б) 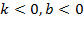
в) 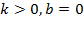
г) Константная функция, т.к. график параллелен оси 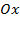 , т.е.
, т.е.  , а
, а  .
.
Задача №6. По виду графика определить знаки коэффициентов общего вида функции 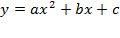 :
:
а) 
б) 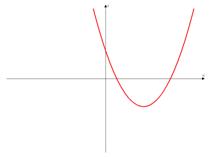
в) 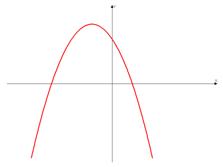
Решение. Вспомним, как параметры 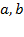 и
и  определяют положение параболы.
определяют положение параболы.
а) Ветви вниз, следовательно, 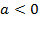 .
.
Точка пересечения с осью  .
.
Иксовая координата вершины  .
.
б) Ветви вверх, следовательно, 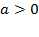 .
.
Точка пересечения с осью  .
.
Иксовая координата вершины 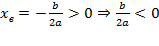 , т.к. неизвестное число при делении на положительное дает отрицательный результат, то это число отрицательное, следовательно,
, т.к. неизвестное число при делении на положительное дает отрицательный результат, то это число отрицательное, следовательно, 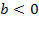 .
.
в) Ветви вниз, следовательно, 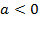 .
.
Точка пересечения с осью 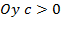 .
.
Иксовая координата вершины 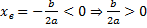 , т.к. неизвестное число при делении на отрицательное дает в результате положительное, то это число отрицательное, следовательно,
, т.к. неизвестное число при делении на отрицательное дает в результате положительное, то это число отрицательное, следовательно,  .
.
И теперь переходим к рассмотрению примеров на преобразование графиков функций.
Задача №7. Построить графики функций: а) 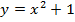 ; б)
; б) 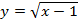 ; в)
; в) 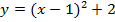 ; г)
; г) 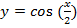 ; д)
; д)  .
.
Решение. Когда сложная функция получена из простейшей путем нескольких преобразований, то преобразования графиков выполняются в порядке арифметических действий с аргументом, например, умножение идет до сложения и т.п.
а) 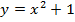
Преобразование в одно действие типа  .
.
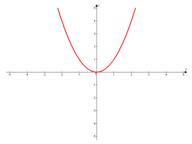

Сдвигаем график вверх на 1: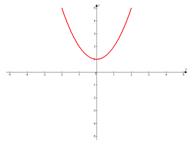
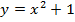
б) 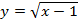
Преобразование в одно действие типа  .
.
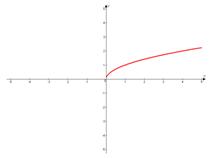

Сдвигаем график вправо на 1:
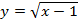
в) 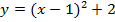
В этом примере два преобразования, выполним их в порядке действий: сначала действия в скобках  , затем сложение
, затем сложение  .
.


Сдвигаем график вправо на 1:


Сдвигаем график вверх на 2:
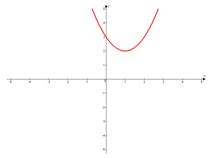

Конечно же, можно построить эту функцию как квадратичную после раскрывания скобок. Проверьте это самостоятельно.
г)
Этап урока, методы и приёмы | Время | Содержание. Деятельность учителя | Деятельность учащихся | УУД |
1. Орг. момент. Словес.: слово учителя. | 1 | Приветствие учителя. | Приветствовать учителя | Р: принимают и сохраняют учебную задачу. |
2. Повторение ранее изученного Словес.: беседа | 1-3 | — В мире искусства существует много разных картин. Все они написаны художниками .Давайте посмотрим на эти картины. — Как называются картины, выполненные в цвете ? (живопись) — Как называются художники, которые пишут живописные картины? (художник-живописец) — Посмотрите на эти изображения( слайд с графикой) — Здесь нет ярких красок. — Чем художник рисовал эти картины(карандашом, черной гелиевой ручкой…. ) — Такой вид работы называется графика. | Слушать учителя, отвечать на вопросы | Р: Умение пользоваться полученной информацией, умение рассказывать по плану |
3. Знакомство с новым материалом | — А как вы думаете, как называют художника, который выполняет работы в графике?(художник — график). — В чем красота графических произведений? Благодаря чему они так выразительны?(таинственное мерцание светлого, чёрного, серого, фантастичность изображений…) — Сегодня на уроке мы будем создавать графическую открытку. — Посмотрите на эти открытки. Что на них изображено? (цветы, ягодки, трава) | формулировать тему, принимать и усваивать учебную задачу | ||
4. Анализ работ | 1-2 | — А сейчас все подойдут к доске и мы с вами рассмотрим изображения, выполненные в графике. — С помощью чего нарисованы изображения? ( точки, линии, штрихи, спирали) — Почему в этом месте получилось темно( показывает на тень в рисунке, скопление точек в тени). | Ответы на вопросы | Р:Умение самостоятельно определять круг задач |
5. Педагогический показ. Демонстрационный: объяснение, показ. | 2-3 | — Сегодня мы будем рисовать на вот таких маленьких красивых медальончиках. ( показать вырезанные медальоны разной формы) — Мы будем создавать графическую открытку, которая называется графическая миниатюра. Миниатюра, то есть мини- маленькая, поэтому наши открытки получатся вот такими маленькими. — Как вы поняли сюжетом у открытки будет?( фрагмент природы) -Сейчас на своих разных по форме медальонах, я вам покажу, как нужно выполнять эту работу. — На одном я нарисую красивую веточку с листочками и ягодками, а сверху нарисую бабочку. Затем заполню все внутри штрихами, точками или спиралями. — Затем, чтобы выделить края медальончика, выполню узор-бордюр. — На втором медальончике я нарисую цветы, а сверху опять рисую бабочку. Внутри также заполню штрихами и точками и украшу край медальона узором. — Когда ваш медальон будет выполнен, возьмите картон любого цвета, разделите его пополам и приклейте медальон на него. — Для вас я принесла свою готовую открытку, посмотрите. | Наблюдают и усваивают приёмы и порядок выполнения работы. Принимают общую задачу. | П: умение следить и усваивать практические приёмы работы. Р: умение воспринимать задачу, мобильно выполнять работу. Формирование ответственного творческого отношения к работе. |
6. Практическая работа. | 15-20 | Используйте только штрихи и линии. Вам нужно нарисовать графически какой-либо элемент природы. А сейчас приступайте к работе. Желаю вам успехов и хорошей творческой работы. Я думаю, что вы с легкостью справитесь с этим задание и в конце урока у нас будет много красивых графических миниатюр. | Самостоятельно выполняют задание. | Р: умение организовывать свою учебную задачу. Учиться определять степень успешности выполнения своей работы, давать оценку работе. |
7. Итог урока. | 2-3 | — Ребята, время выполнения творческой работы подошло к концу, пожалуйста, заканчивайте свою работу. Давайте полюбуемся работами друг друга. Приносим свои работы и кладем их на пол у доски. — Какие работы наиболее творческие? — Я очень довольна вашей работой! Молодцы ребята! | Анализировать продленную работу на уроке, оценивать свои силы, высказывать своё мнение. | Р: самооценка, умение анализировать результаты своего труда и труда других. |