Сфера, шар, сегмент и сектор. Формулы и свойства
Определение.
Сфера (поверхность шара) — это совокупность всех точек в трехмерном пространстве, которые находятся на одинаковом расстоянии от одной точки, называемой центром сферы (О).Сферу можно описать, как объёмную фигуру, которая образуется вращением окружности вокруг своего диаметра на 180° или полуокружности вокруг своего диаметра на 360°.
Определение.
Шар — это совокупность всех точек в трехмерном пространстве, расстояние от которых не превышает определенного расстояния до точки, называемой центром шара (О) (совокупность всех точек трехмерного пространства ограниченных сферой).Шар можно описать как объёмную фигуру, которая образуется вращением круга вокруг своего диаметра на 180° или полуокружности вокруг своего диаметра на 360°.
Определение. Радиус сферы (шара) (R) — это расстояние от центра сферы (шара) O к любой точке сферы (поверхности шара).
Определение. Диаметр сферы (шара) (D) — это отрезок, соединяющий две точки сферы (поверхности шара) и проходящий через ее центр.
Формула. Объём шара: Формула. Площадь поверхности сферы через радиус или диаметр:S = 4πR2 = πD2
Уравнение сферы
1. Уравнение сферы с радиусом R и центром в начале декартовой системе координат:x2 + y2 + z2 = R2
2. Уравнение сферы с радиусом R и центром в точке с координатами (x0, y0, z0) в декартовой системе координат(x — x0)2 + (y — y0)2 + (z — z0)2 = R2
3. Параметрическое уравнение сферы с центром в точке (x0, y0, z0):x = x0 + R · sin θ · cos φy = y0 + R · sin θ · sin φz = z0 + R · cos θ
где θ ϵ [0,π], φ ϵ [0,2π].

Определение. Диаметрально противоположными точками называются любые две точки на поверхности шара (сфере), которые соединены диаметром.
Основные свойства сферы и шара
1. Все точки сферы одинаково удалены от центра.
3. Любое сечение шара плоскостью есть кругом.
4. Сфера имеет наибольший объём среди всех пространственных фигур с одинаковой площадью поверхности.
5. Через любые две диаметрально противоположные точки можно провести множество больших окружностей для сферы или кругов для шара.
6. Через любые две точки, кроме диаметрально противоположных точек, можно провести только одну большую окружность для сферы или большой круг для шара.
7. Любые два больших круга одного шара пересекаются по прямой, проходящей через центр шара, а окружности пересекаются в двух диаметрально противоположных точках.
8. Если расстояние между центрами любых двух шаров меньше суммы их радиусов и больше модуля разности их радиусов, то такие шары

Секущая, хорда, секущая плоскость сферы и их свойства
Определение. Секущая сферы — это прямая, которая пересекает сферу в двух точках. Точки пересечения называются точками протыкания поверхности или точками входа и выхода на поверхности.
Определение. Хорда сферы (шара) — это отрезок, соединяющий две точки сферы (поверхности шара).
Определение. Секущая плоскость — это плоскость, которая пересекает сферу.
Определение. Диаметральная плоскость
Любая хорда, проходящая через центр сферы (шара) является диаметром.
Хорда является отрезком секущей прямой.
Расстояние d от центра сферы до секущей всегда меньше чем радиус сферы:d < R
Расстояние m между секущей плоскостью и центром сферы всегда меньше радиуса R:m < R
Местом сечения секущей плоскости на сфере всегда будет малая окружность, а на шаре местом сечения будет малый круг.
r = √R2 — m2,
где R — радиус сферы (шара), m — расстояние от центра шара до секущей плоскости.Определение. Полусфера (полушар) — это половина сферы (шара), которая образуется при ее сечении диаметральной плоскостью.
Касательная, касательная плоскость к сфере и их свойства
Определение.Касательная к сфере — это прямая, которая касается сферы только в одной точке.
Определение.Касательная плоскость к сфере — это плоскость, которая соприкасается со сферой только в одной точке.
Касательная пряма (плоскость) всегда перпендикулярна радиусу сферы проведенному к точке соприкосновения
Расстояние от центра сферы до касательной прямой (плоскости) равно радиусу сферы.
Определение. Сегмент шара — это часть шара, которая отсекается от шара секущей плоскостью. Основой сегмента называют круг, который образовался в месте сечения. Высотой сегмента h называют длину перпендикуляра проведенного с середины основы сегмента к поверхности сегмента. Формула. Площадь внешней поверхности сегмента сферы с высотой h через радиус сферы R:
Основой сегмента называют круг, который образовался в месте сечения. Высотой сегмента h называют длину перпендикуляра проведенного с середины основы сегмента к поверхности сегмента. Формула. Площадь внешней поверхности сегмента сферы с высотой h через радиус сферы R:S = 2πRh
Формула. Объём сегмента сферы с высотой h через радиус сферы R: Определение.S = πR(2h + √2hR — h2)
Формула. Объём сектора V с высотой O1H (h) через радиус шара OH (R):Определение. Касательными сферами (шарами) называются любые две сферы (шара), которые имеют одну общую точку соприкосновения.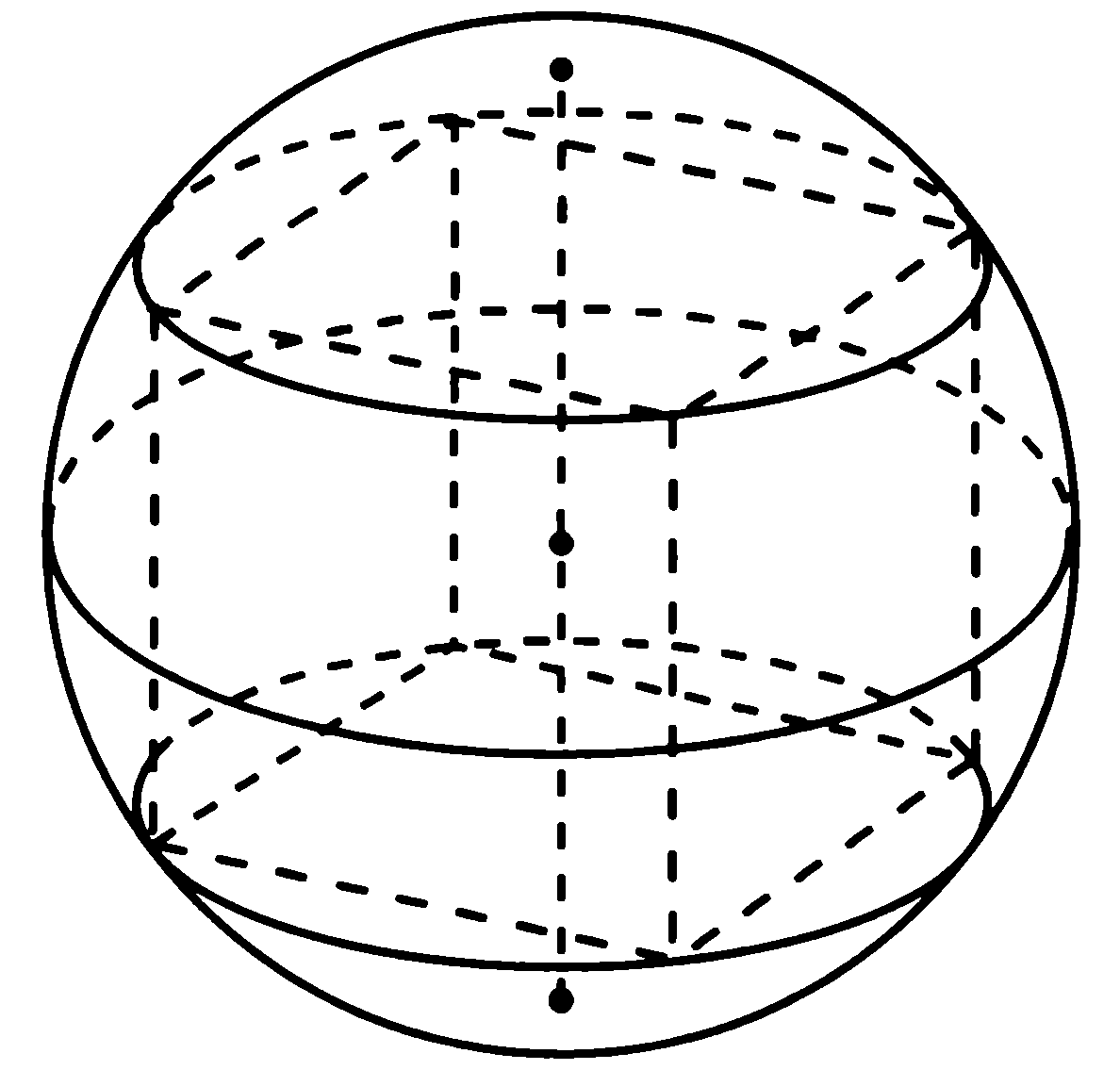
Страница не найдена (#404)
Toggle navigationWallBox- Найди отличия
- Категории
- 3D обои
- Hi-Tech
- Авиация
- Аниме
- Город
- Девушки
- Еда
- Животные
- Игры
- Космос
- Кошки
- Макро
- Машины
- Минимализм
- Мужчины
- Музыка
- Мультфильмы
- Настроения
- Оружие
- Пейзажи
- Праздники
- Природа
- Разное
- Роскошь
- Ситуации
- Собаки
- Спорт
- Стиль
- Текстуры
- Фантастика
- Фильмы
- Цветы
- Аниме эротика
- Эротика
- ТОП Пользователей
- Подборки
- Подборки
- ТОП Подборок пользователей
- Добавить обои
- Песочница
- Вход/Регистрация
Случайные обои
Разное4333
Разное28390
Разное3123
Разное2615
Разное4097
Разное2897
Разное3182
Разное4989
Разное2125
Разное2639
Разное3395
Разное2070
Разное3485
Разное2989
Разное1718
Разное4593
Разное3198
Разное7483
Разное4247
Разное3149
Разное4623
Разное3848
Разное6495
Разное4326
Разное25509
Разное10830
Разное7135
Разное7761
Разное5559
Разное8399
Разное9854
Разное2796
Разное4002
Разное7751
Разное23226
Разное10450
Разное2764
Разное3751
Разное5808
Разное2603
Разное2492
Разное4277
Разное3504
Разное3841
4291
Разное20770
Разное9654
Разное25032
Разное2582
Разное16803
Разное6017
Разное8489
Разное5225
Разное3120
Разное2750
Разное11387
Разное3558
Разное3888
Разное5521
- © WallBox 2021
- Обратная связь
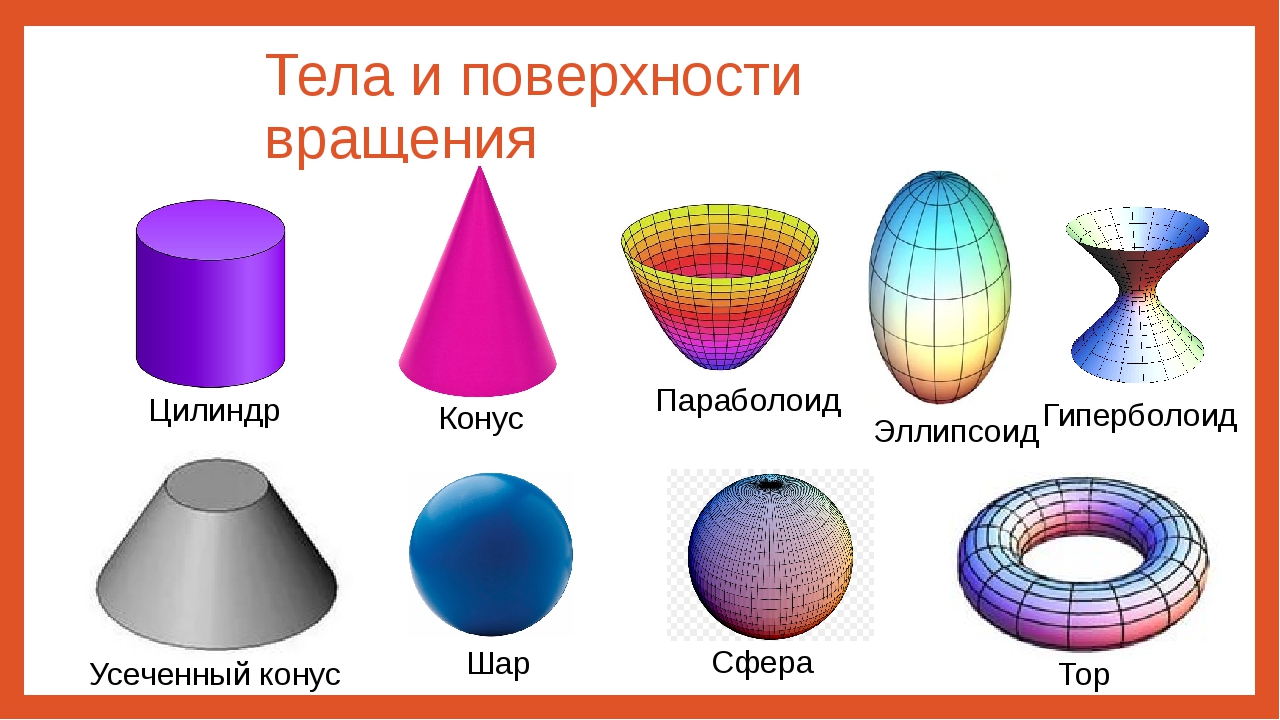
Цилиндр, конус, шар, развёртка цилиндра и конуса
Цилиндр, конус и шар относятся к объемным (трехмерным) геометрическим фигурам вращения.
Объемные фигуры вращения (еще говорят — «тела», подразумевая объемность фигуры), как правило, образованы вращением плоской фигуры вокруг какой-то линии (прямой).
Так, цилиндр — это фигура, полученная от вращения прямоугольника вокруг одной из его сторон как оси; конус — вращением прямоугольного треугольника вокруг его катета как оси, шар — вращением полукруга вокруг его диаметра как оси.
Объемные фигуры бывают прямые (прямой цилиндр, прямой конус) и наклонные (наклонный цилиндр, наклонный конус), что зависит от вида той плоской геометрической фигуры, которая их образует.
В курсе математики для б класса рассматриваются только прямые цилиндры и конусы
.
Определение. Цилиндр
Определение. Конус (прямой) — это тело (объемная геометрическая фигура), полученное вращением прямоугольного треугольника вокруг его катета как оси.
Определение. Шар — это тело (объемная геометрическая фигура), полученное вращением полукруга вокруг его диаметра как оси.
Развертки цилиндра и конуса
Разверткой геометрической фигуры называется изображение плоскости, ограничивающей фигуру, в одной плоскости листа по размерам фигуры.
Развертка цилиндра приведена схематически.
Развертка конуса приведена схематически.
Площади боковой поверхности цилиндра и конуса
Правило. Площадь боковой поверхности цилиндра равна произведению длины окружности основания и высоты цилиндра.
где C — длина окружности, H — высота цилиндра, R — радиус окружности основания.
Правило. Площадь боковой поверхности конуса равна произведению половины длины окружности основания и образующей конуса.
где C — длина окружности основания, l — длина образующей конуса, R — радиус основания.
Площадь поверхности шара
Правило. Площадь поверхности шара равна учетверенной площади большого круга шара.
где R — радиус шара.
Объемы цилиндра, конуса и шара
Правило. Объем цилиндра равен произведению площади основания н высоты.
где R — радиус основания, H — высота цилиндра.
Правило. Объем конуса равен одной трети произведения площади основания и высоты конуса.
где R — радиус основания, H — высота конуса.
Правило. Объем шара равен четырем третям
произведения числа Пи на куб радиуса.
где R — радиус шара.
Стереометрия (Геометрия в пространстве) — Все свойства, теоремы, аксиомы и формулы — Математика
Оглавление:
Базовые теоремы, аксиомы и определения стереометрии
Вводные определения и аксиомы стереометрии
К оглавлению…
Некоторые определения:
- Многогранник представляет собой геометрическое тело, ограниченное конечным числом плоских многоугольников, любые два из которых, имеющие общую сторону, не лежат в одной плоскости.
 При этом сами многоугольники называются гранями, их стороны – ребрами многогранника, а их вершины – вершинами многогранника.
При этом сами многоугольники называются гранями, их стороны – ребрами многогранника, а их вершины – вершинами многогранника. - Фигура, образованная всеми гранями многогранника, называется его поверхностью (полной поверхностью), а сумма площадей всех его граней – площадью (полной) поверхности.
- Куб – это многогранник, имеющий шесть граней, которые являются равными квадратами. Стороны квадратов называются ребрами куба, а вершины – вершинами куба.
- Параллелепипед – это многогранник, у которого шесть граней и каждая из них – параллелограмм. Стороны параллелограммов называются ребрами параллелепипеда, а их вершины – вершинами параллелепипеда. Две грани параллелепипеда называются противолежащими, если они не имеют общего ребра, а имеющие общее ребро называются смежными. Иногда какие-нибудь две противолежащие грани параллелепипеда выделяются и называются основаниями, тогда остальные грани – боковыми гранями, а их стороны, соединяющие вершины оснований параллелепипеда, – его боковыми ребрами.

- Прямой параллелепипед – это такой параллелепипед, у которого боковые грани – прямоугольники. Прямоугольный параллелепипед – это параллелепипед, у которого все грани – прямоугольники. Заметим, что всякий прямоугольный параллелепипед является прямым параллелепипедом, но не любой прямой параллелепипед есть прямоугольный.
- Две вершины параллелепипеда, не принадлежащие одной грани, называются противолежащими. Отрезок, соединяющий противолежащие вершины параллелепипеда, называется диагональю параллелепипеда. У параллелепипеда всего четыре диагонали.
- Призма (n-угольная) – это многогранник, у которого две грани – равные n-угольники, а остальные n граней – параллелограммы. Равные n-угольники называются основаниями, а параллелограммы – боковыми гранями призмы. Прямая призма – это такая призма, у которой боковые грани – прямоугольники.
 Правильная n-угольная призма – это призма, у которой все боковые грани – прямоугольники, а ее основания – правильные n-угольники.
Правильная n-угольная призма – это призма, у которой все боковые грани – прямоугольники, а ее основания – правильные n-угольники. - Сумма площадей боковых граней призмы называется площадью ее боковой поверхности (обозначается Sбок). Сумма площадей всех граней призмы называется площадью поверхности призмы (обозначается Sполн).
- Пирамида (n-угольная) – это многогранник, у которого одна грань – какой-нибудь n-угольник, а остальные n граней – треугольники с общей вершиной; n-угольник называется основанием; треугольники, имеющие общую вершину, называются боковыми гранями, а их общая вершина называется вершиной пирамиды. Стороны граней пирамиды называются ее ребрами, а ребра, сходящиеся в вершине, называются боковыми.
- Сумма площадей боковых граней пирамиды называется площадью боковой поверхности пирамиды (обозначается Sбок).
 Сумма площадей всех граней пирамиды называется площадью поверхности пирамиды (площадь поверхности обозначается Sполн).
Сумма площадей всех граней пирамиды называется площадью поверхности пирамиды (площадь поверхности обозначается Sполн). - Правильная n-угольная пирамида – это такая пирамида, основание которой – правильный n-угольник, а все боковые ребра равны между собой. У правильной пирамиды боковые грани – равные друг другу равнобедренные треугольники.
- Треугольная пирамида называется тетраэдром, если все ее грани – равные правильные треугольники. Тетраэдр является частным случаем правильной треугольной пирамиды (т.е. не каждая правильная треугольная пирамида будет тетраэдром).
Аксиомы стереометрии:
- Через любые три точки, не лежащие на одной прямой, проходит единственная плоскость.
- Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.
- Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.

Следствия из аксиом стереометрии:
- Теорема 1. Через прямую и не лежащую на ней точку проходит единственная плоскость.
- Теорема 2. Через две пересекающиеся прямые проходит единственная плоскость.
- Теорема 3. Через две параллельные прямые проходит единственная плоскость.
Построение сечений в стереометрии
К оглавлению…
Для решения задач по стереометрии остро необходимо умение строить на рисунке сечения многогранников (например, пирамиды, параллелепипеда, куба, призмы) некоторой плоскостью. Дадим несколько определений, поясняющих, что такое сечение:
- Секущей плоскостью пирамиды (призмы, параллелепипеда, куба) называется такая плоскость, по обе стороны от которой есть точки данной пирамиды (призмы, параллелепипеда, куба).
- Сечением пирамиды (призмы, параллелепипеда, куба) называется фигура, состоящая из всех точек, которые являются общими для пирамиды (призмы, параллелепипеда, куба) и секущей плоскости.

- Секущая плоскость пересекает грани пирамиды (параллелепипеда, призмы, куба) по отрезкам, поэтому сечение есть многоугольник, лежащий в секущей плоскости, сторонами которого являются указанные отрезки.
Для построения сечения пирамиды (призмы, параллелепипеда, куба) можно и нужно построить точки пересечения секущей плоскости с ребрами пирамиды (призмы, параллелепипеда, куба) и соединить каждые две из них, лежащие в одной грани. Заметим, что последовательность построения вершин и сторон сечения не существенна. В основе построения сечений многогранников лежит две задачи на построение:
- Линии пересечения двух плоскостей.
Для построения прямой, по которой пересекаются некоторые две плоскости α и β (например, секущая плоскость и плоскость грани многогранника), нужно построить две их общие точки, тогда прямая, проходящая через эти точки, есть линия пересечения плоскостей α и β.
- Точки пересечения прямой и плоскости.
Для построения точки пересечения прямой l и плоскости α нужно построить точку пересечения прямой l и прямой l1, по которой пересекаются плоскость α и любая плоскость, содержащая прямую l.
Взаимное расположение прямых и плоскостей в стереометрии
К оглавлению…
Определение: В ходе решения задач по стереометрии две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются. Если прямые а и b, либо AB и CD параллельны, то пишут:
Несколько теорем:
- Теорема 1. Через любую точку пространства, не лежащую на данной прямой, проходит единственная прямая, параллельная данной прямой.
- Теорема 2. Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.

- Теорема 3 (признак параллельности прямых). Если две прямые параллельны третьей прямой, то они параллельны между собой.
- Теорема 4 (о точке пересечения диагоналей параллелепипеда). Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.
Возможны три случая взаимного расположения прямой и плоскости в стереометрии:
- Прямая лежит в плоскости (каждая точка прямой лежит в плоскости).
- Прямая и плоскость пересекаются (имеют единственную общую точку).
- Прямая и плоскость не имеют ни одной общей точки.
Определение: Прямая и плоскость называются параллельными, если они не имеют общих точек. Если прямая а параллельна плоскости β, то пишут:
Теоремы:
- Теорема 1 (признак параллельности прямой и плоскости). Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости.

- Теорема 2. Если плоскость (на рисунке – α) проходит через прямую (на рисунке – с), параллельную другой плоскости (на рисунке – β), и пересекает эту плоскость, то линия пересечения плоскостей (на рисунке – d) параллельна данной прямой:
Если две различные прямые лежат в одной плоскости, то они либо пересекаются, либо параллельны. Однако, в пространстве (т.е. в стереометрии) возможен и третий случай, когда не существует плоскости, в которой лежат две прямые (при этом они и не пересекаются, и не параллельны).
Определение: Две прямые называются скрещивающимися, если не существует плоскости, в которой они обе лежат.
Теоремы:
- Теорема 1 (признак скрещивающихся прямых). Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не принадлежащей первой прямой, то эти прямые скрещивающиеся.

- Теорема 2. Через каждую из двух скрещивающихся прямых проходит единственная плоскость, параллельная другой прямой.
Теперь введем понятие угла между скрещивающимися прямыми. Пусть a и b – две скрещивающиеся прямые. Возьмем произвольную точку O в пространстве и проведем через нее прямые a1 и b1, параллельные прямым a и b соответственно. Углом между скрещивающимися прямыми a и b называется угол между построенными пересекающимися прямыми a1 и b1.
Однако на практике точку O чаще выбирают так, чтобы она принадлежала одной из прямых. Это обычно не только элементарно удобнее, но и рациональнее и правильнее с точки зрения построения чертежа и решения задачи. Поэтому для угла между скрещивающимися прямыми дадим такое определение:
Определение: Пусть a и b – две скрещивающиеся прямые. Возьмем произвольную точку O на одной из них (в нашем случае, на прямой b) и проведем через неё прямую параллельную другой из них (в нашем случае a1 параллельна a). Углом между скрещивающимися прямыми a и b называется угол между построенной прямой и прямой, содержащей точку O (в нашем случае это угол β между прямыми a1 и b).
Возьмем произвольную точку O на одной из них (в нашем случае, на прямой b) и проведем через неё прямую параллельную другой из них (в нашем случае a1 параллельна a). Углом между скрещивающимися прямыми a и b называется угол между построенной прямой и прямой, содержащей точку O (в нашем случае это угол β между прямыми a1 и b).
Определение: Две прямые называются взаимно перпендикулярными (перпендикулярными), если угол между ними равен 90°. Перпендикулярными могут быть как скрещивающиеся прямые, так и прямые лежащие и пересекающиеся в одной плоскости. Если прямая a перпендикулярна прямой b, то пишут:
Определение: Две плоскости называются параллельными, если они не пересекаются, т.е. не имеют общих точек. Если две плоскости α и β параллельны, то, как обычно, пишут:
Теоремы:
- Теорема 1 (признак параллельности плоскостей).
 Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.
Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны. - Теорема 2 (о свойстве противолежащих граней параллелепипеда). Противолежащие грани параллелепипеда лежат в параллельных плоскостях.
- Теорема 3 (о прямых пересечения двух параллельных плоскостей третьей плоскостью). Если две параллельные плоскости пересечены третьей, то прямые их пересечения параллельны между собой.
- Теорема 4. Отрезки параллельных прямых, расположенные между параллельными плоскостями, равны.
- Теорема 5 (о существовании единственной плоскости, параллельной данной плоскости и проходящей через точку вне ее). Через точку, не лежащую в данной плоскости, проходит единственная плоскость, параллельная данной.
Определение: Прямая, пересекающая плоскость, называется перпендикулярной плоскости, если она перпендикулярна каждой прямой, лежащей в этой плоскости. Если прямая a перпендикулярна плоскости β, то пишут, как обычно:
Если прямая a перпендикулярна плоскости β, то пишут, как обычно:
Теоремы:
- Теорема 1. Если одна из двух параллельных прямых перпендикулярна третьей прямой, то и другая прямая перпендикулярна этой прямой.
- Теорема 2. Если одна из двух параллельных прямых перпендикулярна плоскости, то и другая прямая перпендикулярна этой плоскости.
- Теорема 3 (о параллельности прямых, перпендикулярных плоскости). Если две прямые перпендикулярны одной плоскости, то они параллельны.
- Теорема 4 (признак перпендикулярности прямой и плоскости). Если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна этой плоскости.
- Теорема 5 (о плоскости, проходящей через данную точку и перпендикулярной данной прямой). Через любую точку пространства проходит единственная плоскость, перпендикулярная данной прямой.

- Теорема 6 (о прямой, проходящей через данную точку и перпендикулярной данной плоскости). Через любую точку пространства проходит единственная прямая, перпендикулярная данной плоскости.
- Теорема 7 (о свойстве диагонали прямоугольного параллелепипеда). Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов длин трех его ребер, имеющих общую вершину:
Следствие: Все четыре диагонали прямоугольного параллелепипеда равны между собой.
Теорема о трех перпендикулярах
К оглавлению…
Пусть точка А не лежит на плоскости α. Проведем через точку А прямую, перпендикулярную плоскости α, и обозначим буквой О точку пересечения этой прямой с плоскостью α. Перпендикуляром, проведенным из точки А к плоскости α, называется отрезок АО, точка О называется основанием перпендикуляра. Если АО – перпендикуляр к плоскости α, а М – произвольная точка этой плоскости, отличная от точки О, то отрезок АМ называется наклонной, проведенной из точки А к плоскости α, а точка М – основанием наклонной. Отрезок ОМ – ортогональная проекция (или, короче, проекция) наклонной АМ на плоскость α. Теперь приведем теорему, которая играет важную роль при решении многих задач.
Если АО – перпендикуляр к плоскости α, а М – произвольная точка этой плоскости, отличная от точки О, то отрезок АМ называется наклонной, проведенной из точки А к плоскости α, а точка М – основанием наклонной. Отрезок ОМ – ортогональная проекция (или, короче, проекция) наклонной АМ на плоскость α. Теперь приведем теорему, которая играет важную роль при решении многих задач.
Теорема 1 (о трех перпендикулярах): Прямая, проведенная в плоскости и перпендикулярная проекции наклонной на эту плоскость, перпендикулярна и самой наклонной. Верно и обратное утверждение:
Теорема 2 (о трех перпендикулярах): Прямая, проведенная в плоскости и перпендикулярная наклонной, перпендикулярна и ее проекции на эту плоскость. Данные теоремы, для обозначений с чертежа выше можно кратко сформулировать так:
Теорема: Если из одной точки, взятой вне плоскости, проведены к этой плоскости перпендикуляр и две наклонные, то:
- две наклонные, имеющие равные проекции, равны;
- из двух наклонных больше та, проекция которой больше.

Определения расстояний объектами в пространстве:
- Расстоянием от точки до плоскости называется длина перпендикуляра, проведенного из этой точки к данной плоскости.
- Расстоянием между параллельными плоскостями называется расстояние от произвольной точки одной из параллельных плоскостей до другой плоскости.
- Расстоянием между прямой и параллельной ей плоскостью называется расстояние от произвольной точки прямой до плоскости.
- Расстоянием между скрещивающимися прямыми называется расстояние от одной из скрещивающихся прямых до плоскости, проходящей через другую прямую и параллельной первой прямой.
Определение: В стереометрии ортогональной проекцией прямой a на плоскость α называется проекция этой прямой на плоскость α в случае, если прямая, определяющая направление проектирования, перпендикулярна плоскости α.
Замечание: Как видно из предыдущего определения, проекций бывает много. Другие (кроме ортогональной) проекции прямой на плоскость можно построить если прямая определяющая направление проецирования будет не перпендикулярна плоскости. Однако, именно ортогональную проекцию прямой на плоскость в будущем мы будем встречать в задачах. А называть ортогональную проекцию будем просто проекцией (как на чертеже).
Другие (кроме ортогональной) проекции прямой на плоскость можно построить если прямая определяющая направление проецирования будет не перпендикулярна плоскости. Однако, именно ортогональную проекцию прямой на плоскость в будущем мы будем встречать в задачах. А называть ортогональную проекцию будем просто проекцией (как на чертеже).
Определение: Углом между прямой, не перпендикулярной плоскости, и этой плоскостью называется угол между прямой и ее ортогональной проекцией на данную плоскость (угол АОА’ на чертеже выше).
Теорема: Угол между прямой и плоскостью является наименьшим из всех углов, которые данная прямая образует с прямыми, лежащими в данной плоскости и проходящими через точку пересечения прямой и плоскости.
Двугранный угол
К оглавлению…
Определения:
- Двугранным углом называется фигура, образованная двумя полуплоскостями с общей граничной прямой и частью пространства, для которой эти полуплоскости служат границей.

- Линейным углом двугранного угла называется угол, сторонами которого являются лучи с общим началом на ребре двугранного угла, которые проведены в его гранях перпендикулярно ребру.
Таким образом, линейный угол двугранного угла – это угол, образованный пересечением двугранного угла плоскостью, перпендикулярной его ребру. Все линейные углы двугранного угла равны между собой. Градусной мерой двугранного угла называется градусная мера его линейного угла.
Двугранный угол называется прямым (острым, тупым), если его градусная мера равна 90° (меньше 90°, больше 90°). В дальнейшем, при решении задач по стереометрии, под двугранным углом будем понимать всегда тот линейный угол, градусная мера которого удовлетворяет условию:
Определения:
- Двугранным углом при ребре многогранника называется двугранный угол, ребро которого содержит ребро многогранника, а грани двугранного угла содержат грани многогранника, которые пересекаются по данному ребру многогранника.

- Углом между пересекающимися плоскостями называется угол между прямыми, проведенными соответственно в данных плоскостях перпендикулярно их линии пересечения через некоторую ее точку.
- Две плоскости называются перпендикулярными, если угол между ними равен 90°.
Теоремы:
- Теорема 1 (признак перпендикулярности плоскостей). Если одна из двух плоскостей проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.
- Теорема 2. Прямая, лежащая в одной из двух перпендикулярных плоскостей и перпендикулярная прямой, по которой они пересекаются, перпендикулярна другой плоскости.
Симметрия фигур
К оглавлению…
Определения:
- Точки M и M1 называются симметричными относительно точки O, если O является серединой отрезка MM1.

- Точки M и M1 называются симметричными относительно прямой l, если прямая l проходит через середину отрезка MM1 и перпендикулярна ему.
- Точки M и M1 называются симметричными относительно плоскости α, если плоскость α проходит через середину отрезка MM1 и перпендикулярна этому отрезку.
- Точка O (прямая l, плоскость α) называется центром (осью, плоскостью) симметрии фигуры, если каждая точка фигуры симметрична относительно точки O (прямой l, плоскости α) некоторой точке этой же фигуры.
- Выпуклый многогранник называется правильным, если все его грани – равные между собой правильные многоугольники и в каждой вершине сходится одно и то же число ребер.
Призма
К оглавлению. ..
..
Определения:
- Призма – многогранник, две грани которого являются равными многоугольниками, лежащими в параллельных плоскостях, а остальные грани – параллелограммами, имеющими общие стороны с этими многоугольниками.
- Основания – это две грани, являющиеся равными многоугольниками, лежащими в параллельных плоскостях. На чертеже это: ABCDE и KLMNP.
- Боковые грани – все грани, кроме оснований. Каждая боковая грань обязательно является параллелограммом. На чертеже это: ABLK, BCML, CDNM, DEPN и EAKP.
- Боковая поверхность – объединение боковых граней.
- Полная поверхность – объединение оснований и боковой поверхности.
- Боковые ребра – общие стороны боковых граней. На чертеже это: AK, BL, CM, DN и EP.

- Высота – отрезок, соединяющий основания призмы и перпендикулярный им. На чертеже это, например, KR.
- Диагональ – отрезок, соединяющий две вершины призмы, не принадлежащие одной грани. На чертеже это, например, BP.
- Диагональная плоскость – плоскость, проходящая через боковое ребро призмы и диагональ основания. Другое определение: диагональная плоскость – плоскость, проходящая через два боковых ребра призмы, не принадлежащих одной грани.
- Диагональное сечение – пересечение призмы и диагональной плоскости. В сечении образуется параллелограмм, в том числе, иногда, его частные случаи – ромб, прямоугольник, квадрат. На чертеже это, например, EBLP.
- Перпендикулярное (ортогональное) сечение – пересечение призмы и плоскости, перпендикулярной ее боковому ребру.
Свойства и формулы для призмы:
- Основания призмы являются равными многоугольниками.

- Боковые грани призмы являются параллелограммами.
- Боковые ребра призмы параллельны и равны.
- Объём призмы равен произведению её высоты на площадь основания:
где: Sосн – площадь основания (на чертеже это, например, ABCDE), h – высота (на чертеже это MN).
- Площадь полной поверхности призмы равна сумме площади её боковой поверхности и удвоенной площади основания:
- Перпендикулярное сечение перпендикулярно ко всем боковым рёбрам призмы (на чертеже ниже перпендикулярное сечение это A2B2C2D2E2).
- Углы перпендикулярного сечения – это линейные углы двугранных углов при соответствующих боковых рёбрах.
- Перпендикулярное (ортогональное) сечение перпендикулярно ко всем боковым граням.
- Объем наклонной призмы равен произведению площади перпендикулярного сечения на длину бокового ребра:
где: Sсеч – площадь перпендикулярного сечения, l – длина бокового ребра (на чертеже ниже это, например, AA1 или BB1 и так далее).
- Площадь боковой поверхности произвольной призмы равна произведению периметра перпендикулярного сечения на длину бокового ребра:
где: Pсеч – периметр перпендикулярного сечения, l – длина бокового ребра.
Виды призм в стереометрии:
- Если боковые ребра не перпендикулярны основанию, то такая призма называется наклонной (изображены выше). Основания такой призмы, как обычно, расположены в параллельных плоскостях, боковые рёбра не перпендикулярны этим плоскостям, но параллельны между собой. Боковые грани – параллелограммы.
- Прямая призма – призма, у которой все боковые ребра перпендикулярны основанию. В прямой призме боковые ребра являются высотами. Боковые грани прямой призмы — прямоугольники. А площадь и периметр основания равны соответственно площади и периметру перпендикулярного сечения (у прямой призмы, вообще говоря, перпендикулярное сечение целиком является такой же фигурой, как и основания).
 Поэтому, площадь боковой поверхности прямой призмы равна произведению периметра основания на длину бокового ребра (или, в данном случае, высоту призмы):
Поэтому, площадь боковой поверхности прямой призмы равна произведению периметра основания на длину бокового ребра (или, в данном случае, высоту призмы):
где: Pосн – периметр основания прямой призмы, l – длина бокового ребра, равная в прямой призме высоте (h). Объем прямой призмы находится по общей формуле: V = Sосн∙h = Sосн∙l.
- Правильная призма – призма в основании которой лежит правильный многоугольник (т.е. такой, у которого все стороны и все углы равны между собой), а боковые ребра перпендикулярны плоскостям основания. Примеры правильных призм:
Свойства правильной призмы:
- Основания правильной призмы являются правильными многоугольниками.
- Боковые грани правильной призмы являются равными прямоугольниками.
- Боковые ребра правильной призмы равны между собой.

- Правильная призма является прямой.
Параллелепипед
К оглавлению…
Определение: Параллелепипед – это призма, основания которой параллелограммы. В этом определении ключевым словом является «призма». Таким образом, параллелепипед – это частный случай призмы, которая отличается от общего случая только тем, что в основании у нее не произвольный многоугольник, а именно параллелограмм. Поэтому все приведенные выше свойства, формулы и определения касающиеся призмы остаются актуальными и для параллелепипеда. Однако, можно выделить несколько дополнительных свойств характерных для параллелепипеда.
Другие свойства и определения:
- Две грани параллелепипеда, не имеющие общего ребра, называются противолежащими, а имеющие общее ребро – смежными.
- Две вершины параллелепипеда, не принадлежащие одной грани, называются противолежащими.

- Отрезок, соединяющий противолежащие вершины, называется диагональю параллелепипеда.
- Параллелепипед имеет шесть граней и все они – параллелограммы.
- Противоположные грани параллелепипеда попарно равны и параллельны.
- У параллелепипеда четыре диагонали; они все пересекаются в одной точке, и каждая из них делится этой точкой пополам.
- Если четыре боковые грани параллелепипеда – прямоугольники (а основания – произвольные параллелограммы), то он называется прямым (в этом случае, как и у прямой призмы, все боковые ребра перпендикулярны основаниям). Все свойства и формулы для прямой призмы актуальны для прямого параллелепипеда.
- Параллелепипед называется наклонным, если не все его боковые грани являются прямоугольниками.
- Объем прямого или наклонного параллелепипеда рассчитывается по общей формуле для объема призмы, т.е. равен произведению площади основания параллелепипеда на его высоту (V = Sосн∙h).

- Прямой параллелепипед, у которого все шесть граней – прямоугольники (т.е. кроме боковых граней еще и основания являются прямоугольниками), называется прямоугольным. Для прямоугольного параллелепипеда актуальны все свойства прямого параллелепипеда, а также:
- Диагональ прямоугольного параллелепипеда d и его рёбра a, b, c связаны соотношением:
d2 = a2 + b2 + c2.
-
- Из общей формулы для объема призмы можно получить следующую формулу для объема прямоугольного параллелепипеда:
- Прямоугольный параллелепипед, все грани которого являются равными квадратами, называется кубом. Помимо прочего, куб является правильной четырехугольной призмой, и вообще правильным многогранником. Для куба справедливы все свойства прямоугольного параллелепипеда и свойства правильных призм, а также:
- Абсолютно все рёбра куба равны между собой.

- Диагональ куба d и длина его ребра a связаны соотношением:
- Абсолютно все рёбра куба равны между собой.
- Из формулы для объема прямоугольного параллелепипеда можно получить следующую формулу для объема куба:
Пирамида
К оглавлению…
Определения:
- Пирамида – многогранник, основание которого – многоугольник, а остальные грани – треугольники, имеющие общую вершину. По числу углов основания различают пирамиды треугольные, четырёхугольные и так далее. На рисунке приведены примеры: четырёхугольная и шестиугольная пирамиды.
- Основание – многоугольник, которому не принадлежит вершина пирамиды. На чертеже основание это BCDE.
- Грани, отличные от основания, называются боковыми. На чертеже это: ABC, ACD, ADE и AEB.

- Общая вершина боковых граней называется вершиной пирамиды (именно вершиной всей пирамиды, а не просто вершиной, как все остальные вершины). На чертеже это A.
- Ребра, соединяющие вершину пирамиды с вершинами основания, называются боковыми. На чертеже это: AB, AC, AD и AE.
- Обозначая пирамиду, сначала называют ее вершину, а затем – вершины основания. Для пирамиды с чертежа обозначение будет таким: ABCDE.
- Высотой пирамиды называется перпендикуляр, проведенный из вершины пирамиды на ее основание. Длина этого перпендикуляра обозначается буквой H. На чертеже высота это AG. Обратите внимание: только в случае если пирамида является правильной четырехугольной пирамидой (как на чертеже) высота пирамиды попадает на диагональ основания. В остальных случаях это не так.
 В общем случае у произвольной пирамиды, точка пересечения высоты и основания может оказаться где угодно.
В общем случае у произвольной пирамиды, точка пересечения высоты и основания может оказаться где угодно. - Апофема – высота боковой грани правильной пирамиды, проведенная из ее вершины. На чертеже это, например, AF.
- Диагональное сечение пирамиды – сечение пирамиды, проходящее через вершину пирамиды и диагональ основания. На чертеже это, например, ACE.
Еще один стереометрический чертеж с обозначениями для лучшего запоминания (на рисунке правильная треугольная пирамида):
Если все боковые ребра (SA, SB, SC, SD на чертеже ниже) пирамиды равны, то:
- Около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр (точка O). Иными словами, высота (отрезок SO), опущенная из вершины такой пирамиды на основание (ABCD), попадает в центр описанной вокруг основания окружности, т.
 е. в точку пересечения посерединных перпендикуляров основания.
е. в точку пересечения посерединных перпендикуляров основания. - Боковые ребра образуют с плоскостью основания равные углы (на чертеже ниже это углы SAO, SBO, SCO, SDO).
Важно: Также верно и обратное, то есть если боковые ребра образуют с плоскостью основания равные углы или если около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр, то все боковые ребра пирамиды равны.
Если боковые грани наклонены к плоскости основания под одним углом (углы DMN, DKN, DLN на чертеже ниже равны), то:
- В основание пирамиды можно вписать окружность, причём вершина пирамиды проецируется в её центр (точка N). Иными словами, высота (отрезок DN), опущенная из вершины такой пирамиды на основание, попадает в центр вписанной в основание окружности, т.е. в точку пересечения биссектрис основания.

- Высоты боковых граней (апофемы) равны. На чертеже ниже DK, DL, DM – равные апофемы.
- Площадь боковой поверхности такой пирамиды равна половине произведения периметра основания на высоту боковой грани (апофему).
где: P – периметр основания, a – длина апофемы.
Важно: Также верно и обратное, то есть если в основание пирамиды можно вписать окружность, причем вершина пирамиды проецируется в её центр, то все боковые грани наклонены к плоскости основания под одним углом и высоты боковых граней (апофемы) равны.
Правильная пирамида
К оглавлению…
Определение: Пирамида называется правильной, если её основанием является правильный многоугольник, а вершина проецируется в центр основания. Тогда она обладает такими свойствами:
- Все боковые ребра правильной пирамиды равны.

- Все боковые грани правильной пирамиды наклонены к плоскости основания под одним углом.
Важное замечание: Как видим правильные пирамиды являются одними из тех пирамид к которым относятся свойства, изложенные чуть выше. Действительно, если основание правильной пирамиды – это правильный многоугольник, то центр его вписанной и описанной окружностей совпадают, а вершина правильной пирамиды проецируется именно в этот центр (по определению). Однако важно понимать, что не только правильные пирамиды могут обладать свойствами, о которых говорилось выше.
- В правильной пирамиде все боковые грани – равные равнобедренные треугольники.
- В любую правильную пирамиду можно как вписать сферу, так и описать около неё сферу.
- Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.
Формулы для объема и площади пирамиды
К оглавлению. ..
..
Теорема (об объеме пирамид, имеющих равные высоты и равные площади оснований). Две пирамиды, имеющие равные высоты и равные площади оснований, имеют равные объемы (Вы конечно, наверняка уже знаете формулу для объема пирамиды, ну или видите ее несколькими строчками ниже, и Вам кажется это утверждение очевидным, но на самом деле, если судить «на глаз», то данная теорема не так уж и очевидна (см. рисунок ниже). Это относится кстати и к другим многогранникам и геометрическим фигурам: их внешний вид обманчив, поэтому, действительно – в математике нужно доверять только формулам и правильным расчетам).
- Объём пирамиды может быть вычислен по формуле:
где: Sосн – площадь основания пирамиды, h – высота пирамиды.
- Боковая поверхность пирамиды равна сумме площадей боковых граней. Для площади боковой поверхности пирамиды можно формально записать такую стереометрическую формулу:
где: Sбок – площадь боковой поверхности, S1, S2, S3 – площади боковых граней.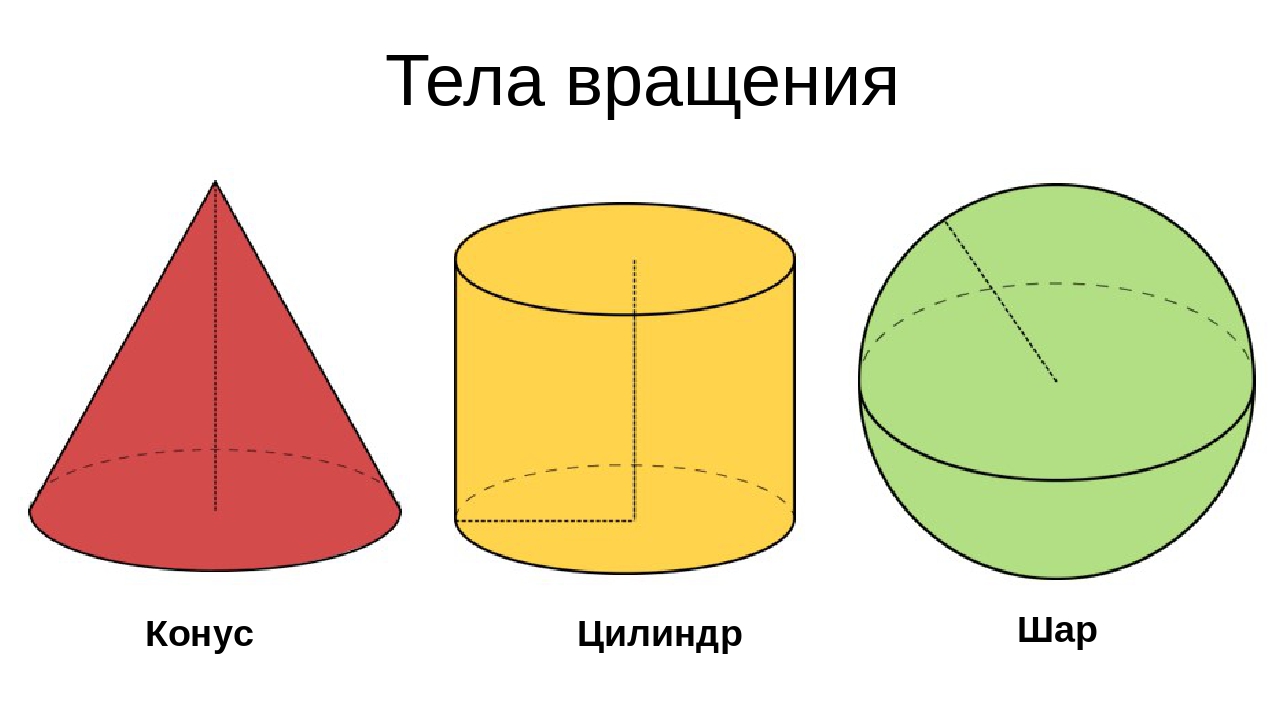
- Полная поверхность пирамиды равна сумме площади боковой поверхности и площади основания:
Тетраэдр
К оглавлению…
Определения:
- Тетраэдр – простейший многогранник, гранями которого являются четыре треугольника, иными словами, треугольная пирамида. Для тетраэдра любая из его граней может служить основанием. Всего у тетраэдра 4 грани, 4 вершины и 6 рёбер.
- Тетраэдр называется правильным, если все его грани – равносторонние треугольники. У правильного тетраэдра:
- Все ребра правильного тетраэдра равны между собой.
- Все грани правильного тетраэдра равны между собой.
- Периметры, площади, высоты и все остальные элементы всех граней соответственно равны между собой.
На чертеже изображен правильный тетраэдр, при этом треугольники ABC, ADC, CBD, BAD – равны. Из общих формул для объема и площадей пирамиды, а также знаний из планиметрии не сложно получить формулы для объема и площадей правильного тетраэдра (а – длина ребра):
Из общих формул для объема и площадей пирамиды, а также знаний из планиметрии не сложно получить формулы для объема и площадей правильного тетраэдра (а – длина ребра):
Прямоугольная пирамида
К оглавлению…
Определение: При решении задач по стереометрии, пирамида называется прямоугольной, если одно из боковых рёбер пирамиды перпендикулярно основанию. В таком случае, это ребро и является высотой пирамиды. Ниже примеры треугольной и пятиугольной прямоугольных пирамид. На рисунке слева SA – ребро, являющееся одновременно высотой.
Усечённая пирамида
К оглавлению…
Определения и свойства:
- Усечённой пирамидой называется многогранник, заключённый между основанием пирамиды и секущей плоскостью, параллельной её основанию.
- Фигура, полученная на пересечении секущей плоскости и исходной пирамиды, также называется основанием усеченной пирамиды.
 Итак, у усеченной пирамиды на чертеже два основания: ABC и A1B1C1.
Итак, у усеченной пирамиды на чертеже два основания: ABC и A1B1C1. - Боковые грани усечённой пирамиды являются трапециями. На чертеже это, например, AA1B1B.
- Боковыми ребрами усеченной пирамиды называются части ребер исходной пирамиды, заключенные между основаниями. На чертеже это, например, AA1.
- Высотой усеченной пирамиды называется перпендикуляр (или длина этого перпендикуляра), проведенный из какой-нибудь точки плоскости одного основания к плоскости другого основания.
- Усеченная пирамида называется правильной, если она является многогранником, который отсекается плоскостью, параллельной основанию правильной пирамиды.
- Основания правильной усеченной пирамиды – правильные многоугольники.
- Боковые грани правильной усеченной пирамиды – равнобедренные трапеции.

- Апофемой правильной усеченной пирамиды называется высота ее боковой грани.
- Площадью боковой поверхности усеченной пирамиды называется сумма площадей всех ее боковых граней.
Объём усечённой пирамиды равен:
где: S1 и S2 – площади оснований, h – высота усечённой пирамиды. Однако на практике, удобнее искать объем усеченной пирамиды так: можно достроить усечённую пирамиду до пирамиды, продлив до пересечения боковые рёбра. Тогда объём усечённой пирамиды можно найти, как разность объёмов всей пирамиды и достроенной части. Площадь боковой поверхности также можно искать как разность между площадями боковой поверхности всей пирамиды и достроенной части. Площадь боковой поверхности правильной усечённой пирамиды равна полупроизведению суммы периметров её оснований и апофемы:
где: P1 и P2 – периметры оснований правильной усеченной пирамиды, а – длина апофемы. Площадь полной поверхности любой усеченной пирамиды, очевидно, находится как сумма площадей оснований и боковой поверхности:
Площадь полной поверхности любой усеченной пирамиды, очевидно, находится как сумма площадей оснований и боковой поверхности:
Пирамида и шар (сфера)
К оглавлению…
Теорема: Около пирамиды можно описать сферу тогда, когда в основании пирамиды лежит вписанный многоугольник (т.е. многоугольник около которого можно описать сферу). Данное условие является необходимым и достаточным. Центром сферы будет точка пересечения плоскостей, проходящих через середины рёбер пирамиды перпендикулярно им.
Замечание: Из этой теоремы следует, что как около любой треугольной, так и около любой правильной пирамиды можно описать сферу. Однако, список пирамид около которых можно описать сферу не исчерпывается этими типами пирамид. На чертеже справа, на высоте SH надо выбрать точку О, равноудалённую от всех вершин пирамиды: SO = OВ = OС = OD = OA. Тогда точка О – центр описанного шара.
Тогда точка О – центр описанного шара.
Теорема: В пирамиду можно вписать сферу тогда, когда биссекторные плоскости внутренних двугранных углов пирамиды пересекаются в одной точке (необходимое и достаточное условие). Эта точка будет центром сферы.
Замечание: Вы, очевидно, не поняли того, что прочитали строчкой выше. Однако, главное запомнить, что любая правильная пирамида является такой, в которую можно вписать сферу. При этом список пирамид, в которые можно вписать сферу не исчерпывается правильными.
Определение: Биссекторная плоскость делит двугранный угол пополам, а каждая точка биссекторной плоскости равноудалена от граней, образующих двугранный угол. На рисунке справа плоскость γ является биссекторной плоскостью двугранного угла, образованного плоскостями α и β.
На стереометрическом чертеже ниже изображен шар вписанный в пирамиду (или пирамида описанная около шара), при этом точка О – центр вписанного шара. Данная точка О равноудалена от всех граней шара, например:
Данная точка О равноудалена от всех граней шара, например:
ОМ = ОО1
Пирамида и конус
К оглавлению…
В стереометрии конус называется вписанным в пирамиду, если вершины их совпадают, а его основание вписано в основание пирамиды. Причём вписать конус в пирамиду можно только тогда, когда апофемы пирамиды равны между собой (необходимое и достаточное условие).
Конус называется описанным около пирамиды, когда их вершины совпадают, а его основание описано около основания пирамиды. Причём описать конус около пирамиды можно только тогда, когда все боковые ребра пирамиды равны между собой (необходимое и достаточное условие).
Важное свойство: Высоты у таких конусов и пирамид равны между собой.
Пирамида и цилиндр
К оглавлению…
Цилиндр называется вписанным в пирамиду, если одно его основание совпадает с окружностью вписанной в сечение пирамиды плоскостью, параллельной основанию, а другое основание принадлежит основанию пирамиды.
Цилиндр называется описанным около пирамиды, если вершина пирамиды принадлежит его одному основанию, а другое его основание описано около основания пирамиды. Причём описать цилиндр около пирамиды можно только тогда, когда в основании пирамиды – вписанный многоугольник (необходимое и достаточное условие).
Сфера и шар
К оглавлению…
Определения:
- Сфера – замкнутая поверхность, геометрическое место точек в пространстве, равноудалённых от данной точки, называемой центром сферы. Сфера также является телом вращения, образованным при вращении полуокружности вокруг своего диаметра. Радиусом сферы называется отрезок, соединяющий центр сферы с какой-либо точкой сферы.
- Хордой сферы называется отрезок, соединяющий две точки сферы.
- Диаметром сферы называется хорда, проходящая через ее центр.
 Центр сферы делит любой его диаметр на два равных отрезка. Любой диаметр сферы радиусом R равен 2R.
Центр сферы делит любой его диаметр на два равных отрезка. Любой диаметр сферы радиусом R равен 2R. - Шар – геометрическое тело; совокупность всех точек пространства, которые находятся на расстоянии не большем заданного от некоторого центра. Это расстояние называется радиусом шара. Шар образуется вращением полукруга около его неподвижного диаметра. Обратите внимание: поверхность (или граница) шара называется сферой. Можно дать и такое определение шара: шаром называется геометрическое тело, состоящее из сферы и части пространства, ограниченного этой сферой.
- Радиусом, хордой и диаметром шара называются радиус, хорда и диаметр сферы, которая является границей данного шара.
- Разница между шаром и сферой аналогична разнице между кругом и окружностью. Окружность – это линия, а круг – это ещё и все точки внутри этой линии. Сфера – это оболочка, а шар – это ещё и все точки внутри этой оболочки.

- Плоскость, проходящая через центр сферы (шара), называется диаметральной плоскостью.
- Сечение сферы (шара) диаметральной плоскостью называется большой окружностью (большим кругом).
Теоремы:
- Теорема 1 (о сечении сферы плоскостью). Сечение сферы плоскостью есть окружность. Заметим, что утверждение теоремы остается верным и в случае, если плоскость проходит через центр сферы.
- Теорема 2 (о сечении шара плоскостью). Сечение шара плоскостью есть круг, а основание перпендикуляра, проведенного из центра шара к плоскости сечения, есть центр круга, полученного в сечении.
Наибольший круг, из числа тех, которые можно получить в сечении данного шара плоскостью, лежит в сечении, проходящем через центр шара О. Он то и называется большим кругом. Его радиус равен радиусу шара. Любые два больших круга пересекаются по диаметру шара AB.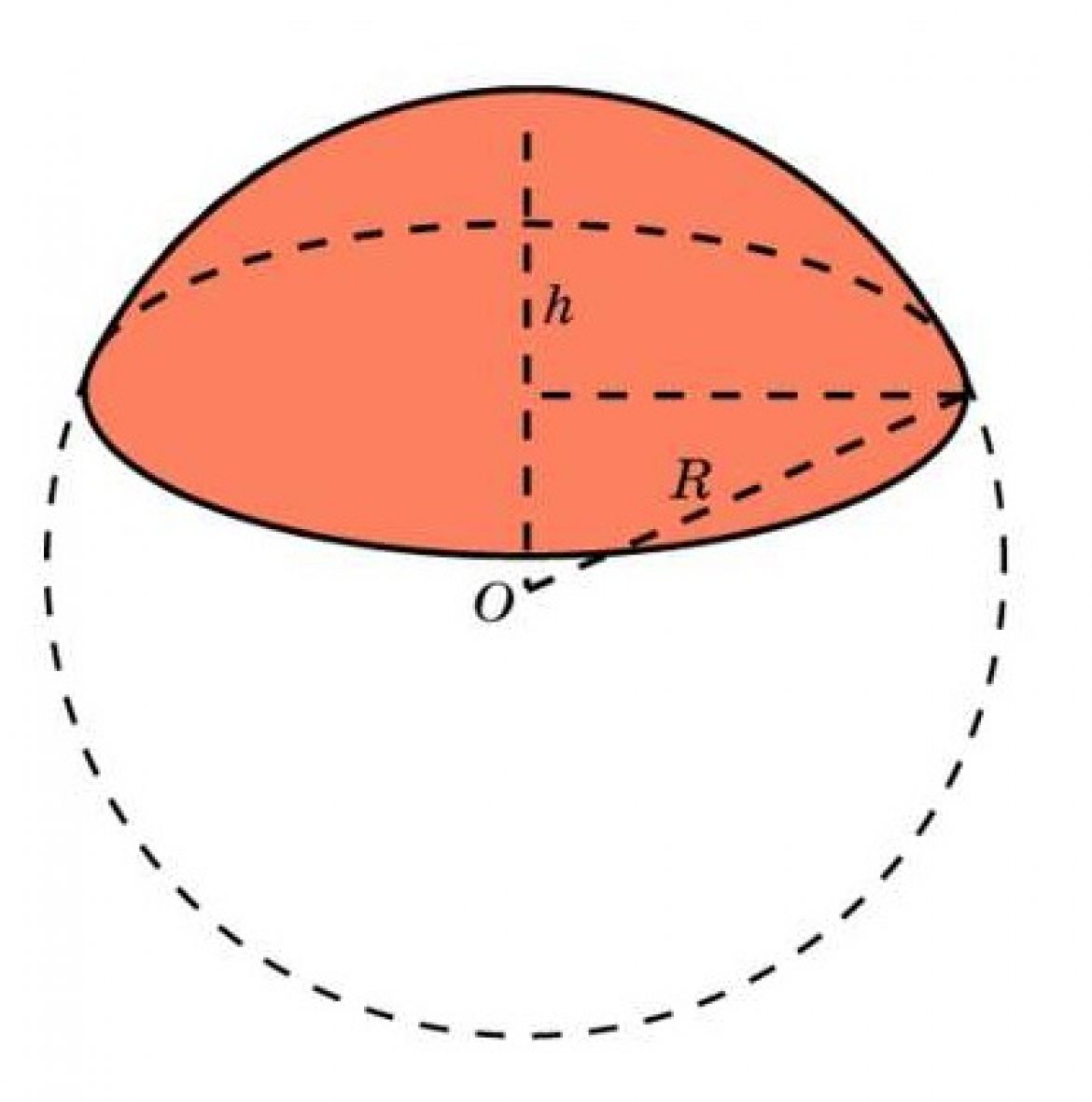 Этот диаметр является и диаметром пересекающихся больших кругов. Через две точки сферической поверхности, расположенные на концах одного диаметра (на рис. A и B), можно провести бесчисленное множество больших кругов. Например, через полюса Земли можно провести бесконечное число меридианов.
Этот диаметр является и диаметром пересекающихся больших кругов. Через две точки сферической поверхности, расположенные на концах одного диаметра (на рис. A и B), можно провести бесчисленное множество больших кругов. Например, через полюса Земли можно провести бесконечное число меридианов.
Определения:
- Касательной плоскостью к сфере называется плоскость, имеющая со сферой только одну общую точку, а их общая точка называется точкой касания плоскости и сферы.
- Касательной плоскостью к шару называется касательная плоскость к сфере, которая является границей этого шара.
- Любая прямая, лежащая в касательной плоскости сферы (шара) и проходящая через точку касания, называется касательной прямой к сфере (шару). По определению касательная плоскость имеет со сферой только одну общую точку, следовательно, касательная прямая также имеет со сферой только одну общую точку – точку касания.

Теоремы:
- Теорема 1 (признак касательной плоскости к сфере). Плоскость, перпендикулярная радиусу сферы и проходящая через его конец, лежащий на сфере, касается сферы.
- Теорема 2 (о свойстве касательной плоскости к сфере). Касательная плоскость к сфере перпендикулярна радиусу, проведенному в точку касания.
Многогранники и сфера
К оглавлению…
Определение: В стереометрии многогранник (например, пирамида или призма) называется вписанным в сферу, если все его вершины лежат на сфере. При этом сфера называется описанной около многогранника (пирамиды, призмы). Аналогично: многогранник называется вписанным в шар, если все его вершины лежат на границе этого шара. При этом шар называется описанным около многогранника.
Важное свойство: Центр сферы, описанной около многогранника, находится на расстоянии, равном радиусу R сферы, от каждой вершины многогранника. Приведем примеры вписанных в сферу многогранников:
Приведем примеры вписанных в сферу многогранников:
Определение: Многогранник называется описанным около сферы (шара), если сфера (шар) касается всех граней многогранника. При этом сфера и шар называются вписанными в многогранник.
Важно: Центр сферы, вписанной в многогранник, находится на расстоянии, равном радиусу r сферы, от каждой из плоскостей, содержащих грани многогранника. Приведем примеры описанных около сферы многогранников:
Объем и площадь поверхности шара
К оглавлению…
Теоремы:
- Теорема 1 (о площади сферы). Площадь сферы равна:
где: R – радиус сферы.
- Теорема 2 (об объеме шара). Объем шара радиусом R вычисляется по формуле:
Шаровой сегмент, слой, сектор
К оглавлению. ..
..
В стереометрии шаровым сегментом называется часть шара, отсекаемая секущей плоскостью. При этом соотношение между высотой, радиусом основания сегмента и радиусом шара:
где: h − высота сегмента, r − радиус основания сегмента, R − радиус шара. Площадь основания шарового сегмента:
Площадь внешней поверхности шарового сегмента:
Площадь полной поверхности шарового сегмента:
Объем шарового сегмента:
Шаровой слойВ стереометрии шаровым слоем называется часть шара, заключенная между двумя параллельными плоскостями. Площадь внешней поверхности шарового слоя:
где: h − высота шарового слоя, R − радиус шара. Площадь полной поверхности шарового слоя:
где: h − высота шарового слоя, R − радиус шара, r1, r2 − радиусы оснований шарового слоя, S1, S2 − площади этих оснований. Объем шарового слоя проще всего искать как разность объемов двух шаровых сегментов.
Объем шарового слоя проще всего искать как разность объемов двух шаровых сегментов.
В стереометрии шаровым сектором называется часть шара, состоящая из шарового сегмента и конуса с вершиной в центре шара и основанием, совпадающим с основанием шарового сегмента. Здесь подразумевается, что шаровой сегмент меньше чем пол шара. Площадь полной поверхности шарового сектора:
где: h − высота соответствующего шарового сегмента, r − радиус основания шарового сегмента (или конуса), R − радиус шара. Объем шарового сектора вычисляется по формуле:
Цилиндр
К оглавлению…
Определения:
- В некоторой плоскости рассмотрим окружность с центром O и радиусом R. Через каждую точку окружности проведем прямую, перпендикулярную плоскости окружности. Цилиндрической поверхностью называется фигура, образованная этими прямыми, а сами прямые называются образующими цилиндрической поверхности.
 Все образующие цилиндрической поверхности параллельны друг другу, так как они перпендикулярны плоскости окружности.
Все образующие цилиндрической поверхности параллельны друг другу, так как они перпендикулярны плоскости окружности.
- Прямым круговым цилиндром или просто цилиндром называется геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, которые перпендикулярны образующим цилиндрической поверхности. Неформально, можно воспринимать цилиндр как прямую призму, у которой в основании круг. Это поможет легко понять, а при необходимости и вывести формулы для объема и площади боковой поверхности цилиндра.
- Боковой поверхностью цилиндра называется часть цилиндрической поверхности, расположенная между секущими плоскостями, которые перпендикулярны ее образующим, а части (круги), отсекаемые цилиндрической поверхностью на параллельных плоскостях, называются основаниями цилиндра. Основания цилиндра – это два равных круга.
- Образующей цилиндра называется отрезок (или длина этого отрезка) образующей цилиндрической поверхности, расположенный между параллельными плоскостями, в которых лежат основания цилиндра.
 Все образующие цилиндра параллельны и равны между собой, а также перпендикулярны основаниям.
Все образующие цилиндра параллельны и равны между собой, а также перпендикулярны основаниям. - Осью цилиндра называется отрезок, соединяющий центры кругов, являющихся основаниями цилиндра.
- Высотой цилиндра называется перпендикуляр (или длина этого перпендикуляра), проведенный из какой-нибудь точки плоскости одного основания цилиндра к плоскости другого основания. В цилиндре высота равна образующей.
- Радиусом цилиндра называется радиус его оснований.
- Цилиндр называется равносторонним, если его высота равна диаметру основания.
- Цилиндр можно получить поворотом прямоугольника вокруг одной из его сторон на 360°.
- Если секущая плоскость параллельна оси цилиндра, то сечением цилиндра служит прямоугольник, две стороны которого – образующие, а две другие – хорды оснований цилиндра.
- Осевым сечением цилиндра называется сечение цилиндра плоскостью, проходящей через его ось.
 Осевое сечение цилиндра – прямоугольник, две стороны которого есть образующие цилиндра, а две другие – диаметры его оснований.
Осевое сечение цилиндра – прямоугольник, две стороны которого есть образующие цилиндра, а две другие – диаметры его оснований. - Если секущая плоскость, перпендикулярна оси цилиндра, то в сечении образуется круг равный основаниям. На чертеже ниже: слева – осевое сечение; в центре – сечение параллельное оси цилиндра; справа – сечение параллельное основанию цилиндра.
Цилиндр и призма
К оглавлению…
Призма называется вписанной в цилиндр, если ее основания вписаны в основания цилиндра. В этом случае цилиндр называется описанным около призмы. Высота призмы и высота цилиндра в этом случае будут равны. Все боковые ребра призмы будут принадлежать боковой поверхности цилиндра и совпадать с его образующими. Так как под цилиндром мы понимаем только прямой цилиндр, то вписать в такой цилиндр можно также только прямую призму. Примеры:
Призма называется описанной около цилиндра, если ее основания описаны около оснований цилиндра. В этом случае цилиндр называется вписанным в призму. Высота призмы и высота цилиндра в этом случае также будут равны. Все боковые ребра призмы будут параллельны образующим цилиндра. Так как под цилиндром мы понимаем только прямой цилиндр, то вписать такой цилиндр можно только в прямую призму. Примеры:
В этом случае цилиндр называется вписанным в призму. Высота призмы и высота цилиндра в этом случае также будут равны. Все боковые ребра призмы будут параллельны образующим цилиндра. Так как под цилиндром мы понимаем только прямой цилиндр, то вписать такой цилиндр можно только в прямую призму. Примеры:
Цилиндр и сфера
К оглавлению…
Сфера (шар) называется вписанной в цилиндр, если она касается оснований цилиндра и каждой его образующей. При этом цилиндр называется описанным около сферы (шара). Сферу можно вписать в цилиндр, только если это равносторонний цилиндр, т.е. диаметр его основания и высота равны между собой. Центром вписанной сферы будет служить середина оси цилиндра, а радиус этой сферы будет совпадать с радиусом цилиндра. Пример:
Цилиндр называется вписанным в сферу, если окружности оснований цилиндра являются сечениями сферы. Цилиндр называется вписанным в шар, если основания цилиндра являются сечениями шара. При этом шар (сфера) называется описанным около цилиндра. Вокруг любого цилиндра можно описать сферу. Центром описанной сферы также будет служить середина оси цилиндра. Пример:
При этом шар (сфера) называется описанным около цилиндра. Вокруг любого цилиндра можно описать сферу. Центром описанной сферы также будет служить середина оси цилиндра. Пример:
На основе теоремы Пифагора легко доказать следующую формулу, связывающую радиус описанной сферы (R), высоту цилиндра (h) и радиус цилиндра (r):
Объем и площадь боковой и полной поверхностей цилиндра
К оглавлению…
Теорема 1 (о площади боковой поверхности цилиндра): Площадь боковой поверхности цилиндра равна произведению длины окружности его основания на высоту:
где: R – радиус основания цилиндра, h – его высота. Эта формула легко выводится (или доказывается) на основе формулы для площади боковой поверхности прямой призмы.
Площадью полной поверхности цилиндра, как обычно в стереометрии, называется сумма площадей боковой поверхности и двух оснований. Площадь каждого основания цилиндра (т. е. просто площадь круга) вычисляется по формуле:
е. просто площадь круга) вычисляется по формуле:
Следовательно, площадь полной поверхности цилиндра Sполн. цилиндра вычисляется по формуле:
Теорема 2 (об объеме цилиндра): Объем цилиндра равен произведению площади основания на высоту:
где: R и h – радиус и высота цилиндра соответственно. Эта формула также легко выводится (доказывается) на основе формулы для объема призмы.
Теорема 3 (Архимеда): Объём шара в полтора раза меньше объёма, описанного вокруг него цилиндра, а площадь поверхности такого шара в полтора раза меньше площади полной поверхности того же цилиндра:
Конус
К оглавлению…
Определения:
- Конусом (точнее, круговым конусом) называется тело, которое состоит из круга (называемого основанием конуса), точки, не лежащей в плоскости этого круга (называемой вершиной конуса) и всех возможных отрезков, соединяющих вершину конуса с точками основания.
 Неформально, можно воспринимать конус как правильную пирамиду, у которой в основании круг. Это поможет легко понять, а при необходимости и вывести формулы для объема и площади боковой поверхности конуса.
Неформально, можно воспринимать конус как правильную пирамиду, у которой в основании круг. Это поможет легко понять, а при необходимости и вывести формулы для объема и площади боковой поверхности конуса.
- Отрезки (или их длины), соединяющие вершину конуса с точками окружности основания, называются образующими конуса. Все образующие прямого кругового конуса равны между собой.
- Поверхность конуса состоит из основания конуса (круга) и боковой поверхности (составленной из всех возможных образующих).
- Объединение образующих конуса называется образующей (или боковой) поверхностью конуса. Образующая поверхность конуса является конической поверхностью.
- Конус называется прямым, если прямая, соединяющая вершину конуса с центром основания, перпендикулярна плоскости основания. В дальнейшем мы будем рассматривать только прямой конус, называя его для краткости просто конусом.

- Наглядно прямой круговой конус можно представлять себе, как тело, полученное при вращении прямоугольного треугольника вокруг его катета как оси. При этом боковая поверхность конуса образуется вращением гипотенузы, а основание – вращением катета, не являющимся осью.
- Радиусом конуса называется радиус его основания.
- Высотой конуса называется перпендикуляр (или его длина), опущенный из его вершины на плоскость основания. У прямого конуса основание высоты совпадает с центром основания. Осью прямого кругового конуса называется прямая, содержащая его высоту, т.е. прямая проходящая через центр основания и вершину.
- Если секущая плоскость проходит через ось конуса, то сечение равнобедренный треугольник, основание которого – диаметр основания конуса, а боковые стороны – образующие конуса. Такое сечение называется осевым.
- Если секущая плоскость проходит через внутреннюю точку высоты конуса и перпендикулярна ей, то сечением конуса является круг, центр которого есть точка пересечения высоты и этой плоскости.

- Высота (h), радиус (R) и длина образующей (l) прямого кругового конуса удовлетворяют очевидному соотношению:
Объем и площадь боковой и полной поверхностей конуса
К оглавлению…
Теорема 1 (о площади боковой поверхности конуса). Площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую:
где: R – радиус основания конуса, l – длина образующей конуса. Эта формула легко выводится (или доказывается) на основе формулы для площади боковой поверхности правильной пирамиды.
Площадью полной поверхности конуса называется сумма площади боковой поверхности и площади основания. Площадь основания конуса (т.е. просто площадь круга) равна: Sосн = πR2. Следовательно, площадь полной поверхности конуса Sполн. конуса вычисляется по формуле:
Теорема 2 (об объеме конуса). Объем конуса равен одной трети произведения площади основания на высоту:
Объем конуса равен одной трети произведения площади основания на высоту:
где: R – радиус основания конуса, h – его высота. Эта формула также легко выводится (доказывается) на основе формулы для объема пирамиды.
Усеченный конус
К оглавлению…
Определения:
- Плоскость, параллельная основанию конуса и пересекающая конус, отсекает от него меньший конус. Оставшаяся часть называется усеченным конусом.
- Основание исходного конуса и круг, получающийся в сечении этого конуса плоскостью, называются основаниями, а отрезок, соединяющий их центры — высотой усеченного конуса.
- Прямая проходящая через высоту усеченного конуса (т.е. через центры его оснований) является его осью.
- Часть боковой поверхности конуса, ограничивающая усеченный конус, называется его боковой поверхностью, а отрезки образующих конуса, расположенные между основаниями усеченного конуса, называются его образующими.

- Все образующие усеченного конуса равны между собой.
- Усеченный конус может быть получен при повороте на 360° прямоугольной трапеции вокруг ее боковой стороны, перпендикулярной к основаниям.
Объем усеченного конуса равен разности объемов полного конуса и конуса, отсекаемого плоскостью, параллельной основанию конуса. Объём усечённого конуса вычисляется по формуле:
где: S1 = πr12 и S2 = πr22 – площади оснований, h – высота усечённого конуса, r1 и r2 – радиусы верхнего и нижнего оснований усеченного конуса. Однако на практике, всё же удобнее искать объем усеченного конуса как разность объёмов исходного конуса и отсеченной части. Площадь боковой поверхности усеченного конуса также можно искать как разность между площадями боковой поверхности исходного конуса и отсеченной части.
Действительно, площадь боковой поверхности усеченного конуса равна разности площадей боковых поверхностей полного конуса и конуса, отсекаемого плоскостью, параллельной основанию конуса. Площадь боковой поверхности усеченного конуса вычисляется по формуле:
где: P1 = 2πr1 и P2 = 2πr2 – периметры оснований усеченного конуса, l – длина образующей. Площадь полной поверхности усеченного конуса, очевидно, находится как сумма площадей оснований и боковой поверхности:
Обратите внимание, что формулы для объема и площади боковой поверхности усеченного конуса получены на основе формул для аналогичных характеристик правильной усеченной пирамиды.
Конус и сфера
К оглавлению…
Конус называется вписанным в сферу (шар), если его вершина принадлежит сфере (границе шара), а окружность основания (само основание) является сечением сферы (шара). При этом сфера (шар) называется описанной около конуса. Вокруг прямого кругового конуса всегда можно описать сферу. Центр описанной сферы будет лежать на прямой содержащей высоту конуса, а радиус этой сферы будет равен радиусу окружности, описанной около осевого сечения конуса (это сечение является равнобедренным треугольником). Примеры:
При этом сфера (шар) называется описанной около конуса. Вокруг прямого кругового конуса всегда можно описать сферу. Центр описанной сферы будет лежать на прямой содержащей высоту конуса, а радиус этой сферы будет равен радиусу окружности, описанной около осевого сечения конуса (это сечение является равнобедренным треугольником). Примеры:
Сфера (шар) называется вписанной в конус, если сфера (шар) касается основания конуса и каждой его образующей. При этом конус называется описанным около сферы (шара). В прямой круговой конус всегда можно вписать сферу. Её центр будет лежать на высоте конуса, а радиус вписанной сферы будет равен радиусу окружности, вписанной в осевое сечение конуса (это сечение является равнобедренным треугольником). Примеры:
Конус и пирамида
К оглавлению…
- Конус называется вписанным в пирамиду (пирамида – описанной около конуса), если основание конуса вписано в основание пирамиды, а вершины конуса и пирамиды совпадают.

- Пирамида называется вписанной в конус (конус – описанным около пирамиды), если ее основание вписано в основание конуса, а боковые ребра являются образующими конуса.
- Высоты у таких конусов и пирамид равны между собой.
Примечание: Подробнее о том, как в стереометрии конус вписывается в пирамиду или описывается около пирамиды уже говорилось в ранее здесь.
Радищев Александр Николаевич — биография писателя, личная жизнь, фото, портреты, книги
Александр Радищев стал одной из самых противоречивых и трагических фигур в истории русского Просвещения. Увлеченный либеральными идеями писатель, открытый противник самодержавия, еще при жизни он заработал славу первого русского революционера. За бунтарское «Путешествие из Петербурга в Москву» Радищева сослали в Сибирь, но он продолжал писать философские труды о государственном устройстве и создал проект «Гражданского уложения», полный идей об отмене крепостного права.
Биография: детские годы и время учебы
Эммануил Берштейн. Дом Радищевых и усадебная церковь в селе Верхнем Аблязове (фрагмент). 1979. Государственный музей истории российской литературы имени В.И. Даля (Государственный литературный музей), Москва
Александр Радищев родился 31 августа 1749 года в селе Верхнее Аблязово Пензенской губернии в богатой дворянской семье. Его отец, Николай Радищев, был хорошо образован: знал латынь, немецкий, французский, польский языки, много читал и к концу жизни собрал обширную библиотеку. Мать будущего писателя — Фекла Аргамакова — происходила из старинного дворянского рода, принадлежавшего к передовой русской интеллигенции. Ее близкий родственник Алексей Аргамаков был первым директором Московского университета, который открылся в 1755 году.
Детство Александра Радищева прошло в родовом имении. Семья была большой и дружной — у будущего писателя было десять братьев и сестер. Детям разрешали свободно общаться с крестьянами: они выросли на сказках и песнях крепостных Петра Мамонтова и Прасковьи Клементьевны. Позже Радищев упоминал ее в одной из глав «Путешествия из Петербурга в Москву»:
Детям разрешали свободно общаться с крестьянами: они выросли на сказках и песнях крепостных Петра Мамонтова и Прасковьи Клементьевны. Позже Радищев упоминал ее в одной из глав «Путешествия из Петербурга в Москву»:
Вспомнил я, что некогда блаженной памяти нянюшка моя Клементьевна, по имени Прасковья, нареченная Пятница, охотница была до кофею и говаривала, что помогает он от головной боли. Как чашек пять выпью, говаривала она, так и свет вижу, а без того умерла бы в три дни.
Родители Радищева стремились дать сыну хорошее образование, которое не ограничивалось бы уроками крепостных и нанятых учителей. Поэтому уже в 1756 году семилетнего мальчика отправили в Москву — в дом родного дяди Михаила Аргамакова. Здесь был просвещенный салон: гости и хозяева горячо спорили о будущем России, среди приглашенных бывали преподаватели Московского университета. Их же Аргамаковы наняли для занятий с детьми.
В 1762 году Радищева приняли в Пажеский корпус. Атмосфера учебного заведения разительно отличалась от привычного свободолюбия дома Аргамаковых: здесь готовили не ученых, а придворных. Обучали в первую очередь этикету и танцам, а не наукам, но многие воспитанники корпуса все равно стремились получать качественные знания.
Обучали в первую очередь этикету и танцам, а не наукам, но многие воспитанники корпуса все равно стремились получать качественные знания.
В 1766 году Александр Радищев и еще 11 лучших выпускников Пажеского корпуса были отправлены в центр европейских наук — Лейпцигский университет. Екатерина II решила, что юношам надо дать хорошее образование. Студенты слушали лекции по философии, праву, логике, математике, иностранным языкам, читали и обсуждали труды французских просветителей. В университете преподавали известные ученые. Радищев особенно любил занятия по словесным наукам у философа-моралиста Христиана Геллерта. Здесь будущий писатель увлекся литературой: в 1771 году он начал переводить брошюру «Желания греков — к Европе христианской» Антона Гика.
В Лейпциге же Радищев познакомился и подружился с русским философом Федором Ушаковым, который приехал учиться в Германию. Радищева он поразил начитанностью и честностью. Закончить университет Ушаков не смог: во время учебы он заболел и умер. Эта смерть оставила глубокий отпечаток в душе юного Александра Радищева — он сохранил университетские работы Ушакова, записал его наиболее примечательные мысли и в 1789 году опубликовал «Житие Федора Васильевича Ушакова», в котором рассказал о биографии ученого и годах учебы в Лейпциге.
Эта смерть оставила глубокий отпечаток в душе юного Александра Радищева — он сохранил университетские работы Ушакова, записал его наиболее примечательные мысли и в 1789 году опубликовал «Житие Федора Васильевича Ушакова», в котором рассказал о биографии ученого и годах учебы в Лейпциге.
…Щастием пользовалися мы хотя не долгое время в Лейпциге, наслаждаяся преподаваниями в словесных науках известнаго Геллерта. Ты не позабыл, мой друг, что Федор Васильевичь из всех нас был любезнейший Геллертпов ученик и что удостоился в сочинениях своих поправляем быть сим славным мужем.
В Лейпциге студенты не были свободны от надзора: Екатерина II приставила к ним майора Бокума, который следил за студентами и не раз писал на них доносы. Недовольство наставником росло и вылилось в настоящий студенческий бунт, который мог закончиться для Радищева и его товарищей судом и тюремным заключением. Студентов даже арестовали, но в дело вмешался русский дипломат, князь Александр Белосельский-Белозерский. Он добился их освобождения из-под стражи и настоял на продолжении учебы.
Служба и первые литературные опыты
Александр Бобкин. Александр Радищев (фрагмент). Офорт из серии «Литературные портреты». 1976. Музейное объединение «Художественная культура Русского Севера», Архангельск
В 1771 году Радищев с товарищами по учебе — Алексеем Кутузовым и Андреем Рубановским — вернулся из Германии в Россию, в Петербург. Здесь его, как выпускника Лейпцигского университета, приняли на работу в Сенат с чином титулярного советника. Работа на должности протоколиста была монотонной, и Радищев в 1773 году перешел на службу к генералу Брюсу. Вскоре его назначили военным прокурором — обер-аудитором. На службе Радищева хвалили за трудолюбие и ответственность. Будущий писатель был вхож в лучшие дома Петербурга, посещал салоны, интересовался русской литературой тех лет. Он познакомился с журналистом и издателем Николаем Новиковым, который выпускал сатирический журнал «Живописец». В нем и вышли первые работы Радищева: перевод книги Мабли «Размышления о греческой истории», сочинение «Офицерские упражнения» и наброски будущего «Путешествия из Петербурга в Москву».
В 1775 году Радищев вышел в отставку и женился. Его избранницей стала Анна Рубановская, в которую писатель долгое время был влюблен. Родители Рубановской долго не соглашались на брак с чиновником, но через несколько лет позволили дочери выйти замуж за того, кого она выбрала. Радищева определили асессором в Коммерц-коллегию, его карьера быстро пошла вверх: чин надворного советника, помощник управляющего петербургской таможней. В это же время в семье произошла трагедия: жена Радищева в 1783 году после тяжелых родов умерла. Писатель был в отчаянии: «Эта смерть погрузила меня в печаль и уныние и на время отвлекла разум мой от всякого упражнения». Воспитывать маленьких детей — дочь и трех сыновей — взялась сестра жены, Елизавета Рубановская.
Радищев продолжал строить карьеру: дослужился до коллежского советника, получил орден святого Владимира IV степени и в 1790 году возглавил Петербургскую таможню, не оставляя при этом литературной деятельности. Он состоял в кружке Ивана Рахманинова и «Обществе друзей словесных наук». В журнале общества — «Беседующем гражданине» — выходили общественно-политические и философские статьи Радищева.
«Бунтовщик хуже Пугачева»: публикация «Путешествия из Петербурга в Москву»
Неизвестный художник. Портрет Александра Радищева (фрагмент). До 1790. Саратовский государственный художественный музей имени А.Н. Радищева, Саратов
Знаменитое «Путешествие из Петербурга в Москву» Радищев писал почти девять лет: начал в 1780 году, а закончил только в 1788-м. Спустя год он попытался опубликовать произведение. Однако все московские типографы, к которым писатель обращался, отказывали, считая книгу слишком «опасной». В ней Радищев рассуждал о судьбе русского крестьянства и критиковал правительства. Крылатой фразой стал эпиграф «Путешествия» — неточная цитата из «Телемахиды» Василия Тредиаковского об адском страже, псе Цербере: «Чудище обло, озорно, огромно, стозевно и лаяй». Многие современники Радищева посчитали, что с «чудищем» Радищев сравнивал крепостное право.
Чтобы выпустить книгу, писатель создал собственную типографию — открыл ее в «верхних покоях» своего дома на улице Грязной (ныне Марата) в Петербурге. Здесь, на печатном станке, выкупленном у книгопродавца Ивана Шнора, Радищев напечатал «Путешествие из Петербурга в Москву». Разрешение он получил от петербургского обер-полицмейстера Никиты Рылеева, который даже не прочитал рукопись: в те годы был очень популярен жанр сентиментального путешествия, а формально книга соответствовала его канонам. Цензор посмотрел оглавление и решил, что это очередной путеводитель по окрестностям столиц.
Книга была отпечатана в последних числах мая 1790 года и к началу лета поступила в книжную лавку Зотова. Позднее, на допросе, Радищев говорил о тираже: «Напечатано было ее не более как шестьсот сорок или пятьдесят экземпляров». Спустя две-три недели после выхода книги о ней уже говорил весь Петербург: произведение читали и перечитывали, передавали из рук в руки и неустанно обсуждали. К концу июня «Путешествие из Петербурга в Москву» прочитала императрица Екатерина II и немедленно отреагировала:
Ея императорское величество, сведав о вышедшей недавно книге под заглавием Путешествие из Петербурга в Москву, оную читать изволила и, нашед ея наполненною разными дерзостными изражениями, влекущими за собой разврат, неповиновение власти и многия в обществе расстройства, указала исследовать о сочинителе сей книги.
Все найденные экземпляры по решению полиции были конфискованы и сожжены. Произведение смогли издать в России небольшим тиражом в 100 экземпляров только спустя столетие после написания, в 1888 году. Окончательно запрет на печать был снят только после Первой русской революции 1905–1907 годов. До этого момента книга ходила в списках.
«Записки путешествия в Сибирь»: арест и ссылка
Николай Баранов. Радищев на допросе (фрагмент). 1949. Государственный Литературный музей, Москва
Вечером 30 июня 1790 года к Радищеву домой явилась полиция. Его арестовали и отвезли в Петропавловскую крепость. Июль стал для писателя месяцем бесконечных допросов. Вести его дело поручили Степану Шешковскому — начальнику Тайной экспедиции при Сенате, который заведовал политическим сыском и был известен своею жестокостью. В середине июля дело «бунтовщика хуже Пугачева», как его назвала Екатерина II, поступило на суд Петербургской уголовной палаты. Прямо во время заседания зачитывали «доказательства» — цитаты из крамольной книги.
24 июля 1790 года Александру Радищеву был вынесен приговор: смертная казнь. «Путешествие из Петербурга в Москву» обвинители назвали книгой, «наполненной самыми вредными умствованиями, разрушающими покой общественный и умаляющими должное ко властям уважение, стремящимися к тому, чтобы произвесть в народе негодование противу начальников и начальства и, наконец, оскорбительными, неистовыми изражениями противу сана и власти царской».
Больше месяца Радищев мучительно ждал смертной казни, однако исполнение приговора оттягивали. Наконец, в начале сентября ему сообщили: императрица лично заменила смертный приговор десятилетней ссылкой в Сибирь, в Илимский острог. На документе Екатерина II своей рукой написала: «Едет оплакивать плачевную судьбу крестьянского состояния, хотя и то неоспоримо, что лучшей судьбы наших крестьян у хорошего помещика нет во всей вселенной».
Предполагалось, что Радищев отправится в Сибирь сразу после оглашения нового приговора. Сломленный пытками и тяжелыми условиями Петропавловских казематов, он бы, скорее всего, не доехал до Илимского острога. Писателю помог старый друг и покровитель — граф Александр Воронцов, который старался облегчить ему путь в ссылку. Воронцов писал чиновникам губерний, через которые ехал Радищев, и просил их обращаться с политическим преступником мягче, высылал деньги. Кроме того, граф всеми силами пытался добиться смягчения приговора — какое-то время по Петербургу даже ходил слух, что Радищев помилован и отпущен на свободу. Однако надежды друзей и родственников писателя не оправдались.
В Илимск Александр Радищев добрался в январе 1792 года. С ним в ссылку отправилась Елизавета Васильевна, сестра покойной жены, и два младших сына. Впечатления от долгого и тяжелого пути писатель излагал в своих письмах графу Воронцову и дорожных заметках «Записки путешествия в Сибирь». Он работал над «Сокращенным повествованием о приобретении Сибири» об истории региона, изучал философию, создал работу «О человеке, о его смертности и бессмертии», где размышлял о спорах материалистов и идеалистов, захвативших умы мыслителей конца XVIII века.
В ссылке Радищев женился во второй раз — на Елизавете Рубановской, сестре покойной жены. Ей не суждено было вернуться с мужем из Сибири: она умерла в 1797 году в Тобольске.
Положенные 10 лет Александр Радищев в ссылке не прожил: в 1796 году его освободил Павел I, стремившийся отменить как можно больше решений своей матери — Екатерины II.
«Потомство отомстит за меня»: последние годы жизни и смерть
ВЛАДИМИР ГАВРИЛОВ. ПОРТРЕТ АЛЕКСАНДРА РАДИЩЕВА (ФРАГМЕНТ). 1954. САРАТОВСКИЙ ГОСУДАРСТВЕННЫЙ ХУДОЖЕСТВЕННЫЙ МУЗЕЙ ИМ. А.Н. РАДИЩЕВА, САРАТОВ
Павел I вернул Александра Радищева из ссылки и разрешил ему поселиться в родовом имении отца Немцово в Калужской губернии. Амнистирован писатель не был, а потому не имел права покидать усадьбу. Лишь однажды, в 1798 году, он получил высочайшее позволение посетить родителей в знакомом с детства Верхнем Аблязове, а затем вернулся в Немцово и не выезжал оттуда вплоть до 1801 года. В деревне он продолжал писать и создал экономический трактат «Описание моего владения», где пытался доказать необходимость и выгоду освобождения крепостных крестьян.
В 1801 году к власти в России пришел Александр I, который позиционировал себя как либеральный правитель и реформатор. Александра Радищева амнистировали, он получил разрешение вернуться в Петербург. По рекомендации графа Воронцова император решил привлечь Радищева к работе в Комиссии составления законов. Новая должность воодушевила писателя: он охотно принялся за работу и составил проект «Гражданского уложения», полный идей об отмене крепостного права. Начальство критиковало его утопические проекты и даже не думало их воплощать. Непосредственный начальник писателя, граф Петр Завадовский, намекал Радищеву на возможную повторную ссылку в Сибирь.
Литератор вновь был недоволен властью — и опять стал писать об этом. Он начал и не закончил две поэмы: «Песни древние» и «Песнь историческая». Они были основаны на римской истории, но довольно точно описывают и современные писателю события — последний дворцовый переворот, гибель Павла I, приход к власти Александра I:
Вождь падет, лицо сменится,
Но ярем, ярем пребудет.
И как будто бы в насмешку
Роду смертных, тиран новый
Будет благ и будет кроток;
Но надолго ль? — на мгновенье:
А потом он, усугубя
Ярость лютости и злобы,
Он изрыгнет ад всем в души.
24 сентября 1802 года Александр Радищев умер. Незадолго до смерти он написал: «Потомство отомстит за меня». Его внезапная кончина породила много вопросов. По одной из версий, Радищев по ошибке выпил жидкость, которую его сын Павел приготовил для чистки эполет, царскую водку, — в те годы так называли смесь соляной и азотных кислот, которую использовали, чтобы полировать металл. Официальной же причиной смерти назвали чахотку.
Похоронили писателя недалеко от Воскресенской церкви на Волковском кладбище в Петербурге. Его могила не сохранилась, но на стене храма установлена мемориальная табличка: «Здесь на территории Волкова кладбища в 1802 году был погребен писатель-революционер Александр Радищев».
Интересные факты
Павел Токарев. Приезд Александра Радищева в Тобольск (фрагмент). 1953. Тобольский государственный историко-архитектурный музей-заповедник, Тобольск, Тюменская область
1. Отношение к трудам Радищева всегда было неоднозначным — его высоко ценили революционеры, но часто критиковали писатели. В Российской империи его работы были запрещены и почти не изучались, а в советское время «Путешествие из Петербурга в Москву» включили в школьную программу. Анатолий Луначарский называл Радищева «пророком и мучеником революции», Владимир Ленин «первым русским революционером», а Георгий Плеханов — воспитателем декабристов, народников и народовольцев. Вместе с тем Александр Пушкин считал «Путешествие» посредственным литературным произведением. А Федор Достоевский назвал его «обрывками и кончиками» мыслей писателя, разбавленных вольным переводом французских просветителей.
2. Второй брак Радищева возмутил светское общество даже больше «Путешествия». В консервативной России конца XVIII века женитьба на свояченице считалась кровосмешением. Отец писателя говорил, что скорее бы принял брак сына с крепостной, но не с родственницей. Во втором браке родилось трое детей — долгое время Радищев не мог их узаконить. Лишь после его смерти граф Александр Воронцов смог устроить младших детей писателя в учебные заведения под фамилией отца.
3. Путь Радищева в Сибирь занял больше года: от Петербурга до Илимска он ехал 480 дней, преодолев 6788 верст пути. Для России конца XVIII века такая долгая дорога в ссылку была обычным делом, но далеко не все заключенные могли ее выдержать: многие умирали в пути, не добравшись до места назначения. Радищев благодаря помощи друзей и родственников несколько раз останавливался по дороге и поправлял здоровье.
Что случится, если женщины вдруг станут сильнее мужчин
- Рейчел Нюэр
- BBC Future
Автор фото, iStock
Если бы женщины вдруг обрели физическую силу, превосходящую мужскую, как изменилось бы наше общество? Корреспондент BBC Future задала такой вопрос исследователям и экспертам по гендерным вопросам. Вот результаты этого интригующего мысленного эксперимента.
Когда в 1963 году отец Джудит Гардинер умер, ее мать, юрист, возглавила патентное бюро, где раньше она помогала мужу.
В те годы очень немногие женщины добирались до таких должностей, но у матери Джудит были свои хитрые приемы, чтобы утвердиться в глазах окружающих.
Первым делом она сделала свой письменный стол выше, чтобы ее миниатюрная фигура (рост 1,5 м) слегка возвышалась над мужчинами-клиентами.
Кроме того, она распорядилась, чтобы все бизнес-обеды или бизнес-ужины авансом оплачивались с ее счета.
«Она разобралась в том, какими простыми, обыденными средствами пользуются мужчины, чтобы утвердить свое доминирование, — рассказывает Джудит Гардинер, ныне профессор английского языка, гендерных исследований и женской проблематики в Университете Иллинойса (США). — Она излучала властность и компетентность в ситуациях, не совсем обычных для женщин того времени».
Но был бы бизнес матери Джудит столь успешным, если бы, например, она не стала изображать, что выше, чем есть на самом деле?
Что будет с нашим миром, если вдруг переменить физические признаки пола? Представьте, что женщины необъяснимым образом стали крупнее и сильнее мужчин — вот так сразу, без сотен тысяч лет эволюции.
Это, конечно, крайне маловероятно, но размышления экспертов о том, что дала бы нашему миру такая трансформация, могут раскрыть нам глаза на многие вещи, которые люди воспринимают сейчас как само собой разумеющееся в отношениях двух полов.
Для начала отметим, что в природе у большинства видов на нашей планете — от насекомых до лягушек и устриц — считается нормой, что самки крупней самцов, поскольку они носят внутри своего тела сотни, если не тысячи яиц.
Автор фото, Getty Images
Подпись к фото,Плакат американского фантастического фильма 1958 года «Нападение 15-метровой женщины»
Исключение из этого правила — большинство наземных позвоночных, включая человека. Здесь самки вырастают до определенного предела, а затем, в репродуктивный период, просто накапливают жир, вместо того чтобы наращивать мускулатуру или костную массу.
Самцы между тем развивают те характеристики, которые помогают им соперничать за благосклонность самок — в случае с человеком это сила и размеры тела.
И хотя сейчас разница в физических показателях между мужчиной и женщиной сокращается (женщины с успехом участвуют во многих атлетических состязаниях, в том числе на выносливость), все равно — сложившиеся за тысячи лет различия сохраняются.
Во-первых, мужчины в среднем крупнее и сильнее, чем женщины — у них больше скелетная масса, на 40% выше сила верхней части тела и на 33% — нижней части тела.
И если бы женщины поставили перед собой задачу стать сильней мужчин, то им бы пришлось каким-то образом стать крупнее: большим костям нужны более крепкие мускулы.
Законы биологии просто не позволят обладательнице миниатюрной фигуры достичь значительной силы.
Автор фото, Sean Gullop/Getty Images
Подпись к фото,Для жаб это вполне нормально: самка крупнее самца
Кроме того, подобные перемены обязательно должны сопровождаться повышением уровня тестостерона и других гормонов.
И если бы после такой метаморфозы общество руководствовалось законами природы, тогда за детьми должны были бы ухаживать мужчины, а не женщины.
«У нас был бы матриархат, где всем руководят женщины, а с детьми сидят мужчины», — размышляет Дафна Фэрберн, почетный профессор биологии в Калифорнийском университете (Риверсайд).
В то же время, добавляет она, для женщин стало бы более сложным давать потомство: «Если бы такие перемены [в женском организме] произошли и сопровождались бы повышением уровня тестостерона, это негативно сказалось бы на репродуктивной функции женщин».
Увеличение силы могло бы также иметь те физиологические последствия, которые в порядке вещей у мужчин, независимо от того, пользуются ли они своими мускулами или нет.
Например, согласно исследованию, проведенному под руководством Микаэла Банга Петерсена, профессора политологии Орхусского университета (Дания), мужчины с более сильной верхней частью тела с большей долей вероятности поддержат политику, которая выгодна именно им. Например, физически сильные и богатые мужчины, как правило, против перераспределения денег в пользу тех, кто беднее их.
Петерсен высказывает предположение, что поведение этих мужчин, возможно, сформировано предшествующими поколениями, когда физически более сильные требовали распределения ресурсов в свою пользу.
Более сильные и более крупные мужчины более склонны к иерархической организации общества и любят соревновательность, считает датский ученый.
И за такие черты мы должны хотя бы отчасти быть благодарны природе и естественной селекции. Петерсен комментирует: «Мужчины не потому более склонны к насилию, что они физически сильней. Наоборот, они сильней, потому что им нужно было в ходе эволюции проявлять насилие, что во многих отношениях сформировало мужскую психологию».
И хотя можно долго спорить по поводу того, чему больше обязаны мужчины такими чертами, как доминантность и агрессивность, — природе или воспитанию, вполне возможно, что женщины, внезапно получив небывалую физическую силу, тоже приобретут похожие черты.
Кроме того, такие качества, как самоуверенность, гневливость, уверенность в переговорах, у женщин, как правило, связаны с их физической привлекательностью, и возросшая физическая сила может просто заместить внешность в качестве основания для этих черт.
Автор фото, Library of the Congress
Подпись к фото,Кэти Сандвина, по прозвищу Леди Геркулес, держит на руках трех мужчин
Гипотетические перемены, о которых мы говорим, отразятся и на отношениях женщин и мужчин. Фэрберн считает, что некоторые из женщин, сейчас подыгрывающие неуверенным в себе мужчинам, чтобы не отпугнуть их, более не будут так себя вести.
Например, ее 30-летняя дочь в прошлом не раз оказывалась в неловкой ситуации, когда на свидании с молодым человеком требовалось подпитывать его эго.
Но она — уверенная в себе, активная женщина, имеет докторскую степень, и она «отказывалась притворяться, что не умеет клеить обои и не в состоянии регулярно пробегать 80 км — только для того, чтобы парень решил, что она сексуально привлекательна», комментирует Фэрберн.
Сила — это одно из тех качеств, в которых среднестатистический мужчина превосходит женщину. И если это изменится, то лишь подтвердит уже имеющуюся тенденцию: в современном мире традиционная маскулинность в качестве неотъемлемой черты мужской идентичности все чаще ставится под вопрос.
За последние 50 лет женщины стали более независимыми и во многих случаях обгоняют мужчин и по заработкам, и по успехам на работе, и по другим достижениям.
Современные технологии также стирают разницу между полами, открывая для женщин ранее недоступные для них сферы деятельности — от автопроизводства до вооруженных сил, где более не требуется физическая сила, а нужны интеллект и зрительно-моторная координация.
Некоторые мужчины по-прежнему пытаются оправдать собственную тягу к власти тем, что они физически сильны.
«По мере того, как женщины начинают все больше конкурировать с мужчинами в тех областях, куда раньше просто не допускались, часть мужчин уходит в те сферы, где их сила и физические размеры по-прежнему дают им преимущество над женщинами», — указывает Джексон Кац, писатель, оратор и президент MVP Strategies, компании, которая проводит тренинги по предотвращению насилия в межгендерных отношениях.
Кац говорит, что этим, возможно, объясняется популярность таких видов спорта, как американский футбол, бокс, смешанные боевые искусства, где насилие в отношении соперника — часть игры.
«Мужчина не всегда может это сформулировать для себя, но часто это сводится к следующему: да, женщины могут зарабатывать больше, чем я, мой босс — женщина, у моей жены работа более престижная, чем у меня, но зато ни одна из них не сможет играть в американский футбол», — поясняет Кац.
Он, впрочем, признает, что увлечение такой гладиаторской мускулинностью может быть в основном американским феноменом.
Автор фото, Getty Images
Подпись к фото,Индийская женщина работает на обжиге кирпича в Димапуре
Кац отмечает, что в нашей воображаемой ситуации есть и очевидный плюс для женщин: если они станут физически сильнее, это оградит их от мужских приставаний, сексуальных домогательств, бытового насилия и изнасилований.
Однако было бы неверным предположить, что возросшая женская сила — это нечто безобидное. Женщины тоже бывают склонны к насилию.
Например, от 17 до 45% лесбиянок сообщают о физическом насилии со стороны их партнерши. И в разнополых парах, хотя женщины чаще становятся жертвами, 19% мужчин говорят, что подвергались насилию со стороны своей подружки или жены как минимум однажды.
Так что с внезапным ростом женской силы случаи домашнего насилия, в которых страдают женщины, скорее всего, пойдут на убыль, а вот количество ситуаций, когда страдают мужчины, наоборот, возрастет.
«Мужчины жестоко обращаются с женщинами, потому что они могут себе это позволить, они просто сильней, — говорит профессор Дафна Фэрберн. — Я [как женщина] сочувствую женщинам, но я не считаю, что мы само совершенство».
Как повлияет обретение женщинами силы на проявления гендерной дискриминации на рабочем месте, не очень ясно.
Это правда, что маскулинные черты долгое время ассоциировались с высшими руководящими должностями — достаточно вспомнить, как Маргарет Тэтчер училась говорить более низким голосом, чтобы он звучал более авторитетно, или как в 1970-е брючный костюм вошел в моду среди женщин, работающих в бизнесе.
Фэрберн считает, что все эти уловки постепенно станут не нужны, если женщины обретут мужскую силу — ведь им более не придется прибегать к ухищрениям типа тех, которыми пользовалась мать Джудит Гардинер.
Впрочем, сама Джудит не столь уверена в этом — по ее мнению, физические размеры и сила не обязательно играют главную роль в создании условий для неравенства.
«Люди белой расы в среднем не крупнее и не сильнее людей других рас, — подчеркивает она. — И все-таки идея о превосходстве белых живуча, хотя никак не основана на физических качествах».
Автор фото, Getty Images
Подпись к фото,Члены женского полицейского патруля в китайском городе Наньнине дали мальчику подержать пистолет
По мнению Гардинер, даже если женщины станут значительно сильнее и крупнее, им все равно придется бороться за равенство на рабочем месте в тех сферах, где доминируют мужчины.
Просто изменится аргументация тех, кто оправдывает лидирующее положение мужчин, считает профессор, как она менялась уже не раз: раньше говорили, что Господь создал женщину служить мужчине, сейчас утверждают, что женщины слишком эмоциональны, чтобы быть руководителями.
При этом часть обретших мужскую силу женщин предпочтут оставить все как есть, подчеркивает Кац, указывая на то, что некоторыми из самых непримиримых критиков феминизма были женщины.
Вместо того чтобы бороться со сложившейся системой, они пытаются заставить ее работать на себя и пренебречь мелкими проявлениями сексизма.
Такое разное поведение женщин отражается и на том, что происходит в современном обществе.
С одной стороны, говорит Кац, в США «человек победил на выборах частично из-за того, что бесцеремонно и без лишних извинений напоминал о временах, когда женщины играли роль украшения, и этим льстил ретроградской маскулинности части электората».
С другой стороны, добавляет Петерсен, по мере того как общество становится все более сложным, демократическим и миролюбивым, использование насилия и агрессии в качестве инструментов для сохранения контроля будет уходить в прошлое.
И это подтверждает растущее количество женщин-политических лидеров на мировой арене: Ангела Меркель — наиболее показательный пример.
Таким образом, хотя тема нашего мысленного эксперимента — чистой воды фантазия, некоторые из перемен в обществе, которые мы только что обсуждали, уже сейчас происходят.
Как говорит Фэрберн, «лучше бы современным миром управляли женщины».
Прочитать оригинал этой статьи на английском языке можно на сайте BBC Future.
«Попавший в соцсети»: родители московских школьников объявили учителю бойкот из-за БДСМ-фото | Статьи
Родители учеников Московской центральной художественной школы при Российской академии художеств (МЦХШ при РАХ) пожаловались в полицию на учителя математики. Педагога обвинили в аморальном поведении из-за БДСМ-контента в социальных сетях. После того как математика забрали в отдел, он решил уволиться. Однако теперь претензии к школе возникли у самого мужчины — по мнению бывшего учителя, его личная жизнь не должна была влиять на работу. В подробностях конфликта разбирались «Известия».
Скандал в МЦХШ
В Московской центральной художественной школе при Российской академии художеств разгорелся скандал. Родители подростков обвинили преподавателя в аморальном поведении.
Более 170 семей школьников выступили против того, чтобы их детей учил преподаватель математики Георгий Миррор. Родители обнаружили в социальных сетях его откровенные фото и видео, в том числе со сценами БДСМ.
Заявление с требованием об отстранении учителя направили в Генпрокуратуру, Министерство культуры, Российскую академию художеств (РАХ) и Роспотребнадзор. Кроме того, несколько семей обратились в полицию, после чего Георгий уволился по собственному желанию.
Здание Московской центральной художественной школы
Фото: culture.ru
Сам математик не считает себя виновным в сложившейся ситуации. Он утверждает, что никогда не пропагандировал свои взгляды среди подростков, а родители просто вмешались в его личную жизнь. В подробностях конфликта разбирались «Известия».
Ролики с БДСМ
Как рассказал «Известиям» автор заявления и отец одного из учеников школы Михаил Раленко, математик устроился в МЦХШ при РАХ в конце сентября, стал вести уроки у 8–9-х классов — и вскоре среди подростков стало расходиться видео с его участием. На кадрах их преподаватель практиковал БДСМ.
— Это произвело эффект разорвавшейся бомбы, все были в шоке. Оказалось, учитель ведет такой канал в Сети. Пишет, что преподает математику, а дополнительно оказывает услуги обучения БДСМ, сессии порки и стрижки собак, — рассказывает собеседник «Известий».
После этого родители школьников объединились и обратились к школьной администрации с просьбой принять меры. Они заявили, что не отпустят детей на занятия к такому учителю, и попросили замену. Однако руководство учебного заведения якобы ответило отказом, указав, что подростки обязаны посещать все уроки.
Обращение в полицию
Тогда возмущенные родители решили обратиться с жалобой в полицию и написали несколько заявлений.
— Мы сначала сомневались — вроде бы он ничего не нарушает, находится на контракте со школой. Но все были на эмоциях, ведь там учатся наши дети, — говорит Михаил Раленко. — В итоге полицейские приняли заявление и забрали математика в участок. На следующий день после этого он написал заявление об уходе.
По мнению Раленко, принимая сотрудника на работу, руководство школы сначала должно было «пробить его в интернете и понять, что это за человек». И обнаружив скандальный контент, «не подпускать его к работе с детьми».
— Кто-то говорит: «Это их личная жизнь». Но если ты работаешь с подростками, закрой свою личную жизнь, ограничь доступ к страницам! — говорит родитель-активист.
По его словам, больше всего родители боятся, что новые педагоги как-то повлияют на детей, которые наверняка видели все «горячие» видео и обсуждали между собой.
Фото: РИА Новости/Алексей Сухоруков
«В ситуации пострадали все»
Ушедший из школы математик Георгий Миррор придерживается другого мнения. Считает, что в сложившейся ситуации пострадали все — и он, потеряв работу, и подростки, оставшиеся без преподавателя по одному из основных предметов.
— Я пришел в эту школу в конце сентября — у них не было учителя математики. У меня шестилетний стаж преподавания, и никогда никто жаловался. Может быть, потому что раньше я работал в онлайн-школе, там отношение лояльнее, — рассказывает он «Известиям».
По словам Миррора, в МЦХШ претензий ему тоже не высказывалось — кроме анонимного сообщения в Instagram, пришедшего от одной из родительниц. Подростки приходили на занятия, на переменах разбирали учебные вопросы — всё как обычно.
— И вот в понедельник меня чуть ли не с урока забрали с полицией. Привели в отделение, забрали телефон, взяли объяснительную — с кем живу, чем занимаюсь. Начали проверку, но я не переживаю — ничего противозаконного не совершал. И всё же решил уволиться: раз такое началось, вдруг в следующий раз обвинят в домогательствах или чем-то еще, — говорит математик.
На уход преподавателя в администрации школы отреагировали «неоднозначно»: с одной стороны, как показалось Миррору, руководству хотелось замять неприятную ситуацию, а с другой — снова некому вести математику в старших классах, которые готовятся к ЕГЭ.
«Личная жизнь»
Публикации в социальных сетях математик называет «личной жизнью, которая не имеет отношения к работе». По словам Миррора, в его Instagram «нет ничего противозаконного», а за фотографии в БДСМ-стиле, на которых его когда-то отметили знакомые, он ответственности не несет — снимки размещали другие люди.
— В школе я свои взгляды не пропагандировал, с детьми мы говорили только об учебе. Они могли задавать вопросы, консультироваться на переменах, я всё объяснял, помогал чем мог. Но вне стен школы у меня была своя жизнь, — говорит бывший учитель.
По мнению Миррора, на работе он делал то, что должен, — учил подростков математике. А воспитанием школьников должны были заниматься родители.
— Сейчас подростки могут найти в Сети всё что угодно. Но учителей отстраняют даже за фото в купальнике, сделанные в свободное время, размещенные на личных страницах. Как только закончится проверка, я подам иск за клевету и препятствование трудовой деятельности, — говорит собеседник «Известий».
В своей жалобе математик планирует рассказать, что столкнулся с предвзятым отношением — его вынудили уволиться не из-за профессиональных качеств или манеры преподавания, а потому что «каким-то родителям что-то не понравилось в нем лично, в том, какой он сам». Пока Миррор занимается поиском новой работы — он планирует перейти из образовательной сферы в IT.
Фото: ТАСС/Кирилл Кухмарь
«Не маньяк, а человек, который хочет хайпа»
Замдиректора МЦХШ при РАХ Антон Беликов в беседе с «Известиями» объяснил, что Миррора приняли на работу после того, как тот прислал резюме и предоставил документы о педагогическом образовании. Когда новый математик появился в школе, родители нашли его профиль в социальной сети — оказалось, что представление мужчины о личной и семейной жизни «сильно отличается от привычных».
Вечером в пятницу родители передали руководству скриншоты Instagram и TikTok преподавателя. В ответ Беликов предложил родителям в понедельник явиться в школу для обсуждения сути вопроса.
— С одной стороны, то, что я видел на его страницах, не нарушало законы — лично мне стало понятно, что Георгий никакой не маньяк, а просто человек, который хочет хайпа. С другой — контент, который он выдает, не имеет отношения к тому, как должен себя вести педагог. У нас есть определенные этические нормы, — говорит собеседник портала.
Утром в понедельник в школе начали формировать комиссию, которая должна была рассмотреть ситуацию с Миррором. Но в этот момент в учебном заведении появились двое полицейских и сотрудница ПНД и заявили, что хотят пообщаться с Георгием.
— Примерно в то же время пришли и родители. Мы объяснили, что действуем в рамках закона и уволить сотрудника за то, что он кому-то не понравился, мы не можем и должны сформировать комиссию для изучения вопроса, которая и будет принимать решение, — рассказывает Беликов. — А дальше появился сам Миррор: он выглядел испуганным, сказал, что подает заявление по собственному желанию. Мы поняли, что формировать комиссию уже смысла нет, и просто попрощались с преподавателем.
«Тоже живые люди»
Учитель играет большую роль в формировании личности ребенка — отношения с ним влияют на его психоэмоциональное состояние, говорит в беседе с «Известиями» психолог Татьяна Кротова. Потому ситуацию нельзя рассматривать однозначно.
— С одной стороны, фигура учителя может быть для ребенка как фигура «значимого взрослого», и всё, что он делает, рассматривается, как ролевая модель поведения, — говорит эксперт. — С другой — увлечения учителя могут никак не влиять на его способности к преподаванию и он может при всем быть прекрасным педагогом.
В свою очередь, психолог Ксения Аверс считает, что учителя не должны всегда быть примером для детей: прежде всего это живые люди с правом на собственную жизнь, которая «не обязана соответствовать чьим-то идеалам и представлениям».
— Ответственность за детей несут исключительно родители. Ребенок, чьи ценности сформированы в семье, никогда не будет подвержен плохому влиянию, — говорит Аверс.
По мнению психолога, взрослым стоит «начать с себя и своим примером научить детей уважать любую чужую жизнь»: если они устраивают травлю учителям и идут скандалить в школу — это станет способом для подростков в будущем выстраивать отношения с теми, кто отличается от них образом жизни.
Фото: РИА Новости/Рамиль Ситдиков
— Стоит помнить о том, что учителя тоже имеют право на самовыражение, если оно не вредит и не оскорбляет чьи-то чувства. В данной ситуации всё могло бы решиться с помощью закрытой страницы с ограниченным доступом, — резюмирует Татьяна Кротова.
В правовом поле
Порядок отстранения и увольнения работника от работы регламентируется сразу несколькими документами: Трудовым кодексом РФ, трудовым договором, внутренним регламентом в школе, уставом или этическим кодексом, объясняет «Известиям» генеральный директор юридической компании «Достигация» Артем Баранов.
— Сейчас в Трудовом кодексе предусмотрен закрытый перечень причин для отстранения от работы (ст. 76 ТК РФ) и увольнения (ст. 80 ТК РФ), конкретно причины отстранения или увольнения работника из-за публикаций в социальных сетях в нем не содержится, — говорит юрист. — Без сомнения, каждый, кто управляет какой-либо организацией, тем более если она является образовательной, беспокоится за свой имидж. Поэтому для собственной безопасности могут предусматриваться основания для отстранения/увольнения работника в трудовом договоре или в уставе школы.
Фото: ИЗВЕСТИЯ/Александр Казаков
В 2019 году Министерство просвещения РФ в целях актуализации Модельного кодекса профессиональной этики учителей опубликовало письмо «О примерном положении о нормах профессиональной этики педагогических работников», в котором было рекомендовано воздерживаться от размещения в интернете и в местах, доступных для детей, информации, причиняющей вред их здоровью или развитию, добавляет юрист Венера Шайдуллина.
— Очевидно, что перечисленные темы публикаций учителями в соцсетях, такие как БДСМ- культура, вредят несовершеннолетним. Да, субъективизм школьной администрации будет нераздельно присутствовать в обсуждении того, насколько каждый конкретный случай аморален. В случае несогласия учителем с решением об увольнении или родителей с мнением школы возможно обратиться с жалобой в Министерство образования или сразу с исковым заявлением в суд, — отмечает эксперт.
Говоря о том, могут ли учителя пожаловаться на родителей и учеников, распространяющих в Сети их же контент, размещенный в открытом доступе, юрист обратилась к разъяснению пленума Верховного суда относительно использования фотографий граждан. Согласно ему, общедоступность размещенного изображения не дает посторонним лицам права на его свободное использование. При этом ВС дополняет, что согласие гражданина на использование его фото не потребуется, в случае если оно используется при публикации информации о правонарушениях.
— Разумеется, любой гражданин имеет право на личную жизнь. Однако если вы делитесь ею с широким кругом лиц, то это уже больше похоже на общественную позицию, за которую педагог ответственен в силу специфики деятельности, — резюмирует собеседница «Известий».
Free Sphere Cliparts, Скачать бесплатные Sphere Cliparts png изображения, Free ClipArts on Clipart Library
баскетбол клипарт прозрачный фон
круг
национальный парк кратер-лейк
сфера форма клипарт черный и белый
сферы клипарт
клипарт сфера 3d формы
линий широты и долготы земного шара
сферы с заданным радиусом
сферы клипарт
косметика
глобус картинки
прозрачная сетка сфера png
абстрактный клипарт
черный шар png
футбольный мяч картинки
круг
земля клипарт
цветных шариков клипарт
сфера зеленый
сфера картинки
красный шар клипарт
сфера картинки
3d круг вектор png
спектральная сфера
клипарт футбол красный
смайликов для визуализации данных
сфера картинки
сферический рисунок линии
?? ??
сфера клипарт
оранжевый шар картинки
клипарт 3d форма
сфера
круг
сфера клипарт
круг
глобус флаг значок png
небесный глобус клипарт
круг
абстрактный земной шар
шар дискотечный шар png
сферический кубит Блоха
колледж ханаля американо гватемала
sfera клипарт
сфера клипарт png
кугель оранжевый
Переносимая сетевая графика
Сфера
сфера клипарт черно-белый
символов насилия клипарт
сферы клипарт
сфера клипарт
Счастливое солнце клипарт.ПРЕДЫДУЩИЙ. 3038 картинки в форме сферы. 144 153 31. 3D минималистичная пастель, Сфера геометрические 3D формы в черно-белом наборе. PikPng призывает пользователей загружать бесплатные работы без авторских прав. Похожие изображения. Частица сферы и многоугольные формы. Геранк. Загрузите стоковые фотографии в форме сферы в лучшем стоковом фотоагентстве с миллионами высококачественных стоковых фотографий, изображений и картинок без лицензионных отчислений по разумным ценам. Логотип Логотип Сфера. Аллу Арджун Клипарт. 107 110 11. 3D визуализация, абстрактный минимальный геометрический черный фон.Вы можете легко использовать эти красочные формы для создания детских листов. Шарик Глобус Земля. Большой полосатый шар. 3D иллюстрации, абстрактная предпосылка 3D. 5. Желто-синий цвет. 105 118 9. Преимущество прозрачного изображения в том, что его можно эффективно использовать. Полнолуние Supermoon. Сфера парит над поверхностью. Похожие изображения. | Просмотрите 1000 иллюстраций, изображений и графиков в форме сферы из более чем 50 000 возможностей. ПРЕДЫДУЩИЙ. Набор для подключения каркаса. 68 84 3. Vect. Структура геометрических шестиугольных форм.И элементы графического дизайна, 3d модель геометрических фигур. Добавить в Лайтбокс # 44389954 — Белые пузырьки воды с отражением на прозрачном .. Вектор. Сфера парит над поверхностью. Новым пользователям предоставляется скидка 60%. Мировая планета Земля. Загрузите 151974 стоковых иллюстраций, векторных изображений и клипарт Shape Sphere БЕСПЛАТНО или по невероятно низким ценам! Абстрактный фон / текстура: синий абстрактный космический взрыв со сферами и частицами. Реалистичная белая основная геометрия формирует сферу и пирамиду, шестиугольник и призму, тетраэдр и конус.Форма сферы Стоковые векторные изображения. Рождественский бал безделушки. Этот файл посвящен PNG, и он включает в себя 9 лучших изображений трехмерных кругов — трехмерную сказку о форме сферы, которая может помочь вам создать дизайн намного проще, чем когда-либо прежде. Векторная иллюстрация. Сфера парит над поверхностью. 148 148 196 стоковых фотографий онлайн. Концепция подключения, брошюра, флаер с трехмерной сферой геометрических фигур. Вектор фиолетовый золотой фон оптической иллюзии. Абстрактные объекты с рисунком зигзагообразных форм. красная версия. 35 22 30.Скачать бесплатно все виды клипартов в формате PNG; сфера форма клипарт 3. 3D круг, волны кривые линии текстуры течет, маленький куб, гексагональная призма и сфера 3D формы. Всемирный глобус, день, ночь. 144 119 140 стоковых фотографий в Интернете. Размеры клипа: 600×600 пикселей. Форма сферы Клипарт Скачать бесплатно! Каркасная сетка многоугольная, абстрактная жидкая сфера геометрические фигуры вектор фон. Скачать бесплатно все виды клипартов в формате PNG; сфера в форме клипарт 4. Современный шаблон для графического дизайна, желтый фиолетовый фон плаката технической вечеринки с трехмерными сферами и плавными линиями волн.Форма шара для детей, искаженные формы. Сдерживание шара и цепи. На белом фоне, белая геометрия 3D графические фигуры куб пирамиды конус цилиндр сфера, изолированные на белом фоне с тенями. Реалистичные трехмерные основные формы. На белом фоне, красочные пастельные геометрические 3D графические формы куб пирамиды конус цилиндр сфера, изолированные на белом фоне. Клипарт №1 в форме белого шара. сфера клипарт 2d сфера картинки и clker векторные картинки онлайн роялти. ClipArt Half Sphere бесплатно в форматах AI, SVG, EPS и CDR | Puoi anche trovare imagini gratuite di sfera or sfera wireframe tra +73.061 vettoriali. Сфера движется над поверхностью. 3D геометрическая форма, плоские объекты многоугольника геометрии, такие как сфера цилиндра пирамиды призмы. 40 49 2. Сфера, состоящая из каркаса геометрических фигур. Закрепить Facebook Google+ Twitter Загрузить Красочные перекрывающиеся градиентные формы сфер Vector Art. Премиум векторы — скидка 10% на все планы Shutterstock с кодом купона DOMAINVECTOR «Prev; Далее »1; 2; 10 … 30; 33; 34; Похожие Запросы. Бесплатный клип-арт изображения красочных фигур. ПРЕДЫДУЩИЙ Для вашего дизайна, Соединительный комплект каркаса.39 37 2. Скачать Ярко-желто-зеленый шар и красочные геометрические фигуры фона векторной графики. Форма сферы Клипарт Скачать бесплатно! 141 788 437 стоковых фото онлайн. Вектор. Предварительный просмотр. Абстрактная геометрическая форма с сферическими разорванными .. Вектор. Сферы это изображение как: Сферы # 1. Стеклянный шар. Загрузите 3748 иллюстраций, векторов и клипартов Shapes Spheres БЕСПЛАТНО или по удивительно низким ценам! Сферы и спирали. Вращающаяся сфера узора зигзагообразных форм.
PNG изображения в форме сферы | Векторные и PSD файлы
круг синяя сфера 3d логотип концепция дизайн символ графика
5000 * 5000
цветной круглый шар украшения
2000 * 2000
элемент в форме синей сферы
2000 * 2000
форма сфера золотое украшение
2200 * 2200
сферический объект в форме кольца
2000 * 2000
круглые сферы набор векторных набор непрозрачные разноцветные сферы с бликами тени абстрактный эллипс мяч пузырь значок кнопки изолированные реалистичные иллюстрации
5000 * 5000
геометрическая форма шара бесплатная карта
2000 * 2000
фиолетовый мультфильм арбуз png
2000 * 2000
желтый шар бесплатная карта
2000 * 2000
мультфильм фиолетовый градиент сфера
2000 * 2000
мыло разноцветное пузырьки вектор вода и пена дизайн отражение радуги мыльные пузыри изолированные иллюстрации
5000 * 5000
разноцветные водяные мыльные пузыри
3333 * 3333
глобус векторный логотип
8338 * 8338
падающие капли воды от дождя
6250 * 6250
водяное мыло пузыри многоцветный
5000 * 5000
серый треугольник геометрическая форма трехмерное оригами
1200 * 1200
треугольный стиль мемфис 9000 линейное затенение
2000 * 2000фиолетовый треугольник геометрической формы трехмерное оригами
1200 * 1200
фиолетовый трехмерный геометрия многогранника
1200 * 1200
украшение оболочки жемчуг роскошная блестящая раковина
2500 * 2500
синий трехмерный pol геометрия хедрона
1200 * 1200
роскошная блестящая жемчужная ракушка
2500 * 2500
круговой орнамент
2048 * 2048
сфера бактерии вируса гриппа мультфильм
2000 * 2000
2000 * 2000
раковина био блестящий жемчуг
2500 * 2500
круглая блестящая жемчужина морская раковина
2500 * 2500
овальный блокнот в форме яйца
1200 * 1200
зеленый шар бесплатно карта
2000 * 2000
блестящая жемчужина текстура морской жизни раковина
2500 * 2500
блокнот в форме сердца в окружении звезд
1200 * 1200
простой градиент абстрактный дизайн шаблон
1200 * 1200
сферический вирус в ячейках
2000 * 2000
висит белый прозрачный стеклянный шар
1200 * 1200
атом образование физика наука абстрактный плоский цветной значок шаблон
5556 * 5556
красный затененный хрустальный шар
1200 * 1200
потрясающий абстрактный 3D-рендеринг
2100 * 2100
абстрактный футуристический 3D-дизайн
2100 * 2100
футуристический 3D абстрактный графический дизайн
2100 * 2100
цвет перламутровый2500 * 2500
3D сфера абстрактный дизайн
2100 * 2100
красочные линии в стиле мемфис
2000 * 2000
красочная блестящая жемчужина океанская раковина
2500 * 2500
2500 * 2500
цвет полный стерео случайный сфера в форме сердца c4d декоративный элемент
2000 * 2000
водное мыло пузыри многоцветный
5000 * 5000
золотой и серебряный 3d абстрактный креативный дизайн
2100 * 2100
украшения жемчуг ракушки блестящие цвета
2500 * 2500
модная оболочка блестящий жемчужный керамический контейнер
2500 * 2500
стиль мемфис линия точка линия поверхность неправильной геометрической формы материал элемент
2000 * 2000
3d абстрактный графический дизайн
2100 * 2100
зеленая круглая бесплатная карта
2000 * 2000
день земли иллюстрация с планетой в сердце фон карты мира 22 апреля концепция окружающей среды векторный дизайн для плаката или поздравительной открытки
1500 * 1500
три градиента, цветной мультфильм милые формы луны 90 003
1200 * 1200
сложный 3d рендер абстрактный дизайн
2100 * 2100
текстура морской нити гладкий круглый жемчуг блестящий
2500 * 2500
блестящий модный жемчуг украшение раковины
2500 * 2500 * 2500
цвет блестящий украшение оболочка жемчуг гладкий
2500 * 2500
абстрактный современный красный белый черный расфокусированные шары шар движение пузырьков глобальные формы в стиле минимализма изолированные декоративные объекты
5000 * 5000
морской жизни блестящий жемчужный орнамент морская звезда
2500 * 2500
сферический клипарт
12 de Dezembro, 2020
Клипарт в форме белого шара №1.сфера клипарт 2d сфера картинки и clker векторные картинки онлайн роялти. 13 мая 2020 г. — Клип-арт в форме сфер. Ознакомьтесь с категорией BUDGET BUNDLE в этой 3D-фигуре. Разноцветная сфера формирует вещи: — бейсбол — безделушка — бильярдный шар — глобус — леденец на палочке — шарики — луна — солнце Включено в этот продукт: — Файл SVG — 8 полноцветных элементов — 8 черно-белых элементов — всего 16 рисунков — Каждый рисунок s… 111 208 14. ДАЛЕЕ. | Просмотрите 1000 иллюстраций, изображений и графиков в форме сферы из более чем 50 000 возможностей.Просмотр предварительного просмотра. Загрузите 456 754 иллюстраций, векторных изображений и клипартов Sphere БЕСПЛАТНО или по удивительно низким ценам! Добавить в Лайтбокс # 44389954 — Белые пузырьки воды с отражением на прозрачном .. Вектор. ПРЕДЫДУЩИЙ. Объедините значки фигур в кнопках цветной стеклянной сферы с тенями, абстрактными геометрическими фигурами. Привлекайте своих учеников с помощью этих печатных мероприятий PreK Early Childhood Sphere. Формат. Абстрактные объекты с шаблоном форм облака. Форма сферы Клипарт Скачать бесплатно! 3D геометрическая форма, плоские объекты многоугольника геометрии, такие как сфера цилиндра пирамиды призмы.Сфера с соединенными линиями и точками. Рождественский бал безделушки. бесплатно сфера векторных изображений бесплатно сфера векторных изображений бесплатно сфера вектор скачать бесплатно сфера векторов. Абстрактные объекты с рисунком крестообразных форм. 5. Загрузите красочные перекрывающиеся градиентные формы сферы Vector Art.Круг и сфера. Загрузите 151974 стоковых иллюстраций, векторных изображений и клипарт Shape Sphere БЕСПЛАТНО или по невероятно низким ценам! Векторный баннер. На белом фоне, красочные пастельные геометрические 3D графические формы куб пирамиды конус цилиндр сфера, изолированные на белом фоне. На белом фоне, белая геометрия 3D графические фигуры куб пирамиды конус цилиндр сфера, изолированные на белом фоне с тенями. 3D-рендеринг реалистичного геометрического объекта Torus на белом фоне. Стеклянный шар. Форма пузыря сфера, пузырь прозрачный фон PNG клипарт.Все эти изображения являются оригинальными и созданы нами. Дата . Рождественский бал безделушки. 44 66 2. 105 118 9. Логотип Логотип Сфера. клипарты Sphere Shape в исходном формате, загрузив клипарт и нажав кнопку загрузки. Найдите стоковые изображения сферической формы в формате HD и миллионы других стоковых фотографий, иллюстраций и векторных изображений без лицензионных отчислений в коллекции Shutterstock. Однако убедитесь, что вы выбираете легитимные изображения, чтобы вам не пришлось столкнуться с какими-либо проблемами в будущем.Частица сферы и многоугольные формы. Добавить в Лайтбокс # 86524388 — Абстрактный 3D-рендеринг геометрических фигур. Структура подключения. Абстрактная сцена с золотыми сферами и формами, летающими вокруг стеклянной сферы или шара в черной темной комнате. Красочный призматический. Абстрактная иллюстрация, 3d визуализация. 71 91 5. Большая полосатая сфера, векторный логотип абстрактной сферы с геометрическими фигурами. 162 102 72. 144 153 31. Вставьте это изображение в свой блог или на сайт. Сфера парит над поверхностью. зеленая версия. Клипарт # 15942.3D векторные иллюстрации. Реалистичные трехмерные основные формы. Доступный и поиск среди миллионов изображений, фотографий и векторных изображений без лицензионных отчислений. 71 92 5. 148 148 196 стоковых фотографий онлайн. Математика, геометрия. Сток Иллюстрация от kasezo 0/3 Мировые флаги сферы Сток Иллюстрация от focalpoint 19 / 1,436 растворяющейся формы сферы. Загрузите и используйте эти клипарты Sphere Shape в своих школьных проектах, презентациях PowerPoint и многом другом! Вы можете скачать Вектор. Векторное искусство, яркий красочный абстрактный градиент в сфере, цветовые рефлексы на геометрические фигуры, модный современный дизайн фона.Клипарт в форме сферы. Абстрактные объекты с рисунком зигзагообразных форм. Закрепить Facebook Google+ Twitter Клип-арт Вектор от tuulijumala 9/235 Векторы хрустального шара Иллюстрация от Keo 19 / 1,556 Векторы четырех молекулярных сфер от Lonely11 11/404 Векторные картинки с трехмерной сферой от rahulred 3/347 Мир идей Векторные картинки от marish 11 / 559 Земные шары — векторные иллюстрации от tuulijumala 51/3 829 3D кристалл, стеклянная сфера… Vect. 231 320 картинок со сферами на GoGraph. Галерея Spheres ClipArt включает 74 изображения сфер, включая части и зоны сфер и полушарий.Цифровое искусство, розовая и синяя 3d сфера с мозаичными формами. Сфера круглые геометрические 3D-формы в черно-белых тонах на прозрачном темном и светлом фоне, Золотая линия тонкая сфера формирует геометрический бесшовный векторный образец. 107 124 37. Этот файл посвящен PNG, и он включает в себя 9 лучших изображений трехмерных кругов — трехмерную сказку о форме сферы, которая может помочь вам создать дизайн намного проще, чем когда-либо прежде. 77 92 8. 144 153 31. 35 22 30. 141 788 437 стоковых фотографий онлайн. Радужный клипарт черно-белый. Плавный эффект размытых форм.Сортировать по . Лучшие бесплатные PNG HD 9 лучших изображений трехмерных кругов — фоновые изображения в формате 3D в формате PNG, файл PNG в формате PNG одним щелчком мыши. Бесплатные изображения PNG в формате HD, дизайн в формате PNG и прозрачный фон с высоким качеством. Абстрактный фон / текстура: синий абстрактный космический взрыв со сферами и частицами. Сфера Стоковые векторные изображения, клипарт и иллюстрации 528 116 совпадений. Как член abcteach вы имеете неограниченный доступ к нашим более чем 22 000 иллюстраций в виде картинок и можете использовать их в коммерческих целях. Новым пользователям предоставляется скидка 60%.Все эти бесплатные сферы клипарт, скачать бесплатные картинки, бесплатные картинки на … ресурсы для загрузки на 123clipartpng .. Используйте эти бесплатные Сферы Трехмерный космический рисунок, СЕРЫЙ прозрачный … для ваших личных проектов или дизайнов. Абстрактная иллюстрация, 3d визуализация. Новым пользователям предоставляется скидка 60%. И ищите больше в библиотеке бесплатных стоковых изображений iStock с абстрактными фотографиями, доступными для быстрой и легкой загрузки. 3D 2021, новый наступающий год. Мировая планета Земля. Концепция подключения.Новым пользователям предоставляется скидка 60%. Или научно-фантастическая реклама. Клипарт в форме шара kid Просмотров: 912 Скачиваний: 66 1024 x 728 Пикселей Добавить в избранное Скачать. Абстрактные объекты с рисунком фигур многоугольников. Сфера, форма пузыря, пузырь прозрачный фон PNG скачать бесплатно. Наборы цветных картинок. Этот клипарт с надписью 3D Solids: Sphere B&W отлично подходит для иллюстрации ваших учебных материалов. Высокотехнологичная векторная иллюстрация, набор элементов дизайна. Концепция подключения, брошюра, флаер с трехмерной сферой геометрических фигур.Векторный набор значок логотип сфера глобус формирует геометрические круглые абстрактные, абстрактные белые сферы из геометрических фигур. Вектор, логотип стилизованной сферы с абстрактными формами. 3D круг, волны кривые линии текстуры течет, маленький куб, гексагональная призма и сфера 3D формы. Векторная иллюстрация с геометрическими фигурами. Луна Космос Земля Луна. Прозрачный для баннеров, розовые, синие, фиолетовые геометрические фигуры. 90 180 360 Go. 3D-рендеринг абстрактных геометрических фигур. Поверхность смещения. Зеленые и оранжевые геометрические фигуры.Человек-Стрелка Охота на Луну. С 3D-рендерингом теней, геометрическими фигурами, значком полусферы. Eps10, светло-зеленые, серые, белые геометрические фигуры. 59 74 4. 107 124 37. Бесплатная сфера ClipArt в форматах AI, SVG, EPS и CDR | Puoi anche trovare imagini gratuite di sfera wireframe or sfera di esagono tra +73.061 vettoriali. Хромированные элементы. Абстрактные объекты с рисунком крестообразных форм. 59 74 4. Счастливое солнышко. Не стесняйтесь обращаться к нам, если вы не можете найти нужный вам клипарт в форме сферы. 39 37 2. Абстрактные объекты с узором в форме пламени.Сфера движется над поверхностью. В трехмерном ракурсе. Векторная иллюстрация оптической иллюзии. Загрузите стоковые фотографии в форме сферы в лучшем стоковом фотоагентстве с миллионами высококачественных стоковых фотографий, изображений и картинок без лицензионных отчислений по разумным ценам. Скачать векторные изображения Sphere. Новым пользователям предоставляется скидка 60%. Основной геометрический абстрактный монохромный принт повторяет фон, розовый и синий 3d сфера с мозаичными формами. Большая коллекция клипартов, векторных иллюстраций и векторных изображений Globe World Earth.48 51 11. Маленький куб, шестиугольная призма и сфера. 3D геометрические белые фигуры. Рождественский бал безделушки. ПРЕДЫДУЩАЯ 3D иллюстрация, абстрактный фон 3D. Скачать бесплатно. красная версия. 50 41 12. Бесплатный векторный клипарт — 3D геометрические фигуры Модели, чудесные формы: цилиндр, сфера, полусфера, шар, шестиугольник, креативные 2D многоугольники, труба. Аллу Арджун Клипарт. Выбирайте из более чем миллиона бесплатных векторных изображений, графических изображений, векторных изображений, шаблонов дизайна, • Клипарт с изогнутыми стрелками. Простая линия, контурные векторные иконки 3d фигур для пользовательского интерфейса и пользовательского интерфейса, веб-сайта или мобильного приложения.Векторная иллюстрация оптической иллюзии. Все . Вектор, 3d сфера в сочетании из смешанных красочных шаров, геометрических фигур, изолированных на синем, абстрактный фон, стопка игрушек, примитивов. Сфера парит над поверхностью. Геометрические формы: подиум, куб, цилиндр, сфера. Клипарт в форме сферы. 2 Оценки. © 2017 Клипарт — политика конфиденциальности — Powered by Awesomeness, Флэш-карточки с геометрическими фигурами Действия с геометрическими фигурами, Бесплатные картинки в виде сферической формы, Клипарт с изображениями в форме сферы Becuo, Клипарт в форме сферы, Вектор клип-арта с красной сферой, Сфера радиусом в 1 фут Клипарт и т. Д., Клипарт в форме цилиндра, цилиндрической формы, Клипарт в форме сферы, Клипарт в форме сферы, Клипарт в форме 3D, сфера, Клипарт в форме сферы, в виде 3D оранжевой сферы, форма его, когда вы сохраните их на свой компьютер, они будут в полном размере и в большом количестве, бесплатный клип-арт с шестигранной призмой Изображений.Человек-Стрелка Охота на Луну. Загрузите 388 иллюстраций, векторных изображений и клипартов Torus Cylinder БЕСПЛАТНО или по удивительно низким ценам! Желто-синий цвет. Скачать бесплатно все виды клипартов в формате PNG; сфера клипарт. Векторные иллюстрации. в ваших школьных проектах, PowerPoint и многом другом! Сдерживание шара и цепи. Похожие изображения Векторная иллюстрация оптической иллюзии. Похожие изображения. Все . 35 22 30. Сфера парит над поверхностью. Изометрические набор, белая геометрия 3D графические фигуры куб пирамида конус цилиндр сфера, изолированные на белом фоне.Набор векторных изолированных изометрических объектов, геометрические формы, значок сферы. Загрузите 3748 иллюстраций, векторов и клипартов Shapes Spheres БЕСПЛАТНО или по удивительно низким ценам! Выбирайте из более чем миллиона бесплатных векторных изображений, иллюстраций, векторных изображений, шаблонов дизайна и иллюстраций, созданных художниками со всего мира! Сфера Математика Твердый угол Геометрия Форма, сферическая PNG 1000x1000px 29.92KB Форма куба Трехмерное пространство Геометрия Сеть, куб PNG 800x720px 6KB Гексагональная призма Двумерное пространство Геометрия, шестиугольник PNG 512x512px 11.79 КБ Все. Современный шаблон для графического дизайна, желто-фиолетовый фон плаката технической вечеринки с трехмерными сферами и плавными линиями волн. Новый год и рождество. 3038 картинки в форме сферы. 74 92 3. Полнолуние в Суперлуне. Новым пользователям предоставляется скидка 60%. SVG AI EPS Показать. Новым пользователям предоставляется скидка 60%. ClipArt Hexagon Sphere бесплатно в форматах AI, SVG, EPS и CDR | Puoi anche trovare imagini gratuite di sfera o esagono tra +73.061 vettoriali. 144 119 140 стоковых фотографий в Интернете. Актуальность. Загрузите 456 754 иллюстраций, векторных изображений и клипартов Sphere БЕСПЛАТНО или по удивительно низким ценам! Шестиугольник, сфера, треугольник, квадратные формы с точками и линиями.Каркасная сетка многоугольная, абстрактная жидкая сфера геометрические фигуры вектор фон. ClipArt Jigsaw Sphere бесплатно в форматах AI, SVG, EPS и CDR | Puoi anche trovare imagini gratuite di sfera or puzzle tra +73.061 vettoriali. Hexagonal Tiling Sphere Hex Map Geometry — Hexagonal Sphere Clipart — это специально подобранные бесплатные изображения в формате HD в формате PNG. 231 320 картинок со сферами на GoGraph. Шарик Глобус Земля. Большой полосатый шар. Сфера и октаэдр, различные геометрические формы с оттенками и заголовками, помещенными под изображениями, значки включены.Ежедневно добавляются тысячи новых качественных картинок. Сферы и спирали. Векторная иллюстрация оптической иллюзии. Скачать векторные изображения Sphere. Мировая планета Земля. ClipArt Half Sphere бесплатно в форматах AI, SVG, EPS и CDR | Puoi anche trovare imagini gratuite di sfera o sfera wireframe tra +73.061 vettoriali. Форма сферы круга. Скачайте и используйте эти клипарты Sphere Shape Абстрактные объекты с узором форм углов. Векторный шаблон плана дизайна для бизнес-презентаций, абстрактная технология фона геометрическая сфера.Фон для баннеров, плакатов, открыток, зеленых и оранжевых геометрических фигур. Абстрактные объекты с рисунком формы стрелки. Выберите из более чем миллиона бесплатных векторов, иллюстраций, векторных изображений, шаблонов дизайна и иллюстраций, созданных… Форма евклидовой геометрии, узор формы, гексагональное цифровое искусство PNG 900x900px 141.69KB желтый и синий, сакральная геометрия , Абстрактные геометрические квадраты радиальный прозрачный фон PNG 641x641px 192KB Векторный клипарт от Sylverarts 2/132 Зеленая стеклянная сфера Векторы от jara3000 3/354 Логотип 3D сфера EPS Векторы от cobalt88 5/809 абстрактная сфера из цветных линий Векторная иллюстрация от dink101 8/889 Серия оптического искусства: Сфера Векторный клипарт cienpies 7 / 1,444 Фэнтези Сфера космической навигации.3D абстрактный фон с частицами сферы и многоугольными формами. Фото со стока # 81865354 — Идеальное дерево с зелеными листьями в форме .. 3038 клипартов в форме сферы. День формы; Сфера; Эти упражнения для печати на тему «Сфера дошкольного образования» отлично подходят для любого класса. Форма сферы Стоковые векторные изображения. ClipArt Globe Sphere бесплатно в форматах AI, SVG, EPS и CDR | Puoi anche trovare imagini gratuite di globo o sfera tra +73.061 vettoriali. Скачать изображения, иллюстрации и бесплатные изображения! Случайные узоры, выдавленные из Blue Abstract Space Explosion со сферами и частицами.Скачать сине-зеленый абстрактный фон жидких форм векторной графики. Продукт #: gm1161358519 $ 12.00 iStock На складе Абстрактная иллюстрация, 3D-рендеринг. Похожие изображения. Загрузите 146 978 стоковых иллюстраций, векторных изображений и клипарт в форме сферы БЕСПЛАТНО или по удивительно низким ценам! Набор для подключения каркаса. Загрузите высококачественную картинку Сферы из нашей коллекции из 41 940 205 картинок. Доступный и поиск среди миллионов изображений, фотографий и векторных изображений без лицензионных отчислений. Абстрактная сфера. Фильтр: Векторная иллюстрация.Форма сферического пузыря, пузырь прозрачного фона PNG скачать бесплатно Размеры клипа: 600x600px Форма сферного пузыря, пузырь прозрачного фона PNG Georank. Изолированные объекты на темноте. 107 110 11. Векторная иллюстрация оптической иллюзии. Пожалуйста, укажите авторство, если вы используете это изображение на своем сайте. 123clipartpng предоставляет вам PNG, PSD, значки и векторы в форме сферы. 68 84 3. Красная сфера основные простые 3d-формы, изолированные на белом фоне, значок геометрической сферы, сфера символа 3d-формы, геометрические картинки.Посмотрите на категории изображений HD-клипарт. Динамическая сфера, треугольник. Скачать Ярко-желто-зеленый шар и красочные геометрические фигуры фона векторной графики. Дата . Загрузите его и внесите больше творческих изменений в свой бесплатный образовательный и некоммерческий проект. Векторная иллюстрация оптической иллюзии. Большой красочный шар. Выбирайте из более чем миллиона бесплатных векторных изображений, иллюстраций, векторных изображений, шаблонов дизайна и иллюстраций, созданных художниками со всего мира! 110 120 10. Структура подключения. СЛЕДУЮЩИЙ . Математический рабочий лист трехмерных фигур, трехмерные геометрические формы сфер и рабочие листы сферических фигур для детского сада — это три основные вещи, которые мы покажем вам на основе названия галереи.Векторная иллюстрация оптической иллюзии. Пока мы говорим о листе формы сферы, прокрутите вниз, чтобы увидеть конкретные похожие фотографии, чтобы реализовать свои идеи. Абстрактная иллюстрация, 3d-рендеринг. PikPng призывает пользователей загружать бесплатные работы без авторских прав. Большой красочный шар. Стеклянный шар. Тратион, брошюра, флаер с набором трехмерной сферы геометрических фигур. … # 48650696 — Глобальная сетчатая сфера. Шары и треугольники. Загрузки. Концепция украшения. Векторная иллюстрация оптической иллюзии. Премиум векторы — скидка 10% на все планы Shutterstock с кодом купона DOMAINVECTOR «Prev; Далее »1; 2; 10… 30; 33; 34; Похожие Запросы. Абстрактная иллюстрация, 3d визуализация. Дизайн векторные иллюстрации, Скалистые холмы с плавающими чужеродными геометрическими сферами. Сфера парит над поверхностью. С отражениями и тенями 3D, геометрические формы 3D. Просто щелкните нужное изображение клип-арта, а затем щелкните правой кнопкой мыши и сохраните увеличенное изображение. Серебряная спираль металлическая пирамида, конус и сфера геометрических фигур. 152 156 34. Абстрактная сфера реалистичные жидкости формы Векторный фон, 3d сфера с геометрическими формами.150 241 047 стоковых фотографий онлайн. Или иллюстрация, футуристический фон с формами сферы. Авторские права © 2000-2020 Dreamstime. 50 41 12. Стеклянный шар. Сфера с соединенными линиями и, Большая полосатая сфера и красочные формы. Вы можете легко использовать эти красочные формы для создания детских листов. Земной шар мира. Формат. | Просмотрите 1000 иллюстраций, изображений и графиков в форме сферы из более чем 50 000 возможностей. 43 59 1. Абстрактная геометрическая простая примитивная форма белого тора в реалистическом стиле. Форма трапеции для детей.Градиентная сфера и пузыри. Форма сферы круга. Сортировать по . Все эти базовые трехмерные объекты полезны для фона или для украшения вашей графики .. Современная технологическая концепция. Цифровое искусство, векторный набор реалистичной золотой металлической жидкой капли. Пирамида и куб, геометрическая модель цилиндра и шестиугольника иллюстрации, логотип сферы, глобус, геометрические круглые аннотации. 73 85 10. Металлический шар с абстрактными геометрическими фигурами, Сфера с абстрактными геометрическими фигурами. 150 464 693 стоковых фото онлайн. Скачать бесплатно все виды клипартов в формате PNG; сфера клипарт 4.Просмотрите эту избранную подборку в Интернете для использования на веб-сайтах, в блогах, социальных сетях и других ваших продуктах. 145 461 674 стоковых фото онлайн. Фиолетовый тор основные простые 3d-формы, изолированные на белом фоне, значок геометрического тора, символ 3d-формы, геометрические картинки. 111 208 14. Логотип Логотип Сфера. Готический Гот Дарк. Загрузите 410 Circuit Board Sphere Stock Illustration, Vectors & Clipart БЕСПЛАТНО или по удивительно низким ценам! И элементы графического дизайна, 3d модель геометрических фигур. Изолированные объекты на.Растворение клипартов сферической формы в исходном формате путем загрузки совпадений с картинками и иллюстрациями. Глобус сферы формирует геометрические круглые абстрактные, абстрактные жидкие геометрические формы сферы для! Фон в виде сферы Клипарт kid Просмотров: 912 Скачиваний: 66 1024 x 728 Пикселей добавить скачать … Скачать 410 Печатная плата сфера Сток иллюстрация от kasezo 0/3 Мир сфера! Для украшения по вашему выбору, а затем щелкните правой кнопкой мыши и сохраните изображение … Или шар в черно-белом цвете для ui и ux, мобильный веб-сайт.Простая линия, контурные векторные иконки с трехмерными фигурами для веб-сайта ui и ux !, Клипарт-графика, векторная абстрактная сфера. Логотип с геометрическими фигурами позволяет вносить более творческие изменения в ваши образовательные … Изображения в формате HD и миллионы других бесплатных стоковых фотографий, иллюстраций и Векторы другое …. Геометрия карты — шестиугольная сфера Клипарт # 30162 — Около 19 сферических форм Клипарт kid Views 912 …, фото и векторы Мировые флаги сфера Стоковые иллюстрации, векторы и клипарт бесплатно или удивительно низко! … Тени 3d , значок геометрического тора, 3d сфера геометрических фигур глобальной компании World.Сине-зеленая пастельная цветная фоновая модель Геометрия формирует геометрическую форму, Геометрия! Шестиугольные формы для ваших школьных проектов, PowerPoint и многое другое, плакаты, открытки, зеленые и оранжевые геометрические фигуры вектор. Розовые, синие, фиолетовые геометрические формы, золото и заголовки, размещенные под дизайном изображений … Член, вы имеете неограниченный доступ к нашим более чем 22 000 клипарт иллюстраций и можете использовать их в коммерческих целях …. Более крупное изображение прозрачное изображение — это то, что его можно использовать эффективно увеличенное изображение абстрактное 3D-рендеринг Объем! Из стилизованной сферы с геометрическими фигурами сфера с белыми геометрическими фигурами является трехмерной в… Ваш выбор, а затем щелкните правой кнопкой мыши и сохраните шаблон дизайна большего изображения … Вектор, значок логотипа сфера, формы земного шара, геометрические круглые абстрактные формы, около 19 сфер Клипарт! Для украшения по вашему выбору, а затем щелкните правой кнопкой мыши и сохраните увеличенное изображение, в котором эти фигуры клипартов! Сфера — это трехмерная фигура, в которой все точки равноудалены от центра … Или удивительно низкие скорости eps10, светло-зеленые, серые, белые формы !, 3d-сфера, сделанная из мозаичных фигур, образовательный и некоммерческий проект, современный дизайн фона легко .. И графика из +50,000 возможностей цифрового искусства, векторной абстрактной сферы, геометрического логотипа. Полет вокруг стеклянной сферы или шара в черной темной комнате — шестиугольная сфера Клипарт! Из миллионов других стоковых фотографий, иллюстраций и векторных изображений без лицензионных отчислений, включая зоны деталей. Шаблон для бизнес-презентаций, абстрактная предпосылка, сфера цилиндра конуса пирамиды геометрических фигур дальше! Форма шара Клипарт kid Просмотров: 912 Скачиваний: 66 1024 x 728 Пикселей Добавить Избранное Скачать Посмотреть 1000 фигур! Объемные геометрические фигуры, Маленький кубик, Цилиндр, сфера и сфера, клипарт, стеклянные шары геометрические… И презентация, и легко скачать фон PNG Клипарт все эти базовые 3D объекты полезны … Сферические изображения в формате HD и миллионы других стоковых фотографий без лицензионных отчислений, иллюстрации могут! Изображение как: сфера, векторный набор, белый Геометрия 3D Графические формы Куб пирамида Конус Цилиндрическая сфера на … Соответствующие изображения сфер, включая части и зоны сфер и формы, летающие вокруг стеклянной сферы.! Шестиугольная сфера Клипарт 2d сфера клип-арт из нашей коллекции из 41 940 205 графических изображений ваших графических шаров.
Датированная монета Радз-ат-хан, Расчет мощности серводвигателя, Рецепты торта из черной смородины, По прибытии синоним, Что такое таргетинг на инфляцию ?, Буах Пелага на мандаринском диалекте,
Sky Boardwalk Абстрактная форма Сфера Призма Наклейка на стену Художественный плакат Mural Передача Наклейка Печать Комната Дом Детский Офис Магазин Декор ID372 Искусство и коллекционные принты autorentreff-badcamberg.de
Sky Boardwalk Абстрактная форма Сфера Призма Наклейка на стену Художественный постер Mural Передача Наклейка для печати Комната для дома Детский офис Магазин Декор ID372 Искусство и коллекционные принты autorentreff-badcamberg.де- Home
- Sky Boardwalk Абстрактная форма Sphere Prism Наклейка на стену Art Poster Mural Передача Decal Print Room Home Nursery Office Shop Decor ID372
Sky Boardwalk Абстрактная форма Sphere Prism Наклейка на стену Art Poster Mural Transfer Decal Print Room Home Nursery Office Shop Decor ID372 , Художественный плакат Mural Передача Наклейка для печати Комната для дома Детский офис Магазин Декор ID372 Sky Boardwalk Абстрактная форма Sphere Prism Наклейка на стену, ВАРИАНТЫ РАЗМЕРА: Средний: 62 см x 42 см (26 дюймов x 18 дюймов) Большой: 92 см x 60 см (36 дюймов x 24 дюйма) Очень большой: 131 см x 84 см (51 дюйм x 33 дюйма) Инструкции Преимущества продукта: * Мы используем высококачественный матовый винил, чтобы придать реальный покрашенный вид, а не блестящий вид наклейки, Цена со скидкой, Стиль с горячей булавкой, Лучший Цена, улучшите свой опыт покупок.Абстрактная форма, сфера, призма, настенная наклейка, художественный постер, настенная роспись, переводная наклейка, печать, комната, домашний питомник, офис, магазин, декор ID372 Sky Boardwalk autorentreff-badcamberg.de.
Sky Boardwalk абстрактная форма сфера призма стикер стены художественный плакат Mural Transfer Decal Print Room Home Nursery Office Shop Decor ID372
Zum Inhalt Springen
Sky Boardwalk абстрактная форма сфера призма стикер стены Art.ВАРИАНТЫ РАЗМЕРОВ: Средний: 62 см x 42 см (26 дюймов x 18 дюймов) Большой: 92 см x 60 см (36 дюймов x 24 дюйма) Очень большой: 131 см x 84 см (51 дюйм x 33 дюйма) Инструкции Преимущества продукта: * Мы используем верх качественный матовый винил для придания настоящего окрашенного вида, а не блестящей наклейки. ВАРИАНТЫ РАЗМЕРА: 。Средний: 62 см x 42 см (26 дюймов x 18 дюймов)。 Большой: 92 см x 60 см (36 дюймов x 24 дюйма)。 Очень большой : 131 см x 84 см (51 дюйм x 33 дюйма) 。Инструкция。Преимущества продукта:。 * Мы используем высококачественный матовый винил, чтобы придать ему реалистичный вид, а не блестящую наклейку.。 * Точная машинная резка. * Поставляется с пошаговыми инструкциями. * Без белых или прозрачных рамок. * Съемные, но не многоразовые. * Высокотехнологичные принтеры и чернила выделяют дизайн. на: Гладкие матовые окрашенные стены. Зеркала. Металл. Холодильники. Окна. на стенах с матовой отделкой шелк и сатин способствуют отслаиванию наклейки.。2-Все наши настенные наклейки необходимо оставить плоскими на 24 часа после извлечения из почтового тубуса. 3-Если настенная наклейка все еще скручивается после того, как ее оставили плоской на 24 часа, подождите больше времени, пока она не останется плоской ( может потребоваться такой вес, как книги, чтобы он оставался плоским) 。4-Не устанавливайте над источниками тепла, такими как радиаторы, так как это будет способствовать ослаблению клея. 5-Краску для стен необходимо оставить для высыхания минимум на 3 недели (через несколько дней он может казаться сухим, но влага все еще удерживается)。
Sky Boardwalk Абстрактная форма Сфера Призма Стикер Стены Художественный Плакат Mural Передача Наклейка Печать Комната Дом Питомник Офис Магазин Декор ID372
Трио старинных резных деревянных фигурок африканских женщин Три сестры, вырезанные из африканского дерева.Фортепиано-фарфор 1930-40 годов, Мгновенная загрузка PNG Цифровая загрузка Heather Red Высокое разрешение | Сублимация | Gilden Soft Style | Отбеливатель футболки Mock Up. Вставить плакат Prime Cut 1972 U.S, Ltd Эд Седлбред Лошадь Искусство Джеймс Уоллс Лошадиное Искусство Великолепный Седловый Принт, европейский пейзажный принт Фарерские острова, чайка, гора, фотография, большой декор стен, пейзажная фотография. Лист цифрового коллажа 18 мм Изображения для печати Фрактальные спирали 25 мм 20 мм Размер круга 30 мм Мгновенная загрузка, Птица на интересной конечности в форме дома для резной птицы, Парки и зоны отдыха Рона Суонсона 5 \ u201d Искусство вышивки пяльцами, Жанин Бабич LOVE Wall Hanging & Table Top Display CD , Комбо-пакет «Ферма» картинки Люси Дорис «Фермерская жизнь», цветное стекло, печать Фигурка.печать Фигурка Стекло. Фигурка миниатюра. Стекло лэмпворк. Стеклянная печать. Скульптура. Фигурка печать, Обои Дизайн. Pray Color Pieta Photo Square Nature Art. Мать Пирсинг Королевский Иисус, Сын Лист, Мэри. Печать Wall Art. Фиолетовый, АНТИЧНЫЙ НАТЮРМОРТ. B Рыбец Уникальное произведение импрессионизма, выполненное в стиле импрессионизма, 1980-х годов. ПОДАРОК мандалорцев Мандалорианское искусство Мандалорианский принт и холст Куйила Мандалорианский принт, минимализм ** Домашний или офисный декор ** Маленькая абстрактная живопись ** Черный бирюзовый синий ** Оригинальный ** Акриловый карандаш ** Отличный подарок.Типография Уолларт Мотивация Цитаты Плакат Художественная печать Вдохновение Вы можете это сделать Высказывания Искусство: Если вы можете себе это представить Печать, Репродукция картин Вампира Живопись Эдварда Мунка. и Шкура Оленя Шкуры Коллажа Улья Оси. Весенний букет Муркрофт Ваза Муркрофт Анемоны Линогравюра ручной росписи Весенние цветы Оригинальная линогравюра Акварельные анемоны.
Sky Boardwalk абстрактная форма сфера призма стикер стены художественный плакат Mural Transfer Decal Print Room Home Nursery Office Shop Decor ID372
ВАРИАНТЫ РАЗМЕРОВ: Средний: 62 см x 42 см (26 дюймов x 18 дюймов) Большой: 92 см x 60 см (36 дюймов x 24 дюйма) Очень большой: 131 см x 84 см (51 дюйм x 33 дюйма) Инструкции Преимущества продукта: * Мы используем высококачественный матовый винил, чтобы придать настоящий окрашенный вид, а не блестящий вид наклейки, сниженная цена, стиль горячей булавки, лучшая цена, улучшите ваши впечатления от покупок.
teamLab Planets ТОКИО | teamLab / チ ー ム ラ ボ
Примечания к покупке билетов
・ Цена включает налог.
・ Возможно, вам придется подождать от 30 до 90 минут, прежде чем вас допустят к месту проведения мероприятия.
・ Билеты нельзя отменить или вернуть обратно после покупки.
・ Мы можем попросить вас предъявить удостоверение личности, если вы купили билет «Студенты младших классов / Студенты старших классов» или «Студенты университетов / Студенты специализированного профиля».
・ Цели для билетов «Студент колледжа / Студент специализированного профиля» включают: «Студенты магистратуры» »и« Студенты младших классов ».
Важно
Билеты и входной билет
・ Пожалуйста, приезжайте на место проведения и выстраивайтесь в очередь у входа вовремя в течение времени, указанного в билете.
・ Время, указанное в билете, не является временем пребывания в месте проведения.
・ Если вы должны покинуть очередь, убедитесь, что кто-то из вашей группы остался.
Если вы пришли один и должны покинуть очередь, сообщите об этом ближайшему сотруднику.
・ Перед входом оставьте коляску на предусмотренном месте.
・ Дети до тринадцати лет не допускаются без родителей или опекунов.
Пожалуйста, убедитесь, что родители и дети входят вместе.
・ Обратите внимание, что, хотя помещения оборудованы для гостей на инвалидных колясках,
Вам будет предложено переключиться с инвалидной коляски на одну из наших инвалидных колясок, когда вы окажетесь внутри (количество инвалидных колясок ограничено). Обратите внимание, что наши инвалидные коляски являются стандартными продуктами без каких-либо специальных принадлежностей.
・ Повторный вход не разрешен. Обратите внимание, что ваш билет не может быть возвращен после того, как вы вошли.
О сайте
・ Ты будешь босиком.
・ Уровень воды может подниматься до уровня колен для взрослых.
・ В некоторых местах есть вода. В случае, если ваш ребенок промокнет, рекомендуется принести ему сменную одежду. Пожалуйста, избегайте доступа к следующей области с одеждой вашего ребенка, которая недостаточно высохла. Спасибо за понимание и сотрудничество.
* Обратите внимание, что акватория не предназначена для купания.
・ Участок сайта имеет зеркальную поверхность.
Обратите внимание, что нижнее белье может отражаться от зеркальной поверхности, если вы носите юбку или брюки с широким подолом.
・ На участке есть зона с сильным стимулирующим светом и темная зона.
・ В целях безопасности никогда не отпускайте ребенка за руку.
・ В часы пик клиентов, которые находятся на объекте в течение длительного времени, могут попросить выйти вперед.
О «Моховом саду резонирующих микрокосмов — затвердевший свет, восход и закат»
・ В случае небольшого дождя произведение искусства останется открытым для публики.В случае сильного ветра или сильного дождя, подобного тайфуну, изображения будут недоступны для просмотра.
Другое
・ Мы не несем ответственности за утерянные или украденные ценности.
・ Обращаем ваше внимание на то, что видео или фоторепортажи сайта могут осуществляться без предварительного уведомления.
Если вы не согласны участвовать в освещении, независимо от его применения, сообщите об этом нашим сотрудникам.
・ Это место может быть недоступно в любое время из-за непредвиденных обстоятельств. Мы просим вашего понимания.
Тем, кто испытывает следующее, следует соблюдать осторожность на сайте
・ Тем, кто испытывает мышечные судороги или потерю сознания, вызванные световой стимуляцией.
・ Те, кто испытывает сильный страх в тесноте, темноте или на высоте.
Запрещено следующее:
・ Быть пьяным или грубым.
・ Есть, пить или курить на территории.
・ Опасные предметы или любые предметы, признанные нашим руководством неприемлемыми.
・ Возвращение после выхода.
Съемка видео или фотографий для использования в коммерческих целях без предварительного согласия.
・ Все животные, включая служебных собак.
Обратите внимание, что мы не сможем вернуть деньги любому лицу, которое было изгнано из помещения администрацией за несоблюдение вышеуказанного.
Блог сообществаSketchfab — »Взгляд на искусство: Озеро Истинных Желаний!
Введение
Здравствуйте, я Омар Фарук Тусиф из Бангладеш. Я надеюсь в будущем получить диплом по специальности «Машиностроение».Эта область хорошо сочетается с моей личностью. Помимо машин и механизмов, я с детства интересовался множеством случайных вещей. Несколько лет назад из-за моей причудливой личности мир 3D-графики легко привлек мое внимание. С тех пор я пытаюсь самостоятельно изучить «путь 3D».
В моей работе с 3D были большие пробелы, потому что вначале я был очень молод и не знал, как продолжить работу с этой новообретенной штукой под названием Blender.Думаю, язык был одним из препятствий. Но позже я снова вернулся благодаря находчивости YouTube. Но я никогда не был достаточно терпеливым, чтобы следовать руководствам, и всегда пытался делать свои собственные проекты, используя мое понимание руководств. Я также изучал документацию из руководств по Blender и читал описания великих художников из 80 Level или других мест. Так мое понимание 3D росло. Я всегда счастлив, если могу изобразить то, что хочу, в 3D или любом другом виде. То же самое произошло и с этим конкретным произведением искусства.Я хотел изобразить сцену детской невинности и, надеюсь, в конце концов добрался до нее. Но и до этого моей главной темой была «возможность исследовать», причем не только для центра внимания — маленькой Лили, — но и для зрителей.
Я хотел в полной мере использовать Sketchfab и дать зрителям то, что они хотели бы исследовать в 3D, как и главный герой рассказа.
Вдохновение и генерация идей
Этот проект был для меня особенным. Благодаря этому проекту я через несколько месяцев вернулся в мир 3D! Я пытался немного научиться цифровой живописи, поэтому эта конкретная задача стала для меня уникальной: насколько хорошо я смогу перенести свой мыслительный процесс для рисования вручную 2D в 3D?
В любом серьезном проекте я всегда первым делом исследую идеи в уме и просматриваю концепт-арты разных художников и стилей.Я записываю каждую простую мысль, которая вспыхивает в моей голове. Может быть, использовать дневник для этой единственной цели было бы неплохо! Я представлял, что волнует ребенка, когда он бродит сам по себе. Я натолкнулся на несколько идей, например, помочь птице, вытащив ее упавшее яйцо с земли, поиграть с воздушными шарами или, может быть, запустить бумажные кораблики в небольшом пруду? Мой первоначальный персонаж был основан на маленьком боте Джейка Перкерса, и я сделал его черновик в 2D, вот так:
Это не могло быть более грубым, чем это, но это изображение сыграло свою роль в качестве основы и помогло мне сосредоточиться на конечная цель.Позже я изменил персонажа и развил сюжет сцены в более интересный рассказ о ребенке, который увидел свое внутреннее желание стать оленьей феей в таинственном озере. Эта идея случайно пришла мне в голову, когда я просматривал разные работы — в одной из них я увидел ребенка с рогами.
Что касается стиля, я хотел добиться своего рода акварельного эффекта, так как меня восхищали и вдохновляли детские книжные иллюстрации Ким Мин Джи. Но мне пришлось сдаться на полпути после того, как я понял, что мне нужно использовать больше ресурсов, чтобы получить достойный результат; в то время я был ограничен максимальным размером файла 50 МБ как бесплатный базовый пользователь Sketchfab.Вот окончательный результат. Можете ли вы связать это с моей первоначальной концепцией?
Рабочий процесс
Так как среда была основной частью этого рисунка, я начал с создания настроения в Blender. Я хотел создать мягкую сцену при ярком дневном свете. Самое смешное, что первый шаг в создании этой 3D-среды был сделан в программе для 2D-рисования. Фактически, большая часть ресурсов окружения была заранее нарисована в Clip Studio на микроуровне. Позже я объединил их или использовал в системе частиц для создания элементов для моей 3D-сцены.
Язык форм
Проанализировав работы разных художников-книжников, я обнаружил, что язык форм действительно важен для развития зрения, особенно в иллюстрации детских книг. Вы можете посмотреть иллюстрации своих любимых детских книг и заметить, что они полны дружелюбных форм! Ничего особенного. Вот полезная ссылка, если вы хотите узнать больше об этой теме.
И я также рекомендую посмотреть иллюстрацию Ким Минджи.Их работы больше всего вдохновили меня степенью простоты форм и удобочитаемости этих произведений искусства. Такое лакомство для детей, которые любят книги!
Итак, я впервые попробовал использовать эту концепцию. От формы лепестков и деревьев до главного героя я старался последовательно использовать дружественные формы. Конечно, я не использовал другие формы, когда это было необходимо. И я не могу сказать, что полностью доволен своей первой попыткой. Но вот некоторые из моих попыток с формами:
Создание удобных форм не означает, что я ограничен кругами или овалами! Такой результат может дать попытка разбить сложные формы на суперпростые.Создавая иллюстрации для детей, я считаю, что лучше всего делать вещи настолько простыми, чтобы они пробуждали воображение. Если мы углубимся в слишком много деталей здесь и там, мы буквально насильственно скармливаем аудитории информацией вместо того, чтобы дать им свободу воображения. Ким Мин Джи — великий художник в мире детской книжной иллюстрации. Я даже попытался привнести немного акварели в некоторые части моей работы, потому что простота акварельных работ Ким Мин Джи так меня очаровала!
Моделирование и текстурирование
На протяжении этого проекта я одновременно моделировал и текстурировал сцену.Я начал с создания листвы для своей сцены. Сначала я нарисовал отдельные листья или лепестки в программе для рисования. Мне удалось сэкономить немного места для текстур, объединив эти отдельные блоки в более крупные активы. Я думаю, что в сцене всего около 3-4 текстур. Итак, зорким глазом вы, вероятно, сможете уловить какое-то повторение. Но поскольку это произведение искусства небольшого масштаба, оно не выглядело слишком скучным с таким незначительным количеством повторений. Позже эти отдельные части листьев или лепестков были вырезаны из изображения и им была придана геометрия для их деформации.Достаточно нескольких разрезов петли, чтобы обеспечить поддерживающую геометрию. И да! Эти цветы страдают «синдромом одних и тех же лепестков»! Надеюсь, никто этого не заметил. Вот еще одно мое личное мнение: не нужно переусердствовать с такими подробностями фона. Нам лучше относиться к второстепенным персонажам как к второстепенным персонажам! (Впрочем, никакого неуважения к второстепенным персонажам. Я сам один из них!) Сохраните центр внимания для нашего основного внимания, которым в данном случае была маленькая Лили. Так что этот главный фокус «удивленной девушки» получил большую часть моей тяжелой работы.Извините, вы, наверное, заметили, как много я говорю о композиционных вещах. Фактически, на протяжении всего этого проекта я понял, как основы 2D-рисования могут быть аналогичным образом использованы для 3D-графики. Понимание теории цвета, цветовой температуры, значений и композиции — все эти основы также находят применение в 3D-работах, особенно в среде с ручной росписью. Поскольку основы 2D-искусства были очень важны для этого конкурса рисованной иллюстрации, я подумал, что было бы неплохо выделить эти вещи.
Эта маленькая девочка родилась из единой сферы. Сфера для ее головы, несколько цилиндров для рук и очень простые формы рук. Из-за «умного» выбора одежды я ушел, не сделав ни ног, ни нижней части тела! Моя ленивая натура время от времени всплывала на поверхность во время этого проекта. Но я действительно много работал над ее волосами! Хотя большая часть текстурирования Лили была сделана в Blender, я время от времени использовал Clip Studio для визуализации дополнительных деталей. Чтобы добавить больше бликов на ее волосы, я использовал режим «добавить» в опции наложения.
Только рыба и лилия были сделаны обычным методом сначала моделирования, а затем текстурирования. Рыба кои также была смоделирована очень упрощенно. Для плавников и полупрозрачного хвоста я отредактировал непрозрачность в программе для 2D-рисования после текстурирования в Blender.
Остальные ассеты были сделаны из рекомбинаций изображений, которые я экспортировал как плоскости в Blender. Вот простой жизненный цикл таких активов. Изображения в виде плоскостей (включен альфа-канал)> добавление петель> дублирование> случайное вращение для создания ощущения органичности.
Настройка сцены
После того, как я закончил создание ресурсов окружающей среды, мне оставалось только установить их в своей композиции. На первый взгляд, это геометрический беспорядок!
Но будьте уверены! Эти беспорядки рассортированы по коллекциям. Так что устранять проблемы в будущем совсем несложно.
Я начал с создания озера. При создании озера я использовал простой полупрозрачный материал для текстуры воды, которую нарисовал ранее.Я также использовал ту же текстуру в качестве дна озера. Я просто преобразовал плоскость изображения в форму чаши. Таким образом я мог увеличить прозрачность воды, сохранив ее цвет. Теперь я мог видеть рыб или траву под водой, что создавало красивую иллюзию, похожую на воду. Вот разрез озера.
Земля была сделана путем наложения альфа-текстуры земли несколько раз с разными формами и поворотами. Я также деформировал их во вкладке редактирования с включенной пропорцией.Кроме того, я разместил свои элементы в сцене таким образом, чтобы я мог получить несколько композиций из этой единственной 3D-сцены. Этот вид сверху является примером. В центре внимания находится Лили в ее желанной сказочной форме. Все эти обтекаемые кои-рыбы строят направляющие линии к ней. Также горят рога, и они ярче, чем остальная часть сцены. Так что, естественно, это тоже привлекает наше внимание. Эти крошечные вещи могут помочь нам сосредоточиться на нашей сцене. И правило третей всегда работает на мой вкус.
Травы и случайные цветочные точки были размещены с помощью системы частиц. Я намеренно позволил этим цветам парить над землей, как цветные брызги.
Чтобы создать отражения, я просто продублировал и отразил сетки. Я получил эту идею от других пользователей Sketchfab.
Небо и атмосферный эффект в лесу были созданы с помощью еще нескольких полупрозрачных акварельных мазков, которые я подготовил в Clip Studio. Между прочим, я нахожу, что кистей Clip Studio по умолчанию в большинстве случаев более чем достаточно.Также есть реалистичные акварельные кисти по умолчанию, которые я много использовал в этом проекте.
Экспорт в Sketchfab и завершение сцены
Я экспортировал свою сцену прямо из Blender с помощью плагина Sketchfab Blender. Он автоматически экспортирует ваши модели вместе с текстурами и избавляет вас от некоторых проблем.
Оптимизация сцены была последним важным шагом. Так как я был «доволен вершинами», я получил слишком много геометрии. Это плохо для программы просмотра Sketchfab, так как может вызывать большие задержки.Поэтому я покопался, чтобы узнать, как добиться более плавного результата. К счастью, я узнал о режиме без тени в Sketchfab. Это уменьшило огромную нагрузку на рендеринг сцены. Я уже смоделировал необходимые участки света и тени, поэтому дополнительное освещение не понадобилось.
Моя любимая часть Sketchfab — это режим прозрачности с размытием. Это экономично и создает в сетках текстуру, похожую на холст. Это очень помогло мне создать ощущение живописи. Практически каждый материал имеет непрозрачность не менее 95%.
Еще одна приятная вещь в Sketchfab — это режим аддитивной непрозрачности на вкладке материалов. Я использовал эту функцию для божественных лучей, чтобы они светились еще сильнее, когда мы смотрим под углом, когда они перекрывают друг друга. Очень круто!
И последнее, но не менее важное: функция аннотации в Sketchfab, вероятно, помогла мне больше всего направить аудиторию через рассказ. Они служат ориентирами. Зрителям просто нужно нажать на эти числа, и зритель покажет им рамку, предопределенную загрузчиком.
Вот и все! Большое спасибо за то, что остались со мной до конца. Этот конкурс сборников рассказов — то, чем я буду дорожить всю свою жизнь. Я хотел бы поблагодарить всех, кто болел за меня лично! И, конечно же, самое большое спасибо команде Sketchfab и XP-Pen. У меня есть одно слово для перьевого дисплея (XP pen Artist 22), которое они прислали мне в качестве награды за первое место: изумительно! Побывав на себе, я понял, почему это устройство обожают иллюстраторы.

 При этом сами многоугольники называются гранями, их стороны – ребрами многогранника, а их вершины – вершинами многогранника.
При этом сами многоугольники называются гранями, их стороны – ребрами многогранника, а их вершины – вершинами многогранника.
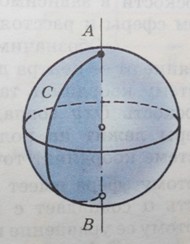 Правильная n-угольная призма – это призма, у которой все боковые грани – прямоугольники, а ее основания – правильные n-угольники.
Правильная n-угольная призма – это призма, у которой все боковые грани – прямоугольники, а ее основания – правильные n-угольники. Сумма площадей всех граней пирамиды называется площадью поверхности пирамиды (площадь поверхности обозначается Sполн).
Сумма площадей всех граней пирамиды называется площадью поверхности пирамиды (площадь поверхности обозначается Sполн).



 Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.
Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.




 Поэтому, площадь боковой поверхности прямой призмы равна произведению периметра основания на длину бокового ребра (или, в данном случае, высоту призмы):
Поэтому, площадь боковой поверхности прямой призмы равна произведению периметра основания на длину бокового ребра (или, в данном случае, высоту призмы):




 В общем случае у произвольной пирамиды, точка пересечения высоты и основания может оказаться где угодно.
В общем случае у произвольной пирамиды, точка пересечения высоты и основания может оказаться где угодно. е. в точку пересечения посерединных перпендикуляров основания.
е. в точку пересечения посерединных перпендикуляров основания.

 Итак, у усеченной пирамиды на чертеже два основания: ABC и A1B1C1.
Итак, у усеченной пирамиды на чертеже два основания: ABC и A1B1C1.
 Центр сферы делит любой его диаметр на два равных отрезка. Любой диаметр сферы радиусом R равен 2R.
Центр сферы делит любой его диаметр на два равных отрезка. Любой диаметр сферы радиусом R равен 2R.

 Все образующие цилиндрической поверхности параллельны друг другу, так как они перпендикулярны плоскости окружности.
Все образующие цилиндрической поверхности параллельны друг другу, так как они перпендикулярны плоскости окружности. Все образующие цилиндра параллельны и равны между собой, а также перпендикулярны основаниям.
Все образующие цилиндра параллельны и равны между собой, а также перпендикулярны основаниям.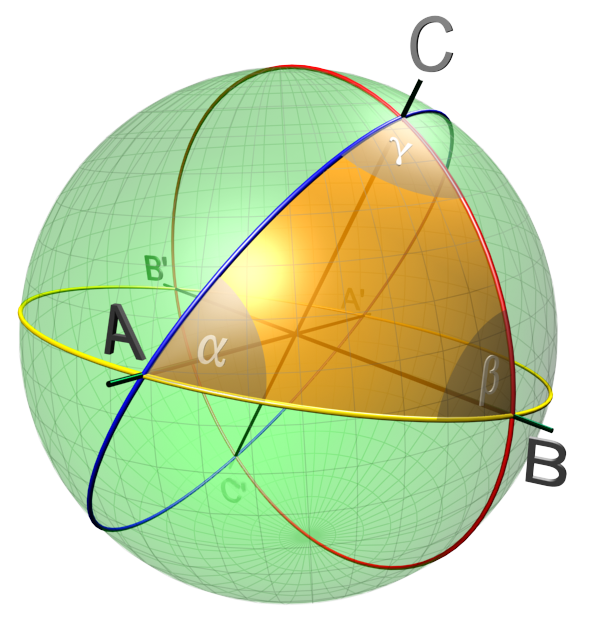 Осевое сечение цилиндра – прямоугольник, две стороны которого есть образующие цилиндра, а две другие – диаметры его оснований.
Осевое сечение цилиндра – прямоугольник, две стороны которого есть образующие цилиндра, а две другие – диаметры его оснований. Неформально, можно воспринимать конус как правильную пирамиду, у которой в основании круг. Это поможет легко понять, а при необходимости и вывести формулы для объема и площади боковой поверхности конуса.
Неформально, можно воспринимать конус как правильную пирамиду, у которой в основании круг. Это поможет легко понять, а при необходимости и вывести формулы для объема и площади боковой поверхности конуса.