Частотное разложение на 3 частоты: Рецепты частотного разложения

Рецепты частотного разложения

Метод частотного разложения, на мой взгляд – это лучшая на сегодняшний день технология, позволяющая отдельно работать с детализацией и цветом. Для тех, кому интересны теоретические основы этого метода, рекомендую почитать соответствующие материалы в ЖЖ Андрея Журавлева, так как не вижу смысла дублировать то, что уже было сделано до меня, причем, максимально подробно, с описанием математики.

Мы же с вами коснемся чисто практических аспектов и нюансов применения данного метода, рассмотрим как достоинства, так и недостатки, а точнее, ограничения различных способов реализации метода частотного разложения.

Если вы уже сталкивались с этим методом, то знаете, что существует несколько способов его реализации.

Разложение на две частоты с помощью фильтров Размытие по Гауссу (Gaussian Blur) и Цветовой контраст (High Pass).

 Именно этот метод получил поначалу самое широкое распространение в сети. Он прост в реализации, но имеет некоторые ограничения в применении.

Для начала кратко рассмотрим сам метод.

Для того, чтобы разложить изображение на две частоты, нужно выполнить следующие операции:

1. Создаем копию фонового слоя или объединяем видимые слои на отдельный слой.

2. Называем ее как-то осмысленно, исходя из того, что этот слой будет являться основой для дальнейших действий. Например, Base или Основа.

3. Делаем две копии слоя Base. Первую называем Low или Низкая частота, вторую, соответственно, High или Высокая частота.

4. Дальнейшие действия зависят от того, на какую составляющую мы будем ориентироваться. Если нам важно вынести на слой

High всю хорошую текстуру, оставив более крупные дефекты на слое Low, то поступаем следующим образом:

5. К слою High применяем фильтр Цветовой контраст (High Pass) с таким радиусом, чтобы видеть только ту текстуру кожи, которая нам нужна.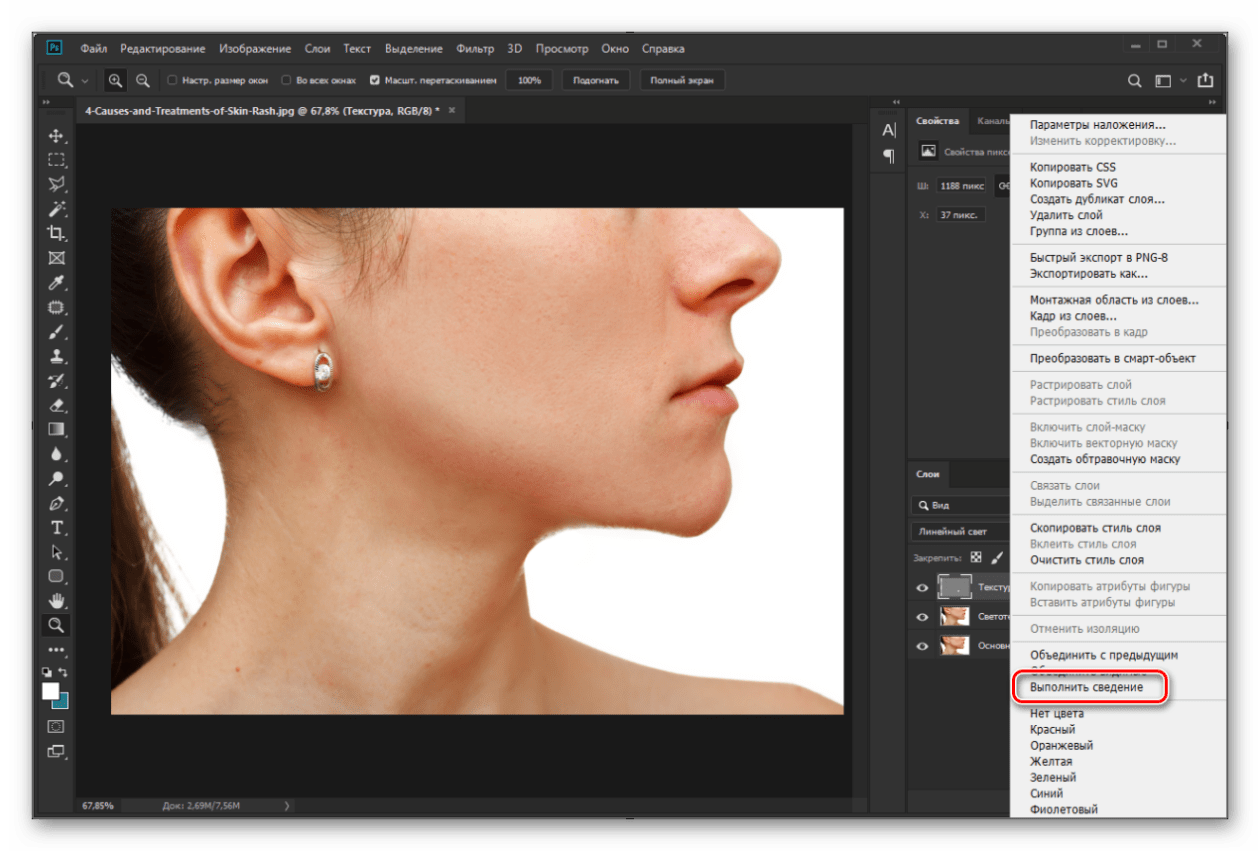 Радиус не должен быть слишком малым, иначе часть хорошей текстуры уйдет на слой с низкой частотой, то есть

Low. Также он не должен быть и слишком большим, чтобы не выносить на слой с высокой частотой те самые, более крупные дефекты в виде локальных объемов, от которых нам необходимо избавляться.

Неправильный выбор радиуса фильтра Цветовой контраст. Слишком большой радиус.

 Неправильный выбор радиуса фильтра Цветовой контраст. Слишком маленький радиус. 

Оптимальный радиус фильтра Цветовой контраст

6. Подобрав необходимый радиус фильтра Цветовой контраст (High Pass), например, 5 пикселей, запоминаем его и применяем. Очень желательно прописать радиус фильтра в названии слоя. Например,

High 5. Дело в том, что если вас неожиданно отвлекут от работы, например, телефонным звонком, вы вполне можете забыть значение и тогда придется начинать все заново.

7. Применяем фильтр Размытие по Гауссу (Gaussian Blur) с таким же радиусом, то есть, в данном случае, 5 пикселей.

8. Меняем режим наложения слоя High на Линейный свет (Linear light)

9. Снижаем контраст слоя High в два раза. Для этого создаем корректирующий слой Яркость/Контрастность, включаем параметр Использовать прежние и ставим значение контраста на минус 50. Применяем через обтравочную маску к слою High.

10. Мы разложили изображение на две частоты. Теперь можно по отдельности работать с детализацией, цветом и объемом. Я не буду подробно останавливаться на процессе, так как подробнее вы можете узнать об этом, купив запись онлайн мастер-класса «Частотное разложение — просто как 2х2»

11. Если же нам важно наоборот, контролировать, какие дефекты останутся на низкой частоте, то есть, работа с низкой частотой в приоритете, то нужно сначала отключить видимость слоя

High, затем подобрать нужный радиус Размытия по Гауссу для слоя Low, прописать это значение в названии слоя, а затем, включив видимость слоя High, применить фильтр Цветовой контраст с тем же радиусом, что и фильтр Размытие по Гауссу. Далее все аналогично.

12. После этого можно создать дополнительные слои для ретуши низкочастотной и высокочастотной составляющих.

Достоинства метода: простота в освоении даже для новичков, возможность временно усилить текстуру для ретуши путем простого отключения корректирующего слоя, снижающего контраст.

Недостатки и ограничения метода: недостаточная гибкость, по сравнению с разложением изображения на три пространственных частоты, опасность появления артефактов на контрастных границах при работе на слое с текстурой, некоторая математическая неточность, обусловленная особенностью математики фильтра Цветовой контраст (подробнее об этом можно почитать здесь). Впрочем, надо отметить, что в 99% случаев этой погрешностью можно пренебречь, так как вы сами при ретуши вносите гораздо более существенные «погрешности», несоизмеримо большие.

Разложение на две частоты с помощью операции вычитания.

Для реализации этого метода нужно выполнить следующее:

1. Сделайте копию фонового слоя или копию видимых слоев, аналогично предыдущему алгоритму.

2. Точно также сделайте две копии, назвав одну Low, а другую High.

3. Отключите видимость слоя High.

4. Подберите радиус размытия для слоя Low, примените фильтр Размытие по Гауссу.

5. Перейдите на слой High. Если вы работаете с глубиной цвета 8 бит, то примените команду Внешний канал (Apply Image), установив следующие параметры – слой

Low, канал RGB, режим наложения Вычитание, масштаб 2, сдвиг 128. Если вы работаете с глубиной цвета 16 бит, то примените команду Внешний канал, установив следующие параметры – слой Low, канал RGB, инвертировать, режим наложения Добавление, масштаб 2, сдвиг 0.

Параметры команды Внешний канал для режима 8 бит

Параметры команды Внешний канал для режима 16 бит

6. Измените режим наложения слоя

High на Линейный свет (Linear light).

Достоинства метода: более аккуратная математика, отсутствие «проблемы High Pass», возможность применения любых фильтров размытия, а не только Размытия по Гауссу. Например, за счет применения фильтра Размытие по поверхности можно полностью решить проблему грязи на контрастных границах, легкость применения при построении «частотных эквалайзеров», то есть, многополосного разложения на пространственные частоты.

Недостатки метода: необходимость дополнительных операций для визуализации высокой частоты. Как выполнить такую визуализацию, я расскажу в конце статьи. Также к недостаткам (скорее к особенностям) метода можно отнести недостаточный контраст слоя

High, что вызывает необходимость создания дополнительного корректирующего слоя, повышающего контраст, для облегчения ретуши высокочастотной составляющей. Точно также, метод имеет недостаточную гибкость, по сравнению с разложением на три пространственных частоты.

Разложение на три полосы частот.

Обеспечивает гораздо большую гибкость в работе, чем двухполосные методы. В частности, на низкой частоте можно полностью сосредоточиться на крупных участках, цвете, светотеневом рисунке, на высокую частоту вынести только необходимую текстуру, а все остальное оставить на промежуточной, средней частоте. В диапазон средних частот попадают такие дефекты как родинки, прыщи, пигментация кожи, веснушки, целлюлит, растяжки и т.д. Ретушируя среднюю полосу частот, мы избавляемся от этих дефектов. Иногда можно встретить рекомендации размывать среднюю полосу или просто вырубать ее черным цветом на маске. Я считаю такой подход несколько некорректным, так как именно ретушь средней полосы частот даст гораздо лучший результат.

Именно метод с разложением на три полосы частот я использую для ретуши фотографий, к которым предъявляются очень высокие требования по качеству постобработки. Подробный процесс ретуши со всеми объяснениями вы сможете найти в обучающем

онлайн-курсе с домашними заданиями «Секреты профессиональной ретуши»

Как разложить изображение на три пространственных частоты:

1. Делаем базовый слой, как описано выше.

2. Создаем три копии слоя, называя их соответственно Low, Mid и High.

3. Подбираем радиус фильтра Цветовой контраст для слоя High. На этом слое будет только текстура кожи, без излишней информации о локальных объемах и дефектах. Радиус фильтра прописываем в названии слоя.

4. Подбираем радиус фильтра Размытие по Гауссу для слоя Low. Основным критерием здесь является размытие дефектов мелких и средних размеров. Должны остаться только дефекты относительно крупные, такие как следы крупных родимых или пигментных пятен, неровностей светотеневого рисунка. Однако, переусердствовать тоже не следует, иначе средняя частота получится слишком широкой. Как показала практика, оптимальное соотношение между высокой и низкой частотой в большинстве случаев лежит в пределах от 1:3 до 1:4, то есть, радиус размытия в 3-4 раза больше радиуса фильтра Цветовой контраст. Прописываем радиус фильтра в названии слоя.

5. Все, что лежит между этими радиусами, будет вынесено в среднюю полосу частот. Для этого переходим на слой Mid и выполняем вычитание из него слоя Low. Делаем это с помощью команды Внешний канал, аналогично тому, как делали разложение на две частоты. Таким образом мы убиваем двух зайцев: получаем честный математический алгоритм, что критично для довольно больших радиусов, а также имеем возможность использовать на слое НЧ любые фильтры размытия, отличные от гауссова.

6. Размываем слой Mid по Гауссу с радиусом, который использован на слое High для фильтра Цветовой контраст.

7. Меняем режим наложения слоя Mid на Линейный свет.

8. Меняем режим наложения слоя High на Линейный свет. Уменьшаем контраст этого слоя в два раза, аналогично первому методу.

9. Теперь мы сможем работать раздельно с тремя пространственными частотами.

Достоинства метода: больше гибкости в работе, более качественный результат ретуши.

Недостатки метода: те же, что и у метода с разложением на две частоты, требуется больше времени для ретуши, так как приходится работать на трех слоях, вместо двух. Сложность в освоении метода, если нет необходимых базовых знаний Photoshop.

Полосовой фильтр.

Этот метод в зарубежных источниках имеет название Inverted High Pass, однако, по аналогии с электрическими фильтрами, здесь имеет место простое подавление некоторой полосы частот, то есть это аналог режекторного или полосового фильтра.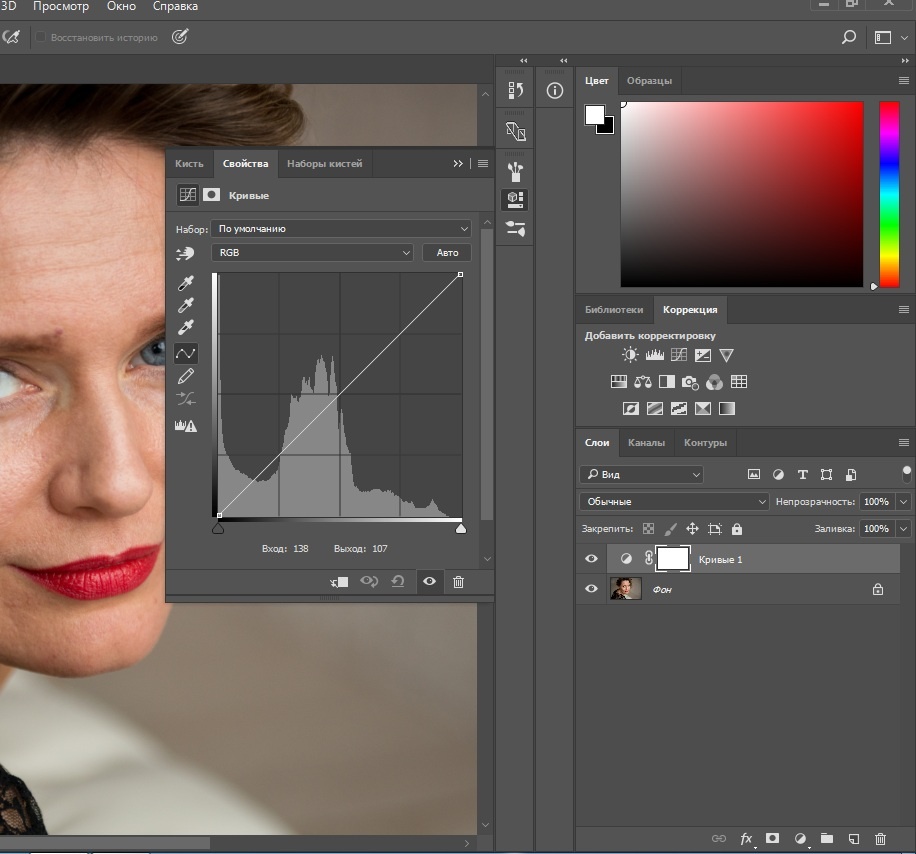

Полосовой фильтр хорошо использовать для быстрой ретуши, когда требуется с минимальными затратами времени и приемлемым для массовых работ качеством избавиться от дефектов в средней полосе частот.

Алгоритм действий:

1. Делаем копию фонового слоя, называя ее, например, Fast Retouch, то есть Быстрая Ретушь.

2. Размываем данный слой по Гауссу с таким радиусом, чтобы убрать ненужные локальные объемы.

3. Вычитаем из размытого слоя исходный, то есть, в данном случае процесс происходит наоборот, так как в предыдущих методах мы вычитали из исходного слоя как раз размытый. Делаем это с помощью команды Внешний канал.

4. Изменяем режим наложения слоя Fast Retouch на Линейный свет. Мы должны увидеть размытую картинку.

5. Теперь снова размываем данный слой по Гауссу, только теперь с радиусом в 2-4 раза меньшим, проявляя мелкую текстуру кожи. Мы получим изображение, которое выглядит несколько необычно.

6. Прячем данный слой в черную маску и белой кистью проявляем его в нужных местах. При этом избегайте работы вблизи контрастных границ, так как получите грязь на этих местах.

Впрочем, проблему грязи на контрастных границах довольно легко решить. Уже догадались как?

Правильно! Использовать для размытия фильтр, оставляющий четкие границы, например, Размытие по поверхности.

Достоинства метода: простота и эффективность, быстрота в применении для массовой обработки. В отличие от плагинов, более контролируемый результат.

Недостатки метода: отсутствие какой-либо гибкости в работе, невозможно получить результат высокого качества.

Многополосное разложение или «эквалайзер».

Для упрощения процесса ретуши можно модифицировать предыдущий метод, раскладывая изображение на несколько пространственных частот, с использованием различных радиусов для размытия изображения. Таким образом мы получим возможность, работая по маске слоя, быстро убирать дефекты различных размеров.

Алгоритм создания эквалайзера:

1. Определяемся со значениями радиусов, которые будем использовать. Обычно используются значения 5, 10, 15, 25, 40 пикселей, но вы можете выбирать любые, которые вам подходят.

2. Создаем базовый слой, как в предыдущих методах.

3. Создаем необходимое количество копий, по числу радиусов плюс один слой. В данном случае шесть копий базового слоя.

4. Называем копии осмысленно, например, по диапазонам радиусов, то есть, 40, 40-25, 25-15, 15-10, 10-5, 5.

5. Отключаем все слои выше слоя 40. Размываем этот слой по Гауссу с радиусом 40 пикселей

6. Включаем вышележащий слой 40-25, переходим на него и выполняем вычитание слоя 40 с помощью команды Внешний канал.

7. Размываем данный слой по Гауссу с радиусом 25 пикселей.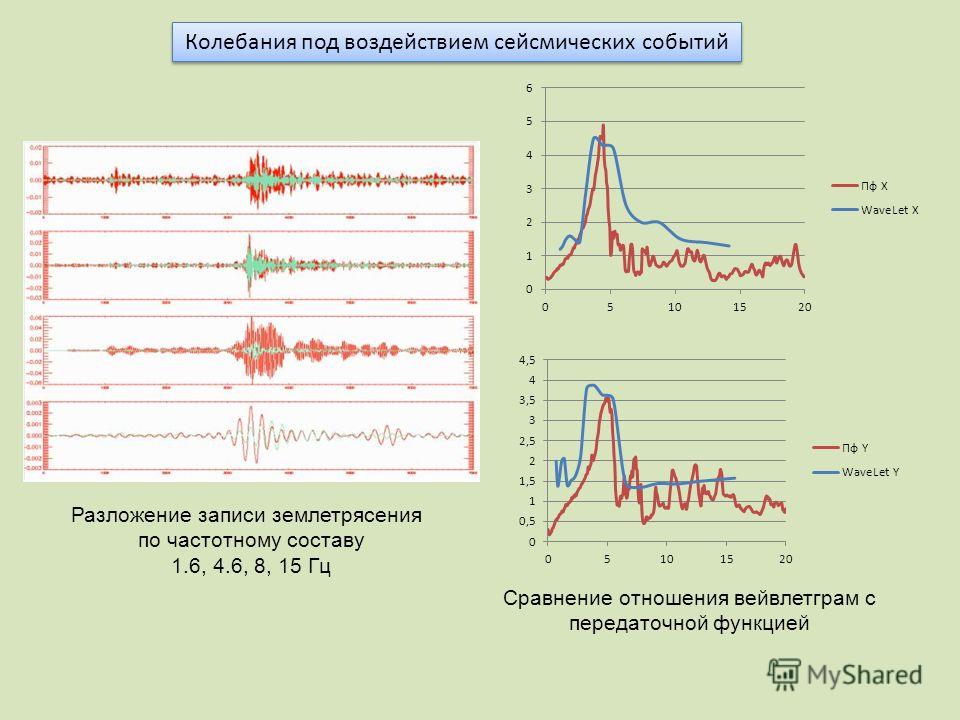 Получаем полосу частот от 40 до 25 пикселей.

8. Меняем режим наложения на Линейный свет.

9. Переходим на слой 25-15 и, ВНИМАНИЕ! Не включаем видимость слоя!

10. Выполняем вычитание из данного слоя содержимого всех слоев. То есть, в настройках команды Внешний канал в качестве источника нужно поставить Объединено. Таким образом мы вычтем из данного слоя изображение, размытое на 25 пикселей.

11. Теперь включаем видимость слоя 25-15 и меняем режим наложения на Линейный свет.

12. Размываем слой 25-15 на 15 пикселей.

13. Повторяем операции с другими слоями. Последний слой, с названием 5, не размываем, так как на нем будет находиться текстура с размерами элементов до 5 пикселей.

14. Таким образом, мы получаем эквалайзер пространственных частот. Теперь мы можем как ослаблять нужный диапазон частот, так и усиливать его. Ослабление производится путем наложения маски слоя и рисования по нужным местам черной кистью с необходимой непрозрачностью. Усиление производится с помощью корректирующего слоя, например, Кривые, действующего через обтравочную маску на конкретный слой. Поднимая контраст простым поворотом кривой против часовой стрелки, мы усиливаем контраст слоя, тем самым усиливая видимость данной полосы частот.

Достоинства метода: возможность быстрого подавления или усиления в выбранных полосах частот, таким образом можно значительно ускорить процесс ретуши.

Недостатки метода: сложность в реализации для начинающих, накопление ошибок округления из-за большого количества слоев, при работе вблизи контрастных границ те же проблемы с грязью из-за ореолов размытия.

Частотное разложение без потерь.

Все предыдущие способы разложения изображения на пространственные частоты имеют общий недостаток (хотя это скорее особенность), возникающий из-за целочисленной арифметики Photoshop, то есть, из-за округления чисел до целых при расчете. В результате, например, 5 разделить на 2 будет равно уже не 2.5, а 3.

Поэтому, если вынести изображение, получаемое частотным разложением, на отдельный слой и сравнить его с исходником, наложив в режиме Разница (Difference) и сильно подняв контраст, мы увидим, что изображения имеют небольшое отличие друг от друга.

Как правило, это отличие не превышает один-два тоновых уровня. Те изменения, которые вносятся впоследствии в картинку при ретуши, несоизмеримо больше. Поэтому не следует обращать на это внимания.

Однако, если для вас все же критична даже такая микроскопическая разница, можете воспользоваться способом честного частотного разложения, без потерь.

Для режима 8 бит алгоритм будет следующий:

1. Создаем базовый слой. Делаем три копии базового слоя.

2. Называем первый слой Low, следующий High_Dark, и верхний High_Light.

3. Отключаем видимость слоев High_Light и High_Dark.

4. Размываем слой Low с необходимым радиусом. При этом можно использовать любые фильтры размытия.

5. Включаем слой High_Dark. Переходим на него. Применяем команду Внешний канал со следующими настройками: источник слой Low, канал RGB, инвертировать, режим наложения Линейный осветлитель (Linear Dodge).

6. Меняем режим наложения слоя High_Dark на Линейный затемнитель (Linear Burn).

7. Включаем слой High_Light и переходим на него. Применяем команду Внешний канал со следующими настройками: источник слой Low, канал RGB, инвертировать, режим наложения Линейный затемнитель.

8. Меняем режим наложения слоя High_Light на Линейный осветлитель.

Если вынести разложенную картинку на отдельный слой с помощью комбинации клавиш CTRL+ALT+SHIFT+E, то при наложении ее на исходную в режиме Разница, с предельно усиленным контрастом, мы ничего не увидим. То есть, метод обеспечивает математически точное частотное разложение. К сожалению, в режиме 16 бит данный метод имеет видимую погрешность. Для 16 бит используется несколько другой алгоритм, который также дает погрешность, но уже на уровне единичных пикселей, что абсолютно некритично.

9. Таким образом, мы получаем два слоя для текстуры – один High_Light со светлой составляющей на черном фоне и второй High_Dark с темной составляющей на белом фоне. Ретушь текстуры в данном случае придется производить в два этапа, сначала одну составляющую, затем другую.

Достоинства метода: математически точное частотное разложение, без погрешностей.

Недостатки метода: необходимость ретуши высокочастотной составляющей в два этапа.

Алгоритм визуализации высокочастотной составляющей.

При работе с фильтрами размытия, такими как Размытие по поверхности (Surface Blur) или Медиана (Median) имеется определенная проблема. Заключается она в том, что довольно часто хочется реализовать видимость высокочастотной составляющей, как будто мы применяем фильтр Цветовой контраст. Это необходимо для того, чтобы иметь возможность контролировать, какая текстура будет впоследствии вынесена на высокочастотный слой.

Для визуализации высокочастотной составляющей я предложил следующий метод, который основан на знании математики режимов наложения и особенностей работы фильтров в Photoshop. Теперь этот метод используют многие ретушеры и преподаватели в различных онлайн и оффлайн школах, обучающих обработке изображений.

Алгоритм визуализации следующий:

1. Создаем базовый слой. Делаем две копии, называем одну Low, другую High. Слой High отключаем.

2. Копируем слой Low, называем копию Temp, что означает временный.

3. Слой Temp инвертируем и устанавливаем непрозрачность 50%. Получаем 50% серый.

4. Теперь над слоем Temp создаем временный корректирующий слой Инверсия (Invert).

5. Для дополнительного усиления контраста, чтобы лучше видеть текстуру, желательно создать еще один временный корректирующий слой Кривые, закрутив кривую RGB против часовой стрелки вокруг центральной точки.

6. Теперь, если мы будем размывать каким-либо фильтром слой Low, мы увидим серую картинку с текстурой, как будто мы применяем фильтр Цветовой контраст.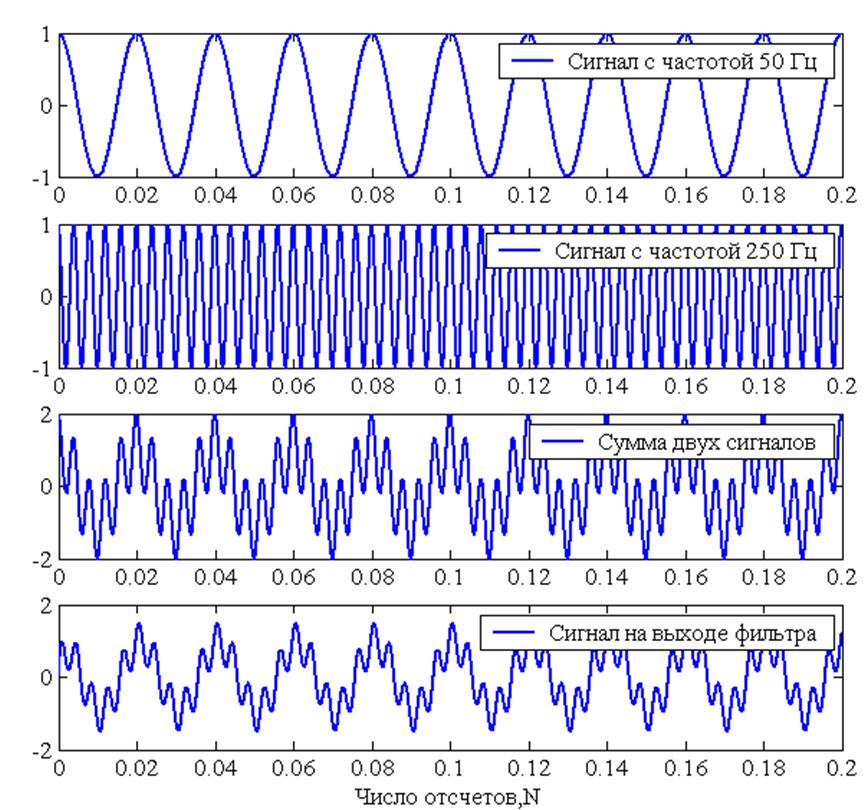 В данном случае я применил фильтр Медиана

7. Подобрав таким образом параметры фильтра, применяем его, удаляем все временные слои.

8. Затем включаем слой High и получаем высокочастотную составляющую путем вычитания с помощью команды Внешний канал.

Надеюсь, что данный сборник рецептов поможет вам лучше разобраться в использовании метода частотного разложения для ретуши в различных его вариациях. 

Более подробно о самых современных методиках быстрой ретуши вы можете узнать из записи онлайн-мастер-класса «Частотное разложение 2.0. Эксклюзивные методики быстрой ретуши» (предупреждаю, что материал там не для начинающих).

А для тех, кто делает только первые шаги в ретуши, рекомендую запись моего трехдневного онлайн-марафона по ретуши «Сделай первые шаги в ретуши портретов»

По всем вариантам частотного разложения вы можете записать экшены и использовать их в своей работе. Пусть это будет вашим домашним заданием.

Автор: Евгений Карташов

Частотное разложение. ULTIMATE | Виртуальная школа Profile

Частотное разложение. ULTIMATE

Цикл завершен. Начавшаяся 4 года назад история подошла к логическому концу. Я не изобретал этот прием, мне просто удалось вытащить его из узкого кулуарного круга «крутых профи» и запустить в широкие массы. Само название «частотка» — яркое тому доказательство. Огромное спасибо Александру Миловскому за подсказку, позволившую мне открыть Америку через форточку (так мой дед называл изобретение для себя лично чего-либо уже известного окружающим). Именно из его статьи шагнул в массы термин «частотное разложение».

1. ТЕОРИЯ

Разложение в спектр.

В 1807 году Жан Батист Жозеф Фурье подготовил доклад «О распространении тепла в твёрдом теле», в котором использовал разложение функции в тригонометрический ряд

При таком преобразовании функция представляется в виде суммы синусоидальных колебаний (гармоник) с различной амплитудой

Любой сигнал может быть представлен в таком виде, а все образующие его гармоники вместе называются спектром

В 1933 году Владимир Александрович Котельников сформулировал и доказал теорему, согласно которой любой сигнал с конечным спектром может быть без потерь восстановлен после оцифровки, при условии, что частота дискретезации будет как минимум в два раза выше частоты верхней гармоники сигнала

Что такое пространственные частоты.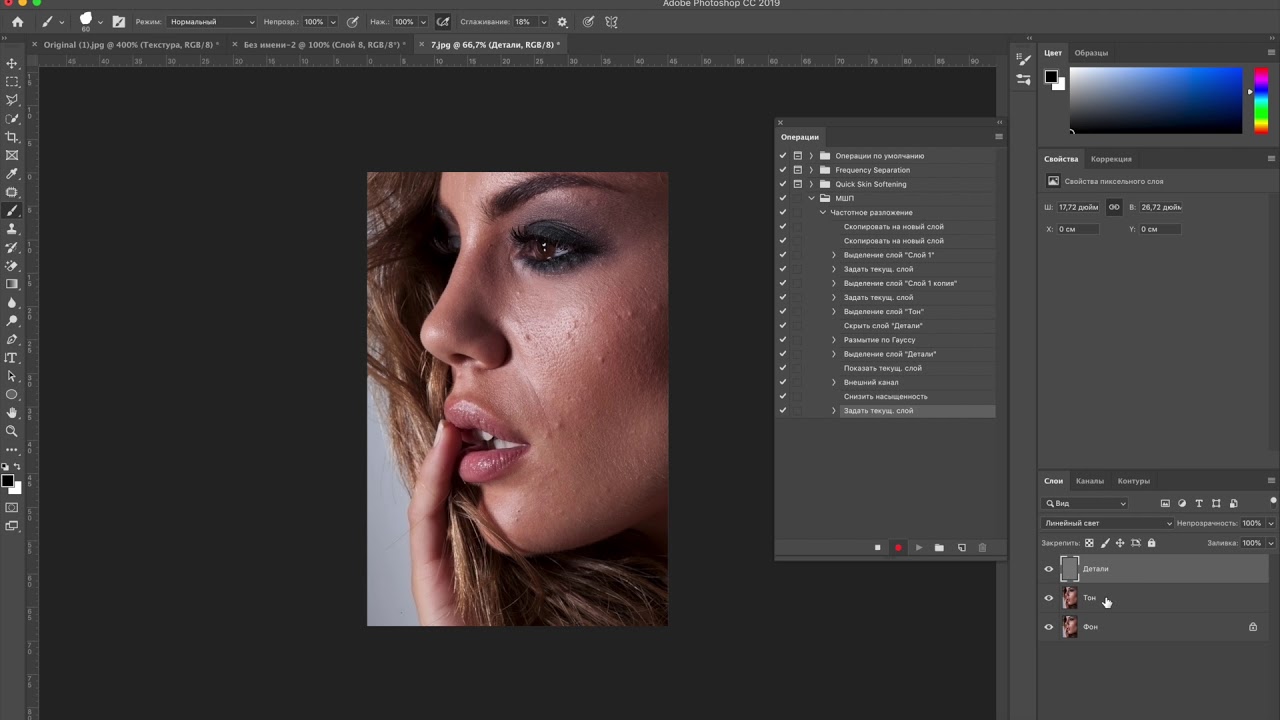

Частота с которой меняется яркость при перемещении по горизонтали или вертикали

Изображение — это двумерный сигнал (яркость меняется при перемещении по горизонтали и вертикали), поэтому общая решетка образуется из двух решеток различных ориентаций — горизонтальной и вертикальной

Чем выше частота, тем быстрее меняется яркость, тем мельче детали которые она задает

Самые мелкие детали — это перепады яркости на контрастных контурах

Разложение на полосы частот.

Для эффективной обработки сигнала нет необходимости раскладывать его в спектр, достаточно разложить его на несколько полос, содержащих все гармоники ниже или выше определеной частоты

Самые низкие частоты задают общее распределение яркости и, как следствие, цвета

Средние частоты уточняют эту картинку принося основные объемы объектов

Верхние частоты добавляют самую мелкую детализацию — фактуру поверхностей

Дополнительные материалы:

Алексей Шадрин. «Управление визуальным объемом изображений»Александр Миловский. «Муар нам только снится»

2. ПРОСТОЕ РАЗЛОЖЕНИЕ НА 2 ПОЛОСЫ ЧАСТОТ

Фильтры нижних и верхних частот.

Gaussian Blur — фильтр нижних пространственных частот

Чем больше Raduis, тем более крупные детали убираются, тем ниже оставшиеся частоты

High Pass — фильтр верхних пространственных частот, дополнительный к Gaussian Blur

High Pass показывает детали, которые убрал Gaussian Blur при том же значении Radius

Эти детали отображаются в виде отклонения от средне-серого цвета (отклонения от средней яркости в каждом канале)

Сложение исходного изображение из частотных полос.

Добавить эти отклонения к исходному изображению может режим Linear Light

Контраст ВЧ-слоя надо понизить в два раза вокруг средней яркости (тон 128), чтобы скомпенсировать заложенное в Linear Light удвоение

Это можно сделать при помощи кривых (Curves) подняв черную точку в позицию (0; 64) и опустив белую в позицию (255; 192)

Можно понизить контраст при помощи Brightness/Contrast с установкой Contrast -50 и активированным ключем Use Legacy

Вместо понижения контраста можно уменьшить до 50% непрозрачность слоя, но в этом случае регулятор Opasityиспользовать нельзя, а нужно воспользоваться регулятором Fill

Дополнительные материалы:

Андрей Журавлев. «Ретушь портрета на основе частотного разложения»

3. DODGE & BURN

Идеология Dodge & Burn.

Основная идея этой техники: ручное осветление излишне темных и затемнение слишком светлых участков для придания объекту более гладкой и правильной формы

Таким же образом усиливаются или дорисовываются недостающие объемы

Классически реализуется при помощи инструментов Dodge Tool и Burn Tool, но эти инструменты допускают только деструктивную обработку

Может быть реализована при помощи режимов наложения или корректирующих кривых с рисованием по макске слоя

Реализация Dodge & Burn при помощи режимов наложения.

Для сильной перерисовки свето-теневого рисунка используются режимы наложения Multiply и Screen

Рисование производится на пустых или залятых нейтральными для данных режимов цветом слоях

Основным преимуществом такой работы является большая сила воздействия: Multiply способен затемнять даже белый объект, а Screen осветлять даже черный

Дополнительным плюсом является возможность работать разным цветом на одном слое и простота выбора цвета: его можно брать с самого изображения

Минусом (особенно для начинающих) является уже упомянутая сила воздействия, заставляющая точно контролировать свои движения

Для легкой финальной правки применяют слой в режиме Soft Light (прозрачный или залитый средне-серым)

Плюсами являются: мягкость и визуальная однородность воздействия; ограниченный диапазон воздейстывий; отсутствие воздействия на белые и черные участки

Реализация Dodge & Burn при помощи кривых.

Затемнение и осветление производится при помощи корректирующих слоев кривых (Curves), а необходимые участки прорисовываются по их маскам

При затемнении происходит повышение, а при осветлении понижение, насыщенности изображения. Для их компенсации к каждому слою кривых через маску вырезания (Create Clipping Mask) добавляется слой Hue/Saturation

К плюсам метода можно отнести большую (по сравнению с использованием режимов наложения) гибкость последующих настроек

Минусом является невозможность вносить разные оттенки цвета при помощи одного корректирующего слоя

Для самостоятельного изучения:

Алиса Еронтьева и Дмитрий Никифоров. «Портретная ретушь»

4. ИНСТРУМЕНТЫ ИХ НАСТРОЙКИ

Почему выгодно править частотные полосы по отдельности.

При ретуши необходимо согласовывать цвет и его переходы с одной стороны и фактуру поверхности с другой

При исправлении формы крупных объектов выгодно использовать пониженную непрозрачность

Для сохранения мелких объектов (фактура поверхности) необходимо использовать 100% непрозрачность

Мягкая граница кисти у штампа — вынужденный компромисс между этими двумя требованиями

Жесткий стык между однородными однотипными фактурами заметен не будет

Выбор радиуса при разложении на две полосы частот.

Для Gaussian Blur выгодно задавать большой радиус, чтобы максимально убрать фактуру

Для High Pass выгодно задавать малый радиус, чтобы не пропустить объемы

Конкретное значение выбирается как компромиссный вариант между этими двумя условиями

При этом учитывается детали какой крупности мы относим к фактуре

Визуализация при выборе радиуса разложения.

Радиус Gaussian Blur удобнее подбирать плавно увеличивая его, пока не исчезнут ненужные детали

Радиус High Pass удобнее подбирать плавно уменьшая его, пока не пропадут ненужные объемы

Если более важной является форма, радиус удобнее подбирать ориентируясь на содержимое НЧ (размытая картинка)

Если более важной является фактура поверхности, радиус удобнее подбирать ориентируясь на содержимое ВЧ («хайпасная» картинка)

Зависимость радиусов от размера лица и крупности дефектов.

Пропорции среднего лица (ширина к высоте) составляют примерно один к полутора

При вычислении радиусов удобнее отталкиваться от высоты лица, так как она меньше зависит от ракурса съемки

Для удаления аккуратной фактуры кожи необходимо взять значение Radius порядка 1/280 — 1/250 от высоты лица

Для удаления мелких дефектов (прыщи, морщины и т.п.) необходимо взять значение Radius порядка 1/100 — 1/120 от высоты лица

Для удаления крупных дефектов (подглазины, шрамы и т.п.) необходимо взять значение Radius порядка 1/50 — 1/60 от высоты лица

5. РЕТУШЬ ПРИ РАЗЛОЖЕНИИ НА 2 ПОЛОСЫ ЧАСТОТ

Ретушь НЧ-составляющей — исправление формы.

Находящуюся на НЧ слое форму удобно ретушировать при помощи инструментов Clone Stamp, Brush и Mixer Brush

Штампом работаем с мягкой кистью и пониженной непрозрачностью

Можно работать на новом прозрачном слое с настройкой штампа Sample: Current & Below

При этом на экран можно вывести общий вид картинки, а не только НЧ слоя.

Кисть (Brush Tool) удобно использовать для закрашивания локальных дефектов (пробойные блики, проваальные тени и т.п.) телесным цветом

Mixer Brush используется для быстрого разглаживания лишних объемов

Ретушь ВЧ-составляющей исправление фактуры.

Работаем штампом с жесткой кистью и 100% непрозрачностью

Можно работать на новом прозрачном слое с настройкой штампа Sample: Current & Below и отображением только ВЧ слоя

Чтобы ретушировать глядя на финальную картинку надо работать на самом ВЧ слое (его копии) с настройкой штампа Sample: Current Layer

Чтобы иметь возможность откатиться к исходному состоянию ретушь проводят на копии слоя ВЧ с применением к нему команды Create Clipping Mask

Для лучшего контроля над деталями можно временно включить корректирующий слой кривых, повышающий контраст ВЧ составляющей

При отсутствии на изображении необходимой текстуры можно перенести ее с другой фотографии

Как работает Healing Brush.

На НЧ слое после размытия на участках рядом с контрастной границей появляется цвет соседней области

На ВЧ слое вдоль контрастных границ появляются ореолы противоположных цветов

Если в процессе ретуши ВЧ слоя убрать ореол на финальной картинке на этом участке появится цвет соседней области

Healing Brush переносит фактуру с донорской области, подгоняя цвет и яркость под ретушируемого участка под цвет и яркость его окрестностей

Его работа построена на алгоритме частотного разложения, а значение радиуса привязано к размер кисти

6. ОТДЕЛЬНЫЕ ПРИЕМЫ РЕТУШИ

Как побрить человека.

Вынести волоски (щетину) на ВЧ слой и заменить их фактурой чистой кожи

Если щетина была темная, поправить цвет на НЧ слое

Внимательно следите за фактурой, она сильно отличается на разных участках лица

«Брить» мужчину тяжело, поскольку на лице не хватает нужной фактуры

При необходимости нужную фактуру кожи можно взять с другой фотографии

Борьба с пробойными бликами. Ретушь НЧ.

Изображение раскладывается на две полосы с установками обеспечивающими полный переход фактуры кожи на ВЧ слой

На НЧ слое участки пробойных бликов закрашиваются цветом кожи

При необходимости на них наносится свето-теневой рисунок передающий объем объекта

Борьба с пробойными бликами. Ретушь ВЧ.

Если блик пробойный и вообще не содержал фактуры, она переносится с целых участков кожи

Если блик близок к пробойному и фактура кожи все-таки содержится, после ретуши НЧ она визуально усилится

Чтобы смягчить этот эффект можно наложить на нее фактуру с более гладких участков на отдельном слое с пониженной непрозрачностью

7. «ЧЕСТНОЕ» РАЗЛОЖЕНИЕ НА 2 ПОЛОСЫ ЧАСТОТ

Ошибка High Pass.

Максимальный диапазон разностей яркости от -256 (вычитаем белый из черного) до 256 (вычитаем черный из белого) составляет 512 тоновых уровней

Максимально возможные отклонения от средней яркости от -128 (затемнение) до 127 (осветление)

При наличии мелких деталей на массивном фоне отличающихся по яркости более чем на 128 уровней High Pass ошибается

Обычно это случается на точечных бликах расположенных на темном объекте

Чем больше радиус размытия, тем больше сама ошибка и вероятность ее появления.

На практике, при малых радиусах разница является «гомеопатической» и рассматривать ее как реальную проблему можно только с академической точки зрения

При больших радиусах ошибка составляет реальную проблему, поскольку «гасит» мелкие блики

Создание ВЧ составляющей вычитанием НЧ из оригинала.

Альтернативой High Pass является наложение на исходное изображение размытой версии при помощи команды Apply Image в режиме Subtract с установками Scale:2 Offset:128

В поле Offset (смещение) задается значение яркости вокруг которого будет откладываться результат вычитания

В поле Scale устанавливается во сколько раз будет уменьшаться результат вычитания перед добавлением к значению Offset

Диапазон установок Scale от 1 до 2, то есть контраст можно понизить максимум в 2 раза

Применять корректирующий слой понижающий контраст в этом случае не нужно, поскольку он уже понижен установкой Scale:2

Особенности разложения 16-битных изображений.

При вычислении ВЧ через команду Subtract у 16-битных изображений появляется ошибка величиной в 1 восьмибитный (128 шестнадцатибитных) уровень

Вероятно, это связано с тем, что реально вычисления происходят в пятнадцатибитном виде

Чтобы избежать этой ошибки при работе в 16-битном режиме вместо команды Subtract используют команду Add с активированным ключом Invert и установками Scale:2 Offset:0

Использование Surface Blur для получения НЧ составляющей.

В случае применения для получения НЧ составляющей Gaussian Blur вдоль контрастных границ создаются сильные ореолы

Ретушь в области ореолов может привести к «затягиванию» на объект цвета соседнего фона

Проблема проявляется тем более сильно, чем больше радиус размытия, поскольку в этом случае ореолы становятся более массивными и плотными

Чтобы избежать такой проблемы НЧ составляющую можно создавать при помощи фильтра Surface Blur

Границы, имеющие перепад яркости больше уровня установленного регулятором Threshold, не размываются

На практике удобнее всего подобрать значение Radius при установленном на максимум Threshold, а потом уменьшать значение Threshold до восстановления контрастных границ

8. АВТОМАТИЗАЦИЯ ПРОЦЕССА

Запись универсального экшена для разложения на 2 полосы частот.

Все операции выполняются со слоями, созданными самим экшеном

Слой создается командой Layer > New Layer и сразу переименовывается

Текущее изображение помещается на него при помощи команды Image > Apply Image с установкой Layer: Merged

Переключения между слоями выполняются при помощи шоткатов «Alt»+«[» и «Alt»+«]»

Для возможности переключения вместо отключения видимости слоя его непрозрачность уменьшается до нуля

При необходимости перемещение слоев выполняются командами Layer > Arange

В качестве подсказки перед применением Gaussian Blur в экшен вставляется команда Stop с комментариями по подбору радиуса

При регулярном применении Stop можно деактивировать или удалить

Преимущества «честного» разложения при работе с экшенами.

При записи экшена количество стандартных операций не является критичным

При этом важно минимизировать количество операций, требующих участия пользователя

Вычисление ВЧ составляющей через наложение НЧ на копию исходного слоя избавляет пользователя от задания радиуса для фильтра High Pass

Дополнительным плюсом такого метода является возможность применить для размытия не Gaussian Blur, а какой-нибудь другой фильтр

Создание набора экшенов для разложения на 2 полосы.

Сделать набор экшенов с жестко заданными значениями радиуса можно на основе универсального экшена

Для этого нужно убрать команду Stop, отключить диалоговое окно в Gaussian Blur и настроить его радиус на требуемый

Для удобства последующей работы с файлом к названиям слоев Low и High можно сразу добавить приписку со значением радиуса размытия

Экшен для пакетной обработки с настройкой по первому кадру.

При обработке серии фотографий с одинаковой крупностью объектов было бы удобно один раз вручную подобрать нужный радиус разложения, а потом применять его ко всей серии

Это можно сделать, если вместо прямого вызова конкретного фильтра вписать в экшен команду вызова последнего использовавшегося фильтра

Теперь достаточно один раз вызвать нужный фильтр (в рамках стандартного экшена или отдельно), настроить его параметры и он будет применяться при всех следующих запусках экшена

9. РАЗЛОЖЕНИЕ НА 3 ПОЛОСЫ ЧАСТОТ

Зачем раскладывают картинку на три полосы.

Чаще всего задача такого разложения — вынести все дефекты в среднюю полосу частот

Таким образом можно бороться с объектами определенного типоразмера, например веснушками

Кроме того, в средних частотах находится большинство «старящих» элементов: глубина морщин, жилистость, вены, провисания, мешки под глазами и т.п.

Реже ретушируются все три полосы, в этом случае процесс аналогичен разделению на 2 полосы, но позволяет проще работать объектами разного типоразмера

Как это сделать.

Для НЧ увеличиваем радиус Gaussian Blur пока не останется чистая форма

Для ВЧ уменьшаем радиус High Pass пока не останется чистая фактура

Создаем между нами слой средних частот применив к нему сначала High Pass с радиусом который использовался для создания НЧ, а потом Gaussian Blur с радиусом который использовался для создания ВЧ

Универсальное правило: High Pass следующего слоя имеет такой же радиус, как Gaussian Blur предыдущего

Теперь можно ретушировать средние частоты не обращая внимание не только на фактуру, но и на разницу цвета исходной и ретушируемой области

При «честном» разложении средние частоты получаются вычитанием из исходного изображения низких и высоких

Автоматизация разложение на три полосы.

Для создания ВЧ удобно использовать High Pass, поскольку он позволяет более наглядно подобрать радиус

В процессе подбора уменьшаем радиус High Pass пока на ВЧ не останется чистая фактура

Вместо High Pass можно использовать Gaussian Blur с визуализацией ВЧ составляющей

Слой средних частот можно получить вычитая из исходного изображения верхние и нижние частоты

10. УПРОЩЕННЫЙ МЕТОД РЕТУШИ СРЕДНИХ ЧАСТОТ (INVERTED HIGH PASS)

Почему можно упростить ретушь средних частот.

Ретушируя средние частоты мы прежде всего убираем лежащие в них излишние локальные объемы

Это можно сделать проще, не раскладывая изображение на три полосы, а выделить среднюю и вычесть ее из исходника

Вычитание должно быть локальным: только на участках где присутствует лишний объем, пропорционально степени его подавления

Как это сделать.

Подбирать радиус для High Pass удобнее через Gaussian Blur (через НЧ составляющую) и наоборот

Делаем копию исходного слоя

Вызываем Gaussian Blur, плавно увеличиваем радиус пока не исчезнут ненужные детали, запоминаем его значение и нажимаем Cansel

Вызываем High Pass, плавно уменьшаем радиус пока не пропадут ненужные объемы, запоминаем его значение и вводим радиус подобранный на предыдущем шаге

Применяем Gaussian Blur с радиусом подобранным на предыдущем шаге

Инвертируем изображение

В два раза понижаем контраст вокруг средней точки

Переключаем режим наложения на Linear Light

На слой вычитающий средние частоты из исходного изображения набрасываем черную маску

Белой кистью по маске прорисовываем те участки, на которых нужно подавить крупные детали

Автоматизация процесса.

Все рутинные операции записываются в экшен

Полоса средних частот получается вычитанием из исходного изображения НЧ и ВЧ полос с подобранными пользователем радиусами

За счет этого визуализация оказывается наиболее комфортной

Подбор верхнего радиуса можно делать после наложения на исходное изображение инвертированной СЧ+ВЧ составляющей. В этом случае используется Gaussian Blur и на размытой картинке начинает проступать чистая фактура

Чем приходится расплачиваться за скорость.

Результат ручной ретуши выглядите естественно прежде всего из-за сохранения мелких неоднородностей

За скорость и простоту приходится расплачиваться механистически правильной формой объектов, что визуально удешевляет работу

Соотношение радиусов обычно выбирают 1:3 или меньше, иначе результат будет выглядеть слишком неестественным

Для более тонкой работы соотношение радиусов берут примерно 1:2 и производят несколько циклов разложения с разными значениями вилки

При ретуши второстепенных участков можно брать соотношение 1:4 и даже больше

Для самостоятельного изучения:

Евгений Карташов. «Рецепты частотного разложения»

11. ЧАСТОТНОЕ РАЗЛОЖЕНИЕ И ДРУГИЕ ИНСТРУМЕНТЫ PHOTOSHOP

Средние частоты и Clarity.

Алгоритм работы Clarity строится на усилении (ослаблении) средних пространственных частот

При этом работа идет только по яркостной составляющей изображения

Повышение и ослабление Clarity не симметрично

Инструмент использует интеллектуальное размытие с сохранением контрастных контуров напоминающее Surface Blur, но не совпадающее с ним

При умеренных значениях можно рекомедовать использование Clarity в конвертере, при условии, что в дальнейшем изображение не будет подвергаться «сильной» обработке

Высокие частоты и повышение резкости.

Искусственное повышение резкости есть ни что иное, как усиление самых верхних из содержащихся в изображении частот.

При подготовке пейзажей основной проблемой является замыливание (исчезновение) сверх мелкой детализации (трава) вследствии нехватки разрешения.

Аналогичная проблема встает при подготовке изображений с мелкими деталями для размещения в интернете

Создать визуально ощущение наличия сверх мелких деталей можно добавив в изображение мелкий шум, согласованный с его элементами

Для этого повышаем резкость классическим способом, но оставляем это повышение только на низко контрастных областях

Проще всего это сделать используя Surface Blur в качестве фильтра, создающего нерезкую маску

12. В ЗАВЕРШЕНИИ РАЗГОВОРА

Для чего еще можно применять частотное разложение

Частотное разложение — это универсальный метод применимый к любому жанру фотографии

Убирать складки на ткани или других материалах

С его помощью можно смягчать слишком жесткие тени

Избавляться от разводов оставшихся после общей ретуши

Решать любые задачи, требующие различной работы с общей формой и мелкими деталями

Почему после частотного разложения картинка выглядит плохо?

Ретушь — это процесс не поддающийся автоматизации

Частотное разложение не делает ретушь за вас, оно лишь упрощает решение некоторых проблем

Увлекшись возможностью решить все «несколькими размашистыми мазками», при использовании частотного разложения ретушеры нередко позволяют себе работать халтурно

Будьте честны перед собой, не сваливайте собственные ошибки и халтуру на «плохую методику»

Чтобы избежать такой ловушки можно разделить процесс на два этапа

При помощи частотного разложения быстро поправить форму и разобраться с сильными огрехами фактуры (пробойные блики, грубая фактура и т.п.)

Последующую доработку производить при помощи привычных реализаций Dodge & Burn, чтобы обеспечить остаточную неоднородность и естественность изображения

Для самостоятельного изучения:

ModelMayhem.com — RAW! Beauty Robot.Сергей Брежнев «Частотное разложение vs Dodge&Burn»

«Adobe Photoshop. Продвинутый уровень». Занятие 9.

Конспект к девятому занятию курса «Adobe Photoshop. Продвинутый уровень» в его гибридной версии, стартовавшей в 2019 году. Курс состоит из 5 видоезанятий и 5 онлайн занятий. Конспекты сделаны только для видеозанятий, поскольку на онлайн занятиях идет разбор пройденной темы и домашних заданий. Здесь можно посмотреть полное описание и программу курса.

Перед записью на любой курс по Adobe Photoshop очень рекомендую прйти тест на знание программы. Как показывает опыт, самостоятельная оценка собственных знаний не всегда адекватно отражает их действительный уровень.

Дополнительные материалы — материалы, рекомендованные к изучению в процессе прохождения курса.
Для самостоятельного изучения — материалы, рассчитанные на самостоятельное освоение не только в процессе, но и по окончании курса.

Для стандартизации внешнего вида, обеспечения стабильности и удобства доступа, данные материалы представлены в виде документов Evernote с упрощенным форматированием. Чтобы перейти к оригиналу статьи, кликните по адресу сайта непосредственно под ее названием.

Для лучшей связи конспекта и занятия в соответствующих местах помещены миниатюры разбираемых в этот момент изображений.

Задачи на занятие
1. Освоить ручное разложение на 2 и 3 полосы пространственных частот
2. Научиться подбирать радиус разложения под конкретную задачу
3. Наработать первичные навыки пользования инструментами при ретуши низких и верхних частот
4. Разобрать автоматизацию процесса и настройки экшенов под свои собственные задачи

Дополнительные материалы:
Андрей Журавлев «Частотное разложение. Ultimate. Конспект и видео»
Евгений Карташов. «Рецепты частотного разложения»
Для самостоятельного изучения:
Liveclasses. Частотное разложение на пальцах
Liveclasses. Управление визуальным объемом и резкостью изображений
Liveclasses. Зрительное восприятие: от физиологии к образу
Алексей Шадрин. «Управление визуальным объемом фотографических изображений»
Александр Миловский. «Муар нам только снится»

Тема 9. Разложение на пространственные частоты.

9.1 Что такое пространственные частоты

• Пространственная частота — это частота с которой меняется яркость при перемещении по горизонтали или вертикали


• Чем выше частота, тем быстрее меняется яркость, соответственно тем мельче детали, которые она задает


• Низкие частоты задают общее распределение яркости и цвета на изображении, проявляя самую общую форму объектов


• Средние частоты уточняют картинку, созданную низкими частотами, привнося в нее локальные контрасты, то есть форму и объемы более мелкой детализации


• Верхние частоты добавляют самую мелкую детализацию и фактуру поверхностей


• Самые верхние частоты отвечают за микро контрасты на контрастных границах, то есть за резкость этих границ

9.2 Общие принципы частотного разложения

• Для выделения низких частот используются низкочастотные фильтры, которыми в Photoshop являются все фильтры размытия


• Чем больше значения параметра Radius (Радиус), тем более крупная детализация будет подвергаться размытию и исчезать с низкочастотного слоя, тем ниже будут оставшиеся на нем частоты


• Если для выделения низких пространственных частот используется фильтр Gaussian Blur (Размытие по Гауссу), то для выделения верхних пространственных частот можно использовать взаимно-дополнительный к нему фильтр High Pass (Краевой контраст), применив его с таким же значением параметра Radius (Радиус)


• Фильтр High Pass (Краевой контраст) выдает результат вычитания размытой картинки из исходной, то есть показывает детали, которые размыл на изображении Gaussian Blur (Размытие по Гауссу), при применении с таким же значением параметра Radius (Радиус)


• Эти детали отображаются в виде отклонения от средне-серого цвета (отклонения от средней яркости в каждом канале)


• Создание очередной частотной полосы нужно производить на базе исходного изображения, скопировав его на новый слой


• Чтобы добавить получившуюся на высокочастотном слое детализацию к расположенному ниже размытому изображению можно использовать режим наложения Linear Light (Линейный свет)


• Поскольку режим Linear Light (Линейный свет) добавляет к ниже лежащему изображению удвоенное отклонения яркости текущей картинки от средне-серого, перед наложением нужно понизить контраст высокочастотного слоя в два раза относительно средней яркости


• Это можно сделать при помощи кривых (Curves) подняв черную точку в позицию (0; 64) и опустив белую в позицию (255; 192)


• Категорически нельзя использовать для понижения контраста высокочастотного слоя уменьшение его непрозрачности до 50%, поскольку такая манипуляция не дает правильный результат!!!


• После разложения изображения на частотные полосы и сложения из них композитной картинки нужно сравнить ее с исходном. Если разницы нет, значит все было сделано правильно

9.3 Часто совершаемые ошибки

• Ошибка 1: для создания новой частотной полосы используется копия не исходного, а уже размытого изображения


• Результатом такой ошибки будет отсутствие мелких деталей на изображении


• Ошибка 2: несовпадения значения параметра Radius (Радиус) у фильтров Gaussian Blur (Размытие по Гауссу) и High Pass (Краевой контраст)


• Если значение Radius (Радиус) у Gaussian Blur (Размытие по Гауссу) было больше, чем у High Pass (Краевой контраст), произойдет выпадение некоторой полосы средних частот, и на изображении будет заметен некоторый эффект размытия, напоминающий работу софт-фильтра, при сохранении резкости мелких деталей


• Если значение Radius (Радиус) у Gaussian Blur (Размытие по Гауссу) было меньше, чем у High Pass (Краевой контраст), произойдет усиление некоторой полосы средних частот, и на изображении усилится объем мелких и средних деталей. Результат будет напоминать применение регулировки Clarity (Четкость) в конвертере


• Ошибка 3: в настройках кривых крайние точки окажутся не в позициях (0; 64) для точки черного, и (255; 192) для точки белого


• В зависимости от того, в какую сторону от правильного положения сместится кривая, результат получится немного светлее или темнее исходника


• Ошибка 4: режим наложения Linear Light (Линейный свет) задается корректирующему слою кривых, задача которого снизить контраст высокочастотной картинки


• В результате такого наложения контраст деталей на высокочастотном слое сильно увеличится, что на композитной версии будет выглядеть как сильный перешарп


• Ошибка 5: для сложения картинки был использован не режим Linear Light (Линейный свет), а какой-то другой


• В результате фактура с высокочастотного слоя проявится недостаточно активно и картинка будет выглядеть слегка размытой


• Ошибка 6: непрозрачность какого-то из слоев будет меньше 100%


• В зависимости от того, с каким слоем это произойдет, мелкая детализация либо усилится, либо ослабится


• Уменьшение непрозрачности слоя может произойти если во время работы с ним была задета цифровая клавиша на клавиатуре

9.4 Инструменты и настройки. Низкие частоты

• Ретушь полосы частот производится на копии слоя соответствующей полосы частот, что позволяет, с одной стороны, сохранить неизменным исходное изображение соответствующей частотной полосы, а с другой стороны, в процессе ретуши не обращаться к информации за пределами слоя, на котором производится ретушь


• Ретушь на слое низких частот как правило делается полупрозрачными инструментами с максимально мягкими кистями, поскольку это позволяет более мягко и плавно сопрягать полутоновые переходы


• Работа инструментом «Штамп» (Clone Stamp Tool) с полупрозрачной мягкой кистью позволяет плавно наносить на ретушируемые участки новый цвет, не теряя при этом контраста фактуры


• Работа инструментом «Кисть» (Brush Tool) с полупрозрачной мягкой кистью позволяет закрашивать сильно выбивающиеся по яркости и цвету участки в цвет в цвет окрестных областей


• При работе инструментом «Кисть» (Brush Tool) нужно стараться не наносить много мазков одним и тем же цветом на одно место, поскольку это приводит к появлению однородно окрашенных плоских пятен


• Чтобы минимизировать подобный эффект можно регулярно забирать цвет для рисования с близлежащих участков, кликая по ним с зажатой клавишей «Alt»


• Для разглаживая полутоновых переходов можно использовать инструмент «Микс-кисть» (Mixer Brush Tool), который является более продвинутой версией инструмента «Палец» (Smudge Tool), и занимается «растиранием» уже имеющейся на изображении краски


• В поле Current brush load (Текущая заполненность кисти) в палитре Options (Параметры) нужно отдать команду Clean Brush (Очистить кисть) и убедиться, что в данном поле отображается клетчатая пиктограмма, обозначающая непрозрачность


• В противном случае инструмент будет не просто растирать уже присутствующие на изображении краски, но и добавлять имеющийся на нем цвет


• Кнопка Load the brush after each stroke (Заполнять кисть после каждого мазка) должна быть деактивирована, чтобы кисть не запоминала краску, забранную на предыдущем мазке


• Кнопка Clean the brush after each stroke (Чистить кисть после каждого штриха) должна быть активирована, чтобы кисть очищалась от краски, которую могла забрать на предыдущем мазке


• Настройки параметров Wet (Влажн.), Load (Заполн.), Mix (Смеш.) нужно установить на 25%-30%, поскольку именно при таких настройках микс-кисть наиболее аккуратно имитирует растирающую краски на изображении


• С помощью настройки параметра Flow (Наж.) меняем скорость, с которой инструмент вносит изменения в изображение


• Ключ Sample All Layers (Все сл.) должен быть дезактивирован, чтобы при вкрученном отображении верхних частот не происходил их перенос на слой ретуши нижних частот


• Для выравнивания неоднородностей при сохранении полутонового перехода движения микс-кистью производятся вдоль линий сохранения яркости (вдоль границы перехода)


• Для выравнивания неоднородностей с одновременным удалением (разглаживанием) полутонового перехода движения микс-кистью производятся поперек линий сохранения яркости (поперек границы перехода)

9.5 Инструменты и настройки. Высокие частоты

• Ретушь полосы частот производится на копии слоя соответствующей полосы частот, что позволяет, с одной стороны, сохранить неизменным исходное изображение соответствующей частотной полосы, а с другой стороны, в процессе ретуши не обращаться к информации за пределами слоя, на котором производится ретушь


• Это особенно важно при ретуши верхних частот, если при этом хочется видеть на экране ужо собранное финальное изображение


• Ретушь верхних частот производится штампом с максимальной жесткой кистью и стопроцентной непрозрачностью, это позволяет предотвратить замаливание фактур на полупрозрачных участках заплатки


• Основной особенностью при такой работе является настройка штампа Sample: Curent Layer (Образец: Активный слой)


• Если оставить штампу привычную настройку Sample: Curent & Below (Образец: Активный и ниже), при ретуши с визуализацией всех пространственных частот (на экране готовое изображение) на высокочастотный слой будет переноситься композитное изображение, что приведет к неадекватно виду картинки


• Визуально это будет проявляться в виде появления на коже пятен «позолоты» или «йода»


• Особое внимание нужно уделить ретуши участков в окрестностях контрастных границ, поскольку при применении для разложения фильтров Gaussian Blur (Размытие по Гауссу) и High Pass (Краевой контраст) на высокочастотном слое в этой зоне появляются ореолы, а их удаление приводит к затягиванию на участок цвета с противоположной стороны границы


• Использование других инструментов кроме штампа при ретуши верхних частот нецелесообразно

9.6 Подбор радиуса

• Радиус при разложении выбирается исходя из желания ретушера «выдавить» дефекты на верхнюю или нижнюю полосу частот


• Данное желание зависит не только от навыков работы конкретного ретушера с теми или иными инструментами, но и от его личных пристрастий и привычек


• Если ретушеру удобнее исправлять дефекты на верхних частотах, радиус подбирается настолько большим, чтобы все неровности ушли с низких частот


• В таком случае удобнее делать визуализацию по низкой частоте, то есть начинать с применения фильтра Gaussian Blur (Размытие по Гауссу), плавно увеличивая радиус до такого минимального значения, при котором дефекты перестанут отображаться на низких частотах


• Если ретушеру удобнее исправлять дефекты на нижних частотах, радиус подбирается настолько маленьким, чтобы все неровности остались на низких частотах


• В таком случае удобнее делать визуализацию по верхней частоте, то есть начинать с применения фильтра High Pass (Краевой контраст), задав изначально достаточно большой радиус и плавно уменьшая его до такого максимального значения, при котором дефекты перестанут отображаться на верхних частотах


• Для ретуши портретов можно указать приблизительные соотношения размеров лица и значения параметра Radius (Радиус), при которых с низких частот удаляются детали определенного типоразмера


• При вычислении радиусов удобнее отталкиваться от высоты лица, так как она меньше зависит от ракурса съемки


• Для удаления аккуратной фактуры кожи необходимо взять значение Radius (Радиус) порядка 1/280 — 1/250 от высоты лица


• Для удаления мелких дефектов (прыщи, морщины и т.п.) необходимо взять значение Radius (Радиус) порядка 1/100 — 1/120 от высоты лица


• Для удаления крупных дефектов (подглазины, шрамы и т.п.) необходимо взять значение Radius (Радиус) порядка 1/50 — 1/60 от высоты лица

9.7 Ретушь верхних частот

• Разложение начинается с применения фильтра Gaussian Blur (Размытие по Гауссу), у которого плавно увеличивается радиус до такого минимального значения, при котором дефекты перестанут отображаться на низких частотах


• Высокочастотный слой формируется при помощи фильтра High Pass (Краевой контраст), который применяется со значением Radius (Радиус), аналогичным использованному на предыдущем шаге в фильтре Gaussian Blur (Размытие по Гауссу)


• Ретушь производится на копии высокочастотного слоя, либо помещенного с ним в одну группу, либо привязанного к оригиналу с помощью команды Create Clipping Mask (Создать обтравочную маску)


• Для ретуши используется штамп с максимальной жесткой непрозрачной кистью и настройкой Sample: Curent Layer (Образец: Активный слой)


• Таким образом с изображения легко удаляются мелкие дефекты: родинки, прыщики, морщинки, мелкие шрамы, сосуды и капилляры (как на склере глаза, так и просвечивающие через кожу), выбившиеся из прически волоски, щетина и пушок на лице, края контрастных границ, и т.п.


• Для лучшего контроля над деталями можно временно отключить корректирующий слой кривых, понижающий контраст высокочастотного слоя (или включить слой кривых, повышающий контраст высокочастотного слоя при честном разложении)

9.8 Ретушь низких частот

• Разложение начинается с применения фильтра High Pass (Краевой контраст), у которого задается изначально достаточно большой радиус и плавно уменьшается до такого максимального значения, при котором дефекты перестанют отображаться на верхних частотах


• Низкочастотный слой формируется при помощи фильтра Gaussian Blur (Размытие по Гауссу), который применяется со значением Radius (Радиус), аналогичным использованному на предыдущем шаге в фильтре High Pass (Краевой контраст)


• Ретушь производится на копии высокочастотного слоя, для удобства и единообразия помещенного с ним в одну группу, либо привязанного к оригиналу с помощью команды Create Clipping Mask (Создать обтравочную маску), хотя это и не обязательно


• Для ретуши на первом этапе может использоваться инструмент «Кисть» (Brush Tool), а в последующем инструменты «Штамп» (Clone Stamp Tool) и «Микс-кисть» (Mixer Brush Tool)


• Все инструменты применяются с максимально мягкими полупрозрачными кистями


• Таким образом с изображения можно легко удалить как пятна, созданные светл-теневым рисунком, то есть неровности на различных материалах (кожа, ткань, обивки мягких поверхностей, твердые поверхности и т.п.), так и пятна созданные различной окраской разных участков объекта (пигментные пятна и покраснения на коже, неоднородности окраски древесины, пятна жира и краски на любой поверхности и т.п.)

9.9 Ретушь двух полос частот

• Существуют дефекты, которые невозможно выдавить на отдельную полосу частот, поэтому их приходится ретушировать как на низких, на и на высоких частотах


• Чаще всего такими дефектами являются слишком жесткие акцентированные тени или объекты со слишком резкими и четкими краями


• Преимущество такого подхода, по сравнению с ретушью композитного изображения, состоит в том, что работа с формой и цветом производится на низкочастотной составляющей, без оглядки на фактуру поверхности и резкие края, а ретушь жестких границ делается на высокочастотной составляющей, без привязки к цвету конкретного участка изображения

9.10 Ретушь «металлических» бликов на коже

• Слишком яркие блики на коже, часто называемые «металлическими», яркий пример дефекта, который нужно ретушировать на двух полосах частот


• Разложение производится с таким радиусом, чтобы вся фактура кожи и мелкие детали «ушли» на верхние частоты


• Ретушь нижних частот начинается с закрашивания особенно ярких участков бликов с помощью инструмента «Кисть» (Brush Tool) (подробности настроек и применения смотри в разделе 9.4)


• Если ретушеру это более удобно, работу инструментом «Кисть» (Brush Tool) можно заменить на «Штамп» (Clone Stamp Tool)


• После выравнивания цвета на участках бликов производится их разглаживание с помощью инструмента «Микс-кисть» (Mixer Brush Tool)


• Сначала движения этим инструментом делаются только в центр блика, таким образом цвет с окрестных участков «натягивается» на ликующую область, еще больше выравнивая ее по сравнению с соседними участками


• После этого растирка делается через область блика в обе стороны, чтобы максимально сгладить и смягчить полутоновые переходы на данном участке


• После ретуши низких частот не забудьте про верхние!


• Если блик пробойный и вообще не содержал фактуры, она переносится с целых участков кожи


• Если фактура на бликах изначально была, она будет более контрастной, чем на остальных участках изображения, поэтому ее контраст нужно понизить


• Чтобы фактура не выглядела «замыленной», при понижении ее контраста нужно замещать ее другой фактурой


• Выделяем на изображении подходящий по размеру участок высокочастотного слоя с подходящей фактурой и копируем его на отдельный слой


• Переносим эту заплатку на место блика и уменьшаем ее непрозрачность, таким образом смягчая изначально слишком контрастную фактуру, и частично сохраняя ее для обеспечения более естественного вида изображения

9.11 Ретушь и продление однородных фонов

• После ретуши на достаточно однородных участках с низко контрастной фактурой часто остаются достаточно крупные низко контрастные пятна


• Для удаления этих пятен проще всего разложить изображение на пространственные частоты, выдавив всю фактуру на высоко частотный слой, а после этого отретушировать низко частотный слой полупрозрачной мягкой кистью или аналогичным штампом


• При необходимости продлить достаточно однородный фон поступаем аналогично: раскладываем изображения, выдавив всю фактуру на высоко частотный слой, на низких частотах продолжаем фон при помощи градиентной или обычной заливки, дорабатывая его большой мягкой полупрозрачной кистью, а на верхних частотах просто планируем имеющуюся на фоне фактуру

Тема 10. Сложные варианты разложения и автоматизация.

10.1 Разложение без применения фильтра High Pass (Краевой контраст)

• Вычисление верхних частот можно проводить без применения фильтра High Pass (Краевой контраст), и тому есть три причины


• Во-первых, фильтр High Pass (Краевой контраст) дает ошибку


• Во-вторых, применение этого фильтра невозможно, если для размытия используется не Gaussian Blur (Размытие по Гауссу), а другой фильтр размытия


• В-третьих, когда при написании экшена нужно избавить пользователя от необходимости запоминать радиус и вводить его второй раз


• Про «ошибку High Pass»: при вычитании размытой версии из исходной максимальный диапазон составляет от -256 (вычитаем белый из черного) до 256 (вычитаем черный из белого), то есть 512 значений


• В то же время, максимально возможные отклонения от средней яркости на высокочастотном слое составляют от -128 (затемнение) до 127 (осветление)


• При наличии мелких деталей на массивном фоне отличающихся по яркости более чем на 128 уровней High Pass (Краевой контраст) ошибается, обычно это случается на точечных бликах расположенных на темном объекте


• Чем больше радиус размытия, тем больше сама ошибка и вероятность ее появления, хотя на практике, при малых радиусах разница является «гомеопатической» и рассматривать ее как реальную проблему можно только с академической точки зрения


• При больших радиусах данная ошибка составляет реальную проблему, поскольку «гасит» мелкие блики


• Альтернативой High Pass (Краевой контраст) является создание высокочастотного слоя путем наложения на копию исходного изображения его размытой версии при помощи команды Apply Image (Внешний канал) в режиме Subtract (Вычитание) с установками Scale: (Масштаб:) 2 Offset: (Сдвиг:) 128


• В поле Scale: (Масштаб:) устанавливается во сколько раз будет уменьшаться результат вычитания наложенной яркости из исходной, а в поле Offset: (Сдвиг:) задается какое значение нужно добавить к получившемуся результату


• При помощи таких настроек диапазон значений после вычитания (-256: 256) приводится к имеющемуся у нас в распоряжении диапазону яркостей (0; 256)


• Применять корректирующий слой кривых понижающий контраст к высокочастотному слою в данном случае не нужно, поскольку он уже понижен установкой Scale: (Масштаб:) 2

10.2 Настройки для 16-битных изображений

• При вычислении высокочастотной составляющей при помощи режима наложения Subtract (Вычитание) у 16-битных изображений появляется ошибка величиной в 1 восьмибитный (128 шестнадцатибитных) уровень


• Чтобы избежать этой ошибки при работе в 16-битном режиме вместо режима наложения Subtract (Вычитание) используют режим Add (Добавление) с активированным ключом Invert (Инвертировать) и установками Scale: (Масштаб:) 2 Offset: (Сдвиг:) 0

10.3 Применение альтернативных фильтров размытия

• «Честное» вычисление высокочастотной составляющей позволяет перейти от применения фильтра Gaussian Blur (Размытие по Гауссу) к любым другим фильтрам размытия


• В случае применения для получения низкочастотной составляющей фильтра Gaussian Blur (Размытие по Гауссу) вдоль контрастных границ создаются сильные ореолы, ретушь в этой области может привести к «затягиванию» на объект цвета соседнего фона


• Данная проблема проявляется тем более сильно, чем больше радиус размытия, поскольку в этом случае ореолы становятся более массивными и плотными


• Чтобы избежать такой проблемы низкочастотную составляющую можно создавать при помощи фильтра Surface Blur (Размытие по поверхности)


• При использовании Surface Blur (Размытие по поверхности) границы, имеющие перепад яркости больше уровня установленного регулятором Threshold (Изогелия), практически не размываются


• На практике удобнее всего подобрать значение Radius (Радиус) при установленном на максимум параметре Threshold (Изогелия), а потом уменьшать значение Threshold (Изогелия) до восстановления резкости контрастных границ


• Такой прием упрощает ретушь высокочастотной составляющей в окрестностях контрастных границ, а при переделке фонов облегчает и доработку низкочастотной составляющей в этой же зоне


• Как более простая и быстрая альтернатива фильтру Surface Blur (Размытие по поверхности) может использоваться фильтр Median (Медиана), впрочем, в некоторых случаях, этот фильтр может оказаться даже более полезен, чем Surface Blur (Размытие по поверхности)

10.4 Разложение на 3 полосы частот

• Основная идея разложения на три полосы частот состоит в том, чтобы выдавить все дефекты на слой средних частот


• Таким образом можно бороться с объектами определенного типоразмера, например веснушками


• Кроме того, в средних частотах находится большинство «старящих» элементов: глубина морщин, жилистость, вены, провисания, мешки под глазами и т.п.


• Реже ретушируют все три полосы, в этом случае процесс аналогичен разделению на 2 полосы, но позволяет проще работать объектами разного типоразмера


• В целом такое разложение напоминает разложение на два полосы частот, только значения параметра Radius (Радиус) на начальном этапе выбираются не одинаковыми


• Сначала для низкочастотной составляющей, для фильтра Gaussian Blur (Размытие по Гауссу), подбираем такой значение Radius (Радиус), чтобы с нее исчезли все ненужные неровности


• Потом формируем высокочастотную составляющую, подобрав такое значение фильтра High Pass (Краевой контраст), чтобы на ней не проявлялись ненужные неровности


• В конце формируем вреднечатотную составляющую, начав работу с копии исходного изображения, и применив к ней фильтр High Pass (Краевой контраст) с такими же настройками, как у Gaussian Blur (Размытие по Гауссу), примененному к слою низких частот, и Gaussian Blur (Размытие по Гауссу) с такими же настройками, как у High Pass (Краевой контраст), примененному к слою верхних частот


• Для сложения картинки понижаем в два раза контраст средних и верхних частот вокруг средне-серого и накладываем их в режиме Linear Light (Линейный свет) на лежащее ниже изображение


• Ретушь средних частот производится аналогично описанной ранее ретуши нижних частот


• Преимущество данного метода в том, что даже при очень размашистых и неаккуратных движениях, аккуратная форма объекта сохранится, поскольку она находится на низких частотах, которые мы не затрагиваем

10.5 Упрощенная ретушь средних частот

• Ретушируя средние частоты, мы прежде всего убираем лежащие в них излишние локальные объемы, это можно сделать проще, не раскладывая изображение на три полосычастот, а выделив только среднечастотную составляющую, вычесть ее из исходного изображения


• Вычитание должно быть локальным: только на участках где присутствует лишний объем, пропорционально степени его подавления


• Подбор значения Radius (Радиус) для выделения средних частот аналогичен предыдущему примеру, поэтому фильтры придется использовать «шиворот-навыворот», то есть подбирать радиус для High Pass (Краевой контраст) удобнее через Gaussian Blur (Размытие по Гауссу) и наоборот


• Делаем копию исходного слоя, вызываем Gaussian Blur (Размытие по Гауссу), плавно увеличиваем радиус пока не исчезнут ненужные детали, запоминаем его значение и нажимаем Cansel (Отмена)


• Вызываем High Pass (Краевой контраст), задаем заведомо большой радиус и плавно уменьшаем его, пока не пропадут ненужные объемы, запоминаем его значение и вводим радиус, подобранный на предыдущем шаге, применяем Gaussian Blur (Размытие по Гауссу) с радиусом подобранным на предыдущем шаге


• Желательно, чтобы значения Radius (Радиус) отличались не больше, чем в три раза, иначе будет удаляться слишком широкая полоса частот, что приведет к неестественно равномерной форме


• Инвертируем изображение командой Image > Adjustments > Invert (Изображение > Коррекция > Инверсия)


• В два раза понижаем контраст вокруг средней точки с помощью прямой коррекции: Image > Adjustments > Curves (Изображение > Коррекция > Кривые)


• Меняем режим наложения получившегося слоя на Linear Light (Линейный свет)


• На слой, вычитающий средние частоты из исходного изображения, добавляем черную маску


• Белой кистью по маске прорисовываем те участки, на которых нужно подавить крупные детали


• Данный прием нужно с аккуратностью применять к коже, поскольку он дает слишком правильную, механистически-чистую форму, что смотрится не естественно


• Однако, такой прием идеально подходит для разглаживая одежды, драпировок, и всего, что мы воспринимаем как «не кожу»

10.6 Устройство и работа экшенов

• Для ускорения и оптимизации процесса работы все рутинные операции можно записать в экшена, оставив на долю человека только подбор радиуса


• Преимущество экшенов перед панельками и плагинами состоит в том, что пользователь может самостоятельно их модифицировать, настроив под свои задачи


• Процесс написания и модернизации экшенов не входит в рамки данного курса, поэтому на все возникшие вопросы преподаватель может факультативно ответить на онлайн занятии


• Экшен «2_FB_Low» — разложение на две полосы частот с визуализацией по нижней полосе, для ретуши используются слои помеченные красным цветом, для усиления деталей можно включить видимость корректирующего слоя кривых


• Экшен «2_FB_High» — разложение на две полосы частот с визуализацией по верхней полосе, для ретуши используются слои помеченные красным цветом, для усиления деталей можно включить видимость корректирующего слоя кривых


• Экшен «3_FB» — разложение на три полосы частот, визуализация разделения между низкими и средними частотами делается по низкой частоте (первый подбор радиуса), визуализация разделения между средними и верхними частотами делается по верхней частоте (второй подбор радиуса), для ретуши используются слои помеченные красным цветом


• Экшен «Inverted_HighPass» — упрощенный метод ретуши (подавления) средних частот, визуализация разделения между низкими и средними частотами делается по низкой частоте (первый подбор радиуса), визуализация разделения между средними и верхними частотами делается по верхней частоте (второй подбор радиуса), для ретуши нужно рисовать белым цветом на маске слоя «Inverted_HighPass»

© Андрей Журавлев (aka zhur74), 2012 г.
Редакция третья (2020 г.) переработанная и дополненная.
Первая публикаци https://zhur74.livejournal.com/101357.html

Советы и хитрости: техника частотного разложения | Фотограф — Александр Золотухин

Если вы читали мою предыдущую статью — Профессиональная портретная ретушь: техника частотного разложения, то вы уже знаете что такое частотное разложение и как им пользоваться. Если нет, пожалуйста сначала прочитайте ту статью.

Тут я хочу рассказать вам некоторые советы и хитрости по использованию техники частотного разложения, которые помогут вам работать эффективнее и получать лучшее качество. В конце статьи вы можете скачать бесплатные экшены, чтобы применять эту технику быстро и автоматически (нужно подписаться на блог, чтобы получить ссылку на загрузку).

Что же, давайте начнем.

1. Всегда используйте метод Apply Image.

Если ваша цель — получить качественный результат, никогда не используйте метод High Pass для разложения на частоты. В предыдущей статье я уже упоминал, что High Pass не корректен математически, в отличие от Apply Image. Вот простой тест, чтобы увидеть погрешность. Я разделил изображение методом High Pass, сгрупировал получившиеся слои и изменил режим наложения группы на Difference. И вот что я получил:

Отчетливо видны не черные пиксели и линии — это и есть разница между оригинальным изображением и разложенным на частоты, или говоря математическим языком, погрешность. Я немного повысил контрастность, чтобы разница была видна отчетливее, потому что на уменьшенном изображении на сайте она не так заметна. Можете повторить это сами дома, это не опасно 🙂

Если не хотите потерять в качестве еще до того, как начнете собственно редактирование, используйте Apply Image.

2. Используйте 16-битную глбину цвета, если это возможно.

Это касается редактирования изображений всегда. Чем выше глубина цвета изображения — тем лучше. 16-битные изображения в значительно меньшей степени страдают постеризацией. Подробнее этот аспект описывается в статье Глубина цвета. 8 бит или 16 бит.

Но что касается именно техники частотного разложения — этот тот факт, что 8-битные изображения, в отличие от 16-битных, не имеют настоящего 50% серого! На слое высоких частот 50% серый означает не оказывать никакого влияния на низлежащий слой при наложении в режиме Linear Light. Потому возможностьиметь реальные 50% серые пиксели будет очень к стати.

Давайте начнем с простой математики. Представьсте себе что у нас нечетное количество цветов, скажем 5, где 1 — белый, 5 — черный. ТОгда 2 будет светло-серым, 3 — 50% серым и 4 — темно-серым.

Но что будет если у нас нечетное количество цветов? Давайте рассмотрим случай с 6 цветами. На значениях 3 и 4 мы получаем 40% и 60% серый. Наш средний-серый будет где-то на 3,5, но цвета могут быть представлены только целыми числами. Это означает что при четном количестве цветов 50% серый не существует.

Теперь вернемся к 8 и 16-битным цветам.

8-битные цвета представлены значениями от 0 до 255, это дает нам 256 цветов. 256 — это четное число, так что истинного среднего серого цвета в 8-битном режиме не будет. Значение 127,5 будет округлено до 128.

16-битный цвет в Фотошопе на амом деле 15-битный + 1 цвет. 2¹⁵ = 32768. Добавляем еще 1 цвет и получаем 32769 — нечетное число, в котором 50% серый вполне возможен.

 3. Не трогайте оригинальные слои.

Как я уже упоминал в предыдущей статье, всегда используйте отдельные слои любой коррекции, чтобы иметь возможность в любой момент вернуться к любому этапу ретуши. Когда выолняете низкочастотную ретушь, используйте отдельные слои для мешков под глазами, морщинок, мимических складок и прочего. можно использовать любые типы слоев над слоем Low Frequency в режиме наложения Normal. Таким образом вы сможете быстро снизить эффект отдельных коррекций снизив непрозрачность соответствующих слоев. Это дает намного больше гибкости и ускоряет работу. Можно конечно держать все эти изменения на одном слое и при необходимости пользоваться маской слоя, но это не так удобно и не так быстро, как если у вас будут отдельные слои.

4. Раскладываем изображение на 3 и более разных частоты.

Это процедура чуть более сложная (потому в конце статьи прилагается набор бесплатных экшенов для автоматизации) и на мой взгляд довольно бесполезная, но может быть она кому-то пригодится. Покажу на примере разложения на 3 частоты:

1. Создайте 3 копии слоя Background: Low Frequency, Med Frequency, High Frequency.
2. Примените фильтр Gaussian Blur с большим радиусом. к слою Low Frequency.
3. Выбираем слой Med Frequency и запускаем Image -> Apply Image. В графе Layer выбираем слой Low Frequency. Остальные настройки в зависимости от битности изображения.
4. Меняем режим наложения слоя Med Frequency на Linear Light.
5. Размываем слой Med Frequency с таким радиусом, чтобы пропали только самы мелкие детали, которые уйдут на слой High Frequency (можно воспользоваться фильтром High Pass чтобы точнее прикинуть радиус).
6. Выделите слои Med Frequency и Low Frequency, нажмите Cmd+Option+Shift+E / Ctrl+Alt+Shift+E чтобы объединть эти слои на новом слое. Назовите его Help.
7. Выбираем слой High Frequency и запускаем Image -> Apply Image. В графе Layer выбираем слой Help. Остальные настройки в зависимости от битности изображения.
8. Меняем  режим наложения слоя High Frequency на Linear Light.
9. Удаляем слой Help.

По такому же алгоритму можно разложить изображение и на большее число частот.

5. Повышение резкости и микроконтраста с помощью частотного разложения.

Техника частотного разложения открывает кучу возможностей не только для ретуши, но и многих других типов обработки. Повышение микроконтраста может значительно улучшить вид пейзажа и даже портрета. Оно делает изображение более резким, четким, выделяет все мельчайшие детали изображения. Оно делает фотографии очень похожими на HDR фотографии с тонмаппингом.
Запомните: делайте это только после того, как закончите ретушь, в противном случае вы сделаете все не исправленные дефекты еще более заметными.

Шарпинг (повышение резкости)

1. Выделите все высокочастотные слои (оригинальный и корретирующий). Нажмите Cmd+Option+E / Ctrl+Alt+E чтобы объединить их на новом слое.
2. Измените режим наложения получившегося слоя на Linear Light. Вы сразу же увидете как подскочила резкость изображения.
3. Добавьте маску слоя удерживая Option / Alt. Появится новая черная маска..
4. Рисуйте белой кистью по маске в тех областях, где хотите добавить больше резкости.

Повышение микроконтраста

Тут мы также будем использовать технику частотного разложения, основанную на методе Apply Image. Принцип похож на то что мы делали ранее, но тут мы будем раскладывать изображение на 2 слоя так, чтобы на одном слое остались детали с высоким изначальным микроконтрастом, а на другом — с низким.

1. Объедините все видимые слои на новый (Cmd+Option+Shift+E / Ctrl+Alt+Shift+E). Назовите его SurfBlur_Base.
2. Создайте копию слоя SurfBlur_Base и назовите её MicroContrast.
3. Примените фильтр Surface Blur к слою SurfBlur_Base. Чем выше радиус, тем больше микроконтраста получат детали изображения. Порог (Threshold) определяет какие детали получат больше микроконтраста, а какие нет. При низком пороге эффект будет влиять только на детали с низким изначальным микроконтрастом, а при высоком пороге эффект будет заметен даже на объектах с высоким изначальным микроконтрастом.
4. Выберите слой MicroContrast. Перейдите в Image -> Apply Image. Выберите слой SurfBlur_Base в графе Layer, прочие опции в зависимости от битности изображения, и нажмите ОК.
5. Поменяйте режим наложения слоя MicroContrast на Linear Light. Сейчас ваше изображение должно выглядеть также как изначально.
6. Создайте копию (Cmd+J / Ctrl+J) слоя MicroContrast. Сразу после этого вы должны увидеть улучшение микроконтраста.
7. Примените маску к этому слою, если нужно.

6. Старайтесь чтобы ваши фотографии выглядели натурально.

После того как как закончите ретушь, поиграйтесь с прозрачность слоев. Часто бывает, что фото с меньшим количеством правок выглядит лучше и натуральнее.

7. Пользуйтесь экшенами.

В принципе техника не так уж и сложна, когда поймешь как она работает и научишься пользоваться. Но вот выполнять каждый раз кучу механических шагов вручную — не самое приятное занятие. Чтобы всё это автоматизировать и придумали экшены. Можете создать свой собственный набор экшенов по собственному вкусу или воспользоваться моими экшенами. Их можно скачать бесплатно заполнив форму ниже. Всего их 7 и они охватывают широкий спектр способов применения техники частотного разложения.
Вот их список:
1. High Pass Frequency Separation.
2. 2 Frequencies Separation — Apply Image, 8-bit
3. 2 Frequencies Separation — Apply Image, 16-bit
4. 3 Frequencies Separation — Apply Image, 8-bit
5. 3 Frequencies Separation — Apply Image, 16-bit
6. Micro-contrast increasing — 8-bit
7. Micro-contrast increasing — 16-bit

Вы можете скачать бесплатные экшены по ссылке ниже:

Скачать бесплатные экшены

4.7 / 5 ( 20 голосов )

Метод частотного разложения · Мир Фотошопа

Профессиональные ретушёры использую много разных техник ретуши кожи. В этом уроке Вы изучите одну из базовых техник ретуши называемую частотным разложением. Она используется для быстрого разглаживания кожи без потери детализации.

Что такое частотное разложение?

Частотное разложение — это жаргон, используемый в мире ретуши, для описания техники разглаживания кожи. Техника основывается на разделении изображения на две «частоты».

1. Слой низкой частоты: слой для смягчения, на котором находятся только тона и оттенки.
2. Слой высокой частоты: слой резкости и мелких деталей.

Как разгладить кожу аэрографом, используя метод частотного разложения?

1. Подготовьте слой к обратимому редактированию

Преобразуйте слой фотографии в смарт-объект. Благодаря ему Вы сможете изменять настройки фильтров в любое время.

Создайте две копии слоя. Верхнюю назовите «High Frequency Layer», а нижнюю — «Low Frequency Layer».

2. Создание слоя высокой частоты

Выберите верхний слой и примените фильтр High Pass (Filter ? Other ? High Pass). В результате получится серый слой с эффектом тиснения на деталях. Установите радиус на 3 пикселя.

Установите режим наложения Linear Light и получите очень сильную резкость. Этот слой поможет восстановить детализацию на фотографии.

3. Традиционный и современный вариант размытия

Обычно к слою с низкой частотой применяют фильтр Gaussian Blur, который противоположен фильтру High Pass. Вместо повышения детализации он размазывает изображение так, чтобы стали видны только тона.

Однако традиционный способ не всегда даёт хорошие результаты. Он создаёт эффект рассеянного свечения и делает кожу искусственной. Поэтому вместо традиционного метода мы будем использовать современный, подразумевающий применение фильтра Surface Blur. Он даёт более реалистичное изображение и сохраняет края объектов чёткими. Ниже можете сравнить два фильтра:

4. Создание слоя низкой частоты

Выберите нижнюю копию и примените фильтр Surface Blur (Filter ? Blur ? Surface Blur).

5. Настройка слоя высокой частоты

Уменьшите непрозрачность верхнего слоя, чтобы уменьшить чрезмерную резкость. Начните с 50%.

6. Настройка слоя низкой частоты

Вернёмся к нижнему слою. Кликните дважды на названии фильтра, чтобы открыть настройки. Установите Threshold на максимум и настройте радиус так, чтобы тона кожи стали плавными и всё изображение размытым.

Уменьшите Threshold, чтобы детали стали снова появляться. Возможно Вам потребуется несколько раз перенастраивать фильтр.

7. Объединение слоёв

Оба слоя поместите в одну группу (Ctrl + G) и назовите её «Frequency Separation».

8. Маска группы

К группе добавьте маску и залейте её чёрным цветом. Белой кистью верните эффект разглаживания на отдельные участки лица.

<iframe src=»https://www.youtube.com/embed/R8WVR2VroSc?rel=0″ frameborder=»0″ allowfullscreen></iframe>

На этом можно закончить урок. Так как мы работали со смарт-объектом, Вы в любой момент можете открыть его и изменить изображение. Если вдруг решите почистить кожу инструментом Spot Healing Brush Tool, лучше работать на отдельном слое. В настройках инструмента нужно включить Sample All Layers.

<iframe src=»https://www.youtube.com/embed/vgUkq-sxG7A?rel=0″ frameborder=»0″ allowfullscreen></iframe>

Результат до и после:

Молниеносное разложение фото на три полосы частот – запись экшна

Приветствую всех посетителей блога! Сегодня на повестке дня – разложение картинки на три полосы частот довольно часто применяемое в повседневной практике обработки изображений. Тему я начал здесь рассказом о двух полосах, однако сегодня обещаю больше драйва. Да, я «запилил» по этому поводу небольшой видос, думаю так будет более понятно.

Создание частотного разложения на три полосы

И так приступим. Для начала я создал пару слоев выше фонового для того чтобы имитировать обычный процесс ретуши. Согласитесь, далеко не всегда бывает так что мы начинаем «частотно разлагать» с фонового слоя.

Затем запустил процесс записи операции используя одноименную панель, познакомится с таким процессом можно по этой ссылке. По ходу работы создал стек из слоев для низкой, средней и высокой частоты используя команду дублирования слоев из одноимённого меню фотошопа.

При помощи размытия по гауссу очистил низкочастотный слой от «ненужных» элементов. Затем применив «Цветовой контраст», один из примеров его использования описан здесь, но уже с другими настройками «очистил» слой высокочастотный. Осталось поработать со средними частотами.

Применение команды Внешний канал (Apply Image)

Используя команду Внешний канал вычел из средних частот верхние и нижние. Затем накинул на этот канал маску слоя. Ниже добавил слой в режиме наложения «Мягкий свет», о основных режимах наложения применяемых при редактировании фото читайте тут, для применения на нем техники D&B при корректировании основных объемов изображения.

На этом собственно все готовую операцию если лень видео смотреть и записывать можно скачать по этой ссылке, пирожок слоёв ей создаваемый перед вами

На этом сегодня все, надеюсь эта техника найдет применение в вашей практике обработки фото.

Первичная чистка и частотное разложение

Исходная фотография

Привет! Меня зовут Саша, я один из основателей платформы для творческих людей “ТВОРЧmachine”.

Мы записали цикл бесплатных видеоуроков по естественной обработке портретов, который состоит из трёх частей:

1. Первичная чистка и частотное разложение.
2. Dodge and Burn, ретушь глаз.
3. Глобальный контраст и добавление объёма в кожу, подготовка к публикации во ВКонтакте.

В первом 7-минутном видеоуроке из цикла я рассказываю, как на фотографиях избавляюсь от временных проблемных зон на коже базовыми инструментами Adobe Photoshop, а также демонстрирую один из вариантов механики ретуши под названием “Частотное разложение”.

Частотное разложение в фотографии — это приём, используемый фотографами и ретушёрами, основанный на разложении частот (в классическом варианте на низкую, среднюю и высокую). В низкой находится основное распределение цвета и яркости, в средней — объёмы объектов, а в высокой — мелкая детализация.

В нашем примере мы используем упрощённый вариант — деление только на “низы” и “верха”.

Исходная фотография

Начинаем ретушь с дублирования основного слоя (Ctrl+J для Win, cmd+J для Mac). Анализируя временные проблемные зоны (которые не преследуют человека всю жизнь: прыщики, болячки и синяки, неуложенные волосы и др.), выбираем подходящий инструмент для лучшего результата. Я использую в большинстве случаев два:

• Patch Tool (Заплатка) — универсальный вариант для работы с кожей, позволяет практически бесследно убирать изъяны разных размеров.
• Healing Brush Tool (Лечащая кисть) — хорошо работает с волосами.

Результат после первичной чистки

Следующий этап: разложить изображение на две частоты: верхнюю и нижнюю. Нижняя — общее распределение яркости и цвета, верхняя — вся текстура и детализация. Создаём две копии получившего слоя после первичной чистки. Один из них для удобства назовём Low, другой — High.

К слою Low, на который мы выносим яркость и цвет, применяем Filter—Noise—Median.

Значение радиуса зависит от конкретного случая. Алгоритм выбора: необходимо размыть фотографию настолько, чтобы переходы между светом и тенью были различимы, но плавны. В нашем случае это значение равно 15.

Переходим на слой High. Чтобы вынести на него текстуру, идём по пути Image—Apply Image.

В открывшемся окне, как видно на следующей картинке, выбираем в пункте Layer слой с нижней частотой (Low) в режиме наложения Add (Добавление), включаем инвертирование, значение Scale устанавливаем на 2, Offset — 0. Нажимаем ОК.

Слою High меняем режим наложения на Linear Light (Линейный свет) и объединяем со слоем Low в группу.

Итак, подготовительный этап закончен. Далее будем работать только с нижней частотой (слой Low), не переживая за потерю детализации или текстуры, ведь она осталась на слое High.

Принцип дальнейшей работы прост: выравниваем необходимые (на субъективный взгляд каждого) области по яркости и цвету, тем самым визуально прикрывая на фотографии проблемные зоны — в нашем примере это участки под глазами, носогубные складки и т.д.

Для работы переходим на слой Low и берём инструмент Mixer Brush Tool (Микс-кисть, находится на панеле “Наборы кистей”).

Устанавливаем в верхней панели кисти значение в отрезке 20-22 для параметров Wet, Load, Mix, Flow. В нашем примере мы использовали 21.

Границы кисти должны быть мягкими.

Во время работы с микс-кистью движения должны быть плавными. Направление — из зоны с хорошим паттерном на область, где нужно избавляться от проблем с яркостью или цветом. Таким образом проходим все необходимые места.

 

Если действия кажутся слишком внушительными, что сказывается на естественности и реализме фотографии, то значения непрозрачности группы можно снизить, например, до 60-70%.

На этом мы заканчиваем ретушь портрета, проделав первичную чистку базовыми инструментами Adobe Photoshop и используя приём “Частотное разложение”. В большинстве случаев на этом результате можно остановиться, однако существуют и другие механики ретуши, дополняющие этот приём или раскрывающиеся полноценно и самостоятельно. Например, техника Dodge and Burn, об одном варианте которой я расскажу вам в следующем материале.

Результат после первичной чистки и частотного разложения

Видеоурок

Подписывайтесь на ТВОРЧmachine в социальных сетях:

 

Frequency Decomposition — обзор

3.2 Разделение источников многоканального звука

В этом разделе мы кратко представляем основы разделения источников многоканального звука. Эта презентация ограничена основным материалом, необходимым для понимания следующего обсуждения MASS в дикой природе. На самом деле, цель этой главы не состоит в том, чтобы подробно представить теоретические основы и принципы разделения источников и формирования луча, даже ограничиваясь аудиоконтекстом: этому вопросу посвящено множество публикаций, включая книги [13,26,33,61,89] и обзорные статьи [20,48,106].

Сотни методов усиления многоканального аудиосигнала были предложены в литературе за последние 40 лет по двум историческим направлениям. Обработка массива микрофонов возникла из теории обработки массива датчиков для телекоммуникаций и была сосредоточена в основном на локализации и улучшении речи в шумной или реверберирующей среде [14,18,25,49,84], в то время как MASS позже был популяризирован Сообщество машинного обучения, и оно рассматривало сценарии «коктейльной вечеринки» с участием нескольких источников звука, смешанных вместе [26,89,106,113,136,137].Эти два направления исследований сошлись в последнее десятилетие, и сегодня их трудно различить. Методы разделения источников больше не обязательно являются слепыми, и в большинстве из них используются те же теоретические инструменты, модели импульсной характеристики и принципы пространственной фильтрации, что и в методах улучшения речи.

Формализация задачи MASS начинается с формализации сигнала смеси. Наиболее общее выражение для линейной смеси сигналов источников J , записанных микрофонами I :

(3.1) x (t) = ∑j = 1Jyj (t) + b (t) ∈RI,

, где yj (t) ∈RI — многоканальное изображение j -го исходного сигнала sj (t) [128] с учетом эффекта распространения звука от места расположения излучаемого источника до микрофонов (каждая запись yij (t) из yj (t) является изображением sj (t) на микрофоне i ). b (t) — коэффициент шума датчика. В большинстве исследований MASS эффект распространения звука от источника j до микрофона i моделируется как линейный инвариантный во времени фильтр импульсной характеристики aij (t), и мы имеем

(3.2) x (t) = ∑j = 1J∑τ = 0La − 1aj (τ) sj (t − τ) + b (t).

Вектор aj (τ) содержит все ответы aij (t) для i∈ [1, I], которые, как предполагается, имеют одинаковую длину La для удобства. В зависимости от приложения цель MASS состоит в том, чтобы оценить либо исходные изображения yj (t), либо (одноканальные) исходные сигналы sj (t) по наблюдению x (t).

Современные методы MASS обычно начинаются с частотно-временного (TF) разложения временных сигналов, обычно с применением кратковременного преобразования Фурье (STFT) [29].На это есть две основные причины. Во-первых, подходы, основанные на моделях, могут использовать преимущества очень конкретной структуры разреженных аудиосигналов в плоскости TF [115]: небольшая часть исходных коэффициентов TF имеет значительную энергию. Таким образом, исходные сигналы, как правило, намного меньше перекрываются в области TF, чем во временной области, что, естественно, способствует разделению. Во-вторых, принято считать, что на каждой частоте процесс сверточного микширования во временной области (3.2) преобразуется с помощью STFT в простое произведение между исходными коэффициентами STFT и коэффициентами дискретного преобразования Фурье (DFT) фильтра смешения, см. e.г. [4,91,107,109,110,146,147] и многие другие исследования:

(3.3) x (f, n) ≈∑j = 1Jaj (f) sj (f, n) + b (f, n) = A (f) s (f , n) + b (f, n),

где x (f, n), sj (f, n) и b (f, n) — СТПФ для x (τ), b (τ) и sj ( τ) соответственно, а aj (f) собирает ДПФ элементов aj (τ), известных как акустические передаточные функции (ATF). Векторы ATF объединяются в матрицу A (f), а исходные сигналы sj (f, n) складываются в вектор s (f, n). Во многих практических сценариях A (f) заменяется соответствующей матрицей относительной передаточной функции (RTF), для которой каждый столбец нормализуется своей первой записью.При такой нормализации первая строка A (f) состоит из «1», а исходные сигналы sj (f, n) заменяются их изображением на первом микрофоне. ²

Как далее обсуждается в разделе 3.3.3, (3.3) является приближением, которое допустимо, если длина импульсных характеристик смесительных фильтров короче, чем длина анализа окна STFT. В литературе и далее это приближение называется приближением мультипликативной передаточной функции (МПФ) [9] или узкополосным приближением [71].

MASS-методы затем можно разделить на четыре (неисключительные) категории [48,137]. Во-первых, методы разделения, основанные на анализе независимых компонентов (ICA), заключаются в оценке фильтров демиксирования, которые максимизируют независимость разделенных источников [26,61]. Методы ICA на TF-домен широко исследованы [103, 110, 127]. К сожалению, основанные на ICA методы подвержены хорошо известным проблемам неоднозначности масштабов и перестановки источников по частотным элементам [3], которые обычно должны решаться как этап постобработки [62,119,120].Кроме того, эти методы нельзя напрямую применять к недоопределенным смесям.

Во-вторых, методы, основанные на анализе разреженных компонентов (SCA) и двоичном маскировании, основываются на предположении, что только один источник активен в каждой точке TF [4,91,118,146] (большинство методов рассматривают только один активный источник в каждом бине TF, хотя в принципе подходы SCA и ICA можно комбинировать, учитывая до – активных источников в каждом бункере TF). Эти методы часто основываются на некотором виде кластеризации источников в домене TF, обычно на основе пространственной информации, извлеченной из предшествующей идентификации фильтра смешивания.Следовательно, для такого рода методов проблема разделения источников часто связана с проблемой локализации источника (где находятся источники излучения?).

В-третьих, более современные методы основаны на вероятностных генеративных моделях в области STFT и связанных с ними алгоритмах оценки параметров и вывода источников [137]. Последние в основном основаны на хорошо известной методологии максимизации ожидания (EM) [30] и т.п. (то есть методах итеративной чередующейся оптимизации). Одним из популярных подходов является моделирование коэффициентов STFT источника с помощью комплексной локальной гауссовой модели (LGM) [37,45,82,148], часто в сочетании с моделью неотрицательной матричной факторизации (NMF) [74], применяемой к спектральной плотности мощности источника. (PSD) матрица [6,44,107,109], которая напоминает такие новаторские работы, как [12].Это позволяет резко сократить количество параметров модели и (до некоторой степени) облегчить проблему перестановки источников. Источники звука обычно разделяются с помощью фильтров Винера, построенных на основе изученных параметров. Такой подход был расширен на супергауссовские (или с тяжелым хвостом) распределения для моделирования разреженности аудиосигнала в области TF [98], а также на полностью байесовскую структуру путем рассмотрения априорных распределений для (источника и / или микширования). процесс) параметры модели [66].Обратите внимание, что, что касается методов SCA / двоичного маскирования, оценка параметров смешения и само разделение источников — это два разных этапа, которые часто обрабатываются поочередно в рамках методологии, основанной на принципах электромагнитной совместимости.

Методы, принадлежащие к четвертой категории, можно в целом классифицировать как методы формирования луча, что примерно эквивалентно линейной пространственной фильтрации . Формирователь луча — это вектор w (f) = [w1 (f),…, wI (f)] T, содержащий один комплексный весовой коэффициент для каждого микрофона, который применяется к x (n, f).Выход wH (f) x (n, f) может быть преобразован обратно во временную область с помощью обратного STFT. Изначально формирователи луча относились к пространственным фильтрам, основанным на направлении прихода (DOA) исходного сигнала, и только позже были обобщены на любые линейные пространственные фильтры. Формирователи луча на основе DOA все еще широко используются, особенно когда решающее значение имеют простота реализации и ее надежность. Однако ожидается, что характеристики этих формирователей луча ухудшатся по сравнению с современными формирователями луча, которые учитывают весь акустический путь [46].Вес формирователя луча устанавливается в соответствии с конкретным критерием оптимизации. Многие критерии формирования луча можно найти в общей литературе [134]. В сообществе обработки речи используется формирователь луча с минимальной дисперсией без искажений (MVDR) [46], формирователь луча с максимальным отношением сигнал / шум (MSNR) [142], многоканальный фильтр Винера (MWF) [34], в частности его искажение речи взвешенный вариант (SDW-MWF) [35] и формирователь луча с линейно ограниченной минимальной дисперсией (LCMV) [92], широко используются.

Можно утверждать, что до сих пор подход формирования луча приводил к более эффективным промышленным приложениям реального мира, чем «общий» подход MASS. Это заключается в различии между (а) усилением пространственно фиксированного доминирующего целевого речевого сигнала от фонового шума (возможно, состоящего из нескольких источников) и (б) четким разделением нескольких исходных сигналов, которые все рассматриваются как представляющие интерес сигналы, которые смешиваются с аналогичными мощность (проблема коктейльной вечеринки). Первую проблему, как правило, решить проще, чем вторую.Другими словами, второй можно рассматривать как продолжение первого. В любом случае, как мы сейчас увидим, проблемы обработки в естественных условиях в каждом случае остаются сложными.

Частотное разложение — обзор

3.2 Разделение источников многоканального звука

В этом разделе мы кратко представляем основы разделения источников многоканального звука. Эта презентация ограничена основным материалом, необходимым для понимания следующего обсуждения MASS в дикой природе.На самом деле, цель этой главы не состоит в том, чтобы подробно представить теоретические основы и принципы разделения источников и формирования луча, даже ограничиваясь аудиоконтекстом: этому вопросу посвящено множество публикаций, включая книги [13,26,33,61,89] и обзорные статьи [20,48,106].

Сотни методов усиления многоканального аудиосигнала были предложены в литературе за последние 40 лет по двум историческим направлениям. Обработка массива микрофонов возникла из теории обработки массива датчиков для телекоммуникаций и была сосредоточена в основном на локализации и улучшении речи в шумной или реверберирующей среде [14,18,25,49,84], в то время как MASS позже был популяризирован Сообщество машинного обучения, и оно рассматривало сценарии «коктейльной вечеринки» с участием нескольких источников звука, смешанных вместе [26,89,106,113,136,137].Эти два направления исследований сошлись в последнее десятилетие, и сегодня их трудно различить. Методы разделения источников больше не обязательно являются слепыми, и в большинстве из них используются те же теоретические инструменты, модели импульсной характеристики и принципы пространственной фильтрации, что и в методах улучшения речи.

Формализация задачи MASS начинается с формализации сигнала смеси. Наиболее общее выражение для линейной смеси сигналов источников J , записанных микрофонами I :

(3.1) x (t) = ∑j = 1Jyj (t) + b (t) ∈RI,

, где yj (t) ∈RI — многоканальное изображение j -го исходного сигнала sj (t) [128] с учетом эффекта распространения звука от места расположения излучаемого источника до микрофонов (каждая запись yij (t) из yj (t) является изображением sj (t) на микрофоне i ). b (t) — коэффициент шума датчика. В большинстве исследований MASS эффект распространения звука от источника j до микрофона i моделируется как линейный инвариантный во времени фильтр импульсной характеристики aij (t), и мы имеем

(3.2) x (t) = ∑j = 1J∑τ = 0La − 1aj (τ) sj (t − τ) + b (t).

Вектор aj (τ) содержит все ответы aij (t) для i∈ [1, I], которые, как предполагается, имеют одинаковую длину La для удобства. В зависимости от приложения цель MASS состоит в том, чтобы оценить либо исходные изображения yj (t), либо (одноканальные) исходные сигналы sj (t) по наблюдению x (t).

Современные методы MASS обычно начинаются с частотно-временного (TF) разложения временных сигналов, обычно с применением кратковременного преобразования Фурье (STFT) [29].На это есть две основные причины. Во-первых, подходы, основанные на моделях, могут использовать преимущества очень конкретной структуры разреженных аудиосигналов в плоскости TF [115]: небольшая часть исходных коэффициентов TF имеет значительную энергию. Таким образом, исходные сигналы, как правило, намного меньше перекрываются в области TF, чем во временной области, что, естественно, способствует разделению. Во-вторых, принято считать, что на каждой частоте процесс сверточного микширования во временной области (3.2) преобразуется с помощью STFT в простое произведение между исходными коэффициентами STFT и коэффициентами дискретного преобразования Фурье (DFT) фильтра смешения, см. e.г. [4,91,107,109,110,146,147] и многие другие исследования:

(3.3) x (f, n) ≈∑j = 1Jaj (f) sj (f, n) + b (f, n) = A (f) s (f , n) + b (f, n),

где x (f, n), sj (f, n) и b (f, n) — СТПФ для x (τ), b (τ) и sj ( τ) соответственно, а aj (f) собирает ДПФ элементов aj (τ), известных как акустические передаточные функции (ATF). Векторы ATF объединяются в матрицу A (f), а исходные сигналы sj (f, n) складываются в вектор s (f, n). Во многих практических сценариях A (f) заменяется соответствующей матрицей относительной передаточной функции (RTF), для которой каждый столбец нормализуется своей первой записью.При такой нормализации первая строка A (f) состоит из «1», а исходные сигналы sj (f, n) заменяются их изображением на первом микрофоне. ²

Как далее обсуждается в разделе 3.3.3, (3.3) является приближением, которое допустимо, если длина импульсных характеристик смесительных фильтров короче, чем длина анализа окна STFT. В литературе и далее это приближение называется приближением мультипликативной передаточной функции (МПФ) [9] или узкополосным приближением [71].

MASS-методы затем можно разделить на четыре (неисключительные) категории [48,137]. Во-первых, методы разделения, основанные на анализе независимых компонентов (ICA), заключаются в оценке фильтров демиксирования, которые максимизируют независимость разделенных источников [26,61]. Методы ICA на TF-домен широко исследованы [103, 110, 127]. К сожалению, основанные на ICA методы подвержены хорошо известным проблемам неоднозначности масштабов и перестановки источников по частотным элементам [3], которые обычно должны решаться как этап постобработки [62,119,120].Кроме того, эти методы нельзя напрямую применять к недоопределенным смесям.

Во-вторых, методы, основанные на анализе разреженных компонентов (SCA) и двоичном маскировании, основываются на предположении, что только один источник активен в каждой точке TF [4,91,118,146] (большинство методов рассматривают только один активный источник в каждом бине TF, хотя в принципе подходы SCA и ICA можно комбинировать, учитывая до – активных источников в каждом бункере TF). Эти методы часто основываются на некотором виде кластеризации источников в домене TF, обычно на основе пространственной информации, извлеченной из предшествующей идентификации фильтра смешивания.Следовательно, для такого рода методов проблема разделения источников часто связана с проблемой локализации источника (где находятся источники излучения?).

В-третьих, более современные методы основаны на вероятностных генеративных моделях в области STFT и связанных с ними алгоритмах оценки параметров и вывода источников [137]. Последние в основном основаны на хорошо известной методологии максимизации ожидания (EM) [30] и т.п. (то есть методах итеративной чередующейся оптимизации). Одним из популярных подходов является моделирование коэффициентов STFT источника с помощью комплексной локальной гауссовой модели (LGM) [37,45,82,148], часто в сочетании с моделью неотрицательной матричной факторизации (NMF) [74], применяемой к спектральной плотности мощности источника. (PSD) матрица [6,44,107,109], которая напоминает такие новаторские работы, как [12].Это позволяет резко сократить количество параметров модели и (до некоторой степени) облегчить проблему перестановки источников. Источники звука обычно разделяются с помощью фильтров Винера, построенных на основе изученных параметров. Такой подход был расширен на супергауссовские (или с тяжелым хвостом) распределения для моделирования разреженности аудиосигнала в области TF [98], а также на полностью байесовскую структуру путем рассмотрения априорных распределений для (источника и / или микширования). процесс) параметры модели [66].Обратите внимание, что, что касается методов SCA / двоичного маскирования, оценка параметров смешения и само разделение источников — это два разных этапа, которые часто обрабатываются поочередно в рамках методологии, основанной на принципах электромагнитной совместимости.

Методы, принадлежащие к четвертой категории, можно в целом классифицировать как методы формирования луча, что примерно эквивалентно линейной пространственной фильтрации . Формирователь луча — это вектор w (f) = [w1 (f),…, wI (f)] T, содержащий один комплексный весовой коэффициент для каждого микрофона, который применяется к x (n, f).Выход wH (f) x (n, f) может быть преобразован обратно во временную область с помощью обратного STFT. Изначально формирователи луча относились к пространственным фильтрам, основанным на направлении прихода (DOA) исходного сигнала, и только позже были обобщены на любые линейные пространственные фильтры. Формирователи луча на основе DOA все еще широко используются, особенно когда решающее значение имеют простота реализации и ее надежность. Однако ожидается, что характеристики этих формирователей луча ухудшатся по сравнению с современными формирователями луча, которые учитывают весь акустический путь [46].Вес формирователя луча устанавливается в соответствии с конкретным критерием оптимизации. Многие критерии формирования луча можно найти в общей литературе [134]. В сообществе обработки речи используется формирователь луча с минимальной дисперсией без искажений (MVDR) [46], формирователь луча с максимальным отношением сигнал / шум (MSNR) [142], многоканальный фильтр Винера (MWF) [34], в частности его искажение речи взвешенный вариант (SDW-MWF) [35] и формирователь луча с линейно ограниченной минимальной дисперсией (LCMV) [92], широко используются.

Можно утверждать, что до сих пор подход формирования луча приводил к более эффективным промышленным приложениям реального мира, чем «общий» подход MASS. Это заключается в различии между (а) усилением пространственно фиксированного доминирующего целевого речевого сигнала от фонового шума (возможно, состоящего из нескольких источников) и (б) четким разделением нескольких исходных сигналов, которые все рассматриваются как представляющие интерес сигналы, которые смешиваются с аналогичными мощность (проблема коктейльной вечеринки). Первую проблему, как правило, решить проще, чем вторую.Другими словами, второй можно рассматривать как продолжение первого. В любом случае, как мы сейчас увидим, проблемы обработки в естественных условиях в каждом случае остаются сложными.

Частотно-временное разложение — SEG Wiki

Рассмотрим форму волны или сигнал с как функцию времени t . Например, синусоида с некоторой амплитудой a и на некоторой частоте f может быть определена как

s (t) = asin⁡ (2πft) {\ displaystyle s (t) = a \ sin (2 \ pi ft)}.

Мы можем реализовать эту математическую функцию как подпрограмму, обычно также называемую функцией на языке программирования Python. Поскольку компьютеры живут в дискретном мире, мы необходимо оценить функцию в течение некоторого времени и с некоторой частотой дискретизации:

 def sine_wave (f, a, duration, sample_rate):
    t = np.arange (0, продолжительность, 1 / частота_выборки)
    вернуть a * np.sin (2 * np.pi * f * t), t 

Теперь мы можем вызвать эту функцию, передав ей частоту f = 261.63 Гц. Мы просим 0,25 с при частоте дискретизации 10 кГц.

 с, t = sine_wave (f = 261,63,
                   а = 1,
                   продолжительность = 0,25,
                   sample_rate = 10e3) 

Это приводит к следующему сигналу, обычно называемому временным рядом , который мы визуализируем, отображая с в зависимости от времени t :

Я изобразил результирующий массив в виде линии, но на самом деле это серия дискретных точек, представленных в Python в виде массива чисел, начиная с этих четырех:

 массив ([0., 0,1636476, 0,32288289, 0,47341253]) 

Построим первые 80 точек:

Когда воздух вибрирует с этой частотой, мы слышим среднюю C или C4. Вы можете услышать примечание для себя в блокноте Jupyter, сопровождающем эту статью, по адресу https://github.com/seg/tutorials-2018. (Блокнот также содержит весь код для построения графиков.) Код для рендеринга массива s как аудио очень короткий:

 из IPython.display импорт аудио
fs = 10e3
Аудио (с, частота = fs) 

Этот сигнал только 0.25 сек, а покачиваний уже много. Нам бы очень хотелось, чтобы сейсмические исследования проводились на такой частоте! Большинство сейсмических данных воспроизводятся только на нижних 20-30 клавишах 88-клавишного пианино — действительно, самая нижняя клавиша — это A0, которая на 27,5 Гц выше пиковой частоты многих более старых съемок.

Если бы мы хотели узнать частоту этого сигнала, мы могли бы предположить, что это чистый тон, и просто посчитать количество циклов в единицу времени. Но естественные сигналы редко бывают монотонными, поэтому давайте сделаем более интересный сигнал.Мы можем использовать нашу функцию, чтобы сделать аккорд до мажор с тремя нотами (C4, E4 и G4), передав векторы столбцов (путем изменения формы массивов) для частоты f и амплитуды a :

 f = np.array ([261.6, 329.6, 392.0])
a = np.array ([1.5, 0.5, 1])
s, t = sine_wave (f = f.reshape (3, 1),
                 a = a.reshape (3, 1),
                 продолжительность = 0,25,
                 sample_rate = 10e3) 

Результатом является набор из трех синусоидальных кривых длиной 0,25 с:

Суммарный сигнал определяется суммой трех кривых:

 s = np.сумма (s, ось = 0) 

Преобразование Фурье

Хотя этот смешанный или политонный сигнал представляет собой просто сумму трех чистых тонов, определение компонентов уже не является тривиальным делом. Здесь на помощь приходит преобразование Фурье.

Мы не будем вдаваться в подробности того, как работает преобразование Фурье. Лучшее объяснение, которое я видел за последнее время, — это вступительное видео Гранта Сандерсона. Дело в том, что преобразование описывает сигналы как смесь периодических компонентов.Давай попробуем это на нашем аккорде.

Сначала мы сужаем сигнал, умножая его на функцию окна . Идеальные чистые тона имеют бесконечную длительность, а сужение помогает предотвратить влияние краев нашего конечного сигнала на преобразование Фурье.

 s = s * np. Черный человек (размер s) 

Оконная функция (зеленый) имеет эффект постепенного изменения сигнала:

Поскольку функция s определена для данного момента времени t , мы называем это представление сигнала временной областью .(е) {\ displaystyle {\ hat {s}} (f)}). Это новое представление называется частотной областью. Он состоит из массива коэффициентов Фурье :

 S = np.fft.fft (s) 

Вспомогательная функция fftfreq () возвращает массив частот, соответствующих коэффициентам. Интервал частотной выборки определяется длительностью сигнала с : чем длиннее сигнал, тем меньше интервал частотной выборки. (Точно так же короткие интервалы выборки по времени соответствуют широкой полосе частот.)

 freq = np.fft.fftfreq (s.size, d = 1 / 10e3) 

Результатом является массив из коэффициентов Фурье , большинство из которых равны нулю. Но на частотах в хорде и около них коэффициенты большие. Результат: «рецепт» аккорда в терминах синусоидальных монотонов.

Это называется спектром сигнала s . Он показывает величину каждой частотной составляющей.

Частотно-временное представление

Теперь мы знаем, как расплетать политонические сигналы, но давайте введем еще одну сложность — сигналы, компоненты которых меняются со временем.Такие сигналы называются нестационарными . Например, представьте себе монотонный сигнал, тон которого меняется в какой-то момент (см. в Блокноте код, который генерирует этот сигнал):

Мы можем вычислить преобразование Фурье этого сигнала, как и раньше:

 s * = np.blackman (размер s)
S = np.fft.fft (s)
freq = np.fft.fftfreq (s.size, d = 1 / 10e3) 

И построить график амплитуды S относительно частотного массива freq :

Он очень похож на спектр, который мы создали ранее, но без средней частоты.Пики немного более разбросаны, потому что длительность каждого сигнала вдвое меньше, чем была. (Общий принцип неопределенности распределяет сигналы по частоте по мере того, как они становятся более компактными во времени.)

Дело в том, что нет большой разницы между спектром двух смешанных сигналов и спектром двух последовательных сигналов. Если мы заботимся о локализации сигналов во времени (делаем!), это проблема. Одно из решений — обратиться к частотно-временным представлениям .Пытаясь одновременно разбить сигнал по времени и частоте, они предлагают способ одновременно пользоваться преимуществами обоих доменов.

Библиотека построения графиков matplotlib Python предлагает удобный способ построения частотно-временного графика, также известного как спектрограмма . В одной строке кода он создает график 2D-изображения, показывающий частоту в зависимости от времени.

 _ = plt.specgram (s, Fs = 1 / 10e3,
                   NFFT = 512, noverlap = 480) 

Приложив немного больше усилий, мы можем получить очень обширное представление о наших данных:

График использует алгоритм, называемый кратковременным преобразованием Фурье или STFT.Это просто выполняет преобразование Фурье в скользящем окне длиной NFFT , при этом точек перекрытия перекрываются с предыдущим окном. Мы хотим, чтобы NFFT был длинным, чтобы получить хорошее частотное разрешение, и мы хотим, чтобы noverlap был большим, чтобы получить хорошее временное разрешение.

Обратите внимание, что мы не можем точно увидеть точную частоту компонентов - они не работают достаточно долго, чтобы их определить. Есть некоторая неуверенность в сроках перехода, потому что для получения приличного частотного разрешения нам нужен более длинный сегмент сигнала (в данном случае 512 отсчетов) - поэтому мы теряем информацию о времени.Но в целом этот сюжет лучше, чем только спектр: мы можем видеть, что есть по крайней мере два сильных сигнала с частотами около 250 и 400 Гц, и что изменение происходит примерно через 0,125 с.

Произведение фортепианной музыки может напоминать такой сюжет. Поскольку клавиши пианино могут воспроизводить только одну ноту, спектрограмма фортепианной музыки выглядит как серия горизонтальных линий:

Существует сильное сходство между этим частотно-временным разложением и обозначением нотоносца:

Оказывается, что наиболее интересные сигналы - и, возможно, все естественные сигналы - являются политоническими и нестационарными.По этой причине, хотя временные ряды часто полезны, частотно-временное разложение может быть очень показательным. Вот несколько примеров; в каждом случае частота отложена по вертикальной оси, а время - по горизонтальной оси. Цвета указывают на мощность от низкой (синий) до высокой (желтый) (пропорционально квадрату амплитуды).

Вот человеческий голос, говорящий "SEG". Сонорантные гласные имеют гармоники (горизонтальные полосы), тогда как свистящие звуки «S» и первой части «G» имеют шумоподобные спектральные отклики.

Эта спектрограмма показывает 5-секундную серию щебетаний летучих мышей. Я обозначил 18 кГц, приблизительный предел слышимости взрослого человека, оранжевой линией, и если вы слушаете звук этого сигнала в Ноутбук, вы можете убедиться, что щебетание едва слышно при нормальной скорости воспроизведения; только при замедлении клипа их можно будет отчетливо услышать.

Наконец, вот вулканический «крик» - гармонический тремор, предшествующий взрывному извержению на горе Редут, Аляска, в марте 2009 года. Звучит невероятно в аудио, но спектрограмма тоже интересно.В отличие от чириканья летучей мыши, этот 15-минутный временной ряд должен быть ускорен, чтобы его услышать.

Продолжить изучение

Все рисунки в этой записной книжке можно воспроизвести с помощью кода из записной книжки Jupyter, прилагаемой к этой статье по адресу https://github.com/seg/tutorials-2018. Вы даже можете запустить код в облаке и поиграть с ним в браузере. Ничего не сломаешь - не волнуйся!

В хранилище вы также найдете больше сигналов, синтетических и естественных, от биений сердца и загадочного подводного щебета до гравитационных волн и сейсмических трасс.Мало того, есть блокнот, в котором показано, как использовать другой алгоритм - непрерывное вейвлет-преобразование - для получения другого типа частотно-временного анализа.

Удачного разложения!

Автор, ответственный за переписку

• Автор, ответственный за переписку: Мэтт Холл, Agile Scientific, Махоун-Бэй, Новая Шотландия, Канада. Электронная почта: mattagilescientific.com

Благодарности

Фортепианная запись BWV846 Баха имеет лицензию CC-BY Кимико Ишизака на http: // welltemperedclavier.орг. Данные щебета летучих мышей лицензированы CC-BY-NC пользователем http://freesound.org klankschap. Спасибо Алисии Хотовек-Эллис за ее помощь с данными о Маунт Редут, зарегистрированными обсерваторией вулкана Аляски Геологической службы США.

Внешние ссылки

Метод извлечения нейронных компонентов, связанных на разных частотах

Abstract

Перцепционные, моторные и когнитивные процессы основаны на разнообразных взаимодействиях между удаленными областями человеческого мозга. Такие взаимодействия могут осуществляться за счет фазовой синхронизации колебательных сигналов.Синхронизация нейронов в основном изучалась в том же частотном диапазоне, например, в альфа- или бета-диапазонах частот. Тем не менее, недавние исследования показывают, что популяции нейронов также могут демонстрировать фазовую синхронизацию между различными частотными диапазонами. Однако извлечение таких межчастотных взаимодействий в записях ЭЭГ / МЭГ остается методологически сложной задачей. Здесь мы представляем новый метод для надежного извлечения межчастотных синхронизированных фаз. Обобщенная кросс-частотная декомпозиция (GCFD) восстанавливает временные ходы синхронизированных нейронных компонентов, их пространственных фильтров и паттернов.Наш метод расширяет предыдущее состояние техники, кросс-частотное разложение (CFD), на весь диапазон частот: он работает для любых f 1 и f 2 всякий раз, когда f 1 : f 2 - рациональное число. GCFD дает компактное описание нелинейно взаимодействующих нейронных источников на основе их межчастотной фазовой связи. Мы успешно проверили новый метод в симуляциях и протестировали его на реальных записях ЭЭГ, включая данные состояния покоя и установившиеся визуально вызванные потенциалы (SSVEP).

Ключевые слова: перекрестная связь , ЭЭГ и МЭГ, межфазная связь, колебания мозга, локализация источника

1. Введение

Синхронизация между популяциями нейронов считается ключевым механизмом, лежащим в основе взаимодействий между отдельными группами нейронов. Согласно гипотезе коммуникации через когерентность (CTC), эффективная коммуникация между двумя группами нейронов возможна только тогда, когда колебания синхронизированы по фазе (когерентны) (Fries, 2015).

Среди различных явлений синхронизации взаимодействия в одной и той же полосе частот (с соотношением 1: 1, т. Е. Гамма-гамма, альфа-альфа или бета-бета) в основном изучены и хорошо охарактеризованы как на людях (Varela et al. , 2001; Halgren et al., 2002; Howard et al., 2003; Palva et al., 2005) и у животных (Womelsdorf et al., 2017). Эти согласованные взаимодействия присутствуют как во время выполнения задач, так и в состоянии покоя. В исследовании MEG было показано, что выраженная фазовая синхронность 1: 1 присутствует в состоянии покоя для всех частотных диапазонов и по всей коре, тогда как локальная 1: r , r ≥ 2, фазовая синхронность увеличивается во время решения задач. в диапазоне бета-альфа и гамма-альфа над задними областями правого полушария (Palva et al., 2005). Между тем, дальнодействующая фазовая синхронизация альфа-диапазона связана с обработкой внимания и рабочей памяти (Palva and Palva, 2011). Синхронизация в диапазонах бета и гамма частот и их пространственные закономерности указывают на активацию зрительного внимания и формирование визуального представления (Siebenhühner et al., 2016). Установлено, что бета-фазовая синхронизация сопровождает обучение слухомоторному ритму (Edagawa, Kawasaki, 2017). Синхронизация нулевой фазы гамма-диапазона может быть связана с сенсорной репрезентацией в обонятельной луковице (Li and Cleland, 2017).

В дополнение к внутренней синхронизации частот, связь между двумя полосами частот также наблюдалась у людей (Sauseng et al., 2008; Jirsa and Müller, 2013; Akiyama et al., 2017; Palva and Palva, 2017) и в записях животных. (Chrobak and Buzsáki, 1998). Такая кросс-частотная синхронизация нейронных колебаний в двух различных частотных диапазонах является активной темой исследований (Palva, Palva, 2017). Фактически, недавние экспериментальные результаты предполагают, что перекрестная частотная связь между пространственно распределенными источниками может лежать в основе динамического формирования функциональных сетей мозга, участвующих в перцепционной, когнитивной и моторной деятельности (как описано в Hyafil et al., 2015).

Было обнаружено несколько типов перекрестной частотной связи: амплитудно-амплитудная, межфазная, межфазная перекрестная связь (Canolty et al., 2006; Jensen and Colgin, 2007). Согласно недавним открытиям, разные типы межчастотной связи связаны с различными функциональными ролями. Например, тета-колебания влияют на фазу или мощность гамма-колебаний в слуховых цепях во время обработки речи (Giraud and Poeppel, 2012; Hyafil et al., 2015). Перекрестная частотная связь между гамма-мощностью и альфа-фазой отражает индивидуальную способность кодировать память (Park et al., 2016).

Особенно важной формой нейронных взаимодействий является межфазная синхронизация, поскольку она представляет собой стабильные временные спайковые отношения между удаленными нейронными колебаниями и, следовательно, напрямую координирует фазовую связь быстрых и медленных колебаний (Siebenhühner et al., 2016) . Считается, что фазовая синхронизация интегрирует и координирует нейронную активность (Jirsa and Müller, 2013; Akiyama et al., 2017). Есть свидетельства того, что межчастотная фазовая синхронизация между тета- и альфа-гамма, а также между альфа- и бета-гамма-колебаниями отражает нагрузку на задачи рабочей памяти (Siebenhühner et al., 2016). Межчастотная фазовая связь лежит в основе недавних нейрофизиологических наблюдений на животных: взаимодействия тета-гамма нейронов в гиппокампе (Belluscio et al., 2012). Взаимодействие между колебаниями альфа-, тета-, бета- и гамма-диапазонов в лобно-корковых областях и их модуляция, по-видимому, играют решающую роль в высших когнитивных функциях (Palva and Palva, 2017), таких как рабочая память (Chaieb et al., 2015), интеграция памяти и процессы внимания (Sauseng et al., 2008).

Хотя это потенциально важно для когнитивных функций и вычислений мозга, связь между фазами нелегко охарактеризовать в неинвазивных записях, поскольку распространенные методы страдают от ряда трудностей, таких как несинусоидальный характер колебаний, нестационарность сигналов и большого количества шума в данных ЭЭГ (Никулин, Брисмар, 2006; Hyafil et al., 2015; Lozano-Soldevilla et al., 2016). Особенно сложная проблема связана с объемной проводимостью, которая приводит к одновременному обнаружению одного и того же сигнала на многих датчиках, что усложняет выделение отдельных источников нейронов, показывающих кросс-частотную синхронизацию. Один из способов решения этой проблемы - использовать моделирование обратного источника. Однако этот подход также имеет ограничения из-за неединственности получаемых решений. Наконец, для извлечения связанных сигналов могут использоваться методы пространственного разложения, такие как SPoC (Source Power Comodulation) и CFD (Cross Frequency Decomposition).Последний, будучи высокоэффективным, ограничен соотношением 1: r (Никулин и др., 2012). Следовательно, необходимы новые методы для надежной оценки межчастотной фазовой связи.

Чтобы избежать ограничений предыдущих методов, в настоящем исследовании мы предлагаем новый подход для выделения компонентов, демонстрирующих межчастотную фазовую связь. Мы называем этот новый метод Generalized Cross-Frequency Decomposition (GCFD). GCFD - это обобщение CFD (Никулин и др., 2012) и использует нелинейные методы для извлечения наиболее сильных ритмических компонентов в сочетании с соотношением частот p : q . Этот метод применим к широкому диапазону перекрестных частотных взаимодействий по сравнению с предыдущими современными методами CFD. Мы протестировали работу GCFD как в моделировании, так и на реальных данных ЭЭГ (стационарные визуально вызванные потенциалы (SSVEP) и наборы данных в состоянии покоя).

2. Методы

2.1. Межчастотная фазовая синхронизация

Пусть с ( t ) будет ходом сигнала с действительным знаком во времени.Мгновенная фаза с ( t ) определяется следующим образом. Сигнал s ( t ) сначала комплексифицируется:

, где H (·) - преобразование Гильберта, а i - мнимая единица. Комплексный сигнал s ~ (t) называется аналитическим сигналом для с ( t ) и допускает следующую факторизацию

с ~ (t) = A (t) · eiφ (t), A (t ) ∈ℝ, A≥0, φ (t) ∈ℝ,

, где A ( t ) называется мгновенной амплитудой с ( t ), а φ ( t ), определенная по модулю 2π, ее мгновенная фаза называется .

Для изучения обычной 1: 1 фазовой синхронизации двух узкополосных сигналов с 1 ( t ) и с 2 ( t ) с той же центральной частотой f , мы наблюдаем их циклическая разность фаз

Δφ (t): = φ2 (t) -φ1 (t) mod2π

в достаточно большом временном окне t = 1 .. T . В случае полного отсутствия синхронности эмпирическое распределение вероятности Δφ ( t ) во временном окне будет равномерным на отрезке [0, 2π].Любое существенное отклонение от равномерного распределения указывает на наличие взаимодействия между мгновенными фазами с 1 ( t ) и с 2 ( t ). Сильная форма этого - когда Δφ ( t ) имеет ярко выраженное унимодальное распределение на [0, 2π]. Это означает, что для некоторого c ∈ [0, 2π] почти в каждый момент времени мы наблюдаем, что φ 2 ( t ) −φ 1 ( t ) ≈ c .Это называется фазовой синхронизацией .

Теперь обобщим это на случай, когда центральные частоты f 1 и f 2 из с 1 ( t ) и s 2 ( t ) различны, но рационально связаны:

см. Rosenblum et al. (2001). Изучение синхронности между такими сигналами - основная цель данной статьи. Чтобы проанализировать этот случай, мы снова вычисляем их мгновенные фазы φ 1 и φ 2 , но теперь мы рассматриваем обобщенную циклическую разность фаз

Δφp, q (t): = pφ2 (t) -qφ1 (t) mod2π.

Теперь мы говорим, что с 1 и с 2 находятся в межчастотной фазовой синхронизации (CFS) , если распределение Δφ p, q ( t ) не является -униформа.

Мы используем следующее значение Phase Locking Value (Rosenblum et al., 2001; Palva et al., 2005) для оценки силы CFS между с 1 и с 2 во временном окне. т = 1.. T :

PLVp, q (φ1, φ2) = 1T | ∑t = 1..TeiΔφp, q (t) |.

(1)

2.2. Предварительная обработка

В случае записей, полученных эмпирическим путем, сырые данные Э / МЭГ проверяются и очищаются от мерцаний и других мышечных артефактов. Это делается путем применения независимого анализа компонентов (алгоритм FastICA, см. Hyvärinen et al., 2001) и удаления всех компонентов, связанных с артефактами. В конце концов, у нас есть многоканальный сигнал E / MEG с одним или несколькими непрерывными временными интервалами, свободными от артефактов, которые называются эпохами .

Очищенные данные Э / МЭГ затем подвергаются низкочастотной фильтрации в широкой полосе, начиная с 0,5 Гц примерно до 150% от наивысшей частоты, которая будет использоваться в анализе. Если нас интересует межчастотное взаимодействие между ритмом 20 Гц и ритмом 30 Гц, высокая частота среза фильтра будет 45 Гц. Это сделано для дальнейшей очистки данных от любого высокочастотного шума.

2.3. Алгоритм GCFD

Общий рабочий процесс предлагаемого метода представлен на рисунке, а подробности будут представлены в следующих разделах.Метод состоит из следующих основных шагов:

Схема алгоритма.

1. выберите один диапазон, который представляет « эталонный» диапазон - P, а другой представляет « соответствует» диапазон - Q;

2. идентифицирует один или несколько компонентов-кандидатов для эталонной полосы;

3. для другой частоты, используя нелинейную оптимизацию, найдите уникальные компоненты, которые наиболее синхронизированы с кандидатами в эталонный ритм;

4. выводит пары, которые демонстрируют лучшую синхронизацию.

Ниже мы подробно рассмотрим каждый из этих шагов, а также некоторые вспомогательные шаги.

2.3.1. Выбор эталонной полосы

В следующем анализе полосы частот f 1 и f 2 играют две разные роли. Сначала мы выбираем несколько самых сильных ритмических компонентов из эталонной полосы с помощью пространственно-спектральной декомпозиции, см. Подраздел 2.3.2. Эти компоненты становятся нашими опорными сигналами. Во-вторых, для каждого из эталонных сигналов мы находим компонент в соответствующей полосе, который наиболее синхронен с ритмической активностью в эталонном сигнале.Это делается с помощью нового метода кросс-частотной подгонки фазы (XPF), который составляет основу данной статьи.

Если нет особых причин предпочитать f 1 f 2 или наоборот в качестве эталонного диапазона, мы рекомендуем выбирать диапазон с меньшей частотой. Таким образом, полиномиальные выражения в процедуре нелинейной оптимизации имеют более низкие степени, и, следовательно, метод сходится быстрее и является более точным. В дальнейшем мы всегда предполагаем, что f 1 является эталонной полосой, а f 2 - подходящей полосой.

Здесь мы подчеркиваем, что XPF асимметричен относительно порядка полос частот f 1 и f 2 . То есть тот же анализ, но с переставленными местами полосами, как правило, не гарантирует получение тех же результатов. Однако численные эксперименты на смоделированных данных показывают, что, хотя результаты могут быть разными, оба подхода очень близки к истине. Пространственные шаблоны для компонентов в подходящей полосе в среднем обнаруживаются более точно, чем пространственные шаблоны для компонентов в эталонной полосе, мы подробно остановимся на этом в следующих разделах.

2.3.2. Пространственно-спектральная декомпозиция

Для опорной полосы частот f 1 мы выполняем процедуру декомпозиции, которая позволяет нам выделить соответствующие колебательные компоненты и уменьшить размерность данных. Среди таких процедур метод пространственно-спектральной декомпозиции (SSD) (Никулин и др., 2011) показал особенно хорошие результаты в симуляционных тестах. Это связано с тем, что SSD лучше приспособлен для обработки узкополосных сигналов по сравнению с более общими методами, такими как ICA.

По сути, SSD максимизирует отношение сигнал / шум, которое определяется как отношение мощности в узкой полосе частот, представляющей интерес, к мощности шума в окружающих фланговых диапазонах частот. См. Nikulin et al. (2011), где представлено полное описание SSD, и (Никулин и др., 2012), раздел 3, где представлена ​​его компактная схема. Мы используем SSD в GCFD два раза. В первый раз мы используем SSD для извлечения самых сильных ритмических компонентов в эталонной полосе, см. Подраздел 2.3.1. Во второй раз мы выполняем SSD, чтобы снизить вычислительную сложность задачи нелинейной оптимизации за счет уменьшения эффективного количества компонентов в полосе соответствия, см. Подраздел 2.4.

Для следующего анализа из эталонной полосы мы берем только компоненты с наибольшими собственными значениями и отбрасываем остальную часть сигнального пространства эталонной полосы. В каждом конкретном наборе данных может быть разное количество этих важных компонентов. Мы рекомендуем сначала использовать количество компонентов по умолчанию, равное 5, и при необходимости изменить его позже.

2.3.3. Кросс-частотная подгонка фазы (XPF)

Подгонка межчастотной фазы (XPF) - это основная процедура GCFD. Его входами являются один узкополосный опорный сигнал r ( t ) на частоте f 1 и набор нескольких узкополосных сигналов m 1 ( t ),…, м I ( t ) на частоте f 2 , где f 1 : f 2 = p : q с целыми положительными числами p , q и t = 1.. Т . Во время стандартного рабочего процесса GCFD опорные сигналы - это компоненты от SSD, которые один за другим подаются в XPF. Другой возможный сценарий, описанный в подразделе 2.5, - это когда одиночный опорный сигнал известен априори . Затем XPF применяется только один раз, используя этот конкретный сигнал и набор сигналов в подходящей полосе.

Мы предполагаем, что м i представляет собой линейную комбинацию неизвестного «целевого» сигнала с ( t ), который находится в межчастотной фазовой синхронизации (CFS) с r ( t ) и I N компоненты шума n i :

(m1 ⋮ mI) T = (sn1 ⋮ nIN) T · P,

(2)

где P - это матрица с действительным знаком ( I N + 1) -by- I , называемая матрицей пространственного смешивания или матрицей пространственного шаблона .Сначала мы стремимся восстановить коэффициенты w i ∈ ℝ такие, что s (t) = ∑iwimi (t). Эти коэффициенты называются пространственным фильтром или просто фильтром . Если P было квадратной матрицей, то w i было бы первым столбцом P −1 .

Для каждого канала r ( t ) и m i ( t ) мы вычисляем их комплексные аналитические сигналы r ~ (t) = r (t) + iH (r) (t ) и m ~ i (t) = mi (t) + iH (mi) (t), где H (·) - преобразование Гильберта, а i - мнимая единица.Сигналы r ~ (t), m ~ i (t) представляют собой-значные временные ряды, такие, что для каждых t = 1 .. T имеет

Re (r ~ (t)) = r (t), Re (m ~ i (t)) = mi (t).

Теперь для r ~ (t) выполняем так называемое искажение частоты в q раз . А именно, мы составляем новый-значный сигнал r ~ [q] (t) такой, что

| r ~ [q] (t) | = | r ~ (t) |, Arg (r ~ [q] ( t)) = q · Arg (r ~ (t)).

(3)

Эквивалентный способ записать это:

r ~ [q] (t) = r ~ (t) q | r ~ (t) | q-1 для каждого t∈1..T.

Обратите внимание на разницу между обозначениями (·) [ q ] и (·) q .Мы сохраняем последнее для стандартной комплексной мощности

По построению, всякий раз, когда какой-либо другой сигнал g ( t ) отображает синхронизацию p : q с r ~ (t), он также находится в p : 1 синхронизация с r ~ [q] (t), и наоборот. q -я степень r ~ (t) q сигнала r ~ (t) имеет то же свойство, но менее удобна для вычислительных целей, поскольку ее величина | r ~ (t) | q может быть либо очень маленькой, либо очень большой для больших значений q .

Как указано в Nikulin et al. (2012), максимизация корреляции между узкополосными сигналами аналогична максимизации их когерентности. Ранее было замечено, что когерентность в первую очередь отражает фазовую синхронизацию (Nolte et al., 2004), но она также измеряет корреляцию амплитуд между двумя сигналами. Когерентность представляет собой фазовую синхронизацию, взвешенную по амплитудной комодуляции (Nolte et al., 2004; Friston et al., 2012). Мезейова и Палуш (2012), однако, показали, что на практике фазовая синхронизация (измеряемая с помощью индекса синхронизации) и когерентность могут давать аналогичные результаты.Кроме того, Nolte et al. (2004) заметили, что для эмпирических сигналов не совсем ясно, можно ли предположить независимость между амплитудой и фазой. Более того, авторы утверждали, что при очень низком отношении сигнал / шум фаза может сильно пострадать, и, следовательно, когерентность (которая включает ковариацию амплитуды) может дать более надежные результаты, чем индекс синхронизации.

Основываясь на этом свидетельстве, мы будем максимизировать корреляцию между-значными сигналами s ~ 1p и s ~ 2, где s ~ 1 = s + iH (s1), s ~ 2 = s + iH (s2) - это аналитические сигналы для с 1 , с 2 .Мы можем найти коэффициенты w i как решение задачи оптимизации

argminwi∈ℝ∑t | (∑iwim ~ i (t)) p-r ~ [q] (t) | 2 =?

(4)

Обратите внимание, что, хотя и m ~ i (t), и r ~ [q] (t) являются комплексными, мы все еще ищем коэффициенты w i в реальный космос. Таким образом, это частный случай ограниченной нелинейной задачи наименьших квадратов (см., Например, Schittkowski, 1988).Стандартный подход - начать со случайного предположения для w i и итеративно спуститься до локального минимума. На практике несколько современных высокоуровневых вычислительных комплексов предлагают компактные решатели для задач ограниченного нелинейного метода наименьших квадратов. В нашей реализации мы использовали функцию lsqnonlin из MATLAB. Те, кто предпочитает Python, могут использовать функцию scipy.optimize.least_squares из пакета SciPy, которая обеспечивает аналогичную функциональность.

2.3.4. Вернуться к пространственным шаблонам

Наконец, для каждого опорного компонента r ( t ) в полосе частот f 1 у нас есть коэффициенты пространственного фильтра w i и компонент с ( t ) = ∑ w i м i ( t ) в соответствующем частотном диапазоне f 2 , который находится в межчастотной фазовой синхронизации с r ( т ).Теперь мы явно вычисляем значение межчастотной фазовой синхронизации (1) из r ( t ) и s ( t ) и выбираем пару ( r, s ) с наибольшим PLV.

Последний шаг - преобразовать пространственные фильтры для вновь обнаруженных компонентов в соответствующие пространственные паттерны (см. Haufe et al., 2014). Подход, предложенный Parra et al. (2005) основан на предположении, что источники взаимно некоррелированы, и дает компактную формулу

, где p - искомый образец, s (t) = ∑iwimi (t), и M = ( m i ) - матрица пространственных сигналов датчиков в полосе частот f 2 .Этот расчет эквивалентен (Haufe et al., 2014) умножению ковариационной матрицы данных в M с фильтром w .

Конечным результатом алгоритма является наиболее синхронная пара ( r, s ) вместе с соответствующими пространственными фильтрами и пространственными шаблонами. Эти пространственные паттерны теперь могут быть визуализированы как топографии кожи головы, см. Пример на Рис. 3 .

2.4. Вторичный твердотельный накопитель

Поскольку вычислительная сложность основной задачи нелинейной оптимизации быстро возрастает по мере увеличения количества каналов N (приблизительно, примерно на ~ N 3 , в зависимости от конкретного решателя), иногда это полезно. чтобы уменьшить размер проблемы.Для этого мы проецируем исходное пространство датчика в линейное подпространство меньшего размера. Мы применяем пространственно-спектральную декомпозицию (см. Подраздел 2.3.2) к узкополосным сигналам на частоте f 2 и пренебрегаем всеми, кроме 15 наиболее значимых компонентов. Например, для N = 60 датчиков это дает ускорение примерно в 4 3 = 64 раза. Для большего количества датчиков этот шаг становится еще более важным.

Затем применяем ту же процедуру нелинейной оптимизации (см. П. 2.3.3) к тому же опорному сигналу и первым 15 компонентам SSD в качестве сигналов соответствия. Это возможно, потому что оптимизация фактически не использует информацию о реальном характере положения датчиков и одинаково хорошо работает для таких «виртуальных датчиков». Наконец, каждый пространственный образец p ′ длины 15, обнаруженный в пространстве виртуальных датчиков, должен быть преобразован обратно в исходное пространство датчика:

, где p - пространственный образец длиной N в пространстве реального датчиков и S - это матрица N × 15 пространственных шаблонов компонентов SSD.

Обратите внимание, что такая оптимизация скорости может происходить за счет снижения точности алгоритма, потому что поиск лучшего пространственного фильтра затем выполняется в некотором 15-мерном подпространстве, а не во всем пространстве фильтра. Таким образом, в некоторых случаях можно отключить эту опцию. Однако эта опция чрезвычайно полезна для быстрого грубого поиска синхронизированных компонентов по множеству комбинаций частотных диапазонов.

2.5. Опорный сигнал

r известный априори

В некоторых экспериментальных сценариях мы можем захотеть изучить синхронизацию колебаний мозга с определенным сигналом, который уже известен.Например, Байрактароглу и др. (2011) провели исследование кортико-мышечной когерентности между сигналом одноканальной электромиограммы и данными многоканальной ЭЭГ. Другой пример - увлечение нейрональной активности зрительной коры на периодическое мерцание экрана. В таком случае шаг SSD не требуется перед основной процедурой нелинейной оптимизации. Другой подходящий пример для этого сценария - запись потенциала локального поля (LFP) с хорошим SNR. Во всех этих случаях метод пропускает шаги (а) и (б), вспомните раздел 2.3, и сразу переходим к пункту (c), поскольку нам нужна только процедура XPF без остальной части алгоритма GCFD. Мы будем называть эту усеченную версию рабочего процесса отдельной процедурой XPF .

Мы провели численное моделирование, чтобы оценить способность отдельного XPF справляться с этими ситуациями с известными опорными сигналами. Эти тесты показали, что в этом режиме общее качество восстановления шаблона для синхронизированных источников значительно лучше, чем у более сложного полного алгоритма GCFD (см. Ниже).Более того, отделенный XPF может точно реконструировать источник при больших значениях p и q , протестированных до p, q = 5. Подробности см. В подразделе 3.1.

2.6. Общая фазовая синхронизация

Выше мы искали компоненты межчастотной фазовой синхронизации:

Более слабое состояние, называемое , межчастотная фазовая синхронизация требует только постоянной разницы между адаптированными циклическими фазами сигналов:

To Для поиска межчастотных составляющих с фазовой синхронизацией в сигнале E / MEG мы модифицируем формулу (3) для искажения частоты опорных составляющих.Мы выбираем целое число K ≈10 и определяем комплексные сигналы r ~ [q, k] как

| r ~ [q, k] (t) | = | r ~ (t) |, Arg (r ~ [q, k] (t)) = q · Arg (r ~ (t)) + kK2π

(5)

для k = 0 .. K −1. Затем мы запускаем вышеуказанные алгоритмы для каждого k = 1 .. K −1 и ищем компоненты с самым высоким PLV среди всех прогонов.

Наш предварительный анализ показал, что распределение разностей фаз между компонентами довольно широкое, что указывает на то, что нет необходимости точно выравнивать фазы обоих сигналов, чтобы иметь разность 0 или π.Аналогичное число K = 12 было успешно использовано в другом исследовании для оптимизации когерентности (Bayraktaroglu et al., 2012).

2.7. Моделирование

Для тестов производительности алгоритмов мы выбрали соотношения p : q , которые с наибольшей вероятностью продемонстрируют межчастотную фазовую синхронизацию в записях Э / МЭГ человеческого мозга:

p: q = 1: 2,1: 3, 1: 4,2: 1,2: 3,3: 1,3: 2,3: 4,4: 1,4: 3.

(6)

Мы стремились моделировать фазовые взаимодействия между тета, альфа, бета и низкими гамма-колебаниями.Некоторые из них, например альфа: бета (1: 2), ранее наблюдались в записях Э / МЭГ. Для каждого отношения p : q мы провели 100 независимых рандомизированных симуляций мозговой активности и проверили, насколько точным был наш алгоритм, восстанавливающий истинные синхронизированные источники.

Для каждого моделирования мы сначала сгенерировали 5 независимых пар перекрестно-синхронизированных колебательных сигналов с различным соотношением частот p : q . Процедура для каждой пары была следующей.Мы генерировали белый шум длительностью 150 секунд, дискретизированный с частотой 200 Гц. Затем этот шум подвергался полосовой фильтрации в диапазоне частот 9-11 Гц с использованием двух проходов фильтра Баттерворта, одного прямого и одного обратного. Такие два прохода позволяют нейтрализовать любые фазовые искажения, вызванные артефактами одного прохода фильтра (Mitra and Kuo, 2001). Затем мы исказили по частоте две копии этого сигнала в p и q раз соответственно. Это дало нам пару p : q -синхронизированных сигналов в полосах частот около 10 p Гц и 10 q Гц.

Кроме того, мы использовали 100 взаимно независимых источников шума со спектром мощности 1/ f (так называемый розовый шум ). Такой спектр мощности типичен для записи Э / МЭГ мозга человека.

Каждый из 10 синхронизированных колебательных сигналов и 100 шумовых сигналов соответствует соответствующему диполю тока, случайно выбранному из узлов треугольной мозаичной корковой мантии. Ориентация диполя также была рандомизирована. Мы использовали реалистичную модель прямого проводника с тремя отсеками (Nolte and Dassios, 2005), основанную на главе Монреальского неврологического института (MNI) (Evans et al., 1994) для расчета смоделированных сигналов датчиков ЭЭГ по сигналам источников. Каждая моделированная запись ЭЭГ имела 64 канала, соответствующих стандартным положениям датчиков.

Кроме того, мы нормализовали отношения сигнал / шум (SNR) всех наших сигналов, которые мы определяем как отношение средней дисперсии сигналов по каналам для каждого проецируемого сигнального диполя и средней дисперсии по каналам для всего совокупный прогнозируемый шум. Мы проверили производительность нашего алгоритма для значений SNR, равных 0.1, 0.5, 1.0, 2.0, см. Ниже.

Затем для каждого моделирования мы запускали алгоритм GCFD реконструкции источника, описанный в подразделах 2.2–2.4. Результирующие пространственные шаблоны для восстановленных источников в полосе частот f ₁ затем сравниваются с истинными шаблонами, которые известны a priori по дизайну.

В дополнение к этим симуляциям мы также выполнили симуляции для случая 2: 3 (SNR = 0,5), смешивая пять компонентов в диапазоне частот 20 Гц, но соответствующие составляющие 30 Гц были получены путем деформации частоты других пяти составляющих 10 Гц, которые были не зависит от первых 10 Гц компонентов..

Обратите внимание, что восстановленные шаблоны не имеют определенного порядка, связанного с исходными шаблонами. Чтобы найти фактическую ошибку восстановления для каждого сигнала, требуется процедура сортировки. А именно, мы рассчитали все попарные расхождения паттернов между всеми восстановленными паттернами и всеми исходными паттернами. Затем мы использовали жадный алгоритм для сопоставления восстановленных шаблонов с исходными шаблонами: сначала мы находим пару восстановленного шаблона и исходного шаблона с наименьшим расхождением, а затем мы удаляем их оба из наборов шаблонов.Затем мы повторяем процедуру с оставшимися шаблонами, чтобы найти второе наилучшее совпадение и так далее .

Каждая симуляция дает вектор из 5 чисел расходимости паттернов. Умножив на 100 симуляций, в итоге мы получим 500 чисел для каждого отношения частот p : q и каждого значения SNR. См. Подраздел 3.2 и Рисунок 3 для результатов и обсуждения.

2.8.2. Эмпирические данные

Что касается эмпирических данных, нам не хватает информации о базовых шаблонах истинности, и, таким образом, мы не можем напрямую измерить расхождения между базовыми шаблонами истинности и предполагаемыми шаблонами.В этом случае мы скорее используем расхождение шаблона как меру сходства между двумя шаблонами, относящимися к компонентам с перекрестной частотной связью.

2.9. Реальные записи ЭЭГ

2.9.1. Состояние покоя

Алгоритм GCFD был протестирован на данных ЭЭГ, полученных в Центре познания и принятия решений НИУ ВШЭ, Москва. Все экспериментальные процедуры были одобрены местным этическим комитетом. Участники подписали форму информированного согласия.В эксперименте ЭЭГ участвовали 32 здоровых человека (12 мужчин, правши, средний возраст 23 года). Данные ЭЭГ регистрировали с помощью 60 активных электродов BrainVision actiCHamp (Brain Products GmbH) по расширенной версии системы 10–20. Данные были дискретизированы с частотой 500 Гц. Активные каналы сравнивали со средним значением двух сосцевидных электродов. Электроокулограмма записывалась с помощью электродов, размещенных на наружном уголке глаза и ниже правого глаза. Записи ЭЭГ были отфильтрованы в автономном режиме в диапазоне частот 0.5–40 Гц. Спектральный анализ с помощью БПФ (быстрое преобразование Фурье) проводился с окном Хэммингса 3 секунды. Участники удобно рассаживались перед темным экраном в течение 10 минут, не сводя глаз с креста перед собой.

Для последовательного автономного анализа данные ЭЭГ были субдискретизированы до 200 Гц, длина данных составила 10 минут. Мы уменьшили размер сигнала, используя 5 самых мощных компонентов SSD в обоих интересующих частотных диапазонах p ^* f ₁ ± 1 Гц и q ^* f ₂ ± 1 Гц .Настройки для SSD были следующие: диапазон частот среза для полосового фильтра был p ^* f ₁ ± 1 Гц и q ^* f ₂ ± 1 Гц; диапазон частот среза для самых низких и самых высоких частот, определяющих интервалы фланкирования, составлял p ^* f ₁ ± 3 Гц и q ^* f ₂ ± 3 Гц; Диапазон частот среза для полосового фильтра составлял p ^* f ₁ ± 2 Гц и q ^* f ₂ ± 2 Гц.Мы искали самые сильные синхронные компоненты для p : q , равных 2: 1 и 2: 3, и базовых частот из альфа-диапазона частот (8–12 Гц). Например, максимальное значение PLV для p : q = 2: 3 могло быть достигнуто при базовой частоте 9,5 Гц, что означало бы, что большинство синхронизированных 2: 3 компонентов находятся на частотах 19 Гц и 28,5 Гц.

2.9.2. Устойчивые визуальные вызванные потенциалы

Для демонстрации работы GCFD мы использовали данные ЭЭГ, полученные в Центре когнитивных исследований и принятия решений НИУ ВШЭ, Москва, с устойчивыми визуально вызванными потенциалами (SSVEP), которые регистрировались для BCI эксперименты (Ишкан, Никулин, 2018).Все экспериментальные процедуры были одобрены местным этическим комитетом. Участники подписали форму информированного согласия. В эксперименте приняли участие 24 здоровых человека (возраст 18–41 год). ЭЭГ регистрировали с частотой дискретизации 1 кГц усилителем ActiCHamp с использованием программного обеспечения PyCorder (Brain Products) с 60 каналов actiCHamp. Полосовой фильтр с частотами отсечки 0,53 и 40 Гц был применен к необработанным данным для удаления составляющей постоянного тока и высокочастотных артефактов. Во время эксперимента испытуемые должны были смотреть на экран компьютера с одним периодически мерцающим кружком.Эта установка, как известно, вызывает периодические потенциалы, известные как устойчивые визуальные вызванные потенциалы (SSVEP), в зрительной коре головного мозга субъектов с той же частотой, что и частота мерцания (Friman et al., 2007). Эксперимент был разбит на 3-секундные сегменты. Для каждого сегмента частота мерцания была случайным образом выбрана из четырех фиксированных значений: 5,45, 8,57, 12, 15 Гц.

Для последовательного анализа GCFD мы объединили все 3-секундные пробные записи в один 75-секундный многоканальный сигнал для каждого объекта и каждой частоты мерцания.Поскольку необработанные данные были отфильтрованы с помощью фильтра высоких частот с частотой 0,53 Гц перед объединением, не было никаких смещений между эпохами, и, таким образом, последующая фильтрация не приводила к появлению артефактов, что также было подтверждено визуальным осмотром.

Мы уменьшили размер сигнала, используя 15 самых мощных компонентов SSD в обоих интересующих частотных диапазонах p ^* f ₁ ± 1 Гц и q ^* f ₂ ± 1 Гц . Для SSD использовались следующие настройки: диапазон частот среза полосового фильтра p ^* f ₁ ± 1 Гц и q ^* f ₂ ± 1 Гц; диапазон частот среза для самых низких и самых высоких частот, определяющих интервалы фланкирования, составлял p ^* f ₁ ± 3 Гц и q ^* f ₂ ± 3 Гц; Диапазон частот среза для полосового фильтра составлял p ^* f ₁ ± 2 Гц и q ^* f ₂ ± 2 Гц.Для удобства вычислений в нашем анализе мы аппроксимировали реальные частоты мерцания 5,45, 8,57, 12, 15 Гц с целочисленными частотами 6, 9, 12, 15 Гц соответственно.

2.9.3. Статистическое тестирование

Мы использовали непараметрический критерий перестановки для оценки статистической значимости результатов (Maris and Oostenveld, 2007). В нашем подходе тестовая статистика была получена из GCFD, примененного к случайно переставленным данным.

Мы разделили записи и объединили сегменты в случайном порядке из данных, относящихся к поиску пространственного фильтра w , при сохранении порядка сегментов в опорном сигнале, который описан в разделе 2.3.1. Обратите внимание, что эта рандомизация была выполнена до нахождения пространственных фильтров w , так что все остальные шаги сохраняются, как и в основном анализе.

Затем мы запустили наш алгоритм на переставленной записи и получили новый парный сигнал для опорного сигнала. Затем мы создали распределение перестановок, повторив эту процедуру 1000 раз и вычислив для каждой пары соответствующее значение фазовой синхронизации (1). Нулевая гипотеза при этом тесте на перестановку заключалась в том, что все переставленные пары и исходная пара принадлежали одному и тому же распределению.Наконец, мы вычислили P-значение для исходной пары сигналов, и если оно было меньше 0,05, мы пришли к выводу, что результат был статистически значимым.

Это часто используемый подход для непараметрического тестирования перестановок (Hesterberg et al., 2005; Maris et al., 2007), который сохраняет спектры сигналов и все шаги оптимизации, таким образом представляя надежную процедуру для управления эффектами переоснащение.

3. Результаты

3.1. Тест отсоединенного XPF

Сначала мы проверили, насколько точно процедура отсоединенного XPF (вспомните Подраздел 2.3.3) восстанавливает пространственные структуры источников в сценарии, когда истинные источники предоставляются в качестве опорных сигналов, и, таким образом, нам нужно только найти компоненты с перекрестно-частотной связью в подходящей полосе. Обратите внимание, что это также действительное моделирование эксперимента, когда захватывающий сигнал известен из других источников, таких как кардиограмма, миограмма, колебательный сигнал от транскраниальной стимуляции переменным током, визуальный или слуховой сигнал и т. Д. Подробности см. В подразделе 2.5. . Для каждой пары

p: q = 1: 2,1: 3,1: 4,2: 1,2: 3,3: 1,3: 2,3: 4,4: 1,4: 3

(8)

и каждый SNR = 1.0, 0.5, 0.1 мы выполнили 100 симуляций, аналогичных описанным в подразделе 2.7. Результаты представлены на рисунке. Мы видим удивительно хорошую производительность для всех SNR и для всех пар p : q с соответствующим расхождением модели <0,05.

Точность восстановления паттерна оторванного XPF.

В этом тесте мы практически устранили все ошибки, связанные с производительностью алгоритма SSD на этапе первоначального извлечения эталонных компонентов.Как мы покажем позже, недостаточно чистое извлечение компонентов SSD может привести к ошибкам реконструкции для алгоритма GCFD, сравните рисунки, 4 .

В целом результаты этого теста демонстрируют, что процедура оптимизации ядра работает хорошо для всех протестированных соотношений частот, которые часто встречаются в исследованиях синхронизации сигналов E / MEG.

3.2. Моделирование для алгоритма GCFD

Моделирование, основанное на реалистичном моделировании напора, показало, что алгоритм GCFD надежно восстанавливает перекрестно-частотные компоненты на разных частотах, относящиеся друг к другу через рациональные числа p : q , по крайней мере, до p, q ≤ 4.Это значительное улучшение по сравнению с базовым алгоритмом кросс-частотной декомпозиции (CFD) (Никулин и др., 2012), который был пригоден только для случая p = 1 и q ≤ 3.

На рисунке показан пример реконструкции 5 смоделированных источников 30 Гц, синхронизированных с 5 другими источниками 20 Гц. В этом примере p : q = 3: 2 и SNR = 0,1 для полос частот 30 и 20 Гц. Рисунок демонстрирует, что восстановленные топографии источников 30 и 20 Гц были очень похожи на смоделированные изображения.

Шаблоны источников (SP) и восстановленные шаблоны (RP) для 5 пар смоделированных синхронизированных источников на 20 и 30 Гц. SNR = 0,1. Цветовая шкала в произвольных единицах.

Чтобы измерить общее качество восстановления шаблона алгоритма GCFD, мы выполнили серию из 100 симуляций для каждого из соотношений частот (6) p : q = 1: 2, 1: 3, 1: 4, 2: 1 , 2: 3, 3: 1, 3: 2, 3: 4, 4: 1, 4: 3 и отношения сигнал / шум = 1,0, 0,5, 0,1. Результаты показаны на рисунке.

Точность восстановления шаблона для всего GCFD.

Естественно, что по мере уменьшения отношения сигнал / шум для каждого фиксированного отношения p : q мы наблюдали постепенное снижение точности восстановления структуры. Однако для всех частотных соотношений даже при SNR ≥0,1 средняя ошибка все еще была очень маленькой, не более 0,08. Результаты отдельного теста XPF, см. Подраздел 3.1, показывают, что основной источник снижения точности связан с недостаточной производительностью SSD.

В целом мы пришли к выводу, что для всех протестированных частот и отношения сигнал / шум ≥0.1, точность восстановления структуры достаточна для анализа синхронизированных источников в реальных записях Э / МЭГ.

При моделировании несвязанных источников мы наблюдали, что при SNR = 0,5 расходимость диаграмм составляла в среднем 0,33, что по крайней мере в 15 раз больше, чем расходимость диаграмм, характерных для связанных источников. Такие значения расхождения рисунков указывают на то, что извлеченные топографии сильно отличались от топографий исходных несвязанных источников. Это, в свою очередь, указывает на то, что при моделировании, когда источники не связаны, GCFD не может восстановить смоделированные компоненты.

3.3. Реальные записи ЭЭГ

3.3.1. Состояние покоя

Сначала мы проверили, как работает GCFD для записей ЭЭГ в состоянии покоя, описанных в 2.9.1. Мы выбрали 8 субъектов с наиболее выраженными пиками мощности в альфа-, бета- и гамма-диапазоне частот и провели анализ GCFD для выявления синхронных источников с перекрестно-частотной связью. Базовые частоты были взяты из альфа-диапазона 8–12 Гц. На рисунке показаны результаты для типичного объекта, для которого мы выполнили поиск в соотношении 2: 1 и 2: 3 с базовой частотой, равной 9.9 Гц. На рисунке представлены все пары сигналов, восстановленные GCFD для всех участников.

Примеры кросс-частотных синхронных колебаний, обнаруженных с помощью алгоритма GCFD для поиска 2: 1 и 2: 3. (A) Для данных состояния покоя. (B) Для записи с SSVEP 12 Гц.

Пары всех компонентов (2: 1 и 2: 3) от всех субъектов, извлеченные с помощью GCFD для поиска 2: 1 (слева) и 2: 3 (справа). (A) Для данных состояния покоя. (B) Для записи с SSVEP 12 Гц.

Для отношения частот 2: 1 большинство (92%) вычисленных значений фазовой синхронизации были статистически значимыми. Однако корреляция между PLV и дивергенцией паттернов не была особенно сильной ( R ² = 0,49), что указывает на то, что только часть данных, вероятно, представляет связь из-за несинусоидальной формы нейронных колебаний.

Для соотношения частот 2: 3 только 20% PLV были статистически значимыми. Мы также проанализировали взаимосвязь между силой фазовой связи и релевантной расходимостью паттернов.Мы наблюдали отрицательную корреляцию для случая 2: 1 ( p -значение = 7 · 10 ⁻⁶ ) и отсутствие корреляции для 2: 3 ( p -значение = 0,11).

3.3.2. Устойчивые визуальные вызванные потенциалы

Мы также протестировали GCFD на сигналах устойчивых визуальных вызванных потенциалов (SSVEP), описанных в 2.9.2. Цель состояла в том, чтобы продемонстрировать, что наш подход может найти гармоники, синхронизированные по фазе между частотами, сигналов SSVEP с частотами, относящимися друг к другу посредством рационального соотношения p : q для p, q ≤ 4.Мы выполнили анализ GCFD для 24 субъектов с частотами мерцания 5,45, 8,57, 12 и 15 Гц. Мы использовали частоту визуальной стимуляции в качестве базовой частоты и установили соотношение p : q в соответствии с исследованными гармониками сигнала SSVEP. На рисунке показаны результаты типичного испытуемого с частотой визуальной стимуляции 12 Гц, где выполнялись поиски 2: 1 и 2: 3. Мы наблюдали пары сигналов с похожими пространственными паттернами, которые предполагают, что соответствующие источники нейронов находятся в зрительной коре.Более того, мы наблюдали значительно высокие значения PLV между компонентами с разными частотами. Значимость результатов проверялась с помощью перестановочных тестов, описанных ранее в подразделе 2.9.3. Тесты на перестановки показали, что 44 и 28% пар были значимы для взаимодействий 2: 1 и 2: 3 соответственно. На рисунке показаны все пары сигналов, обнаруженные методом GCFD в записях ЭЭГ с частотой стимуляции 12 Гц для поиска 2: 1 и 2: 3. Дивергенция паттернов была рассчитана в соответствии с 7. Это указывает на сходство между двумя топографиями.Никакой существенной корреляции между PLV и расхождением паттернов не наблюдалось для 2: 1 ( p -значение = 0,10) и 2: 3 ( p -значение = 0,13).

4. Обсуждение

Мы представили новый алгоритм для обнаружения и выделения межчастотных межфазных синхронизированных нейронных компонентов. Обобщенная кросс-частотная декомпозиция способна реконструировать как временные ходы синхронизированных нейронных компонентов, так и соответствующие пространственные фильтры и паттерны.

Мы показали, что GCFD способен обнаруживать синхронность между частотами, связанными рациональным соотношением p: q, для p, q ≤ 4.Новый метод расширяет предыдущий уровень техники, кросс-частотное разложение (CFD) (Никулин и др., 2012), на более общий диапазон частотных пар. Однако для p, q > 4 обнаружение межчастотной синхронизации затруднительно, потому что область фазовой синхронизации очень узкая и возможная синхронизация, вероятно, будет скрыта шумом. Это общая проблема обнаружения межчастотных взаимодействий, которая не является специфической для алгоритма GCFD (Pikovsky et al., 2001).

4.1. Ограничения предыдущих методов

Наиболее распространенным подходом является расчет кросс-частотной синхронизации в пространстве датчиков (Schanze, Eckhorn, 1997; Tass et al., 1998; Carlqvist et al., 2005; Palva et al., 2005; Никулин и др.) Brismar, 2006; Sauseng et al., 2008; Darvas et al., 2009; Siebenhühner et al., 2016). Одна из ловушек анализа в сенсорном пространстве заключается в том, что топографии источника невозможно идентифицировать из-за проблемы смешения, связанной с объемной проводимостью. Другой подход (Tass et al., 2003) основан на инверсном моделировании исходных сигналов, которые затем попарно проверяются на наличие межчастотной синхронизации путем вычисления значений фазовой синхронизации по всем парам вокселей мозга. Этот подход требует обширных исправлений статистических ошибок типа I. Более того, эти сравнения создают большую сложность нейронных отношений, которые, однако, не обязательно связаны с истинной нейронной сложностью. В случае обратного моделирования также важно обратить внимание на общую неоднозначность обратной реконструкции.

4.2. Преимущества и ограничения GCFD

Численное моделирование показало, что GCFD может восстанавливать взаимодействующие источники, даже если они замаскированы очень сильным шумом (SNR = 0,1), см. Рисунок. Извлечение нелинейно взаимодействующих компонентов было замечательно хорошим, показывая только небольшую ошибку (<0,08) в восстановленных шаблонах даже в очень сложной ситуации, когда SNR = 0,1. В этом исследовании мы используем SSD, который является одним из лучших методов извлечения сигналов с низким отношением сигнал / шум (Никулин и др., 2011). GCFD зависит от производительности SSD, так как ошибки извлечения SSD для опорных сигналов могут влиять на качество окончательной реконструкции шаблона, см. Подразделы 2.3.2, 3.1. GCFD также имеет асимметрию производительности по отношению к свопу p и q из-за его зависимости от начального SSD. Мы показали при моделировании, что отдельный XPF, который использует уже доступные опорные сигналы, работает значительно лучше по сравнению со всем GCFD, см. Раздел 3.Однако GCFD не ограничивается использованием SSD для получения опорных сигналов. Здесь можно использовать компоненты, извлеченные с помощью другого подхода к разложению, такого как ICA, или непосредственно доступные сигналы, такие как кардиограмма, миограмма, визуальный или слуховой сигнал и т. Д. Это может быть особенно полезно при анализе межчастотных корково-мышечных взаимодействий, когда опорные сигналы получаются с поверхности. ЭМГ. Фактически, в недавнем обзоре подчеркивалась важность кросс-частотных взаимодействий для лучшего понимания корково-спинномозгового моторного контроля (Yang et al., 2017). Мы считаем, что метод GCFD может быть ценным подходом в этом отношении.

4.3. Истинные и ложные межчастотные взаимодействия

При поиске межчастотной синхронизации всегда есть возможность обнаружить CFS не из-за подлинных взаимодействий нейронов, но также из-за несинусоидальной формы колебаний (Gaarder and Speck, 1967; Jürgens et al., 1995; Никулин, Брисмар, 2006). Это связано с тем, что несинусоидальные волны представляют собой сумму синусоидальных волн на основной и гармонической частотах (которые являются целыми кратными базовой частоте), и эти синусоидальные волны затем будут демонстрировать кросс-частотную синхронизацию.Например, (Никулин и Брисмар, 2006) в численном эксперименте показали, что, когда сигнал ЭЭГ не является синусоидальным, он демонстрирует ложную альфа-бета-фазовую связь.

Чтобы контролировать этот побочный эффект, мы вычислили расхождение паттернов между пространственными паттернами опорного сигнала и синхронизированными ритмическими компонентами. Если паттерны были похожи, мы считали их гармониками. Для случая 2: 1 мы наблюдали много подобных моделей с высоким PLV. Этого не было в случае связи 2: 3, где мы наблюдали меньшее количество аналогичных паттернов и среднее значение PLV было ниже.

Мы показали, что GCFD может применяться для поиска фазовой связи в случаях, когда мы используем предварительно выбранные пики на основе спектров, как показано на рисунке в состоянии покоя, а также для случаев, когда известна априорная информация об опорных спектрах, что и имеет место для эксперимента SSVEP, рис. Все пары, найденные GCFD, представлены на рисунке. В экспериментах на ЭЭГ мы не обнаружили особенно сильной корреляции между сходством паттернов и силой межчастотной фазовой синхронизации.Это, в свою очередь, указывает на то, что извлеченные межчастотные взаимодействия маловероятны из-за присутствия гармоник, поскольку в этом случае корреляция между подобием структуры и значениями PLV будет очень сильной. Более того, чувствительность GCFD как к подлинным, так и к «гармоническим» межчастотным взаимодействиям имеет дополнительные преимущества, поскольку может позволить более точное извлечение несинусоидальных нейронных колебаний, важных для систем интерфейса мозг-компьютер, основанных на известном мю-ритме. иметь вторую и даже третью гармоники.Наличие межчастотных взаимодействий в динамике состояния покоя, как мы наблюдали в настоящем исследовании, является особенно интересным случаем, поскольку это может указывать на вычислительную готовность нейронных сетей к участию в обработке информации, распределенной по различным областям коры, производящим колебательные сигналы. активность на разных частотах.

В качестве направления для будущих исследований было бы интересно применить GCFD для исследования роли межчастотной фазовой синхронизации между различными сетями, демонстрируя сильную внутричастотную связь, в различных когнитивных задачах, предлагаемых для такой интеграции, е.г., в зрительной рабочей памяти (Siebenhühner et al., 2016). Наша работа демонстрирует, что алгоритм GCFD может быть легко использован для исследования таких сложных межчастотных взаимодействий.

Понимание функций аудиоданных, преобразования Фурье, БПФ и спектрограммы для системы распознавания речи | Картик Чаудхари

Быстрое преобразование Фурье (БПФ) - математический алгоритм, который вычисляет Дискретное преобразование Фурье (ДПФ) заданной последовательности. Единственное различие между FT (преобразование Фурье) и FFT состоит в том, что FT рассматривает непрерывный сигнал, а FFT принимает дискретный сигнал в качестве входного. DFT преобразует последовательность (дискретный сигнал) в ее частотные составляющие точно так же, как FT для непрерывного сигнала. В нашем случае у нас есть последовательность амплитуд, выбранных из непрерывного звукового сигнала. Алгоритм DFT или FFT может преобразовать этот дискретный сигнал временной области в частотный.

Обзор алгоритма БПФ

Простая синусоида для понимания БПФ

Чтобы понять результат БПФ, давайте создадим простую синусоиду. Следующий фрагмент кода создает синусоидальную волну с частотой дискретизации = 100, амплитудой = 1 и частотой = 3 .Значения амплитуды вычисляются каждые 1/100 секунды (частота дискретизации) и сохраняются в списке с именем y1. Мы передадим эти дискретные значения амплитуды для вычисления ДПФ этого сигнала с помощью алгоритма БПФ.

Если вы нанесете эти дискретные значения (y1), сохраняя номер выборки на оси x и значение амплитуды на оси y, он сгенерирует красивый график синусоидальной волны, как показано на следующем снимке экрана -

Теперь у нас есть последовательность амплитуд, сохраненная в список y1. Мы передадим эту последовательность алгоритму БПФ, реализованному scipy.Этот алгоритм возвращает список yf из комплексных амплитуд частот , найденных в сигнале. Первая половина этого списка возвращает термины с положительной частотой, а другая половина возвращает термины с отрицательной частотой, которые аналогичны положительным. Вы можете выбрать любую половину и вычислить абсолютные значения для представления частот, присутствующих в сигнале. Следующая функция берет образцы в качестве входных данных и строит график частот -

На следующем графике мы построили частоты для нашей синусоидальной волны, используя указанную выше функцию fft_plot.Вы можете видеть, что этот график ясно показывает одно значение частоты, присутствующее в нашей синусоиде, равное 3. Кроме того, он показывает амплитуду, связанную с этой частотой, которую мы оставили равной 1 для нашей синусоидальной волны.

Чтобы проверить выходной сигнал БПФ для сигнала, имеющего на более одной частоты , давайте создадим еще одну синусоидальную волну. На этот раз мы оставим частоту дискретизации = 100, амплитуду = 2 и значение частоты = 11 . Следующий код генерирует этот сигнал и строит синусоидальную волну -

Сгенерированная синусоида выглядит как на графике ниже.Было бы более плавно, если бы мы увеличили частоту дискретизации. Мы сохранили частоту дискретизации = 100 , потому что позже мы добавим этот сигнал к нашей старой синусоиде.

Очевидно, функция БПФ также покажет одиночный всплеск с частотой = 11 для этой волны. Но мы хотим увидеть, что произойдет, если мы сложим эти два сигнала с одинаковой частотой дискретизации, но с разными значениями частоты и амплитуды. Здесь последовательность y3 будет представлять результирующий сигнал.

Если мы построим сигнал y3, он будет выглядеть примерно так -

Если мы передадим эту последовательность (y3) нашей функции fft_plot. Он генерирует для нас следующий частотный график. Он показывает два пика для двух частот, присутствующих в нашем результирующем сигнале. Таким образом, наличие одной частоты не влияет на другую частоту в сигнале. Также следует отметить, что амплитуды частот находятся на линии с нашими сгенерированными синусоидальными волнами.

БПФ для нашего аудиосигнала

Теперь, когда мы увидели, как этот алгоритм БПФ дает нам все частоты в данном сигнале. давайте попробуем передать в эту функцию наш исходный аудиосигнал. Мы используем тот же аудиоклип, который мы ранее загрузили в питон, с частотой дискретизации = 16000 .

Теперь посмотрите на следующий график частот. Этот сигнал «длиной 3 секунды» состоит из тысяч различных частот. Амплитуды значений частот> 2000 очень малы, так как большинство этих частот, вероятно, вызвано шумом.Мы наносим на график частоты в диапазоне от 0 до 8 кГц, потому что наш сигнал был дискретизирован с частотой дискретизации 16k, и согласно теореме дискретизации Найквиста он должен иметь только частоты ≤ 8000 Гц (16000/2).

Сильные частоты находятся в диапазоне от 0 до 1 кГц только потому, что этот аудиоклип был человеческой речью. Мы знаем, что в типичной человеческой речи этот диапазон частот доминирует.

Структура прогнозирования с функцией частотно-временной локализации для обнаружения начала сейсмических событий

Abstract

Обнаружение начала P-волны в сейсмических сигналах имеет жизненно важное значение для сейсмологов, поскольку оно не только важно для разработки систем раннего предупреждения, но также помогает в оценке параметров сейсмического источника.Все существующие методы обнаружения начала P-волны основаны на сочетании статистической обработки сигналов и идей моделирования временных рядов. Однако эти методы неадекватно отражают некоторые передовые идеи, существующие в литературе по обнаружению неисправностей, особенно те, которые основаны на прогнозной аналитике. В сочетании с методом частотно-временной (t-f) / временной спектральной локализации эффективность таких методов значительно повышается. В этой работе предлагается новый автоматический детектор и сборщик P-волн в реальном времени в структуре прогнозирования с функцией частотно-временной локализации.Предлагаемый подход предоставляет широкий набор возможностей для точного обнаружения начала P-волны, особенно в условиях низкого отношения сигнал / шум (SNR), которых не могут достичь все существующие методы. Основная идея состоит в том, чтобы отслеживать разницу в квадратах величин предсказаний на один шаг вперед и измерений в частотно-временных диапазонах со статистически определенным порогом. Предлагаемая структура по существу вмещает любую подходящую методологию прогнозирования и частотно-временное преобразование.Мы демонстрируем предлагаемую структуру путем развертывания моделей авторегрессивного интегрированного скользящего среднего (ARIMA) для прогнозов и хорошо известного преобразования дискретных вейвлет-пакетов с максимальным перекрытием (MODWPT) для проекции измерений t-f. Возможности и эффективность предложенного метода, особенно в обнаружении P-волн, встроенных в измерения с низким SNR, проиллюстрированы на синтетическом наборе данных и 200 наборах данных в реальном времени, охватывающих четыре различных географических региона. Сравнение с тремя широко используемыми детекторами, а именно STA / LTA, AIC и DWT-AIC, показывает улучшенную скорость обнаружения событий с низким SNR, лучшую точность обнаружения и выбора, снижение частоты ложных тревог и устойчивость к выбросам в данных.В частности, предлагаемый метод дает уровень обнаружения 89% и уровень ложных тревог 11,11%, что значительно лучше, чем у существующих методов.

Образец цитирования: Аггарвал К., Мухопадхья С., Тангирала А.К. (2021) Структура прогнозирования с функцией частотно-временной локализации для обнаружения начала сейсмических событий. PLoS ONE 16 (4): e0250008. https://doi.org/10.1371/journal.pone.0250008

Редактор: Хао Сунь, Северо-Восточный университет, США

Поступила: 26.10.2020; Одобрена: 29 марта 2021 г .; Опубликован: 22 апреля 2021 г.

Авторские права: © 2021 Aggarwal et al.Это статья в открытом доступе, распространяемая в соответствии с условиями лицензии Creative Commons Attribution License, которая разрешает неограниченное использование, распространение и воспроизведение на любом носителе при условии указания автора и источника.

Доступность данных: Все файлы данных доступны через веб-службы IRIS (URL https://service.iris.edu/.), Включая сетевой IU и станции ANMO, MAJO, ANTO и TSUM.

Финансирование: Авторы получили частичное финансирование этой работы от Совета по исследованиям в области ядерных наук (BRNS).Дополнительного внешнего финансирования для этого исследования получено не было.

Конкурирующие интересы: Авторы заявили, что конкурирующих интересов не существует.

Введение

Точное обнаружение и определение P-волн - наиболее важный шаг в разработке систем раннего предупреждения (EWS). Естественно, эта тема вызвала большой интерес у сейсмологов, поскольку существует огромное количество литературы, охватывающей шестидесятилетнюю историю [1–6]. Среди репертуара существующих методов лишь некоторые из них широко используются [2, 7] из-за их простоты и разумного успеха.В принципе, требования к любому детектору / сборщику: (i) точность обнаружения, (ii) низкий уровень ложных тревог, (iii) устойчивость к выбросам, (iv) способность обнаруживать сейсмограммы низкого качества, (v) способность для обработки недостающих данных и, наконец, (vi) простота реализации или простота. Нельзя ожидать, что ни один из существующих или перспективных методов удовлетворяет всем заявленным требованиям, поскольку они противоречат друг другу. Например, можно пожертвовать простотой ради точности и надежностью ради точности, особенно в условиях низкого отношения сигнал / шум (SNR).Кроме того, ожидается, что любой метод в максимально возможной степени учитывает дополнительные аспекты, связанные с процессами и измерениями, такие как (i) слабый и возникающий характер волны, (ii) форма P-волны изменяется в зависимости от источника и географическое положение, (iii) маскирование P-волны естественным или искусственным шумом, и (iv) влияние полосы пропускания прибора, шума, дисперсии и т. д. на зарегистрированный сигнал (измерение). Возможно, удастся разработать метод, который может обслуживать P-волны разной силы, меняющиеся шумовые условия и географические регионы; однако метод может быть адаптирован для конкретного прибора.Основная мотивация для этой работы заключается в том, что существующие методы не обязательно эффективны в условиях низкого отношения сигнал / шум, поскольку мы рассуждаем путем критического обзора преобладающей литературы ниже, а также предлагаем некоторые полезные точки зрения. Более того, существует обширная литература о методах обнаружения неисправностей, особенно тех, которые основаны на прогнозирующих моделях, для инженерных систем [8], которые потенциально могут быть адаптированы для расширенного обнаружения начала P-волны. Этот путь практически не исследовался в литературе по анализу сейсмических данных.В этой статье мы представляем новую систему прогнозирования с возможностью частотно-временной локализации для обнаружения P-волн путем объединения основанных на модели методов обнаружения неисправностей в технологическом проектировании и основанных на проекции методов анализа сигналов.

Предлагаемая структура не обязательно ограничивается обнаружением сейсмических событий, но является довольно общей в том смысле, что ее можно использовать для обнаружения неисправностей в других областях. Объем данной презентации ограничен одноканальными сейсмическими сигналами.Положительным ответвлением предлагаемой структуры является то, что она облегчает реконструкцию зубца P после его обнаружения. Спешим добавить, что эта идея находится на начальной стадии и требует достаточной проработки и проверки, выходящей за рамки данной работы. Мы предполагаем два потенциальных преимущества полностью разработанного алгоритма реконструкции P-зубца. Во-первых, реконструированный или оцененный (отфильтрованный) зубец P можно затем использовать для построения библиотеки математических моделей для зубца P. Разработанную эмпирическую модель P-волны можно использовать для обнаружения начала с помощью фильтров Калмана или байесовских методов, в которых несколько скрытых переменных (или состояний) соответствуют динамике P-волны.Восстановленная P-волна также может использоваться в так называемом сопоставлении сценариев, где входящая P-волна может быть сопоставлена ​​со словарем исторически реконструированных P-волн для оценки параметров источника без использования информации о S-волнах. Это исследовательские идеи, которые составляют темы для будущих исследований. Мы вернемся к описанию основных характеристик предлагаемой системы прогнозирования в следующем обсуждении.

Основная идея предлагаемой структуры состоит в том, чтобы отслеживать разницу квадратов абсолютной величины между данными и прогнозами на один шаг вперед в области t-f с помощью порога, управляемого данными.Работа в структуре прогнозирования позволяет пользователю выделить событие даже в условиях низкого отношения сигнал / шум, в то время как инструмент t-f предлагает локализацию в полосах частот на желаемых временных интервалах. Локализацию в плоскости t-f можно рассматривать как функцию увеличения, которая позволяет пользователю увеличивать интересующие полосы частот, тем самым значительно улучшая SNR, поскольку отброшенные полосы частот уносят значительное количество шума. Основные преимущества этой работы по сравнению с существующими методами tf состоят в том, что она (i) соизмерима с шумовыми характеристиками, что приводит к минимальной чувствительности к выбросам или робастному обнаружению , (ii) предлагает более гибкий выбор полосы частот путем декомпозиции как более низкие, так и более высокие частоты на каждом уровне, что приводит к точному обнаружению , и (iii) это позволяет пользователю отбросить шум в нежелательных tf-диапазонах, что приводит к улучшенному SNR .Здесь уместно сделать важное замечание о преобладающем определении отношения сигнал / шум. Однако это консервативный показатель, который хорошо подходит для методов временной области или тех, которые работают со всеми частотными диапазонами. Когда речь идет о методах на основе частотно-временной локализации, ограниченное по полосе отношение сигнал / шум, определяемое как отношение энергии коэффициентов tf сигнала к энергии коэффициентов шума tf в желаемой полосе частот, лучше подходит для понимания их эффективность. В силу своего определения SNR с ограниченной полосой частот может быть высоким, даже если стандартное SNR очень низкое.Этот аспект по существу объясняет, почему методы t-f-локализации могут превосходить чистые методы временной или частотной области.

Предлагаемая структура демонстрируется путем развертывания моделей авторегрессивного интегрированного скользящего среднего (ARIMA) для прогнозов и дискретного вейвлет-пакетного преобразования с максимальным перекрытием (MODWPT) для t-f-разложения данных на игрушечном примере и 200 наборов сейсмических данных в реальном времени. MODWPT обеспечивает двустороннюю декомпозицию, что делает его лучше других методов локализации t-f.Сравнительный анализ с методами STA / LTA, AIC и WPT-AIC представлен, чтобы продемонстрировать превосходство предложенного метода. Предварительные идеи конкретной применяемой методологии были представлены на конференции [9], где мы продемонстрировали ее применимость, не ссылаясь на какие-либо общие рамки или оценку P-волны с использованием восстановленного сигнала. Более того, [9] не предписывает метод выбора диапазона t-f и исключает какой-либо сравнительный анализ с существующими методами для различных наборов данных с различными сценариями SNR.

Остальная часть статьи организована следующим образом. Сначала мы рассмотрим существующую литературу по обнаружению и выбору начала P-зубца. Затем мы описываем предлагаемую структуру, лежащую в основе методологию и участвуем в кратком обсуждении важнейших параметров, определяемых пользователем, которые определяют эффективность всего алгоритма. Затем мы рассмотрим пример, включающий синтетический процесс, чтобы продемонстрировать предлагаемую структуру. Затем следует широкое применение метода для обнаружения продольных волн в 200 наборах данных с разных станций, которые характеризуются диапазоном отношения сигнал / шум и магнитуды землетрясений.Статья завершается рефлексивным резюме работы и направлениями будущих исследований.

Обзор литературы

Большинство существующих детекторов / сборщиков основаны на отслеживании резких изменений характеристик сигнала, таких как амплитуда, энергия, частота, статистика более высокого порядка и т. Д., Либо в исходной области, либо в преобразованной области по прибытии. сейсмического события [1–4, 10–14]. Среди этих методов широко используются STA / LTA (краткосрочное среднее / долгосрочное среднее) [2] и его варианты [15, 16] для упрощения вычислений и онлайн-реализации.Принцип работы методов STA / LTA основан на сравнении отношения энергий в коротком и длинном окне с порогом. Эти методы приводят к высокому уровню ложных тревог из-за того, как они отделяют шум от сигнала. Это неотъемлемый недостаток всех методов измерения во временной области из-за незнания частотного содержания P-волны. Более того, поскольку используются только свойства времени, эти методы чувствительны к выбросам. Присущие методам временной области ограничения вдохновили на разработку нескольких методов частотной области, в которых частота или энергия используются в качестве функции для обнаружения начала P-волны [1, 3, 12].Однако на практике эти методы не получили широкого внимания, поскольку они используют весь частотный диапазон (от 0 до частоты Найквиста), тем самым не обеспечивая каких-либо конкретных преимуществ перед их аналогами во временной области. Истинная выгода достигается только путем объединения достоинств работы в обеих областях. Таким образом, исследователи разработали частотно-временные детекторы, учитывающие временные свойства и частотную информацию сейсмического сигнала. Возможности в смешанной области, особенно с использованием инструментов время-частота (tf), таких как непрерывное и дискретное вейвлет-преобразование (CWT, DWT) [13, 14], кратковременное преобразование Фурье (STFT) [5] и разложение по эмпирическим модам (EMD). ) [6], широко использовались в этой связи.Общая идея, лежащая в основе этих методов, включает проецирование данных в область t-f (или временную шкалу) и поиск функции либо в смешанной области, либо в восстановленном сигнале. Последние достижения в этих методах сочетают в себе преимущества методов временной области с инструментами t-f [7, 17, 18] для повышения скорости обнаружения сейсмических сигналов с низким отношением сигнал / шум. Независимо от того, как инструменты t-f использовались в сейсмической литературе, их использование включало только разложение низкочастотного содержимого (приближения) в каждом масштабе, тем самым ограничивая локализацию низкими частотными диапазонами.Это одностороннее разложение не всегда может содержать информацию о P-зубцах.

В начале 1990-х годов были разработаны методы на основе шаблонов для обнаружения слабых событий, встроенных в шум [19–22]. Эти методы сравнивают сходство между сигналом землетрясения и структурой события (шаблоном). [23] предложили метод обнаружения локальных событий, встроенных в локальный стационарный фоновый шум. Большинство методов, основанных на паттернах, либо используют фиксированный шаблон P-волны, либо предполагают, что рассматриваемый сигнал имеет определенные особенности.Более того, различные другие факторы, такие как сложные механизмы источников и зависимость частоты P-волн от местоположения источника и станции, ограничивают применимость этих детекторов к исключительным ситуациям, таким как афтершоки и повторяющиеся источники.

В последние годы были предложены детекторы, основанные на машинном обучении / глубоком обучении (ML / DL) [24, 25]. Метод [24] предоставляет вероятности, связанные с существованием землетрясения и двух разных сейсмических фаз для каждой временной точки, с помощью кодеров, которые по сути фиксируют временные зависимости в сейсмических данных.Декодеры состоят из тщательно разработанного набора сетевых моделей глубокого обучения, состоящих из десятков слоев и около 372000 настраиваемых параметров для обнаружения и выбора прихода сейсмической фазы. Метод, предложенный [25], использует капсульную нейронную сеть (CapsNet) для выбора прихода P-волны. CapsNet состоит из трех основных уровней для классификации данных как шума и сигнала землетрясения с последующим извлечением времени прихода P-волны. В обеих работах показано, что обученные сложные модели обеспечивают высокоточное обнаружение и выборку; однако подходы включают не только обширные данные (в том смысле, что для обучения моделей требуются огромные объемы данных), но также включают проектирование очень сложной архитектуры модели.Наконец, несмотря на их высокий уровень сложности, построение этих моделей может привести к неприемлемому уровню ложных тревог. Средство, предложенное в [24], заключается в явном включении спектральных характеристик сейсмических сигналов.

Очевидно, что существующую литературу по обнаружению начала P-волны можно классифицировать несколькими различными способами в зависимости от принятых точек зрения. Несколько полезных перспектив можно получить, выбрав классификацию литературы на основе принятого подхода, а именно: (i) методы, основанные на признаках, (ii) методы, основанные на распознавании образов, и (iii) методы, основанные на моделях.Большинство существующих методов обнаружения основаны на признаках, в то время как подходы, основанные на шаблонах и моделях, используются лишь в небольшом количестве методов. Независимо от принятого подхода реализация может быть непосредственно на необработанных данных (во временной области), в области преобразования (обычно в частотной области) или в смешанной (например, частотно-временной) области. Преимущество работы в смешанной области состоит в том, что характеристики сигнала могут быть захвачены одновременно во временном интервале и полосе частот. Следовательно, поскольку сейсмический сигнал является многомасштабным (каждый масштаб связан с полосой частот), P-волна лучше выделяется в смешанной области по сравнению с сигналом временной области, особенно для условий низкого отношения сигнал / шум.Более того, поскольку характеристики сигнала сконцентрированы в относительно меньшей области (более низкие диапазоны частот), нежелательный шум в более высоких частотных диапазонах можно игнорировать, что приводит к улучшенному обнаружению. Таким образом, очевидно, что реализации во временной области являются наиболее широко используемыми, за ними следуют относительно более свежие работы в смешанной области [13, 17], в то время как реализациям в области преобразования уделяется очень мало внимания. В классе реализаций смешанной области существует подмножество методов, которые работают с проекциями (на выбранный набор базисных функций или атомов, таких как вейвлеты) или коэффициентов , в то время как оставшееся подмножество использует реконструированных или отфильтровал сигналов, где конкретное преобразование используется по существу как фильтр для выбора известных компонентов сейсмических измерений.Существенным преимуществом подходов, основанных на проекции, перед подходами, основанными на реконструкции, является то, что желаемые характеристики в сигнале сильно локализованы в области проекции по сравнению с временным доменом (восстановленный сигнал). Более того, коэффициенты проекции не так сильно коррелированы, как восстановленный сигнал, что приводит к сравнительно разреженному представлению в области проекции.

Методы, основанные на моделях, предлагают привилегию использования прогнозного подхода к проблеме обнаружения, чего нет в методах без моделей.Эти подходы широко использовались в технологическом проектировании, особенно для обнаружения неисправностей [8], идеи из которых, однако, еще предстоит полностью использовать при анализе сейсмических данных. Несколько методов, широко известных как сборщики AR-AIC, появились в конце 1980-х и 1990-х годах, построили модели временных рядов и отслеживали соответствующий критерий Akaike-Information (AIC) [26–28]. Сборщики AR-AIC превосходят детекторы STA / LTA; однако эти методы предполагают, что шум и событие являются локально стационарными, и не обеспечивают надлежащего обоснования для использования моделей AR.Более того, технически нецелесообразно моделировать P-волну как случайный процесс. В вышеупомянутых работах общая тенденция состоит в том, чтобы исследовать AIC, а не прогнозы, тем самым не используя в полной мере преимущества подхода, основанного на модели. Существенным преимуществом работы с прогнозирующими подходами является то, что измерения раскладываются на прогнозируемый компонент и ошибку прогнозирования (что не объясняется моделью). Первым следствием этого разложения является то, что ошибка предсказания имеет меньшую дисперсию, чем ошибка измерения - степень, в которой она меньше, зависит от предсказуемой составляющей.Чем выше сила предсказуемого компонента в измерении, тем меньше дисперсия ошибки предсказания. Во-вторых, любая особенность, которая не содержится в исторической записи, появится в ошибке предсказания вместе с непредсказуемой частью измерения. Относительно легче обнаружить «новые» сигналы в ошибках прогнозирования, чем при исходном измерении, поскольку отношение сигнал / шум значительно увеличивается в области ошибок прогнозирования. Таким образом, прогнозный подход, естественно, лучше подходит для обработки измерений с низким SNR, чем методы, которые не входят в структуру прогнозирования.Излишне говорить, что качество метода, основанного на прогнозировании, зависит от качества модели. С этой целью авторы данной работы в отдельном исследовании разработали систематическую методологию построения статистически подходящих моделей временных рядов для сейсмического шума [29]. Эта работа по существу основана на разработанных моделях и использует преимущества модели прогнозирования, особенно для обработки ситуаций с низким отношением сигнал / шум.

Предлагаемая структура

В этом разделе представлены подробности предлагаемой структуры прогнозирования для точного обнаружения и захвата P-волны в сейсмическом сигнале с использованием данных вертикального канала.Предлагаемая структура по существу состоит из двух частей, как показано на рис. 1, одна из которых обеспечивает точное обнаружение, а другая отвечает за точное определение P-волны. Прогностические модели разрабатываются во временной области, в то время как обнаружение выполняется в области t-f с помощью инструмента преобразования t-f. Принцип обнаружения с использованием предлагаемого метода заключается в следующем. Для заданного временного окна оцененная модель шума приведет к оптимальным прогнозам, если окно содержит фоновый шум.Напротив, прогнозы будут плохими, если окно содержит данные о событии. Кроме того, как следствие работы с прогнозами в области t-f, по прибытии сейсмического события происходит резкое изменение разности квадратов абсолютной величины коэффициентов t-f. Это изменение выделяется с помощью порога, предупреждающего об обнаружении события. Пост-обнаружение, выбор (определение времени начала события) осуществляется путем ранжирования выделенных диапазонов t-f с учетом того, что разница в квадрате абсолютной величины более заметна в определенных диапазонах t-f, относящихся к частоте P-волны, чем в других диапазонах.Такое ранжирование не только облегчает выбор, но и восстановление сигнатуры P-волны, которая, как упоминалось выше, является новой и потенциально полезной на продвинутых этапах анализа сейсмических данных. Предлагаемая структура графически изображена на рис. 1. Эта схема описывает шаги, реализованные в окне данных.

Сначала предположим, что N наблюдений (что соответствует длительности T = NT _с с, где T _с - интервал дискретизации) сейсмического сигнала y [ k ] доступны онлайн, где N - это параметр, определяемый пользователем (подробности см. Ниже).Процедура состоит из следующих шагов:

1. Построить окно данных
   Состояние в данный момент k = N + ( n - 1) S , где S - определяемый пользователем скользящий параметр, а n - это индекс окна (изначально установлен на 1), построить окно из N прошлых наблюдений следующим образом: (1) где w _n - вектор размером N × 1.
2. Вычислить прогнозы на один шаг вперед
   Используя модель временных рядов, разработанную в автономном режиме, вычислить прогнозы наблюдений на один шаг вперед в окне,
3. Данные проекта и прогнозы с использованием инструмента tf
   Разложите как входящие данные, w _n [ k ], так и прогнозы, [ k ∣ k - 1] в tf domain up до желаемого уровня L с помощью подходящего инструмента tf.На каждом уровне l ( l = 1, 2, ⋯, L ) коэффициенты tf обозначаются как C ( l , ω _{c , i} ): { C ( l , ω _{c , i} , k )}, где на уровне l , C ( l , ω _{c i} ) - 2 ^l × N матрица, ω _{c , i} представляет центральную частоту i ^th ( i = 1, ⋯ , B _l ) частотный диапазон, а k представляет момент времени.Обратите внимание, что максимальный индекс полосы частот на каждом уровне l составляет B _l = 2 ^l .
4. Вычислить квадрат абсолютной величины в диапазонах t-f
   Квадрат абсолютной величины проекций данных и прогнозов в диапазоне i ^th t-f на каждом уровне l определяется как: (2) (3) где и - проекции сигнала и прогнозов соответственно, а ω _{c , i} - центральная частота, как определено ранее.
5. Вычислить среднее абсолютное отклонение (μAD)
   В окне n ^th w _n [ k ], среднее абсолютное отклонение разницы в квадратах абсолютных величин между проекциями данных и прогнозы в диапазоне i ^th tf на каждом уровне l определяется как: (4) где разница, E _d , определяется как (5) мкАД , как известно, является смещенной оценкой стандартного отклонения, поэтому мы работаем со скорректированным смещением мкАД , (6) где, К = 1.25 - это поправочный коэффициент, который численно определяется для случайной величины E _d посредством моделирования Монте-Карло (см. Приложение S1 в файле S1). Обратите внимание, что E _d ( l , ω _{c , i} ) приблизительно следует гамма-распределению, которое определяется эмпирическим путем.
6. Сравните μAD в выбранных диапазонах t-f с соответствующими пороговыми значениями , чтобы обнаружить резкие изменения.
   Пусть δ _{l , i} будет вектором B _l порогов для фонового шума в соответствующих диапазонах t-f. Если окно, w _n [ k ] содержит только сейсмический шум, тогда μAD _{l , i} ( n ) в tf диапазонах не будет изменяться, поскольку k варьируется, однако, μAD _{l , i} ( n ) резко увеличивается в определенных tf диапазонах по достижении P-волны в w _n [ к ].
7. Принять решение
   Отметить те диапазоны, для которых μAD _{l , i} ( n )> δ _{l ,24 i} и для всех диапазонов уровни.
   • Нет обнаружения : в случае, если событие не обнаружено, установите флаг обнаружения на 0, сдвиньте окно с длиной скольжения ( S ) и перейдите к шагу 8. Выбор S основан на различных факторах. такие как SNR, частота дискретизации данных и тип сейсмического события и т. д.
   • Обнаружение : При обнаружении события выполните следующие действия.
     1. Установите флаг обнаружения на 1.
     2. Точно выберите начало события, уменьшив длину окна и повторив шаги для обнаруженного сегмента данных. Новая длина рабочего окна в обнаруженном сегменте также зависит от SNR, частоты дискретизации и т. Д. Данных. Обычно для выбора события в обнаруженном сегменте используется окно длительностью 1-2 секунды, потому что P-волна является сигналом короткой продолжительности.
     3. Выберите «лучшие» диапазоны t-f. Полосы, которые выделены на этапе 6 (по прибытии P-волны), ранжируются в порядке возрастания времени начала обнаружения и выбираются для , выбирая начало P-волны. Динамический выбор представляющих интерес пакетов (диапазонов) в отличие от работы с заранее определенным набором диапазонов из анализа исторических данных делает подход адаптивным к форме P-волны, местоположению источника-станции и т. Д. Кроме того, поскольку выбранный tf диапазоны обычно охватывают частоту P-волны, их можно использовать для восстановления сигнатуры P-волны во временной области, которая, в свою очередь, может использоваться как минимум для двух различных расширенных анализов сейсмических данных (см. раздел Введение для краткое описание).Мы считаем, что это положительный результат предлагаемой методики.
8. Повторите шаги выше для онлайн-обнаружения сейсмического события.

Эффективность предлагаемого метода зависит от различных параметров или переменных. Сводка с кратким описанием и оптимальными значениями (для параметров, определяемых пользователем) этих параметров представлена ​​в таблице 1. Оптимальные значения параметров, управляемых данными, варьируются в зависимости от наборов данных и, следовательно, представлены в таблице как DD (зависит от данных).Влияние этих параметров на производительность предложенного алгоритма обсуждается позже в следующих разделах.

Эффективность предлагаемой структуры демонстрируется с использованием широко используемой модели временных рядов, известной как модель ARIMA для целей прогнозирования, и хорошо зарекомендовавшего себя инструмента tf, а именно MODWPT на основе вейвлет-преобразования в качестве инструмента tf для декомпозиции данные в tf диапазонах. Модели ARIMA - это линейные модели временных рядов, которые, по сути, улавливают интегрирующие эффекты путем разработки моделей ARMA на основе разностных рядов [30].Основное уравнение модели ARIMA ( p , d , m ) определяется следующим образом: (7) где, q ⁻¹ - оператор обратного сдвига, ϕ _i и θ _j - коэффициенты AR и MA порядка p и m соответственно, d - это степень разности, а e [ k ] - гауссовский белый шум с нулевым средним (не коррелированный по времени) дисперсии.Оценка моделей ARIMA включает идентификацию порядков моделей p , d , q , где d - это степень разности, а p и q представляет порядок коэффициентов AR и MA, p + q параметры модели и дисперсия движущей силы. Неизвестные оцениваются с использованием алгоритма оценки максимального правдоподобия.

MODWPT - это обобщение вейвлет-преобразования, в котором сигнал разлагается на низкочастотные и высокочастотные полосы, а низкочастотные (приближения) и высокочастотные (детали) коэффициенты дополнительно разлагаются на поддиапазоны на каждом уровне [ 31].На рис. 2 показана схема MODWPT, где каждый блок называется вейвлет-пакетом (также называемым узлом). Каждый пакет соответствует определенной полосе частот. Отображение частот для пакетов MODWPT до уровня 4 приведено в таблице 2 для частоты дискретизации 20 Гц. Диапазон частот, охватываемый каждой полосой для другой частоты дискретизации F _с , может быть пересчитан прямым способом как 0- F _с /4, F _с /4 - F _с /2 на уровне 1 и т. Д.

Рис. 2. Схема разложения MODWPT до уровня 4.

«A» и «D» относятся к аппроксимации и детализации соответственно. Целое число в правом верхнем углу каждого поля указывает номер пакета в порядке возрастания частоты.

https://doi.org/10.1371/journal.pone.0250008.g002

Здесь уместно сделать замечание о требованиях к данным и сложности модели для выбранного класса прогнозной модели. Около 10 минут данных достаточно, чтобы получить достаточно хорошую оценку модели.Во-вторых, количество настраиваемых параметров ограничено примерно 20. Таким образом, как с точки зрения требований к данным, так и с точки зрения сложности модели, выбранная модель на несколько порядков ниже по сравнению с методами на основе DL. Это дает реальную возможность обновлять модель по мере получения потоковых данных. В-третьих, данные не должны подвергаться маркировке и другим этапам предварительной обработки, как того требуют преобладающие модели DL.

Результаты и обсуждения

В этом разделе эффективность предложенного метода проиллюстрирована с помощью синтетических данных с переменным SNR и 200 наборов сейсмических данных в реальном времени, характеризующихся диапазоном SNR и магнитудой землетрясения.

Применение к синтетическим наборам данных

Основная цель этого раздела - проиллюстрировать применение предложенной структуры для обнаружения кратковременного сигнала для изменения SNR с помощью синтетических данных.

Генерация данных.

Синтетические данные y [ k ]: { k = 1, 2,…, 50000} могут быть представлены как (8) где s [ k ] представляет желаемый кратковременный сигнал, генерируемый с использованием экспоненциально затухающей синусоидальной волны, а v [ k ] представляет цветной шум.Сигнал с [ k ] задается (9) где f ₀ фиксируется на частоте 1,8 Гц, сигнал s [ k ] дискретизируется при 20 отсчетах в секунду (sps), а значения a и b изменяются для изменения отношения сигнал / шум. . Подробная информация о различных значениях a и b вместе с SNR и SNR с ограниченным диапазоном суммирована в таблице 3. Шумовая последовательность v [ k ] генерируется с использованием реалистичной модели временных рядов, разработанной для реальных -временной сейсмический шум от станции ЦУМ, Намибия, Африка.Процесс генерации данных для v [ k ] определяется как (10) (11) где e [ k ] - гауссовский белый шум с нулевым средним с дисперсией σ ² = 155,78.

Результаты для синтетических данных.

Учитывая измерения y [ k ], метод направлен на точное обнаружение и определение начала сигнала s [ k ]. Реализация предлагаемой структуры подробно проиллюстрирована для случая 1 данных, а результаты суммированы для остальных случаев.Данные случая 1 (SNR = 0,021) показаны на рисунке 3. Начальные 10000 точек данных используются для оценки модели прогнозирующего ARIMA (4, 1, 8) и вычисления порога в каждом пакете. Используя скользящее окно из 240 отсчетов со скользящим шагом из 10 отсчетов, оба значения w _n [ k ] и разлагаются в частотно-временной области с использованием вейвлетов Добеши 4 (дБ4) через MODWPT. μAD разности квадратов абсолютных величин коэффициентов MODWPT w _n [ k ] и во всех пакетах сравнивается с порогом в соответствующих пакетах.По прибытии сигнала s [ k ] выделяются определенные диапазоны t-f (пакеты 8, 18, 17 и 30 для данных случая 1). На рис. 4 показаны выбранные пакеты в порядке возрастания начала обнаружения. Пакеты, которые обнаруживают начало s [ k ] с минимальными выборками s [ k ] в w _n [ k ], получают более высокий приоритет. Также можно заметить, что, когда движущееся окно не содержит никаких событий, никакие пакеты не выделяются (представлен значением 0 на верхнем графике рис. 4).Наличие 1 указывает на выделенные пакеты. µAD в разных пакетах вместе с порогом показано на рис. 5. Для целей выбора в обнаруженном сегменте для выбранных пакетов используется скользящее окно из 20 выборок со сдвигом в 1 отсчет. Для данных случая 1 метод выбирает начало с [ k ] с ошибкой в ​​3 отсчета.

Рис. 4. Выбор пакета.

График вверху отображает выбранные пакеты на лету на основе ранжирования выделенных пакетов.Ось Y представляет время начала окна в ранжированном порядке (сверху вниз). Наличие 1 указывает на обнаружение, а 0 означает отсутствие обнаружения. Продолжительность выделенных пакетов показана на нижнем графике, где ось X представляет начало рабочего окна.

https://doi.org/10.1371/journal.pone.0250008.g004

Рис. 5. μAD в выделенных пакетах.

В некоторых пакетах (30, 14 и 17) происходит внезапное увеличение мкАД , в то время как в других пакетах (16 показано на рисунке, но оно сохраняется для остальных пакетов) мкАД всегда ниже порога.

https://doi.org/10.1371/journal.pone.0250008.g005

На рис. 6 показан восстановленный сигнал с использованием выбранных пакетов. Для реконструкции используются данные от k = 19500 до k = 20500. Начало сигнала s [ k ] ясно видно в восстановленном сигнале даже для случая низкого отношения сигнал / шум. Основная цель восстановления сигнала - получить математическую модель для сигнала s [ k ] на основе измерений.Это может быть чрезвычайно полезно при получении модели P-волны, которая иначе отсутствует в литературе.

Точно так же мы применили предложенный метод к остальным четырем случаям, и было замечено, что метод обнаруживает начало s [ k ] даже для случаев чрезвычайно низкого отношения сигнал / шум. Причина точного обнаружения, особенно для сценариев с низким SNR, заключается в том, что сигнал сильно локализован в области t-f. Кроме того, ограниченное по полосе SNR выше стандартного SNR для всех случаев, указанных в таблице 3.Последний рассматривает полосу частот от 0 до частоты Найквиста (в данном случае 10 Гц), в то время как первая охватывает частоты в желаемой полосе (от 1,25 до 2,5 Гц). Этим объясняется улучшенная производительность предложенного метода даже для случаев чрезвычайно низкого отношения сигнал / шум. Из рисунка 7 также видно, что с увеличением SNR выделяется больше пакетов.

Приложение к сейсмическим данным в реальном времени

Способность и эффективность предложенной схемы для обнаружения начала P-волны проиллюстрирована с использованием 200 наборов сейсмических данных в реальном времени различных магнитуд и отношения сигнал / шум (SNR).Данные собираются с четырех разных станций: ANMO (Нью-Мексико, США), ANTO (Турция), MAJO (Мацусиро, Япония) и TSUM (Намибия, Африка), и они находятся в свободном доступе на Incorporated Research Institutions for Seismology (IRIS). Ссылка на веб-сайт, с которого можно напрямую загрузить наборы данных, предоставляется в S2 Data в S1 File. Из 200 наборов данных 173 содержат сейсмические события, в то время как 27 не содержат событий, т. Е. Не содержат никаких сейсмических событий (шума). Величина наборов данных подразделяется на четыре категории: (i) Mag ≤2.5, (ii) 2,5 6, чтобы оценить эффективность предлагаемого метода. Подробности всех наборов данных сведены в Таблицу 4, где SNR _BL означает SNR с ограничением полосы частот. Для наборов данных в реальном времени SNR _BL - это отношение энергии коэффициентов t-f сигнала в обнаруженном сегменте к энергии коэффициентов шума t-f в выделенных диапазонах t-f. Мы также сравнили производительность предлагаемой структуры с STA / LTA, сборщиком AIC и сборщиком DWT-AIC.Время, указанное на веб-сайте IRIS, считается эталонным.

Данные вертикального канала с низкой магнитудой (<2,5) и низким SNR (<2), полученными на разных станциях, показаны на рисунке 8 (a) (SNR = -0,7), рисунке 8 (d) (SNR = 1,5) и рисунке 8. (г) (SNR = 0,001). Фиг.8 (b), 8 (e) и 8 (h) изображают среднее абсолютное отклонение, соответствующее пакетам 8, 35 и 31 соответственно. Как видно из рисунков 8 (c), 8 (f) и 8 (i) (увеличенные снимки данных), алгоритм выбирает события с низкой магнитудой и низким SNR с высокой точностью (менее 0.2 секунды) по сравнению со временем начала события, указанным на веб-сайте IRIS.

Рис. 8. Результаты обнаружения событий для наборов данных с низким SNR.

Графики (a), (d), (g) показывают данные вертикального канала со станций MAJO, ANTO и ANMO соответственно, где вертикальная черная сплошная линия указывает начало истинного события, о котором сообщается на веб-сайте IRIS, графики ( b), (e), (h) изображает соответствующие μ AD в выбранных пакетах. Сплошная горизонтальная линия на средних графиках - это пороговое значение для соответствующих пакетов.Увеличенные снимки соответствующих данных с выбранными событиями показаны на графиках (c), (f) и (i), где красные вертикальные линии указывают время, в которое предлагаемый метод выбирает событие. Графики (c), (f), (i) показывают увеличенный снимок данных с выбранными событиями.

https://doi.org/10.1371/journal.pone.0250008.g008

Для целей обнаружения и отбора исходные 10-минутные данные используются для разработки прогнозных моделей и вычисления порога в выбранных пакетах. Фоновый шум на каждой станции моделируется с использованием моделей ARIMA подходящего порядка.Например, шум в ANMO моделируется с использованием ARIMA (5, 1, 3), ANTO с использованием ARIMA (4, 1, 6), MAJO с использованием ARIMA (6, 1, 5) и TSUM с использованием ARIMA (4, 1, 8). ) модель. И данные, и прогнозы на один шаг вперед раскладываются в частотно-временной (t-f) области с использованием вейвлета Добеши 4 (db4) до уровня 4 для данных 20 выборок в секунду (sps) и уровня 5 для данных 40 sps. Для большинства наборов данных пакеты 8, 9, 16, 17, 18, 19, 21 выбираются для данных 20 sps. В дополнение к пакетам, выбранным для данных 20 sps, пакеты 27, 31, 32, 32, 33, 35 также выбираются для данных 40 sps.Скользящее окно ( w _n [ k ]) длиной 240 отсчетов с скользящей длиной ( S ) 5 отсчетов используется для обнаружения события. Для точного выбора в обнаруженном сегменте используется окно в 1 секунду с длиной скольжения в 1 образец.

Сравнительное исследование обнаруженных событий с истинным началом проводится на всех 200 наборах данных для проверки надежности предлагаемого метода. На рис. 9 показано, что точность обнаружения увеличивается с увеличением отношения сигнал / шум.На верхнем рисунке изображена ошибка обнаружения в наборах данных разной магнитуды, загруженных со станции ANMO. Число в верхней части каждой полосы представляет ошибку обнаружения в образцах, где положительное число указывает на раннее обнаружение, а отрицательное число указывает на задержку. Цифры, написанные красным цветом, указывают на пропущенные события. Соответствующие SNR показаны на нижнем графике рис. 9. Кроме того, для данных станции ANMO из 42 событий на рис. 9 метод не может обнаружить 4 события (столбцы с номерами красного цвета вверху).Для некоторых наборов данных алгоритм обнаруживает событие немного раньше, несмотря на низкий SNR (<1 дБ). Также проводится сравнительное исследование различных данных SNR для анализа точности предложенного алгоритма для разных SNR. Скорость обнаружения предлагаемого метода для низкого отношения сигнал / шум (<1 дБ) показана на рисунке 10. Некоторые наборы данных с низкой магнитудой имеют несколько событий в непосредственной близости. Для таких наборов данных алгоритм выбирает более сильное событие среди всех событий (полоса серого цвета на рис. 10). На рис.11 показано, что алгоритм выбирает события с высоким SNR с высокой точностью (<0.02 сек). Для сценариев отсутствия событий (фоновый шум) алгоритм выбирает ложные события в 3 наборах данных из 27, как показано на рис. 11.

Рис 11. Ошибка обнаружения.

Левый график отображает скорость обнаружения предложенного алгоритма для высокого отношения сигнал / шум> 1 дБ. Правый график показывает частоту ложных срабатываний предложенного метода для фонового шума, где красный квадрат указывает на отсутствие обнаружения в шуме, а синий прямоугольник указывает на ложное обнаружение событий в фоновом шуме.

https: // doi.org / 10.1371 / journal.pone.0250008.g011

Чтобы проиллюстрировать важность выбора пакета (диапазон t-f), выбраны данные вертикального канала с более чем одним событием от станции TSUM (mag Ml0.8). Как показано на рис. 12 (b), пакет 16 не может обнаружить какое-либо из событий, пакет 9 (рис. 12 (c)) точно обнаруживает второе событие, пропуская главное событие (представляющее интерес). Однако, как видно на рис. 12 (d), пакет 27 обнаруживает оба события с высокой точностью. Следовательно, если пользователь выбирает неправильные пакеты (диапазоны t-f), алгоритм либо не сможет выбрать событие, либо пропустит его.По сравнению с существующими методами и временем события, указанным на веб-сайте IRIS, алгоритм успешно выбирает событие с чрезвычайно низким SNR и низкой магнитудой с высокой точностью (менее 2,5 с).

Рис. 12. Результаты обнаружения событий малой величины.

Вертикальный канал станции TSUM (a) данные с двумя событиями - сплошная вертикальная черная линия указывает истинное начало интересующего сейсмического события, а пунктирная черная цветная линия указывает второе событие в данных. Графики (b), (c) и (d) отображают μ AD, соответствующие пакетам 9, 16 и 27 соответственно, а график (e) представляет собой увеличенный снимок данных - красная вертикальная линия указывает время, в которое предлагаемый алгоритм выбирает событие с низкой магнитудой.

https://doi.org/10.1371/journal.pone.0250008.g012

Эффективность предлагаемого метода дополнительно оценивается путем сравнения его с широко используемыми детекторами STA / LTA, AIC и сборщиками DWT-AIC. Набор определяемых пользователем параметров, таких как длина окна, выбор вейвлета и т. Д., Регулирует производительность каждого из этих методов. Эти параметры оптимизированы для каждой станции. Для детектора STA / LTA данные сначала фильтруются с использованием фильтра Баттерворта 4 ^{-го порядка} с полосой пропускания 0.2–2 Гц, прежде чем оценивать характеристическую функцию. Длительность окон STA и LTA составляет 0,3 и 12 секунд соответственно. Для сборщика DWT-AIC данные разлагаются до масштаба 7 с использованием вейвлета Добеши 4. Из рис. 12 (e) видно, что как детектор STA / LTA, так и сборщики AIC не могут обнаружить или выбрать событие с низкой величиной и низким SNR, в то время как сборщик DWT-AIC выбирает более поздние фазы (поверхностные волны). Далее, рис. 13 и 14 (а) позволяют сделать вывод, что для событий с магнитудой <2.5, все три существующих метода не могут обнаружить / выбрать начало события. Однако 20% более поздних фаз (поверхностные волны) были обнаружены детектором STA / LTA, 24% были выбраны сборщиком AIC, а 62% - сборщиком DWT-AIC. С другой стороны, 20% вступлений P-волн в событиях с низкой магнитудой выбраны с низкой точностью, а 50% более поздних фаз были обнаружены с использованием предложенного метода.

Скорость обнаружения предлагаемого метода сравнивается с широко используемым детектором STA / LTA, а скорость обнаружения сравнивается с пикерами AIC и DWT-AIC.Ошибки обнаружения и выбора предлагаемого метода и существующих детекторов и сборщиков показаны на рисунках 13 и 14 соответственно.

Для событий с магнитудой от 2,5 до 4 (SNR <1 дБ) STA / LTA не может обнаружить начало P-волны почти во всех наборах данных (рис. 13). STA / LTA обнаруживает приход P-волны только в одном из 61 набора данных, однако было обнаружено около 20% более поздних фаз. Предлагаемый метод, с другой стороны, обнаруживает около 84% событий с точностью ≤2.5 сек. Как показано на рис. 14, широко используемые сборщики также не могут выбрать большинство событий с низкой магнитудой и низким отношением сигнал / шум. Сборщики AIC и DWT-AIC выбирают 3% и 8% прихода P-волны соответственно с точностью менее 5 секунд. Сборщик DWT-AIC выбирает 54% более поздних фаз, в то время как сборщик AIC выбирает только 39%. Предлагаемый метод захватывает 56% прихода продольной волны с высокой точностью (<0,05 с), а захват 33% - с точностью 2,5 с. Предлагаемый метод не позволяет отобрать только 11% пришедших.Для событий более высокой магнитуды (категория 3: 4 6) обнаруживаются и выбираются всеми четырьмя методами с максимальной ошибкой 1,25 секунды. Прибытие P-волны обнаруживается / выбирается точно (с ошибкой 0) в 10 наборах данных из 34 с помощью STA / LTA, 16 с помощью AIC и 22 с помощью сборщика DWT-AIC.С другой стороны, предлагаемый метод точно выбирает приход P-волны в 32 наборах данных.

Мы также сравнили производительность этих методов на основе частоты ложных тревог, т. Е. Обнаружения события при отсутствии события. Таким образом, все три существующих метода и предлагаемый метод реализованы на сейсмическом шуме (данные без событий). 27 наборов данных без событий тщательно отобраны в том смысле, что мы рассмотрели импульсный шум (шум с импульсными всплесками), шум в ночное время (меньше культурной активности) и днем ​​(культурные мероприятия вносят значительный вклад в шум), чтобы изучить функцию устойчивости. предлагаемого каркаса.Из рисунка 15 видно, что предлагаемый метод превосходит существующие методы в том, что он приводит к меньшему количеству ложных срабатываний, чем другие методы.

Таким образом, предлагаемый метод превосходит существующие методы, выделяя 63% приходов P-волн с высокой точностью (менее 0,05 с), при этом обнаруживая 27,6% приходов приходов с точностью менее 2,5 с. В таблице 5 приведены сведения о точности обнаружения / выбора и частоте ложных срабатываний (FAR) различных методов. Предлагаемый метод превосходит существующие методы по обоим показателям.

Как обсуждалось ранее, производительность предложенного алгоритма зависит от определенных управляемых данными и определяемых пользователем параметров. Следующий подраздел посвящен анализу чувствительности этих параметров.

Ключевые параметры

Производительность предлагаемой структуры зависит от выбора таких параметров, как длина окна, скользящий параметр (параметры настройки), порог и т. Д. Влияние этих параметров на производительность обсуждается ниже.

1. Параметры настройки : Такие параметры, как длина окна и параметр скольжения, регулируют работу детектора и сборщика.
   
   1. Длина окна (N) : Выбор подходящей длины окна для онлайн-обнаружения и отбора является одним из важнейших шагов. Существует компромисс между длиной окна и частотой обнаружения. Более короткое окно с маленьким значением N приводит к увеличению ошибки типа I (частота ложных тревог; обнаружение событий при отсутствии событий) из-за повышенной чувствительности к небольшим изменениям данных.С другой стороны, выбор более широкого окна, большего N , снижает ошибку типа I за счет увеличения ошибки типа II (частота обнаружения; вероятность пропуска события при наличии событий) из-за пониженной чувствительности к небольшие изменения. Следовательно, необходимо выбрать окно подходящей длины, обеспечивающее низкую частоту ложных тревог без ущерба для скорости обнаружения.
   2. Длина скольжения (S) : выбор S зависит от того, является ли цель алгоритма обнаружением или точным выбором события.Для целей обнаружения можно выбрать более крупный S , а для точного выбора события следует использовать более короткий S .
   Влияние этих параметров на характеристики предлагаемого метода показано на рис. 16. В целях иллюстрации рассматриваются данные со станции ANMO. Ошибка обнаружения, указанная на вертикальной оси графика, определяется как разница между истинным началом события и обнаруженным предлагаемым методом. Как показано на рис. 16 (а), ошибка обнаружения уменьшается с увеличением длины окна.Однако после достижения минимумов ошибка увеличивается с увеличением длины окна. Как видно из рис. 16 (b), ошибка обнаружения увеличивается с увеличением длины скольжения для фиксированной длины окна в 240 выборок.
2. Порог ( δ ) : В этой работе мы используем управляемый данными статический порог, вычисляемый в автономном режиме из исторических данных без событий (фоновый шум). Порог меняется в зависимости от диапазона t-f, потому что каждый диапазон t-f содержит информацию об ограничении диапазона. Следовательно, использование одного и того же порога для всех диапазонов t-f приводит к ошибочному обнаружению.
3. Уровень декомпозиции (L) : Этот параметр определяет общее количество полос t-f в разложении t-f. L играет жизненно важную роль в определении точности обнаружения предлагаемой структуры. При более низком значении L ширина полосы t-f выше, что приводит к большему вкладу шума и, следовательно, к плохому обнаружению. Однако, если значение L выбрано как высокое, полоса пропускания каждого диапазона t-f уменьшается, что приводит к потере желаемой функции из-за разделения информации на несколько диапазонов, тем самым пропуская событие.

Рис. 16. Чувствительность критических параметров.

Влияние (а) переменной длины окна для фиксированной длины скольжения из 5 выборок и (б) переменной длины скольжения для фиксированной длины окна в 240 выборок на производительность предложенного метода. Вертикальная ось указывает ошибку обнаружения для различных параметров настройки. Кружки синего цвета указывают на ошибку обнаружения, а сплошная линия красного цвета - это аппроксимированная кривая для обоих параметров.

https: // doi.org / 10.1371 / journal.pone.0250008.g016

Заключение

В этой работе представлена ​​новая структура прогнозирования с функцией частотно-временной локализации для обнаружения и выбора начала P-волны в сейсмических измерениях. Эта работа не только нова, но и важна, поскольку преодолевает ключевой недостаток существующих методов обработки измерений низкого отношения сигнал / шум. Кроме того, он использует преимущества прогнозной аналитики и функцию увеличения масштаба методов частотно-временного преобразования.Основной вклад в эту работу заключался в (i) расширении применимости прогностической структуры с tf-локализацией для эффективного обнаружения и выбора сейсмического события, особенно для случаев с низким SNR, (ii) оперативном выборе подходящих tf-диапазонов для улучшения точность обнаружения и (iii) оптимальный выбор параметров настройки для снижения частоты ложных тревог. Разработанный сборщик обеспечивает элегантную технику обнаружения и захвата, соизмеримую со свойствами шума, и сильно локализован в области t-f.Следовательно, он устойчив к выбросам и обеспечивает точное обнаружение сейсмограмм с низким отношением сигнал / шум с минимальным количеством ложных срабатываний. Предлагаемый метод по своей конструкции обладает некоторыми желательными характеристиками, такими как низкая частота ложных тревог, устойчивость к выбросам и, что очень важно, способность обнаруживать P-волны на сейсмограммах низкого качества. Одним из наиболее важных шагов, которые придают предлагаемому методу возможность обнаруживать события с низким SNR, является выбор диапазонов t-f, который выполняется с помощью процедуры ранжирования.Наконец, использование изменчивости разницы энергий между данными и прогнозами в области t-f в качестве статистики для проведения теста обнаружения делает его чувствительным к приходу P-волны. Дополнительным преимуществом предлагаемого метода, который имеет значительный потенциал в математическом моделировании P-волн, является то, что он облегчает восстановление сигнатур P-волн из сейсмических измерений, что ранее не рассматривалось в опубликованной литературе.

Мы продемонстрировали предлагаемую структуру с использованием моделей ARIMA в качестве средств прогнозирования и максимального перекрытия DWT для частотно-временных проекций измерений и прогнозов.Модели ARIMA были построены с использованием систематической процедуры, разработанной авторами и опубликованной в другом месте. Реализация почти 200 наборов данных с различными характеристиками показала, что предложенная структура не только устойчива к выбросам (низкий уровень ложных тревог в зашумленных данных), но также способна обнаруживать события с чрезвычайно низким SNR (<0,13) и низкой магнитудой (<0,9). . Предлагаемая структура превосходит широко используемые методы STA / LTA, AIC и DWT-AIC, особенно для событий с низким SNR.

Успех предложенной схемы и ее способность обнаруживать в условиях чрезвычайно низкого отношения сигнал / шум не следует рассматривать как совпадение, поскольку успех предлагаемого метода основан на ограниченном по полосе соотношении сигнал / шум, а не на общепринятом SNR, широко используемом критерии.Ограниченное по полосе SNR высокое, даже если стандартное SNR очень низкое для анализируемых событий. Это связано со значительными различиями частотно-временных распределений события и характеристик сейсмического шума (многомасштабный характер сейсмических измерений). По своей конструкции существующие методы не используют высокое значение SNR с ограниченной полосой пропускания или, скорее, многомасштабный характер данных и, следовательно, не работают в сценариях с низким SNR. Любой метод, который увеличивает t-f-характеристики данных, потенциально может выиграть от ограниченного полосы пропускания SNR.Добавление уровня прогнозов и сравнение различий в характеристиках между двумя уровнями (данные и прогнозы) значительно улучшает различительную способность метода обнаружения. По сути, это основная идея предлагаемой структуры и рационализирует преимущества, которые она приносит для решения интересующей проблемы.

Благодарности

Идея этой работы была концептуализирована К. Аггарвалом и А. К. Тангиралой. Все наборы данных для исследования были подготовлены, загружены и обработаны К.Аггарвал с помощью С.Мухопадхая. К. Аггарвал сформулировал систематическую методологию и провел формальный анализ под руководством А. К. Тангирала и С. Мухопадхьяя. Результаты были подтверждены А. К. Тангиралой и С. Мухопадхяй. Рукопись написана и подготовлена ​​К. Аггарвалом, редактирование - А. К. Тангирала. Отзывы, предоставленные С. Мухопадхьяем и А. К. Тангиралой о рукописи, сформировали рукопись до уровня подачи.

Список литературы

1. 1.МакГарр А., Хофманн Р. Б., Волос Г. Д.. Процесс спектров сигналов в движущемся временном окне. Геофизика. 1964. 29 (2): 212–220.
2. 2. Аллен Р.В. Автоматическое распознавание землетрясений и определение времени по единичным трассам. Бюллетень сейсмологического общества Америки. 1978. 68 (5): 1521–1532.
3. 3. Гофорт Т., Херрин Э. Алгоритм автоматического обнаружения сейсмических сигналов, основанный на преобразовании Уолша. Бюллетень сейсмологического общества Америки. 1981. 71 (4): 1351–1360.
4. 4.Сарагиотис CD, Hadjileontiadis LJ, Panas SM. Фазовая идентификация трехкомпонентных сейсмограмм на основе статистики более высокого порядка в области избыточного вейвлет-преобразования. В: Статистика высшего порядка, 1999. Труды семинара по обработке сигналов IEEE на. IEEE; 1999. стр. 396–399.
5. 5. Хафез А.Г., Хан Т.А., Кохда Т. Обнаружение начала землетрясения с использованием спектрального отношения на многопороговом частотно-временном поддиапазоне. Цифровая обработка сигналов. 2009. 19 (1): 118–126.
6. 6.Ли Х, Шан Х, Моралес-Эстебан А., Ван З. Идентификация появления слабых событий в фазе P: приложение для выбора информационного критерия Акаике на основе разложения по эмпирическим модам. Компьютеры и науки о Земле. 2017; 100: 57–66.
7. 7. Li X, Shang X, Wang Z, Dong L, Weng L. Идентификация приходов P-фазы с шумом: улучшенный метод эксцесса на основе DWT и STA / LTA. Журнал прикладной геофизики. 2016; 133: 50–61.
8. 8. Венкатасубраманиан В, Ренгасвами Р., Инь К., Кавури С.Н.Обзор обнаружения и диагностики сбоев процесса: Часть I: Методы, основанные на количественных моделях. Компьютеры и химическая инженерия. 2003. 27 (3): 293–311.
9. 9. Аггарвал К., Мухопадхьяй С., Тангирала А.К. Обнаружение начала P-волны в сейсмических сигналах с помощью преобразования пакета вейвлет. В: 2019 58-я ежегодная конференция Общества инженеров КИПиА Японии (SICE). IEEE; 2019. стр. 1513–1518.
10. 10. Сарагиотис CD, Hadjileontiadis LJ, Panas SM.PAI-S / K: надежная автоматическая схема определения прихода P-фазы сейсмических данных. IEEE Transactions по наукам о Земле и дистанционному зондированию. 2002. 40 (6): 1395–1404.
11. 11. Куперкох Л., Мейер Т., Ли Дж., Фридрих В., Группа EW. Автоматическое определение времени прихода P-фазы на региональных и местных расстояниях с использованием статистики более высокого порядка. Международный геофизический журнал. 2010. 181 (2): 1159–1170.
12. 12. Шенса MJ. Детектор отклонения - его теория и оценка на короткопериодических сейсмических данных.Texas Instruments Inc., Далласская группа оборудования; 1977.
13. 13. Tibuleac IM, Herrin E. Автоматический метод определения времени прихода Lg с использованием вейвлет-преобразований. Письма о сейсмологических исследованиях. 1999. 70 (5): 577–595.
14. 14. Анант К.С., Даула Ф.У. Методы вейвлет-преобразования для фазовой идентификации трехкомпонентных сейсмограмм. Бюллетень сейсмологического общества Америки. 1997. 87 (6): 1598–1612.
15. 15. Баер М., Крадолфер У.Автоматический выбор фазы для локальных и телесейсмических событий. Бюллетень сейсмологического общества Америки. 1987. 77 (4): 1437–1445.
16. 16. Холерс М., Астер Р., Янг С., Бейригер Дж., Харрис М., Мур С. и др. Сравнение выбранных алгоритмов запуска для автоматического обнаружения фазы глобальной сейсмики и событий. Бюллетень сейсмологического общества Америки. 1998. 88 (1): 95–106.
17. 17. Шан Х, Ли Х, Вен Л. Улучшение пикирования прихода фазы P сейсмических данных на основе шумоподавления вейвлетов и пикировщика эксцесса.Журнал сейсмологии. 2018; 22 (1): 21–33.
18. 18. Галиана-Мерино Дж. Дж., Роса-Херранц Дж. Л., Паролаи С. Seismic P Выбор фазы с использованием критерия на основе эксцесса в области стационарного вейвлета. IEEE Transactions по наукам о Земле и дистанционному зондированию. 2008. 46 (11): 3815–3826.
19. 19. Джозвиг М. Распознавание образов для обнаружения землетрясений. Бюллетень сейсмологического общества Америки. 1990. 80 (1): 170–186.
20. 20. Харрис ДБ. Метод корреляции формы волны для идентификации взрывов в карьере.Бюллетень сейсмологического общества Америки. 1991. 81 (6): 2395–2418.
21. 21. ВанДекар Дж., Кроссон Р. Определение времен прихода относительной фазы телесейсмических сигналов с использованием многоканальной взаимной корреляции и метода наименьших квадратов. Бюллетень сейсмологического общества Америки. 1990. 80 (1): 150–169.
22. 22. Гиббонс С.Дж., Рингдал Ф., Кверна Т. Сейсмограммы отношения к скользящему среднему: стратегия улучшения характеристик корреляционного детектора. Международный геофизический журнал.2012; 190 (1): 511–521.
23. 23. Ахуайри Э.С., Аглиз Д., Атмани А. и др. Автоматическое обнаружение и выбор прихода P-волны в локально стационарном шуме с использованием взаимной корреляции. Цифровая обработка сигналов. 2014; 26: 87–100.
24. 24. Мусави С.М., Эллсуорт В.Л., Чжу В., Чуанг Л.Й., Бероза Г.К. Трансформатор землетрясений - внимательная модель глубокого обучения для одновременного обнаружения землетрясений и выбора фазы. Связь природы. 2020; 11 (1): 1–12. pmid: 32770023
25. 25.Саад О.М., Чен Ю. Обнаружение землетрясений и выбор времени прихода P-волн с использованием капсульной нейронной сети. IEEE Transactions по наукам о Земле и дистанционному зондированию. 2020 ;.
26. 26. Леонард М., Кеннет Б. Многокомпонентные авторегрессионные методы анализа сейсмограмм. Физика Земли и планетных недр. 1999. 113 (1-4): 247–263.
27. 27. Таканами Т., Китагава Г. Новая эффективная процедура для оценки времени начала сейсмических волн.Журнал физики Земли. 1988. 36 (6): 267–290.
28. 28. Слиман Р., Ван Эк Т. Надежный автоматический выбор P-фазы: онлайн-реализация для анализа записей широкополосных сейсмограмм. Физика Земли и недр планет. 1999. 113 (1-4): 265–275.
29. 29. Аггарвал К., Мухопадхьяй С., Тангирала А.К. Статистическая характеристика и моделирование сейсмического шума временными рядами; 2020.
30. 30. Box GE, Jenkins GM, Reinsel GC, Ljung GM.Анализ временных рядов: прогнозирование и контроль. Джон Уайли и сыновья; 2015.
31. 31. Уолден А.Т., Кристан А.С. Дискретное дискретное вейвлет-пакетное преобразование с фазовой коррекцией и его применение для интерпретации хронирования событий. Труды Лондонского королевского общества, серия A: математические, физические и инженерные науки. 1998. 454 (1976): 2243–2266.

Потеря и восстановление частоты при обнаружении неисправностей подшипников качения | Китайский журнал машиностроения

В этом разделе обсуждается взаимодействие сигнала неисправности подшипника с использованием смоделированного сигнала.{- \ xi t} \ cos (2 \ uppi {f_ {n}} t + \ phi_ {n}), $$

(2)

, где B обозначает амплитуду импульсного отклика, \ (f_ {n} \) - возбужденная собственная частота, \ (\ phi_ {n} \) - начальный фазовый угол, \ (\ xi \) - коэффициент затухания для одной степени свободы (SDOF), \ (\ xi = \ alpha 2 \ uppi {f_ {n}} \), где \ (\ alpha \) обозначает относительный коэффициент демпфирования.

Игнорируя влияние проскальзывания роликов, сигнал вибрации, возникающий из-за локального повреждения подшипника, может быть выражен как

$$ y (t) = \ sum \ nolimits_ {k = 0} ^ {N} {[A_ { k} \ delta (t - kT_ {d})} \ otimes s (t)], $$

(3)

где символ \ (\ otimes \) обозначает свертку.

Из приведенных выше экспериментальных случаев в спектре обнаружены несколько полос резонансных частот, т. Е. Полосы частот около 1500 Гц и 2800 Гц на рисунке 2 (b), 2800 Гц и 4000 Гц на рисунке 2 (c), 1200 Гц, 2700 Гц и 3600 Гц на рисунке 3. Таким образом, фактический сигнал неисправности подшипника представляет собой совокупность нескольких импульсных характеристик с разными резонансными частотами. Путь передачи различных резонансных откликов на преобразователь различается для разных компонентов. Таким образом, собранный сигнал вибрации представляет собой мультирезонансный отклик с разницей во времени.Также сообщается о двух импульсных характеристиках в сигнале вибрации подшипника со сколами, когда элемент качения входит в скол и выходит из него [21].

В следующих разделах анализ частотной области (амплитуда и фаза) смоделированного сигнала в формуле. (3), а затем используется сигнал неисправности подшипника с двойной резонансной частотой для обсуждения взаимодействия в сигнале неисправности подшипника. {{j [\ phi (f - kf_ {d} - f_ {n) }) + \ phi_ {n}]}}}.\ hfill \\ \ end {align} $$

(6)

Таким образом, \ (Y (f) \) имеет дискретный спектр, а соответствующая фаза является суммой \ (\ phi (f) \) и \ (\ phi_ {n} \).

Моделируются два разных резонансных отклика, возбуждаемых ударом одного периода. Частота дискретизации установлена ​​на 8192 Гц, \ (T_ {d} \) установлена ​​на 128 точек дискретизации, соответствующая характеристическая частота равна 64 Гц. И амплитуда импульсных сил, и импульсные характеристики установлены равными 1, коэффициент затухания \ (\ xi \) равен 600, и всего 8192 отсчета используются для дальнейшего анализа.Собственная частота установлена ​​на 1000 Гц (первый отклик) и 2000 Гц (второй отклик), соответственно. На рисунках 7 и 8 показаны два смоделированных отклика с начальными фазами 0 °. Судя по спектрам, два сигнала имеют одинаковую характеристическую частоту, а амплитуда низкочастотных составляющих (64 Гц и его гармоники низкого порядка) примерно одинакова. Линии спектра симметричны относительно центральной (резонансной) частоты.

Рисунок 7

Отклик 1 (собственная частота: 1000 Гц, фаза: 0 °): ( a ) временная форма волны, ( b ) спектр БПФ

Рисунок 8

Отклик 2 (собственная частота: 2000 Гц, фаза: 0 °): ( a ) временная форма волны, ( b ) спектр БПФ

Параметры первого отклика остаются постоянными, второй отклик накладывается при разных условиях.Условия наложения перечислены в таблице 2. Результаты наложения представлены на рисунках 9, 10, 11, 12. По сравнению с исходным откликом (рисунок 7 и рисунок 8) результаты наложения показали, что спектр сильно различается из-за различных условий наложения. . Как показано на рисунке 10 (b), результат наложения при условии 2 показывает, что характеристическая частота (64 Гц) и ее гармоники низкого порядка едва ли могут быть обнаружены в спектре. Явление потери частоты наблюдается при моделировании, когда два отклика имеют противоположную фазу.В то же время амплитуда пиков около 1500 Гц в два раза больше, чем у исходного отклика. Исходя из результата наложения при условии 1, амплитуда низкочастотных компонентов на рисунке 9 (b) примерно вдвое больше, чем у исходного отклика, а амплитуда пиков около 1500 Гц почти равна исходному значению.

Таблица 2 Условия наложения Рисунок 9

Результат наложения при условии 1: ( a ) временной сигнал, ( b ) спектр БПФ

Рисунок 10

Результат наложения при условии 2: ( a ) временной сигнал, ( b ) спектр БПФ

Теоретический расчет по формуле.(6) указывает, что амплитуда наложенного отклика в спектре является векторной суммой амплитуды каждого отклика. Из уравнения. Согласно (5), фазы двух экспоненциальных функций затухания приближаются к -90 ° в низкочастотной полосе. Когда начальная фаза \ (\ phi_ {n} \) установлена ​​на ноль (условие 1), заключительная фаза двух ответов почти одинакова (приблизительно - 90 °). Следовательно, разность фаз двух откликов в полосе низких частот составляет почти 0 °, а амплитуда наложенного отклика является суммой амплитуды каждого отклика.Точно так же, когда начальная фаза второго отклика установлена ​​на - 180 ° (условие 2), разность фаз двух откликов составляет - 180 °, и амплитуда двух откликов компенсируется друг другом. Таким образом, потеря частоты наблюдается при условии наложения два.

На рисунках 11 и 12 показаны результаты наложения, когда начальная позиция второго отклика сдвинута вправо на 32 точки. Некоторые гармоники, например, гармоника второго порядка (2 N) характеристической частоты на Рисунке 11 (b) и 4 N на Рисунке 12 (b), практически не видны.Очевидно, что изменяются и другие гармоники, включая резонансные частоты и частоты их боковых полос.

Рисунок 11

Результат наложения при условии 3: ( a ) временной сигнал, ( b ) спектр БПФ

Рисунок 12

Результат наложения при условии 4: ( a ) временная форма волны, ( b ) спектр БПФ

Влияние начальной позиции в ответе два можно легко объяснить свойством сдвига во времени преобразования Фурье:

$$ \ begin {array} {* {20} c} {\ text {If}} & { \ begin {array} {* {20} c} {x (t) \ leftrightarrow X (f)} & {\ text {then}} \\ \ end {array}} \\ \ end {array} \ begin { массив} {* {20} c} {} & {x (t - t_ {0}) \ leftrightarrow X (f)} \\ \ end {array} e ^ {{- j2 \ uppi {f} t_ {0 }}}, $$

(7)

где \ (X (f) \) - преобразование Фурье \ (x (t) \), \ (t_ {0} \) - временная задержка.

Второй ответ начинается с 32 точки, что составляет четверть периода, фазовые задержки первых четырех гармоник рассчитываются как \ (- {\ uppi \ mathord {\ left / {\ vphantom {\ uppi 2}) } \ right. \ kern-0pt} 2} \), \ (- \ pi \), \ ({\ pi \ mathord {\ left / {\ vphantom {\ pi 2}} \ right. \ kern-0pt} 2} \), 0. Из-за сдвига во времени второго отклика между двумя откликами при 2 Н (рис. 11 (b)) при условии 3 и 4 Н (рис. 11) создается общая разность фаз - 180 ° (рис. 12 (б)) при условии 4.

Согласно теоретическим расчетам и моделированию, кратко описан механизм взаимодействия сигнала неисправного подшипника. Когда тела качения ударяют о локальную неисправность внутреннего или внешнего кольца, возникает удар, который вызывает высокочастотные резонансы всей конструкции между подшипником и преобразователем. Собранный сигнал вибрации неисправного подшипника состоит из мультирезонансного отклика. Конечная амплитуда гармоник в спектре - это векторная сумма амплитуды каждого отклика.