8 угольник как нарисовать: Как нарисовать восьмиугольник циркулем

Как нарисовать восьмиугольник циркулем

• Попроси больше объяснений
• Следить
• Отметить нарушение

Маня568 26.02.2013

Ответ

Проверено экспертом

Вспомогательная задача:
Разделить данный отрезок АВ пополам или провести серединный перпендикуляр к отрезку (рис. 1 внизу)
Из концов отрезка АВ одним и тем же радиусом, большим половины отрезка АВ провести две дуги. Через точки их пересечения проводим прямую. Это серединный перпендикуляр к отрезку АВ.

Построение правильного восьмиугольника:
Проводим диаметр АВ. Строим CD – серединный перпендикуляр к АВ.
Хорду СВ делим пополам – прямая KL.
Хорду АС делим пополам – прямая MN.
Соединяем точки A, M, C, K, B, N, D и L. Получили правильный восьмиугольник.

Построение правильного пятиугольника.
Строим два перпендикулярных диаметра АВ и CD.
Делим пополам отрезок ОА – точка Е.
Из Е радиусом ЕС проводим дугу, которая пересекает ОВ в точке F.

Из С радиусом CF проводим дугу, которая пересекает окружность в точке G. CG – сторона правильного пятиугольника.
Проводим радиусом CG из точки G как из центра дугу, которая пересекает окружность в точке K. GK – вторая сторона.
И т.д.
Получаем правильный пятиугольник CGKLM.

Деление окружности на равные части и по­строение правильных вписанных многоуголь­ников можно выполнить как циркулем, так и с помощью угольников и рейсшины.

Деление окружности на четыре равные части и построение пра­вильного вписанного четырех­угольника. Две взаимно перпендикулярные центровые линии делят окружность на четыре равные части (рис. 115, а). Соединив точки пе­ресечения этих линий с окружностью прямы­ми, получают правильный вписанный четырех­угольник.

Деление окружности на восемь равных частей и построение пра­вильного вписанного восьмиуголь­ника. Две взаимно перпендикулярные линии, проведенные под углом 45° к центровым ли­ниям с помощью угольника с углами 45, 45 и 90° и рейсшины (рис.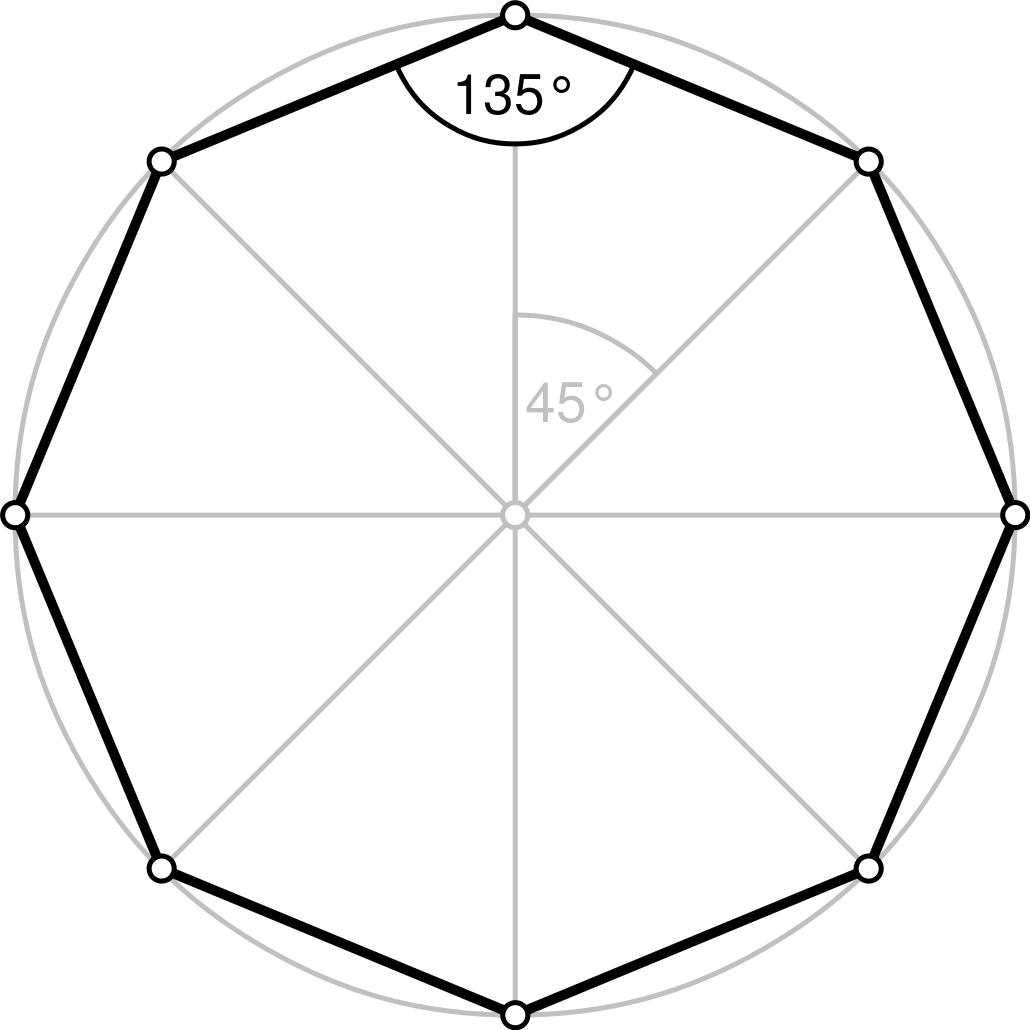 115, б), вместе с центро­выми линиями разделят окружность на восемь равных частей.

Деление окружности на восемь равных час­тей можно выполнить циркулем. Для этого из точек 1 и 3 (точки пересечения центровых линий с окружностью) произвольным радиусом делаются засечки до взаимного пересечения, тем же радиусом делают две засечки из точек 3 и 5 (рис. 115, в). Через точки пересечения засечек и центр окружности проводят прямые линии до пересечения с окружностью в точках 2, 4, 6, 8.

Если полученные восемь точек соединить последовательно прямыми линиями, то полу­чится правильный вписанный восьмиугольник (рис. 115, в).

Деление окружности на три рав­ные части и построение правиль­ного вписанного треугольника вы­полняют с помощью циркуля или угольника с углами 30, 60 и 90° и рейсшины.

При делении окружности циркулем на три равные части из любой точки окружности, на­пример из точки Л пересечения центровых ли­ний с окружностью (рис. 116, а и б), проводят дугу радиусом R, равным радиусу данной ок­ружности, получают точки 1 и 2.

Третья точка деления (точка 3) будет находиться на про­тивоположном конце диаметра, проходящего через точку Л. Последовательно соединив точ­ки 1, 2 и 3, получают правильный вписанный треугольник. При построении правильного впи­санного треугольника, если задана одна из его вершин, например точка 1, находят точку А. Для этого через заданную точку 1 проводят диаметр (рис. 116, в). Точка А будет находить­ся на противоположном конце этого диаметра. Затем проводят дугу радиусом R равным ра­диусу данной окружности, получают точки 2 и 3.

При делении окружности на три равные час­ти с помощью угольника и рейсшины через точку 1 под углом 60° проводят две прямые линии до пересечения с окружностью в точках 2 и 3 (рис. 117, а, б), точки 2 и 3 соединяют и получают правильный вписанный треугольник (рис. 117, в).

Деление окружности на шесть равных частей и построение пра­вильного вписанного шестиуголь­ника выполняют с помощью угольника с уг­лами 30, 60 и 90° и рейсшины или циркуля. При делении окружности на шесть равных частей циркулем из двух концов одного диа­метра радиусом, равным радиусу данной окруж­ности, проводят дуги до пересечения с окруж­ностью в точках 2, 6 и 3, 5 (рис.

118). Последовательно соединив полученные точки, полу­чают правильный вписанный шестиугольник. Деление окружности на шесть равных час-1ен и построение правильного вписанного шестиугольника с помощью угольника и рейс­шины показано на рис. 119 и 120. Деление окружности на двенад­цать равных частей и построение правильного вписанного двенад­цатиугольника выполняют с помощью угольника с углами 30, 60 и 90° и рейсшины или циркуля.

При делении окружности циркулем из четы­рех концов двух взаимно перпендикулярных диаметров окружности проводят радиусом, рав­ным радиусу данной окружности, дуги до пере­сечения с окружностью (рис. 121). Соединив по­лученные точки, получают двенадцатиугольник.

При построении двенадцатиугольника с по­мощью угольника и рейсшины точки деления строят, как показано на рис.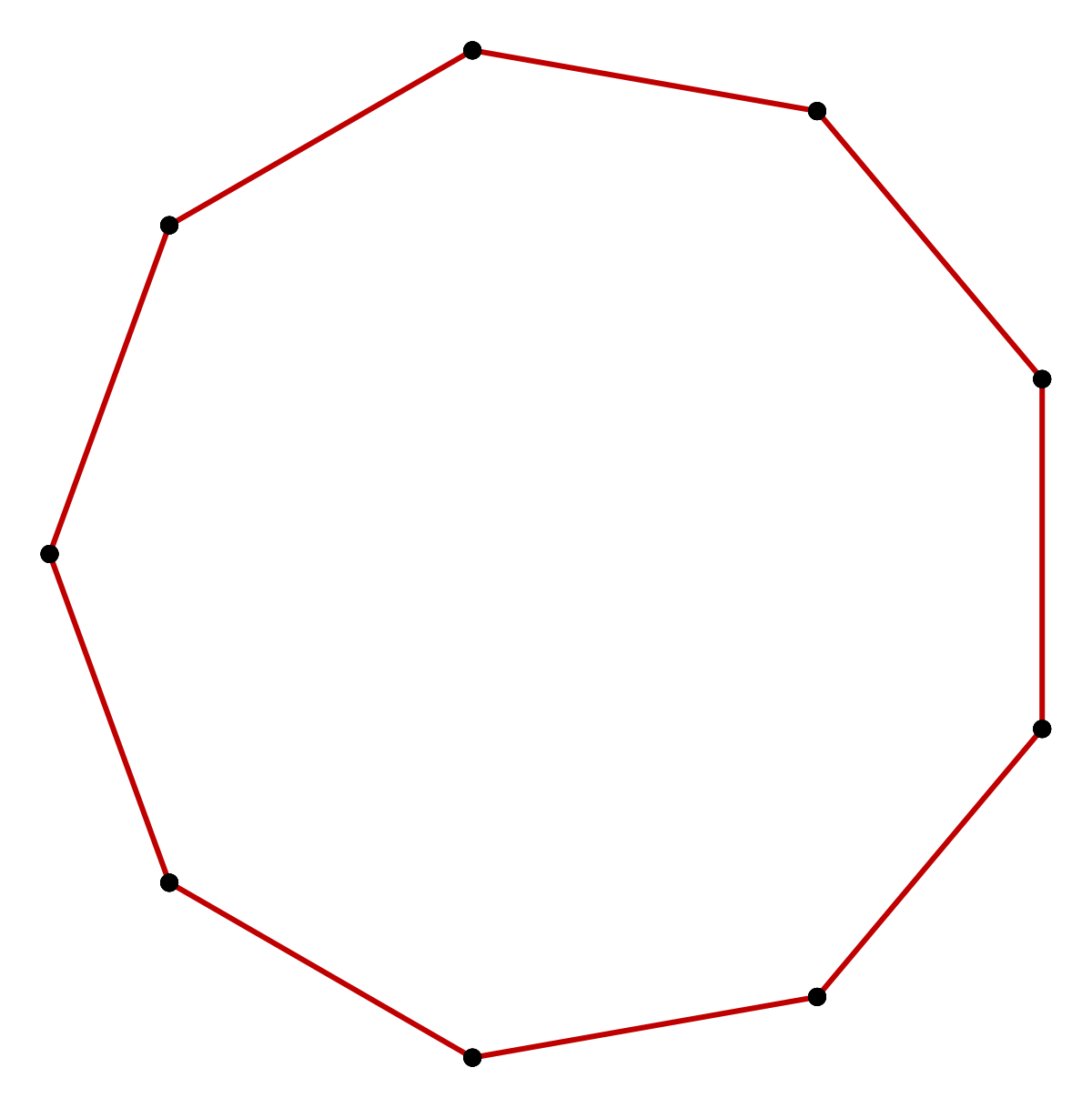 119 и 120.

Деление окружности на пять и десять равных частей и построе­ние правильного вписанного пяти­угольника и десятиугольника пока­зано на рис. 122.

Половину любого диаметра (радиус) делят пополам (рис. 122, а), получают точку А. Из точки А, как из центра, проводят дугу радиу­сом, равным расстоянию от точки А до точки 1, до пересечения со второй половиной этого диаметра, в точке В (рис. 122, б). Отрезок 1В равен хорде, стягивающей дугу, длина которой равна 1 /₅ длины окружности. Делая засечки на окружности (рис. 122, в) радиусом R, равным отрезку 1В, делят окруж­ность на пять равных частей. Начальную точку 1 выбирают в зависимости от расположения пятиугольника. Из точки / строят точки 2 и 5 (рис. 122, в), затем из точки 2 строят точку 3, а из точки 5 строят точку 4. Расстояние от точки 3 до точки 4 проверяют циркулем; если расстояние между точками 3 и 4 равно отрезку 1В, то построения были выполнены точно. Нельзя выполнять засечки последовательно, в одну сторону, так как происходит набегание ошибок и последняя сторона пятиугольника получается перекошенной.

Последовательно соединив найденные точки, получают пяти­угольник (рис. 122, г).

Деление окружности на десять равных час­тей выполняют аналогично делению окруж­ности на пять равных частей (рис. 122), но сначала делят окружность на пять частей, на­чиная построение из точки /, а затем из точ­ки 6, находящейся на противоположном конце диаметра (рис. 123, а). Соединив последова­тельно все точки, получают правильный впи­санный десятиугольник (рис. 123, б).

Деление окружности на семь и четырнадцать равных частей и по­строение правильного вписанного семиугольника и четырнадцатиугольника показано на рис. 124 и 125.

Из любой точки окружности, например точ­ки Л, радиусом заданной окружности проводят дугу (рис. 124, а) до пересечения с окруж­ностью в точках В и D. Соединим точки В и D прямой. Половина полученного отрезка (в данном случае отрезок ВС) будет равна хорде, которая стягивает дугу, составляющую 1 /₇ дли­ны окружности.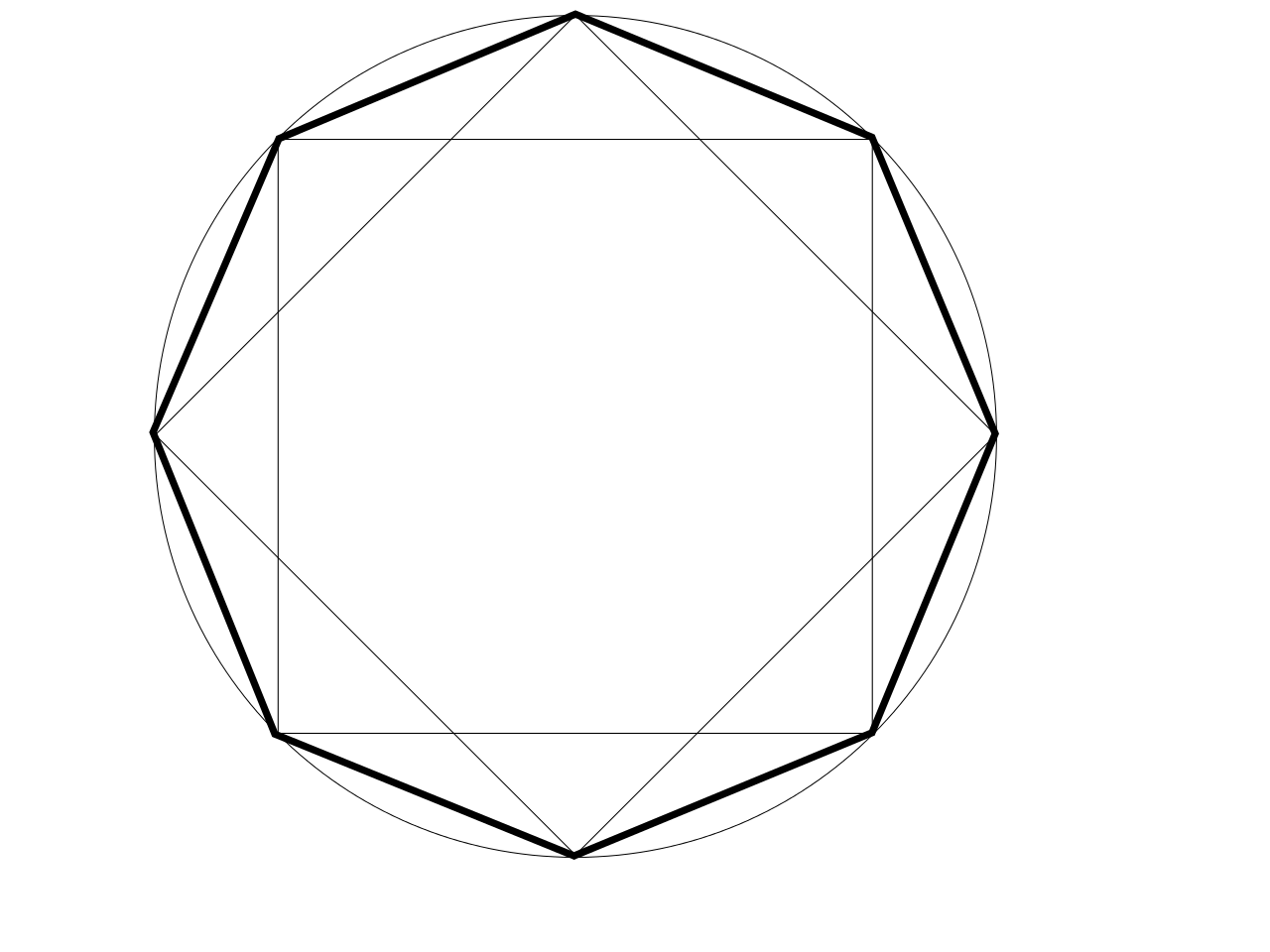

Радиусом, равным отрезку ВС, делают засечки на окружности в последова­тельности, показанной на рис. 124, б. Соединив последовательно все точки, получают правиль­ный вписанный семиугольник (рис. 124, в).

Деление окружности на четырнадцать рав­ных частей выполняется делением окружности на семь равных частей два раза от двух точек (рис. 125, а).

Сначала окружность делится на семь рав­ных частей от точки /, затем то же построение выполняется от точки 8. Построенные точки соединяют последовательно прямыми линиями и получают правильный вписанный четырна-дцатиугольник (рис. 125, б).

СОПРЯЖЕНИЯ

Рассматривая детали, видим, что в их конст­рукции часто одна поверхность переходит в другую. Обычно эти переходы делают плав­ными, что повышает прочность деталей и де­лает их более удобными в работе. На чертеже поверхности изображаются линиями, которые также плавно переходят одна в другую.

На рис. 126, а изображена деталь, в которой плавные переходы одних плоскостей в другие представляют собой цилиндрические поверхнос­ти. На чертеже (рис. 126, б) эти плоскости изо­бражены прямыми линиями, а цилиндрические поверхности — дугами окружностей. Плавные переходы от одной прямой к другой в этих случаях выполняются дугой заданного радиуса.

Плавный переход одной цилиндрической поверхности в другую может являться цилинд­рической поверхностью (рис. 127, а). На черте­же эти цилиндрические поверхности изобра­жены дугами окружностей, (рис. 127, б). В этом случае плавный переход одной дуги окруж­ности в другую осуществляется дугой окруж­ности заданного радиуса.

На рис. 126, а и 127, а рассмотрены простей­шие примеры плавных переходов поверхностей. В чертежах более сложных деталей плавные переходы между поверхностями изображают­ся различными сочетаниями прямых, окруж­ностей и их дуг. Вариантов таких сочетаний может быть много, но их объединяет од­но — плавность перехода. Такой плавный пе­реход одной линии (поверхности) в другую ли­нию (поверхность) называют сопряжени­ем. При построении сопряжения необходимо определить границу, где кончается одна линия и начинается другая, т.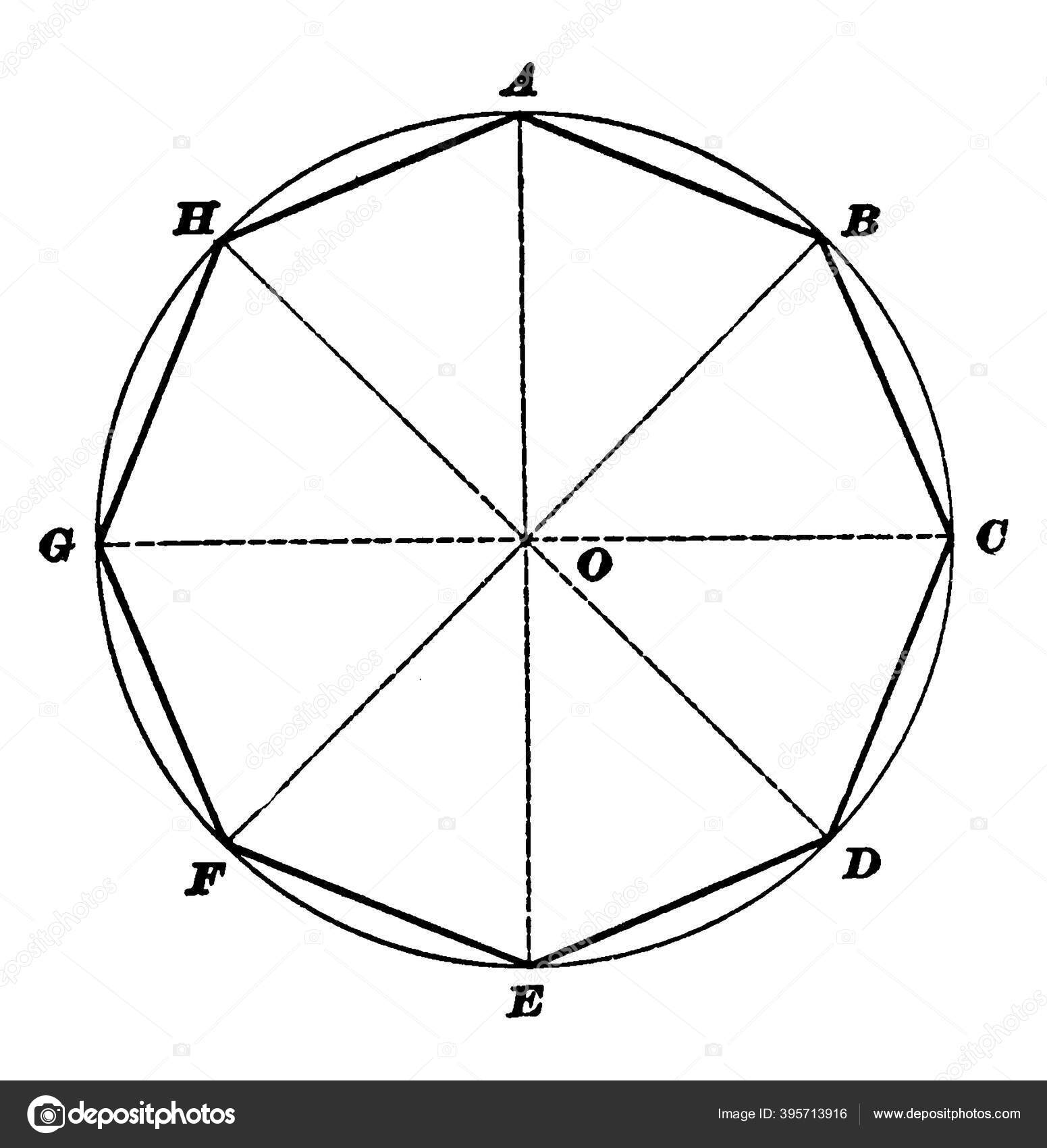 е. найти на чертеже точку перехода, которая называется точкой сопряжения или точкой касания.

Задачи на сопряжения условно можно раз­делить на три группы.

Первая группа задачвключает в себя зада­чи на построение сопряжений, где участвуют прямые линии. Это может быть непосредствен­ное касание прямой и окружности, сопряжение двух прямых дугой заданного радиуса, а также проведение касательной прямой к двум окружностям.

Построение окружности, каса­тельной к прямой, связано с нахождени­ем точки касания и центра окружности.

Задана горизонтальная прямая АВ, требует­ся построить окружность радиусом R, касательную к данной прямой (рис. 128). Точка касания выбирается произвольно. Так как точка касания не задана, то окружность ра­диуса R может коснуться данной прямой в любой точке. Таких окружностей можно про­вести множество. Центры этих окружностей (O₁, О₂и т. д.) будут находиться на одина­ковом расстоянии от заданной прямой, т. е. на линии, расположенной параллельно заданной прямой АВ на расстоянии, равном радиусу заданной окружности (рис. 128). Назовем эту линию линией центров. Проведем линию центров параллельно прямой АВ на расстоя­нии R. Так как центр касательной окруж­ности не задан, возьмем любую точку на линии центров, например точку О. Прежде чем про­водить касательную окружность, следует опре­делить точку касания. Точка касания будет лежать на перпендикуляре, опущенном из точ­ки О на прямую АВ. В пересечении перпендику­ляра с прямой АВ получим точку К, которая будет точкой касания. Из центра О радиусом R от точки К проведем окружность. Задача решена.

В детали, которая изображена на рис. 129, а, пластина плавно переходит в цилиндр. При выполнении чертежа этой детали необходимо построить плавный переход прямой в окруж­ность.

Задача аналогична предыдущей, но до­полнена условием, что точка касания задана, так как задан размер А (рис. 129, б), который определяет величину прямолинейного участка.

Отложив размер Л, находят точку касания (точку /С), затем из точки К восставляют пер­пендикуляр, на котором откладывают радиус R заданной окружности, и находят центр ок­ружности (точку О). При обводке сначала от точки касания проводится дуга заданного ра­диуса, а потом — прямая.

Из сказанного следует:

1) центр окружности, касательной к прямой, лежит на прямой (линия центров), проведенной параллельно заданной прямой, на расстоянии, равном радиусу данной окружности;

Не нашли то, что искали? Воспользуйтесь поиском:

В черчении зачастую требуется строить положительные многоугольники. Так, скажем, положительные восьмиугольники применяются на щитах дорожных знаков.

Вам понадобится

Инструкция

1. Пускай задан отрезок, равный длине стороны желанного восьмиугольника. Требуется возвести верный восьмиугольник. Первым шагом постройте равнобедренный треугольник на заданном отрезке, применяя отрезок, как основание. Для этого вначале постройте квадрат со стороной, равной отрезку, проведите в нем диагонали. Сейчас постройте биссектрисы углов при диагоналях (на рисунке биссектрисы указаны синим), на пересечении биссектрис образуется вершина равнобедренного треугольника, стороны которого равны радиусу окружности, описанной вокруг верного восьмиугольника.

2. Постройте окружность с центром в вершине треугольника. Радиус окружности равен стороне треугольника. Сейчас разведите циркуль на расстояние, равное величине заданного отрезка. Отложите это расстояние на окружности, начиная от всякого конца отрезка. Объедините все полученные точки в восьмиугольник.

3. Если же задана окружность, в которую должен быть вписан восьмиугольник, то построения будут еще проще. Постройте две перпендикулярные друг другу осевые линии, проходящие через центр окружности. На пересечении осевых и окружности получатся четыре вершины грядущего восьмиугольника. Осталось поделить расстояние между этими точками на дуге окружности напополам, дабы получить еще четыре вершины.

Верный треугольник – тот, у которого все стороны владеют идентичной длиной. Исходя из этого определения, построение сходственной разновидности треугольник а является нетрудной задачей.

Вам понадобится

• Линейка, лист разлинованной бумаги, карандаш

Инструкция

1. Взять лист чистой бумаги, разлинованной в клеточку, линейку и подметить на бумаге три точки так, дабы они находились на идентичном друг от друга расстоянии (рис.1)

2. С подмогой линейки объединить подмеченные на листе точки ступенчато, друг за ином так, как это показано на рисунке 2.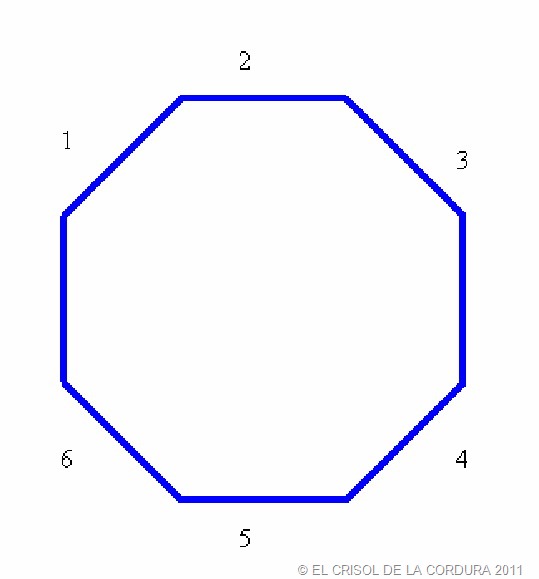

Обратите внимание!
В верном (равностороннем) треугольнике все углы равны 60 градусам.

Полезный совет
Равносторонний треугольник так же является и равнобедренным. Если треугольник равнобедренный, то это обозначает, что 2 из 3-х его сторон равны, а третья сторона считается основанием. Всякий положительный треугольник является равнобедренным, в то время как обратное заявление не правильно.

Восьмиугольник – это, по своей сути, два квадрата, смещенных касательно друг друга на 45° и объединенных на вершинах цельной линией. А потому, для того дабы положительно изобразить такую геометрическую фигуру, нужно твердым карандашом дюже опрятно, по правилам начертить квадрат либо круг, с которыми и проводить последующие действия. Изложение ориентировано на длину стороны, равной 20 см. А значит, при расположении чертежа рассматривайте, дабы вертикальная и горизонтальная линии длиной 20 см умещались на листе бумаги.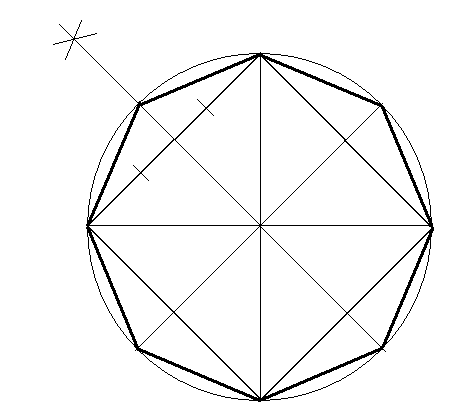

Вам понадобится

• Линейка, прямоугольный треугольник, транспортир, карандаш, циркуль, лист бумаги

Инструкция

1. Метод 1. Начертите внизу горизонтальную линию длиной 20 см. После этого с одной стороны подметьте транспортиром прямой угол, тот, что составляет 90°. То же самое дозволено сделать с поддержкой прямого треугольника. Проведите вертикальную линию и подметьте 20 см. Проделайте те же самые манипуляции с иной стороны. Объедините две полученные точки горизонтальной линией. В итоге получилась геометрическая фигура – квадрат.

2. Для того дабы возвести 2-й (смещенный) квадрат, потребуется центр фигуры. Для этого поделите всякую сторону квадрата на 2 части. Объедините вначале 2 точки параллельных верхней и нижней сторон, а потом точки боковых сторон. Проведите через центр квадрата 2 прямые линии, перпендикулярные касательно друг друга. Начиная от центра, отмерьте на новых прямых длину по 10 см, что в результате даст 4 прямые линии.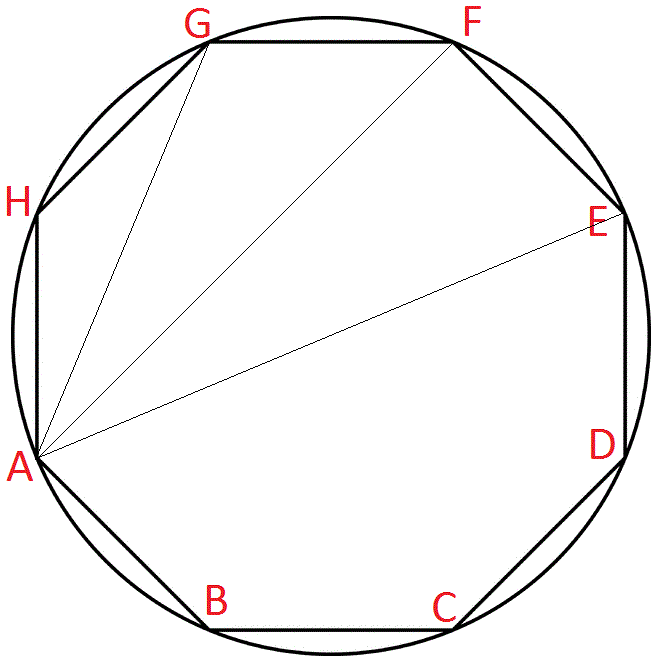 Объедините 4 полученные наружные точки между собой, в итоге чего получится 2-й квадрат. Сейчас всякую точку из 8 полученных углов объедините между собой. Таким образом, будет начерчен восьмиугольник.

3. Метод 2. Для этого потребуется циркуль, линейка и транспортир. От центра листа с поддержкой циркуля начертите круг диаметром 20 см (радиус 10 см). Через центральную точку проведите прямую линию. После этого начертите вторую перпендикулярную ей линию. То же самое дозволено исполнить с подмогой транспортира либо прямого треугольника. В итоге круг будет поделен на 4 равные части. Дальше всякий из секций поделите еще на 2 части. Для этого также дозволено воспользоваться транспортиром, отмеряя 45° либо прямоугольным треугольником, тот, что приложите острым углом в 45° и проведите лучи. От центра на всякой прямой линии отмерьте по 10 см. В итоге получатся 8 «лучиков», которые объедините между собой. В итоге получится восьмиугольник.

4. Метод 3. Для этого так же начертите круг, проведите через середину линию.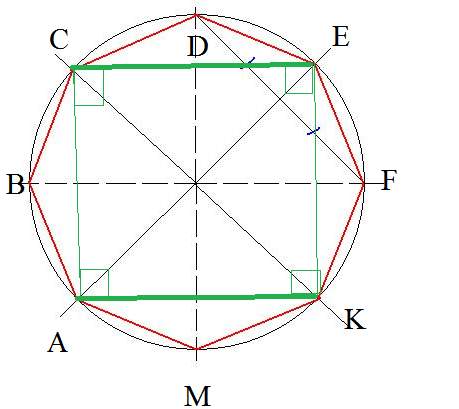 После этого возьмите транспортир, поставьте его на центр и отмеряйте углы, рассматривая, что всякий секция восьмиугольника имеет в центре угол 45° . Позже этого на полученных лучах отмерьте длину в 10 см. и объедините их между собой. Восьмиугольник готов.

Полезный совет
Делайте чертеж твердым карандашом, побочные линии на котором после этого легко дозволено будет удалить

Верный восьмиугольник – это геометрическая фигура, у которой всякий угол составляет 135?, и все стороны между собою равны. Эта фигура дюже зачастую используется в архитектуре, к примеру, при постройке колон, а также при изготовлении дорожного знака STOP. Как же нарисовать положительный восьмиугольник?

Вам понадобится

Инструкция

1. Нарисуйте вначале квадрат. После этого проведите окружность так, дабы квадрат оказался внутри круга. Сейчас проведите две осевые серединные линии квадрата – горизонтальную и вертикальную до пересечения с кругом. Объедините прямыми отрезками точки пересечения осей с кругом и точки прикосновения описанной окружности с квадратом. Таким образом, получите стороны верного восьмиугольника.

2. Нарисуйте верный восьмиугольник иным методом. Вначале начертите окружность. После этого проведите горизонтальную линию через ее центр. Подметьте точку пересечения крайней правой границы окружности с горизонталью. Эта точка будет являться центром еще одной окружности, радиусом равным предыдущей фигуре.

3. Проведите вертикальную линию через точки пересечения 2-й окружности с первой. Поставьте ножку циркуля в точку пересечения вертикали с горизонталью и начертите небольшой круг радиусом, равным расстоянию от центра крошечной окружности до центра начального круга.

4. Начертите прямую линию через две точки – центр начального круга и точку пересечения вертикали и крошечной окружности. Продолжите ее до пересечения с рубежом изначальной фигуры. Это будет точка вершины восьмиугольника. Циркулем подметьте еще одну точку, проведя окружность с центром в точке пересечения крайней правой рубежом начального круга с горизонталью и радиусом, равным расстоянию от центра к теснее имеющейся вершине восьмиугольника.

5. Проведите прямую линию через две точки – центр начального круга и последнюю новообразованную точку. Продолжите прямую линию до пересечения с границами первоначальной фигуры.

6. Объедините прямыми отрезками ступенчато: точку пересечения горизонтали с правой рубежом начальной фигуры, после этого по часовой стрелке все образовавшиеся точки, включая точки пересечения осей с первоначальной окружностью.

“>

Как нарисовать правильный восьмиугольник

Ответ

Проверено экспертом

Вспомогательная задача:
Разделить данный отрезок АВ пополам или провести серединный перпендикуляр к отрезку (рис. 1 внизу)
Из концов отрезка АВ одним и тем же радиусом, большим половины отрезка АВ провести две дуги. Через точки их пересечения проводим прямую. Это серединный перпендикуляр к отрезку АВ.

Построение правильного восьмиугольника:
Проводим диаметр АВ. Строим CD — серединный перпендикуляр к АВ.
Хорду СВ делим пополам — прямая KL.
Хорду АС делим пополам — прямая MN.
Соединяем точки A, M, C, K, B, N, D и L. Получили правильный восьмиугольник.

Построение правильного пятиугольника.
Строим два перпендикулярных диаметра АВ и CD.
Делим пополам отрезок ОА — точка Е.
Из Е радиусом ЕС проводим дугу, которая пересекает ОВ в точке F.
Из С радиусом CF проводим дугу, которая пересекает окружность в точке G. CG — сторона правильного пятиугольника.
Проводим радиусом CG из точки G как из центра дугу, которая пересекает окружность в точке K. GK — вторая сторона.
И т.д.
Получаем правильный пятиугольник CGKLM.

Деление окружности на равные части и по­строение правильных вписанных многоуголь­ников можно выполнить как циркулем, так и с помощью угольников и рейсшины.

Деление окружности на четыре равные части и построение пра­вильного вписанного четырех­угольника. Две взаимно перпендикулярные центровые линии делят окружность на четыре равные части (рис. 115, а). Соединив точки пе­ресечения этих линий с окружностью прямы­ми, получают правильный вписанный четырех­угольник.

Деление окружности на восемь равных частей и построение пра­вильного вписанного восьмиуголь­ника. Две взаимно перпендикулярные линии, проведенные под углом 45° к центровым ли­ниям с помощью угольника с углами 45, 45 и 90° и рейсшины (рис. 115, б), вместе с центро­выми линиями разделят окружность на восемь равных частей.

Деление окружности на восемь равных час­тей можно выполнить циркулем. Для этого из точек 1 и 3 (точки пересечения центровых линий с окружностью) произвольным радиусом делаются засечки до взаимного пересечения, тем же радиусом делают две засечки из точек 3 и 5 (рис. 115, в). Через точки пересечения засечек и центр окружности проводят прямые линии до пересечения с окружностью в точках 2, 4, 6, 8.

Если полученные восемь точек соединить последовательно прямыми линиями, то полу­чится правильный вписанный восьмиугольник (рис. 115, в).

Деление окружности на три рав­ные части и построение правиль­ного вписанного треугольника вы­полняют с помощью циркуля или угольника с углами 30, 60 и 90° и рейсшины.

При делении окружности циркулем на три равные части из любой точки окружности, на­пример из точки Л пересечения центровых ли­ний с окружностью (рис. 116, а и б), проводят дугу радиусом R, равным радиусу данной ок­ружности, получают точки 1 и 2. Третья точка деления (точка 3) будет находиться на про­тивоположном конце диаметра, проходящего через точку Л. Последовательно соединив точ­ки 1, 2 и 3, получают правильный вписанный треугольник. При построении правильного впи­санного треугольника, если задана одна из его вершин, например точка 1, находят точку А. Для этого через заданную точку 1 проводят диаметр (рис. 116, в). Точка А будет находить­ся на противоположном конце этого диаметра. Затем проводят дугу радиусом R равным ра­диусу данной окружности, получают точки 2 и 3.

При делении окружности на три равные час­ти с помощью угольника и рейсшины через точку 1 под углом 60° проводят две прямые линии до пересечения с окружностью в точках 2 и 3 (рис. 117, а, б), точки 2 и 3 соединяют и получают правильный вписанный треугольник (рис. 117, в).

Деление окружности на шесть равных частей и построение пра­вильного вписанного шестиуголь­ника выполняют с помощью угольника с уг­лами 30, 60 и 90° и рейсшины или циркуля. При делении окружности на шесть равных частей циркулем из двух концов одного диа­метра радиусом, равным радиусу данной окруж­ности, проводят дуги до пересечения с окруж­ностью в точках 2, 6 и 3, 5 (рис. 118). Последовательно соединив полученные точки, полу­чают правильный вписанный шестиугольник. Деление окружности на шесть равных час-1ен и построение правильного вписанного шестиугольника с помощью угольника и рейс­шины показано на рис. 119 и 120. Деление окружности на двенад­цать равных частей и построение правильного вписанного двенад­цатиугольника выполняют с помощью угольника с углами 30, 60 и 90° и рейсшины или циркуля.

При делении окружности циркулем из четы­рех концов двух взаимно перпендикулярных диаметров окружности проводят радиусом, рав­ным радиусу данной окружности, дуги до пере­сечения с окружностью (рис. 121). Соединив по­лученные точки, получают двенадцатиугольник.

При построении двенадцатиугольника с по­мощью угольника и рейсшины точки деления строят, как показано на рис. 119 и 120.

Деление окружности на пять и десять равных частей и построе­ние правильного вписанного пяти­угольника и десятиугольника пока­зано на рис. 122.

Половину любого диаметра (радиус) делят пополам (рис. 122, а), получают точку А. Из точки А, как из центра, проводят дугу радиу­сом, равным расстоянию от точки А до точки 1, до пересечения со второй половиной этого диаметра, в точке В (рис.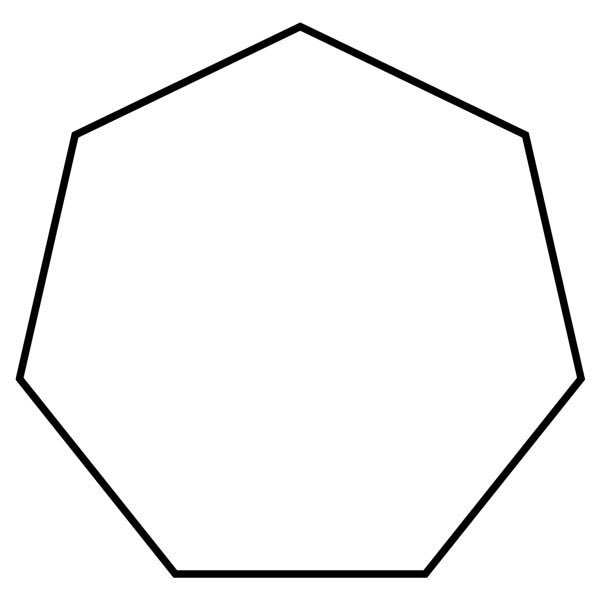 122, б). Отрезок 1В равен хорде, стягивающей дугу, длина которой равна 1 /₅ длины окружности. Делая засечки на окружности (рис. 122, в) радиусом R, равным отрезку 1В, делят окруж­ность на пять равных частей. Начальную точку 1 выбирают в зависимости от расположения пятиугольника. Из точки / строят точки 2 и 5 (рис. 122, в), затем из точки 2 строят точку 3, а из точки 5 строят точку 4. Расстояние от точки 3 до точки 4 проверяют циркулем; если расстояние между точками 3 и 4 равно отрезку 1В, то построения были выполнены точно. Нельзя выполнять засечки последовательно, в одну сторону, так как происходит набегание ошибок и последняя сторона пятиугольника получается перекошенной. Последовательно соединив найденные точки, получают пяти­угольник (рис. 122, г).

Деление окружности на десять равных час­тей выполняют аналогично делению окруж­ности на пять равных частей (рис. 122), но сначала делят окружность на пять частей, на­чиная построение из точки /, а затем из точ­ки 6, находящейся на противоположном конце диаметра (рис.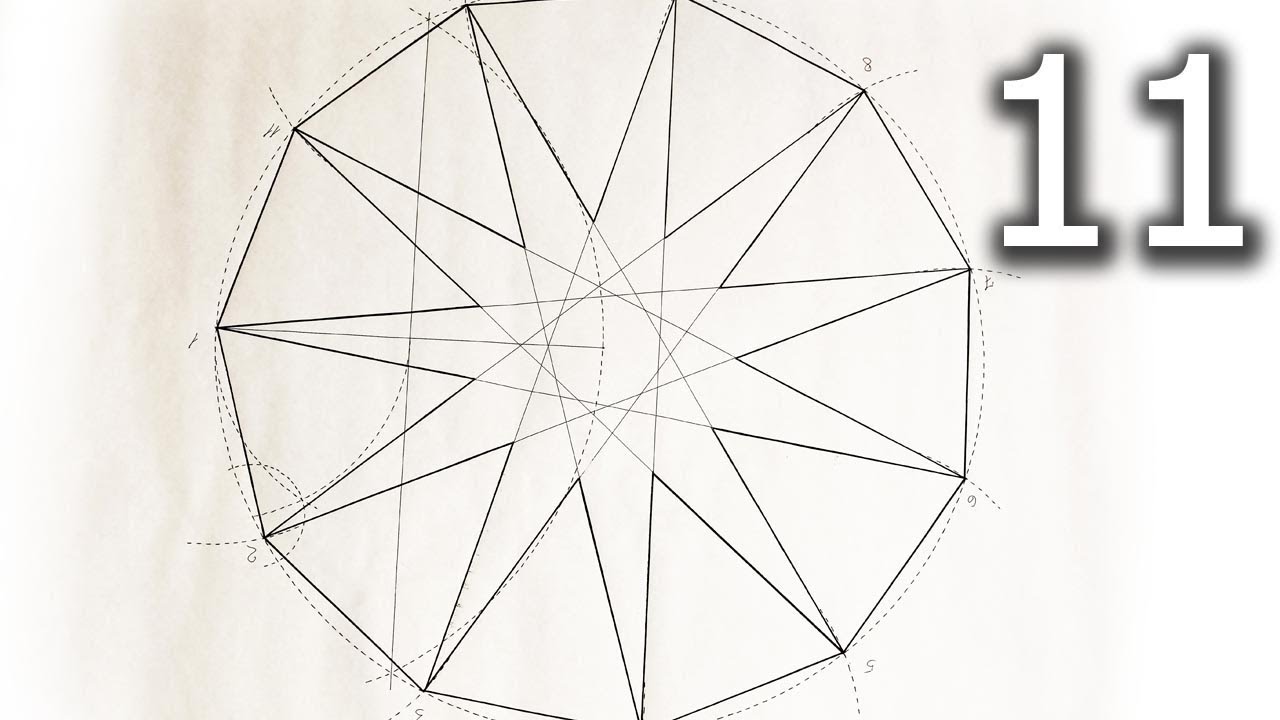 123, а). Соединив последова­тельно все точки, получают правильный впи­санный десятиугольник (рис. 123, б).

Деление окружности на семь и четырнадцать равных частей и по­строение правильного вписанного семиугольника и четырнадцатиугольника показано на рис. 124 и 125.

Из любой точки окружности, например точ­ки Л, радиусом заданной окружности проводят дугу (рис. 124, а) до пересечения с окруж­ностью в точках В и D. Соединим точки В и D прямой. Половина полученного отрезка (в данном случае отрезок ВС) будет равна хорде, которая стягивает дугу, составляющую 1 /₇ дли­ны окружности. Радиусом, равным отрезку ВС, делают засечки на окружности в последова­тельности, показанной на рис. 124, б. Соединив последовательно все точки, получают правиль­ный вписанный семиугольник (рис. 124, в).

Деление окружности на четырнадцать рав­ных частей выполняется делением окружности на семь равных частей два раза от двух точек (рис.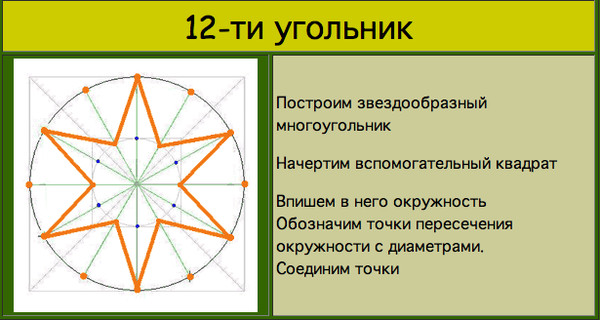 125, а).

Сначала окружность делится на семь рав­ных частей от точки /, затем то же построение выполняется от точки 8. Построенные точки соединяют последовательно прямыми линиями и получают правильный вписанный четырна-дцатиугольник (рис. 125, б).

СОПРЯЖЕНИЯ

Рассматривая детали, видим, что в их конст­рукции часто одна поверхность переходит в другую. Обычно эти переходы делают плав­ными, что повышает прочность деталей и де­лает их более удобными в работе. На чертеже поверхности изображаются линиями, которые также плавно переходят одна в другую.

На рис. 126, а изображена деталь, в которой плавные переходы одних плоскостей в другие представляют собой цилиндрические поверхнос­ти. На чертеже (рис. 126, б) эти плоскости изо­бражены прямыми линиями, а цилиндрические поверхности — дугами окружностей. Плавные переходы от одной прямой к другой в этих случаях выполняются дугой заданного радиуса.

Плавный переход одной цилиндрической поверхности в другую может являться цилинд­рической поверхностью (рис. 127, а). На черте­же эти цилиндрические поверхности изобра­жены дугами окружностей, (рис. 127, б). В этом случае плавный переход одной дуги окруж­ности в другую осуществляется дугой окруж­ности заданного радиуса.

На рис. 126, а и 127, а рассмотрены простей­шие примеры плавных переходов поверхностей. В чертежах более сложных деталей плавные переходы между поверхностями изображают­ся различными сочетаниями прямых, окруж­ностей и их дуг. Вариантов таких сочетаний может быть много, но их объединяет од­но — плавность перехода. Такой плавный пе­реход одной линии (поверхности) в другую ли­нию (поверхность) называют сопряжени­ем. При построении сопряжения необходимо определить границу, где кончается одна линия и начинается другая, т. е. найти на чертеже точку перехода, которая называется точкой сопряжения или точкой касания.

Задачи на сопряжения условно можно раз­делить на три группы.

Первая группа задачвключает в себя зада­чи на построение сопряжений, где участвуют прямые линии. Это может быть непосредствен­ное касание прямой и окружности, сопряжение двух прямых дугой заданного радиуса, а также проведение касательной прямой к двум окружностям.

Построение окружности, каса­тельной к прямой, связано с нахождени­ем точки касания и центра окружности.

Задана горизонтальная прямая АВ, требует­ся построить окружность радиусом R, касательную к данной прямой (рис. 128). Точка касания выбирается произвольно. Так как точка касания не задана, то окружность ра­диуса R может коснуться данной прямой в любой точке. Таких окружностей можно про­вести множество. Центры этих окружностей (O₁, О₂и т. д.) будут находиться на одина­ковом расстоянии от заданной прямой, т. е. на линии, расположенной параллельно заданной прямой АВ на расстоянии, равном радиусу заданной окружности (рис. 128). Назовем эту линию линией центров. Проведем линию центров параллельно прямой АВ на расстоя­нии R. Так как центр касательной окруж­ности не задан, возьмем любую точку на линии центров, например точку О.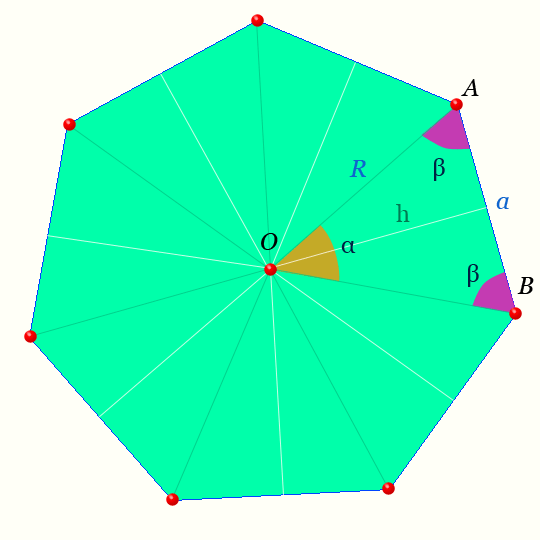 Прежде чем про­водить касательную окружность, следует опре­делить точку касания. Точка касания будет лежать на перпендикуляре, опущенном из точ­ки О на прямую АВ. В пересечении перпендику­ляра с прямой АВ получим точку К, которая будет точкой касания. Из центра О радиусом R от точки К проведем окружность. Задача решена.

В детали, которая изображена на рис. 129, а, пластина плавно переходит в цилиндр. При выполнении чертежа этой детали необходимо построить плавный переход прямой в окруж­ность.

Задача аналогична предыдущей, но до­полнена условием, что точка касания задана, так как задан размер А (рис. 129, б), который определяет величину прямолинейного участка.

Отложив размер Л, находят точку касания (точку /С), затем из точки К восставляют пер­пендикуляр, на котором откладывают радиус R заданной окружности, и находят центр ок­ружности (точку О). При обводке сначала от точки касания проводится дуга заданного ра­диуса, а потом — прямая.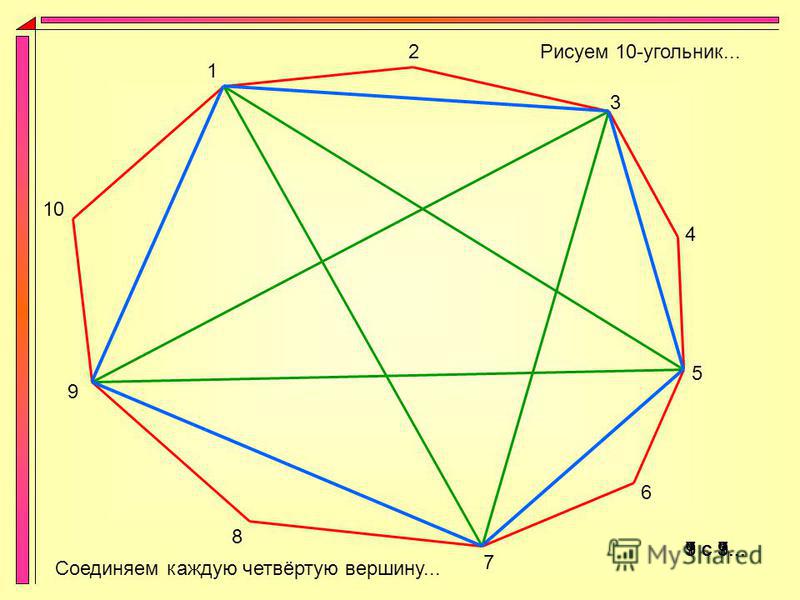

Из сказанного следует:

1) центр окружности, касательной к прямой, лежит на прямой (линия центров), проведенной параллельно заданной прямой, на расстоянии, равном радиусу данной окружности;

Не нашли то, что искали? Воспользуйтесь поиском:

Здесь легко и интересно общаться. Присоединяйся!

Умеете построить угол 45 градусов?
Для этого надо от конца первой стороны построить угол -90 и в нём построить биссектрису продлите биссектрису в противоположную сторону и отложите туда длину стороны.

Всё повторить ещё 5 раз и замкнуть 8-угольник.

Если не нравится,
1. нарисуйте перекрестье двух перпендикулярных линий
2. постройте биссектрисы всех четырёх прямых углов
3. получили 8 лучей, надо к каждому лучу построить по две параллельные линии,
отстоящие на половину стороны 8-угольника, Длина этой стороны должна быть задана в начале задания.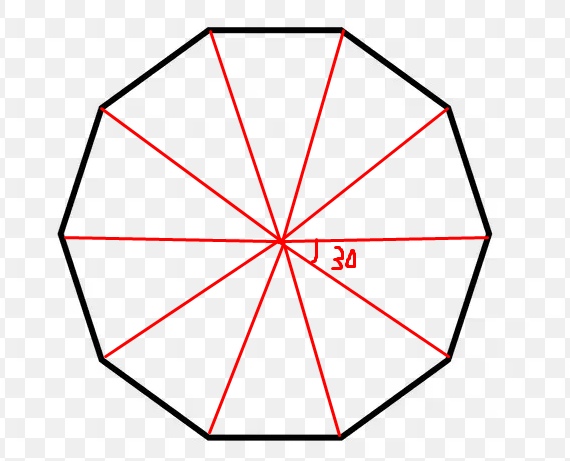
4. Не принимая во внимание 8 первоначальных лучей, найдите точки пересечения всех остальных шестнадцати линий, соедините 8 точек, лежащих дальше всего от центра, ломаной линией, поочерёдно переходя к следующей ближайшей точке. Получится правильный 8-угольник.

Только циркулем и линейкой? ! —не знаю.
А так — угол вычислить, и порядок.

При помощи циркуля проведите окружность. Отметьте ее центр.

Сделайте отметки на концах любого диаметра окружности. Это первые две вершины будущего восьмиугольника.

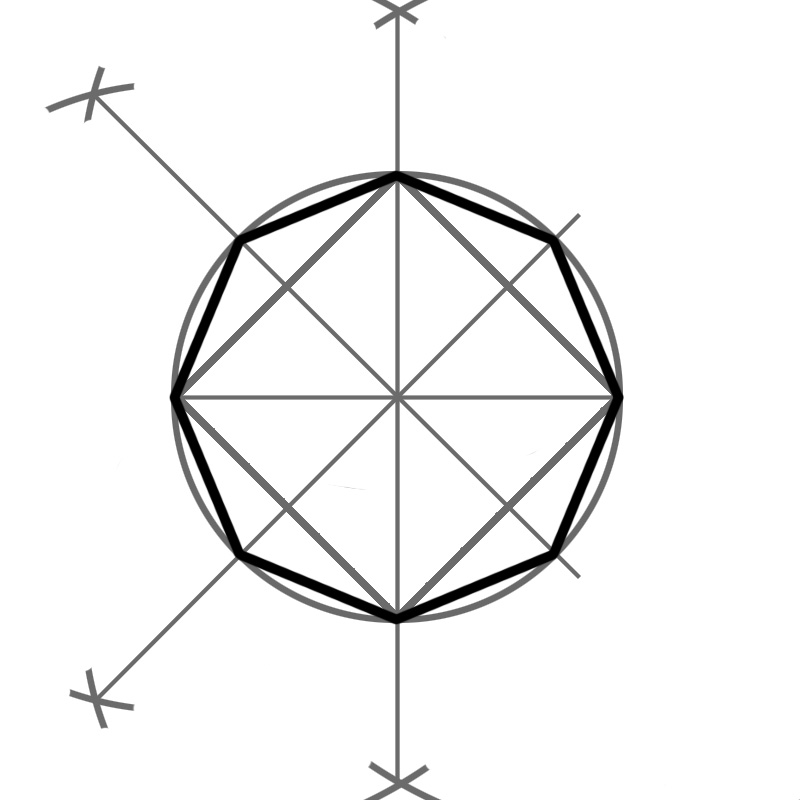
Установите раствор циркуля, равный диаметру окружности. Поставив иглу циркуля в одну из отмеченных на предыдущем этапе точек, сделайте засечки выше и ниже окружности. Старайтесь делать их не слишком короткими, поскольку они должны будут пересекаться с засечками, которые вы сделаете на следующем этапе.

Поставьте иглу циркуля в другую отмеченную точку и точно так же сделайте засечки выше и ниже окружности. Если провести прямую линию между точками пересечения засечек, то она пройдет через центр окружности, разделив первоначальный диаметр точно пополам, и будет к нему перпендикулярна.

Приложите линейку к двум найденным точкам и сделайте отметки на окружности там, где ее пересекает построенный перпендикуляр. Вы разделили окружность на четыре равные части, и найденные вами точки являются вершинами квадрата, вписанного в окружность. Первоначальный диаметр и его перпендикуляр, найденный на предыдущем этапе, служат диагоналями этого квадрата.

Чтобы завершить построение правильного восьмиугольника, нужно найти перпендикуляры к сторонам квадрата.

Установите раствор циркуля, равный стороне квадрата. Поместите иглу циркуля в любую вершину квадрата и сделайте засечки по обеим ее сторонам вне окружности.

Повторите процедуру с двумя вершинами квадрата, смежными с первой. У вас должны получиться две точки в местах пересечения засечек.

Приложите линейку так, чтобы она проходила через любую из найденных точек и центр окружности. Сделайте две отметки на окружности там, где ее пересекает полученная прямая. Повторите то же самое со второй найденной точкой.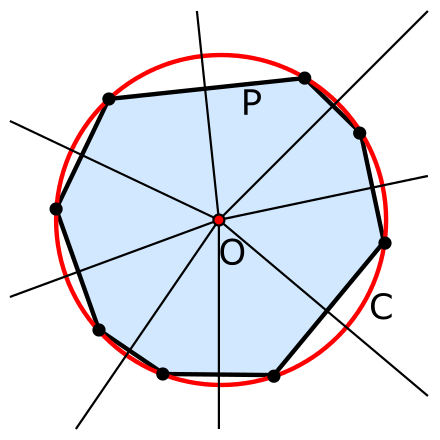 Теперь у вас есть восемь точек, делящих окружность на восемь равных частей. Это и есть вершины правильного восьмиугольника.

При помощи линейки соедините последовательно все восемь найденных точек. Построение завершено.

Построить равнобедренный треугольник (любого размера) с углом при вершине 45.

На основании треугольника отложить отрезок с длиной, равной длине стороны восьмиугольника, который следует построить.

Из конца отрезка провести прямую, параллельную боковой стороне треугольника, примыкающей к началу отрезка, до пересечения её с второй боковой стороной треугольника.

Отрезок от вершины треугольника до найденной точки и будет являться радиусом окружности, описанной вокруг искомого 8-угольника.

Ув. Джойстик. В вопросе автора длина стороны считается заданной.

1) Продолжить данный отрезок А1 в одну из сторон.
2) Провести перпендикуляр к отрезку А1.
3) Построить биссектрису полученного прямого угла.
4) На биссектрисе отложить новый отрезок А2 такой же длины,
как у А1.
5) Повторить 7 раз операции 1-4, начиная с отрезка А2.

«>

Как начертить правильный 8 угольник. Как построить правильный восьмиугольник

Куклин Алексей

Работа носит реферативный характер с элементами исследовательской деятельности. В ней рассматриваются различные способы построения правильных n-угольников. В работе содержится подробный ответ на вопрос о том, что всегда ли можно построить n-угольник с помощью циркуля и линейки. К работе прилагается презентация, которую можно найти на данном мини-сайте.

Скачать:

Предварительный просмотр:

Чтобы пользоваться предварительным просмотром создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com

Предварительный просмотр:

https://accounts.google.com

Подписи к слайдам:

Построение правильных многоугольников Работу выполнил: ученик 9 класса «В» МБОУ СОШ № 10 Куклин Алексей

Правильные многоугольники Правильным многоугольником называют выпуклый многоугольник, у которого все стороны и углы равны. Перейти к примерам Выпуклым многоугольником называется многоугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.

Назад Правильные многоугольники

Основоположниками раздела математики о правильных многоугольниках являлись древнегреческие ученые. Одними из них были Архимед и Евклид.

Доказательство существования правильного n-угольника Если n (число углов многоугольника) больше 2, то такой многоугольник существует. Попробуем построить 8ми угольник и доказать это. Доказательство

Возьмем окружность произвольного радиуса с центром в точке О. Разделим её на некоторое число равных дуг, в нашем случае 8. Для этого проведем радиусы так, чтобы получилось 8 дуг, и угол между двумя ближайшими радиусами был равен 360°: количество сторон (в нашем случае 8), соответственно каждый угол будет равен 45°.

3. Получаем точки A1, A2, A3, A4, A5, A6, A7, A8. Поочередно соединяем их и получаем правильный восьмиугольник. Назад

Построение правильного многоугольника по стороне с использованием поворота Правильный многоугольник можно построить, зная его углы. Мы знаем, что сумма углов выпуклого n-угольника равна 180°(n — 2). Из этого можно вычислить угол многоугольника, разделив сумму на n. Углы Построение

Угол правильного: 3-угольника равен 60° 4-угольника равен 90° 5-угольника равен 108° 6-угольника равен 120° 8-угольника равен 135° 9-угольника равен 140° 10-угольника равен 144° 12-угольника равен 150° Градусная мера углов правильных треугольников Назад

Предварительный просмотр:

Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com

Подписи к слайдам:

В 1796 году одним из величайших математиков всех времён Карл Фридрих Гаусс показал возможность построения правильных n-угольников, если выполняется равенство, где n – количество углов, а k-любое натуральное число. Тем самым получилось, что в пределах 30 возможно деление окружности на 2, 3, 4, 5, 6, 8, 10, 12, 15, 16, 17, 20, 24, 30 равных частей. В 1836 году Ванцель доказал, что правильные многоугольники, не удовлетворяющие данному равенству при помощи линейки и циркуля построить нельзя. Теорема Гаусса

Построение треугольника Построим окружность с центром в точке О. Построим еще одну окружность того же радиуса проходящую через точку О.

3. Соединим центры окружностей и одну из точек их пересечения, получив правильный многоугольник. Назад Построение треугольника

Построение шестиугольника 1. Построим окружность с центром в точке О. 2. Проведем прямую линию через центр окружности. 3. Проведем дугу окружности того же радиуса с центром в точке пересечения прямой с окружностью до пересечения с окружностью.

4. Проведем прямые через центр начальной окружности и точки пересечения дуги с этой окружностью. 5. Соединяем точки пересечения всех прямых с исходной окружностью и получаем правильный шестиугольник. Построение шестиугольника

Построение четырёхугольника Построим окружность с центром в точке О. Проведем 2 взаимно перпендикулярных диаметра. Из точек в которых диаметры касаются окружности проводим другие окружности данного радиуса до их пересечения (окружностей).

Построение четырёхугольника 4. Проводим прямые через точки пересечения окружностей. 5. Соединяем точки пересечения прямых и окружности и получаем правильный четырехугольник.

Построение восьмиугольника Можно построить любой правильный многоугольник у которого в 2 раза больше углов, чем у данного. Построим восьмиугольник при помощи четырехугольника. Соединим противоположные вершины четырехугольника. Проведем биссектрисы углов образованных пересекающимися диагоналями.

4. Соединим точки, лежащие на окружности, получив при этом правильный восьмиугольник. Построение восьмиугольника

Предварительный просмотр:

Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com

Подписи к слайдам:

Построение десятиугольника Построим окружность с центром в точке О. Проведем 2 взаимно перпендикулярных диаметра. Разделим радиус окружности пополам и из получившейся на нем точки проведем окружность проходящую через точку О.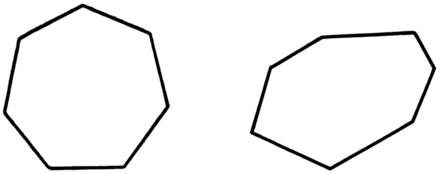

Построение десятиугольника 4. Проведем отрезок из центра маленькой окружности к точки в которой большая окружность касается своего радиуса. 5. Из точки соприкосновения большой окружности и её радиуса проведем окружность так, что она будет соприкасаться с маленькой.

Построение десятиугольника 6. Из точек пересечения большой и полученной окружностей проведем окружности построенные в прошлый раз и так будем проводить до тех пор пока соседние окружности не соприкоснутся. 7. Соединим точки и получим десятиугольник.

Построение пятиугольника Для построения правильного пятиугольника нужно во время построения правильного десятиугольника соединить поочередно не все точки, а через одну.

Приблизительное построение правильного пятиугольника методом Дюрера Построим 2 окружности проходящие через центр друг друга. Соединим центры прямой, получив одну из сторон пятиугольника. Соединим точки пересечения окружностей.

Приблизительное построение правильного пятиугольника методом Дюрера 4. Проведем еще одну окружность того же радиуса с центром в точке пересечения двух других окружностей. 5. Проведем 2 отрезка как указано на рисунке.

Приблизительное построение правильного пятиугольника методом Дюрера 6. Соединим точки соприкосновения этих отрезков с окружностями с концами построенной стороны пятиугольника. 7. Достроим до пятиугольника.

Приблизительное построение правильного пятиугольника методами Коваржика, Биона

Построение вписанного в окружность правильного шестиуголь­ника. Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения доста­точно разделить окружность на шесть равных частей и соединить най­денные точки между собой (фиг. 60, а).

Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг. 60, б), строим стороны 1 -6, 4-3, 4-5 и 7-2, после чего прово­дим стороны 5-6 и 3-2.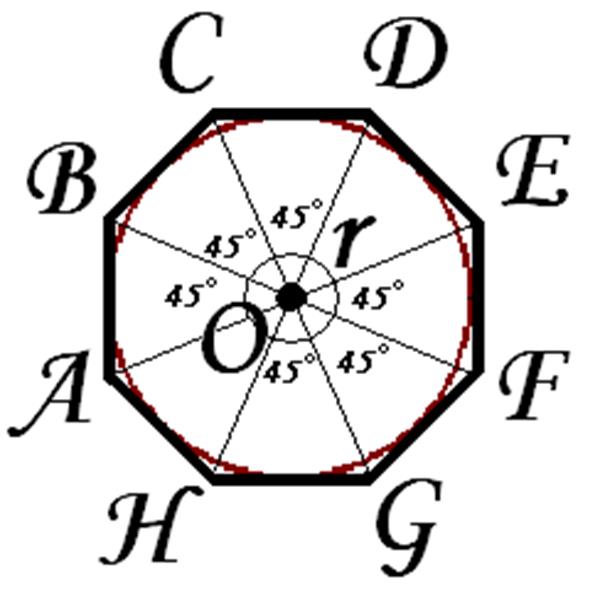

Построение вписанного в окружность равностороннего треуголь­ника . Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного цир­куля.

Рассмотрим два способа построения вписанного в окружность рав­ностороннего треугольника.

Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, прове­дённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0-1-2 равен 30°, то для нахождения стороны

1-2 достаточно построить по точке 1 и стороне 0-1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1-2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2-3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 прово­дим прямую, которая определит третью вершину треугольника.

Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вер­шины через одну, то получится равносторонний треугольник.

Для построения треугольника (фиг. 61, б) намечаем на диаметре вершину-точку 1 и проводим диаметральную линию 1-4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окруж­ностью в точках 3 и 2. Полученные точки будут двумя другими вер­шинами искомого треугольника.

Построение квадрата, вписанного в окружность . Это построение можно выполнить при помощи угольника и циркуля.

Первый способ основан на том, что диагонали квадрата пере­секаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные сто­роны квадрата 4-1 и 3-2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1-2 и 4-3.

Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра (фиг. 62, б).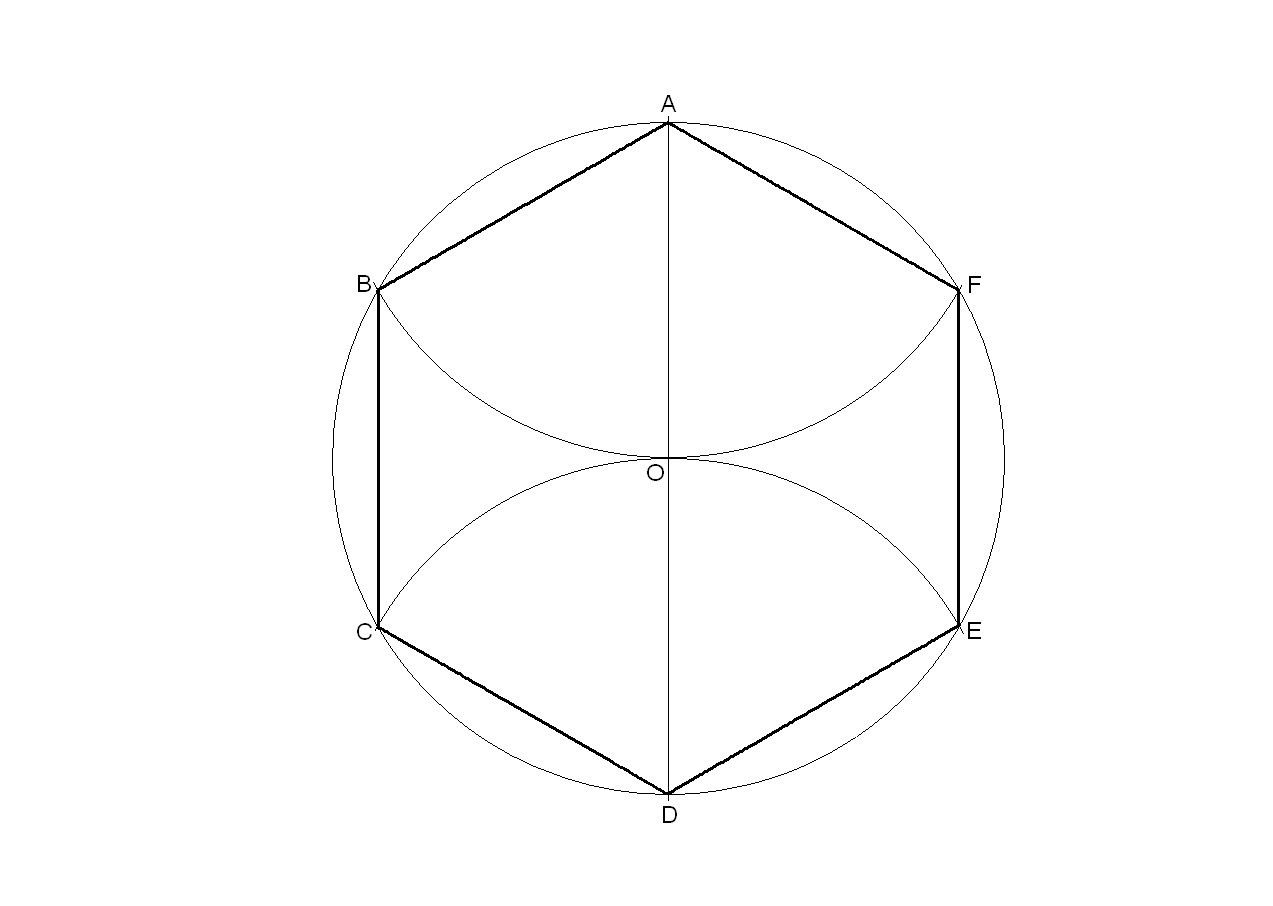 Намечаем на концах двух взаимно перпендикулярных диа­метров точки А, В и С и из них радиусом у описываем дуги до вза­имного их пересечения.

Далее через точки пересечения дуг проводим вспомогательные пря­мые, отмеченные на фигуре сплошными линиями. Точки их пересече­ния с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.

Построение вписанного в окружность правильного пятиугольника.

Чтобы вписать в окружность правильный пятиугольник (фиг. 63), про­изводим следующие построения.

Намечаем на окружности точку 1 и принимаем её за одну из вер­шин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точ­ках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника.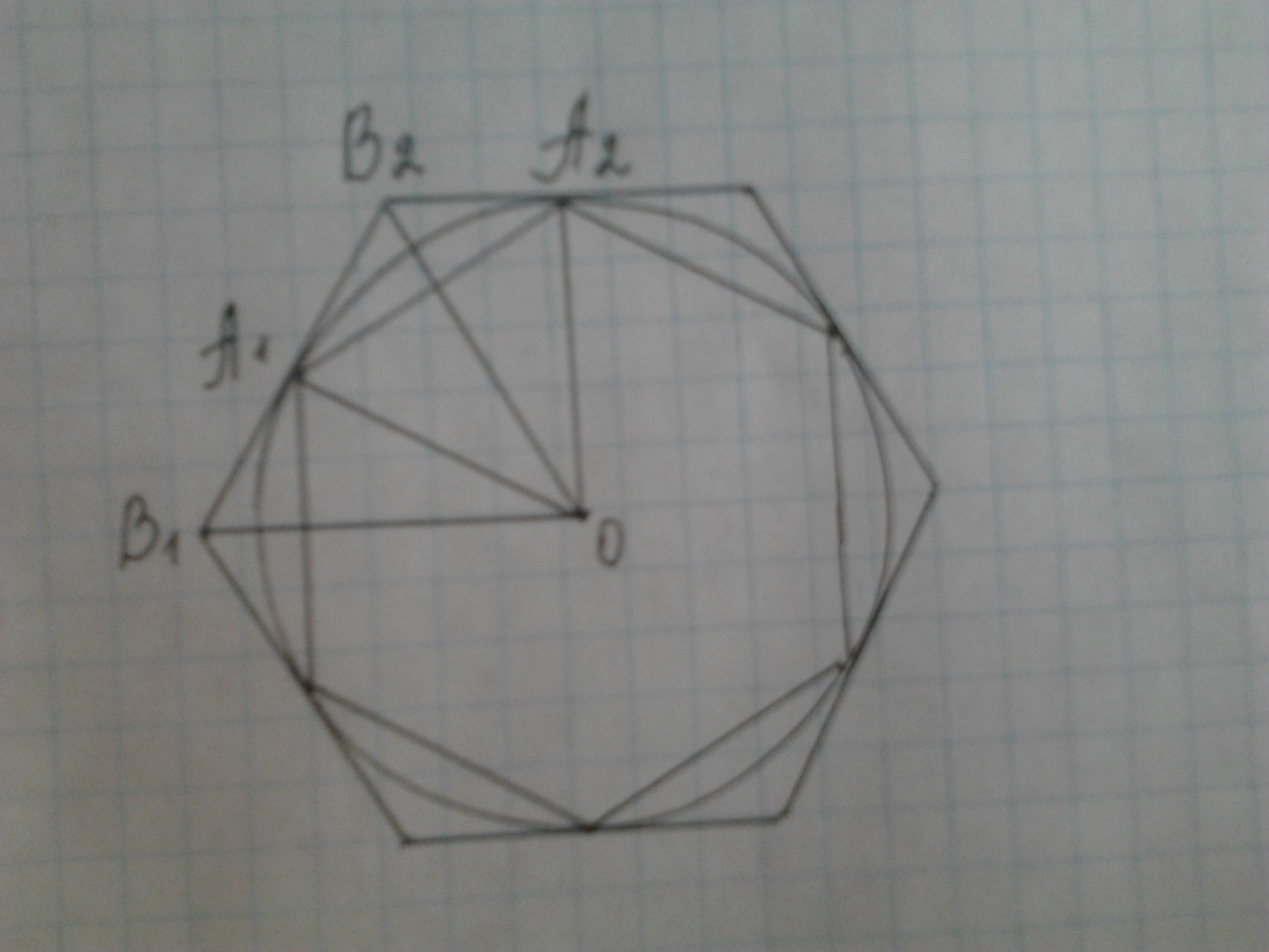 Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вер­шины 3 и 4. Найденные точки последовательно соединяем между собой.

Построение правильного пятиугольника по данной его стороне.

Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую.

Получим точку 1-вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведён­ными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.

Построение вписанного в окружность правильного семиугольника.

Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг.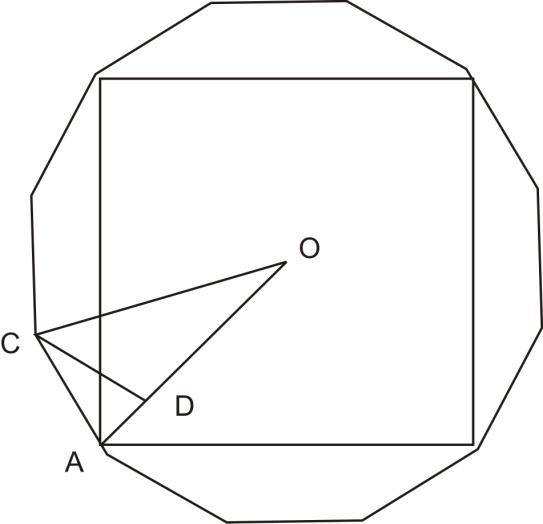 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиу­сом, равным диаметру окружности D, описываем дугу до пересечения с про­должением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, прово­дим из полюса F через чётные деления вертикального диаметра лучи, пересече­ние которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем после­довательно между собой. Семиугольник может быть построен путём проведе­ния лучей из полюса F и через нечётные деления вертикального диаметра.

Приведённый способ годен для построения правильных многоуголь­ников с любым числом сторон.

Деление окружности на любое число равных частей можно произ­водить также, пользуясь данными табл. 2, в которой приведены коэф­фициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.

Построение правильных многоугольников — техническое черчение. Как построить правильный восьмиугольник Как построить правильный 8 угольник

В черчении зачастую требуется строить положительные многоугольники. Так, скажем, положительные восьмиугольники применяются на щитах дорожных знаков.

Вам понадобится

• – циркуль
• – линейка
• – карандаш

Инструкция

1. Пускай задан отрезок, равный длине стороны желанного восьмиугольника. Требуется возвести верный восьмиугольник. Первым шагом постройте равнобедренный треугольник на заданном отрезке, применяя отрезок, как основание. Для этого вначале постройте квадрат со стороной, равной отрезку, проведите в нем диагонали. Сейчас постройте биссектрисы углов при диагоналях (на рисунке биссектрисы указаны синим), на пересечении биссектрис образуется вершина равнобедренного треугольника, стороны которого равны радиусу окружности, описанной вокруг верного восьмиугольника.

2. Постройте окружность с центром в вершине треугольника. Радиус окружности равен стороне треугольника. Сейчас разведите циркуль на расстояние, равное величине заданного отрезка. Отложите это расстояние на окружности, начиная от всякого конца отрезка. Объедините все полученные точки в восьмиугольник.

3. Если же задана окружность, в которую должен быть вписан восьмиугольник, то построения будут еще проще. Постройте две перпендикулярные друг другу осевые линии, проходящие через центр окружности. На пересечении осевых и окружности получатся четыре вершины грядущего восьмиугольника. Осталось поделить расстояние между этими точками на дуге окружности напополам, дабы получить еще четыре вершины.

Верный треугольник – тот, у которого все стороны владеют идентичной длиной. Исходя из этого определения, построение сходственной разновидности треугольник а является нетрудной задачей.

Вам понадобится

• Линейка, лист разлинованной бумаги, карандаш

Инструкция

1. Взять лист чистой бумаги, разлинованной в клеточку, линейку и подметить на бумаге три точки так, дабы они находились на идентичном друг от друга расстоянии (рис.1)

2. С подмогой линейки объединить подмеченные на листе точки ступенчато, друг за ином так, как это показано на рисунке 2.

Обратите внимание!
В верном (равностороннем) треугольнике все углы равны 60 градусам.

Полезный совет
Равносторонний треугольник так же является и равнобедренным. Если треугольник равнобедренный, то это обозначает, что 2 из 3-х его сторон равны, а третья сторона считается основанием. Всякий положительный треугольник является равнобедренным, в то время как обратное заявление не правильно.

Восьмиугольник – это, по своей сути, два квадрата, смещенных касательно друг друга на 45° и объединенных на вершинах цельной линией. А потому, для того дабы положительно изобразить такую геометрическую фигуру, нужно твердым карандашом дюже опрятно, по правилам начертить квадрат либо круг, с которыми и проводить последующие действия. Изложение ориентировано на длину стороны, равной 20 см. А значит, при расположении чертежа рассматривайте, дабы вертикальная и горизонтальная линии длиной 20 см умещались на листе бумаги.

Вам понадобится

• Линейка, прямоугольный треугольник, транспортир, карандаш, циркуль, лист бумаги

Инструкция

1. Метод 1. Начертите внизу горизонтальную линию длиной 20 см. После этого с одной стороны подметьте транспортиром прямой угол, тот, что составляет 90°. То же самое дозволено сделать с поддержкой прямого треугольника. Проведите вертикальную линию и подметьте 20 см. Проделайте те же самые манипуляции с иной стороны. Объедините две полученные точки горизонтальной линией. В итоге получилась геометрическая фигура – квадрат.

2. Для того дабы возвести 2-й (смещенный) квадрат, потребуется центр фигуры. Для этого поделите всякую сторону квадрата на 2 части. Объедините вначале 2 точки параллельных верхней и нижней сторон, а потом точки боковых сторон. Проведите через центр квадрата 2 прямые линии, перпендикулярные касательно друг друга. Начиная от центра, отмерьте на новых прямых длину по 10 см, что в результате даст 4 прямые линии. Объедините 4 полученные наружные точки между собой, в итоге чего получится 2-й квадрат. Сейчас всякую точку из 8 полученных углов объедините между собой. Таким образом, будет начерчен восьмиугольник.

3. Метод 2. Для этого потребуется циркуль, линейка и транспортир. От центра листа с поддержкой циркуля начертите круг диаметром 20 см (радиус 10 см). Через центральную точку проведите прямую линию. После этого начертите вторую перпендикулярную ей линию. То же самое дозволено исполнить с подмогой транспортира либо прямого треугольника. В итоге круг будет поделен на 4 равные части. Дальше всякий из секций поделите еще на 2 части. Для этого также дозволено воспользоваться транспортиром, отмеряя 45° либо прямоугольным треугольником, тот, что приложите острым углом в 45° и проведите лучи. От центра на всякой прямой линии отмерьте по 10 см. В итоге получатся 8 «лучиков», которые объедините между собой. В итоге получится восьмиугольник.

4. Метод 3. Для этого так же начертите круг, проведите через середину линию. После этого возьмите транспортир, поставьте его на центр и отмеряйте углы, рассматривая, что всякий секция восьмиугольника имеет в центре угол 45° . Позже этого на полученных лучах отмерьте длину в 10 см. и объедините их между собой. Восьмиугольник готов.

Полезный совет
Делайте чертеж твердым карандашом, побочные линии на котором после этого легко дозволено будет удалить

Верный восьмиугольник – это геометрическая фигура, у которой всякий угол составляет 135?, и все стороны между собою равны. Эта фигура дюже зачастую используется в архитектуре, к примеру, при постройке колон, а также при изготовлении дорожного знака STOP. Как же нарисовать положительный восьмиугольник?

Вам понадобится

• – альбомный лист;
• – карандаш;
• – линейка;
• – циркуль;
• – ластик.

Инструкция

1. Нарисуйте вначале квадрат. После этого проведите окружность так, дабы квадрат оказался внутри круга. Сейчас проведите две осевые серединные линии квадрата – горизонтальную и вертикальную до пересечения с кругом. Объедините прямыми отрезками точки пересечения осей с кругом и точки прикосновения описанной окружности с квадратом. Таким образом, получите стороны верного восьмиугольника.

2. Нарисуйте верный восьмиугольник иным методом. Вначале начертите окружность. После этого проведите горизонтальную линию через ее центр. Подметьте точку пересечения крайней правой границы окружности с горизонталью. Эта точка будет являться центром еще одной окружности, радиусом равным предыдущей фигуре.

3. Проведите вертикальную линию через точки пересечения 2-й окружности с первой. Поставьте ножку циркуля в точку пересечения вертикали с горизонталью и начертите небольшой круг радиусом, равным расстоянию от центра крошечной окружности до центра начального круга.

4. Начертите прямую линию через две точки – центр начального круга и точку пересечения вертикали и крошечной окружности. Продолжите ее до пересечения с рубежом изначальной фигуры. Это будет точка вершины восьмиугольника. Циркулем подметьте еще одну точку, проведя окружность с центром в точке пересечения крайней правой рубежом начального круга с горизонталью и радиусом, равным расстоянию от центра к теснее имеющейся вершине восьмиугольника.

5. Проведите прямую линию через две точки – центр начального круга и последнюю новообразованную точку. Продолжите прямую линию до пересечения с границами первоначальной фигуры.

6. Объедините прямыми отрезками ступенчато: точку пересечения горизонтали с правой рубежом начальной фигуры, после этого по часовой стрелке все образовавшиеся точки, включая точки пересечения осей с первоначальной окружностью.

Видео по теме

Построение вписанного в окружность правильного шестиуголь­ника. Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения доста­точно разделить окружность на шесть равных частей и соединить най­денные точки между собой (фиг. 60, а).

Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг. 60, б), строим стороны 1 -6, 4-3, 4-5 и 7-2, после чего прово­дим стороны 5-6 и 3-2.

Построение вписанного в окружность равностороннего треуголь­ника . Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного цир­куля.

Рассмотрим два способа построения вписанного в окружность рав­ностороннего треугольника.

Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, прове­дённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0-1-2 равен 30°, то для нахождения стороны

1-2 достаточно построить по точке 1 и стороне 0-1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1-2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2-3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 прово­дим прямую, которая определит третью вершину треугольника.

Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вер­шины через одну, то получится равносторонний треугольник.

Для построения треугольника (фиг. 61, б) намечаем на диаметре вершину-точку 1 и проводим диаметральную линию 1-4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окруж­ностью в точках 3 и 2. Полученные точки будут двумя другими вер­шинами искомого треугольника.

Построение квадрата, вписанного в окружность . Это построение можно выполнить при помощи угольника и циркуля.

Первый способ основан на том, что диагонали квадрата пере­секаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные сто­роны квадрата 4-1 и 3-2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1-2 и 4-3.

Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра (фиг. 62, б). Намечаем на концах двух взаимно перпендикулярных диа­метров точки А, В и С и из них радиусом у описываем дуги до вза­имного их пересечения.

Далее через точки пересечения дуг проводим вспомогательные пря­мые, отмеченные на фигуре сплошными линиями. Точки их пересече­ния с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.

Построение вписанного в окружность правильного пятиугольника.

Чтобы вписать в окружность правильный пятиугольник (фиг. 63), про­изводим следующие построения.

Намечаем на окружности точку 1 и принимаем её за одну из вер­шин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точ­ках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вер­шины 3 и 4. Найденные точки последовательно соединяем между собой.

Построение правильного пятиугольника по данной его стороне.

Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую.

Получим точку 1-вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведён­ными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.

Построение вписанного в окружность правильного семиугольника.

Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиу­сом, равным диаметру окружности D, описываем дугу до пересечения с про­должением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, прово­дим из полюса F через чётные деления вертикального диаметра лучи, пересече­ние которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем после­довательно между собой. Семиугольник может быть построен путём проведе­ния лучей из полюса F и через нечётные деления вертикального диаметра.

Приведённый способ годен для построения правильных многоуголь­ников с любым числом сторон.

Деление окружности на любое число равных частей можно произ­водить также, пользуясь данными табл. 2, в которой приведены коэф­фициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.

Куклин Алексей

Работа носит реферативный характер с элементами исследовательской деятельности. В ней рассматриваются различные способы построения правильных n-угольников. В работе содержится подробный ответ на вопрос о том, что всегда ли можно построить n-угольник с помощью циркуля и линейки. К работе прилагается презентация, которую можно найти на данном мини-сайте.

Скачать:

Предварительный просмотр:

Чтобы пользоваться предварительным просмотром создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com

Предварительный просмотр:

https://accounts.google.com

Подписи к слайдам:

Построение правильных многоугольников Работу выполнил: ученик 9 класса «В» МБОУ СОШ № 10 Куклин Алексей

Правильные многоугольники Правильным многоугольником называют выпуклый многоугольник, у которого все стороны и углы равны. Перейти к примерам Выпуклым многоугольником называется многоугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.

Назад Правильные многоугольники

Основоположниками раздела математики о правильных многоугольниках являлись древнегреческие ученые. Одними из них были Архимед и Евклид.

Доказательство существования правильного n-угольника Если n (число углов многоугольника) больше 2, то такой многоугольник существует. Попробуем построить 8ми угольник и доказать это. Доказательство

Возьмем окружность произвольного радиуса с центром в точке О. Разделим её на некоторое число равных дуг, в нашем случае 8. Для этого проведем радиусы так, чтобы получилось 8 дуг, и угол между двумя ближайшими радиусами был равен 360°: количество сторон (в нашем случае 8), соответственно каждый угол будет равен 45°.

3. Получаем точки A1, A2, A3, A4, A5, A6, A7, A8. Поочередно соединяем их и получаем правильный восьмиугольник. Назад

Построение правильного многоугольника по стороне с использованием поворота Правильный многоугольник можно построить, зная его углы. Мы знаем, что сумма углов выпуклого n-угольника равна 180°(n — 2). Из этого можно вычислить угол многоугольника, разделив сумму на n. Углы Построение

Угол правильного: 3-угольника равен 60° 4-угольника равен 90° 5-угольника равен 108° 6-угольника равен 120° 8-угольника равен 135° 9-угольника равен 140° 10-угольника равен 144° 12-угольника равен 150° Градусная мера углов правильных треугольников Назад

Предварительный просмотр:

Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com

Подписи к слайдам:

В 1796 году одним из величайших математиков всех времён Карл Фридрих Гаусс показал возможность построения правильных n-угольников, если выполняется равенство, где n – количество углов, а k-любое натуральное число. Тем самым получилось, что в пределах 30 возможно деление окружности на 2, 3, 4, 5, 6, 8, 10, 12, 15, 16, 17, 20, 24, 30 равных частей. В 1836 году Ванцель доказал, что правильные многоугольники, не удовлетворяющие данному равенству при помощи линейки и циркуля построить нельзя. Теорема Гаусса

Построение треугольника Построим окружность с центром в точке О. Построим еще одну окружность того же радиуса проходящую через точку О.

3. Соединим центры окружностей и одну из точек их пересечения, получив правильный многоугольник. Назад Построение треугольника

Построение шестиугольника 1. Построим окружность с центром в точке О. 2. Проведем прямую линию через центр окружности. 3. Проведем дугу окружности того же радиуса с центром в точке пересечения прямой с окружностью до пересечения с окружностью.

4. Проведем прямые через центр начальной окружности и точки пересечения дуги с этой окружностью. 5. Соединяем точки пересечения всех прямых с исходной окружностью и получаем правильный шестиугольник. Построение шестиугольника

Построение четырёхугольника Построим окружность с центром в точке О. Проведем 2 взаимно перпендикулярных диаметра. Из точек в которых диаметры касаются окружности проводим другие окружности данного радиуса до их пересечения (окружностей).

Построение четырёхугольника 4. Проводим прямые через точки пересечения окружностей. 5. Соединяем точки пересечения прямых и окружности и получаем правильный четырехугольник.

Построение восьмиугольника Можно построить любой правильный многоугольник у которого в 2 раза больше углов, чем у данного. Построим восьмиугольник при помощи четырехугольника. Соединим противоположные вершины четырехугольника. Проведем биссектрисы углов образованных пересекающимися диагоналями.

4. Соединим точки, лежащие на окружности, получив при этом правильный восьмиугольник. Построение восьмиугольника

Предварительный просмотр:

Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com

Подписи к слайдам:

Построение десятиугольника Построим окружность с центром в точке О. Проведем 2 взаимно перпендикулярных диаметра. Разделим радиус окружности пополам и из получившейся на нем точки проведем окружность проходящую через точку О.

Построение десятиугольника 4. Проведем отрезок из центра маленькой окружности к точки в которой большая окружность касается своего радиуса. 5. Из точки соприкосновения большой окружности и её радиуса проведем окружность так, что она будет соприкасаться с маленькой.

Построение десятиугольника 6. Из точек пересечения большой и полученной окружностей проведем окружности построенные в прошлый раз и так будем проводить до тех пор пока соседние окружности не соприкоснутся. 7. Соединим точки и получим десятиугольник.

Построение пятиугольника Для построения правильного пятиугольника нужно во время построения правильного десятиугольника соединить поочередно не все точки, а через одну.

Приблизительное построение правильного пятиугольника методом Дюрера Построим 2 окружности проходящие через центр друг друга. Соединим центры прямой, получив одну из сторон пятиугольника. Соединим точки пересечения окружностей.

Приблизительное построение правильного пятиугольника методом Дюрера 4. Проведем еще одну окружность того же радиуса с центром в точке пересечения двух других окружностей. 5. Проведем 2 отрезка как указано на рисунке.

Приблизительное построение правильного пятиугольника методом Дюрера 6. Соединим точки соприкосновения этих отрезков с окружностями с концами построенной стороны пятиугольника. 7. Достроим до пятиугольника.

Приблизительное построение правильного пятиугольника методами Коваржика, Биона

CorelDRAW Graphics Suite — Учебные пособия

Автор: Анна Мария Лопес Лопес (Anna María López López)

Этот урок был опубликован одним из первых на сайте www.CORELCLUB.org, который в 1996 году был известен как «Anna’s CorelClub Spain».

Благодаря своему успеху среди пользователей продуктов Corel этот урок был впоследствии включен в несколько моих книг. Кроме того, я преподавала эту технику на курсах и семинарах, посвященных CorelDRAW.

Пришла пора сдуть пыль с этого учебного пособия и сделать его широко доступным.

Этот несложный прием позволяет добиться интересных творческих результатов с помощью трех простых инструментов CorelDRAW: Многоугольник, Указатель и Форма.

Процесс создания многоугольников в CorelDRAW интуитивно понятен. Когда в версии 6 впервые был представлен инструмент Многоугольник, постоянные пользователи CorelDRAW по достоинству оценили его универсальность и интерактивность.

На первый взгляд этот инструмент не создает впечатление креативного инструмента с широкими возможностями, ведь он предназначен для создания многосторонних многоугольников. Этот урок убедит вас в обратном.

Для начала нам нужно начертить простой многоугольник. Для этого щелкните инструмент «Многоугольник» и протащите курсор в окне рисования, пока многоугольник не достигнет желаемых размеров.

Совет: для создания симметричного многоугольника (многоугольника с равными сторонами) удерживайте клавишу Ctrl, а для создания многоугольника от центра наружу — клавишу Shift.

После того, как многоугольник создан, выделите его с помощью инструмента Указатель. Количество сторон многоугольника может быть изменено в любой момент. Для этого в поле Точки или стороны на панели свойств нужно ввести число сторон. Помните, что для внесения изменений в объект его нужно выделить с помощью инструмента Указатель.

У нашего многоугольника 8 восемь сторон (восьмиугольник).

После того, как многоугольник создан, щелкните инструмент Форма и нарисуйте окно вокруг многоугольника.

Будут выделены два узла, а на панели свойств отобразятся параметры редактирования узлов. Нажмите значок Преобразовать в кривые.

На первый взгляд изменения не будут заметны. Однако, щелкнув один из узлов или путь многоугольника с помощью инструмента Форма и протащив курсор внутрь или наружу, вы заметите, что стороны многоугольника искривляются. Это позволяет создавать разнообразные формы. Посмотрите:

Вы можете продолжать изменять форму многоугольника. Для этого нужно щелкнуть и перетащить узлы и опорные маркеры.

Кроме того, к многоугольнику можно применить заливку цветом. Как видите, здесь я залила многоугольник черным цветом, щелкнув нужный образец цвета на цветовой палитре.

Замечательная особенность состоит в том, что в течение всего процесса исходный многоугольник можно модифицировать — изменять количество сторон многоугольника можно столько раз, сколько нужно.

Каждый раз при изменении количества сторон многоугольника будет создаваться новая фигура.

Попробуйте: выделите многоугольник и измените количество сторон. Для этого в поле Точки или стороны на панели свойств введите нужное число. Как и в этом примере, ваш многоугольник будет автоматически преобразован в новую форму.

Это может показаться удивительным, но все формы на изображении ниже были созданы с помощью этой техники. Щелкнув изображение*, вы можете загрузить исходный файл (http://www.corelclub.org/tutoriales/practicas/ejercicio-tutorial-poligonos-corelclub.cdr).

*Объем этого .cdr файла — 31 КБ. Чтобы сохранить его на своем компьютере, щелкните ссылку правой кнопкой мыши и выберите «Сохранить ссылку как». Затем файл можно будет открыть в CorelDRAW.

Вы сможете взаимодействовать с каждым многоугольником в этом файле и убедиться в универсальности и огромных возможностях инструмента CorelDRAW Многоугольник.

—————

Этот урок разработала Анна Мария Лопес Лопес (Anna María López López) — многопрофильный дизайнер, основатель www.corelclub.org и автор многочисленных книг по цифровому дизайну, таких как www.cursodisenografico.net.

Источник: http://www.corelclub.org/tutorial-poligonos-coreldraw/

Занятие 8 — Программирование на Scratch

Тема: Ящик «Перо».

Задачи:

• Познакомиться с командами ящика «Перо»;
• Вспомнить координаты на сцене;
• Закрепить использование циклических алгоритмов.

1. Ящик «Перо»

На сцене спрайт может оставлять рисунки. Для работы с рисование в Scratch предназначен ящик «Перо». Рассмотрим команды этого ящика:

Задание 8.1

Создадим проект, в котором спрайт будет рисовать. При нажатии клавиши клавиатуры, спрайт будет рисовать различные объекты:

• клавиша «1»- спрайт рисует цифру «1»;
• клавиша «2» — цифру «2»;
• клавиша «3» — цифру «3»;
• клавиша «4» — спрайт рисует квадрат;
• клавиша «6» — спрайт рисует шестиугольник;
• клавиша «8» — спрайт рисует восьмиугольник.

1. Создайте новый проект.

2. Выберите спрайта, а сцену оставьте белой.

3. Зададим начальные значения событием «Когда щелкнут по флажку«. «Очистим» сцену и «Опустим перо«, чтобы дальнейшие движения спрайта оставляли след. Спрайту можно дать команду «Спрятаться» или, если Вы хотите его видеть, «Показаться«.

4. Для того, чтобы выполнить проект нам понадобиться команда ящика «События» — «Когда клавиша … нажата«. Попробуем нарисовать цифру 1. Нам понадобятся координаты на сцене. Например цифру 1 можно нарисовать по следующим координатам:

Тогда скрипт можно записать так:5. Цифры 2 и 3 попробуйте нарисовать сами. Также используйте события «Когда клавиша … нажата«.

6. Для того, чтобы нарисовать квадрат воспользуемся циклом. «Повторим 4» раза движение вперед и поворот на 90 градусов.

Количество углов (и сторон) фигуры — 4, поэтому повторяем 4 раза.

Чтобы посчитать угол, разделим 360 на количество углов — четыре, получим 90 градусов.

7. Нарисуем шестиугольник. Повторить нужно будет 6 раз, а угол 360:6=60 градусов.

8. Попробуйте самостоятельно нарисовать восьмиугольник. Сколько раз повториться цикл? На какой угол нужно будет повернуться?

9. Сохраните проект под название «Рисование», откройте доступ к своему проекту.

Объект Многоугольник в Автокаде — как построить его в AutoCAD различными способами

[Уроки Автокад] Как нарисовать (начертить) многоугольник в AutoCAD

---

Команда рисования в AutoCAD

Многоугольник

Определение

Многоугольник в Автокад — является замкнутой 2D-полилинией, состоящей из трех и более сегментов. Правильный многоугольник — это многоугольник у которого все стороны и углы равны.

Инструмент

Инструмент Автокад Многоугольник — строит правильный многоугольник либо по конечным точкам одной стороны, либо по точке центра и радиусу вписанной или описанной окружности.

Команда

МН-Угол

Объект

Полилиния

Команда МН-Угол в AutoCAD

За создание в Автокад правильного многоугольника отвечает команда MH-Угол.

Вызвать данную команду можно следующими способами (начать построение в AutoCAD многоугольника):

• построить многоугольник в Автокад можно из строки меню пункт Рисование — строка Многоугольник;
• начертить его можно из ленты инструментов на вкладке «Главная» — в группе Рисование кнопка Многоугольник;
• нарисовать многоугольник в Автокад можно из классической панели инструментов Рисование кнопка Многоугольник;
• либо прописать наименование команды в командной строке МН-Угол.

Построение многоугольника в Автокад вписанного в окружность

Как уже отмечалось, в вписанный в AutoCAD многоугольник в окружность задается центральной точкой и расстоянием от центра до любой из вершин. Следовательно, радиус описанной окружности — это расстояние от центра многоугольника до одной из его вершин.

Вызываем команду МН-Угол. В командной строке появляется запрос:

Число сторон <4>:

В ответ на который вы должны ввести число сторон, которое должно быть у многоугольника в AutoCAD (от 3 до 1024). Введем значение 5. Нажимаем «Enter». Появляется следующий запрос:

Укажите центр многоугольника:

Зададим центр многоугольника в AutoCAD щелчком мыши. Система отобразит запрос:

Задайте параметр размещения [Вписанный в окружность/Описанный вокруг окружности] <В>:

Выбираем опцию «Вписанный в окружность». Отобразится предварительный вид многоугольника AutoCAD, который прикреплен к линии, проходящей из заданного центра до указателя. Размер его будет изменяться вместе с изменением положения указателя. В командной строке появится запрос:

Радиус окружности:

Радиус окружности можно задать, введя значение в командную строку или щелчком мыши, указав точку на чертеже. Введем значение 20 мм в командную строку и нажмем «Enter». Правильный пятиугольник (многоугольник) в Автокад с радиусом описанной окружности 20 мм построен.

Как начертить многоугольник в AutoCAD описанный вокруг окружности

Многоугольник Автокад описанный вокруг окружности задается центральной точкой и расстоянием от центра до средней точки одной из его сторон. Следовательно, радиус вписанной окружности — это расстояние от центра многоугольника до средней точки одной из его сторон.

Вызываем команду «МН-Угол». Система отобразит запрос:

Число сторон <5 — предыдущее значение>:

Соглашаемся со значением по умолчанию, нажимаем «Enter». Появляется следующий запрос:

Укажите центр многоугольника:

Указываем в Автокад центр многоугольника. Появляется запрос в командной строке:

Задайте параметр размещения [Вписанный в окружность/Описанный вокруг окружности] <В>:

Выбираем опцию «Описанный вокруг окружности» команды МН-Угол. Отобразится предварительный вид многоугольника Автокад, который прикреплен к линии, проходящей из заданного центра до указателя, соответствующего середине одной из сторон многоугольника. Размер многоугольника в Автокад будет изменяться вместе с изменением положения указателя. В командной строке появится запрос:

Радиус окружности:

Повторим ввод координат и зададим радиус описанной окружности с помощью задания относительных полярных координат. Введем в командную строку следующее значение @20<0, что означает:

• «@» — отсчет координат ведется от центральной точки многоугольника Автокад;
• «20» — расстояние от центральной точки, т.е. радиус вписанной окружности;
• «<» обозначение полярности координат — возможности привязки к определенному углу;
• «0» — значение угла, т.е. 0 градусов.

Правильный многоугольник в Автокад с радиусом вписанной окружности 20 мм построен.

Совет

Задав радиус вписанной или описанной окружности в командной строке путем ввода значения радиуса, многоугольник в Автокад автоматически выравнивается так, чтобы его нижняя сторона располагалась параллельно оси X текущей ПСК. Если задать радиус при помощи мыши (различными методами задания координат), то можно повернуть многоугольник вокруг центра на нужный угол.

Как построить многоугольник по конечным точкам одной стороны (по стороне)

Как в Автокад начертить многоугольник по стороне (алгоритм):

Вызываем команду МН-Угол в AutoCAD. В командной строке появляется запрос:

Число сторон <5 — предыдущее значение>:

Соглашаемся со значением по умолчанию, т.е. 5 сторон многоугольника Автокад. Нажимаем «Enter». Система отобразит запрос:

Укажите центр многоугольника или [Сторона]:

Выбираем опцию «Сторона», чтобы начать строить в AutoCAD многоугольник по одной из сторон. Появляется следующий запрос:

Первая конечная точка стороны:

Укажем первую конечную точку стороны многоугольника Автокад щелчком мыши. Отобразиться его предварительный вид, который прикреплен к линии, проходящей от заданной первой конечной точки стороны до второй конечной точки. Появится запрос:

Вторая конечная точка стороны:

Вторую конечную точку стороны многоугольника в AutoCAD можете указать щелчком мыши или вводом координат в командную строку. Укажем точку щелчком мыши.

Правильный пятиугольник (многоугольник) в Автокад произвольных размеров по стороне построен.

Полезные уроки схожих тематик и рекомендации

Рекомендую ознакомиться с подобными уроками по Автокад:

Читайте и смотрите также:

Курсы, самоучители Автокад:

1. 2D проектирование.
2. 3D моделирование.
3. Начертательная геометрия.
4. Инженерная графика.
5. План дома.
6. Сборочный чертеж цилиндрической зубчатой передачи.
7. Модель кухни 3D.

Видео «Как начертить прямоугольник и правильный многоугольник в Автокад»

Как поэтапно нарисовать восьмиугольник? — Mvorganizing.org

Как нарисовать восьмиугольник поэтапно?

Создайте восьмиугольник из квадрата

1. Шаг 1. Разделите на части. Разделите длину на три части.
2. Шаг 2: Разделите на 9 квадратов. Нарисуйте по разметке 9 маленьких квадратов.
3. Шаг 3. Создайте восьмиугольник из 9 квадратов. Нарисуйте линии так, чтобы восьмиугольник был виден в 9 квадратах.
4. Шаг 4: Сотрите восьмиугольник.

Как нарисовать 8-сторонний многоугольник?

Обычный восьмиугольник. Нарисуйте большой круг в центре страницы. Нарисуйте прямую горизонтальную линию, разделяющую круг на равные части. Нарисуйте прямую вертикальную линию (также разделяющую круг на равные части), центр которой будет пересекаться с центром горизонтальной линии.

Как построить правильный восьмиугольник с заданной стороной?

С помощью транспортира отметьте угол 135 ° относительно вашей линии. На любом конце линии найдите и отметьте угол 135 °.Нарисуйте линию той же длины, что и первая, под углом 135 градусов к исходной линии. Это вторая сторона восьмиугольника.

Как называется 4-сторонняя форма?

четырехугольник

Как называется 6-сторонняя форма?

шестигранник

Как называется 100-сторонняя форма?

га

У шестиугольников 6 равных сторон?

У правильного шестиугольника шесть равных сторон и шесть равных внутренних углов.

Как называется 8-сторонняя форма?

В геометрии восьмиугольник (от греческого ὀκτάγωνον oktágōnon, «восемь углов») представляет собой восьмиугольник или восьмиугольник.Правильный восьмиугольник имеет символ Шлефли {8}, а также может быть построен как квазирегулярный усеченный квадрат t {4}, который чередует два типа ребер.

Как называется 13-сторонняя форма?

Tridecagon

Как называется 20-гранная форма?

icosagon

Какая форма самая большая?

мириагон

Есть ли двусторонняя форма?

В геометрии двуугольник — это многоугольник с двумя сторонами (ребрами) и двумя вершинами. У правильного двуугольника оба угла равны и обе стороны равны, он обозначается символом Шлефли {2}.

методов построения правильных многоугольников, подходящих для вводных уроков

Охочуку Н. Стивен

Кафедра химии, факультет естественных и прикладных наук, Педагогический университет Игнатия Аджуру, Порт-Харкорт, Нигерия

Адрес для корреспонденции: Охочуку Н.Стивен, факультет химии, факультет естественных и прикладных наук, Педагогический университет Игнатиуса Аджуру, Порт-Харкорт, Нигерия.

Электронная почта:

Авторские права © 2016 Научно-академическое издательство. Все права защищены.

Эта работа находится под лицензией Creative Commons Attribution International License (CC BY).
http: // creativecommons.org / licenses / by / 4.0 /

Аннотация

Введение правильных многоугольников и их построение всегда включало правильные шестиугольники и правильные восьмиугольники. Вводные конструкции правильных шестиугольников представляют собой использование кругов, разделенных на шесть равных секторов с использованием радиуса круга, в то время как в случае восьмиугольников используется разбиение кругов на восемь равных секторов.После этого конструкции различных классов правильных многоугольников исследуются с использованием либо базового угла, либо внешнего угла, либо другого сложного метода, свойственного конкретному семейству многоугольников. В этой статье представлены новые методы построения каждого семейства правильных многоугольников от 3-угольника до 9-угольника (от трехугольника до девятиугольника), которые подходят для вводных классов. Методы, перечисленные для каждого семейства правильных многоугольников, настолько просты, что вызывают интерес к построению многоугольников другими методами.Методы, представленные здесь для использования во вводных уроках, хотя и простые, также проходят как стандартные методы для построения конкретного семейства правильных многоугольников.

Ключевые слова: Вводные способы построения многоугольника

Цитируйте эту статью: Охочуку Н.Стивен, Методы построения правильных многоугольников, подходящие для вводных уроков, Американский журнал математики и статистики , Vol. 6 No. 6, 2016, pp. 242-250. DOI: 10.5923 / j.ajms.20160606.04.

Краткое содержание статьи

1. Введение

2. Методология

2.2. Построение правильного «треугольника» (равностороннего треугольника) стороны AB

2.2.1. Построение правильного «треугольника» (равностороннего треугольника) стороны AB прямым методом, рисунок 2

2.2.2. Построение правильного треугольника (равностороннего треугольника) методом сектора круга, рисунок 3

2.2.3. Построение правильного треугольника (равностороннего треугольника) методом пересекающихся окружностей, рисунок 4

2.3. Построение правильного Тетрагона (Квадрата)

2.3.1. Построение правильного тетрагона (квадрата) стороны AB методом пересекающихся кругов, рис. 5а

2.3.2. Построение квадрата квадрантным методом, рис. 6

2.3.3. Тетрагон через данный равнобедренный прямоугольный треугольник ABC, рис. 7

2.4. Строительство Правильного Пентагона

2.4.1. Из равностороннего треугольника с той же стороны. Метод треугольника / круга, рисунок 8

2.4.2. Правильный пятиугольник из трех пересекающихся коллинеарных кругов, рис. 8a

2.5. Построение правильного шестиугольника известной стороны AB

2.5.1. Шестиугольник от любого равностороннего треугольника через перпендикулярную сторону или биссектрису угла, рисунок 9

2.5.2. Шестиугольник из равностороннего треугольника с той же стороной AB посредством процедуры увеличения, рисунок 10

2.5.3. Построение шестиугольника из пересекающихся кругов с центрами в вершинах равностороннего треугольника, рис. 11

2.6. Правильный семиугольник

2.6.1. Развертка из треугольника с помощью процедуры множественного круга, рисунок 12

2.6.2. Правильный семиугольник из треугольника с помощью процедуры создания нескольких кругов, альтернативная процедура, рисунок 13

2.7. Октагон. Развитие правильного восьмиугольника из квадрата той же стороны AB

2.7.1. Создание правильного восьмиугольника из квадрата той же стороны через изготовленные стороны, рис. 14

2.7.2. Создание правильного восьмиугольника из квадрата той же стороны через полученные биссектрисы сторон и внутренних углов, рис. 15

2.7.3. Обычный восьмиугольник из обычного треугольника, рисунок 16

2.8. Обычный Нонагон

3. Результаты и обсуждение

3.1. Конструкции треугольника

3.2. Конструкция Tetragon

3.3. Пентагоны

3.4. Шестиугольники

3.5. Гептагон

3.6. Октагоны

3.7. Нонагоны.

3.8. Общие комментарии к методам

3.8.1. Важность равностороннего треугольника в построении многоугольника

3.8.2. Дополнительные наблюдения

3.8.3. Угловые конструкции

4. Выводы

1.Введение

Как общее определение, многоугольник определяется как любая геометрическая фигура, ограниченная тремя или более сторонами; а правильный многоугольник — это многоугольник с равными сторонами и равными углами основания / внешнего основания [1-3]. Равносторонние треугольники и квадраты квалифицируются как правильные многоугольники не только по приведенному выше определению, но и потому, что они также подчиняются правилам, регулирующим правильные многоугольники. В некоторых учебниках [1] правильные многоугольники начинаются с пятиугольников, но в этой статье, как и в других работах [2-5], правильные многоугольники начинаются с равносторонних треугольников и квадратов.Эти два семейства (равносторонние треугольники и квадраты) играют важную роль в этой работе. По определению, геометрические плоские фигуры, ограниченные замкнутыми прямыми линиями в качестве сторон, являются многоугольниками; треугольники и четырехугольники образуют младшие семьи.

Вводные уроки по правильным многоугольникам и их построению обычно демонстрируются в основном с правильными шестиугольниками [2], потому что правильные шестиугольники можно легко построить простыми методами, которые находятся в пределах элементарной геометрии плоскости, рис. 1.Правильный восьмиугольник иногда также используется, потому что его внешний базовый угол легко построить путем деления круга на восемь равных секторов, как в случае правильного шестиугольника, который построен с помощью правильных многоугольников, которые проиллюстрированы с использованием их деления круга на шесть. равные секторы, рисунок 1. Другие обычные методы строительства, включающие угловые конструкции и перенос углов. Более того, у многих правильных многоугольников есть основания / внешние углы, которые трудно построить; хотя сейчас есть простые и легкие методы [6] построения любого угла.Даже при этом использование новых методов требует построения углов и копирования их в нужное место в качестве средства разгрузки рабочего пространства. Все это может внушить страх учащемуся. Поэтому необходимо искать другие способы введения построения семейств многоугольников, особенно нижних семейств, которые всегда используются на уроках, с помощью простых методов, которые также могут вызвать интерес к построениям в плоской геометрии.

Рисунок 1. Иллюстрации построения многоугольника

Разработанные таким образом методы должны также быть аутентичными процедурами для построения проиллюстрированных правильных многоугольников и требовать только базовых знаний в области геометрии плоскости. Это основная цель данной статьи. Предлагаемые здесь методы могут вызвать у новичка интерес к построению правильных многоугольников до уровня, на котором необходимо использование передовых практик. Эти простые методы, лишенные специальных конструкций и копирования углов, которые загромождают рабочее пространство вспомогательными линиями, описаны ниже.

2. Методология

2.1. Как указано выше, правильные многоугольники начинаются с равностороннего треугольника, проходящего через квадрат, пятиугольник, шестиугольник, семиугольник, восьмиугольник и заканчивая более высокими элементами. Любой метод построения правильного многоугольника приемлем, но более полезен, когда метод строит правильный многоугольник с известной длиной стороны с самого начала. Методы, описанные здесь, достигают цели. Круги играют важную роль в последующих построениях; поэтому, чтобы упростить наименование кругов, круг, обозначенный как круг A, является кругом с центром A.С этого момента именованный многоугольник или многоугольник означает обычный тип.

2.2. Построение правильного «треугольника» (равностороннего треугольника) стороны AB

2.2.1. Построение правильного «треугольника» (равностороннего треугольника) стороны AB прямым методом, рис. 2

Рис. 2. Построение правильного треугольника (равностороннего треугольника) прямым методом

(a ). Рядом с центром прямой PQ отметьте расстояние AB, рисунок 2.

(б). А как центр и радиус AB поворачивают дугу над AB.

(в). B как центр и тот же радиус пересекает дугу в C. Соедините AC и BC. Фигура ABC — это треугольник (равносторонний треугольник).

2.2.2. Построение правильного треугольника (равностороннего треугольника) Метод кругового сектора, рисунок 3

Рисунок 3. Построение правильного треугольника (равносторонний треугольник): метод кругового сектора

(a) .На прямой PQ отметьте точку A. Центр A радиусом AB нарисуйте окружность A, которая разрезает PQ в точках D и E.

(b). Центр E и радиус AB отсекают окружность A в точках B и F; центр D того же радиуса, разрезать окружность A в точках C и E. Соедините AB, BC и AC, чтобы получить треугольник ABC.

2.2.3. Построение правильного треугольника (равностороннего треугольника) Метод пересекающихся окружностей, рисунок 4

Рисунок 4. Построение правильного треугольника (равносторонний треугольник) Метод пересекающихся окружностей

(a ).Нарисуйте сторону AB треугольника ABC, фигура 4. Центр A радиусом AB нарисуйте окружность A; центр B того же радиуса нарисуйте окружность B, чтобы пересечь ее с окружностью A в точках C и D. Соедините AC и BC, чтобы получить треугольник ABC.

2.3. Строительство правильного Тетрагона (Квадрата)

2.3.1. Построение правильного тетрагона (квадрата) стороны AB методом пересекающихся кругов, рис. 5a

Рис. 5. Построение квадрата стороны AB: метод пересекающихся кругов

( ).Рядом с центром PQ отметьте AB. Центр A, радиус AB, нарисуйте окружность A; центр B, такого же радиуса нарисуйте окружность B, пересекающуюся с окружностью A в точке E над AB; центр E того же радиуса нарисуйте окружность E, отсекающую окружность A в точке F и окружность B в точке G.

(b). Центр F с тем же радиусом вырезки окружности E в H; центр G и такой же радиус разрезают окружность E в точке K. Соедините AH, чтобы разрезать окружность A в точке D; присоединитесь к BK, чтобы разрезать круг B в C. Присоединитесь к DC. ABCD — четырехугольник (квадрат). В качестве альтернативы , на прямой XY отметьте PQ = QR. PQ = AB, рисунок 5b.

(а). Центр P, радиус PQ начертить окружность P; центр R того же радиуса, нарисуйте окружность R; центр Q, тот же радиус нарисуйте окружность Q, которая разрезает окружность P в точках E и F и окружность R в точках G и H. Соедините FE и HG, образуя каждую линию вверх и пересекающуюся с XY в точках A и B соответственно.

(б). Центр A, резка FE с таким же радиусом, полученная в D, центр B, резка HG с таким же радиусом, полученная в C. Соедините CD. ABCD — это квадрат.

2.3.2. Построение квадрата квадрантным методом, рисунок 6

Рисунок 6.Построение квадрата методом квадранта

(а). В точке A на прямой PQ постройте ∠RAQ = 45 °, рис. 6.

(b). Центр A и удобный радиус AB разрезают AR в точке D. Проведите вниз перпендикуляр от D к O на PQ.

(в). Центр O и радиус AO начертите окружность O, которая разрезает PQ в точке C и DO, полученную в точке B. Соедините AB, BC и CD. ABCD — четырехугольник.

2.3.3. Тетрагон через данный равнобедренный прямоугольный треугольник ABC, рисунок 7

Рисунок 7. Построение квадрата с помощью метода конгруэнтных прямоугольных равнобедренных треугольников

(a). Нарисуйте равнобедренный прямоугольный треугольник ACB с горизонтальным основанием (длинной стороной AC).

(б). Центр Радиус AB отклоняет дугу ниже AC; центр C того же радиуса разрезает дугу в точке D. Соедините AD и DC, чтобы получить квадрат ABCD.

2.4. Строительство Правильного Пентагона

2.4.1. Из равностороннего треугольника с той же стороны. Метод треугольника / круга, рисунок 8

Рисунок 8. Строительство Пентагона. Метод треугольника / круга

(а). Нарисуйте равносторонний треугольник ABF с вершиной F вертикально под AB, рис. 8. Центр A и радиус AB нарисуйте окружность A; центр B того же радиуса, нарисуйте круг B, который пересекается с кругом A в точках F и G; присоединяйтесь к FG, производящему вверх. Центр F, тот же радиус нарисуйте окружность F, которая разрезает окружность A в точке H, FG в точке J и окружность B в точке K.

(b). Присоединитесь к KJ, чтобы разрезать круг A в точке E; присоединиться к HJ, производя разрезание круга B в точке C.Присоединяйтесь к AE и BC.

(в). Центр C, вырез FG с таким же радиусом, полученный в D; присоединяйтесь к CD и DE. Пятиугольник — это ABCDE.

2.4.2. Правильный пятиугольник из пересекающихся трех коллинеарных кругов, рисунок 8a

Рисунок 8a. Правильный Пентагон от пересечения трех коллинеарных окружностей

(a). На отметке XY равные точки пересечения PQ = QR.

(б). Центр P, радиус PQ начертить окружность P; центр R того же радиуса начертить окружность R; центр Q того же радиуса нарисуйте окружность Q, которая разрезает окружность A в точках F и G и окружность R в точках H и J.

(в). Пусть общая хорда FG (не нарисована) окружностей P и Q разрезает XY в точке A, а общая хорда HJ (не нарисована) окружностей Q и R разрезает XY в точке B; центр. Тот же радиус PQ вырезать окружность P в точке E; центр B тот же радиус разрезает окружность R в точке C. Соедините AE и BC.

(d) Центр C дуги поворота того же радиуса над окружностью Q. Центр E того же радиуса пересекает эту дугу над окружностью Q в точке D. Соедините CD и DE. ABCDE — правильный пятиугольник.

2,5. Конструкция правильного шестиугольника известной стороны AB

2.5.1. Шестиугольник от любого равностороннего треугольника через перпендикулярную сторону или биссектрису угла, рис. 9

Рис. 9. Шестиугольник от любого треугольника через угол или биссектрису перпендикулярной стороны Метод

(a). Нарисуйте любой равносторонний треугольник PQR, цифра 9; пусть перпендикулярные (или угловые) биссектрисы PQ и QR (или ∠P и ∠Q) пересекаются в точке O. Соедините RO, образуя все три биссектрисы в обе стороны.

(б). Центр O и радиус AB (сторона шестиугольника) нарисуйте окружность O, которая пересекает биссектрисы в точках A, (A находится на OP), B, C, D, E и F в направлении против часовой стрелки.Присоединяйтесь к ABCDEF как к правильному шестиугольнику.

2.5.2. Шестиугольник из равностороннего треугольника той же стороны AB с помощью процедуры увеличения, рисунок 10

Рисунок 10. Шестиугольник из треугольника той же стороны с помощью процедуры увеличения

(a). Нарисуйте данный равносторонний треугольник PFE (ΔPFE = ΔABC), продолжая PF до M и PE до N, рисунок 10.

(b). Центр F, радиус PF срез PM в точке A; центр A, срез PM того же радиуса в точке Q; центр E, такой же радиус резания PN в точке D; центр D, такой же радиус резания PN в точке R.Присоединяйтесь к QR. Центр Отрезок QR с таким же радиусом в точке B и центр D срез с таким же радиусом RQ в точке C.

(c). Присоединяйтесь к AB и CD. ABCDEF — правильный шестиугольник.

2.5.3. Рис. 11

Рис. 11. Создание шестиугольника из пересекающихся окружностей с центрами в вершинах равностороннего треугольника

(а). Нарисуйте равносторонний (треугольник) ABG, рисунок 11.Центр A радиус AB нарисуйте окружность A; центр B того же радиуса нарисуйте круг B и центр G того же радиуса нарисуйте круг G, который разрезает круг A в точке F и круг B в точке C.

(b). Центр F такой же разрез радиуса G в E и центр C, такой же радиус разрезания G в D. Соедините BC, CD, DE, EF и FA. ABCDEF — шестиугольник.

2,6. Обычный семиугольник

2.6.1. Развертка из треугольника с помощью процедуры множественного круга, рисунок 12

Рисунок 12. Обычный семиугольник через треугольник

(а). Около середины прямой XY нарисуйте треугольник ABM, рисунок 12, с вершиной M вертикально ниже AB. Центр A, радиус AB нарисуйте круг A, который разрезает XY в точке H; центр B того же радиуса нарисуйте окружность B, которая разрезает XY в точке J, а также окружность A в точках M и N, соедините MN, производя движение вверх.

(б). Центр M, такого же радиуса нарисуйте круг M, который пересекает круг A в точке P; обведите B у R и MN у O.

(в). Центр H того же радиуса нарисуйте окружность H; центр P того же радиуса вырезать окружность H в точке Q.

(г). Центр J того же радиуса нарисуйте окружность J; центр R того же радиуса вырезать окружность J у S.

(e). Присоединитесь к QO, чтобы разрезать круг B в точке C; присоединитесь к SO, чтобы разрезать круг A в точке G. Присоединитесь к BC и AG.

(ф). Центр O срез MN того же радиуса выполнен в точке T, разрез по центру T и разрез MN с таким же радиусом снова выполнен в точке E.

(g). Центр E тот же радиус начертания окружности E. Центр G такой же радиус вырезания окружности E в точке F, центр C и такой же радиус вырезания окружности E в точке D. Соедините GF, FE, ED и DC. ABCDEFG — это сторона AB правильного семиугольника, через процедуру треугольника с множеством пересекающихся окружностей, рисунок 11.

2.6.2. Правильный семиугольник из треугольника с помощью процедуры с несколькими кругами, альтернативная процедура, рисунок 13

Рисунок 13. Гептагон из треугольника; Альтернативная процедура

(а). Нарисуйте треугольник ABH, образующий AB в обоих направлениях к X и Y. Центр A, радиус AB нарисуйте окружность A; центр B, тот же радиус нарисуйте круг B, который разрезает окружность A в точках H и J. Присоединитесь к HJ, производя движение вверх.

(б). Центр H, разрез HJ с таким же радиусом, полученный в K; центр K, одинаковый радиус срезают равные пересечения вдоль HJ, полученные в L и E.Соедините AE и EB, которые разрезают окружность A в точке M и окружность B в точке N соответственно.

(в). Центр E, тот же радиус, нарисуйте круг E, который разрезает AE в точке O и BE в точке P соответственно. Центр O, окружность A с таким же радиусом в точке G; центр P, тот же радиус, вырезать окружность B в точке C.

(d). Центр M, окружность среза E с таким же радиусом в точке F; центр N, окружность E с таким же радиусом в точке D. Соедините BC, CD, DE, EF, FG и GA, чтобы сформировать правильный 7-угольник.

2.7. Октагон. Развитие правильного восьмиугольника из квадрата той же стороны AB

2.7.1. Рис.14.Развитие правильного восьмиугольника из квадрата той же стороны через созданные стороны, Рисунок 14

Рисунок 14. Развитие правильного восьмиугольника той же стороны AB, что и данный квадрат, через созданные стороны

( а). Нарисуйте квадрат PQRS, где PQ равно AB (дано), образуя стороны в обе стороны, рис. 14. Пусть O будет пересечением диагоналей.

(б). Центр P радиус PO вырез SP, произведенный в A. Центр радиус O OA начертите окружность O, которая разрезает полученные стороны в точках A, B, C, D, E, F, G и H (в направлении против часовой стрелки).Соедините соседние точки, чтобы получился правильный восьмиугольник со стороной AB.

2.7.2. Рис. 15

Рис. 15. Развитие правильного восьмиугольника той же стороны AB, что и данный квадрат, через полученные биссектрисы угла. внутренние углы и стороны

(а). Нарисуйте квадрат PQRS, где PQ равно AB (дано), рис. 15.

Нарисуйте серединные перпендикулярные стороны сторон и биссектрисы углов, образующие каждую биссектрису в обе стороны.Пусть O — пересечение этих биссектрис. Производим SP и QP.

(б). Центр P радиус PO вырез SP, произведенный в J. Центр радиуса O OJ начертите окружность O, которая разрезает RP, полученный в A, и полученные линии в точках J, B, C, D, E, F, G, H и K (против часовой стрелки) . Соедините соседние точки (исключая K и J), чтобы получить правильный восьмиугольник ABCDEFG стороны AB.

2.7.3. Правильный восьмиугольник из обычного треугольника, рисунок 16

Рисунок 16. Правильный восьмиугольник из треугольника

Правильный восьмиугольник можно построить из правильного треугольника следующим образом.

(а). Нарисуйте правильный треугольник ABJ с горизонтальным основанием AB и вершиной J вертикально над AB. Произведите AB в обоих направлениях к XY соответственно. Обратите внимание, что точки A, B и J обозначают треугольник.

Центр A, радиус AB, нарисуйте круг A, который разрезает XY в точке K рядом с X. Центр B, тот же радиус нарисуйте круг B, который разрезает XY в L и окружность A в M и J.

Центр J, тот же радиус, нарисуйте круг J, который разрезает окружность A в точке N и окружность B в точке O.

Центр N, тот же радиус, нарисуйте окружность N, которая разрезает окружность J в точке P.Присоединитесь к AP, которая разрезает круг A в точке Q; производите AP вверх.

Центр O, тот же радиус, нарисуйте круг O, разрезающий круг J в точке R. Присоединитесь к BR, разрезающему круг B в точке S; производят BR вверх.

(б). С точками K и P в качестве центров и одинакового радиуса разделите ∠PAK пополам и пусть биссектриса пересекает окружность A в точке H. Соедините AH.

С точками S и L в качестве центров и одинаковым радиусом разделите пополам ∠SBL и пусть биссектриса пересекает окружность B в точке C. Соедините BC.

(в). Центр H, тот же радиус, поверните дугу над H; центр Q, тот же радиус, дуга разреза в G.Присоединяйтесь к HG.

Центр C, тот же радиус, поверните дугу над C; центр S, тот же радиус, дуга разреза в D. Соедините CD.

Центр G, тот же радиус, разрез AP произведен на F; присоединиться к FG.

Центр D, тот же радиус, вырез BR произведен в точке E; присоединиться к DE. ABCDEFGH — правильный восьмиугольник.

2,8. Обычный неугольник

Рис. 17. Обычный неугольник

(a) Нарисуйте прямую линию XY и отметьте AB, рисунок 17.

(b).Центр A и радиус AB начертить окружность A; Центр B, тот же радиус, нарисуйте круг B, который разрезает окружность A в точках K и L. Соедините KL, производя движение вверх. Центр L, вырез LK с таким же радиусом на M.

(c). Центр M, радиус 3AB, вырез KL, полученный в F. Центр F, радиус AB, начертите окружность F. Присоединитесь к FA, которая разрезает окружность F в N и окружность A в O. Присоединитесь к FB, которая разрезает окружность F в точке P и окружность B в точке Q.

(г). Центр N, радиус AB, отрезок окружности F в точке G, соединение FG; центр O, тот же радиус разрезает окружность A в точке J. Соедините AJ.

Центр P, тот же радиус AB, отрезок окружности F в точке E, соединение EF; центр Q, такая же окружность, разрезанная adius, B в C, соединяется с BC.

(д). Центр G, тот же радиус AB, поверните дугу ниже G, центр J, тот же радиус пересекает дугу в H. Соедините GH и HJ. Центр E с таким же радиусом поверните дугу ниже E, центр C, тот же радиус пересекает эту дугу в D. Соедините DC и DE. ABCDEFGHJ — правильный шестиугольник.

3. Результаты и обсуждение

3.1. Конструкции треугольника

Конструкция треугольника в разделе 2.2.1 рис. 2 является обычным модным методом. Стороны равны, потому что они имеют одинаковый радиус, а внутренние углы равны 60 °.Примечание: любые смежные точки на окружности можно соединить, а также с центром круга, чтобы получить треугольник.

Метод кругового сектора (раздел 2.2.2, рис. 3) основан на том факте, что радиус круга делит круг на шесть равных секторов. У каждого сектора прямые стороны равны радиусу круга. Хорда сектора равна радиусу окружности.

В методе пересекающихся окружностей, раздел 2.2.3 рис. 4, который используется как вводное построение правильного треугольника [5].два круга имеют общие радиусы. Остальные стороны — такие же равные радиусы равных кругов. Итак, треугольник равносторонний. Примечание: процедура такая же, как и при прямом методе; в прямом методе показаны только соответствующие дуги окружностей раздела 2.2.3.

3.2. Конструкция тетрагона

В разделе 2.3.1, построение тетрагона путем пересечения окружностей, рис. 5a, окружности F, E и G имеют равный радиус и коллинеарны, а окружность E пересекается с окружностями F и G в точках H и K соответственно и они разделены радиусом, HA параллельна KB, оба перпендикулярны AB и разнесены по радиусу (поскольку AB является общим радиусом для всех окружностей).AD равен и параллелен BC, поэтому DC касается окружностей A и B, а также равен AB и параллелен им. Таким образом, AB = BC = AD = DC и внутренние углы равны 90 ° каждый, следовательно, ABCD — квадрат. На рисунке 5b A и B являются серединами PQ и QR, поэтому AB = PQ. AD ǁ BC оба перпендикулярны XY и AD = DC (одинаковый радиус). Итак, ABCD — квадрат. Вышеупомянутый метод, особенно рисунок 5b, — это быстрый и удобный способ построить квадрат без ошибок.

В разделе 2.3.2 рис. 6 каждый квадрант имеет прямоугольный равнобедренный треугольник e.грамм. ΔAOD и любые два соседних квадранта, образующие полукруг, составляют прямоугольный равнобедренный треугольник, например Δ ACD под прямым углом к ​​D, с AC (диаметром) в качестве длинной стороны и с равными хордами, как у двух других сторон. Комбинация ΔADC с его конгруэнтным треугольником ΔABC (в другом полукруге) с общим основанием AC с помощью процесса, описанного в разделе 2.3.2, дает квадрат ABCD. Построение квадрата ABCD можно было бы укоротить после шага (а), используя центр A с радиусом AD для поворота дуги, пересекающей AR в точке D и проходящей ниже PQ; центр D с тем же радиусом выреза PQ в точке C; центр C, тот же радиус пересекает дугу ниже PQ в точке B.Соединение AB, BC и CD даст требуемый квадрат. Первая процедура принята для ясности на уроке по использованию квадранта для построения квадрата, а также для исключения путаницы с процедурой, описанной в разделе 2.3.3, которая аналогична.

В разделе 2.3.3, рисунок 7, равнобедренный прямоугольный треугольник имеет две равные стороны с включенным прямым углом. Два таких равных треугольника, имеющих общее более длинное основание, образуют квадрат.

3.3. Пентагоны

Есть два метода построения правильных пятиугольников: с помощью внешнего / внутреннего угла основания или путем развертки из правильного треугольника [4] (равносторонний треугольник).Эти методы не просты, чтобы их можно было использовать в качестве демонстрационных. С введением раздела 2.4.2 можно продемонстрировать построение правильного пятиугольника. Конструкция использует круги одного радиуса, чтобы построить правильный пятиугольник из равностороннего треугольника с той же стороной, так что стороны построенного пятиугольника равны сторонам треугольника. Построение внутреннего угла CBA (правильного пятиугольника) с использованием линии HJC не является ортодоксальным методом, но дает ожидаемый результат.На рис. 8а в разделе 2.4.2 показана новая простая конструкция пятиугольника. Точки A и B являются серединами PQ и QR соответственно, поэтому AB равен радиусу любого из кругов. Процедура регулярного треугольника и круга представляет собой интересную практику. Заслуживает упоминания построение правильного пятиугольника с помощью процедуры, полученной путем применения продвинутой алгебры к построению многоугольника [5]. Процедура, хотя и простая, не позволяет построить правильный пятиугольник с заданной длиной стороны, поэтому она не описывается и не включается здесь.

3.4. Шестиугольники

У правильного шестиугольника есть много простых и удобных методов, подходящих для вводных уроков, кроме метода деления окружности круга на его радиус (рис. 1). Правильные шестиугольники могут быть построены любым из методов, использующих равносторонний треугольник, как показано выше в разделах с 2.5.1 по 2.5.3, включая разделение круга на шесть равных частей с использованием радиуса круга для получения шестиугольника на рисунке 1.

Шестиугольник из угловой или перпендикулярной стороны биссектрисы треугольника (сечение 2.5.1) имеет ту же сторону, что и секторный треугольник; OA = OB (радиусы одного круга), каждый угол при O равен 60 °, поэтому каждый базовый угол в треугольнике OAB равен 60 °, поэтому ∠ABO равносторонний, а OA = OB = AB = сторона равностороннего треугольника сектора. Радиус окружности O (как в случае метода равномерного разбиения окружности на шесть частей на фиг.1) определяет длину стороны шестиугольника.

В увеличенном равностороннем треугольнике, раздел 2.5.2, каждый из маленьких треугольников, скажем, PFE, является равносторонним.По построению FE = FA, поэтому ABCDEF — правильный шестиугольник с заданной стороной. Этот метод и разделение круга на шесть равных секторов подходят для правильных шестиугольников с очень короткими сторонами.

В разделе 2.5.3 использование системы трех кругов с равносторонним треугольником аналогично иллюстрации, показанной на рисунке 1; вершина G равностороннего треугольника на рисунке 11 определяет центр окружности на рисунке 1, точки пересечения A, B, C и F на окружности G являются вершинами шестиугольника, а AB — длина каждой стороны шестиугольника. шестиугольник на рисунке 11.AB (сторона треугольника) — это радиус каждой из окружностей на рисунке 11.

3.5. Гептагон

До сих пор обычный семиугольник не демонстрировался из-за сложности его построения из внешнего или внутреннего угла. Метод, описанный в разделе 2.6.2, рисунок 13, является новым и может использоваться в качестве демонстрационной конструкции. Опять же, построение внешнего угла CBY (правильного семиугольника) с использованием линии QOC, рис. 12, не является ортодоксальным методом, хотя и дает ожидаемый результат.Однако оказывается, что точка J (рис. 8), которая совпадает с точкой O на рис. 12, является полезной точкой при построении правильных многоугольников с нечетными номерами с помощью процедуры «треугольник-круг». Эта точка, K рис. 13 в разделе 2.6.2, используется в альтернативной процедуре построения семиугольника. Процедура правильного треугольника и круга здесь представляет интересную практику, как и в случае с пятиугольником.

3,6. Октагоны

Помимо метода разделения круга на восемь равных частей, показанного на рисунке 1, существуют другие методы, которые можно использовать для обучения построению правильных восьмиугольников.Эти методы включают построение под разными углами, которые в этой статье мы пытаемся найти минимально. В связи с этим метод приведения квадрата к правильному восьмиугольнику по Блейки [7] путем отсечения вычисленных равных длин от каждой вершины квадрата исключен из этого отчета, как и другие в той же категории, потому что сторона многоугольника длина должна быть измерена или рассчитана. Введение этих других новых методов упрощает дело.

В разделе 2.7.1 рисунок 14 (восьмиугольник от четырехугольника через образованные стороны четырехугольника), OP = PA = PH по конструкции; AB ² = PQ ² = 2OP ² = 2PH ² = HA ² . Следовательно, AB = HA = PQ.

В разделе 2.7.2 (рис. 15) используются диагонали и перпендикулярные биссектрисы для построения правильного восьмиугольника. Квадрат разделен биссектрисой на восемь равных частей (секторов); круг с центром O и радиусом OJ разделен на восемь равных секторов, как в четырехугольнике.Круг O разрезает QP, полученный при K, PJ = PK, сектор KOJ (линии OK и OJ не показаны) = сектор AOB (те же радиусы и угол сектора 45 °). Итак, KJ = AB. Но AB = PQ (по построению или ΔKPJ ≡ ΔPOQ SAS). Следовательно, KJ = PQ = AB. Примечание: если квадраты на рисунках 14 и 15 одинаковы, построенные восьмиугольники одинаковы.

В разделе 2.7.3, рис. 16 восьмиугольник построен как треугольник с процедурой с использованием окружности. В этом методе много кругов, поэтому он может сбивать с толку, но он показывает, что n-угольники от n = 3 до 9, которые здесь рассматриваются, могут быть построены с помощью обычного метода с помощью тригона / круга.

3,7. Нонагоны.

Раздел 2.8, рис. 17, строит правильный 9-угольник (нонагон) с помощью процедуры треугольника / окружности, метода, обычно используемого в этой работе. Этот новый метод построения многоугольника включен, потому что несколько иллюстративных примеров построения многоугольников обычно заканчиваются восьмиугольником, последним наиболее легко построенным многоугольником. Процедура проста и может быть использована.

3.8. Общие комментарии к методам

Цель этой статьи — представить простые методы построения нижних членов многоугольников во вводных учебных классах.Такие методы должны быть лишены построения и / или копирования углов, которые загромождают рабочую плоскость, а также должны давать многоугольник с известной длиной стороны. Представленные здесь методы соответствуют этим целям.

3.8.1. Важность равностороннего треугольника в построении многоугольника

Ранее во введении было сказано, что равносторонний треугольник играет важную роль в построении многоугольника. Используя метод, представленный здесь для каждого семейства многоугольников, все они могут быть созданы из правильных треугольников с помощью построений с использованием окружностей.Одно очевидное наблюдение состоит в том, что многоугольник с четным числом сторон, треугольник, используемый в процедуре триагома и круга, — это тот, вершина которого находится вертикально над горизонтальным основанием, в то время как у многоугольников с нечетным числом сторон вершина используемого треугольника находится вертикально ниже горизонтальное основание. На самом деле есть два правильных треугольника с общей базой (основание строящегося многоугольника), образованных двумя пересекающимися окружностями (константа для всех построений этим методом), вертикально противоположные вершины этих двух треугольников с общим основанием являются точками пересечения. пересечения двух кругов.

Получается, что равносторонний треугольник является основным элементом при построении любого правильного многоугольника, когда он соединен с кругами того же радиуса. Правильный четырехугольник (квадрат) также является важным элементом при построении правильного 8-угольника, сечения 2.7.1 на рис. 14 и сечения 2.7.2 на рис. 15. Правильный 6-угольник также может быть получен из правильного четырехугольника (квадрата). такой же длины стороны. Нарисован квадрат. Нарисуется середина диагонали O как центр и сторона квадрата как радиус окружности O.Равное разбиение окружности окружности O на сектора и ее радиуса дает точки вдоль окружности в виде вершин правильного 6-угольника. Этот метод аналогичен равному разделению круга на шесть секторов (рис. 1) во вводной части с квадратом, обозначающим центр и радиус круга и, следовательно, сторону шестиугольника.

Другой аспект процедуры треугольника-окружности — использование постоянного радиуса (стороны треугольника) на всем протяжении построения. Это упрощает конструкцию после того, как можно правильно определить необходимые центры.

3.8.2. Дополнительные наблюдения

Дополнительные наблюдения, полезные для учащегося, включают следующее: линия, проходящая через точки пересечения двух окружностей, перпендикулярна линии центров; если два круга имеют общий радиус, линия, проходящая через точки пересечения, является серединным перпендикуляром линии центров, например. линия GF в разделе 2.4.1 на рисунке 8 и может использоваться в разделе 2.5.1, рисунок 9, чтобы получить угол или боковые биссектрисы треугольника; но для перегруженности рабочего пространства показаны только релевантные дуги.В общем, любая дуга, нарисованная в конструкции, является частью круга (общая рабочая лошадка / помощник в плоских геометрических конструкциях) с известным центром.

3.8.3. Конструкции углов

Одной из основных трудностей при построении правильных многоугольников является невозможность построить большую часть основания или внешнего угла основания. До сих пор такие углы копируются с транспортира до появления методов равнораспределения углов на любое количество частей [6]. Разделы 2.4.1 и 2.4.2 представляют два соответствующих метода построения 72 (внешний угол правильного пятиугольника), а в разделе 2.5.3 на рисунке 12 показана модификация раздела 2.4.1 для построения 51 ³ / ₇ ^o (внешний угол правильного семиугольника). Эти методы предполагают существование других методов построения углов некоторых из этих многоугольников, которые не были исследованы.

4. Выводы

Для вводного обучения по правильным многоугольникам достаточно простых построений.Эти новые методы подробно описаны в разделах 2.2.2, 2.3.1, 2.3.2, 2.3.3, 2.4.2, 2.5.1, 2.5.2, 2.5.3, 2.6.1, 2.6.2, 2.7.1. , 2.7.2, 2.7.3 и 2.8 — это новые методы, которые могут быть добавлены к любым существующим процедурам, используемым для иллюстративных построений. Инструктор может выбрать один из множества перечисленных методов. Эти методы, хотя и просты, в равной степени являются стандартными процедурами, применимыми к каждому классу полигонов. Для новичков, имеющих предварительные навыки геометрического построения, эти конструкции не только будут легко усвоены, но и вызовут больший интерес, чтобы побудить их к более высоким методам построения в этой области.

Каталожные номера

---

[1]	Бамиро О. А., Элеква И., Околи Онединма А. С. Б, Окори О. О. и Аньяболу И. С. 1985. Вводная технология для школ и колледжей. Evans Brothers (Nigeria Publishers) Ltd, Джерико Роуд, Ибадан, Нигерия, стр. 14.
[2]	Macrea M F, Kalejaiye A O, Chima Z I, Garba G U, Channon J B, MacLeish Smith A и Head H C.2008. Новая общая математика для старших классов средней школы UBE Edition. Pearson Educational Ltd, Edinburh Gate, Harlow, Essex CM 20 2EJ, England, p9.
[3]	Бейли, Дэй, ФРЕЙ, Ховард, Хатченс, Маклейн, Мур-Харрис, Олт, Пелфри, При, Вильхабер и Уиллард. Математика: приложения и концепции, курс 2. Флоридское издание, fl.msmaths.net McGraw Hill Glencoe. Нью-Йорк. Глава 10-7 с. 446-447.
[4]	Центр сравнительного обучения и адаптации, CESAC.1986. Вводная технология для младших классов средней школы Учебник 2, стр. 16.
[5]	Динамика Polygons.org Построение правильных многоугольников.
[6]	Охочуку, Н. С. 2015. Равнораспределение плоских геометрических углов на любое количество частей. Журнал прикладной математики, 5 (4). Pp84 — 87. http://journal.sapub.org/am.
[7]	Блейки Дж. Математика среднего уровня. Кливер-Хьюм Пресс Лтд.Я постараюсь быть очень эффективным с текстом, поэтому буду описывать только шаги, требующие некоторых пояснений. Убедитесь, что на бумаге достаточно свободного места для следующих шагов. Вы можете увидеть, сколько места вам понадобится, по размеру бумаги на этой картинке. Шаг 2 Шаг 3 Шаг 4 Шаг 5 Шаг 6 Шаг 7 Шаг 8 Шаг 9 Обесцветьте все линии построения, «отпечатав» разминаемый ластик на бумаге.. Шаг 10 Дождитесь полного высыхания чернил и сотрите все линии построения. Шаг 11 Чтобы добавить цвета, обязательно сначала нарисуйте цветные контуры правильным цветом или карандашом. Если ваша цель — стать настоящим мангакой и создать собственных персонажей манги, обязательно попробуйте несколько раз нарисовать Гона по памяти. Всегда сравнивайте рисунок с оригиналом и исправляйте обнаруженные ошибки. Делайте это, пока не будете довольны результатом.Хироши (рисунок Бьянки) [PDF] Раздел 8. Гл. 8. \\\ «Более трех сторон \\\» 1 Раздел 8. Гл. 8. «Более трех сторон» 1. С помощью линейки нарисуйте ВЫПУКЛЫЕ многоугольники с 4, 5, 6 и 7 сторонами … Раздел 8. Гл. 8. «Более трех сторон» 1. Используйте линейку, чтобы нарисовать ВЫПУКЛЫЕ многоугольники с 4, 5, 6 и 7 сторонами. 2. На каждой рисуйте все диагонали ТОЛЬКО ОДНОГО ВЕРТЕКСА. Диагональ — это отрезок, соединяющий две непоследовательные вершины.Обратите внимание на количество образованных треугольников. 3. Составьте таблицу: Многоугольник. # сторон. # треугольников. Сумма внутренних углов A. Зависит ли сумма внутренних углов от того, является ли многоугольник выпуклым? Проверьте эту идею, нарисовав на бумаге несколько невыпуклых многоугольников (например, тот, что справа) и определите, имеет ли значение, является ли многоугольник выпуклым. Объясните свои выводы. B. Найдите сумму внутренних углов 100-угольника. Объясните свои рассуждения. 1.Какова сумма внутренних углов четырехугольника? 2. Какова сумма внешних углов восьмиугольника? 1. Сколько сторон у многоугольника, если сумма его внутренних углов равна 1260 °? 1. Каков размер внутреннего угла правильного шестиугольника? 2. Каков размер внешнего угла правильного треугольника? 1. Внешний угол правильного многоугольника составляет 36 °. Сколько сторон у многоугольника? 2. Внутренний угол правильного многоугольника составляет 60 °.Сколько у него сторон? Имя ——————————————————————— Дата ————————————— Практика B УРОК 8.1 Для использования в уроке «Определение углов в многоугольниках» Найдите сумму размеров внутренних углов указанного выпуклого многоугольника. 1. Шестиугольник 2. Додекагон 3. 11-угольник 4. 15-угольник 5. 20-угольник 6. 40-угольник Сумма размеров внутренних углов выпуклости. дан многоугольник.Классифицируйте многоугольник по количеству сторон. 8. 5408 9. 9008 10. 18008 11. 25208 12. 39608 13. 50408 14. 59408 15. 86408 17. 18. Найдите значение x. 16. 105 142 140 124 x 88 3x 2x Авторские права © Houghton Mifflin Harcourt Publishing Company. Все права защищены. 86 93 75 x 2x 34x 124 102 19. 158 1 6x 146 64 УРОК 8.1 7. 1808 24x 110 20. 21. 60 60 8x 100 2x x 6x 6x 22. Каков размер каждого внешнего угла правильного шестиугольника? 23. Размеры внешних углов выпуклого четырехугольника равны 908, 10×8, 5×8 и 458. Какова мера наибольшего внешнего угла? 24.Размеры внутренних углов выпуклого восьмиугольника составляют 45×8, 40×8, 1558, 1208, 1558, 38×8, 1588 и 41×8. Какова мера наименьшего внутреннего угла? Найдите размеры внутреннего и внешнего углов указанного многоугольника. 25. Правильный треугольник 26. Правильный восьмиугольник 27. Правильный 16-угольник 28. Правильный 45-угольник 29. Правильный 60-угольник 30. Правильный 100-угольник Справочник по вопросам геометрии 8-7 Имя —————————————————————— УРОК 8.1 Дата ———————————— Практика B (продолжение) Для использования с уроком «Найти угловые меры в многоугольниках» В упражнениях 31–34 найдите значение n для каждого описан обычный n-угольник. 31. Каждый внутренний угол правильного n-угольника имеет меру 1408. 32. Каждый внутренний угол правильного n-угольника имеет меру 175,28. 33. Каждый внешний угол правильного n-угольника имеет меру 458. 34. Каждый внешний угол правильного n-угольника имеет размер 38. 35. Хранилище для хранения Вид сбоку навеса для хранения показан ниже.Найдите значение x. Затем определите размер каждого угла. A УРОК 8.1 2x E 2x B 2x D C 36. Палатки Вид на палатку спереди показан ниже. Найдите значение x. Затем определите размер каждого угла. N (2x 1 20) (2x 1 20) RM x x S 37. Доказательство Поскольку все меры внутреннего угла правильного n-угольника совпадают, вы можете найти размер каждого отдельного внутреннего угол.Измерение каждого (n 2 s внутреннего угла правильного n-угольника равно}. Напишите доказательство абзаца, чтобы доказать это утверждение. 8-8 Справочник по главе по геометрии Copyright © Houghton Mifflin Harcourt Publishing Компания. Все права защищены. PQO 140 150 150 Имя —————————————————————— Дата —————————— ——— Практикум по решению проблем: решение смешанных задач Для использования с уроками «Найти меры углов в многоугольниках», «Использовать свойства параллелограммов» и «Показать, что четырехугольник — это параллелограмм» 1.Многоступенчатая задача Форма Illinois может быть аппроксимирована многоугольником, как показано. ILLINOIS Springfield 5. Расширенный ответ Вершины четырехугольника JKLM — это J (22, 4), K (5, 7), L (3, 21) и M (24, 24). а. Используйте то, что вы знаете о наклонах линий, чтобы доказать, что JKLM — параллелограмм. Объясните свои рассуждения. б. Используйте формулу расстояния, чтобы показать, что JKLM — параллелограмм. Объяснять. 6. Кратковременный отклик. Угол параллелограмма на 18 градусов меньше, чем в 5 раз больше, чем прилегающий угол.Объясните, как найти размеры всех внутренних углов параллелограмма. б. Какова сумма размеров внутренних углов многоугольника? c. Какова сумма размеров внешних углов многоугольника? 2. Задача с несколькими шагами. Используйте циркуль, транспортир и линейку для деталей (a) — (c) ниже. а. Нарисуйте большой угол размером 1408. Отметьте одинаковые длины по бокам углов. б. От конца одного из равных отрезков в части (а) проведите вторую сторону другого угла, равного 1408.Отметьте еще одну совпадающую длину вдоль этой новой стороны. c. Продолжайте рисовать углы размером 1408 с совпадающими сторонами, пока не сформируется многоугольник. Сколько сторон у многоугольника? d. Проверьте ответ на часть (c) с помощью математики. 3. Открытый. Нарисуйте четырехугольник, у которого одна пара равных сторон и одна пара параллельных сторон, но не параллелограмм. 4. Ответ с сеткой. Выпуклый восьмиугольник имеет внутренних углов с размерами 1328, 1348, 1468, 1478, 1508, 1588, x8 и 2×8.Найдите значение x. 8-42 Справочник по главам по геометрии 7. Фотографы с расширенным откликом могут использовать ножничные подъемники для съемки сверху. Поперечные балки лифта образуют параллелограммы, которые вместе перемещаются, поднимая и опуская платформу. Воспользуйтесь схемой параллелограмма ABCD ниже. D B A C а. Что такое mŽ C, когда mŽ A 5 1208? б. Предположим, вы уменьшаете mŽ A. Что происходит с mŽ C? c. Предположим, вы увеличиваете mŽ A.Что происходит с AD? d. Предположим, вы уменьшаете mŽ A. Что происходит с общей высотой ножничного подъемника? Объяснять. Авторские права © Houghton Mifflin Harcourt Publishing Company. Все права защищены. а. Сколько сторон у многоугольника? Ответы к главе 8 Урок 8.1 Определение углов в многоугольниках 18. 1058 19. около 128,68; около 51,48 Учебное пособие 22. 172,88; 7,28 23, около 174,98; около 5,18 20,1508; 308 21.около 158,88; около 21,28 24, около 177,18; около 2,98 25. 24 26. 150 3. правильный пятиугольник; 1088 27. 72 28. 30 29. №; Многоугольник будет иметь 5. правильный семиугольник; около 1298 6. правильный восьмиугольник; 1358 Практический уровень A 1. 14408 2. 19808 3. 27008 4. 28808 5. 36008 6. 41408 7. 50408 8. 57608 9. 66608 10. 9 11. 14 12. 20 13. 28 14. 32 15. 44 16. 93 17. 127 18. 85 19. 71 20. 52 21. 36 22. 1508 23. 248 24. 1208; 608 25. 1448; 368 26,1568; 248 27,1628; 188 28.1688; 128 29, 1708; 108 30. 4 31. 5 32. 8 33. 10 34. 4 35. 6 36. 9 37. 12 38. а. 4; четырехугольник b. 3608 г. 3608 39, 1358 40, 1358; 458 Практический уровень B 1. 7208 2. 18008 3. 16208 4. 23408 5. 32408 6. 68408 7. треугольник 8. пятиугольник 9. семиугольник 10. двенадцатигранник 11. 16-угольник 12. 24-угольник 13. 30- гон 14. 35-угольник 15. 50-угольник 16. 121 17. 56 18. 5 19. 64 20. 30 21. 9 22. 408 23. 1508 24. 1148 25. 608; 1208 26,1358; 458 27,157,58; 22,58, 28,1728; 88 29,1748; 68 30,176,48; 3,68 31,9 32,75 33,8 34.120 35. х 5 60; mŽ A 5 mŽ B 5 mŽ E 5 1208 и mŽ C 5 mŽ D 5 908 36. x 5 70; mŽ M 5 mŽ S 5 708, mŽ N 5 mŽ R 5 1608, mŽ O 5 mŽ Q 5 1508 и mŽ P 5 1408 37. Пусть A — правильный n-угольник, а x8 — мера каждого интерьера Ž. Тогда сумма интерьера? равно n + x8. По внутреннему пространству многоугольника? Теорема, сумма мер интерьера? из A составляет (n 2 2) + 1808. (n 2 2) + 180 . Итак, n + x8 5 (n 2 2) + 1808, или x 5} n Практический уровень C 1. 34208 2. 59408 3. 86408 4. 10 5. 19 6.23 7. 38 8. 47 9. 51 10. 83 11. 17 12. 8 13. 16 14. 13 15. 3 16. 1408 17. 1058 14,4 стороны, что невозможно. 30. Да; У многоугольника будет 18 сторон. 31. Да; У многоугольника будет 72 стороны. 32. Да; У многоугольника будет 30 сторон. 33. всегда 34. никогда 35. всегда 36. иногда 37. x 5 13,5; mŽA 5 1178, mŽB 5 868, mŽC 5 1348, mŽD 5 868, mŽE 5 1178 38. x 5 16; mŽF 5 808, mŽG 5 1608, mŽH 5 1458, mŽJ 5 1308, mŽK 5 1458, mŽL 5 1608, mŽM = 808 39. По теореме о внутренних углах многоугольника (n 2 2) + 1808 5 сумма размеров внутренних углов.По определению правильного многоугольника все внутренние углы равны. Таким образом, сумма мер внутренних углов равна (n + x) 8. Это означает, что (n 2 2) + 1808 5 (n + x) 8. Умножение (n 2 2) на 180 дает 180n 2 360 5 nx. Вычитание nx с обеих сторон и прибавление 360 к обеим сторонам дает 180n 2 nx 5 360. Вынося n из левой части уравнения, получаем n (180 2 x) 5 360. Деление ОТВЕТЫ 1. равносторонний треугольник; 608 2. квадрат; 908 4. правильный шестиугольник; 1208 Авторские права © Houghton Mifflin Harcourt Publishing Company.Все права защищены. Четырехугольники 360 . обе стороны на (180 2 x) дает n 5} 180 2 x Учебное пособие 1. 18008 2. пятиугольник 3. 71 4. 438 Мастер-класс по решению проблем: пример 1. 1408, 408 2. Внутренний угол нонагон на 208 больше внутреннего угла шестиугольника. Внешний угол шестиугольника на 208 больше внутреннего угла шестиугольника. 3. 1358, 458 4. 55 Упражнение 1 1. a. } x 2 tan 728 квадратных единиц 4 2 x b.} (tan 728) 1 x 2 (sin 728) 1 x 2 (cos 728) (sin 728) 4 квадратных единиц c. x 2 (sin 728) 1 x 2 (cos 728) (sin 728) квадратные единицы} s2 1 1 2. a. } s2 квадратных единиц b. } (s2 + Ï 2 s2 +}) 4 2 2 квадратных единицы Справочник по главам по геометрии A13 Метод диагонали со ступенчатой ​​диагональю на восемь участков, 125 мм Чтобы построить правильный восьмиугольник по диагонали, т.е. о. внутри ■ заданного круга (Рис. 2/29) 1. Нарисуйте круг и вставьте диаметр AE. 2. Постройте еще одну диагональ CO, перпендикулярную первой диагонали. 3. Разделите четыре квадранта пополам, чтобы разрезать круг в B. D. F иH. ABCDEFGH — это требуемый восьмиугольник. Для построения правильного восьмиугольника по диаметру, т.е. в пределах заданного квадрата (Рис. 2/30) 1. Постройте квадратный ПОРС. длина стороны равна диаметру. 2. Нарисуйте диагонали SQ и PR так, чтобы пересечь м T. 3. С центрами P.Q. R и S рисуют четыре дуги радиусом PT (a QT = RT = ST), чтобы разрезать квадрат в A, B. C, D. E. F. GandH. ABCDEFGH — это требуемый восьмиугольник Для построения любого многоугольника g i van, учитывая длину aside Есть три довольно простых способа построить правильный многоугольник. Два метода требуют простых вычислений, а третий требует очень тщательного построения. Если быть точным. Показаны все три метода. Конструкции подходят для любого многоугольника, и для их иллюстрации выбран семиугольник (семь сторон).Метод 1 (Рис. 2/31) 1. Нарисуйте линию AB, равную длине одной из сторон, и проведите AB до P. 2. Вычислите внешний угол многоугольника, разделив 360® на количество сторон. В данном случае угол экстенора составляет 360 * / 7 — 51 377. 3. Нарисуйте внешний угол PBC так, чтобы BC-AB. 4 Биссектрисы AB и BC пересекаются в 0 5 Нарисуйте окружность с центром 0 и радиусом OA (- OB — OC). 6. Сойдите по сторонам фигуры от C до D. D до E. и т. Д.ABCDEFG — это требуемый семиугольник. 1. Нарисовал линию A8, длина которой равна одному o! сторона». 2. От прямолинейного полукруга E, радиус AB до встречи BA, произведенный в P. 3. Разделите полукруг на такое же количество равных частей, поскольку у предлагаемого многоугольника есть стороны. Это может быть сделано методом проб и энор или расчетом (18077 -25 5 * / 7 для каждой дуги). 4. Проведите линию от A до точки 2 (для ВСЕХ полигонов). Это образует вторую сторону многоугольника. 5.Разделите пополам AB и A2 до пересечения в 0. 6. С центром O нарисуйте окружность радиуса OB (- OA — 02). 7. Сойдите по сторонам фигуры от B до C. C к D и т. Д. ABCDEFG — требуемый септаугольник 1. Проведите линию GA, равную по длине одной из сторон 2. Поперечный GA. 3. Из A постройте угол 45 **, чтобы пересечь биссектрису в точке 4. 4. Постройте из G угол 60p, чтобы пересечь биссектрису в точке 6. 5.Разделите пополам между точками 4 и 6, чтобы получить точку 5. Точка 4 — это центр круга, содержащего квадрат. Точка 5 — это центр круга, содержащего пятиугольник. Точка 6 — центр окружности, содержащей шестиугольник. Отметив точки на одинаковом расстоянии, можно получить центры окружностей, содержащих любой правильный многоугольник. 6. Отметьте точку 7 так, чтобы от 6 до 7 — от 5 до 6 (от — 4 до 5). 7. С центром в точке 7 нарисуйте круг, пересчитывая 7 к A (- 7 к G). 8.Сойдите по сторонам фигуры от A до B. От B до C. и т. Д. ABCDEFG — это требуемый семиугольник. Построить правильный многоугольник по диагонали e. 1. Начертите данную окружность и вставьте диаметр AM. 2. Разделите диаметр на такое количество частей, которое имеет стороны многоугольника. 3. С центром M нарисуйте дугу. радиус MA С центром A нарисуйте еще одну дугу того же радиуса, чтобы пересечь первую дугу в N. 4. Нарисуйте N2 и произведите пересечение круга в B (для любого многоугольника). 5. AB — первая сторона многоугольника. Шагните с другой стороны 8C. CO. И др. ABCDE — искомый многоугольник. Для построения • правильного многоугольника по диаметру e (Рис. 2/36) 1. Рисует линию MN. 2. Из некоторой точки A на прямой проведите полукруг любого удобного радиуса. 3. Разделите полукруг на такое же количество равных секторов, как многоугольник имеет стороны (в данном случае 9, т.е. 208 интервалов). 4. От точки A проведите радиальные линии через точки с 1 по 8. 5. Если многоугольник имеет четное число сторон, через A проходит только один диаметр. В этом случае разделите известный диаметр пополам, чтобы получить центр 0. Если, как в этом случае, через A проходят два диаметра ( никогда не может быть больше двух), затем разделите оба диаметра пополам до пересечения в 0. 6. С центром O и радиусом OA нарисуйте окружность, чтобы пересечь радиальные линии в C, D. E, F. G и H. 7. От A отметки AB и AJ равны CD. DE и др. ABCDEFG H J — искомый многоугольник. Показанные выше конструкции ни в коем случае не являются всеми конструкциями, которые могут потребоваться от вас. но они являются представителями того типа, с которым вы можете встретиться. Если ваша геометрия требует дополнительной практики, стоит доказать эти построения евклидовыми доказательствами. Чтобы ответить на многие из приведенных ниже вопросов, необходимо знать некоторые геометрические теоремы, и доказывая приведенные выше конструкции, вы убедитесь, что вы с ними знакомы. Упражнения 2 1.Постройте равносторонний треугольник со сторонами 60 мм. 2. Постройте равнобедренный треугольник с периметром 135 мм и высотой 65 мм. 3. Постройте треугольник с углами основания 60 * и 45 * и высотой 76 мм. 4. Постройте треугольник с основанием 55 мм. высота 62 мм и вертикальный угол 37} *. 6. Постройте треугольник с периметром 160 мм и сторонами в соотношении 3: 5: 6. 6. Постройте треугольник с периметром 170 мм и соотношением сторон 7: 3: 5. 7. Постройте треугольник с периметром 115 мм. высота 40 мм, вертикальный угол 45 *. 8. Постройте треугольник с основанием 62 мм. высота 50 мм и вертикальный угол 60 *. Теперь нарисовал аналогичный треугольник с периметром 250 мм . 9. Постройте клубок с периметром 125 мм, стороны которого находятся в соотношении 2: 4: 5. Теперь нарисуйте аналогичный треугольник, периметр которого равен 170 мм. 10. Постройте квадрат со стороной 50 мм.Путем построения найдите середину каждой стороны и соедините точки прямыми линиями, чтобы получить второй квадрат 11. Постройте квадрат с диагональю 68 мм. 12. Постройте квадрат с диагональю 85 мм. 13. Постройте параллелограмм с двумя сторонами длиной 42 мм и 90 мм и углом между ними 67 дюймов. 14. Постройте прямоугольник с диагональю 55 мм и длиной с одной стороны 35 мм. 15. Постройте ромб, если длина диагонали 75 мм, а длина одной стороны — 44 мм. 16. Постройте трапецию, учитывая, что параллельные стороны имеют длину 50 мм и 80 мм и находятся на расстоянии 45 мм друг от друга. 17. Постройте правильный шестиугольник. Сторона 45 мм. 18. Постройте правильный шестигранник, если диаметр равен 75 мм. 19. Постройте правильный шестиугольник внутри круга диаметром 80 мм. Все углы шестиугольника должны лежать на окружности . 20. Постройте квадрат со стороной 100 мм. Внутри квадрата постройте правильный восьмиугольник. Четыре противоположные стороны восьмиугольника должны лежать на сторонах квадрата . 21.Постройте следующие правильные многоугольники: пятиугольник, сторона 65 мм, семиугольник, сторона 55 мм. негон. сторона 45 мм. десятиугольник, сторона 36 мм. 22. Постройте правильный пятиугольник диаметром 82 мм. 23. Постройте правильный семиугольник внутри круга радиусом 60 мм. Углы семиугольника должны лежать на окружности круга. Читать здесь: Jrheberrechtlich geschtztes Material Была ли эта статья полезной? Свойства многоугольника Что такое многоугольник? Замкнутая плоская фигура, состоящая из нескольких соединенных отрезков. вместе.Стороны не пересекаются. Ровно две стороны встречаются на каждая вершина. Типы | Формулы | Запчасти | Специальные многоугольники | Имена Типы многоугольников Обычные — все углы равны и все стороны одинаковой длины. Правильные многоугольники бывают равносторонними и равносторонними. Equiangular — все углы равны. Равносторонний — все стороны одинаковой длины. Convex — прямая линия, проведенная через выпуклый многоугольник , пересекает не более двух сторон . Каждый внутренний угол составляет менее 180 °. Вогнутая — можно провести хотя бы одну прямую линию вогнутый многоугольник, который пересекает более двух сторон . По крайней мере, один внутренний угол больше 180 °. Формулы многоугольника (N = количество сторон и S = ​​длина от центра до угла) Площадь правильного многоугольника = (1/2) N sin (360 ° / N) S 2 Сумма внутренних углов многоугольника = (N — 2) x 180 ° Число диагоналей в многоугольнике = 1/2 N (N-3) Число треугольников (когда вы проводите все диагонали из одного вершина) в многоугольнике = (N — 2) Части многоугольника Сторона — один из отрезков прямой которые составляют многоугольник. Vertex — точка, где две стороны встретиться. Две или более из этих точек называются вершинами. Диагональ — линия, соединяющая две вершины, не являющиеся стороной. Внутренний угол — Уголок сформированный двумя соседними сторонами внутри многоугольника. Внешний угол — Уголок сформированный двумя соседними сторонами вне многоугольника. Особые полигоны Особые Четырехугольники — квадрат, ромб, параллелограмм, прямоугольник и трапеция. Специальный Треугольники — правый, равносторонний, равнобедренный, разносторонний, острый, тупой. Многоугольник Имена Общепринятые имена Стороны Имя п N-угольник 3 Треугольник 4 Четырехугольник 5 Пентагон 6 Шестиугольник 7 Гептагон 8 Восьмиугольник 10 Десятиугольник 12 Додекагон Предложены имена для других полигонов. Стороны Имя 9 Нонагон, Эннеагон 11 Undecagon, Hendecagon 13 Tridecagon, Triskaidecagon 14 Тетрадекагон, Тетрадекагон 15 Пентадекагон, Пентакайдекагон 16 Шестиугольник, Шестиугольник 17 Гептадекагон, Гептадекагон 18 Октадекагон, Октадекагон 19 Enneadecagon, Enneakaidecagon 20 Икосагон 30 Триаконтагон 40 Тетрактагон 50 Пентаконтагон 60 Шестигранник 70 Гептаконтагон 80 Octacontagon 90 Эннеаконтагон 100 Гектогон, Гекатонтагон 1 000 Чилигон 10 000 Мириагон Чтобы создать имя, объедините префикс + суффикс Стороны Префикс 20 Icosikai… 30 Триаконтакт … 40 Tetracontakai … 50 Пентаконтаки … 60 Hexacontakai… 70 Heptacontakai … 80 Octacontakai … 90 Эннеаконтакай … + Стороны Суффикс +1 …henagon +2 … digon +3 … тригон +4 … четырехугольник +5 …пентагон +6 … шестигранник +7 … семиугольник +8 … восьмиугольник +9 …enneagon Примеры: 46-сторонний многоугольник — Tetracontakaihexagon 28-сторонний многоугольник — Icosikaioctagon Однако многие люди используют форму n-угольник, например, 46-угольник или 28-угольник. этих имен. Многоугольники вкратце Мы долгое время уделяли внимание треугольникам и четырехугольникам.Но в этих геометрических джунглях существует гораздо больше форм, чем просто трех- и четырехгранные животные. Есть фигуры с пятью, шестью, семью и даже сорока двумя сторонами. И нам не пойдет на пользу держать головы под землей, как страусы, делая вид, что их не существует. Если вы еще не догадались, полигонов — это замкнутые двумерные фигуры, состоящие только из отрезков прямых линий. Таким образом, треугольники и четырехугольники являются примерами многоугольников, но углы, кривые и окружности не обязательны. Что касается именования полигонов, мы обычно называем их греческими префиксами (например, «три-» и «окто-»), которые соответствуют количеству их сторон. Конечно, после определенного момента это утомляет. Вот почему после 12 сторон мы просто называем их 13-угольными, 28-угольными и 146-угольными. Легче запоминать и легче писать. Нам это нравится. шестиугольник 076 Стороны Название многоугольника 3 треугольник 4 четырехугольник 5 пятиугольник 6 7 семиугольник 8 восьмиугольник 9 неугольник 10 десятиугольник 11 ундекагон 12 додекагон n n -угольник Как и четырехугольники, эти разные типы многоугольников также имеют диагонали.(Кроме треугольников, неважно, насколько сильно они или .) Но сколько именно диагоналей будет у этих многоугольников? Начнем с рисования непересекающихся диагоналей . У четырехугольника может быть только одна такая диагональ. Рисование в другом будет пересекаться с первым, и их не зря называют «непересекающимися». Если мы возьмем пятиугольник, мы можем нарисовать две диагонали, которые не пересекаются. Ключ состоит в том, чтобы нарисовать ровно столько, чтобы разделить многоугольник на треугольники. Когда мы смотрим на шестиугольники, мы можем разбить их на 4 различных треугольника, используя любые 3 непересекающиеся диагонали. Когда мы переходим к семиугольникам, мы можем иметь 4 непересекающиеся диагонали. Это может быть какое-то странное математическое вуду … или это может быть особая связь между многоугольниками и треугольниками? По сути, это сводится к тому, что выпуклый многоугольник с n сторонами можно разделить на n — 2 различных треугольника, на n — 3 непересекающихся диагонали. Если мы вернемся к нашему шведскому столу многоугольников, мы знаем, что треугольник имеет внутренние углы, которые в сумме составляют 180 °. Четырехугольник имеет внутренние углы в сумме 360 °. Как оказалось, пятиугольники имеют внутренние углы 540 °, а шестиугольники имеют внутренние углы 720 °. Больше математического вуду? Не так много. Многоугольник со сторонами n имеет внутренние углы, которые в сумме составляют ( n — 2) × 180 °. Пример задачи Используя треугольники, определите общую меру внутренних углов четырехугольника. Нарисуем одну диагональ, соединяющую B и D через четырехугольник ABCD . Получаем два треугольника: Δ ABD и Δ BCD . Мера внутреннего ABC — это просто сумма мер ∠1 и ∠2. Мера ADC — это сумма мер 3 и 4. Между тем, BAD и ∠ BCD являются общими для треугольников и четырехугольника. Если сложить углы обоих треугольников вместе, получится 180 ° + 180 ° = 360 °.Это в точности подтверждает то, что мы уже знали. Так держать, нам. Если бы мы сделали то же самое для пятиугольника, мы бы разбили пятиугольник на три треугольника, каждый из которых дает 180 ° к сумме внутренних углов пятиугольника. Добавление каждого из этих вкладов дает нам 540 °. Это также согласуется с нашей формулой, поскольку ( n — 2) × 180 °, когда n = 5, равно (5 — 2) × 180 ° = 3 × 180 ° = 540 °. До сих пор мы придерживались треугольников и четырехугольников. Теперь, когда мы расширяем наш геометрический вкус, нам следует расширить наш словарный запас. Правильный многоугольник — это многоугольник, стороны которого равны, а углы равны. Итак, правильный треугольник — это хорошо знакомый равносторонний треугольник. Правильный четырехугольник нам больше известен как квадрат. Это потому, что единственный четырехугольник, который одновременно является равносторонним и , является квадратом. Мы можем считать стороны, мы можем считать углы и мы можем считать диагонали. (Вы знаете, кто любит считать? Счет.) Число непересекающихся диагоналей, как мы уже знаем, равно n — 3, где n — количество сторон многоугольника.Но как насчет общего количества диагоналей, даже если они и пересекаются? Что ж, каждая вершина может иметь те же n — 3 диагонали, но мы будем считать каждую диагональ дважды (по одной для каждой вершины), поэтому мы должны разделить это число на 2. В итоге мы получим формулу для числа диагоналей в n -гон. Пример задачи Сколько градусов в восьмиугольнике? Сколько может быть непересекающихся и пересекающихся диагоналей? У восьмиугольников 8 сторон, поэтому n = 8.Теперь все, что нам нужно сделать, это применить наши формулы (и вспомнить, что означает каждая из них). Начнем с количества градусов. ( n — 2) × 180 ° = (8 — 2) × 180 ° = 6 × 180 ° = 1080 ° Теперь о количестве непересекающихся и пересекающихся диагоналей. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт