29.11.2017 Городской мастер-класс «Технология «Симметричное рисование» «
Для педагогов дошкольного образования, начального образования, дополнительного образования, прочих специальностей
Городской мастер-класс
Дата проведения: 29.11.2017
Время проведения: 16:00 — 17:30
Ведущая: Иванковская Светлана Анатольевна, преподаватель-психолог Центра ДПО «АНЭКС»
Описание:
Цель: ознакомление слушателей с технологий симметричного рисования.
Вопросы для обсуждения:
- Симметричное рисование как инструментарий развития конгнитивных процессов ребенка.
- Симметричное рисование как инструментарий развития мелкой моторики рук ребенка.
- Симметричное рисование как инструментарий коррекции поведения ребенка.
Упражнения для развития межполушарного взаимодействия улучшают мыслительную деятельность,
синхронизируют работу полушарий, способствуют улучшению запоминания, повышают устойчивость внимания, облегчают процесс письма.
Пожалуйста, зарегистрируйтесь на МААМ. Копировать можно только зарегистрированным пользователям МААМ. Адрес публикации: http://www.maam.ru/detskijsad/korekcija-giperaktivnogo-povedenija-detei-sredstvami-netradicionyh-izobrazitelnyh-tehnik-v-srednei-grupe-detskogo-sada.html
Список секций:
Секция 1. «Понятие симметрии для дошкольников. Формирование понятий»
Секция 2. «Приемы работы с гиперактивными детьми на уроке в начальной школе»
Секция 3. «Структура индивидуальной образовательной программы для коррекции поведения детей »
Записаться на мероприятие и оставить свои тезисы
Осевая симметрия рисунки по геометрии 8 класс
В природе симметрия встречается очень часто. Ее можно наблюдать в расположении органов у животных, в строении листьев и цветов растений, во взмахе крыльев, одним словом везде. А человек взял на вооружение этот инструмент, и использует его и в проектировании сложных объектов, и в искусстве, а так же в других сферах деятельности. Различают осевую и центральную симметрию, а чтобы разобраться какая между ними разница, надо изучить рисунки из этой статьи.

Осевая симметрия.

Центральная симметрия — симметрия относительно точки.
У равностороннего треугольника три оси симметрии.
На тетрадном листочке.
Зеркальное отражение.
Квадрат имеет четыре оси симметрии.
Центральная симметрия в квадратах.
Ось симметрии в творчестве.
Осевая симметрия.
Относительно одной точки. Все отрезки равны.
Симметрия относительно прямой.
Ось — воображаемая линия, делящая тело на две равные половины.
В художестве.
Симметричное рисование предметов правильной формы
Если на минутку задуматься и представить у себя в воображении какой-либо предмет, то в 99% случаев фигура, пришедшая на ум, будет правильной формы. Лишь 1 % людей, точнее их воображение, нарисует замысловатый объект, выглядящий совсем неправильно или непропорционально. Это скорее исключение из правил и относится к нетрадиционно размышляющим личностям с особым взглядом на вещи. Но возвращаясь к абсолютному большинству, стоит сказать, что существенная доля правильных предметов все же преобладает. В статье пойдет речь исключительно о них, а именно о симметричном рисовании таковых.
Изображение правильных предметов: всего несколько шагов до законченного рисунка
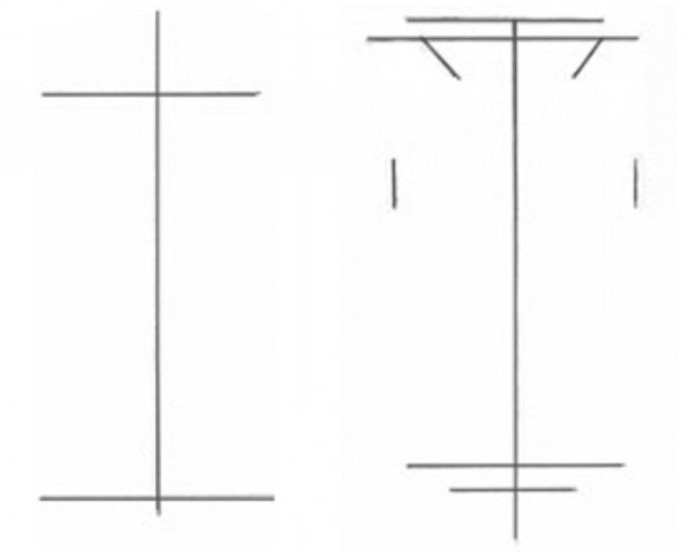
Прежде чем приступить к рисованию симметричного предмета, нужно его выбрать. В нашем варианте это будет ваза, но даже если она никак не напоминает то, что решили изображать вы, не отчаивайтесь: все шаги абсолютно идентичны. Придерживайтесь последовательности и все получится:
- У всех предметов правильной формы есть так называемая центральная ось, которую при симметричном рисовании обязательно стоит выделить. Для этого можно даже воспользоваться линейкой и провести по центру альбомного листа прямую линию.
- Далее внимательно посмотрите на выбранный вами предмет и постарайтесь перенести его пропорции на лист бумаги. Сделать это несложно, если с обеих сторон проведенной заранее линии, наметить легкие штрихи, которые впоследствии станут очертаниями рисуемого предмета. В случае с вазой необходимо выделить горлышко, донышко и самую широкую часть корпуса.
- Не забывайте о том, что симметричное рисование не терпит неточностей, поэтому если есть некоторые сомнения относительно намеченных штрихов, или вы не уверены в правильности собственного глазомера, перепроверьте отложенные расстояния при помощи линейки.
- Последний шаг — соединение всех линий воедино.
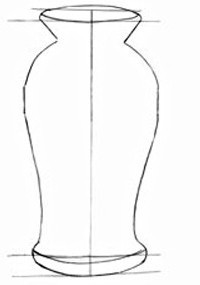
Симметричное рисование доступно компьютерным пользователям
В силу того что большинство окружающих нас предметов имеют правильные пропорции, иначе говоря симметричны, разработчики компьютерных приложений создали программы, в которых легко можно нарисовать абсолютно все. Достаточно лишь скачать их и наслаждаться творческим процессом. Однако помните, машина никогда не станет заменой остро наточенному карандашу и альбомному листу.
Осевая и центральная симметрия — урок. Математика, 6 класс.
Симметрия — слово греческого происхождения, как и многие другие слова, которые связаны с математикой. Оно означает соразмерность, наличие определённого порядка, закономерности в расположении частей. Смотря на объекты вокруг, мы не раз восклицаем: «Какая симметрия!»

Люди с давних времён использовали симметрию в рисунках, орнаментах, предметах быта, в архитектуре, художестве, строительстве.
Но симметрия широко распространена и в природе, где не было вмешательства человеческой руки. Её можно наблюдать в форме листьев и цветов растений, в расположении различных органов животных, в форме кристаллических тел, в порхающей бабочке, загадочной снежинке, морской звезде.

Пока рассмотрим две симметрии на плоскости: относительно точки и прямой.
Центральная симметрия
Симметрию относительно точки называют центральной симметрией.
Точки M и M1 симметричны относительно некоторой точки \(O\), если точка \(O\) является серединой отрезка MM1.

Точка \(O\) называется центром симметрии.
Алгоритм построения центрально-симметричных фигур.

Построим треугольник A1B1C1, симметричный треугольнику \(ABC\) относительно центра (точки) \(O\):
1. для этого соединим точки \(A\), \(B\), \(C\) с центром \(O\) и продолжим эти отрезки;
2. измерим отрезки \(AO\), \(BO\), \(CO\) и отложим с другой стороны от точки \(O\) равные им отрезки AO=OA1;BO=OB1;CO=OC1;
3. соединим получившиеся точки отрезками и получим треугольник A1B1C1, симметричный данному треугольнику \(ABC\).
Фигуры, симметричные относительно некоторой точки, равны.
Фигура симметрична относительно центра симметрии, если для каждой этой точки фигуры симметричная ей точка также лежит на этой фигуре. Такая фигура имеет центр симметрии (фигура с центральной симметрией).
Осевая симметрия
Осевая симметрия — это симметрия относительно проведённой прямой (оси).
Точки M и M1 симметричны относительно некоторой прямой (оси симметрии), если эти точки лежат на прямой, перпендикулярной данной, и на одинаковом расстоянии от оси симметрии.

Алгоритм построения фигуры, симметричной относительно некоторой прямой.

Построим треугольник A1B1C1, симметричный треугольнику \(ABC\) относительно красной прямой:
1. для этого проведём из вершин треугольника \(ABC\) прямые, перпендикулярные оси симметрии, и продолжим их дальше на другой стороне оси.
2. Измерим расстояния от вершин треугольника до получившихся точек на прямой и отложим с другой стороны прямой такие же расстояния.
3. Соединим получившиеся точки отрезками и получим треугольник A1B1C1, симметричный данному треугольнику \(ABC\).
Фигуры, симметричные относительно прямой, равны.
Фигура считается симметричной относительно прямой, если для каждой точки рассматриваемой фигуры симметричная для неё точка относительно данной прямой также находится на этой фигуре. Прямая является в этом случае осью симметрии фигуры.
Иногда у фигур несколько осей симметрии:
- для неразвёрнутого угла существует единственная ось симметрии — это биссектриса данного угла.
- Для равнобедренного треугольника есть единственная ось симметрии.
- Для равностороннего треугольника — три оси.
- Для прямоугольника и ромба существуют две оси симметрии.
- Для квадрата — целых четыре.
- Для окружности осей симметрии бесчисленное множество — это каждая прямая, которая проходит через центр этой фигуры.
- Есть фигуры без осей симметрии — это параллелограмм и треугольник, все стороны которого различны.
