Линейно-конструктивный рисунок шестигранной призмы | СПЛАЙН
ЦЕЛЬ ЗАДАНИЯ. Научиться изображать шестигранную призму в различных положениях.
ПОСТАНОВКА ЗАДАНИЯ. Изучите различные способы построения правильного шестиугольника, сделайте рисунки шестиугольников, проверьте правильность их построения. На основе шестиугольников постройте шестигранные призмы.
РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ ЗАДАНИЯ.
Рассмотрите шестигранную призму на рис. 3.52 и ее ортогональные проекции на рис. 3.53. В основании шестигранной призмы (шестигранника) лежат правильные шестиугольники, боковые грани — одинаковые прямоугольники. Для того, чтобы правильно изобразить шестигранник в перспективе, необходимо сначала научиться грамотно изображать в перспективе его основание (рис. 3.54). В шестиугольнике на рис. 3.55 вершины обозначены цифрами от одного до шести.
Если соединить точки 1 и 3, 4 и 6 вертикальными прямыми, можно заметить, что эти прямые вместе с точкой центра окружности делят диаметр 5— 2 на четыре равных отрезка (эти отрезки обозначены дугами).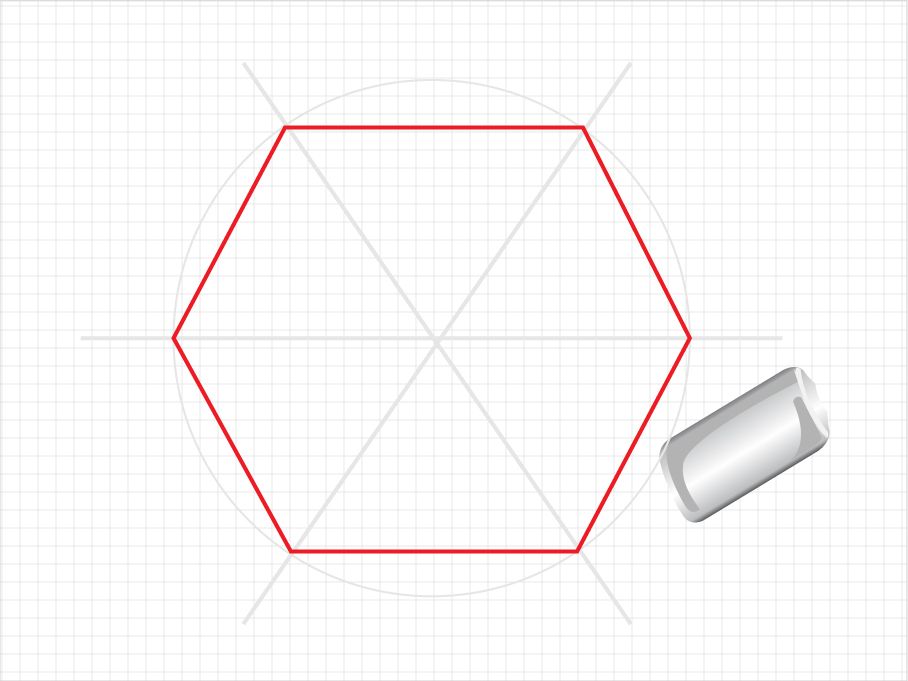
Построить правильный шестиугольник по представлению можно двумя способами: на основе описанной окружности и на основе квадрата.
На основе описанной окружности. Рассмотрите рис. 3.56. Все вершины правильного шестиугольника принадлежат описанной окружности, радиус которой равен стороне шестиугольника.
Горизонтальный шестиугольник
Изобразите горизонтальный эллипс произвольного раскрытия, т.е. описанную окружность в перспективе. Теперь необходимо найти на ней шесть точек, являющихся вершинами шестиугольника. Проведите любой диаметр данной окружности через ее центр (рис. 3.57).
Крайние точки диаметра — 5 и 2, лежащие на эллипсе, являются вершинами шестиугольника. Для нахождения остальных вершин необходимо разделить этот диаметр на четыре одинаковых отрезка. Диаметр уже разделен точкой центра окружности на два радиуса, остается разделить каждый радиус пополам. На перспективном рисунке все четыре отрезка равномерно сокращаются при удалении от зрителя (рис. 3.58). Теперь проведите через середины радиусов — точки А и В — прямые, перпендикулярные прямой 5— 2. Найти их направление можно при помощи касательных к эллипсу в точках 5 и 2 (рис. 3.59). Эти касательные будут перпендикулярны диаметру 5— 2, а прямые, проведенные через точки А и В параллельно этим касательным, будут также перпендикулярны прямой 5— 2. Обозначьте точки, полученные на пересечении этих прямых с эллипсом, как 1, 3, 4, 6 (рис. 3.60). Соедините все шесть вершин прямыми линиями (рис. 3.61).
Для нахождения остальных вершин необходимо разделить этот диаметр на четыре одинаковых отрезка. Диаметр уже разделен точкой центра окружности на два радиуса, остается разделить каждый радиус пополам. На перспективном рисунке все четыре отрезка равномерно сокращаются при удалении от зрителя (рис. 3.58). Теперь проведите через середины радиусов — точки А и В — прямые, перпендикулярные прямой 5— 2. Найти их направление можно при помощи касательных к эллипсу в точках 5 и 2 (рис. 3.59). Эти касательные будут перпендикулярны диаметру 5— 2, а прямые, проведенные через точки А и В параллельно этим касательным, будут также перпендикулярны прямой 5— 2. Обозначьте точки, полученные на пересечении этих прямых с эллипсом, как 1, 3, 4, 6 (рис. 3.60). Соедините все шесть вершин прямыми линиями (рис. 3.61).
Проверьте правильность вашего построения разными способами. Если построение верно, то линии, соединяющие противоположные вершины шестиугольника, пересекаются в центре окружности (рис.
Вертикальный шестиугольник
В таком шестиугольнике прямые, соединяющие точки 1 и 3, 6 и 4, а также касательные к описанной окружности в точках 5 и 2, имеют вертикальное направление и сохраняют его на перспективном рисунке. Таким образом, проведя две вертикальные касательные к эллипсу, найдем точки 5 и 2 (точки касания). Соедините их прямой линией, а затем разделите полученный диаметр 5— 2 на 4 равных отрезка, учитывая их перспективные сокращения (рис. 3.65). Проведите вертикальные прямые через точки А и В, а на их пересечении с эллипсом найдите точки 7, 3, 6 и 4. Затем последовательно соедините точки 1— 6 прямыми (рис. 3.66). Правильность построения шестиугольника проверьте аналогично предыдущему примеру.
Описанный способ построения шестиугольника позволяет получить эту фигуру на основе окружности, изобразить которую в перспективе проще, чем
квадрат заданных пропорций.
ения на основе квадрата позволяет легко изобразить шестигранник в том случае, когда на рисунке уже есть куб, иными словами, когда пропорции квадрата и направление его сторон определены.
На основе квадрата. Рассмотрите рис. 3.67. Вписанный в квадрат шестиугольник по горизонтальному направлению 5— 2 равен стороне квадрата, а по вертикали — меньше ее длины.
Вертикальный шестиугольник
Нарисуйте вертикальный квадрат в перспективе. Проведите через пересечение диагоналей прямую, параллельную его горизонтальным сторонам. Разделите полученный отрезок 5— 2 на четыре равные части и проведите через точки А и В вертикальные прямые (рис. 3.68).
 3.69).
3.69).Гэризонтальный шестиугольник строится в той же последовательности (рис. 3.70 и 3.71).
Этот способ построения уместен только для шестиугольников с достаточным раскрытием. В случае, если раскрытие шестиугольника незначительно, лучше воспользоваться способом на основе описанной окружности. Для проверки шестиугольника, построенного через квадрат, можно использовать уже известные вам методы.
Кроме того существует еще один — описать вокруг полученного шестиугольника окружность (на вашем рисунке — эллипс). Все вершины шестиугольника должны принадлежать этому эллипсу.
Овладев навыками изображения шестиугольника, вы свободно перейдете к изображению шестигранной призмы. Внимательно рассмотрите схему
на рис. 3.72, а также схемы построения шестигранных призм на основе описанной окружности (рис. 3.73; 3.74 и 3.75) и на основе квадрата (рис. 3.76; 3.77 и 3.78).
Изобразите вертикальные и горизонтальные шестигранники различными способами.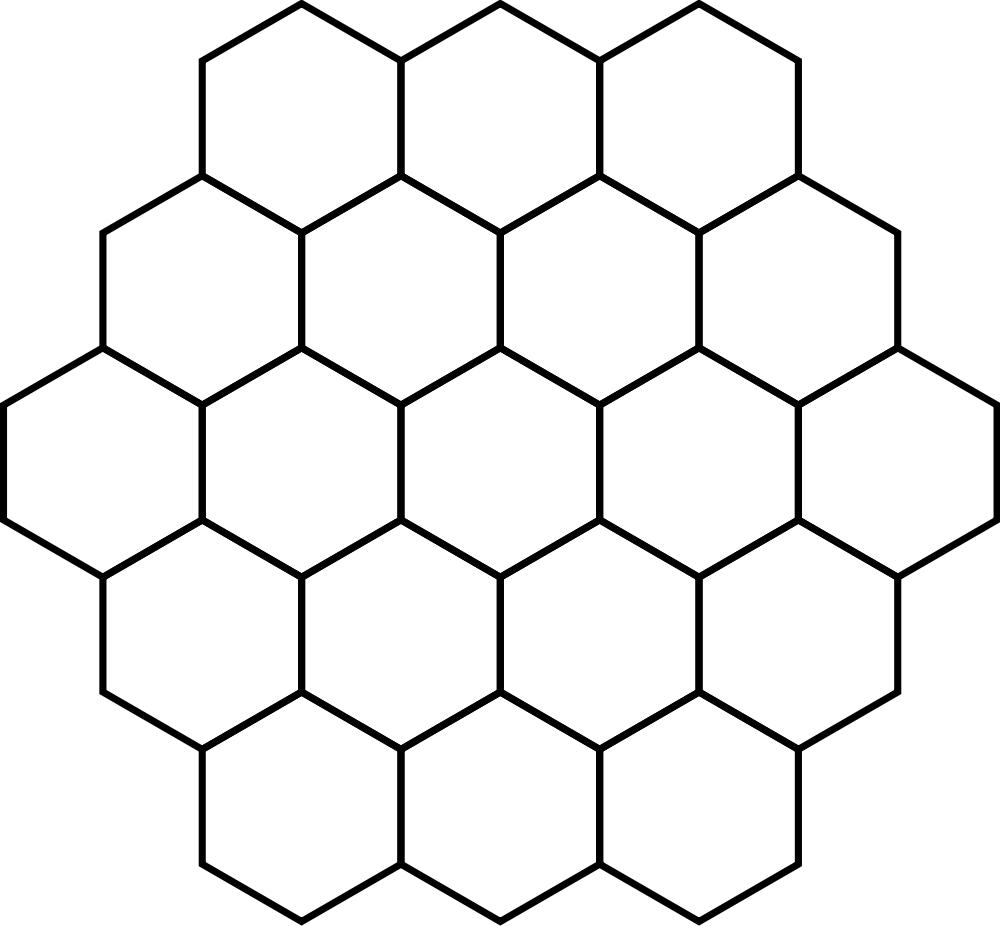 На рисунке вертикального шестигранника длинные стороны боковых граней будут параллельными друг другу вертикальными прямыми, а шестиугольник
На рисунке вертикального шестигранника длинные стороны боковых граней будут параллельными друг другу вертикальными прямыми, а шестиугольник
основания будет тем больше раскрыт, чем дальше он находится от линии горизонта. На рисунке горизонтального шестигранника длинные стороны боковых граней будут сходиться в точке схода на горизонте, а раскрытие шестиугольника основания будет тем больше, чем дальше от зрителя он находится. Изображая шестигранник, следите также за тем, чтобы параллельные грани обоих оснований сходились в перспективе (рис. 3.79; 3.80).
Как правильно начертить шестигранник
Обычно при вычерчивании болта или гайки, на учебных чертежах, студенты пользуются двумя способами. Первый – это взять ГОСТ, на тот элемент, который вычерчиваешь, и начертить его по размерам, а второй – начертить тот же самый элемент по расчетам. Расчеты не сложные. Но у студентов всегда возникает вопрос: почему размеры сделанные по расчетам не совпадают с размерами по ГОСТу.
Это явление на самом деле обычное, так как из расчетов мы получаем «условные» разметы, проще говоря – приблизительные. Но это другая тема, а нас в данной статье интересует – как начертить головку болта (или гайки), так чтобы она соответствовала размерам, взятым из ГОСТов.
В ГОСТ обычно указывается размер болта под ключ ( S ) и наружный диаметр головки болта ( D ). Для того что бы вычертить шестигранник (а именно так и выглядит головка болта) при помощи циркуля, достаточно будет знать диаметр круга описанного вокруг него (параметр D ), но в таком случае мы не получим того размера под ключ который нам нужно. Можете проверить – если не верите.
Значит, данный способ нам не подходит, так как нам важен именно размер «под ключ» (параметр S ). Соответственно будем чертить шестигранник немного другим способом…
1. Вычерчиваем оси
2. Намечаем центр нашего шестигранника и проводим линии под углом 30 градусов к горизонтали (или вертикали, если шестигранник развернут на 90 градусов).
3. Проводим вертикальные прямые, на расстоянии S /2 от вертикальной оси справа и слева. На пересечении линий намечаем точки граней.
4. Откладываем расстояние U (между противоположными углами) по вертикали.
5. Соединяем все точки воедино и получаем искомую фигуру.
Теперь все расстояния, между гранями головки болта (или гайки), будут равны параметру S – размеру под ключ.
В широком смысле шестиугольник — это многоугольник с шестью углами. У правильного же шестиугольника углы и стороны равны. Нарисовать такой шестиугольник можно при помощи рулетки и транспортира, грубый шестиугольник — при помощи круглого предмета и линейки или еще более грубый шестиугольник — при помощи интуиции и карандаша. Если вы хотите знать, как нарисовать шестиугольник различными способами, просто читайте далее.
Научимся изображать шестигранную призму в различных положениях.
Изучите различные способы построения правильного шестиугольника, сделайте рисунки шестиугольников, проверьте правильность их построения. На основе шестиугольников постройте шестигранные призмы.
На основе шестиугольников постройте шестигранные призмы.
Рассмотрите шестигранную призму на рис. 3.52 и ее ортогональные проекции на рис. 3.53. В основании шестигранной призмы (шестигранника) лежат правильные шестиугольники, боковые грани — одинаковые прямоугольники. Для того, чтобы правильно изобразить шестигранник в перспективе, необходимо сначала научиться грамотно изображать в перспективе его основание (рис. 3.54). В шестиугольнике на рис. 3.55 вершины обозначены цифрами от одного до шести. Если соединить точки 1 и 3, 4 и 6 вертикальными прямыми, можно заметить, что эти прямые вместе с точкой центра окружности делят диаметр 5 — 2 на четыре равных отрезка (эти отрезки обозначены дугами). Противоположные стороны шестиугольника параллельны друг другу и прямой, проходящей через его центр и соединяющей две вершины (например, стороны 6 — 1 и 4 — 3 параллельны прямой 5 — 2). Эти наблюдения помогут вам построить шестиугольник в перспективе, а также проверить правильность этого построения. Построить правильный шестиугольник по представлению можно двумя способами: на основе описанной окружности и на основе квадрата.
Построить правильный шестиугольник по представлению можно двумя способами: на основе описанной окружности и на основе квадрата.
На основе описанной окружности. Рассмотрите рис. 3.56. Все вершины правильного шестиугольника принадлежат описанной окружности, радиус которой равен стороне шестиугольника.
Линейно-конструктивный рисунок шестигранной призмы Линейно-конструктивный рисунок шестигранной призмы Линейно-конструктивный рисунок шестигранной призмы
Горизонтальный шестиугольник. Изобразите горизонтальный эллипс произвольного раскрытия, т. е. описанную окружность в перспективе. Теперь необходимо найти на ней шесть точек, являющихся вершинами шестиугольника. Проведите любой диаметр данной окружности через ее центр (рис. 3.57). Крайние точки диаметра — 5 и 2, лежащие на эллипсе, являются вершинами шестиугольника. Для нахождения остальных вершин необходимо разделить этот диаметр на четыре одинаковых отрезка. Диаметр уже разделен точкой центра окружности на два радиуса, остается разделить каждый радиус пополам.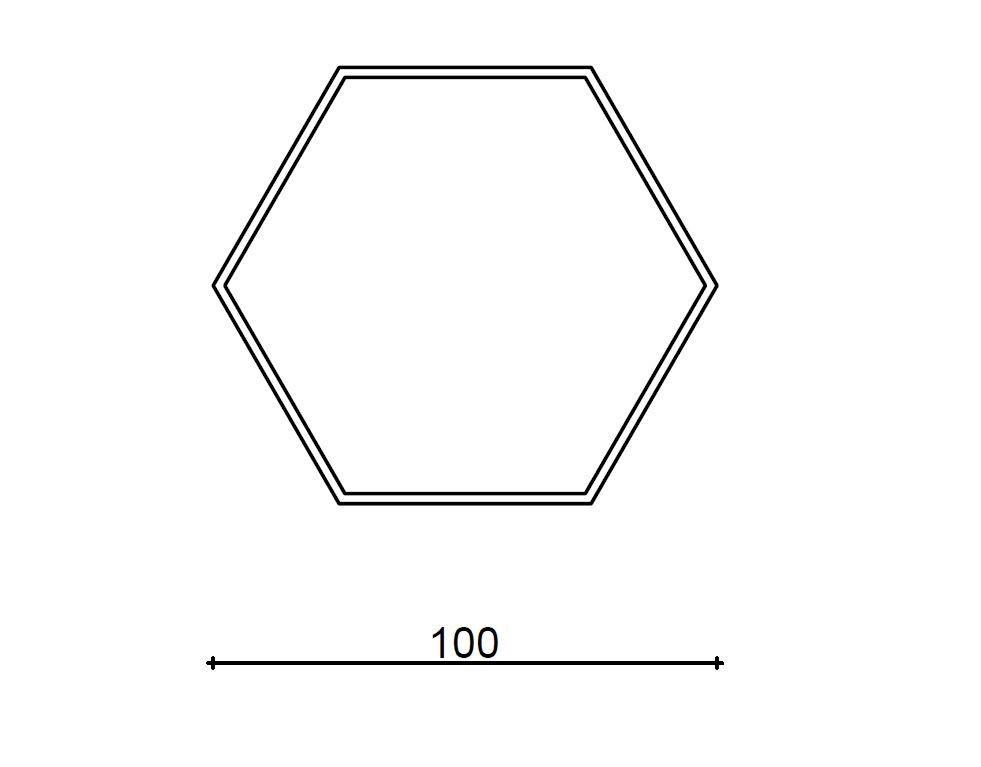 На перспективном рисунке все четыре отрезка равномерно сокращаются при удалении от зрителя (рис. 3.58). Теперь проведите через середины радиусов — точки А и В — прямые, перпендикулярные прямой 5 — 2. Найти их направление можно при помощи касательных к эллипсу в точках 5 и 2 (рис. 3.59). Эти касательные будут перпендикулярны диаметру 5 — 2, а прямые, проведенные через точки А и В параллельно этим касательным, будут также перпендикулярны прямой 5 — 2. Обозначьте точки, полученные на пересечении этих прямых с эллипсом, как 1, 3, 4, 6 (рис. 3.60). Соедините все шесть вершин прямыми линиями (рис. 3.61).
На перспективном рисунке все четыре отрезка равномерно сокращаются при удалении от зрителя (рис. 3.58). Теперь проведите через середины радиусов — точки А и В — прямые, перпендикулярные прямой 5 — 2. Найти их направление можно при помощи касательных к эллипсу в точках 5 и 2 (рис. 3.59). Эти касательные будут перпендикулярны диаметру 5 — 2, а прямые, проведенные через точки А и В параллельно этим касательным, будут также перпендикулярны прямой 5 — 2. Обозначьте точки, полученные на пересечении этих прямых с эллипсом, как 1, 3, 4, 6 (рис. 3.60). Соедините все шесть вершин прямыми линиями (рис. 3.61).
Проверьте правильность вашего построения разными способами. Если построение верно, то линии, соединяющие противоположные вершины шестиугольника, пересекаются в центре окружности (рис. 3.62), а противоположные стороны шестиугольника параллельны соответствующим диаметрам (рис. 3.63). Еще один способ проверки показан на рис. 3.64.
Вертикальный шестиугольник. В таком шестиугольнике прямые, соединяющие точки 7 и 3, б и 4, а также касательные к описанной окружности в точках 5 и 2, имеют вертикальное направление и сохраняют его на перспективном рисунке. Таким образом, проведя две вертикальные касательные к эллипсу, найдем точки 5 и 2 (точки касания). Соедините их прямой линией, а затем разделите полученный диаметр 5 — 2 на 4 равных отрезка, учитывая их перспективные сокращения (рис. 3.65). Проведите вертикальные прямые через точки А и Б, а на их пересечении с эллипсом найдите точки 1,3,6л4. Затем последовательно соедините точки 1 — 6 прямыми (рис. 3.66). Правильность построения шестиугольника проверьте аналогично предыдущему примеру.
Таким образом, проведя две вертикальные касательные к эллипсу, найдем точки 5 и 2 (точки касания). Соедините их прямой линией, а затем разделите полученный диаметр 5 — 2 на 4 равных отрезка, учитывая их перспективные сокращения (рис. 3.65). Проведите вертикальные прямые через точки А и Б, а на их пересечении с эллипсом найдите точки 1,3,6л4. Затем последовательно соедините точки 1 — 6 прямыми (рис. 3.66). Правильность построения шестиугольника проверьте аналогично предыдущему примеру.
Описанный способ построения шестиугольника позволяет получить эту фигуру на основе окружности, изобразить которую в перспективе проще, чем квадрат заданных пропорций. Поэтому данный способ построения шестиугольника представляется наиболее точным и универсальным. Способ построения на основе квадрата позволяет легко изобразить шестигранник в том случае, когда на рисунке уже есть куб, иными словами, когда пропорции квадрата и направление его сторон определены.
На основе квадрата. Рассмотрите рис. 3.67. Вписанный в квадрат шестиугольник по горизонтальному направлению 5 — 2 равен стороне квадрата, а по вертикали — меньше ее длины.
3.67. Вписанный в квадрат шестиугольник по горизонтальному направлению 5 — 2 равен стороне квадрата, а по вертикали — меньше ее длины.
Вертикальный шестиугольник. Нарисуйте вертикальный квадрат в перспективе. Проведите через пересечение диагоналей прямую, параллельную его горизонтальным сторонам. Разделите полученный отрезок 5 — 2 на четыре равные части и проведите через точки А и В вертикальные прямые (рис. 3.68). Линии, ограничивающие шестиугольник сверху и снизу, не совпадают со сторонами квадрата. Изобразите их на некотором расстоянии (1114 а) от горизонтальных сторон квадрата и параллельно им. Соединив найденные таким образом точки 1 и 3 с точкой 2, а точки 6 и 4 — с точкой 5, получим шестиугольник (рис. 3.69).
Горизонтальный шестиугольник строится в той же последовательности (рис. 3.70 и 3.71).
Этот способ построения уместен только для шестиугольников с достаточным раскрытием. В случае, если раскрытие шестиугольника незначительно, лучше воспользоваться способом на основе описанной окружности.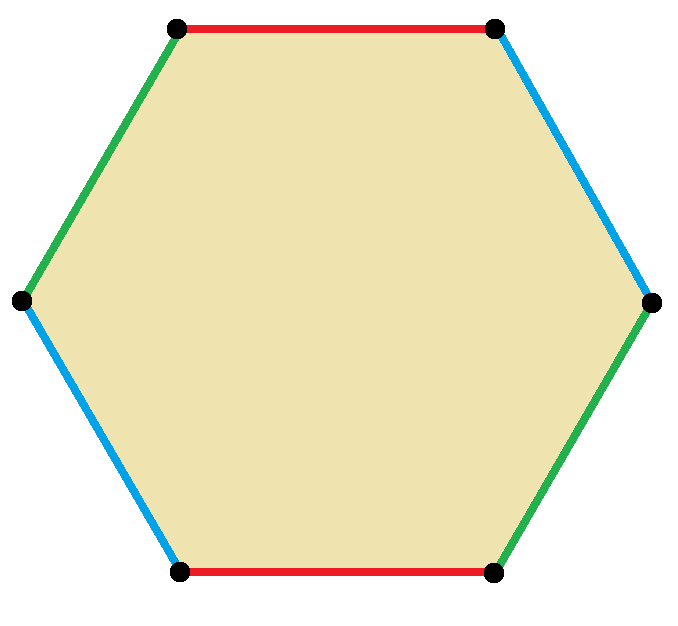 Для проверки шестиугольника, построенного через квадрат, можно использовать уже известные вам методы.
Для проверки шестиугольника, построенного через квадрат, можно использовать уже известные вам методы.
Линейно-конструктивный рисунок шестигранной призмы Линейно-конструктивный рисунок шестигранной призмы
Кроме того существует еще один — описать вокруг полученного шестиугольника окружность (на вашем рисунке — эллипс). Все вершины шестиугольника должны принадлежать этому эллипсу.
Овладев навыками изображения шестиугольника, вы свободно перейдете к изображению шестигранной призмы. Внимательно рассмотрите схему на рис. 3.72, а также схемы построения шестигранных призм на основе описанной окружности (рис. 3.73; 3.74 и 3.75) и на основе квадрата (рис. 3.76; 3.77 и 3.78). Изобразите вертикальные и горизонтальные шестигранники различными способами. На рисунке вертикального шестигранника длинные стороны боковых граней будут параллельными друг другу вертикальными прямыми, а шестиугольник основания будет тем больше раскрыт, чем дальше он находится от линии горизонта. На рисунке горизонтального шестигранника длинные стороны боковых граней будут сходиться в точке схода на горизонте, а раскрытие шестиугольника основания будет тем больше, чем дальше от зрителя он находится. Изображая шестигранник, следите также за тем, чтобы параллельные грани обоих оснований сходились в перспективе (рис. 3.79; 3.80).
Изображая шестигранник, следите также за тем, чтобы параллельные грани обоих оснований сходились в перспективе (рис. 3.79; 3.80).
Линейно-конструктивный рисунок шестигранной призмы Линейно-конструктивный рисунок шестигранной призмы
8.1. Шестиугольник. Разоблаченный логотип, или Психогеометрия
8.1. Шестиугольник
Да что там хваленый немецкий порядок. Вот у муравьев – настоящий «орднунг». И чего они не стали хозяевами планеты?
Козьма Прутков, сельский учитель, бывший фронтовик
Шестиугольная плитка крепче держится.
Мнение штукатуров
Вместе весело шагать по просторам, по просторам!
Из детской песенки
Разом нас багато, нас не подолати.
Непереводимый слоган 2004 года
Медовые соты вкуснейшая вещь, да уж слишком больно обходятся.
Медведь Мишка
Дресс-код – та же униформа, только в мирное время.
Из корпоративного этикета
Мы едины или просто все клонированы?
Открытый вопрос
ШЕСТИУГОЛЬНИК – особая фигура, аналогов у которой поистине нет. Она обладает свойством, которое нигде больше не повторяется так ярко, функционально и выразительно. А для нашей цивилизации еще и предельно актуально. На современном языке это именуется «корпоративным духом» и «корпоративной религией». Впрочем, можно додуматься и до «бренд-рая» на основе все той же корпоративной религии[3].
Она обладает свойством, которое нигде больше не повторяется так ярко, функционально и выразительно. А для нашей цивилизации еще и предельно актуально. На современном языке это именуется «корпоративным духом» и «корпоративной религией». Впрочем, можно додуматься и до «бренд-рая» на основе все той же корпоративной религии[3].
Но давайте вначале рассмотрим психогеометрическую сущность самого шестиугольника. Его изображение представлено на рис. 8.1. У фигуры отчетливо выражен центр. В этом аспекте шестиугольник чем-то сродни кругу. Однозначно есть своя идеология, единство и целостность. Шестиугольник обладает ярко выраженной самостью. Поэтому во внешних «варягах» совершенно не нуждается. Управление из центра идет по стратегическим радиальным каналам по направлению к углам. Административная иерархия четко прослеживается. Проще говоря, шестиугольник знает, что нужно делать, и умеет эффективно выстроить свой менеджмент.
Есть два ударных угла. Что весьма немаловажно. Можно концентрировать силы на главных направлениях. А в общем-то, в наличии еще четыре дополнительных угла по круговой обороне, потому-то и шестиугольник. Попробуй подкатись без тщательной рекогносцировки. Шестиугольник умеет очень хорошо защищать свою территорию и свои интересы вовне ее. Своего рода скрытая агрессия, неумолимая и весьма беспощадная. Железно работает правило: «кто не с нами – тот против нас». Однако авантюрного риска в этой фигуре совершенно нет. Исключено.
А в общем-то, в наличии еще четыре дополнительных угла по круговой обороне, потому-то и шестиугольник. Попробуй подкатись без тщательной рекогносцировки. Шестиугольник умеет очень хорошо защищать свою территорию и свои интересы вовне ее. Своего рода скрытая агрессия, неумолимая и весьма беспощадная. Железно работает правило: «кто не с нами – тот против нас». Однако авантюрного риска в этой фигуре совершенно нет. Исключено.
Обратим также внимание на внутренние производственные возможности, на рисунке зона производства заштрихована (рис. 8.2). Шестиугольник особенно удачно сочетает логику и иррациональность в своей тактике и стратегии. Где надо – работать, где надо – атаковать (углы-то выступающие). Добавьте к этому единство идеологии и диктат центра. Поистине неотразимое сочетание. И все как-то целостно объединено.
Но главная фишка все же в другом. Шестиугольник может. производить себе подобных! Скажем, для круга, треугольника либо овала это просто физически невозможно, да и немыслимо.![]() Зато шестиугольник очень легко объединяется с себе подобными в некую ячеистую сеть, которая непрерывно множится (рис. 8.3). Такова уж его конфигурация. Она позволяет устанавливать связи в самых различных направлениях. Создавая, например, сеть однотипных филиалов. Что и есть отличительным признаком корпорации (от позднелатинского corporatio – объединение, сообщество). Впрочем, можно применять термин «множение» либо «клонирование». Наверное, это так увлекательно – бесконечно расширяться и строить мир по своему плану и подобию. Идея, многократно воспроизведенная, становится очевидным материальным и духовным могуществом. Применительно к шестиугольнику мы можем говорить об уникальной способности к самовоспроизводству. Своего рода матричная система. В естественной природе идеально применяемая некоторыми видами насекомых. Муравьи, термиты, осы, пчелы, шершни расширяют свой ареал по одному и тому же «строительному генплану». И если вы встанете у них на пути, то, скорее всего, вас заставят ретироваться.
Зато шестиугольник очень легко объединяется с себе подобными в некую ячеистую сеть, которая непрерывно множится (рис. 8.3). Такова уж его конфигурация. Она позволяет устанавливать связи в самых различных направлениях. Создавая, например, сеть однотипных филиалов. Что и есть отличительным признаком корпорации (от позднелатинского corporatio – объединение, сообщество). Впрочем, можно применять термин «множение» либо «клонирование». Наверное, это так увлекательно – бесконечно расширяться и строить мир по своему плану и подобию. Идея, многократно воспроизведенная, становится очевидным материальным и духовным могуществом. Применительно к шестиугольнику мы можем говорить об уникальной способности к самовоспроизводству. Своего рода матричная система. В естественной природе идеально применяемая некоторыми видами насекомых. Муравьи, термиты, осы, пчелы, шершни расширяют свой ареал по одному и тому же «строительному генплану». И если вы встанете у них на пути, то, скорее всего, вас заставят ретироваться. Либо придется принять вызов и приступить к активным контрмерам. Третьего, увы, не дано. Правда, в бизнесе и политике есть еще третий вариант, а именно – инкорпорироваться в множащуюся структуру. Стать ее частью, филиалом и безоговорочно принять правила игры корпорации. Тем самым получив надежную «крышу» и гарантию того, что тонуть в случае чего придется всем «титаником». У шестиугольника неважно с адаптацией к внешней среде. Это уж точно не ромб. Изменять свою структуру он никак не желает. Приходится применять иную глобальную стратегию выживания. Чтобы предвидеть будущее, его надо создать однотипным и сделать управляемым. Что шестиугольник активно и претворяет в жизнь. Зачастую в нашей цивилизации это очень даже неплохо получается. Хотя все же бывают досадные сбои. Даже идеальный план не может учесть все факторы. И уж тем более, когда имеешь дело со временем, пространством и бытием в его сущности. Хотя, все мировые религии довольно устойчиво процветают многие и многие века. Чем не удачное клонирование некой парадигмы? Современный бизнес таким устойчивым долголетием похвастаться не может.
Либо придется принять вызов и приступить к активным контрмерам. Третьего, увы, не дано. Правда, в бизнесе и политике есть еще третий вариант, а именно – инкорпорироваться в множащуюся структуру. Стать ее частью, филиалом и безоговорочно принять правила игры корпорации. Тем самым получив надежную «крышу» и гарантию того, что тонуть в случае чего придется всем «титаником». У шестиугольника неважно с адаптацией к внешней среде. Это уж точно не ромб. Изменять свою структуру он никак не желает. Приходится применять иную глобальную стратегию выживания. Чтобы предвидеть будущее, его надо создать однотипным и сделать управляемым. Что шестиугольник активно и претворяет в жизнь. Зачастую в нашей цивилизации это очень даже неплохо получается. Хотя все же бывают досадные сбои. Даже идеальный план не может учесть все факторы. И уж тем более, когда имеешь дело со временем, пространством и бытием в его сущности. Хотя, все мировые религии довольно устойчиво процветают многие и многие века. Чем не удачное клонирование некой парадигмы? Современный бизнес таким устойчивым долголетием похвастаться не может. Другие темпы и другие правила эволюции. Для мощных корпоративных структур в том числе.
Другие темпы и другие правила эволюции. Для мощных корпоративных структур в том числе.
Да, еще несколько слов о пространственном положении фигуры. Шестиугольник весьма самодостаточен, автономен, идеологичен, он обладает собственной базой воспроизводства, и потому ему, как и ромбу, больше всего подходит вертикальное положение, когда ударные углы смотрят вверх и вниз (рис. 8.1). Но бывают ситуации, когда шестиугольник вынужден ложиться на бок (рис. 8.5). Скорее всего, из-за чисто прагматических интересов. Приоритеты экспансии оказались несколько более заземленными, нежели ожидалось. Здесь уже не до мегаломании. Приходится ближе на более понятном языке контактировать со средой обитания и как-то с ней сосуществовать. Пусть даже получая далеко не ту прибыль, которая предполагалась. В реальной жизни корпорации слишком запоздало прибегают к стратегии «перемен на понижение». Комплекс успеха не позволяет поступить иначе. Тем более что управленческий механизм корпорации-шестиугольника отлажен безупречно для исполнения единой миссии.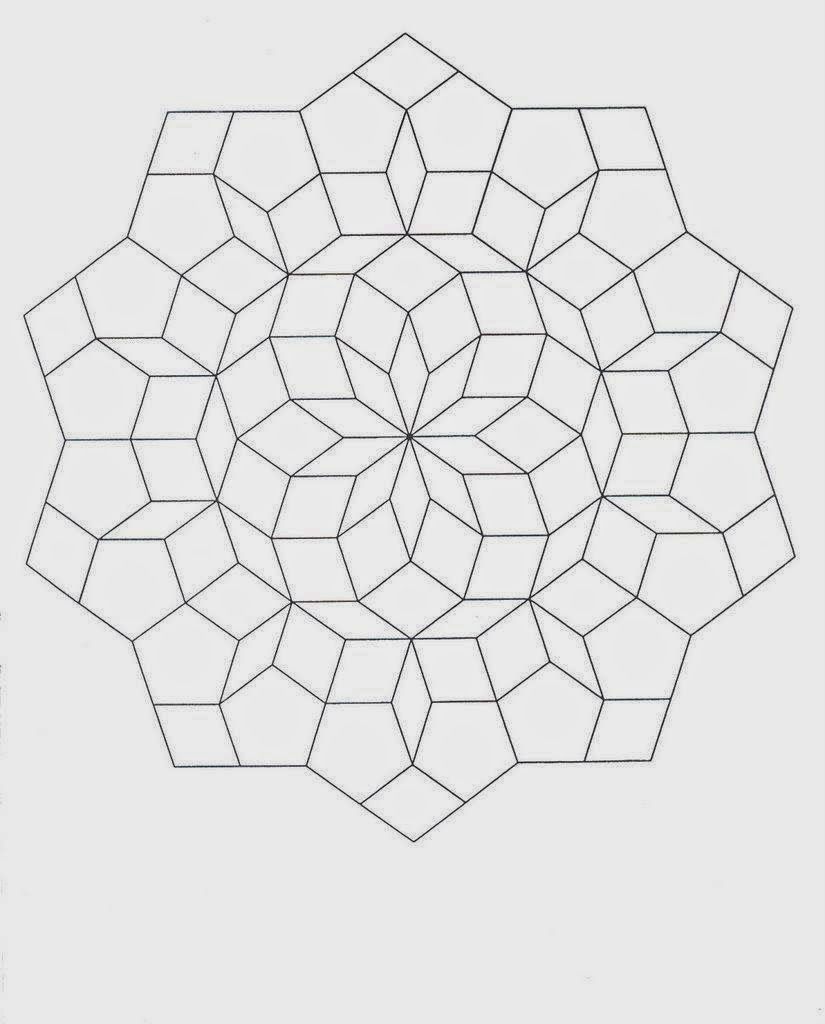 Для отдаленных географически и этнически филиалов тоже. Хотя там могли бы действовать гораздо более продуктивно, что называется, по обстановке. Однако указания из штаб-квартиры не оспариваются. Безусловно, можно упорствовать до бесконечности, надеясь на непобедимую силу корпоративного духа. Вот только где теперь мамонты и динозавры?
Для отдаленных географически и этнически филиалов тоже. Хотя там могли бы действовать гораздо более продуктивно, что называется, по обстановке. Однако указания из штаб-квартиры не оспариваются. Безусловно, можно упорствовать до бесконечности, надеясь на непобедимую силу корпоративного духа. Вот только где теперь мамонты и динозавры?
ЛЮДИ И ФИРМЫ КОРПОРАТИВНОГО ДУХА. Здесь ответ однозначен – им это очень нравится. Достигать высот можно различными путями. В данном случае лучше под надежной и могущественной крышей. Сопричастность к великому делу порой захватывает дух не хуже любого индивидуального экстрима. И при этом есть масса плюсов. Прежде всего не надо терзаться со смыслом жизни, личной миссией, вечными «гамлетовскими» вопросами и прочими неврозами выбора и принятия решения. Корпоративная религия в прямом смысле даст покой душе. Что в наше время очень даже немало. Стимул к успеху также налицо. Финансовое поощрение, атрибуты власти, чувство собственной значимости мало кого оставят равнодушными. Остается лишь денно и нощно стараться не выпасть из генерального русла. Люди корпоративного духа всегда исполнительные и превосходные работники. Им нравится по утрам облачаться в «деловую униформу» и с наслаждением приступать к порученным делам. Соты множатся, и это приятно. Причитающееся вознаграждение – тем более. И после затяжных праздничных выходных опять тянет обрести привычный смысл «времяпрожития» в офисе, с которым уже почти сроднился. Тем более что преданность и деловой энтузиазм (а если он еще и сверхактивный) корпорацией только поощряются.
Остается лишь денно и нощно стараться не выпасть из генерального русла. Люди корпоративного духа всегда исполнительные и превосходные работники. Им нравится по утрам облачаться в «деловую униформу» и с наслаждением приступать к порученным делам. Соты множатся, и это приятно. Причитающееся вознаграждение – тем более. И после затяжных праздничных выходных опять тянет обрести привычный смысл «времяпрожития» в офисе, с которым уже почти сроднился. Тем более что преданность и деловой энтузиазм (а если он еще и сверхактивный) корпорацией только поощряются.
Никаких сомнений и только сплошной позитив в работе, общении и, безусловно, настроении. Пожалуй, по психологической атмосфере коммунистические субботники эпохи начала строительства советского социализма здесь могут и проигрывать. Для корпоративного духа важна исключительно добровольная мотивация быть сопричастным. Снова подчеркнем – не безвозмездно. Особенно для адептов (фр. adepte – сторонник, приверженец, лат. adeptus – достигший) от бизнеса.
Для фирмы, правда, очень бурный корпоративный рост может сыграть плохую шутку. Все оборотные и наличные активы окажутся втянутыми в дело. Свободные деньги иссякнут, и может возникнуть угроза локального дефолта по неотложным платежам. А если еще незаметно подкрадется более глобальный кризис мирового сообщества, тогда станет совсем плохо. Корпорации, в отличие от фирм, гораздо легче идут с молотка по столь низкой цене, о которой даже никогда и не мечталось. Работники будут несказанно шокированы. Как же так? Незыблемый дотоле муравейник вдруг разорен! Подобный суперстресс корпоративному человеку весьма трудно будет пережить. Придется стремглав подыскивать новую ячейку. А в общем-то, корпорации и их работники очень боятся любых перемен. И уж тем более непредсказуемых, а то и угрожающих вызовов внешней среды и эпохи. Как, впрочем, и любая другая империя. Но здесь стабильность и величие именно в создании сети по единому образу и подобию, исходя из первоначального эскиза. Шестиугольники (человек и фирма) терпеливы и могут долго ждать своего часа для успешного клонирования. Сотовая сеть сразу и просто так не возникает. Ей предшествует скрытый от посторонних глаз латентный период. Поэтому до конца всю правду вы так и не узнаете. Публичность и откровенность все же разные вещи.
Сотовая сеть сразу и просто так не возникает. Ей предшествует скрытый от посторонних глаз латентный период. Поэтому до конца всю правду вы так и не узнаете. Публичность и откровенность все же разные вещи.
СОТОВЫЙ КОНТАКТ, или ДЕЛОВАЯ КОММУНИКАЦИЯ ШЕСТИУГОЛЬНИКА. Уже сама постановка вопроса слегка проблематична. Шестиугольнику, который сам себя воспроизводит, союзники и партнеры не особенно-то и нужны. По идее. На практике все несколько иначе. Сотовое клонирование имеет как своих союзников, так и врагов. Нейтралитет, впрочем, тоже возможен, но лишь до поры до времени. Экспансия – она и есть экспансия, даже если существует лишь в одиночном проекте.
С квадратом и прямоугольником может наблюдаться нечто вроде симбиоза. Все-таки нужда в производственном аспекте требует системности, рационального подхода и отлаженного хода воспроизводства. Главное, чтобы квадрат ни в коем случае не мешал корпоративному расширению. Сравните рис. 8.6 и 8.7. В первом случае с гармонией несколько не сложилось. Квадрат не позволяет ему вовсю клонироваться. Да и сама рациональная система квадрата серьезно подменена чужеродным корпоративным духом. Рано или поздно шестиугольник сбросит оболочку квадрата, использовав ее лишь как мимикрию. На рис. 8.7 ситуация гораздо благоприятнее. Вместо иррациональной корпоративной харизмы шестиугольника – исключительно голый расчет и строго системный подход во всех делах. Штаб-квартира в виде квадрата диктует свою волю будущему клонированию и созданию сети.
Квадрат не позволяет ему вовсю клонироваться. Да и сама рациональная система квадрата серьезно подменена чужеродным корпоративным духом. Рано или поздно шестиугольник сбросит оболочку квадрата, использовав ее лишь как мимикрию. На рис. 8.7 ситуация гораздо благоприятнее. Вместо иррациональной корпоративной харизмы шестиугольника – исключительно голый расчет и строго системный подход во всех делах. Штаб-квартира в виде квадрата диктует свою волю будущему клонированию и созданию сети.
Вариант наиболее удачного симбиоза с прямоугольником уже показан на рис. 8.2. Только полное слияние и тотальное растворение прямоугольника в структуре шестиугольника. Другие варианты не рассматриваются.
С кругом у шестиугольника общая склонность к идеологическому центру. Ну а два идеолога, да еще «центровых», далеко не всегда находят общий язык. Тем более что круг иррационален и мистичен, а шестиугольник скорее рационалист и руководствуется сугубо прагматичным подходом в своих делах. Поэтому представить шестиугольник внутри круга можно (рис. 8.8), но, как и в случае с наружным квадратом, гармонии здесь нет. Круг уж больно не любит что-либо впускать внутрь себя, да еще в зоне сакральной идеи. Все, ей теперь конец. Там уже диктат идеологии шестиугольника. Хотя и шестиугольнику не совсем уютно. Из круга как-то надо будет вырваться. А круги не склонны просто за так кого-либо из своих объятий выпускать. А вдруг удастся переделать шестиугольник под себя? Все-таки некое тождество наличествует.
8.8), но, как и в случае с наружным квадратом, гармонии здесь нет. Круг уж больно не любит что-либо впускать внутрь себя, да еще в зоне сакральной идеи. Все, ей теперь конец. Там уже диктат идеологии шестиугольника. Хотя и шестиугольнику не совсем уютно. Из круга как-то надо будет вырваться. А круги не склонны просто за так кого-либо из своих объятий выпускать. А вдруг удастся переделать шестиугольник под себя? Все-таки некое тождество наличествует.
Но вот если круг окажется внутри шестиугольника (рис. 8.9), то можно смело предположить, что внутри корпорации имеется еще один, более закрытый идеологический центр. Корпоративный дух служит некой наружной оболочкой, что, однако, не мешает корпорации развиваться. До тех пор пока круг не начнет ради своих идей отбирать слишком много оборотных средств. А так, скорее всего, и будет. Если босс со своим ближайшим окружением вдруг увлекся религией, то менеджеры-практики начнут подыскивать другое рабочее место. Тандем «корпорация + религия» – это все же не «корпоративная религия». Но тем не менее в наше время подобное слияние только набирает обороты.
Но тем не менее в наше время подобное слияние только набирает обороты.
Но вот с треугольником и ромбом никакого глубокого идейного слияния у шестиугольника не предвидится. Для объяснения почему, здесь даже рисунков не требуется. Эти фигуры по своей жесткой и независимой природе не склонны куда-либо инкорпорироваться. Корпорация их может использовать только методом аутсорсинга, т. е. временные контракты для оказания определенной услуги. Шестиугольник, тем более в сотовом варианте, не любит идти на слишком большой риск. Есть, что терять. Треугольнику и ромбу это как раз не страшно, ибо они для такой работы и предназначены. Но вот с корпоративным духом будет посложней. Строптивость, видите ли. Да и нежелание годами высиживать карьеру.
С овалом, овоидом и каплей тоже судьба не сложится. Уж больно разный стиль жизни и решаемые задачи. Миссия тоже совершенно разная. Тем более что названные фигуры динамичны, а шестиугольник таковым не является. Опять же, тот же овоид имеет свою идеологию и знает, куда двигаться.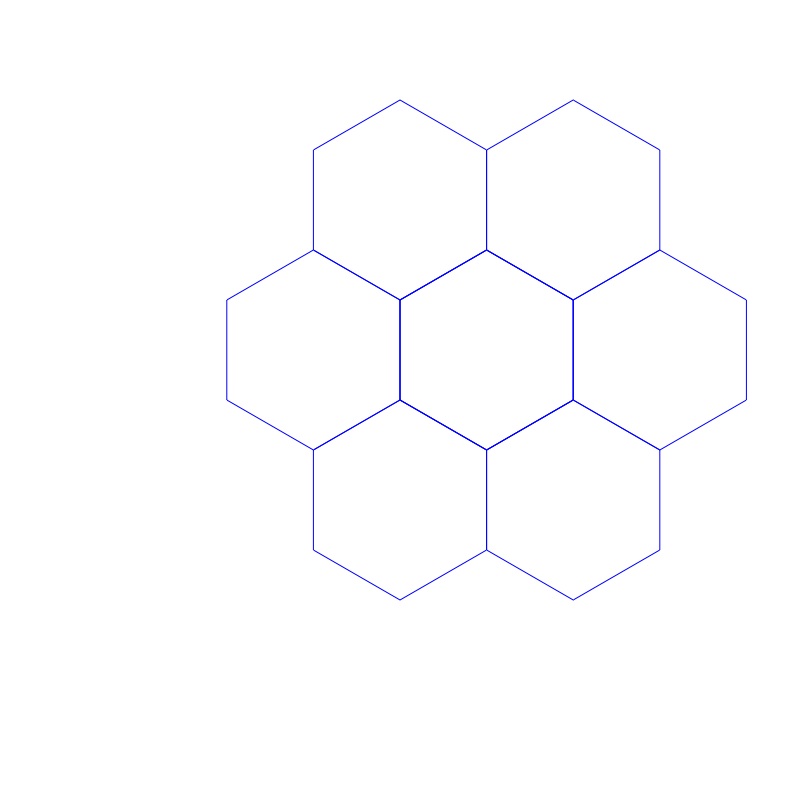 Биполярный овал внесет только ненужную полярность для центричного шестиугольника. А у капли слишком короткий срок жизни. Стабильной корпорации такой сценарий и даром не нужен. Сеть должна в своем существовании стремиться к вечности.
Биполярный овал внесет только ненужную полярность для центричного шестиугольника. А у капли слишком короткий срок жизни. Стабильной корпорации такой сценарий и даром не нужен. Сеть должна в своем существовании стремиться к вечности.
МОНОЦВЕТИЕ КОРПОРАТИВНОЙ СТРУКТУРЫ. Пожалуй, начнем с того, что для логотипов шестиугольник очень даже подходит. Особенно если будет красиво выложен фрагмент ячеистой структуры (см. рис. 8.3). Все хотят быть стабильными и развивающимися. Да еще и согласно своему стратегическому бизнес-плану. Осталось лишь удачно выбрать корпоративный стиль. И цветовое решение логотипа, в котором шестиугольник – ключевая фигура.
Белый шестиугольник динамично стремится в будущее, легко находит альтернативы своего клонирования, привлекает партнеров и работников. Но у него «забелены» истоки и, собственно, сама корпоративная миссия. Такое ощущение, что корпорация непрерывно находится в поиске чего-то нового. Может быть, в этом и суть миссии? В любом случае сочетание цвета и формы здесь неожиданно, но может сработать.
Желтый, равно как и оранжевый, добавит позитивной активности, но внесет легкомыслие и повышенную трату ресурсов. Для корпорации не совсем подходящий вариант. Разве что она специализируется на дорожно-строительных работах. Там действительно много тратят и почти всегда не укладываются в смету.
Зато отлично подойдет глубокий золотистый цвет. Лучше без полировки, т. е. не зеркальный. Престижность и уверенность. И никаких сомнений. Успех корпорации будет всегда обеспечен!
Алый шестиугольник активный и весьма импульсивно атакующий среду. Корпоративный дух едва ли не приравнен к духу боевому. Чем-то напоминает самурайство в бизнесе. Можно и так развивать сеть. Хотя темновато-красный шестиугольник уже более глубокий и уравновешенный, при сохранении корпоративной «боевитости». Но еще лучше – вишневый и пурпурный. Поистине императорские цвета, а корпорации именно это и нужно. Глубина развертывания сотовой сети только усилится за счет чувствования внутренних и внешних процессов без ослабления мощи экспансии.![]() Только теперь она будет более взвешенной. Малиновый еще больше усилит коммуникативные качества корпоративного духа как внутри структуры, так и с внешней средой, но слабым малиновый шестиугольник казаться не будет.
Только теперь она будет более взвешенной. Малиновый еще больше усилит коммуникативные качества корпоративного духа как внутри структуры, так и с внешней средой, но слабым малиновый шестиугольник казаться не будет.
Соты черного цвета покажутся уж очень мрачными и, следовательно, потерявшими вкус к жизни. Черный сжимает и уходит вглубь, а здесь как раз и нужны активная внешняя экспансия и позитивный имидж развертывания сети. Не подойдет черный цвет для корпоративных задач.
Серый в любых оттенках, кроме очень бледного, а также серебристо-серый очень даже ничего. Хорошая динамика, отлично разработанные стратегия и тактика продвижения, внимания к внешней среде и мощная аналитика собственных проблем и задач. Полная толерантность и внимание ко всему. В сером цвете корпорацию точно лихорадить не будет. Все будет происходить без эксцессов, что для шестиугольника немаловажно.
Цвет металла шестиугольникам надо также избегать. Внешняя среда начнет более активно сопротивляться политике экспансии. И тогда сотовая сеть начнет восприниматься агрессивно. Зачем это делать?
И тогда сотовая сеть начнет восприниматься агрессивно. Зачем это делать?
Намного лучше темно-синий, а также фиолетовый цвет. У структуры появляется внутренняя глубина процессов и собственно самого корпоративного духа. Чувство внешней среды также усилится. Главное, чтобы корпоративный дух постепенно не подменился духом религиозным. Тогда уже будет не до дальнейшего развертывания. Зато комфортно в слитном единстве.
Хотите, чтобы в коллективах корпорации сохранялись дружелюбные отношения между коллегами и работа не воспринималась как трудовая повинность? Тогда выбирайте приятный голубой, т. е. более интенсивный и не бледный.
ПОПУТНОЕ ДОПОЛНЕНИЕ К ТЕМЕ. ВОСЬМИУГОЛЬНИКИ по своей форме начинают «округляться» и являются переходным звеном к кругу. Нет доминирующих ударных углов, а центр, в сравнении с шестиугольником, выражен еще более. Правда, внешний контур фигуры пока рациональный, хотя совершенно лишен жесткости. Так что дорожный знак «Движение без остановки запрещено» хоть и в алом цвете, но водителей не раздражает.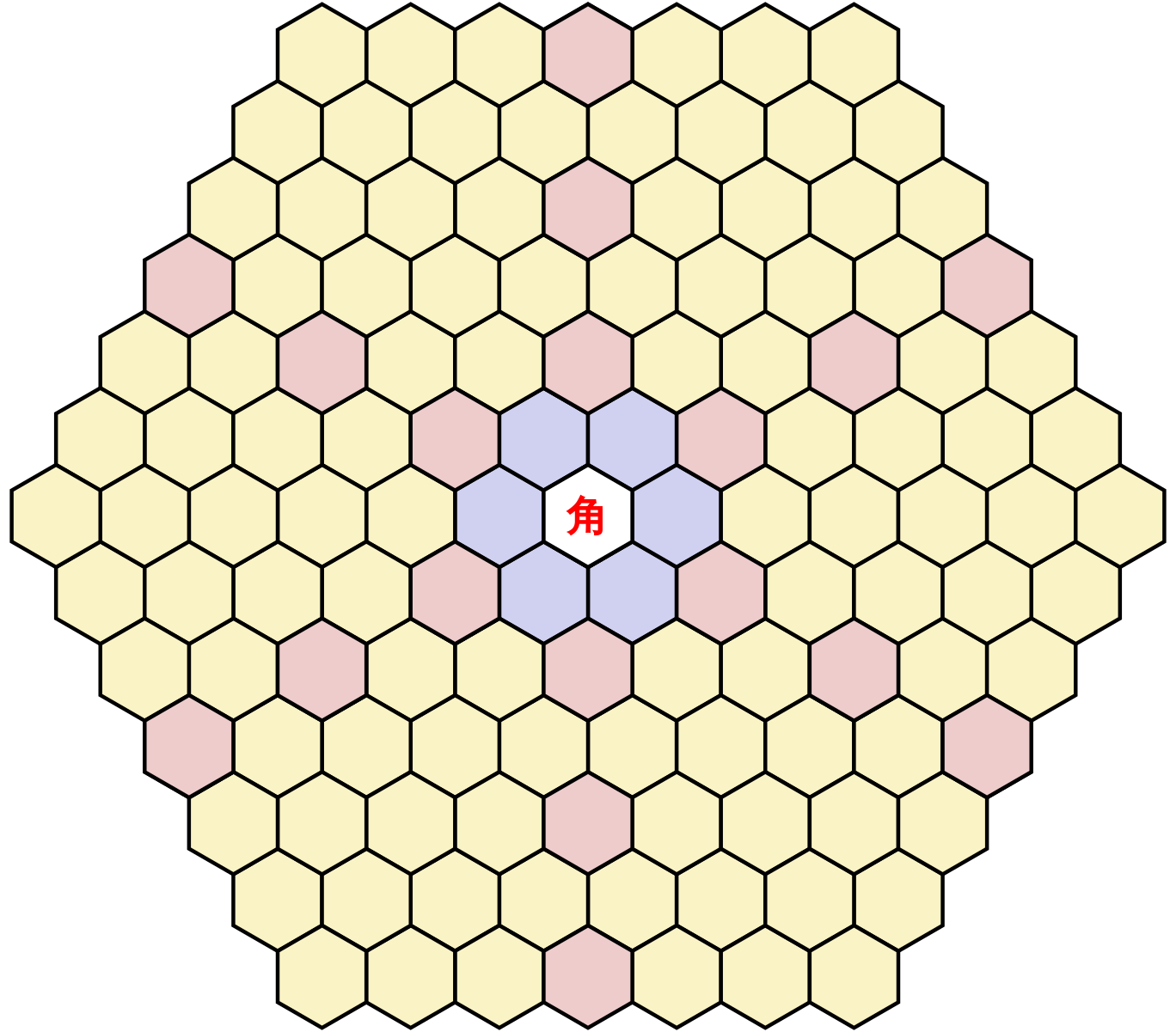 Тем более что команда «STOP» написана белым, а значит, еще облегчает команду приоритета, психологически снимая агрессивные установки водителей, которые вынуждены остановиться. Как говорится, «стали, подождали, а дальше все опять будет». И еще один очень важный момент относительно восьмиугольника. У этой фигуры резко ослаблена тенденция создавать ячеистые структуры. Это, скорее всего, будет монофирма со своей внутренней идеологией и уравновешенной деловой коммуникацией с партнерами. Удачно для логотипа, если бы только не прочно сложившаяся ассоциация с упомянутым дорожным знаком.
Тем более что команда «STOP» написана белым, а значит, еще облегчает команду приоритета, психологически снимая агрессивные установки водителей, которые вынуждены остановиться. Как говорится, «стали, подождали, а дальше все опять будет». И еще один очень важный момент относительно восьмиугольника. У этой фигуры резко ослаблена тенденция создавать ячеистые структуры. Это, скорее всего, будет монофирма со своей внутренней идеологией и уравновешенной деловой коммуникацией с партнерами. Удачно для логотипа, если бы только не прочно сложившаяся ассоциация с упомянутым дорожным знаком.
Данный текст является ознакомительным фрагментом.
Продолжение на ЛитРесРисунок Пентагона, шестиугольника в Pygame
Я пытаюсь создать функции, которые могут рисовать пятиугольник, шестиугольник и т. д. Беспокоясь об алгоритме, должен ли я сравнивать строки с
д. Беспокоясь об алгоритме, должен ли я сравнивать строки с pygame.draw.line ? Похоже, что слишком много работы вокруг определения координат линий. Есть ли простой способ нарисовать их? Кроме того, я не знаю другой библиотеки, которая могла бы нарисовать эти вещи. Я знаю только Pygame, есть ли еще один ?
Поделиться Источник GLHF 15 марта 2015 в 18:05
2 ответа
- Как создать форму Пентагона для изображения Аватара?
Я не могу понять, как создать форму Пентагона для изображения аватара пользователя (или .svg). Ищу форму, которая указывает вниз, а не сверху. Я нашел примеры здесь http://css-tricks.com/examples/ShapesOfCSS/ , но не знаю, как заполнить изображение в такой форме. Фоновая недвижимость тоже не будет…
- Обрезать UIImage в форме шестиугольника?
Итак, я видел решения для того, как обрезать UIImages в определенные формы, но как насчет шестиугольника ? Мысль: подкласс UIImage, изменить метод drawRect, чтобы рисовать только определенные разделы? EDIT: если быть более точным, я надеюсь сохранить границы изображения одинаковыми, но сделать.
 ..
..
6
Вы можете нарисовать его с помощью lines . Вам нужно только сгенерировать список вершин с помощью простой тригонометрии.
Что-то вроде этого (если я не ошибся):
def draw_ngon(Surface, color, n, radius, position):
pi2 = 2 * 3.14
for i in range(0, n):
pygame.draw.line(Surface, color, position, (cos(i / n * pi2) * radius + position[0], sin(i / n * pi2) * radius + position[1]))
return pygame.draw.lines(Surface,
color,
True,
[(cos(i / n * pi2) * radius + position[0], sin(i / n * pi2) * radius + position[1]) for i in range(0, n)])
Поделиться ciechowoj 15 марта 2015 в 18:15
0
Вы можете использовать pygame.draw.polygon(surface, color, point_list) для рисования многоугольника.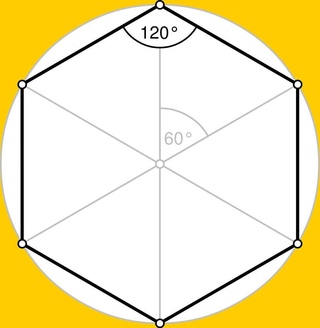 В этом случае вы можете использовать тригонометрию для создания списка вершин и передачи его в качестве параметра
В этом случае вы можете использовать тригонометрию для создания списка вершин и передачи его в качестве параметра point_list . Вот функция, которая рисует любой правильный многоугольник, имеющий vertex_count вершин:
def draw_regular_polygon(surface, color, vertex_count, radius, position):
n, r = vertex_count, radius
x, y = position
pygame.draw.polygon(surface, color, [
(x + r * cos(2 * pi * i / n), y + r * sin(2 * pi * i / n))
for i in range(n)
])
Вы можете запустить эту демонстрацию и увидеть эту функцию в действии, изменив количество вершин с помощью клавиш со стрелками UP / DOWN.
Поделиться Arthur Khazbs 24 августа 2019 в 14:47
Похожие вопросы:
Pygame рисунок не отображается в окне Pygame
Итак, я тестировал pygame и хотел нарисовать простой прямоугольник. Когда я запускаю код, нет никаких сообщений об ошибках, но прямоугольник не появляется в окне. То, что я вижу, — это пустое белое…
Когда я запускаю код, нет никаких сообщений об ошибках, но прямоугольник не появляется в окне. То, что я вижу, — это пустое белое…
Проект Пентагона в c++
Су… я пишу проект Пентагона для своего класса c++, и, честно говоря, сейчас я не очень хорошо справляюсь с работой и другими классами. Итак… нам нужно сделать программу Пентагона, которая будет…
Проект Пентагона в c++ с классами
Итак, мне нужно создать проект Пентагона, и я немного запутался. Я имею в виду, что он отлично работает, но мне не хватает одного класса, в котором должен быть какой-то код. Назначение есть:…
Как создать форму Пентагона для изображения Аватара?
Я не могу понять, как создать форму Пентагона для изображения аватара пользователя (или .svg). Ищу форму, которая указывает вниз, а не сверху. Я нашел примеры здесь…
Обрезать UIImage в форме шестиугольника?
Итак, я видел решения для того, как обрезать UIImages в определенные формы, но как насчет шестиугольника ? Мысль: подкласс UIImage, изменить метод drawRect, чтобы рисовать только определенные. ..
..
Площадь шестиугольника вне окружности
Пусть будет круг радиусом r. Я хочу узнать площадь шестиугольника, нарисованного вокруг круга. Дополнено образцовое изображение, за исключением того, что мне нужно, чтобы все были шестиугольника, а…
Рисование шестиугольника
Используя Firemonkey XE2, я смог использовать компонент TCube для создания кубической карты, но теперь мне нужна карта шестиугольника. Не было никакого варианта для формы шестиугольника 3d, которую…
Нахождение положения Пентагона внутри круга
Я пытаюсь нарисовать маленькие круги над углами Пентагона внутри круга. Мне известна следующая информация. Радиус окружности равен 50. Центр окружности равен x = 100, y = 100 Как я могу получить…
Просмотреть изображение шестиугольника в NS
Как я могу создать такой компонент, как NS? Как придать форму шестиугольника ImageView Я хочу создать компонент изображения, который имеет вид шестиугольника, но я не могу понять, как правильно. ..
..
Pygame Рисунок (На Пасху)
Мне было интересно, как нарисовать cloud на pygame. Единственное, что я умею делать, — это делать правильные круги и эллипсы. Кроме того, Пожалуйста, скажите мне, как нарисовать кролика или…
Как построить призму. Правильное изображение фигуры на рисунке
Овладеть базовыми знаниями в области рисунка необходимо каждому начинающему художнику, независимо от выбранного стиля живописи. Обучение рисунку происходит поэтапно, и одной из важнейших тем является построение геометрических фигур. Сначала ученики осваивают плоские объекты, а потом переходят к объемным – в частности, призмам.
В зависимости от фигуры, лежащей в основании, призма бывает треугольной, четырехугольной, пятиугольной и так далее. Рассмотрим процесс рисования на примере четырехгранной и шестигранной призмы.
Рисуем четырехгранную призму
Четырехгранная призма строится по тому же плану, что и куб, поэтому логично сначала освоить рисование этой фигуры. Обе они – это простые геометрические тела, имеющие прямые грани. Однако если у куба все грани являются квадратами, то у призмы квадраты – это только основания, а боковые грани – прямоугольники.
Обе они – это простые геометрические тела, имеющие прямые грани. Однако если у куба все грани являются квадратами, то у призмы квадраты – это только основания, а боковые грани – прямоугольники.
Объект рисуют в точности так же, как и куб, длина которого затем увеличивается по горизонтали или вертикали (в зависимости от положения предмета).
Как правило, длина увеличивается в полтора раза, однако это зависит от того, во сколько раз высота фигуры превышает ширину основания призмы.
Сначала нужно нанести на лист бумаги общие габариты фигуры при помощи легких линий карандашом.
Затем нужно найти, где будет находиться переднее вертикальное ребро, и провести линию, на которой отложить высоту тела. После этого намечаются наклоны ребер. Затем прорисовываются все невидимые грани.
Шестигранная призма
Основой для построения шестигранной призмы является четырехгранная. Передняя поверхность делится пополам по вертикали и горизонтали с учетом перспективы, если тело изображено в ракурсе. Затем вписываем в поверхность эллипс. Горизонтальная ось, пересекающая поверхность, делится еще раз пополам с учетом перспективы. Ставим точки в местах пересечения получившихся вертикалей с окружностью. Соединяем их между собой и с углами.
Затем вписываем в поверхность эллипс. Горизонтальная ось, пересекающая поверхность, делится еще раз пополам с учетом перспективы. Ставим точки в местах пересечения получившихся вертикалей с окружностью. Соединяем их между собой и с углами.
Точно такой же шестиугольник нужно нарисовать на задней стороне четырехгранной призмы, а затем соединить его с первым нарисованным шестиугольником. Таким образом, у нас получится шестигранная призма, вписанная в четырехгранную.
Чтобы показать объем вашей призмы, нужно обозначить светотени. В первую очередь нужно заштриховать поверхности в тени и те, на которые тень падает. После этого нужно проработать самые освещенные поверхности.
Зачем уметь строить эту геометрическую фигуру?
Научиться изображать геометрические тела, в том числе и призмы, необходимо всем будущим художникам.
С построения этих объектов начинается учебный процесс во всех заведениях. А уже после этого студенты постепенно переходят к изображению розеток, капителей, портрета и фигуры человека.
Если вы освоите этот объект, то в дальнейшем вам будет проще изображать различные предметы, строящиеся на его основе. В частности, у вас не возникнет трудностей с различными коробками и упаковками, бытовой техникой, зданиями и так далее.
Рисование геометрических тел также входит и в экзаменационную программу для поступления в художественный вуз. Однако с первого раза построить правильную фигуру с соблюдением пропорции и перспективы получается далеко не у каждого. Поэтому будет лучше, если в процессе подготовки к экзаменам вы потратите на изображение призмы достаточно времени, тогда на самом вступительном испытании будете чувствовать себя уверенно. С каждым разом изображение призмы будет даваться все легче.
В школе-студии К.Э. Арутюновой «Мастер рисунка» учат работать с геометрическими телами. К каждому ученику применяется индивидуальный подход с учетом его уровня и времени до сдачи вступительного экзамена. Преподаватель подробно разбирает со студентами все работы, обращает внимание на ошибки и помогает их исправить.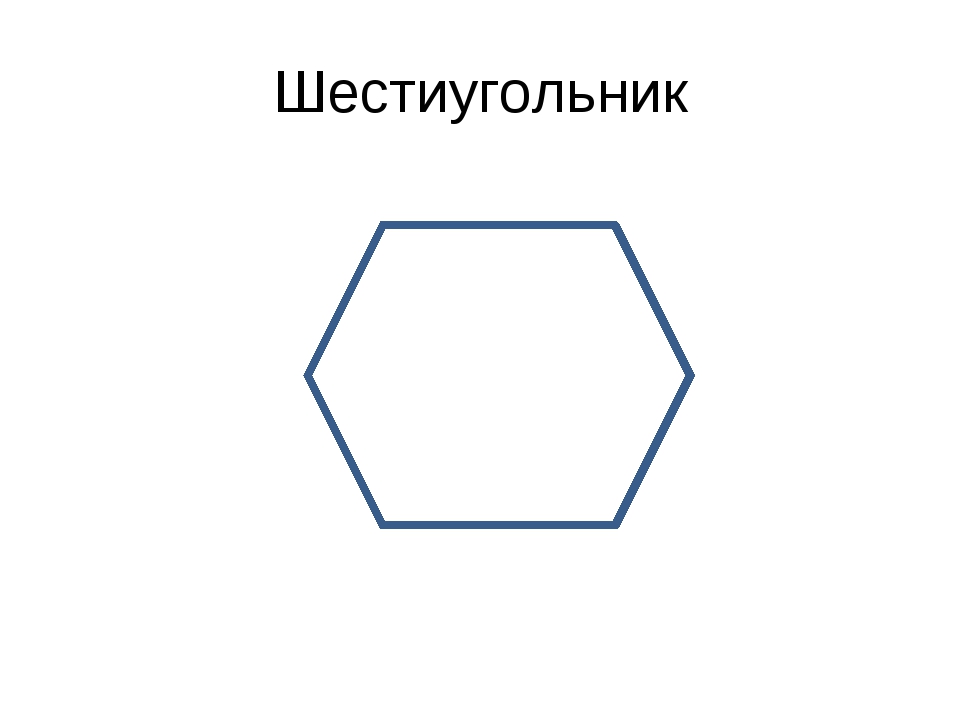
Готовитесь ли вы к поступлению в художественный вуз или просто хотите научиться для себя, без основ вам не обойтись. Независимо от того, в каком стиле вы собираетесь работать позднее, начать изучение все равно необходимо с базовых знаний. Запишитесь на занятия по телефону в Москве или через специальную форму на сайте.
Похожие записи
%d1%88%d0%b5%d1%81%d1%82%d0%b8%d1%83%d0%b3%d0%be%d0%bb%d1%8c%d0%bd%d0%b8%d0%ba PNG, векторы, PSD и пнг для бесплатной загрузки
естественный цвет bb крем цвета
1200*1200
green environmental protection pattern garbage can be recycled green clean
2000*2000
дизайн плаката премьера фильма кино с белым вектором экрана ба
1200*1200
набор векторных иконок реалистичные погоды изолированных на прозрачной ба
800*800
схема бд электронный компонент технологии принципиальная схема технологическая линия
2000*2000
вектор поп арт иллюстрацией черная женщина шопинг
800*800
blue series frame color can be changed text box streamer
1024*1369
аэрозольный баллончик увлажняющий лосьон bb cream парфюм для рук
3072*4107
в первоначальном письме bd логотипа
1200*1200
Крутая музыка вечеринка певца креативный постер музыка Я Май Ба концерт вечер К
3240*4320
bb крем ню макияж косметика косметика
1200*1500
bd письмо 3d круг логотип
1200*1200
чат комментарий образование синий значок на абстрактных облако сообщение
5556*5556
в первоначальном письме ба логотипа
1200*1200
82 летняя годовщина логотип дизайн шаблона иллюстрацией вектор
4083*4083
простая инициализация bb b геометрическая линия сети и логотип цифровых данных
2276*2276
в первоначальном письме bd логотип шаблон
1200*1200
в первоначальном письме bd шаблон векторный дизайн логотипа
1200*1200
элегантный серебряный золотой bb позже логотип значок символа
1200*1200
облака комиксов
5042*5042
круглая буквица bd или db дизайн логотипа вектор
5000*5000
88 летний юбилей векторный дизайн шаблона иллюстрация
4083*4083
Красивая розовая и безупречная воздушная подушка bb крем косметика постер розовый красивый розовый Нет времени На воздушной
3240*4320
bb логотип
2223*2223
bb логотип письмо дизайн вектор простые и минималистские ключевые слова lan
1202*1202
82 летняя годовщина векторный дизайн шаблона иллюстрация
4083*4083
Векторная иллюстрация мультфильм различных овощей на деревянном ба
800*800
bb логотип дизайн шаблона
2223*2223
bb крем элемент
1200*1200
номер 82 золотой шрифт
1200*1200
bb логотип градиент с абстрактной формой
1200*1200
три группы 3d реалистичное декоративное яйцо с золотым цветом на гнезде bd с золотым всплеском текстовый баннер
5000*5000
ма дурга лицо индуистский праздник карта
5000*5000
b8 b 8 письма и номер комбинации логотипа в черном и gr
5000*5000
серые облака png элемент для вашего комикса bd
5042*5042
bd письмо логотип
1200*1200
88 лет юбилей празднования вектор шаблон дизайн иллюстрация
4187*4187
bd письмо логотип
1200*1200
bb градиентный логотип с абстрактной формой
1200*1200
3d золотые числа 81 с галочкой на прозрачном фоне
1200*1200
88 год юбилея векторный дизайн шаблона иллюстрация
4083*4083
жидкая подушка крем bb
1200*1200
bb кремовый плакат белый макияж косметический На воздушной подушке
3240*4320
номер 88 3d рендеринг
2000*2000
номер 81 3d рендеринг
2000*2000
в первоначальном письме bd логотип шаблон
1200*1200
81 год лента годовщина
5000*3000
83 лет юбилей празднования вектор шаблон дизайна иллюстрация
4187*4187
red bb cream cartoon cosmetics
2500*2500
3d модель надувной подушки bb cream
2500*2500
Правильный шестиугольник, площадь правильного шестиугольника
youtube.com/embed/SHPetQYqlus?list=PL_ROP0qHFB3njfNcvjC6zgeSD-SRcsb04″ frameborder=»0″ allowfullscreen=»»/>
Знаете ли вы, как выглядит правильный шестиугольник?
Этот вопрос задан не случайно. Большинство учащихся 11 класса не знают на него ответа.
Правильный шестиугольник — такой, у которого все стороны равны и все углы тоже равны.
Железная гайка. Снежинка. Ячейка сот, в которых живут пчелы. Молекула бензола. Что общего у этих объектов? — То, что все они имеют правильную шестиугольную форму.
Многие школьники теряются, видя задачи на правильный шестиугольник, и считают, что для их решения нужны какие-то особые формулы. Так ли это?
Проведем диагонали правильного шестиугольника. Мы получили шесть равносторонних треугольников.
Мы знаем, что площадь правильного треугольника: .
Тогда площадь правильного шестиугольника — в шесть раз больше.
, где — сторона правильного шестиугольника.
Обратите внимание, что в правильном шестиугольнике расстояние от его центра до любой из вершин одинаково и равно стороне правильного шестиугольник.
Значит, радиус окружности, описанной вокруг правильного шестиугольника, равен его стороне.
Радиус окружности, вписанной в правильный шестиугольник, нетрудно найти.
Он равен .
Теперь вы легко решите любые задачи ЕГЭ, в которых фигурирует правильный шестиугольник.
Ты нашел то, что искал? Поделись с друзьями!
. Найдите радиус окружности, вписанной в правильный шестиугольник со стороной .
Радиус такой окружности равен .
Ответ: .
. Чему равна сторона правильного шестиугольника, вписанного в окружность, радиус которой равен 6?
Мы знаем, что сторона правильного шестиугольника равна радиусу описанной вокруг него окружности.
Ответ: .
Как построить правильный шестиугольник по одной стороне с помощью циркуля и линейки или линейки
Как построить
правильный шестиугольник
учитывая одну сторону. Строительство начинается с нахождения центра шестиугольника, а затем его рисования. описанный круг
который представляет собой круг, проходящий через каждый
вершина.
Затем компас обходит круг, отмеченный с каждой стороны.
описанный круг
который представляет собой круг, проходящий через каждый
вершина.
Затем компас обходит круг, отмеченный с каждой стороны.
Пошаговые инструкции для печати
Вышеупомянутая анимация доступна как распечатываемый лист с пошаговыми инструкциями, который можно использовать для изготовления раздаточных материалов или когда компьютер недоступен.
Объяснение метода
Эта конструкция очень похожа на построение шестиугольника, вписанного в круг, за исключением того, что нам дан не круг, а одна из сторон. Шаги 1-3 нужны, чтобы нарисовать этот круг, и с тех пор конструкции такие же.
Центр круга находится с использованием того факта, что радиус правильного шестиугольника (расстояние от центра до вершины) равна длине каждой стороны. См. Определение шестиугольника.
Проба
Изображение ниже — это окончательный рисунок из приведенной выше анимации.
| Аргумент | Причина | |
|---|---|---|
| 1 | ABCDEF — шестигранник | Это многоугольник с шестью сторонами.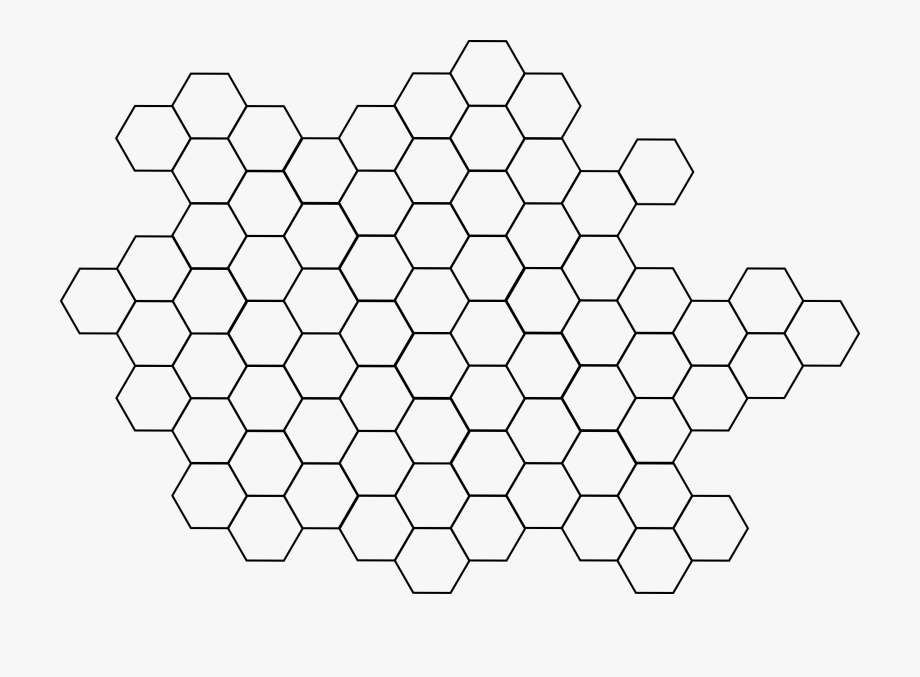 См. Определение шестиугольника. См. Определение шестиугольника. |
| 2 | AB, BC, CD, DE, EF, FA все совпадают. | Нарисовано с той же шириной компаса AF. |
| 3 | A, B, C, D, E, F все лежат на окружности O | По конструкции |
| 4 | ABCDEF — правильный шестиугольник | Из (1), (2).Все его вершины лежат на окружности, а все стороны равны. Это определяет правильный шестиугольник. Видеть Определение и свойства правильного многоугольника |
— Q.E.D
Попробуйте сами
Щелкните здесь, чтобы распечатать рабочий лист, содержащий две проблемы, которые можно попробовать. Когда вы перейдете на страницу, используйте команду печати браузера, чтобы распечатать столько, сколько хотите. Печатная продукция не защищена авторскими правами.Другие конструкции, страницы на сайте
Строки
Уголки
Треугольники
Правые треугольники
Центры треугольника
Окружности, дуги и эллипсы
Полигоны
Неевклидовы конструкции
(C) Открытый справочник по математике, 2011 г.
Все права защищены.
Рисование шестиугольников
Рисование шестиугольниковВведение
Многие настольные ролевые игры используют карту, нарисованную на шестиугольниках, чтобы показать, где находятся игроки и другие объекты. Они делают это, потому что шестиугольники имеют одинаковое расстояние от центра до центра, как бы вы ни иди туда, где нет квадратов.
К сожалению, рисовать квадраты на экране намного проще, чем рисование шестиугольников. Обнаружение попаданий и позиционирование тоже проще, поэтому большинство компьютерных программ заканчиваются использованием квадратов или, по крайней мере, прямоугольники.Хотя это вполне приемлемо, это не так. эффективен и предлагает другой игровой опыт.
В Интернете есть много интересных ресурсов, посвященных играм.
Некоторые из них говорят об использовании гексов, но не говорят о том, как
на самом деле нарисовать их, или как сделать что-нибудь полезное, например, проверку нажатия. Возможно, если вы не так плохо разбираетесь в математике, как я, это
простая вещь, и у вас не будет проблем. Однако это
потребовал от меня некоторых усилий, и я подумал, что напишу это здесь, чтобы
кому-то другому, возможно, не придется делать то же самое.
Возможно, если вы не так плохо разбираетесь в математике, как я, это
простая вещь, и у вас не будет проблем. Однако это
потребовал от меня некоторых усилий, и я подумал, что напишу это здесь, чтобы
кому-то другому, возможно, не придется делать то же самое.
Представляющие шестигранники
Есть несколько предложений по хранению содержимого шестиугольники на веб-странице, URL-адрес которой я не могу найти в настоящий момент. я нашел большинство из них более сложны, чем нужно, и обнаружили, что хранение содержимое гексов в двумерном массиве работало лучше всего. А сетка гексов на самом деле просто сетка, но со смещением строки на половину шестнадцатеричный. Хранить это намного проще, чем другие предложения, которые я читал.
Мой друг тангалор очень помог мне понять это.Мы с ним разработали быстрый способ рисования гексов, который не совсем пятно и нарисовал неправильные шестиугольники. В думая, что я сделал там, привел меня сюда.
Шестигранник для чертежа
Как я понял
Рисование настоящего правильного шестиугольника долгое время сбивало меня с толку. я
наконец сел с миллиметровой бумагой, карандашами и шестигранником.
бумагу и начал делать каракули. В конце концов я понял, что
что правильный шестиугольник можно разбить на прямоугольник, а четыре
прямоугольные треугольники.Как только я это узнал, все сложилось довольно хорошо.
я
наконец сел с миллиметровой бумагой, карандашами и шестигранником.
бумагу и начал делать каракули. В конце концов я понял, что
что правильный шестиугольник можно разбить на прямоугольник, а четыре
прямоугольные треугольники.Как только я это узнал, все сложилось довольно хорошо.
Это
hex показывает треугольники, о которых я говорю. Углы в разумных пределах
легко понять; каждый внутренний угол правильного шестиугольника равен 120
градусов, и мы знаем, что красные линии перпендикулярны
зеленая линия; это должен быть треугольник 30-60-90, и определить 30
и стороны 60 градусов довольно просты.
После того, как вы разбили шестиугольник на красивые треугольники, он станет немного проще, как увидеть то, что вы хотите знать.В регулярном шестиугольник, все стороны одинаковой длины. Извлекая один треугольник, а маркировка сторон дает нам имена, с которыми можно работать.
Если
вы посмотрите на весь шестигранник выше, вы увидите, что если вы знаете
длины всех трех сторон этого треугольника, вы можете нанести точки на
сетка, чтобы нарисовать шестиугольник довольно легко. И поскольку мы знаем один из
длины сторон, мы можем получить остальное через какой-нибудь старый добрый
модная тригонометрия.
И поскольку мы знаем один из
длины сторон, мы можем получить остальное через какой-нибудь старый добрый
модная тригонометрия.
Нам нужно знать A, B и C.Нам дается Ц.
Мы можем вычислить сторону A из этого:
Это довольно разумная формула.
Другая похожа, но не сводится к такой красивой ясности. номера:
Sin 60 — это константа, которую можно вычислить или сохранить как константа (0,866) в вашей программе с той степенью точности, с которой вы чувствую потребность в использовании.
То есть:
(дано)
Рисование шестигранника
Чтобы нарисовать гексагон, вам нужно вычислить точки для каждого
точка шестигранника. Есть два способа нарисовать шестиугольник, один, называемый
Север-Юг имеет параллельные края, идущие вертикально на странице.
Другой, называемый Восток-Запад, имеет параллельные края, идущие
по горизонтали. Используя длину, указанную выше, он становится красивым. просто подсчитать очки для шестигранника.
просто подсчитать очки для шестигранника.
Я пронумеровал точки шестиугольника, чтобы просто показать, что который; числа не имеют никакого отношения ни к чему.
Север-Юг
Гексагон Север-Юг можно нарисовать, используя следующие точки.
Путевая точка | Координата X | Координата Y |
|---|---|---|
1 | 0 | А + С |
2 | 0 | А |
3 | Б | 0 |
4 | 2 * В | А |
5 | 2 * В | А + С |
6 | Б | 2 * С |
Восток-Запад
Гексагон Восток-Запад можно нарисовать, используя следующие точки.
Путевая точка | Координата X | Координата Y |
|---|---|---|
1 | 0 | Б |
2 | А | 0 |
3 | А + С | 0 |
4 | 2 * С | Б |
5 | А + С | 2 * В |
6 | А | 2 * В |
Python — рисование шестиугольника с использованием графики черепахи
Python — рисование шестиугольника с использованием графики черепахи
В этой статье мы узнаем, как создать шестиугольник, используя графику черепахи в Python. Для этого сначала нужно узнать, что такое Turtle Graphics.
Для этого сначала нужно узнать, что такое Turtle Graphics.
Черепаха графика
Turtle — это функция Python, подобная доске для рисования, которая позволяет нам приказывать черепахе рисовать по всему ней! Мы можем использовать множество функций черепахи, которые могут перемещать черепаху. Turtle входит в состав библиотеки turtle. Модуль turtle можно использовать как объектно-ориентированным, так и процедурно-ориентированным способами.
Вот некоторые из наиболее часто используемых методов:
- вперед (длина): перемещает перо вперед на единицу x.
- назад (длина): перемещает перо в обратном направлении на единицу x.
- вправо (угол): поверните перо по часовой стрелке на угол x.
- влево (угол): поверните перо против часовой стрелки на угол x.
- penup (): остановить рисование пера черепахи.
- pendown (): начать рисование ручки черепахи.

Подход —
- Определите экземпляр для черепахи .
- Для шестиугольника выполнить петлю 6 раз.
- В каждой итерации перемещайте черепаху на 90 единиц вперед и перемещайте ее влево на 300 градусов.
- Это будет шестиугольник.
Ниже представлена реализация вышеуказанного подхода на языке Python.
Python3
|
Выход:
Шестиугольник для изготовления черепах
Внимание компьютерщик! Укрепите свои основы с помощью курса Python Programming Foundation и изучите основы.
Для начала подготовьтесь к собеседованию. Расширьте свои концепции структур данных с помощью курса Python DS .
Калькулятор шестиугольника| 6-сторонний многоугольник
Сотовый узор — почему 6-сторонняя форма так распространена в природе
Сотовый узор состоит из правильных шестиугольников, расположенных рядом .Они полностью заполняют всю покрываемую ими поверхность, поэтому между ними нет дыр. Этот сотовый узор появляется не только в сотах (сюрприз!), Но также и в многих других местах в природе . Фактически, он настолько популярен, что можно сказать, что это форма по умолчанию, когда действуют конфликтующие силы, а сферы невозможны из-за характера проблемы.
Фактически, он настолько популярен, что можно сказать, что это форма по умолчанию, когда действуют конфликтующие силы, а сферы невозможны из-за характера проблемы.
От пчел «ульев» до трещин в горных породах через органическую химию (даже в строительных блоках жизни: белках) правильные шестиугольники являются наиболее распространенной многоугольной формой, существующей в природе.И тому есть причина: углы шестиугольника. Угол 120º является наиболее механически устойчивым из всех, и по совпадению это также угол , под которым стороны встречаются в вершинах , когда мы выстраиваем шестиугольники бок о бок. Для полного описания важности и преимуществ правильных шестиугольников рекомендуем посмотреть видео выше. Тем, кто заядлый читатель, читайте дальше (вы можете проверить, насколько быстро вы читаете, с помощью калькулятора скорости чтения).
То, как углы 120º распределяют силы (и, в свою очередь, напряжение) между двумя сторонами шестиугольника, делает его очень стабильной и механически эффективной геометрией.Это значительное преимущество шестиугольников. Еще одним важным свойством правильных шестиугольников является то, что они могут заполнять поверхность без промежутков между ними (вместе с правильными треугольниками и квадратами). Вдобавок ко всему, обычная 6-сторонняя форма имеет наименьшего периметра для наибольшей площади среди этих заполняющих поверхность многоугольников, что, очевидно, делает ее очень эффективной.
Очень интересный пример на видео выше — это мыльных пузырей .Когда вы создаете пузырь, используя воду, мыло и немного собственного дыхания, он всегда имеет сферическую форму. Это связано с тем, что объем сферы является самым большим из любого другого объекта для данной площади поверхности.
Однако, когда мы складываем пузыри вместе на плоской поверхности, сфера теряет свое преимущество в эффективности , поскольку сечение сферы не может полностью покрыть двумерное пространство. Следующая лучшая форма с точки зрения объема и площади поверхности также наилучшим образом уравновешивает межпузырьковое натяжение, которое создается на поверхности пузырьков.Речь, конечно же, идет о нашем всемогущем шестиугольнике .
Следующая лучшая форма с точки зрения объема и площади поверхности также наилучшим образом уравновешивает межпузырьковое натяжение, которое создается на поверхности пузырьков.Речь, конечно же, идет о нашем всемогущем шестиугольнике .
Пузыри представляют интересный способ визуализации преимуществ шестиугольника над другими формами, но это не единственный способ. В природе, как мы уже упоминали, существует примеров гексагональных образований , в основном из-за напряжений и напряжений в материале. К сожалению, мы не можем подробно остановиться на них. Тем не менее, можно назвать несколькими местами, где в природе можно встретить правильные шестиугольные узоры :
- Соты
- Органические соединения
- Стеки пузырей
- Скальные образования (например, Дорога гигантов)
- Глаза насекомых
- …
Богна Шик и Альваро Диес
Геометрические конструкции и касания — инженерный чертеж
1 Опишите дугу с центром A и радиусом больше половины AB.
2 Повторите с тем же радиусом из точки B, дуги пересекаются в точках C и D.
3 Соедините C с D, чтобы разделить дугу AB пополам.
Найти центр заданной дуги AB (рис. 9.4)
1 Нарисуйте два аккорда, AC и BD.
2 Bisect AC и BD, как показано; биссектрисы пересекутся в точке E.
3 Центр дуги — точка E.
Радиус окружности
Чтобы вписать круг в данный треугольник ABC (рис. 9.5)
1 Разделите пополам любые два угла, как показано, так, чтобы биссектрисы пересекались в точке D.
2 Центр вписанной окружности — точка D.
Описать окружность вокруг треугольника ABC (рис. 9.6)
1 Разделите пополам любые две стороны треугольника, как показано, так, чтобы биссектрисы пересекались в точке D.
2 Центром описываемой окружности является точка D.
Чтобы нарисовать шестиугольник с учетом расстояния по углам
1 Нарисуйте вертикальные и горизонтальные центральные линии и круг с диаметром, равным заданному расстоянию.
2 Сойдите с радиуса вокруг круга, чтобы получить шесть равноотстоящих точек, и соедините точки, чтобы получить требуемый шестиугольник.
Радиус круга
1 Нарисуйте вертикальные и горизонтальные центральные линии и окружность с диаметром, равным заданному расстоянию.
2 Используя угольник 60 °, нарисуйте точки на окружности на расстоянии 60 ° друг от друга.
3 Соедините эти шесть точек прямыми линиями, чтобы получить требуемый шестиугольник.
\ 60 ° | Тройник | ||
V 1 |
Чтобы нарисовать шестиугольник с учетом расстояния между квартирами (рис. 9.8)
1 Нарисуйте вертикальные и горизонтальные центральные линии и круг с диаметром, равным заданному расстоянию.
2 Используйте угольник 60 ° и тройник, как показано, чтобы получить шесть сторон.
Угольник 60 °
Угловой профиль 60 °
- Тройник
Для рисования правильного восьмиугольника с учетом расстояния по углам (рис. 9.9)
Повторите инструкции на рис. 9.7 (b), но используйте квадрат под углом 45 °, затем соедините восемь точек, чтобы получить требуемый восьмиугольник.
Нарисовать правильный восьмиугольник с учетом расстояния между квартирами (рис.9.10)
Повторите инструкции на рис. 9.8, но используйте квадрат под 45 °, чтобы получить требуемый восьмиугольник.
Угловой угол 45 °
Угловой квадрат 45 °
Для рисования правильного многоугольника с учетом длины сторон (рис. 9.11)
Обратите внимание, что правильный многоугольник определяется как плоская фигура, ограниченная прямыми линиями одинаковой длины и содержащая углы одинакового размера. Предположим, что в этом примере количество сторон равно семи.
1 Начертите заданную длину одной стороны AB и радиусом AB опишите полукруг.
2 Разделите полукруг на семь равных углов с помощью транспортира и через второе деление от левой соединительной линии A2.
3 Проведите радиальные линии от точки A до точек 3, 4, 5 и 6.
4 С радиусом AB и центром в точке 2 опишите дугу, которая соответствует продолжению линии A3, показанной здесь как точка F.
Повторите то же самое с радиусом AB и центром F, чтобы пересечь линию A4 в точке E. Соедините точки, как показано, чтобы создать требуемый многоугольник.
Рисование шестиугольника бумагой.js · GitHub
Рисование шестиугольника с помощью Paper.js · GitHubМгновенно делитесь кодом, заметками и фрагментами.
Рисование шестиугольника с помощью Paper.js
// Создаем путь Paper. js, чтобы провести в нем линию: js, чтобы провести в нем линию: | |
| var hexagon = новый путь (); | |
| // Раскрасьте наш путь в черный цвет | |
| шестигранник.strokeColor = ‘черный’; | |
| // Сколько точек мы хотим, чтобы наш объект имел | |
| вар баллов = 6; | |
| // Насколько он должен быть большим | |
| var radius = 60; | |
| // От 0 до 2PI — это круг, поэтому разделите его на количество точек | |
| // в нашем объекте и на сколько радиан мы должны поместить новый | |
| // точка, чтобы нарисовать фигуру | |
var angle = ((2 * Math. ИП) / баллы); ИП) / баллы); | |
| // Для такого количества вершин в форме добавляем точку | |
| для (i = 0; i <= points; i ++) { | |
| // Добавляем новую точку к объекту | |
| hexagon.add (новая точка ( | |
| // Радиус * Мат.cos (количество радианов точки) — позиция x | |
| радиус * Math.cos (угол * i), | |
| // То же самое с Math.sin для позиции y точки | |
| радиус * Math.sin (угол * i) | |
| )); | |
| } | |
| // Сдвинуть форму так, чтобы она полностью отображалась на холсте | |
шестигранник. position.x + = 200; position.x + = 200; | |
| шестиугольник. Положение.y + = 200; |
Как нарисовать невозможный шестиугольник
Легко, пошагово Учебное пособие по рисованию невозможного шестиугольникаНажмите ЗДЕСЬ, чтобы сохранить учебное пособие в Pinterest!
Что такое невозможный объект? Эти рисунки, также называемые невозможными или неразрешимыми фигурами, являются разновидностью оптической иллюзии.Двумерная фигура кажется трехмерной, но ее геометрия не похожа ни на что, что могло бы существовать в реальном мире. Невозможные объекты использовались в интригующих произведениях искусства на протяжении всего двадцатого века.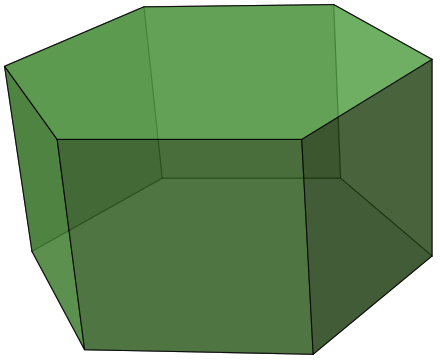
Невозможный шестиугольник в этом руководстве по рисованию основан на треугольнике Пенроуза, который был создан художником в 1934 году. Многоугольники Пенроуза, такие как этот шестиугольник, построены путем добавления дополнительных сторон к треугольнику Пенроуза.
Прокрутите вниз, чтобы загрузить этот учебник в формате PDF.
Однако оптическая иллюзия становится менее яркой по мере добавления сторон. Таким образом, шестиугольник может показаться искривленным, заплетенным или скрученным, а не «невозможным».
Шестиугольники — обычные конструкции как в искусстве, так и в природе. Вы знали? Соты сделаны из маленьких шестиугольников пчелиного воска. Интересно, что шестиугольник позволяет покрыть большое пространство как можно меньшим количеством воска. Эффективная структура также очень сильна.
Другие гексагональные фигуры в природе включают структуру некоторых скал и кристаллов (таких как Дорога гигантов в Ирландии), части панциря черепахи, несколько снежинок и постоянное образование облаков на планете Сатурн.
Хотите нарисовать невозможный шестиугольник? Сделать это легко и весело с помощью этого простого пошагового руководства по рисованию фигур. Все, что вам понадобится, это карандаш, ручка или маркер и лист бумаги. Вы также можете раскрасить законченный рисунок.
Если вам понравился этот урок, см. Также следующие руководства по рисованию: Невозможный треугольник, Бейсбольная бита и Бейсбол.
Разблокируйте БЕСПЛАТНЫЕ и ПЕЧАТНЫЕ уроки рисования и раскрашивания! Узнать большеПошаговая инструкция по рисованию невозможного шестиугольника
Чертеж невозможного шестиугольника — шаг 11.Начните с рисования шестиугольника. Шестиугольник — это правильная шестигранная фигура, у которой все стороны одинаковой длины.
Рисование невозможного шестиугольника — шаг 2 2. Проведите короткую линию, идущую от верхнего угла шестиугольника. От этой линии вытяните более длинную линию, параллельную стороне шестиугольника. Затем от конца этой линии протяните прямую, параллельную следующей стороне шестиугольника. Обратите внимание, что расстояние между линией и второй стороной больше, чем между линией и первой стороной.
Обратите внимание, что расстояние между линией и второй стороной больше, чем между линией и первой стороной.
3. Проведите короткую прямую линию, идущую от следующего угла шестиугольника. Вытяните от него прямую, параллельную стороне шестиугольника.
Рисование невозможного шестиугольника — шаг 44. Вытяните короткую прямую линию от нижнего угла шестиугольника. От этой линии проведите прямую, параллельную нижней части шестиугольника. Затем протяните еще одну линию вверх, параллельно следующей стороне шестиугольника.
Чертеж невозможного шестиугольника — шаг 55.Проведите короткую линию от оставшегося нижнего угла шестиугольника. Оттуда проведите прямую линию, параллельную стороне шестиугольника. Затем проведите еще одну линию, параллельную следующей стороне шестиугольника.
Рисование невозможного шестиугольника — шаг 6 6. Проведите короткую прямую линию, выходящую из следующего угла шестиугольника. Затем протяните прямую линию, параллельную стороне шестиугольника.
Затем протяните прямую линию, параллельную стороне шестиугольника.
7. Проведите короткую прямую линию от последнего угла шестиугольника.Оттуда вытяните прямую линию, параллельную вершине шестиугольника.
Рисование невозможного шестиугольника — шаг 88. Начните соединять внешние края невозможного шестиугольника. Вытяните короткие линии от верхнего угла и сбоку фигуры. Затем соедините эти линии с существующими линиями, заключив верхнюю и верхнюю часть фигуры.
Рисование невозможного шестиугольника — шаг 99. Проведите короткую линию, идущую от нижнего угла шестиугольника. Затем соедините все линии с открытым концом, пока фигура не станет полностью замкнутой.
Завершите рисунок «Невозможный шестиугольник»Раскрасьте и закрасьте свой невозможный шестиугольник. Обратите внимание, как штриховка в нашем примере делает трехмерную иллюзию более яркой.
Хотите рисовать больше невозможных объектов? Ознакомьтесь с нашими руководствами по рисованию искусственных объектов для создания невозможных треугольников, кубов, квадратов, сердец, лестниц и многого другого.![]()

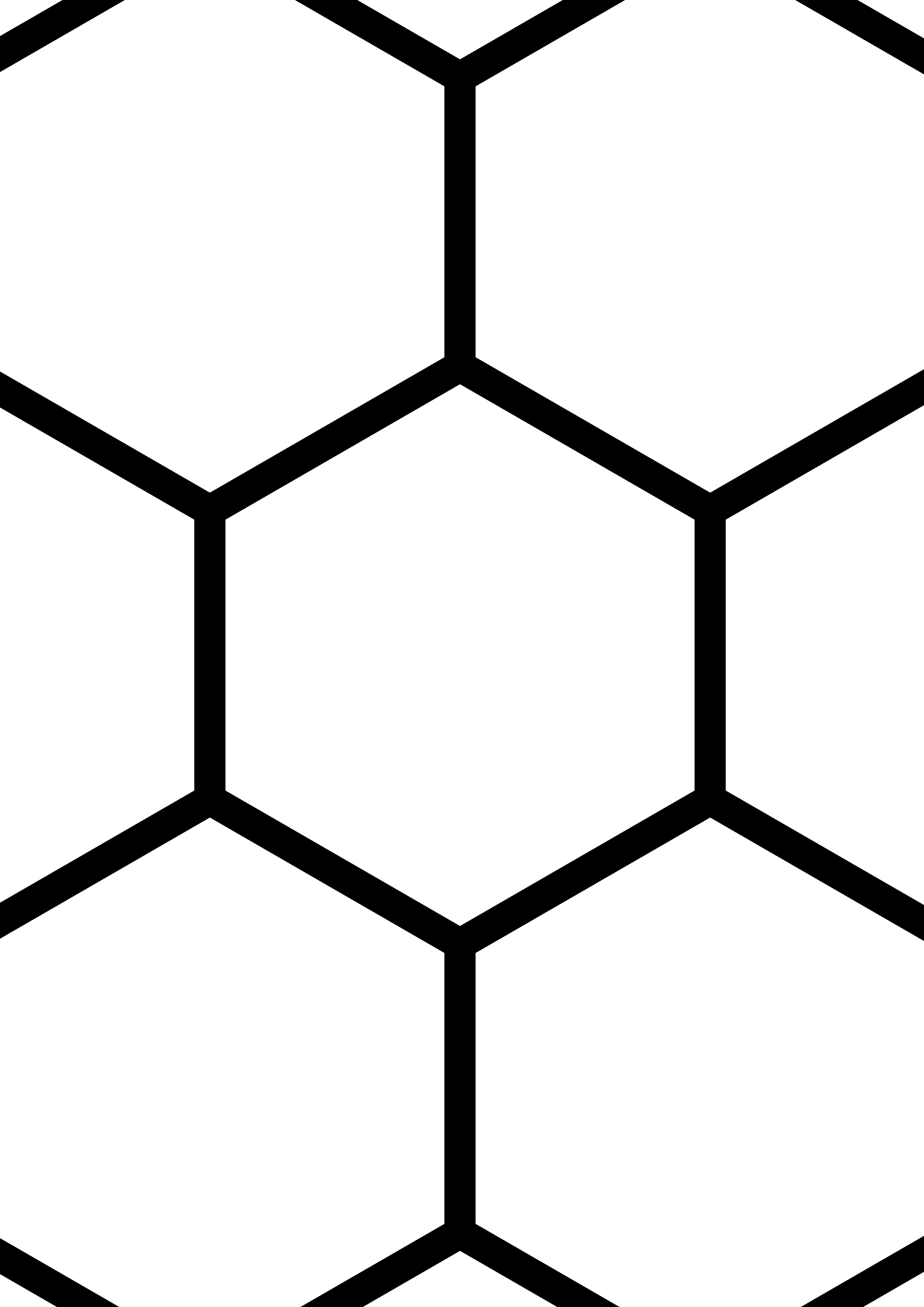 ..
..
 forward (
forward (