Ресемплинг это: Передискретизация — Википедия – Ресемплинг — это… Что такое Ресемплинг?

alexxlab
Разное |

Содержание

Ресемплинг — это… Что такое Ресемплинг?

Иллюстрация эффекта наложения спектров при децимации изображения. Сверху — исходное изображение. Слева снизу — уменьшенное в два раза с фильтрацией. Справа снизу — уменьшенное в два раза без фильтрации (с наложением спектров).

Передискретиза́ция (англ. resampling) в обработке сигналов — изменение частоты дискретизации дискретного (чаще всего цифрового) сигнала. Алгоритмы передискретизации широко применяются при обработке звуковых сигналов, радиосигналов и изображений.

В англоязычной литературе применяются также термины downsampling для обозначения понижения частоты дискретизации и upsampling для её повышения.

Понятие передискретизации не следует смешивать с процедурой дискретизации сигнала с запасом по частоте дискретизации (англ. oversampling).

Общие принципы

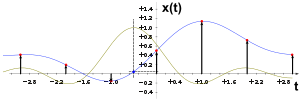
Вычисление промежуточного отсчёта дискретного сигнала с помощью идеального фильтра нижних частот. Синия кривая — исходный непрерывный сигнал, зелёная — импульсная характеристика идеального ФНЧ.

Согласно теореме Котельникова любой непрерывный сигнал с финитным спектром (то есть таким спектром, что спектральные составляющие, соответствующие частотам выше некоторой частоты f0, отсутствуют) может быть представлен в виде отсчётов дискретного сигнала с частотой дискретизации fd > 2f0. При этом такое преобразование является взаимно однозначным, то есть при соблюдении условий теоремы Котельникова по дискретному сигналу можно восстановить исходный сигнал с финитным спектром без искажений.

При передискретизации отсчёты сигнала, соответствующие одной частоте дискретизации, вычисляются по имеющимся отсчётам этого же сигнала, соответствующим другой частоте дискретизации (при этом предполагается, что обе частоты дискретизации соответствуют условиям теоремы Котельникова). Идеальная передискретизация эквивалентна восстановлению непрерывного сигнала по его отсчётам с последующей дискретизацией его на новой частоте.

Точное вычисление значения исходного непрерывного сигнала в определённой точке производится следующим образом:

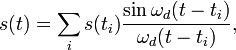
\,\!s(t)=\sum_i s(t_i) \frac{\sin \omega_d(t-t_i)}{\omega_d(t-t_i)},

где s(ti) — i-й отсчёт сигнала, ti — момент времени, соответствующий этому отсчёту, s(t) — интерполированное значение сигнала в момент времени t.

Сложность практического применения этого выражения заключается в том, что функция 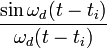\frac{\sin \omega_d(t-t_i)}{\omega_d(t-t_i)} не является финитной, поэтому для вычисления значения сигнала в определённый момент времени необходимо обработать бесконечное число его отсчётов (как в прошлом, так и в будущем). В реальной жизни интерполяция осуществляется с помощью других фильтров, при этом выражение для неё принимает следующий вид:

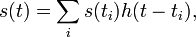
\,\!s(t)=\sum_i s(t_i) h(t-t_i),

где h(t) — импульсная характеристика соответствующего восстанавливающего фильтра. Вид этого фильтра выбирается в зависимости от задачи.

Прямое вычисление новых отсчётов сигнала по вышеприведённым формулам требует значительных вычислительных ресурсов и нежелательно для приложений реального времени. Существуют важные частные случаи передискретизации, для которых вычисление новых отсчётов производится проще:

  • децимация — уменьшение частоты дискретизации в целое число раз;
  • интерполяция в узком смысле — увеличение частоты дискретизации в целое число раз.

При таких ограничениях становится удобным применение цифровых фильтров для передискретизации.

Передискретизация с помощью цифровых фильтров

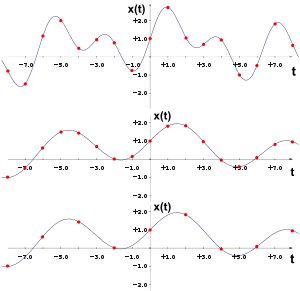
\,\!s(t)=\sum_i s(t_i) h(t-t_i),

Иллюстрация алгоритма децимации дискретного сигнала (с коэффициентом 2). Красные точки обозначают отсчеты, сплошные линии — непрерывный сигнал, представлением которого эти отсчеты являются. Сверху — исходный сигнал. В середине — этот же сигнал после фильтрации в цифровом фильтре нижних частот. Снизу — децимированный сигнал.

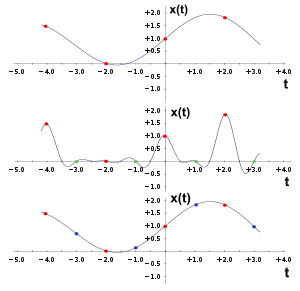
\,\!s(t)=\sum_i s(t_i) h(t-t_i),

Иллюстрация алгоритма интерполяции дискретного сигнала (с коэффициентом 2). Красные точки обозначают исходные отсчеты сигнала, сплошные линии — непрерывный сигнал, представлением которого эти отсчеты являются. Сверху — исходный сигнал. В середине — этот же сигнал со вставленными нулевыми отсчётами (зеленые точки). Снизу — интерполированный сигнал (синие точки — интерполированные значения отсчётов).

Децимация

Децимацией называют уменьшение частоты дискретизации в целое число раз (далее

N). Децимация цифрового сигнала производится в два этапа:

  1. Цифровая фильтрация сигнала с целью удаления высокочастотных составляющих, не удовлетворяющих условиям теоремы Котельникова для новой частоты дискретизации;
  2. Удаление (отбрасывание) лишних отсчетов (сохраняется каждый N-й отсчёт).

Первый этап необходим для исключения наложения спектров, природа которого аналогична наложению спектров при первоначальной дискретизации аналогового сигнала. Наложение спектров особенно заметно на тех участках сигнала, которые содержат значительные высокочастотные спектральные составляющие. Так, на приведённых в начале статьи фотографиях небо практически не подвергнулось наложению спектров, но эффект бросается в глаза, если обратить внимание на резкие переходы (такие как чёткие линии зданий и дорожной разметки).

При программной реализации алгоритма децимации «лишние» отсчёты не удаляются, а просто не вычисляются. При этом число обращений к цифровому фильтру уменьшается в N раз.

Интерполяция

Под интерполяцией в узком смысле понимают увеличение частоты дискретизации сигнала в целое число раз путем вычисления промежуточных отсчетов по уже имеющимся. Идеальная интерполяция позволяет точно восстановить значения сигнала в промежуточных отсчётах.

Стандартный алгоритм интерполяции заключается в следующем:

  • вставка нулевых отсчетов на место отсчетов, которые необходимо вычислить;
  • фильтрация сигнала цифровым фильтром нижних частот для того, чтобы убрать спектральные составляющие сигнала, которых заведомо не могло быть в исходном сигнале согласно теореме Котельникова.

Точность этого метода ограничивается невозможностью реализации фильтра нижних частот с идеально прямоугольной частотной характеристикой.

При программной реализации интерполяции нулевые отсчёты не участвуют в вычислении полинома, что позволяет оптимизировать процесс вычисления.

Комбинация интерполяции и децимации

Для того, чтобы изменить частоту дискретизации сигнала в 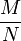\frac{M}{N}

раз (M и N — целые положительные числа), можно сначала провести интерполяцию, увеличив частоту дискретизации в M раз, а затем с помощью децимации уменьшить её в N раз. Фильтрацию сигнала достаточно произвести всего один раз — между интерполяцией и децимацией.

Недостатком данного метода является необходимость фильтрации сигнала на повышенной в M раз частоте дискретизации, что требует значительных вычислительных ресурсов. При этом соответствующая частота может во много раз превосходить как исходную, так и окончательную частоту передискретизации, особенно если M и N — близкие большие числа. Так, например, при передискретизации звукового сигнала с 44100 Гц до 48000 Гц этим методом необходимо увеличить частоту дискретизации в 160 раз до 7056000 Гц и затем уменьшить её в 147 раз до 48000 Гц. Таким образом, в данном примере вычисления приходится производить на частоте дискретизации более 7 МГц.

Передискретизация с помощью полифазных фильтров

Метод передискретизации с помощью полифазных фильтров аналогичен предыдущему, с тем отличием, что в нём вместо одного фильтра, работающего на высокой частоте дискретизации, используется несколько фильтров, работающих на низкой частоте. При этом удаётся добиться сокращения количества необходимых вычислений, так как для каждого отсчёта необходимо вычислить выход только одного из этих фильтров.

Передискретизация с помощью дискретного преобразования Фурье

Передискретизация с помощью ДПФ используется для повышения частоты дискретизации в целое или дробное число раз. Алгоритм работает только с конечными отрезками сигнала. Пусть

N — начальное число отсчётов, M — число отсчётов в передискретизованном сигнале. Алгоритм включает в себя следующие операции:

1. Вычисляется ДПФ исходного сигнала (чаще всего по алгоритму быстрого преобразования Фурье).

2. В середину спектра вставляется необходимое число нулевых компонент:

2.1. если N нечётное:
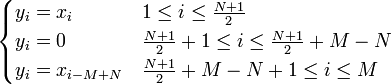
\begin{cases} y_i=x_i & 1 \le i \le \frac{N+1}{2} \\ y_i=0 & \frac{N+1}{2}+1 \le i \le \frac{N+1}{2}+M-N\\ y_{i}=x_{i-M+N} & \frac{N+1}{2}+M-N+1 \le i \le M \end{cases}
2.2. если N чётное
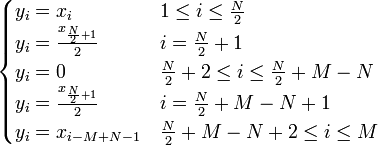
\begin{cases} y_i=x_i & 1 \le i \le \frac{N}{2} \\ y_i=\frac{x_{\frac{N}{2}+1}}{2} & i=\frac{N}{2}+1 \\ y_{i}=0 & \frac{N}{2}+2 \le i \le \frac{N}{2}+M-N \\ y_i=\frac{x_{\frac{N}{2}+1}}{2} & i=\frac{N}{2}+M-N+1 \\ y_i=x_{i-M+N-1} & \frac{N}{2}+M-N+2 \le i \le M \end{cases}

3. Вычисляется обратное ДПФ.

Ограничением этого метода является то, что, как и любой метод, основанный на ДПФ, он даёт точный результат только для периодического дискретного сигнала. Для обработки непериодических сигналов необходимо применять оконные функции и выбирать отрезки сигнала для вычисления ДПФ таким образом, чтобы их концы перекрывались.

Применения

Широко применяется как аппаратная (на основе специализированных микросхем или FPGA), так и программная (на базе процессоров общего назначения или сигнальных процессоров) реализация алгоритмов передискретизации.

Выбор конкретной реализации алгоритма передискретизации является результатом компромисса между качеством преобразования и его вычислительной сложностью. Основным параметром, влияющим на эти характеристики, является близость используемых цифровых фильтров к идеальным. Более качественные фильтры требуют больше ресурсов для вычисления.

На практике передискретизация в большинстве случаев ведёт к потере информации о сигнале по следующим причинам:

  • при уменьшении частоты дискретизации сигнал необходимо отфильтровать с целью удаления высокочастотных спектральных составляющих, которые не соответствуют условиям теоремы Котельникова для новой частоты дискретизации;
  • вычисления, производимые над цифровыми (квантованными по уровню) сигналами ведут к необратимым ошибкам округления.

Таким образом, при увеличении частоты дискретизации с последующим уменьшением её до исходного значения качество сигнала будет потеряно (если только высокая частота не кратна низкой).

При обработке звука

Оборудование, предназначенное для воспроизведения цифрового звука, как правило, рассчитано на вполне определённую частоту дискретизации сигнала непосредственно перед цифро-аналоговым преобразованием (для многих звуковых карт эта частота составляет 48000 Гц). Все звуковые сигналы с другими частотами дискретизации должны быть рано или поздно передискретизованы.

Передискретизация звукового сигнала на требуемую частоту может осуществляться мультимедиа-проигрывателем, драйвером звуковой карты или самой звуковой картой. Использование программы-проигрывателя для данной цели может быть оправдано, если есть желание избежать аппаратной передискретизации звука (или передискретизации драйвером) с целью добиться более высокого качества (при большей загрузке центрального процессора). Однако программная передискретизация воспроизводимого материала на частоту, отличную от частоты, поддерживаемой оборудованием, не имеет смысла и приводит только к потере качества сигнала.

Существуют программные передискретизаторы звуковых сигналов с открытым исходным кодом:

  • SRC (Secret Rabbit Code) или libsamplerate[1] — существует плагин для [2] — существуют плагины для foobar2000.

Также передискретизация поддерживается программами-редакторами звука.

При обработке изображений

Изменение разрешения является одной из распространённых операций обработки изображений. Передискретизация, приближенная к идеальной (с минимизацией наложения спектров), не всегда является желательной. Выбор фильтра для передискретизации является результатом компромисса между типом и выраженностью артефактов и вычислительной сложностью преобразования (актуальной для приложений реального времени).

Типичные артефакты при изменении разрешения изображения:

Для передискретизации изображений применяется большое число фильтров, которые можно классифицировать следующим образом[3]:

  1. Фильтры интерполяционного типа, обладающие сравнительно узкой импульсной характеристикой. К ним относятся, в частности, треугольный фильтр, производящий билинейную интерполяцию и полином Лагранжа, с помощью которого можно реализовать бикубическую интерполяцию. Применение таких фильтров позволяет осуществить передискретизацию изображения достаточно быстро.
  2. Фильтры с колоколообразной характеристикой, такие как фильтр Гаусса. Эти фильтры хорошо справляются с пикселизацией, звоном и алиасингом, а также отфильтровывают высокочастотные шумы. Их недостаток — заметное размытие изображения.
  3. Оконные sinc-фильтры. Sinc-фильтр — это идеальный фильтр нижних частот. Как говорилось выше, он не может быть реализован. Однако если частотную характеристику sinc-фильтра умножить на оконную функцию, получится реализуемый фильтр с хорошими спектральными свойствами. При применении данных фильтров к изображениям удаётся сохранить относительно высокую чёткость (даже при увеличении разрешения), но может быть сильно заметен эффект звона. Одним из наиболее часто применяемых фильтров данного типа является фильтр Ланцоша.

При обработке радиосигналов

При демодуляции цифровых сигналов желательно, чтобы частота дискретизации сигнала была кратна его скорости манипуляции (иначе говоря, чтобы на каждый символ приходилось одинаковое число отсчётов сигнала). Однако частота дискретизации входного сигнала с АЦП, как правило, фиксирована, а скорость манипуляции может меняться. Решением является передискретизация сигнала.

Примечания

  1. ↑ Secret Rabbit Code (aka libsamplerate)
  2. ↑ Shibatch Audio Tools
  3. ↑ Resize and Scaling на сайте программы

    Литература

    1. Richard G. Lyons Understanding digital signal processing. — Addison Wesley, 1997. — 517 с. — ISBN 0-201-63467-8
    2. Л. Рабинер, Б. Гоулд Теория и применение цифровой обработки сигналов = Theory and Application of Digital Signal Processing. — М.: Мир, 1978. — 848 с.
    3. Романюк Ю.А. Основы цифровой обработки сигналов. В 3-х ч. Ч.1. Свойства и преобразования дискретных сигналов: Учебное пособие. — М.: МФТИ, 2005. — 332 с. — ISBN 5-74-170144-2

    Wikimedia Foundation. 2010.

  • Реселлинг
  • Ресивер

Смотреть что такое «Ресемплинг» в других словарях:

  • Ресемплинг (статистика) — Эта статья предлагается к удалению. Пояснение причин и соответствующее обсуждение вы можете найти на странице Википедия:К удалению/2 июля 2012. Пока процесс обсуждения н …   Википедия

  • Апскейлинг — Стиль этой статьи неэнциклопедичен или нарушает нормы русского языка. Статью следует исправить согласно стилистическим правилам Википедии …   Википедия

  • Sony Vegas — Pro Разработчик Sony Операционная система Microsoft Windows Последняя версия 12.0.367 (26 сентября 2012) Лицензия Проприетарная Сайт …   Википедия

  • DeaDBeeF — DeaDBeeF …   Википедия

  • JPEGView — Главное окно JPEGView с выдвинутой панелью обработки Тип Просмотр и редактирование фотографий …   Википедия

Ресемплинг. Цифровая кирпичная стена против теории заговора. Рождественская сказка для любителей чистого звука

Ни в одной области электроники не скопилось столько мифов,
как в области Hi-Fi и Hi-End устройств для воспроизведения звука.
Ударим Рождественской Историей по одному из них!

Когда старый год уже проводили, Новый встретили сначала в узком семейном кругу, а затем с более дальними родственниками, когда закончились или пришли в негодность новогодние салаты и стало отпускать похмелье…

Те, кто не захотел или не смог встречать Новый Год в Дальнем Зарубежье, начинают ощущать на себе зов персонального компьютера.

Именно для них и предназначена моя рождественская история, об основах ресемплинга — технологии, позволившей значительно улучшить качество воспроизведения дисков формата Аудио CD в начале тысячелетия. Именно тогда для воспроизведения 16 битных записей начали применять 18 и даже 20 битные цифро-аналоговые преобразователи. С первого взгляда это выглядело как маркетинговая уловка производителей, направленная на извлечение дополнительной порции денег из кошельков доверчивых аудиофилов, но в этот раз сторонники теории заговоров могут курить в сторонке. На самом деле это было удачной попыткой улучшить качество воспроизведения и снизить цену дорогостоящей профессиональной аппаратуры. История старая, но поучительная, во многом актуальная и по сей день.

Цифро-аналоговый преобразователь digital-to-analog DAC является сердцем любой аудиовопроизводящей системы, использующей в качестве источника компакт диски. На него возложена сложная и деликатная задача раскодирования последовательности 16-битных чисел и преобразования её в формат, воспринимаемый человеческим ухом.

В далёком 1983 году появился первый культовый CD проигрыватель Magnavox со сдвоенным 14 битным конвертором, но уже к началу века многие системы высококачественного воспроизведения CD дисков имели 18, а то и 20 битные преобразователи. Почему?

Немного теории, почти без формул


Концепция цифро-аналоговых преобразований покоится на двух китах: частоте дискретизации sampling и разрядности quantization.

Для воспроизведения звука в PCM формате мы должны через равные промежутки времени преобразовывать цифровые значения в соответствующие им аналоговые величины напряжения или тока. Частота этих преобразований и является частотой дискретизации. Согласно теореме Найквиста, таким образом возможно воспроизводить сигналы с частотой не выше половины частоты дискретизации. Наиболее распространённые форматы, которые способны воспроизводить сигналы с частотой воспринимаемой человеческим ухом общепринята цифра 20 кГц, имеют частоты дискретизации в 44.1 и 48 КГц.


Первый до сих пор широко используется в звуковых компакт дисках (CDDA, англ. Compact Disc Digital Audio, также называемый англ. Audio CD и Red Book), а второй зародился в ряде стандартов для профессиональной звукозаписывающей аппаратуры.

Давайте вообразим себе что при записи звуковой сигнал попадает на идеальный аналогово-цифровой преобразователь. Он не имеет собственных шумов и искажений и преобразует мгновенное значение поступающего на него сигнала в цифровое с заданной разрядностью, ну например в 16 бит, как это принято в формате Audio CD. В таком случае, теоретически достижимый динамический диапазон сигнала (соотношение между оцифрованными сигналами с самым большим и маленьким уровнями) будет составлять 98.1 dB. Для вычисления этой величины часто используют приближённую формулу, согласно которой каждый лишний бит добавляет 6 децибел к теоретически достижимому динамическому диапазону. Для 16 битного сигнала мы получим:

6dB/bit*16bits=96dB.

Реальный музыкальный сигнал чаще всего состоит не из чистого тона, а из смеси большого количества быстро меняющих свою частоту и амплитуду гармоник. Для гармоник, имеющих амплитуду менее одного разряда АЦП, невозможно восстановить корреляцию с исходным сигналом и они в результате операции кодирования-декодирования превращаются в белый шум. Кроме этого, шумы генерируются быстро изменяющимися сигналами с большой амплитудой, которых много скажем в поп музыке.

От идеальных приближений к реальной жизни. Проблемы первых CD проигрывателей


Со времён начала использования цифровых технологий в звукозаписи ведётся постоянная гонка за увеличение их производительности и уменьшение стоимости. Первые CD проигрыватели имели единственный параллельный DAC и две входные цепи, которые поочерёдно подавали на него сигналы то правого, то левого каналов. Мгновенные уровни аналоговых сигналов на выходе DAC фиксировались с помощью специальных цепей на время между двумя считываниями и попеременно поступали на отдельные усилители правого и левого каналов. Это порождало дополнительные искажения, величина которых зависела от разности мгновенных звуковых уровней каналов. Под напором критики ауидофилов производители вынуждены были перейти на схему с отдельными DAC для каждого из каналов.

На выходе DAC присутствует ступенчатый сигнал, который не слишком похож на плавный исходный, в нём существуют неприятные на слух искажения. Давайте для упрощения представим что на вход была подана единственная гармоника с частотой 1 КГц. Операция восстановления оцифрованного сигнала приводит фактически к возникновению интермодуляционных искажений между исходным сигналом и частотой дискретизации — в нашем случае 44.1 КГц. (Механизм возникновения интермодуляционных искажений и ликбез по гармоникам при необходимости ищите в моей прошлой статье).

Несмотря на то, что паразитные гармоники лежат за пределами человеческого уха, они оказывают неблагоприятное воздействие на усилительный тракт и от них лучше избавиться.

В ранних моделях аппаратуры для воспроизведения цифрового контента для этого использовались фильтры, которые имели плоскую характеристику до частоты в 20 кГц, а далее резкое ослабление уровня на 80дБ и более. В английской терминологии такие фильтры называют brick-wall, на русском иногда именуют по аналогии “кирпичной стеной”. Проблема заключалась в том, что аналоговые ФНЧ высокого порядка очень чувствительны к точности значений пассивных компонентов, из которых они состоят. Ещё больше осложняют ситуацию требуемые номиналы выбивающиеся за пределы стандартного ряда и особые требования к качеству этих компонентов, которое необходимо для достижения минимального вклада в искажение сигнала. В результате, стоимость данных фильтров получалась запредельной, но самое печальное — они не смогли удовлетворить запросы аудиофилов, поскольку данные фильтры имели большие фазовые искажения, особенно на краях воспроизводимого диапазона. Поэтому звучание ранних версий CD проигрывателей несмотря на высокую стоимость аудиофилы характеризовали как “песочное” (gritty).

Цифровые фильтры спешат на помощь. Oversampling на пальцах


Серьёзным шагом в направлении улучшения качества звука а главное его доступности было внедрение технологии передискретизации сигнала, которой собственно и посвящена данная статья.

Для того, чтобы пояснить её сущность давайте представим процесс восстановления сигнала с так любимой ГОСТами частотой 1 КГц. На рисунке A представлен ряд сэмплов составляющих сигнал, которые появляются на выходе DAC, а правее спектральные составляющие второго и третьего порядков, содержащиеся в сигнале на выходе DAC. Можно заметить, что сигнал является ни чем иным, как продуктом интермодуляционных искажений между исходным тоном с частотой 1 КГц и частой оцифровки 44.1 КГц.

Увеличим частоту дискретизации сигнала в четыре раза путём элементарной операции — добавления лишних трёх сэмплов между двумя соседними, каждый из которых имеет нулевые значения, как показано на рисунке C. Одновременно с этим добавим два младших разряда в каждый сэмпл, также заполнив их нулями. Теперь мы получили 18 битные значения сэмплов. В результате этой операции спектр сигнала фактически не изменился, но на самом деле произошло фундаментальное изменение. Гармоники второго порядка, вызванные частотой дискретизации стали частью спектра основного сигнала. Производные же гармоники переместились выше частоты 44.1 кГц. Это показано на рисунке D.

В области же спектра основного сигнала с успехом можно применить цифровую фильтрацию, что мы и сделаем, использовав цифровой фильтр высокого порядка, с АЧХ показанный на рисунке F. Физически мы получаем дополнительные промежуточные точки между имеющимися сэмплами сигнала, которые сглаживают переходы между двумя значениями за счёт появления дополнительных двух разрядов в представлении амплитуды.

Теперь, когда всю тяжёлую и грязную работу выполнил цифровой фильтр мы подаём результирующий сигнал с частотой дискретизации в 44.1*4 =176.4 КГц, на DAC.

Осталось добавить вишенку на наш тортик — пропустить сигнал через простейший аналоговый фильтр третьего порядка, который отлично справится с подавлением гармоник в заданном диапазоне и не внесёт при этом заметных фазовых искажений.

Результат — спектр полученного сигнала стал гораздо ближе к исходному, паразитные составляющие в нём сильно ослаблены, а фазовые искажения сведены к минимуму благодаря возможностям цифровой фильтрации.


Аппаратная реализация


На рисунке представлена аппаратная реализация описанного выше решения. Операции передискретизации и цифровой фильтрации выполняет микросхема CXD1088Q производства фирмы SONY — одним из прародителей формата Audio CD. Несложная логическая схема поочерёдно запускает преобразование двух отдельных 18 битных DAC AD1860.

Какие же преимущества мы получили в результате наших цифровых фокусов?

  • Снижение интермодуляционных искажений
  • Низкие фазовые искажения, вносимые фильтром
  • Отличное подавление высших гармоник, возникающий в процессе цифро-аналогового преобразования, которые могут служить источником возникновения интермодуляционных искажений в усилительном тракте
  • Применение ЦАП с большей разрядностью позволяет уменьшить нелинейности преобразования и коэффициент гармонических искажений в силу того, что они имеют лучшие параметры
  • Благодаря использованию специализированных чипов вместо сложных аналоговых фильтров, снизилась цена реализации, размеры и потребляемая мощность аппаратного решения.

Каждому яблоку место упасть, каждому вору возможность украсть…


Как любая хорошая рождественская история, эта имеет хэппиенд. От внедрения новой технологии кажется выиграли все:

Производители профессиональной аппаратуры и CD проигрывателей в сегменте Hi Fi смогли улучшить качество звука и значительно увеличить повторяемость параметров своих изделий в процессе производства.

Любители качественного звука получили проигрыватели дисков с улучшенными параметрами за разумную цену.

Законченные аудиофилы теперь могут ворчать о том, какой крутой звук был у старых аппаратов с аналоговыми фильтрами пока всё не испортила цифра и охотиться за винтажной техникой.

Ну а избранные производители хайэнда могут создавать единичные экземпляры устройств, тщательно подбирая компоненты аналогового фильтра с характерным названием “кирпичная стена”, получая при этом аппараты с индивидуальным звучанием обусловленным в основном вносимыми фильтрами фазовыми и не только искажениями и задирать их ценник до небес.

Более подробное сравнение работы аналоговых и цифровых фильтров и ответы на характерные вопросы читайте в следующей статье
.

При подготовке публикации были использованы материалы статьи DAC ICs: How Many Bits is Enought? под авторством Robert Adams

Ресамплинг — это… Что такое Ресамплинг?

Иллюстрация эффекта наложения спектров при децимации изображения. Сверху — исходное изображение. Слева снизу — уменьшенное в два раза с фильтрацией. Справа снизу — уменьшенное в два раза без фильтрации (с наложением спектров).

Передискретиза́ция (англ. resampling) в обработке сигналов — изменение частоты дискретизации дискретного (чаще всего цифрового) сигнала. Алгоритмы передискретизации широко применяются при обработке звуковых сигналов, радиосигналов и изображений.

В англоязычной литературе применяются также термины downsampling для обозначения понижения частоты дискретизации и upsampling для её повышения.

Понятие передискретизации не следует смешивать с процедурой дискретизации сигнала с запасом по частоте дискретизации (англ. oversampling).

Общие принципы

Вычисление промежуточного отсчёта дискретного сигнала с помощью идеального фильтра нижних частот. Синия кривая — исходный непрерывный сигнал, зелёная — импульсная характеристика идеального ФНЧ.

Согласно теореме Котельникова любой непрерывный сигнал с финитным спектром (то есть таким спектром, что спектральные составляющие, соответствующие частотам выше некоторой частоты f0, отсутствуют) может быть представлен в виде отсчётов дискретного сигнала с частотой дискретизации fd > 2f0. При этом такое преобразование является взаимно однозначным, то есть при соблюдении условий теоремы Котельникова по дискретному сигналу можно восстановить исходный сигнал с финитным спектром без искажений.

При передискретизации отсчёты сигнала, соответствующие одной частоте дискретизации, вычисляются по имеющимся отсчётам этого же сигнала, соответствующим другой частоте дискретизации (при этом предполагается, что обе частоты дискретизации соответствуют условиям теоремы Котельникова). Идеальная передискретизация эквивалентна восстановлению непрерывного сигнала по его отсчётам с последующей дискретизацией его на новой частоте.

Точное вычисление значения исходного непрерывного сигнала в определённой точке производится следующим образом:

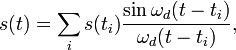
\,\!s(t)=\sum_i s(t_i) \frac{\sin \omega_d(t-t_i)}{\omega_d(t-t_i)},

где s(ti) — i-й отсчёт сигнала, ti — момент времени, соответствующий этому отсчёту, s(t) — интерполированное значение сигнала в момент времени t.

Сложность практического применения этого выражения заключается в том, что функция 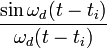\frac{\sin \omega_d(t-t_i)}{\omega_d(t-t_i)} не является финитной, поэтому для вычисления значения сигнала в определённый момент времени необходимо обработать бесконечное число его отсчётов (как в прошлом, так и в будущем). В реальной жизни интерполяция осуществляется с помощью других фильтров, при этом выражение для неё принимает следующий вид:

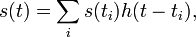
\,\!s(t)=\sum_i s(t_i) h(t-t_i),

где h(t) — импульсная характеристика соответствующего восстанавливающего фильтра. Вид этого фильтра выбирается в зависимости от задачи.

Прямое вычисление новых отсчётов сигнала по вышеприведённым формулам требует значительных вычислительных ресурсов и нежелательно для приложений реального времени. Существуют важные частные случаи передискретизации, для которых вычисление новых отсчётов производится проще:

  • децимация — уменьшение частоты дискретизации в целое число раз;
  • интерполяция в узком смысле — увеличение частоты дискретизации в целое число раз.

При таких ограничениях становится удобным применение цифровых фильтров для передискретизации.

Передискретизация с помощью цифровых фильтров

\,\!s(t)=\sum_i s(t_i) h(t-t_i),

Иллюстрация алгоритма децимации дискретного сигнала (с коэффициентом 2). Красные точки обозначают отсчеты, сплошные линии — непрерывный сигнал, представлением которого эти отсчеты являются. Сверху — исходный сигнал. В середине — этот же сигнал после фильтрации в цифровом фильтре нижних частот. Снизу — децимированный сигнал.

\,\!s(t)=\sum_i s(t_i) h(t-t_i),

Иллюстрация алгоритма интерполяции дискретного сигнала (с коэффициентом 2). Красные точки обозначают исходные отсчеты сигнала, сплошные линии — непрерывный сигнал, представлением которого эти отсчеты являются. Сверху — исходный сигнал. В середине — этот же сигнал со вставленными нулевыми отсчётами (зеленые точки). Снизу — интерполированный сигнал (синие точки — интерполированные значения отсчётов).

Децимация

Децимацией называют уменьшение частоты дискретизации в целое число раз (далее N). Децимация цифрового сигнала производится в два этапа:

  1. Цифровая фильтрация сигнала с целью удаления высокочастотных составляющих, не удовлетворяющих условиям теоремы Котельникова для новой частоты дискретизации;
  2. Удаление (отбрасывание) лишних отсчетов (сохраняется каждый N-й отсчёт).

Первый этап необходим для исключения наложения спектров, природа которого аналогична наложению спектров при первоначальной дискретизации аналогового сигнала. Наложение спектров особенно заметно на тех участках сигнала, которые содержат значительные высокочастотные спектральные составляющие. Так, на приведённых в начале статьи фотографиях небо практически не подвергнулось наложению спектров, но эффект бросается в глаза, если обратить внимание на резкие переходы (такие как чёткие линии зданий и дорожной разметки).

При программной реализации алгоритма децимации «лишние» отсчёты не удаляются, а просто не вычисляются. При этом число обращений к цифровому фильтру уменьшается в N раз.

Интерполяция

Под интерполяцией в узком смысле понимают увеличение частоты дискретизации сигнала в целое число раз путем вычисления промежуточных отсчетов по уже имеющимся. Идеальная интерполяция позволяет точно восстановить значения сигнала в промежуточных отсчётах.

Стандартный алгоритм интерполяции заключается в следующем:

  • вставка нулевых отсчетов на место отсчетов, которые необходимо вычислить;
  • фильтрация сигнала цифровым фильтром нижних частот для того, чтобы убрать спектральные составляющие сигнала, которых заведомо не могло быть в исходном сигнале согласно теореме Котельникова.

Точность этого метода ограничивается невозможностью реализации фильтра нижних частот с идеально прямоугольной частотной характеристикой.

При программной реализации интерполяции нулевые отсчёты не участвуют в вычислении полинома, что позволяет оптимизировать процесс вычисления.

Комбинация интерполяции и децимации

Для того, чтобы изменить частоту дискретизации сигнала в 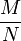\frac{M}{N} раз (M и N — целые положительные числа), можно сначала провести интерполяцию, увеличив частоту дискретизации в M раз, а затем с помощью децимации уменьшить её в N раз. Фильтрацию сигнала достаточно произвести всего один раз — между интерполяцией и децимацией.

Недостатком данного метода является необходимость фильтрации сигнала на повышенной в M раз частоте дискретизации, что требует значительных вычислительных ресурсов. При этом соответствующая частота может во много раз превосходить как исходную, так и окончательную частоту передискретизации, особенно если M и N — близкие большие числа. Так, например, при передискретизации звукового сигнала с 44100 Гц до 48000 Гц этим методом необходимо увеличить частоту дискретизации в 160 раз до 7056000 Гц и затем уменьшить её в 147 раз до 48000 Гц. Таким образом, в данном примере вычисления приходится производить на частоте дискретизации более 7 МГц.

Передискретизация с помощью полифазных фильтров

Метод передискретизации с помощью полифазных фильтров аналогичен предыдущему, с тем отличием, что в нём вместо одного фильтра, работающего на высокой частоте дискретизации, используется несколько фильтров, работающих на низкой частоте. При этом удаётся добиться сокращения количества необходимых вычислений, так как для каждого отсчёта необходимо вычислить выход только одного из этих фильтров.

Передискретизация с помощью дискретного преобразования Фурье

Передискретизация с помощью ДПФ используется для повышения частоты дискретизации в целое или дробное число раз. Алгоритм работает только с конечными отрезками сигнала. Пусть N — начальное число отсчётов, M — число отсчётов в передискретизованном сигнале. Алгоритм включает в себя следующие операции:

1. Вычисляется ДПФ исходного сигнала (чаще всего по алгоритму быстрого преобразования Фурье).

2. В середину спектра вставляется необходимое число нулевых компонент:

2.1. если N нечётное:
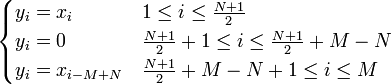
\begin{cases} y_i=x_i & 1 \le i \le \frac{N+1}{2} \\ y_i=0 & \frac{N+1}{2}+1 \le i \le \frac{N+1}{2}+M-N\\ y_{i}=x_{i-M+N} & \frac{N+1}{2}+M-N+1 \le i \le M \end{cases}
2.2. если N чётное
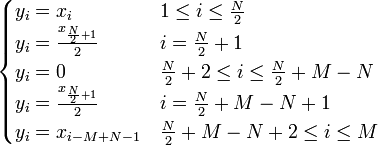
\begin{cases} y_i=x_i & 1 \le i \le \frac{N}{2} \\ y_i=\frac{x_{\frac{N}{2}+1}}{2} & i=\frac{N}{2}+1 \\ y_{i}=0 & \frac{N}{2}+2 \le i \le \frac{N}{2}+M-N \\ y_i=\frac{x_{\frac{N}{2}+1}}{2} & i=\frac{N}{2}+M-N+1 \\ y_i=x_{i-M+N-1} & \frac{N}{2}+M-N+2 \le i \le M \end{cases}

3. Вычисляется обратное ДПФ.

Ограничением этого метода является то, что, как и любой метод, основанный на ДПФ, он даёт точный результат только для периодического дискретного сигнала. Для обработки непериодических сигналов необходимо применять оконные функции и выбирать отрезки сигнала для вычисления ДПФ таким образом, чтобы их концы перекрывались.

Применения

Широко применяется как аппаратная (на основе специализированных микросхем или FPGA), так и программная (на базе процессоров общего назначения или сигнальных процессоров) реализация алгоритмов передискретизации.

Выбор конкретной реализации алгоритма передискретизации является результатом компромисса между качеством преобразования и его вычислительной сложностью. Основным параметром, влияющим на эти характеристики, является близость используемых цифровых фильтров к идеальным. Более качественные фильтры требуют больше ресурсов для вычисления.

На практике передискретизация в большинстве случаев ведёт к потере информации о сигнале по следующим причинам:

  • при уменьшении частоты дискретизации сигнал необходимо отфильтровать с целью удаления высокочастотных спектральных составляющих, которые не соответствуют условиям теоремы Котельникова для новой частоты дискретизации;
  • вычисления, производимые над цифровыми (квантованными по уровню) сигналами ведут к необратимым ошибкам округления.

Таким образом, при увеличении частоты дискретизации с последующим уменьшением её до исходного значения качество сигнала будет потеряно (если только высокая частота не кратна низкой).

При обработке звука

Оборудование, предназначенное для воспроизведения цифрового звука, как правило, рассчитано на вполне определённую частоту дискретизации сигнала непосредственно перед цифро-аналоговым преобразованием (для многих звуковых карт эта частота составляет 48000 Гц). Все звуковые сигналы с другими частотами дискретизации должны быть рано или поздно передискретизованы.

Передискретизация звукового сигнала на требуемую частоту может осуществляться мультимедиа-проигрывателем, драйвером звуковой карты или самой звуковой картой. Использование программы-проигрывателя для данной цели может быть оправдано, если есть желание избежать аппаратной передискретизации звука (или передискретизации драйвером) с целью добиться более высокого качества (при большей загрузке центрального процессора). Однако программная передискретизация воспроизводимого материала на частоту, отличную от частоты, поддерживаемой оборудованием, не имеет смысла и приводит только к потере качества сигнала.

Существуют программные передискретизаторы звуковых сигналов с открытым исходным кодом:

  • SRC (Secret Rabbit Code) или libsamplerate[1] — существует плагин для [2] — существуют плагины для foobar2000.

Также передискретизация поддерживается программами-редакторами звука.

При обработке изображений

Изменение разрешения является одной из распространённых операций обработки изображений. Передискретизация, приближенная к идеальной (с минимизацией наложения спектров), не всегда является желательной. Выбор фильтра для передискретизации является результатом компромисса между типом и выраженностью артефактов и вычислительной сложностью преобразования (актуальной для приложений реального времени).

Типичные артефакты при изменении разрешения изображения:

Для передискретизации изображений применяется большое число фильтров, которые можно классифицировать следующим образом[3]:

  1. Фильтры интерполяционного типа, обладающие сравнительно узкой импульсной характеристикой. К ним относятся, в частности, треугольный фильтр, производящий билинейную интерполяцию и полином Лагранжа, с помощью которого можно реализовать бикубическую интерполяцию. Применение таких фильтров позволяет осуществить передискретизацию изображения достаточно быстро.
  2. Фильтры с колоколообразной характеристикой, такие как фильтр Гаусса. Эти фильтры хорошо справляются с пикселизацией, звоном и алиасингом, а также отфильтровывают высокочастотные шумы. Их недостаток — заметное размытие изображения.
  3. Оконные sinc-фильтры. Sinc-фильтр — это идеальный фильтр нижних частот. Как говорилось выше, он не может быть реализован. Однако если частотную характеристику sinc-фильтра умножить на оконную функцию, получится реализуемый фильтр с хорошими спектральными свойствами. При применении данных фильтров к изображениям удаётся сохранить относительно высокую чёткость (даже при увеличении разрешения), но может быть сильно заметен эффект звона. Одним из наиболее часто применяемых фильтров данного типа является фильтр Ланцоша.

При обработке радиосигналов

При демодуляции цифровых сигналов желательно, чтобы частота дискретизации сигнала была кратна его скорости манипуляции (иначе говоря, чтобы на каждый символ приходилось одинаковое число отсчётов сигнала). Однако частота дискретизации входного сигнала с АЦП, как правило, фиксирована, а скорость манипуляции может меняться. Решением является передискретизация сигнала.

Примечания

  1. ↑ Secret Rabbit Code (aka libsamplerate)
  2. ↑ Shibatch Audio Tools
  3. ↑ Resize and Scaling на сайте программы

    Литература

    1. Richard G. Lyons Understanding digital signal processing. — Addison Wesley, 1997. — 517 с. — ISBN 0-201-63467-8
    2. Л. Рабинер, Б. Гоулд Теория и применение цифровой обработки сигналов = Theory and Application of Digital Signal Processing. — М.: Мир, 1978. — 848 с.
    3. Романюк Ю.А. Основы цифровой обработки сигналов. В 3-х ч. Ч.1. Свойства и преобразования дискретных сигналов: Учебное пособие. — М.: МФТИ, 2005. — 332 с. — ISBN 5-74-170144-2

    Wikimedia Foundation. 2010.

  • Рерихианство
  • Ресдайн

Что такое DPI и ресемплинг

Что такое DPI и ресемплинг

Вернуться к разделу «Материалы по сканированию и оцифровке бумажных книг».

Что такое DPI и ресемплинг

По материалам книги Сибил и Эмиль Айриг
«Сканирование — профессиональный подход».

Введение

Создавая электронные версии бумажных книг (в формате DjVu), необходимо знать некоторые основные базовые понятия из области сканирования и преобразования изображений. Это поможет создавать электронные книги лучшего качества, а также находить общий язык с единомышленниками.

К таким базовым понятиям относятся, например, «DPI» и «ресемплинг».

Виды разрешения

Исходная чёрно-белая или цветная страница бумажной книги имеет непрерывный тон — смежные цвета или оттенки плавно переходят друг в друга. Однако компьютеры не могут воспринять ничего непрерывного, для того, чтобы поместить в компьютер цифровую копию бумажной страницы, её нужно разбить на дискретные единицы — пикселы.

Пиксел, или элемент изображения, является минимальной единицей измерения данных изображения. Каждый пиксел имеет однородный цвет. Компьютер же воспроизводит цифровые изображения путём моделирования непрерывных тонов с помощью этих маленьких дискретных элементов.

Понятие «разрешение» имеет несколько различных значений:

  • Плотность информации, которую сканирующее устройство может вводить на дюйм (входное разрешение, или разрешение при сканировании).

  • Полный объём информации в растровом изображении (разрешение изображения).

  • Число дискретных горизонтальных и вертикальных элементов, которые может одновременно отображать компьютерный монитор (экранное разрешение).

Важно различать эти значения.

Во всех случаях разрешение описывает либо общее количество, либо плотность графической информации в пикселях на единицу площади цифрового изображения (при масштабе 100%).

Единицы разрешения

Все оцифровывающие устройства — сканеры, цифровые фото- и видеокамеры и т.д., имеют несколько общих функций:

— Преобразуют аналоговую (реальную) информацию в цифровые данные, которые могут использоваться компьютером.

— Генерируют растровые изображения, состоящие из матриц чёрно-белых, серых полутоновых или цветных пикселов (элементов изображения).

Примечание: Растровые изображения часто называют также битовыми изображениями, но между ними имеется важное различие. Термин «растровое изображение» описывает состоящие из пикселов изображения независимо от их цветовых характеристик. Битовые изображения (bitmap) содержат только чёрно-белые пикселы.

— Считывают или производят выборку исходного изображения, измеряя значения градаций серого или цвета для каждого элемента выборки.

Входное разрешение сканера описывает плотность, с которой сканирующее устройство производит выборку информации в данной области (обычно на дюйм или на сантиметр) в ходе оцифровки.

PPI (пикселы на дюйм)

Программные интерфейсы многих оцифровывающих устройств описывают частоту дискретизации в ppi или пикселах на дюйм. Многие цифровые фото- и видеокамеры имеют единое фиксированное входное разрешение, а в сканерах обычно имеется диапазон возможных разрешений. При этом с ростом частоты дискретизации сканирующего устройства размер генерируемых пикселов уменьшается. Это легко понять, если мысленно попробовать упаковать 50 сардин в банку, предназначенную для 25 сардин стандартного размера. 50 сардин поместятся в ней только в том случае, если они вдвое меньше стандартных 25.

Термин «пикселы» может также указывать полный объём информации, которую оцифрованное изображение содержит по горизонтали и по вертикали (например, 800 х 400 пикселов). Этот вариант использования описывает скорее разрешение изображения, чем входное разрешение. Наконец, многие используют термин «пикселы» для описания экранного разрешения — числа горизонтальных и вертикальных дискретных визуальных элементов, которые может отображать компьютерный монитор, — например, 1024 х 768 пикселов. В отличие от размера пикселов, которые вводит сканирующее устройство, размер пикселов на компьютерном мониторе остается постоянным. Следовательно, монитор отображает все пикселы каждого изображения с единым фиксированным размером. Это объясняет, почему изображение, сканированное с разрешением 300 ppi, отображается на мониторе компьютера Macintosh с разрешением всего 72 ppi и выглядит намного большим на экране, чем в печати.

DPI (точки на дюйм) Многие журналисты и некоторые программные интерфейсы сканирования всё ещё используют термин dpi (точки на дюйм) для описания разрешения при сканировании, или входного разрешения. Однако с технической точки зрения число точек на дюйм описывает выходное разрешение, представляя горизонтальную плотность меток, которые имиджсеттеры и лазерные принтеры типа PostScript делают в ходе печати. Будьте внимательны и не путайте эти два термина - подразумевайте «ppi» всякий раз, когда видите в интерфейсе сканера «dpi».

Виды разрешения сканера

Одним из важнейших критериев при выборе сканера или бесплёночной цифровой камеры должно быть максимальное входное разрешение конкретного сканирующего устройства. Изготовители определяют это максимальное значение двумя способами: как оптическое разрешение или как интерполированное разрешение.

Оптическое разрешение

Оптическое разрешение описывает объём реальной информации, который может ввести оптическая система сканирующего устройства. Факторы, определяющие оптическое разрешение, зависят от типа оцифровывающего устройства. В планшетных, листовых, ручных сканерах и многих сканерах для обработки слайдов и диапозитивов максимальное оптическое разрешение зависит от трёх факторов:

а). Количества отдельных датчиков в линейке ПЗС в перемещающейся сканирующей головке. ПЗС («приборы с зарядовой связью») — это твердотельный электронный компонент, состоящий из множества крошечных датчиков, которые регистрируют аналоговый электрический заряд, пропорциональный интенсивности падающего на них света).

b). Максимальной ширины оригинала, который может обработать сканер. Например, линейка ПЗС из 5100 ячеек в сканере, принимающем оригиналы шириной до 8,5 дюймов, позволяет получить максимальное горизонтальное оптическое разрешение 600 ppi.

с). Расстояние смещения сканирующей головки по оригинальному изображению. Оно определяет вертикальное разрешение, которое может быть выше, чем горизонтальное.

В цифровых фото- и видеокамерах, а также некоторых сканерах для обработки диапозитивов обычно используется прямоугольная матрица (а не перемещающаяся линейка) ПЗС, определяющая общее число пикселов, которые могут вводиться по любому направлению.

Примечание: Изготовители планшетных сканеров часто приводят вертикальное оптическое разрешение вдвое большее, чем горизонтальное, например, 600 х 1200 ppi. Механизм перемещения этих сканеров отрабатывает «полушаги», сдвигая головку на половину пиксела за шаг, что приводит к перекрыванию пикселов. Для получения окончательного значения уровней цвета или серого сканер должен выполнить математическое усреднение. «Истинное» оптическое разрешение этих сканеров ниже (например, 600 х 600 ppi), оно также приводит к наилучшей чёткости изображения и уменьшает шум.

Интерполированное разрешение

С другой стороны, максимальное интерполированное разрешение устройства представляет кажущийся объём информации, который сканер может вводить с помощью алгоритмов реализуемых процессором и/или программным обеспечением. Алгоритмы интерполяции не добавляют реальных деталей в изображение, они лишь добавляют пикселы, просто усредняя значения цвета или градаций серого в смежных пикселах и вставляя между ними новый пиксел. Интерполированное разрешение часто в два или более раз выше, чем оптическое.

Остерегайтесь маркетинговых уловок — там, где важно качество, имеет значение только оптическое разрешение. Интерполяция добавляет «псевдоинформацию», которая может быть приемлема для дешёвых публикаций или компаний с ограниченными средствами, но никогда не будет работать в цветных изображениях большого формата, где жизненно важны детальная структура и широкий тоновый диапазон. Интерполяция также приводит к «смягчению» изображения и необходимости более серьёзного увеличения контраста на границах между областями. Если вы часто сканируете для высококачественной печати, то лишь выиграете, вложив дополнительные деньги в сканер с более высоким оптическим разрешением.

Атрибуты пикселов

Каждый пиксел растрового изображения имеет четыре основные характеристики — размер, тоновое значение, глубину цвета и позицию. Эти четыре атрибута определяют разрешение, причем каждый это делает по-своему.

Размер пиксела (физический размер)

Все пикселы одного изображения имеют одинаковый размер. Изначально размер пиксела определён разрешением, с которым было сканировано или оцифровано изображение. Так, разрешение в 600 пикселов на дюйм указывает, что размер каждого пиксела равен 1/600 дюйма. При более высоком входном разрешении генерируются пикселы меньшего размера, что, в свою очередь, обеспечивает большее количество информации и вероятных деталей на единицу измерения, а также большую плавность тоновых переходов. При более низком разрешении пикселы имеют больший размер, наблюдается меньше деталей на единицу измерения и изображение имеет мозаичную структуру. Размер и количество пикселов определяют количество информации, содержащейся в изображении. Можно изменить размер пиксела в любой момент производственного процесса, изменив разрешение. При этом если изображение выводится на печать, то автоматически изменится размер отпечатка.

Значение цвета или тона (номер цвета)

Сканеры и цифровые камеры присваивают определенное значение цвета или оттенка серого каждому пикселу изображения. Эффект непрерывности тона возникает из-за того, что пикселы очень малы и соседние пикселы только немного отличаются друг от друга по цвету или тону. Изображения, сканированные с помощью устройств с широким динамическим диапазоном, наилучшим образом передают непрерывность тона. Динамический диапазон — это аппаратная чувствительность сканера к тончайшим цветовым оттенкам на сканируемом изображении. Динамический диапазон зависит от битовой разрядности сканера, соотношения сигнал/шум, типа лампы подсветки, непрерывной коррекции тона и т.д. Чем дороже сканер, тем шире его динамический диапазон.

Глубина цвета (битовая разрядность)

Конечно, каждому отдельному пикселу можно приписать лишь одно значение, но существует такая характеристика, как разрядность битового представления цвета (или глубина цвета) оцифровывающего устройства, определяющая количество возможных цветов или тонов. Каждый дополнительный бит приводит к росту размера графических файлов и, соответственно, потребности в свободном месте на жёстком диске, хотя при этом увеличивается гладкость переходов между смежными цветами и тонами.

Позиция пиксела (координаты)

Растровое изображение представляет собой сетку дискретных пикселов, каждый из которых имеет определенные горизонтальные и вертикальные координаты внутри сетки. В большинстве основных программ редактирования изображений можно узнать координаты любого пиксела, поместив над ним инструмент Eyedropper (пипетка). Физические размеры сетки, определяемой общим количеством пикселов и разрешением, задают относительное положение пикселов.

Повторная выборка изображений, или ресемплинг

Большинство цифровых изображений имеют следующие размерные характеристики:

1. Физические размеры (длина и ширина) в дюймах (миллиметрах, точках и т.д.). Это, в общем-то, довольно условная величина, которая показывает, какую площадь экрана монитора или страницы при печати на принтере будет занимать данное изображение при масштабе 100%.

2. Печатные (пиксельные) размеры (длина и ширина) в пикселях (процентах).

3. Разрешение (пикселы/дюймы, пикселы/сантиметры). Это определённое соотношение предыдущих величин.

Все 3 вида этих характеристик являются переменными величинами.

Многие профессионалы-графики не понимают, чем изменение физических размеров изображения отличается от повторной выборки. При изменении физических размеров пропорционально изменяется разрешение при неизменном информационном содержании (размере файла). С другой стороны, повторная выборка, или ресемплинг, всегда связана с изменением объёма информации в изображении и может включать независимые изменения любой из трёх (или всех) размерных характеристик файлов. Ресемплинг всегда изменяет количество пикселей и размер файла. Поскольку это влечет за собой интерполяцию и усреднение, повторную выборку следует использовать только в том случае, если сканированное изображение оригинала содержит или слишком много, или слишком мало информации для высококачественного вывода.

Профессионалы художественной графики используют термин субдискретизация (downsampling), или уменьшение размеров изображения, для описания уменьшения числа пикселов в изображении и термин интерполяция (upsampling), или увеличение размеров изображения, чтобы описать увеличение числа пикселов.

Усреднение значений пиксела происходит в обоих случаях. При правильном проведении субдискретизации устраняются ненужные детали, в то время как при увеличении пиксельных размеров изображения добавляются псевдодетали. Оба способа являются компромиссными и воздействуют на качество изображения, но субдискретизация редко приводит к видимому ухудшению качества изображения, потому что она обычно сопровождается уменьшением размера изображения, а увеличение пиксельных размеров изображения почти всегда приводит к ухудшению изображения.

Повторную выборку изображения можно провести с помощью двух базовых методов — ручного масштабирования или через диалоговое окно типа Image Size (размер изображения), где в цифровой форме определяется изменение разрешения или размеров. Второй метод намного точнее и дает возможность точно проконтролировать количество добавляемой или отбрасываемой информации.

Чем руководствоваться при повторной выборке

Используйте алгоритм повторной выборки самого высокого качества, поддерживаемый вашим пакетом редактирования изображений, чтобы минимизировать видимые потери. Так, например, Photoshop предлагает выбор трех опций: Bicubic (бикубическая), Bilinear (билинейная) и Nearest Neighbor (ближайший сосед). Опция Bicubic выполняет наиболее сложное усреднение значений пикселов; метод Bilinear производит более мягкий просмотр, уменьшающий вероятность артефактов; и Nearest Neighbor выполняется быстро, но приводит к более видимой ступенчатости изображения.

Не производите повторную выборку одного изображения более, чем один раз. Каждое изменение объёма информации в изображении связано с потерями, так что не стоит разбираться в причинах ухудшения второго, третьего (и далее) поколения.

Субдискретизация более надежна, чем увеличение пиксельных размеров изображения, с точки зрения уменьшения потерь качества изображения, особенно если физический размер выводимого изображения уменьшается. Детали, потерянные при проведении субдискретизации, все равно нельзя было вывести на печать.

Пример ресемплинга

Как уже было сказано, изменение разрешения не обязательно предполагает ресемплинг. Всего возможны 2 варианта:

1. Изменение разрешения с ресемплингом. При этом всегда изменяется количество пикселей и размер файла. Это часто связано с риском ухудшения качества изображения. Подварианты:

a). При чрезмерном уменьшении разрешения (с понижающим ресемплингом) может возникнуть угроза целостности и детальности изображения («нарастание мозаичности»).

b). При сильном увеличении разрешения (с повышающим ресемплингом) может ухудшиться чёткость и проработка деталей изображения (т.к. процесс интерполяции не добавляет «реальных» деталей). Этот дефект можно частично компенсировать с помощью фильтра наложения нерезкой маски. (Соблюдайте осторожность при наложении нерезкой маски на изображения низкого разрешения — во всех случаях, кроме светлых изображений, это может привести к нежелательным эффектам возникновения ореола).

2. Изменение разрешения без ресемплинга не меняет информационное содержание файла, а только автоматически и пропорционально меняет физические размеры изображения (в мм) так, чтобы оставить неизменными размеры в пикселях по длине и ширине. Можно наоборот — поменять физические размеры изображения — при этом пропорционально изменится разрешение. В любом случае количество пикселей, размер и качество изображения не изменятся.

Рассмотрим примеры повышения и понижения разрешения изображения с ресемплингом и без него (в Adobe Photoshop 5.0):

Исходная картинка:

Файл в формате Color TIFF LZW.
Пример 1. Повышение разрешения (в 2 раза):

a). Без ресемплинга:

Размер файла не изменился.

b). С ресемплингом:

Размер файла возрос в 2,87 раза (примерно в 3 раза).
Пример 2. Понижение разрешения (в 2 раза):

a). Без ресемплинга:

Размер файла не изменился.

b). С ресемплингом:

Размер файла уменьшился в 3,36 раза (примерно в 3 раза).
Ссылки

Связь между ppi, lpi и dpi

DPI в Википедии

Разрешение (компьютерная графика) в Википедии

Автор: monday2000.

24 мая 2006 г.

E-Mail  (monday2000 [at] yandex.ru)


5 главных алгоритмов сэмплинга / Habr

Работа с данными — работа с алгоритмами обработки данных.

И мне приходилось работать с самыми разнообразными на ежедневной основе, так что я решил составить список наиболее востребованных в серии публикаций.

Эта статья посвящена наиболее распространённым способам сэмплинга при работе с данными.


Допустим, если вы хотите сделать выборку, где каждый элемент имеет равную вероятность быть выбранным.

Ниже мы выбираем 100 таких элементов из датасета.

sample_df = df.sample(100)



Допустим, нам нужно оценить среднее количество голосов за каждого кандидата на выборах. Голосование проходит в трёх городах:

В городе A живёт 1 миллион рабочих

В городе B живёт 2 миллиона художников

В городе C живёт 3 миллиона пенсионеров

Если мы попытаемся взять равновероятные выборки по 60 человек среди всего населения, то они наверняка будут разбалансированы относительно разных городов, а потому предвзяты, что приведёт к серьёзной ошибке в предсказаниях.

Если же мы специально сделаем выборку из 10, 20 и 30 человек из городов A, B и C соответственно, то ошибка будет минимальной.

На Python это можно сделать так:

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y,
                                                    stratify=y, 
                                                    test_size=0.25)



Мне нравится такая формулировка задачи:

Допустим, у вас есть поток элементов большого неизвестного размера, по которым можно итерироваться только один раз.

Создайте алгоритм, произвольно выбирающий элемент из потока так, как если бы любой элемент мог быть выбран с равной вероятностью.

Как это сделать?

Допустим, нам надо выбрать 5 объектов из бесконечного потока, так чтобы каждый элемент в потоке мог быть выбран равновероятно.

import random
def generator(max):
    number = 1
    while number < max:
        number += 1
        yield number
# Создаём генератор потока
stream = generator(10000)
# Делаем резервуарный сэмплинг
k=5
reservoir = []
for i, element in enumerate(stream):
    if i+1<= k:
        reservoir.append(element)
    else:
        probability = k/(i+1)
        if random.random() < probability:
            # Сохраняем элемент из потока, удаляя ранее добавленный 
             reservoir[random.choice(range(0,k))] = element
print(reservoir)
------------------------------------
[1369, 4108, 9986, 828, 5589]

Доказать, что каждый элемент мог быть выбран равновероятно можно математически.

Как?

Когда дело доходит до математики, лучше попытаться начать решение с небольшого частного случая.

Так что давайте рассмотрим поток, состоящий из 3-х элементов, где нам нужно выбрать только 2.

Мы видим первый элемент, сохраняем его в списке, так как в резервуаре ещё есть место. Мы видим второй элемент, сохраняем его в списке, так как в резервуаре ещё есть место.

Мы видим третий элемент. Здесь становится интереснее. Мы сохраним третий элемент с вероятностью 2/3.

Давайте теперь посмотрим итоговую вероятность первого элемента быть сохранённым:

Вероятность вытеснения первого элемента из резервуара равна вероятности третьего элемента быть выбранным, умноженной на вероятность что именно первый элемент из двух будет выбран для вытеснения. То есть:

2/3 * 1/2 = 1/3 

То есть конечная вероятность первого элемента быть сохранённым:

1 — 1/3 = 2/3 

Абсолютно такую же логику можно применить и для второго элемента, распространив её в дальнейшем на большее количество элементов при увеличении резервуара.

То есть каждый элемент будет сохранён с вероятностью 2/3 или в общем случае k/n.




Источник

Слишком часто в жизни встречаются несбалансированные наборы данных.

Широко применяемый в таком случае способ называется ресэмплинг (в русском переводе иногда говорят «передискретизация» — прим. перев.). Его суть заключается либо в удалении элементов из слишком большого набора (андерсэмплинг) и/или добавлении большего количества элементов в недостаточно большой набор (оверсэмплинг).

Давайте для начала создадим какие-нибудь несбалансированные наборы.

from sklearn.datasets import make_classification
X, y = make_classification(
    n_classes=2, class_sep=1.5, weights=[0.9, 0.1],
    n_informative=3, n_redundant=1, flip_y=0,
    n_features=20, n_clusters_per_class=1,
    n_samples=100, random_state=10
)
X = pd.DataFrame(X)
X['target'] = y

Теперь случайный андерсэмплинг и оверсэмплинг мы можем выполнять вот так:

num_0 = len(X[X['target']==0])
num_1 = len(X[X['target']==1])
print(num_0,num_1)
# случайный андерсэмплинг
undersampled_data = pd.concat([ X[X['target']==0].sample(num_1) , X[X['target']==1] ])
print(len(undersampled_data))
# случайный оверсэмплинг
oversampled_data = pd.concat([ X[X['target']==0] , X[X['target']==1].sample(num_0, replace=True) ])
print(len(oversampled_data))
------------------------------------------------------------
OUTPUT:
90 10
20
180


imbalanced-learn (imblearn) — это питоновская библиотека для борьбы с проблемами несбалансированных наборов данных.

Она содержит несколько различных методов для проведения ресэмплинга.


a. Андерсэмплинг с использованием Tomek Links:

Один из предоставляемых методов называется «Tomek Links». «Links» в данном случае — пары элементов из разных классов, находящиеся поблизости.

Используя алгоритм мы в конечном итоге удалим элемент пары из большего набора, что позволит классификатору отработать лучше.


Источник
from imblearn.under_sampling import TomekLinks

tl = TomekLinks(return_indices=True, ratio='majority')
X_tl, y_tl, id_tl = tl.fit_sample(X, y)

b. Оверсэмплинг со SMOTE:

В SMOTE (Способ Передискретизации Синтезированных Меньшинств) мы создаём элементы в непосредственной близости от уже существующих в меньшем наборе.


Источник
from imblearn.over_sampling import SMOTE

smote = SMOTE(ratio='minority')
X_sm, y_sm = smote.fit_sample(X, y)

Но в imblearn существуют и другие способы андерсэмплинга (Cluster Centroids, NearMiss, и т.д.) и оверсэмплинга (ADASYN и bSMOTE), которые тоже могут пригодиться.



Алгоритмы — кровь науки о данных.

Сэмплинг — одна из важнейших областей в работе с данными и выше приведён только поверхностный обзор.

Хорошо выбранная стратегия сэмплинга может потянуть весь проект за собой. Выбранная плохо приведёт к ошибочным результатам. Поэтому выбор нужно делать с умом.

Передискретизация (oversampling) | Основы электроакустики

Это дискретизация сигнала с частотой, превышающей основную частоту дискретизации. Передискретизации может быть аналоговой, когда с повышенной частотой делаются выборки исходного сигнала, или цифровой, когда между уже существующими цифровыми отсчетами вставляются дополнительные, рассчитанные путем интерполяции. Другой способ получения значений промежуточных отсчетов состоит во вставке нулей, после чего вся последовательность подвергается цифровой фильтрации. В АЦП используется аналоговая передискретизация, в ЦАП — цифровая.

 Передискретизация используется для упрощения конструкций АЦП и ЦАП. По условиям задачи на входе АЦП и выходе ЦАП должен быть установлен аналоговый фильтр с АЧХ, линейной в рабочем диапазоне и круто спадающей за его пределами. Реализация такого аналогового фильтра весьма сложна; в то же время при повышении частоты дискретизации вносимые ею отражения спектра пропорционально отодвигаются от основного сигнала, и аналоговый фильтр может иметь гораздо меньшую крутизну среза.

 Другое преимущество передискретизации состоит в том, что ошибки амплитудного квантования (шум дробления), распределенные по всему спектру квантуемого сигнала, при повышении частоты дискретизации распределяются по более широкой полосе частот, так что на долю основного звукового сигнала приходится меньшее количество шума. Каждое удвоение частоты снижает уровень шума квантования на 3 дБ; поскольку один двоичный разряд эквивалентен 6 дБ шума, каждое учетверение частоты позволяет уменьшить разрядность преобразователя на единицу.

 Передискретизация вместе с увеличением разрядности отсчета, интерполяцией отсчетов с повышенной точностью и выводом их на ЦАП надлежащей разрядности позволяет несколько улучшить качество восстановления звукового сигнала. По этой причине даже в 16-разрядных системах нередко применяются 18- и 20-разрядные ЦАП с передискретизацией. АЦП и ЦАП с передискретизацией за счет значительного уменьшения времени преобразования могут обходиться без схемы выборки-хранения.

Передискретизация с помощью цифровых фильтров  Выбор фильтра для передискретизации Выбор функции h(t) обуславливается компромиссом между качеством передискретизации (то есть близости её к идеальной) и вычислительной сложностью этого процесса. В принципе, для передискретизации может быть использован любой фильтр нижних частот с необходимой частотой среза. КИХ-фильтры применяются для этих задач чаще, чем БИХ-фильтры, из-за возможности построения КИХ-фильтров с линейной фазо-частотной характеристикой.

Чаще всего при передискретизации используются следующие классы цифровых фильтров:

  • 1. Фильтры, построенные, исходя из критерия близости частотной характеристики к частотной характеристике идеального фильтра нижних частот:
  •  Оконные sinc-фильтры (англ. windowed-sinc filters) — их импульсная характеристика h(t) получается путём умножения импульсной характеристики идеального ФНЧ на оконную функцию,
  •  Равноволновые фильтры Чебышёва.
  • 2. Классические способы интерполяции функций (часто применяются для изображений):
  •  Линейные интерполяторы,
  •  Интерполяторы Лагранжа (частный случай — кубическая интерполяция).
  • 3. CIC-фильтры (каскады гребёнчатых фильтров и интеграторов).Этот класс фильтров не использует умножений при вычислении, что позволяет сэкономить вычислительные ресурсы.

Процесс уменьшения частоты дискретизации сигнала называется децимацией. Иногда этот термин употребляют только для уменьшения частоты дискретизации в целое число раз (далее N). Децимация цифрового сигнала с целым коэффициентом производится в два этапа:

  •   Цифровая фильтрация сигнала с целью удаления высокочастотных составляющих, не удовлетворяющих условиям теоремы Котельникова для новой частоты дискретизации;
  • Удаление (отбрасывание) лишних отсчетов (сохраняется каждый N-й отсчёт).

В англоязычной литературе второй из этих этапов иногда обозначают термином downsampling. В обиходе этот термин может употребляться как синоним термина «децимация».
Первый этап необходим для исключения наложения спектров, природа которого аналогична наложению спектров при первоначальной дискретизации аналогового сигнала. Наложение спектров особенно заметно на тех участках сигнала, которые содержат значительные высокочастотные спектральные составляющие. Так, на приведённых в начале статьи фотографиях небо практически не подвергнулось наложению спектров, но эффект становится заметным, если обратить внимание на резкие переходы.
При программной реализации алгоритма децимации «лишние» отсчёты не удаляются, а просто не вычисляются. При этом число обращений к цифровому фильтру уменьшается в N раз. При аппаратной реализации экономии можно достичь путём использования полифазных фильтров. Интерполяцией называют увеличение частоты в целое или дробное число раз путем вычисления промежуточных отсчетов по уже имеющимся. Идеальная интерполяция позволяет точно восстановить значения сигнала в промежуточных отсчётах.
Стандартный алгоритм интерполяции сигнала с целым коэффициентом заключается в следующем:

  •    вставка нулевых отсчетов на место отсчетов, которые необходимо вычислить;
  •    фильтрация сигнала цифровым фильтром нижних частот для того, чтобы убрать спектральные составляющие сигнала, которых заведомо не могло быть в исходном сигнале согласно теореме Котельникова; выход фильтра умножается на коэффициент интерполяции для нормирования.

В англоязычной литературе первый из этих этапов иногда обозначается термином upsampling. При этом в обиходе этот термин может употребляться как синоним термина «интерполяция».
При программной реализации интерполяции нулевые отсчёты не участвуют в вычислении выходного сигнала фильтра, что позволяет оптимизировать процесс вычисления. При аппаратной реализации для экономии ресурсов возможно использование полифазных фильтров.

Комбинация интерполяции и децимации  Для того, чтобы изменить частоту дискретизации сигнала в \frac{M}{N} раз (M и N — целые положительные числа), можно сначала увеличить частоту дискретизации в M раз, а затем уменьшить её в N раз. Фильтрацию сигнала достаточно произвести всего один раз — между интерполяцией и децимацией. Недостатком данного метода является необходимость фильтрации сигнала на повышенной в M раз частоте дискретизации, что требует значительных вычислительных ресурсов. При этом соответствующая частота может во много раз превосходить как исходную, так и окончательную частоту передискретизации, особенно если M и N — близкие большие числа. Так, например, при передискретизации звукового сигнала с 44100 Гц до 48000 Гц этим методом необходимо увеличить частоту дискретизации в 160 раз до 7056000 Гц и затем уменьшить её в 147 раз до 48000 Гц. Таким образом, в данном примере вычисления приходится производить на частоте дискретизации более 7 МГц.

Метод передискретизации с помощью полифазных фильтров аналогичен предыдущему, с тем отличием, что в нём вместо одного фильтра, работающего на высокой частоте дискретизации, используется несколько фильтров, работающих на низкой частоте. При этом удаётся добиться сокращения количества необходимых вычислений, так как для каждого отсчёта необходимо вычислить выходной сигнал только одного из этих фильтров. Полифазный фильтр представляет собой набор небольших фильтров, работающих параллельно, каждый из которых обрабатывает только подмножество отсчётов сигнала (если всего имеется N фильтров, каждый фильтр будет обрабатывать только каждый N-й отсчёт).Полифазные фильтры применяются для передискретизации как с целым, так и с дробным коэффициентом.

Передискретизация с помощью дискретного преобразования Фурье Передискретизация с помощью ДПФ используется для повышения частоты дискретизации в целое или дробное число раз. Алгоритм работает только с конечными отрезками сигнала. Пусть N — начальное число отсчётов, M — число отсчётов в передискретизованном сигнале. Алгоритм включает в себя следующие операции:
1. Вычисляется ДПФ исходного сигнала (чаще всего по алгоритму быстрого преобразования Фурье).
2. В середину спектра вставляется необходимое число нулевых компонент:
    2.1. если N нечётное:  \begin{cases} y_i=x_i & 1 \le i \le \frac{N+1}{2} \\ y_i=0 & \frac{N+1}{2}+1 \le i \le \frac{N+1}{2}+M-N\\ y_{i}=x_{i-M+N} & \frac{N+1}{2}+M-N+1 \le i \le M \end{cases}
    2.2. если N чётное:   \begin{cases} y_i=x_i & 1 \le i \le \frac{N}{2} \\ y_i=\dfrac{x_{\frac{N}{2}+1}}{2} & i=\frac{N}{2}+1 \\ y_{i}=0 & \frac{N}{2}+2 \le i \le \frac{N}{2}+M-N \\ y_i=\dfrac{x_{\frac{N}{2}+1}}{2} & i=\frac{N}{2}+M-N+1 \\ y_i=x_{i-M+N} & \frac{N}{2}+M-N+2 \le i \le M \end{cases}
3. Вычисляется обратное дискретное преобразование Фурье с нормировкой. Любой метод, основанный на ДПФ, предназначен в первую очередь для периодических дискретных сигналов. Для обработки непериодических сигналов необходимо выбирать отрезки сигнала для вычисления ДПФ таким образом, чтобы их концы перекрывались. Широко применяется как аппаратная (на основе специализированных микросхем или FPGA, так и программная (на базе процессоров общего назначения  или сигнальных процессоров реализация алгоритмов передискретизации.

Выбор конкретной реализации алгоритма передискретизации является результатом компромисса между качеством преобразования и его вычислительной сложностью. Основным параметром, влияющим на эти характеристики, является близость используемых цифровых фильтров к идеальным. Более качественные фильтры требуют больших ресурсов для вычисления. 

На практике передискретизация в большинстве случаев ведёт к потере информации о сигнале по следующим причинам:

  •     при уменьшении частоты дискретизации сигнал необходимо отфильтровать с целью удаления высокочастотных спектральных составляющих, которые не соответствуют условиям теоремы Котельникова для новой частоты дискретизации;
  •     неизбежная неидеальность применяемых цифровых фильтров;
  •     вычисления, производимые над цифровыми (квантованными по уровню) сигналами ведут к необратимым ошибкам округления.

Таким образом, при увеличении частоты дискретизации с последующим уменьшением её до исходного значения качество сигнала будет потеряно (если только высокая частота не кратна низкой).

 

Ресемплинг (статистика) — это… Что такое Ресемплинг (статистика)?

В статистике, Ресемплинг — передискретизация — группа методов, выполняющих одно из следующих действий:

Jackknife

Jackknifine похож на бутстреппинг, используется для получения статистических выводов об оценке смещения и для оценки стандартной ошибки (дисперсия) статистики, когда случайная выборка наблюдений используются для расчета. Основная идея Jackknife оценки дисперсии заключается в систематическом пересчете статистической оценки убирая одно или несколько наблюдений на время от выборочной совокупности. Из этого нового набора реплик статистики, оценка смещения и оценка дисперсии статистики может быть вычислена.

Требуют особого внимания при применении Jackknifine, в частности, удаление наблюдений-1 Jackknifine. Она должна быть использована только с гладким дифференцируемым статистики, а именно: суммы, пропорции, соотношения, нечетные коэффициенты, коэффициенты регрессии и т.д., но не с медианами или квантилями. Это , может стать практическим недостатком (или нет, в зависимости от потребностей пользователя). Этот недостаток, как правило, аргумент против Jackknifine в пользу загрузки. Более общие jackknifes, чем удаление-1, такие, как удаление м Jackknife, решить эту проблему для медианы и квантилей, ослабив требования гладкости для последовательной оценки дисперсии.

Как правило, с Jackknife легче применять сложные схемы выборки по сравнению с бустреппингом. Комплекс схем отбора проб может привести к расслоению, несколько этапов (кластеризации), различные выборки вес (без ответа коррективы, калибровки, после стратификации) и в неравной вероятностью дизайна выборки. Теоретические аспекты и бутстреппинга и Jackknife можно найти в, [1], в то время как общее введение можно посмотреть здесь [2]

Сравнение бустреппинга и Jackknifine

Оба метода, бутстреппинг и Jackknife, оценивают изменчивость статистики по изменчивости выборки, а не из параметрических предположениях. Обобщенный Jackknife, удаление м наблюдений, может рассматриваться как случайное приближение к бутсреппигу. Оба метода дают аналогичные численные результаты, поэтому каждый из них может рассматриваться как приближение к другому. Несмотря на огромные теоретические различия в их математические идеи, основная практическая разница для пользователей статистических данных является то, что бутстреппинг дает разные результаты при повторении тех же данных, в то время как Jackknife дает точно такой же результат каждый раз. Из-за этого Jackknife является популярным, когда оценки необходимо проверить несколько раз перед публикацией (например, официальная статистика агентства). С другой стороны, когда эта функция проверки не является критическим, идея бустреппинга является предпочтительным (например, исследования в физике, экономике, биологии). Следует ли использовать бутсреппинг или Jackknife может больше зависеть от нестатистических проблем, а от оперативных аспектов обследования. бутсреппинг представляет собой мощный и простой способ оценить не только дисперсию точки оценки, но все ее распространения. С другой стороны, Jackknife дает только оценку дисперсии. Это может быть достаточно для базового статистического вывода (например, для проверки гипотез, или для оценки доверительные интервалы). Таким образом, Jackknife является специализированным методом оценки отклонений в то время как бустреппинг может использоваться для оценки всех параметров распределения.

«Бустреппинг может быть применен как для дисперсии и проблемы распределения оценки. Тем не менее, оценки бустреппинга не так хороши, как Jackknife или БРР ( сбалансированный повторяется репликации , под ред. примечание) дисперсия оценки с точки зрения эмпирических результатов. Кроме того, оценка дисперсии бустреппингом обычно требует больше вычислений, чем Jackknife или BRR. Таким образом, бустреппинг в основном рекомендуется для оценки распределения ». [3]

Литература

  1. ↑ Shao, J. and Tu, D. (1995). The Jackknife and Bootstrap. Springer-Verlag, Inc.
  2. ↑ Wolter, K.M. (2007). Introduction to Variance Estimation. Second Edition. Springer, Inc.
  3. ↑ Shao, J. and Tu, D. (1995). The Jackknife and Bootstrap. Springer-Verlag, Inc. pp. 281.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *