Многоугольник — Википедия
Материал из Википедии — свободной энциклопедии
 Тринадцатиугольник — многоугольник с 13 углами и 13 вершинами.
Тринадцатиугольник — многоугольник с 13 углами и 13 вершинами.Многоуго́льник — геометрическая фигура, обычно определяемая как часть плоскости, ограниченная замкнутой ломаной, звенья которой не пересекаются.
 Многоугольники
МногоугольникиСуществуют три различных варианта определения многоугольника; последнее определение является наиболее распространённым.
- Плоская замкнутая ломаная — наиболее общий случай;
- Плоская замкнутая ломаная без самопересечений, любые два соседних звена которой не лежат на одной прямой;
- Часть плоскости, ограниченная замкнутой ломаной без самопересечений — плоский многоугольник; в этом случае сама ломаная называется
В любом случае вершины ломаной называются вершинами многоугольника, а её звенья — сторонами многоугольника.
Связанные определения[править | править код]
- Вершины многоугольника называются соседними, если они являются концами одной из его сторон.
- Стороны многоугольника называются смежными, если они прилегают к одной вершине.
- Отрезки, соединяющие несоседние вершины многоугольника, называются диагоналями.
- Углом (или внутренним углом) многоугольника при данной вершине называется угол, образованный его сторонами, сходящимися в этой вершине, и находящийся во внутренней области многоугольника. В частности, угол может превосходить 180°, если многоугольник невыпуклый.
- Внешним углом выпуклого многоугольника при данной вершине называется угол, смежный внутреннему углу многоугольника при этой вершине. В общем случае внешний угол — разность между 180° и внутренним углом, он может принимать значения от −180° до 180°.
- Выпуклый многоугольник это многоугольник, который лежит по одну сторону от любой прямой, содержащей его сторону (то есть продолжения сторон многоугольника не пересекают других его сторон). Существуют и другие эквивалентные определения выпуклого многоугольника.
- Выпуклый многоугольник называется
- Многоугольник, у которого равны все стороны и все углы, но который имеет самопересечения, называется правильным звёздчатым многоугольником, например, пентаграмма и октаграмма.
- Многоугольник называется вписанным в окружность, если все его вершины лежат на одной окружности.
- Многоугольник называется описанным около окружности, если все его стороны касаются некоторой окружности.
- Сумма внутренних углов плоского n{\displaystyle n}-угольника без самопересечений равна (n−2)⋅180∘{\displaystyle (n-2)\cdot 180^{\circ }}.
- Число диагоналей всякого n{\displaystyle n}-угольника равно n⋅(n−3)2{\displaystyle {\tfrac {n\cdot (n-3)}{2}}}.
Площадь[править | править код]
- Пусть {(Xi,Yi)},i=1,2,…,n{\displaystyle \{(X_{i},Y_{i})\},i=1,2,…,n} — последовательность координат соседних друг другу вершин n{\displaystyle n}-угольника без самопересечений . Тогда его площадь вычисляется по формуле Гаусса:
- S=12|∑i=1n(Xi+Xi+1)(Yi−Yi+1)|{\displaystyle S={\frac {1}{2}}\left|\sum \limits _{i=1}^{n}(X_{i}+X_{i+1})(Y_{i}-Y_{i+1})\right|}, где (Xn+1,Yn+1)=(X1,Y1){\displaystyle (X_{n+1},Y_{n+1})=(X_{1},Y_{1})}.
Квадрируемость фигур[править | править код]
С помощью множества многоугольников определяется квадрируемость и площадь произвольной фигуры на плоскости. Фигура F{\displaystyle F} называется квадрируемой, если для любого ε>0{\displaystyle \varepsilon >0} существует пара многоугольников P{\displaystyle P} и Q{\displaystyle Q}, такие что P⊂F⊂Q{\displaystyle P\subset F\subset Q} и S(Q)−S(P)<ε{\displaystyle S(Q)-S(P)<\varepsilon }, где S(P){\displaystyle S(P)} обозначает площадь P{\displaystyle P}.
- Многогранник — обобщение многоугольника в размерности три, замкнутая поверхность, составленная из многоугольников, или тело, ей ограниченное.
| Многоугольники | |
|---|---|
| Звёздчатые многоугольники | |
| Паркеты на плоскости | |
| Правильные многогранники и сферические паркеты | |
| Многогранники Кеплера — Пуансо | |
| Соты | |
| Четырёхмерные многогранники |
|
Многоугольник — определение и основные понятия, виды и свойства фигур
Многоугольником называется геометрическая фигура, которая со всех сторон ограничена замкнутой ломаной линией. При этом количество звеньев ломаной не должно быть меньше трех. Каждая пара отрезков ломаной имеет общую точку и образует углы. Количество углов совместно с количеством отрезков ломаной являются основными характеристиками многоугольника. В каждом многоугольнике количество звеньев ограничивающей замкнутой ломаной совпадает с количеством углов.
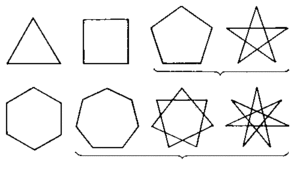
Сторонами в геометрии принято называть звенья ломаной линии, которая ограничивает геометрический объект. Вершинами называют точки соприкосновения двух соседних сторон, по количеству которых получают свои названия многоугольники.
Если замкнутая ломаная состоит из трех отрезков, она носит название треугольника; соответственно, из четырех отрезков — четырехугольником, из пяти — пятиугольником и пр.
Для обозначения треугольника или четырехугольника пользуются заглавными латинскими буквами, обозначающими его вершины. Буквы называют по порядку — по часовой стрелке или против нее.
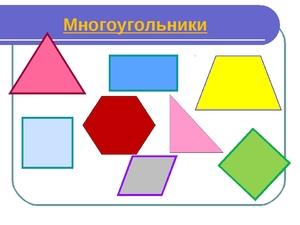
Основные понятия
Описывая определение многоугольника, следует учитывать некоторые смежные геометрические понятия:
- Если вершины являются концами одной стороны, они называются соседними.
- Если отрезок соединяет между собой несоседние вершины, то он имеет название диагонали. У треугольника не может быть диагоналей.
- Внутренний угол — это угол при одной из вершин, который образован двумя его сторонами, сходящимися в этой точке. Он всегда располагается во внутренней области геометрической фигуры. Если многоугольник невыпуклый, его размер может превосходить 180 градусов.
- Внешний угол при определенной вершине — это угол смежный с внутренним при ней же. Иными словами, внешним углом можно считать разность между 180° и величиной внутреннего угла.
- Сумма величин всех отрезков носит название периметра.
- Если все стороны и все углы равны — он носит название правильного. Правильными могут быть только выпуклые.
Как уже упоминалось выше, названия многоугольных геометрических строятся исходя из количества вершин. Если у фигуры их количество равняется n, она носит название n-угольника:
- Многоугольник называется плоским, если ограничивает конечную часть плоскости. Эта геометрическая фигура может быть вписанной в окружность или описанной вокруг окружности.
- Выпуклым называется n-угольник, который соответствует одному из условий, приведенных ниже.
- Фигура расположена по одну сторону от прямой линии, которая соединяет две соседних вершины.
- Эта фигура служит общей частью или пересечением нескольких полуплоскостей.
- Диагонали располагаются внутри многоугольника.
- Если концы отрезка располагаются в точках, которые принадлежат многоугольнику, весь отрезок принадлежит ему.
- Фигура может называться правильной, если у нее все отрезки и все углы равны. Примерами могут служить квадрат, равносторонний треугольник или правильный пятиугольник.
- Если n-угольник невыпуклый, все стороны и углы его равны, а вершины совпали с таковыми правильного n-угольника, он называется звездчатым. У таких фигур могут иметься самопересечения. Примерами могут служить пентаграмма или гексаграмма.
- Треугольник или четырехугольник называется вписанным в окружность, когда все его вершины располагаются внутри одной окружности. Если же стороны этой фигуры имеют точки соприкосновения с окружностью, это многоугольник описанным около некоторой окружности.
Любой выпуклый n-угольник можно поделить на треугольники. При этом количество треугольников бывает меньше количества сторон на 2.
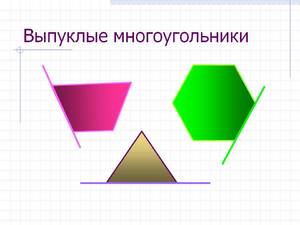
Виды фигур
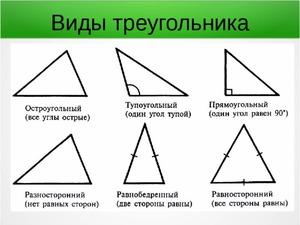
Треугольник
Это многоугольник с тремя вершинами и тремя отрезками, соединяющими их. При этом точки соединения отрезков не лежат на одной прямой.
Точки соединения отрезков — это вершины треугольника. Сами отрезки называются сторонами треугольника. Общая сумма внутренних углов каждого треугольника равняется 180°.
По соотношениям между сторонами все треугольники можно подразделять на несколько видов:
- Равнобедренные — треугольники, у которых равны два отрезка из трех.
- Разносторонние — если длина всех отрезков разная.
Кроме того, принято различать следующие треугольники:
- Остроугольные.
- Прямоугольные.
- Тупоугольные.
Четырехугольник
Четырехугольником называется плоская фигура, имеющая 4 вершины и 4 отрезка, которые их последовательно соединяют.
- Если все углы четырехугольника прямые — эта фигура называется прямоугольником.
- Прямоугольник, у которого все стороны имеют одинаковую величину, называется квадратом.
- Четырехугольник, все стороны которого равны, называется ромбом.
На одной прямой не может находиться сразу три вершины четырехугольника.
Видео
Дополнительную информацию о многоугольниках вы найдете в этом видео.
Многоугольники. Видеоурок. Геометрия 8 Класс
Тема: Четырехугольники
Урок: Многоугольники
В курсе геометрии мы изучаем свойства геометрических фигур и уже рассмотрели простейшие из них: треугольники и окружности. При этом мы обсуждали и конкретные частные случаи этих фигур, такие как прямоугольные, равнобедренные и правильные треугольники. Теперь пришло время поговорить о более общих и сложных фигурах – многоугольниках.
С частным случаем многоугольников мы уже знакомы – это треугольник (см. Рис. 1).

Рис. 1. Треугольник
В самом названии уже подчеркивается, что это фигура, у которой три угла. Следовательно, в многоугольнике их может быть много, т.е. больше, чем три. Например, изобразим пятиугольник (см. Рис. 2), т.е. фигуру с пятью углами.
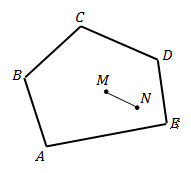
Рис. 2. Пятиугольник. Выпуклый многоугольник
Определение.Многоугольник – фигура, состоящая из нескольких точек (больше двух) и соответствующего количества отрезков, которые их последовательно соединяют. Эти точки называются
Определение.Правильный многоугольник – это выпуклый многоугольник, у которого все стороны и углы равны.
Любой многоугольник разделяет плоскость на две области: внутреннюю и внешнюю. Внутреннюю область также относят к многоугольнику.
Иными словами, например, когда говорят о пятиугольнике  , имеют в виду и всю его внутреннюю область, и границу. А ко внутренней области относятся и все точки, которые лежат внутри многоугольника, т.е. точка
, имеют в виду и всю его внутреннюю область, и границу. А ко внутренней области относятся и все точки, которые лежат внутри многоугольника, т.е. точка 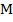
Многоугольники еще иногда называют n-угольниками, чтобы подчеркнуть, что рассматривается общий случай наличия какого-то неизвестного количества углов (n штук).
Определение. Периметр многоугольника – сумма длин сторон многоугольника.
Теперь надо познакомиться с видами многоугольников. Они делятся на выпуклые и невыпуклые. Например, многоугольник, изображенный на Рис. 2, является выпуклым, а на Рис. 3 невыпуклым.

Рис. 3. Невыпуклый многоугольник
Определение 1. Многоугольник называется выпуклым, если при проведении прямой через любую из его сторон весь многоугольник лежит только по одну сторону от этой прямой. Невыпуклыми являются все остальные многоугольники.
Легко представить, что при продлении любой стороны пятиугольника на Рис. 2 он весь окажется по одну сторону от этой прямой, т.е. он выпуклый. А вот при проведении прямой через 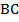 в четырехугольнике на Рис. 3 мы уже видим, что она разделяет его на две части, т.е. он невыпуклый.
в четырехугольнике на Рис. 3 мы уже видим, что она разделяет его на две части, т.е. он невыпуклый.
Но существует и другое определение выпуклости многоугольника.
Определение 2. Многоугольник называется выпуклым, если при выборе любых двух его внутренних точек и при соединении их отрезком все точки отрезка являются также внутренними точками многоугольника.
Демонстрацию использования этого определения можно увидеть на примере построения отрезков  на Рис. 2 и 3.
на Рис. 2 и 3.
Определение. Диагональю многоугольника называется любой отрезок, соединяющий две не соседние его вершины.
Для описания свойств многоугольников существуют две важнейшие теоремы об их углах: теорема о сумме внутренних углов выпуклого многоугольника и теорема о сумме внешних углов выпуклого многоугольника. Рассмотрим их.
Теорема. О сумме внутренних углов выпуклого многоугольника (n-угольника).
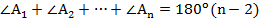 , где
, где  – количество его углов (сторон).
– количество его углов (сторон).
Доказательство 1. Изобразим на Рис. 4 выпуклый n-угольник.
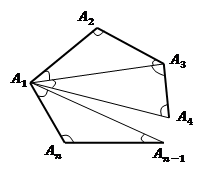
Рис. 4. Выпуклый n-угольник
Из вершины 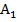 проведем все возможные диагонали. Они делят n-угольник на
проведем все возможные диагонали. Они делят n-угольник на  треугольника, т.к. каждая из сторон многоугольника образует треугольник, кроме сторон, прилежащих к вершине
треугольника, т.к. каждая из сторон многоугольника образует треугольник, кроме сторон, прилежащих к вершине 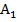 . Легко видеть по рисунку, что сумма углов всех этих треугольников как раз будет равна сумме внутренних углов n-угольника. Поскольку сумма углов любого треугольника –
. Легко видеть по рисунку, что сумма углов всех этих треугольников как раз будет равна сумме внутренних углов n-угольника. Поскольку сумма углов любого треугольника – 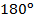 , то сумма внутренних углов n-угольника:
, то сумма внутренних углов n-угольника:
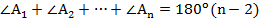 , что и требовалось доказать.
, что и требовалось доказать.
Доказательство 2. Возможно и другое доказательство этой теоремы. Изобразим аналогичный n-угольник на Рис. 5 и соединим любую его внутреннюю точку со всеми вершинами.

Рис. 5.
Мы получили разбиение n-угольника на n треугольников (сколько сторон, столько и треугольников). Сумма всех их углов равна сумме внутренних углов многоугольника и сумме углов при внутренней точке, а это угол  . Имеем:
. Имеем:
 , что и требовалось доказать.
, что и требовалось доказать.
Доказано.
По доказанной теореме видно, что сумма углов n-угольника зависит от количества его сторон (от n). Например, в треугольнике 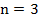 , а сумма углов
, а сумма углов 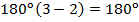 . В четырехугольнике
. В четырехугольнике  , а сумма углов –
, а сумма углов – 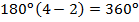 и т.д.
и т.д.
Теорема. О сумме внешних углов выпуклого многоугольника (n-угольника).
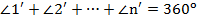 , где
, где  – количество его углов (сторон), а
– количество его углов (сторон), а  , …,
, …,  – внешние углы.
– внешние углы.
Доказательство. Изобразим выпуклый n-угольник на Рис. 6 и обозначим его внутренние и внешние углы.

Рис. 6. Выпуклый n-угольник с обозначенными внешними углами
Т.к. внешний угол связан со внутренним как смежные, то  и аналогично для остальных внешних углов. Тогда:
и аналогично для остальных внешних углов. Тогда:
 .
.
В ходе преобразований мы воспользовались уже доказанной теоремой о сумме внутренних углов n-угольника 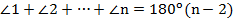 .
.
Доказано.
Из доказанной теоремы следует интересный факт, что сумма внешних углов выпуклого n-угольника равна  от количества его углов (сторон). Кстати, в отличие от суммы внутренних углов.
от количества его углов (сторон). Кстати, в отличие от суммы внутренних углов.
Далее мы более подробно будем работать с частным случаем многоугольников – четырехугольниками. На следующем уроке мы познакомимся с такой фигурой, как параллелограмм, и обсудим его свойства.
Список литературы
- Александров А.Д. и др. Геометрия, 8 класс. – М.: Просвещение, 2006.
- Бутузов В.Ф., Кадомцев С.Б., Прасолов В.В. Геометрия, 8 класс. – М.: Просвещение, 2011.
- Мерзляк А.Г., Полонский В.Б., Якир С.М. Геометрия, 8 класс. – М.: ВЕНТАНА-ГРАФ, 2009.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Profmeter.com.ua (Источник).
- Narod.ru (Источник).
- Xvatit.com (Источник).
Домашнее задание
- № 43, 42 (а, б, в, г, з), 46 (а, б), 47 (а,б). Бутузов В.Ф., Кадомцев С.Б., Прасолов В.В. Геометрия, 8 класс. – М.: Просвещение, 2011.
- Существует ли выпуклый многоугольник, сумма углов которого равна: а)
 ; б)
; б)  ; в)
; в)  ?
? - Найдите углы четырехугольника, если они пропорциональны числам 2, 3, 10 и 21. Выпуклый или невыпуклый этот четырехугольник?
- Вершины выпуклого пятиугольника соединены через одну. Найдите сумму углов при вершинах полученной «звезды».
Многогранники. Виды многогранников. Объём. Видеоурок. Геометрия 9 Класс
До сих пор мы подробно изучали геометрические фигуры на плоскости. Действительно, несмотря на трехмерность окружающего нас мира, часто мы воспринимаем его двумерным, плоским.
Например, используя навигатор, мы представляем себе плоскую модель города. Укладывая паркет на пол, мастер тоже решает двумерную задачу. Такие задачи возникают довольно часто, поэтому мы уделили им много внимания.
Но не любую задачу можно свести к плоской модели. Например: сколько воды помещается в стакан. Здесь необходимо вычислять объем. Но до этого мы говорили только о двух измерениях – длине и ширине. И, как следствие, о площади – как о характеристике места на плоскости, которое занимает фигура.
Чтобы ввести понятие объема, нужно добавить третье измерение – высоту. Действительно, чтобы задать положение объекта на прямой, достаточно одной координаты, на плоскости (например, на карте) – уже двух. А вот в пространстве понадобится три координаты (см. рис. 1).

Рис. 1. Сверху вниз: задание положения объекта на прямой, плоскости, в пространстве
На этом уроке мы приступаем к изучению той части геометрии, которая занимается решением задач в трех измерениях. Называется она стереометрией (от греч. «сте́рео»: στερεός – твердый, пространственный).
Вспомним, что сначала мы рассматривали прямую (одномерное пространство) (см. рис. 2). На ней у нас основными фигурами были отрезки, их мы характеризовали длиной.

Рис. 2. Прямая
Затем мы рассмотрели плоскость – бесконечное множество прямых (см. рис. 3). Здесь разнообразие фигур существенно увеличилось и появились новые характеристики: длина границы (периметр) и площадь.
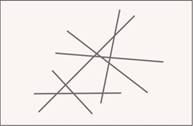
Рис. 3. Плоскость
Теперь мы рассмотрим пространство – бесконечное множество плоскостей (см. рис. 4). В качестве геометрических фигур будут выступать преимущественно различные тела, которые мы будем характеризовать площадью границы (площадь поверхности) и объемом.
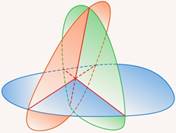
Рис. 4. Пространство
Очень многие объекты стереометрии имеют аналоги в планиметрии. Например: куб и квадрат, шар и круг (соответственно, их границы: сфера и окружность) (см. рис. 5). Кроме того, конечно, все плоские фигуры продолжают существовать и в трехмерном пространстве: точка, прямая, плоскость остаются и в стереометрии основными неопределяемыми понятиями. Но теперь различных плоскостей существует бесконечное число.

Рис. 5. Куб и квадрат; шар и круг
При этом, если мы выберем конкретную плоскость и на ней будут лежать какие-либо знакомые нам уже фигуры: точки, прямые, многоугольники, то мы получим планиметрию в миниатюре и будем применять на этой плоскости все наши знания, полученные ранее. Этот стандартный прием мы будем часто использовать при решении стереометрических задач – свести их к одной или нескольким планиметрическим, которые мы уже умеем решать (так называемый принцип «вылить воду из чайника»).
Итак, точки, прямые, плоскости достаются нам в наследство из планиметрии. Новыми объектами будут многогранники, которые имеют прямую аналогию с многоугольниками.
Многоугольник представляет собой часть плоскости, ограниченной пересекающимися прямыми (см. рис. 6). Отрезки этих прямых называются сторонами многоугольника. Точки пересечения – вершинами. Аналогично образуются многогранники.

Рис. 6. Многоугольник
Если несколько плоскостей, пересекаясь, отделили область пространства, то она и называется многогранником (см. рис. 7, 8). Части плоскостей называются гранями. Отрезки, по которым они пересекаются, называются ребрами. А точки, куда сходятся ребра, называются вершинами.

Рис. 7. Плоскости, пересекаясь, отделили область пространства – многогранник 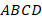 (треугольную пирамиду)
(треугольную пирамиду)
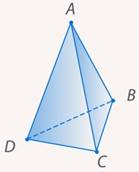
Рис. 8. Треугольная пирамида 
Треугольник – это многоугольник с минимально возможным количеством сторон – с тремя. А каково минимальное количество граней у многогранника? Т. е. сколькими плоскостями можно отделить часть пространства от остального пространства?
Как бы мы ни пересекали три плоскости, создать замкнутую область не получится.
А вот четыре плоскости вполне достаточно. Мы получаем многогранник с четырьмя гранями, т. е. четырехгранник. Но обычно его называют тетраэдр, что по-гречески и означает четырехгранник (см. рис. 9).

Рис. 9. Тетраэдр
Как бы ни был расположен тетраэдр, мы не можем увидеть сразу все грани и ребра (см. рис. 10).
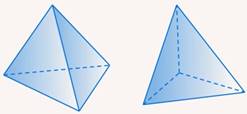
Рис. 10. Возможные расположения тетраэдра
Договорились те ребра, которые мы видим, обозначать сплошной линией, а невидимые для нас – пунктиром. Сколько ребер не видно, зависит от ориентации многогранника. Мы можем расположить тетраэдр таким образом, что невидимыми будут даже три ребра.
Оптический обман
На самом деле, количество «видимых» и «невидимых» ребер тетраэдра зависит от точки, из которой мы на него смотрим (см. рис. 11, 12, 13).

Рис. 11. Видны две грани тетраэдра

Рис. 12. Видна одна грань тетраэдра
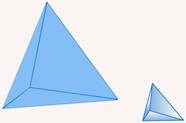
Рис. 13. Видны три грани тетраэдра
Точно так же и в жизни – в зависимости от точки расположения наблюдателя, увиденное им будет различаться, даже если он смотрит на один и тот же объект. Почему мы вообще невидимые линии рисуем по-другому и отмечаем пунктиром? Потому что в противном случае один и тот же рисунок может относиться к разным объектам.
Например, куб, изображенный на рисунке (см. рис. 14), может занимать одно из двух положений (с видимой верхней и видимой нижней гранью) (см. рис. 15). И если не обозначить пунктиром невидимые линии, то нельзя однозначно сказать, какое.

Рис. 14. Куб Неккера
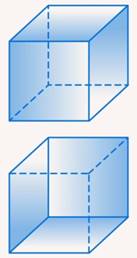
Рис. 15. Два положения куба – с видимой верхней и видимой нижней гранью
Изображенный куб называется кубом Неккера и относится к оптическим иллюзиям. Если нарисовать его таким образом (см. рис. 16), то он окажется невозможным объектом, который не может существовать в реальности.

Рис. 16. Куб, являющийся невозможным объектом, который не может существовать в реальности
Вершины многогранников, как и у многоугольников, обозначаются большими латинскими буквами. Указывая конкретный многогранник, нужно указать его тип и перечислить все вершины. Например, тетраэдр 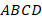 . Увеличивая количество граней, мы получим многообразие многогранников (см. рис. 17) от очень простых до изощренных, изобразить которые будет достаточно сложно.
. Увеличивая количество граней, мы получим многообразие многогранников (см. рис. 17) от очень простых до изощренных, изобразить которые будет достаточно сложно.

Рис. 17. Многогранники
Для успешного изучения свойств многогранников их нужно классифицировать и выбрать для начала самые простые, на которые можно будет разбить более сложные.
Подход такой же, какой был с многоугольниками в планиметрии (начали с треугольников).
Когда мы начали классифицировать многоугольники, то разделили их на два типа:
выпуклые и невыпуклые. Выпуклость многоугольника означала, что если через любую его сторону провести прямую, то весь многоугольник будет лежать с одной стороны от этой прямой (см. рис. 18). А у невыпуклого хотя бы одна из таких прямых разбивает многоугольник на части (см. рис. 19). Иначе это же свойство формулировалось так: если для любых двух точек, лежащих внутри многоугольника, отрезок, их соединяющий, тоже целиком лежит внутри, то такой многоугольник выпуклый.

Рис. 18. Выпуклый многоугольник
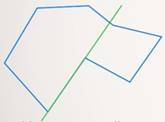
Рис. 19. Невыпуклый многоугольник
Ровно такой же подход используется в случае многогранников. Их точно так же делят на две группы: выпуклые и невыпуклые. Если в многограннике провести плоскость через любую грань и весь многогранник всегда будет оставаться с одной стороны, то его будут называть выпуклым (см. рис. 20). Если хотя бы одна такая плоскость разрезает многогранник, то он невыпуклый (см. рис. 21). Либо можно использовать второе определение, как и в случае многоугольников. У выпуклого многогранника вместе с любыми двумя точками, ему принадлежащими, ему принадлежит и весь отрезок, их соединяющий.
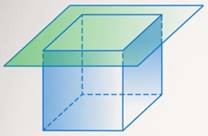
Рис. 20. Выпуклый многогранник

Рис. 21. Невыпуклый многогранник
В дальнейшем мы будем заниматься только выпуклыми многогранниками как более простыми для изучения.
Среди выпуклых многогранников мы выделим две группы наиболее простых и одновременно изучаемых (т. е. тех, о свойствах которых мы можем сделать какие-то полезные выводы): призмы и пирамиды (см. рис. 22). Это не значит, что других выпуклых многогранников не бывает. Бывают. Мы с некоторыми познакомимся, но основное внимание уделим именно призмам и пирамидам.

Рис. 22. Призма и пирамида
Возьмем два равных многоугольника и расположим один строго над другим, вершина над вершиной. Соединим попарно соответствующие вершины многоугольников. Полученный многогранник называется прямой призмой (см. рис. 23).

Рис. 23. Прямая призма 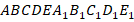
Две грани, образованные равными многоугольниками, называются нижним основанием и верхним основанием. Остальные грани называются боковыми гранями. Все боковые грани прямой призмы являются прямоугольниками. Боковые ребра равны друг другу и вертикальны.
Теперь сдвинем верхнее основание (крышку) в сторону, но без поворота и наклона. Боковые ребра наклонятся в одну сторону, но сохранят параллельность друг другу. Боковые грани теперь не прямоугольники, а параллелограммы. Получившийся многогранник называется наклонной призмой (см. рис. 24).

Рис. 24. Наклонная призма 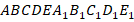
Если мы повернем одно основание относительно другого, перекрутим нашу призму, то она перестанет считаться призмой (см. рис. 25). Более того, если хорошо присмотреться, то наш многогранник перестает быть даже выпуклым. Такие многогранники мы рассматривать уже не будем.

Рис. 25. Пример многогранника, не являющегося призмой
Дадим строгое определение: призма – это многогранник, две грани которого являются равными многоугольниками, лежащими в параллельных плоскостях, а остальные грани – параллелограммами, имеющими общие стороны с этими многоугольниками.
Многоугольник, лежащий в основании, определяет название призмы. Например, если лежит треугольник – треугольная призма, четырехугольник – четырехугольная;  -угольник –
-угольник –  -угольная (см. рис. 26).
-угольная (см. рис. 26).

Рис. 26. Треугольная, четырехугольная,  -угольная призмы
-угольная призмы
Не путайте количество вершин у призмы и количество вершин у одного основания.
У  -угольной призмы
-угольной призмы 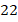 вершины:
вершины:  снизу и
снизу и  сверху.
сверху.
Если в основании призмы лежит правильный многоугольник, а сама призма прямая, то призма называется правильной. Например, если в основании прямой призмы лежит правильный (равносторонний) треугольник, то мы имеем дело с правильной треугольной призмой (см. рис. 27). Если в основании прямой призмы лежит правильный четырехугольник (квадрат), то призма называется правильной четырехугольной (см. рис. 28).
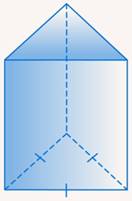
Рис. 27. Правильная треугольная призма

Рис. 28. Правильная четырехугольная призма
Любой предмет, который стоит у нас на столе, имеет высоту. Конечно, иногда определить высоту объекта довольно сложно – например, чему она будет равна у такого предмета (см. рис. 29)? В таких случаях обычно за высоту принимают наибольшее возможное значение расстояния от основания до верхней точки.

Рис. 29. Пример, когда сложно определить высоту объекта
Но у призмы высоту можно строго определить. Если призму поставить на стол на нижнее основание, то все точки верхнего основания находятся на одной высоте – как у прямой призмы, так и у наклонной. Т. е. высота призмы – это расстояние от любой точки верхнего основания до нижнего.
Опустим из любой точки верхнего основания перпендикуляр на плоскость нижнего основания. Полученный отрезок и будет называться высотой призмы (см. рис. 30).

Рис. 30. Высоты у прямой и наклонной призм
В прямой призме любое боковое ребро является высотой. В наклонной призме это не так. Более того, высота, в наклонной призме может вообще не попасть ни на одно из оснований (см. рис. 31). Подобная ситуация нам встречалась, например, с тупоугольным треугольником, когда высота проводится не к основанию треугольника, а к его продолжению.
Рис. 31. Высота наклонной призмы не попала ни на одно из оснований
Призмой с минимальным количеством граней является треугольная призма. На уроках физики, изучая тему преломления света, вы рассматривали разложение пучка белого света в спектр. Там использовалась треугольная призма (см. рис. 32).

Рис. 32. Треугольная призма используется при изучении преломления света на уроках физики
Но в быту не так много предметов имеют эту форму. Например, вращающиеся элементы в рекламных щитах (см. рис. 33).

Рис. 33. Вращающиеся элементы в рекламных щитах имеют форму треугольной призмы
Зато четырехугольные призмы окружают нас буквально повсюду. А если конкретно, прямые призмы, в основании которых лежит прямоугольник. Такую форму имеет кирпич, смартфон, книга, спичечный коробок и многое другое. В силу такой важности этой формы для них придумали даже отдельные дополнительные названия. Разберемся с ними.
Призма, в основании которой лежит параллелограмм, называется параллелепипедом (см. рис. 34).Легко понять, что у параллелепипеда не только основания являются параллелограммами, но и все боковые грани.

Рис. 34. Параллелепипед
Поэтому можно дать другое определение: параллелепипед – это шестигранник (а у него в самом деле шесть граней), у которого все грани являются параллелограммами.
Если боковые ребра параллелепипеда перпендикулярны основаниям, то его называют прямым параллелепипедом (см. рис. 35). Т. е. смысл понятий «прямая призма» и «прямой параллелепипед» одинаковы.

Рис. 35. Прямой параллелепипед
Боковые ребра прямого параллелепипеда являются уже не просто параллелограммами, а прямоугольниками. Обратите внимание, что в основании прямого параллелепипеда у нас пока продолжает лежать произвольный параллелограмм.
Если в основании прямого параллелепипеда тоже лежит прямоугольник, т. е. все грани стали прямоугольниками, то такой параллелепипед называется прямоугольным.
К сожалению, по рисунку параллелепипеда мы не можем понять, является он просто прямым или прямоугольным. Дело в том, что когда мы смотрим на плоскость основания под углом, то прямоугольник мы, скорее всего, увидим как параллелограмм (см. рис. 36). Поэтому, чтобы не было недоразумений, тип параллелепипеда нужно указывать в описании.

Рис. 36. Плоскость основания (прямоугольник) под углом
Вот этот самый прямоугольный параллелепипед мы особо часто и наблюдаем вокруг себя в быту. Если вас попросят склеить коробку, не уточняя ее форму, скорее всего, вы сделаете ее в форме прямоугольного параллелепипеда.
Ну и самым «ровным», самым «правильн
Многоугольники — урок. Геометрия, 8 класс.
Ломаной называется фигура, которая состоит из точек и соединяющих их отрезков.
Точки называются вершинами ломаной, а отрезки — звеньями ломаной.
Виды ломаных
Ломаная называется замкнутой, если у неё концы совпадают.

Если концы ломаной не совпадают, то она называется незамкнутой.

Ломаная называется простой, если она не имеет самопересечений. Обе ломаные выше являются простыми.
На следующем рисунке — ломаная с самопересечением.

Многоугольник
Многоугольник — это простая замкнутая ломаная линия и конечная часть
плоскости, которую она ограничивает.
Вершины ломаной линии называются вершинами многоугольника, а её звенья — сторонами многоугольника.
Отрезок, соединяющий две вершины, не лежащие на одной стороне, называется диагональю многоугольника.
\(A\), \(B\), \(C\), \(D\), \(E\) — вершины;
\(AB\), \(BC\), \(CD\), \(DE\), \(AE\) — стороны;
\(AC\), \(AD\), \(BE\), \(BD\), \(CE\) — диагонали.
Многоугольник, у которого все углы меньше 180°, называется выпуклым многоугольником.
Пятиугольник \(ABCDE\) является выпуклым многоугольником.
Сумма углов выпуклого \(n\)-угольника
В общем случае многоугольник можно назвать \(n\)-угольником, это означает, что у данного многоугольника \(n\) сторон и \(n\) вершин.
Сумма углов выпуклого \(n\)-угольника равна 180°⋅n−2.
Любой выпуклый многоугольник можно разделить на треугольники. Количество треугольников на \(2\) меньше, чем количество сторон в многоугольнике.
Сумма внутренних углов любого треугольника равна 180°.
Поэтому сумма углов выпуклого \(n\)-угольника равна 180°⋅n−2.
Пример:
вычисли сумму внутренних углов выпуклого одиннадцатиугольника.

Можно нарисовать рисунок, но это не обязательно для решения задачи.
Используем формулу:
180°⋅n−2=180°⋅11−2=180°⋅9=1620°.
Многоугольник — Википедия. Что такое Многоугольник
Материал из Википедии — свободной энциклопедии| Тринадцатиугольник | |
|---|---|
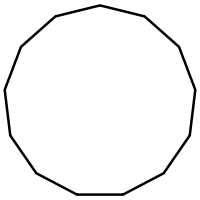 |
Многоуго́льник — это геометрическая фигура, обычно определяемая как часть плоскости ограниченная замкнутой ломаной.
Варианты определений
 Многоугольники
МногоугольникиСуществуют три различных варианта определения многоугольника; последнее определение является наиболее распространённым.
- Плоская замкнутая ломаная — наиболее общий случай;
- Плоская замкнутая ломаная без самопересечений, любые два соседних звена которой не лежат на одной прямой;
- Часть плоскости, ограниченная замкнутой ломаной без самопересечений — плоский многоугольник; в этом случае сама ломаная называется контуром многоугольника.
В любом случае вершины ломаной называются вершинами многоугольника, а её отрезки — сторонами многоугольника.
Связанные определения
- Вершины многоугольника называются соседними, если они являются концами одной из его сторон.
- Стороны многоугольника называются смежными, если они прилегают к одной вершине.
- Отрезки, соединяющие несоседние вершины многоугольника, называются диагоналями.
- Углом (или внутренним углом) многоугольника при данной вершине называется угол, образованный его сторонами, сходящимися в этой вершине, и находящийся во внутренней области многоугольника. В частности, угол может превосходить 180°, если многоугольник невыпуклый.
- Внешним углом выпуклого многоугольника при данной вершине называется угол, смежный внутреннему углу многоугольника при этой вершине. В общем случае внешний угол — это разность между 180° и внутренним углом, он может принимать значения от −180° до 180°.
Виды многоугольников
Многоугольник, вписанный в окружность Многоугольник, описанный около окружности- Выпуклый многоугольник это многоугольник, который лежит по одну сторону от любой прямой, содержащей его сторону (то есть продолжения сторон многоугольника не пересекают других его сторон). Существуют и другие эквивалентные определения выпуклого многоугольника.
- Выпуклый многоугольник называется правильным, если у него равны все стороны и все углы, например равносторонний треугольник, квадрат и правильный пятиугольник.
- Многоугольник, у которого равны все стороны и все углы, но который имеет самопересечения, называется правильным звёздчатым многоугольником, например, пентаграмма и октаграмма.
- Многоугольник называется вписанным в окружность, если все его вершины лежат на одной окружности.
- Многоугольник называется описанным около окружности, если все его стороны касаются некоторой окружности.
Свойства
- Сумма внутренних углов плоского n{\displaystyle n}-угольника без самопересечений равна (n−2)⋅180∘{\displaystyle (n-2)\cdot 180^{\circ }}.
- Число диагоналей всякого n{\displaystyle n}-угольника равно n⋅(n−3)2{\displaystyle {\tfrac {n\cdot (n-3)}{2}}}.
Площадь
- Пусть {(Xi,Yi)},i=1,2,…,n{\displaystyle \{(X_{i},Y_{i})\},i=1,2,…,n} — последовательность координат соседних друг другу вершин n{\displaystyle n}-угольника без самопересечений . Тогда его площадь вычисляется по формуле Гаусса:
- S=12|∑i=1n(Xi+Xi+1)(Yi−Yi+1)|{\displaystyle S={\frac {1}{2}}\left|\sum \limits _{i=1}^{n}(X_{i}+X_{i+1})(Y_{i}-Y_{i+1})\right|}, где (Xn+1,Yn+1)=(X1,Y1){\displaystyle (X_{n+1},Y_{n+1})=(X_{1},Y_{1})}.
Квадрируемость фигур
С помощью множества многоугольников определяется квадрируемость и площадь произвольной фигуры на плоскости. Фигура F{\displaystyle F} называется квадрируемой, если для любого ε>0{\displaystyle \varepsilon >0} существует пара многоугольников P{\displaystyle P} и Q{\displaystyle Q}, такие что P⊂F⊂Q{\displaystyle P\subset F\subset Q} и S(Q)−S(P)<ε{\displaystyle S(Q)-S(P)<\varepsilon }, где S(P){\displaystyle S(P)} обозначает площадь P{\displaystyle P}.
Вариации и обобщения
- Многогранник — обобщение многоугольника в размерности три, замкнутая поверхность, составленная из многоугольников, или тело, ей ограниченное.
| Многоугольники | |
|---|---|
| Звёздчатые многоугольники | |
| Паркеты на плоскости | |
| Правильные многогранники и сферические паркеты | |
| Многогранники Кеплера — Пуансо | |
| Соты | |
| Четырёхмерные многогранники |
|
Правильные многоугольники — урок. Геометрия, 9 класс.
Правильными называют многоугольники, у которых равны все стороны и все углы.
На рисунке видны некоторые правильные многоугольники: треугольник, четырёхугольник (квадрат), пятиугольник и шестиугольник.

Если в правильных выпуклых многоугольниках провести диагонали, то образуются правильные вогнутые многоугольники:
из диагоналей пятиугольника получается пентаграмма, из диагоналей шестиугольника — гексаграмма, а из диагоналей семиугольника — даже две разные гептаграммы.

Если провести все диагонали из одной вершины, любой \(n\)-угольник можно поделить на \(n-2\) треугольника, таким образом сумма всех внутренних углов определяется по формуле 180°⋅n−2.

Так как все углы правильного \(n\)-угольника равны, то величина одного внутреннего угла равна 180°⋅n−2n.
Около любого правильного многоугольника можно описать и вписать в него окружность, при этом совпадают центры обеих окружностей, и эту точку называют центром многоугольника.
Вписанная окружность касается всех сторон, описанная окружность проходит через все вершины.

∡AOH=360°n;∡AOK=360°2n=180°n.
В треугольнике \(AOK\) связаны сторона \(a\) (половина стороны \(AH\)), радиус описанной окружности \(OA = R\) и радиус вписанной окружности \(OK = r\).
a2=R⋅sin180°n;a=2R⋅sin180°n;R=a2sin180°n;a2=r⋅tg180°n;a=2r⋅tg180°n;r=a2tg180°n;r=R⋅cos180°n;R=rcos180°n.
Так как \(n\)-угольник состоит из \(n\) треугольников, равных \(AOH\), то
Sn−уг.=n⋅SAOH=n⋅AH⋅r2=p⋅r2.
Для правильного треугольника и квадрата дополнительно в силе все формулы, которые были рассмотрены в курсе геометрии.

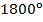 ; б)
; б) 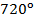 ; в)
; в) 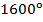 ?
?