Как сделать пятиугольник: Как рисовать правильный пятиугольник с помощью циркуля. Правильный пятиугольник. Получение с помощью полоски бумаги — DesignLessons – все о дизайне

Содержание

Как рисовать правильный пятиугольник с помощью циркуля. Правильный пятиугольник. Получение с помощью полоски бумаги

Правильный пятиугольник представляет собой геометрическую фигуру, которая образовывается пересечением пяти прямых, создающих пять одинаковых углов. Такая фигура носит название — пентагон. С пятиугольником тесно связана работа художников — их рисунки строятся на основе правильных геометрических фигур. Для этого необходимо знать то, как быстро построить пентагон.

Чем интересна эта фигура? Форму пентагона имеет здание Министерства обороны Соединенных Штатов Америки . Это можно увидеть на фото, сделанных с высоты полета. В природе не существует кристаллов и камней, форма которых напоминала бы пентагон. Только в этой фигуре количество граней совпадает с числом диагоналей.

Параметры правильного пятиугольника

Прямоугольный пятиугольник, как и каждая фигура в геометрии, имеет свои параметры. Зная необходимые формулы, можно рассчитать эти параметры, что облегчит процесс построения пентагона.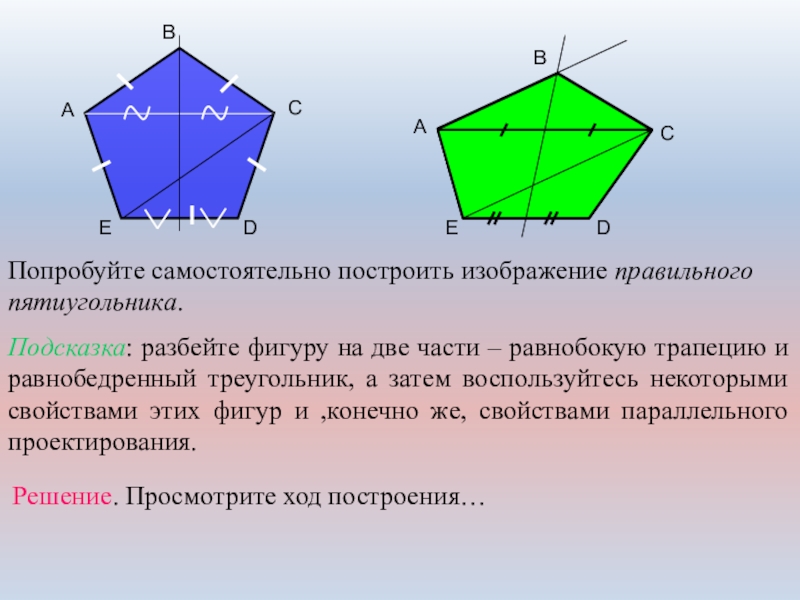

Способы и формулы расчетов:

сумма всех углов в многоугольниках равна 360 градусам. В правильном пятиугольнике все углы равны, соответственно, центральный угол находится таким способом: 360/5 = 72 градуса;
внутренний угол находится таким образом: 180*(n -2)/ n = 180*(5−2)/5 = 108 градусов. Сумма всех внутренних углов: 108*5 = 540 градусов.

Сторона пентагона находится с помощью параметров, которые уже даны в условии задачи:

если вокруг пятиугольника описана окружность и известен ее радиус, сторона находится по такой формуле: a = 2*R*sin (α/2) = 2*R*sin (72/2) = 1,1756*R.
Если известен радиус вписанной в пентагон окружности, то формула расчета стороны многоугольника: 2*r*tg (α/2) = 2*r*tg (α/2) = 1,453*r.

При известной величине диагонали пентагона его сторона рассчитывается таким образом: а = D/1,618.

Площадь пентагона так же , как и его сторона, зависит от уже найденных параметров:

с помощью известного радиуса вписанной окружности площадь находится так: S = (n*a*r)/2 = 2,5*a*r.
описанная вокруг пятиугольника окружность позволяет найти площадь по такой формуле: S = (n*R2*sin α)/2 = 2,3776*R2.
в зависимости от стороны пентагона: S = (5*a2*tg 54°)/4 = 1,7205* a2.

Построение пентагона

Построить правильный пятиугольник можно с помощью линейки и циркуля, на основе вписанной в него окружности или одной из сторон.

Как начертить пятиугольник на основе вписанной окружности? Для этого необходимо запастись циркулем и линейкой и сделать такие шаги:

Сначала необходимо начертить окружность с центром О, после чего на ней выбрать точку, А — вершину пентагона. От центра к вершине проводится отрезок.
Затем строится перпендикулярная прямой ОА отрезок, который также проходит через О — центр окружности. Его пересечение с окружностью обозначается точкой В. Отрезок О. В. делится пополам точкой С.
Точка С станет центром новой окружности, проходящей через А. Точка D — это ее пересечение с прямой ОВ в границах первой фигуры.
После этого проводится третья окружность через D, центром которой является точка А. Она пересекается с первой фигурой в двух точках, их необходимо обозначить буквами Е и F.
Следующая окружность имеет центр в точке Е и проходит через А, а ее пересечение с первоначальной находится в новой точке G.
Последняя окружность в этом рисунке проводится через точку, А с центром F. На ее пересечении с начальной ставится точка Н.
На первой окружности после всех проделанных шагов появились пять точек, которые необходимо соединить отрезками. Таким образом получился правильный пятиугольник АЕ G Н F.

Как построить правильный пятиугольник иным способом? С помощью линейки и циркуля пентагон можно построить немного быстрее. Для этого необходимо:

Cначала необходимо с помощью циркуля нарисовать окружность, центр которой — точка О.
Чертится радиус ОА — отрезок, который откладывается на окружность. Его делят пополам точкой В.
Перпендикулярно радиусу ОА начерчивается отрезок ОС, точки В и С соединяются прямой.
Следующим шагом является отложение длины отрезка ВС с помощью циркуля на диаметральной линии. Перпендикулярно отрезку ОА появляется точка D. Точки В и D соединяются, образуя новый отрезок.

Для того, чтобы получить величину стороны пентагона, необходимо соединить точки С и D.
D с помощью циркуля переносится на окружность и обозначается точкой Е. Соединив Е и С, можно получить первую сторону правильного пятиугольника. Следуя этой инструкции можно узнать о том, как быстро построить пятиугольник с равными сторонами, продолжая построение остальных его сторон подобно первой.

В пятиугольнике с одинаковыми сторонами диагонали равны и образуют пятиконечную звезду, которая называется пентаграммой. Золотое сечение — это отношение величины диагонали к стороне пентагона.

Пентагон непригоден для полного заполнения плоскости. Использование любого материала в этой форме оставляет промежутки или образует наложения. Хотя природных кристаллов этой формы не существует в природе, но при образовании льда на поверхности гладких медных изделий возникают молекулы в виде пентагона, которые соединены в цепочки.

Наиболее простой способ получить правильный пятиугольник из полоски бумаги — завязать ее узлом и немного придавить. Этот способ полезен для родителей детей-дошкольников, которые хотят научить своих малышей распознавать геометрические фигуры.

Видео

Посмотрите, как можно быстро начертить пятиугольник.

Построение вписанного в окружность правильного шестиугольника. Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой (фиг. 60, а).

Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг. 60, б), строим стороны 1 -6, 4-3, 4-5 и 7-2, после чего проводим стороны 5-6 и 3-2.

Построение вписанного в окружность равностороннего треугольника . Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля.

Рассмотрим два способа построения вписанного в окружность равностороннего треугольника.

1-2 достаточно построить по точке 1 и стороне 0-1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1-2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2-3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника.

Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вершины через одну, то получится равносторонний треугольник.

Для построения треугольника (фиг. 61, б) намечаем на диаметре вершину-точку 1 и проводим диаметральную линию 1-4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника.

Построение квадрата, вписанного в окружность . Это построение можно выполнить при помощи угольника и циркуля.

Первый способ основан на том, что диагонали квадрата пересекаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные стороны квадрата 4-1 и 3-2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1-2 и 4-3.

Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра (фиг. 62, б). Намечаем на концах двух взаимно перпендикулярных диаметров точки А, В и С и из них радиусом у описываем дуги до взаимного их пересечения.

Далее через точки пересечения дуг проводим вспомогательные прямые, отмеченные на фигуре сплошными линиями. Точки их пересечения с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.

Построение вписанного в окружность правильного пятиугольника.

Чтобы вписать в окружность правильный пятиугольник (фиг. 63), производим следующие построения.

Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой.

Построение правильного пятиугольника по данной его стороне.

Получим точку 1-вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведёнными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.

Построение вписанного в окружность правильного семиугольника.

Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг.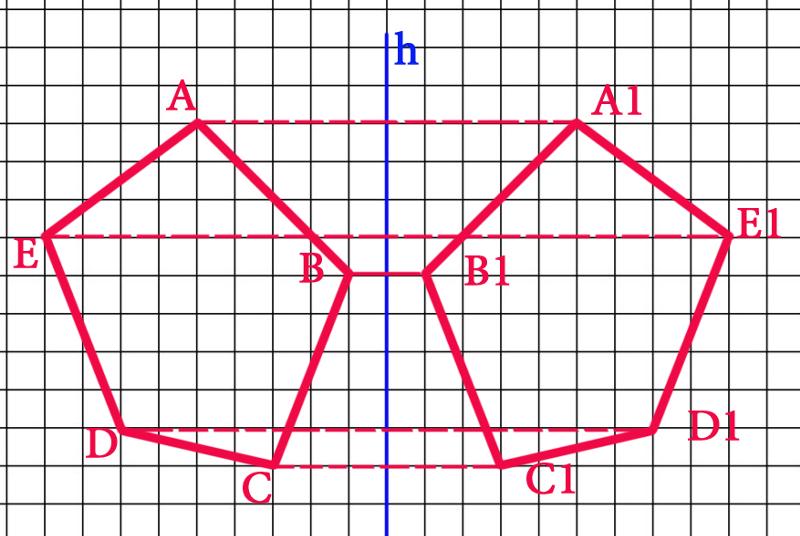 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проводим из полюса F через чётные деления вертикального диаметра лучи, пересечение которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.

Приведённый способ годен для построения правильных многоугольников с любым числом сторон.

Деление окружности на любое число равных частей можно производить также, пользуясь данными табл. 2, в которой приведены коэффициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.

Построение вписанного в окружность правильного пятиугольника. Дан правильный многоугольник, число сторон которого представляет собой произведение натуральных чисел k и m, где m>2. Как построить правильный m-угольник? Гаусс показал также возможность построения правильного 257-угольника с помощью циркуля и линейки.

Построить пятиугольник и поможет именно эта окружность. В первую очередь необходимо построить циркулем окружность. Аналогичным образом необходимо построить еще один круг. Центр его в G. Точка пересечения его с первоначальной окружностью пусть будет H. Это последняя вершина правильного многоугольника.

Правда, процесс это достаточно длительный, как, впрочем, и построение любого правильного многоугльника с нечетным количеством сторон. Она и представляет собой многоугольник, остается только ввести параметры. Число сторон может достигать 1024. Можно использовать и командную строку, в зависимости от версии набрав « _polygon» или «мн.-угол».

Деление окружности на равные части и вписывание правильных многоугольников.

Введите туда цифру «5» и нажмите Enter. Вам будет предложено определить центр пятиугольника. Можно обозначить их как (0,0), но могут быть и любые другие данные. Пятиугольник может быть описанным вокруг окружности или вписанным в нее, но можно построить его и по заданному размеру стороны. Пятиугольник по заданной стороне сначала строится точно так же. Выберите «Рисование», замкнутую полилинию и введите число сторон.

В командной строке наберите координаты начальной и конечной точек одной из сторон пятиугольника. После этого пятиугольник появится на экране. Таким нехитрым способом можно построить не только пятиугольник. Для того чтобы построить треугольник, необходимо разведите ножки циркуля на расстояние, равное радиусу окружности.

Две точки пересечения окружностей, а так же точка, в которой была ножка циркуля образуют три вершины правильного треугольника. Оказалось, что есть несколько различных вариантов построения правильного пятиугольника, разработанных известными математиками.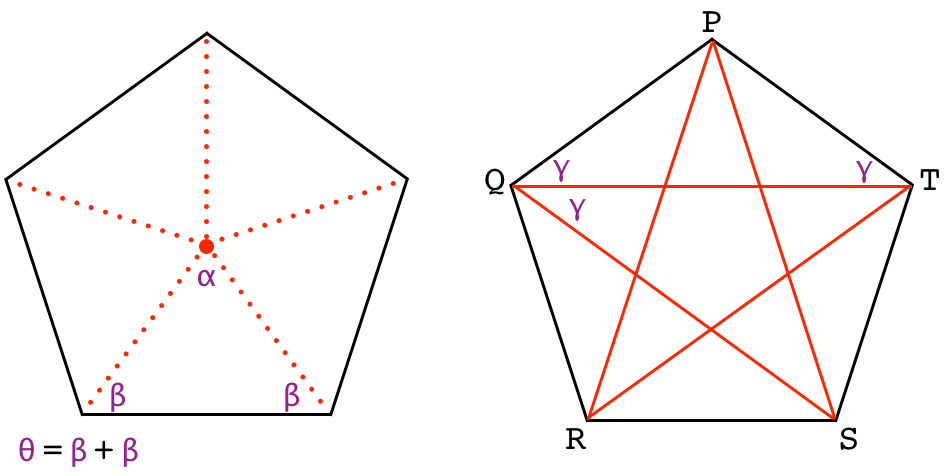 Восьмиугольник — это геометрическая фигура с восемью углами. Правильный восьмиугольник – это восьмиугольник, у которого все стороны (и углы) равны. Эта статья расскажет вам, как сделать восьмиугольник.

Окружность, дуги и многоугольники.

Определите длину стороны восьмиугольника (углы правильного восьмиугольника известны). На листе бумаги при помощи линейки нарисуйте прямую линию выбранной длины. Это первая сторона восьмиугольника (нарисуйте ее так, чтобы оставить место для рисования других сторон). Используя транспортир, отложите угол в 135o (от начала или конца первой стороны). Нарисуйте третью линию выбранной длины под углом в 135o ко второй линии. Продолжайте до тех пор, пока у вас не получится правильный восьмиугольник.

Таким образом, чем больше окружность, тем больше фигура (и наоборот). Нарисуйте вторую большую окружность, установив иглу циркуля в центре первой окружности. Установите иглу циркуля в прямо противоположной точке пересечения внутренней (малой) окружности и ее диаметра. У вас получится «глаз» в середине окружности. Нарисуйте две дуги, пересекающие внутреннюю окружность.

Построение правильных многоугольников по заданной стороне

Сотрите окружности, линии и дуги, оставив только восьмиугольник. Таким образом, вы придадите ему восьмиугольную форму. Используйте линейку, чтобы убедиться, что все стороны получились равными (так как вы делаете правильный восьмиугольник). Не загибайте углы так, чтобы они соприкасались друг с другом; в этом случае вы получите не восьмиугольник, а небольшой квадрат. Зачастую, когда говорят «восьмиугольник», имеют в виду правильный восьмиугольник.

Смотреть что такое «Правильный пятиугольник» в других словарях:

Таким образом, создав фигуру с восемью сторонами разной длины, вы получите неправильный восьмиугольник. Существуют многоугольники с пересекающимися сторонами. Например, пятиконечная звезда является многоугольником с пересекающимися сторонами. Правильные многоугольники уже в глубокой древности считались символом красоты и совершенства. Практическая задача построения таких многоугольников с помощью циркуля и линейки имеет давнюю историю.

Лишь в 1796 г. К. Ф. Гаусc доказал принципиальную невозможность этого построения с помощью только циркуля и линейки. В настоящем параграфе мы предлагаем вам самим поискать способы построения правильных многоугольников, вписанных в данную окружность или имеющих заданную сторону. Не менее важное практическое значение имеют методы приближенного построения в тех случаях, когда точное построение циркулем и линейкой неосуществимо.

Правильный пятиугольник — это многоугольник, у которого все пять сторон и все пять углов равны между собой. Вокруг него легко описать окружность. Теперь на окружности радиуса AО от любой точки последовательно отложим 11 дуг, каждая из которых равна дуге АВ. Получим вершины правильного двенадцатиугольника. Построение правильного пятиугольника по данной его стороне. Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника.

Задача построения верного пятиугольника сводится к задаче деления окружности на пять равных частей. От того что верный пятиугольник – это одна из фигур, содержащая в себе пропорции золотого сечения, его построением издавна интересовались живописцы и математики. Сейчас обнаружены несколько методов построения верного многоугольника, вписанного в заданную окружность.

Вам понадобится

– линейка
– циркуль

Инструкция

1. Видимо, что если возвести верный десятиугольник, а после этого объединить его вершины через одну, то получим пятиугольник. Для построения десятиугольника начертите окружность заданного радиуса. Обозначьте ее центр буквой O. Проведите два перпендикулярных друг друга радиуса, на рисунке они обозначены как OA1 и OB. Радиус OB поделите напополам с подмогой линейки либо способом деления отрезка напополам с подмогой циркуля. Постройте маленькую окружность с центром C в середине отрезка OB радиусом, равным половине OB.Объедините точку C с точкой A1 на начальной окружности по линейке. Отрезок CA1 пересекает вспомогательную окружность в точке D. Отрезок DA1 равен стороне верного десятиугольника, вписанного в данную окружность. Циркулем подметьте данный отрезок на окружности, после этого объедините точки пересечения через одну и вы получите положительный пятиугольник.

2. Еще один метод обнаружил немецкий художник Альбрехт Дюрер. Дабы возвести пятиугольник по его методу, начните вновь с построения окружности. Вновь подметьте ее центр O и проведите два перпендикулярных радиуса OA и OB. Радиус OA поделите напополам и середину подметьте буквой C. Установите иглу циркуля в точку C и раскройте его до точки B. Проведите окружность радиуса BC до пересечения с диаметром начальной окружности, на котором лежит радиус OA. Точку пересечения обозначьте D. Отрезок BD – сторона положительного пятиугольника. Отложите данный отрезок пять раз на начальной окружности и объедините точки пересечения.

3. Если же требуется возвести пятиугольник по его заданной стороне, то вам надобен 3-й метод. Начертите по линейке сторону пятиугольника, обозначьте данный отрезок буквами A и B.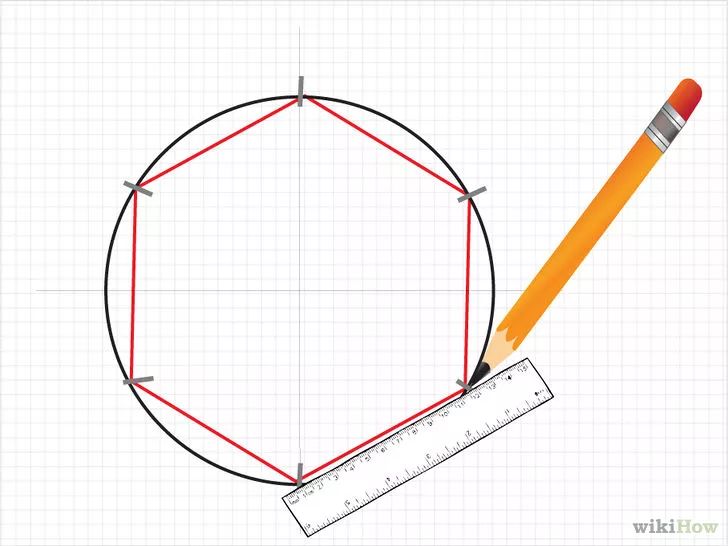 Поделите его на 6 равных частей. Из середины отрезка AB проведите луч, перпендикулярный отрезку. Постройте две окружности радиусом AB и центрами в A и B, как если бы вы собирались разделять отрезок напополам. Эти окружности пересекаются в точке С. Точка C при этом лежит на луче, исходящем перпендикулярно вверх из середины AB. Отложите от C вверх по этому лучу расстояние, равное 4/6 от длины AB, обозначьте эту точку D. Постройте окружность радиуса AB с центром в точке D. Пересечение этой окружности с двумя вспомогательными построенными ранее даст последние две вершины пятиугольника.

Тема деления окружности на равные части с целью построения верных вписанных многоугольников издавна занимала умы древних ученых. Эти тезисы построения с использованием циркуля и линейки были высказаны еще в эвклидовых «Началах». Впрочем лишь через два тысячелетия эта задача была всецело решена не только графически, но и математически.

Инструкция

1. Приближенное построение положительного пятиугольника методом А. Дюрера, с подмогой циркуля и линейки (через две окружности с всеобщим радиусом, равным стороне пятиугольника ).

2. Построение верного пятиугольника на основе положительного десятиугольника, вписанного в окружность (объединив вершины десятиугольника через одну).

3. Графическое построение через вычисленный внутренний угол пятиугольника с поддержкой транспортира и линейки (сумма углов выпуклого n-угольника равна Sn=180°(n – 2), т.к. у положительного многоугольника все углы равны). При n=5, S5=5400, тогда величина угла 1080.А так же с поддержкой окружности и 2-х лучей, выходящих из ее центра, при условии, что угол между ними равен 720, т.к. (36005=720). Их пересечение с окружностью даст отрезок, равный стороне пятиугольника .

4. Еще один легкой графический метод: поделить диаметр заданной окружности AB на три части (AC=CD=DE). Из точки D опустить перпендикуляр до пересечения с окружность в точках E, F.Проведя прямые через отрезки EC и FC до пересечения с окружностью, получим точки G, H.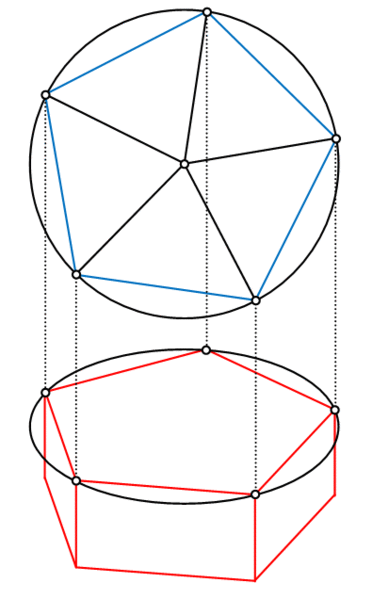 Точки G,E,B,F,H – вершины положительного пятиугольника .

5. Построение с поддержкой приема Биона (дозволяющего возвести верный вписанный в окружность многоугольник с любым числом сторон n по заданному соотношению).Скажем: для n=5. Возведем положительный треугольник ABC, где AB – диаметр заданной окружности. Обнаружим на AB точку D, по дальнейшему соотношению: AD: AB = 2: n. При n=5, AD=25*AB. Проведем прямую через CD до пересечения с окружностью в точке E. Отрезок AE – сторона верного вписанного пятиугольника .При n=5,7,9,10 погрешность построения не превышает 1%. С возрастанием n, погрешность приближения растёт, но остаётся поменьше 10,3%.

6. Построение по заданной стороне по способу Л. Да Винчи (применяя соотношение между стороной многоугольника (аn) и апофемой (ha): аn/2: ha =3/(n-1), которое дозволено выразить так: tg180°/n =3/(n-1)).

7. Всеобщий метод построения положительных многоугольников по заданной стороне по способу Ф. Коваржика (1888 г.), на основе правила Л. да Винчи.Цельный метод построения положительного n-угольника на основании теоремы Фалеса.Дозволено добавить только, что приближенные способы построения многоугольников подлинны, примитивны и прекрасны.

Существуют два основных метода построения верного многоугольника с пятью сторонами. Оба они полагают применение циркуля, линейки и карандаша. 1-й метод представляет собой вписывание пятиугольника в окружность, а 2-й метод базируется на заданной длине стороны вашей грядущей геометрической фигуры.

Вам понадобится

Циркуль, линейка, карандаш

Инструкция

1. 1-й метод построения пятиугольника считается больше «типичным». Для начала постройте окружность и как-либо обозначьте ее центр (обычно для этого применяется буква О). После этого проведите диаметр этой окружности (назовем его АВ) и поделите один из 2-х полученных радиусов (скажем, ОА) ровно напополам. Середину этого радиуса обозначим буквой С.

2. Из точки О (центра начальной окружности) проведите еще один радиус (ОD), тот, что будет сурово перпендикулярен проведенному ранее диаметру (АВ). После этого возьмите циркуль, поставьте его в точку С и отмерьте расстояние до пересечения нового радиуса с окружностью (СD). Это же расстояние отложите на диаметре АВ. Вы получите новую точку (назовем ее Е). Отмерьте циркулем расстояние от точки D до точки Е – оно будет равно длине стороны вашего грядущего пятиугольника .

3. Поставьте циркуль в точку D и отложите на окружности расстояние, равное отрезку DЕ. Повторите эту процедуру еще 3 раза, а после этого объедините точку D и 4 новые точки на начальной окружности. Получившаяся в итоге построения фигура будет верным пятиугольником.

4. Дабы возвести пятиугольник иным методом, для начала начертите отрезок. Скажем, это будет отрезок АВ длиной 9 см. Дальше поделите ваш отрезок на 6 равных частей. В нашем случае длина всякой части будет составлять 1,5 см. Сейчас возьмите циркуль, поставьте его в один из концов отрезка и проведите окружность либо дугу с радиусом, равным длине отрезка (АВ). После этого переставьте циркуль в иной конец и повторите операцию. Полученные окружности (либо дуги) пересекутся в одной точке. Назовем ее C.

5. Сейчас возьмите линейку и проведите прямую через точку С и центр отрезка AB. После этого начиная от точки С отложите на этой прямой отрезок, составляющий 4/6 отрезка AB. 2-й конец отрезка обозначим буквой D. Точка D будет являться одной из вершин грядущего пятиугольника . Из этой точки проведите окружность либо дугу с радиусом, равным АВ. Эта окружность (дуга) пересечет ранее построенные вами окружности (дуги) в точках, являющихся двумя недостающими вершинами пятиугольника . Объедините эти точки с вершинами D, А и В, и построение положительного пятиугольника будет закончено.

Видео по теме

Луч — это прямая линия, проведенная из точки и не имеющая конца. Существуют и другие определения луча: скажем, «…это прямая, ограниченная точкой с одной стороны». Как положительно начертить луч и какие принадлежности для черчения вам потребуются?

Вам понадобится

Лист бумаги, карандаш и линейка.

Инструкция

1. Возьмите лист бумаги и подметьте в произвольном месте точку. После этого приложите линейку и проведите линию, начиная с указанной точки и до бесконечности. Эта нарисованная линия и именуется лучом. Сейчас подметьте на луче еще одну точку, к примеру, буквой C. Линия от исходной и до точки C будет именоваться отрезком. Если вы примитивно начертите линию и не подметите правда бы одну точку, то эта прямая не будет являться лучом.

2. Нарисовать луч в любом графическом редакторе либо в том же MSOffice не труднее, чем вручную. Для примера возьмите программу Microsoft Office 2010. Зайдите в раздел «Вставка» и выберите элемент «Фигуры». В выпадающем списке выберите фигуру «Линия». Дальше курсор примет вид крестика. Дабы начертить ровную линию, нажмите клавишу «Shift»и проведите линию требуемой длины. Сразу позже начертания откроется вкладка «Формат». Теперь у вас нарисована примитивно прямая линия и отсутствует фиксированная точка, а исходя из определения, луч должен быть лимитирован точкой с одной стороны.

3. Дабы сделать точку в начале линии, сделайте следующее: выделите нарисованную линию и вызовите контекстное меню, нажав правую кнопку мыши.

4. Выберите пункт «Формат фигуры». В меню слева выберите пункт «Тип линии». Дальше обнаружьте заголовок «Параметры линий» и выберите «Тип начала» в виде кружочка. Там же вы можете настроить толщину линий начала и конца.

5. Уберите выделение с линии и увидите, что в начале линии возникла точка. Для создания надписи нажмите кнопку «Нарисовать надпись» и сделайте поле, где будет находиться надпись. Позже написания надписи кликните на свободное место и она активируется.

6. Луч благополучно нарисован и заняло это каждого несколько минут. Рисование луча в иных редакторах осуществляется по такому же тезису. При нажатой клавише «Shift» неизменно будут рисоваться пропорциональные фигуры. Славного пользования.

Видео по теме

Обратите внимание!
Отношение диагонали верного пятиугольника к его стороне составляет золотое сечение (иррациональное число (1+√5)/2).Весь из пяти внутренних углов пятиугольника равен 108°.

Полезный совет
Если объединить вершины верного пятиугольника диагоналями, то получится пентаграмма.

Уровень сложности: Несложно

1 шаг

Сначала, выбирайте, где разместить центр окружности. Там нужно поставить начальную точку, пусть она называется О. С помощью циркуля вычерчиваем вокруг нее окружность заданного диаметра или радиуса.

2 шаг

Затем проводим две оси через точку О, центр окружности, одна горизонтальная, другая под 90 градусов по отношению к ней – вертикальная. Точки пересечения по горизонтали назовем слева на право А и В, по вертикали, сверху вниз – М и Н. Радиус, который лежит на любой оси, например, на горизонтальной в правой части, делим пополам. Это можно сделать так: циркуль с радиусом известной нам окружности устанавливаем острием в точку пересечения горизонтальной оси и окружности – В, отчеркиваем пересечения с окружностью, полученные точки называем, соответственно сверху вниз – С и Р, соединяем их отрезком, который будет пересекать ось ОВ, точку пересечения называем К.

3 шаг

Соединяем точки К и М и получаем отрезок КМ, устанавливаем циркуль в точку М, задаем на нем расстояние до точки К и очерчиваем метки на радиусе ОА, эту точку называем Е, далее ведем циркуль до пересечения с левой верхней частью окружности ОМ. Эту точку пересечения называем F. Расстояние равное отрезку МЕ является искомой стороной равностороннего пятиугольника. При этом точка М будет являться одной вершиной встраиваемого в окружность пятиугольника, а точка F – другой.

4 шаг

Далее из полученных точек по всей окружности отчерчиваем циркулем расстояния, равные отрезку МЕ, всего точек должно получиться 5. Соединяем все точки отрезками – получаем пятиугольник, вписанный в окружность.

При черчении будьте аккуратны в измерениях расстояний, не допускайте погрешностей, чтобы пятиугольник действительно полчился равносторонним

Начерти от руки треугольник квадрат круг пятиугольник. Построение правильного пятиугольника. Деление окружности на равные части и вписывание правильных многоугольников

Деление окружности на равные части и вписывание правильных многоугольников.

Окружность, дуги и многоугольники.

Построение правильных многоугольников по заданной стороне

Смотреть что такое «Правильный пятиугольник» в других словарях:

{2}};

Правильный пятиугольник (греч. πενταγωνον ) — геометрическая фигура , правильный многоугольник с пятью сторонами.

Свойства

Додекаэдр — единственный из правильных многогранников , грани которого представляют собой правильные пятиугольники.
Пентагон — здание Министерства обороны США имеет форму правильного пятиугольника.
Правильный пятиугольник — правильный многоугольник с наименьшим количеством углов из тех, которыми нельзя замостить плоскость.
В природе не существует кристаллов с гранями в форме правильного пятиугольника.
Пятиугольник со всеми его диагоналями является проекцией 4-симплекса.

См. также

Напишите отзыв о статье «Правильный пятиугольник»

Примечания



По числу сторон

Правильные

Треугольники

Четырёхугольники

См. также



Многоугольники

Звёздчатые многоугольники

Паркеты на плоскости

Правильные многогранники и сферические паркеты

Многогранники Кеплера — Пуансо

Соты

Четырёхмерные многогранники

Отрывок, характеризующий Правильный пятиугольник

Петя не знал, как долго это продолжалось: он наслаждался, все время удивлялся своему наслаждению и жалел, что некому сообщить его. Его разбудил ласковый голос Лихачева.
– Готово, ваше благородие, надвое хранцуза распластаете.
Петя очнулся.
– Уж светает, право, светает! – вскрикнул он.
Невидные прежде лошади стали видны до хвостов, и сквозь оголенные ветки виднелся водянистый свет. Петя встряхнулся, вскочил, достал из кармана целковый и дал Лихачеву, махнув, попробовал шашку и положил ее в ножны. Казаки отвязывали лошадей и подтягивали подпруги.
– Вот и командир, – сказал Лихачев. Из караулки вышел Денисов и, окликнув Петю, приказал собираться.

Быстро в полутьме разобрали лошадей, подтянули подпруги и разобрались по командам. Денисов стоял у караулки, отдавая последние приказания. Пехота партии, шлепая сотней ног, прошла вперед по дороге и быстро скрылась между деревьев в предрассветном тумане. Эсаул что то приказывал казакам. Петя держал свою лошадь в поводу, с нетерпением ожидая приказания садиться. Обмытое холодной водой, лицо его, в особенности глаза горели огнем, озноб пробегал по спине, и во всем теле что то быстро и равномерно дрожало.
– Ну, готово у вас все? – сказал Денисов. – Давай лошадей.
Лошадей подали. Денисов рассердился на казака за то, что подпруги были слабы, и, разбранив его, сел. Петя взялся за стремя. Лошадь, по привычке, хотела куснуть его за ногу, но Петя, не чувствуя своей тяжести, быстро вскочил в седло и, оглядываясь на тронувшихся сзади в темноте гусар, подъехал к Денисову.
– Василий Федорович, вы мне поручите что нибудь? Пожалуйста… ради бога… – сказал он. Денисов, казалось, забыл про существование Пети. Он оглянулся на него.
– Об одном тебя пг»ошу, – сказал он строго, – слушаться меня и никуда не соваться.
Во все время переезда Денисов ни слова не говорил больше с Петей и ехал молча. Когда подъехали к опушке леса, в поле заметно уже стало светлеть. Денисов поговорил что то шепотом с эсаулом, и казаки стали проезжать мимо Пети и Денисова. Когда они все проехали, Денисов тронул свою лошадь и поехал под гору. Садясь на зады и скользя, лошади спускались с своими седоками в лощину. Петя ехал рядом с Денисовым. Дрожь во всем его теле все усиливалась. Становилось все светлее и светлее, только туман скрывал отдаленные предметы. Съехав вниз и оглянувшись назад, Денисов кивнул головой казаку, стоявшему подле него.
– Сигнал! – проговорил он.
Казак поднял руку, раздался выстрел. И в то же мгновение послышался топот впереди поскакавших лошадей, крики с разных сторон и еще выстрелы.
В то же мгновение, как раздались первые звуки топота и крика, Петя, ударив свою лошадь и выпустив поводья, не слушая Денисова, кричавшего на него, поскакал вперед. Пете показалось, что вдруг совершенно, как середь дня, ярко рассвело в ту минуту, как послышался выстрел. Он подскакал к мосту. Впереди по дороге скакали казаки. На мосту он столкнулся с отставшим казаком и поскакал дальше. Впереди какие то люди, – должно быть, это были французы, – бежали с правой стороны дороги на левую. Один упал в грязь под ногами Петиной лошади.
У одной избы столпились казаки, что то делая. Из середины толпы послышался страшный крик. Петя подскакал к этой толпе, и первое, что он увидал, было бледное, с трясущейся нижней челюстью лицо француза, державшегося за древко направленной на него пики.
– Ура!.. Ребята… наши… – прокричал Петя и, дав поводья разгорячившейся лошади, поскакал вперед по улице.
Впереди слышны были выстрелы. Казаки, гусары и русские оборванные пленные, бежавшие с обеих сторон дороги, все громко и нескладно кричали что то. Молодцеватый, без шапки, с красным нахмуренным лицом, француз в синей шинели отбивался штыком от гусаров. Когда Петя подскакал, француз уже упал. Опять опоздал, мелькнуло в голове Пети, и он поскакал туда, откуда слышались частые выстрелы. Выстрелы раздавались на дворе того барского дома, на котором он был вчера ночью с Долоховым. Французы засели там за плетнем в густом, заросшем кустами саду и стреляли по казакам, столпившимся у ворот. Подъезжая к воротам, Петя в пороховом дыму увидал Долохова с бледным, зеленоватым лицом, кричавшего что то людям. «В объезд! Пехоту подождать!» – кричал он, в то время как Петя подъехал к нему.
– Подождать?.. Ураааа!.. – закричал Петя и, не медля ни одной минуты, поскакал к тому месту, откуда слышались выстрелы и где гуще был пороховой дым. Послышался залп, провизжали пустые и во что то шлепнувшие пули. Казаки и Долохов вскакали вслед за Петей в ворота дома. Французы в колеблющемся густом дыме одни бросали оружие и выбегали из кустов навстречу казакам, другие бежали под гору к пруду. Петя скакал на своей лошади вдоль по барскому двору и, вместо того чтобы держать поводья, странно и быстро махал обеими руками и все дальше и дальше сбивался с седла на одну сторону. Лошадь, набежав на тлевший в утреннем свето костер, уперлась, и Петя тяжело упал на мокрую землю. Казаки видели, как быстро задергались его руки и ноги, несмотря на то, что голова его не шевелилась. Пуля пробила ему голову.
Переговоривши с старшим французским офицером, который вышел к нему из за дома с платком на шпаге и объявил, что они сдаются, Долохов слез с лошади и подошел к неподвижно, с раскинутыми руками, лежавшему Пете.
– Готов, – сказал он, нахмурившись, и пошел в ворота навстречу ехавшему к нему Денисову.
– Убит?! – вскрикнул Денисов, увидав еще издалека то знакомое ему, несомненно безжизненное положение, в котором лежало тело Пети.
– Готов, – повторил Долохов, как будто выговаривание этого слова доставляло ему удовольствие, и быстро пошел к пленным, которых окружили спешившиеся казаки. – Брать не будем! – крикнул он Денисову.

Эта фигура является многоугольником с минимальным количеством углов, которым невозможно замостить площадь. Только у пятиугольника количество диагоналей совпадает с количеством его сторон. Воспользовавшись формулами для произвольного правильного многоугольника, можно определить все необходимые параметры, которые имеет пентагон. Например, вписать его в окружность с заданным радиусом либо построить на базе заданной боковой стороны.

Как правильно начертить луч и какие принадлежности для черчения вам понадобятся? Возьмите листок бумаги и отметьте в произвольном месте точку. Затем приложите линейку и проведите линию, начиная с указанной точки и до бесконечности. Чтобы начертить ровную линию, нажмите клавишу «Shift»и проведите линию нужной длины. Сразу после начертания откроется вкладка «Формат». Уберите выделение с линии и увидите, что в начале линии появилась точка. Для создания надписи нажмите кнопку «Нарисовать надпись» и создайте поле, где будет находиться надпись.

Первый способ построения пятиугольника считается более «классическим». Получившаяся в результате построения фигура будет правильным пятиугольником. Двенадцатиугольник не является исключением, поэтому его построение будет невозможным без применения циркуля. Задача построения правильного пятиугольника сводится к задаче деления окружности на пять равных частей. Начертить пентаграмму можно с использованием простейших инструментов.

Я долго бился пытаясь этого добиться и самостоятельно найти пропорции и зависимости, но мне этого не удалось. Оказалось, что есть несколько различных вариантов построения правильного пятиугольника, разработанных известными математиками. Инересным моментов является то, что арифметически эту задачу решить только приблизительно точно, поскольку придется использовать иррациональные числа. Зато ее можно решить геометрически.

Деление окружностей. Точки пересечения этих линий с окружностью и являются вершинами квадрата. В окружности радиуса R (Шаг 1) следует провести вертикальный диаметр. В точке сопряжения N прямой и окружности прямая является касательной к окружности.

Получение с помощью полоски бумаги

Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля. Чтобы построить сторону 2-3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника. Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.

А на другой конец нитки устанавливаемые карандаш и одержим. Если умеете чертить звезду, но не умеете пятиугольник, начертите звезду карандашом, затем соедините между собой соседние концы звезды, а саму звезду потом сотрите. Затем положите лист бумаги (лучше его закрепить на столе при помощи четырёх кнопок или иголочек). Приколите эти 5 полосочек к листку бумаги кнопками или иголочками, чтобы они оставались неподвижными. Затем обведите полученный пятиугольник и снимите эти полосочки с листка.

Например, нам нужно нарисовать пятиконечную звезду (пентаграмму) для картины о Советском прошлом или о настоящем Китая. Правда для этого нужно уметь создать рисунок звезды в перспективе. Точно так же вы сможете нарисовать фигуру карандашом на бумаге. Как правильно нарисовать звезду, что бы она выглядела ровно и красиво, сразу не ответишь.

С центра опусти на окружность 2 луча, чтоб угол между ними был 72 градуса (транспортиром). Деление круга на пять частей осуществляется с помощью обычного циркуля или транспортира. Поскольку правильный пятиугольник — это одна из фигур, содержащая в себе пропорции золотого сечения, его построением издавна интересовались живописцы и математики. Эти принципы построения с применением циркуля и линейки были изложены еще в эвклидовых «Началах».

Если под руками нет циркуля, то можно нарисовать простую звезду с пятью лучами затем просто соединить эти лучи. как видим на картинке ниже получается абсолютно правильный пятиугольник.

Математика сложная наука и у нее много своих секретиков, некоторые из них весьма забавны. Если вы увлекаетесь такими вещами советую найти книгу Забавная математика.

Окружность можно нарисовать не только при помощи циркуля. Можно, например, использовать карандаш и нитку. Отмеряем нужный диаметр на нитке. Один конец плотно зажимаем на листе бумаги, где будем чертить окружность. А на другой конец нитки устанавливаемые карандаш и одержим. Теперь действует как с циркулем: натягиваем нить и по окружности слегка надавливая карандашом чкртим окружность.

Внутри окружности рисуем крестьян от центра: вертикальная линия и горизонтальная линия. Точка пересечения вертикальной линии и окружности будет вершиной пятиугольника (точка 1). Теперь правую половину горизонтальной линии делим пополам (точка 2). Измеряем расстояние от этой точки до вершины пятиугольника и этот отрезок откладывает влево от точки 2 (точка 3). При помощи нитки и карандаша проводим от точки 1 радиусом до точки 3 дугу, пересекающую первую окружность слева и справа — точки пересечения будут вершинами пятиугольника. Обозначим их точка 4 и 5.

Теперь от точки 4 делаем дугу, пересекающую окружность в нижней части, радиусом равной длине от точки 1 до 4 — это будет точкой 6. Точно так же и от точки 5 — обозначим точкой 7.

Остатся соединить наш пятиугольник с вершинами 1, 5, 7, 6, 4.

Я знаю как построить простой пятиугольник с помощью циркуля: Строим окружность, отмечаем пять точек, соединяем их. Можно построить пятиугольник с равными сторонами, для этого нам еще понадобится транспортир. Просто те же самые 5 точек ставим по транспортиру. Для этого отмечаем углы по 72 градуса. После чего также соединяем отрезками и получаем нужную нам фигуру.

Зеленую окружность можно чертить произвольным радиусом. В эту окружность будем вписывать правильный пятиугольник. Без циркуля начертить точно окружность нельзя, но это не обязательно. Окружность и все дальнейшие построения можно выполнять от руки. Далее через центр окружности О нужно провести две взаимно перпендикулярные прямые и одну из точек пересечения прямой с окружностью обозначить А. Точка А будет вершиной пятиугольника. Радиус ОВ разделим пополам и поставим точку С. Из точки С проводим вторую окружность радиусом АС. Из точки А проводим третью окружность радиусом АD. Точки пересечения третьей окружности с первой (Е и F)будут также вершинами пятиугольника. Из точек Е и F радиусом АЕ делаем засечки на первой окружности и получаем остальные вершины пятиугольника G и H.

Адептам черного искусства: что бы просто, красиво и быстро нарисовать пятиугольник, следует начертить правильную, гармоничную основу для пентаграммы (пятиконечная звезда) и соединить окончания лучей этой звезды посредством прямых, ровных линий. Если все было сделано верно — соединительная черта вокруг основы и будет искомым пятиугольником.

(на рисунке — завершенная, но незаполненная пентаграмма)

Для тех, кто неуверен в правильности начертания пентаграммы: возьмите за основу витрувианского человека Да Винчи (см. ниже)

Если нужен пятиугольник — тыкаете произвольным образом 5 точке и их внешний контур будет пятиугольником.

Если нужен правильный пятиугольник, то без математического циркуля это построение совершить невозможно, поскольку без него нельзя провести два одинаковых, но не параллельных отрезка. Любой другой инструмент, который позволяет провести два одинаковых, но не параллельных отрезка эквивалентен математическому циркулю.

Сначала надо надо начертить круг, потом направляющие, потом второй пунктирный круг, находим верхнюю точку, потом отмеряем два угла верхние, от них чертим нижние. Заметьте, радиус циркуля один и тот же при всем построении.

Вс зависит от того, какой пятиугольник вам необходим. Если любой, то ставите пять точек и соединяете их между собой(естествено точки ставим не по прямой линии). А если нужен пятиугольник правильно формы, возьмите любые пять по длине(полосок бумаги, спичек, карандашей и т.п), выложите пятиугольник и обчертите его.

Пятиугольник можно начертить, к примеру, из звезды. Если умеете чертить звезду, но не умеете пятиугольник, начертите звезду карандашом, затем соедините между собой соседние концы звезды, а саму звезду потом сотрите.

Второй способ. Вырежьте полосочку из бумаги, длиной, равной желаемой стороне пятиугольника, а шириной узкой, допустим 0.5 — 1 см. Как по шаблону, вырежьте по этой полосочке ещ четыре таких же полосочки, чтобы их получилось всего 5.

Затем положите лист бумаги (лучше его закрепить на столе при помощи четырх кнопок или иголочек). Затем наложите эти 5 полосочек на листок так, чтобы они образовали пятиугольник. Приколите эти 5 полосочек к листку бумаги кнопками или иголочками, чтобы они оставались неподвижными. Затем обведите полученный пятиугольник и снимите эти полосочки с листка.

Если нет циркуля и нужно построить пятиугольник, то я могу посоветовать следующее. Я и сама так строила. Можно начертить правильную пятиконечную звезду. И после этого, чтобы получить пятиугольник, просто нужно соединить все вершины звезды. Вот так и получится пятиугольник. Вот что мы получим

Ровными чрными линии мы соединили вершины звезды и получили пятиугольник.

Параметры правильного пятиугольника

сумма всех углов в многоугольниках равна 360 градусам. В правильном пятиугольнике все углы равны, соответственно, центральный угол находится таким способом: 360/5 = 72 градуса;
внутренний угол находится таким образом: 180*(n -2)/ n = 180*(5−2)/5 = 108 градусов. Сумма всех внутренних углов: 108*5 = 540 градусов.

Сторона пентагона находится с помощью параметров, которые уже даны в условии задачи:

если вокруг пятиугольника описана окружность и известен ее радиус, сторона находится по такой формуле: a = 2*R*sin (α/2) = 2*R*sin (72/2) = 1,1756*R.
Если известен радиус вписанной в пентагон окружности, то формула расчета стороны многоугольника: 2*r*tg (α/2) = 2*r*tg (α/2) = 1,453*r.
При известной величине диагонали пентагона его сторона рассчитывается таким образом: а = D/1,618.

Площадь пентагона так же , как и его сторона, зависит от уже найденных параметров:

с помощью известного радиуса вписанной окружности площадь находится так: S = (n*a*r)/2 = 2,5*a*r.
описанная вокруг пятиугольника окружность позволяет найти площадь по такой формуле: S = (n*R2*sin α)/2 = 2,3776*R2.
в зависимости от стороны пентагона: S = (5*a2*tg 54°)/4 = 1,7205* a2.

Построение пентагона

Сначала необходимо начертить окружность с центром О, после чего на ней выбрать точку, А — вершину пентагона. От центра к вершине проводится отрезок.
Затем строится перпендикулярная прямой ОА отрезок, который также проходит через О — центр окружности. Его пересечение с окружностью обозначается точкой В. Отрезок О. В. делится пополам точкой С.
Точка С станет центром новой окружности, проходящей через А. Точка D — это ее пересечение с прямой ОВ в границах первой фигуры.
После этого проводится третья окружность через D, центром которой является точка А. Она пересекается с первой фигурой в двух точках, их необходимо обозначить буквами Е и F.
Следующая окружность имеет центр в точке Е и проходит через А, а ее пересечение с первоначальной находится в новой точке G.
Последняя окружность в этом рисунке проводится через точку, А с центром F. На ее пересечении с начальной ставится точка Н.
На первой окружности после всех проделанных шагов появились пять точек, которые необходимо соединить отрезками. Таким образом получился правильный пятиугольник АЕ G Н F.

Cначала необходимо с помощью циркуля нарисовать окружность, центр которой — точка О.
Чертится радиус ОА — отрезок, который откладывается на окружность. Его делят пополам точкой В.
Перпендикулярно радиусу ОА начерчивается отрезок ОС, точки В и С соединяются прямой.
Следующим шагом является отложение длины отрезка ВС с помощью циркуля на диаметральной линии. Перпендикулярно отрезку ОА появляется точка D. Точки В и D соединяются, образуя новый отрезок.
Для того, чтобы получить величину стороны пентагона, необходимо соединить точки С и D.
D с помощью циркуля переносится на окружность и обозначается точкой Е. Соединив Е и С, можно получить первую сторону правильного пятиугольника. Следуя этой инструкции можно узнать о том, как быстро построить пятиугольник с равными сторонами, продолжая построение остальных его сторон подобно первой.

Видео

Посмотрите, как можно быстро начертить пятиугольник.

Как сделать правильный пятиугольник. Как построить пятиугольник с помощью циркуля

Толковый словарь Ожегова гласит, что пятиугольник представляет собой ограниченную пятью пересекающимися прямыми, образующими пять внутренних углов, а также любой предмет подобной формы. Если у данного многоугольника все стороны и углы одинаковые, то он называется правильным (пентагоном).

Чем интересен правильный пятиугольник?

Именно в такой форме было построено всем известное здание Минобороны Соединенных Штатов. Из объемных правильных многогранников лишь додекаэдр имеет грани в форме пентагона. А в природе напрочь отсутствуют кристаллы, грани которых напоминали бы собой правильный пятиугольник. Кроме того, эта фигура является многоугольником с минимальным количеством углов, которым невозможно замостить площадь. Только у пятиугольника количество диагоналей совпадает с количеством его сторон. Согласитесь, это интересно!

Основные свойства и формулы

Воспользовавшись формулами для произвольного правильного многоугольника, можно определить все необходимые параметры, которые имеет пентагон.

Центральный угол α = 360 / n = 360/5 =72°.
Внутренний угол β = 180° * (n-2)/n = 180° * 3/5 = 108°. Соответственно, сумма внутренних углов составляет 540°.
Отношение диагонали к боковой стороне равно (1+√5) /2, то есть (примерно 1,618).
Длина стороны, которую имеет правильный пятиугольник, может быть рассчитана по одной из трех формул, в зависимости от того, какой параметр уже известен:

если вокруг него описана окружность и известен ее радиус R, то а = 2*R*sin (α/2) = 2*R*sin(72°/2) ≈1,1756*R;
в случае, когда окружность c радиусом r вписана в правильный пятиугольник, а = 2*r*tg(α/2) = 2*r*tg(α/2) ≈ 1,453*r;
бывает так, что вместо радиусов известна величина диагонали D, тогда сторону определяют следующим образом: а ≈ D/1,618.

Площадь правильного пятиугольника определяется, опять-таки, в зависимости от того, какой параметр нам известен:
если имеется вписанная или описанная окружность, то используется одна из двух формул:

S = (n*a*r)/2 = 2,5*a*r либо S = (n*R 2 *sin α)/2 ≈ 2,3776*R 2 ;

площадь можно также определить, зная лишь длину боковой стороны а:

S = (5*a 2 *tg54°)/4 ≈ 1,7205* a 2 .

Правильный пятиугольник: построение

Данную геометрическую фигуру можно построить по-разному. Например, вписать его в окружность с заданным радиусом либо построить на базе заданной боковой стороны. Последовательность действий была описана еще в «Началах» Евклида примерно 300 лет до н.э. В любом случае, нам понадобятся циркуль и линейка. Рассмотрим способ построения с помощью заданной окружности.

1. Выберите произвольный радиус и начертите окружность, обозначив ее центр точкой O.

2. На линии окружности выберите точку, которая будет служить одной из вершин нашего пятиугольника. Пусть это будет точка А. Соедините точки О и А прямым отрезком.

3. Проведите прямую через точку О перпендикулярно к прямой ОА. Место пересечения этой прямой с линией окружности обозначьте, как точку В.

4. На середине расстояния между точками О и В постройте точку С.

5. Теперь начертите окружность, центр которой будет в точке С и которая будет проходить через точку А. Место ее пересечения с прямой OB (оно окажется внутри самой первой окружности) будет точкой D.

6. Постройте окружность, проходящую через D, центр которой будет в А. Места ее пересечения с первоначальной окружностью нужно обозначить точками Е и F.

7. Теперь постройте окружность, центр которой будет в Е. Сделать это надо так, чтобы она проходила через А. Ее другое место пересечения оригинальной окружности нужно обозначить

8. Наконец, постройте окружность через А с центром в точке F. Обозначьте другое место пересечения оригинальной окружности точкой H.

9. Теперь осталось только соединить вершины A, E, G, H, F. Наш правильный пятиугольник будет готов!

Уровень сложности: Несложно

1 шаг

2 шаг

3 шаг

4 шаг

При черчении будьте аккуратны в измерениях расстояний, не допускайте погрешностей, чтобы пятиугольник действительно полчился равносторонним

8 июня 2011

Первый способ — по данной стороне S с помощью транспортира.

Проводим прямую и откладываем на ней AB = S; принимаем эту линию за радиус и этим радиусом из точек A и В описываем дуги: далее с помощью транспортира строим в этих точках углы в 108°, стороны которых пересекутся с дугами в точках С и D; из этих точек радиусом АВ = 5 описываем дуги, которые пересекутся в Е, и прямыми линиями соединяем точки Л, С, Е, D, В.

Полученный пятиугольник — искомый.

Второй способ. Проведем окружность радиусом r. Из точки А циркулем проводим дугу радиуса AM до пересечения в точках В и С с окружностью. Соединяем В и С линией, которая пересечет горизонтальную ось в точке Е.

Затем из точки Е проводим дугу, которая пересечет горизонтальную линию в точке О. Описываем, наконец, из точки F дугу, которая пересечет окружность в точках Н и К. Отложив по окружности расстояние FO = FH = FK пять раз и соединив точки деления линиями, получим правильный пятиугольник.

Третий способ. В данный круг вписать правильный пятиугольник. Проводим два взаимно перпендикулярных диаметра АВ и МС. Делим радиус АО точкой Е пополам. Из точки Е, как из центра, проводим дугу окружности радиуса ЕМ и засекаем ею диаметр АВ в точке F. Отрезок MF равен стороне искомого правильного пятиугольника. Раствором циркуля, равным MF, делаем засечки N 1 , Р 1 , Q 1 , К 1 и соединяем их прямыми.

На рисунке построен шестиугольник по данной стороне.

Прямой АВ = 5, как радиусом, из точек А и В описываем дуги, которые пересекутся в С; из этой точки тем же радиусом описываем окружность, на которой сторона А В отложится 6 раз.

Шестиугольник ADEFGB — искомый.

«Отделка комнат при ремонте»,
Н.П.Краснов

Первый способ построения. Проводим горизонтальную (АВ) и вертикальную (CD) оси и из точки их пересечения М откладываем в соответствующем масштабе полуоси. Наносим малую полуось от точки М на большой оси до точки Е. Эллипс, первый способ построения Делим BE на 2 части и одну наносим от точки М на большой оси (до F или H)…

Основанием для нанесения росписи служат полностью законченные окраской поверхности стен, потолков и других конструкций; роспись делается по высококачественным клеевым и масляным окраскам, сделанным под торцовку или флейц. Приступая к разработке эскиза отделки, мастер должен ясно представить себе всю композицию в бытовой обстановке и отчетливо осознать творческий замысел. Только при соблюдении этого основного условия можно правильно…

Обмер выполненных работ, за исключением особо оговоренных случаев, производится по площади действительно обработанной поверхности с учетом ее рельефа и за вычетом необработанных мест. Для определения действительно обработанных поверхностей при малярных работах следует пользоваться переводными коэффициентами, приведенными в таблицах. А. Деревянные оконные устройства (обмер производится по площади проемов по наружному обводу коробок) Наименование устройств Коэффициент при…

Вам понадобится

– линейка
– циркуль

Инструкция

4. Еще один легкой графический метод: поделить диаметр заданной окружности AB на три части (AC=CD=DE). Из точки D опустить перпендикуляр до пересечения с окружность в точках E, F.Проведя прямые через отрезки EC и FC до пересечения с окружностью, получим точки G, H.Точки G,E,B,F,H – вершины положительного пятиугольника .

Вам понадобится

Циркуль, линейка, карандаш

Инструкция

Видео по теме

Вам понадобится

Лист бумаги, карандаш и линейка.

Инструкция

Видео по теме

Полезный совет
Если объединить вершины верного пятиугольника диагоналями, то получится пентаграмма.

Построение вписанного в окружность правильного шестиугольника.

Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой.

Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4, строим стороны 1 — 6, 4 — 3, 4 — 5 и 7 — 2, после чего проводим стороны 5 — 6 и 3 — 2.

Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля. Рассмотрим два способа построения вписанного в окружность равностороннего треугольника.

Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, проведённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0 — 1 — 2 равен 30°, то для нахождения стороны 1 — 2 достаточно построить по точке 1 и стороне 0 — 1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1 — 2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2 — 3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника.

Для построения треугольника намечаем на диаметре вершину точку 1 и проводим диаметральную линию 1 — 4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника.

Это построение можно выполнить при помощи угольника и циркуля.

Первый способ основан на том, что диагонали квадрата пересекаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные стороны квадрата 4 — 1 и 3 -2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1 — 2 и 4 — 3.

Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра. Намечаем на концах двух взаимно перпендикулярных диаметров точки А, В и С и из них радиусом у описываем дуги до взаимного их пересечения.

Построение вписанного в окружность правильного пятиугольника.

Чтобы вписать в окружность правильный пятиугольник, производим следующие построения. Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой.

Построение правильного пятиугольника по данной его стороне.

Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую. Далее от точки К на этой прямой откладываем отрезок, равный 4/6 AB. Получим точку 1 -вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведёнными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.

Построение вписанного в окружность правильного семиугольника.

Приведённый способ годен для построения правильных многоугольников с любым числом сторон.

Длины сторон правильных вписанных многоугольников.

В первой колонке этой таблицы указаны числа сторон правильного вписанного многоугольника, а во второй — коэффициенты. Длина стороны заданного многоугольника получится от умножения радиуса данной окружности на коэффициент, соответствующий числу сторон этого многоугольника.

Правильный пятиугольник — это… Что такое Правильный пятиугольник?

Правильный пятиугольник

Правильный пятиугольник (греч. πενταγωνον) — геометрическая фигура, правильный многоугольник с пятью сторонами.

Свойства

Построение правильного пятиугольника

Площадь правильного пятиугольника рассчитывается по любой из формул:

где — радиус описанной окружности, — радиус вписанной окружности, — диагональ, — сторона.

Высота правильного пятиугольника:

Диагонали правильного пятиугольника являются трисектрисами его внутренних углов.
Отношение диагонали правильного пятиугольника к стороне равно золотому сечению, то есть числу .

Поэтому радиус вписанной окружности, радиус описанной окружности, высоту и площадь правильного пятиугольника можно вычислить и без использования тригонометрических функций:

Радиус вписанной окружности:

Радиус описанной окружности:

Правильным пятиугольником невозможно заполнить плоскость без промежутков (см. также Паркет)
Отношение площадей правильного пятиугольника и другого правильного пятиугольника, образованного пересечением диагоналей исходного

где — отношение золотого сечения.

Построение

Построение правильного пятиугольника

Правильный пятиугольник может быть построен с помощью циркуля и линейки, или вписыванием его в заданную окружность, или построением на основе заданной стороны. Этот процесс описан Евклидом в его «Началах» около 300 года до н. э.

Вот один из методов построения правильного пятиугольника в заданной окружности:

Постройте окружность, в которую будет вписан пятиугольник и обозначьте её центр как O. (Это зелёная окружность на схеме справа).
Выберите на окружности точку A, которая будет одной из вершин пятиугольника. Постройте прямую через O и A.
Постройте прямую перпендикулярно прямой OA, проходящую через точку O. Обозначьте одно её пересечение с окружностью, как точку B.
Постройте точку C посередине между O и B.
Проведите окружность с центром в C через точку A. Обозначьте её пересечение с прямой OB (внутри первоначальной окружности) как точку D.
Проведите окружность с центром в A через точку D, пересечение данной окружности с оригинальной (зелёной окружностью) обозначьте как точки E и F.
Проведите окружность с центром в E через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку G.
Проведите окружность с центром в F через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку H.
Постройте правильный пятиугольник AEGHF.

Альтернативный метод построения правильного многоугольника с помощью линейки и циркуля

Получение с помощью полоски бумаги

Правильный пятиугольник можно получить, завязав узлом полоску бумаги.

Overhand knot of a paper strip

В природе

Исследования формирования водяного льда на ровной поверхности меди при температурах 100—140 K показали, что сначала на поверхности возникают цепочки молекул шириной около 1 нм не гексагональной, а пентагональной структуры.^[1]

Интересные факты

Пентагон

Додекаэдр — единственный из правильных многогранников, грани которого представляют собой правильные пятиугольники.
Пентагон — здание Министерства обороны США имеет форму правильного пятиугольника.
Правильный пятиугольник — правильный многоугольник с наименьшим количеством углов из тех, которыми нельзя замостить плоскость.
В природе не существует кристаллов с гранями в форме правильного пятиугольника.

См. также

Примечания

Как сделать правильный пятиугольник с помощью циркуля. Как построить и нарисовать правильный пятиугольник по окружности. Построение правильных многоугольников по заданной стороне

Правильный пятиугольник — это многоугольник, у которого все пять сторон и все пять углов равны между собой. Вокруг него легко описать окружность. Построить пятиугольник и поможет именно эта окружность.

Инструкция

В первую очередь необходимо построить циркулем окружность. Центр окружности пусть совпадает с точкой O. Проведите оси симметрии перпендикулярные друг другу. В точке пересечения одной из этих осей с окружностью поставьте точку V. Эта точка будет вершиной будущего пятиугольник а. В точке пересечения другой оси с окружностью расположите точку D.

На отрезке OD найдите середину и отметьте в ней точку А. После этого нужно построить циркулем окружность с центром в этой точке. Кроме того, она должна проходить через точку V, то есть, радиусом CV. Точку пересечения оси симметрии и этой окружности обозначьте за В.

После этого при помощи циркуля проведите окружность такого же радиуса, поставив иголку в точку V. Пересечение этой окружности с первоначальной обозначьте как точку F. Эта точка станет второй вершиной будущего правильного пятиугольник а.

Теперь нужно провести такую же окружность через точку Е, но с центром в F. Пересечение только что проведенной окружности с первоначальной обозначьте как точку G. Эта точка так же станет еще одной из вершин пятиугольник а. Аналогичным образом необходимо построить еще один круг. Центр его в G. Точка пересечения его с первоначальной окружностью пусть будет H. Это последняя вершина правильного многоугольника.

У вас должно получиться пять вершин. Остается их просто соединить по линейке. В результате всех этих операций вы получите вписанный в окружность правильный пятиугольник .

Построение правильных пятиугольников можно с помощью циркуля и линейки. Правда, процесс это достаточно длительный, как, впрочем, и построение любого правильного многоугльника с нечетным количеством сторон. Современные компьютерные программы позволяют сделать это за несколько секунд.

Вам понадобится

— компьютер с программой AutoCAD.

Инструкция

Найдите в программе AutoCAD верхнее меню, а в нем — вкладку «Главная». Нажмите на нее левой клавишей мыши. Появится панель «Рисование». Появятся разные типы линий. Выберите замкнутую полилинию. Она и представляет собой многоугольник, остается только ввести параметры. AutoCAD. Позволяет рисовать самые разные правильне многоугольники. Число сторон может достигать 1024. Можно использовать и командную строку, в зависимости от версии набрав « _polygon» или «мн.-угол».

Вне зависимости от того, пользуетесь ли вы командной строкой или контекстными меню, на экране у вас появится окошко, в которое предлагается ввести количество сторон. Введите туда цифру «5» и нажмите Enter. Вам будет предложено определить центр пятиугольника. Вбейте в появившееся окошко координаты. Можно обозначить их как (0,0), но могут быть и любые другие данные.

Выберите нужный способ построения. . AutoCAD предлагает три варианта. Пятиугольник может быть описанным вокруг окружности или вписанным в нее, но можно построить его и по заданному размеру стороны. Выберите нужный вариант и нажмите на ввод. В случае необходимости задайте радиус окружности и тоже нажмите enter.

Пятиугольник по заданной стороне сначала строится точно так же. Выберите «Рисование», замкнутую полилинию и введите число сторон. Правой клавишей мыши вызовите контекстное меню. Нажмите команду «edge” или «сторона”. В командной строке наберите координаты начальной и конечной точек одной из сторон пятиугольника. После этого пятиугольник появится на экране.

Все операции можно выполнять с помощью командной строки. Например, для построения пятиугольника по стороне в русскоязычной версии программы введите букву «с». В англоязычной версии это будет «_e”. Чтобы построить вписанный или описанный пятиугольник, введите после определения количества сторон буквы «о» или «в» (либо же английские «_с» или «_i»)

Таким нехитрым способом можно построить не только пятиугольник. Для того чтобы построить треугольник, необходимо разведите ножки циркуля на расстояние, равное радиусу окружности. Затем в любую точку установите иглу. Проведите тонкую вспомогательную окружность. Две точки пересечения окружностей, а так же точка, в которой была ножка циркуля образуют три вершины правильного треугольника.

Построение вписанного в окружность правильного шестиугольника.

Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4, строим стороны 1 — 6, 4 — 3, 4 — 5 и 7 — 2, после чего проводим стороны 5 — 6 и 3 — 2.

Это построение можно выполнить при помощи угольника и циркуля.

Построение вписанного в окружность правильного пятиугольника.

Построение правильного пятиугольника по данной его стороне.

Построение вписанного в окружность правильного семиугольника.

Приведённый способ годен для построения правильных многоугольников с любым числом сторон.

Длины сторон правильных вписанных многоугольников.

{2}};

Свойства

Додекаэдр — единственный из правильных многогранников , грани которого представляют собой правильные пятиугольники.
Пентагон — здание Министерства обороны США имеет форму правильного пятиугольника.
Правильный пятиугольник — правильный многоугольник с наименьшим количеством углов из тех, которыми нельзя замостить плоскость.
В природе не существует кристаллов с гранями в форме правильного пятиугольника.
Пятиугольник со всеми его диагоналями является проекцией 4-симплекса.

См. также

Напишите отзыв о статье «Правильный пятиугольник»

Примечания

\frac{{t^2 \sqrt {25 + 10\sqrt 5 } }}{4} = \frac{5R^2}{4}\sqrt{\frac{5+\sqrt{5



По числу сторон

Правильные

Треугольники

Четырёхугольники

См. также



Многоугольники

Звёздчатые многоугольники

Паркеты на плоскости

Правильные многогранники и сферические паркеты

Многогранники Кеплера — Пуансо

Соты

Четырёхмерные многогранники

Отрывок, характеризующий Правильный пятиугольник

8 июня 2011

Первый способ — по данной стороне S с помощью транспортира.

На рисунке построен шестиугольник по данной стороне.

«Отделка комнат при ремонте»,
Н.П.Краснов

Положительный пятиугольник – это многоугольник, у которого все пять сторон и все пять углов равны между собой. Вокруг него легко описать окружность. Возвести пятиугольник и поможет именно эта окружность.

Инструкция

1. В первую очередь нужно возвести циркулем окружность. Центр окружности пускай совпадает с точкой O. Проведите оси симметрии перпендикулярные друг другу. В точке пересечения одной из этих осей с окружностью поставьте точку V. Эта точка будет вершиной грядущего пятиугольник а. В точке пересечения иной оси с окружностью расположите точку D.

2. На отрезке OD обнаружьте середину и подметьте в ней точку А. Позже этого надобно возвести циркулем окружность с центром в этой точке. Помимо того, она должна проходить через точку V, то есть, радиусом CV. Точку пересечения оси симметрии и этой окружности обозначьте за В.

3. Позже этого при помощи циркуля проведите окружность такого же радиуса, поставив иголку в точку V. Пересечение этой окружности с изначальной обозначьте как точку F. Эта точка станет 2-й вершиной грядущего верного пятиугольник а.

4. Сейчас необходимо провести такую же окружность через точку Е, но с центром в F. Пересечение только что проведенной окружности с изначальной обозначьте как точку G. Эта точка так же станет еще одной из вершин пятиугольник а. Аналогичным образом нужно возвести еще один круг. Центр его в G. Точка пересечения его с изначальной окружностью пускай будет H. Это последняя вершина верного многоугольника.

5. У вас должно получиться пять вершин. Остается их легко объединить по линейке. В итоге всех этих операций вы получите вписанный в окружность положительный пятиугольник .

Построение положительных пятиугольников дозволено с поддержкой циркуля и линейки. Правда, процесс это довольно долгий, как, однако, и построение всякого положительного многоугльника с нечетным числом сторон. Современные компьютерные программы разрешают сделать это за несколько секунд.

Вам понадобится

– компьютер с программой AutoCAD.

Инструкция

1. Обнаружьте в программе AutoCAD верхнее меню, а в нем — вкладку «Основная». Нажмите на нее левой клавишей мыши. Появится панель «Рисование». Появятся различные типы линий. Выберите замкнутую полилинию. Она и представляет собой многоугольник, остается только ввести параметры. AutoCAD. Дозволяет рисовать самые различные правильне многоугольники. Число сторон может добиваться 1024. Дозволено применять и командную строку, в зависимости от версии набрав « _polygon» либо «мн.-угол».

2. Вне зависимости от того, пользуетесь ли вы командной строкой либо контекстными меню, на экране у вас появится окошко, в которое предлагается ввести число сторон. Введите туда цифру «5» и нажмите Enter. Вам будет предложено определить центр пятиугольника. Вбейте в появившееся окошко координаты. Дозволено обозначить их как (0,0), но могут быть и всякие другие данные.

3. Выберите необходимый метод построения. . AutoCAD предлагает три варианта. Пятиугольник может быть описанным вокруг окружности либо вписанным в нее, но дозволено возвести его и по заданному размеру стороны. Выберите надобный вариант и нажмите на ввод. В случае необходимости задайте радиус окружности и тоже нажмите enter.

4. Пятиугольник по заданной стороне вначале строится верно так же. Выберите «Рисование», замкнутую полилинию и введите число сторон. Правой клавишей мыши вызовите контекстное меню. Нажмите команду «edge” либо «сторона”. В командной строке наберите координаты исходной и финальной точек одной из сторон пятиугольника. Позже этого пятиугольник появится на экране.

5. Все операции дозволено исполнять с поддержкой командной строки. Скажем, для построения пятиугольника по стороне в русскоязычной версии программы введите букву «с». В англоязычной версии это будет «_e”. Дабы возвести вписанный либо описанный пятиугольник, введите позже определения числа сторон буквы «о» либо «в» (либо же английские “_с” либо “_i”)

Видео по теме

Полезный совет
Таким нехитрым методом дозволено возвести не только пятиугольник. Для того дабы возвести треугольник, нужно разведите ножки циркуля на расстояние, равное радиусу окружности. После этого в всякую точку установите иглу. Проведите тонкую вспомогательную окружность. Две точки пересечения окружностей, а так же точка, в которой была ножка циркуля образуют три вершины положительного треугольника.

Правильный пятиугольник — построение, свойства и формулы

Бывают задачи на построение и нахождение некоторых геометрических параметров правильного пятиугольника. Построить фигуру непросто. Для этого математики рекомендуют несколько методик, позволяющих выполнить операцию более точно или за короткий промежуток времени. У фигуры есть свойства, а также формулы, позволяющие найти ее геометрические характеристики.

Точное построение фигуры

Специалисты рекомендуют некоторую последовательность действий, по которым построить правильный пятиугольник очень просто. Для операции необходимы обыкновенная тетрадь в клеточку, циркуль, карандаш, резинка и линейка. Следует выполнить некоторые шаги:

Построить окружность с центром в некоторой точке О.

Провести два диаметра. Они должны пересекаться под прямым углом.

Поставить точку V (пересечение окружности с одним из диаметров), которая является вершиной фигуры.

По левой стороне поставить точку D. Это пересечение диаметра (оси симметрии) с окружностью.

Отметить на отрезке OD точку А, которая делит его пополам.

Выполнить построение вспомогательной окружности, центром которой является точка, полученная в 5 пункте. Кроме того, круг с радиусом CV должен проходить через V.

Точку, полученную при пересечении диаметра и окружности, нужно обозначить литерой B.

Нарисовать окружность с радиусом, равным CV, из точки V.

Отметить пересечение круга с первой окружностью, центром которой является точка О. Искомое место пересечения обозначить литерой F (вторая вершина пентагона).

Поставить иглу циркуля в точку F и провести окружность через Е.

Обозначить пересечение окружностей с центрами в F и O точкой G, которая будет вершиной пентагона.

Аналогичным образом проделать шаг 11, только центр выбрать не в F, а в G. Полученную точку следует обозначить литерой H (последняя вершина фигуры).

Соединить пять точек (СVEFG) между собой с помощью линейки.

Если все пункты алгоритма выполнены правильно, то должен получиться пентагон, изображенный на рисунке 1:

Этот способ следует применять для точных построений и чертежей деталей. Однако для решения задач, в которых необходимо схематически изобразить пятиугольник, этот вариант не подойдет.

Алгоритм Биона

Прием Биона является менее точным методом, чем первый. Он позволяет построить любой правильный многоугольник, вписанный в произвольный круг. Для операции необходимо воспользоваться алгоритмом (шаблоном) Биона, имеющим такой вид:

Начертить окружность с центром в точке О и радиусом R.

Провести в ней диаметр АD.

Построить правильный (равносторонний) треугольник с одной из сторон, равной диаметру.

Поделить диаметр на несколько равных частей (АС = СE = ED), количество которых вычисляется по формуле: (n — 2). Переменная «n» эквивалентна количеству граней правильного многоугольника, то есть n = 3. Соотношение можно записать следующей зависимостью: АС = [1 / (n — 2)] * AD = AD / 3.

Провести из точек С и Е прямые, перпендикулярные диаметру.

Точки пересечения прямых с окружностью обозначить F и G.

Если соединить точки, то получится пентагон ABDFG.

Погрешность построения многоугольника с 5, 7, 9 и 10 сторонами при использовании алгоритма довольно маленькая. Ее значения равно 3,2%. Однако при n>10 погрешность составляет не более 11%.

Приближенные методы

Существует несколько методов, позволяющих приближенно изобразить фигуру. Однако оптимальным является построение пентагона (рис. 2), используя две окружности (описанную и вписанную).

Метод известного математика А. Дюрера является оптимальным среди остальных, поскольку на построение затрачивается минимальное количество времени. Для его реализации следует выполнить определенные шаги алгоритма Дюрера:

Начертить произвольную окружность с центром в точке О.

Не вынимая иглу циркуля из точки О, выполнить построение другой окружности. Ее радиус нужно уменьшить таким образом, чтобы общий радиус R был равен стороне пятиугольника.

Отметить на окружности с большим радиусом две произвольные точки. При этом следует руководствоваться правилом: прямая, проходящая через них, должна касаться малой окружности в одной точке (касательная).

Отметить следующую точку, чтобы можно было соединить ее с предыдущей. Правило при этом должно соблюдаться.

Аналогично проделать операции с другими сторонами пентагона.

Существует еще один метод — построение пятиугольника из десятиугольника, который вписан в окружность. Для этого следует соединить его вершины через одну. Однако способ рекомендуется применять только в том случае, когда исходная фигура уже имеется. Кстати, его следует строить также методом А. Дюрера.

Математики рекомендуют еще один простой способ. Для его реализации необходимо начертить окружность с диаметром АD. После этого его нужно поделить на 3 равные части, то есть AB = BC = CD. Затем из точки С следует опустить перпендикуляры на окружность. Обозначить места пересечения точками E и F. Проделать такую же процедуру с точкой B, обозначив пересечения точками G и H. Остается лишь соединить все точки отрезками.

Признаки и свойства

Не всегда получается верно идентифицировать пятиугольник. Для этого математики предлагают признаки, которые применимы только к правильной фигуре. К ним можно отнести следующие:

Стороны равны между собой.

Любой угол правильного пятиугольника равен остальным его углам.

Следует отметить, что признаки справедливы для любого правильного многогранника. Пять осей симметрии имеет правильный пятиугольник (сколько сторон, столько и осей). Пентагон обладает некоторыми свойствами, которые будут очень полезны при решении задач. К ним можно отнести следующие:

Равенство сторон.

Углы равны по 108 градусов.

Центры вписанной и описанной окружностей совпадают.(1/2)] / 2.

Однако свойств недостаточно при решении задач, поскольку существуют некоторые формулы и соотношения для нахождения основных параметров пентагона.

Расчет параметров

С помощью соотношений можно легко найти необходимые характеристики любой фигуры. Однако в некоторых источниках не указаны условные обозначения известного параметра пентагона. Это существенно затрудняет понимание формулы, а также ее дальнейшее использование. Перед изучением следует нарисовать фигуру и обозначить некоторые величины, которыми могут быть диагонали, стороны, апофемы и радиусы.

Рекомендуется использовать различные литеры или буквенные обозначения. Недопустимо пронумеровывать вершины, поскольку при вычислениях можно ошибиться. Нельзя использовать вместо букв цифры при обозначениях. Например, пентагон ABCDE является правильной записью. Допускается применение чисел в индексах, а именно, в пятиугольнике правильного типа ABCDE при пересечении его диагоналей образовался пентагон A1B1C1D1E1.

Математики рекомендуют обозначать только промежуточные фигуры или их проекции литерами с индексами. Для каждой новой фигуры следует вводить другие обозначения. Не следует использовать зарезервированные переменные. Например, центр окружности в точке P является недопустимой записью, поскольку такой буквой обозначается периметр.

Условные обозначения

Для нахождения основных величин пентагона следует обозначить некоторые его параметры. Фигура имеет следующие обозначения:

Сторона: a.

Радиус вписанной и описанной окружностей: r и R соответственно.

Площадь: S.

Периметр и полупериметр: P и p соответственно.

Диагональ: d.

Отношение золотого сечения: Ф.

Значения сторон равны между собой. Площадь правильного пятиугольника — характеристика двумерной фигуры, которая показывает ее размерность. Периметром называется сумма всех 5 сторон.(1/2).

Таким образом, при решении задач необходимо знать основные признаки, свойства, соотношения и формулы для нахождения основных характеристик пентагона. Практика обязательна, поскольку теоретические знания без практического применения бесполезны.

ГеометрияСвойства диагоналей ромба — основные формулы и доказательство теоремы

ГеометрияДодекаэдр — свойства, вид и структура двенадцатигранника

Как сделать пятиугольник с помощью циркуля. Построение правильного пятиугольника

Инструкция

Вам понадобится

— компьютер с программой AutoCAD.

Инструкция

Деление окружности на равные части и вписывание правильных многоугольников.

Окружность, дуги и многоугольники.

Построение правильных многоугольников по заданной стороне

Смотреть что такое «Правильный пятиугольник» в других словарях:

Параметры правильного пятиугольника

сумма всех углов в многоугольниках равна 360 градусам. В правильном пятиугольнике все углы равны, соответственно, центральный угол находится таким способом: 360/5 = 72 градуса;
внутренний угол находится таким образом: 180*(n -2)/ n = 180*(5−2)/5 = 108 градусов. Сумма всех внутренних углов: 108*5 = 540 градусов.

Сторона пентагона находится с помощью параметров, которые уже даны в условии задачи:

если вокруг пятиугольника описана окружность и известен ее радиус, сторона находится по такой формуле: a = 2*R*sin (α/2) = 2*R*sin (72/2) = 1,1756*R.
Если известен радиус вписанной в пентагон окружности, то формула расчета стороны многоугольника: 2*r*tg (α/2) = 2*r*tg (α/2) = 1,453*r.
При известной величине диагонали пентагона его сторона рассчитывается таким образом: а = D/1,618.

Площадь пентагона так же , как и его сторона, зависит от уже найденных параметров:

с помощью известного радиуса вписанной окружности площадь находится так: S = (n*a*r)/2 = 2,5*a*r.
описанная вокруг пятиугольника окружность позволяет найти площадь по такой формуле: S = (n*R2*sin α)/2 = 2,3776*R2.
в зависимости от стороны пентагона: S = (5*a2*tg 54°)/4 = 1,7205* a2.

Построение пентагона

Сначала необходимо начертить окружность с центром О, после чего на ней выбрать точку, А — вершину пентагона. От центра к вершине проводится отрезок.
Затем строится перпендикулярная прямой ОА отрезок, который также проходит через О — центр окружности. Его пересечение с окружностью обозначается точкой В. Отрезок О. В. делится пополам точкой С.
Точка С станет центром новой окружности, проходящей через А. Точка D — это ее пересечение с прямой ОВ в границах первой фигуры.
После этого проводится третья окружность через D, центром которой является точка А. Она пересекается с первой фигурой в двух точках, их необходимо обозначить буквами Е и F.
Следующая окружность имеет центр в точке Е и проходит через А, а ее пересечение с первоначальной находится в новой точке G.
Последняя окружность в этом рисунке проводится через точку, А с центром F. На ее пересечении с начальной ставится точка Н.
На первой окружности после всех проделанных шагов появились пять точек, которые необходимо соединить отрезками. Таким образом получился правильный пятиугольник АЕ G Н F.

Cначала необходимо с помощью циркуля нарисовать окружность, центр которой — точка О.
Чертится радиус ОА — отрезок, который откладывается на окружность. Его делят пополам точкой В.
Перпендикулярно радиусу ОА начерчивается отрезок ОС, точки В и С соединяются прямой.
Следующим шагом является отложение длины отрезка ВС с помощью циркуля на диаметральной линии. Перпендикулярно отрезку ОА появляется точка D. Точки В и D соединяются, образуя новый отрезок.
Для того, чтобы получить величину стороны пентагона, необходимо соединить точки С и D.
D с помощью циркуля переносится на окружность и обозначается точкой Е. Соединив Е и С, можно получить первую сторону правильного пятиугольника. Следуя этой инструкции можно узнать о том, как быстро построить пятиугольник с равными сторонами, продолжая построение остальных его сторон подобно первой.

{2}};

Свойства

Додекаэдр — единственный из правильных многогранников , грани которого представляют собой правильные пятиугольники.
Пентагон — здание Министерства обороны США имеет форму правильного пятиугольника.
Правильный пятиугольник — правильный многоугольник с наименьшим количеством углов из тех, которыми нельзя замостить плоскость.
В природе не существует кристаллов с гранями в форме правильного пятиугольника.
Пятиугольник со всеми его диагоналями является проекцией 4-симплекса.

См. также

Напишите отзыв о статье «Правильный пятиугольник»

Примечания



По числу сторон

Правильные

Треугольники

Четырёхугольники

См. также



Многоугольники

Звёздчатые многоугольники

Паркеты на плоскости

Правильные многогранники и сферические паркеты

Многогранники Кеплера — Пуансо

Соты

Четырёхмерные многогранники

Отрывок, характеризующий Правильный пятиугольник

5.3. Золотой пятиугольник; построение Евклида.

Замечательный пример «золотого сечения» представляет собой правильный пятиугольник – выпуклый и звездчатый (рис. 5).

Для построения пентаграммы необходимо построить правильный пятиугольник.

Пусть О — центр окружности, А — точка на окружности и Е — середина отрезка ОА. Перпендикуляр к радиусу ОА, восстановленный в точке О, пересекается с окружностью в точке D. Пользуясь циркулем, отложим на диаметре отрезок CE = ED. Длина стороны вписанного в окружность правильного пятиугольника равна DC. Откладываем на окружности отрезки DC и получим пять точек для начертания правильного пятиугольника. Соединяем углы пятиугольника через один диагоналями и получаем пентаграмму. Все диагонали пятиугольника делят друг друга на отрезки, связанные между собой золотой пропорцией.

Каждый конец пятиугольной звезды представляет собой золотой треугольник. Его стороны образуют угол 36° при вершине, а основание, отложенное на боковую сторону, делит ее в пропорции золотого сечения.

Есть и золотой кубоид- это прямоугольный параллелепипед с ребрами, имеющими длины 1.618, 1 и 0.618.

Теперь рассмотрим доказательство, предложенное Евклидом в «Началах».

Посмотрим теперь, как Евклид использует золотое сечение для того, чтобы построить угол в 72 градуса – именно под таким углом видна сторона правильного пятиугольника

из центра описанной окружности. Начнем с

отрезка АВЕ, разделенного в среднем и

Итак, пусть АС=АЕ. Обозначим через a равные углы ЕВС и СЕВ. Так как АС=АЕ, то угол АСЕ также равен a. Теорема о том, что сумма углов треугольника равна 180 градусов, позволяет найти угол ВСЕ: он равен 180-2a, а угол ЕАС — 3a — 180. Но тогда угол АВС равен 180-a. Суммируя углы треугольника АВС получаем,

180=(3a -180) + (3a-180) + (180 — a)

Откуда 5a=360, значит a=72.

Итак, каждый из углов при основании треугольника ВЕС вдвое больше угла при вершине, равного 36 градусов. Следовательно, чтобы построить правильный пятиугольник, необходимо лишь провести любую окружность с центром в точке Е, пересекающую ЕС в точке Х и сторону ЕВ в точке Y: отрезок XY служит одной из сторон вписанного в окружность правильного пятиугольника; Обойдя вокруг всей окружности, можно найти и все остальные стороны.

Докажем теперь, что АС=АЕ. Предположим, что вершина С соединена отрезком прямой с серединой N отрезка ВЕ. Заметим, что поскольку СВ=СЕ, то угол СNЕ прямой. По теореме Пифагора:

CN 2 = а 2 – (а/2j) 2 = а 2 (1-4j 2)

Отсюда имеем (АС/а) 2 = (1+1/2j) 2 + (1-1/4j 2) = 2+1/j = 1 + j =j 2

Итак, АС = jа = jАВ = АЕ, что и требовалось доказать

5.4.Спираль Архимеда.

Последовательно отсекая от золотых прямоугольников квадраты до бесконечности, каждый раз соединяя противоположные точки четвертью окружности, мы получим довольно изящную кривую. Первым внимание на неё обратил древнегреческий ученый Архимед, имя которого она и носит. Он изучал её и вывел уравнение этой спирали.

В настоящее время спираль Архимеда широко используется в технике.

6.Числа Фибоначчи.

С золотым сечением косвенно связано имя итальянского математика Леонардо из Пизы, который известен больше по своему прозвищу Фибоначчи (Fibonacci — сокращенное filius Bonacci, то есть сын Боначчи)

В 1202г. им была написана книга «Liber abacci», то есть «Книга об абаке» . «Liber abacci» представляет собой объемистый труд, содержащий почти все арифметические и алгебраические сведения того времени и сыгравший заметную роль в развитии математики в Западной Европе в течение нескольких следующих столетий. В частности, именно по этой книге европейцы познакомились с индусскими («арабскими») цифрами.

Сообщаемый в книге материал поясняется на большом числе задач, составляющих значительную часть этого трактата.

Рассмотрим одну такую задачу:

«Сколько пар кроликов в один год от одной пары рождается?

Некто поместил пару кроликов в некоем месте, огороженном со всех сторон стеной, дабы узнать, сколько пар кроликов родится в течение этого года, если природа кроликов такова, что через месяц пара кроликов воспроизведет другую, а рождают кролики со второго месяца после своего рождения»

Месяцы	1	2	3	4	5	6	7	8	9	10	11	12
Пары кроликов	2	3	5	8	13	21	34	55	89	144	233	377

Перейдем теперь от кроликов к числам и рассмотрим следующую числовую последовательность:

u 1 , u 2 … u n

в которой каждый член равен сумме двух предыдущих, т.е. при всяком n>2

u n =u n -1 +u n -2 .

Данная последовательность асимптотически (приближаясь все медленнее и медленнее) стремится к некоторому постоянному соотношению. Однако, это соотношение иррационально, то есть представляет собой число с бесконечной, непредсказуемой последовательностью десятичных цифр в дробной части. Его невозможно выразить точно.

Если какой-либо член последовательности Фибоначчи разделить на предшествующий ему (например, 13:8), результатом будет величина, колеблющаяся около иррационального значения 1.61803398875… и через раз то превосходящая, то не достигающая его.

Асимптотическое поведение последовательности, затухающие колебания ее соотношения около иррационального числа Ф могут стать более понятными, если показать отношения нескольких пеpвых членов последовательности. В этом примере приведены отношения второго члена к первому, третьего ко второму, четвертого к третьему, и так далее:

1:1 = 1.0000, что меньше фи на 0.6180

2:1 = 2.0000, что больше фи на 0.3820

3:2 = 1.5000, что меньше фи на 0.1180

5:3 = 1.6667, что больше фи на 0.0486

8:5 = 1.6000, что меньше фи на 0.0180

По мере продвижения по суммационной последовательности Фибоначчи каждый новый член будет делить следующий со все большим и большим приближением к недостижимому Ф.

Человек подсознательно ищет Божественную пропорцию: она нужна для удовлетворения его потребности в комфорте.

Пpи делении любого члена последовательности Фибоначчи на следующий за ним получается просто обратная к 1.618 величина (1: 1.618=0.618). Hо это тоже весьма необычное, даже замечательное явление. Поскольку пеpвоначальное соотношение – бесконечная дpобь, у этого соотношения также не должно быть конца.

При делении каждого числа на следующее за ним через одно, получаем число 0.382

Подбирая таким образом соотношения, получаем основной набор коэффициентов Фибоначчи: 4.235 ,2.618 ,1.618,0.618,0.382,0.236.Упомянем также 0.5.Все они играют особую роль в природе и в частности в техническом анализе.

Тут необходимо отметить, что Фибоначчи лишь напомнил свою последовательность человечеству, так как она была известна еще в древнейшие времена под названием Золотое сечение.

Золотое сечение, как мы видели, возникает в связи с правильным пятиугольником, поэтому и числа Фибоначчи играют роль во всем, что имеет отношение к правильным пятиугольникам — выпуклым и звездчатым.

Ряд Фибоначчи мог бы остаться только математическим казусом, если бы не то обстоятельство, что все исследователи золотого деления в растительном и в животном мире, не говоря уже об искусстве, неизменно приходили к этому ряду как арифметическому выражению закона золотого деления. Ученые продолжали активно развивать теорию чисел Фибоначчи и золотого сечения. Ю. Матиясевич с использованием чисел Фибоначчи решает 10-ю проблему Гильберта (о решении Диофантовых уравнений). Возникают изящные методы решения ряда кибернетических задач (теории поиска, игр, программирования) с использованием чисел Фибоначчи и золотого сечения. В США создается даже Математическая Фибоначчи-ассоциация, которая с 1963 года выпускает специальный журнал.

Одним из достижений в этой области является открытие обобщенных чисел Фибоначчи и обобщенных золотых сечений. Ряд Фибоначчи (1, 1, 2, 3, 5, 8) и открытый им же «двоичный» ряд чисел 1, 2, 4, 8, 16…(то есть ряд чисел до n , где любое натуральное число, меньшее n можно представить суммой некоторых чисел этого ряда) на первый взгляд совершенно разные. Но алгоритмы их построения весьма похожи друг на друга: в первом случае каждое число есть сумма предыдущего числа с самим собой 2 = 1 + 1; 4 = 2 + 2…, во втором – это сумма двух предыдущих чисел 2 =1 + 1, 3 = 2 + 1, 5 = 3 + 2…. Нельзя ли отыскать общую математическую формулу, из которой получаются и «двоичный» ряд, и ряд Фибоначчи?

Действительно, зададимся числовым параметром S, который может принимать любые значения: 0, 1, 2, 3, 4, 5… Рассмотрим числовой ряд, S + 1 первых членов которого – единицы, а каждый из последующих равен сумме двух членов предыдущего и отстоящего от предыдущего на S шагов. Если n-й член этого ряда мы обозначим через S (n), то получим общую формулу S (n) = S (n – 1) + S (n – S – 1).

Очевидно, что при S = 0 из этой формулы мы получим «двоичный» ряд, при S = 1 –ряд Фибоначчи, при S = 2, 3, 4. новые ряды чисел, которые получили название S-чисел Фибоначчи.

В общем виде золотая S-пропорция есть положительный корень уравнения золотого S-сечения x S+1 – x S – 1 = 0.

Нетрудно показать, что при S = 0 получается деление отрезка пополам, а при S = 1 – знакомое классическое золотое сечение.

Отношения соседних S-чисел Фибоначчи с абсолютной математической точностью совпадают в пределе с золотыми S-пропорциями! То есть золотые S-сечения являются числовыми инвариантами S-чисел Фибоначчи.

7.Золотое сечение в искусстве.

7.1. Золотое сечение в живописи.

Переходя к примерам «золотого сечения» в живописи, нельзя не остановить своего внимания на творчестве Леонардо да Винчи. Его личность – одна из загадок истории. Сам Леонардо да Винчи говорил: «Пусть никто, не будучи математиком, не дерзнет читать мои труды».

Нет сомнений, что Леонардо да Винчи был великим художником, это признавали уже его современники, но его личность и деятельность останутся покрытыми тайной, так как он оставил потомкам не связное изложение своих идей, а лишь многочисленные рукописные наброски, заметки, в которых говорится «обо всем на свете».

Портрет Монны Лизы (Джоконды) долгие годы привлекает внимание исследователей, которые обнаружили, что композиция рисунка основана на золотых треугольниках, являющихся частями правильного звездчатого пятиугольника..

Также пропорция золотого сечения проявляется в картине Шишкина. На этой знаменитой картине И. И. Шишкина с очевидностью просматриваются мотивы золотого сечения. Ярко освещенная солнцем сосна (стоящая на первом плане) делит длину картины по золотому сечению. Справа от сосны — освещенный солнцем пригорок. Он делит по золотому сечению правую часть картины по горизонтали.

В картине Рафаэля «Избиение младенцев» просматривается другой элемент золотой пропорции — золотая спираль. На подготовительном эскизе Рафаэля проведены красные линии, идущие от смыслового центра композиции — точки, где пальцы воина сомкнулись вокруг лодыжки ребенка — вдоль фигур ребенка, женщины, прижимающей его к себе, воина с занесенным мечом и затем вдоль фигур такой же группы в правой части эскиза. Неизвестно, строил ли Рафаэль золотую спираль или чувствовал её.

Т.Кук использовал при анализе картины Сандро Боттичелли «рождение Венеры» золотое сеченеие.

7.2. Пирамиды золотого сечения.

Широко известны медицинские свойства пирамид, особенно золотого сечения. По некоторым наиболее распространенным мнениям, комната, в которой находится такая пирамида, кажется больше, а воздух — прозрачнее. Сны начинают запоминаться лучше. Также известно, что золотое сечение широко применялась в архитектуре и скульптуре. Примером тому стали: Пантеон и Парфенон в Греции, здания архитекторов Баженова и Малевича

8. Заключение.

Необходимо сказать, что золотое сечение имеет большое применение в нашей жизни.

Было доказано, что человеческое тело делится в пропорции золотого сечения линией пояса.

Раковина наутилуса закручена подобно золотой спирали.

Благодаря золотому сечению был открыт пояс астероидов между Марсом и Юпитером – по пропорции там должна находиться ещё одна планета.

Возбуждение струны в точке, делящей её в отношении золотого деления, не вызовет колебаний струны, то есть это точка компенсации.

На летательных аппаратах с электромагнитными источниками энергии создаются прямоугольные ячейки с пропорцией золотого сечения.

Джоконда построена на золотых треугольниках, золотая спираль присутствует на картине Рафаэля «Избиение младенцев».

Пропорция обнаружена в картине Сандро Боттичелли «Рождение Венеры»

Известно много памятников архитектуры, построенных с использованием золотой пропорции, в том числе Пантеон и Парфенон в Афинах, здания архитекторов Баженова и Малевича.

Иоанну Кеплеру, жившему пять веков назад, принадлежит высказывание: «Геометрия обладает двумя великими сокровищами. Первое — это теорема Пифагора, второе — деления отрезка в крайнем и среднем отношении»

Список литературы

1. Д. Пидоу. Геометрия и искусство. – М.: Мир, 1979.

2. Журнал «Наука и техника»

3. Журнал «Квант», 1973, № 8.

4. Журнал «Математика в школе», 1994, № 2; № 3.

5. Ковалев Ф.В. Золотое сечение в живописи. К.: Выща школа, 1989.

6. Стахов А. Коды золотой пропорции.

7.Воробьев Н.Н. «Числа Фибоначчи» — М.: Наука 1964

8. «Математика — Энциклопедия для детей» М.: Аванта +, 1998

9. Информация из интернета.

Матриц Фибоначчи и так называемых «золотых» матриц, новые компьютерные арифметики, новая теорию кодирования и новая теория криптографии. Суть новой науки, в пересмотре с точки зрения золотого сечения всей математики, начиная с Пифагора, что, естественно, повлечет в теории новые и наверняка очень интересные математические результаты. В практическом отношении – «золотую» компьютеризацию. А поскольку…

Не повлияют на этот результат. Основание золотой пропорции является инвариантом рекурсивных соотношений 4 и 6. В этом проявляется «устойчивость» золотого сечения, одного из принципов организации живой материи. Так же, основание золотой пропорции является решением двух экзотических рекурсивных последовательностей (рис 4.) Рис. 4 Рекурсивных последовательности Фибоначчи так…

Уха — j5, а расстояние от уха до макушки — j6 . Таким образом, в этой статуе мы видим геометрическую прогрессию со знаменателем j: 1, j, j2, j3, j4, j5, j6. (рис.9). Таким образом, золотое сечение – один из основополагающих принципов в искусстве античной Греции. Ритмы сердца и мозга. Равномерно бьется сердце человека – около 60 ударов в минуту в состоянии покоя. Сердце как поршень сжимает…

Как нарисовать идеальный пятиугольник

Используя несколько простых математических и геометрических инструментов, мы покажем вам , как нарисовать идеальный пятиугольник . Не нужно сходить с ума или тратить два ластика целиком. Достижение пятиугольника , где каждая сторона равна с углами, которые соприкасаются, возможно, как мы объясним ниже.

Следующие шаги:

Первый шаг к нарисуйте идеальный пятиугольник — это отметить точку в центре вашего листа.Поместите циркуль в точку и нарисуйте идеальный круг. Если у вас есть время, вот и другие способы нарисовать круг.

Используя центральную точку и транспортир, разделите круг на 5 точек. В круге 360 °, а 360/5 = 72 °. Итак, вы должны отмечать точку через каждые 72 градуса. Чтобы получить правильное измерение, используйте транспортир, чтобы получить идеальное измерение для вашего пятиугольника .

Подключите каждую соседнюю точку. Теперь у вас есть пятиугольник.

Если вы хотите нарисовать пентаграмму вместо пятиугольника: вместо того, чтобы соединять соседние точки вместе, вы должны соединить каждую точку с двумя противоположными точками.

Сотрите круг, если он вам больше не нужен.

Можно также нарисовать пятиугольник с помощью циркуля и линейки, если дан круг. Это будет полезно для определенных упражнений, а также может быть применено, когда вам не нужно иметь определенный размер по бокам.

Нарисуйте круг с радиусом циркуля A и центром A B.
Нарисуйте второй круг с тем же радиусом с центром на A.
Пересечение обоих кругов будет обозначено C.
Проведите линейкой прямую линию через точки A и C.
Нарисуйте еще одну прямую линию через B и C.
Эта вторая линия даст вам пересечение с первым кругом, который будет D.
Нарисуйте прямую линию от A до D.
Это создаст третье пересечение между вторым кругом и этой последней линией. Это будет пересечение E.
Установите компас на расстоянии между C и E и нарисуйте круг с центром в B.
Этот третий круг будет пересекать первую прямую линию. Это пересечение будет F.
Нарисуйте исходный круг еще раз.
Установите компас на расстояние между E и F. Это даст вам длину кромки идеального пятиугольника.
С помощью циркуля нарисуйте линии заданной длины.
Объедините каждую отметку, которую вы создали с помощью компаса. Теперь у вас есть пятиугольник.

Этот метод может быть более сложным, но он со 100% точностью и даст вам идеальный пятиугольник.

Если вы хотите прочитать статьи, похожие на Как нарисовать идеальный пятиугольник , мы рекомендуем вам посетить нашу категорию «Ремесла и досуг».

как сложить правильный пятиугольник из квадрата

Квадрат и пятиугольник, кажется, обитают в разных мирах.Прямые углы квадрата кажутся несовместимыми с интересной формой пятиугольника. На первый взгляд кажется маловероятным, что вы можете сбросить одну от другой. Поговорка «Отсюда нельзя попасть». приходит на ум. Тем не менее, благодаря общей связи с золотой серединой вы можете создать правильный пятиугольник из квадратного листа бумаги.

Ступеньки

Сложите квадратный лист бумаги пополам. Открыть.
Загните диагональ правой половины.
Загните нижний край вверх так, чтобы он совпадал с последней складкой.
Согните по существующей линии сгиба так, чтобы точка касалась левого нижнего угла бумаги. Открыть.
Согните бумагу так, чтобы складка проходила через верхнюю середину бумаги, а левый край бумаги касался пересечения двух складок в правой половине бумаги.
Загните угол бумаги обратно по линии сгиба на бумаге под ним. Раскройте бумагу.
Сложите бумагу еще раз пополам.
Загните по предыдущей складке.
Сложите новую складку пополам.
Загните вниз вдоль края бумаги.
Согните так, чтобы правый край совпал с краем.
Загните горную складку в месте стыка краев, загибая нижнюю часть назад за верхнюю часть.
Согните острую складку вдоль края показанной бумаги. Эта складка будет пятиугольником.
Откройте бумагу, чтобы увидеть пятиугольник.

Банкноты

Эта последовательность складок основана на том факте, что отношение диагонали пятиугольника к краю является золотой серединой (). Первые пять шагов создают линейный сегмент нужной длины. Остальные шаги копируют этот сегмент в правильные места вокруг пятиугольника.
Предполагая, что квадрат имеет ширину 2 единицы, каждая сторона пятиугольника должна быть длиной единицы. Чтобы получить это значение, решите указанную выше пропорцию:
Сгиб, созданный на шаге 2, представляет собой квадратный корень из 5 единиц длины.Шаг 4 отмечает точку 1 на этой складке. Остаток — это отрезок правильной длины.
Есть более простой способ сложить примерно правильный пятиугольник, начиная с листа бумаги формата А4. Этот метод основан на том факте, что страница формата A4 представляет собой квадратный корень в два раза больше ее ширины. Складывание противоположных углов вместе создает складку под углом 54,7 ° (арктангенс квадратного корня из двух), который близок к углу 54 °, который можно использовать для построения пятиугольника.

Ссылки

Инструкция, как сложить примерно правильный пятиугольник из листа бумаги формата А4.

Список литературы

http://www.erclc.org/StaffPages/David/Origami/OrigamiPentagon.htm

правильных пятиугольников

правильных пятиугольников Углы в равнобедренных треугольниках

В треугольнике ABC с AB = AC углы между равными сторонами равны.Пусть a = угол BAC и пусть b = угол ABC = угол ACB.

Используя теорему о сумме углов, если известно a, то определяется b, а если b задано, то определяется a.

Запишите отношения:

а =

б =

Некоторые важные примеры

а	б
90
	60
	36
72

Сумма углов в выпуклых многоугольниках (неофициальная версия)
Мы знаем, что сумма углов при вершинах треугольника на плоскости всегда равна 180 градусам.Теорема о суммах углов для многоугольников в целом будет тщательно разработана позже, а пока это будет краткое неформальное введение.
Четырехугольник
Пусть ABCD — четырехугольник. Если диагональ AC (продолженная до прямой) такова, что B находится с одной стороны от AC, а D — с другой, то ABCD делится на объединение двух треугольников ABC и CDA.
В этом случае сумма углов ABCD составляет 360 градусов, что является суммой углов двух треугольников, поскольку 180 + 180 = 360 градусов.
Для выпуклого четырехугольника, такого как левый, это работает для любого выбора диагонали. Для невыпуклого четырехугольника справа мы выбрали одну диагональ, которая делит четырехугольник на два треугольника.
Пентагоны
Если мы разделим пятиугольник на треугольники, как на рисунке слева внизу, пятиугольник состоит из трех треугольников, поэтому сумма углов будет 180 + 180 + 180 = 3 * 180 = 540 градусов.
Однако невыпуклый пятиугольник справа — более сложный случай.Если у нас есть фигура на странице, мы всегда можем найти способ нарисовать сегменты, чтобы разделить пятиугольник на 3 треугольника, но как мы можем доказать это во всех случаях? Как мы можем доказать разбиение треугольников на многоугольники с большим количеством вершин? Это не только теоретическая проблема, но и практическая проблема информатики. Если многоугольник задан на плоскости с помощью координат, как можно указать компьютеру разделить его на треугольники? Мы вернемся к этому вопросу позже. На данный момент мы делаем разумное предположение, что любые встречающиеся нам пятиугольники можно разделить на 3 треугольника.Это, безусловно, верно для выпуклых, как мы видим на рисунке слева.
Вопрос : Правильный пятиугольник определяется как пятиугольник, у которого все углы равны и все стороны равны. Какой должен быть угол в каждой вершине?
Ответ :

Равнобедренные треугольники в правильном пятиугольнике
Для правильного многоугольника мы видели, что угол каждой вершины равен 108 = 3 * 180/5 градусов.
На этом рисунке начертите диагональ переменного тока.
Объясните, почему треугольник ABC является равнобедренным.

Запишите размеры углов треугольника ABC. На рисунке обозначьте каждый угол треугольника ABC числом градусов в угле.

Затем нарисуйте диагональ AD и аналогичным образом обозначьте размеры углов в треугольнике ADE. Почему треугольник ADE конгруэнтен треугольнику ABC?

Объясните, почему треугольник CAD является равнобедренным треугольником.

Наконец, используя то, что вы сейчас знаете обо всех углах с вершиной в A, запишите величину угла CAD, а затем обозначьте размеры других углов треугольника ACD.

Пусть s = || AB | и пусть d = | AC |. Назовите углы в треугольнике, подобном (1) треугольнику со сторонами s-s-d и (2) треугольнику со сторонами d-d-s.

Углы в пятиугольнике и пентаграмме

Знакомая пятиконечная звезда или пентаграмма также является правильной фигурой с равными сторонами и одинаковыми углами.
Пентаграмму можно нарисовать, нарисовав все диагонали правильного пятиугольника.
На предыдущей странице мы видели углы некоторых равнобедренных треугольников. В частности, появились углы 36, 72 и 108 градусов. На этом рисунке выше отметьте все углы в 36 градусов одиночной меткой, отметьте углы в 72 градуса двойной меткой и все углы в 108 градусов тройной меткой.
Передаточные числа в правильном пятиугольнике

Обозначим пересечение AC и BD буквой F.
Теперь, временно игнорируя остальную часть фигуры, сконцентрируйтесь на этом треугольнике с подтреугольником. Обозначьте все углы на рисунке их размерами.
Объясните, основываясь на углах, почему каждый из подтреугольников представляет собой равнобедренный треугольник.
При том, что | AC | = d и | CD | = s, что такое | CD |?

Используя аналогичные треугольники, найдите уравнение, связывающее s и d.

Пусть теперь отношение r = d / s.Перепишите уравнение как уравнение относительно r. (Других переменных не должно быть.) Затем решите относительно r.

Треугольник и пятиугольник
Привет, Оливия.
Зеленый треугольник равнобедренный, поэтому, если вы знаете величину угла между общими сторонами (внешний конец) и длину основания (сторона, общая с красным пятиугольником), то вы можете найти площадь треугольника. .
Во-первых, угол на вершине: вспомните, что сумма углов четырехугольника равна 360 градусам.Вы также должны знать, что сумма углов 5-сторонней фигуры равна 540, потому что для любого замкнутого n-угольника сумма углов равна 180 (n-2) .
Для правильного пятиугольника, как на вашей диаграмме, все углы одинаковы, поэтому каждый внутренний угол составляет 540/5 = 108 градусов.
Теперь подумайте о раскрашенном четырехугольнике (не обращайте внимания на цвет и общую сторону треугольника и пятиугольника. Это четырехгранная форма, поэтому сумма углов равна 360. Но вы уже знаете, что мера трех углов — 108 каждый.
Таким образом, оставшийся угол (вершина треугольника) равен 360 — 3 (108) = 360 — 324 = 36 градусов.
Теперь, когда мы знаем величину угла, нам нужна длина основания треугольника, которая равна длине стороны правильного пятиугольника, площадь которого известна.
Давайте нарисуем центр пятиугольника и разделим его на 5 равных треугольников, затем разделим пополам один из этих 5 на два равных прямоугольных треугольника:
По симметрии вы должны увидеть, что внутренние углы пятиугольника в 108 градусов составляют углы в 54 градуса.Также по симметрии пять треугольников равнобедренные, поэтому, когда мы делим один из них (зеленой линией), мы делим длину стороны пополам с помощью перпендикуляра. Таким образом, мы разделили пятиугольник на 10 эквивалентных прямоугольных треугольников с углом 54 градуса.
Давайте обозначим несколько вещей в этом прямоугольном треугольнике:
Какова площадь этого треугольника? Площадь любого треугольника равна половине основания, умноженной на высоту, поэтому площадь этого треугольника равна ½xw . Поскольку в пятиугольнике десять таких треугольников, площадь пятиугольника равна 10 (½xw) .Но вам говорят, что это 800 см ², поэтому 800 = 10 (½xw) , что сокращается до 160 = xw .
Используя тригонометрию, мы знаем, что тангенс угла в 54 градуса равен противоположной длине на соседней длине, поэтому tan (54) = x / w , что мы можем переписать как w tan (54) = x .
Так как это равно x, давайте подставим его в наше предыдущее уравнение:
160 = xw = (w загар (54)) w = w ² загар (54).
Теперь мы можем найти w:
160 / tan (54) = w ².
w = 10,782 см.
Теперь давайте разделим этот зеленый равнобедренный треугольник таким же образом:
Мы разделили угол кончика пополам, поэтому 36/2 = 18 градусов. Таким образом, зеленый треугольник представляет собой сумму двух равных прямоугольных треугольников. Так как каждый из них имеет площадь ½wy, зеленая зона — это просто wy.
Снова используя тригонометрию, tan (18) = w / y , поэтому y = w / tan (18) .Это означает, что зеленая область равна wy = w ² / tan (18) .
А так как w = 10,782 см, имеем
Зеленая область = (10,782) ² / tan (18) = 357,8 см ².
Cheers,
Стивен Ла Рок.
10 фактов о Пентагоне, которые вы, вероятно, не знали> ДЕПАРТАМЕНТ ОБОРОНЫ США> Сюжет
1
Знаете, почему Пентагон — это пятиугольник?
Территория, по которой Пентагон планировалось пройти сначала, была ограничена с пяти сторон дорогами, поэтому архитекторы спроектировали пятистороннее здание.Президент Франклин Делано Рузвельт беспокоился, что размещение здания в этом месте будет мешать обзору Вашингтона с Арлингтонского кладбища, поэтому он решил переместить его на его нынешнее место, но сохранил пятисторонний дизайн.
2
11 сентября имеет двойное значение для Пентагона.
Строители заложили основу для Пентагона 11 сентября 1941 года, ровно за 60 лет до сентября.11 ноября 2001 г., теракты. 3
Пентагон большой. Очень большой.
Это самое большое в мире малоэтажное офисное здание. Все здание Капитолия США могло поместиться внутри любого из пяти клиньев здания. Он имеет 6 500 000 квадратных футов офисных площадей (в три раза больше площади Эмпайр-стейт-билдинг!), 7 754 окна и 17,5 миль коридоров.Тем не менее, его конструкция со спицами и кольцами означает, что пройти между двумя самыми дальними точками в здании можно всего за 7 минут. 4
Строители бережно относились к материалам.
Во время строительства строители смогли сохранить достаточно стали, чтобы построить линкор. А 689 000 тонн песка и гравия, которые использовались для изготовления железобетона здания, в том числе 41 000 бетонных свай, поступили из близлежащей реки Потомак.
5
До 2011 года в Пентагоне был только один пассажирский лифт. И это было зарезервировано для министра обороны.
В рамках 17-летней реконструкции, завершившейся в 2011 году, в здании было установлено 70 пассажирских лифтов. До этого люди, которые не могли пользоваться лестницей, использовали длинные пандусы для перемещения между этажами. Пандусы все еще там, но слухи о гонках офисных кресел сильно преувеличены.
6
Этот проект ремонта? Вероятно, это спасло тысячи жизней.
Пентагон разделен на пять клиньев, и проект реконструкции клин за клином заходил клин за клином, когда террористы направили рейс 77 American Airlines в Пентагон 11 сентября 2001 года, убив 189 человек. Самолет упал в Ведж 3, где только что закончились ремонтные работы, но только около 800 из 4500 человек, которые обычно работали бы там, вернулись в свои офисы.А новая спринклерная система, дополнительная структурная опора и взрывостойкие окна помогли свести к минимуму повреждения здания, что, вероятно, спасло дополнительные жизни. 7
Пентагон был первым зданием без сегрегации в Вирджинии.
Пентагон был создан, когда сегрегация была законом в Вирджинии. Но в прошлом году Рузвельт подписал указ, запрещающий дискриминацию государственных служащих по признаку расы, вероисповедания, цвета кожи или национального происхождения.Таким образом, Пентагон стал единственным зданием в Вирджинии, где не применялась сегрегация. Поскольку сегрегация была законом штата, Пентагон был построен с вдвое большим количеством ванных комнат, чем необходимо для несегрегированного здания такого размера.
8
Он был построен в рекордные сроки.
Более 15000 рабочих находились на объекте круглосуточно, а нехватка офисных помещений в военное время привела к тому, что рабочие переехали еще до того, как строительство Пентагона было полностью завершено.Строительство завершилось 15 января 1943 года, всего через 16 месяцев после начала. Однако скорость стоит денег: изначально бюджет составлял 35 миллионов долларов, а окончательная стоимость составила 63 миллиона долларов, то есть более 900 миллионов долларов в сегодняшних деньгах.
9
Этот же парень курировал строительство Пентагона и атомной бомбы.
Полковник Лесли Гровс, офицер инженерного корпуса армии, возглавил строительство Пентагона в августе 1941 года.Он работал шесть дней в неделю в своем офисе в Вашингтоне. Затем по воскресеньям он посещал проект, который, по его мнению, больше всего нуждался в его личном внимании. Позже Гроувс сказал о своем пребывании в Пентагоне, что «надеялся попасть на театр военных действий, чтобы я мог найти немного покоя». Вместо этого ему было поручено руководить Манхэттенским проектом — усилиями Америки по созданию атомной бомбы.
10
Какое-то время в Пентагоне была секретная аварийная площадка.
Гроув был широко известен как крутой босс. Один из его заместителей, армейский майор Роберт Фурман, должен был находиться в Пентагоне в любое время дня и ночи. Иногда он целыми днями не ходил домой. Чтобы немного поспать, Фурман приказал подрядчикам Пентагона построить секретную квартиру между стенами того, что впоследствии станет артиллерийской дивизией армии. Он и некоторые другие заместители Гроува использовали квартиру, чтобы взять несколько букетов, принять душ и вернуться к работе.Фурман продолжал использовать квартиру во время официальных поездок обратно в Вашингтон, когда он служил офицером разведки в Манхэттенском проекте, но был вынужден передать ключи в 1943 году, когда его обнаружили офицеры по боеприпасам, когда он выходил из квартиры.
Хотите больше? Посетите Pentagon Tours, чтобы узнать больше о здании и о том, как пройти экскурсию.
Формирующие многоугольники | Справка SketchUp
Нужна шестиугольная форма, чтобы продемонстрировать макет вашего пчеловодческого хозяйства? Хотите значок пятиугольника, чтобы проиллюстрировать пятиэтапный план развития? Инструмент «Многоугольник» LayOut позволяет рисовать многоугольник с любым количеством сторон.(Ну, почти любое число: многоугольники должны иметь как минимум три стороны.)
Инструмент «Многоугольник» () можно найти на панели инструментов по умолчанию или выбрав «Инструменты »> «Многоугольник » в строке меню.
Чтобы нарисовать многоугольник, выполните следующие действия:
Выберите инструмент Многоугольник .
Щелкните в области рисования, чтобы разместить центральную точку многоугольника. Или используйте поле «Измерения», чтобы указать точную центральную точку, введя абсолютные координаты относительно верхнего левого угла области рисования.Например, чтобы разместить центральную точку на 5,5 дюйма по оси X и на 4,25 дюйма вниз по оси Y, введите [5,5 дюйма, 4,25 дюйма] и нажмите . Введите (Microsoft Windows) или . ).
(Необязательно) По умолчанию многоугольники имеют 5 сторон. Чтобы указать необходимое количество сторон, нажмите клавишу Стрелка вверх или Стрелка вниз . Или введите число и букву s . Например, если вам нужно 6 сторон, как показано на следующем рисунке, введите 6s и нажмите . Введите или . Верните .
Переместите курсор внутрь или наружу от центральной точки, чтобы изменить размер многоугольника, и щелкните, чтобы закончить форму. Или используйте поле «Измерения», чтобы указать радиус. Значение радиуса может быть единицей измерения или значением точки. Например, введите 3 « и нажмите . Введите или . Верните . Вы можете продолжать изменять количество сторон и радиус, пока не нарисуете еще один многоугольник или не выберете другой инструмент.
Инструмент «Многоугольник» может также выполнять несколько других задач:
При рисовании многоугольника удерживайте нажатой клавишу Shift , чтобы зафиксировать сторону многоугольника относительно красной или зеленой оси.
Сразу после создания многоугольника дважды щелкните в области рисования, чтобы продублировать многоугольник. Вы можете продолжать дважды щелкать, чтобы создать столько копий, сколько вам нужно.
Совет: Если вы ошиблись при рисовании многоугольника, нажмите Esc , чтобы начать заново.
Как нарисовать пятиугольник с помощью компаса
Пятиугольник — это пятиугольник, стороны которого равны по длине. Это может быть полезная форма при изготовлении реквизита; он также может служить основой для пятигранной звезды.Может быть сложно разметить с помощью стандартных инструментов для рисования, но с помощью метода, описанного ниже, вы можете нарисовать его только с помощью циркуля и линейки.
Начните с круга, размер которого идеально подходит для вашего пятиугольника; то есть каждый угол вашего пятиугольника будет касаться внешней стороны вашего круга.
Рисунок 1
В моем круге я нарисовал две перпендикулярные линии, проходящие через центральную точку O. Там, где они пересекают круг, я пометил A, X, Y и Z (A будет верхней точкой пятиугольника, поэтому поместите это соответственно).
Я разделил линию OY пополам, чтобы найти точку M; то есть M находится точно на полпути между O и Y.
Рисунок 2
Поместите циркуль на M и вытяните его так, чтобы карандаш касался A. Нарисуйте дугу, пересекающую линию XO; мы назовем это пересечение «R».
Рисунок 3
Переместите точку циркуля на A и вытяните его так, чтобы карандаш касался R. Теперь радиус вашего циркуля равен длине сторон вашей пентаграммы. Когда вы рисуете дугу от R до вашего круга, вы найдете точку «B».
Рис. 4
Когда вы перемещаете компас для поворота на B и рисуете дугу, он пересекает круг в двух точках: A и в новой точке «C».
Рисунок 5
Вернув компас к точке А, нарисуйте дугу, пересекающую правую сторону круга, чтобы найти букву «Е».
Рисунок 6
Переместите циркуль в положение E и нарисуйте дугу, чтобы найти «D». На картинке выше я нарисовал дугу так, чтобы она дважды пересекала круг, в точке D и снова в точке A. На самом деле этого делать не нужно.
Чтобы проверить, что у вашего пятиугольника пять равных сторон, вы можете поставить точку компаса на D.