Как сделать 3: как сделать вид от 3 лица на самолете спереди? бф1

Как сделать скриншот экрана на телефоне Xiaomi Mi Max 3

Рейтинг телефона: (3.75 — 8 голосов)

Современный смартфон обладает рядом полезных функций. Например, владелец мобильного устройства в любой момент может сделать скриншот экрана. Выполнение подобной операции поможет, когда пользователь найдет интересную информацию и захочет ее запечатлеть. В такой ситуации не придется фотографировать экран на другой девайс, поскольку достаточно будет сделать скриншот на телефоне Xiaomi Mi Max 3.

Когда можно сделать скриншот на Xiaomi Mi Max 3

Производитель телефона не ограничивает владельца вариантами создания скрина. Сделать скриншот можно в абсолютно любой момент: во время просмотра фильма, игрового процесса или переписки в мессенджере. Главное условие для получения снимка – смартфон должен быть включен и разблокирован.

Создание скриншота на Xiaomi Mi Max 3 при помощи клавиш

Самый простой способ создать скрин экрана – воспользоваться определенной комбинацией клавиш:

1. Открыть раздел меню, который нужно запечатлеть.
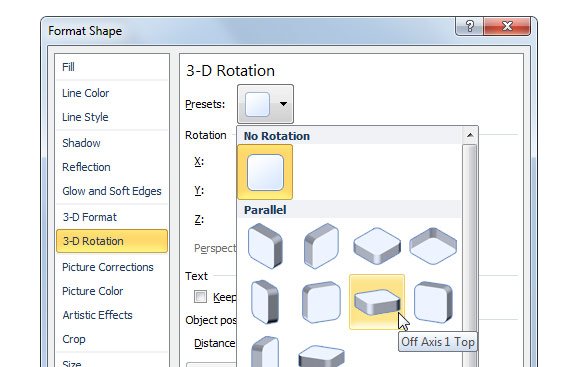
2. Одновременно зажать кнопку питания и нижнюю качельку регулировки громкости.
3. Дождаться появления информации о том, что картинка готова.

После выполнения указанных действий в нижней части экрана появится графическое уведомление об успешном создании скрина. Получившийся кадр можно сразу же открыть, нажав на его иконку после зажатия клавиши понижения громкости и кнопки питания.

Если снимок экрана на Xiaomi Mi Max 3 сделать не получается, рекомендуется ознакомиться с альтернативными комбинациями кнопок, которые приведены в этом материале. Кроме того, существуют и другие способы создания скрина без использования клавиш телефона.

Способ создания скриншота через панель уведомлений

Этот способ будет лучшим выходом из ситуации, когда кнопки смартфона по какой-либо причине не работают, и скрин не создается. В качестве альтернативного варианта предлагается выполнить следующие действия:

1. Разблокировать смартфон.
2. Перейти в раздел меню, где требуется сделать скриншот.
3. Опустить шторку уведомлений свайпом сверху вниз.
4. Нажать на иконку «Screenshot» или «Снимок экрана».

Как и в случае со снимком через горячие клавиши, уведомление о создании скрина сразу же появится на экране смартфона Андроид. Получившийся скрин можно открыть или сделать другой кадр из этого или другого меню.

Где хранятся скриншоты

Чтобы ознакомиться с получившимся снимком экрана, достаточно открыть приложение «Галерея» и перейти в альбом «Screenshots» или «Скриншоты».

Еще один способ быстро найти скрин выглядит следующим образом:

1. Запустить «Проводник» или «Диспетчер файлов».
2. Открыть папку «Pictures».
3. Перейти в «Screenshots».

В открывшемся разделе меню появятся скрины, которые были сделаны за все время использования смартфона.

Как удалить или передать снимок экрана

В момент, когда пользователь открывает кадр через «Галерею» или «Диспетчер файлов», перед ним появляется полный функционал взаимодействия с изображением. К примеру, владелец телефона может удалить один или сразу же несколько снимков экрана в пару кликов:

1. Открыть папку, где лежит скрин.
2. Удержать палец на его иконке.
3. Нажать кнопку «Удалить».

Еще один способ – открыть само изображение через «Галерею» и выбрать ид доступных опций параметр «Удалить». После подтверждения операции скриншот будет удален из памяти телефона.

В случае, когда требуется передать скрин через мессенджер или другим способом, можно воспользоваться той же инструкцией. Единственное отличие заключается в том, что вместо нажатия кнопки «Удалить» нужно кликнуть на «Передать», выбрать способ отправки и координаты получателя. Таким образом, отправка скрина не отличается от передачи любого другого изображения с телефона.

Поделитесь страницей с друзьями:

Если все вышеперечисленные советы не помогли, то читайте также:

Как прошить Xiaomi Mi Max 3

Как получить root-права для Xiaomi Mi Max 3

Как сделать сброс до заводских настроек (hard reset) для Xiaomi Mi Max 3

Как разблокировать Xiaomi Mi Max 3

Как перезагрузить Xiaomi Mi Max 3

Что делать, если Xiaomi Mi Max 3 не включается

Что делать, если Xiaomi Mi Max 3 не заряжается

Что делать, если компьютер не видит Xiaomi Mi Max 3 через USB

Как сделать сброс FRP на Xiaomi Mi Max 3

Как обновить Xiaomi Mi Max 3

Как записать разговор на Xiaomi Mi Max 3

Как подключить Xiaomi Mi Max 3 к телевизору

Как почистить кэш на Xiaomi Mi Max 3

Как сделать резервную копию Xiaomi Mi Max 3

Как отключить рекламу на Xiaomi Mi Max 3

Как очистить память на Xiaomi Mi Max 3

Как увеличить шрифт на Xiaomi Mi Max 3

Как раздать интернет с телефона Xiaomi Mi Max 3

Как перенести данные на Xiaomi Mi Max 3

Как разблокировать загрузчик на Xiaomi Mi Max 3

Как восстановить фото на Xiaomi Mi Max 3

Как сделать запись экрана на Xiaomi Mi Max 3

Где находится черный список в телефоне Xiaomi Mi Max 3

Как настроить отпечаток пальца на Xiaomi Mi Max 3

Как заблокировать номер на Xiaomi Mi Max 3

Как включить автоповорот экрана на Xiaomi Mi Max 3

Как поставить будильник на Xiaomi Mi Max 3

Как изменить мелодию звонка на Xiaomi Mi Max 3

Как включить процент заряда батареи на Xiaomi Mi Max 3

Как отключить уведомления на Xiaomi Mi Max 3

Как отключить Гугл ассистент на Xiaomi Mi Max 3

Как отключить блокировку экрана на Xiaomi Mi Max 3

Как удалить приложение на Xiaomi Mi Max 3

Как восстановить контакты на Xiaomi Mi Max 3

Где находится корзина в Xiaomi Mi Max 3

Как установить WhatsApp на Xiaomi Mi Max 3

Как сделать скриншот для других моделей телефонов

ЗК РФ Статья 39.

28. Случаи и основания перераспределения земель и (или) земельных участков, находящихся в государственной или муниципальной собственности, и земельных участков, находящихся в частной собственности / КонсультантПлюс

ЗК РФ Статья 39.28. Случаи и основания перераспределения земель и (или) земельных участков, находящихся в государственной или муниципальной собственности, и земельных участков, находящихся в частной собственности

КонсультантПлюс: примечание.

О разъяснении положений п. 1 ст. 39.28 см. п. 7 ст. 3.6 ФЗ от 25.10.2001 N 137-ФЗ.

1. Перераспределение земель и (или) земельных участков, находящихся в государственной или муниципальной собственности, и земельных участков, находящихся в частной собственности, допускается в следующих случаях:

1) перераспределение таких земель и (или) земельных участков в границах застроенной территории, в отношении которой заключен договор о развитии застроенной территории, осуществляется в целях приведения границ земельных участков в соответствие с утвержденным проектом межевания территории;

2) перераспределение таких земель и (или) земельных участков в целях приведения границ земельных участков в соответствие с утвержденным проектом межевания территории для исключения вклинивания, вкрапливания, изломанности границ, чересполосицы при условии, что площадь земельных участков, находящихся в частной собственности, увеличивается в результате этого перераспределения не более чем до установленных предельных максимальных размеров земельных участков;

3) перераспределение земель и (или) земельных участков, находящихся в государственной или муниципальной собственности, и земельных участков, находящихся в собственности граждан и предназначенных для ведения личного подсобного хозяйства, огородничества, садоводства, индивидуального жилищного строительства, при условии, что площадь земельных участков, находящихся в собственности граждан, увеличивается в результате этого перераспределения не более чем до установленных предельных максимальных размеров земельных участков;

(в ред. Федерального закона от 29.07.2017 N 217-ФЗ)

4) земельные участки образуются для размещения объектов капитального строительства, предусмотренных статьей 49 настоящего Кодекса, в том числе в целях изъятия земельных участков для государственных или муниципальных нужд.

(в ред. Федерального закона от 08.03.2015 N 48-ФЗ)

2. Перераспределение земель и (или) земельных участков, находящихся в государственной или муниципальной собственности, и земельных участков, находящихся в частной собственности, осуществляется на основании соглашения между уполномоченными органами и собственниками земельных участков. При этом указанное соглашение должно содержать сведения о возникновении права государственной или муниципальной собственности и (или) права частной собственности на образуемые земельные участки.

3. Перераспределение земель и (или) земельных участков, находящихся в государственной или муниципальной собственности, и земельных участков, находящихся в частной собственности, осуществляется в соответствии с утвержденным проектом межевания территории либо при отсутствии такого проекта в соответствии с утвержденной схемой расположения земельного участка.

4. Обязательными приложениями к указанному в пункте 2 настоящей статьи соглашению являются кадастровый паспорт земельного участка или кадастровые паспорта земельных участков, которые образуются в результате перераспределения земель и (или) земельного участка, находящихся в государственной или муниципальной собственности, и земельного участка, находящегося в частной собственности.

5. Увеличение площади земельных участков, находящихся в частной собственности, в результате перераспределения таких земельных участков и земель и (или) земельных участков, находящихся в государственной или муниципальной собственности, осуществляется за плату, размер которой определяется:

1) в порядке, установленном Правительством Российской Федерации, в отношении земельных участков, находящихся в федеральной собственности;

2) в порядке, установленном органом государственной власти субъекта Российской Федерации, в отношении земельных участков, находящихся в собственности субъекта Российской Федерации, земель или земельных участков, государственная собственность на которые не разграничена;

3) в порядке, установленном органом местного самоуправления, в отношении земельных участков, находящихся в муниципальной собственности.

Открыть полный текст документа

Как сделать полный сброс настроек Apple Watch? 3 способа!

Всем категорический привет! Давайте поступим максимально неожиданно и решительно «разорвём шаблон» классических инструкций из «этого вашего интернета» — сразу перейдём к делу и выясним, каким образом можно сделать полный сброс абсолютно любой модели Apple Watch до заводских настроек.

Не будем, так сказать, тянуть кота за причинное место — животных нужно любить:)

Итак, мало кто знает (техническая поддержка Apple, извините, но это камень в ваш огород), что существует аж три разных способа «забабахать» Hard Reset часов от компании Apple! Начнём, конечно же, с классики…

Способ №1. Сбросить Apple Watch при помощи iPhone

Всё максимально просто:

1. Берём iPhone, который находится в паре с Apple Watch.
2. На рабочем столе iPhone находим приложение «Watch» — открываем.
3. Находим настройку «Основные».
4. Прокручиваем экран вниз.
5. Видим пункт «Сброс».
6. Нажимаем, выбираем «Стереть контент и настройки Apple Watch», соглашаемся.
7. Победа!

Ваши Apple Watch полностью «чисты» — на них нет никакой информации.

Вы спросите: «А если iPhone отсутствует?».

Я отвечу: «Тогда…».

Способ №2. Очистить Apple Watch при помощи часов

Опять-таки ничего сложного:

1. Берём часы, открываем меню, переходим в «Настройки».
2. Выбираем пункт «Основные».
3. Прокручиваем экран вниз — видим нужный нам пункт «Сброс».
4. Жмём на «Стереть контент и настройки».
5. Ура!

Apple Watch вернулись к своему заводскому состоянию.

Способ №3. Hard Reset Apple Watch при помощи кнопок

Пригодится в том случае, когда пара ещё не создана, а очистить Apple Watch очень нужно.

Как, например, это происходило у меня, когда я никак не мог обновить WatchOS.

Ух, были времена!

В общем, порядок действий будет таким:

1. Ставим часы на зарядку.
2. Несколько секунд жмём на колёсико Digital Crown.
3. На экране часов появляется надпись: «Повторить поиск? Заводские настройки устройства будут восстановлены».
4. Выбираем «Сбросить».
5. Ок? Ок!

Спустя некоторое время Apple Watch будут сброшены до состояния «как из магазина» — можно обновлять прошивку, создавать пару с iPhone и заниматься другими полезными вещами.

Например, написать комментарий и рассказать — что помогло, а что нет.

P.S. Задавайте вопросы, делитесь личным опытом, ставьте «лайки», жмите на кнопки социальных сетей, не болейте и будьте счастливы. Потому что… а почему бы и нет?:)

3 оригинальные идеи — Ozon Клуб

Кактусы не входит в список самых популярных растений, используемых для украшения интерьера. Между тем, они достаточно декоративны, а флористическая композиция из кактусов и других суккулентов может стать неожиданным и приятным подарком.

Крыжановская Яна

19 Декабря

Пустынный ландшафт

Кактусы – это типичные жители пустынь. Они хорошо приживаются в песчаной почве и привычны к длительному отсутствию воды. Миниатюрный пустынный ландшафт, сделанный своими руками, выглядит эстетично и не требует большого ухода. Для создания композиции вам понадобится плоский низкий горшок наподобие тех, которые используются для выращивания бонсая, галька, почва для кактусов, песок, газета, малярная кисть и собственно мини-кактусы видов «Клейстокактус Штрауса», «Маммиллярия», «Опунция» и цветущая «Ребуция». Не забудьте запастись садовыми инструментами и плотными перчатками.

Кактусы не переносят застой воды, поэтому уложите на дно горшка достаточное количество гальки для оттока жидкости. Убедитесь в том, что выбранные вами растения подходят по размеру для данной композиции. Расставьте их в выбранном порядке, не вынимая из горшков. Имеет смысл на передний план высадить кактусы меньшего размера, а на задний — более высокие и крупные растения. Насыпьте в горшок часть почвы и начинайте пересадку растений. Оберните кактус газетой, сложенной в несколько слоев. Это предотвратит повреждение иголок и защитит ваши руки.

Старайтесь не засаживать кактусы очень плотно. Заполните пустоты между растениями оставшейся почвой, используя ложку. С помощью малярной кисти очистите растения от возможных загрязнений. Обильно полейте почву. После этого распределите по поверхности достаточное количество песка с помощью ложки, чтобы придать всей композиции вид пустынного ландшафта. Если место позволяет, разместите между кактусами несколько крошечных перекати-поле, приобрести которые можно во флористической лавке или изготовить самостоятельно.

Растительный террариум или флорариум

Для его создания понадобится крупная стеклянная ваза или аквариум понравившейся формы. Поместите на дно емкости слой гальки толщиной в 1-2 см для дренажа. Заполните емкость почвой на две трети. Приступаем к высадке растений. На заднем фоне расположите высокий «Трихоцереус», а на переднем – яркие «Гимнокалициумы Михановича» с шапочками красного, розового и желтого цвета, привитыми на зеленый стебель. Центральным звеном композиции может стать «Каменная роза» – эффектный суккулент, хорошо сочетающийся с кактусами. Добавьте еще почвы. По поверхности распределите тонкий слой белой гальки.

Оригинальным и неожиданным подарком станет миниатюрный дзен-сад

Такая композиция может украсить практически любое помещение: ванную комнату, рабочий кабинет, гостиную. Используйте стеклянную емкость с асимметричными краями или низкий деревянный ящик. Наполните дзен-сад белым, черным или цветным песком. Высадите в песок крошечные шарообразные кактусы, например, «Эхинопсисы», заменив ими традиционные для этого вида искусства камни. Дополните композицию деревянной или металлической палочкой, с помощью которой владелец будет рисовать узоры на песке.  

Как сделать расчет по страховым взносам в 1с 8.3?

Данные о налогах во внеоборотные фонды, например, пенсионный, медицинский, социальный или страхование, отражаются в отчете “Расчеты по страховым взносам”.

Данный отчет необходимо подавать за 1 квартал, за 9 месяцев и за год. В отчете будет формироваться информация о работниках организации за период.

С 2017 года была утверждена новая единая форма — отчет, который отображает уплату страховых взносов в налоговые органы и предоставляется в территориальные налоговые инспекции.

Для организаций, в которых численность сотрудников превышает 25 человек, отчет необходимо подавать в электронном виде.

Тарифы в программе 1С Бухгалтерия предприятия 3.0

В программе тарифа по страховым взносам можно посмотреть через пункт меню “Зарплата и кадры” — “Настройка зарплаты” и выбрать раскрывающийся список “Классификаторы”. Далее, нажав на гиперссылку “Страховые взносы”, пользователь сможет просмотреть все тарифы.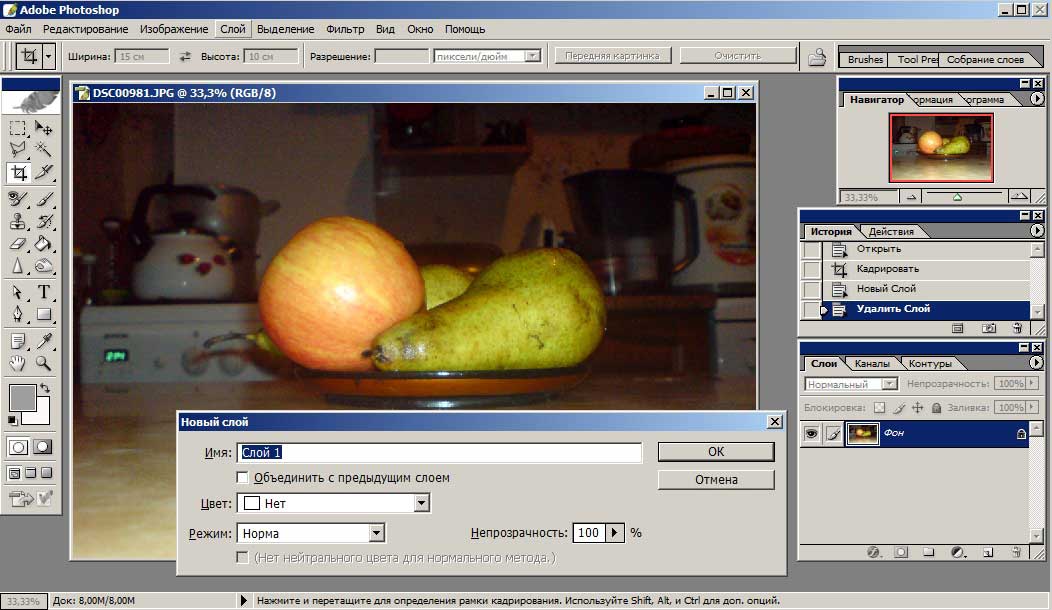

Также данный функционал можно открыть, используя пункт меню “Администрирование”: выбрать “Параметры учета” и нажать на гиперссылку “Настройка зарплаты”.

Формирование расчетов

При начислении зарплаты сотрудникам или оформления больничного листа программа формирует начисление по страховым взносам автоматически.

В документе “Начисление заработной платы” начисление страховых взносов можно посмотреть в колонке “Взносы”, и при нажатии на гиперссылку суммы откроется форма, в которой будет указана сумма начисления.

При оформлении больничного листа будут отражаться расходы за счет ФСС. Данные расходы будут отображаться в Приложении 3 раздел 1.

Формирование отчета РСВ

Чтобы сформировать отчет, необходимо перейти в пункт меню “Отчеты” и выбрать “Регламентированные отчеты”.

В окне 1С — отчетности необходимо нажать на кнопку “Создать”, после чего выбрать отчет из справочника.

Форма выбора отчета состоит из двух вкладок. На первой вкладке отображаются избранные отчеты, а на второй — весь список отчетов. На второй вкладке можно выбрать необходимые отчеты и напротив названия отчета установить звездочку, после чего данный отчет будет доступен на первой вкладке.

Отчет “Расчет по страховым взносам находится в группе “Налоговая отчетность”.

После нажатия на кнопку “Выбрать” программа предложит выбрать, за какой период сформировать отчет и по какой организации, если в программе ведется учет по нескольким организациям.

Создается чистый бланк, который заполняется после нажатия на кнопку “Заполнить”.

Так как отчет состоит из нескольких разделов, рассмотрим некоторые из них.

Раздел 1 — будут отображаться суммы к уплате, таких как:

• страховые взносы,
• взносы на медстраховку,
• страховые взносы на социальное страхование.

Приложение 2 к Разделу 1 — указываются расходы за счет ФСС, суммы взносов и налоговая база на обязательное соцстрахование.

Приложение 3 к Разделу 1 — будут отображаться суммы расходов на обязательное социальное страхование.

Раздел 3 — заполняется общая информация по каждому сотруднику.

После того как отчет будет заполнен, в программе можно сделать проверку. Для этого необходимо воспользоваться кнопкой “Проверка” .

Также в программе можно сформировать отдельный отчет “Проверка расчетов страховых взносов”, который позволит пользователю дельно просмотреть информацию о начислениях.

Чтобы открыть отчет, необходимо перейти в пункт меню “Зарплата и кадры”, выбрать “Отчеты по зарплате”.

Из списка необходимо выбрать отчет “Проверка расчетов взносов”.

В отчете указать, за какой период необходимо сформировать данные, выбрать организацию и нажать на кнопку “Сформировать”.

Как сделать математику в Python 3 с операторами

Вступление

Числа чрезвычайно распространены в программировании. Они используются для представления таких вещей, как размеры экрана, географическое положение, деньги и баллы, количество времени, которое проходит в видео, позиции игровых аватаров и цвета при назначении числовых кодов.

Умение эффективно выполнять математические операции в программировании является важным навыком, который необходимо развивать из-за того, как часто вы будете работать с числами. Хотя понимание математики на высоком уровне, безусловно, может помочь вам стать лучшим программистом, это не является обязательным условием. Если у вас нет знаний по математике, постарайтесь думать о математике как о инструменте для достижения того, чего вы хотели бы достичь, и как способ улучшить ваше логическое мышление.

Мы будем работать с двумя наиболее используемыми числовыми типами данных Python: * integer * и * float *:

• Integers — целые числа, которые могут быть положительными, отрицательными или 0 (…, + -1 + `, + 0 + , + 1 + `,…).

• Floats являются действительными числами, они содержат десятичную точку (как в +9.0+ `или + -2.25 + `).

В этом руководстве рассматриваются операторы, которые могут использоваться с числовыми типами данных в Python.

операторы

• Оператор * — это символ или функция, обозначающая операцию. Например, в математике знак плюс или + — это оператор, который указывает сложение.

В Python мы увидим некоторые знакомые операторы, перенесенные из математики, но другие операторы, которые мы будем использовать, специфичны для компьютерного программирования.

Вот краткая справочная таблица математических операторов в Python. В этом руководстве мы рассмотрим все следующие операции.

Operation	What it returns
x + y	Sum of x and y
x — y	Difference of x and y
-x	Changed sign of x
+x	Identity of x
x * y	Product of x and y
x / y	Quotient of x and y
x // y	Quotient from floor division of x and y
x % y	Remainder of x / y
x ** y	x to the y power

Мы также расскажем о compound assignment операторов, включая + + = + `и + * = + , которые объединяют арифметический оператор с оператором + = + `.

Сложение и вычитание

В Python операторы сложения и вычитания работают так же, как в математике. Фактически, вы можете использовать язык программирования Python в качестве калькулятора.

Давайте рассмотрим несколько примеров, начиная с целых чисел:

Вместо передачи целых чисел непосредственно в оператор + print +, мы можем инициализировать переменные для обозначения целочисленных значений:

a = 88
b = 103

print(a + b)

Поскольку целые числа могут быть как положительными, так и отрицательными числами (и 0 тоже), мы можем добавить отрицательное число с положительным числом:

c = -36
d = 25

print(c + d)

Дополнение будет вести себя аналогично с поплавками:

e = 5.5
f = 2.5

print(e + f)

Поскольку мы добавили два числа с плавающей точкой, Python возвратил значение с плавающей точкой с десятичным знаком.

Синтаксис для вычитания такой же, как и для сложения, за исключением того, что вы смените свой оператор со знака плюс (+) на знак минуса (+ - +):

g = 75.67
h = 32

print(g - h)

Здесь мы вычли целое число из числа с плавающей точкой. Python вернет число с плавающей точкой, если хотя бы одно из чисел, участвующих в уравнении, является числом с плавающей точкой.

Унарные арифметические операции

Унарное математическое выражение состоит только из одного компонента или элемента, и в Python знаки плюс и минус могут использоваться как один элемент в паре со значением, чтобы возвращать идентичность значения (+) или изменять знак значение (+ - +).

Хотя знак «плюс» обычно не используется, он указывает идентичность значения. Мы можем использовать знак плюс с положительными значениями:

Когда мы используем знак плюс с отрицательным значением, он также возвращает идентификатор этого значения, и в этом случае это будет отрицательное значение:

При отрицательном значении знак плюс возвращает такое же отрицательное значение.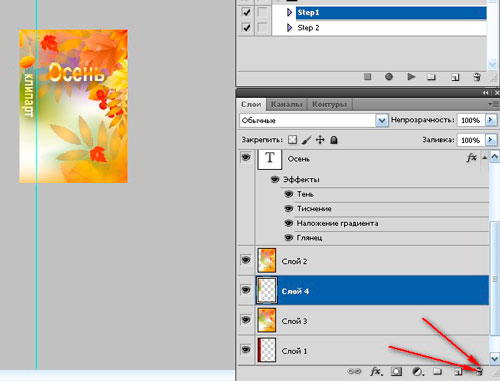

Знак минус, напротив, меняет знак значения. Итак, когда мы передадим положительное значение, мы обнаружим, что знак минус перед значением вернет отрицательное значение:

В качестве альтернативы, когда мы используем унарный оператор со знаком минус с отрицательным значением, будет возвращено положительное значение:

Унарные арифметические операции, обозначенные знаком плюс и минусом, будут возвращать либо идентификатор значения в случае ++ i +, либо знак противоположного значения, как в + -i +.

Умножение и деление

Как сложение и вычитание, умножение и деление будут выглядеть очень похоже на то, как они делают в математике. Знак, который мы будем использовать в Python для умножения, это + * +, а знак, который мы будем использовать для деления, это + / +.

Вот пример выполнения умножения в Python с двумя значениями с плавающей запятой:

k = 100. 1
l = 10.1

print(k * l)

Когда вы делите в Python 3, ваш частный всегда будет возвращаться как число с плавающей запятой, даже если вы используете два целых числа:

m = 80
n = 5

print(m / n)

Это одно из major изменений между Python 2 и Python 3 , Подход Python 3 дает дробный ответ, так что когда вы используете + / + для деления + 11 + на + 2 +, будет получено частное от + 5.5 + . В Python 2 частное, возвращаемое для выражения `+11 / 2 +, равно + 5 +.

Оператор + / + в Python 2 выполняет * деление по полу *, где для частного + x + возвращаемое число является наибольшим целым числом, меньшим или равным + x +. Если вы запустите приведенный выше пример + print (80/5) + с Python 2 вместо Python 3, вы получите + 16 + в качестве вывода без десятичного знака.

В Python 3 вы можете использовать + // + для разделения этажей. Выражение +100 // 40 + вернет значение + 2 +. Разделение по этажам полезно, когда вам нужно, чтобы коэффициент был в целых числах.

Модульное

Оператор +% + является модулем, который возвращает остаток, а не частное после деления. Это полезно, например, для поиска чисел, кратных одному и тому же номеру.

Давайте посмотрим на модуль в действии:

o = 85
p = 15

print(o % p)

Чтобы сломать это, 85, деленное на 15, возвращает частное 5 с остатком 10. Значение + 10 + — это то, что возвращается здесь, потому что оператор по модулю возвращает остаток от выражения деления.

Если мы используем два числа с плавающей точкой по модулю, то значение остатка будет возвращено для остатка:

q = 36.0
r = 6.0

print(o % p)

В случае 36.0, разделенных на 6.0, остатка нет, поэтому возвращается значение + 0.0 +.

Как сделать стейки в духовке? 3 безупречных рецепта

Как же запах жарящегося мяса возбуждает аппетит! Даже когда будущие стейки только только подготавливают к маринованию, воображение уже рисует мяско с дымком на тарелке. И, желательно, большой кусок. 

Само понятие «стейк» стало в Украине довольно расплывчатым. Вне ресторанов и стейк-хаусов стейками становятся куски мяса (в основном — ошейка), толсто нарезанные поперек волокон. Они могут быть разного размера, но часто отличаются толщиной. Их жарят на двойной решетке для гриля, зажав между ее частями. Это блюдо действительно близко к оригинальному стейку — от переплетений толстой проволоки на мясе появляется нужная  «ребристость». При хорошем маринаде и правильной прожарке блюдо получается аппетитным и мягким.

В условиях обычной, домашней кухни многие пытаются жарить стейк на обычной сковородке. Но в лучшем случае получаются слишком толстые и непрожаренные «подошвы». Профессионалы рекомендуют при отсутствии сковороды-гриль приготовить его в духовке. Так сделать стейк не только проще, но и полезнее для организма. Кроме того, вероятность, что мясо пригорит, сократится до минимума.

В статье есть три пошаговых руководства, как готовить стейк в духовом шкафу. С их помощью можно приготовить сочное мясное или рыбное блюдо.

Стейк из свинины

Гурманы убеждены, что настоящий стейк можно приготовить только из говядины. Но свинина — не только более популярна, но и более доступна в Украине. Из нее можно сделать блюдо и на сковородке-гриль (например, Ardesto Gemini), и в духовке.

К выбору мяса нужно подойти ответственно, скупиться здесь не стоит. Правильным решением станет ошеек. В этой части туши есть необходимые жировые прослойки, без которых стейк во время готовки становится жестким. Чем равномернее они чередуются с мясом, тем сочнее получится блюдо.

Можно использовать и вырезку – ее удобнее нарезать и проще найти в продаже. Но из нее приготовить свиной стейк – не самая удачная идея, так как мясо может получиться сухим. Выход – запечь его в духовке или электропечи, завернув в фольгу. Так стейк будет томиться в собственном соку, что сделает его мягче и сочнее.

Важно: Стейк из замороженного мяса будет безвкусным. Поэтому готовьте только из свежей охлажденной свинины.

Ингредиенты (на 3 персоны)

1. Свинной ошеек – 0,5 кг.
2. Лук – 3-4 средних луковки.
3. Чеснок – 4-5 зубчиков.
4. Соль, специи.

Порядок действий

Перед готовкой мясо для стейка заранее вынимается из холодильника – его температура должна соответствовать той, что в помещении.

Ошеек промывается под проточной водой и подсушивается с помощью бумажных полотенец. Далее мясо нарезается толстыми частями по 2,5-3 см. Если сделать тоньше – это уже будут не стейки, а заготовки для шницелей.

Будущие стейки натереть приправами. Их набор зависит от вкуса тех, кто будет их есть. 

Но можно выбирать специи и в зависимости от сезона. Так, в весенне-летний период актуальна пряная, свежая, легкая смесь: например, на основе средиземноморских трав, базилика. В холодное время года согреет и разбудит аппетит комбинация на основе смеси перцев, хмели-сунели, имбиря и кардамона. Но главное – не переборщить, чтобы приправы не «забили» вкус мяса, а дополнили и подчеркнули его. 

Чтобы добавить солнца пасмурному дню, стоит добавить немного куркумы и кориандра, а также зелени – петрушки, кинзы, укропа. Лучше свежей, конечно, но и сушеная или замороженная тоже сойдет. Травки напомнят о весне и тепле. Солить свиные стейки нужно прямо перед тем, как приготовить в духовке-гриль.

Читайте также: Как выбрать электродуховку

Пока нагревается духовка, луковицы нужно нарезать крупненько, а зубчики чеснока — наоборот, потоньше. В подготовленных кусках ошейка делаются маленькие надрезы, которые начиняют чесночным слайсами.

В отрезы фольги, которые по размеру должны быть такими, чтобы в них можно было завернуть стейки без щелей, выложить нарезанный лук, а на него – мясо. Теперь его можно подсолить. Стейки нужно плотно, можно даже в несколько слоев, завернуть в фольгу и переложить в форму (подойдет Ardesto Tasty).

В духовке на обычном режиме мясо нужно запекать примерно 40 минут. Это как раз полная прожарка (Well done), именно так рекомендуется готовить свинину.

Спустя нужное время стейки нужно вынуть из духового шкафа, вытащить аккуратно из фольги и удалить чеснок с помощью зубочисток, вилки или кончика ножа. После этого куски мяса разложить на решетке и запекать в духовке в режиме «гриль» минут десять (не больше!). Оставшаяся вода как раз успеет испариться, и стейки будут приятного золотистого цвета.

Перед подачей готовые стейки нужно несколько минут подержать под фольгой, чтобы они «дошли». Украсить блюдо можно, полив соусом или добавив немного измельченной зелени, овощной нарезки. Стейки прекрасно себя чувствуют и без гарнира, но немного картофеля фри или постного овощного салата лишними не будут. 

Стейк из говядины

Приготовить говяжий стейк немного сложнее. Зато при готовке этого мяса можно варьировать степени прожарки: медиум, с кровью — кому что нравится. Из говядины блюдо можно сделать не только на сковороде-гриль, но и в духовке.

По правилам, нужно брать именно мясо бычков, а не коров. При практически идентичном процессе приготовления, кушанье из коровьего мяса называется бифштекс.

Если есть время и возможность подобрать идеальное мясо, нужно уделить внимание возрасту бычка и тому, как и чем его кормили. В идеале, к моменту забоя животное должно быть не старше полутора лет. Что касается питания, то от одной травы мясо будет нежным, но пресноватым. А такие необходимые характерные «мраморные» прожилки появятся, только если бычку давали и зерновой корм.

Существует несколько разновидностей стейков из говядины. Их тип зависит от того, с какой части было срезано мясо. Готовить говяжий стейк в духовке или на сковороде нужно из вырезки или филе, предпочтительно со спины. В этих кусках мяса есть специальные жировые прослойки, которые плавятся во время готовки и делают стейк сочным и очень вкусным. Филейные же части таких прослоек не имеют, но отличаются нежным, мягким вкусом.

Важно знать: На стейки никогда не берут парное мясо. Наоборот, перед использованием оно должно «дойти».

Мясо для стейка лучше брать свежее, охлажденное. Если ситуация сложилась таким образом, что придется использовать мороженую говядину, ее нужно правильно разморозить. Быстрая разморозка в микроволновой печи или теплой воде «убьет» все вкусовые качества мяса. Начать разморозку нужно за сутки до готовки, переложив его в основное отделение холодильника. Чем медленнее мясо вернется к нормальной температуре, тем больше шансов получить вкусную еду.

Если выбор пал на заготовки, то есть уже нарезанную говядину, перед покупкой следует проверить их толщину. Правильный вариант — это 2,5-3 сантиметра. Если же покупается цельный кусок, выбирать нужно, сразу прикинув в уме, как можно будет его порезать.

Ингредиенты

1. Говядина или телятина – 1 кг.
2. Соевый соус.
3. Пряности.
4. Оливковое или другое растительное масло без запаха – четверть стакана.
5. Соль.

Порядок действий

Говядина комнатной температуры промывается и нарезается кусками толщиной в 2-3 см. Потом нужно подсушить мясо бумажными полотенцами.

Чтобы сделать маринад, в удобной мисочке соединяют соевый соус, 15 мл масла и приправ. Предварительно соевый соус следует попробовать, так как некоторые фирмы выпускают его излишне соленым. В таком случае дополнительная соль будет ни к чему.

Читайте также: Гусь в духовке: 4 этапа приготовления идеального праздничного блюда

Заготовки стейков нужно опустить в смесь для маринования, чтобы они были полностью им покрыты, и оставить на час или чуть дольше. Емкость желательно накрыть пищевой пленкой, чтобы мясо не обветривалось. Мариновать можно как в холодильнике, так и без него.

Спустя указанное время мясо нужно вынуть из маринада и дать ему стечь. Можно сделать это с помощью дуршлага, выстеленного несколькими слоями марли.

Сковороду-гриль (хорошо подойдет для этого Ardesto или Pensofal) нужно очень хорошо нагреть на плите, но не дать ей дымиться. Каждый стейк натирается небольшим количеством растительного масла с обеих сторон и быстро поджаривается до зарумянивания. Пары минут на каждую сторону будет вполне достаточно.

После обжарки заготовки перекладывают в посуду для запекания и готовят в течение четверти часа в печи при температуре 180-200 градусов. Чтобы стейки были еще вкуснее, сразу после запекания их нужно оставить полежать на столе на деревянной досточке под фольгой приблизительно на четверть часа.

Результат

Правильно жарить стейк из телятины в духовке научится и новичок. Для этого не нужны сноровка и опыт, как у шефа. Немного внимания и сосредоточенности на деталях, качественная говядина и хорошее настроение – и вот уже на тарелке ждет сочное, мягкое мясо. Лучший гарнир, который подойдет к этому  великолепному кушанью – бокал сухого красного.

Стейк из рыбы

Приготовить стейк из красной рыбы, семги к примеру, можно как из целой рыбки, так и используя заготовки, каждая из которых рассчитана на одну порцию. В духовке можно запечь восхитительные стейки из лосося и форели. 

Определяющим критерием выбора рыбы должна быть свежесть. Если есть выбор между целой тушкой на подушке из льда и уже нарезанными стейками, но замороженными, лучше отдать предпочтение целой — даже если это дороже. В перемороженной рыбе уже есть излишки воды, которые негативно повлияют на ее вкус.

Если вариантов нет, и есть только замерзшая рыбка, размораживать ее нужно аккуратно и не спеша. И делать это, как и в случае с мясом, нужно на нижней полке холодильника хотя бы сутки. Самое плохое, что можно сделать – это разморозка в теплой воде. Рыба, которая была во льду, возьмет в себя еще лишнюю воду. Блюдо будет разваливаться при готовке и получится безвкусным.

Целую тушку тунца или зубатки сперва нужно тщательно промыть (можно даже с мочалкой), удалить голову, хвостовую часть и срезать плавники. Непотрошеную — нужно разрезать вдоль живота и вынуть внутренности. И только после этого приходит время разделать рыбину на стейки, чтобы затем приготовить в духовке. Толщина должна быть побольше, чем у мясных: 4-5 см, точно не менее 2,5 см.

Ингредиенты (на 4 порции)

• Красная рыба в виде стейков – 4 куска.
• Пара лимончиков.
• Четверть чашки растительного масла без запаха.
• Пряности, крупная соль.

Порядок действий

Рыбку подготовить: если нужно — разморозить, довести до комнатной температуры. Стейки аккуратной промыть и промокнуть полотенцами из бумаги.

Для улучшения вкуса рыбные стейки следует промариновать, но недолго. Для этого части рыбки нужно натереть смесью из сока половины лимона, 30 мл масла и небольшого количества специй. Подойдут белый молотый перец, имбирь, орегано, майоран.

Духовой шкаф (например, ELECTROLUX) разогреть. Пока он греется, стейки перекладывают в фольгу, каждый – отдельно. Можно дополнительно натереть растительным маслом, украсить веточкой розмарина. Сдобрить рыбку морской солью и завернуть в фольгу. Переложить в удобную форму для запекания или на противень.

Читайте также: Украинский борщ в духовке — 3 вкусных рецепта

Запекать в печке нужно чуть меньше получаса. После этого листики фольги следует развернуть и оставить рыбку в духовом шкафу еще минут на 10, чтобы подрумянилась. Так же можно доготовить блюдо на решетке. Тогда рыбные стейки будут не только вкусными, но и с нужной ребристостью.

Результат

Рыбные стейки захочется съесть еще до того, как они будут готовы. И все благодаря аппетитному аромату рыбы из духовки. Но чтобы это блюдо произвело действительно ошеломляющий эффект, его нужно правильно подать.

Для красивой подачи рекомендуется выбрать одноцветную, лучше белую, тарелку большого диаметра (идеальный вариант — Ardesto Lucca). На нее аккуратно переложить стейк из рыбы, рядом положить кусочек лимона, немного розмарина. Также для украшения можно использовать свежую зелень, несколько помидоров «черри». Органично будет смотреться специальный соус для рыбы из сметаны или жирных сливок.

Вывод такой: свежее мясо, фольга, качественный духовой шкаф и немного вдохновения – и можно вкушать собственноручно сделанный стейк. Те же, кто предпочитает рыбу, могут угостить себя и гостей утонченным кушаньем из форели или семги. А если вдруг с первого раза блюдо не выйдет безупречным — не стоит расстраиваться. Следует помнить: это — нормально. Умение приходит с опытом, главное — начать.

Видео Как приготовить стейки из свинины в духовке

Как рассчитать 1/2, 1/3, 1/4 числа

Добро пожаловать в блог Smartick! В этой статье мы узнаем , как вычислить половинки, трети и четверти . Эти выражения используются не только в математических задачах, но и в повседневной жизни.

Вы знаете, что это такое? Вы умеете их рассчитывать? Из этого поста вы поймете, как легко вычислить половинки, трети и четверти.

Половинки

Половина эквивалентна дроби: 1/2.Следовательно, это половина любой суммы. Половинки рассчитываются путем деления на 2.

Например:

Половина 10 = 1/2 10 = 10/2 = 5.

Половина 34 = 1/2 34 = 34/2 = 17.

Три половинки 14 = 3/2 14 = 3 x 14/2 = 3 x 7 = 21.

Третьего

Одна треть эквивалентна дроби: 1/3. Следовательно, это треть суммы. Третьи рассчитываются путем деления на 3.

Например:

Одна треть от 24 = 1/3 от 24 = 24/3 = 8.

Одна треть от 33 = 1/3 от 33 = 33/3 = 11.

Пять третей от 15 = 5/3 из 15 = 5 x 15/3 = 5 x 5 = 25.

Четвертые

Одна четвертая эквивалентна дроби: 1/4. Следовательно, это четверть суммы. Четвертые рассчитываются путем деления на 4.

Например:

Одна четвертая от 20 = ¼ из 20 = 20/4 = 5.

Одна четвертая из 28 = ¼ из 28 = 28/4 = 7.

Семь четвертых от 8 = 7/4 от 8 = 7 x 8/4 = 7 x 2 = 14.

Вы узнали о половинках, третях и четвертях? Не стесняйтесь поделиться этим постом со своими друзьями и коллегами, чтобы они тоже могли учиться. И помните, что для изучения этих расчетов и многого другого лучше всего зарегистрироваться на Smartick и попробовать его бесплатно!

Подробнее:

Развлечение — любимый способ обучения нашего мозга

Дайан Акерман

Smartick — увлекательный способ изучения математики

• 15 веселых минут в день
• Адаптируется к уровню вашего ребенка
• Миллионы учеников с 2009 года

Команда по созданию контента.
Многопрофильная и многонациональная команда, состоящая из математиков, учителей, профессоров и других специалистов в области образования!
Они стремятся создать максимально возможное математическое содержание.

Как умножить на 3

Способы умножения на 3

Давайте изучим несколько различных способов умножения на 3.

Подсчет пропусков

Подсчет пропусков — один из способов умножения на 3. При пропуске подсчета на 3 вы произносите числа 3, 6 , 9, 12, 15, 18, 21, 24, 27, 30, 33 и так далее.Делая это, вы фактически умножаете на 3.

Пропустить подсчет	Задача умножения
3	3 х 1
6	3 х 2
9	3 х 3
12	3 х 4
15	3 х 5

Знаете ли вы, используя подсчет пропусков, что 3 x 6 будет равняться? 3, 6, 9, 12, 15… 18!

Повторное сложение

Вы также можете использовать повторное сложение или многократное сложение чисел, чтобы умножить на 3. Например, если у вас была задача 3 x 2, вы можете сложить 3 два раза и получить ответ . Итак, 3 + 3 = 6, что равносильно 3 x 2 = 6. Теперь вы попробуете. Каков ответ на задачу умножения 3 x 4 с помощью повторного сложения? Чтобы получить ответ, сложите 3 четыре раза следующим образом: 3 + 3 + 3 + 3, чтобы получить ответ 12, в результате чего 3 x 4 = 12.

Использование групп

Вы можете использовать равных групп или групп с одинаковым числом, чтобы умножить их на 3. Нарисуйте на бумаге три круга — это показывает, что мы будем умножать на 3. Теперь нарисуйте по одной точке в каждой. круг. Сколько всего точек у вас сейчас? У вас есть 3 точки, и вы только что показали задачу умножения 3 x 1 = 3. Давайте попробуем другую. Добавьте еще 4 точки к каждому кругу — теперь каждый круг имеет 5 точек. Теперь ваша картинка показывает задачу умножения 3 x 5, и когда вы сложите все точки вместе, вы увидите, что 3 x 5 = 15! Весело, правда?

Теперь я хочу, чтобы вы взглянули на картинку ниже и написали задачу умножения, которую он показывает.Не подглядывайте, пока не закончите!

Если вы написали 3 x 8 = 24, вы правы. На рисунке показаны 3 круга с 8 точками в каждом, всего 24 точки.

Использование массива

Массив — это упорядоченный порядок объектов в строках и столбцах. Вы можете создавать разные массивы, умножая их на 3. Посмотрите на картинку. Показанный массив представляет собой 3 строки на 4 столбца или задачу 3 x 4. Используя этот массив, вы можете вычислить, что 3 x 4 = 12, посчитав все точки.

Пример использования массива для 3 x 4

Твоя очередь! Сделайте массив 3 x 6. При использовании массива вам нужно выяснить, сколько строк и столбцов вам нужно. Поскольку мы умножаем на 3, нам нужно будет сделать 3 ряда точек. В каждой строке нам нужно поставить 6 точек, чтобы выполнить эту задачу умножения. Теперь ваш массив должен отображать 3 строки с 6 точками в каждой. Итак, ваш массив теперь показывает проблему умножения 3 x 6.Подсчитав все точки, которые вы только что нарисовали, вы можете определить, что 3 x 6 = 18!

Резюме урока

Некоторые из различных способов умножения на 3: повторное сложение , равных групп и массив . Используйте тот, который лучше всего подходит для вас, и продолжайте практиковаться!

Как делать математику в Python 3 с операторами

Введение

Числа чрезвычайно распространены в программировании. Они используются для представления таких вещей, как размеры экрана, географическое положение, деньги и очки, количество времени, которое проходит в видео, положения игровых аватаров и цвета посредством присвоения числовых кодов.

Умение эффективно выполнять математические операции в программировании — важный навык, который нужно развивать, потому что вам придется часто работать с числами. Хотя понимание математики на высоком уровне, безусловно, может помочь вам стать лучшим программистом, это не является обязательным условием. Если у вас нет математического образования, попробуйте рассматривать математику как инструмент для достижения того, чего вы хотите достичь, и как способ улучшить свое логическое мышление.

Мы будем работать с двумя наиболее часто используемыми числовыми типами данных Python, целыми числами и с плавающей запятой :

• Целые числа — это целые числа, которые могут быть положительными, отрицательными или 0 (…, -1 , 0 , 1 ,…).
• Float — это действительные числа, они содержат десятичную точку (как в 9.0 или -2.25 ).

В этом руководстве будут рассмотрены операторы, которые можно использовать с числовыми типами данных в Python.

Предварительные требования

У вас должен быть установлен Python 3 и настроена среда программирования на вашем компьютере или сервере. Если у вас не настроена среда программирования, вы можете обратиться к руководствам по установке и настройке для локальной среды программирования или среды программирования на вашем сервере, соответствующей вашей операционной системе (Ubuntu, CentOS, Debian и т. Д.))

Операторы

Оператор — это символ или функция, обозначающая операцию. Например, в математике знак плюс или + — это оператор, обозначающий сложение.

В Python мы увидим некоторые знакомые операторы, перенесенные из математики, но другие операторы, которые мы будем использовать, специфичны для компьютерного программирования.

Вот краткая справочная таблица математических операторов в Python. В этом руководстве мы рассмотрим все следующие операции.

Эксплуатация	Что возвращает
х + у	Сумма x и y
х — у	Разница x и y
-x	Изменен знак x
+ x	Идентификационный номер x
х * у	Произведение x и y
х / у	Частное x и y
х // у	Коэффициент от деления этажа x и y
x% y	Остаток от х / у
х ** у	x до y мощность

Мы также рассмотрим составные операторы присваивания, включая + = и * = , которые объединяют арифметический оператор с оператором = .

Сложение и вычитание

В Python операторы сложения и вычитания работают аналогично математике. Фактически, вы можете использовать язык программирования Python в качестве калькулятора.

Информация: Чтобы следовать примеру кода в этом руководстве, откройте интерактивную оболочку Python в своей локальной системе, выполнив команду python3 . Затем вы можете копировать, вставлять или редактировать примеры, добавляя их после приглашения >>> .

Давайте рассмотрим несколько примеров, начиная с целых чисел:

  печать (1 + 5)
  

  
 Выход 
 6
  

Вместо того, чтобы передавать целые числа непосредственно в оператор print , мы можем инициализировать переменные для обозначения целочисленных значений:

  а = 88
б = 103

печать (a + b)
  

  
 Выход 
 191
  

Поскольку целые числа могут быть как положительными, так и отрицательными (а также 0), мы можем добавить отрицательное число к положительному числу:

  с = -36
d = 25

печать (c + d)
  

  
 Выход 
-11
  

Сложение будет вести себя аналогично с числами с плавающей запятой:

  е = 5.5
f = 2,5

печать (e + f)
  

  
 Выход 
 8,0
  

Поскольку мы сложили вместе два числа с плавающей запятой, Python вернул значение с плавающей запятой с десятичным разрядом.

Синтаксис вычитания такой же, как и для сложения, за исключением того, что вы измените свой оператор со знака плюс ( + ) на знак минус (–):

  г = 75,67
в = 32

печать (г - ч)
  

  
 Выход 
 43,67
  

Здесь мы вычли целое число из числа с плавающей запятой.Python вернет число с плавающей запятой, если хотя бы одно из чисел, участвующих в уравнении, является числом с плавающей запятой.

Унарные арифметические операции

Унарное математическое выражение состоит только из одного компонента или элемента, а в Python знаки плюс и минус могут использоваться как один элемент в паре со значением, чтобы вернуть идентичность значения ( + ) или изменить знак значения. ( - ).

Знак плюс, хотя и не используется обычно, указывает на идентичность значения.Мы можем использовать знак плюса с положительными значениями:

  я = 3,3
печать (+ я)
  

  
 Выход 
 3,3
  

Когда мы используем знак плюса с отрицательным значением, он также возвращает идентичность этого значения, и в этом случае это будет отрицательное значение:

  к = -19
печать (+ j)
  

  
 Выход 
-19
  

При отрицательном значении знак «плюс» возвращает то же отрицательное значение.

Знак минус также меняет знак значения.Итак, когда мы передаем положительное значение, мы обнаруживаем, что знак минус перед значением возвращает отрицательное значение:

  я = 3,3
печать (-i)
  

  
 Выход 
 -3,3
  

В качестве альтернативы, когда мы используем унарный оператор со знаком минус с отрицательным значением, будет возвращено положительное значение:

  к = -19
печать (-j)
  

  
 Выход 
 19
  

Унарные арифметические операции, обозначенные знаком плюс и минус, возвращают либо идентичность значения в случае + i , либо знак, противоположный значению, как в случае -i .

Умножение и деление

Как сложение и вычитание, умножение и деление будут очень похожи на то, как они действуют в математике. Знак, который мы будем использовать в Python для умножения, — * , а знак, который мы будем использовать для деления, — /.

Вот пример умножения в Python с двумя значениями с плавающей запятой:

  к = 100,1
l = 10,1

печать (к * л)
  

  
 Выход 
 1011.0099999999999
  

Когда вы делите в Python 3, ваше частное всегда будет возвращаться как число с плавающей запятой, даже если вы используете два целых числа:

  м = 80
п = 5

печать (м / п)
  

  
 Выход 
 16.0
  

Это одно из основных различий между Python 2 и Python 3. Подход Python 3 дает дробный ответ, поэтому при использовании / для деления 11 на 2 будет возвращено частное 5,5 . В Python 2 частное, возвращаемое для выражения 11/2 , равно 5 .

Оператор

Python 2 / выполняет деление этажа , где для частного x возвращаемое число является наибольшим целым числом, меньшим или равным x .Если вы запустите приведенный выше пример print (80/5) с Python 2 вместо Python 3, вы получите 16 в качестве вывода без десятичного разряда.

В Python 3 вы можете использовать // для выполнения разделения этажей. Выражение 100 // 40 вернет значение 2 . Деление этажей полезно, когда вам нужно, чтобы частное было целым.

по модулю

Оператор % является модулем, который возвращает остаток, а не частное после деления.Это полезно, например, для поиска чисел, кратных одному и тому же числу.

Давайте посмотрим на модуль в действии:

  о = 85
р = 15

печать (o% p)
  

  
 Выход 
 10
  

Чтобы разбить это, 85, деленное на 15, возвращает частное 5 с остатком 10. Здесь возвращается значение 10 , потому что оператор по модулю возвращает остаток выражения деления.

Если мы используем два числа с плавающей запятой по модулю, для остатка будет возвращено значение с плавающей запятой:

  q = 36.0
г = 6,0

печать (o% p)
  

  
 Выход 
 0,0
  

В случае деления 36,0 на 6,0 остатка нет, поэтому возвращается значение 0,0 .

Мощность

Оператор ** в Python используется для возведения числа слева в степень правой степени. То есть в выражении 5 ** 3 5 возводится в 3-ю степень. В математике мы часто видим это выражение в виде 5³, а на самом деле 5 умножается само на себя в 3 раза.В Python мы получили бы тот же результат 125 , запустив либо 5 ** 3 , либо 5 * 5 * 5 .

Давайте посмотрим на пример с переменными:

  с = 52,25
t = 7

печать (дерьмо)
  

  1063173305051.292
  

Повышение числа с плавающей запятой 52,25 до степени 7 с помощью оператора ** приводит к возврату большого значения с плавающей запятой.

Приоритет оператора

В Python, как и в математике, мы должны помнить, что операторы будут оцениваться в порядке приоритета, а не слева направо или справа налево.

Если мы посмотрим на следующее выражение:

  и = 10 + 10 * 5
  

Мы можем читать его слева направо, но помните, что сначала будет выполнено умножение, поэтому, если мы вызовем print (u) , мы получим следующее значение:

  
 Выход 
 60
  

Это потому, что 10 * 5 оценивается как 50 , а затем мы добавляем 10 , чтобы вернуть 60 в качестве окончательного результата.

Если вместо этого мы хотим добавить значение 10 к 10 , а затем умножить эту сумму на 5 , мы можем использовать круглые скобки, как в математике:

  и = (10 + 10) * 5
печать (u)
  

  
 Выход 
 100
  

Один из способов запомнить порядок работы — использовать аббревиатуру PEMDAS :

Заказать	Письмо	Стенды для
1	п.	P аренте
2	E	E xponent
3	M	M повторение
4	D	D ivision
5	А	A ddition
6	S	S убирание

Возможно, вы знакомы с другим сокращением порядка операций, например BEDMAS или BODMAS .Какую бы аббревиатуру вы ни выбрали, постарайтесь помнить ее при выполнении математических операций в Python, чтобы получить ожидаемые результаты.

Операторы присвоения

Самый распространенный оператор присваивания — тот, который вы уже использовали: знак равенства = . Оператор присваивания = присваивает значение справа переменной слева. Например, v = 23 присваивает значение целого числа 23 переменной v .

При программировании обычно используются составные операторы присваивания, которые выполняют операцию над значением переменной, а затем присваивают полученное новое значение этой переменной. Эти составные операторы объединяют арифметический оператор с оператором = , поэтому для сложения мы объединим + с = , чтобы получить составной оператор + = . Давайте посмотрим, как это выглядит:

  Вт = 5
ш + = 1
печать (ш)
  

  
 Выход 
 6
  

Сначала мы устанавливаем переменную w равной значению 5 , затем мы использовали составной оператор присваивания + = , чтобы добавить правое число к значению левой переменной , а затем присвоить результат Вт .

Операторы составного присваивания часто используются в случае для циклов , которые вы будете использовать, если хотите повторить процесс несколько раз:

  для x в диапазоне (0, 7):
    х * = 2
    печать (х)
  

  
 Выход 
 0
2
4
6
8
10
12
  

С помощью цикла for мы смогли автоматизировать процесс оператора * = , который умножил переменную w на число 2 , а затем присвоил результат переменной w для следующей итерации для цикла.

Python имеет составной оператор присваивания для каждого из арифметических операторов, обсуждаемых в этом руководстве:

  y + = 1 # добавить, затем присвоить значение

y - = 1 # вычесть, затем присвоить значение

y * = 2 # умножить и присвоить значение

y / = 3 # разделить, затем присвоить значение

y // = 5 # разделить этаж, затем присвоить значение

y ** = 2 # увеличить до степени, затем присвоить значение

y% = 3 # вернуть остаток, затем присвоить значение
  

Операторы составного присваивания могут быть полезны, когда что-то нужно постепенно увеличивать или уменьшать, или когда вам нужно автоматизировать определенные процессы в вашей программе.

Заключение

В этом руководстве описаны многие операторы, которые вы будете использовать с целочисленными и числовыми типами данных с плавающей запятой. Если вы хотите продолжить чтение о числах в Python, вы можете перейти к встроенным функциям Python 3 для работы с числами.

Чтобы узнать больше о других типах данных, взгляните на Общие сведения о типах данных в Python 3 и узнайте о том, как преобразовывать типы данных, прочитав Как преобразовывать типы данных в Python 3.

3 НОМЕР: ЧТО ЕСТЬ ЗНАТЬ? | Сложим: помощь детям в изучении математики

	классических времен, написал бумагу в форме письма королю своего города, объясняя, как писать такие очень большие числа.Архимед, однако, не зашел так далеко, чтобы изобрести десятичную систему счисления с возможностью неограниченного расширения.
22.	Knuth, 1974, стр. 323.
23.	Steen, 1990. См. Морроу и Кенни, 1998, для получения более подробной информации об алгоритмах.
24.	Точки с многоточием «…» в выражении являются важной частью абстрактной математической записи, компактно обозначающей пропуск необходимых терминов (для достижения м, в данном случае ).

Ссылки

Бер, М.Дж., Харел, Г., Пост, Т., И Леш Р. (1992). Рациональное число, соотношение и пропорция. В D.A.Grouws (Ed.), Справочник по исследованиям по преподаванию и изучению математики (стр. 296–333). Нью-Йорк: Макмиллан.

Bruner, J.S. (1966). К теории обучения . Кембридж, Массачусетс: Belknap Press.

Куоко, А. (Ред.). (2001). Роли представления в школьной математике (Ежегодник Национального совета учителей математики 2001 г.).Рестон, Вирджиния: NCTM.

Дюваль Р. (1999). Представление, видение и визуализация: когнитивные функции в математическом мышлении. Основные вопросы для обучения. В F.Hitt & M.Santos (Eds.), Proceedings of the двадцать первого ежегодного собрания Североамериканского отделения Международной группы психологии математического образования (том 1, стр. 3–26). Колумбус, Огайо: Информационный центр ERIC по естествознанию, математике и экологическому образованию. (ERIC Document Reproduction Service No.ED 433 998).

Фройденталь, Х. (1983). Дидактическая феноменология математических структур . Дордрехт, Нидерланды: Рейдел.

Грино, Дж. Г., и Холл, Р. (1997). Практика репрезентации: изучение репрезентативных форм и их изучение. Дельта Фи Каппан , 78 , 1–24. Доступно: http://www.pdkintl.org/kappan/kgreeno.htm. [10 июля 2001 г.].

Капут,]. (1987). Системы представлений и математика.В C.Janvier (Ed.), Проблемы представления в преподавании и изучении математики (стр. 19–26). Хиллсдейл, Нью-Джерси: Эрлбаум.

Knuth, D.E. (1974). Информатика и ее отношение к математике. American Mathematical Monthly , 81 , 323–343.

Лакофф, Г., & Нуньес, Р.Э. (1997). Метафорическая структура математики: набросок когнитивных основ математики, основанной на разуме. В Л.D.English (Ed.), Математические рассуждения: аналогии, метафоры и образы (стр. 21–89). Махва, Нью-Джерси: Эрлбаум.

Морроу, Л.Дж., и Кенни, М.Дж. (ред.). (1998). Преподавание и изучение алгоритмов в школьной математике (Ежегодник Национального совета учителей математики за 1998 год). Рестон, Вирджиния: NCTM.

Пимм, Д. (1995). Символы и значения в школьной математике . Лондон: Рутледж.

Рассел, Б.(1919). Введение в математическую философию . Нью-Йорк: Макмиллан.

Сфард А. (1997). Комментарий: О метафорических корнях концептуального роста. В L.D. English (Ed.), Математические рассуждения: аналогии, метафоры и изображения (стр. 339–371). Махва, Нью-Джерси: Эрлбаум.

Калькулятор дробей

Калькулятор выполняет базовые и расширенные операции с дробями, выражениями с дробями, объединенными с целыми числами, десятичными знаками и смешанными числами.Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Решайте задачи с двумя, тремя или более дробями и числами в одном выражении.

Правила для выражений с дробями:

Fractions — просто используйте косую черту между числителем и знаменателем, т.е. для пяти сотых введите 5/100 . Если вы используете смешанные числа, не забудьте оставить один пробел между целой и дробной частью.
Косая черта разделяет числитель (число над дробной чертой) и знаменатель (число ниже).

Смешанные числа (смешанные дроби или смешанные числа) записываются как целые числа, разделенные одним пробелом и дробью, т. Е. 1 2/3 (с тем же знаком). Пример отрицательной смешанной дроби: -5 1/2 .
Поскольку косая черта является одновременно знаком для дробной линии и деления, мы рекомендуем использовать двоеточие (:) в качестве оператора деления дробей, то есть 1/2: 3 .

Десятичные числа (десятичные числа) вводятся с десятичной запятой . , и они автоматически переводятся в дроби — i.е. 1,45 .

Двоеточие : и косая черта / являются символом деления. Может использоваться для деления смешанных чисел 1 2/3: 4 3/8 или может использоваться для записи сложных дробей, например, 1/2: 1/3 . 1/2
• сложение дробей и смешанных чисел: 8/5 + 6 2/7
• деление целого и дробного числа: 5 ÷ 1/2
• комплексные дроби: 5/8: 2 2/3
• десятичное в дробное: 0.625
• Дробь в десятичную: 1/4
• Дробь в проценты: 1/8%
• сравнение дробей: 1/4 2/3
• умножение дроби на целое число: 6 * 3/4 ​​
• квадратный корень дроби: sqrt (1/16)
• уменьшение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22
• выражение в скобках: 1 / 3 * (1/2 — 3 3/8)
• сложная дробь: 3/4 от 5/7
• кратная дробь: 2/3 от 3/5
• разделите, чтобы найти частное: 3/5 ÷ 2 / 3

Калькулятор следует известным правилам порядка операций .Наиболее распространенные мнемоники для запоминания этого порядка операций:
PEMDAS — круглые скобки, экспоненты, умножение, деление, сложение, вычитание.
BEDMAS — Скобки, экспоненты, деление, умножение, сложение, вычитание
BODMAS — Скобки, порядок или порядок, деление, умножение, сложение, вычитание.
GEMDAS — Группирующие символы — скобки () {}, экспоненты, умножение, деление, сложение, вычитание.
Будьте осторожны, всегда выполняйте умножение и деление перед сложением и вычитанием .Некоторые операторы (+ и -) и (* и /) имеют одинаковый приоритет и должны вычисляться слева направо.

Задачи с дробями в словах:

следующие математические задачи »

дробей — Рациональные числа — документация Python 3.10.0

Исходный код: Lib / fractions.py

---

Модуль дробей обеспечивает поддержку арифметики рациональных чисел.

Экземпляр Fraction может быть построен из пары целых чисел из другое рациональное число или из строки.

класс фракций. Дробь (числитель = 0 , знаменатель = 1 )

класс фракций. Дробь ( other_fraction )

класс фракций. Дробь ( с плавающей запятой )

класс фракций. Дробь ( десятичная )

класс фракций. Дробь ( строка )

Первая версия требует, чтобы числитель и знаменатель были экземплярами из чисел.Rational и возвращает новый экземпляр Fraction со значением числитель / знаменатель . Если знаменатель равен 0 , он вызывает ZeroDivisionError . Вторая версия требует, чтобы other_fraction является экземпляром чисел. Rational и возвращает Дробь экземпляр с тем же значением.Следующие две версии принимают либо с плавающей запятой , либо десятичный . Десятичный экземпляр и возвращает Дробь экземпляр с точно таким же значением. Обратите внимание, что из-за обычные проблемы с двоичными числами с плавающей запятой (см. Арифметика с плавающей запятой: проблемы и ограничения), аргумент Дробь (1.1) не в точности равна 11/10, и поэтому Fraction (1.1) не возвращает , а возвращает Fraction (11, 10) , как и следовало ожидать. (Но см. Документацию по методу limit_denominator () ниже.) Последняя версия конструктора ожидает строку или экземпляр Unicode. Обычная форма для этого экземпляра:

 [знак] числитель [знаменатель '/']
 

, где необязательный знак может быть либо «+», либо «-» и Числитель и знаменатель (если присутствует) являются строками десятичные цифры. Кроме того, любая строка, представляющая конечный значение и принимается конструктором float также принимается конструктором Fraction .В любой форме входная строка также может иметь начальные и / или конечные пробелы. Вот несколько примеров:

 >>> из импорта дробей Дробь
>>> Дробь (16, -10)
Дробь (-8, 5)
>>> Дробь (123)
Дробь (123, 1)
>>> Дробь ()
Дробь (0, 1)
>>> Дробь ('3/7')
Дробь (3, 7)
>>> Дробь ('-3/7')
Дробь (-3, 7)
>>> Дробь ('1.414213 \ t \ n')
Дробь (1414213, 1000000)
>>> Дробь ('-. 125')
Дробь (-1, 8)
>>> Дробь ('7e-6')
Дробь (7, 1000000)
>>> Дробь (2.25)
Дробь (9, 4)
>>> Дробь (1.1)
Дробь (2476979795053773, 2251799813685248)
>>> из десятичного числа Импорт Десятичный
>>> Дробь (Десятичная дробь ('1.1'))
Дробь (11, 10)
 

Класс Fraction наследуется от абстрактного базового класса номеров.Rational , и реализует все методы и операции из этого класса. Дробь экземпляров можно хэшировать, и должны рассматриваться как неизменяемые. Кроме того, Фракция имеет следующие свойства и методы:

Изменено в версии 3.9. Функция math.gcd () теперь используется для нормализации числителя и знаменатель . math.gcd () всегда возвращает тип int . Ранее тип НОД зависел от числителя и знаменателя .

числитель

Числитель дроби в младшем члене.

Знаменатель

Знаменатель дроби в младшем члене.

as_integer_ratio ()

Вернуть кортеж из двух целых чисел, отношение которых равно в дробь и с положительным знаменателем.

from_float ( flt )

Этот метод класса конструирует Дробь , представляющую точную значение flt , которое должно быть с плавающей точкой . Остерегайтесь этого Fraction.from_float (0.3) — это не то же самое значение, что и Fraction (3, 10) .

Примечание

Начиная с Python 3.2, вы также можете построить Экземпляр фракции непосредственно из поплавка .

from_decimal ( dec )

Этот метод класса конструирует Дробь , представляющую точную значение dec , которое должно быть десятичным .Decimal экземпляр.

limit_denominator ( max_denominator = 1000000 )

Находит и возвращает ближайшую Дробь к self , имеющую знаменатель не более max_denominator.Этот метод полезен для поиска рациональные приближения к заданному числу с плавающей запятой:

 >>> из импорта дробей Дробь
>>> Дробь ('3.1415926535897932'). Limit_denominator (1000)
Фракция (355, 113)
 

или для восстановления рационального числа, представленного в виде числа с плавающей запятой:

 >>> из математического импорта pi, cos
>>> Дробь (cos (pi / 3))
Дробь (4503599627370497, 99254740992)
>>> Дробь (cos (pi / 3)). Limit_denominator ()
Дробь (1, 2)
>>> Дробь (1.1) .limit_denominator ()
Дробь (11, 10)
 

__ этаж__ ()

Возвращает наибольшее значение int <= self . Этот метод может также можно получить через функцию math.floor () :

 >>> от пола импорта математики
>>> этаж (Фракция (355, 113))
3
 

__ceil__ ()

Возвращает наименьшее значение int > = self .Этот метод может также доступны через функцию math.ceil () .

__ вокруг__ ()

__ вокруг__ ( ndigits )

Первая версия возвращает ближайшее int до self , округление от половины до четного. Вторая версия округляет себя до ближайшее кратное Дробь (1, 10 ** ndigits) (логически, если ndigits отрицательно), снова округляя половину в сторону четности.Этот также можно получить доступ через функцию round () .

См. Также

Модуль номеров

Абстрактные базовые классы, составляющие числовую башню.

Как научить умножению за 6 простых шагов

Переход от обучения вычитанию и сложению к умножению обучения - одна из самых сложных задач, с которыми ученики сталкиваются в школе.

Проблемы с этим предметом возникают не только у студентов.

При обучении умножению преподаватели часто начинают с неправильных концепций или слишком быстро прорабатывают уроки. Это может отпугнуть и запугать учащихся, что в конечном итоге может отрицательно сказаться на результатах обучения.

К счастью, существуют известные стратегии, позволяющие избежать этих препятствий.

Используйте приведенное ниже руководство, чтобы узнать, как упростить преподавание и обучение умножению за шесть простых шагов, которые заинтересуют и найдут отклик у студентов.

Раздел A: Шестиступенчатое руководство по обучению умножению

1. Свяжите умножение со сложением

Не начинайте с запоминания. Студенты обычно с трудом запоминают факты умножения с первой попытки, и это может привести к боязни таблицы умножения.

Самый простой способ начать обучение умножению - это закрепить понятие в терминах его отношения к сложению - операции, с которой ваши ученики уже должны быть довольны.

Прежде чем двигаться дальше, убедитесь, что ваши ученики усвоили первый принцип умножения: это просто повторное сложение .

Используйте связанных примеров , подобных приведенному выше, чтобы контекстуализировать этот факт.

Это поможет записать примеры, чтобы учащиеся могли визуализировать идею:

2 x 2 то же самое, что 2 + 2

или

3 x 4 то же самое, что 4 + 4 + 4

2.Начните с числа, кратного нулю и единице

Умножение на ноль: свойство нуля

Выделите для своего класса, что добавление нуля к числу не влияет на его идентичность:

n + 0 = n

Затем объясните, что при умножении любое число , умноженное на ноль, также равно нулю:

nx 0 = 0

Предложите учащимся найти в комнате примеры свойства нуля. Например, в классе с 25 стульями, на каждом из которых не сидит обезьяна, означает, что в классе нет обезьян.

Необязательно, один забавный пример увлекательного математического упражнения для развлечения ваших учеников включает в себя придумывание забавных примеров этого свойства, например 0 x один миллион = 0 ... или ... 0 x бутерброд с ветчиной = 0.

Источник изображения: Шаг во второй класс

Умножение на единицу: свойство идентичности

Короче говоря, свойство идентичности утверждает, что произведение данного числа на единицу и есть само это число: nx 1 = n.

Как и в случае с нулевым свойством, выделите в своем классе, что умножение числа на единицу дает такое же значение.

Чтобы обосновать свойство в контексте реальной жизни, предложите вашему классу подумать об экземплярах свойства identity в классе.

Например,

• Одна группа из восьми столов - это восемь столов
• Одна строка в календаре, показывающая семь дней, равна семи дням

Источник изображения: The Classy Teacher

3. Покройте таблицу умножения, начиная с «легкими» числами

Чтобы повторить, ваши ученики должны теперь понять, что умножение можно рассматривать как повторное сложение.

Им также нужно было время, чтобы умножить числа на ноль и единицу. Хотя им не нужно знать технические термины, учащиеся должны понимать, как работают нулевое свойство и свойство идентичности.

Теперь пришло время сделать один из самых больших скачков: охватить таблицу умножения.

Один эффективный подход работает следующим образом:

• Отобразите диаграмму или верхний слайд таблицы умножения 12 x 12. Если хотите, дополните его экземплярами таблицы умножения для учащихся.Если таблица 12 x 12 кажется слишком сложной, проделайте тот же процесс с таблицей умножения 10 x 10.
• Научите студентов пользоваться таблицей и находить продукты, отслеживая и сопоставляя позиции чисел с помощью вертикальной и горизонтальной осей.

• Теперь поговорим о некоторых моделях, которые вы можете найти на графике. Предложите учащимся подсказки или подсказки. Например, обратите внимание, что каждое кратное десяти оканчивается нулем, а каждое кратное пяти оканчивается нулем или пятью.
• Спросите студентов, какие факты самые простые.Например, единицы и десятки - это просто. Теперь, когда вы обсудили «легкие» факты умножения и то, что делает их легкими, удалите их из таблицы.

Студенты обычно соглашаются, что двойки, пятерки и одиннадцать тоже легко. Продолжайте вычеркивать «простые» числа, пока не дойдете до этапа, который выглядит примерно так:

• Посмотрите на оставшиеся числа вместе со своим классом. Используйте возможность вести динамичное обсуждение и перейти к следующему шагу.

4. Покажите, как свойство коммутативности упрощает задачу

Как и сложение, умножение коммутативно на , что означает , что означает, что порядок множителей не влияет на произведение (ответ).

Другими словами, два числа можно умножить в любом порядке, и произведение будет одинаковым. Например, умножение на 8 x 2 даст вам тот же ответ, что и умножение на 2 x 8.

Если вы эффективно сообщите об этом, это вдохновит ваших учеников.

Покажите своим ученикам, что каждый ответ повторяется, поэтому им нужно выучить только половину оставшихся таблиц. Например, объясните, что обучение 3 x 6 - это то же самое, что обучение 6 x 3!

Если учащиеся уже выучили факты семей из 0–3, то они также знают четыре числа от 4–10 каждое.

Чтобы еще больше усилить свойство коммутативности, вы также можете использовать визуальную модель, подобную показанной выше, и указать, как расположены желтые блоки.

Спросите своих учеников: «Разве это не одно и то же, а разные версии друг друга? Если посчитать общее количество единиц, они одинаковы? »

Помощь учащимся в осознании этого свойства - ключевая часть обучения умножению. Чтобы ученики делали это сами и учились на собственном опыте, попросите ваш класс создать модели, чтобы проиллюстрировать эту идею и доказать, что a x b приводит к тому же продукту, что и b x a .

5. Разделите запоминание на простые шаги

На этом этапе ваши ученики готовы начать запоминать таблицу умножения . Вероятно, они уже начали это делать.

Имейте в виду, что ученикам не всегда очевидно, почему им нужно заучивать факты умножения наизусть. Расскажите о важности понимания значения , стоящего за фактами умножения , и о том, как их можно использовать в повседневных ситуациях.

Хотя существует множество подходов к запоминанию таблицы умножения, вспомните приведенные выше примеры - «простые» числа - как хорошую отправную точку. Продолжая урок, примите во внимание следующие правила:

• Поощряйте студентов и назначьте им время для устной или письменной практики.
• Вводите новые факты умножения один за другим , постепенно и постепенно открывая концепцию для более сложных шагов умножения на 2, 3, 4 и так далее.
• Дайте студентам время попрактиковаться в фактах умножения. Найдите ритм, который хорошо подходит для вашего класса. Если хотите, воспользуйтесь взаимным обучением для учащихся, которые испытывают трудности.
• Запомните факты в стратегическом порядке . Когда ваши ученики освоят 0-3 , переходите к 4-7 , а затем 8-10 . В зависимости от ваших предпочтений вы также можете охватить 11 и 12. Включение более сложных задач в качестве бонуса поможет вам оценить успешных учеников.Некоторые учителя включают несколько более сложных задач в качестве бонуса или для выявления учеников с высокими успеваемостями.

Чтобы облегчить запоминание, держите наглядные материалы под рукой в ​​классе. Независимо от того, сколько раз вы говорите об умножении, всегда полезно иметь физическую копию таблицы в вашем классе.

Если у вас его нет, вы можете заказать его в Интернете менее чем за 10 долларов. Быстрый поиск на Amazon показывает множество вариантов.

Если у вас уже есть плакат, подумайте о приобретении других материалов, которые помогут вам наглядно объяснить функцию умножения.

Например, этот документ является отличным вариантом для дисплеев: он содержит набор из 20 страниц с ответами (как показано ниже) на каждую из таблиц умножения от 1 до 10, с цветовой кодировкой в ​​соответствии с конкретной таблицей, которую они представляют.

6. Представьте ассоциативные и распределительные свойства.

Хотя эти концепции являются более продвинутыми, важно, чтобы ваши ученики усвоили их. Вы обнаружите, что они могут творить чудеса, улучшая умственную математику ваших учеников.

Примечание: Используйте свое усмотрение, представляя свойства ниже.Они не могут быть применимы к учащимся любого года ниже 4-го класса.

Ассоциативное свойство

Правило ассоциативного свойства гласит, что независимо от способа группировки факторов продукт всегда будет одним и тем же.

Например,

( a x b ) x c = a x ( b x c )

или

(1 x 2) x 3 = 1 x (2 x 3)

Ваши ученики могут понять эту концепцию, связав ее со сложением столбцов, посредством чего они группируют слагаемые, чтобы найти сумму.

Студенты также могут научиться группировать факторы любым удобным для них способом в поисках ответа. Вы можете объяснить это правило как расширение указанного выше коммутативного свойства.

Распределительное свойство

Распределительное свойство обозначается как a (b + c) = (ab) + (ac)

Студентам это может показаться сложным, но часто они уже используют это свойство сами по себе как мысленный математический трюк для решения более сложных фактов умножения.

Проще говоря, собственность распространяется - или, как следует из названия, распределяет - значение a поровну до b и c.

Например, для 6 x 8 они могут использовать свойство распределения, чтобы думать: (6 x 5) + (6 x 3) или 30 +18

Чтобы объяснить свойство визуально или тактильные учащиеся, позвольте детям изучить свойство распределения с такими материалами, как чашки и бобы или сетка.

Раздел B: Интересные способы научить умножать

Играть в классные математические игры

Классные математические игры могут избавить от страха перед умножением. Рассмотрим эти два примера, специализирующихся на умножении:

Константы калькулятора

Если калькуляторы в вашем классе имеют постоянную функцию, поощрите своих учеников использовать их для определения кратных любого числа, чтобы найти связь между умножением и сложением.

Как это работает:

• Выберите множитель, например семь, и введите его.
• Нажмите кнопку +, затем нажмите кнопку =. Калькулятор должен снова показать семь.
• Затем продолжайте нажимать кнопку =. Функция константы будет постоянно добавлять семь, показывая увеличивающиеся кратные числа (7, 14, 21, 28 и т. Д.)
• При желании попросите учащихся записать список найденных кратных чисел и побудить их искать закономерности в списке. они придумывают

Таблица умножения Жужжание

Это увлекательное математическое задание, которое мотивирует ваших учеников и укрепляет их знания о таблице умножения.

Шаг a) Выберите конкретную таблицу умножения для использования в упражнении (например, кратное пяти)

Шаг b) Попросите учеников встать и расположить их в определенном порядке, чтобы каждый ученик знал когда придет их очередь

Шаг c) Выберите одного ученика, чтобы посчитать «один». Затем ребенок слева от него считает «два». Следующий ребенок считает «три» и так далее. Когда последовательность становится кратной пяти, ученик кричит «гуд!»

Таким образом, последовательность будет выглядеть следующим образом: один, два, три, четыре, « жужжание, !», Шесть, семь...

Шаг d) Если ученик забывает сказать «жужжание» или говорит это в неподходящее время, он выходит и садится. Последовательность подсчета будет продолжаться до тех пор, пока ученики не достигнут десятикратного пятикратного счета (или по усмотрению учителя), а затем начнется снова.

Победителями финала становятся трое оставшихся в живых детей. Рассмотрите возможность награждения победителей в рамках своей стратегии управления классом.

Чтобы получить больше вдохновения, ознакомьтесь с полным списком из 20 увлекательных математических игр в классе «».

Для активного подхода к обучению математике просмотрите наши 20 забавных и творческих математических заданий - подходов и упражнений, с компьютерами и без них, которые заставят учащихся с нетерпением ждать ваших уроков математики.

Используйте забавные учебники по математике в классе

В нашем обзоре учебников по математике для учащихся мы нашли список исключительных ресурсов для учителей.

Просмотрите номера три, пять и шесть, чтобы найти примеры публикаций, в которых есть функция умножения и которые помогают поддерживать хорошо структурированный учебный план по математике.

Поддержите обучение с помощью математических веб-сайтов

Интернет является домом для огромного количества мощных и полезных образовательных математических веб-сайтов для учителей и студентов.

См. Наш список полезных веб-сайтов по математике для учителей, пятью из которых вы можете поделиться со студентами. Один ресурс - Prodigy, бесплатная математическая игра в соответствии с учебной программой, которую используют более 800 000 учителей и 30 миллионов студентов по всему миру.

Prodigy предлагает материалы по всем основным математическим темам, включая умножение, и охватывает 1–8 классы.

Вы можете превратить обучение в умножение в путешествие, вдохновленное фантазией, где успех учащихся зависит от оттачивания математических навыков в соответствии с учебной программой!

Это также подтверждается количественными исследованиями. В недавнем исследовании мы обнаружили, что школы, зачисленные в Prodigy, показали лучшие результаты и улучшили результаты тестов, чем неактивные школы.