Построение равносторонего треугольника
← →boriskb © (2012-04-11 10:27) [0]
без транспортира и циркуля.
Прямо сейчас понадобилось. Ниего кроме карандаша и линейки без делений нет. Размер стороны можно на глаз.
Научите?
← →
RWolf © (2012-04-11 10:30) [1]
сдаётся мне, для таких фокусов нужны минимум циркуль и линейка.
← →
Jeer © (2012-04-11 10:31) [2]
Сверлишь две дырочки в линейке — вот тебе и циркуль 🙂
← →
CRLF (2012-04-11 10:33) [3]
в нашей нищей школе математик, помнится, кусок мела и тряпку для вытирания доски успешно использовал в качестве циркуля %-)
← →
Boriskb © (2012-04-11 10:33) [4]
> Сверлишь две дырочки в линейке — вот тебе и циркуль 🙂
Ниего кроме карандаша и линейки без делений нет.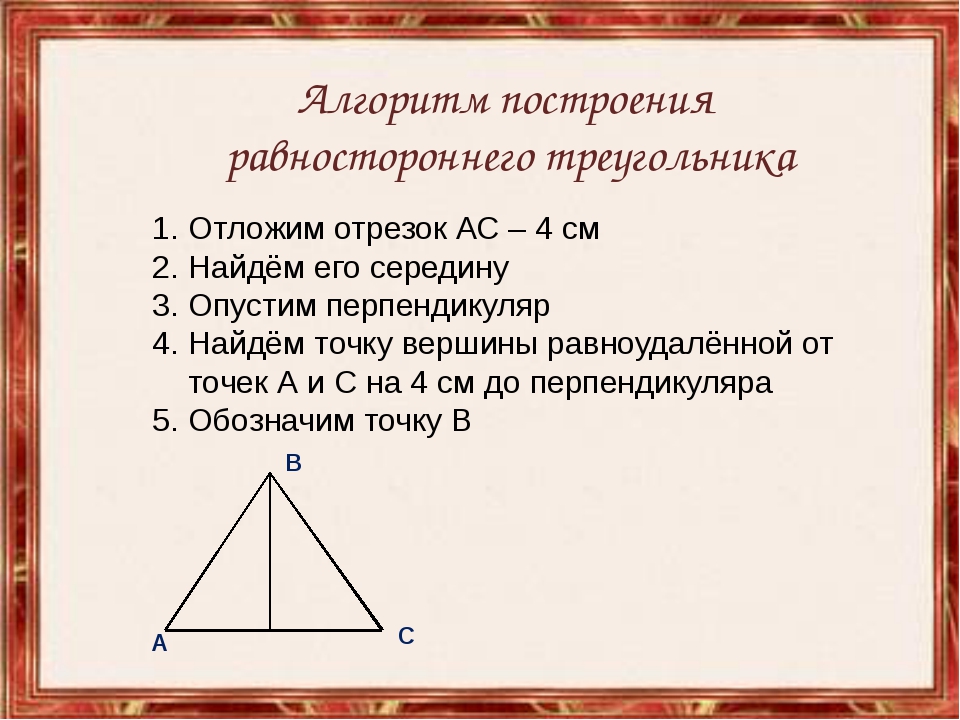
← →
oldman © (2012-04-11 10:33) [5]
высота расчитывается по теореме Пифагора
Проводить перпендикуляр с помощью только линейки научить?
← →
Медвежонок Пятачок © (
ломаем линейку на три примерно равные части.
складываем вместе, карандашом наносим риски с краев.
получили три стороны одинаковой длины.
выкладываем их на листе бумаги, совмещая риски.
вуаля….
← →
Boriskb © (2012-04-11 10:36) [7]
Ладно. Уточним вопрос: как простейшим способом соорудить циркуль?
← →
AV © (2012-04-11 10:37) [8]
> Сверлишь две дырочки в линейке — вот тебе и циркуль 🙂
рисуешь любой треугольник, объявляешь его находящимся в таком искривленном пространстве, что он становится равносторонним по его искривлению.

по сабжу — имхо, никак. Циркуль, все-таки, нужен.
← →
Boriskb © (2012-04-11 10:38) [9]
> oldman © (11.04.12 10:33) [5]
> высота расчитывается по теореме ПифагораПроводить перпендикуляр
> с помощью только линейки научить?
Нет спасибо — лучше науите откладывать на линейке без делений корень из 2
← →
oldman © (2012-04-11 10:38) [10]
> Ладно. Уточним вопрос: как простейшим способом соорудить
> циркуль?
Карандаш, нитка, кнопка
← →
Boriskb © (2012-04-11 10:40) [11]
Блин…
Есть куча графических редакторов, но нет принтера :))
← →
RWolf © (2012-04-11 10:42)
> как простейшим способом соорудить циркуль?
ножницы должны подойти.
← →
oldman © (2012-04-11 10:44) [13]
1. Рисуешь известную тебе одну сторону треугольника AB.
2. С помощью линейки рисуешь с двух сторон равноудаленные параллельные прямые 1 и 2 (прикладывая линейку к АВ и чертя с другой стороны линейки)
3. Находишь на прямой точки A1 и В1, а на прямой 2 точки А2 и В2
(AA1=AA2=BB1=BB2>половины стороны)
4. соединяешь точки пересечения АА1 с ВВ1 и АА2 с ВВ2
← →
sniknik © (2012-04-11 10:46) [14]
> Карандаш, нитка, кнопка
кусок бумаги пробитый в одном месте спичкой в другом карандашом.
← →
Boriskb © (2012-04-11 10:46) [15]
> Карандаш, нитка, кнопка
Это первое что пришло в голову, но нет кнопки. На иголке завязать чтоли… И карандашь обвязать? Амне их надо штук 20 разного размера — с моими кривыми руками я их буду бог знает скаолько времени завязывать…
На иголке завязать чтоли… И карандашь обвязать? Амне их надо штук 20 разного размера — с моими кривыми руками я их буду бог знает скаолько времени завязывать…
По всем соседям уже сбегал.
← →
Boriskb © (2012-04-11 10:47) [16]
> RWolf © (11.04.12 10:42) [12]
> > как простейшим способом соорудить циркуль?ножницы должны
> подойти.
ну вот почему сам не догадался? Пока самый реальный метод.
← →
oldman © (2012-04-11 10:47) [17]
> По всем соседям уже сбегал.
А по магазинам нет?
«Знаю я тут одно место с офигенными циркулями» (ДМБ ©)
← →
Boriskb © (2012-04-11 10:49) [18]
> Пока самый реальный метод
Хотя. . как я след на бумаге от такого циркуля получу? Глазки старенькие уже :))
. как я след на бумаге от такого циркуля получу? Глазки старенькие уже :))
← →
Boriskb © (2012-04-11 10:50)
> А по магазинам нет?
Денег жалко :))
На один раз покупать — потом выбросить..
← →
oldman © (2012-04-11 10:50) [20]
Привяжи карандаш к ножницам!!!
← →
oldman © (2012-04-11 10:54) [21]
> > Карандаш, нитка, кнопка
>
> Это первое что пришло в голову, но нет кнопки. На иголке
> завязать чтоли… И карандашь обвязать? Амне их надо штук
> 20 разного размера — с моими кривыми руками я их буду бог
 ..
..Завязать на карандаше. Отмотать нитку большой длины. Начать с большого треугольника. Малые радиусы получаться путем наматывания нитки вокруг карандаша.
Блин! Я больше не могу смеяться. Закройте ветку.
← →
Boriskb © (2012-04-11 10:56) [22]
> Блин! Я больше не могу смеяться. Закройте ветку.
:))
Еще веселей будет если сам, на практике, попробуешь решить задачу с указанными ограничениями
← →
han_malign (2012-04-11 10:59) [23]
> надо штук 20 разного размера
— нарисуй один большой, и 19-ть вложенных — используй как трафарет…
← →
Плохиш © (2012-04-11 10:59) [24]
Сначала создать трудности, а после героически их решать. Как всё знакомо и не смешно.
Как всё знакомо и не смешно.
← →
RWolf © (2012-04-11 11:01) [25]
почему бы просто не нарисовать треугольник на экране, после чего приложить лист бумаги и отметить на нём вершины треугольника на просвет?
а их уж и линейкой обвести можно.
← →
Inovet © (2012-04-11 11:07) [26]
Так ниток тоже нет.
А у линейкм есть ширина? Прямой угол? Лист сгибать можно?
← →
AV © (2012-04-11 11:09) [27]
имхо, дядя Боря дисер пишет
«Мониторинг инет-сообщества технического уклона по вопросам готовности помочь ближнему»
наиболее реальное — нарисовать, добавить яркости, приложить, обвести.
Я так дочери солдата-победителя нарисовал в школу на А2. Кусками двигал изображение и лист, обводил. Даже на выставку оправили 🙂
Кусками двигал изображение и лист, обводил. Даже на выставку оправили 🙂
← →
Inovet © (2012-04-11 11:11) [28]
> [27] AV © (11.04.12 11:09)
> наиболее реальное — нарисовать, добавить яркости, приложить,
> обвести.
Монитора тоже нет
← →
Boriskb © (2012-04-11 11:15) [29]
Ну хоть тренинг в остроумии получился 🙂
> Монитора тоже нет
Монитор есть :))
Сейчас расскажу историю вопроса.
← →
Inovet © (2012-04-11 11:17) [30]
> [29] Boriskb © (11.04.12 11:15)
> Монитор есть :))
Может и принтер есть?
← →
CRLF (2012-04-11 11:18) [31]
а прямой угол у нас есть?
← →
Inovet © (2012-04-11 11:20) [32]
> [31] CRLF (11. 04.12 11:18)
04.12 11:18)
> а прямой угол у нас есть?
Монитор прямокгольный. Можно положить на стол и пользоваться как прямоугольником.
← →
CRLF (2012-04-11 11:22) [33]
впрочем, не поможет.
← →
Boriskb © (2012-04-11 11:23) [34]
История следущая:
Ко мне пришла внучка — 14 лет . Захотел ей показать сою любимую игрушку в ее возрасте и около того.
Гексафлексагоны http://www.arbuz.uz/z_flex.html
На ней и мои дети выросли. Тогда известный кубик еще не был изобретен
Требуется ее сначала сделать :))
← →
Boriskb © (2012-04-11 11:24) [35]
Циркуль сбегал — купил.
Ножницы бы все равно не подошли — трудно зафиксировать раствор.
← →
Inovet © (2012-04-11 11:25) [36]
> [33] CRLF (11.04.12 11:22)
> впрочем, не поможет.
Чё иа не поможет, очень даже поможет.
← →
Anatoly Podgoretsky © (2012-04-11 11:29) [37]
Бумаги нет
← →
Inovet © (2012-04-11 11:34) [38]
> [37] Anatoly Podgoretsky © (11.04.12 11:29)
> Бумаги нет
Придётся линейку пилить ей же самой и карандашом.
← →
Boriskb © (2012-04-11 11:34) [39]
> Бумаги нет
Да, кстати — тоже не так просто.
Надо было найти подходящий картон белый с обеих сторон. Не так просто.
Еще не знаю — есть ли чем скреплять…
Липкой ленты точно нет. Полезу в аптечку — пластырь рулонный искать…
← →
Inovet © (2012-04-11 11:35) [40]
> [39] Boriskb © (11.04.12 11:34)
> Липкой ленты точно нет.
Скотч надо было вместе с циркулем купить и картон там же.
← →
oldman © (2012-04-11 11:41) [41]
> Скотч надо было вместе с циркулем купить и картон там же.
Проще купить гексафлексагон
← →
Boriskb © (2012-04-11 11:42) [42]
> Inovet © (11.04.12 11:35) [40]
Не понимаете вы ничего в воспитании.
Лучше было бы и циркуль не покупать. Дал слабину…
← →
Труп Васи Доброго © (2012-04-11 11:46) [43]
Найди/создай/отмерь угол в 60 градусов (раздели 180 на 3). Нарисуй этот «длинный» угол на весь ватман, а потом при помощи любой штуки отметь на обоих сторонах угла одинаковое расстояние. Соедини отметки и вот тебе сколь угодно равносторонних треугольников.
← →
Inovet © (2012-04-11 11:47) [44]
> [42] Boriskb © (11.04.12 11:42)
> Не понимаете вы ничего в воспитании.
Внучка может не понять изюминку изготовления и заодно ей станет неинтересна сама суть игрушки. Даже во всяких Очумелых ручках применяют скотч, чтобы понятно было — он же есть в магазине, чем он хуже картона. Ну а нет, так ткашь и нитки с иголкой, но их тоже нет по условию задачи.
← →
Inovet © (2012-04-11 11:49) [45]
> [43] Труп Васи Доброго © (11.04.12 11:46)
> Нарисуй этот «длинный» угол на весь ватман, а потом при
> помощи любой штуки отметь на обоих сторонах угла одинаковое
> расстояние. Соедини отметки и вот тебе сколь угодно равносторонних
> треугольников.
Надо, как оказалось, много одинаковых.
← →
Inovet © (2012-04-11 11:51) [46]
> [43] Труп Васи Доброго © (11.04.12 11:46)
> Найди/создай/отмерь угол в 60 градусов (раздели 180 на 3).
Нечем — нет ничего.
← →
Boriskb © (2012-04-11 11:56) [47]
Задача ясна из [34]
Попробуйте в реале bepyftnt методом проб и ошибок (я их сделал несколько десятков штук) что ни бумага, картон не всякий, иголка и нитка и много чего еще не подойдет для хоть мало мальски долгоживущей игрушки.
> Проще купить гексафлексагон
Это точно — зачем учить арифметику — ведь калькулятор есть :))
← →
Anatoly Podgoretsky © (2012-04-11 11:59) [48]
> Inovet (11.04.2012 11:34:38) [38]
Ничего нет, вот в этом ничего и надо рисовать
← →
CRLF (2012-04-11 12:02) [49]
Ничего есть!
← →
Anatoly Podgoretsky © (2012-04-11 12:13) [50]
> CRLF (11.04.2012 12:02:49) [49]
Ничего есть нельзя.
← →
Игорь Шевченко © (2012-04-11 12:20) [51]
Boriskb © (11.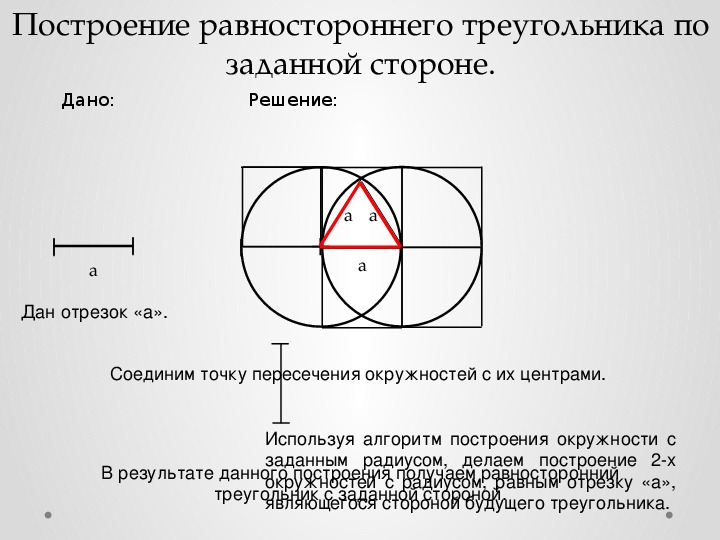 04.12 11:23) [34]
04.12 11:23) [34]
Статья в «Науке и жизни» занимательная была, помнится
← →
Boriskb © (2012-04-11 12:27) [52]
> Игорь Шевченко © (11.04.12 12:20) [51]
Я про них вычитал в книге Мартина Гарднера. Подарила учительница математики. Потом купили еще 3 наименования его книг.
Помнится на этом форуме его уже упоминали
← →
Jeer © (2012-04-11 14:30) [53]
Что-то мне напомнило «Как выжить с товарищем в пустыне без воды» 🙂
Варианты ? 🙂
← →
Думкин © (2012-04-11 14:36) [54]
> Jeer © (11.04.12 14:30) [53]
А товарищ тоже должен выжить?
← →
Anatoly Podgoretsky © (2012-04-11 14:46) [55]
> Думкин (11.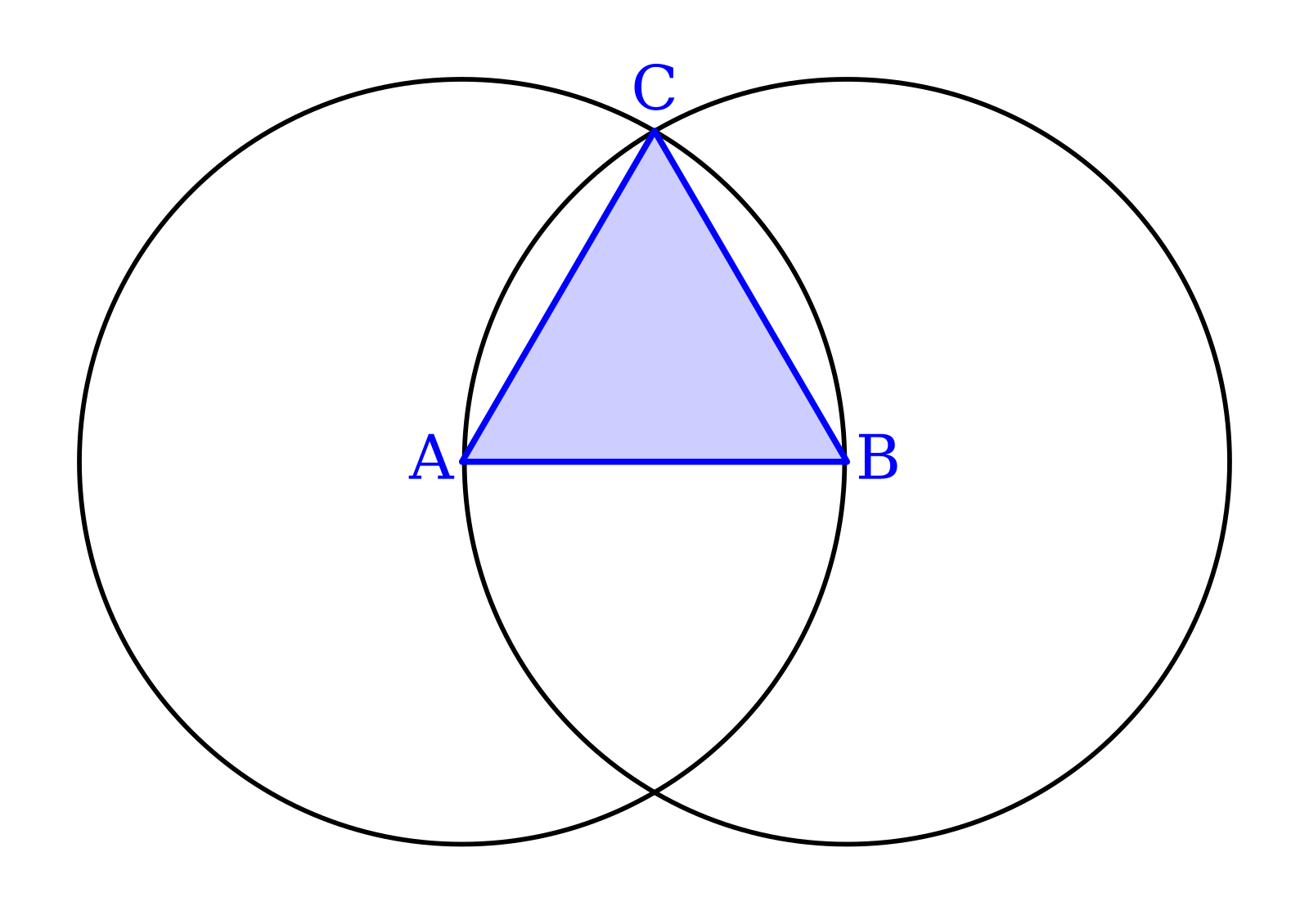 04.2012 14:36:54) [54]
04.2012 14:36:54) [54]
А потом будем выяснить можно ли пить кровь
← →
Думкин © (2012-04-11 14:49) [56]
> Anatoly Podgoretsky © (11.04.12 14:46) [55]
нужно!
Постперестроечный помойный фильм как-то был — так там сын в пустыне папку съел, так и выжил.
← →
Jeer © (2012-04-11 14:58) [57]
> Думкин © (11.04.12 14:36) [54]
>
>
> > Jeer © (11.04.12 14:30) [53]
>
> А товарищ тоже должен выжить?
А как же ? Иначе это уже не товарищ, а корм 🙂
← →
БарЛог © (2012-04-11 15:03) [58]
Я за 20 секунд нарисовал 🙂
Рисуешь квадрат.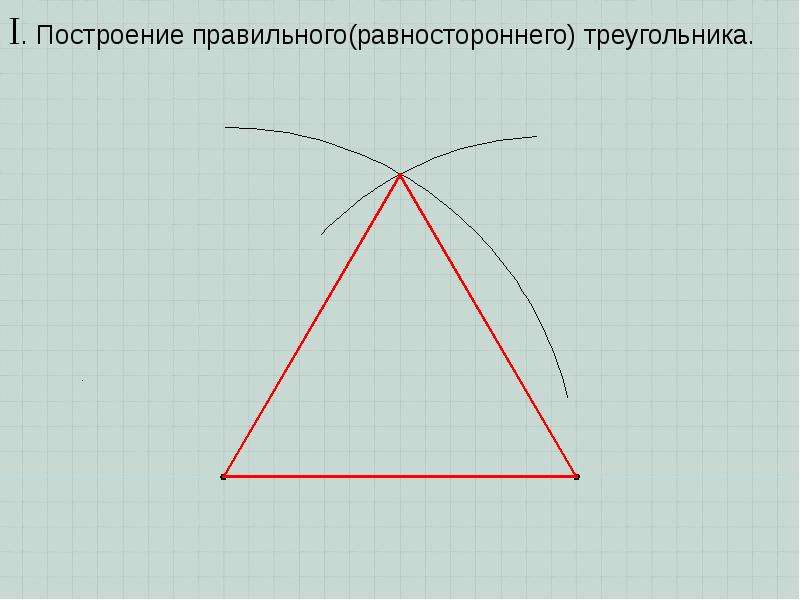 Делишь верхнюю сторону пополам, соединяешь точки.
Делишь верхнюю сторону пополам, соединяешь точки.
Из точки, которая лежит на середине верхней стороны квадрата проводишь отрезки до нижних точек.
← →
Труп Васи Доброго © (2012-04-11 15:12) [59]
> Я за 20 секунд нарисовал 🙂
Учителем тебе не быть! Ничего не понял из твоего «рассказа».
Сдаётся мне что если вырезать из бумаги три одинаковые полоски и сложить из них замкнутую фигуру, то получится совершенно равносторонний треугольник.
← →
boriskb © (2012-04-11 15:13) [60]
> БарЛог © (11.04.12 15:03) [58]
Не понял.
Нарисуй — покажи.
PS
:))
вспомнил анекдот про «не понял»
← →
Inovet © (2012-04-11 15:21) [61]
> [58] БарЛог © (11. 04.12 15:03)
04.12 15:03)
> Рисуешь квадрат
Как?
← →
Boriskb © (2012-04-11 15:21) [62]
К
> boriskb © (11.04.12 15:13) [60]
Старый рабочий передает своё хозяйство молодому.
— Значит так: ты работаешь дежурныи электриком. Утром приходишь — включаешь рубильник. Вечером уходишь — выключаешь. Понял?
-Неа. Не понял.
-Видишь рубильник. Утром его надо включить, люди придут, будут работать. Вечером, все уйдут. В целях пожарной безопасности рубильник дадо выключить. Понял?
-Да не понял я!
-Ну идрит твою… Рубильник знаешь? Включать-выключать умеешь? Утром ты первый приходишь, надо дать электричество цеху — поворачивашь рубильник в эту сторону. Вечером, когда все уйдут, повернешь его в другую сторону — выключишь. Понял?
— Мужик, ты что — тупой чтоли? Я тебе уже сколько раз говорю: Я не понял!! А ты всё переспрашиваешь!
← →
CRLF (2012-04-11 15:32) [63]
> Как?
Кстати. .. Загибаем угол бумажной полоски под 45 градусов (короткий край параллельно длинному краю). Загибаем полоску вдоль катета получившегося треугольника, имеем квадрат.
.. Загибаем угол бумажной полоски под 45 градусов (короткий край параллельно длинному краю). Загибаем полоску вдоль катета получившегося треугольника, имеем квадрат.
← →
icWasya © (2012-04-11 15:44) [64]
Как тот же Гарднер советовал — сначала взять ленту от кассового аппарата.
Если аккуратно сложить втрое лист бумаги — можно получить угол в 60 градусов.
← →
Думкин_ (2012-04-11 15:50) [65]
> А как же ? Иначе это уже не товарищ, а корм 🙂
Какая скучная задача, однако! Но может так оказаться, что в пустыне только товарищ, а не я.
Как с таким товарищем, который в пустыне без воды, выжить — вроде понятно.
А вот если в пустые и он и я. А пустыня — это центр Сахары, то думаю, что привет. Даже та дикая идея, что пробегает по некоторому взаимному сохранению жидкости — кажется безнадежной. И неприятной.
И неприятной.
← →
Inovet © (2012-04-11 15:53) [66]
> [63] CRLF (11.04.12 15:32)
> [64] icWasya © (11.04.12 15:44)
На мой вопрос положительного ответа не было
> [26] Inovet © (11.04.12 11:07)
> А у линейкм есть ширина? Прямой угол? Лист сгибать можно?
И вообще
> [37] Anatoly Podgoretsky © (11.04.12 11:29)
> Бумаги нет
← →
CRLF (2012-04-11 15:59) [67]
> Inovet © (11.04.12 15:53) [66]
У топикстартера задача — сделать гексафлексагон. Как нарисовать сферический квадрат в вакууме, он не спрашивал. Ты спрашиваешь, да. 🙂
← →
CRLF (2012-04-11 15:59) [68]
> Inovet © (11. 04.12 15:53) [66]
04.12 15:53) [66]
У топикстартера задача — сделать гексафлексагон. Как нарисовать сферический квадрат в вакууме, он не спрашивал. Ты спрашиваешь, да. 🙂
← →
Inovet © (2012-04-11 16:18) [69]
> [67] CRLF (11.04.12 15:59)
> Как нарисовать сферический квадрат в вакууме, он не спрашивал.
ТС хочет нарисовать только линейкой, больше ничего нет. Сгибать лист не разрешил. Потом купил циркуль, тут уже всё просто.
← →
CRLF (2012-04-11 16:30) [70]
> Захотел ей показать сою любимую игрушку в ее возрасте и около того.
> Требуется ее сначала сделать :))
Задача — сделать игрушку, а не мысленный эксперимент «как построить всё, не имея ничего» %-)
← →
TUser © (2012-04-11 16:33) [71]
> У топикстартера задача — сделать гексафлексагон.
Только вопрос в топике задан в стиле, на который тут обычно отвечают ссылкой на «Как задавать вопросы хакерам?»
← →
Владислав © (2012-04-11 16:35) [72]
Надо до появления внуков циркуль купить.
← →
CRLF (2012-04-11 16:36) [73]
Обычно разным людям отвечают по-разному, на основе экспертной оценки их предыдущих постов, ага.
← →
boriskb © (2012-04-11 16:43) [74]
Друзья, мне конечно льстит, что меня причисляют к великим писателям (Ведь только в произведениях великих писателей каждый видит что-то своё?).
Но, право же — я не достоин. :))
Всё проще.
Я лишь хотел воказать внучке, чем дед занимался в её возрасте :))
Идействительно, ни линейки нормальной (не говоря о большем) дома давно нет.
Отучились все.
← →
БарЛог © (2012-04-11 18:12) [75]
http://savepic.su/1656425m.jpg
← →
Владислав © (2012-04-11 18:22) [76]
> БарЛог © (11.04.12 18:12) [75]
Ну все бы ничего, но нужен равносторонний.
← →
Inovet © (2012-04-11 18:24) [77]
> [75] БарЛог © (11.04.12 18:12)
> http://savepic.su/1656425m.jpg
И как это сделать одной линейкой?
← →
Inovet © (2012-04-11 18:25) [78]
> [76] Владислав © (11.04.12 18:22)
> Ну все бы ничего, но нужен равносторонний.
Там не понятно какой он.
← →
БарЛог © (2012-04-11 18:30) [79]
> Ну все бы ничего, но нужен равносторонний.
Да, задача не решена 🙁
← →
CRLF (2012-04-11 18:34) [80]
Без эталона прямого угла задачка нерешаема %-)
← →
Дмитрий С © (2012-04-11 18:52) [81]
Тему не читал.
Решение задачи:
Берем линейку, карандаш. Начинаем случайным образом рисовать линии до тех пор пока какие нибудь из них не образуют равносторонний треугольник.
← →
CRLF (2012-04-11 18:54) [82]
А линейка-то зачем?. .
.
← →
boriskb © (2012-04-11 20:04) [83]
Инет всё знает :))
Получаем эталон угла в 60 градусов. Он решит все наши проблемы.
http://505sovetov.ru/231/
Правда получаем вопрос: как построить квадрат? Я думаю в наших условиях можно воспользоваться тетрадкой в клеточку — она у меня есть.
← →
Sha © (2012-04-11 20:10) [84]
> boriskb © (11.04.12 20:04) [83]
> Инет всё знает :))
не верь:
у того треугольника отношение катетов 2:1,
а надо гипотенуза к катету 2:1
← →
Inovet © (2012-04-11 20:18) [85]
> [83] boriskb © (11.04.12 20:04)
> Инет всё знает :))
Врёт инет всё
a — сторона квадрата
a / (1/2 * a) = 2 = tng(CAB)
CAB = 1,1071487177940905030170654601785
CAB <> Pi / 3 = 1,0471975511965977461542144610932
← →
Inovet © (2012-04-11 20:20) [86]
И гнуть ты запретил. Если можно гнуть, то равносторонний легко строится с помощью линейки.
Если можно гнуть, то равносторонний легко строится с помощью линейки.
← →
Inovet © (2012-04-11 20:24) [87]
Ты так плохому научишь внучку.
← →
Boriskb © (2012-04-11 20:25) [88]
> Inovet © (11.04.12 20:18) [85]
Да уж…
Как школьник.
← →
Boriskb © (2012-04-11 20:26) [89]
> И гнуть ты запретил
Где? Цитата?
> Если можно гнуть, то равносторонний легко строится с помощью
> линейки.
Покажи
← →
Sha © (2012-04-11 20:32) [90]
Если у нас есть прямой угол, то задача сводится к построению отрезка длиной 3^1/2. 1/2.
1/2.
← →
Inovet © (2012-04-11 20:34) [91]
> [89] Boriskb © (11.04.12 20:26)
> > И гнуть ты запретил
>
> Где? Цитата?
Ты не ответил на вопрос о гнутье.:)
> [26] Inovet © (11.04.12 11:07)
> А у линейкм есть ширина? Прямой угол? Лист сгибать можно?
> [89] Boriskb © (11.04.12 20:26)
> Покажи
Чертим отрезок на длину линейки. Складываем лист так, чтобы концы отрезка совпали — линия изгиба будет срединным перпендикуляром. Совмежаем один конец линейки с концом отрезка, второй с перпендикуляром, проводим линию. Аналогично поступаем с другим.
← →
Inovet © (2012-04-11 20:35) [92]
> [90] Sha © (11.04.12 20:32)
> то задача сводится к построению отрезка длиной
Делений нет на линейке.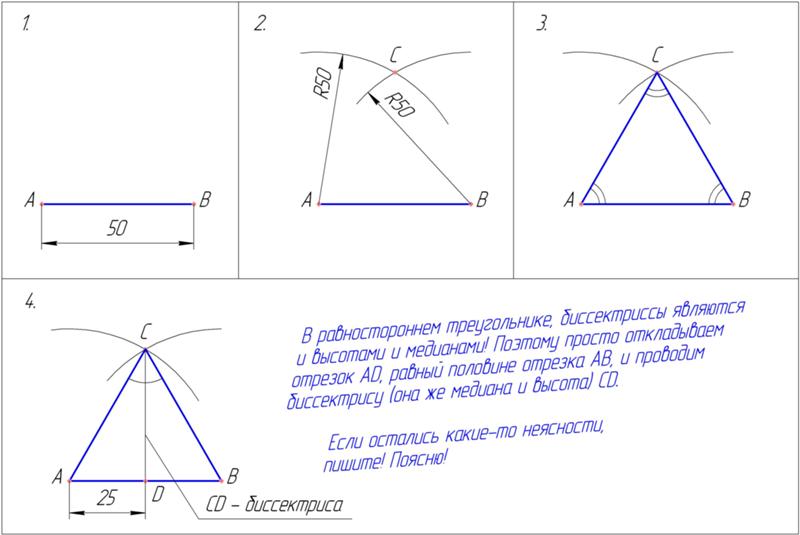
← →
Inovet © (2012-04-11 20:37) [93]
> [92] Inovet © (11.04.12 20:35)
> Делений нет на линейке.
Вообще никаких, тем более логарифмической разметки.
← →
Sha © (2012-04-11 20:38) [94]
> Inovet © (11.04.12 20:35) [92]
> Делений нет на линейке.
Они не нужны.
В качестве единичного отрезка выбери любую длину.
Этого достаточно.
← →
Inovet © (2012-04-11 20:42) [95]
> [94] Sha © (11.04.12 20:38)
> Они не нужны.
А, ну да. Прямой угол тоже двумя сгибаниями можно сделать.
← →
oldman © (2012-04-11 21:02) [96]
> БарЛог © (11. 04.12 18:30) [79]
04.12 18:30) [79]
> Да, задача не решена 🙁
>
> CRLF (11.04.12 18:34) [80]
> Без эталона прямого угла задачка нерешаема %-)
Задача решена еще в [13]
Если на линейке нет делений, до две риски карандашом помогают не прибегать даже к теореме Пифагора.
Построив срединный перпендикуляр найти на нем точку, удаленную от концов отрезка на длину отрезка элементарно.
Кстати, отложив на перпендикуляре длину отрезка, получим эталонный треугольник с углами 30 и 60.
Математики, блин! Геометрия, средняя школа.
← →
oldman © (2012-04-11 21:04) [97]
Елки! Про эталонный треугольник я ошибся. там не 30 и 60!!!
← →
CRLF (2012-04-11 21:07) [98]
> Построив срединный перпендикуляр
Как его построить без циркуля или эталонного прямого угла?
← →
Sha © (2012-04-11 21:09) [99]
> oldman © (11.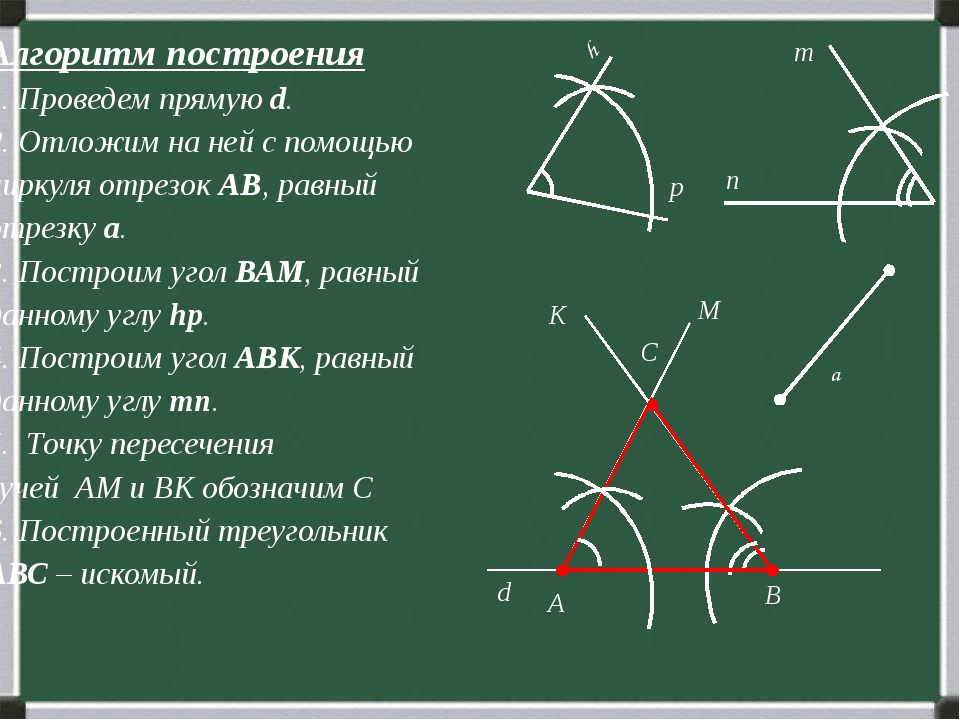 04.12 21:02) [96]
04.12 21:02) [96]
> Построив срединный перпендикуляр найти на нем точку,
> удаленную от концов отрезка на длину отрезка элементарно.
Без циркуля? Это задача на построение или где?
← →
oldman © (2012-04-11 21:19) [100]
> CRLF (11.04.12 21:07) [98]
> Как его построить без циркуля или эталонного прямого угла?
Учитывая [13] и написанное ниже в этом посте, можно. Используя поворот линейки с двумя рисками как циркуль. Вернее, как нахождение угла поворота.
> Sha © (11.04.12 21:09) [99]
> Без циркуля? Это задача на построение или где?
Без циркуля!
Задача на построение в домашних условиях.
Прикладывая первую риску линейки к концу основания, найти точку пересечения перпендикуляра с другой риской можно просто поворачивая линейку.
Да, похоже на циркуль. Но человеку было надо построить треугольник.
А с точки зрения геометрии нужен циркуль.
← →
Sha © (2012-04-11 21:25) [101]
Похоже, есть 2 решения задачи, кпждое при 1 дополнительном условии
1. при условии, что линейка имеет постоянную по длине ширину
2. при условии, что разрешено на любой прямой отмерять некий единичный отрезок
← →
Sha © (2012-04-11 21:28) [102]
> oldman © (11.04.12 21:19) [100]
> Задача на построение в домашних условиях.
немного беременной быть нельзя:
— или на построение
— или в домашних условиях
← →
oldman © (2012-04-11 21:29) [103]
Замечание по поводу.
Что же это за линейка такая, без делений? Это называется как-то по другому. ..
..
← →
oldman © (2012-04-11 21:32) [104]
> Sha © (11.04.12 21:28) [102]
Когда Пифагор сказал землемерам, что может доказать, что квадрат Г равен сумме квадратов К, землемеры сказали: «Мы знаем, что это так по опыту, а доказательство засунь себе…»
Немного беременной быть можно. ты никогда в саду ничего не строил, имея из измерительных инструментов карандаш, молоток и лопату?
← →
Sha © (2012-04-11 21:33) [105]
> oldman © (11.04.12 21:29) [103]
> Что же это за линейка такая, без делений?
В задачах на построение только такие используются
← →
Inovet © (2012-04-11 21:34) [106]
> [103] oldman © (11.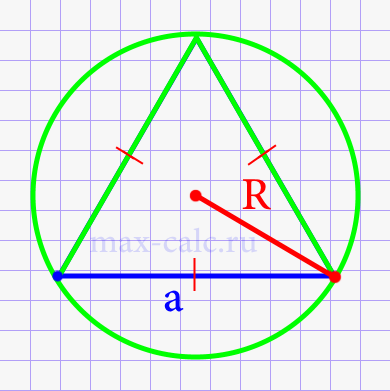 04.12 21:29)
04.12 21:29)
> Что же это за линейка такая, без делений? Это называется
> как-то по другому…
Линейка от линия, а деления уже для измерения длины линии.
← →
CRLF (2012-04-11 21:35) [107]
> 2. при условии, что разрешено на любой прямой отмерять некий
> единичный отрезок
Линейка и есть единичный отрезок
← →
Sha © (2012-04-11 21:37) [108]
> oldman © (11.04.12 21:32) [104]
> ты никогда в саду ничего не строил, имея из измерительных инструментов карандаш, молоток и лопату?
еще как строил и египетский треугольник активно юзал,
только, вроде, задача не для сада была сформулирована
← →
Sha © (2012-04-11 21:41) [109]
> CRLF (11. 04.12 21:35) [107]
04.12 21:35) [107]
> Линейка и есть единичный отрезок
Не совсем так.
В задачах на построение для построения равных по длине отрезков
используется линейка и циркуль, как бы смешно это не звучало.
← →
CRLF (2012-04-11 21:43) [110]
Чего уж тут смешного… Но учитывая, что циркуля у нас нет, придётся линейку в качестве единичного отрезка использовать имхо.
← →
oldman © (2012-04-11 21:47) [111]
> Sha © (11.04.12 21:37) [108]
> только, вроде, задача не для сада была сформулирована
Построение равносторонего треугольника
boriskb © (11.04.12 10:27)
без транспортира и циркуля.
Прямо сейчас понадобилось. Ниего кроме карандаша и линейки без делений нет.
И правда не для сада.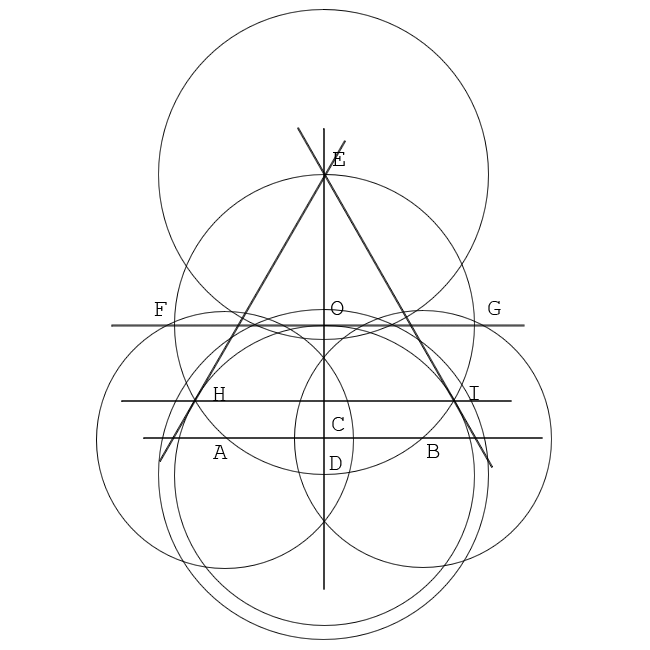 Для детсада.
Для детсада.
В общем, спасибо boriskb© за классную разминку для затекших мозгов. Попахивает разводом в стиле 1 апреля, да ладно.
← →
Sha © (2012-04-11 21:55) [112]
> oldman © (11.04.12 21:47) [111]
Никто задачу в такой формулировке и не решает.
Мне, например, интересно другое:
что надо добавить в условия задачи, чтобы она имела решение?
← →
oldman © (2012-04-11 21:58) [113]
> что надо добавить в условия задачи, чтобы она имела решение?
естественно, циркуль!
← →
MBo © (2012-04-11 22:08) [114]
Достаточно одной таблэтки, т.е. тонкой линейки.
Отмеряем полоску бумаги шириной точно в линейку — приложить, загнуть, оторвать.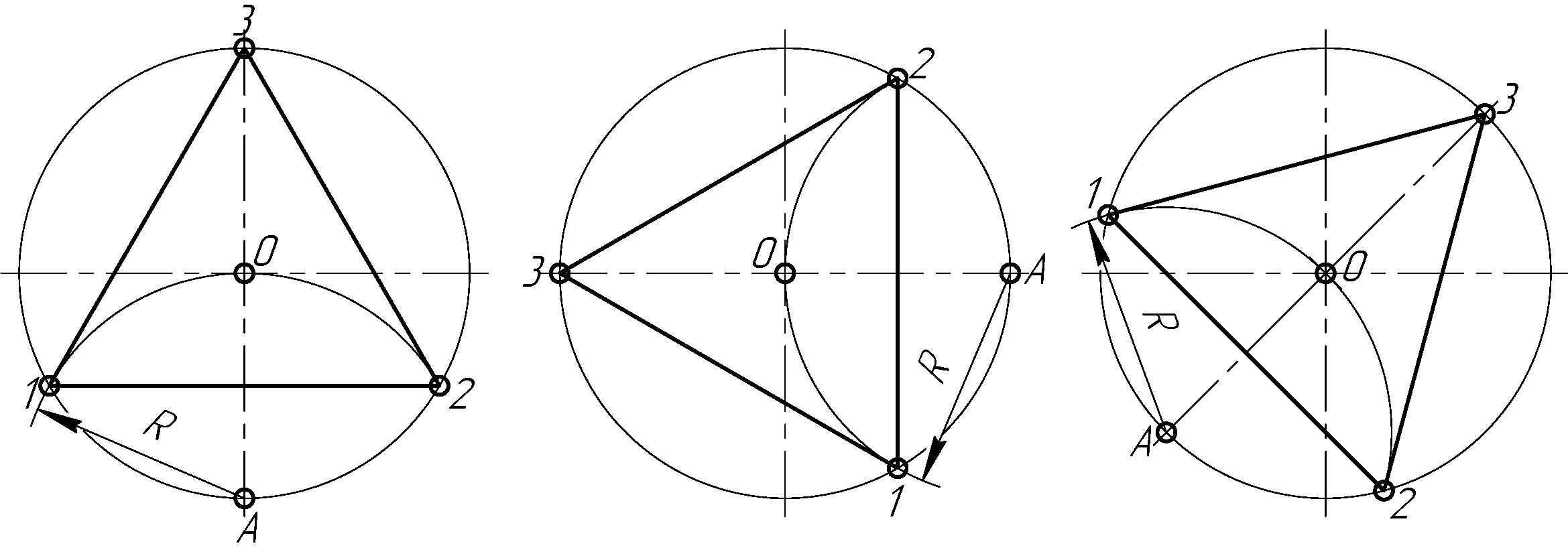 1/2.
1/2.
При помощи вспомогательного треугольника со сторонами,
перпендикулярными только что построенному,
строим треугольник с углом 30 градусов.
← →
Sha © (2012-04-11 22:23) [116]
> MBo © (11.04.12 22:08) [114]
> Ромбы 60-градусные.
а почему у меня параллелограммы не ромбические выходят? )
← →
Anatoly Podgoretsky © (2012-04-11 23:03) [117]
> Inovet (11.04.2012 21:34:46) [106]
Делилка — деление
← →
MBo © (2012-04-11 23:14) [118]
>Sha © (11.04.12 22:23) [116]
Хм… Пусть линейка горизонтальна, ширина линейки А. Половинка параллелограмма симметрична относительно вертикали (угол отражения) — треугольник равнобедренный. Высота треугольника А — как ширина линейки, высота к левому плечу тоже А — как ширина полоски, высота к правому плечу такая же ввиду равнобедренности. Разве три равные высоты не гарантируют, что треугольник равносторонний? Или я что-то упустил?
Высота треугольника А — как ширина линейки, высота к левому плечу тоже А — как ширина полоски, высота к правому плечу такая же ввиду равнобедренности. Разве три равные высоты не гарантируют, что треугольник равносторонний? Или я что-то упустил?
← →
Sha © (2012-04-11 23:35) [119]
> MBo © (11.04.12 23:14) [118]
В теории все верно.
Практическому воплощению могут помешать 3 вещи
1 материал может растягиваться и тогда угол будет гулять
2 материал не растягивается и из большего шага трудно будет
перейти к правильному
3 материал не растягивается и если шаг меньше нужного,
то небольшой зазор между одним краем ленты и линейкой
можно исправить только ценой зазора между витками.
Т.е. получается, что шаг надо угадать сразу.
← →
MBo © (2012-04-11 23:49) [120]
Ну на практике даже и с предварительной разметкой качественный флексагон второго порядка может не с первого раза получиться.
Всё-таки построение фигур с помощью искусственно ограниченных средств подразумевает условность идеальной точности.
← →
Inovet © (2012-04-11 23:50) [121]
> [119] Sha © (11.04.12 23:35)
> то небольшой зазор между одним краем ленты и линейкой
> можно исправить только ценой зазора между витками.
Так атрэзать, всё равно рэзать надо.
← →
Sha © (2012-04-12 00:03) [122]
> MBo © (11.04.12 23:49) [120]
> условность идеальной точности.
Тут даже не ясно с чего мы начинаем.
Примерно так: кладем линейку на бумажную полоску, загибаем концы
полоски навстречу друг другу, если стороны полоски не соприкасаются,
то повторяем процесс…
> Inovet © (11.04.12 23:50) [121]
просто много раз приходилось наматывать полоску не линейку или трубку,
не просто это сделать красиво
← →
MBo © (2012-04-12 05:32) [123]
Блин, у меня уже полтретьего ночи было, жена заинтересовалась рваньём бумажек, объяснял, что я не просто так, а детство вспомнил, гексагексафлексагон собираю 🙂
С накруткой на слесарную линейку вышло довольно коряво. Выворачивается, но всё друг за друга зацепляется, бумага для принтера — быстро рвётся.
Выворачивается, но всё друг за друга зацепляется, бумага для принтера — быстро рвётся.
← →
MBo © (2012-04-12 05:39) [124]
>Тут даже не ясно с чего мы начинаем
Вроде это не вызвало особых затруднений — накидываем виток-два ленты на линейку, подтягиваем не до излома, чуть шевелим вправо-влево до совмещения.
В детстве я, насколько помню, использовал бумагу для слепых (по плотности похоже на перфокарту, но другой консистенции, не хрупкая), у нас была пачка для поделок. Не накручивал, конечно, а предварительную разметку делал. Задним концом иглы двойные швы нужной толщины проминал.
← →
oldman © (2012-04-12 08:05) [125]
> уже полтретьего ночи было, жена заинтересовалась рваньём
> бумажек
А могла и санитаров позвать )))
← →
Sha © (2012-04-12 08:44) [126]
>> что надо добавить в условия задачи, чтобы она имела решение?
> oldman © (11. 04.12 21:58) [113]
04.12 21:58) [113]
> естественно, циркуль!
По условию задачи у ТС нет его. Если есть циркуль, то линейка не нужна.
Решение [115] вполне строгое.
С одним дополнительным требованием, меньше требования наличия циркуля.
← →
oldman © (2012-04-12 08:52) [127]
> Линейка от линия, а деления уже для измерения длины линии.
Линия бесконечна, можно не измерять
← →
Inovet © (2012-04-12 08:55) [128]
> [127] oldman © (12.04.12 08:52)
> Линия бесконечна, можно не измерять
Отрезка линии, но ножниц тоже нет.
← →
han_malign (2012-04-12 09:48) [129]
Вот зараза ведь. 1/2:
1/2:
Нумеруем вершины квадрата по часовой стрелке 1, 2, 3, 4.
Продолжим сторону 1-2 на единичный отрезок, получим точку 5.
На отрезке 1-4 отложим единичный отрезок от точки 4, получим точку 6.
Проведем прямую через точки 6 и 3, отложим на ней единичные отрезки
от точки 3 в обе стороны, получим точки 7 и 8.
Треугольник 7-5-8 равносторонний.
Треугольник 3-5-8 прямоугольный, с углами 90, 30, 60 градусов
Как начертить равнобедренный треугольник в круге. Рисуем треугольник в фотошопе
Как начертить треугольник?
Построение различных треугольников — обязательный элемент школьного курса геометрии. У многих это задание вызывает страх. Но на самом деле, все довольно просто. Далее в статье описано, как начертить треугольник любого типа с помощью циркуля и линейки.
Треугольники бывают
- разносторонние;
- равнобедренные;
- равносторонние;
- прямоугольные;
- тупоугольные;
- остроугольные;
- вписанные в окружность;
- описанные вокруг окружности.

Построение равностороннего треугольника
Равносторонним называется треугольник, у которого все стороны равны. Из всех видов треугольников, начертить равносторонний проще всего.
- С помощью линейки начертите одну из сторон, заданной длины.
- Измерьте ее длину с помощью циркуля.
- Поместите острие циркуля в один из концов отрезка и проведите окружность.
- Переставьте острие в другой конец отрезка и проведите окружность.
- У нас получилось 2 точки пересечения окружностей. Соединяя любую из них с краями отрезка, мы получаем равносторонний треугольник.
Построение равнобедренного треугольника
Данный тип треугольников можно построить по основанию и боковым сторонам.
Равнобедренным называется треугольник, у которого две стороны равны. Для того чтобы начертить равнобедренный треугольник по данным параметрам, необходимо выполнить следующие действия:
- С помощью линейки откладываем отрезок, равный по длине основанию.
 Обозначаем его буквами АС.
Обозначаем его буквами АС. - Циркулем измеряем необходимую длину боковой стороны.
- Рисуем из точки А, а затем из точки С, окружности, радиус которых равен длине боковой стороны.
- Получаем две точки пересечения. Соединив одну из них с точками А и С, получаем необходимый треугольник.
Построение прямоугольного треугольника
Треугольник, у которого один угол прямой, называют прямоугольным. Если нам даны катет и гипотенуза, начертить прямоугольный треугольник не составит труда. Его можно построить по катету и гипотенузе.
Построение тупоугольного треугольника по углу и двум прилегающим сторонам
Если один из углов треугольника тупой (больше 90 градусов), его называют тупоугольным. Чтобы начертить по указанным параметрам тупоугольный треугольник необходимо сделать следующее:
- С помощью линейки откладываем отрезок, равный по длине одной из сторон треугольника. Обозначим его буквами А и D.
- Если в задании уже нарисован угол, и вам необходимо начертить такой же, то на его изображении отложить два отрезка, оба конца которых лежат в вершине угла, а длина равняется указанным сторонам.
 Соедините полученные точки. У нас получился искомый треугольник.
Соедините полученные точки. У нас получился искомый треугольник. - Чтобы его перенести на свой чертеж, вам необходимо измерить длину третьей стороны.
Построение остроугольного треугольника
Остроугольный треугольник (все углы меньше 90 градусов) строится по тому же принципу.
- Нарисуйте две окружности. Центр одной из них лежит в точке D, а радиус равен длине третьей стороны, а у второй центр находится в точке А, а радиус равен длине указанной в задании стороны.
- Соедините одну из точек пересечения окружности с точками А и D. Искомый треугольник построен.
Вписанный треугольник
Для того чтобы начертить треугольник в окружности, нужно помнить теорему, в которой говорится, что центр описанной окружности лежит на пересечении серединных перпендикуляров:
У тупоугольного треугольника центр описанной окружности лежит за пределами треугольника, а у прямоугольного — на середине гипотенузы.
Чертим описанный треугольник
Описанный треугольник — это треугольник, в центре которого нарисована окружность, касающаяся всех его сторон. Центр вписанной окружности лежит на пересечении биссектрис. Для их построения необходимо:
Центр вписанной окружности лежит на пересечении биссектрис. Для их построения необходимо:
Построение вписанного в окружность правильного шестиугольника. Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой (фиг. 60, а).
Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг. 60, б), строим стороны 1 -6, 4-3, 4-5 и 7-2, после чего проводим стороны 5-6 и 3-2.
Построение вписанного в окружность равностороннего треугольника . Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля.
Рассмотрим два способа построения вписанного в окружность равностороннего треугольника.
Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, проведённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0-1-2 равен 30°, то для нахождения стороны
61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, проведённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0-1-2 равен 30°, то для нахождения стороны
1-2 достаточно построить по точке 1 и стороне 0-1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1-2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2-3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника.
Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вершины через одну, то получится равносторонний треугольник.
Для построения треугольника (фиг. 61, б) намечаем на диаметре вершину-точку 1 и проводим диаметральную линию 1-4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника.
Полученные точки будут двумя другими вершинами искомого треугольника.
Построение квадрата, вписанного в окружность . Это построение можно выполнить при помощи угольника и циркуля.
Первый способ основан на том, что диагонали квадрата пересекаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные стороны квадрата 4-1 и 3-2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1-2 и 4-3.
Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра (фиг. 62, б). Намечаем на концах двух взаимно перпендикулярных диаметров точки А, В и С и из них радиусом у описываем дуги до взаимного их пересечения.
Далее через точки пересечения дуг проводим вспомогательные прямые, отмеченные на фигуре сплошными линиями. Точки их пересечения с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.
Точки их пересечения с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.
Построение вписанного в окружность правильного пятиугольника.
Чтобы вписать в окружность правильный пятиугольник (фиг. 63), производим следующие построения.
Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4.![]() Найденные точки последовательно соединяем между собой.
Найденные точки последовательно соединяем между собой.
Построение правильного пятиугольника по данной его стороне.
Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую.
Получим точку 1-вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведёнными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.
Построение вписанного в окружность правильного семиугольника.
Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проводим из полюса F через чётные деления вертикального диаметра лучи, пересечение которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проводим из полюса F через чётные деления вертикального диаметра лучи, пересечение которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
Приведённый способ годен для построения правильных многоугольников с любым числом сторон.
Деление окружности на любое число равных частей можно производить также, пользуясь данными табл. 2, в которой приведены коэффициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.
Равносторонний треугольник в фотошопе рисуется при помощи векторных объектов. Можно нарисовать закрашенный треугольник, можно треугольник с рамкой. Выбираем рисование многоугольников (Polygon tool).
Выбираем рисование многоугольников (Polygon tool).
Рисование многоугольников (Polygon tool)
Выбираем фигуры (гор. клавиша U ), затем Polygon tool (Инструмент Многоугольник), см. скриншот ниже.
Устанавливаем свойство «Fill Pixels».
Выбираем цвет заливки треугольника (первый цвет в панели инструментов), рисуем мышкой треугольник.
Треугольник с рамкой
Треугольник следует рисовать на новом пустом слое , без какой-либо заливки. Создать новый слой можно одновременным нажатием клавиш Alt + Ctrl + Shift + N .
Устанавливаем значение «Paths» (по-русски пути).
Рисуем мышкой треугольник.
Преобразуем векторный треугольник в выделение (Select), нажатием клавиш Ctrl + Enter .
Закрашиваем выделение (в данном случае белым цветом).
Alt + ← BackSpace — первый выбранный цвет.
Ctrl + ← BackSpace — второй выбранный цвет.
В свою бытность «чайником», я столкнулся с необходимостью нарисовать треугольник в Фотошопе. Тогда с этой задачей без посторонней помощи мне справиться не удалось.
Тогда с этой задачей без посторонней помощи мне справиться не удалось.
Оказалось, что все не настолько сложно, как могло показаться на первый взгляд. В этом уроке я поделюсь с Вами опытом в рисовании треугольников.
Существуют два (известных мне) способа.
Первый способ позволяет изобразить равносторонний треугольник. Для этого нам нужен инструмент под названием «Многоугольник» . Находится он в разделе фигур на правой панели инструментов.
Этот инструмент позволяет рисовать правильные многоугольники с заданным числом сторон. В нашем случае их (сторон) будет три.
После настройки цвета заливки
ставим курсор на холст, зажимаем левую кнопку мыши и рисуем нашу фигуру. В процессе создания треугольник можно вращать, не отпуская кнопку мыши.
Полученный результат:
Кроме того, можно нарисовать фигуру без заливки, но с контуром. Линии контура настраиваются в верхней панели инструментов. Там же настраивается и заливка, вернее ее отсутствие.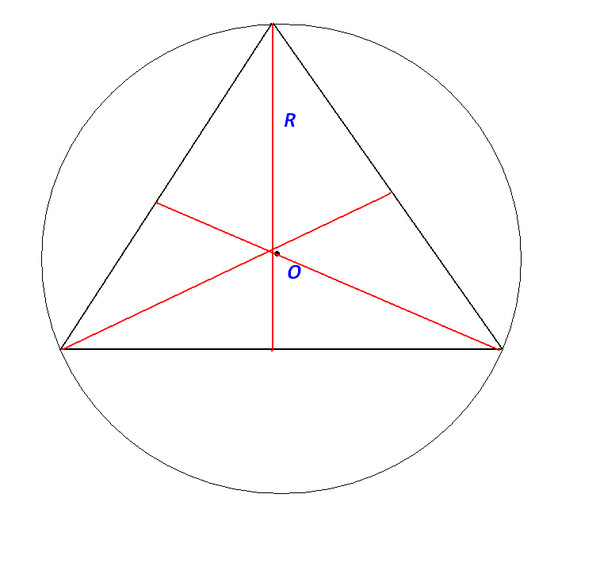
У меня получились такие треугольники:
С настройками можно экспериментировать, добиваясь нужного результата.
Следующий инструмент для рисования треугольников – «Прямолинейное лассо» .
Этот инструмент позволяет рисовать треугольники с любыми пропорциями. Давайте попробуем изобразить прямоугольный.
Для прямоугольного треугольника нам понадобится точно нарисовать прямой (кто бы мог подумать…) угол.
Воспользуемся направляющими. Как работать с направляющими линиями в Фотошопе, читайте в этой статье .
Итак, статью прочитали, тянем направляющие. Одну вертикальную, другую горизонтальную.
Чтобы выделение «притягивалось» к направляющим, включаем функцию привязки.
Затем кликаем правой кнопкой мыши внутри выделения и выбираем, в зависимости от потребностей, пункты контекстного меню «Выполнить заливку» или «Выполнить обводку» .
Цвет заливки настраивается следующим образом:
Для обводки также можно настроить ширину и расположение.
Получаем следующие результаты:
Заливка.
Для получения острых углов обводку нужно выполнять «Внутри» .
После снятия выделения (CTRL+D ) получаем готовый прямоугольный треугольник.
Вот такие два простейших способа рисования треугольников в программе Фотошоп.
Как нарисовать треугольник на листе чтобы вырезать. Как нарисовать несуществующий объемный треугольник поэтапно. Построение остроугольного треугольника
Как нарисовать треугольник? Этому учат в процессе изучения геометрии в школе. Чтобы задание было выполнено правильно, важно точно знать, какой треугольник необходимо изобразить: равносторонний, равнобедренный или же вписанный. Правилам начертания этих фигур будет посвящена данная статья.
Как рисовать треугольник с равными сторонами?
Как нарисовать треугольник, стороны у которого равны? Для этого можно воспользоваться одним из трех методов.
Такая фигура имеет три одинаковые по длине стороны, связанные тремя углами равной ширины. Это может быть сложным для рисования треугольника вручную. Поэтому можно использовать круглый объект для выделения углов.
Это может быть сложным для рисования треугольника вручную. Поэтому можно использовать круглый объект для выделения углов.
Варианты создания фигуры
Обязательно используйте линейку и один из представленных ниже способов:
- Применение циркуля: надо начертить ровную линию. Проведите карандаш вдоль прямого края бумаги. Этот сегмент линии образует одну из сторон. А это означает, что нужно будет чертить вторую и третью линии одинаковой длины, каждая из которых достигает точки под углом 60° от первой линии. Удостоверьтесь, что достаточно места для рисования всех трех сторон!
- Разделите сегмент циркулем. Вставьте карандаш и убедитесь, что он острый! Поместите точку циркуля на один конец сегмента и установите карандаш на другую. Опишите дугу. Не изменяйте установленную «ширину» инструмента от точки циркуля до точки карандаша. Нарисуйте вторую дугу, чтобы она пересекала первую дугу, которую уже нарисовали. Отметьте точку, в которой пересекаются две дуги. Это вершина (верхняя точка) треугольника.
 Он должен лежать в точном центре сегмента линии, который нарисовали. Теперь можете сделать две прямые линии, ведущие к этой точке: по одному от каждого конца «нижнего» сегмента линии. Закончите треугольник. Далее с помощью линейки надо нарисовать еще два сегмента прямой линии — это стороны в треугольнике. Подключите каждый конец исходного сегмента линии к точке, в которой пересекаются дуги. Чтобы закончить работу, сотрите дуги, которые нарисовали, так, чтобы остался только треугольник.
Он должен лежать в точном центре сегмента линии, который нарисовали. Теперь можете сделать две прямые линии, ведущие к этой точке: по одному от каждого конца «нижнего» сегмента линии. Закончите треугольник. Далее с помощью линейки надо нарисовать еще два сегмента прямой линии — это стороны в треугольнике. Подключите каждый конец исходного сегмента линии к точке, в которой пересекаются дуги. Чтобы закончить работу, сотрите дуги, которые нарисовали, так, чтобы остался только треугольник. - Использование объекта с круглой базой: этот совет подойдет для построения дуги. Предложенный метод по сути такой же, как с использованием циркуля.
Указанные советы помогут выяснить, как нарисовать равносторонний треугольник.
Равнобедренный треугольник представляет собой фигуру с двумя равными сторонами и двумя равными углами. Если знаете длину, основание и высоту стороны, это можно сделать только с линейкой и циркулем (или просто циркулем, если заданы размеры).
Как нарисовать равнобедренный треугольник:
- Учитывая все боковые длины.
 Чтобы использовать этот метод, важно знать длину основания треугольника и длину двух равных сторон.
Чтобы использовать этот метод, важно знать длину основания треугольника и длину двух равных сторон. - Учитывая две равные стороны и угол между ними. Чтобы использовать этот метод, нужно знать длину двух равных сторон и измерение угла между этими двумя сторонами.
- Учитывая базовые и смежные углы — необходимо знать длину базы, градусы двух углов, смежных с основанием. Помните, что два угла, смежные с основанием равнобедренного треугольника, будут равны.
- Основа и высота. Нужно знать длину основания треугольника, а также высоту этой геометрической фигуры.
Как нарисовать вписанный треугольник? Выберите круглый объект. Используйте предмет с круглым основанием. Выбор компакт-диска станет хорошим вариантом. Но можно взять и другой объект нужного размера. Для этого метода свойственно, что длина каждой стороны равносторонней геометрической фигуры с тремя углами будет равна размерам радиуса (половине диаметра) круга.
Как нарисовать треугольник, если используете компакт-диск? Представьте себе равносторонний треугольник, который вписывается в верхнюю правую часть компакт-диска. Надо начертить первую из сторон. Радиус круглого объекта — расстояние на полпути до получения желаемого результата. Удостоверьтесь, что линии нарисованы ровно.
С помощью линейки просто выполните измерения диаметра объекта и нарисуйте линию на половину длины. Если ее нет, поместите круглый объект на бумагу, затем тщательно проведите по окружности карандашом. Удалите объект — должен быть идеальный круг. Используйте прямой край, чтобы нарисовать линию через точный центр круга: точку, которая полностью равноудалена от любой точки по окружности круга.
Используйте круглый объект для создания дуги. Поместите объект по отрезку линии, с краем круга, расположенным на одном конце линии. Для обеспечения точности убедитесь, что линия проходит четко через центр круга. Используйте карандаш, чтобы начертить дугу — это четверть пути по окружности.
Начертите еще одну дугу. Теперь сдвиньте круглый объект так, чтобы край касался другого конца сегмента линии.
Подведем итоги
Как начертить треугольник?
Построение различных треугольников — обязательный элемент школьного курса геометрии. У многих это задание вызывает страх. Но на самом деле, все довольно просто. Далее в статье описано, как начертить треугольник любого типа с помощью циркуля и линейки.
Треугольники бывают
- разносторонние;
- равнобедренные;
- равносторонние;
- прямоугольные;
- тупоугольные;
- остроугольные;
- вписанные в окружность;
- описанные вокруг окружности.
Построение равностороннего треугольника
Равносторонним называется треугольник, у которого все стороны равны. Из всех видов треугольников, начертить равносторонний проще всего.
- С помощью линейки начертите одну из сторон, заданной длины.
- Измерьте ее длину с помощью циркуля.
- Поместите острие циркуля в один из концов отрезка и проведите окружность.
- Переставьте острие в другой конец отрезка и проведите окружность.
- У нас получилось 2 точки пересечения окружностей. Соединяя любую из них с краями отрезка, мы получаем равносторонний треугольник.
Построение равнобедренного треугольника
Данный тип треугольников можно построить по основанию и боковым сторонам.
Равнобедренным называется треугольник, у которого две стороны равны. Для того чтобы начертить равнобедренный треугольник по данным параметрам, необходимо выполнить следующие действия:
- С помощью линейки откладываем отрезок, равный по длине основанию. Обозначаем его буквами АС.
- Циркулем измеряем необходимую длину боковой стороны.
- Рисуем из точки А, а затем из точки С, окружности, радиус которых равен длине боковой стороны.
- Получаем две точки пересечения. Соединив одну из них с точками А и С, получаем необходимый треугольник.
Построение прямоугольного треугольника
Треугольник, у которого один угол прямой, называют прямоугольным. Если нам даны катет и гипотенуза, начертить прямоугольный треугольник не составит труда. Его можно построить по катету и гипотенузе.
Построение тупоугольного треугольника по углу и двум прилегающим сторонам
Если один из углов треугольника тупой (больше 90 градусов), его называют тупоугольным. Чтобы начертить по указанным параметрам тупоугольный треугольник необходимо сделать следующее:
- С помощью линейки откладываем отрезок, равный по длине одной из сторон треугольника. Обозначим его буквами А и D.
- Если в задании уже нарисован угол, и вам необходимо начертить такой же, то на его изображении отложить два отрезка, оба конца которых лежат в вершине угла, а длина равняется указанным сторонам. Соедините полученные точки. У нас получился искомый треугольник.
- Чтобы его перенести на свой чертеж, вам необходимо измерить длину третьей стороны.
Построение остроугольного треугольника
Остроугольный треугольник (все углы меньше 90 градусов) строится по тому же принципу.
- Нарисуйте две окружности. Центр одной из них лежит в точке D, а радиус равен длине третьей стороны, а у второй центр находится в точке А, а радиус равен длине указанной в задании стороны.
- Соедините одну из точек пересечения окружности с точками А и D. Искомый треугольник построен.
Вписанный треугольник
Для того чтобы начертить треугольник в окружности, нужно помнить теорему, в которой говорится, что центр описанной окружности лежит на пересечении серединных перпендикуляров:
У тупоугольного треугольника центр описанной окружности лежит за пределами треугольника, а у прямоугольного — на середине гипотенузы.
Чертим описанный треугольник
Описанный треугольник — это треугольник, в центре которого нарисована окружность, касающаяся всех его сторон. Центр вписанной окружности лежит на пересечении биссектрис. Для их построения необходимо:
Построение вписанного в окружность правильного шестиугольника. Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой (фиг. 60, а).
Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг. 60, б), строим стороны 1 -6, 4-3, 4-5 и 7-2, после чего проводим стороны 5-6 и 3-2.
Построение вписанного в окружность равностороннего треугольника . Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля.
Рассмотрим два способа построения вписанного в окружность равностороннего треугольника.
Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, проведённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0-1-2 равен 30°, то для нахождения стороны
1-2 достаточно построить по точке 1 и стороне 0-1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1-2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2-3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника.
Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вершины через одну, то получится равносторонний треугольник.
Для построения треугольника (фиг. 61, б) намечаем на диаметре вершину-точку 1 и проводим диаметральную линию 1-4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника.
Построение квадрата, вписанного в окружность . Это построение можно выполнить при помощи угольника и циркуля.
Первый способ основан на том, что диагонали квадрата пересекаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные стороны квадрата 4-1 и 3-2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1-2 и 4-3.
Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра (фиг. 62, б). Намечаем на концах двух взаимно перпендикулярных диаметров точки А, В и С и из них радиусом у описываем дуги до взаимного их пересечения.
Далее через точки пересечения дуг проводим вспомогательные прямые, отмеченные на фигуре сплошными линиями. Точки их пересечения с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.
Построение вписанного в окружность правильного пятиугольника.
Чтобы вписать в окружность правильный пятиугольник (фиг. 63), производим следующие построения.
Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой.
Построение правильного пятиугольника по данной его стороне.
Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую.
Получим точку 1-вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведёнными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.
Построение вписанного в окружность правильного семиугольника.
Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проводим из полюса F через чётные деления вертикального диаметра лучи, пересечение которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
Приведённый способ годен для построения правильных многоугольников с любым числом сторон.
Деление окружности на любое число равных частей можно производить также, пользуясь данными табл. 2, в которой приведены коэффициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.
Сегодня мы расскажем вам, как легко прослыть художником среди своих друзей или показать девушке, какой ты весь разносторонний (о, они это любят!). Итак начнем!
Нам понадобится: 50 грамм для храбрости, 2 карандаша (один жесткий, другой мягкий), лист бумаги, линейка и ластик. Да начнется магия!
Шаг 1.
Рисуем обычный треугольник – он не должен являть собой венец геометрической мысли: просто соедини три линии.
Шаг 2.
Теперь нарисуй внутри линии, прямо как у нас. Старайся сделаить их одной ширины, ты ж не рукожоп, как мы!
Шаг 3.
Нарисовал? Молодец! Теперь нарисуй еще, как мы показали. Мы знаем, ты устал, но скоро все закончится.
Шаг 4.
Спили вершины треугольника как на рисунке.
Шаг 5.
Теперь обведи все линии, которые выделили мы, жирным карандашом, пером или гелевой ручкой. Или маркером. Или фломастером. Может надо бутерброд забацать?
Шаг 6.
Сотри все ненужное. Мы близко к цели, видишь?
Шаг 7.
Тут мы обратились к богам Олимпа и они нарисовали нам тени. Ты рисуй сам.
Шаг 8.
Теперь можно вырезать наше творение лезвием или ножницами и ломать хрупкие разумы своих друзей. Этот треугольник входит в число фигур, которые геометрически не имеют право на существование или по по-другому “несуществующие фигуры”.
Надеемся, тебе понравилось, ибо мы старались и крали этот урок рисования несуществующего треугольника поэтапно. И теперь тебе лучше нарисовать героев
- карандаш,
- стерка,
- лист бумаги,
- пошаговая интсрукция.
- сперва изобразить треугольник,
- затем все его грани, начиная с внешней,
- заштриховать участки свето-тени, чтобы придать объем фигуре,
- при необходимости разукрасить объект.
Нарисуем треугольник 3D с оптической иллюзией поэтапно.
Сначала рисуем обыкновенный равносторонний треугольник карандашом. Внутри него, параллельно каждой из сторон, проводим по линии на равном расстоянии так, что внутри треугольника получается еще один треугольник.
Вновь проводим параллельные линии, отступив на то же расстояние и рисуя еще один меньший треугольник внутри первых двух.
Жирно проводим контур по периметру сторон большого треугольника, обводя его стороны, но срезая острые углы.
Проводим еще один контур из двух прямых, повторяющих одну сторону среднего и одну сторону меньшего треугольников внутри большого, как показано на рисунке.
Проводим еще по контуру, — две прямые, повторяя стороны треугольников, как на рисунке.
И еще раз делаем те же действия, с другими сторонами, — обводим жирным контуром две прямые, как на рисунке.
Лишние линии убираем. Вот получился 3D треугольник, пока не закрашенный.
Заштриховываем стороны треугольника, придавая изображению объемность. Рисунок готов, треугольник 3D иллюзия .
Посмотрим видео, как рисовать оптическую иллюзию треугольник 3D.
Нарисовать треугольную иллюзию несложно, особенно если есть пошаговая инструкция. Понадобится карандаш, бумага и желательно линейка, с ней будет аккуратнее рисунок. По шагам повторить все действия, а потом затенить с помощью растушевки нужные места.
Как нарисовать треугольник … Да, при этом не простой, а очень сложный с множеством треугольников внутри. Чтобы все его грани проглядывались, а на бумаге он выглядел реалистичным и четким.
Для этого нам потребуется:
Процесс рисования:
Получается необычайная фигура с множеством завихрений. Смотрится немного завораживающе, так как разум пытается продлить все линии и уловить суть.
Видео-инструкция, как нарисовать треугольник на бумаге:
Треугольник Пенроуза или невозможные фигуры. Был придуман в 1953 году художником Оскаром Реутерсвардом. Первый треугольник был сделан из кубиков.
Уникальность этого объекта в том, что посмотрев на прямые палки под определнным углом можно четко увидеть треугольник. Как например вот на этом памятнике.
Узнаем как правильно нарисовать треугольник: этапы выполнения задания
Как нарисовать треугольник? Этому учат в процессе изучения геометрии в школе. Чтобы задание было выполнено правильно, важно точно знать, какой треугольник необходимо изобразить: равносторонний, равнобедренный или же вписанный. Правилам начертания этих фигур будет посвящена данная статья.
Как рисовать треугольник с равными сторонами?
Как нарисовать треугольник, стороны у которого равны? Для этого можно воспользоваться одним из трех методов.
Такая фигура имеет три одинаковые по длине стороны, связанные тремя углами равной ширины. Это может быть сложным для рисования треугольника вручную. Поэтому можно использовать круглый объект для выделения углов.
Варианты создания фигуры
Обязательно используйте линейку и один из представленных ниже способов:
- Применение циркуля: надо начертить ровную линию. Проведите карандаш вдоль прямого края бумаги. Этот сегмент линии образует одну из сторон. А это означает, что нужно будет чертить вторую и третью линии одинаковой длины, каждая из которых достигает точки под углом 60° от первой линии. Удостоверьтесь, что достаточно места для рисования всех трех сторон!
- Разделите сегмент циркулем. Вставьте карандаш и убедитесь, что он острый! Поместите точку циркуля на один конец сегмента и установите карандаш на другую. Опишите дугу. Не изменяйте установленную «ширину» инструмента от точки циркуля до точки карандаша. Нарисуйте вторую дугу, чтобы она пересекала первую дугу, которую уже нарисовали. Отметьте точку, в которой пересекаются две дуги. Это вершина (верхняя точка) треугольника. Он должен лежать в точном центре сегмента линии, который нарисовали. Теперь можете сделать две прямые линии, ведущие к этой точке: по одному от каждого конца «нижнего» сегмента линии. Закончите треугольник. Далее с помощью линейки надо нарисовать еще два сегмента прямой линии – это стороны в треугольнике. Подключите каждый конец исходного сегмента линии к точке, в которой пересекаются дуги. Чтобы закончить работу, сотрите дуги, которые нарисовали, так, чтобы остался только треугольник.
- Использование объекта с круглой базой: этот совет подойдет для построения дуги. Предложенный метод по сути такой же, как с использованием циркуля.
Указанные советы помогут выяснить, как нарисовать равносторонний треугольник.
Рекомендации по построению равнобедренного треугольника
Равнобедренный треугольник представляет собой фигуру с двумя равными сторонами и двумя равными углами. Если знаете длину, основание и высоту стороны, это можно сделать только с линейкой и циркулем (или просто циркулем, если заданы размеры).
Как нарисовать равнобедренный треугольник:
- Учитывая все боковые длины. Чтобы использовать этот метод, важно знать длину основания треугольника и длину двух равных сторон.
- Учитывая две равные стороны и угол между ними. Чтобы использовать этот метод, нужно знать длину двух равных сторон и измерение угла между этими двумя сторонами.
- Учитывая базовые и смежные углы – необходимо знать длину базы, градусы двух углов, смежных с основанием. Помните, что два угла, смежные с основанием равнобедренного треугольника, будут равны.
- Основа и высота. Нужно знать длину основания треугольника, а также высоту этой геометрической фигуры.
Вписанный треугольник
Как нарисовать вписанный треугольник? Выберите круглый объект. Используйте предмет с круглым основанием. Выбор компакт-диска станет хорошим вариантом. Но можно взять и другой объект нужного размера. Для этого метода свойственно, что длина каждой стороны равносторонней геометрической фигуры с тремя углами будет равна размерам радиуса (половине диаметра) круга.
Как нарисовать треугольник, если используете компакт-диск? Представьте себе равносторонний треугольник, который вписывается в верхнюю правую часть компакт-диска. Надо начертить первую из сторон. Радиус круглого объекта – расстояние на полпути до получения желаемого результата. Удостоверьтесь, что линии нарисованы ровно.
С помощью линейки просто выполните измерения диаметра объекта и нарисуйте линию на половину длины. Если ее нет, поместите круглый объект на бумагу, затем тщательно проведите по окружности карандашом. Удалите объект – должен быть идеальный круг. Используйте прямой край, чтобы нарисовать линию через точный центр круга: точку, которая полностью равноудалена от любой точки по окружности круга.
Используйте круглый объект для создания дуги. Поместите объект по отрезку линии, с краем круга, расположенным на одном конце линии. Для обеспечения точности убедитесь, что линия проходит четко через центр круга. Используйте карандаш, чтобы начертить дугу – это четверть пути по окружности.
Начертите еще одну дугу. Теперь сдвиньте круглый объект так, чтобы край касался другого конца сегмента линии.
Подведем итоги
В статье были предоставлены рекомендации, как нарисовать треугольник равносторонний, равнобедренный и вписанный в окружность.
Построение правильных многоугольников. Построение правильных вписанных многоугольников
Для начала разберемся с том, какую окружность можно назвать вписанной в треугольник. Это вам не просто взять и нарисовать в треугольнике фигуру. Ту окружность можно назвать вписанной в треугольник, у которой есть три точки на дуге, соприкасающихся с тремя гранями треугольника.
Из этого определения следует, что в каждый треугольник можно вписать лишь одну единственную возможную окружность, центр которой находится на пересечении трех биссектрис внутренних углов данного треугольника.
Теперь подробнее о том, как вписать окружность в треугольник:
- Находим вершины треугольника, как помним, их три.
- Из каждой вершины необходимо с помощью циркуля провести окружности, можно произвольного радиуса.
- Теперь найдите точку пересечения двух окружностей (эта точка должна находиться на стороне треугольника, которая противоположна делимому углу) и соединяем с делимым углом.
- Такую операцию необходимо провести с каждым из трех углов. У вас получатся в результате три пересекающиеся биссектрисы.
- Центр окружности вписанной в треугольник будет находиться в точки пересечения его биссектрис.
- Далее при помощи циркуля рисуем окружность с центром в полученной точке.
Как вписать треугольник в окружность
Вписанным в окружность треугольником называют треугольник, у которого три вершины соприкасаются с окружностью. Тогда окружность называют описанной вокруг треугольника.
Из этого следует, что радиус этой окружности — это отрезок, соединяющий центр описанной окружности и вершину треугольника. Поэтому для того, чтобы вписать треугольник в окружность необходимо обозначить три точки на окружности и соединить их отрезками.
Внимание, только СЕГОДНЯ!
ДРУГОЕ
Часто в геометрии приходится сталкиваться с описанными окружностями и их радиусами. Это ведет к простому вопросу: как…
Как начертить треугольник?Построение различных треугольников — обязательный элемент школьного курса геометрии. У многих…
Окружность считается вписанной в границы правильного многоугольника, в случае, если лежит внутри него, касаясь при этом…
Для того чтобы найти координаты вершины равностороннего треугольника, если известны координаты двух других его вершин,…
Как разделить окружность на части?Для того чтобы разделить отрезок или угол на равные части, особых навыков не…
Чему равен радиус описанной окружности?Описанной окружностью многоугольника называется такая окружность, которая…
Делить окружность на равное количество частей — это не пустое занятие, нужное лишь для того, чтобы усложнить вам жизнь…
Кто-то из нас математику в школе просто прогуливал, кто-то проболел, а кто-то подзабыл за давностью школьных лет, но…
Диаметром окружности называют отрезок прямой, которая соединяет две наиболее удаленные друг от друга точки окружности,…
Каждый школьник в начальных классах пытался узнать, что такое треугольник и что такое периметр ттреугольника. Попробуем…
Задачи на геометрические построения весьма хорошо развивают пространственное и логическое мышление и потому являются одной из основных частей школьной программы обучения. Как и в любой предметной области, существуют типовые и нетиповые задачи. К типовым задачам можно отнести, например, построение равностороннего треугольника . В процессе построения треугольник оказывается вписанным в окружность . Но как быть, если нужно вписать равносторонний треугольник в окружность , которая уже построена?
Вам понадобится
- — линейка;
- — карандаш;
- — циркуль.
Инструкция
Постройте хорду заданной окружности. При помощи линейки начертите отрезок так, чтобы он пересекал окружность в двух точках. Пусть это будут точки A и B. Желательно, чтобы эти точки были расположены на достаточном удалении друг от друга.
Постройте перпендикуляр, пересекающий отрезок AB и делящий его точкой пересечения на две равные части. Установите между ножками циркуля расстояние, несколько меньшее длины отрезка AB, но заведомо большее длины половины этого отрезка. Установите иглу циркуля в точку A. Вычертите окружность . Установите иглу циркуля в точку B. Вычертите еще одну окружность . Проведите отрезок через точки пересечения вычерченных окружностей так, чтобы он пересек отрезок AB в одной точке (пусть это будет точка C) и первоначальную окружность в двух точках (пусть это будут точки D и E).
Постройте перпендикуляр, пересекающий отрезок DE и делящий его точкой пересечения на две равные части способом, аналогичным описанному во втором шаге. Пусть построенный отрезок пересекает окружность в точках F и G, а отрезок DE в точке O. Точка O будет являться центром окружности.
Установите расстояние между ножками циркуля равным радиусу окружности. Поместите иглу циркуля в точку D. Поместите конец другой ножки циркуля в точку O.
Найдите точки двух углов равностороннего треугольника , вписанного в окружность . Не изменяя положения ножки циркуля с иглой (в точке D) и расстояния между ножками циркуля, установленные на предыдущем шаге, начертите окружность . Эта окружность пересечет первоначальную окружность в двух точках. Пусть это будут точки H и I.
Впишите равносторонний треугольник в окружность . Попарно соедините отрезками точки E, H и I. Треугольник со сторонами EH, HI и EI будет равносторонним и вписанным в заданную изначально окружность .
Согласно определению, если все вершины многоугольника принадлежат окружности, он называется «вписанным». Построить на бумаге такую фигуру несложно, особенно если все составляющие ее стороны имеют одинаковую длину. Для правильного треугольника такое построение может быть выполнено несколькими способами, а выбор наиболее удобного зависит от имеющихся инструментов.
Вам понадобится
- Бумага, карандаш, циркуль, линейка, калькулятор, транспортир.
Инструкция
Если у вас есть возможность использовать при построении транспортир, начните с выбора произвольной точки на окружности, которая должна стать одной из вершин правильного треугольника . Обозначьте ее, например, буквой А.
Начертите вспомогательный отрезок, соединив точку А с центром окружности. К этому отрезку приложите транспортир таким образом, чтобы нулевое деление совпало с центром круга, и поставьте вспомогательную точку у отметки 120°. Через эту точку проведите еще один вспомогательный отрезок с началом в центре круга и окончанием на пересечении с окружностью . Точку пересечения обозначьте буквой В — это вторая вершина вписанного треугольника .
Повторите предыдущий шаг, но транспортир прикладывайте ко второму вспомогательному отрезку, а точку пересечения с окружностью обозначьте буквой С. Больше транспортир не понадобится.
Соедините точки А и В, В и С, С и А. На этом построение правильного треугольника вписанного в окружность будет завершено.
Если транспортира нет, но есть циркуль и калькулятор, то начните с вычисления длины стороны треугольника . Вы наверняка знаете, что ее можно выразить через радиус описанной окружности, умножив его на отношение тройки к квадратному корню из тройки, то есть примерно на 1,732050807568877. Округлите это число до нужной степени точности и умножьте на радиус круга.
Отметьте произвольную точку на окружности и обозначьте ее буквой А — это первая вершина правильного треугольника .
Отложите на циркуле найденную на пятом шаге длину стороны треугольника и начертите вспомогательный круг с центром в точке А. Точки пересечения двух окружностей обозначьте буквами В и С — это две другие вершины вписанного в круг правильного треугольника .
Соедините точки А и В, В и С, С и А и построение будет завершено.
Внимание, только СЕГОДНЯ!
Инструкция
Способ первый. Если вы хотите начертить в окружности правильный треугольник, из ее центра необходимо провести 3 отрезка ОВ, ОС и ОМ под углом 120о друг к другу. Точка О будет совпадать с центром окружности, а точки В, С и М будут находиться на самой окружности. Соедините эти точки между собой и получите равносторонний треугольник ВСМ.
Способ второй. Вам необходимо начертить в окружности треугольник, зная только две его стороны. Выберите на окружности точку О, которая будет являться вершиной треугольника АОС, а известные стороны будут АО и ОС. Из точки О отмерьте отрезок ОА так, чтобы точка А находилась на окружности. Таким же способом начертите отрезок ОС. Соединив точки А и С, получите необходимый треугольник.
Способ третий. Необходимо начертить в окружности треугольник, зная одну сторону и угол, прилегающий к этой стороне. Допустим, что в треугольнике АВС известна сторона АВ и угол ВАС. Начертите отрезок АВ так, чтобы точки А и В лежали на окружности, затем отмерьте угол ВАС и проведите отрезок АС так, чтобы точка С так же находилась на окружности. Соедините точки С и В для окончания построения треугольника.
Способ четвертый. Имеется некий треугольник ТМР. Необходимо нарисовать вокруг него окружность таким образом, чтобы он был вписан в окружность. Проведите перпендикуляры из середины каждой стороны треугольника. Точка их пересечения – точка О, будет являться центром окружности. Соедините точку О с любой вершиной треугольника ТМР, получившийся отрезок будет радиусом окружности.
Треугольник – это многоугольник, у которого три стороны. Равносторонним или правильным треугольником называют треугольник, у которого все стороны и углы равны. Рассмотрим, как можно нарисовать правильный треугольник.
Вам понадобится
- Линейка, циркуль.
Инструкция
Рассмотрим способ с линейкой и циркулем. Построим треугольник АВС. С помощью линейки начертите линию АВ, это будет одна из сторон треугольника , а точки А и В его вершинами.
С помощью циркуля нарисуйте еще одну окружность, центр которой будет в точке В, а радиус равен отрезку ВА.
Окружности будут пересекаться в двух точках. Выберите любую из них. Назовите ее С. Это будет третьей вершиной треугольника.
Соедините вершины между собой. Получившийся треугольник будет правильным. Убедитесь в этом, померив его стороны линейкой.
Рассмотрим способ построения правильного треугольника с помощью двух линеек. Начертите отрезок ОК, он будет одной из сторон треугольника, а точки О и К его вершинами.
С помощью линейки отмерьте отрезок ОЕ, равный отрезку ОК так, чтобы один его конец совпадал с точкой О, а другой находился на прямой m. Точка Е буде третьей вершиной треугольника.
Закончите построение треугольника, соединив точки Е и К. Проверьте правильность построения с помощью линейки.
Обратите внимание
Убедиться в том, что треугольник правильный можете с помощью транспортира, измерив углы.
Полезный совет
Равносторонний треугольник так же можно начертить на листе в клетку с помощью одной линейки. Вместо другой линейки используйте перпендикулярные линии.
Источники:
- Классификация треугольников. Равносторонние треугольники
- Что такое треугольник
- построение правильного треугольника
Если все вершины треугольник а лежат на одной окружности, то в этом случае он называется вписанным, а окружность, соответственно — описанной вокруг него. Построить треугольник на известной окружности очень просто, но как вписать треугольник в круг, если изначально существует именно он?
Вам понадобится
- — циркуль;
- — бумага;
- — карандаш;
- — линейка.
Инструкция
Для любого треугольника всегда возможно построить описанную окружность, поскольку эта кривая однозначно определяется тремя заданными точками.
Чтобы это обнаружить, достаточно предположить, что треугольник задан декартовыми координатами своих вершин. В этом случае радиус и координаты центра окружности, проходящей через все три точки, должны быть решениями системы из трех уравнений второй степени с тремя неизвестными.
Эта система будет иметь единственное решение в том случае, если заданные точки не лежат на одной прямой (в этом последнем случае она вовсе не имеет решений). Но три точки, лежащие на одной прямой, не могут быть вершинами треугольника, следовательно, этот случай можно даже не рассматривать. Итак, решение заведомо существует.
Построение вписанного в окружность правильного шестиугольника. Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой (фиг. 60, а).
Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг. 60, б), строим стороны 1 -6, 4-3, 4-5 и 7-2, после чего проводим стороны 5-6 и 3-2.
Построение вписанного в окружность равностороннего треугольника . Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля.
Рассмотрим два способа построения вписанного в окружность равностороннего треугольника.
Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, проведённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0-1-2 равен 30°, то для нахождения стороны
1-2 достаточно построить по точке 1 и стороне 0-1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1-2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2-3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника.
Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вершины через одну, то получится равносторонний треугольник.
Для построения треугольника (фиг. 61, б) намечаем на диаметре вершину-точку 1 и проводим диаметральную линию 1-4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника.
Построение квадрата, вписанного в окружность . Это построение можно выполнить при помощи угольника и циркуля.
Первый способ основан на том, что диагонали квадрата пересекаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные стороны квадрата 4-1 и 3-2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1-2 и 4-3.
Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра (фиг. 62, б). Намечаем на концах двух взаимно перпендикулярных диаметров точки А, В и С и из них радиусом у описываем дуги до взаимного их пересечения.
Далее через точки пересечения дуг проводим вспомогательные прямые, отмеченные на фигуре сплошными линиями. Точки их пересечения с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.
Построение вписанного в окружность правильного пятиугольника.
Чтобы вписать в окружность правильный пятиугольник (фиг. 63), производим следующие построения.
Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой.
Построение правильного пятиугольника по данной его стороне.
Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую.
Получим точку 1-вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведёнными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.
Построение вписанного в окружность правильного семиугольника.
Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проводим из полюса F через чётные деления вертикального диаметра лучи, пересечение которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
Приведённый способ годен для построения правильных многоугольников с любым числом сторон.
Деление окружности на любое число равных частей можно производить также, пользуясь данными табл. 2, в которой приведены коэффициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.
Построение различных треугольников — обязательный элемент школьного курса геометрии. У многих это задание вызывает страх. Но на самом деле, все довольно просто. Далее в статье описано, как начертить треугольник любого типа с помощью циркуля и линейки.
- разносторонние;
- равнобедренные;
- равносторонние;
- прямоугольные;
- тупоугольные;
- остроугольные;
- вписанные в окружность;
- описанные вокруг окружности.
Построение равностороннего треугольника
Равносторонним называется треугольник, у которого все стороны равны. Из всех видов треугольников, начертить равносторонний проще всего.
- С помощью линейки начертите одну из сторон, заданной длины.
- Измерьте ее длину с помощью циркуля.
- Поместите острие циркуля в один из концов отрезка и проведите окружность.
- Переставьте острие в другой конец отрезка и проведите окружность.
- У нас получилось 2 точки пересечения окружностей. Соединяя любую из них с краями отрезка, мы получаем равносторонний треугольник.
Построение равнобедренного треугольника
Данный тип треугольников можно построить по основанию и боковым сторонам.
Равнобедренным называется треугольник, у которого две стороны равны. Для того чтобы начертить равнобедренный треугольник по данным параметрам, необходимо выполнить следующие действия:
- С помощью линейки откладываем отрезок, равный по длине основанию. Обозначаем его буквами АС.
- Циркулем измеряем необходимую длину боковой стороны.
- Рисуем из точки А, а затем из точки С, окружности, радиус которых равен длине боковой стороны.
- Получаем две точки пересечения. Соединив одну из них с точками А и С, получаем необходимый треугольник.
Построение прямоугольного треугольника
Треугольник, у которого один угол прямой, называют прямоугольным. Если нам даны катет и гипотенуза, начертить прямоугольный треугольник не составит труда. Его можно построить по катету и гипотенузе.
Построение тупоугольного треугольника по углу и двум прилегающим сторонам
Если один из углов треугольника тупой (больше 90 градусов), его называют тупоугольным. Чтобы начертить по указанным параметрам тупоугольный треугольник необходимо сделать следующее:
- С помощью линейки откладываем отрезок, равный по длине одной из сторон треугольника. Обозначим его буквами А и D.
- Если в задании уже нарисован угол, и вам необходимо начертить такой же, то на его изображении отложить два отрезка, оба конца которых лежат в вершине угла, а длина равняется указанным сторонам. Соедините полученные точки. У нас получился искомый треугольник.
- Чтобы его перенести на свой чертеж, вам необходимо измерить длину третьей стороны.
Построение остроугольного треугольника
Остроугольный треугольник (все углы меньше 90 градусов) строится по тому же принципу.
- Нарисуйте две окружности. Центр одной из них лежит в точке D, а радиус равен длине третьей стороны, а у второй центр находится в точке А, а радиус равен длине указанной в задании стороны.
- Соедините одну из точек пересечения окружности с точками А и D. Искомый треугольник построен.
Вписанный треугольник
Для того чтобы начертить треугольник в окружности, нужно помнить теорему, в которой говорится, что центр описанной окружности лежит на пересечении серединных перпендикуляров:
У тупоугольного треугольника центр описанной окружности лежит за пределами треугольника, а у прямоугольного — на середине гипотенузы.
Чертим описанный треугольник
Описанный треугольник — это треугольник, в центре которого нарисована окружность, касающаяся всех его сторон. Центр вписанной окружности лежит на пересечении биссектрис. Для их построения необходимо:
Ещё больше интересного
как начертить треугольник, как начертить треугольник в окружности, как начертить прямоугольный треугольник, как начертить циркулем треугольник, как начертить вписанный треугольник, как начертить описанный треугольник:Из нашей статьи вы узнаете, как начертить треугольник, а именно как изобразить следующие треугольники: разносторонний, равнобедренный, равносторонний, прямоугольный, тупоугольный, остроугольный, вписанный, описанный вокруг окружности, при помощи циркуля и линейки.
Как построить равнобедренный треугольник | Треугольники
Как построить равнобедренный треугольник? Это легко сделать с помощью линейки, карандаша и клеточек тетради.
Построение равнобедренного треугольника начинаем с основания. Чтобы рисунок получился ровным, количество клеточек в основании должно быть четным числом.
Делим отрезок — основание треугольника — пополам.
Вершину треугольника можно выбрать на любой высоте от основания, но обязательно ровно над срединой.
Как построить остроугольный равнобедренный треугольник?
Углы при основании равнобедренного треугольника могут быть только острыми. Чтобы равнобедренный треугольник получился остроугольным, угол при вершине тоже должен быть острым.
Для этого вершину треугольника выбираем повыше, подальше от основания.
Чем выше вершина, тем меньше угол при вершине. Углы при основании при этом, соответственно, увеличиваются.
Как построить тупоугольный равнобедренный треугольник?
С приближением вершины равнобедренного треугольника к основанию градусная мера угла при вершине увеличивается.
Значит, чтобы построить равнобедренный тупоугольный треугольник, вершину выбираем пониже.
Как построить равнобедренный прямоугольный треугольник?
Чтобы построить равнобедренный прямоугольный треугольник, надо вершину выбрать на расстоянии, равном половине основания (это обусловлено свойствами равнобедренного прямоугольного треугольника).
Например, если длина основания — 6 клеточек, то вершину треугольника располагаем на высоте 3 клеточек над серединой основания. Обратите внимание: при этом каждая клеточка у углов при основании делится по диагонали.
Построение равнобедренного прямоугольного треугольника можно начать с вершины.
Выбираем вершину, от нее под прямым углом откладываем равные отрезки вверх и вправо. Это — боковые стороны треугольника.
Соединим их и получим равнобедренный прямоугольный треугольник.
Построение равнобедренного треугольника с помощью циркуля и линейки без делений рассмотрим в другой теме.
Планиметрия (прямая и окружность) / Хабр
Задача 1.3Задача 1.4
Задача 1.6
Задача 1.7
Планиметрия изучется в начальном курсе геометрии и зачастую сводится к решению практических задач без изучения теоретической базы.
В данной статье приводятся альтернативные (подсказкам) решения задач из первого раздела (кроме 1.5) приложения Euclidea (геометрические построения с помощью циркуля и линейки).
Решения задач 1.1, 1.2 и 1.3 основаны на том, что с помощью циркуля и линейки можно построить равносторонний треугольник.
1.1 Построить угол 60° с заданой стороной
1.2 Построить серединный перпендикуляр к отрезку
Рассмотрим
Предложение I, приведённое в «Началах» Евклида
На данной ограниченной прямой построить равносторонний треугольник
Такой треугольник строится на пересечении двух окружностей одного диаметра.
Доказательство того, что этот треугольник является равноcторонним приводится далее в Предложении I «Начал»
1.3 Середина отрезка
Постройте точку, делящую отрезок на две равные части.
Эту задачу можно решить, используя построения из предыдущей задачи, но здесь я буду использовать построения одним только циркулем
Построение одним только циркулем
Итак,
теорема Мора-Маскеронигласит, что
всё, что можно построить с помощью циркуля и линейки, может быть построено с помощью одного циркуля.
Рассмотрим сперва задачу
4.1 Удвоенный отрезокВ книге Я. Перельмана «Занимательная геометрия» приводится решение этой задачи
Из точки В радиусом АВ описываем окружность.
По этой окружности откладываем от точки А расстояние АВ три раза: получаем точку С, очевидно, диаметрально противоположную А. Расстояние АС представляет собой двойное рассрастояние АВ. Проведя окружность из С радиусом ВС, мы можем таким же образом найти точку,
диаметрально противоположную В и, следовательно, удаленную от А на
тройное расстояние АВ, и т. д.
Далее необходимо построить равнобедренный треугольник с основанием, равным
rи длинами боковых сторон, равными
2r.
AEF — равнобедренный треугольник с основанием, равным r и длинами боковых сторон, равными 2r.
AFM — равнобедренный треугольник с основанием, равным r/2 и длинами боковых сторон, равными r.
Ссылка на источник
и построение одной только линейкой
Построение одной только линейкой
Итак,
по теореме Штейнера — Понселе:
любое построение, выполнимое на плоскости циркулем и линейкой, можно выполнить одной линейкой, если нарисована хотя бы одна окружность и отмечен её центр.
Решим вспомогательную задачу:
Провести прямую, параллельную данному отрезку.
Далее в приложении есть похожая задача
5.1 Параллельная прямая через точку.
Поскольку треугольник, образованый пересечением диаметров и прямой, является равнобедренным; и поскольку углы при основании треугольника равны, то и
вписанные углы, образованые пересечением диаметров и прямой равны, а значит данные прямые параллельны.
Далее, решим
Задачу 1из
параграфа 3книги «Геометрические построения на плоскости» (Б.И. Аргунов, М.Б. Балк.)
Задача 1:
Даны две параллельные прямые
аи
bи на одной из них, например
a, отрезок
AB. Построить середину этого отрезка.
Для решения нам понадобится одно вспомогательное предложение («лемма о трапеции»):
Прямая, соединяющая точку пересечения диагоналей трапеции с точкой пересечения продолженных её боковых сторон, делит оба основания трапеции пополам.
Далее в книге приводится доказательство, которое я приводить не буду
Решение:
Изберем произвольную точку P, лежащую вне полосы, ограниченной заданными прямыми
Проведем прямые
PAи
PBи отметим точки
Dи
Cих пересечения прямой
b. Пусть
О— точка пересечения прямых
ACи
BD. Тогда, согласно предыдущей лемме, прямая
POпересечёт отрезок
ABв его середине
M.
Решением задачи 1.3 по методу Штейнера-Понеселе будет:
1.4 Окружность, вписанная в квадрат
Постройте окружность, вписанную в квадрат
.
Общими точками у квадрата и вписанной в него окружности будут середины рёбер квадрата. Середину ребра можно найти, опустив на него перпендикуляр из точки пересечения диагоналей квадрата.
Для того, чтобы построить такой перпендикуляр, решим вспомогательную задачу
2.6 Опустить перпендикуляр
Эта задача есть в книге «Занимательная геометрия»
Из точки A, лежащей вне данной полуокружности, опустить на её диаметр перпендикуляр, обходясь при этом без циркуля. Положение центра полуокружности не указано.
Нам пригодится здесь то свойство треугольника, что все его высоты пересекаются в одной точке. Соединим A с B и C; получим точки D и E. Прямые BE и CD, очевидно, — высоты треугольника ABC. Третья высота — искомый перпендикуляр к BC — должна проходить через пересечение двух других, т.е. через точку M. Проведя по линейке прямую через точки A и M, мы выполним требованиек задачи, не прибегая к услугам циркуля.
Вернёмся к задаче
1.4Опустим перпендикуляр из точки пересечения диагоналей квадрата на одну из его сторон.
Для этого построим окружность с центром, принадлежащим нижнему (горизонтальному) ребру квадрата.
И опустив перпендикуляр из точки пересечения диагоналей квадрата на ребро, найдём середину ребра.
Это же построение можно использовать для решения задачи
2.9 Окружность, касающаяся прямой1.6 Найти центр окружности
Центр окружности можно найти, построив диаметр этой окружности и разделив его пополам; для построения диаметра можно воспользоваться, например,
теоремой Фалесаоб угле, опирающемся на диаметр окружности
Плоский угол, опирающийся на диаметр окружности, — прямой.
Построим две хорды, лежащие под прямым углом друг к другу; соединим противоположные концы хорд
Соответственно,
центром окружностибудет являться точка, лежащая посередине построенного диаметра, т.е. точка, которая делит диаметр пополам.
Эти же построения можно использовать для решения задачи 2.7
2.7 Восстановить перпендикуляр
Построим произвольную окружность, проходящую через точку, из которой необходимо восстановить перпендикуляр.
По теореме Фалеса угол, опирающийся на диаметр, является прямым, а искомым перпендикуляром является хорда, соединяющая точку, из которой необходимо восстановить перпендикуляр, с точкой пересечения диаметра с окружностью.
Ксати, задачу
2.7можно решить, например, так
Эту задачу можно решить с помощью одного циркуля, разделив дугу верхней полуокружности пополам, построив окружность из этой точки, а затем найти точку пересечения прямой и окружности.
Это построение можно использовать и для решения задачи
3.5Определение: касательной к окружности называется прямая, имеющая с окружностью одну общую точку. Касательная к окружности перпендикулярна радиусу, проведённому в точку касания.
Рассмотрим задачу 2.8
2.8 Касательная к окружности в точке
Возвращаясь к предыдущей задаче, эту задачу можно решить построив угол, опирающийся на диаметр окружности по теореме Фалеса
Да, задача навскидку решается за 4Е действия
Доказательство
Докажем, что оранжевая прямая действительно является касательной к исходной окружности. Как показано в
Предложении I«Начал», треугольник, построенный на пересечении двух окружностей является равносторонним.
Рассмотрим равносторонний треугольник с длиной ребра, равной 2r и вершиной, лежащей в центре исходной окружности. Тогда касательной к окружности будет одна из биссектрис/медиан/высот треугольника.
Можно замеить, что оранжевая линия лежит в основании равнобедренного треугольника
Оказывается, такой треугольник можно построить без привязки к центру окружности
Вообще, данные построения можно сделать без использования вспомогательных прямых, а значит эта задача решается в 3Е действия.
Далее, построив перпендикуляр к касательной, найдём диаметр окружности, и, разделив его пополам, найдём центр окружности.
Ещё об одном способе построения касательной к окружности можно узнать из лекции 1.5 курса «Геометрия и группы» А. Савватеева ссылка
1.7 Квадрат, вписанный в окружность
В книге «Занимательная геометрия» рассматривается аналогичная этой задаче
Задача Наполеона
Решим задачу методом Мора-Маскерони.
Построим три окружности радиусом r и две окружности радиусом
В приложении нет такой операции, как перенос раствора циркуля (равного MO), поэтому необходимо использовать дополнительные построения.
Для того, чтобы построить касательную к исходной окружности, параллельную МО, необходимо произвести построения, которые были приведены выше (построить три окружности радиусом r и две окружности радиусом ), но вместо исходной окружности взять окружность, обозначенную на рисунке синим цветом
Т.о. мы перенесли раствор циркуля (равный МО) в точку А.
Далее из точки А необходимо провести окружность c радиусом МО
P.S. Ксати, у создателей приложения есть своя группа в VK vk.com/euclidea
Как построить (нарисовать) равносторонний треугольник
Содержание
- Построить равносторонний треугольник
- Как нарисовать равносторонний треугольник с помощью циркуля
- Как построить равносторонний треугольник, вписанный в круг
- Постройте равносторонний треугольник, вписанный в круг Доказательство
- Как нарисовать равносторонний треугольник
- Нарисуйте доказательство равностороннего треугольника
Построить равносторонний треугольник
Равносторонние треугольники легко построить с помощью циркуля, линейки и карандаша, потому что внутренние углы 60 ° можно найти, используя только радиус круга вокруг треугольника (описанный круг).
Предположим, вам дана длина одной стороны требуемого равностороннего треугольника. Вы должны построить две одинаковые стороны, которые каким-то образом образуют три внутренних угла в 60 °.
Вот сегмент CE:
[вставить чертеж линейного сегмента CE]
- Поместите иглу циркуля для рисования в точку C, затем отрегулируйте рычаг карандаша так, чтобы он касался точки E.
- Поверните дугу вверх, образуя легкую строительную линию.
- Не регулируя компас, переместите стрелку в точку E.
- Поверните дугу вверх от точки C, образуя еще одну легкую строительную линию. [вставить чертеж, показывающий дуги поворота компаса для этих точек]
- В месте пересечения двух дуг находится точка третьей вершины равностороннего треугольника. Назовите это точкой A. Используйте линейку, чтобы соединить точки A и C, точки A и E. У вас есть равносторонний треугольник ACE!
Как нарисовать равносторонний треугольник с помощью компаса
Точки C и E — центры конгруэнтных окружностей с радиусами, равными CE.Длины AC и CE являются радиусами окружности C. Длины AE и CE также являются радиусами окружности E. По переходному свойству:
Три совпадающие стороны означают, что треугольник должен быть равносторонним.
Как построить равносторонний треугольник, вписанный в круг
Предположим, вам дан круг, а не сторона. Предположим, вас попросили построить внутри этого круга равносторонний треугольник:
[вставить чертеж круга S]
Вы знаете только центральную точку, точку S, но из нее вы можете скопировать радиус (расстояние от центра, точки S, до самой окружности).
- Настройте циркуль для рисования и установите радиус.
- Сделайте отметку на круге в любом месте. Установите игольную консоль в эту точку.
- Не меняя циркуля, поверните две небольшие дуги выше и ниже точки окружности, чтобы дуги пересекали окружность.
- Переместите стрелку циркуля для рисования на одну из этих дуг.
- Снова поверните циркуль, чтобы образовать небольшую дугу на окружности.
- Повторите это еще два раза, чтобы создать шесть точек на окружности (исходная точка плюс шесть маленьких дуг, пересекающих ее).
- Используйте линейку, чтобы соединить все остальные точки на окружности. То есть нарисуйте линейные сегменты, скажем, от вашей первой точки на окружности до третьей точки, и еще один линейный сегмент от третьей точки до пятой точки. Еще одна линия, от пятой точки обратно к исходной точке, и вот она. Вы вписали в круг равносторонний треугольник!
[вставьте рисунок, показывающий это, или анимируйте конструкцию трех сторон]
Постройте равносторонний треугольник, вписанный в круг Доказательство
Представьте, что этот равносторонний треугольник состоит из трех меньших равнобедренных треугольников, имеющих точку S как общую вершину.Это означает, что каждый из трех треугольников имеет центральный угол (в точке S) 120 °, полученный путем деления полных 360 ° круга на 3 (количество центральных углов).
Каждый из этих меньших равнобедренных треугольников имеет две вершины на окружности, и каждый имеет одинаковые стороны с другими треугольниками. Таким образом, две из трех сторон треугольников совпадают.
Если две стороны равнобедренного треугольника совпадают, то третья сторона также определяется теоремой стороны-угла-стороны.
Как нарисовать равносторонний треугольник
Этот метод позволяет вам контролировать размер вашего равностороннего треугольника, потому что вы строите его с нуля.
- Настройте циркуль для рисования, чтобы нарисовать круг; назовем его Circle E.
- Используйте линейку, чтобы установить диаметр (отрезок прямой, проходящий через центральную точку E с конечными точками на самой окружности). Обозначьте конечные точки Точки B и R. [вставьте рисунок или анимацию, показывающую эти шаги]
- Не мешая компасу, опустите иглу в точку R и сделайте еще один полный круг. Там, где новый круг пересекает старый в двух точках выше и ниже диаметра BR, обозначьте эти точки A и S.
- Соедините точку B с точкой A, точку A с точкой S и точку A с точкой B. МЕДВЕДЬ замечает, что вы построили равносторонний треугольник!
Нарисуйте доказательство равностороннего треугольника
Вы можете доказать, что треугольник равносторонний, используя свои знания о том, что любой угол, вписанный в полукруг, является прямым углом, что дает вам прямые углы ∠BAR и ∠BSR, что создает два конгруэнтных прямоугольных треугольника △ BAR и △ BSR, имеющих общую гипотенузу, BR .
Таким образом, AB ≅ BS (соответствующие стороны равнобедренных треугольников), что означает, что △ BAS равнобедренный.Это делает BAS и ∠BSA конгруэнтными (углы основания равнобедренного треугольника совпадают). Мы знаем, что ∠ABS составляет 60 °, оставляя два оставшихся угла в сумме до 120 °, так что каждый из них составляет 60 °. Все три внутренних угла △ BAS равны, что делает его равносторонним треугольником.
Следующий урок:
Как построить биссектрису угла
GeoGebra Tutorial 2 — Построение равностороннего треугольника
Это второй учебник из серии GeoGebra Intermediate Tutorial Series .Если вы впервые используете GeoGebra, прочтите серию статей о GeoGebra Essentials. Это руководство решает следующую проблему с использованием GeoGebra.
Примечание: Это руководство было обновлено для GeoGebra 4.2.
В приведенном ниже руководстве команды меню, расположенные в строке меню, выделены коричневым полужирным шрифтом , а подменю обозначены символом > . Например, Параметры> Надпись> Только новые точки означает, что щелкните меню Параметры , выберите Надпись из списка, затем выберите Только новые точки .Инструменты GeoGebra обозначены оранжевым текстом . Например, New Point означает инструмент новой точки.
Задача: Как нарисовать равносторонний треугольник без инструмента «Правильный многоугольник»?
В этом уроке мы имитируем построение циркуля и линейки с помощью инструмента круга. Идея состоит в том, чтобы использовать одно из пересечений двух окружностей и двух центров, чтобы сформировать равносторонний треугольник, как показано на рисунке 1.
Рисунок 1 — Равносторонний треугольник, образованный радиусами двух окружностей
При построении треугольника мы узнаем, как использовать инструмент круга и как отображать внутренний угол многоугольника и длину сегментов.Обратите внимание, что мы также можем нарисовать правильный многоугольник с любой стороной, используя инструмент Правильный многоугольник. Результат этого руководства можно посмотреть здесь.
| 1.) Откройте GeoGebra , а затем выберите Geometry на панели «Перспектива» на боковой панели. | |
| 2.) Щелкните инструмент «Сегмент между двумя точками» и щелкните два разных места в графическом представлении, чтобы построить сегмент AB . | |
| 3.) Если метки точек не отображаются, щелкните инструмент Move , щелкните каждую точку правой кнопкой мыши и выберите Показать метку в контекстном меню. | |
| 4.) Чтобы построить круг с центром A , проходящим через B , щелкните инструмент «Окружность с центром через точку », щелкните точку A, , затем щелкните точку B . Ваш рисунок должен выглядеть так, как показано на рис. , рис. 2 . Рисунок 2 — Окружность с центром A, проходящая через B. | |
| 5.) Чтобы построить еще один круг с центром B , проходящим через A , с кругом с центром, хотя точка все еще активна, щелкните точку B , а затем щелкните точку A . | |
| 6.) Затем мы должны «пересечь» круги. Чтобы пересечь два круга, выберите Пересечь два объекта , затем щелкните окружность обоих кругов.Обратите внимание, что на их пересечении появляются две точки. После шага 6 рисунок должен выглядеть так, как показано на Рисунок 3 . | |
Рисунок 3 — Окружности радиуса AB и пересечения Cand D. | |
| 7.) Нам нужны только три точки: точки A, , B, и C, , чтобы сформировать равносторонний треугольник, поэтому мы скрываем два круга, сегмент AB (не нажимайте точки A . или B при укрытии) и точка D .Для этого щелкните каждый объект правой кнопкой мыши и выберите Показать объект . | |
| 8.) Когда в графическом представлении осталось только три точки, щелкните инструмент Многоугольник и щелкните точки в следующем порядке: A , B , C и затем щелкните A , чтобы закрыть многоугольник. . После шага 8 ваш рисунок должен выглядеть как на рисунке 4. Рисунок 4 — Треугольник, образованный радиусами двух окружностей | |
| 9.) Используя инструмент Move , переместите вершины треугольника. Что вы наблюдаете? | |
| 10.) Вы, наверное, заметили, что ABC — равносторонний треугольник. На самом деле это так. Для проверки мы можем отобразить внутренние углы треугольника. Для этого щелкните инструмент Угол , затем щелкните внутреннюю часть треугольника. | |
| 11.) Что вы наблюдаете? Переместите на вершины треугольника. Ваше наблюдение осталось прежним? | |
| 12.) Вы также можете проверить длину сторон с помощью окна Preferences . Для этого щелкните правой кнопкой мыши одну из сторон треугольника, выберите Свойства объекта из контекстного меню . | |
| 13.) В окне Preferences выберите вкладку Basic . Убедитесь, что установлен флажок Показать метку и выберите Значение из раскрывающегося списка Показать метку . | |
| 14.) Выберите другие стороны треугольника в списке Object , расположенном в левой части окна Preferences , и измените метки на Value, , затем закройте окно, когда закончите. | |
| 15.) Докажите, что построение выше всегда приводит к равностороннему треугольнику. |
Урок двенадцатого класса Построение равностороннего треугольника
Конструирование: равносторонний треугольник Евклида
Чтобы начать мини-урок, я публикую Математический навык №4: я могу конструировать математические модели (MP4) .Я начинаю с указания на то, что существуют разные виды математических моделей. В осеннем семестре мы провели много статистического и алгебраического моделирования; Теперь мы собираемся построить геометрическую модель. Прежде чем приступить к задаче, мы хотим убедиться, что понимаем слово «построить».
Я хочу сказать, что если мы делаем конструкцию, мы не собираемся ничего измерять. Я сравниваю это с некоторыми примерами, сделанными учениками, которые измеряли углы или стороны. Могли бы получиться хорошо, но можно сделать равносторонний, ничего не замерив — вот что подразумевается под построением.Я немного говорю о Евклиде и о том, как он смог доказать всевозможные геометрические теоремы с помощью немного больше, чем линейка ( не линейка! ) и циркуля. «Что меня удивляет, — добавляю я, — так это то, что, избегая измерения, мы на самом деле можем создать еще более точный равносторонний треугольник. В конце мы измерим его углы, чтобы увидеть, что я вам говорю. правда!»
Просматриваем заметки. Студентам может потребоваться небольшая помощь в запоминании того, как пользоваться компасом, это дает время для обзора использования этого инструмента (MP5) .Важно напомнить учащимся, чтобы они не меняли радиус своего компаса после создания первого круга, потому что на следующем шаге мы собираемся создать еще один круг с таким же радиусом.
Язык Шага 2 точен, хотя на первый взгляд сбивает с толку многих студентов. Это прекрасная возможность коснуться идеи того, как медленно следует читать математические утверждения. Один из способов добиться точности (MP6) — это остановиться и убедиться, что вы действительно понимаете точное значение (и порядок!) Каждого тщательно подобранного слова.
На шаге 3 я указываю, что мы используем линейку как линейку — нас не волнует длина линий, мы просто хотим убедиться, что они прямые.
Обсуждение: Сработало?
Когда ученики соединяют точки A, B и C, они часто восхищаются результатом. Совершенно ясно, что это равносторонний треугольник. Из-за того, как они справились с задачей начать наш урок, они больше заинтересованы в достижении этого успешного результата.
Тем не менее, несмотря на то, что нам кажется, я демонстрирую некоторый здоровый скептицизм. «Как мы можем точно сказать, что это равносторонний треугольник?» Я спрашиваю. Ключевое слово находится внизу слайда № 10: , радиус . Я спрашиваю класс, какое отношение имеет радиус к чему-либо, и мы довольно быстро видим, что все три стороны этого треугольника имеют одинаковую длину, потому что каждая является радиусом по крайней мере одного из этих двух конгруэнтных кругов. Для развлечения студенты также могут измерить углы своих треугольников, чтобы убедиться, что все получилось, но это измерение не обязательно; доказательство заключается в том, что каждая сторона треугольника представляет собой радиус.
Чтобы немного предвосхитить наши Круги и Единицы Кругов, я упоминаю, что это не последний раз, когда мы видим радиус круга, соответствующий стороне треугольника.
Эссе 2: Построение правильных многоугольников
Шона Д. Бродерика
Правильные многоугольники — это замкнутые плоские фигуры, состоящие из ребер равной длины и вершин равного размера. Самый простой правильный многоугольник — это равносторонний треугольник, который состоит из трех ребер равной длины и трех углов между каждой парой ребер, составляющих 60 градусов.Три ребра — это наименьшее количество ребер для построения многоугольника, потому что два ребра образуют угол, а одно ребро — сегмент. Полигоны — это замкнутые фигуры. Правильный многоугольник с четырьмя ребрами и есть квадрат. Пять ребер составляют пятиугольник, а шесть — шестиугольник.
Мы исследуем, как построить правильные многоугольники, используя циркуль и линейку, в сравнении с программой динамической геометрии, такой как Sketchpad Geometer.
Сначала рассмотрим построение равностороннего треугольника с помощью линейки и циркуля.Это простейший правильный многоугольник на плоскости. Он состоит из трех сторон.
1. Мы начинаем с рисования произвольной точки A.
2. Затем мы открываем наш компас на фиксированное расстояние и делаем небольшую отметку справа от нашей точки A. Это то место, где в конечном итоге будет наша точка B.
3. Не отрывая циркуль от бумаги, перемещаем конец карандаша вверх и к середине и делаем еще одну отметку. Это будет то место, куда в конечном итоге попадет точка C.
4. Теперь мы помечаем нашу точку B в любом месте отметки.(Почему мы можем отметить его где-нибудь на линии и при этом сохранить определенную длину?)
5. Теперь поместите конец циркуля в точку B и сделайте отметку вверх и до середины, пересекая место, куда пойдет точка C.
6. Отметьте пересечение как точку C.
7. Используя линейку, нарисуйте первую сторону треугольника от A до B.
8. Снова с помощью линейки нарисуйте вторую сторону треугольника от B. по C.
9. Нарисуйте последнюю сторону. На этом мы закончили построение равностороннего треугольника.
Теперь мы сравним этот процесс с процессом, который можно использовать для построения равностороннего треугольника в GSP:
1. Начнем с рисования отрезка произвольной длины. Это будет одна из сторон нашего треугольника.
2. Обозначим точки A для левой точки и B для правой точки.
3. Теперь мы построим круг, используя точку B в качестве центра и точку A в качестве края.
4. Затем мы создаем еще один круг, используя точку A в качестве центра и точку B в качестве края.
5. Строим их пересечение и маркируем его точкой C.
6. Строим отрезок AC.
7. Строим отрезок ВС.
8. Если мы скроем наши круги, у нас теперь есть равносторонний треугольник.
1. Почему эти конструкции работают?
2. Что делает этот треугольник равносторонним в любой из сред?
3. Теряем ли мы что-нибудь или получаем что-нибудь, если учим студентов делать это, используя одно, другое или и то, и другое?
1 (и часть 2).В классе мы обсуждали, что эти равносторонние треугольники работают, потому что две окружности, которые построены, или отметки из двух окружностей, мы увидим, что сегменты треугольника являются радиусами окружностей. Если круги одинакового размера, то радиусы одинакового размера и их положение таково, что они пересекаются в трех точках (центры кругов и их пересечение). Вот диаграмма, которая может помочь:
Мы начали с одного круга и построили два радиуса. Затем мы отразили круг поперек линии, чтобы получилось два круга.
Мы выберем один круг и объединим его с другим, чтобы показать, как радиусы образуют равносторонний треугольник.
По мере приближения мы видим, что радиусы образуют треугольник.
Поскольку круги слились и теперь имеют общие радиусы, образующие основу, мы можем видеть, что, поскольку все радиусы равны, если они перекрываются, образуя основание, а два других соединяются наверху, у нас должен быть равносторонний треугольник.
Остальные части 2. Мы видели, что составляет равносторонний треугольник в GSP, но что касается конструкции из карандаша и бумаги, мы видим, что они такие же, но вместо того, чтобы использовать круги, чтобы показать соответствие радиусов, компас (открытость которого остается постоянной) используется для создания конгруэнтных радиусов.
3. Мы можем немного потерять конструкцию из карандаша и бумаги, потому что круги полностью проиллюстрированы в GSP, а с карандашом и бумагой мы видим только дуги кругов, а равномерное расстояние, созданное компасом, скрыто. Однако я считаю, что оба типа конструкций полезны для того, чтобы у учащихся было более полное представление о конструкциях.
Давайте посмотрим, как построить квадрат. Снова начнем с построения по циркулю и линейке:
1.Мы отмечаем точку А, выставляем циркуль на определенную длину и делаем отметку. Нам нужно сохранить эту длину, поэтому не теряйте ее.
2. Мы отмечаем точку на отметке компаса, B.
3. Затем мы проводим прямую линию через точку A и точку B.
4. Используя компас при текущей настройке, сделайте отметку на слева от точки A и справа от точки B.
5. Если мы хотим сделать квадрат, нам нужно построить перпендикулярные линии, идущие вверх от точек A и B. Итак, чтобы сделать это, нам нужно продлить компас от нашей произвольной длины совсем чуть-чуть.Затем мы размещаем точку на самом левом пересечении и делаем дугу, как показано выше. Затем мы помещаем конец циркуля в точку B и делаем еще одну дугу вокруг точки A, чтобы они пересекались, как показано на рисунке. Повторите этот процесс, чтобы сделать аналогичные дуги вокруг точки B. Начните с точки циркуля на точке A и сделайте дугу вокруг B. Затем поместите точку циркуля на крайнее правое пересечение и сделайте дугу, соединяющуюся с другим. , охватывающую точку B.
6. Сначала сделайте две отметки над точками A и B, используя исходный циркуль произвольной длины.Это будет означать высоту квадрата. Он будет точно такой же длины, как и от A до B, поэтому он будет квадратным. Далее нам нужно выяснить, где будет вершина квадрата. Вот почему мы сделали дуги. Используя линейку, проведите линию от A вверх через две дуги вокруг A и пересеките ее с отметкой сверху. На иллюстрации показано, как это могло теперь выглядеть.
7. Теперь мы закончим построение, проведя перпендикулярную линию вверх от B до отметки и обозначив эту точку пересечения C.Наконец, мы соединяем точку D и точку C, чтобы закончить квадрат.
Теперь мы проиллюстрируем, как можно построить квадрат, используя GSP:
1. Постройте отрезок произвольной длины.
2. Постройте круг, используя A как центр и B как край. В верхней части круга мы отметили расстояние, такое же, как и от A до B.
3.Итак, теперь мы строим перпендикулярную линию через A к отрезку AB. Пересечение этой линии через вершину круга мы обозначим как точка D.
4. Построим теперь перпендикулярную линию через точку D к прямой AD.
5. Затем мы строим еще одну перпендикулярную линию, на этот раз через точку B к прямой AB.
6.Мы обозначаем эту точку C.
.7. Если мы скроем объекты, которые помогли нам в строительстве, мы получим построенный квадрат ABCD.
Комментарий:
Похоже, что причина, по которой это работает, аналогична объяснению равностороннего треугольника. Вот несколько эскизов:
Здесь мы имеем тот же тип конструкции, что и у треугольника.Теперь наши радиусы перпендикулярны и одинаковой длины. Это похоже на атрибуты квадрата.
Теперь мы выделяем две точки на одном круге и объединяем их с другим.
Как только они объединятся, мы увидим квадрат. Просто соединяем верхние точки и у нас будет наш квадрат.
Теперь обратим наше внимание на построение пятиугольника с помощью циркуля и линейки. Сначала я понятия не имел, как это сделать, поэтому мне пришлось использовать Интернет.Есть много разных способов построить пятиугольник. Основное внимание в этом эссе уделяется тому, чтобы показать, как это сделать, и обсудить, почему этот подход работает. Что за математика стоит за этим?
1. Пятиугольник состоит из круга. Каждая из вершин будет пересекаться с краем круга. Итак, сначала строим круг с помощью циркуля. Далее мы проводим линию по центру круга, разделяя его пополам.
2.Нам нужно построить еще одну линию, разделяющую левую половину круга пополам. На рисунке мы сделали это, разделив пополам угол 180 градусов, идущий вниз по середине круга. Для этого выставляем компас на определенную точку открытия. Мы помещаем конец циркуля в центр круга и делаем отметки на обоих лучах на произвольном расстоянии. Затем мы помещаем конец циркуля в сделанные отметки и делаем еще одну отметку в области, где будет проходить деление угла пополам.Создает X, пересечение которого — это то место, где должен пройти луч круга. Проведите линейкой биссектрису угла.
3. Следующая цель — построить середину отрезка, который мы только что нарисовали. Для этого мы открываем компас на произвольное расстояние, которое чуть больше, чем приблизительная средняя точка сегмента. Помещаем конец циркуля в центр круга и делаем отметку дуги как на картинке.Затем мы сохраняем измерение компаса как есть и помещаем точку компаса на пересечение сегмента и края круга и делаем аналогичную отметку. Если компас открыт достаточно далеко, дуги должны пересекаться, как показано. Если эти новые пересечения соединены, пересечение обоих сегментов является средней точкой сегмента.
4. Затем соедините середину найденного сегмента с вершиной круга и с пересечением разделительной линии и края круга.Наша следующая цель — разделить пополам угол, образованный отрезком, от центра к краю и средней точки к краю, как показано на рисунке. Используем те же методы, что и в начале. Раскрываем циркуль на произвольную длину, которая меньше длины отрезков угла. Поместив острие циркуля в вершину угла, делаем отметки на отрезках угла. Затем мы немного закрываем циркуль и помещаем его конец на сделанные нами отметки и делаем новые отметки в направлении центра угла.Эти отметки должны пересекаться под биссектрисой угла. Проведена линия биссектрисы угла от вершины угла через точку X до линии, разделяющей круг на две равные части. (На самом деле, как показано на следующем рисунке, вам нужно продлить биссектрису угла за вертикальную линию.)
5. Следующая цель — построить линию, параллельную горизонтальному сегменту, в точке пересечения вертикального сегмента и биссектрисы угла.Это делается путем размещения точки циркуля в вершине угла, разделенного пополам, и разметки угла дугой, как показано. Там, где биссектриса угла пересекает вертикальный сегмент, поместите точку циркуля и нарисуйте еще одну дугу, как и раньше. Затем мы открываем компас ровно настолько, чтобы переходить от углового сегмента к угловому сегменту на сделанной вами отметке. Затем сделайте еще одну отметку вниз от дуги, которую вы делаете выше, и это пересечение является точкой, где параллельная линия может быть проведена через пересечение биссектрисы угла и вертикальной линии.Давай, сделай так.
6. Соедините точку пересечения нового сегмента и края круга с верхним пересечением вертикальной линии и края круга, и мы построили первую сторону нашего пятиугольника.
7. Теперь нам нужно повторить весь этот процесс, чтобы построить еще три стороны. Четвертую сторону можно соединить с пятой, не делая конструкции.Однако мы все равно делаем его, чтобы убедиться, что фигура построена правильно. Теперь нам просто нужно определиться, с чего начать. Поскольку мы построили сторону, начинающуюся сверху и наклоненную вниз влево, мы делаем наш сегмент, проходящий через центр круга, начиная с последней точки, которую мы только что построили.
8. Повторим этот процесс в другой раз.
9.Повторяем этот процесс еще раз.
10. Теперь мы закончим построением последней стороны, хотя в этом нет необходимости. Теперь у нас есть пятиугольник ABCDE.
Мне также любопытно, что есть математические побочные продукты построения пятиугольника, которые можно наблюдать. Это большой круг на внешней стороне конструкции, прежде чем мы его скроем.Кроме того, внутри пятиугольника есть маленький кружок, если дуги, определяющие середину сегмента, были немного более согласованными. Внутри большого тоже есть маленький пятиугольник. Однако регулярно ли это? Это пропорционально большому пятиугольнику? Если бы конструкция была нарисована идеально, был бы маленький пятиугольник правильным? Означает ли это, что большой пятиугольник не совсем правильный?
Теперь мы покажем тот же процесс, используя GSP:
1.Строим круг произвольной длины. Затем мы проводим линию по центру круга.
2. Затем мы строим перпендикулярную линию к вертикальной линии, проходящей через центр круга. Мы делаем отрезок с линией, которую только что создали, от центра к левому краю. Затем мы строим середину этого отрезка.
3. Оттуда проводим линию, соединяющую среднюю точку с вершиной круга.Это создает угол, а затем мы строим биссектрису угла.
4. Мы строим линию, параллельную предыдущей горизонтальной линии, и пересечение новой линии с краем круга является точкой для создания первой стороны нашего пятиугольника. Теперь рисуем эту сторону. Этот процесс будет повторяться с разными цветами, начиная с боковой точки, которую мы только что построили.
5.Теперь повторяем этот процесс для второй стороны бордового цвета.
6. Повторяем этот процесс еще раз с оранжевым.
7. Мы повторяем этот процесс с розовым или темно-синим цветом, каким бы он ни был. На этом этапе мы можем просто соединить последние две стороны, но, поскольку меня интересовала внутренняя геометрия, я повторил процесс еще раз, чтобы посмотреть, поможет ли точность GSP.
8. Похоже, что в середине этого сооружения происходит много всего. Однако пятиугольник, который, как я думал, находится прямо внутри, не так идеально расположен, как я думал.
9. Если мы скроем все тонкие линии, мы увидим наш пятиугольник.
Вопрос:
Почему это работает?
Ответ:
В классе мы обсуждали использование золотого сечения.В пятиугольнике,
отношение длины красной диагонали к длине стороны равно специальному числу.
Мы будем использовать эту демонстрацию, чтобы показать, как конструкция выше представляет собой пятиугольник. Теперь мы сделаем круг радиуса одной стороны единицы длины:
Затем мы наклеили несколько ярлыков, чтобы облегчить обсуждение:
Во-первых, мы замечаем, что треугольник ABF похож на треугольник AEB .Из этого можно сделать вывод, что:
Тогда через подстановку получаем следующее:
Что дает:
Мы знаем, что фи — это золотое сечение. Таким образом, мы имеем утверждение, что отношение длины диагонали правильного пятиугольника к длине его стороны есть золотое сечение. Теперь посмотрим на нашу конструкцию:
Чтобы обсудить причину, по которой эта конструкция представляет собой пятиугольник, мы используем указанные выше метки.Наша цель — доказать, что отношение диагонали пятиугольника (EF) к стороне (AE) равно фи или золотому сечению, тогда фигура оказывается пятиугольником. Конструкция, изображенная выше, является той же конструкцией, которую мы использовали, за исключением того, что я построил сегмент EO, чтобы облегчить вычисление EF.
Начну с того, что нам дано, что отрезки AO, BO и EO имеют длину 2 единицы. Сегменты BC и CO имеют длину одну единицу, потому что C является средней точкой BO. Если AO равно 2, а CO равно единице, то AC:
Теперь мы можем найти угол ACO с помощью тригонометрии.Следовательно, угол ACO равен:
Таким образом, угол DCO равен половине угла, по определению:
Сегмент DO / 1 равен:
Поскольку мы знаем, что EO равно 2, мы используем теорему Пифагора, чтобы найти ED. Таким образом, ED 2 + DO 2 = EO 2 . Итак, имеем:
Следовательно, ED =
Мы умножаем это выражение на 2, чтобы получить длину EF.Итак, EF =
Мы на полпути к нашей цели. Помните, что мы рассчитываем соотношение длины стороны нашей фигуры к длине диагонали. У нас есть диагональ EF. Теперь мы ищем длину стороны, скажем AE. Мы планируем использовать теорему Пифагора, чтобы найти AE. Мы будем использовать уравнение AE 2 = ED 2 + AD 2 . Мы знаем ED и можем найти AD с выражением 2 — DO. Следовательно, решаем:
Когда мы находим AE и используем наш калькулятор для получения десятичного приближения, мы получаем AE = 2.35114100917. Десятичное приближение для EF = 3,80422606518. Тогда EF / AE = 1,61803398875. Десятичное приближение для золотого сечения — это то же самое, что и мое приближение для EF / AE. Следовательно, эта конструкция дает правильный многоугольник.
Теперь перейдем к разделу о построении шестиугольника с линейкой и циркулем:
1. Начнем с построения круга произвольного размера.
2. Делаем отметку на краю круга с правой стороны.Сохраняя исходный произвольный размер компаса, мы помещаем точку циркуля на эту отметку и отмечаем пересечения круга сверху и снизу.
3. Теперь мы рисуем диаметр круга от верхнего пересечения кругов через центр и продолжаем через противоположный край внизу с помощью нашей линейки.
4. Проделаем то же самое на противоположном перекрестке.
5.Теперь мы можем приступить к построению сторон шестиугольника. Наша первая сторона идет от отмеченной нами правой точки до верхнего пересечения круга.
6. Наша вторая сторона соединяет верхние перекрестки. Но подождите, куда пойдет наша третья сторона?
7. Сделаем нашу третью сторону, построив линию, соединяющую отметки центров наших двух кругов. Если мы продолжим эту линию через другую сторону, у нас будет пересечение слева, которое отмечает точку, где наша третья сторона закончится.Теперь мы можем построить эту третью сторону.
8. Мы рисуем четвертую сторону, начиная с только что созданного пересечения и заканчивая левым нижним пересечением.
9. Наша пятая сторона построена путем соединения нижних перекрестков.
10. Мы закончили конструирование сторон шестиугольника, соединив точки пересечения от правого нижнего до крайней правой отметки.
11.У нас есть шестиугольник!
Хм … Похоже, верх немного криво … Не знаю, почему так получилось. Мы снова спрашиваем, как эта конструкция дает шестиугольник. Связано ли это с умением создавать внутренние или дополнительные углы?
Мы выполняем этот процесс в GSP:
1. Сначала построим круг произвольного размера.
2. Затем мы строим горизонтальную линию от центра круга до края.
3. Затем мы строим еще один круг, используя край первого в качестве центра и центр первого в качестве края.
4. Затем мы строим линию через центр первого круга и верхнее пересечение обоих кругов.
5. Затем мы строим еще одну линию через центр первой окружности, которая проходит через нижнее пересечение окружностей.
6.Теперь мы готовы нарисовать стороны нашего шестиугольника. Первая сторона начинается от нижнего пересечения обоих кругов и идет к центру второго круга.
7. Вторая сторона идет от нижнего пересечения двух кругов до нижнего пересечения первой линии, которую мы нарисовали, и первого круга.
8. Третья сторона идет от нижнего пересечения первой окружности и первой линии до левого пересечения горизонтальной линии и первой окружности.
9. Четвертая сторона идет от пересечения первой окружности и горизонтальной линии до верхнего пересечения первой окружности и второй линии.
10. Пятая сторона идет от верхнего пересечения первого круга и второй линии до верхнего пересечения обоих кругов.
11. Шестая сторона соединяет пятую сторону с первой стороной, и у нас есть шестиугольник.
12.Когда мы скрываем линии и помечаем вершины, мы получаем чистое изображение нашего построенного шестиугольника.
Теперь мы подошли к вопросу о том, как построить семиугольник. Невозможно построить идеально правильный семиугольник, используя только линейку и циркуль, как мы делали раньше. Итак, мой вопрос: почему это так?
Поскольку это невозможно, я считаю, что сейчас хорошее время, чтобы закончить это эссе.
Построение равностороннего треугольника. Евклид I. 1.
Содержание | Введение | Дом
П л а н е г о м е т р и я
Приключение в области языка и логики
на основе
Книга I.Предложение 1
Предложение 1
Формальные части предложения
Молчаливые предположения
ЛОГИЧЕСКАЯ ТЕОРИЯ ПЛОСКОЙ ГЕОМЕТРИИ состоит из первых принципов, за которыми следуют предложения, которые бывают двух видов: теоремы и проблемы. Теорема предлагает утверждение для доказательства. Проблема предлагает задачу, которую нужно выполнить.
Наше первое предложение — это проблема: на данной прямой AB нас попросят нарисовать равносторонний треугольник.Это не сложно.
Поместите конец циркуля в точку A; отрегулируйте циркуль так, чтобы карандаш оказался в точке B; и нарисуйте дугу. Затем с той же настройкой компаса поместите точку в точке B и нарисуйте дугу, позволяя ей пересекать первую в точке C. После рисования прямых линий CA, CB треугольник будет равноугольным.
В формальном доказательстве ниже мы должны сделать три вещи:
1. Надо описать конструкцию.
| 2. | Затем мы должны доказать , что построенная нами фигура на самом деле является равносторонним треугольником; то есть, что он удовлетворяет определению единицы. |
| 3. | Мы должны санкционировать каждое утверждение конструкции и доказательства, цитируя первый принцип. Продолжая, мы подкрепим эти утверждения утверждениями, которые мы уже доказали.Это то, что в математике называется строгостью. |
Это и все формальные доказательства являются упражнениями в риторике, то есть искусстве использования языка как средства убеждения.
Чтобы свести к минимуму прокрутку, повторим цифры.
| 1. | По заданной прямой построить равносторонний треугольник. | |
| 2. | Пусть AB — заданная прямая; | |||
| 3. | нам требуется построить равносторонний треугольник на AB. | |||
| 4. | С центром A и радиусом AB нарисуйте окружность BCD; | |||
| (Постулат 3) | ||||
| 5. | с центром B и радиусом BA, нарисуйте окружность ACE; | |||
| (Постулат 3) | ||||
| 6. | и от точки C, где круги пересекаются, | |||
| 7. | нарисуйте прямые CA и CB. | (Постулат 1) | ||
| 8. | Тогда, поскольку точка A является центром окружности BCD, | ||||||||||||||||||||||
| 9. | AC невероятно похож на AB. | (определение 16) | |||||||||||||||||||||
| 10. | А так как точка B является центром окружности ACE, | ||||||||||||||||||||||
| 11. | BC невероятно похож на AB. | ||||||||||||||||||||||
| 12. | Но мы показали, что CA также равно AB; | ||||||||||||||||||||||
| 13. | , следовательно, CA и CB равны AB. | ||||||||||||||||||||||
| 14. | И вещи, которые равны одному и тому же, равны друг другу; | ||||||||||||||||||||||
| (Аксиома 1) | |||||||||||||||||||||||
| 15. | , следовательно, CA равно CB. | ||||||||||||||||||||||
| 16. | Следовательно, три прямые CA, AB, BC равны одной | ||||||||||||||||||||||
| 17. | другой. | ||||||||||||||||||||||
| 18. | Следовательно, треугольник ABC равносторонний, | (Определение 9) | |||||||||||||||||||||
| 19. | и мы построили его на данной прямой AB. | ||||||||||||||||||||||
| 20. | Это то, что от нас требовалось сделать. | ||||||||||||||||||||||
Это первое предложение не только показывает, как нарисовать эквивалентный треугольник. Это доказывает, что, поскольку мы можем построить , равносторонние треугольники существуют логически. См. Комментарий к определениям.
Ниже приводится руководство к риторике.
Формальные части предложения
Общее утверждение предложения называется его высказыванием.Формулировка этого предложения выделена курсивом в строке 1. В нем говорится о том, что дано и что мы должны заключить или сделать.
После изложения следует изложение, строка 2. Здесь мы применяем то, что дано к конкретной фигуре. Далее следует спецификация, строка 3. Здесь, в отношении этой цифры, мы конкретно указываем, что мы должны доказать или сделать.
Далее идет сама конструкция (строки с 4 по 7), а за ней следует доказательство (строки с 8 по 17).
Наконец, у нас есть закрытие. В заключении мы возвращаемся к высказыванию и подтверждаем то, что мы сделали или показали. Строки с 18 по 20 являются закрывающими.
Проблема, традиционно закрываемая с помощью латинского Quod erat faciendum , буквально «Что и должно было быть сделано», сокращенно Q.E.F. Теорема, завершенная с помощью Quod erat manifestrandum , которое должно было быть доказано, сокращенно Q.E.D. Скоро мы начнем использовать эти закрытия.
Это шесть формальных частей предложения.Стабильность, которую они имели более 2500 лет, проистекает из эстетики ясной демонстрации, которая принадлежит изучению риторики. («Скажите им, что вы собираетесь делать; сделайте это; скажите им, что вы это сделали».)
Цитаты из постулатов, определений и аксиом, которые мы поместили в крайнем правом углу, не были включены в Элементы . Однако стало традицией включать их в качестве руководства к рассуждениям. Мы надеемся, что они не будут отвлекать от изящества демонстраций Евклида; баланс, который нарушается сегодняшними доказательствами из двух столбцов.
Молчаливые предположения
Были ли вам понятны все части предложения? Если нет, то, как только вы поймете, вы можете найти свой собственный способ, более ясный способ выразить это.
Была ли демонстрация убедительной? То есть были ли аргументы действительными и были ли они основаны только на вещах, которые были ранее признаны? Ведь каждое сделанное нами утверждение должно принадлежать к какой-то логической категории. Это должно быть Определение, Постулат, Аксиома или предложение, которые мы уже установили.Это называется аксиоматическим методом.
Или были какие-то неявные предположения? (Слово молчаливое означает не произнесенное; поэтому молчаливое предположение — это то, что явно не указано. Например, если a больше, чем b , а b больше, чем c , тогда a молчаливое предположение может заключаться в том, что a больше, чем c .)
Были ли неявные предположения? Как насчет вывода о том, что два круга действительно пересекаются друг с другом в точке под названием C? (Строка 6.) Гарантирует ли это какой-либо постулат или аксиома? Если нет, можете ли вы предложить такой постулат?
(Такой постулат должен констатировать что-то чрезвычайно очевидное, и поэтому его будет тем труднее сформулировать. Он должен подразумевать, что, когда непрерывная линия существует по обе стороны от другой линии, то в какой-то момент она должна пересекать эту другая строка.)
При строгом рассмотрении любой логической науки делается попытка выявить все неявные предположения.Это означает, что каждое доказательство подвергается поисковому анализу. Мы этого делать не будем. В этот раз мы подняли вопрос о неявных предположениях и оставим его как есть, что не должно мешать студенту задавать вопросы.
Таким образом, математика не является статичным предметом, поскольку всегда будут люди, которые недовольны текущими методами, концепциями и доказательствами. Только поставив под сомнение то, что «очевидно» или что одобрено, наука может когда-либо проникнуть в то, что истинно.
Пожалуйста, «переверните» страницу и решите проблемы.
или
Перейти к следующему предложению.
Содержание | Введение | Дом
Сделайте пожертвование, чтобы TheMathPage оставалась в сети.
Даже 1 доллар поможет.
Авторские права © 2021 Лоуренс Спектор
Вопросы или комментарии?
Эл. Почта: [email protected]
Равносторонний треугольник. Факты для детей
В геометрии равносторонний треугольник — это треугольник, все три стороны которого имеют одинаковую длину, и все три угла также одинаковы и составляют 60 ° каждый.Если нарисована высота, она делит пополам ту сторону, к которой она нарисована, в свою очередь оставляя два отдельных треугольника 30-60-90
Основные свойства
Равносторонний треугольник. Он имеет равные стороны ( a = b = c ), равные углы () и равные высоты ( h a = h b = h c ).Обозначив общую длину сторон равностороннего треугольника как a , мы можем определить, используя теорему Пифагора, что:
Обозначив радиус описанной окружности R , мы можем определить с помощью тригонометрии, что:
- Площадь треугольника
Многие из этих величин имеют простую связь с высотой («h») каждой вершины с противоположной стороны:
- Площадь
- Высота центра с каждой стороны или апофемы
- Радиус окружности, описывающей три вершины, равен .
- Радиус вписанной окружности
В равностороннем треугольнике высота, биссектриса угла, серединный перпендикуляр и медиана каждой стороны совпадают.
Геометрическая конструкция
Равносторонний треугольник легко построить с помощью циркуля и линейки, так как 3 — простое число Ферма. Нарисуйте прямую линию, поместите точку циркуля на один конец линии и проведите дугу от этой точки до другой точки отрезка. Повторите то же самое с другой стороной линии. Наконец, соедините точку пересечения двух дуг с каждым концом отрезка
.Альтернативный метод — нарисовать круг с радиусом r , поместить точку циркуля на круг и нарисовать еще один круг с тем же радиусом.Два круга пересекутся в двух точках. Равносторонний треугольник можно построить, взяв два центра окружностей и любую из точек пересечения.
В обоих методах побочным продуктом является образование vesica piscis.
Доказательство того, что полученная фигура является равносторонним треугольником, является первым предложением в Книге I Элементов Евклида.
Вывод формулы площади
Формула площади относительно длины стороны a может быть получена непосредственно с помощью теоремы Пифагора или с помощью тригонометрии.
Постройте треугольник — объяснение и примеры
Можно построить равносторонние треугольники, равнобедренные треугольники, разносторонние треугольники, острые треугольники, тупые треугольники и прямоугольные треугольники, используя только циркуль и линейку.
Мы уже обсуждали, как сделать равносторонний треугольник, и мы будем использовать этот навык, чтобы помочь нам создать некоторые другие типы треугольников.
Задачи, связанные с построением треугольников, включают построение треугольников с дающей вершиной, заданным сегментом или тремя заданными сегментами.Методы построения также могут помочь нам классифицировать треугольники.
В этом разделе мы рассмотрим:
- Как построить треугольник
- Как построить прямоугольный треугольник с помощью C
- Как построить конгруэнтный треугольник
- Как построить Масштабный треугольник
Как построить треугольник
Каждый раз, когда мы рисуем фигуру, окруженную тремя прямыми сторонами, мы строим треугольник.Мы можем классифицировать эти фигуры по соотношению длин сторон и углов, которые образуют стороны.
У равносторонних треугольников три стороны равной длины, у равнобедренных треугольников ровно две стороны равной длины, а у равносторонних треугольников нет сторон равной длины. У прямоугольных треугольников прямой угол, у тупых треугольников на один угол больше прямого, а у острых треугольников все три угла меньше прямого. Обратите внимание, что у треугольника не может быть более одного прямого или тупого угла.
Как построить прямоугольный треугольник
Если у нас есть прямоугольный треугольник, это означает, что два катета треугольника перпендикулярны. Следовательно, чтобы построить прямоугольный треугольник, мы должны построить линию, перпендикулярную другой линии. Затем мы можем соединить любые две точки на этих линиях линейкой, чтобы получить прямоугольный треугольник.
На показанном рисунке линии AD и BC перпендикулярны. Следовательно, DAB — это прямой угол. Это означает, что треугольники DAB, CAB и EAB являются прямоугольными.
Как построить конгруэнтный треугольник
Что, если нам дан треугольник и мы хотим построить другой треугольник, конгруэнтный ему?
Это немного сложнее, потому что нам нужно использовать несколько конструкций, которые мы делали раньше.
Сначала мы должны построить бесконечную прямую DE, используя любые две точки на плоскости.
Затем мы строим линейный сегмент, равный по длине AC с конечной точкой D. Мы назовем этот сегмент DF. После этого отрезаем отрезок DE, равный по длине AC, построив окружность с центром D и радиусом DF.Мы будем называть пересечение этой окружности и DE, G. DG также будет иметь длину AC, потому что она равна по длине DF, которая равна длине AC.
Затем мы аналогичным образом строим сегмент, равный по длине CB на сегменте GE, который мы назовем GH. Наконец, мы строим отрезок HI, равный длине AB.
Затем мы создаем новую окружность с центром G и радиусом DG. Обозначьте пересечение этого круга и круга с центром H и радиусом HI как J.Затем соедините GJ и HJ. JHG соответствует ACB.
Доказательство конгруэнтности треугольников
Как мы узнаем, что треугольники ABC и JGH конгруэнтны?
Мы знаем, что DG = AC, GH = CB и HI = BA. Поскольку они являются радиусами одного круга, DJ = DG, поэтому DJ = AC по транзитивному свойству. Аналогично, поскольку HI и HJ являются радиусами одной окружности, HI = HJ и HJ = BA. Таким образом, точка A совпадает с точкой J, точка B совпадает с точкой H, а точка C совпадает с точкой G.
Как построить масштабный треугольник
Разносторонний треугольник имеет все три стороны разной длины.
Чтобы построить равносторонний треугольник, выберите три линии разной длины. Как и выше, отрежьте отрезки бесконечной линии равной выбранной длине. Как и раньше, три сегмента должны быть ровно в ряд.
Если отрезаны отрезки AB, BC и CD, мы строим окружности с центром B и радиусом AB, а также с центром C и радиусом CD. Обозначьте пересечение этих двух кругов буквой E, затем соедините AE и DE.Треугольник AED будет иметь сегменты, равные по длине исходной выбранной длине, если исходная длина удовлетворяет неравенству треугольника. В противном случае окружность с центром C и радиусом CD не будет пересекать окружность с центром B и радиусом AB.
Неравенство треугольника
Предположим, нам даны три отрезка разной длины: AB, CD и EF. Неравенство треугольника утверждает, что мы можем построить треугольник со сторонами, равными длинам AB, CD и EF, тогда и только тогда, когда:
- AB + CD> EF
- AB + EF> CD и
- EF + CD> ОБЪЯВЛЕНИЕ.
Все три условия должны быть выполнены; в противном случае мы не сможем построить такой треугольник. Другими словами, мы можем построить треугольник из трех сегментов тогда и только тогда, когда длина любых двух сегментов больше, чем длина третьего сегмента.
Это требование известно как неравенство треугольника.
Примеры
В этом разделе будут рассмотрены общие примеры построения треугольников и их пошаговые решения.
Пример 1
Постройте прямоугольный равнобедренный треугольник.
Пример 1 Решение
Сначала мы построим прямоугольный треугольник. Затем мы отрежем отрезок длинной стороны, равный длине более короткой стороны.
Начните с сегмента AB. Затем постройте равносторонний ABC. Затем постройте биссектрису угла для ACB. Обозначьте пересечение биссектрисы и AB как D.
CDB будет прямоугольным треугольником. Теперь нам нужно отрезать сегмент DC, больший из двух ножек, образующих прямой угол, равный длине DB, меньший.Для этого постройте окружность с центром в точке D и радиусом DB. Обозначьте пересечение DC и этого круга как E. Поскольку DE также является радиусом круга, он равен по длине DB. Следовательно, если мы построим отрезок BE, DBE будет равнобедренным прямоугольным треугольником.
Пример 2
Постройте тупой равнобедренный треугольник.
Пример 2 Решение
Вернемся к построению из примера 1, который показывает прямоугольный равнобедренный треугольник.
Нам нужно построить новый сегмент, DF, чтобы FDB был больше EDB.Мы также хотим, чтобы DF по длине был равен DB.
Затем мы можем выбрать любую точку на окружности круга между A и E в качестве точки F. Затем мы соединяем BF и DF, чтобы создать треугольник.
В этом случае угол EDB состоит из двух меньших углов EDC и CDB. Поскольку CDB является прямым углом, EDC + CDB должен быть больше прямого угла. Таким образом, EDB тупой, и треугольник EDB тоже тупой.
Пример 3
Определите, является ли следующий треугольник острым, прямым или тупым.
Пример 3 Решение
Сначала мы продолжим прямые AB, BC и CA до бесконечных прямых.
Затем мы находим линию, перпендикулярную одной из сторон в каждой вершине. То есть CF перпендикулярно CA, AD перпендикулярно CA, а BE перпендикулярно AB.
Когда мы рассмотрим этот рисунок, мы можем увидеть, как каждый из углов исходного треугольника сравнивается с построенными прямыми углами. Угол CAB лежит внутри угла CAD, который является прямым углом.Таким образом, мы знаем, что CAB — это острое заболевание.
Аналогично, ABC находится внутри ABE. Таким образом, мы знаем, что ABC также является острым.
Наконец, угол ACB состоит из углов ACF и FCB. Поскольку ACF — прямой угол, ACF + FCB должен быть больше прямого угла. Следовательно, мы знаем, что ACB тупой. Следовательно, весь треугольник тупой.
Пример 4
Покажите, что указанные сегменты не удовлетворяют неравенству треугольника.
Пример 4 Решение
Мы можем вырезать сегменты EF, равные по длине AB и CD.
Пусть EG равно AB, а GH равно CD. Когда мы это делаем, мы видим, что H находится внутри сегмента EF. То есть EH меньше EF. Следовательно, EF> EH = EG + EH = CD + AB. Таким образом, отрезки CD и AB не удовлетворяют неравенству треугольника.
Отсюда мы знаем, что невозможно построить треугольник со сторонами длиной AB, CD и EF.
Пример 5
Постройте треугольник, конгруэнтный данному треугольнику так, чтобы вершина, соответствующая A, находилась в точке D.
Пример 5 Решение
Сначала мы создаем бесконечную линию DE, где E — любая точка на плоскости.
Затем нам нужно построить AB и AC на DE так, чтобы каждый сегмент имел конечную точку в D. Мы назовем сегмент равным AB DI, а сегмент — AC DG. Мы делаем это, чтобы гарантировать, что точка D выровняется с точкой A при построении конгруэнтных треугольников.
Затем мы создаем сегмент, равный BC, чтобы иметь конечную точку I. Мы назовем другую конечную точку K.
Теперь мы создаем два круга. Один будет иметь центр I и радиус IK. Другой будет иметь центр D и радиус DG — обозначьте одно из пересечений этих окружностей L.
Теперь мы можем построить отрезки DL и IL. Треугольник DIL будет конгруэнтен исходному треугольнику ABC.
Практические задачи
- Покажите, что треугольник ABC разносторонний.
- Треугольник ABC классифицируют как разносторонний, равносторонний или равнобедренный.
- Покажите, что отрезки удовлетворяют неравенству треугольника, а затем постройте из них треугольник.


 Обозначаем его буквами АС.
Обозначаем его буквами АС. Соедините полученные точки. У нас получился искомый треугольник.
Соедините полученные точки. У нас получился искомый треугольник. Он должен лежать в точном центре сегмента линии, который нарисовали. Теперь можете сделать две прямые линии, ведущие к этой точке: по одному от каждого конца «нижнего» сегмента линии. Закончите треугольник. Далее с помощью линейки надо нарисовать еще два сегмента прямой линии — это стороны в треугольнике. Подключите каждый конец исходного сегмента линии к точке, в которой пересекаются дуги. Чтобы закончить работу, сотрите дуги, которые нарисовали, так, чтобы остался только треугольник.
Он должен лежать в точном центре сегмента линии, который нарисовали. Теперь можете сделать две прямые линии, ведущие к этой точке: по одному от каждого конца «нижнего» сегмента линии. Закончите треугольник. Далее с помощью линейки надо нарисовать еще два сегмента прямой линии — это стороны в треугольнике. Подключите каждый конец исходного сегмента линии к точке, в которой пересекаются дуги. Чтобы закончить работу, сотрите дуги, которые нарисовали, так, чтобы остался только треугольник. Чтобы использовать этот метод, важно знать длину основания треугольника и длину двух равных сторон.
Чтобы использовать этот метод, важно знать длину основания треугольника и длину двух равных сторон.