Фигура сфера картинки: Сфера — Википедия – Сфера, шар, сегмент и сектор. Формулы и свойства

Сфера — Википедия

Сфера (каркасная проекция) Сфера — поверхность шара

Сфе́ра (др.-греч. σφαῖρα «мяч, шар^[1]») — геометрическое место точек в пространстве, равноудаленных от некоторой заданной точки (центра сферы).

Расстояние от точки сферы до её центра называется радиусом сферы. Сфера радиуса 1 называется единичной сферой.

Сфера является поверхностью вращения, образованной при вращении полуокружности вокруг своего диаметра. Площадь сферы в градусной мере с учётом непостоянства значения размеров дуг составляет 41252,96 кв. градусов.

Сфера является частным случаем эллипсоида, у которого все три оси (полуоси, радиусы) равны. Сфера является поверхностью шара. Сфера имеет наименьшую площадь из всех поверхностей, ограничивающих данный объём, также из всех поверхностей с данной площадью сфера ограничивает наибольший объём. Поэтому тела сферической формы встречаются в природе, например, маленькие капли воды при свободном падении приобретают сферическую форму именно из-за минимизации площади поверхности силой поверхностного натяжения.

Объём цилиндра, объём вписанного в него шара, касающегося обоих его оснований, и объём конуса, с вершиной в центре одного основания цилиндра и с основанием, совпадающим с другим основанием цилиндра, находятся в соотношении 3 : 2 : 1^[2].

«Кубок Кеплера»: модель Солнечной системы из пяти правильных многогранников и их вписанных и описанных сфер.

Совершенство сферической формы издавна привлекало внимание мыслителей и учёных, которые с помощью сфер пытались объяснить гармонию окружающего мира. Древнегреческий учёный Пифагор вместе с шарообразной Землёй в центре Вселенной ввёл окружающую Землю удалённую хрустальную сферу, к которой прикреплены звёзды, и семь более близких вращающихся хрустальных сфер, к которым прикреплены Солнце, Луна и пять известных к тому времени планет (исключая Землю). Эта модель впоследствии усложнялась: Евдокс Книдский рассматривал уже 27 подобных сфер, а Аристотель — 55 хрустальных сфер^[3]

. Представления о вращающихся небесных сферах господствовали по крайней мере до средних веков и даже вошли в гелиоцентрическую систему мира Николая Коперника, который назвал свой основной труд «О вращении небесных сфер» (лат. De revolutionibus orbium coelestium).

Небесные сферы со времён Древней Греции были частью более общей концепции гармонии сфер о музыкально-астрономическом устройстве мира, куда также входило понятие «музыка сфер». Эта концепция также существовала как минимум до средневековья. У одного из известнейших астрономов, Иоганна Кеплера, сфера занимала центральное место во всей его системе религиозно-мистических представлений, он писал: «Образ триединого бога есть сферическая поверхность, а именно: бог-отец в центре, бог-сын — на поверхности и святой дух — в симметричном отношении между центром и описанной вокруг него сферической поверхностью»

[4]^[5]. Одно из первых значительных сочинений Кеплера, «Тайна мироздания» (лат. Mysterium Cosmographicum), было посвящено параметрам небесных сфер, Кеплер считал, что он открыл замечательную связь между правильными многогранниками, которых только пять, и небесными сферами шести известных к тому времени планет (включая Землю), являвшимися, по Кеплеру, описанными и вписанными сферами этих многогранников. Представления о гармонии сфер сыграли большую роль при открытии Кеплером третьего закона движений небесных тел (во всяком случае, могут рассматриваться как стимул к поиску астрономических соотношений) ^[6]. Однако у Кеплера небесные сферы являлись уже чисто математическими объектами, а не физически существующими телами. К тому времени Тихо Браге показал, что движение комет, в частности, Большой кометы 1577 года, несовместимо с существованием твердых небесных сфер^[7]. Как удобная математическая модель, осталась одна небесная сфера, с помощью которой астрономы по сей день представляют видимые положения звезд и планет.

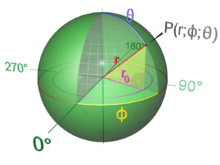
Уравнение сферы в прямоугольной системе координат:

(x−x0)2+(y−y0)2+(z−z0)2=R2,{\displaystyle (x-x_{0})^{2}+(y-y_{0})^{2}+(z-z_{0})^{2}=R^{2},}

где (x0,y0,z0){\displaystyle (x_{0},y_{0},z_{0})} — координаты центра сферы, R{\displaystyle R} — её радиус.

Параметрическое уравнение сферы с центром в точке (x0,y0,z0){\displaystyle (x_{0},y_{0},z_{0})}:

{x=x0+R⋅sin⁡θ⋅cos⁡ϕ,y=y0+R⋅sin⁡θ⋅sin⁡ϕ,z=z0+R⋅cos⁡θ,{\displaystyle {\begin{cases}x=x_{0}+R\cdot \sin \theta \cdot \cos \phi ,\\y=y_{0}+R\cdot \sin \theta \cdot \sin \phi ,\\z=z_{0}+R\cdot \cos \theta ,\\\end{cases}}}

где θ∈[0,π]{\displaystyle \theta \in [0,\pi ]} и ϕ∈[0,2π).{\displaystyle \phi \in [0,2\pi ).}

Гауссова кривизна сферы постоянна и равна 1/R².

Основные геометрические формулы[править | править код]

Площадь поверхности сферы

S=4πr2=πd2.{\displaystyle S=4\pi r^{2}=\pi d^{2}.}

Объём шара, ограниченного сферой

V=43πr3.{\displaystyle V={\frac {4}{3}}\pi r^{3}.}

Площадь сегмента сферы высоты H{\displaystyle H}

S=2πrH{\displaystyle S=2\pi rH}.

Окружность, лежащая на сфере, центр которой совпадает с центром сферы, называется большим кругом (большой окружностью) сферы. Большие окружности являются геодезическими линиями на сфере; любые две из них пересекаются в двух точках. Иными словами, большие круги сферы являются аналогами прямых на плоскости, расстояние между точками на сфере — длина дуги проходящего через них большого круга. Углу же между прямыми на плоскости соответствует двугранный угол между плоскостями больших кругов. Многие теоремы геометрии на плоскости справедливы и в сферической геометрии, существуют аналоги теоремы синусов, теоремы косинусов для сферических треугольников. В то же время, существует немало отличий, например, в сферическом треугольнике сумма углов всегда больше 180 градусов, к трём признакам равенства треугольников добавляется их равенство по трём углам, у сферического треугольника может быть два и даже три прямых угла — например, у сферического треугольника, образованного экватором и меридианами 0° и 90°.

Расстояние между двумя точками на сфере[править | править код]

Если даны сферические координаты двух точек, то расстояние между ними можно найти так:

L=R⋅arccos⁡(cos⁡θ1⋅cos⁡θ2+sin⁡θ1⋅sin⁡θ2⋅cos⁡(ϕ1−ϕ2)).{\displaystyle L=R\cdot \arccos(\cos \theta _{1}\cdot \cos \theta _{2}+\sin \theta _{1}\cdot \sin \theta _{2}\cdot \cos(\phi _{1}-\phi _{2})).}

Однако, если угол θ{\displaystyle \theta } задан не между осью Z и вектором на точку сферы, а между этим вектором и плоскостью XY (как это принято в земных координатах, заданных широтой и долготой), то формула будет такая:

L=R⋅arccos⁡(sin⁡θ1⋅sin⁡θ2+cos⁡θ1⋅cos⁡θ2⋅cos⁡(ϕ1−ϕ2)).{\displaystyle L=R\cdot \arccos(\sin \theta _{1}\cdot \sin \theta _{2}+\cos \theta _{1}\cdot \cos \theta _{2}\cdot \cos(\phi _{1}-\phi _{2})).}

В этом случае θ1{\displaystyle \theta _{1}} и θ2{\displaystyle \theta _{2}} называются широтами, а ϕ1{\displaystyle \phi _{1}} и ϕ2{\displaystyle \phi _{2}} долготами.

В общем случае уравнение (n−1)-мерной сферы (в n-мерном евклидовом пространстве) имеет вид:

∑i=1n(xi−ai)2=r2,{\displaystyle \sum _{i=1}^{n}(x_{i}-a_{i})^{2}=r^{2},}

где (a1,…,an){\displaystyle (a_{1},…,a_{n})} — центр сферы, а r{\displaystyle r} — радиус.

Пересечением двух n-мерных сфер является (n−1)-мерная сфера, лежащая на радикальной гиперплоскости этих сфер.

В n-мерном пространстве могут попарно касаться друг друга (в разных точках) не более n+1 сфер.

n-мерная инверсия переводит (n−1)-мерную сферу в (n−1)-мерную сферу или гиперплоскость.

С трёхмерной сферой связана одна из задач тысячелетия — гипотеза Пуанкаре, в которой утверждается, что всякое односвязное компактное трёхмерное многообразие без края гомеоморфно такой сфере. Эта гипотеза была доказана Г. Я. Перельманом в начале 2000-х годов на основе результатов Ричарда Гамильтона.

Компактные поверхности и их погружения в трёхмерное пространство
Класс гомеоформности компактной триангулируемой поверхности определяется ориентируемостью, числом компонент границы и эйлеровой характеристикой.
Без границы
С границей
Связанные понятия

Сфера, шар, сегмент и сектор. Формулы и свойства

Определение.

Сфера (поверхность шара) — это совокупность всех точек в трехмерном пространстве, которые находятся на одинаковом расстоянии от одной точки, называемой центром сферы (О).

Сферу можно описать, как объёмную фигуру, которая образуется вращением окружности вокруг своего диаметра на 180° или полуокружности вокруг своего диаметра на 360°.

Определение.

Шар — это совокупность всех точек в трехмерном пространстве, расстояние от которых не превышает определенного расстояния до точки, называемой центром шара (О) (совокупность всех точек трехмерного пространства ограниченных сферой).

Шар можно описать как объёмную фигуру, которая образуется вращением круга вокруг своего диаметра на 180° или полуокружности вокруг своего диаметра на 360°.

Определение. Радиус сферы (шара) (R) — это расстояние от центра сферы (шара) O к любой точке сферы (поверхности шара).

Определение. Диаметр сферы (шара) (D) — это отрезок, соединяющий две точки сферы (поверхности шара) и проходящий через ее центр.

Формула. Объём шара: Формула. Площадь поверхности сферы через радиус или диаметр:

S = 4πR² = πD²

Уравнение сферы

1. Уравнение сферы с радиусом R и центром в начале декартовой системе координат:

x² + y² + z² = R²

2. Уравнение сферы с радиусом R и центром в точке с координатами (x₀, y₀, z₀) в декартовой системе координат:

(x — x₀)² + (y — y₀)² + (z — z₀)² = R²

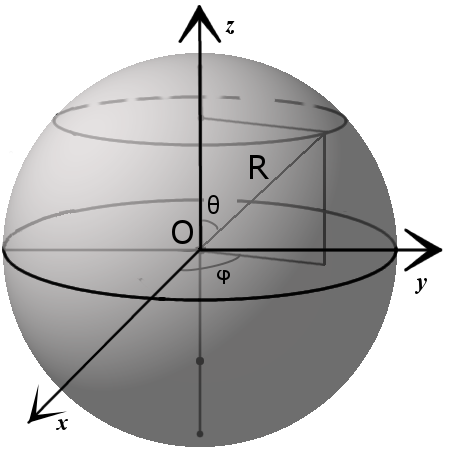3. Параметрическое уравнение сферы с центром в точке (x₀, y₀, z₀):
x = x₀ + R · sin θ · cos φy = y₀ + R · sin θ · sin φz = z₀ + R · cos θ
где θ ϵ [0,π], φ ϵ [0,2π].

Определение. Диаметрально противоположными точками называются любые две точки на поверхности шара (сфере), которые соединены диаметром.

Основные свойства сферы и шара

1. Все точки сферы одинаково удалены от центра.

2. Любое сечение сферы плоскостью является окружностью.

3. Любое сечение шара плоскостью есть кругом.

4. Сфера имеет наибольший объём среди всех пространственных фигур с одинаковой площадью поверхности.

5. Через любые две диаметрально противоположные точки можно провести множество больших окружностей для сферы или кругов для шара.

6. Через любые две точки, кроме диаметрально противоположных точек, можно провести только одну большую окружность для сферы или большой круг для шара.

7. Любые два больших круга одного шара пересекаются по прямой, проходящей через центр шара, а окружности пересекаются в двух диаметрально противоположных точках.

8. Если расстояние между центрами любых двух шаров меньше суммы их радиусов и больше модуля разности их радиусов, то такие шары пересекаются, а в плоскости пересечения образуется круг.

Секущая, хорда, секущая плоскость сферы и их свойства

Определение. Секущая сферы — это прямая, которая пересекает сферу в двух точках. Точки пересечения называются точками протыкания поверхности или точками входа и выхода на поверхности.

Определение. Хорда сферы (шара) — это отрезок, соединяющий две точки сферы (поверхности шара).

Определение. Секущая плоскость — это плоскость, которая пересекает сферу.

Определение. Диаметральная плоскость — это секущая плоскость, проходящая через центр сферы или шара, сеченме образует соответственно большую окружность и большой круг. Большая окружность и большой круг имеют центр, который совпадают с центром сферы (шара).

Любая хорда, проходящая через центр сферы (шара) является диаметром.

Хорда является отрезком секущей прямой.

Расстояние d от центра сферы до секущей всегда меньше чем радиус сферы:

d < R

Расстояние m между секущей плоскостью и центром сферы всегда меньше радиуса R:

m < R

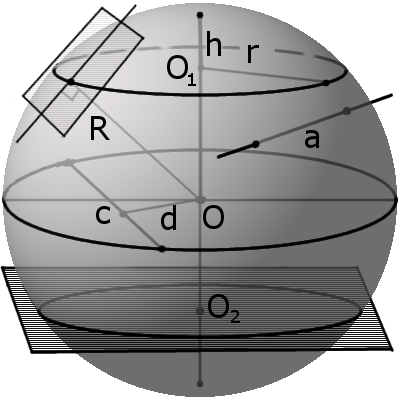
Местом сечения секущей плоскости на сфере всегда будет малая окружность, а на шаре местом сечения будет малый круг. Малая окружность и малый круг имеют свои центры, не совпадающих с центром сферы (шара). Радиус r такого круга можно найти по формуле:

r = √R² — m²,

где R — радиус сферы (шара), m — расстояние от центра шара до секущей плоскости.

Определение. Полусфера (полушар) — это половина сферы (шара), которая образуется при ее сечении диаметральной плоскостью.

Касательная, касательная плоскость к сфере и их свойства

Определение.Касательная к сфере — это прямая, которая касается сферы только в одной точке.

Определение.Касательная плоскость к сфере — это плоскость, которая соприкасается со сферой только в одной точке.

Касательная пряма (плоскость) всегда перпендикулярна радиусу сферы проведенному к точке соприкосновения

Расстояние от центра сферы до касательной прямой (плоскости) равно радиусу сферы.

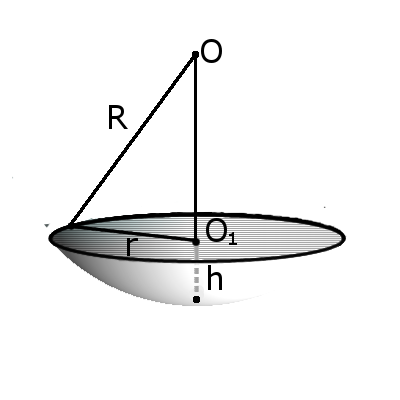Определение. Сегмент шара — это часть шара, которая отсекается от шара секущей плоскостью. Основой сегмента называют круг, который образовался в месте сечения. Высотой сегмента h называют длину перпендикуляра проведенного с середины основы сегмента к поверхности сегмента. Формула. Площадь внешней поверхности сегмента сферы с высотой h через радиус сферы R:

S = 2πRh

Формула. Объём сегмента сферы с высотой h через радиус сферы R: 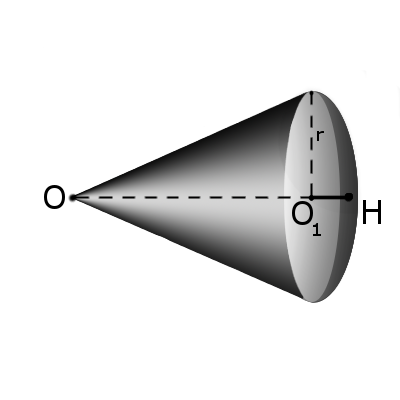Определение. Срез шара — это часть шара, которая образуется в результате его сечения двумя параллельными плоскостями и находится между ними. Определение. Сектором называется часть шара, ограниченная совокупностью всех лучей, исходящих из центра шара О и образующих круг на его поверхности с радиусом r. Формула. Площадь поверхности сектора S с высотой O₁H (h) через радиус шара OH (R):

S = πR(2h + √2hR — h

2)

Формула. Объём сектора V с высотой O₁H (h) через радиус шара OH (R):

Определение. Касательными сферами (шарами) называются любые две сферы (шара), которые имеют одну общую точку соприкосновения. Если расстояние между центрами больше суммы радиусов, то фигуры не касаются и не пересекаются.

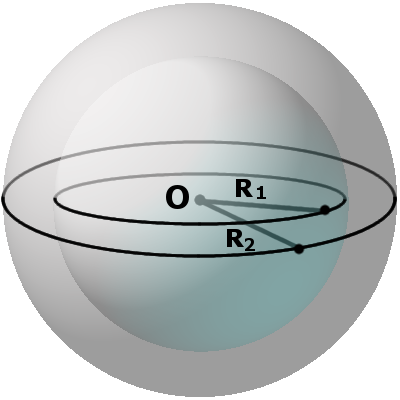Определение. Концентрическими сферами называются любые две сферы, которые имеют общий центр и радиусы различной длины.

Шар и сфера, объем шара, площадь сферы, формулы

Шар и сфера — это прежде всего геометрические фигуры, и если шар — это геометрическое тело, то сфера — это поверхность шара. Этими фигурами интересовались еще многие тысячи лет назад до н.э.

Впоследствии когда было открыто, что Земля — это шар, а небо — небесная сфера, получило развитие новое увлекательное направление в геометрии — геометрия на сфере или сферическая геометрия. Для того, чтобы рассуждать о размере и объеме шара, нужно сначала дать ему определение.

Шар

Шаром радиуса R с центром в точке О в геометрии называют тело, которое создано всеми точками пространство, имеющими общее свойство. Эти точки находятся на расстоянии, не превышающем радиуса шара, то есть заполняют все пространство меньше радиуса шара во все стороны от его центра. Если мы рассмотрим только те точки, которые равноудалены от центра шара — мы будем рассматривать его поверхность или оболочку шара.

Как можно получить шар? Мы можем вырезать из бумаги круг и начать его вращать вокруг его же диаметра. То есть диаметр круга будет осью вращения. Образованная фигура — будет шар. Поэтому шар называют также телом вращения. Потому что он может быть образован путем вращения плоской фигуры — круга.

Возьмем какую-нибудь плоскость и разрежем ею наш шар. Подобно тому как мы режем ножом апельсин. Кусок, который мы отсечем от шара, называется шаровым сегментом.

В Древней Греции умели не только работать с шаром и сферой, как с геометрическими фигурами, например, использовать их при строительстве, а также умели расчитывать площадь поверхности шара и объем шара.

Сфера

Сферой иначе называется поверхность шара. Сфера — это не тело — это поверхность тела вращения. Однако так как и Земля и многие тела имеют сферическую форму, например капля воды, то изучение геометрических соотношений внутри сферы получило большое распространение.

Например, если мы соединим две точки сферы между собой прямой линией, то эта прямая линия назовется хордой, а если эта хорда пройдет через центр сферы, который совпадает с центром шара, то хорда назовется диаметром сферы.

Если мы проведем прямую линию, которая коснется сферы всего в одной точке, то эта линия будет называться касательной. Кроме того, эта касательная к сфере в этой точке будет перпендикулярна к радиусу сферы, проведенному в точку касания.

Если мы продолжим хорду до прямой в одну и другую сторону от сферы, то эта хорда станет называться секущей. Или можно сказать иначе — секущая к сфере содержит в себе ее хорду.

Объем шара

Формула для вычисления объема шара имеет вид:

V=4/3 πR³,

где R — радиус шара.

Если нужно найти объем шарового сегмента — воспользуйтесь формулой:

V _сег=πh²(R-h/3),  h — высота шарового сегмента.

Площадь поверхности шара или сферы

Чтобы вычислить площадь сферы или площадь поверхности шара (это одно и то же):

S=4πR,

где R — радиус сферы.

Архимед очень любил шар и сферу, он даже попросил оставить на его гробницу рисунок, на котором в цилиндр вписан шар. Архимед считал, что объем шара и его поверхность равны двум третьим от объема и поверхности цилиндра, в который вписан шар»

 

 

 

Стоковые векторные изображения Геометрические фигуры сфера

Стоковые векторные изображения Геометрические фигуры сфера | Depositphotos®Абстрактная композиция, вода круг значок эффекта, воздушный шарик в океане раме, круглый блеск, луч света в море шрифт, a4 брошюры титульного листа, кислородной лампочки, элегантный синий фон поверхности, ежедневно периодическое издание, фантазии летчиком моды, творческих Eps10 иллюстрацииАбстрактная композиция, вода круг значок эффекта, воздушный шарик в океане раме, круглый блеск, луч света в море шрифт, a4 брошюры титульного листа, кислородной лампочки, элегантный синий фон поверхности, ежедневно периодическое издание, фантазии летчиком моды, творческих Eps10 иллюстрации

Шар как геометрическая фигура

Шар – это тело, состоящее из всех точек пространства, которые находятся на расстоянии, не большем данного от данной точки. Эта точка называется центром шара, а данное расстояние – радиусом шара. Граница шара называется шаровой поверхностью или сферой. Точками сферы являются все точки шара, которые удалены от центра на расстояние, равное радиусу. Любой отрезок, который соединяет центр шара с точкой шаровой поверхности, тоже называется радиусом. Проходящий через центр шара отрезок, который соединяет две точки шаровой поверхности, называется диаметром. Концы любого диаметра называются диаметрально противоположными точками шара.

Шар является телом вращения, так же как конус и цилиндр. Шар получается при вращении полукруга вокруг  его диаметра как оси.

Площадь поверхности шара можно найти по формулам:

S = 4 πr²

S = πd²,

где r – радиус шара, d – диаметр шара.

Объём шара находится по формуле:

V = 4 / 3 πr³,

где r – радиус шара.

Теорема. Всякое сечение шара плоскостью есть круг. Центр этого круга есть основание перпендикуляра, опущенного из центра шара на секущую плоскость.

Исходя из данной теоремы, если шар с центром O и радиусом R пересечён плоскостью α, то в сечении получается круг радиуса r с центром K. Радиус сечения шара плоскостью можно найти по формуле

 

Из формулы видно, что плоскости, равноудалённые от центра, пересекают шар по равным кругам. Радиус сечения тем больше, чем ближе секущая плоскости к центру шара, то есть чем меньше расстояние ОК. Наибольший радиус имеет сечение плоскостью, проходящей через центр шара. Радиус этого круга равен радиусу шара.

Плоскость, проходящая через центр шара, называется диаметральной плоскостью. Сечение шара диаметральной плоскостью, называется большим кругом, а сечение сферы – большим кругом, а сечение сферы – большой окружностью.

Теорема. Любая диаметральная плоскость шара является его плоскостью симметрии. Центр шара является его центром симметрии.

Плоскость, которая и проходит через точку А шаровой поверхности и перпендикулярна радиусу, проведённому в точку А, называется касательной плоскостью. Точка А называется точкой касания.

Теорема. Касательная плоскость имеет с шаром только одну общую точку – точку касания.

Прямая, которая проходит через точку А шаровой поверхности перпендикулярно к радиусу, проведённому в эту точку, называется касательной.

Теорема. Через любую точку шаровой поверхности проходит бесконечно много касательных, причём все они лежат в касательной плоскости шара.

Шаровым сегментом называется часть шара, отсекаемая от него плоскостью. Круг ABC – основание шарового сегмента. Отрезок MN перпендикуляра, проведенного из центра N круга ABC до пересечения со сферической поверхностью, – высота шарового сегмента. Точка M – вершина шарового сегмента.

Площадь поверхности шарового сегмента можно вычислить по формуле:

S = 2πRh,

где R – радиус большого круга, h – высота шарового сегмента.

Объём шарового сегмента можно найти по формуле:

V = πh²(R – 1/3h),

где R – радиус большого круга, h – высота шарового сегмента.

Шаровой сектор получается из шарового сегмента и конуса, следующим образом. Если шаровой сегмент меньше полушара, то шаровой сегмент дополняется конусом, у которого вершина в центре шара, а основанием является основание сегмента. Если же сегмент больше полушара, то указанный конус из него удаляется.

Шаровой сектор – это часть шара, ограниченная кривой поверхностью сферического сегмента (на нашем рисунке – это AMCB) и конической поверхностью (на рисунке – это OABC), основанием которой служит основание сегмента (ABC), а вершиной – центр шара O.

Объем шарового сектора находится по формуле:

V = 2/3 πR²H.

Шаровый слой – это часть шара, заключённая между двумя параллельными плоскостями (на рисунке плоскостями ABC и DEF), пересекающими сферическую поверхность. Кривая поверхность шарового слоя называется шаровым поясом (зоной). Круги  ABC и DEF – основания шарового пояса. Расстояние NK между основаниями шарового пояса – его высота.

© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Сфера и шар / Многогранники / Справочник по геометрии 7-9 класс

1. Главная
2. Справочники
3. Справочник по геометрии 7-9 класс
4. Многогранники
5. Сфера и шар

Сфера — поверхность, состоящая из всех точек пространства, расположенных на заданном расстоянии от данной точки.

Центр сферы — данная точка (точка О на рисунке выше).

Радиус сферы — данное расстояние (R на рисунке выше), также это любой отрезок, соединяющий центр сферы с какой-либо ее точкой.

Диаметр сферы — отрезок, соединяющий две точки сферы и проходящий через ее центр. Диаметр сферы в два раза больше ее радиуса, т.е. если радиус сферы — R, то ее диаметр — 2R.

Определение

Шар — тело, ограниченное сферой.

Центр, радиус и диаметр сферы называются также центром, радиусом и диаметром шара. Шар радиуса R с центром О содержит все точки пространства, расположенные от точки О на расстоянии, не превышающем R (включая и саму точку О), и не содержит других точек.

Шар также может быть получен вращением полукруга вокруг его диаметра. При этом сфера образуется в результате вращения полуокружности.

Объем шара

Доказательство

Дано: шар радиуса R и объемом V.

Доказать: .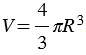

Доказательство:

Воспользуемся принципом Кавальери*. Рассмотрим два тела: половину шара радиуса R и тело Т, представляющее собой цилиндр радиуса R с высотой R, из которого вырезан конус с радиусом основания и высотой R. Представим себе, что оба тела «стоят» на плоскости 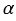(смотри рисунок ниже). Проведем секущую плоскость 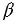, параллельную плоскости 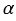и пересекающую радиус шара ОА, перпендикулярный к плоскости 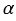, в точке А₁, а высоту ВН конуса — в точке В₁.

Сечение половины шара представляет собой круг, по теореме Пифагора радиус этого круга . Поэтому площадь этого круга .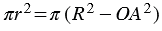

Сечение тела Т представляет собой кольцо, площадь которого равна разности площадей двух кругов: круга радиуса R и круга радиуса В₁В₂ (смотри рисунок выше), т.е. равна . 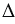 ВВ₁В₂ подобен  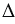ВНК по двум углам ( 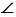В — общий,  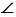ВВ₁В₂=  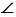ВНК = 90⁰), при этом ВН = НК = R, следовательно, и В₁В₂= ВВ₁ , кроме того, ВВ₁ = ОА₁ (т.к. параллельные плоскости отсекают от параллельных прямых равные отрезки), значит, площадь сечения тела Т равна .

Получаем, что площадь сечения половины шара равна площади сечения тела Т. Поэтому и объем половины шара равен объему этого тела. В свою очередь, объем тела Т можно вычислить как разность объемов цилиндра и конуса:

.

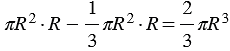Итак, объем половины шара равен , следовательно, объем всего шара 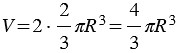. Что и требовалось доказать.

Площадь сферы

Площадь сферы S радиуса R вычисляется по формуле .

Поделись с друзьями в социальных сетях:

Советуем посмотреть:

Предмет стереометрии

Параллельность и перпендикулярность прямых и плоскостей в пространстве

Многогранник

Призма

Параллелепипед

Объём тела

Свойства прямоугольного параллелепипеда

Пирамида

Цилиндр

Конус

Многогранники

Правило встречается в следующих упражнениях:

7 класс

Задание 1224, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1226, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1228, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1230, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1231, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 24, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 25, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1252, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1254, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1255, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

---

© budu5.com, 2020

Пользовательское соглашение

Copyright

Шар — Википедия

Материал из Википедии — свободной энциклопедии

Поверхность шара — сфера
r — радиус шара

Шар — геометрическое тело; совокупность всех точек пространства, находящихся от центра на расстоянии, не больше заданного. Это расстояние называется радиусом шара. Шар образуется вращением полукруга около его неподвижного диаметра. Этот диаметр называется осью шара, а оба конца указанного диаметра — полюсами шара. Поверхность шара называется сферой: замкнутый шар включает эту сферу, открытый шар — исключает.

Если секущая плоскость проходит через центр шара, то сечение шара называется большим кругом. Другие плоские сечения шара называются малыми кругами. Площадь этих сечений вычисляется по формуле πR².

Площадь поверхности S{\displaystyle S} и объём V{\displaystyle V} шара радиуса r{\displaystyle r} (и диаметром d=2r{\displaystyle d=2r}) определяются формулами:

• S= 4πr2{\displaystyle S=\ 4\pi r^{2}}

• S= πd2{\displaystyle S=\ \pi d^{2}}

• V=43πr3{\displaystyle V={\frac {4}{3}}\pi r^{3}}

Доказательство

• V=πd36{\displaystyle V={\frac {\pi d^{3}}{6}}}

Доказательство

d=2r,V=43πr3=43π(d2)3=43πd38=πd36{\displaystyle d=2r,V={4 \over 3}\pi r^{3}={4 \over 3}\pi \left({d \over 2}\right)^{3}={4 \over 3}\pi {\frac {d^{3}}{8}}={\frac {\pi d^{3}}{6}}} Ч. т. д.

Понятие шара в метрическом пространстве естественно обобщает понятие шара в евклидовой геометрии.

Пусть дано метрическое пространство (X,ρ){\displaystyle (X,\rho )}. Тогда

• Шаром (или открытым шаром) с центром в точке x0∈X{\displaystyle x_{0}\in X} и радиусом r>0{\displaystyle r>0} называется множество

Br(x0)={x∈X∣ρ(x,x0)<r}.{\displaystyle B_{r}(x_{0})=\{x\in X\mid \rho (x,x_{0})<r\}.}

• Замкнутым шаром с центром в x0{\displaystyle x_{0}} и радиусом r{\displaystyle r} называется множество

Dr(x0)={x∈X∣ρ(x,x0)⩽r}.{\displaystyle D_{r}(x_{0})=\{x\in X\mid \rho (x,x_{0})\leqslant r\}.}

Замечания[править | править код]

Шар радиуса r{\displaystyle r} с центром x0{\displaystyle x_{0}} также называют r{\displaystyle r}-окрестностью точки x0{\displaystyle x_{0}}.

B1(x)={x},B1(x)¯={x},D1(x)=X.{\displaystyle B_{1}(x)=\{x\},\;{\overline {B_{1}(x)}}=\{x\},\;D_{1}(x)=X.}

Объём[править | править код]

Объём n-мерного шара радиуса R в n-мерном евклидовом пространстве:^[1]

Vn(R)=πn/2Γ(n2+1)Rn,{\displaystyle V_{n}(R)={\frac {\pi ^{n/2}}{\Gamma ({\frac {n}{2}}+1)}}R^{n},}

где Γ — это эйлеровская гамма-функция (которая является расширением факториала на поле нецелых действительных и комплексных чисел). Используя частные представления гамма-функции для целых и полуцелых значений, можно получить формулы объёма n-мерного шара, которые не требуют гамма-функции:

V2k(R)=πkk!R2k{\displaystyle V_{2k}(R)={\frac {\pi ^{k}}{k!}}R^{2k}},

V2k+1(R)=2k+1πk(2k+1)!!R2k+1=2(k!)(4π)k(2k+1)!R2k+1{\displaystyle V_{2k+1}(R)={\frac {2^{k+1}\pi ^{k}}{(2k+1)!!}}R^{2k+1}={\frac {2(k!)(4\pi )^{k}}{(2k+1)!}}R^{2k+1}}.

В формуле для пространства с нечётным количеством размерностей двойной факториал (2k + 1)!! определён для нечётных чисел 2k + 1 в виде произведения: (2k + 1)!! = 1 · 3 · 5 · … · (2k − 1) · (2k + 1).

Обратная функция для выражения зависимости радиуса от объёма:

Rn(V)=Γ(n/2+1)1/nπV1/n{\displaystyle R_{n}(V)={\frac {\Gamma (n/2+1)^{1/n}}{\sqrt {\pi }}}V^{1/n}}.

Эта формула также может быть разделена на две: для пространств с чётным и нечётным количеством размерностей, используя факториал и двойной факториал вместо гамма-функции:

R2k(V)=(k!V)1/2kπ{\displaystyle R_{2k}(V)={\frac {(k!V)^{1/2k}}{\sqrt {\pi }}}},

R2k+1(V)=((2k+1)!!V2k+1πk)1/(2k+1){\displaystyle R_{2k+1}(V)=\left({\frac {(2k+1)!!V}{2^{k+1}\pi ^{k}}}\right)^{1/(2k+1)}}.

Рекурсия[править | править код]

Формулу объёма также можно выразить в виде нескольких рекурсивной функций. Эти формулы могут быть доказаны непосредственно или выведены из основной формулы, представленной выше. Проще всего выразить объём n-мерного шара через объём шара размерности n−2{\displaystyle n-2} (при условии, что они имеют одинаковый радиус):

Vn(R)=2πR2nVn−2(R){\displaystyle V_{n}(R)={\frac {2\pi R^{2}}{n}}V_{n-2}(R)}.

Также существует формула объёма n-мерного шара в зависимости от объёма (n−1)-мерного шара того же радиуса:

Vn(R)=RπΓ(n+12)Γ(n2+1)Vn−1(R){\displaystyle V_{n}(R)=R{\sqrt {\pi }}{\frac {\Gamma ({\frac {n+1}{2}})}{\Gamma ({\frac {n}{2}}+1)}}V_{n-1}(R)}.

То же без гамма-функции:

V2k(R)=Rπ(2k−1)!!2kk!V2k−1(R)=Rπ(2k−1)(2k−3)⋯5⋅3⋅1(2k)(2k−2)⋯6⋅4⋅2V2k−1(R),V2k+1(R)=2R2kk!(2k+1)!!V2k(R)=2R(2k)(2k−2)⋯6⋅4⋅2(2k−1)(2k−3)⋯5⋅3⋅1V2k(R).{\displaystyle {\begin{aligned}V_{2k}(R)&=R\pi {\frac {(2k-1)!!}{2^{k}k!}}V_{2k-1}(R)=R\pi {\frac {(2k-1)(2k-3)\cdots 5\cdot 3\cdot 1}{(2k)(2k-2)\cdots 6\cdot 4\cdot 2}}V_{2k-1}(R),\\V_{2k+1}(R)&=2R{\frac {2^{k}k!}{(2k+1)!!}}V_{2k}(R)=2R{\frac {(2k)(2k-2)\cdots 6\cdot 4\cdot 2}{(2k-1)(2k-3)\cdots 5\cdot 3\cdot 1}}V_{2k}(R).\end{aligned}}}

Пространства младших размерностей[править | править код]

Формулы объёма для некоторых пространств младших размерностей:

Пространства старших размерностей[править | править код]

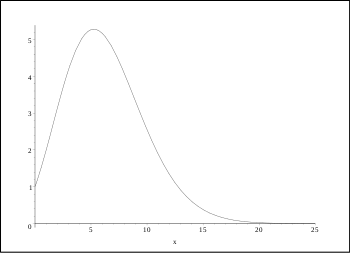Объём гипершара размерности n единичного радиуса в зависимости от n.

При стремлении количества размерностей к бесконечности объём шара единичного радиуса стремится к нулю. Это может быть выведено из рекурсивного представления формулы объёма.

• если d=1{\displaystyle d=1} (пространство — прямая), то

Br(x0)={x∈R∣|x−x0|<r}=(x0−r,x0+r),{\displaystyle B_{r}(x_{0})=\{x\in \mathbb {R} \mid |x-x_{0}|<r\}=\left(x_{0}-{r},x_{0}+{r}\right),}

Dr(x0)={x∈R∣|x−x0|≤r}=[x0−r,x0+r].{\displaystyle D_{r}(x_{0})=\{x\in \mathbb {R} \mid |x-x_{0}|\leq r\}=\left[x_{0}-{r},x_{0}+{r}\right].}

 — открытый и замкнутый отрезок соответственно.

• если d=2{\displaystyle d=2} (пространство — плоскость), то

  Br((x0,y0))={(x,y)∈R2∣(x−x0)2+(y−y0)2<r},{\displaystyle B_{r}((x_{0},y_{0}))=\left\{(x,y)\in \mathbb {R} ^{2}\mid {\sqrt {(x-x_{0})^{2}+(y-y_{0})^{2}}}<r\right\},}

  Dr((x0,y0))={(x,y)∈R2∣(x−x0)2+(y−y0)2≤r}{\displaystyle D_{r}((x_{0},y_{0}))=\left\{(x,y)\in \mathbb {R} ^{2}\mid {\sqrt {(x-x_{0})^{2}+(y-y_{0})^{2}}}\leq r\right\}}

 — открытый и замкнутый диск соответственно.

• если d=3{\displaystyle d=3}, то

  Br((x0,y0,z0))={(x,y,z)∈R3∣(x−x0)2+(y−y0)2+(z−z0)2<r},{\displaystyle B_{r}((x_{0},y_{0},z_{0}))=\left\{(x,y,z)\in \mathbb {R} ^{3}\mid {\sqrt {(x-x_{0})^{2}+(y-y_{0})^{2}+(z-z_{0})^{2}}}<r\right\},}

  Dr((x0,y0,z0))={(x,y,z)∈R3∣(x−x0)2+(y−y0)2+(z−z0)2≤r}{\displaystyle D_{r}((x_{0},y_{0},z_{0}))=\left\{(x,y,z)\in \mathbb {R} ^{3}\mid {\sqrt {(x-x_{0})^{2}+(y-y_{0})^{2}+(z-z_{0})^{2}}}\leq r\right\}}

 — открытый и замкнутый стереометрический шар соответственно.

• В иных метриках шар может иметь иную геометрическую форму. Например, определим в евклидовом пространстве